Empirical Investigation of the Structural Response of Super-Span Soil–Steel Arches During Backfilling
Abstract
1. Introduction
2. Description of the Tested Structure
3. Field Test
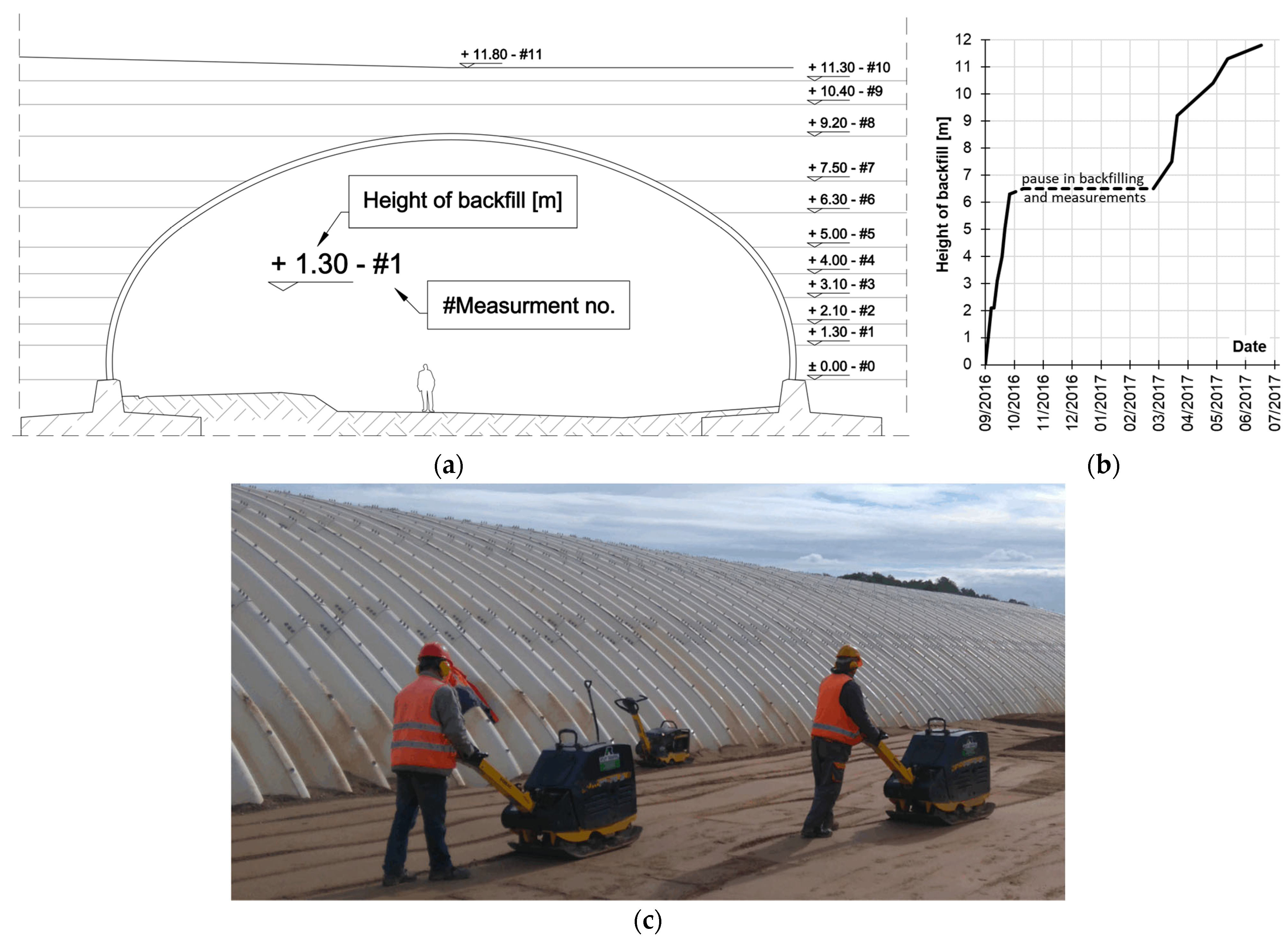
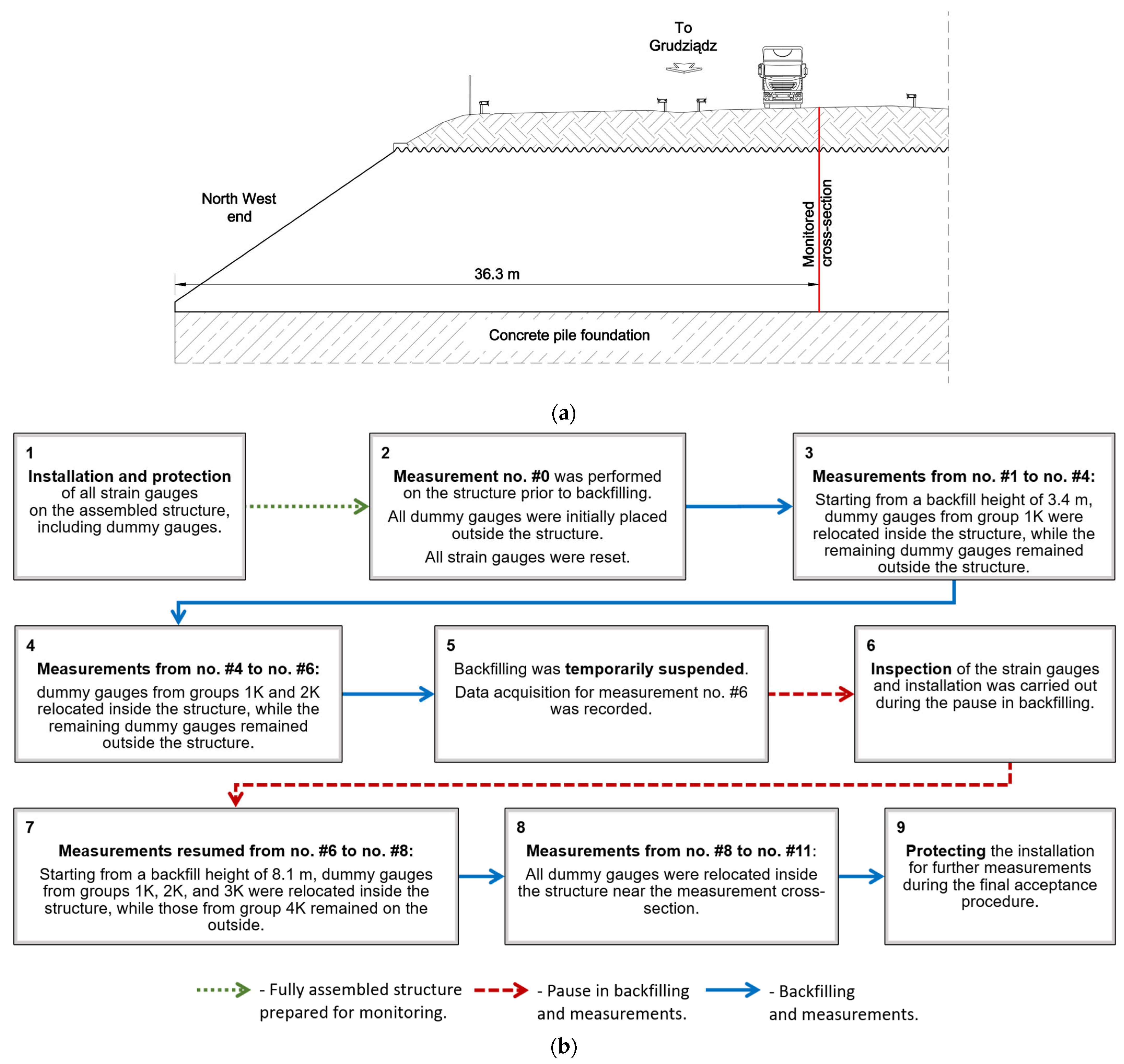
3.1. Backfilling Process
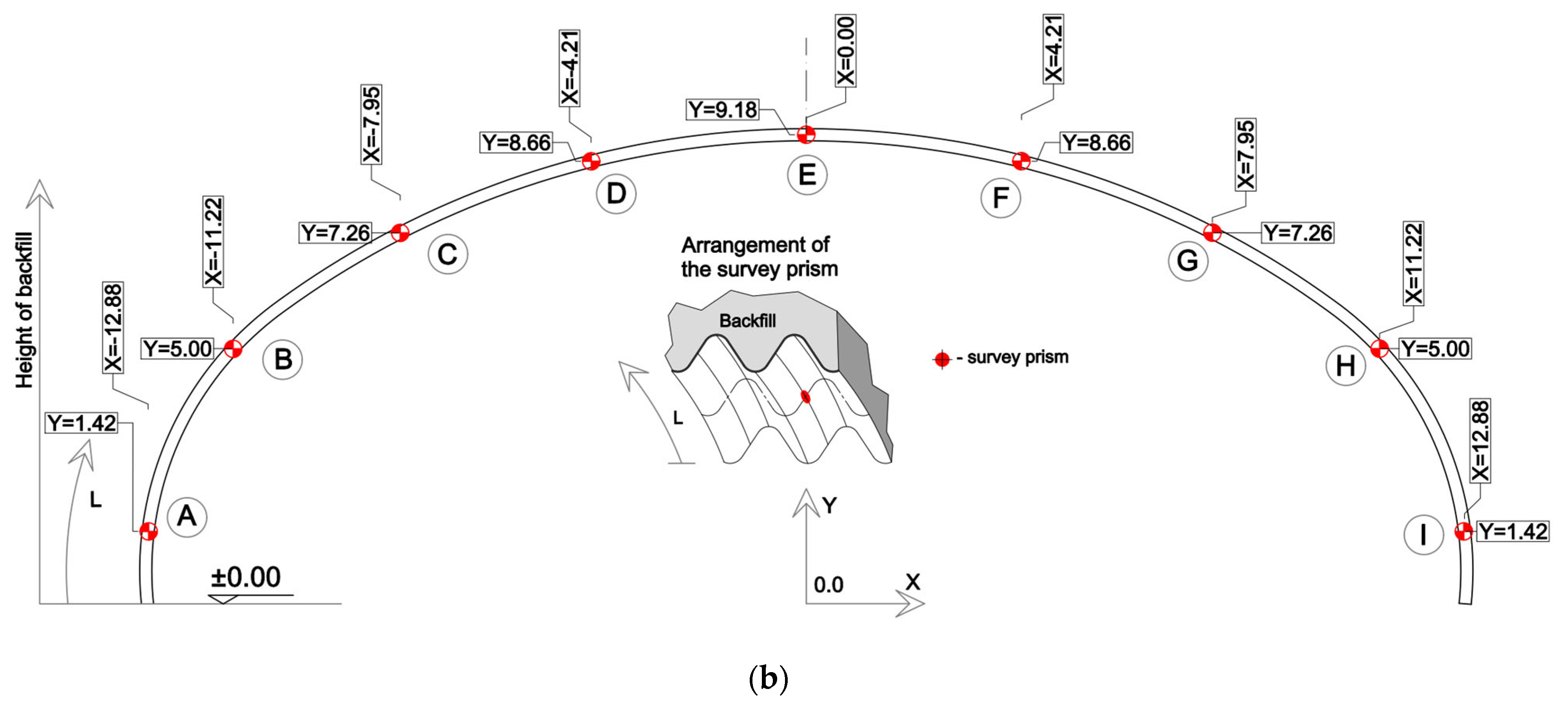
3.2. Instrumentation and Measurement
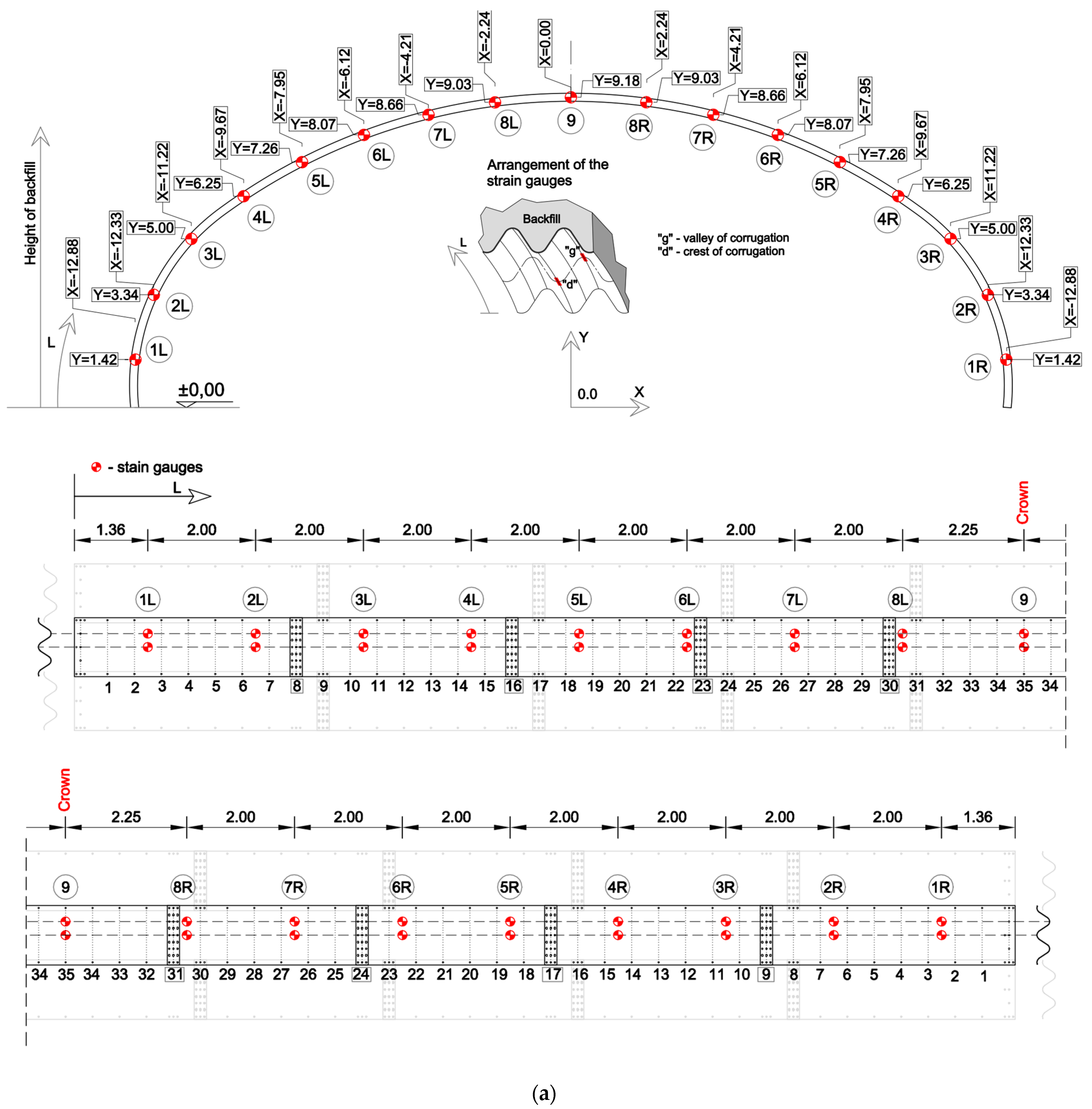
3.3. Strain Measurements
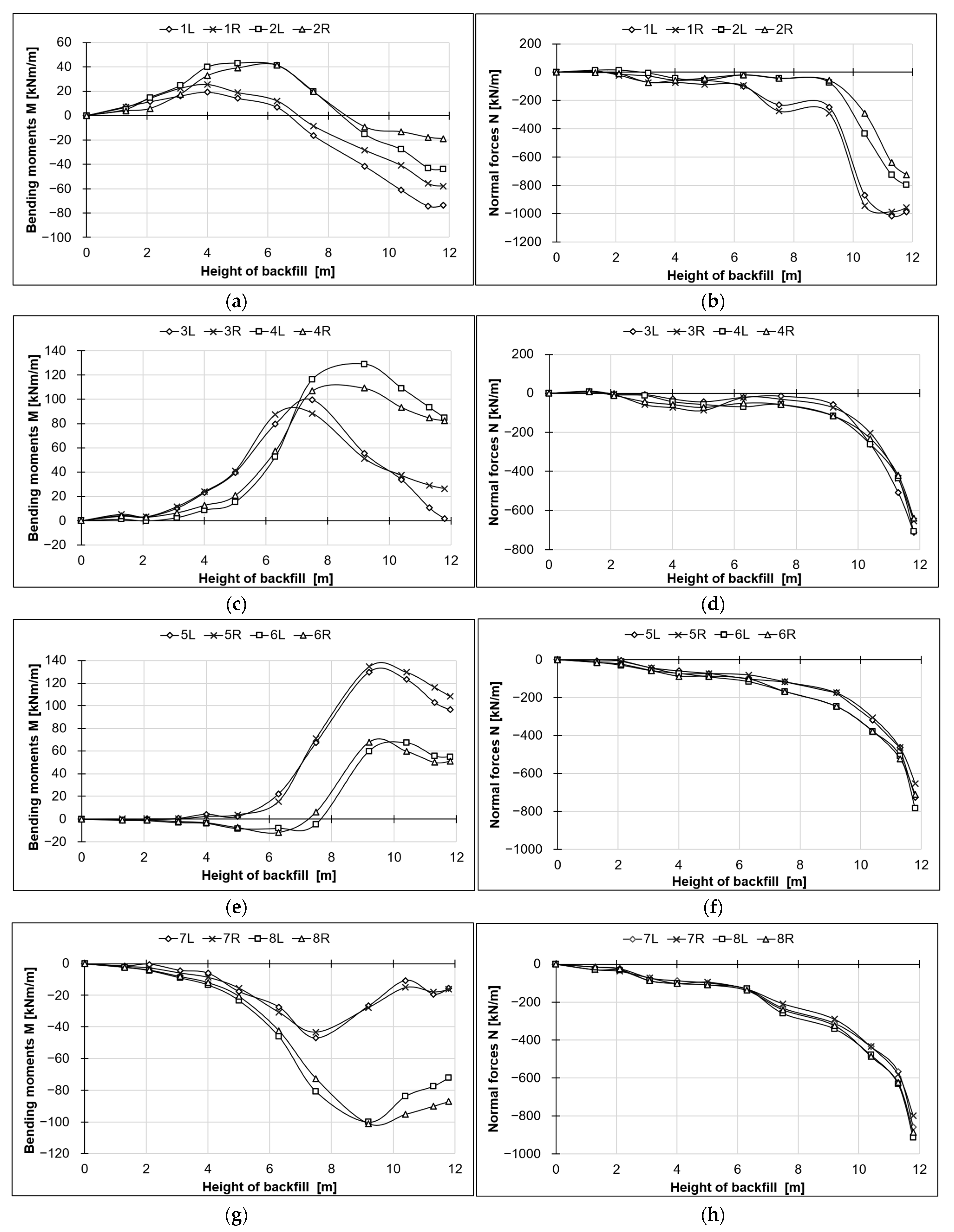
- Group 1K: 1L, 1R, 2L, 2R
- Group 2K: 3L, 3R, 4L, 4R
- Group 3K: 5L, 5R, 6L, 6R
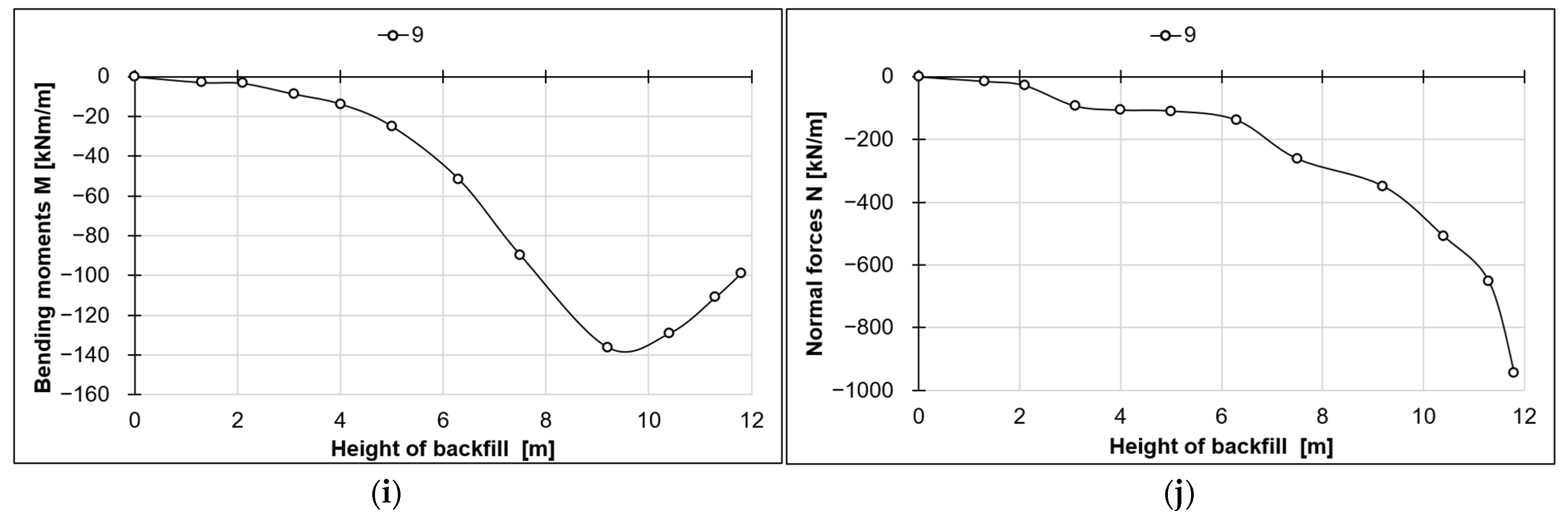
- Group 4K: 7L, 7R, 8L, 8R, 9
3.4. Deflection Measurements
4. Test Results
4.1. Internal Forces Calculations
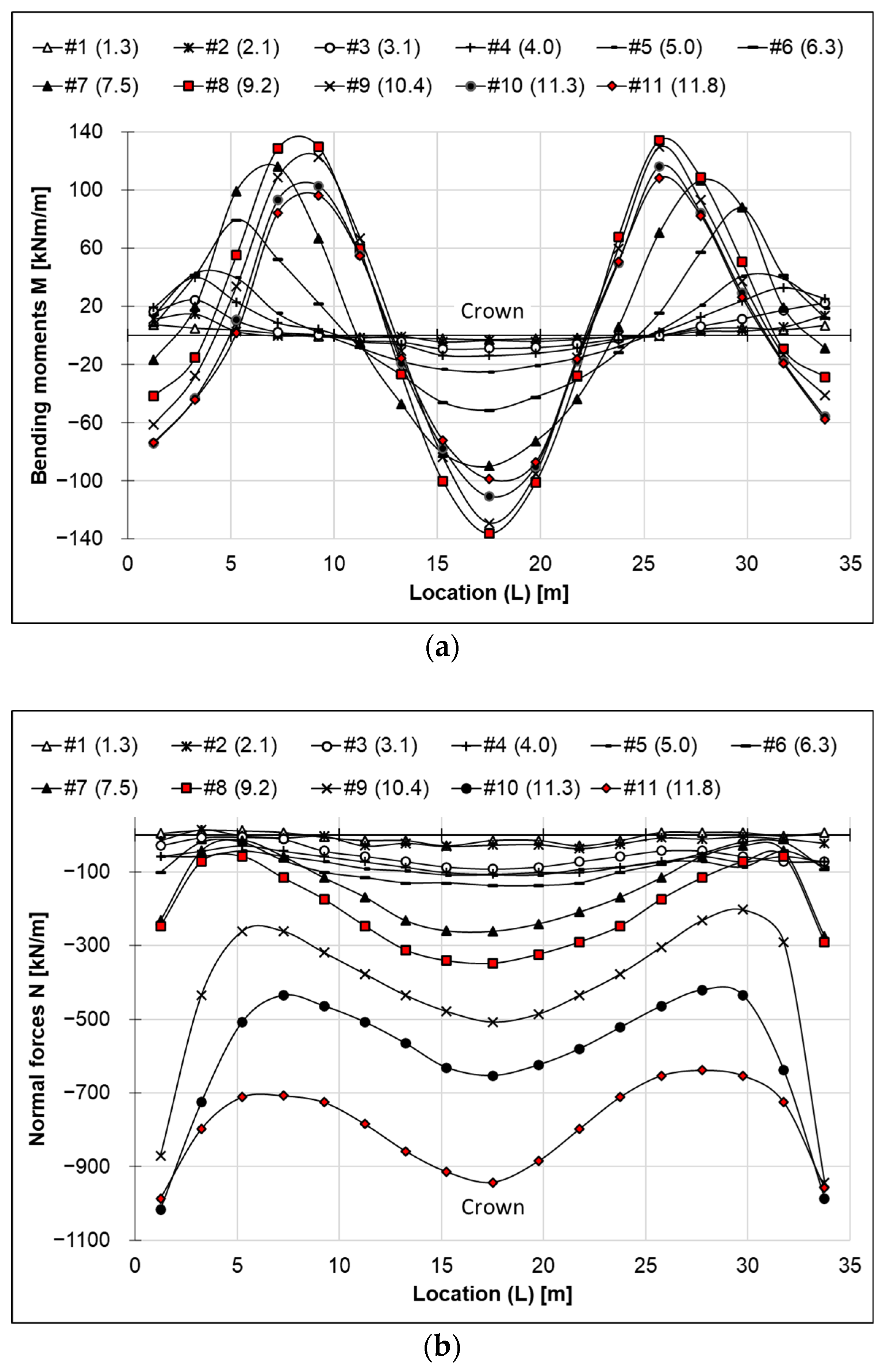
4.2. Internal Forces Distribution
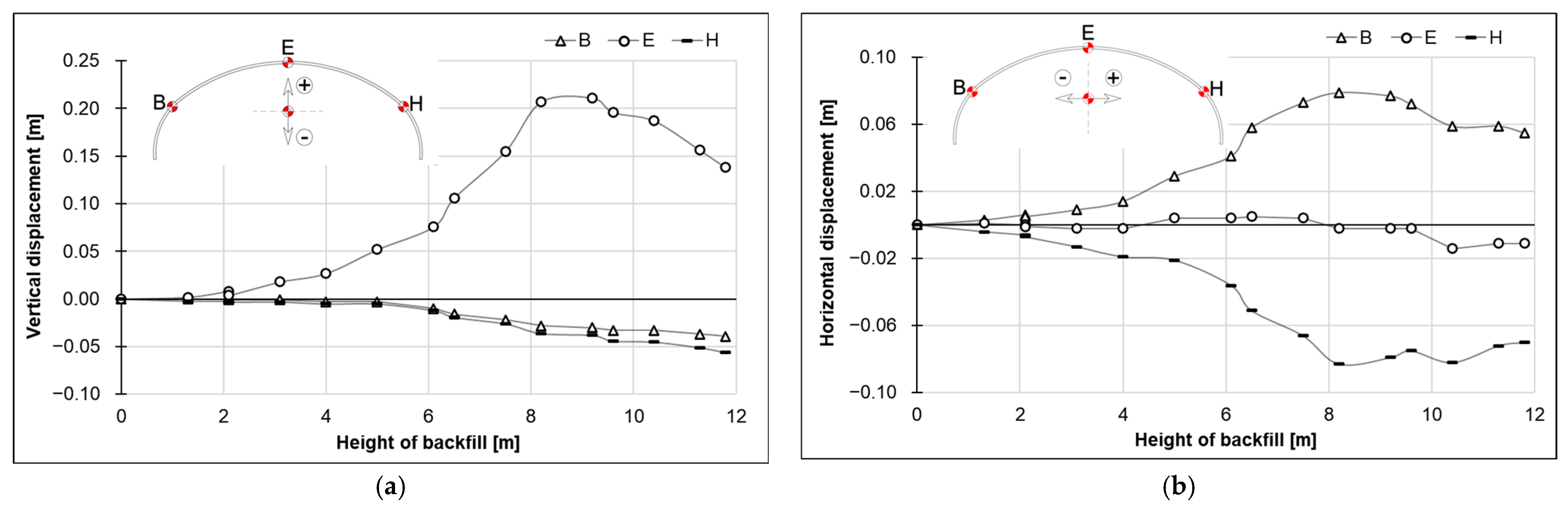
4.3. Displacements
4.4. Summary of Test Results
- The minimum bending moment recorded during backfilling was −136 kNm/m and occurred at Point 9 (crown), when the backfill reached the crown elevation.
- The maximum bending moment recorded was 135 kNm/m and occurred at Point 5R (haunch), also when the backfill was near the crown elevation.
- The highest bending moments were observed when the backfill height reached the crown level. Comparable values were recorded at the crown and haunch zones.
- The minimum axial force (compressive) was −1016 kN/m and was registered at Point 1L after completion of backfilling.
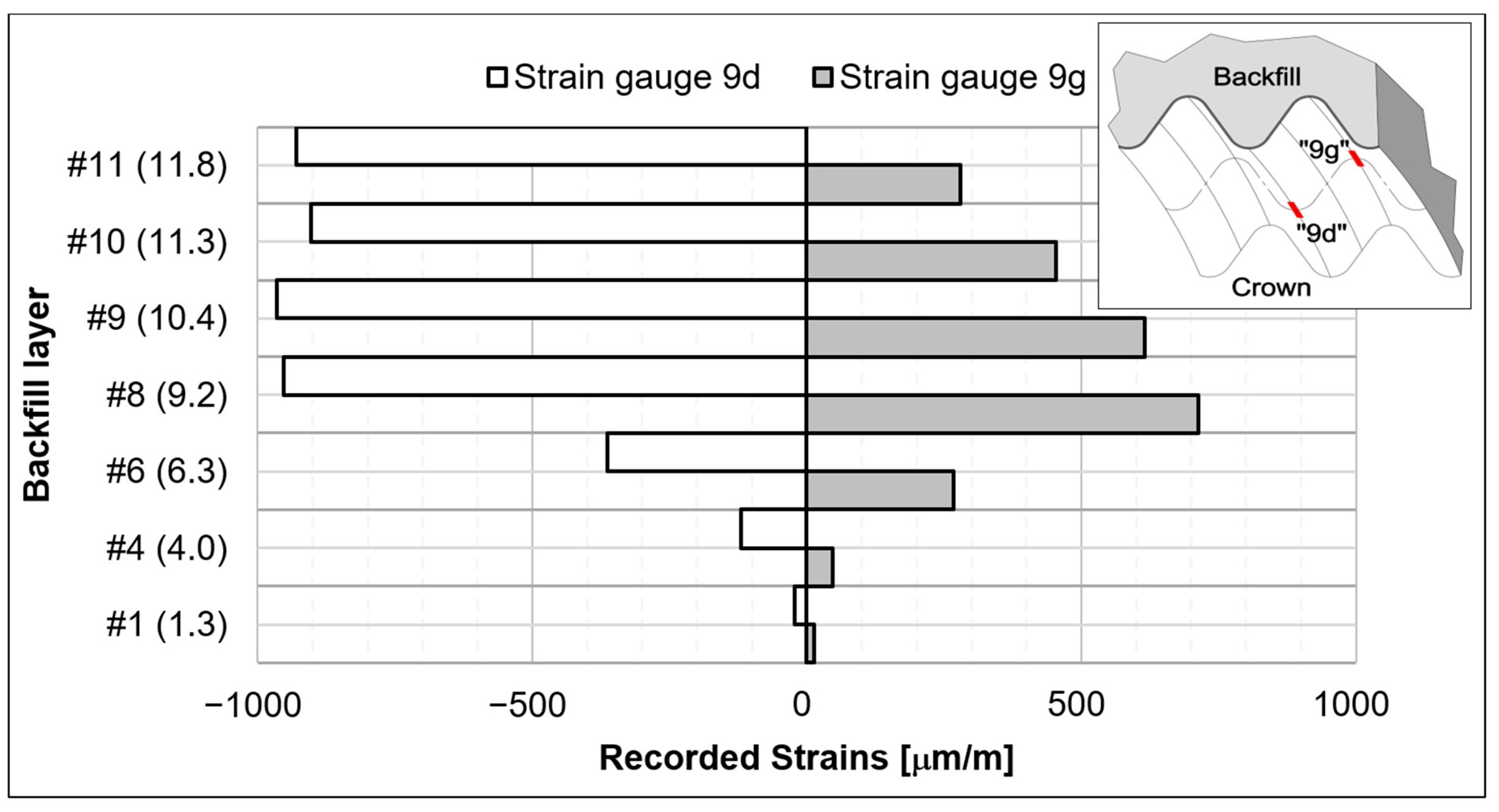
- The maximum absolute strain recorded was 965 μm/m, occurring at the crown during the stage when the backfill was close to the crown elevation.
- The maximum upward displacement of the crown was 211 mm, which was also observed when the backfill was near the crown elevation.
- The maximum horizontal narrowing of the structure was 162 mm, recorded between Points H and B when the backfill height reached 8.6 m above the foundation level.
- A slight asymmetry in the internal forces was observed, corresponding to minor asymmetries in the recorded displacements.
- A reduction in bending moments and a simultaneous increase in axial forces were observed when the backfill height surpassed the crown elevation.
- It was observed that, with increasing backfill height, bending moments and axial forces exhibited divergent trends at measurement points symmetrically distributed along the arch cross-section.
5. Comparison with Design Method
5.1. Internal Forces During Backfilling
5.2. Deformations During Backfilling
6. Summary and Conclusions
- Maximum internal forces and displacements were observed during the backfilling phase, particularly when the fill reached and surpassed the crown level.
- Measured values of bending moments and axial forces were significantly different from those predicted by the SDM, with overestimations of 69% and 152%, respectively, at the crown level, and further inaccuracies at the final cover height.
- The results confirm that the fifth edition of the SDM, originally developed for shallower corrugations and shorter spans, is not suitable for structures with 500 mm × 237 mm corrugation profiles and spans exceeding 25 m.
- Maximum displacements and internal forces occurred during backfilling, underscoring the importance of monitoring throughout the construction process.
- A slight asymmetry in displacements and internal forces was observed, likely resulting from minor differences in construction conditions.
- The results indicate that even with a slight exceedance of the recommended deformation limit, the structural performance remained within safe bounds, highlighting the necessity to update design guidelines for large-span, deeply corrugated soil–steel structures.
- It was observed that with increasing backfill height, bending moments and axial forces exhibited divergent trends at various measurement points located symmetrically along the arch cross-section, as illustrated in the graphs in Figure 7. This behavior of internal forces can be attributed to the varying distances between individual pairs of strain gauges and the longitudinal bolted connections of the steel plates. These connections feature enlarged bolt holes to facilitate bolt installation, which allows for slight relative movement between the joined plates. Such localized displacements may influence the distribution of internal forces in the vicinity of the joints. A second potential cause of the divergent trends in internal forces with increasing backfill height is the possibility of asymmetric backfilling and compaction, or the use of a single work crew compacting the soil alternately on both sides of the arch.
- Updating analytical design methods and guidelines to reflect current manufacturing capabilities, with particular emphasis on modeling the backfilling phase.
- Conducting long-term deformation monitoring of buried soil–steel structures, especially those with spans exceeding 20 m and located within newly constructed embankments.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Janusz, L.; Madaj, A. Engineering Structures from Corrugated Plates. Design and Construction; Transport and Communication Publishers: Warsaw, Poland, 2009. [Google Scholar] [CrossRef]
- Beben, D. Soil Steel Bridges: Design, Maintenance and Durability; Springer Nature: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Legese, A.M.; Sobótka, M.; Machelski, C.; Różański, A. Behaviour of Soil–Steel Composite Structures during Construction and Service: A Review. Arch. Civ. Eng. 2023, 69, 263–292. [Google Scholar] [CrossRef]
- Kunecki, B. Field Test and Three-Dimensional Numerical Analysis of Soil–Steel Tunnel during Backfilling. Transp. Res. Rec. 2014, 2462, 55–60. [Google Scholar] [CrossRef]
- Kunecki, B. Behaviour of Orthotropic Buried Arch Shells under Static and Dynamic Live Load. Ph.D. Thesis, Wrocław University of Science and Technology, Wrocław, Poland, 2006. [Google Scholar]
- Vaslestad, J. Soil Structure Interaction of Buried Culverts. Ph.D. Thesis, Norges Tekniske Høgskole, Institutt for Geoteknikk, Trondheim, Norway, 1990. [Google Scholar]
- Korusiewicz, L.; Kunecki, B. Behaviour of the Steel Box-Type Culvert during Backfilling. Arch. Civ. Mech. Eng. 2011, 11, 637–650. [Google Scholar] [CrossRef]
- Ebeltoft, R.; Larsen, J.O.; Nordal, S. Instrumentation of Buried Flexible Culvert Subjected to Rockfall Loading. In Proceedings of the Joint International Conference on Computing and Decision Making in Civil and Building Engineering, Montréal, QC, Canada, 14–16 June 2006. [Google Scholar]
- Kunecki, B.; Vaslestad, J.; Emdal, A. Long Term Earth Pressure Measurements of Two Large Span Flexible Culverts in Norway. In Bridge Design, Construction and Maintenance; Thomas Telford Publishing: London, UK, 2007; pp. 122–131. [Google Scholar]
- Williams, K.; MacKinnon, S.; Newhook, J. New and Innovative Developments for Design and Installation of Deep Corrugated Buried Flexible Steel Structures. In Proceedings of the 2nd European Conference on Buried Flexible Steel Structures, Wrocław, Poland, 25–27 April 2012. [Google Scholar]
- Embaby, K.; El Naggar, M.H.; El Sharnouby, M. Response Evaluation of Large Span Ultradeep Soil–Steel Bridges to Truck Loading. Int. J. Geomech. 2021, 21, 04021186. [Google Scholar] [CrossRef]
- Embaby, K.; El Naggar, M.H.; El Sharnouby, M. Performance of Large Span Arched Soil–Steel Structures under Soil Loading. Thin Walled Struct. 2022, 172, 108884. [Google Scholar] [CrossRef]
- Miśkiewicz, M.; Sobczyk, B.; Tysiąc, P. Non Destructive Testing of the Longest Span Soil Steel Bridge in Europe—Field Measurements and FEM Calculations. Materials 2020, 13, 3652. [Google Scholar] [CrossRef] [PubMed]
- Kunecki, B.; Janusz, L.; Korusiewicz, L.; Williams, K. Field Tests of Deep Corrugated Super Span Metal Arch during Backfilling. In Proceedings of the TRB 97th Annual Meeting, Washington, DC, USA, 7–11 January 2018. Paper 18-03926. [Google Scholar]
- EN 10149-2; Hot Rolled Flat Products Made of High Yield Strength Steels for Cold Forming—Part 2: Technical Delivery Conditions for Thermomechanically Rolled Steels. The European Committee for Standardization: Brussels, Belgium, 2013.
- M167M/M167-15; Standard Specification for Corrugated Steel Structural Plate, Zinc-Coated, for Field-Bolted Pipe, Pipe-Arches, and Arches. American Association of State Highway and Transportation Officials (AASHTO): Washington, DC, USA, 2015.
- Duncan, J.M. Soil Culvert Interaction Method for Design of Metal Culverts. Transp. Res. Rec. 1978, 678, 1–8. [Google Scholar]
- Duncan, J.M. Behavior and Design of Long Span Metal Culverts. J. Geotech. Eng. Div. 1979, 105, 399–418. [Google Scholar] [CrossRef]
- Pettersson, L.; Sundquist, H. Design of Soil–Steel Composite Bridges; KTH Royal Institute of Technology: Stockholm, Sweden, 2014. [Google Scholar]
- Flener, E.B. Soil–Steel Interaction of Long Span Box Culverts—Performance during Backfilling. J. Geotech. Geoenviron. Eng. 2010, 136, 823–832. [Google Scholar] [CrossRef]
- Kunecki, B.; Korusiewicz, L. Field Test of Super Span Metal Twin Arches during Backfilling. In Proceedings of the TRB 89th Annual Meeting, Washington, DC, USA, 10–14 January 2010. Paper 10-1467. [Google Scholar]
- Elshimi, T.; Mak, A.; Brachman, R.W.I.; Moore, I.D. Behaviour of a Deep Corrugated Large Span Box Culvert during Backfilling. In Proceedings of the Pan American Conference on Teaching and Learning of Geotechnical Engineering, Toronto, ON, Canada, 2–6 October 2011. [Google Scholar]
- Beben, D. Numerical Study of Performance of Soil–Steel Bridge during Soil Backfilling. Struct. Eng. Mech. 2012, 42, 571–587. [Google Scholar] [CrossRef]
- Kunecki, B.; Korusiewicz, L. Field Tests of Large Span Metal Arch Culvert during Backfilling. Roads Bridges–Drogi Mosty 2013, 12, 283–295. [Google Scholar] [CrossRef]
- Maleska, T.; Beben, D. Behaviour of soil-steel composite bridge with various cover depths under seismic excitation. Steel Compos. Struct. 2022, 42, 747–764. [Google Scholar]
- Maleska, T.; Beben, D. Behaviour of Soil–Steel Composite Bridges under Strong Seismic Excitation with Various Boundary Conditions. Materials 2023, 16, 650. [Google Scholar] [CrossRef] [PubMed]
- Maleska, T.; Beben, D. Effect of the soil cover depth on the seismic response in a large-span thin-walled corrugated steel plate bridge. Soil Dyn. Earthq. Eng. 2023, 166, 107744. [Google Scholar] [CrossRef]
- Wu, F.; Liu, B.; Sun, W.; Sun, H.; Zhang, S. Full-Scale Model Tests of Two Box-Type Soil–Steel Structures with Different Crown and Haunch Radii. Materials 2024, 17, 1710. [Google Scholar] [CrossRef] [PubMed]
- Lougheed, A.C. Limit States Testing of a Buried Deep Corrugated Large Span Box Culvert. Master′s Thesis, Queen′s University, Kingston, ON, Canada, 2008. [Google Scholar]
- Elshimi, T.M. Three Dimensional Nonlinear Analysis of Deep Corrugated Steel Culverts. Ph.D. Dissertation, Queen’s University, Kingston, ON, Canada, 2011. [Google Scholar]
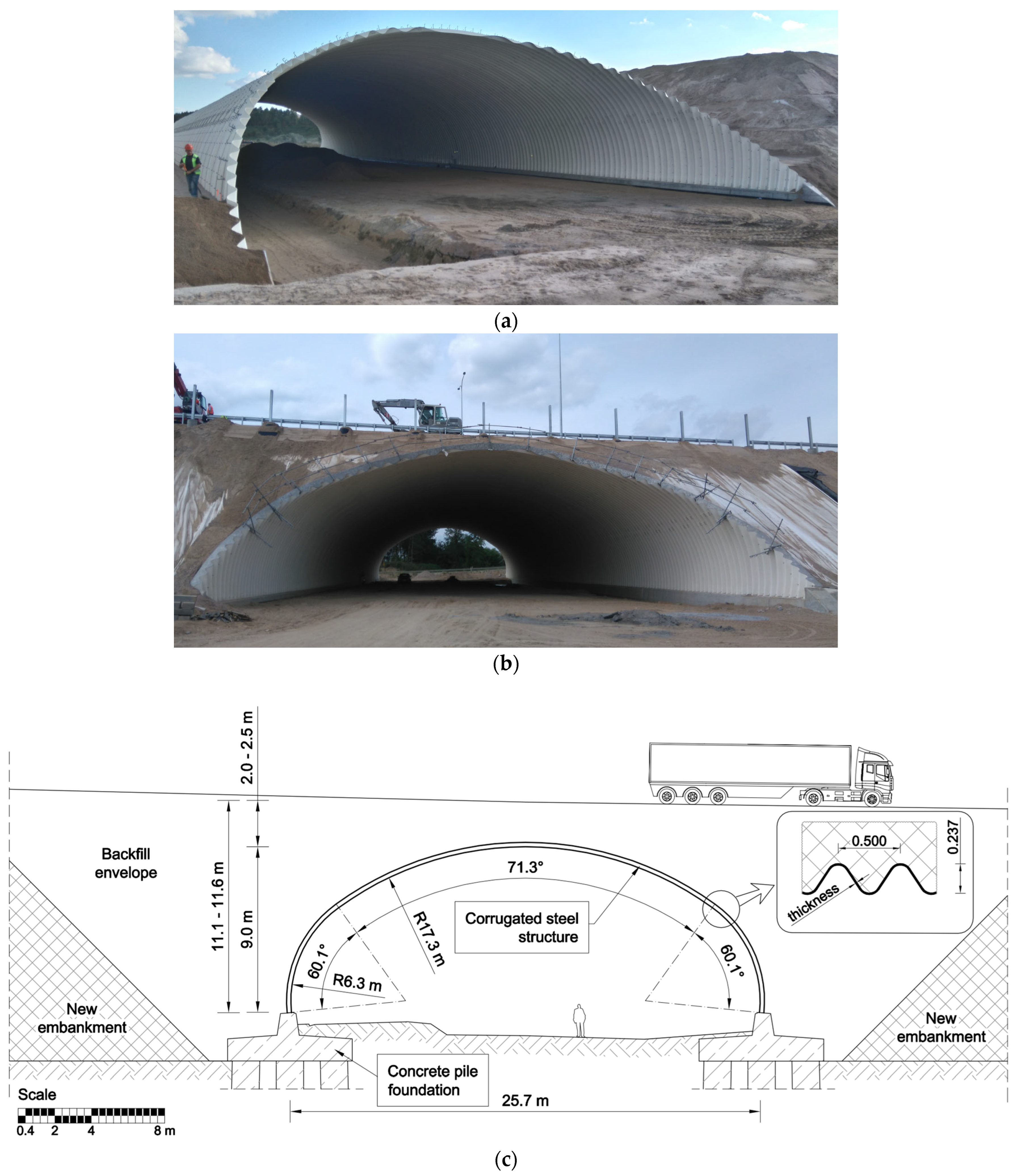

| Profile Dimension (mm × mm) | Cross-Section Area (mm2/mm) | Moment of Inertia (mm4/mm) | Section Modulus (mm3/mm) | Plate Thickness (mm) |
|---|---|---|---|---|
| 500 × 237 | 14.51 | 96,733 | 817.69 | 9.65 |
| Maximum Banding Moment Mmax (kNm/m) | Minimal Banding Moment Mmin (kNm/m) | Maximum Normal Forces Nmax (kN/m) | Minimal Normal Forces Nmin (kN/m) | |
|---|---|---|---|---|
| Registered value | 135 | −136 | 14 | −1016 |
| Point name (location) | 5R (haunch) | 9 (crown) | 2L | 1L |
| Height of backfill (m) | 9.2 | 9.2 | 2.1 | 11.3 |
| Maximum Stress (MPa) | Minimal Stress (MPa) | |
|---|---|---|
| Registered value | 153 | −193 |
| Point name (location) | 5Rd (haunch) | 9d (crown) |
| Height of backfill (m) | 9.2 | 10.4 |
| Maximum Uplift (mm) | Maximum Narrowing (mm) | |
|---|---|---|
| Registered value | 211 | 162 |
| Point name (location) | 9 (crown) | line B–H |
| Height of backfill (m) | 9.2 | 8.6 |
| Backfill Level | Backfill Level (6.3 m) | Crown Level (9.2 m) | Final Level (11.8 m) | |||
|---|---|---|---|---|---|---|
| Internal Forces | Bending Moments (kNm/m) | Normal Forces (kN/m) | Bending Moments (kNm/m) | Normal Forces (kN/m) | Bending Moments (kNm/m) | Normal Forces (kN/m) |
| TEST | −52 | −139 | −137 | −350 | −99 | −943 |
| SDM | n/a | n/a | −230 | −879 | −44 | −1793 |
| Ratio: SDM/TEST | n/a | n/a | 1.69 | 2.52 | 0.45 | 1.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kunecki, B. Empirical Investigation of the Structural Response of Super-Span Soil–Steel Arches During Backfilling. Materials 2025, 18, 3650. https://doi.org/10.3390/ma18153650
Kunecki B. Empirical Investigation of the Structural Response of Super-Span Soil–Steel Arches During Backfilling. Materials. 2025; 18(15):3650. https://doi.org/10.3390/ma18153650
Chicago/Turabian StyleKunecki, Bartłomiej. 2025. "Empirical Investigation of the Structural Response of Super-Span Soil–Steel Arches During Backfilling" Materials 18, no. 15: 3650. https://doi.org/10.3390/ma18153650
APA StyleKunecki, B. (2025). Empirical Investigation of the Structural Response of Super-Span Soil–Steel Arches During Backfilling. Materials, 18(15), 3650. https://doi.org/10.3390/ma18153650






