Strain-Rate Effects on the Mechanical Behavior of Basalt-Fiber-Reinforced Polymer Composites: Experimental Investigation and Numerical Validation
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Dynamic Mechanical Properties Testing of BFRP Composites
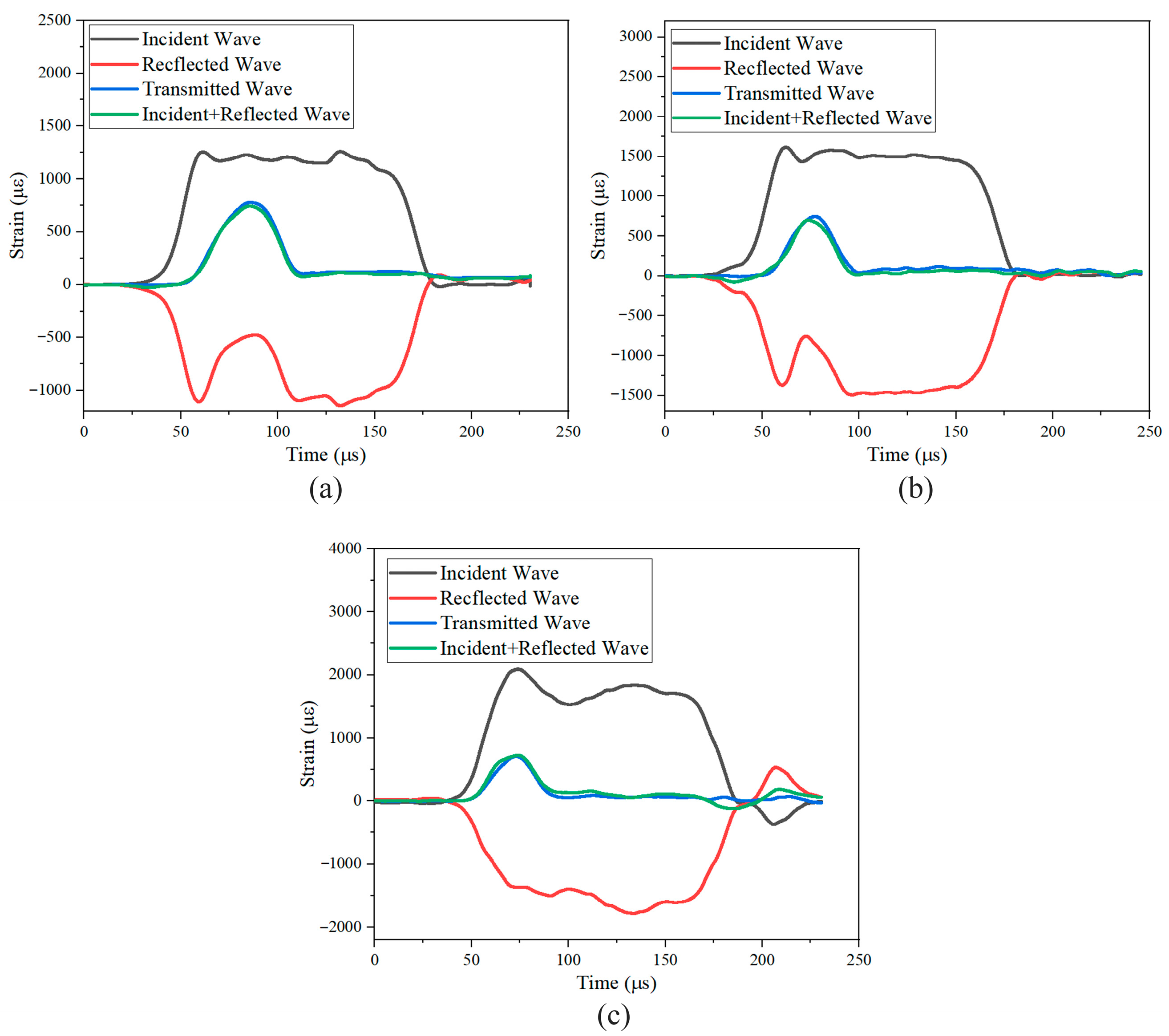
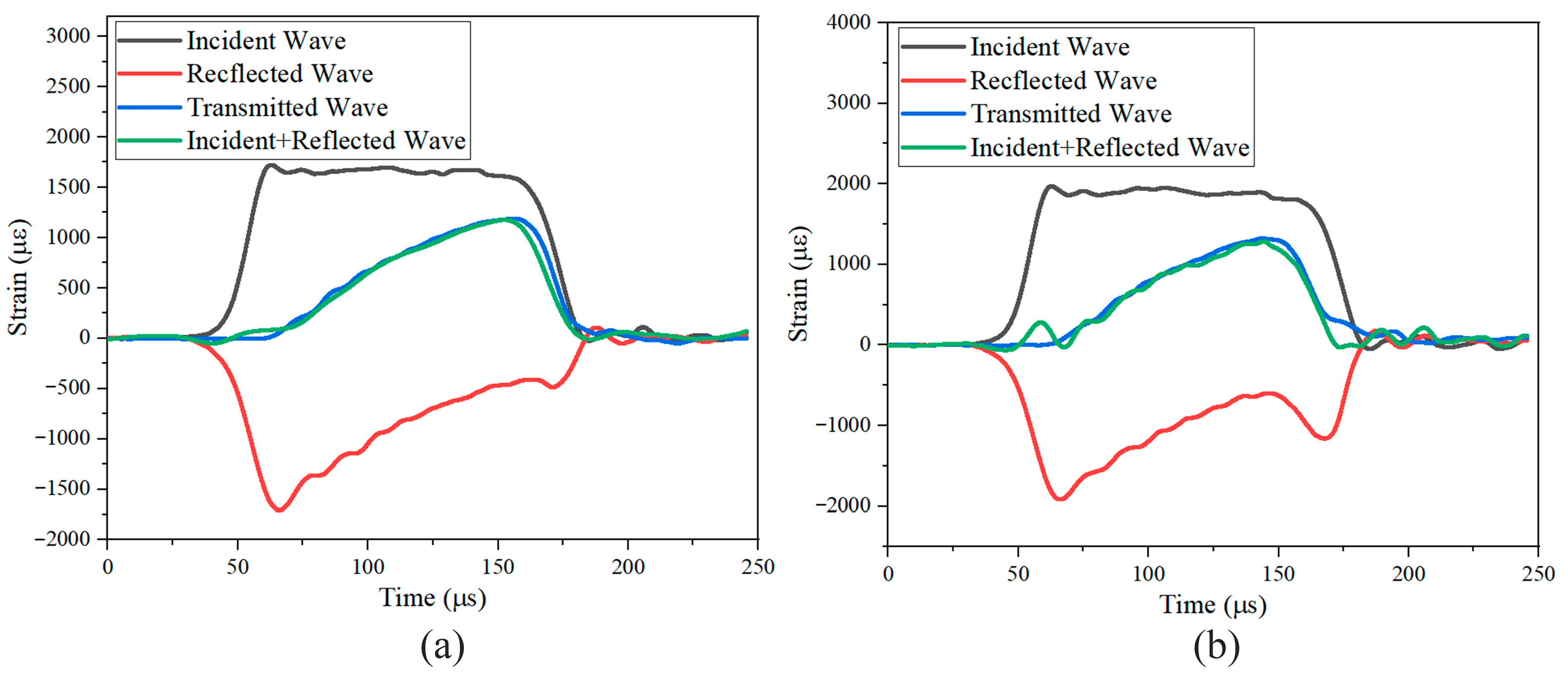
2.2.1. Tensile Mechanical Properties Test
- (1)
- In-Plane Tensile Properties
- (2)
- Out-of-Plane (Z-direction) Tensile Properties
2.2.2. Compressive Mechanical Properties Testing
2.2.3. Shear Mechanical Properties Testing
- (1)
- In-Plane Shear Properties
- (2)
- Out-of-Plane Shear Properties
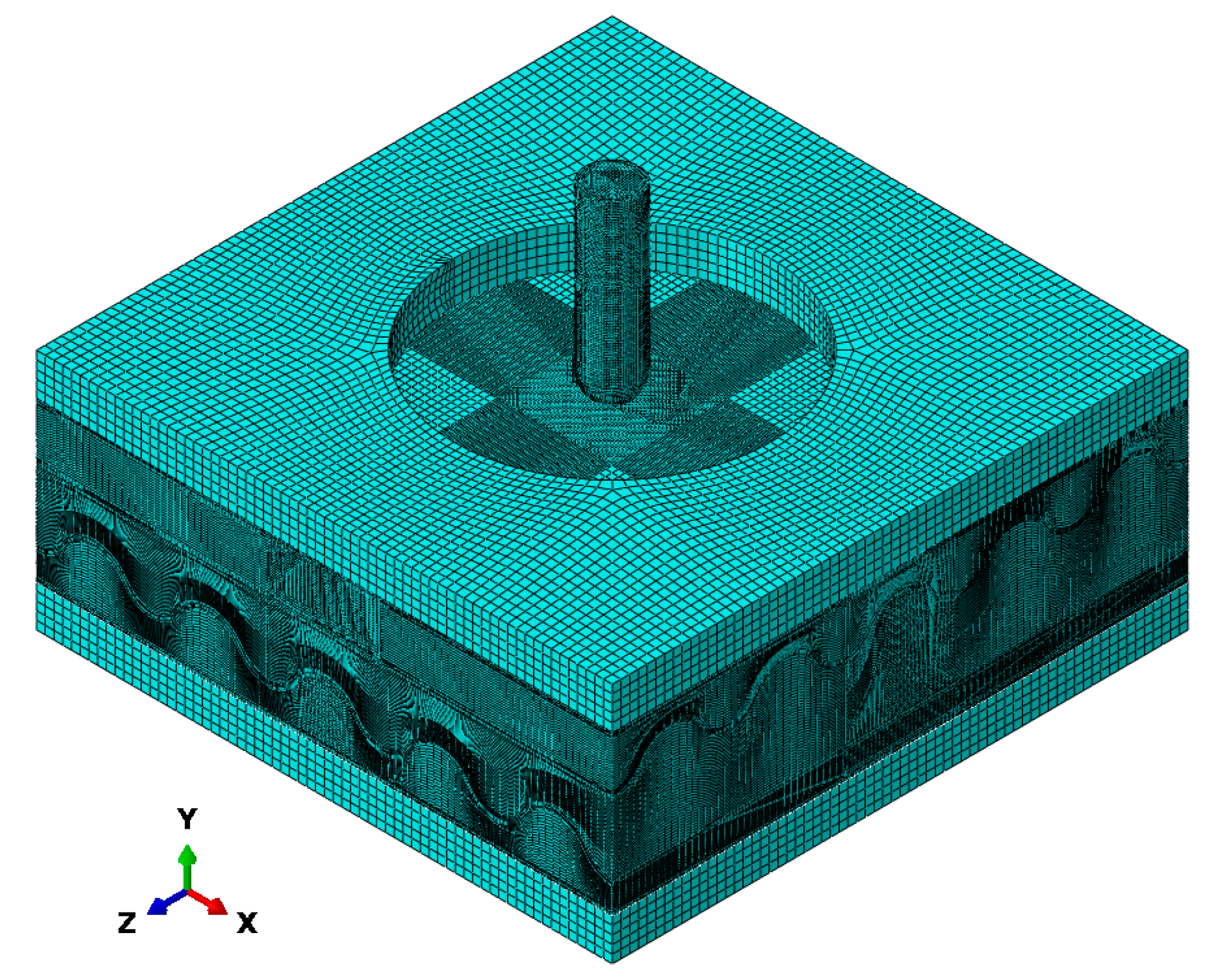
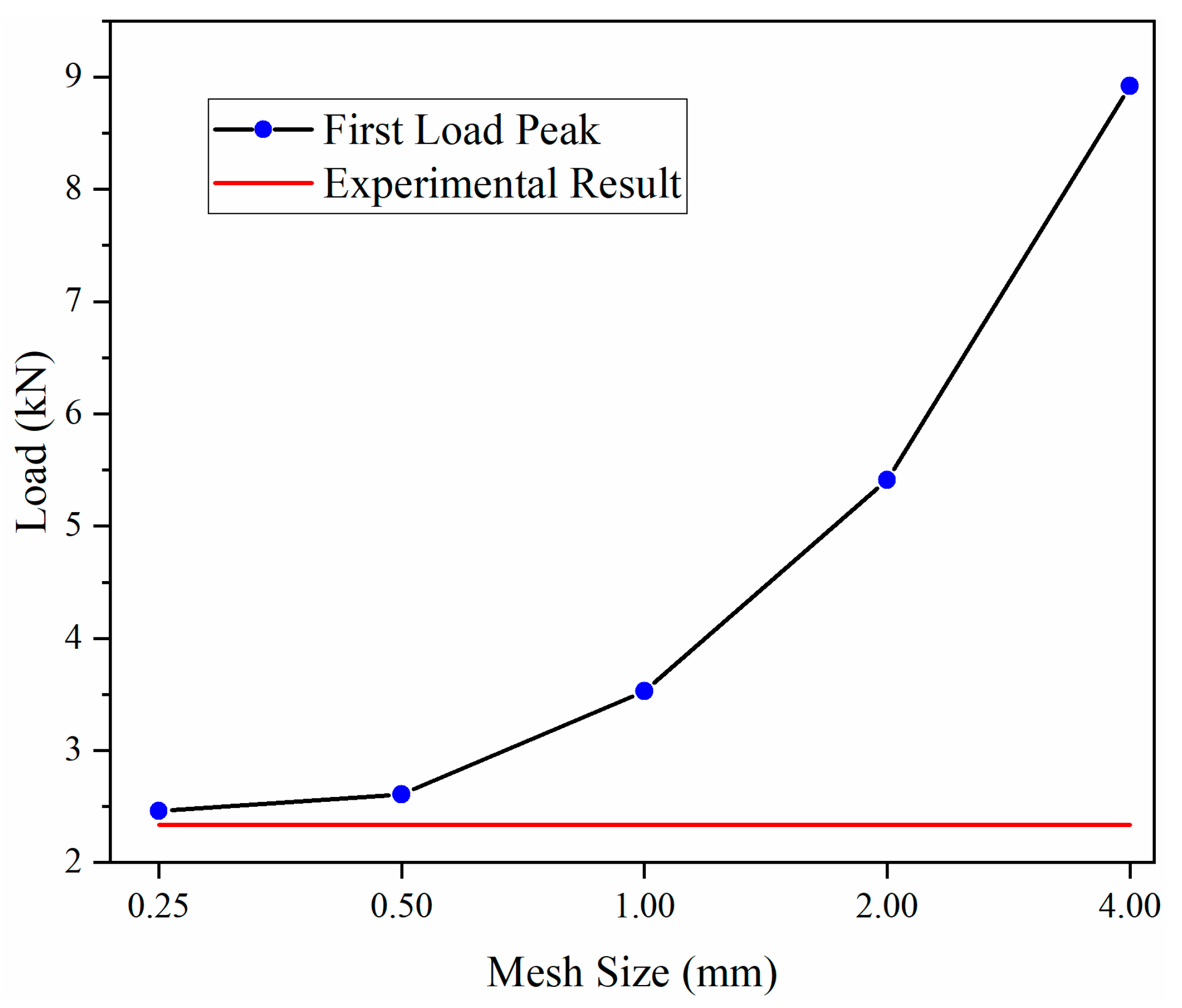
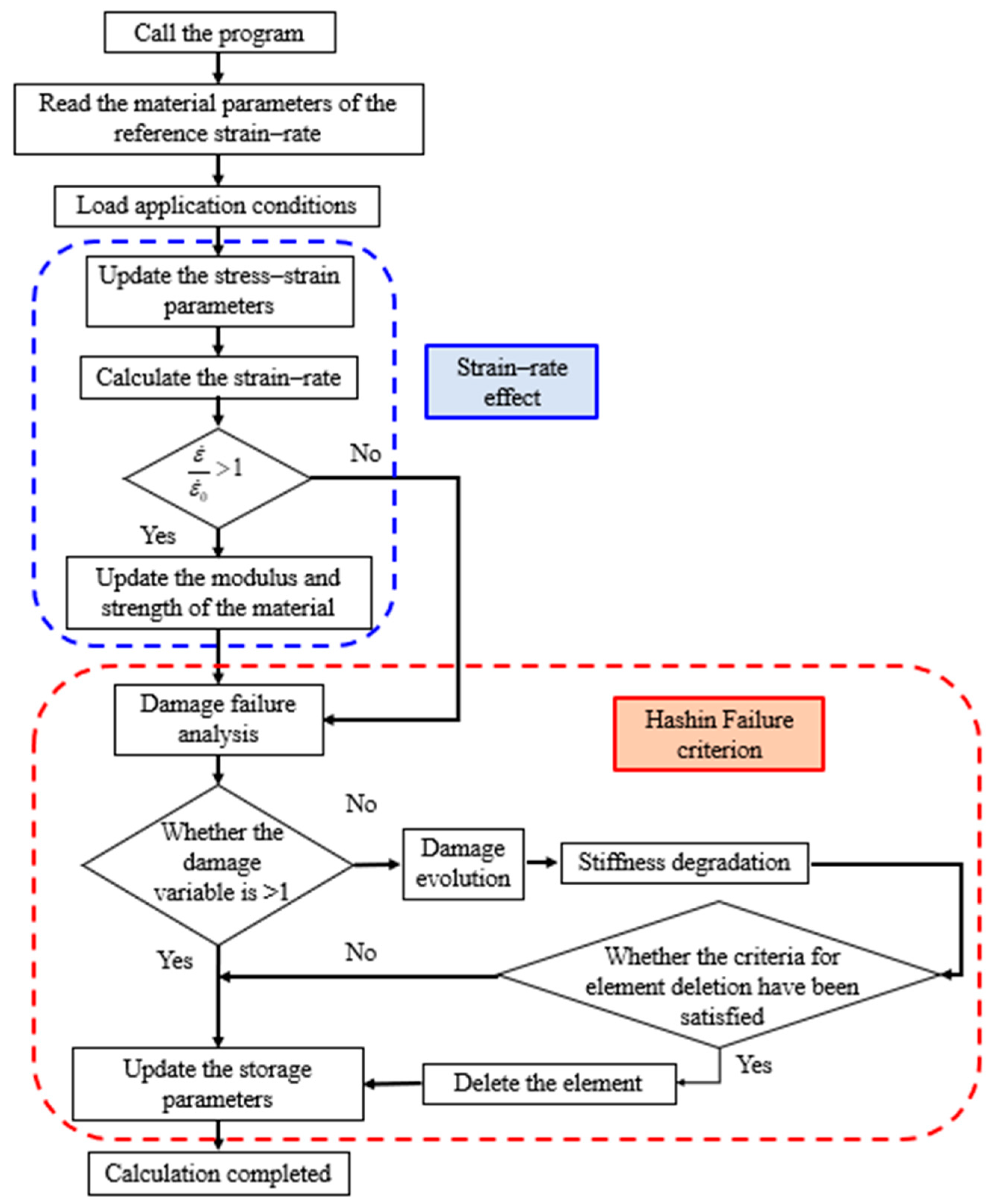
2.3. Validation of the Strain Rate Effect in a Low-Velocity Impact Simulation
3. Results
3.1. In-Plane Tensile Strength
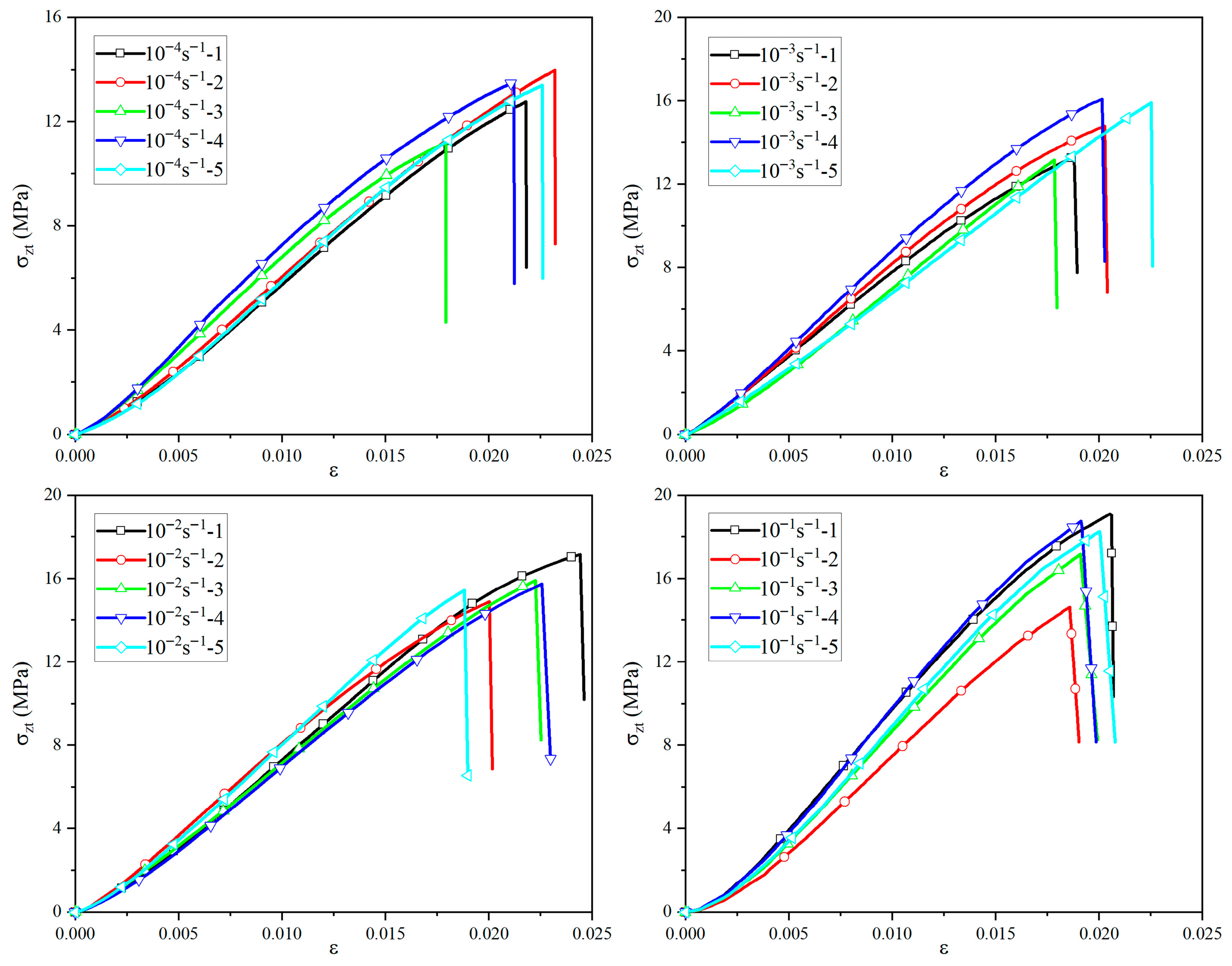
3.2. Out-of-Plane Tensile Strength
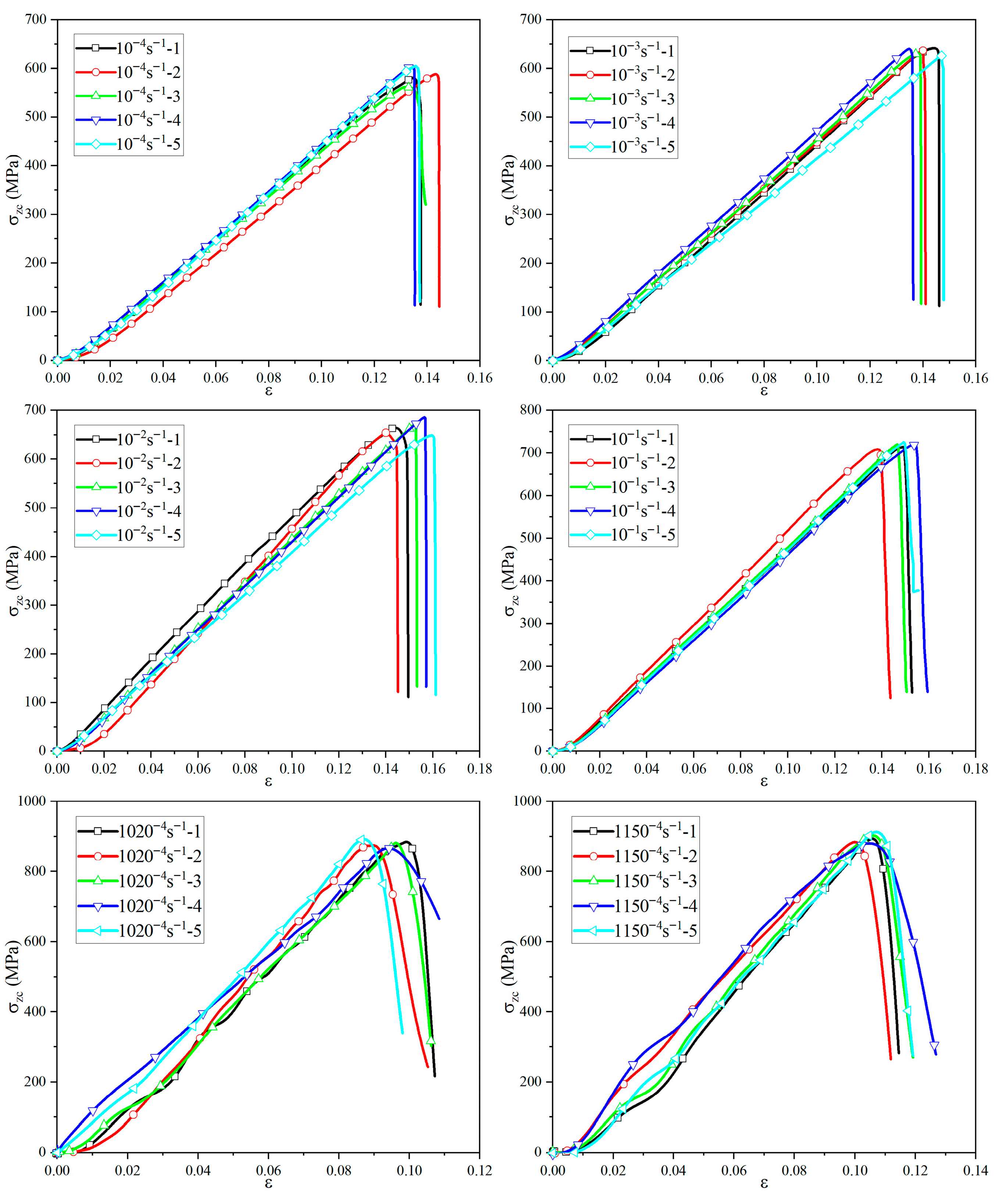
3.3. In-Plane Compressive Strength
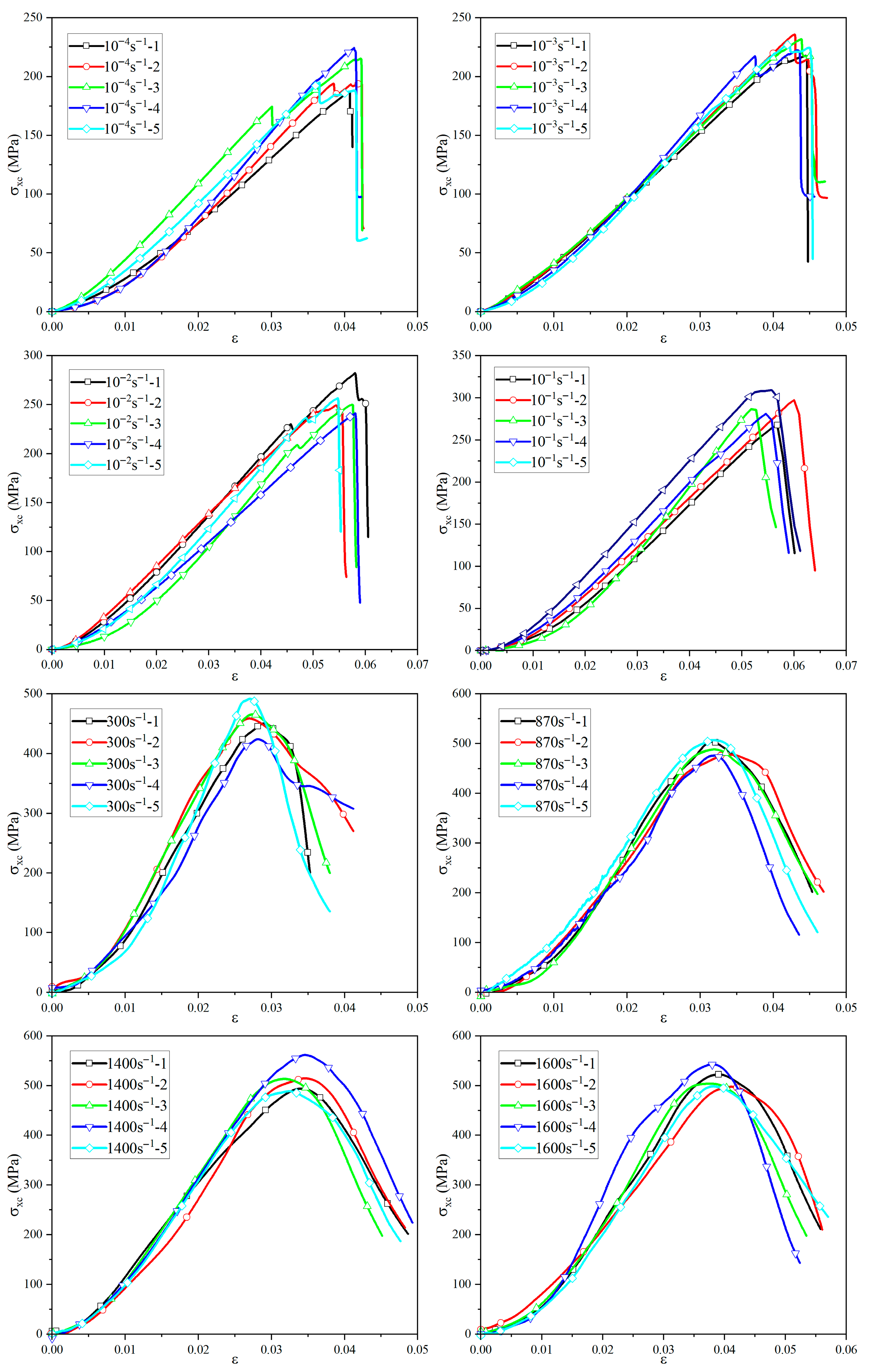
3.4. Out-of-Plane Compressive Strength
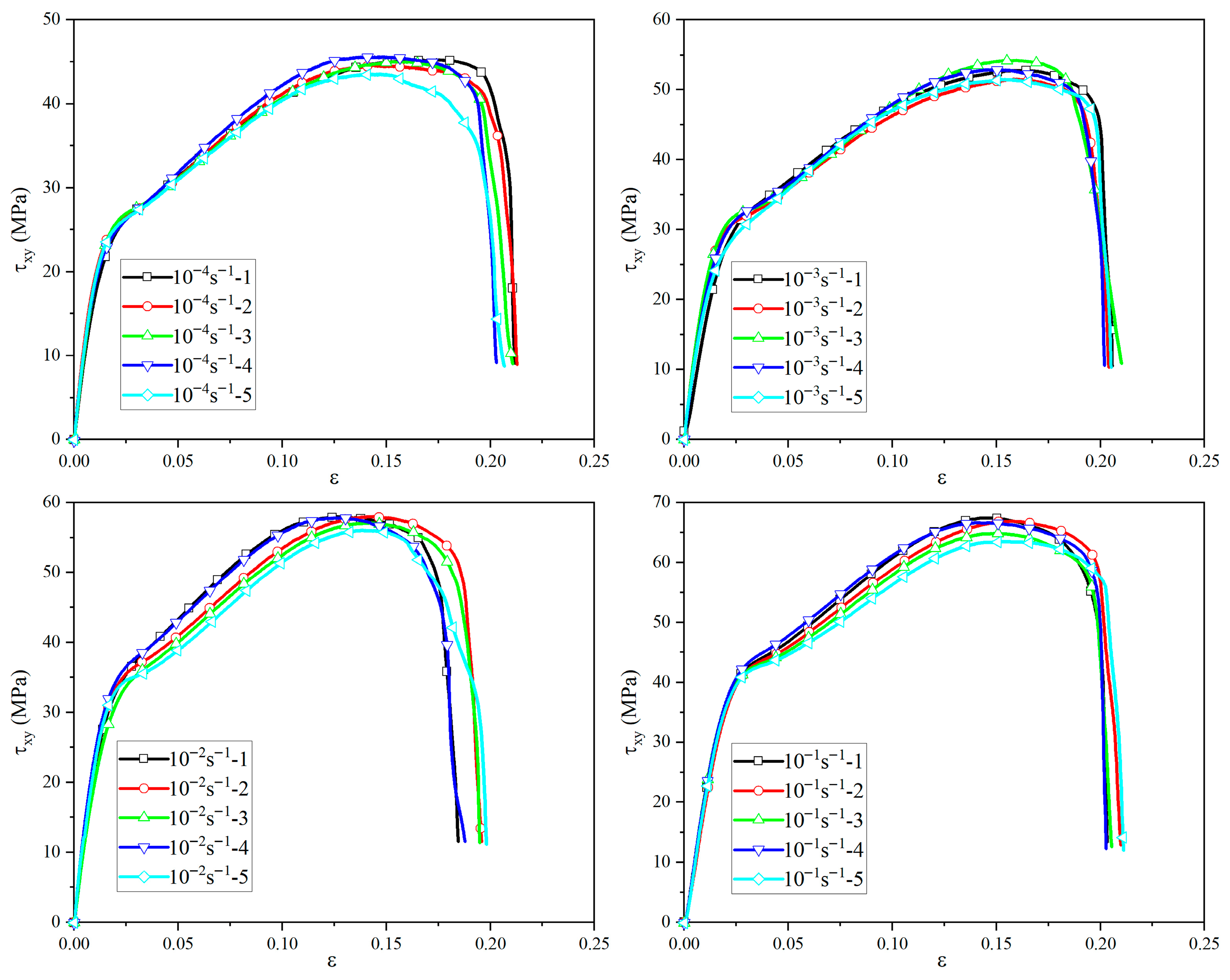
3.5. In-Plane Shear Strength
3.6. Out-of-Plane Shear Strength
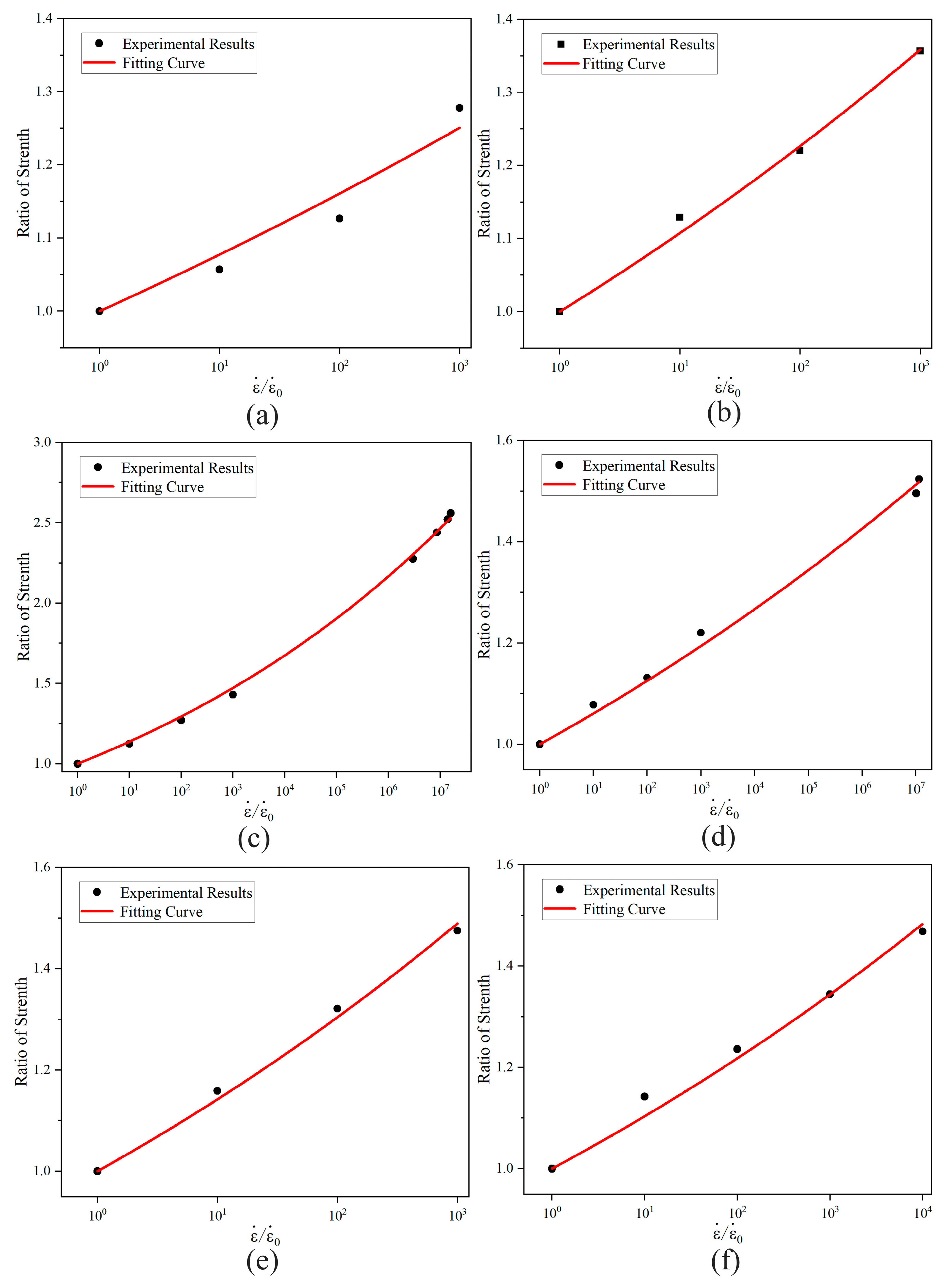
3.7. The Strain Rate Effect of Basalt-Fiber Composite Materials
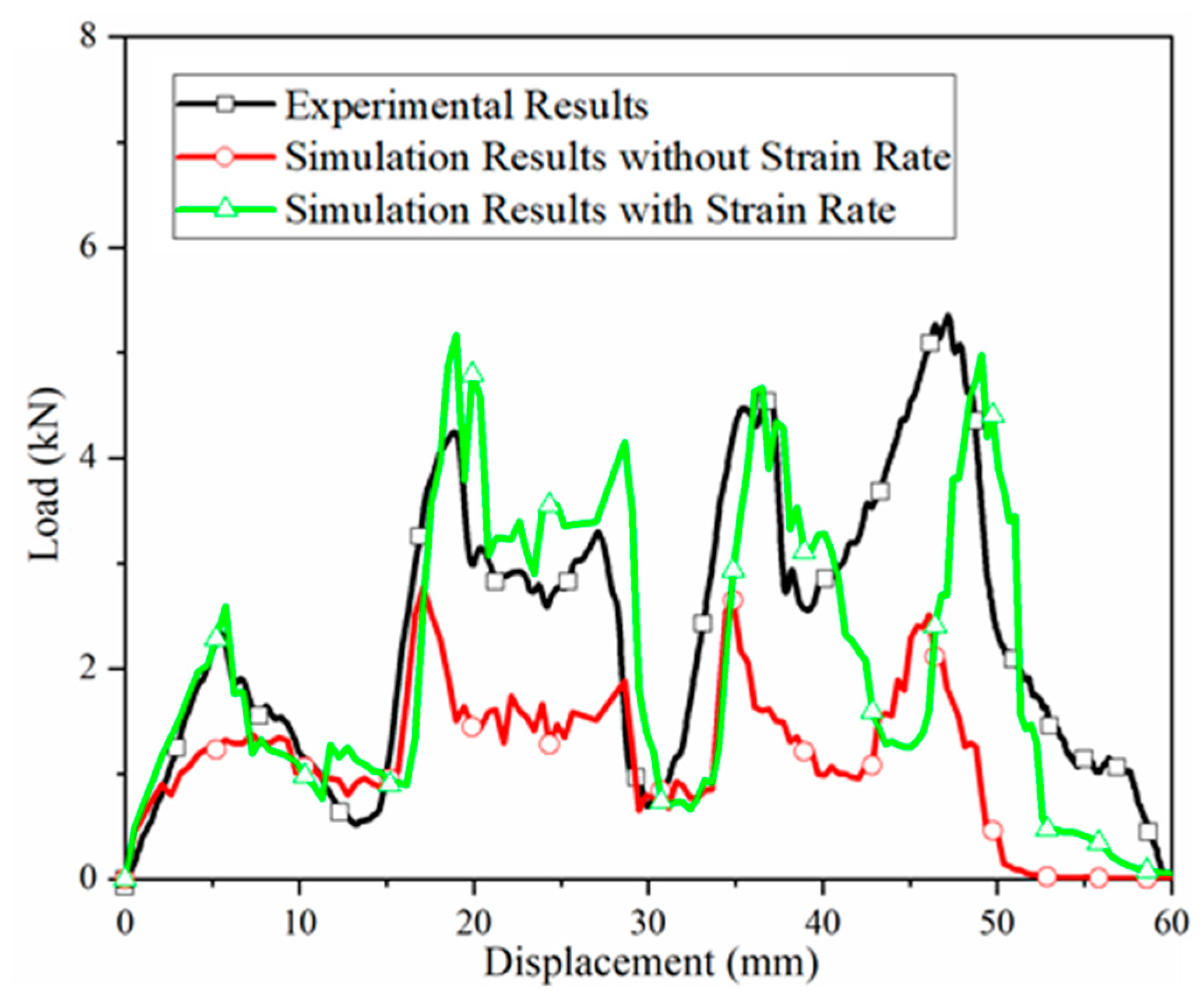
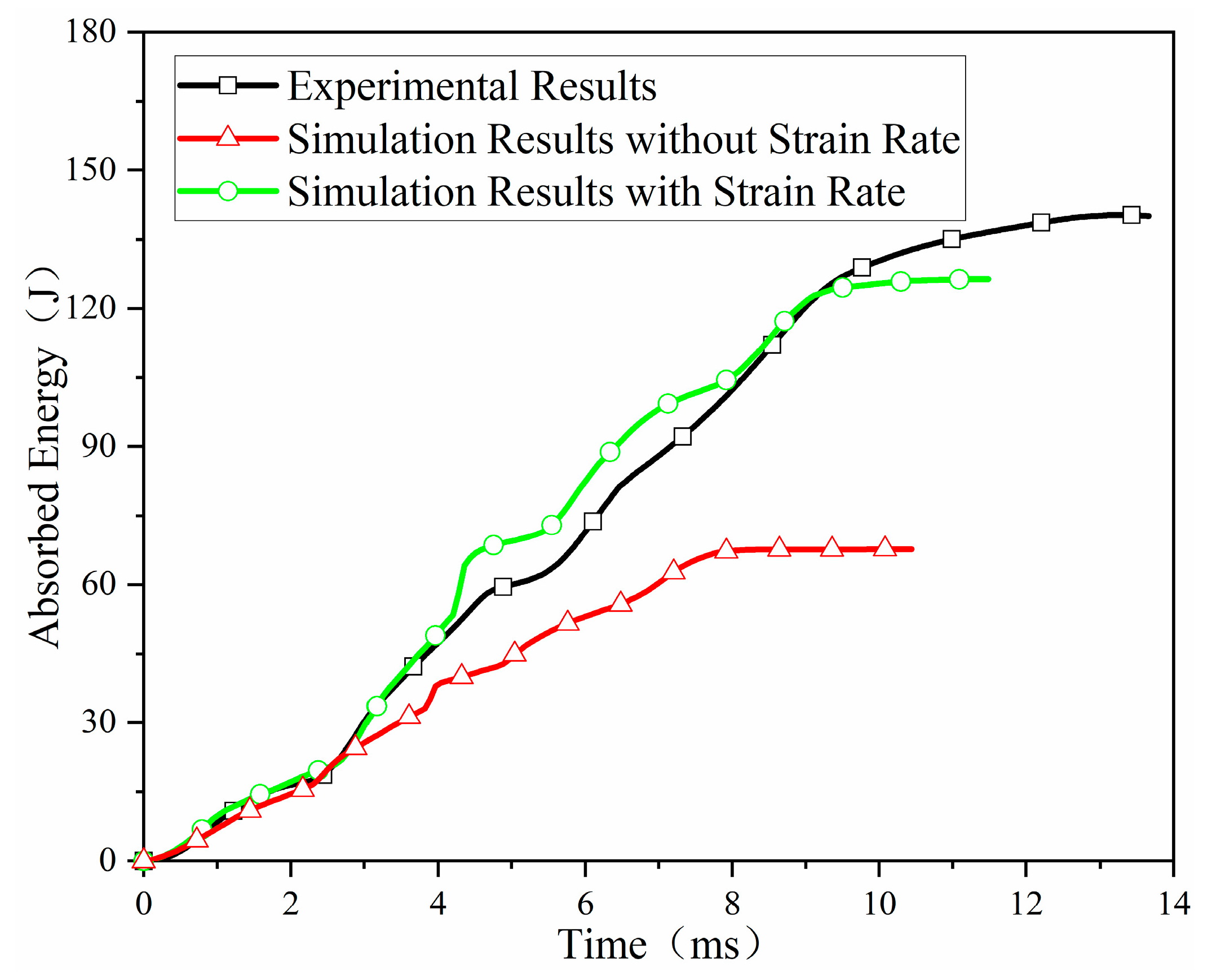
4. Discussion
5. Conclusions
- (1)
- BFRP composites exhibit significant strain-rate dependency, with strength increasing as strain rate increases.
- (2)
- The strain-rate effect is directionally dependent, showing varying sensitivity across different material orientations.
- (3)
- The relationship between strength and strain rate in different directions follows a nonlinear trend, well-described by the established power–law relationships.
- (4)
- The developed strain-rate relationships for BFRP composites were successfully validated in low-velocity impact simulations, demonstrating high accuracy compared to experimental results when incorporated into the numerical model.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A


References
- Mamidi, N.; Delgadillo, R.M.V.; González-Ortiz, A. Engineering of carbon nano-onion bioconjugates for biomedical applications. Mater. Sci. Eng. C 2021, 120, 111698. [Google Scholar] [CrossRef]
- Paknahad, A.; Goudarzi, M.; Kucko, N.W.; Leeuwenburgh, S.C.G.; Sluys, L.J. Calcium phosphate cement reinforced with poly (vinyl alcohol) fibers: An experimental and numerical failure analysis. Acta Biomater. 2021, 119, 458–471. [Google Scholar] [CrossRef]
- Zhang, S.; Caprani, C.C.; Heidarpour, A. Strain rate studies of pultruded glass fibre reinforced polymer material properties: A literature review. Constr. Build. Mater. 2018, 171, 984–1004. [Google Scholar] [CrossRef]
- Harding, M.M.; Ruiz, C. The mechanical behaviour of composite materials under impact loading. Key Eng. Mater. 1997, 141, 403–426. [Google Scholar] [CrossRef]
- Caverzan, A.; Cadoni, E.; di Prisco, M. Tensile behaviour of high performance fibre-reinforced cementitious composites at high strain rates. Int. J. Impact Eng. 2012, 45, 28–38. [Google Scholar] [CrossRef]
- Al-Mosawe, A.; Al-Mahaidi, R.; Zhao, X.L. Engineering properties of CFRP laminate under high strain rates. Compos. Struct. 2017, 180, 9–15. [Google Scholar] [CrossRef]
- Eskandari, S.; Pires, F.M.A.; Camanho, P.P.; Cui, H.; Petrinic, N.; Marques, A.T. Analyzing the failure and damage of FRP composite laminates under high strain rates considering visco-plasticity. Eng. Fail. Anal. 2019, 101, 257–273. [Google Scholar] [CrossRef]
- Kim, M.; Park, T.Y.; Hong, S. Experimental determination of the plastic deformation and fracture behavior of polypropylene composites under various strain rates. Polym. Test. 2021, 93, 107010. [Google Scholar] [CrossRef]
- Li, D.; Han, W.; Jiang, L. High strain rate impact effect and failure behavior of 3D six-directional braided composites. Extrem. Mech. Lett. 2021, 45, 101291. [Google Scholar] [CrossRef]
- Vieille, B.; Albouy, W.; Taleb, L. Viscoelastic viscoplastic model for aeronautical thermoplastic laminates at high temperature: Validation on high stress gradient structures. Compos. Part B Eng. 2016, 90, 278–286. [Google Scholar] [CrossRef]
- Abdul-Latif, A.; Che Man, M.H.; Mansor, S. Inclusion of strain-rate effects in low velocity impact simulation of laminated composites. Appl. Mech. Mater. 2014, 465, 1395–1399. [Google Scholar] [CrossRef]
- Zhang, X.; Hao, H.; Shi, Y.; Cui, J.; Zhang, X. Static and dynamic material properties of CFRP/epoxy laminates. Constr. Build. Mater. 2016, 114, 638–649. [Google Scholar] [CrossRef]
- Xin, S.H. Numerical Simulation of Penetration Resistance of Fiber Reinforced Resin Matrix Composite Laminates. Ph.D. Thesis, University of Science and Technology of China, Hefei, China, 2015. [Google Scholar]
- Gebbeken, N.; Greulich, S. A new material model for SFRC under high dynamic loadings. In Proceedings of the International Conference on Interaction of the Effects of Munitions with Structures, Mannheim, Germany, 5–9 May 2003; pp. 1–16. [Google Scholar]
- Gama, B.Z.; Stanton, R.J.; Gillespie, J.W. Perforation mechanics of thin composites. In Proceedings of the International SAMPE Technical Conference, Long Beach, CA, USA, 6–9 May 2013. [Google Scholar]
- Long, S.; Yao, X.; Wang, H.; Zhang, X. A dynamic constitutive model for fiber-reinforced composite under impact loading. Int. J. Mech. Sci. 2020, 166, 105226. [Google Scholar] [CrossRef]
- Tang, D.; Huang, H.; Fan, Y.; Wang, H.; Peng, Y. Manufacturing and impact resistance of Large-Scale stacked fibre metal laminates. Mater. Des. 2025, 253, 113917. [Google Scholar] [CrossRef]
- Kong, X.; Zhu, Z.; Zheng, C.; Zhou, H.; Wu, W. Numerical investigation on the dynamic behavior of thermoplastic fiber-metal laminates subject to confined explosion loading. Thin-Walled Struct. 2025, 214, 113354. [Google Scholar] [CrossRef]
- Zhang, N.; Qian, X.; Zhang, Q.; Zhou, G.; Xuan, S.; Wang, X.; Cai, D. On strain rate effect and high-velocity impact behavior of carbon fiber reinforced laminated composites. Thin-Walled Struct. 2024, 194 Pt B, 111328. [Google Scholar] [CrossRef]
- Peng, Y.; Wang, X.; Chen, X.; Wang, K.; Huang, Z.; Liu, Z.; Zhang, H. Numerical simulation of the effect of projectile shape and size on the high-velocity impact of carbon fiber reinforced composite laminates. J. Mater. Res. Technol. 2024, 30, 5109–5120. [Google Scholar] [CrossRef]
- Pournoori, N.; Rodera, O.; Jokinen, J.; Hokka, M.; Kanerva, M. Failure prediction for high-strain rate and out-of-plane compression of fibrous composites. Compos. Sci. Technol. 2021, 218, 109141. [Google Scholar] [CrossRef]
- ASTM D3039; Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials. ASTM International: West Conshohocken, PA, USA, 2008.
- ASTM D3518; Standard Test Method for In-plane Shear Response of Polymer Matrix Composite Materials by Tensile Test of a ±45° Laminate. ASTM International: West Conshohocken, PA, USA, 2007.
- ASTM D7291/D7291M-15; Standard Test Method for Through-Thickness “Flatwise” Tensile Strength and Elastic Modulus of a Fiber-Reinforced Polymer Matrix Composite Material. ASTM International: West Conshohocken, PA, USA, 2015.
- ASTM D 2344; Standard Test Method for Short-Beam Strength of Polymer Matrix Composite Materials and Their Laminates. ASTM International: West Conshohocken, PA, USA, 2006.
- Pang, Y.; Yan, X.; Qu, J.; Wu, L. Dynamic response of polyurethane foam and fiber orthogonal corrugated sandwich structure subjected to low-velocity impact. Compos. Struct. 2022, 282, 114994. [Google Scholar] [CrossRef]
- Yao, H.; Pang, Y.; Jiang, L.; Li, Y.; Qu, J. Mechanical Properties and Dynamic Constitutive Model of Polyurethane Foam under Different Strain Rates. Appl. Compos. Mater. 2025, 32, 257–279. [Google Scholar] [CrossRef]
- Bing, Q.; Sun, C.T. Modeling and testing strain rate-dependent compressive strength of carbon/epoxy composites. Compos. Sci. Technol. 2005, 65, 2481–2491. [Google Scholar] [CrossRef]
- Brown, K.A.; Brooks, R.; Warrior, N.A. The static and high strain rate behaviour of a commingled E-glass/polypropylene woven fabric composite. Compos. Sci. Technol. 2010, 70, 272–283. [Google Scholar] [CrossRef]
- Naresh, K.; Shankar, K.; Velmurugan, R.; Gupta, N.K. High strain rate studies for different laminate configurations of bi-directional glass/epoxy and carbon/epoxy composites using DIC. Structures 2020, 27, 2451–2465. [Google Scholar] [CrossRef]










| Strain Rate (s−1) | In-Plane Tensile Strength (MPa) | Average Tensile Strength (MPa) | Standard Deviation (MPa) | ||||
|---|---|---|---|---|---|---|---|
| Specimen 1 | Specimen 2 | Specimen 3 | Specimen 4 | Specimen 5 | |||
| 10−4 | 273.42 | 276.50 | 264.86 | 256.32 | 253.14 | 264.85 | 10.24 |
| 10−3 | 294.33 | 282.95 | 277.42 | 274.58 | 270.23 | 279.90 | 9.29 |
| 10−2 | 307.32 | 307.48 | 297.71 | 291.10 | 288.41 | 298.40 | 8.88 |
| 10−1 | 353.74 | 348.44 | 341.17 | 322.24 | 326.35 | 338.39 | 13.69 |
| Strain Rate (s−1) | Out-of-Plane Tensile Strength (MPa) | Average Tensile Strength (MPa) | Standard Deviation (MPa) | ||||
|---|---|---|---|---|---|---|---|
| Specimen 1 | Specimen 2 | Specimen 3 | Specimen 4 | Specimen 5 | |||
| 10−4 | 11.20 | 13.53 | 12.77 | 13.40 | 13.98 | 12.98 | 1.08 |
| 10−3 | 13.31 | 14.79 | 16.09 | 15.91 | 13.15 | 14.65 | 1.39 |
| 10−2 | 17.15 | 14.90 | 15.92 | 15.75 | 15.43 | 15.83 | 0.83 |
| 10−1 | 18.78 | 19.12 | 18.27 | 17.17 | 14.66 | 17.60 | 1.80 |
| Strain Rate (s−1) | In-Plane Compressive Strength (MPa) | Average Compressive Strength (MPa) | Standard Deviation (MPa) | ||||
|---|---|---|---|---|---|---|---|
| Specimen 1 | Specimen 2 | Specimen 3 | Specimen 4 | Specimen 5 | |||
| 10−4 | 187.07 | 224.23 | 214.90 | 186.85 | 193.93 | 201.39 | 17.15 |
| 10−3 | 235.63 | 231.70 | 224.42 | 222.27 | 217.93 | 226.39 | 7.18 |
| 10−2 | 281.74 | 257.07 | 249.93 | 249.50 | 241.37 | 255.92 | 15.47 |
| 10−1 | 309.18 | 297.24 | 285.48 | 267.40 | 281.05 | 288.07 | 15.91 |
| 300 | 466.23 | 459.06 | 450.14 | 424.56 | 492.40 | 458.48 | 24.65 |
| 870 | 505.15 | 488.27 | 481.60 | 476.89 | 506.45 | 491.67 | 13.52 |
| 1400 | 515.42 | 513.54 | 495.68 | 487.57 | 528.85 | 508.21 | 16.50 |
| 1600 | 522.63 | 520.20 | 497.07 | 498.78 | 542.67 | 516.27 | 18.89 |
| Strain Rate (s−1) | Out-of-Plane Compressive Strength (MPa) | Average Compressive Strength (MPa) | Standard Deviation (MPa) | ||||
|---|---|---|---|---|---|---|---|
| Specimen 1 | Specimen 2 | Specimen 3 | Specimen 4 | Specimen 5 | |||
| 10−4 | 605.66 | 562.37 | 588.04 | 604.63 | 581.85 | 588.51 | 17.90 |
| 10−3 | 630.00 | 626.02 | 642.46 | 638.48 | 639.45 | 635.28 | 6.94 |
| 10−2 | 654.96 | 643.82 | 673.86 | 685.31 | 670.50 | 665.69 | 16.34 |
| 10−1 | 720.21 | 725.61 | 719.51 | 708.98 | 715.09 | 717.88 | 6.22 |
| 1020 | 885.30 | 870.41 | 884.25 | 865.57 | 894.41 | 879.99 | 11.78 |
| 1150 | 905.14 | 888.35 | 895.24 | 879.28 | 913.20 | 896.24 | 13.40 |
| Strain Rate (s−1) | In-Plane Shear Strength (MPa) | Average Shear Strength (MPa) | Standard Deviation (MPa) | ||||
|---|---|---|---|---|---|---|---|
| Specimen 1 | Specimen 2 | Specimen 3 | Specimen 4 | Specimen 5 | |||
| 10−4 | 31.74 | 31.31 | 31.13 | 31.11 | 30.96 | 31.25 | 0.30 |
| 10−3 | 36.92 | 36.51 | 36.06 | 35.82 | 35.74 | 36.21 | 0.50 |
| 10−2 | 43.38 | 43.09 | 40.97 | 40.06 | 38.92 | 41.28 | 1.93 |
| 10−1 | 47.81 | 46.83 | 45.94 | 45.26 | 44.63 | 46.09 | 1.26 |
| Strain Rate (s−1) | Out-of-Plane Shear Strength (MPa) | Average Shear Strength (MPa) | Standard Deviation (MPa) | ||||
|---|---|---|---|---|---|---|---|
| Specimen 1 | Specimen 2 | Specimen 3 | Specimen 4 | Specimen 5 | |||
| 10−4 | 36.81 | 36.01 | 35.47 | 34.97 | 34.26 | 35.50 | 0.97 |
| 10−3 | 42.01 | 41.21 | 40.16 | 40.33 | 39.08 | 40.56 | 1.11 |
| 10−2 | 45.68 | 44.01 | 41.53 | 44.50 | 43.68 | 43.88 | 1.51 |
| 10−1 | 48.37 | 48.16 | 47.82 | 47.60 | 46.71 | 47.73 | 0.64 |
| 100 | 54.63 | 53.40 | 51.47 | 51.32 | 49.85 | 52.13 | 1.88 |
(GPa) | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | ||||
| 25.83 | 25.83 | 9.00 | 23.809 | 4.339 | 4.339 | 0.28 | 0.148 | 0.148 | |
(MPa) | (MPa) | (MPa) | (MPa) | (MPa) | (MPa) | (MPa) | (MPa) | (MPa) | (MPa) |
| 264.85 | 201.40 | 264.85 | 201.40 | 12.98 | 588.34 | 264.85 | 31.25 | 31.25 | 12.98 |
| Load Peaks | Experimental Results (kN) | Simulation Results Without Strain Rates (kN) | Errors | Simulation Results with Strain Rates (kN) | Errors |
|---|---|---|---|---|---|
| First | 2.34 | 1.38 | 41.03% | 2.61 | 11.54% |
| Second | 4.25 | 2.78 | 34.59% | 5.16 | 21.41% |
| Third | 4.49 | 2.63 | 41.43% | 4.66 | 3.79% |
| Fourth | 5.35 | 2.52 | 52.90% | 4.99 | 6.73% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pang, Y.; Wang, C.; Zhao, Y.; Yao, H.; Wang, X. Strain-Rate Effects on the Mechanical Behavior of Basalt-Fiber-Reinforced Polymer Composites: Experimental Investigation and Numerical Validation. Materials 2025, 18, 3637. https://doi.org/10.3390/ma18153637
Pang Y, Wang C, Zhao Y, Yao H, Wang X. Strain-Rate Effects on the Mechanical Behavior of Basalt-Fiber-Reinforced Polymer Composites: Experimental Investigation and Numerical Validation. Materials. 2025; 18(15):3637. https://doi.org/10.3390/ma18153637
Chicago/Turabian StylePang, Yuezhao, Chuanlong Wang, Yue Zhao, Houqi Yao, and Xianzheng Wang. 2025. "Strain-Rate Effects on the Mechanical Behavior of Basalt-Fiber-Reinforced Polymer Composites: Experimental Investigation and Numerical Validation" Materials 18, no. 15: 3637. https://doi.org/10.3390/ma18153637
APA StylePang, Y., Wang, C., Zhao, Y., Yao, H., & Wang, X. (2025). Strain-Rate Effects on the Mechanical Behavior of Basalt-Fiber-Reinforced Polymer Composites: Experimental Investigation and Numerical Validation. Materials, 18(15), 3637. https://doi.org/10.3390/ma18153637





