Temporal Deformation Characteristics of Hydraulic Asphalt Concrete Slope Flow Under Different Test Temperatures
Abstract
1. Introduction
2. Test Procedure
2.1. Sample Preparation
2.2. Developed Test Apparatus
2.3. Test Plan
- (1)
- Initial setup: According to the test plan, the multifunctional sample holder’s slope was set to 1:1.7, and the temperature inside the high-precision temperature control box was programmed to the target T.
- (2)
- Sample installation: Once the temperature inside the high-precision temperature control box stabilized, the box door was opened, and the multifunctional sample holder extracted. High-temperature-resistant adhesive was uniformly applied to the placement table, followed by specimen adhesion.
- (3)
- Laser displacement sensor calibration: The laser displacement sensor was activated and calibrated by adjusting the reference slope board until the beam aligned with the predefined D = 50 mm point from the specimen base (Figure 4).
- (4)
- Test initiation: The multifunctional sample holder with the installed specimen was smoothly pushed back into the high-precision temperature control box, and its door was closed. The laser displacement sensor readings were zeroed before initiating 48 h isothermal testing.
- (5)
- Data acquisition: Real-time slope flow values were recorded and downloaded via the digital twin system throughout testing.
3. Result Analysis
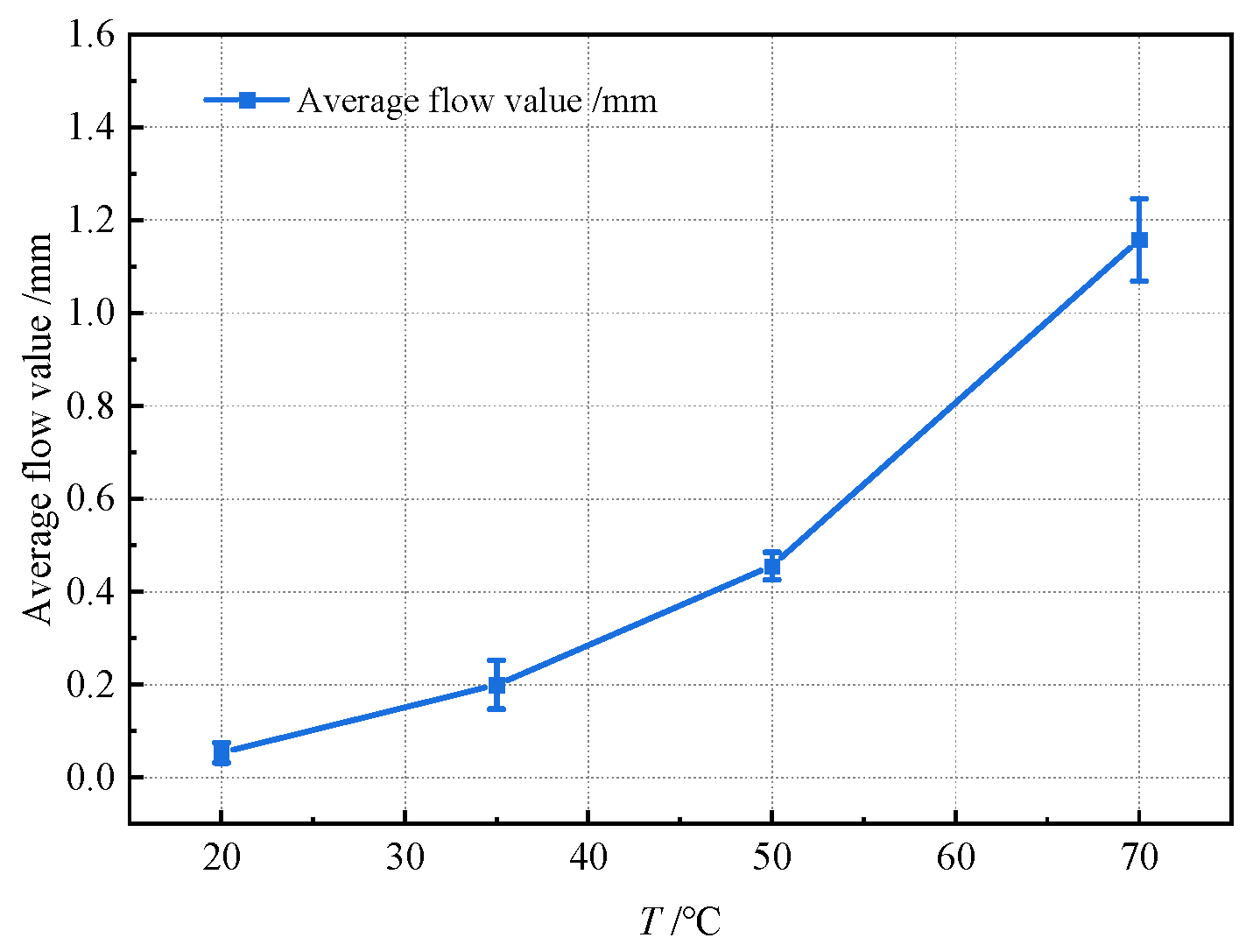
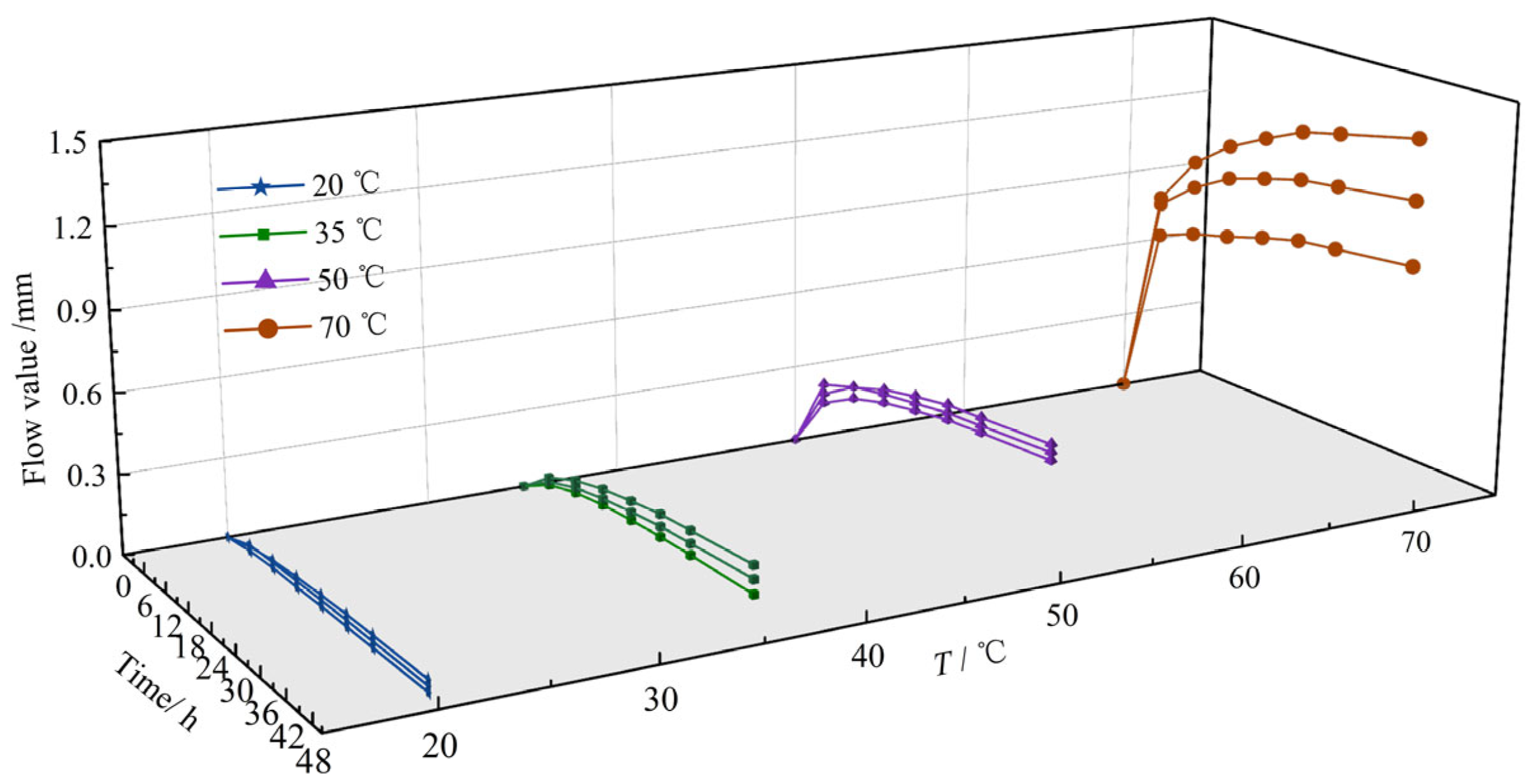
3.1. Temporal Evolution of Slope Flow Value
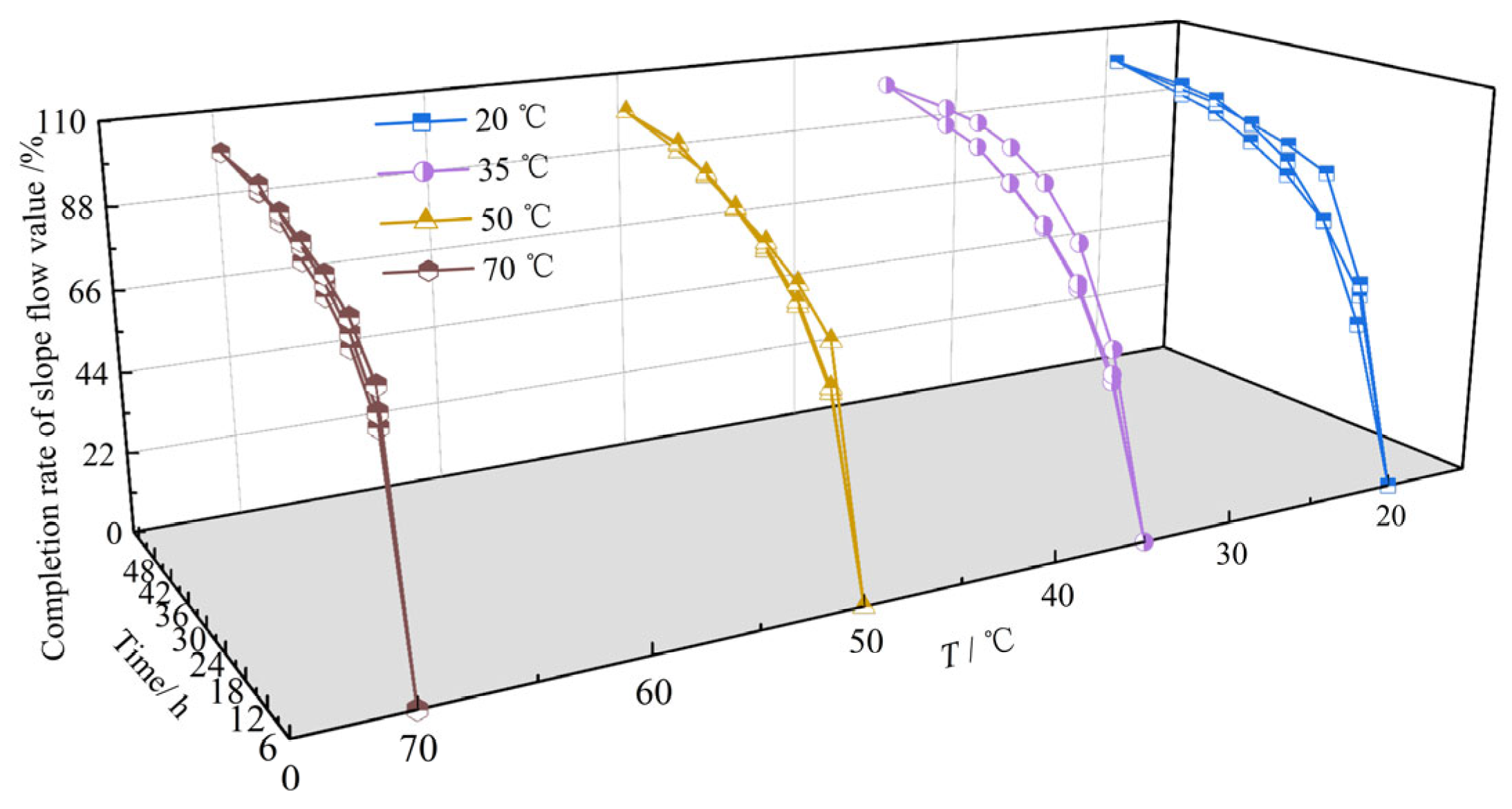
3.2. Temporal Evolution of Slope Flow Completion Rate
3.3. Stage Characterization of Slope Flow Evolution
4. Nonlinear Mechanical Behavior Characteristics of HAC Thermal Stability
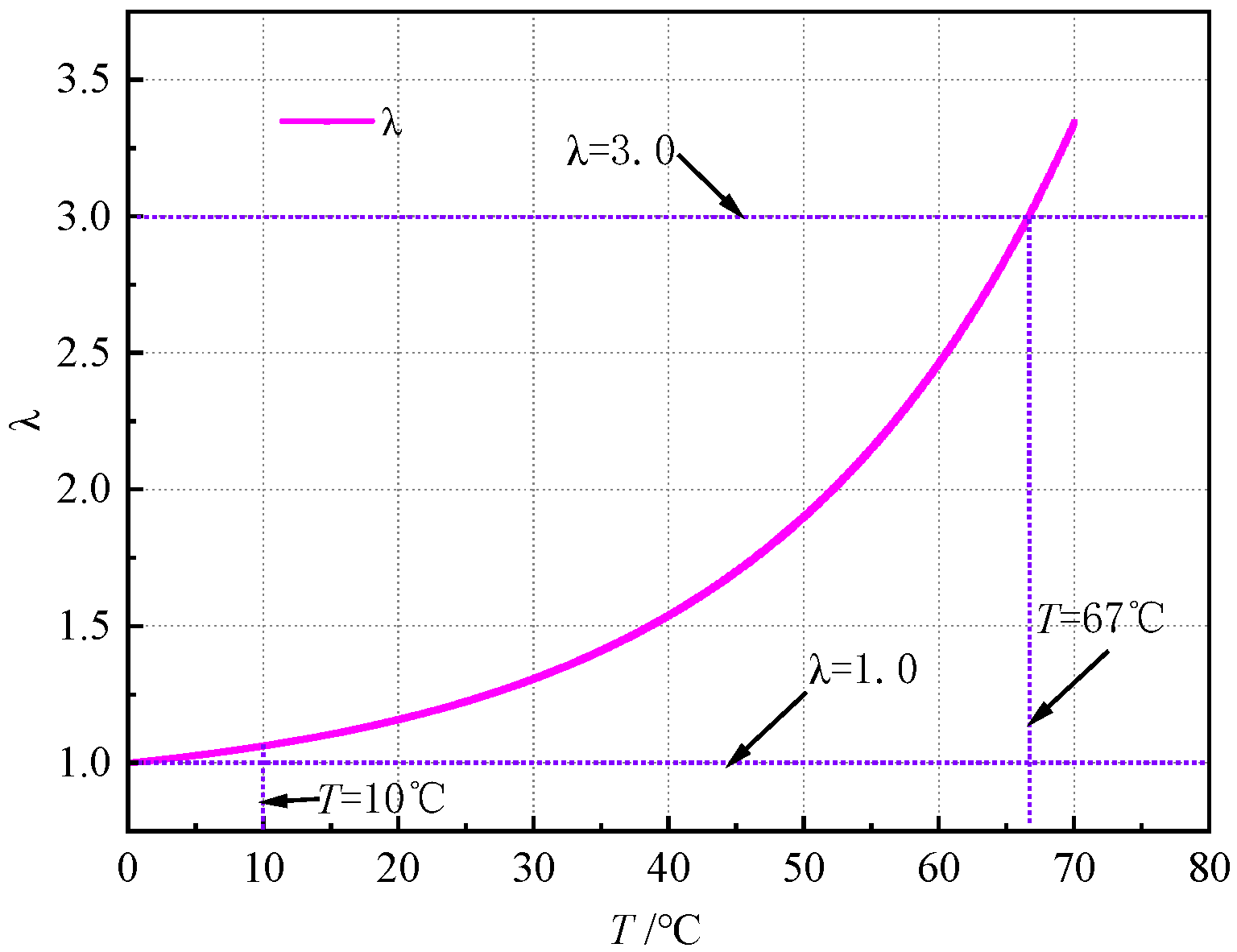
4.1. Thermal Stability Temperature Influence Factor
4.2. Disorder Characteristics of the Thermal Stability Temperature Influence Factor Sequence
5. Discussion
6. Conclusions
- The slope flow deformation of asphalt concrete exhibits a distinct three-stage temporal evolution pattern: (1) Rapid growth stage (0~12 h): The slope flow value increases rapidly, reaching 50~70% of the final deformation. This is attributed to thermal disruption of the primary skeleton structure formed by coarse aggregates. (2) Decelerated growth stage (12~24 h): The growth rate decreases sharply, with deformation attaining 70~90% of the final value. During this stage, an embryonic secondary skeleton forms and progressively develops deformation resistance. (3) Stabilization stage (24~48 h): Deformation stabilizes (>90% completion) as coarse aggregates complete reorganization, establishing a stable secondary skeleton that effectively resists further flow.
- The thermal stability of asphalt concrete is synergistically controlled by the phase-transition behavior of the asphalt binder and the reorganization of coarse aggregates. At elevated temperatures, the asphalt phase transition dominates initial deformation, while coarse aggregate reorganization governs stabilization by forming a secondary skeleton in later stages. When the test temperature exceeds the asphalt’s softening point, the internal system enters an aperiodic oscillatory state. This systematic disordering prevents coarse aggregates from establishing an effective secondary skeleton.
- Beyond the asphalt’s softening point, non-periodic instability compromises aggregate interlocking, accelerating deformation. This necessitates thermal mitigation strategies (e.g., reflective surface coatings) and material optimization (e.g., high-softening-point binders, optimized gradation indices) for slope integrity in pumped-storage facilities.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dong, J.; Ding, Y.X.; Liu, Y.H.; Ning, Z.Y.; Qi, Y.J. Tensile test and discrete element study on recycled aggregate hydraulic asphalt concrete. Constr. Build. Mater. 2024, 450, 138538. [Google Scholar] [CrossRef]
- He, J.X.; Lu, J.N.; Liu, L.; Yang, W.; Yang, H.H.; Chen, P.P.; Ding, X.Y. Bending performance evaluation of large grain hydraulic asphalt concrete based on the coefficient of variation. KSCE J. Civ. Eng. 2024, 28, 3420–3429. [Google Scholar] [CrossRef]
- He, J.X.; Yang, Z.H.; Yang, W.; Liu, L.; Li, H. Long-term water stability of hydraulic asphalt concrete based on time-temperature equivalence. J. Mater. Civ. Eng. 2024, 36, 04024238. [Google Scholar] [CrossRef]
- Rahman, M.M.; Oni, A.O.; Gemechu, E.; Kumar, A. Assessment of energy storage technologies: A review. Energy Convers. Manag. 2020, 223, 113295. [Google Scholar] [CrossRef]
- Xu, X.D.; Wang, Z.X.; Zhu, A.L.; Xia, S.F. Analysis of the influence of environmental factors on the temperature of asphalt concrete facing on reservoir dam. J. Water Resour. Archit. Eng. 2023, 21, 15–29. [Google Scholar]
- Wang, Z.X.; Hao, J.T.; Sun, Z.H.; Ma, B.D.; Xia, S.F.; Li, X.L. Blistering mechanism analysis of hydraulic asphalt concrete facing. Appl. Sci. 2019, 9, 2903. [Google Scholar] [CrossRef]
- Wang, Z.X.; Hao, J.T.; Yang, J.; Cao, Y.; Li, X.L.; Liu, S.J. Experimental study on hydraulic fracturing of high asphalt concrete core rock-fill dam. Appl. Sci. 2019, 9, 2285. [Google Scholar] [CrossRef]
- Tang, R.; Yu, Z.P.; Liu, G.Q.; Li, F.R.; Tang, W.B. Uniaxial dynamic compressive behaviors of hydraulic asphalt concrete under the coupling effect between temperature and strain rate. Materials 2020, 13, 5348. [Google Scholar] [CrossRef]
- Feng, S.; Wang, W.B.; Hu, K.; Höeg, K. Stress-strain-strength behavior of asphalt core in embankment dams during construction. Constr. Build. Mater. 2020, 259, 119706. [Google Scholar] [CrossRef]
- Han, Q.Z.; Song, G.; Wang, Y.Y.; Zhang, Y.B.; Ning, Z.Y. Experimental research on high-temperature stability of asphalt concrete panels of impermeable layers. Appl. Sci. 2023, 13, 7555. [Google Scholar] [CrossRef]
- Adam, K.; Říha, J.; Špano, M. Investigation on the temperature of the asphalt-concrete facing of embankment dams. Int. J. Pavement Res. Technol. 2016, 9, 73–81. [Google Scholar] [CrossRef][Green Version]
- Ning, Z.Y.; Liu, Y.H.; Xue, X. Dynamic compressive behavior of hydraulic asphalt concrete under different temperatures. J. Hydroelectr. Eng. 2019, 38, 24–34. [Google Scholar]
- Ning, Z.Y.; Liu, Y.H.; Wang, W.B. Compressive behavior of hydraulic asphalt concrete under different temperatures and strain rates. J. Mater. Civ. Eng. 2021, 33, 04021013. [Google Scholar] [CrossRef]
- Jin, D.Z.; Xin, K.; Mohammadi, S.; Cetin, B.; You, Z.P. Performance of rubber modified asphalt mixture with tire-derived aggregate subgrade. Constr. Build. Mater. 2024, 499, 138261. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.L.; Liu, J.H.; Li, W.M.; She, L. Optimization of some properties of hydraulic asphalt concrete mix using RSM and NSGA-II. Constr. Build. Mater. 2024, 438, 137317. [Google Scholar] [CrossRef]
- Li, Y.L.; Liu, J.H.; Liu, Y.H.; Zhou, H.; Wen, L.F.; Chen, J.H. Aggregate grading design of skeleton dense hydraulic asphalt concrete. Constr. Build. Mater. 2023, 365, 130031. [Google Scholar] [CrossRef]
- Zhu, J.Q.; Ma, T.; Cheng, H.; Li, T.L.; Fu, J.K. Mechanical properties of high-modulus asphalt concrete containing recycled asphalt pavement: A parametric study. J. Mater. Civ. Eng. 2021, 33, 04021056. [Google Scholar] [CrossRef]
- Meng, X.; Liu, Y.H.; Ning, Z.Y.; Xue, X. Anlysis of factors affectings slope flow of asphalt concrete. Water Resour. Power. 2019, 37, 100–103. [Google Scholar]
- Li, C.; Li, L.L. Criteria for controlling rutting of asphalt concrete materials in sloped pavement. Constr. Build. Mater. 2012, 35, 330–339. [Google Scholar] [CrossRef]
- Cai, Y.Z.; Xiang, P.; Ye, Y. Effect factor analysis of asphalt concrete imperious facing thermal stability with grey relation entropy method. China Rural. Water Hydropower 2014, 1, 135–137. [Google Scholar]
- Zou, C.G.; Hua, Z.; Mo, L.T.; Qi, G.; Liu, Z.X.; Xie, Y.J.; Yu, H.; Ke, J.T. Evaluation on the performance of hydraulic bitumen binders under high and low temperatures for pumped storage power station projects. Materials 2022, 15, 1890. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.B.; Wang, W.B.; Du, X.H.; He, Z.P. Research on the effects of limestone filler content on the behaviors of hydraulic asphalt concrete. J. Hydroelectr. Eng. 2008, 27, 73–77. [Google Scholar]
- Zhang, Y.B.; Wang, W.B.; Lan, X.; Zhao, Y.H. Research on the suitability of acidic gravels for asphalt core of embankment dam. J. Hydraul. Eng. 2012, 43, 460–466. [Google Scholar]
- Sun, Y.; Huang, W.; Xu, G.; Gan, L.; Shen, Z.Z.; Luo, S.; Zhang, H.W.; Feng, Y.X.; Xiong, H.Y.; Shu, Y.K. Experimental investigation on the performance of hydraulic asphalt concrete with varying epoxy system content. Constr. Build. Mater. 2025, 484, 141755. [Google Scholar] [CrossRef]
- Ali, Y.; Irfan, M.; Buller, A.S.; Khan, H.A.; Gul, H.M.F. Factors affecting low-temperature cracking of asphalt pavements: Analysis of field observations using the ordered logistic model. Constr. Build. Mater. 2019, 227, 116608. [Google Scholar] [CrossRef]
- Rys, D.; Judycki, J.; Pszczola, M.; Jaczewski, M.; Mejlun, L. Comparison of low-temperature cracks intensity on pavements with high modulus asphalt concrete and conventional asphalt concrete bases. Constr. Build. Mater. 2017, 147, 478–487. [Google Scholar] [CrossRef]
- Wu, N.; Fu, J.Y. Research on the impact response and chaos characteristics in the dynamic damage evolution process of concrete material. Constr. Build. Mater. 2020, 262, 120921. [Google Scholar] [CrossRef]
- Wang, G.L.; Cao, T.C.; Wen, X.X.; Sun, F.; Zhang, L. Evolution law of selfsuppression of peak energy of single jointed sandstone. J. China Coal Soc. 2021, 46, 211–221. [Google Scholar]
- DL/T5362-2018; Test Code for Hydraulic Asphalt Concrete. China Electric Power Press: Beijing, China, 2018. (In Chinese)
- NB/T 11015-2022; Code for Design of Asphalt Concrete Facings and Cores for Embankment Dams. China Water Resources Press: Beijing, China, 2022. (In Chinese)
- Ning, Z.Y.; Liu, Y.H.; Wang, W.B.; Zhang, K. Experimental study on compressive properties and impermeability of hydraulic asphalt concrete under different temperatures. Shuili Xuebao 2020, 51, 527–535. [Google Scholar]
- Liu, S.; Zhu, D.J.; Yao, Y.M.; Shi, C.J. Effects of strain rate and temperature on the flexural behavior of basalt and glass textile–reinforced concrete. J. Mater. Civ. Eng. 2018, 30, 04018172. [Google Scholar] [CrossRef]
- Ning, Z.Y.; Liu, Y.H.; Wang, Q.; Wang, W.B. Experimental study on the dynamic compressive behavior of asphalt concrete under different temperature. J. Vib. Shock 2021, 40, 243–250. [Google Scholar]
- An, X.X.; Hu, Z.P.; Zhang, L.; Liu, A.L.; Zhang, Y.H.; Li, F.T. Nonlinear energy evolution characteristics of diorite examined by triaxial loading—Unloading and acoustic emission tests. Materials 2022, 15, 6434. [Google Scholar] [CrossRef]
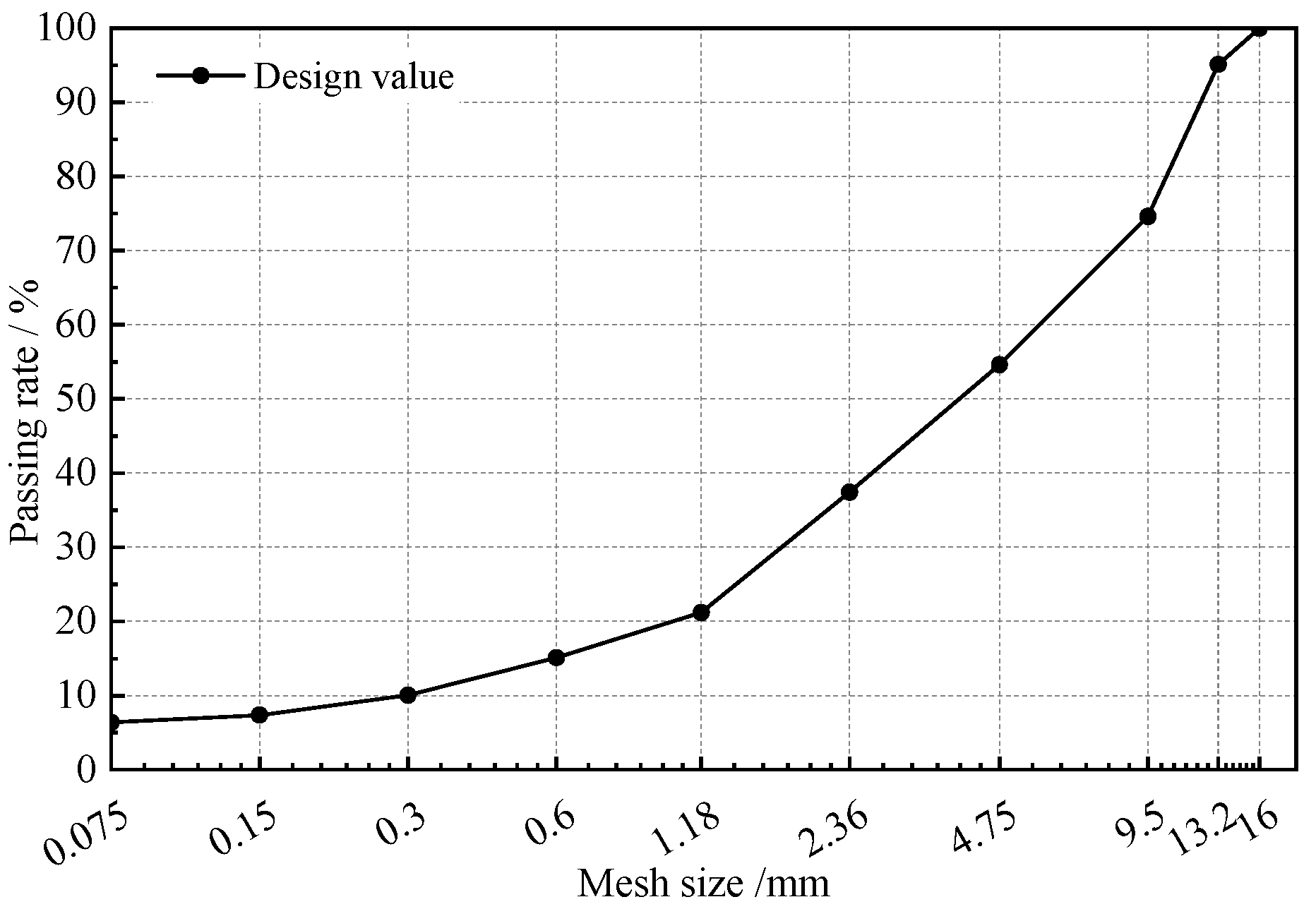

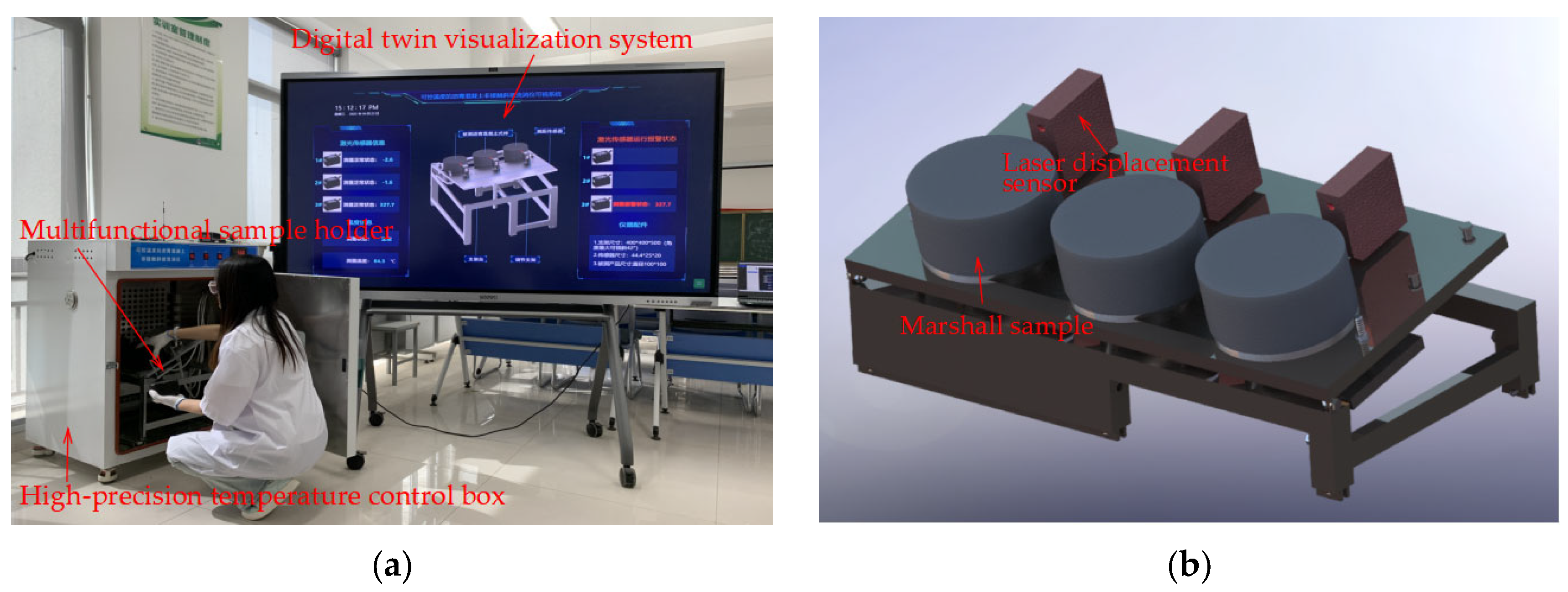
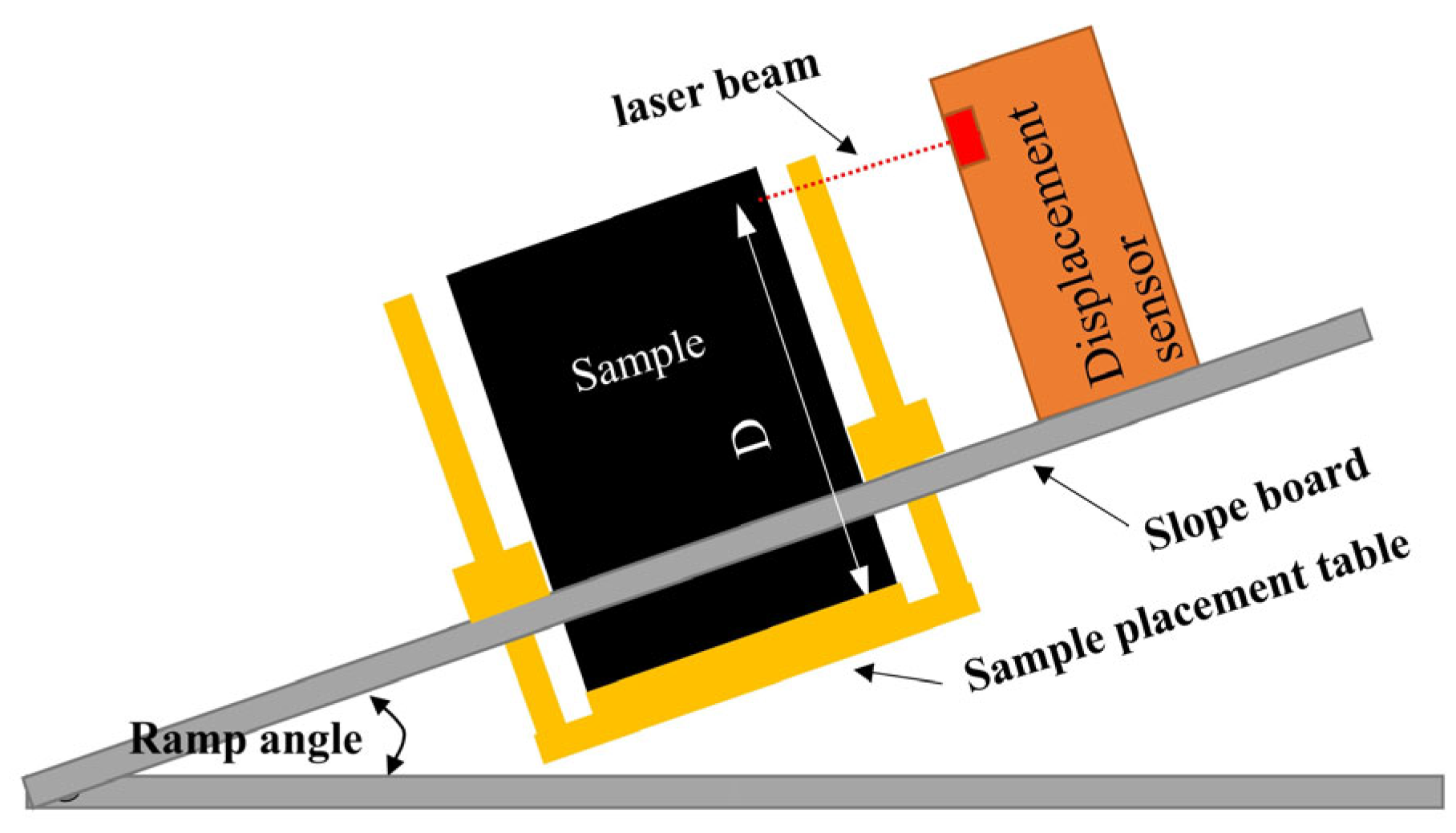

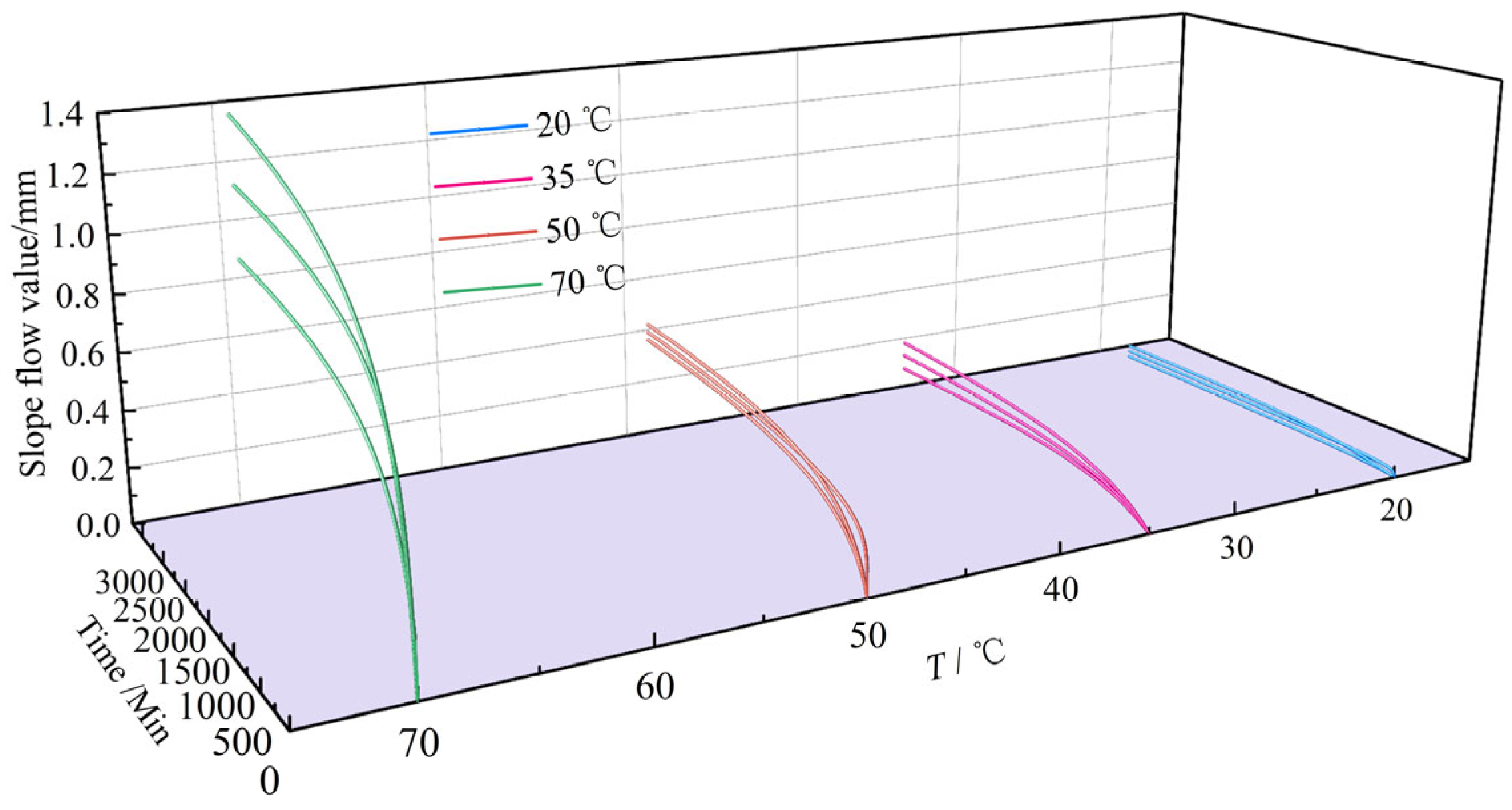



| No. | Variable Name | Variable Value | Other Variables | Number of Samples |
|---|---|---|---|---|
| 1 | Test temperature (T) | 20 °C | Tamp angle α = 30° | 3 |
| 2 | 35 °C | 3 | ||
| 3 | 50 °C | 3 | ||
| 4 | 70 °C | 3 |
| Test Time/h | 6 | 12 | 18 | 24 | 30 | 36 | 48 |
|---|---|---|---|---|---|---|---|
| Average value/% | 52.95 | 70.305 | 81.4825 | 87.68833 | 92.96917 | 96.115 | 100 |
| Standard deviation/% | 4.66 | 4.98 | 4.61 | 3.46 | 2.30 | 1.63 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, X.; Li, J.; Ning, Z. Temporal Deformation Characteristics of Hydraulic Asphalt Concrete Slope Flow Under Different Test Temperatures. Materials 2025, 18, 3625. https://doi.org/10.3390/ma18153625
An X, Li J, Ning Z. Temporal Deformation Characteristics of Hydraulic Asphalt Concrete Slope Flow Under Different Test Temperatures. Materials. 2025; 18(15):3625. https://doi.org/10.3390/ma18153625
Chicago/Turabian StyleAn, Xuexu, Jingjing Li, and Zhiyuan Ning. 2025. "Temporal Deformation Characteristics of Hydraulic Asphalt Concrete Slope Flow Under Different Test Temperatures" Materials 18, no. 15: 3625. https://doi.org/10.3390/ma18153625
APA StyleAn, X., Li, J., & Ning, Z. (2025). Temporal Deformation Characteristics of Hydraulic Asphalt Concrete Slope Flow Under Different Test Temperatures. Materials, 18(15), 3625. https://doi.org/10.3390/ma18153625






