Hysteresis Loops Design for Nanoporous Ferroelectrics
Abstract
1. Introduction
2. Simulation Method
3. Results
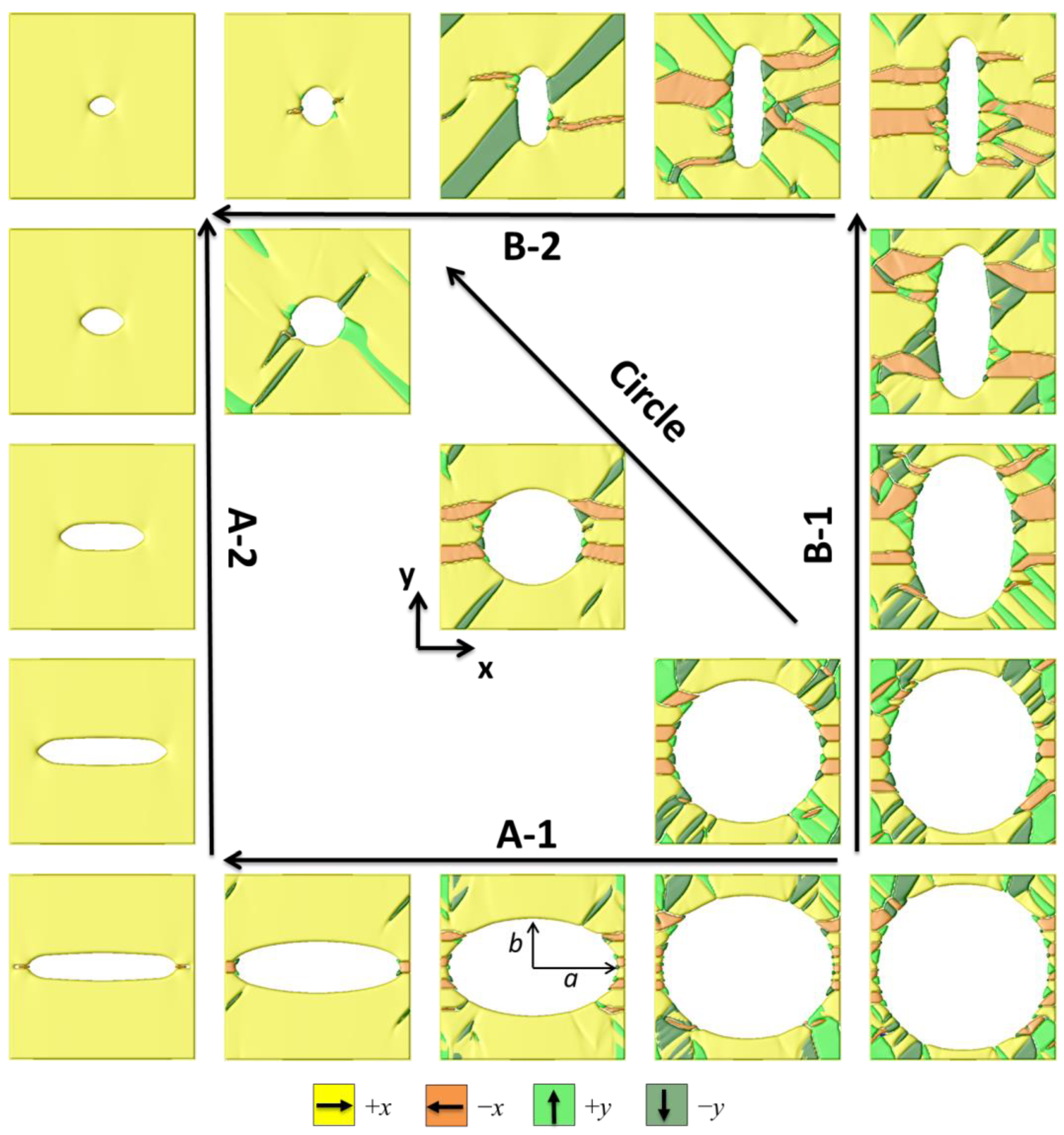
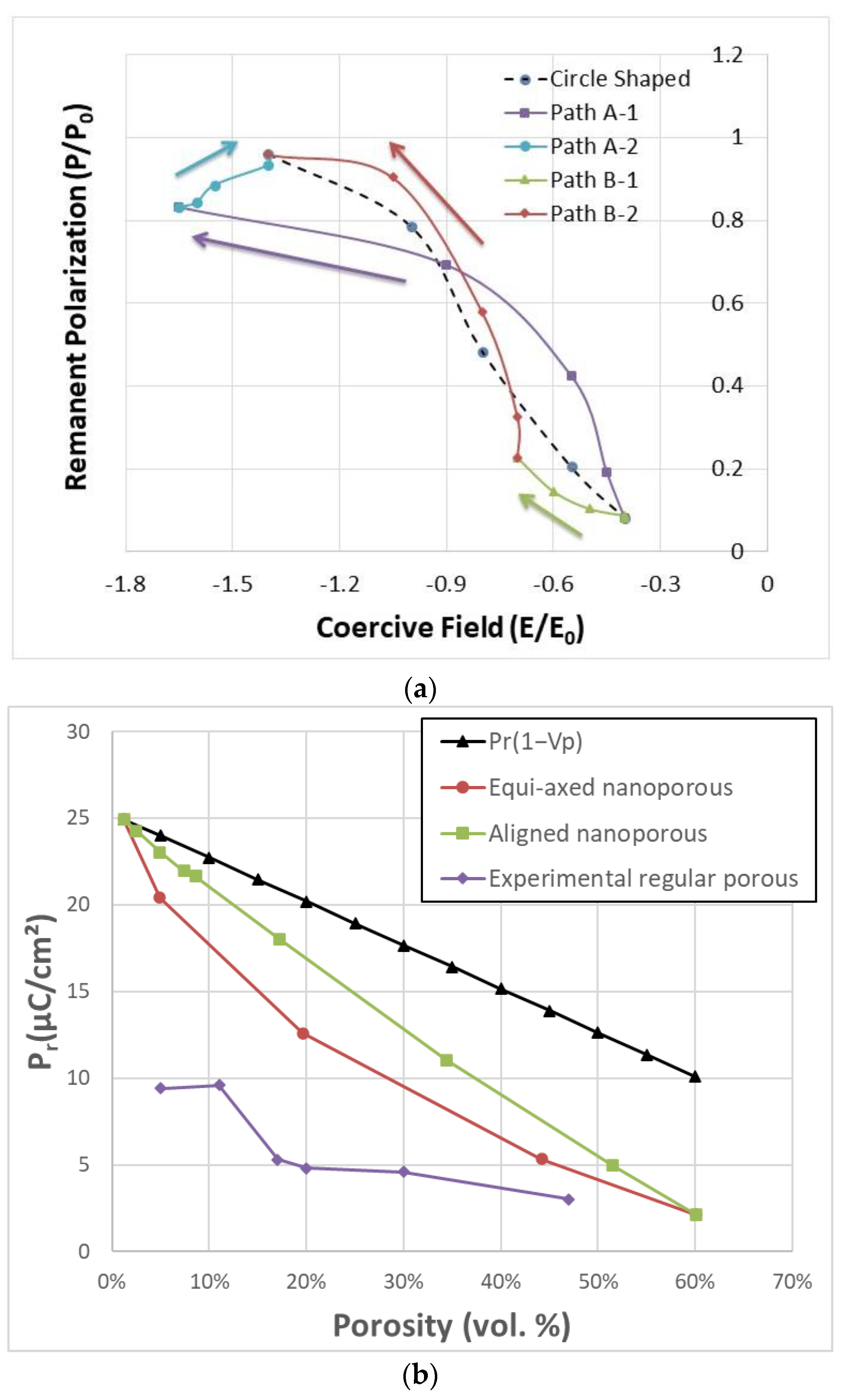
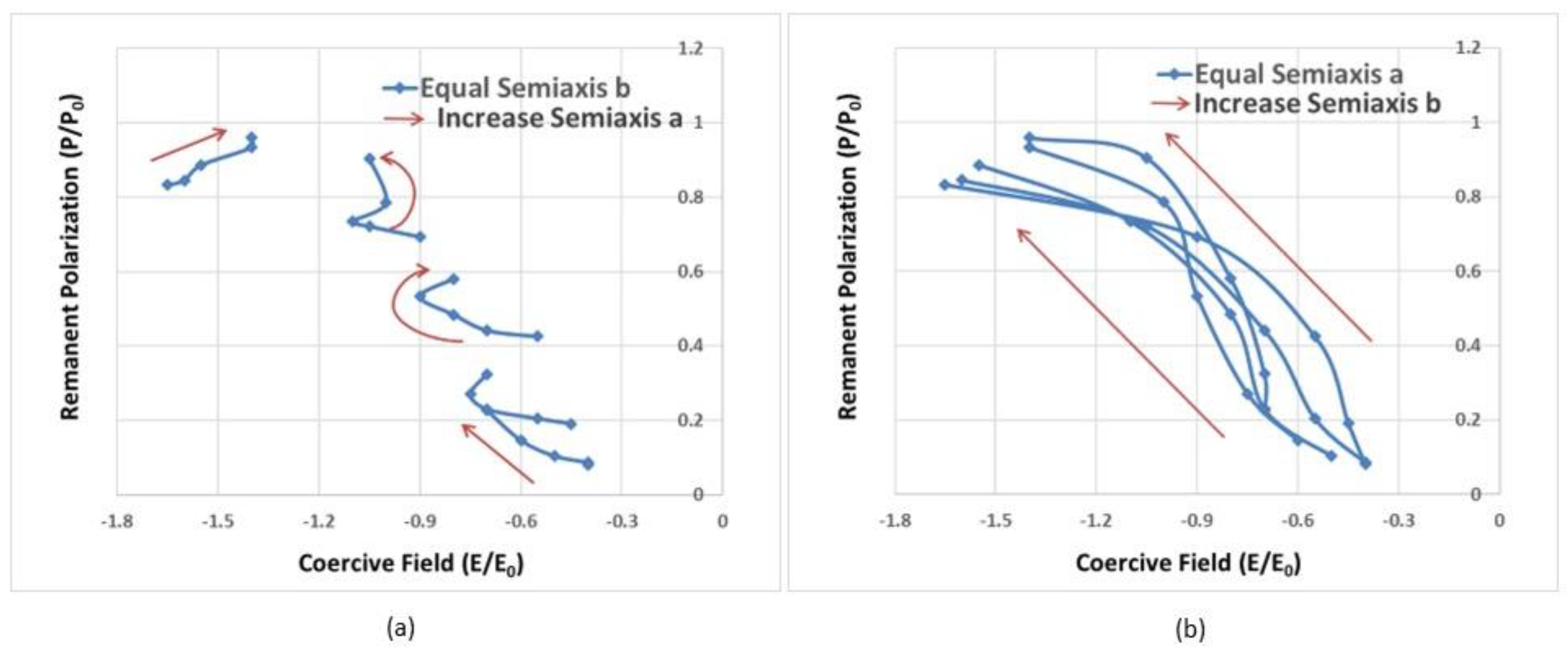
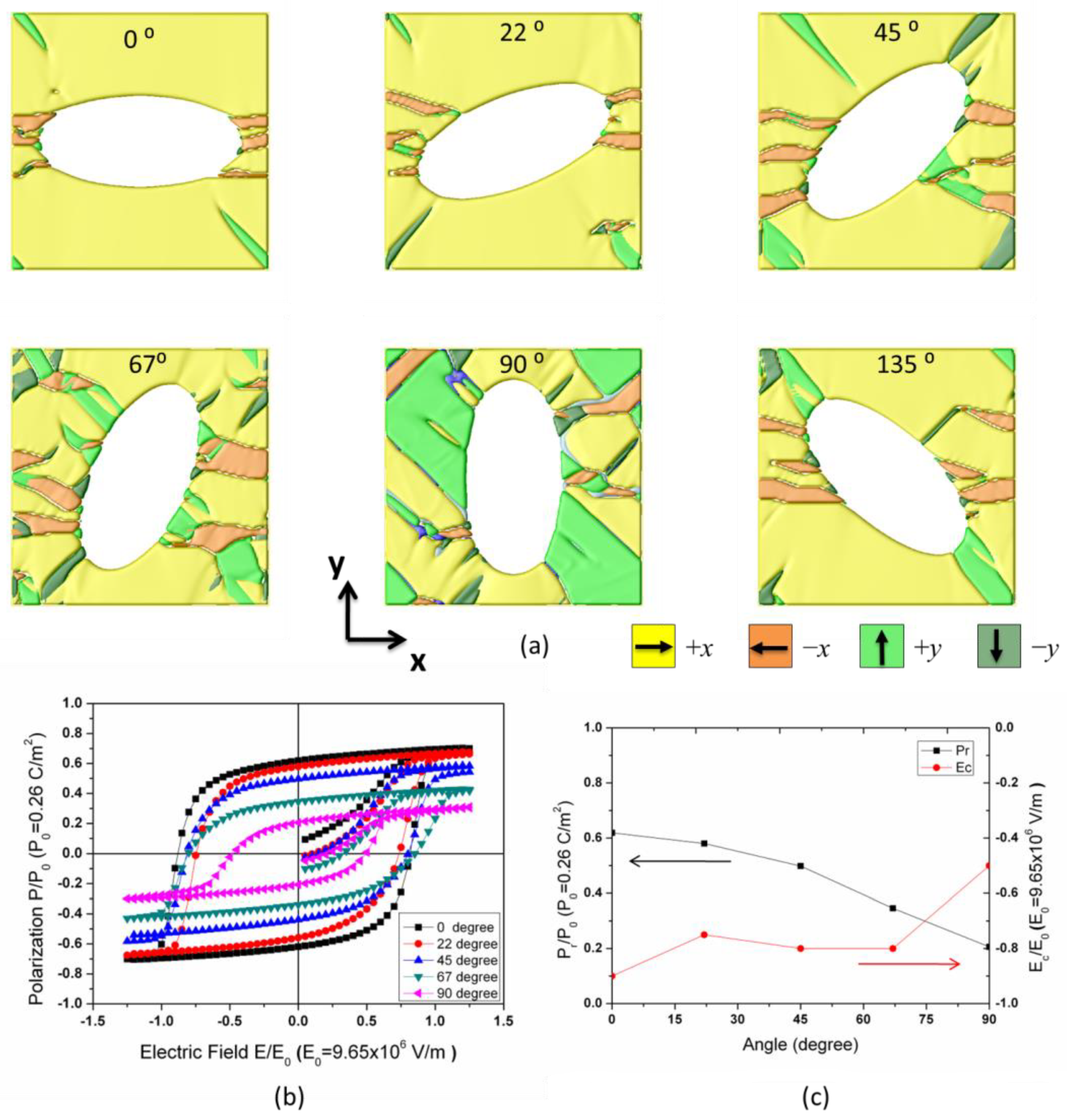
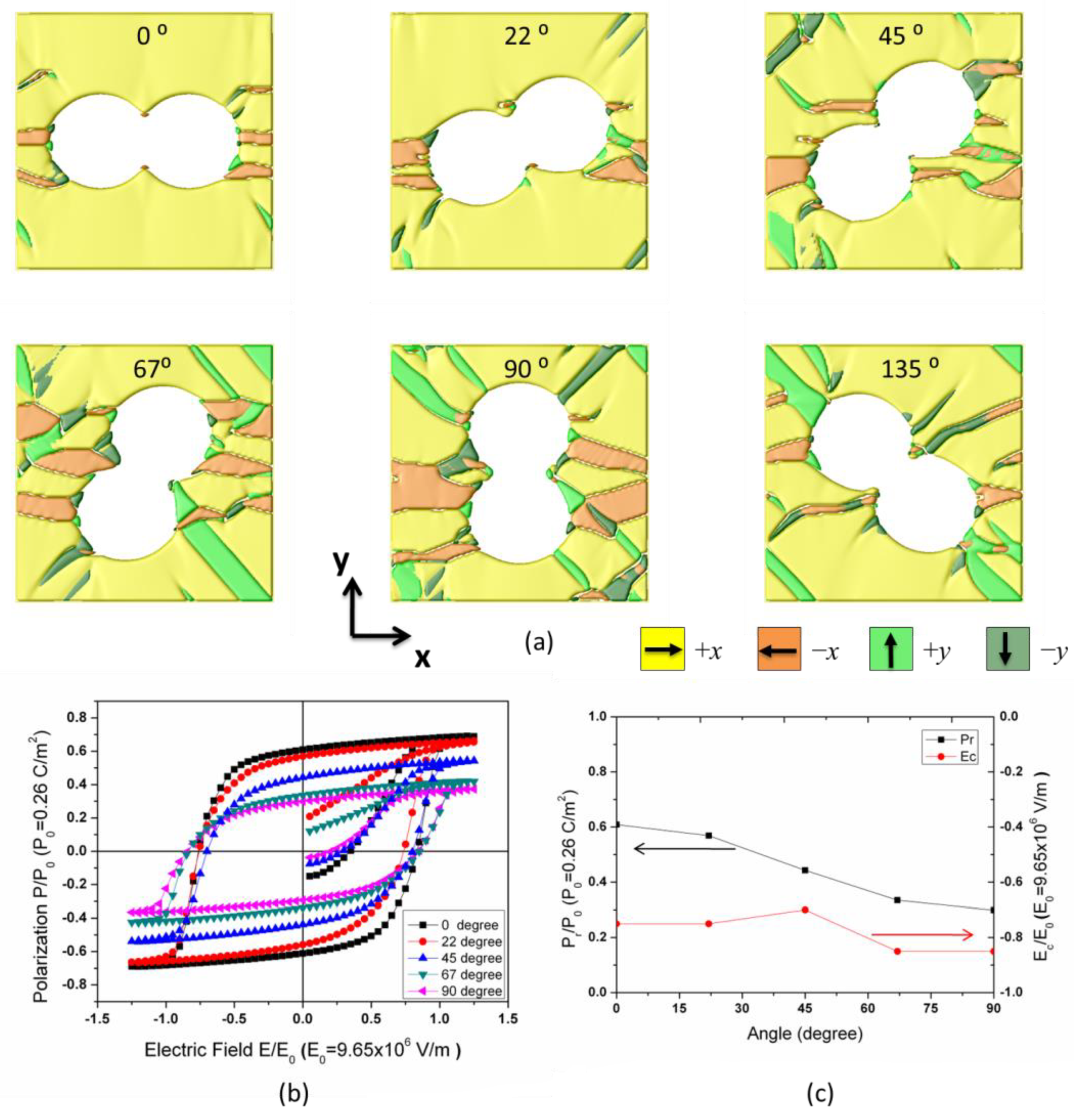
3.1. Hysteresis Loops of Porous Ferroelectrics and the Pr-Ec Diagram
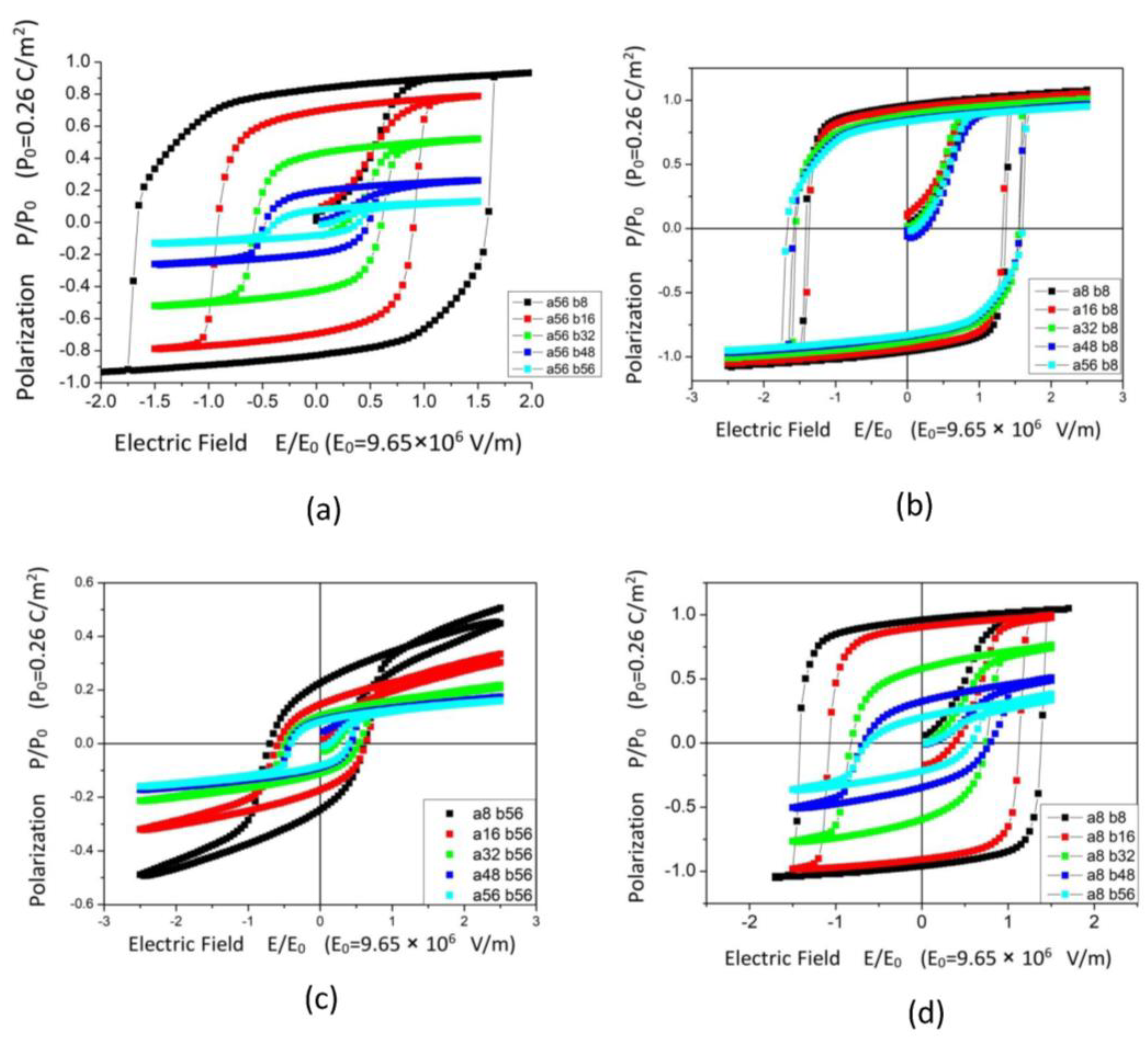
3.2. Design the Hysteresis Loops
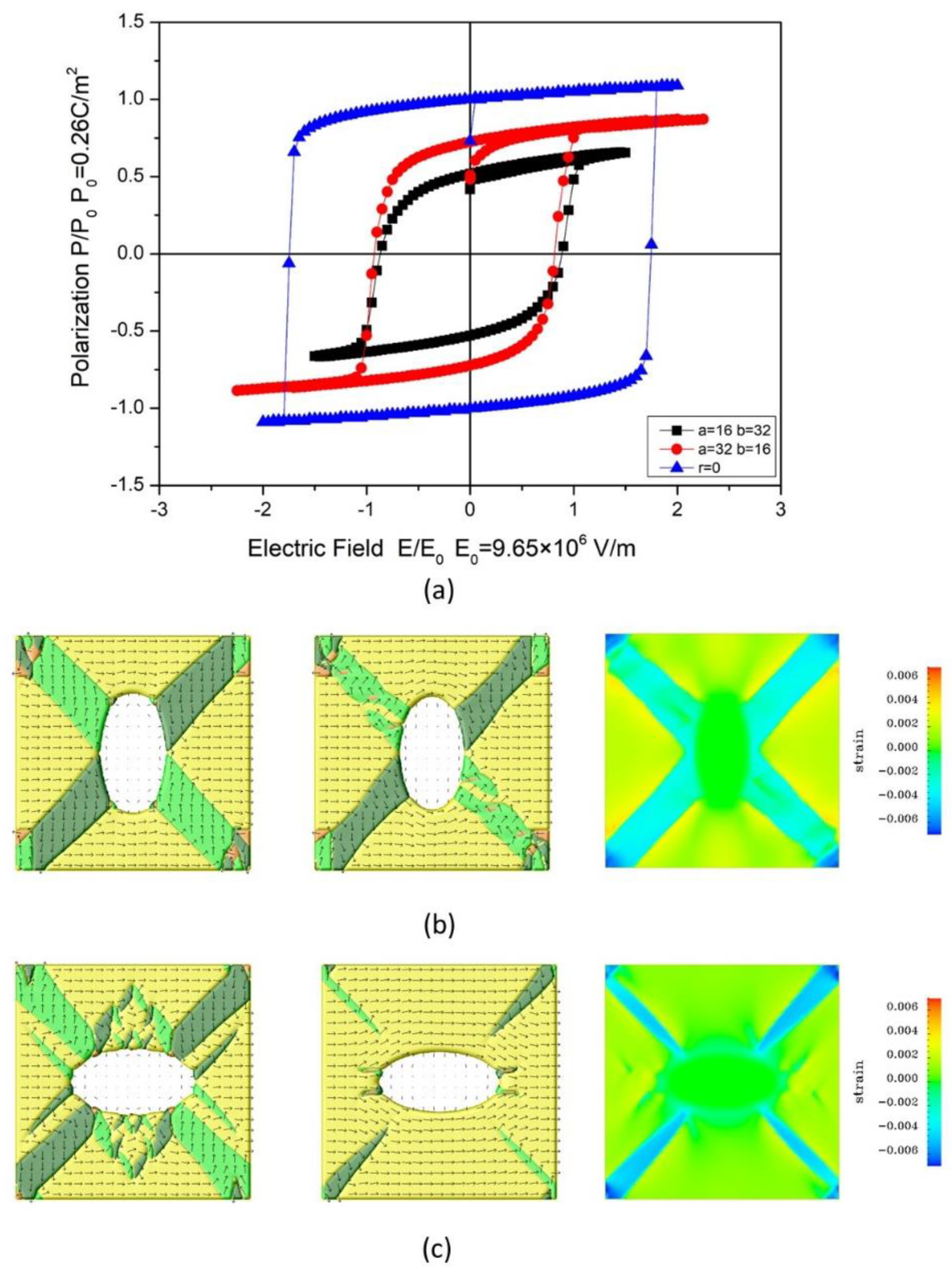
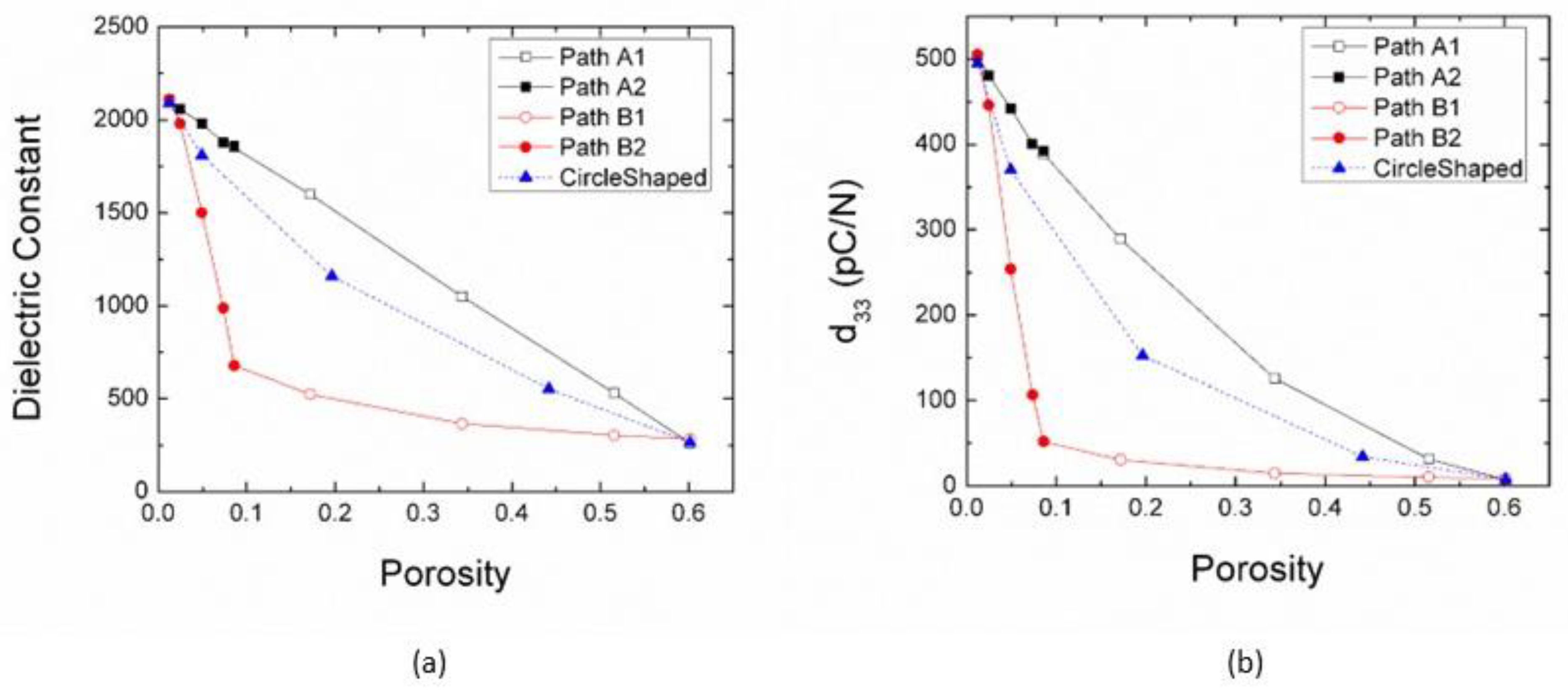
3.3. The Influence on the Dielectric and Piezoelectric Properties
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khachaturyan, R.; Zhukov, S.; Schultheiß, J.; Galassi, C.; Reimuth, C.; Koruza, J.; von Seggern, H.; Genenko, Y.A. Polarization-switching dynamics in bulk ferroelectrics with isometric and oriented anisometric pores. J. Phys. D Appl. Phys. 2017, 50, 045303. [Google Scholar] [CrossRef]
- Curecheriu, L.; Lukacs, V.A.; Padurariu, L.; Stoian, G.; Ciomaga, C.E. Effect of porosity on functional properties of lead-free piezoelectric BaZr0.15Ti0.85O3 porous ceramics. Materials 2020, 13, 3324. [Google Scholar] [CrossRef]
- Martínez-Ayuso, G.; Friswell, M.I.; Haddad Khodaparast, H.; Roscow, J.I.; Bowen, C.R. Electric field distribution in porous piezoelectric materials during polarization. Acta Mater. 2019, 173, 332–341. [Google Scholar] [CrossRef]
- Padurariu, C.; Padurariu, L.; Curecheriu, L.; Ciomaga, C.; Horchidan, N.; Galassi, C.; Mitoseriu, L. Role of the pore interconnectivity on the dielectric, switching and tunability properties of PZTN ceramics. Ceram. Int. 2017, 43, 5767–5773. [Google Scholar] [CrossRef]
- Zhu, S.; Cao, L.; Xiong, Z.; Lu, C.; Gao, Z. Enhanced piezoelectric properties of 3-1 type porous 0.94Bi0.5Na0.5TiO3-0.06BaTiO3 ferroelectric ceramics. J. Eur. Ceram. Soc. 2018, 38, 2251–2255. [Google Scholar] [CrossRef]
- Yap, E.W.; Glaum, J.; Oddershede, J.; Daniels, J.E. Effect of porosity on the ferroelectric and piezoelectric properties of (Ba0.85Ca0.15)(Zr0.1Ti0.9)O3 piezoelectric ceramics. Scr. Mater. 2018, 145, 122–125. [Google Scholar] [CrossRef]
- Gheorghiu, F.; Padurariu, L.; Airimioaei, M.; Curecheriu, L.; Ciomaga, C.; Padurariu, C.; Galassi, C.; Mitoseriu, L. Porosity-dependent properties of Nb-doped Pb(Zr,Ti)O3 ceramics. J. Am. Ceram. Soc. 2017, 100, 647–658. [Google Scholar] [CrossRef]
- Zhang, Y.; Roscow, J.; Lewis, R.; Khanbareh, H.; Topolov, V.Y.; Xie, M.; Bowen, C.R. Understanding the effect of porosity on the polarisation-field response of ferroelectric materials. Acta Mater. 2018, 154, 100–112. [Google Scholar] [CrossRef]
- Yan, M.; Xiao, Z.; Ye, J.; Yuan, X.; Li, Z.; Bowen, C.; Zhang, Y.; Zhang, D. Porous ferroelectric materials for energy technologies: Current status and future perspectives. Energy Environ. Sci. 2021, 14, 6158–6190. [Google Scholar] [CrossRef]
- Zhang, Y.; Bowen, C.R.; Ghosh, S.K.; Mandal, D.; Khanbareh, H.; Arafa, M.; Wan, C. Ferroelectret materials and devices for energy harvesting applications. Nano Energy 2019, 57, 118–140. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, N.; Ola, O.; Xia, Y.; Zhu, Y. Porous ceramics: Light in weight but heavy in energy and environment technologies. Mater. Sci. Eng. R Rep. 2021, 143, 100589. [Google Scholar] [CrossRef]
- Xu, T.; Wang, C.-A. Control of pore size and wall thickness of 3-1 type porous PZT ceramics during freeze-casting process. Mater. Des. 2016, 91, 242–247. [Google Scholar] [CrossRef]
- Mercadelli, E.; Galassi, C. How to Make Porous Piezoelectrics? Review on Processing Strategies. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2021, 68, 217–228. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Wu, Q.; Zhang, C.; Li, Y.; Nie, M.; Wang, Q.; Liu, Y. Porosity manipulation to boost piezoelectric output via supercritical carbon dioxide foaming and surface modification. Mater. Des. 2022, 217, 110616. [Google Scholar] [CrossRef]
- Wang, J.; Wylie-van Eerd, B.; Sluka, T.; Sandu, C.; Cantoni, M.; Wei, X.K.; Kvasov, A.; McGilly, L.J.; Gemeiner, P.; Dkhil, B.; et al. Negative-pressure-induced enhancement in a freestanding ferroelectric. Nat. Mater. 2015, 14, 985–990. [Google Scholar] [CrossRef]
- Kvasov, A.; McGilly, L.J.; Wang, J.; Shi, Z.; Sandu, C.S.; Sluka, T.; Tagantsev, A.K.; Setter, N. Piezoelectric enhancement under negative pressure. Nat. Commun. 2016, 7, 12136. [Google Scholar] [CrossRef]
- Ferreira, P.; Hou, R.Z.; Wu, A.; Willinger, M.G.; Vilarinho, P.M.; Mosa, J.; Laberty-Robert, C.; Boissière, C.; Grosso, D.; Sanchez, C. Nanoporous piezo- and ferroelectric thin films. Langmuir 2012, 28, 2944–2949. [Google Scholar] [CrossRef]
- Matavž, A.; Bradeško, A.; Rojac, T.; Malič, B.; Bobnar, V. Self-assembled porous ferroelectric thin films with a greatly enhanced piezoelectric response. Appl. Mater. Today 2019, 16, 83–89. [Google Scholar] [CrossRef]
- Castro, A.; Ferreira, P.; Rodriguez, B.J.; Vilarinho, P.M. The role of nanoporosity on the local piezo and ferroelectric properties of lead titanate thin films. J. Mater. Chem. C 2015, 3, 1035–1043. [Google Scholar] [CrossRef]
- Chen, F.; Yang, C.; An, Z.; Zhang, X.; Zhou, T.; Chen, N. Direct-ink-writing of multistage-pore structured energy collector with ultrahigh ceramic content and toughness. Mater. Des. 2022, 217, 110652. [Google Scholar] [CrossRef]
- Vorotyntsev, D.A.; Vishnevskiy, A.S.; Seregin, D.S.; Sigov, A.S.; Vorotilov, K.A. Temperature evolution of pore structure in ferroelectric PZT films prepared by molecular self-assembly. J. Adv. Dielectr. 2025, 15, 2550008. [Google Scholar] [CrossRef]
- Suzuki, N.; Osada, M.; Billah, M.; Alothman, Z.A.; Bando, Y.; Yamauchi, Y.; Hossain, M.S. Origin of thermally stable ferroelectricity in a porous barium titanate thin film synthesized through block copolymer templating. APL Mater. 2017, 5, 076111. [Google Scholar] [CrossRef]
- Stancu, V.; Lisca, M.; Boerasu, I.; Pintilie, L.; Kosec, M. Effects of porosity on ferroelectric properties of Pb(Zr0.2Ti0.8)O3 films. Thin Solid Film. 2007, 515, 6557–6561. [Google Scholar] [CrossRef]
- Billah, M.; Terasawa, Y.; Masud, M.K.; Asahi, T.; Hegazy, M.B.Z.; Nagata, T.; Chikyow, T.; Uesugi, F.; Hossain, M.S.A.; Yamauchi, Y. Giant piezoresponse in nanoporous (Ba,Ca)(Ti,Zr)O3 thin film. Chem. Sci. 2024, 15, 9147–9154. [Google Scholar] [CrossRef] [PubMed]
- Delimova, L.; Seregin, D.; Orlov, G.; Zaitseva, N.; Gushchina, E.; Sigov, A.; Vorotilov, K. Porous PZT films: How can we tune electrical properties? Materials 2023, 16, 5171. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Zhou, K.; Zhang, D.; Bowen, C.; Wang, Q.; Zhong, J.; Zhang, Y. Perspective on porous piezoelectric ceramics to control internal stress. Nanoenergy Adv. 2022, 2, 269–290. [Google Scholar] [CrossRef]
- Roscow, J.I.; Pearce, H.; Khanbareh, H.; Kar-Narayan, S.; Bowen, C.R. Modified energy harvesting figures of merit for stress- and strain-driven piezoelectric systems. EPJ Spec. Top. 2019, 228, 1537–1554. [Google Scholar] [CrossRef]
- Huang, J.; Tan, P.; Wang, F.; Li, B. Ferroelectric memory based on topological domain structures: A phase field simulation. Crystals 2022, 12, 786. [Google Scholar] [CrossRef]
- Hou, X.; Li, H.; Shimada, T.; Kitamura, T.; Wang, J. Effect of geometric configuration on the electrocaloric properties of nanoscale ferroelectric materials. J. Appl. Phys. 2018, 123, 124101. [Google Scholar] [CrossRef]
- Chen, H.; Hou, X.; Chen, J.; Chen, S.; Hu, P.; Wu, H.; Wang, J.; Zhu, J. Large electrostrain induced by reversible domain switching in ordered ferroelectric nanostructures with optimized geometric configurations. Nanotechnology 2020, 31, 335714. [Google Scholar] [CrossRef]
- Ma, L.L.; Ji, Y.; Chen, W.J.; Liu, J.Y.; Liu, Y.L.; Wang, B.; Zheng, Y. Direct electrical switching of ferroelectric vortices by a sweeping biased tip. Acta Mater. 2018, 158, 23–37. [Google Scholar] [CrossRef]
- Zhou, M.-J.; Yang, T.; Wang, J.-J.; Ren, Z.; Chen, L.-Q.; Nan, C.-W. Nanopore-induced dielectric and piezoelectric enhancement in PbTiO$_3$ nanowires. Acta Mater. 2020, 187, 146–152. [Google Scholar] [CrossRef]
- Wang, J.-J.; Wang, B.; Chen, L.-Q. Understanding, predicting, and designing ferroelectric domain structures and switching guided by the phase-field method. Annu. Rev. Mater. Res. 2019, 49, 127–152. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, P.; Du, L.; Du, H. Effect of the nanopore on ferroelectric domain structures and switching properties. Comput. Mater. Sci. 2018, 148, 216–223. [Google Scholar] [CrossRef]
- Xie, C.; Zhao, H.; Du, L.; Du, H.; Wu, P. Enhanced ferroelectricity for nanoporous barium titanate: A phase-field prediction. Philos. Mag. Lett. 2021, 101, 341–352. [Google Scholar] [CrossRef]
- Van Lich, L.; Shimada, T.; Wang, J.; Kitamura, T. Self-ordering of nontrivial topological polarization structures in nanoporous ferroelectrics. Nanoscale 2017, 9, 15525–15533. [Google Scholar] [CrossRef] [PubMed]
- Kargupta, R.; Venkatesh, T. Electromechanical response of porous piezoelectric materials. Acta Mater. 2006, 54, 4063–4078. [Google Scholar] [CrossRef]
- Li, Y.; Cross, L.; Chen, L. A phenomenological thermodynamic potential for BaTiO3 single crystals. J. Appl. Phys. 2005, 98, 064101. [Google Scholar] [CrossRef]
- Merz, W.J. Domain Formation and Domain Wall Motions in Ferroelectric BaTiO3 Single Crystals. Phys. Rev. 1954, 95, 690–698. [Google Scholar] [CrossRef]
- Lines, M.E.; Glass, A.M. Principles and Applications of Ferroelectrics and Related Materials; Oxford University Press: New York, NY, USA, 2001. [Google Scholar]
- Geng, L.D.; Jin, Y.M.; Tan, D.Q.; Wang, Y.U. Computational study of nonlinear dielectric composites with field-induced antiferroelectric-ferroelectric phase transition. J. Appl. Phys. 2018, 124, 164109. [Google Scholar] [CrossRef]
- Lukacs, V.A.; Stanculescu, R.; Curecheriu, L.; Ciomaga, C.E.; Horchidan, N.; Cioclea, C.; Mitoseriu, L. Structural and Functional Properties of BaTiO3 Porous Ceramics Produced by Using Pollen as Sacrificial Template. Ceram. Int. 2020, 46, 523–530. [Google Scholar] [CrossRef]
- Jo, J.Y.; Kim, Y.S.; Noh, T.W.; Yoon, J.-G.; Song, T.K. Coercive Fields in Ultrathin BaTiO3 Capacitors. Appl. Phys. Lett. 2006, 89, 232909. [Google Scholar] [CrossRef]
- Sheeraz, M.; Tran, V.D.; Jo, Y.J.; Kim, G.; Cho, S.; Sohn, C.; Kim, I.W.; Shin, Y.H.; Ahn, C.W.; Kim, T.H. Defect Engineering of Ferroelectric Hysteresis in Lead-Free Bi1/2(Na,K)1/2TiO3 Thin Films. ACS Appl. Electron. Mater. 2024, 6, 8328–8338. [Google Scholar] [CrossRef]
- Shen, Z.-Y.; Li, J.-F. Enhancement of Piezoelectric Constant d33 in BaTiO3 Ceramics due to Nano-Domain Structure. J. Ceram. Soc. Jpn. 2010, 118, 940–943. [Google Scholar] [CrossRef]
- Zhang, G.J.; Yang, J.F.; Ohji, T. Fabrication of porous ceramics with unidirectionally aligned continuous pores. J. Am. Ceram. Soc. 2001, 84, 1395–1397. [Google Scholar] [CrossRef]
- Guo, Y.; Peng, B.; Qiu, R.; Dong, G.; Yao, Y.; Zhao, Y.; Zhou, Z.; Liu, M. Self-Rolling-up Enabled Ultrahigh-Density Information Storage in Freestanding Single-Crystalline Ferroic Oxide Films. Adv. Funct. Mater. 2023, 33, 2213668. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Yang, F.; Du, L.; Wang, J.; Liang, Y.; Wu, P. Hysteresis Loops Design for Nanoporous Ferroelectrics. Materials 2025, 18, 3606. https://doi.org/10.3390/ma18153606
Huang X, Yang F, Du L, Wang J, Liang Y, Wu P. Hysteresis Loops Design for Nanoporous Ferroelectrics. Materials. 2025; 18(15):3606. https://doi.org/10.3390/ma18153606
Chicago/Turabian StyleHuang, Xuan, Fengjuan Yang, Lifei Du, Jiong Wang, Yongfeng Liang, and Pingping Wu. 2025. "Hysteresis Loops Design for Nanoporous Ferroelectrics" Materials 18, no. 15: 3606. https://doi.org/10.3390/ma18153606
APA StyleHuang, X., Yang, F., Du, L., Wang, J., Liang, Y., & Wu, P. (2025). Hysteresis Loops Design for Nanoporous Ferroelectrics. Materials, 18(15), 3606. https://doi.org/10.3390/ma18153606




