Predicting the Uniaxial Compressive Strength of Cement Paste: A Theoretical and Experimental Study
Abstract
1. Introduction
1.1. Background and Significance of Cement Paste Strength
1.2. Review of Existing Strength Models for Cementitious Materials
1.3. Research Objectives and Scope
- To develop a theoretical and experimental model for the uniaxial compressive strength of pure cement paste, grounded in the hypothesis that strength is directly proportional to the volumetric density of hydration products. While the fundamental concept of strength–density correlation has roots in classical theories [33,34], our novelty lies in developing a pragmatic yet physically meaningful model that integrates readily measurable parameters (such as paste density) with a refined mechanistic understanding to provide highly accurate predictions across diverse cementitious systems, particularly pure cement pastes. The water–cement ratio will serve as the primary input variable in the initial formulation.
- To extend the model to include the effects of mineral admixtures, with a specific focus on fine powders introduced via aggregate systems (e.g., limestone powder, granite powder). These materials will be treated as functional components that influence hydration kinetics, filler packing, and the resulting microstructure.
- To incorporate curing conditions and age into the model, capturing the effects of environmental variables such as temperature, humidity, and curing duration. These parameters are essential to accurately represent hydration progression and microstructural densification over time.
2. Theoretical Framework for Strength Prediction of Pure Cement Paste
2.1. Fundamental Hypothesis: Strength–Microstructural Compactness Relationship
- Reduced Porosity: Lower total and connected pore volumes diminish stress concentration sites, consequently increasing the effective load-bearing solid area.
- Improved Solid-Phase Continuity: A more interconnected C–S–H network facilitates more efficient internal stress transfer throughout the material under applied loads.
- Suppressed Defect Formation: Denser microstructures inherently inhibit the formation and propagation of critical flaws, such as large pores or microcracks, which often trigger premature failure [27].
2.2. Model for Pure Cement Paste Strength
2.3. Extension for Mineral Admixtures
- Dilution effects due to partial cement replacement by less reactive materials;
- Filler and packing effects through improved particle dispersion and reduced effective porosity;
- Entrapped air, which lowers actual density and weakens microstructural continuity.
3. Materials and Experimental Methods
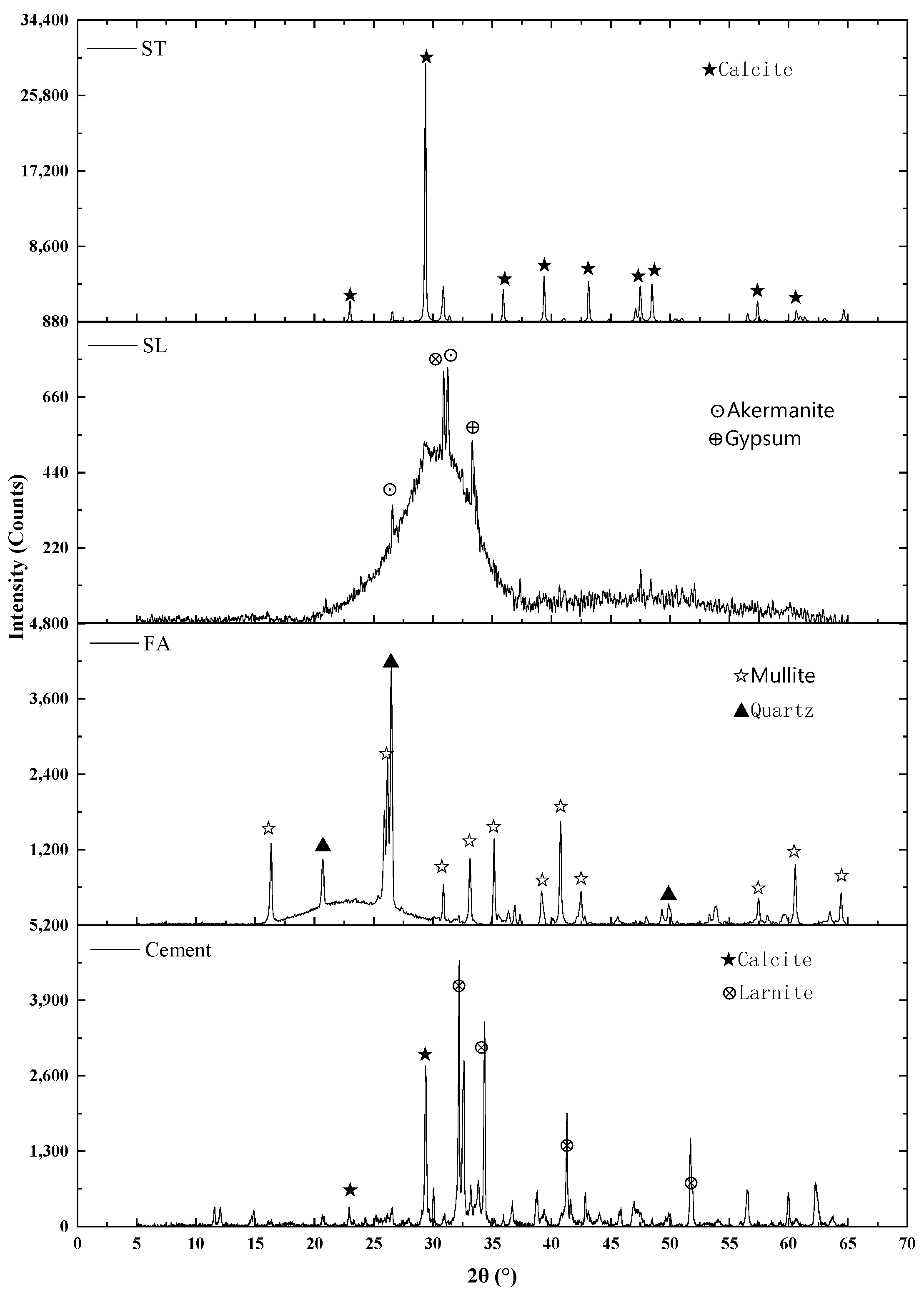
3.1. Cementitious Materials
3.2. Mix Proportions and Specimen Preparation
3.3. Experimental Setup and Visual Documentation
3.4. Cement Pastes with Mineral Additives
4. Results and Analysis
4.1. Strength of Pure Cement Paste
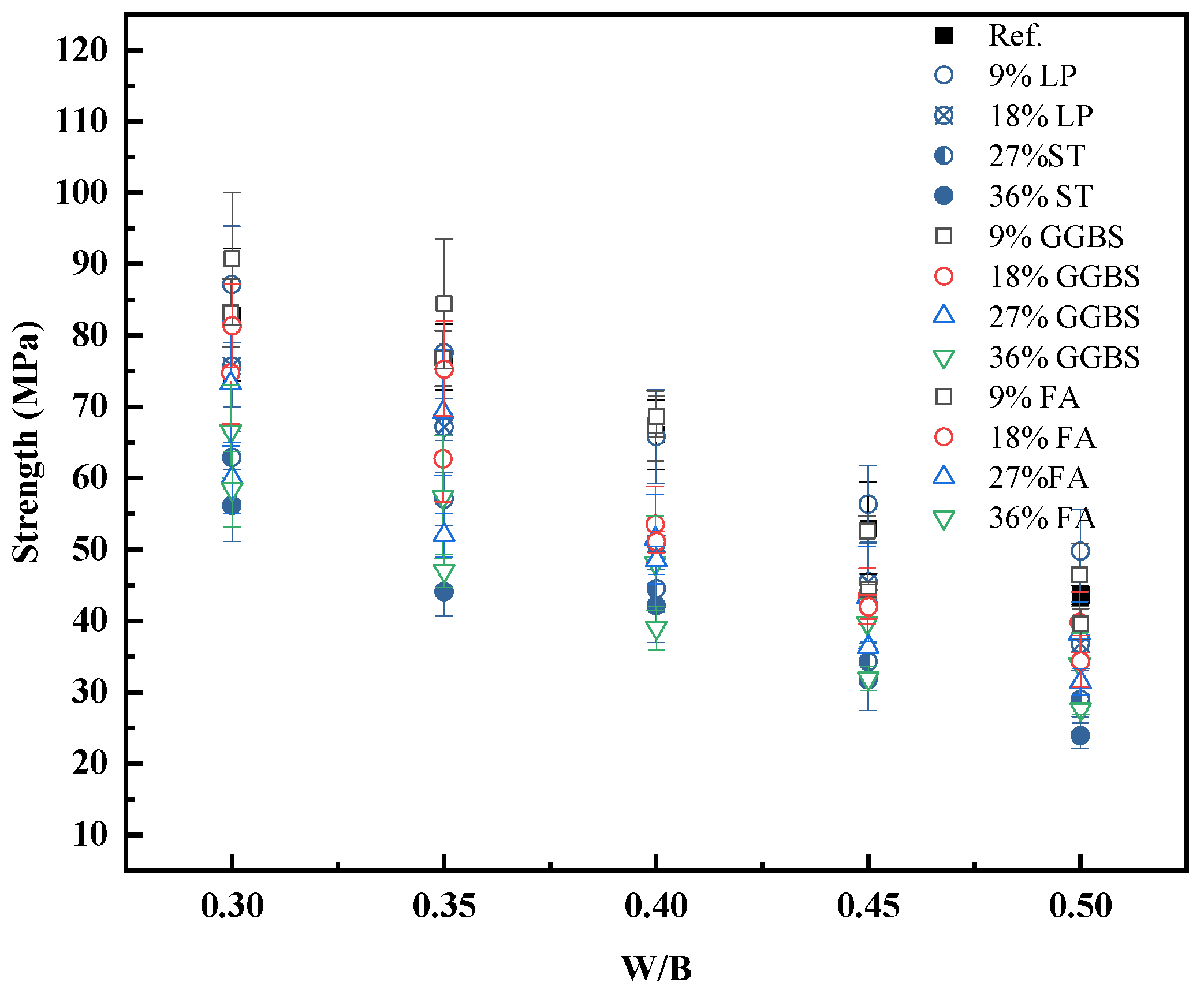
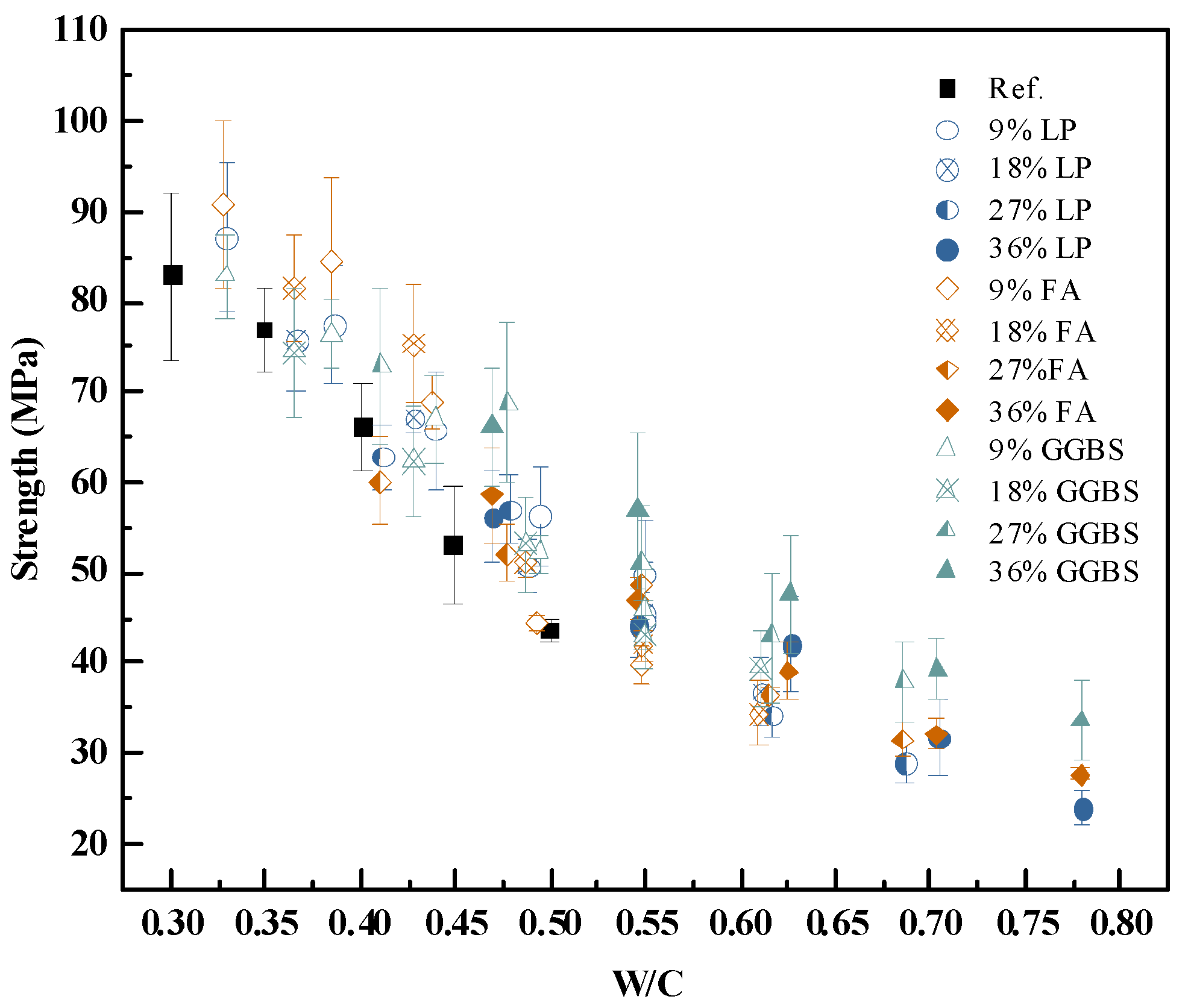
4.2. Influence of Mineral Additives on Strength
5. Conclusions and Outlook
- For pure cement pastes, compressive strength is highly correlated with the water-to-cement ratio (w/c). A semi-empirical model based on paste density and theoretical packing (Equation (5)) was proposed and verified, with a determination coefficient R2 = 0.97.
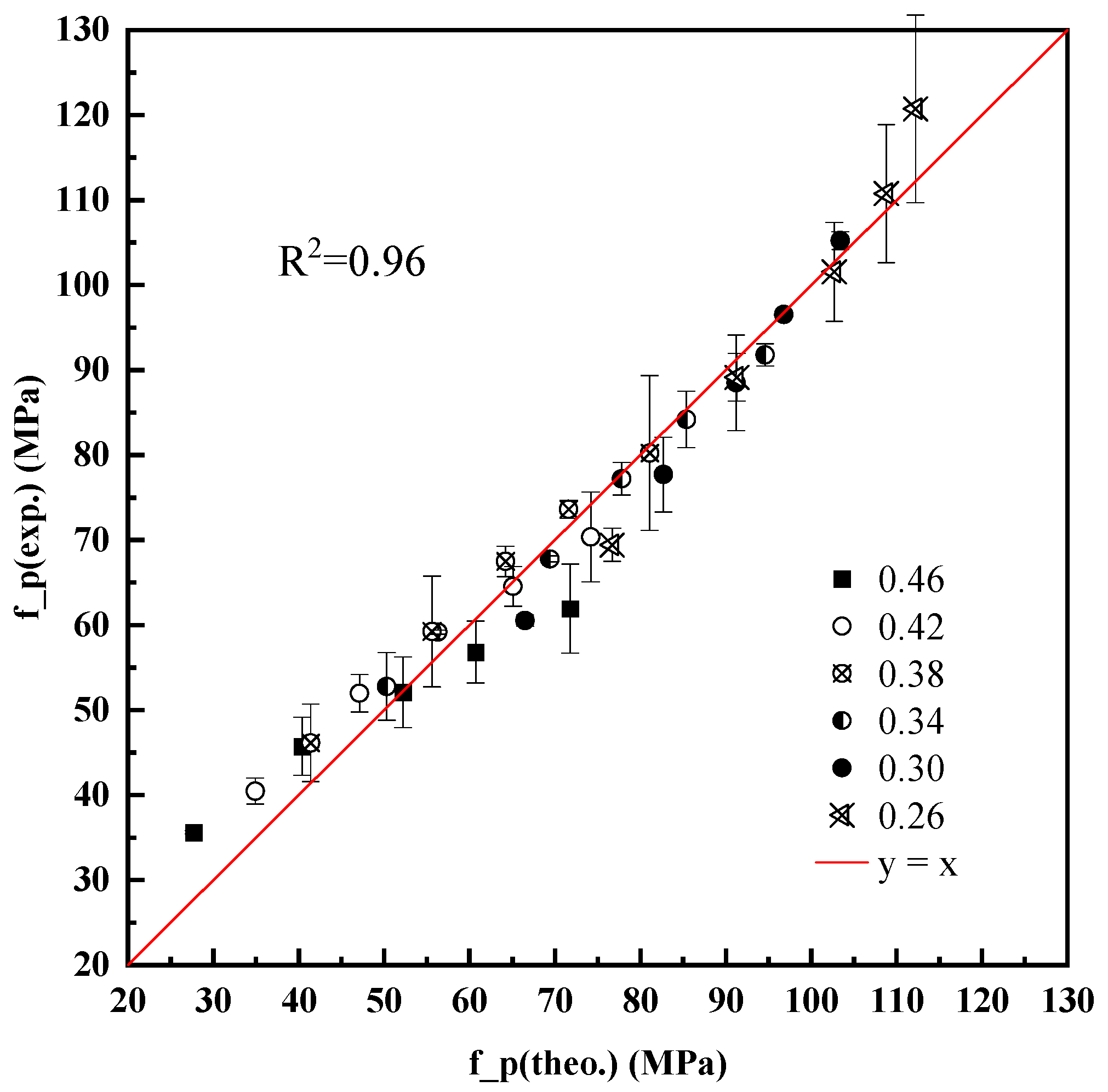
- Strength development over time was modeled using the degree of hydration calculated via an equivalent age approach. This hydration-informed model (Equation (10)) demonstrated excellent agreement with experimental data over multiple curing ages (from 3 to 90 days), with R2 = 0.96.
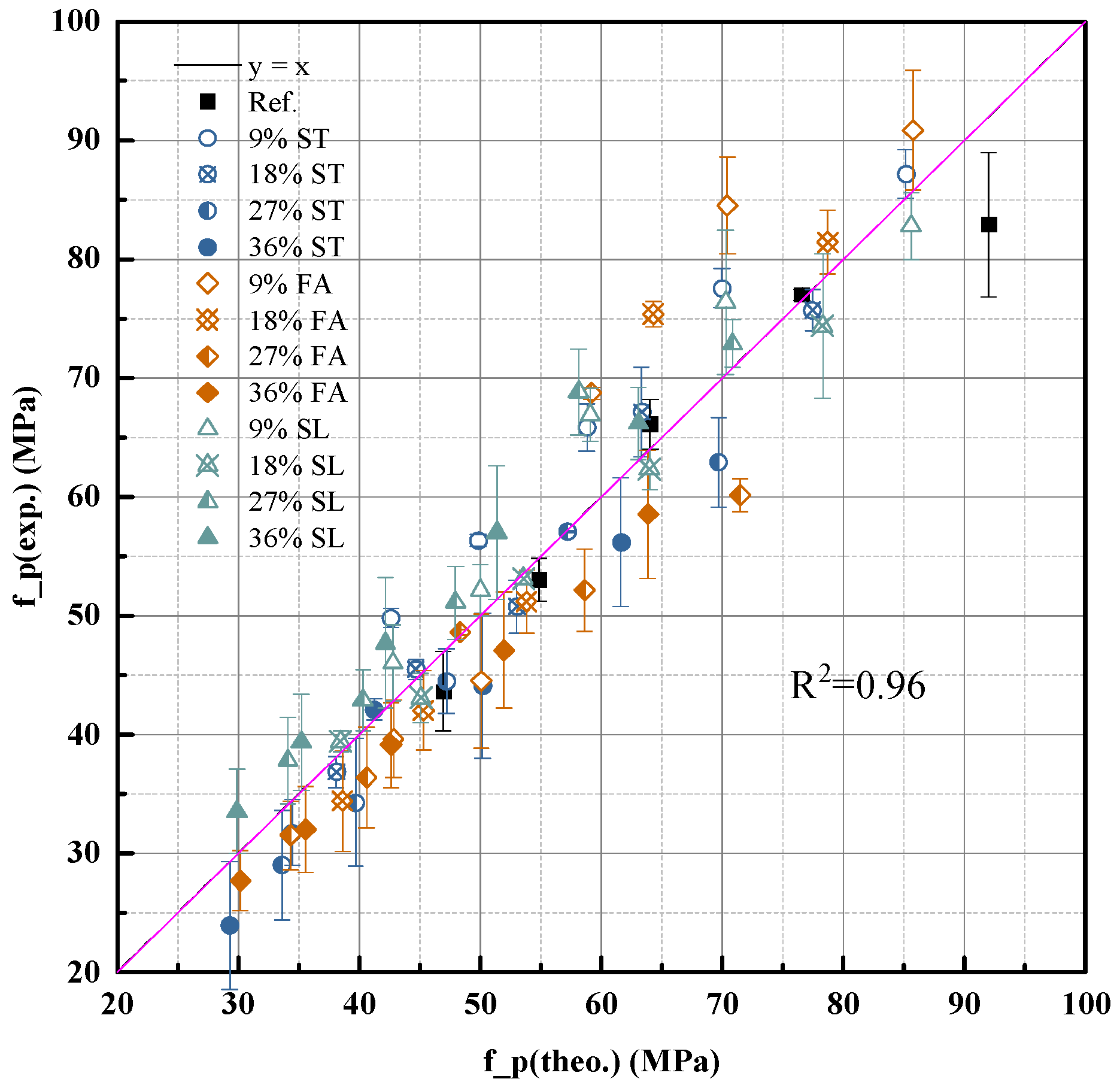
- Mineral additives (fly ash, slag, limestone powder) affect strength primarily through physical filler and dilution effects at early ages. Their influence can be accurately captured by correcting the w/c ratio using measured paste density.
- A density-corrected water–cement ratio was introduced and validated, enabling a unified expression (Equation (11)) that predicts the strength of blended cement pastes with high accuracy using only measurable mix parameters and hydration degree.
- The final model accommodates variation in curing temperature and time, enabling strength prediction across curing conditions by adjusting hydration degree.
- The primary novelty of this research lies in developing a pragmatic yet physically grounded strength prediction model that unifies the effects of diverse mineral additives, including aggregate-derived fines, through a density-corrected water-to-cement ratio. This approach offers a significant advancement over traditional empirical models and computationally intensive microstructural simulations by providing high predictive accuracy with readily measurable parameters, thus enhancing applicability for practical mix design and early-age strength assessment.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xiao, J.; Zou, S.; Poon, C.-S.; Sham, M.L.; Li, Z.; Shah, S.P. We use 30 billion tonnes of concrete each year—here’s how to make it sustainable. Nature 2025, 638, 888–890. [Google Scholar] [CrossRef]
- Yao, X.; Xi, J.; Guan, J.; Wen, L.; Liu, L.; Shangguan, L.; Xu, Z. Experimental study on macro–micro-structural properties and strength prediction model of wastewater concrete. J. Sustain. Cem.-Based Mater. 2023, 13, 577–597. [Google Scholar] [CrossRef]
- Xie, X.; Fan, J.; Guo, P.; Huang, H.; Hu, J.; Wei, J. Composition Design and Fundamental Properties of Ultra-High-Performance Concrete Based on a Modified Fuller Distribution Model. Materials 2023, 16, 700. [Google Scholar] [CrossRef]
- ASTM C109; Standard Test Method for Compressive Strength of Hydraulic Cement Mortars. ASTM International: West Conshohocken, PA, USA, 2024.
- Prongmanee, N.; Noulmanee, A.; Suppaso, T. Rapid, graded sand preparation method using grain size distribution results for cement mortar testing. Can. J. Civ. Eng. 2024, 51, 1023–1040. [Google Scholar] [CrossRef]
- EN 196-1; Methods of Testing Cement—Part 1: Determination of Strength. Comité Européen de Normalisation: Brussels, Belgium, 2016.
- Tassos, C.; Sideris, K.K.; Chatzopoulos, A.; Tzanis, E.; Katsiotis, M.S. Influence of the Type of Cement on the Durability of Concrete Structures Exposed to Various Carbonation Environments in Greece: A Contribution to the Sustainability of Structures. Constr. Mater. 2023, 3, 14–35. [Google Scholar] [CrossRef]
- GB/T 17671; Test Method of Cement Mortar Strength (ISO Method). Standardization Administration of China (SAC): Beijing, China, 2021.
- Zhang, C.; Chen, M.; Liu, R.; Li, X.; Yan, J.; Zhu, Z.; Fan, F. Synergistic Effect of PVA Fiber and PTB Emulsion on Mechanical Properties of Cementitious Composites for Damage Repair in Operating Tunnels. KSCE J. Civ. Eng. 2022, 26, 5222–5239. [Google Scholar] [CrossRef]
- Abebe, D. Comparative Analysis of Selected Concrete Mix Design Methods Based on Cost-Effectiveness. Adv. Civ. Eng. 2022, 2022, 4240774. [Google Scholar]
- Abrams, D.A. Design of Concrete Mixtures; Structural Materials Research Laboratory, Lewis Institute: Chicago, IL, USA, 1919; Volume 1. [Google Scholar]
- Powers, T.C. The Physical Structure and Engineering Properties of Concrete; Portland Cement Association: Washington, DC, USA, 1958. [Google Scholar]
- Wang, H.; Li, P.; An, X.; Wang, D.; Ji, G. The evolution of microstructure and compressive strength of self-compacting concrete affected by early-age loading: Experiments and multi-scale coupling model. Constr. Build. Mater. 2025, 482, 141614. [Google Scholar] [CrossRef]
- Gilkey, H.J. Water-Cement Ratio Versus Strength-Another Look. J. Proc. 1961, 57, 1287–1312. [Google Scholar]
- Stock, A.F.; Hannantt, D.J.; Williams, R.I.T. The effect of aggregate concentration upon the strength and modulus of elasticity of concrete. Mag. Concr. Res. 1979, 31, 225–234. [Google Scholar] [CrossRef]
- Kaplan, M.F. In Flexural and Compressive Strength of Concrete as Affected by the Properties of Coarse Aggregates. J. Proc. 1959, 55, 1193–1208. [Google Scholar]
- Wang, X.; Park, K. Analysis of the compressive strength development of concrete considering the interactions between hydration and drying. Cem. Concr. Res. 2017, 102, 1–15. [Google Scholar] [CrossRef]
- Larrard, F. Concrete Mixture Proportioning: A Scientific Approach; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Han, W. Mechanical Properties of Cement Paste-Aggregate Interface Based on Microhardness of Interface Transition Zone. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2021. [Google Scholar]
- Belie, N.D.; Soutsos, M.; Gruyaert, E. Properties of Fresh and Hardened Concrete Containing Supplementary Cementitious Materials: State-of-the-Art Report of the RILEM Technical Committee 238-SCM, Working Group 4; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Atiş, C.D. High volume fly ash abrasion resistant concrete. J. Mater. Civ. Eng. 2002, 14, 274–277. [Google Scholar] [CrossRef]
- Ferraris, C.F.; Obla, K.H.; Hill, R.L. The influence of mineral admixtures on the rheology of cement paste and concrete. Cem. Concr. Res. 2001, 31, 245–255. [Google Scholar] [CrossRef]
- Scrivener, K.L.; Crumbie, A.K.; Laugesen, P. The Interfacial Transition Zone (ITZ) Between Cement Paste and Aggregate in Concrete. Interface Sci. 2004, 12, 411–421. [Google Scholar] [CrossRef]
- Wu, K.; Zhang, D.; Zhang, X.; Yao, W. The transformation and development of concrete materials—Study on the sixth component of concrete. J. Build. Mater. 2000, 1, 21–25. [Google Scholar]
- Maekawa, K. Multi-Scale Modeling of Structural Concrete; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Bentz, D.P.; Garboczi, E.J. Modelling the leaching of calcium hydroxide from cement paste: Effects on pore space percolation and diffusivity. Mater. Struct. 1992, 25, 523–533. [Google Scholar] [CrossRef]
- Jennings, H.M. A model for the microstructure of calcium silicate hydrate in cement paste. Cem. Concr. Res. 2000, 30, 101–116. [Google Scholar] [CrossRef]
- Constantinides, G.; Ulm, F.-J. The nanogranular nature of C–S–H. J. Mech. Phys. Solids 2007, 55, 64–90. [Google Scholar] [CrossRef]
- Scrivener, K.L.; Nonat, A. Hydration of cementitious materials, present and future. Cem. Concr. Res. 2011, 41, 651–665. [Google Scholar] [CrossRef]
- Thomas, M.D.A. Supplementary Cementing Materials in Concrete; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Papadakis, V.G. Effect of supplementary cementing materials on concrete resistance against carbonation and chloride ingress. Cem. Concr. Res. 2000, 30, 291–299. [Google Scholar] [CrossRef]
- Zhang, M.-H.; Malhotra, V.M. High-Performance Concrete Incorporating Rice Husk Ash as a Supplementary Cementing Material. ACI Mater. J. 1996, 93, 629–636. [Google Scholar] [CrossRef] [PubMed]
- Powers, T.C. The Properties of Fresh Concrete; Wiley: New York, NY, USA, 1968. [Google Scholar]
- Feret, R. Sur la Compacité des Mortiers Hydrauliques; C. Dunod: Paris, France, 1892. [Google Scholar]
- Mayer, E. Properties Of Concrete; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Taylor, H.F. Cement Chemistry; Thomas Telford: London, UK, 1997; Volume 2. [Google Scholar]
- Bumanis, G.; Zorica, J.; Pundienė, I.; Bajare, D. The Workability Kinetics of Phosphogypsum Binder; Vilnius Gediminas Technical University: Vilnius, Lithuania, 2019. [Google Scholar]
- Thomas, M. Optimizing the Use of Fly Ash in Concrete; Portland Cement Association: Skokie, IL, USA, 2007; Volume 5420. [Google Scholar]
- Mehta, P.K.; Monteiro, P.J. Concrete Microstructure, Properties and Materials; McGraw-Hill Education: New York, NY, USA, 2017. [Google Scholar]
- Yu, Z.; Ye, G. The pore structure of cement paste blended with fly ash. Constr. Build. Mater. 2013, 45, 30–35. [Google Scholar] [CrossRef]
- Bentz, D.P.; Stutzman, P.E. Curing, Hydration, and Microstructure of Cement Paste. Mater. J. 2006, 103, 348–356. [Google Scholar]
- GB 175; Common Portland Cement. Standards Press of China (SPC): Beijing, China, 2024.
- GB/T 1345; The Test Sieving Method for Fineness of Cement. Standardization Administration of the People’s Republic of China (SAC): Beijing, China, 2005.
- GB/T 1596; Fly Ash Used for Cement and Concrete. Standardization Administration of the People’s Republic of China (SAC): Beijing, China, 2017.
- GB/T 18046; Ground Granulated Blast-Furnace Slag Used for Cement, Mortar and Concrete. Standardization Administration of the People’s Republic of China (SAC): Beijing, China, 2017.
- GB/T 35164; Limestone Powder Used for Cement, Mortar and Concrete. Standardization Administration of the People’s Republic of China (SAC): Beijing, China, 2017.
- GB/T 208; Test Method for Determining Cement Density. Standardization Administration of the People’s Republic of China (SAC): Beijing, China, 2014.
- Schindler, A.K.; Folliard, K.J. Heat of Hydration Models for Cementitious Materials. Mater. J. 2005, 102, 24–33. [Google Scholar]
- Mills, R. Factors influencing cessation of hydration in water cured cement pastes. In Highway Research Board Special Report; Highway Research Board: Washington, DC, USA, 1966. [Google Scholar]




| Specific Surface Area (m2/kg) | Density (kg/m3) | Standard Consistency (%) | Initial Setting Time (min) | Final Setting Time (MPa) | Compressive Strength (MPa) | |||
|---|---|---|---|---|---|---|---|---|
| 317 | 2990 | 28.4 | 193 | 266 | 5.3 (3 d) | 9.3 (28 d) | 19.3 (3 d) | 43.2 (28 d) |
| Material | Density (g/cm3) | Specific Surface Area (m2/kg) | Surface Area per Volume (m2/m3) |
|---|---|---|---|
| Cement (C) | 2.99 | 315.2 | 0.94 |
| Fly Ash (FA) | 2.35 | 453.4 | 1.07 |
| Slag (GGBFS) | 2.88 | 343.6 | 0.99 |
| Limestone Powder (LP) | 2.7 | 311.2 | 0.84 |
| Parameter | Unit | Cement | FA | GGBFS | LP |
|---|---|---|---|---|---|
| SiO2 | % | 19.5 | 36.5 | 36.0 | 2.0 |
| CaO | % | 63.5 | 25.0 | 43.0 | 54.0 |
| Al2O3 | % | 5.0 | 17.5 | 15.0 | 0.5 |
| MgO | % | 1.5 | 6.0 | 6.0 | 0.5 |
| Fe2O3 | % | 3.5 | 2.5 | 1.5 | 0.2 |
| SO3 | % | 2.0 | 5.0 | 0.3 | 0.1 |
| NazOeq | % | 0.5 | 0.6 | 0.6 | 0.1 |
| LOI | % | 0.6 | 0.7 | 0.5 | 43.0 |
| Mix ID | Cement (g) | Water (g) | w/c Ratio | 28 d Compressive Strength (MPa) |
|---|---|---|---|---|
| 1 | 592 | 178 | 0.3 | 89.5 |
| 2 | 549 | 192 | 0.35 | 77 |
| 3 | 511 | 205 | 0.4 | 66.1 |
| 4 | 479 | 215 | 0.45 | 53 |
| 5 | 450 | 225 | 0.5 | 43.6 |
| Serial Number | w/c | Compressive Strength (MPa) | ||||
|---|---|---|---|---|---|---|
| 3 d | 7 d | 14 d | 28 d | 90 d | ||
| 1 | 0.46 | 27.7 | 40.4 | 52.2 | 60.7 | 71.8 |
| 2 | 0.42 | 34.9 | 47.1 | 56.3 | 65.1 | 74.2 |
| 3 | 0.38 | 41.4 | 55.6 | 64.2 | 71.6 | 81.1 |
| 4 | 0.34 | 50.3 | 69.4 | 77.8 | 85.4 | 94.6 |
| 5 | 0.30 | 66.5 | 82.7 | 91.2 | 96.8 | 103.4 |
| 6 | 0.26 | 76.7 | 91.3 | 102.7 | 108.8 | 112.2 |
| Mix ID | Cement (g) | LP (g) | GGBFS (g) | FA (g) | Water (g) | w/b Ratio | 28 d Compressive Strength (MPa) |
|---|---|---|---|---|---|---|---|
| 1 | 450 | 0 | 0 | 0 | 225 | 0.5 | 44 |
| 2 | 592 | 0 | 0 | 0 | 178 | 0.3 | 86 |
| 3 | 549 | 0 | 0 | 0 | 192 | 0.35 | 77 |
| 4 | 511 | 0 | 0 | 0 | 205 | 0.4 | 66 |
| 5 | 479 | 0 | 0 | 0 | 215 | 0.45 | 53 |
| 6 | 532 | 53 | 0 | 0 | 175 | 0.3 | 87 |
| 7 | 493 | 49 | 0 | 0 | 190 | 0.35 | 72 |
| 8 | 460 | 46 | 0 | 0 | 202 | 0.4 | 61 |
| 9 | 431 | 43 | 0 | 0 | 213 | 0.45 | 50 |
| 10 | 406 | 40 | 0 | 0 | 223 | 0.5 | 42 |
| 11 | 473 | 104 | 0 | 0 | 173 | 0.3 | 76 |
| 12 | 439 | 96 | 0 | 0 | 188 | 0.35 | 67 |
| 13 | 410 | 90 | 0 | 0 | 200 | 0.4 | 51 |
| 14 | 384 | 84 | 0 | 0 | 211 | 0.45 | 46 |
| 15 | 362 | 79 | 0 | 0 | 221 | 0.5 | 37 |
| 16 | 416 | 154 | 0 | 0 | 171 | 0.3 | 66 |
| 17 | 387 | 143 | 0 | 0 | 185 | 0.35 | 57 |
| 18 | 361 | 134 | 0 | 0 | 198 | 0.4 | 45 |
| 19 | 339 | 125 | 0 | 0 | 209 | 0.45 | 34 |
| 20 | 319 | 118 | 0 | 0 | 219 | 0.5 | 29 |
| 21 | 360 | 203 | 0 | 0 | 169 | 0.3 | 56 |
| 22 | 335 | 188 | 0 | 0 | 183 | 0.35 | 44 |
| 23 | 313 | 176 | 0 | 0 | 196 | 0.4 | 42 |
| 24 | 294 | 165 | 0 | 0 | 207 | 0.45 | 32 |
| 25 | 277 | 156 | 0 | 0 | 216 | 0.5 | 24 |
| 26 | 532 | 0 | 0 | 53 | 175 | 0.3 | 91 |
| 27 | 493 | 0 | 0 | 49 | 190 | 0.35 | 75 |
| 28 | 460 | 0 | 0 | 46 | 202 | 0.4 | 59 |
| 29 | 431 | 0 | 0 | 43 | 213 | 0.45 | 45 |
| 30 | 406 | 0 | 0 | 40 | 223 | 0.5 | 40 |
| 31 | 473 | 0 | 0 | 104 | 173 | 0.3 | 82 |
| 32 | 439 | 0 | 0 | 96 | 188 | 0.35 | 66 |
| 33 | 410 | 0 | 0 | 90 | 200 | 0.4 | 51 |
| 34 | 384 | 0 | 0 | 84 | 211 | 0.45 | 42 |
| 35 | 362 | 0 | 0 | 79 | 221 | 0.5 | 35 |
| 36 | 416 | 0 | 0 | 154 | 171 | 0.3 | 70 |
| 37 | 387 | 0 | 0 | 143 | 185 | 0.35 | 62 |
| 38 | 361 | 0 | 0 | 134 | 198 | 0.4 | 49 |
| 39 | 339 | 0 | 0 | 125 | 209 | 0.45 | 37 |
| 40 | 319 | 0 | 0 | 118 | 219 | 0.5 | 32 |
| 41 | 360 | 0 | 0 | 203 | 169 | 0.3 | 59 |
| 42 | 335 | 0 | 0 | 188 | 183 | 0.35 | 47 |
| 43 | 313 | 0 | 0 | 176 | 196 | 0.4 | 39 |
| 44 | 294 | 0 | 0 | 165 | 207 | 0.45 | 32 |
| 45 | 277 | 0 | 0 | 156 | 216 | 0.5 | 28 |
| 46 | 532 | 0 | 53 | 0 | 175 | 0.3 | 83 |
| 47 | 493 | 0 | 49 | 0 | 190 | 0.35 | 76 |
| 48 | 460 | 0 | 46 | 0 | 202 | 0.4 | 57 |
| 49 | 431 | 0 | 43 | 0 | 213 | 0.45 | 52 |
| 50 | 406 | 0 | 40 | 0 | 223 | 0.5 | 46 |
| 51 | 473 | 0 | 104 | 0 | 173 | 0.3 | 84 |
| 52 | 439 | 0 | 96 | 0 | 188 | 0.35 | 62 |
| 53 | 410 | 0 | 90 | 0 | 200 | 0.4 | 53 |
| 54 | 384 | 0 | 84 | 0 | 211 | 0.45 | 43 |
| 55 | 362 | 0 | 79 | 0 | 221 | 0.5 | 39 |
| 56 | 416 | 0 | 154 | 0 | 171 | 0.3 | 73 |
| 57 | 387 | 0 | 143 | 0 | 185 | 0.35 | 62 |
| 58 | 361 | 0 | 134 | 0 | 198 | 0.4 | 51 |
| 59 | 339 | 0 | 125 | 0 | 209 | 0.45 | 43 |
| 60 | 319 | 0 | 118 | 0 | 219 | 0.5 | 38 |
| 61 | 360 | 0 | 203 | 0 | 169 | 0.3 | 66 |
| 62 | 335 | 0 | 188 | 0 | 183 | 0.35 | 57 |
| 63 | 313 | 0 | 176 | 0 | 196 | 0.4 | 48 |
| 64 | 294 | 0 | 165 | 0 | 207 | 0.45 | 39 |
| 65 | 277 | 0 | 156 | 0 | 216 | 0.5 | 34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lian, C.; Zhang, X.; Han, L.; Wen, W.; Han, L.; Wang, L. Predicting the Uniaxial Compressive Strength of Cement Paste: A Theoretical and Experimental Study. Materials 2025, 18, 3565. https://doi.org/10.3390/ma18153565
Lian C, Zhang X, Han L, Wen W, Han L, Wang L. Predicting the Uniaxial Compressive Strength of Cement Paste: A Theoretical and Experimental Study. Materials. 2025; 18(15):3565. https://doi.org/10.3390/ma18153565
Chicago/Turabian StyleLian, Chunming, Xiong Zhang, Lu Han, Weijun Wen, Lifang Han, and Lizhen Wang. 2025. "Predicting the Uniaxial Compressive Strength of Cement Paste: A Theoretical and Experimental Study" Materials 18, no. 15: 3565. https://doi.org/10.3390/ma18153565
APA StyleLian, C., Zhang, X., Han, L., Wen, W., Han, L., & Wang, L. (2025). Predicting the Uniaxial Compressive Strength of Cement Paste: A Theoretical and Experimental Study. Materials, 18(15), 3565. https://doi.org/10.3390/ma18153565





