Testing Using the DCP Probe of a Subgrade Modeled from Difficult-to-Compact Sand in a Calibration Chamber
Abstract
1. Introduction
2. DCP Probe
2.1. DCP Probe Applications
2.2. Interpretation of DCP Soil Testing Results
| Authors (Year) | Formula | Scope of Application | Coefficient of Determination |
|---|---|---|---|
| Webster et al. (1992) [24] | CBR = 292/DCP1.12 | cohesive soils and non-cohesive soils | Not specified |
| Zohrabi and Scott (2003) [31] | CBR = 240 DCP−0.97 | cohesive soils and non-cohesive soils | R2 = 0.89 |
| CBR = 243 [DCP/(1 + w)]−1.01 | R2 = 0.90 | ||
| George et al. (2009) [5] | CBR = 47.32 (DCPI)−0.7852 | lateritic soils | R2 = 0.82 |
| Jordão et al. (2012) [32] | CBR = 980.55 DCP−1.257 | silty clay | R2 = 0.86 |
| Monteiro et al. (2016) [33] | CBR = 143.13 (DCP)−0.879 | silty or clayey gravel and sand | R2 = 0.89 |
| CBR = 43.91 (DCP)−0.547 | clayey soils | R2 = 0.71 | |
| CBR = 58.154 (DCP)−0.397 | stone fragments, gravel, and sand | R2 = 1.00 | |
| Hamid (2017) [18] | Dr = 230.55/(DCPI)0.417 | silty sand; CU = 1.98; (+1% silt) | R2 = 0.98 |
| Dr = 231/(DCPI)0.419 | silty sand; CU = 1.98; (+4% silt) | R2 = 0.98 | |
| Dr = 214/(DCPI)0.405 | silty sand; CU = 1.98; (+8% silt) | R2 = 0.98 | |
| Wilches et al. (2018) [34] | CBR = 112.03/(DCP)0.803 | fine-grained soils, clay | R2 > 0.80 |
| MacRobert et al. (2019) [9] | Dr = −50 logDPI + 148 | sandy soils; CU = 1.2–9.4 | RE = ±11% |
| Dr = −52 log(DPI · D50)0.3 + 150 | RE = ±9% | ||
| Juntasan et al. (2015) [28] | IS = 5.785 ln(N83mm) + 86.654 | silty or clayey gravel sand; ρdmax = 1.821 t/m3; n = 19 | R2 > 0.96 |
| IS = 8.751 ln(N83mm) + 73.902 | fine sand; ρdmax = 1.867 t/m3; n = 10 | R2 > 0.96 | |
| Yang et al. (2015) [7] | K = 131.57 − 1.05w − 5.00PR for w ≤ wopt K = 46.76 − 3.18w − 1.79PR for w ≥ wopt | clay (CH); CU = 5.59 Laboratory tests | R2 = 0.76 R2 = 0.67 |
| K = 134.57 − 1.08w − 5.39PR for w ≤ wopt; n = 18 K = 49.36 − 3.47w − 1.92PR for w ≥ wopt; n = 44 | clay (CH); CU = 5.59 Field tests | R2 = 0.81 R2 = 0.80 | |
| Belicanta et al. (2016) [29] | ; PI (cm/blow) | lateric silty clay | No data |
2.3. Description of the DCP Device
3. Description of the Tests Performed
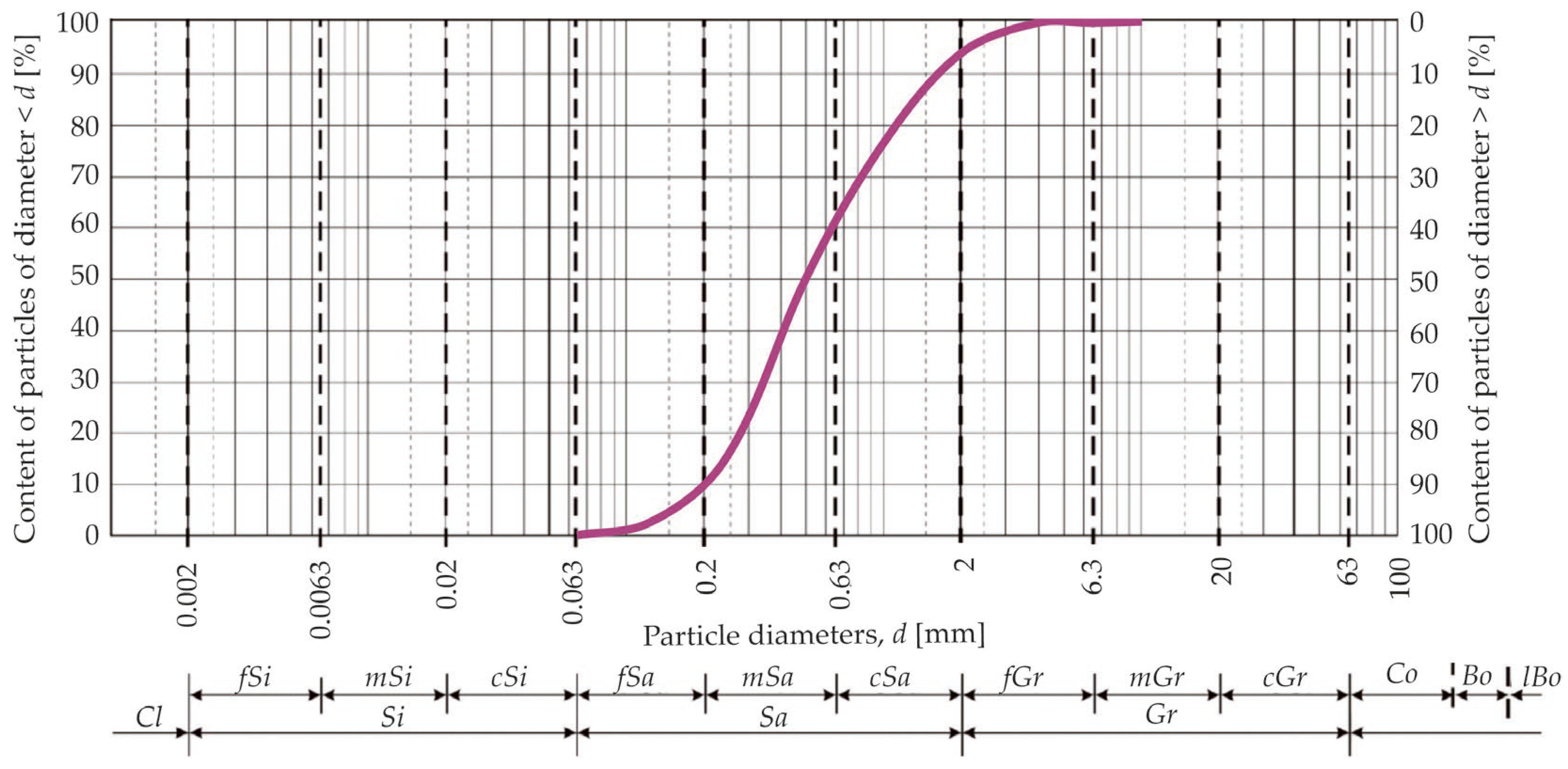
3.1. Description of the Tested Soil
3.2. Calibration Chamber
3.3. Substrate Modeling in a Calibration Chamber
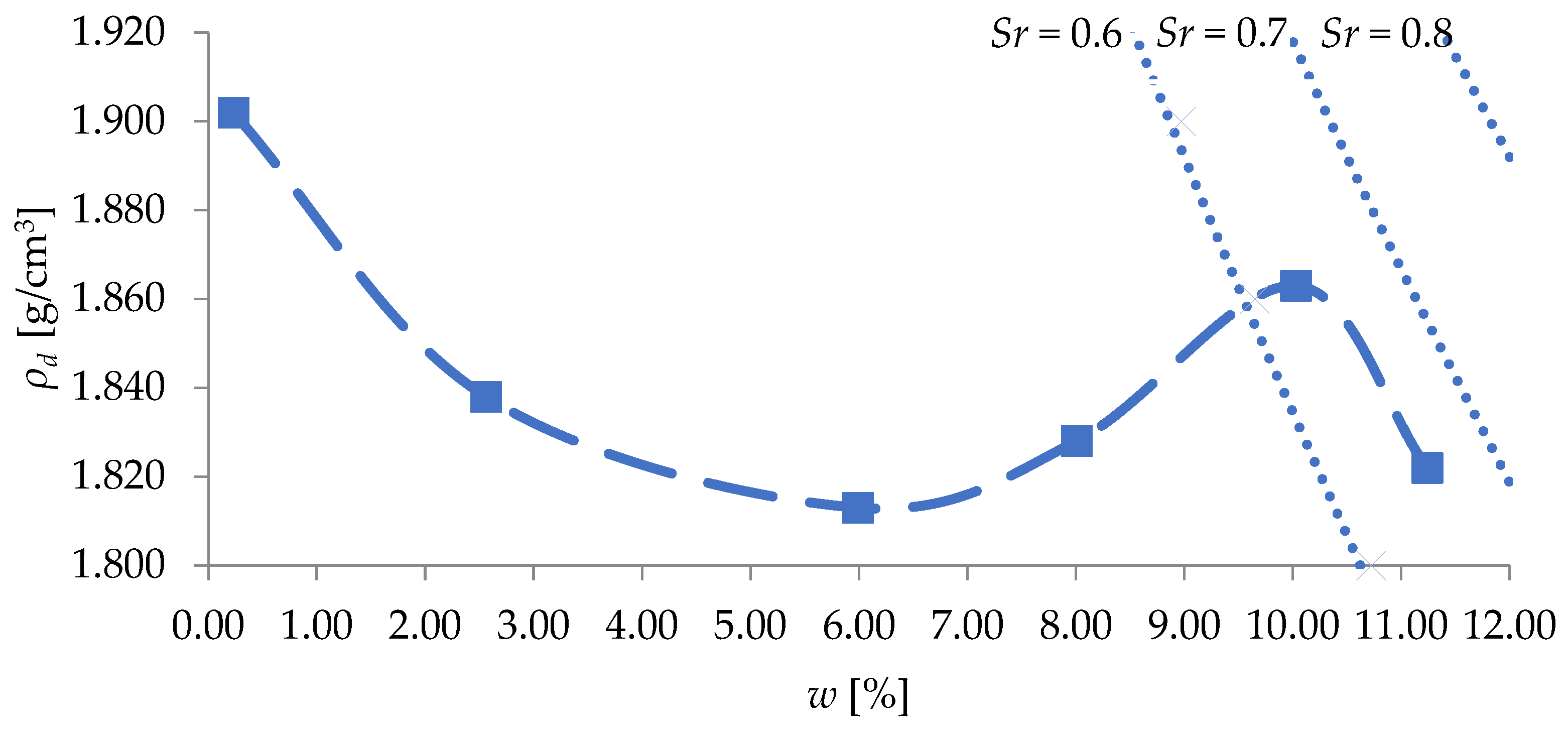
3.4. Measures of Density Tested
3.5. Performing Tests
4. Results
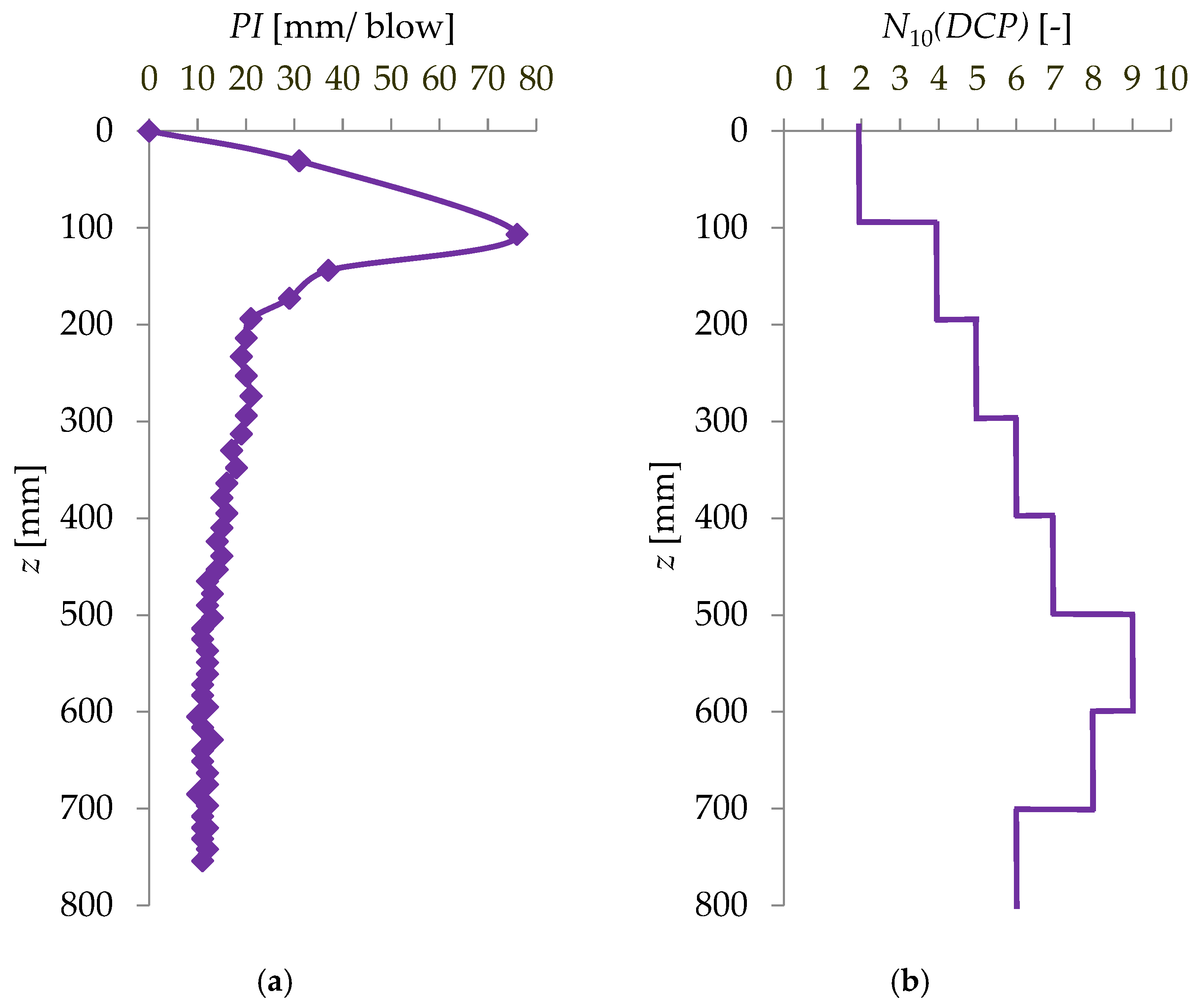
4.1. Summary of Research Results
4.2. Statistical Analysis of Test Results
- (1)
- Which geotechnical parameters are dependent on PI?
- (2)
- Can relationships be developed for the degree of compaction IS based on the results obtained from DCP tests?
5. Conclusions
- The results of DCP testing can be interpreted from the ground surface.
- The DCP test results (PI and N10(DCP)) of sand mainly depend on the test depth z and the degree of compaction IS.
- A statistically significant calibration equation for the DCP probe was developed, which allows determining the degree of compaction IS of the tested sand (Sa) based on the measured values of N10(DCP) and test depth z, with a relative error of RE = ±3%: IS = 0.927 − 0.069z + 0.005N10(DCP) ± 0.013.
- Based on the conducted research and analyses, it is concluded that the DCP probe can be used to assess the compaction index of surface layers of embankments made of poorly graded non-cohesive soil (sand (Sa)), using the developed regression equation Is = f(z, N10(DCP)).
- The DCP probe has great application possibilities for studying the degree of compaction of soils. In this article, the DCP probe was calibrated on one soil type: poorly graded sand. The probe should be calibrated on other cohesionless soils with different grain size distributions.
- Studies will be undertaken on several cohesionless soils with coarser grain sizes, with medium, well, and gap graded.
- Calibration equations for individual soils will be developed. The possibility of generalizing the calibration equations for all cohesionless soils or groups of cohesionless soils will be examined.
- The developed calibration equations will be verified based on field studies on road embankments.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- PN-B-04481:1988; Grunty Budowlane. Badania Próbek Gruntu. Polish Committee for Standardization (PKN): Warsaw, Poland, 1988.
- EN 16907-1:2018; Earthworks—Part 1: Principles and General Rules. CEN: Brussels, Belgium, 2018.
- Hawrysz, M.; Stróżyk, J. Kontrowersyjna interpretacja wyników sondowań dynamicznych w praktyce inżynierskiej. Inżynieria Morska I Geotech 2015, 36, 203–207. [Google Scholar]
- D6951-03:2003; ASTM Standard. Standard Test Method for Use of the Dynamic Cone Penetrometer in Shallow Pavement Applications. ASTM International: West Conshohocken, PA, USA, 2003.
- George, V.; Rao, N.C.; Shivashankar, R. PFWD, DCP and CBR correlations for evaluation of lateritic subgrades. Int. J. Pavement Eng. 2009, 10, 189–199. [Google Scholar] [CrossRef]
- Nguyen, B.T.; Mohajerani, A. A new lightweight dynamic cone penetrometer for laboratory and field applications. Aust. Geomech. 2012, 47, 41–50. [Google Scholar]
- Yang, B.; Zhang, R.; Zha, X.; Liu, C.; Pan, Q. Improved testing method of dynamic cone penetrometer in laboratory for evaluating compaction properties of soil subgrade. Road Mater. Pavement Des. 2015, 17, 487–498. [Google Scholar] [CrossRef]
- Ganju, E.; Kim, H.; Prezzi, M.; Salgado, R.; Siddiki, N.Z. Quality assurance and quality control of subgrade compaction using the dynamic cone penetrometer. Int. J. Pavement Eng. 2016, 19, 966–975. [Google Scholar] [CrossRef]
- MacRobert, C.J.; Bernstein, G.S.; Nchabeleng, M.M. Dynamic Cone Penetrometer (DCP) relative density correlations for sands. Soils Rocks 2019, 42, 201–207. [Google Scholar] [CrossRef]
- PN-S-02205:1998; Roads—Earthwork—Specifications and Testing. Polish Committee for Standardization (PKN): Warsaw, Poland, 1998.
- Salgado, R.; Yoon, S. Dynamic Cone Penetration Test (DCPT) for Subgrade Assessmen. Technical Summary, Technology Transfer and Project Implementation Information, INDOT Research Report, No. FHWA/IN/JTRP-2002/30. 2003. Available online: https://docs.lib.purdue.edu/cgi/viewcontent.cgi?article=1544&context=jtrp (accessed on 22 April 2025).
- Kumar, R.S.; Ajami, A.S.; Valkati, B. Comparative study of grade soil strenght estimation models developed based on CBR, DCP and FWD test results. Int. Adv. Res. J. Sci. Eng. Technol. 2015, 2, 92–102. [Google Scholar] [CrossRef]
- Paige-Green, P.; DuPlessis, L. The Use and Interpretation of the Dynamic Cone Penetrometer (DCP) Test. CSIR Built Environment, Version 2, Pretoria. 2009. Available online: https://rtdcp.co.za/wp-content/uploads/2019/11/The_use_and_interpretation_of_the_Dynamic_Cone_Penetrometer_01.pdf (accessed on 30 April 2025).
- Ayers, M.E.; Thompson, M.R.; Uzarski, D.R. Rapid shear strength evaluation of in situ granular materials. Transp. Res. Rec. 1989, 1227, 134–146. [Google Scholar]
- Al-Amoudi, O.S.B.; Asi, I.M.; Wahhab, H.I.A.-A.; Khan, Z.A. Clegg hammer—California-Bearing Ratio correlations. J. Mater. Civ. Eng. 2002, 14, 512–523. [Google Scholar] [CrossRef]
- Langton, D. The Panda light weight penetrometer for soil investigation and monitoring material compaction. Ground Eng. 1999, 32, 33–37. [Google Scholar]
- Byun, Y.-H.; Hong, W.-T.; Lee, J.-S. Characterization of railway substructure using a hybrid cone penetrometer. Smart Struct. Syst. 2015, 15, 1085–1101. [Google Scholar] [CrossRef]
- Hamid, A.M. Effect of Fine Material on Penetration Resistance. Leadership in Sustainable Infrastructure. In Proceedings of the 2017 Canadian Society for Civil Engineering Conference, CSCE SCGC, Vancouver, BC, Canada, 31 May–3 June 2017; Available online: https://www.researchgate.net/publication/317671646_effect_of_fine_material_on_penetration_resistance (accessed on 23 April 2025).
- Hamid, A.M. The Dynamic cone Penetration Test: A review of its correlations and applications. In Proceedings of the International Conference on Advances in Civil and Environmental Engineering (ACEE), Pulau Pinang, Malaysia, 28–30 July 2015; pp. 1–16. [Google Scholar]
- Stanichevsky, M.; Basio, J.J. The Dynamic Penetration Cone Index as an alternative for the control of a subgrade surface. In Proceedings of the 16th International Conference on Soil Mechanics and Geotechnical Engineering, Osaka, Japan, 12–15 September 2005. [Google Scholar]
- Manjunath, K.C.; Amarnath, M.S. Structural evaluation of low volume road pavements using pavement dynamic cone penetrometr. Int. J. Res. Eng. Technol. (IJRET) 2013, 2, 187–191. [Google Scholar]
- Wu, S.; Sargand, S. Use of Dynamic Cone Penetrometer in Subgrade and Base Acceptance. Ohio Research Institute for Transportation and the Environment (ORITE), Final Technical Report, No. FHWA/ODOT-2007/01. 2007. Available online: https://rosap.ntl.bts.gov/view/dot/39670 (accessed on 29 April 2025).
- Hashemi, M.; Nikudel, M.R. Application of Dynamic Cone Penetrometer test for assessment of liquefaction potential. Eng. Geol. 2016, 208, 51–62. [Google Scholar] [CrossRef]
- Webster, S.L.; Grau, R.H.; Williams, T.P. Description and Application of Dual Mass Dynamic Cone Penetrometer. U.S. Army Corps of Engineers, Waterways Experiment Station, Instruction Report, No. GL-92-3. 1992. Available online: https://apps.dtic.mil/sti/pdfs/ADA251960.pdf (accessed on 28 April 2025).
- Livneh, M. Validation of correlations between a number of penetration tests and in situ California Bearing Ratio tests. Transp. Res. Rec. 1989, 1219, 56–67. [Google Scholar]
- Seyman, E. Laboratory Evaluation of In-Situ Tests as Potential Quality Control/Quality Assurance Tools. Master’s Thesis, Graduate School, LSU Scholarly Repository, Louisiana State University, Baton Rouge, LA, USA, 2003. Available online: https://repository.lsu.edu/gradschool_theses/2601/ (accessed on 25 April 2025).
- Hussein, A.A.; Alshkane, Y.M. Prediction of CBR and Mr of fine grained soil using DCPI. In Proceedings of the 4th International Engineering Conference on Developments in Civil & Computer Engineering Applications, Erbil, Iraq, 12–14 February 2018; pp. 268–282. [Google Scholar]
- Juntasan, P.; Narong, S.; Kaewhanam, N. Evaluation of Highway Subgrade Compaction by Dynamic Cone Penetrometer. Mahasarakham Int. J. Eng. Technol. 2015, 1, 6–10. [Google Scholar]
- Belicanta, A.; Lukiantchuki, J.A.; Reis, J.H. Control of soil compaction in pavement layers: A new approach using the dynamic cone penetrometer (DCP). In Proceedings of the 5th International Conference on Geotechnical and Geophysical Site Characterization (ISC5), Gold Coast, QLD, Australia, 5–9 September 2016. [Google Scholar]
- Kaur, P.; Gill, K.S.; Walia, B.S. Correlation between soaked CBR value and CBR value obtained with dynamic cone penetrometer. Int. J. Res. Eng. Appl. Sci. (IJREAS) 2012, 2, 1243–1250. [Google Scholar]
- Zohrabi, M.; Scott, P.L. The Correlation Between the CBR Value and Penetrability of Pavement Construction Materials. Prepared for Transport for London (Street Management), TRL Report TRL587. 2003. Available online: https://www.trl.co.uk/uploads/trl/documents/TRL587.pdf (accessed on 24 April 2025).
- Jordão, H.P.; de Figueiredo Lopes Lucena, A.E.; das Chagas Filho, M.B.; Rodrigues, J.K.G.; Gama, D.A. Contribution to the project of urban Pavement of Low Volume of Traffic by use of the Dynamic Cone Penetrometer. Soils Rocks 2012, 35, 1–8. [Google Scholar] [CrossRef]
- Monteiro, F.F.; de Oliveira, F.H.L.; Zitllau, O.; de Aguiar, M.F.P.; de Carvalho, L.M.C. CBR value estimation using Dynamic Cone Penetrometer—A case study of Brazil’s Midwest Federal Highway. Electron. J. Geotech. Eng. 2016, 21, 4649–4656. [Google Scholar]
- Wilches, F.J.; Diaz, J.J.F.; Avila, J.R.H. Correlation between California Bearing Ratio (CBR) and Dynamic Cone Penetrometer (DCP) for soil from Sincelejo city in Colombia. Int. J. Appl. Eng. Res. 2018, 13, 2068–2071. [Google Scholar]
- Tymosiak, D. Validation of Selected Methods of Testing Density Measures of Non-Cohesive Soil Compaction. Ph.D. Thesis, Bialystok University of Technology, Bialystok, Poland, 2023. [Google Scholar]
- EN ISO 14688-2:2004; Geotechnical Investigations. Determination and Classification of Soils. Part 2: Principles of Classification. CEN: Brussels, Belgium, 2004.
- CEN ISO/TS 17892-4:2004; European Technical Specification. Geotechnical Investigation and Testing—Laboratory Testing of Soil—Part 4: Determination of Particle Size Distribution. CEN: Brussels, Belgium, 2004.
- EN 13286-2:2010-11; Unbound and Hydraulically Bound Mixtures—Part 2: Test Methods for Laboratory Dry Density and Water Content—Proctor Compaction + Amendment EN 13286-2:2010/AC:2014-07. CEN: Brussels, Belgium, 2010.
- Sulewska, M.J.; Tymosiak, D. Analysis of compaction parameters of the exemplary non-cohesive soil determined by Proctor methods and vibrating table test. Ann. Wars. Univ. Life Sci. Land Reclam. 2018, 50, 99–108. [Google Scholar] [CrossRef]
- CEN ISO/TS 17892-2:2004; European Technical Specification. Geotechnical Investigation and Testing—Laboratory Testing of Soil—Part 2: Determination of Density of Fine Grained Soil. CEN: Brussels, Belgium, 2004.
- CEN ISO/TS 17892-1: 2004; European Technical Specification. Geotechnical Investigation and Testing—Laboratory Testing of Soil—Part 1: Determination of Water Content. CEN: Brussels, Belgium, 2004.
- EN ISO 22476-2:2005; European Standard. Geotechnical Investigation and Testing—Field Testing—Part 2: Dynamic Probing (ISO 22476-2:2005) + Amendment EN ISO 22476-2:2005/A1:2011. CEN: Brussels, Belgium, 2005.
- Stanisz, A. Przystępny Kurs Statystyki z Zastosowaniem STATISTICA PL na Przykładach z Medycyny. T. 1: Statystyki Pod-Stawowe; StatSoft Polska Sp. z o.o.: Kraków, Poland, 2006. [Google Scholar]
- Stanisz, A. Przystępny Kurs Statystyki z Zastosowaniem STATISTICA PL na Przykładach z Medycyny. T. 2: Modele Liniowe i Nieliniowe; StatSoft Polska Sp. z o.o.: Kraków, Poland, 2007. [Google Scholar]
- Peternek, P.; Kośny, M. Kilka uwag o testowaniu istotności współczynnika korelacji. Zesz. Nauk. Wyższej Szkoły Bank. We Wrocławiu 2011, 20, 341–350. [Google Scholar]
- Rabiej, M. Statystyka z Programem STATISTICA; Wydawnictwo Helion: Gliwice, Poland, 2012. [Google Scholar]
- Gruszyński, M.; Mierzejewski, P. Wstęp do Ekonometrii w stu Oknach; Szkoła Główna Handlowa: Warszawa, Poland, 2002. [Google Scholar]
- Daoud, J.I. Multicollinearity and regression analysis. J. Phys. Conf. Ser. 2017, 949, 012009. [Google Scholar] [CrossRef]





| Parameter | Value of Parameter |
|---|---|
| Hammer mass m [kg] | 8 ± 0.01 |
| Hammer drop height h [mm] | 575 ± 10 |
| Apex angle of the cone [°] | 60 ± 1 |
| Diameter of the base of the conical tip d [mm] | 20.0 ± 2.5 |
| Mass of the rod [kg/m] | 1.55 |
| Outer diameter of the rod [mm] | 15.8 |
| Impact energy of the hammer per unit area [kJ/m2] | 143.7 |
| Test result PI [mm/1 blow] | PI (Penetration Index) |
| Geotechnical Parameter | Symbol | Value |
|---|---|---|
| Fraction content: | fgr; csa; mSa; fsa | 5%; 35%; 50%; 10% |
| Grain size distribution: D10, D30, D60 (grain diameters for which 10%, 30%, and 60% of the soil sample, respectively, are finer) | D10 | 0.200 mm |
| D30 | 0.350 mm | |
| D60 | 0.620 mm | |
| Uniformity coefficient | CU = D60/D10 | 3.10 |
| Curvature coefficient | CC = (D30)2/D10·D60 | 0.988 |
| Maximum dry density of the soil | ρdmax | 1.863 g/cm3 |
| Optimum moisture content | wopt | 10.03% |
| Bulk density of the soil | ρ | 1.717–1.903 g/cm3 |
| Moisture content of the soil | w | 3.40–5.81% |
| Dry density of the soil | ρd | 1.649–1.803 g/cm3 |
| Parameter | Dataset1 | Dataset2 | ||||
|---|---|---|---|---|---|---|
| Values Range | Standard Deviation S1 | Coefficient of Variation V1 [%] | Values Range | Standard Deviation S2 | Coefficient of Variation V2 [%] | |
| z [m] | 0.02–0.70 | 0.23 | 68.3 | 0.21–0.70 | 0.15 | 30.3 |
| ρ [g/cm3] | 1.732–1.903 | 0.037 | 2.1 | 1.756–1.903 | 0.042 | 2.3 |
| w [%] | 3.4–5.8 | 0.6 | 12.6 | 3.8–5.8 | 0.6 | 12.1 |
| ρd [g/cm3] | 1.650–1.803 | 0.032 | 1.9 | 1.687–1.803 | 0.034 | 2.0 |
| IS [-] | 0.886–0.968 | 0.017 | 1.9 | 0.906–0.968 | 0.019 | 2.0 |
| PI [mm/1 blow] | 6.0–57.0 | 12.9 | 58.5 | 6.0–30.0 | 5.7 | 40.5 |
| N10(DCP) [blow number/10 cm] | 1.0–17.0 | 4.0 | 69.0 | 4.0–17.0 | 3.4 | 40.4 |
| Dataset1 | |||||||
|---|---|---|---|---|---|---|---|
| Variable | z | ρ | w | ρd | IS | PI | N10(DCP) |
| z | 1.000 | ||||||
| ρ | 0.146 | 1.000 | |||||
| w | 0.239 | 0.498 | 1.000 | ||||
| ρd | 0.100 | 0.962 | 0.253 | 1.000 | |||
| IS | 0.100 | 0.962 | 0.253 | 1.000 | 1.000 | ||
| PI | −0.751 | −0.228 | 0.012 | −0.260 | −0.260 | 1.000 | |
| N10(DCP) | 0.809 | 0.463 | 0.286 | 0.440 | 0.440 | −0.776 | 1.000 |
| Dataset2 | |||||||
| Variable | z | ρ | w | ρd | IS | PI | N10(DCP) |
| z | 1.000 | ||||||
| ρ | 0.025 | 1.000 | |||||
| w | 0.240 | 0.603 | 1.000 | ||||
| ρd | −0.026 | 0.975 | 0.416 | 1.000 | |||
| IS | −0.026 | 0.975 | 0.416 | 1.000 | 1.000 | ||
| PI | −0.409 | −0.451 | −0.022 | −0.512 | −0.512 | 1.000 | |
| N10(DCP) | 0.484 | 0.632 | 0.369 | 0.625 | 0.625 | −0.831 | 1.000 |
 0.99–0.60;
0.99–0.60;  (−0.21)–(−0.60);
(−0.21)–(−0.60);  0.59–0.20;
0.59–0.20;  (−0.61)–(−0.99);
(−0.61)–(−0.99);  0.19–(−0.20).
0.19–(−0.20).| Dataset1 | |||
|---|---|---|---|
| Function | Regression Equation | R2 | Formula No. |
| PI = f(z) | PI = 46.9 − 108.2z + 82.2z2 ± 8.3 | 0.600 | (7) |
| PI = f(IS) | PI = 203.7 − 195.1IS ± 12.6 | 0.068 | (8) |
| N10(DCP) = f(z) | N10(DCP) = 11.9 + 11.0logz ± 2.3 | 0.681 | (9) |
| N10(DCP) = f(IS) | N10(DCP) = −5368.3 + 5392.6IS – 11,369.0logIS ± 3.6 | 0.273 | (10) |
| PI = f(z, IS) | PI = −31.2logz − 293.3logIS ± 8.2 (the intercept is statistically insignificant) | 0.613 | (11) |
| N10(DCP) = f(z, IS) | N10(DCP) = 17.3 + 10.5logz + 182.6logIS ± 1.8 | 0.806 | (12) |
| Dataset2 | |||
| Function | Regression equation | R2 | Formula No. |
| PI = f(IS) | PI = 86.6 − 83.4IS2 ± 5.0 | 0.263 | (13) |
| N10(DCP) = f(z) | N10(DCP) = 12.9 + 14.2logz ± 2.9 | 0.292 | (14) |
| N10(DCP) = f(IS) | N10(DCP) = −97.4 + 113.4IS ± 2.7 | 0.391 | (15) |
| PI = f(z, IS) | PI = 170.9 − 16.5z − 159.7IS ± 4.4 | 0.441 | (16) |
| N10(DCP) = f(z, IS) | N10(DCP) = 20.5 + 14.5logz + 247.4logIS ± 1.9 | 0.691 | (17) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tymosiak, D.; Sulewska, M.J.; Kokoszka, W.; Słowik, M.; Błazik-Borowa, E.; Ożóg, D.; Puchlik, M. Testing Using the DCP Probe of a Subgrade Modeled from Difficult-to-Compact Sand in a Calibration Chamber. Materials 2025, 18, 3548. https://doi.org/10.3390/ma18153548
Tymosiak D, Sulewska MJ, Kokoszka W, Słowik M, Błazik-Borowa E, Ożóg D, Puchlik M. Testing Using the DCP Probe of a Subgrade Modeled from Difficult-to-Compact Sand in a Calibration Chamber. Materials. 2025; 18(15):3548. https://doi.org/10.3390/ma18153548
Chicago/Turabian StyleTymosiak, Dariusz, Maria Jolanta Sulewska, Wanda Kokoszka, Marta Słowik, Ewa Błazik-Borowa, Dominik Ożóg, and Monika Puchlik. 2025. "Testing Using the DCP Probe of a Subgrade Modeled from Difficult-to-Compact Sand in a Calibration Chamber" Materials 18, no. 15: 3548. https://doi.org/10.3390/ma18153548
APA StyleTymosiak, D., Sulewska, M. J., Kokoszka, W., Słowik, M., Błazik-Borowa, E., Ożóg, D., & Puchlik, M. (2025). Testing Using the DCP Probe of a Subgrade Modeled from Difficult-to-Compact Sand in a Calibration Chamber. Materials, 18(15), 3548. https://doi.org/10.3390/ma18153548






