Physics-Informed Neural Networks for Depth-Dependent Constitutive Relationships of Gradient Nanostructured 316L Stainless Steel
Abstract
1. Introduction
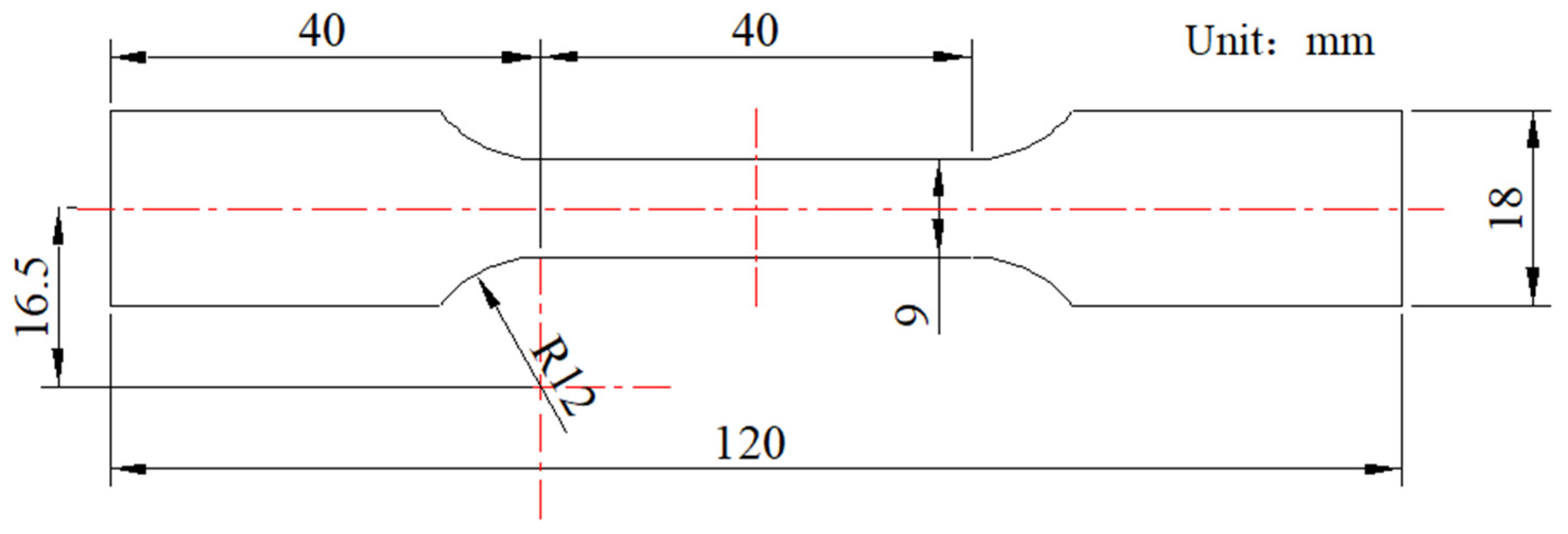
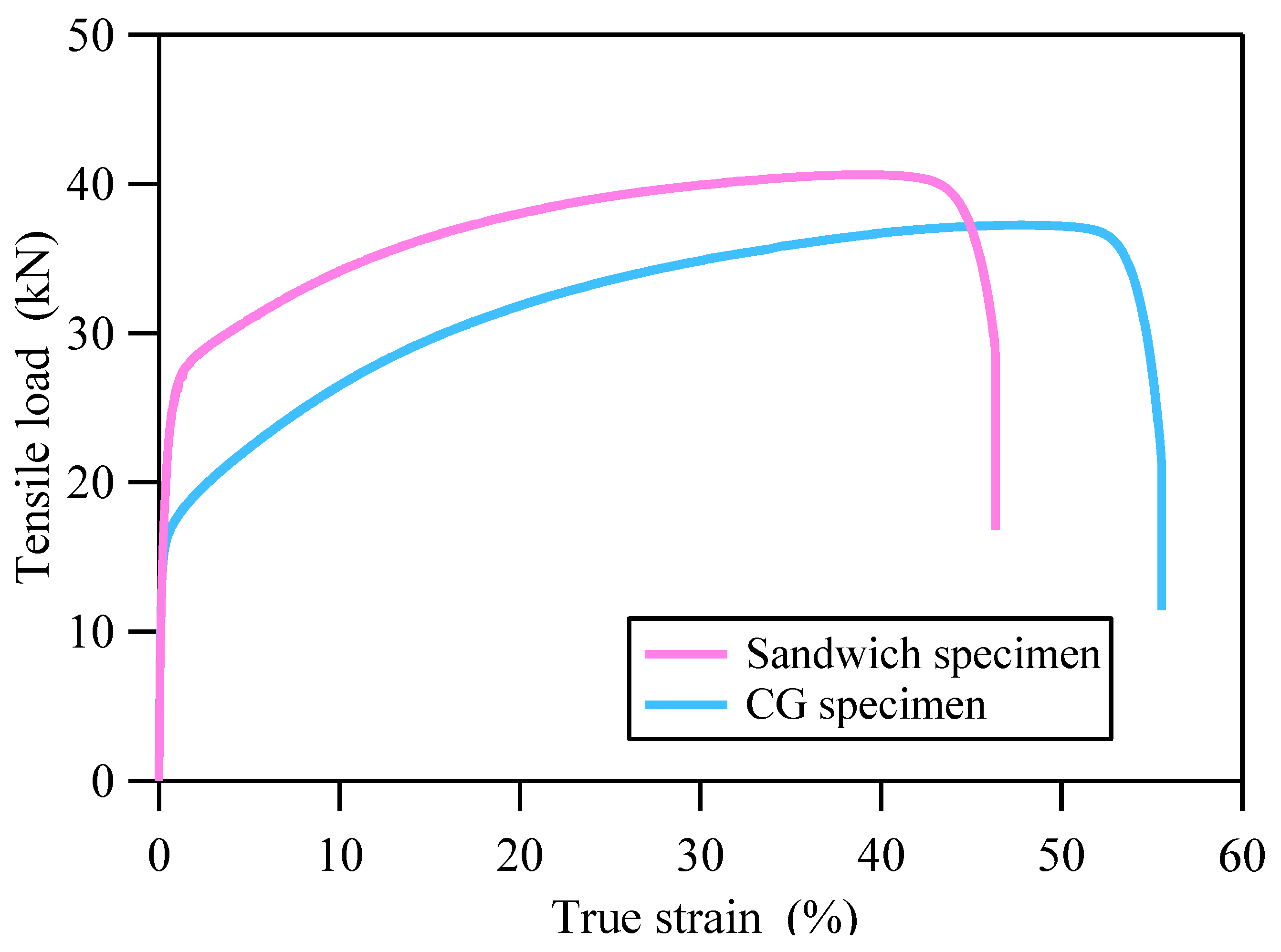
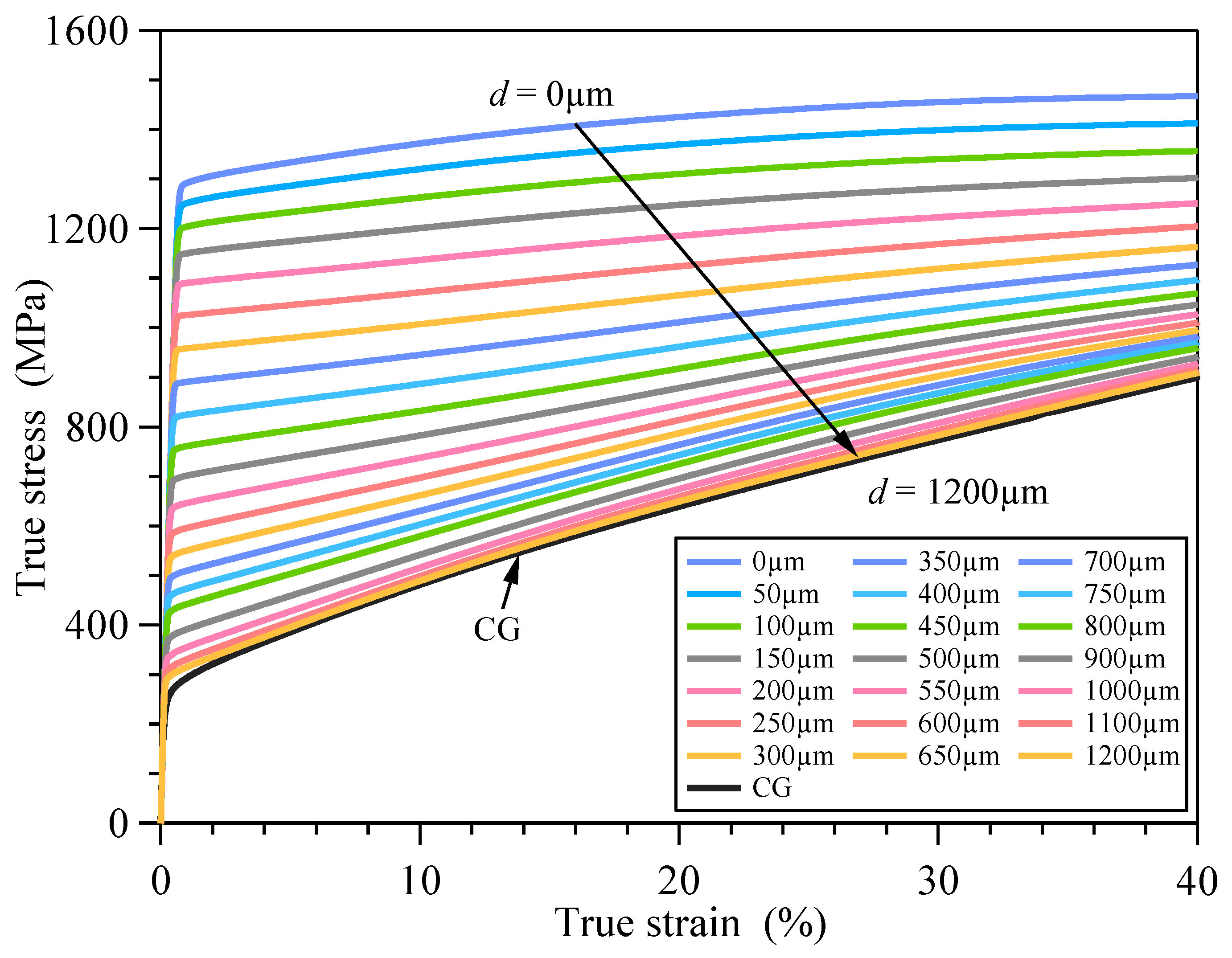
2. Quasi-Static Tensile Test and Hardness Measurement
3. Depth-Dependent PINNs_εH Model
4. Depth-Dependent Constitutive Relationships of GS 316L Stainless Steel
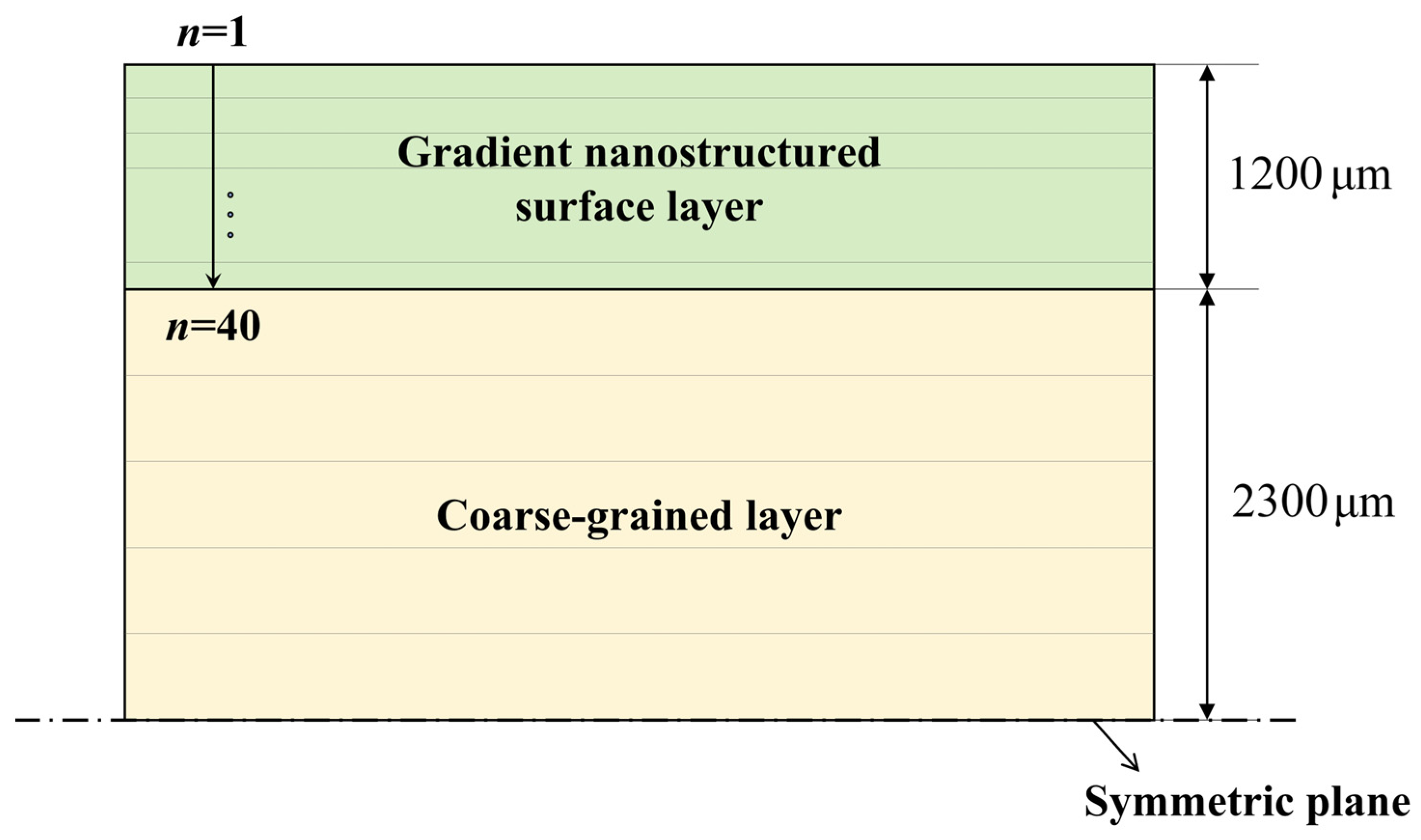
4.1. Laminated Plate Model
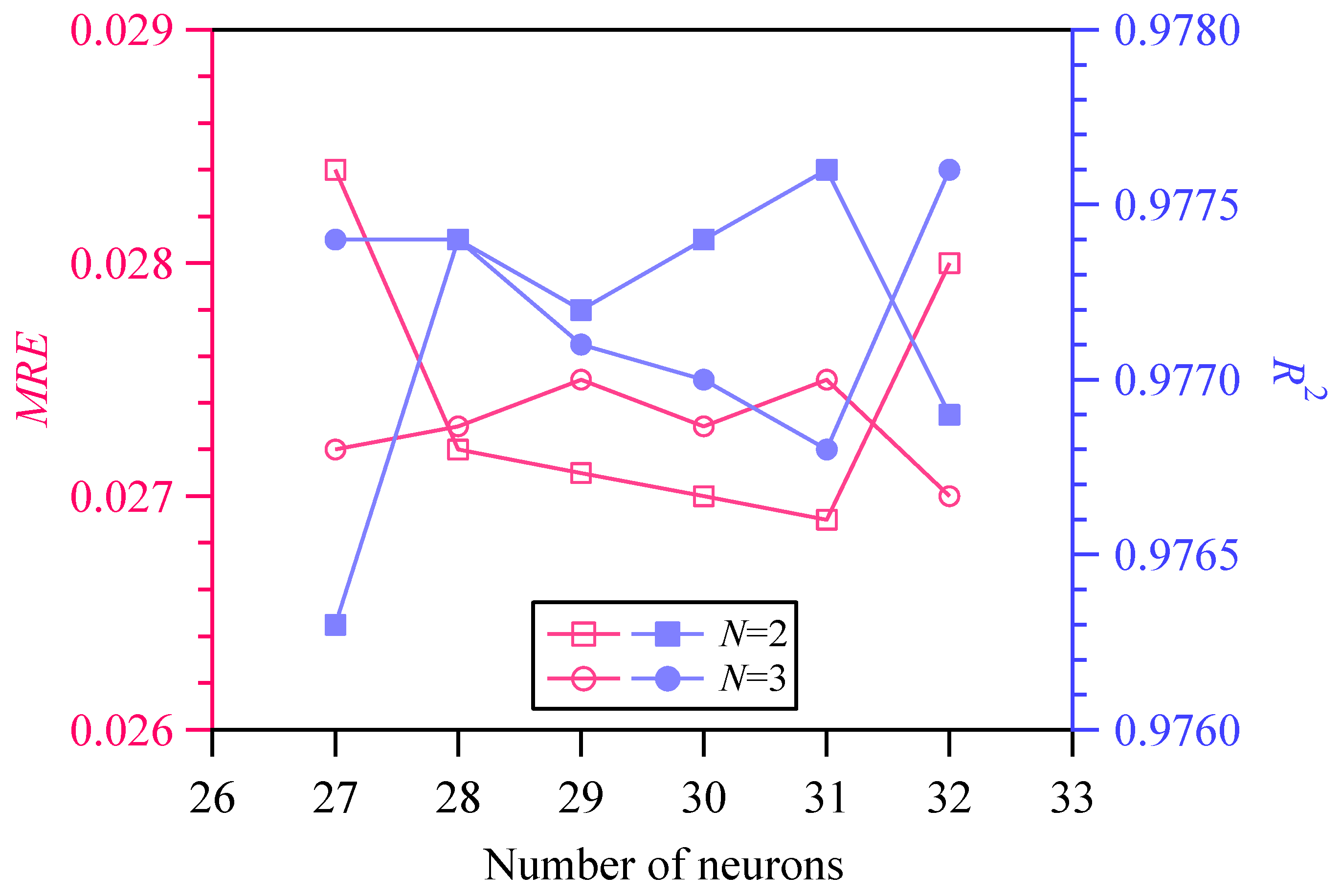
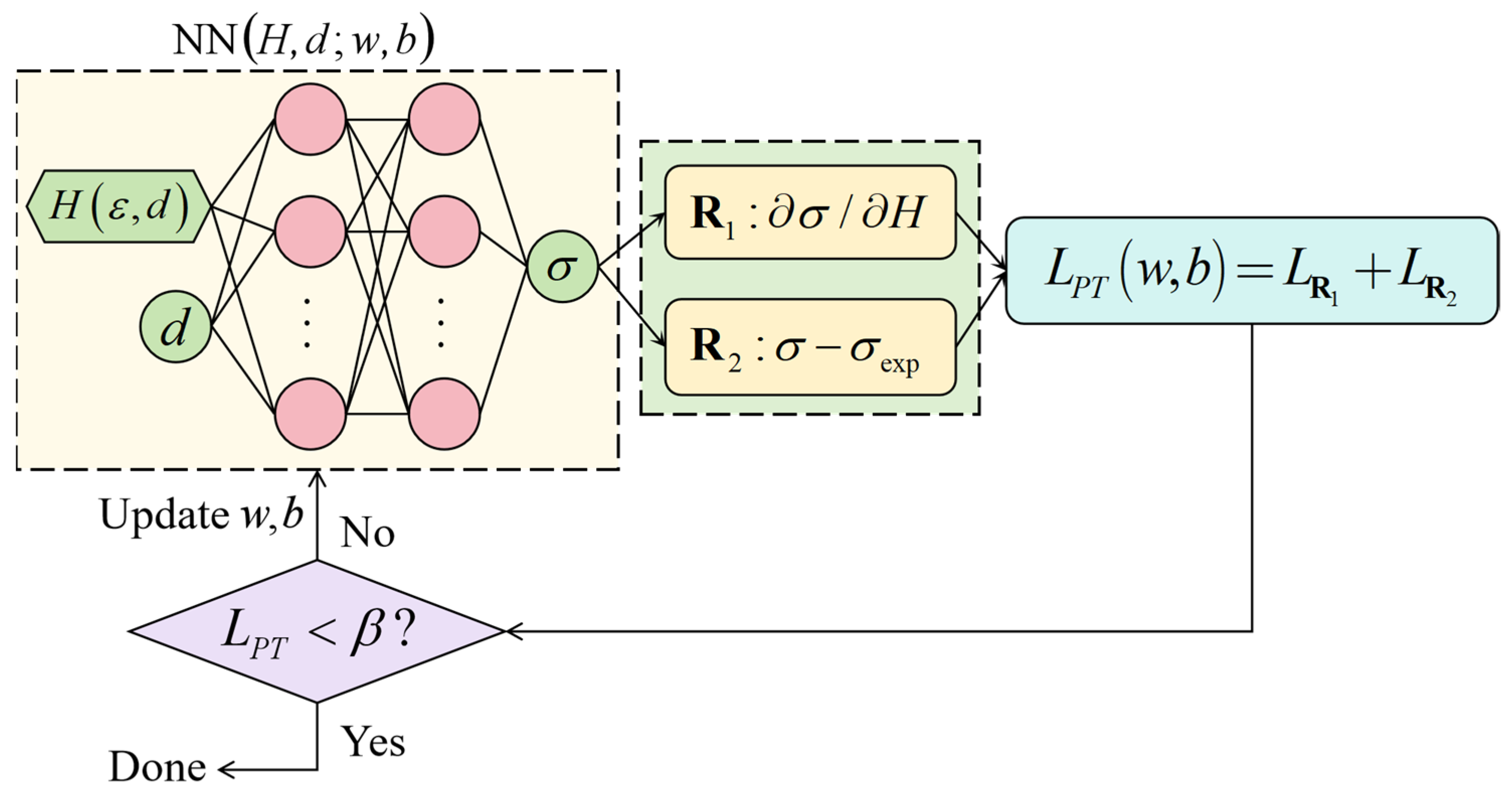
4.2. Depth-Dependent PINNs_Hσ Pre-Trained Model
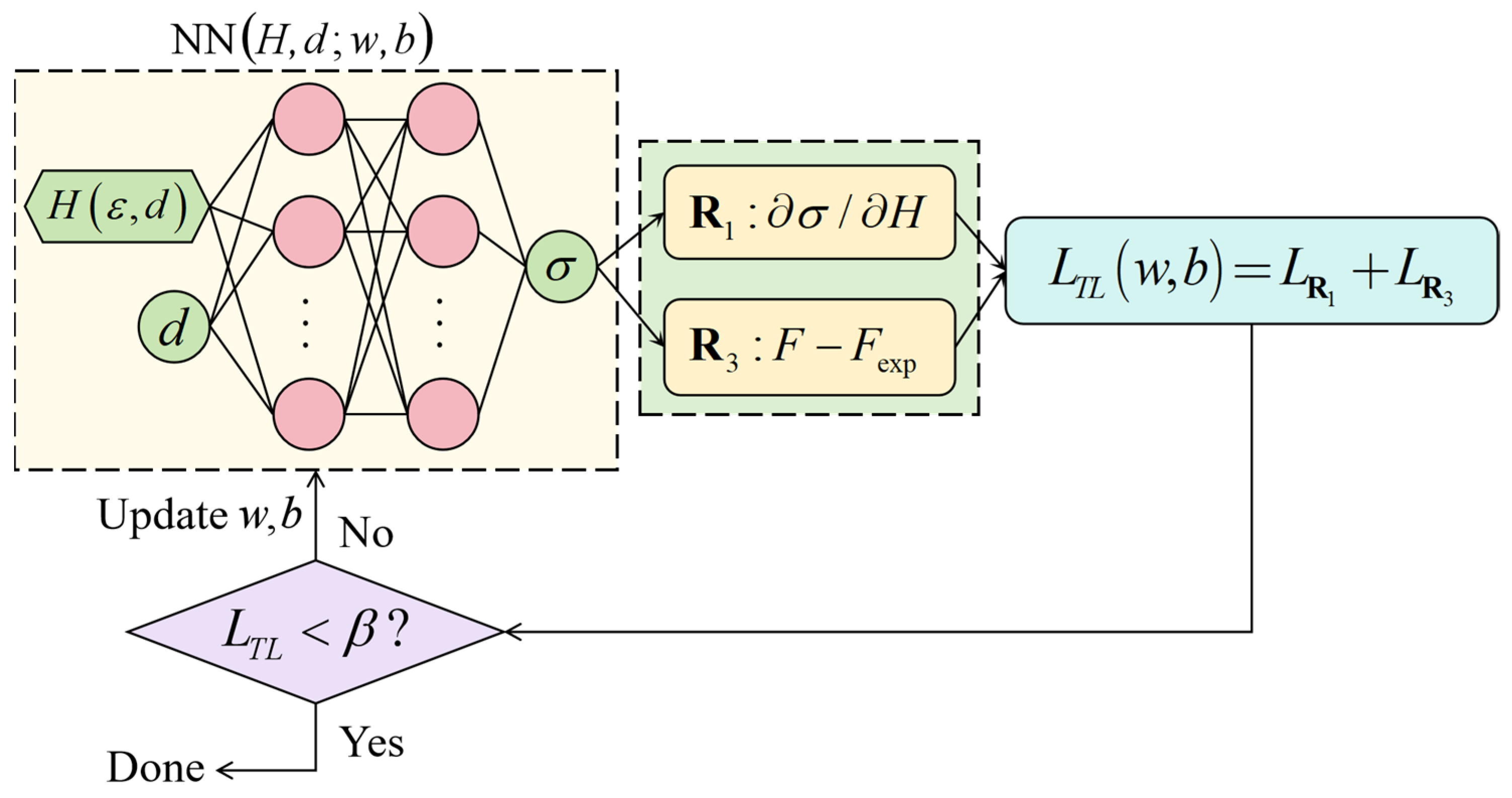
4.3. Depth-Dependent PINNs_Hσ Transfer Learning Model
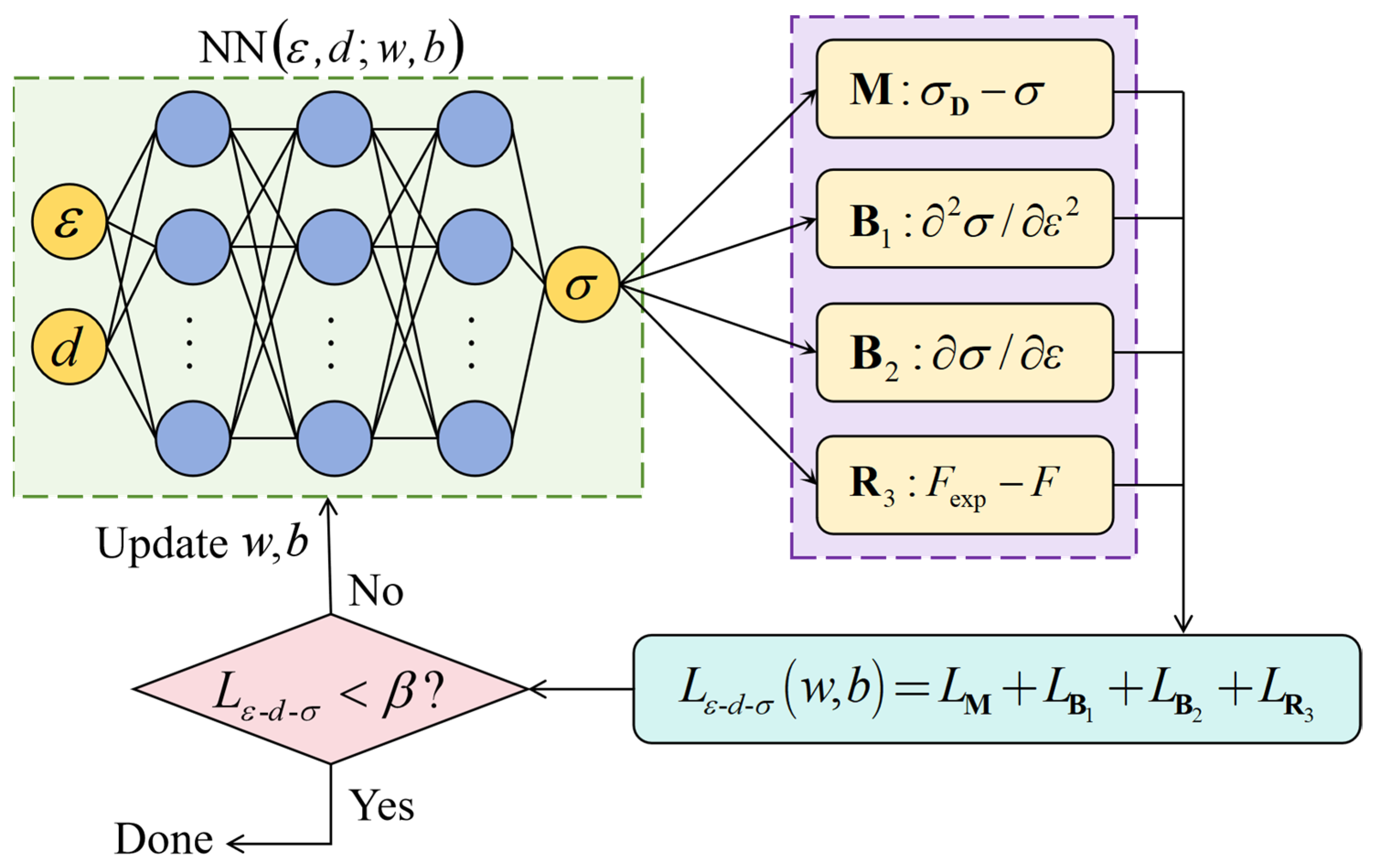
4.4. Depth-Dependent PINNs_εσ Model
5. Validation of Elastic–Plastic Constitutive Relationships of GS 316L Stainless Steel
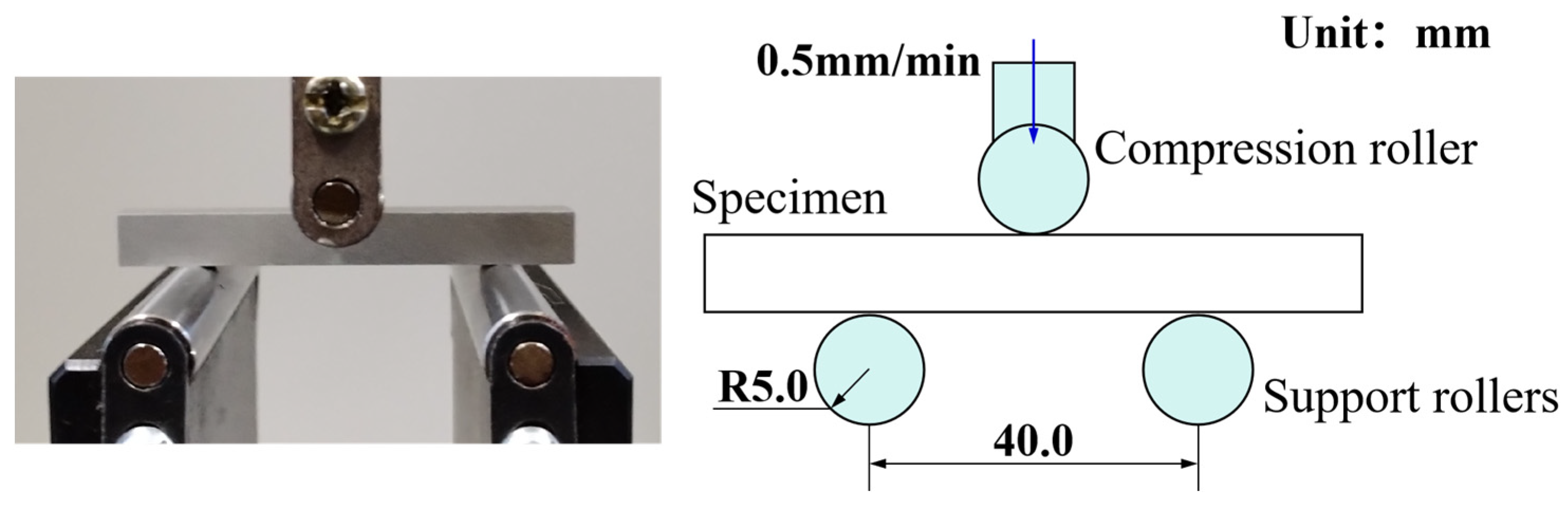
5.1. Three-Point Flexure Test
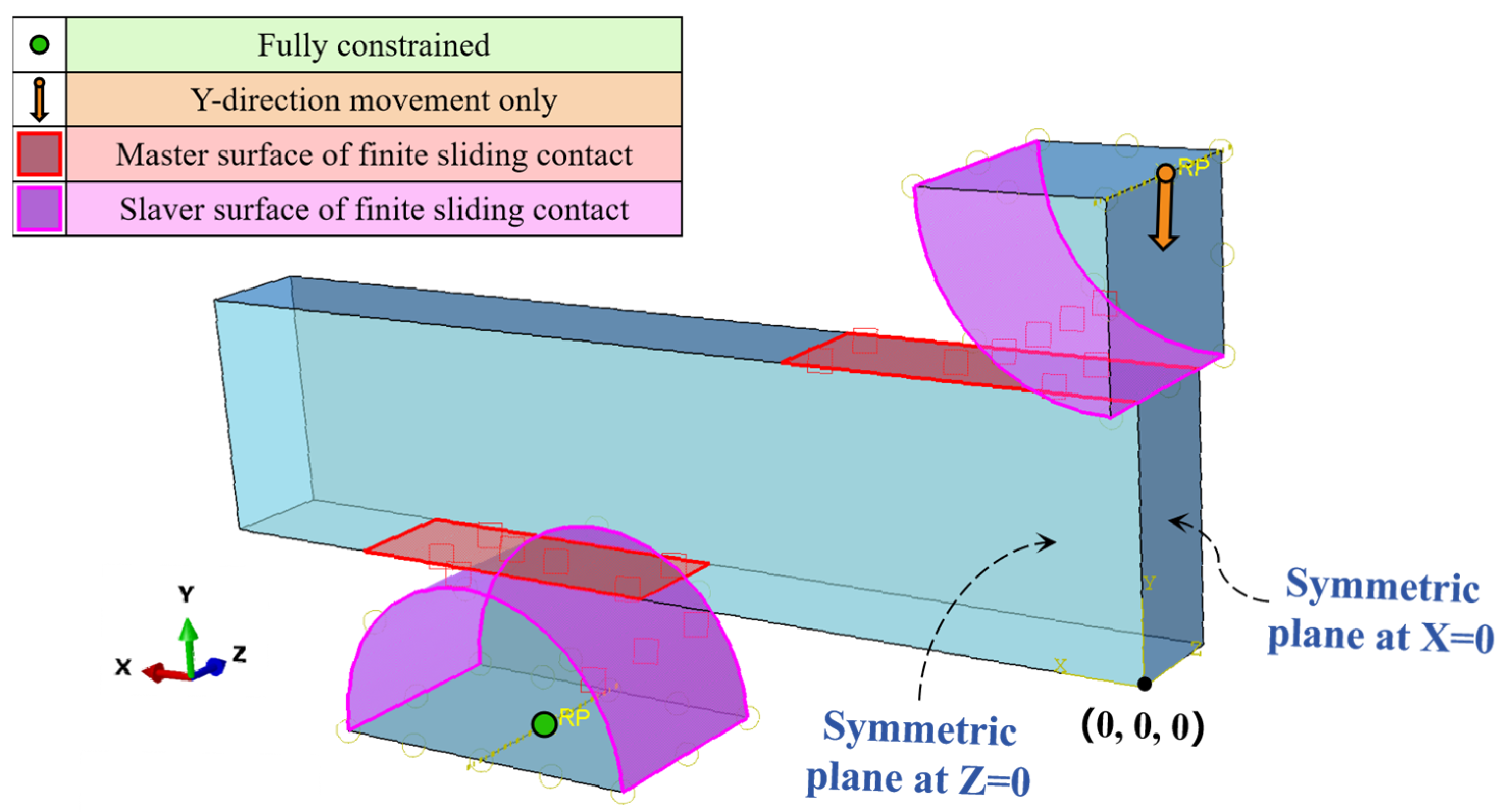
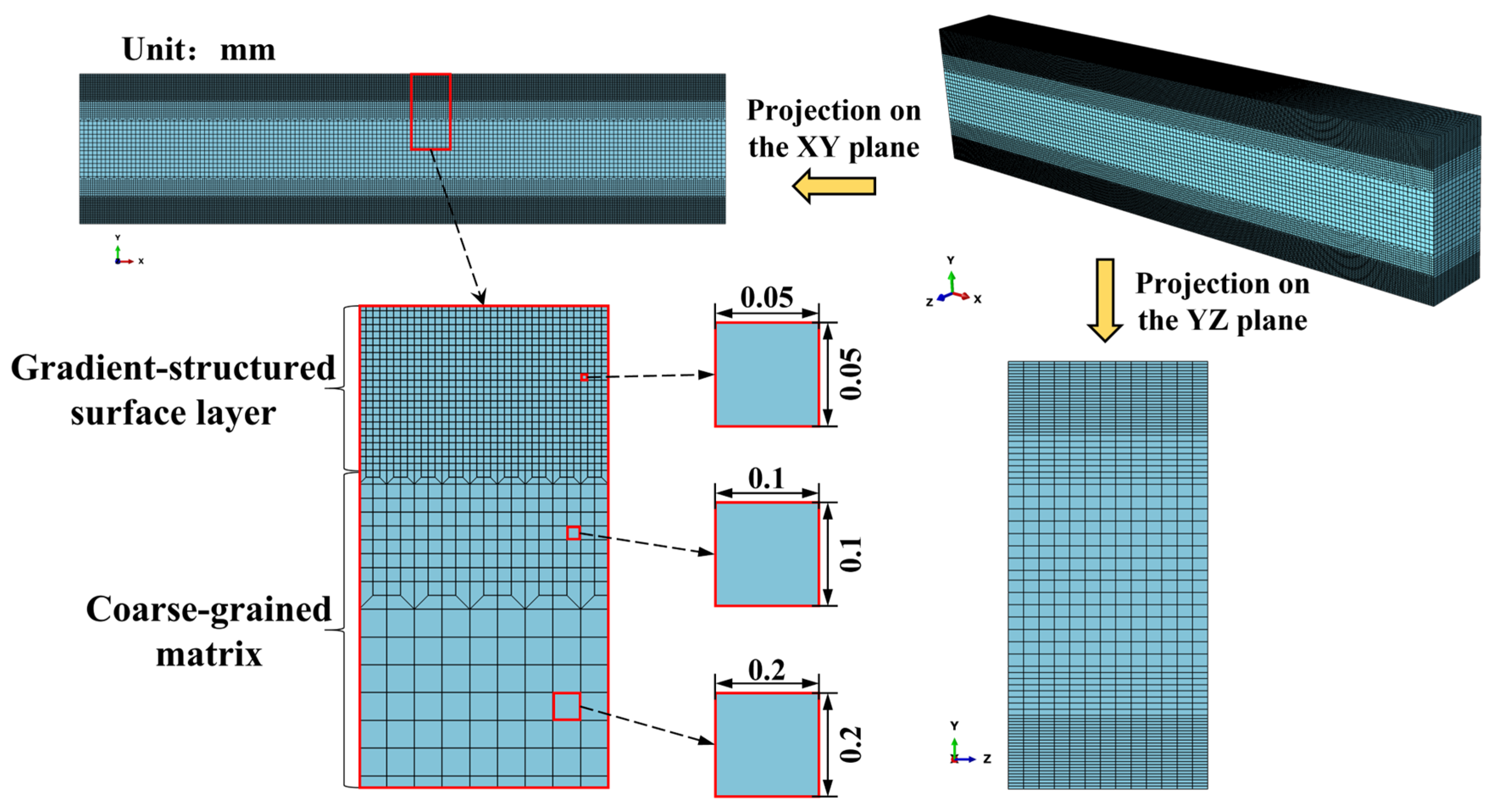
5.2. Finite Element Simulation
5.3. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ritchie, R.O. The conflicts between strength and toughness. Nat. Mater. 2011, 10, 817–822. [Google Scholar] [CrossRef]
- Lu, K.; Lu, L.; Suresh, S. Strengthening Materials by Engineering Coherent Internal Boundaries at the Nanoscale. Science 2009, 324, 349–352. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Jiang, P.; Chen, L.; Yuan, F.; Zhu, Y.T. Extraordinary strain hardening by gradient structure. Proc. Natl. Acad. Sci. USA 2014, 111, 7197–7201. [Google Scholar] [CrossRef]
- He, B.; Hu, B.; Yen, H.; Cheng, G.; Wang, Z.; Luo, H.; Huang, M. High dislocation density–induced large ductility in deformed and partitioned steels. Science 2017, 357, 1029–1032. [Google Scholar] [CrossRef]
- Wu, G.; Chan, K.-C.; Zhu, L.; Sun, L.; Lu, J. Dual-phase nanostructuring as a route to high-strength magnesium alloys. Nature 2017, 545, 80–83. [Google Scholar] [CrossRef]
- Liu, L.; Yu, Q.; Wang, Z.; Ell, J.; Huang, M.X.; Ritchie, R.O. Making ultrastrong steel tough by grain-boundary delamination. Science 2020, 368, 1347–1352. [Google Scholar] [CrossRef]
- Lu, K.; Lu, J. Nanostructured surface layer on metallic materials induced by surface mechanical attrition treatment. Mater. Sci. Eng. A 2004, 375–377, 38–45. [Google Scholar] [CrossRef]
- Fang, T.H.; Li, W.L.; Tao, N.R.; Lu, K. Revealing Extraordinary Intrinsic Tensile Plasticity in Gradient Nano-Grained Copper. Science 2011, 331, 1587–1590. [Google Scholar] [CrossRef] [PubMed]
- Lu, K. Stabilizing nanostructures in metals using grain and twin boundary architectures. Nat. Rev. Mater. 2016, 1, 1–13. [Google Scholar] [CrossRef]
- Tao, N.R.; Wang, Z.B.; Tong, W.P.; Sui, M.L.; Lu, J.; Lu, K. An investigation of surface nanocrystallization mechanism in Fe induced by surface mechanical attrition treatment. Acta Mater. 2002, 50, 4603–4616. [Google Scholar] [CrossRef]
- Liu, X.C.; Zhang, H.W.; Lu, K. Strain-Induced Ultrahard and Ultrastable Nanolaminated Structure in Nickel. Science 2013, 342, 337–340. [Google Scholar] [CrossRef]
- Li, X.; Sun, B.-H.; Guan, B.; Jia, Y.-F.; Gong, C.-Y.; Zhang, X.-C.; Tu, S.-T. Elucidating the effect of gradient structure on strengthening mechanisms and fatigue behavior of pure titanium. Int. J. Fatigue 2021, 146, 106142. [Google Scholar] [CrossRef]
- Huang, H.W.; Wang, Z.B.; Lu, J.; Lu, K. Fatigue behaviors of AISI 316L stainless steel with a gradient nanostructured surface layer. Acta Mater. 2015, 87, 150–160. [Google Scholar] [CrossRef]
- Lei, Y.B.; Wang, Z.B.; Xu, J.L.; Lu, K. Simultaneous enhancement of stress- and strain-controlled fatigue properties in 316L stainless steel with gradient nanostructure. Acta Mater. 2019, 168, 133–142. [Google Scholar] [CrossRef]
- Carneiro, L.; Wang, X.; Jiang, Y. Cyclic deformation and fatigue behavior of 316L stainless steel processed by surface mechanical rolling treatment. Int. J. Fatigue 2020, 134, 105469. [Google Scholar] [CrossRef]
- Nikitin, I.; Scholtes, B.; Maier, H.J.; Altenberger, I. High temperature fatigue behavior and residual stress stability of laser-shock peened and deep rolled austenitic steel AISI 304. Scr. Mater. 2004, 50, 1345–1350. [Google Scholar] [CrossRef]
- Lu, J.Z.; Luo, K.Y.; Zhang, Y.K.; Sun, G.F.; Gu, Y.Y.; Zhou, J.Z.; Ren, X.D.; Zhang, X.C.; Zhang, L.F.; Chen, K.M.; et al. Grain refinement mechanism of multiple laser shock processing impacts on ANSI 304 stainless steel. Acta Mater. 2010, 58, 5354–5362. [Google Scholar] [CrossRef]
- Liu, C.; Liu, D.; Zhang, X.; Liu, D.; Ma, A.; Ao, N.; Xu, X. Improving fatigue performance of Ti-6Al-4V alloy via ultrasonic surface rolling process. J. Mater. Sci. Technol. 2019, 35, 1555–1562. [Google Scholar] [CrossRef]
- Villegas, J.C.; Shaw, L.L. Nanocrystallization process and mechanism in a nickel alloy subjected to surface severe plastic deformation. Acta Mater. 2009, 57, 5782–5795. [Google Scholar] [CrossRef]
- Li, X.; Wang, M.; Xu, L.; Xu, T.; Wu, W.; Pan, S.; Wang, C.; Zhang, W.; Cai, X. Progress in indentation test for material characterization: A systematic review. R. Surf. Interfaces 2024, 17, 100358. [Google Scholar] [CrossRef]
- Prasad, K.E.; Rajesh, K.; Ramamurty, U. Micropillar and macropillar compression responses of magnesium single crystals oriented for single slip or extension twinning. Acta Mater. 2014, 65, 316–325. [Google Scholar] [CrossRef]
- Chen, X.H.; Lu, J.; Lu, L.; Lu, K. Tensile properties of a nanocrystalline 316L austenitic stainless steel. Scr. Mater. 2005, 52, 1039–1044. [Google Scholar] [CrossRef]
- Li, J.; Soh, A.K. Modeling of the plastic deformation of nanostructured materials with grain size gradient. Int. J. Plast. 2012, 39, 88–102. [Google Scholar] [CrossRef]
- Li, J.; Weng, G.J.; Chen, S.; Wu, X. On strain hardening mechanism in gradient nanostructures. Int. J. Plast. 2017, 88, 89–107. [Google Scholar] [CrossRef]
- Li, J.; Chen, S.; Wu, X.; Soh, A.K. A physical model revealing strong strain hardening in nano-grained metals induced by grain size gradient structure. Mater. Sci. Eng. A 2015, 620, 16–21. [Google Scholar] [CrossRef]
- Lyu, H.; Hamid, M.; Ruimi, A.; Zbib, H.M. Stress/strain gradient plasticity model for size effects in heterogeneous nano-microstructures. Int. J. Plast. 2017, 97, 46–63. [Google Scholar] [CrossRef]
- Zeng, Z.; Li, X.; Xu, D.; Lu, L.; Gao, H.; Zhu, T. Gradient plasticity in gradient nano-grained metals. Extrem. Mech. Lett. 2016, 8, 213–219. [Google Scholar] [CrossRef]
- Zhu, L.; Ruan, H.; Chen, A.; Guo, X.; Lu, J. Microstructures-based constitutive analysis for mechanical properties of gradient-nanostructured 304 stainless steels. Acta Mater. 2017, 128, 375–390. [Google Scholar] [CrossRef]
- Zhang, Y.; Fan, J.; Gan, B.; Guo, X.; Ruan, H.; Zhu, L. Constitutive modeling of mechanical behaviors in gradient nanostructured alloys with hierarchical dual-phased microstructures. Acta Mater. 2022, 233, 3197–3212. [Google Scholar] [CrossRef]
- Jin, H.; Zhou, J.; Chen, Y. Grain size gradient and length scale effect on mechanical behaviors of surface nanocrystalline metals. Mater. Sci. Eng. A 2018, 725, 1–7. [Google Scholar] [CrossRef]
- Tao, F.; Liu, X.; Du, H.; Yu, W. Learning composite constitutive laws via coupling Abaqus and deep neural network. Compos. Struct. 2021, 272, 114137. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, X.; Shi, M.; Roters, F.; Kang, G.; Raabe, D. Dislocation mechanism based size-dependent crystal plasticity modeling and simulation of gradient nano-grained copper. Int. J. Plast. 2019, 113, 52–73. [Google Scholar] [CrossRef]
- Lu, X.; Zhao, J.; Wang, Z.; Gan, B.; Zhao, J.; Kang, G.; Zhang, X. Crystal plasticity finite element analysis of gradient nanostructured TWIP steel. Int. J. Plast. 2020, 130, 102703. [Google Scholar] [CrossRef]
- Zhao, J.; Lu, X.; Yuan, F.; Kan, Q.; Qu, S.; Kang, G.; Zhang, X. Multiple mechanism based constitutive modeling of gradient nanograined material. Int. J. Plast. 2020, 125, 314–330. [Google Scholar] [CrossRef]
- Wang, M.; Jiang, S.; Sun, D.; Zhang, Y.; Yan, B. Molecular dynamics simulation of mechanical behavior and phase transformation of nanocrystalline NiTi shape memory alloy with gradient structure. Comput. Mater. Sci. 2022, 204, 111186. [Google Scholar] [CrossRef]
- He, C.-Y.; Yang, X.-F.; Chen, H.; Zhang, Y.; Yuan, G.-J.; Jia, Y.-F.; Zhang, X.-C. Size-dependent deformation mechanisms in copper gradient nano-grained structure: A molecular dynamics simulation. Mater. Today Commun. 2022, 31, 103198. [Google Scholar] [CrossRef]
- Liu, M.; Liang, L.; Sun, W. A generic physics-informed neural network-based constitutive model for soft biological tissues. Comput. Methods Appl. Mech. Eng. 2020, 372, 113402. [Google Scholar] [CrossRef]
- Li, K.-Q.; Yin, Z.-Y.; Zhang, N.; Li, J. A PINN-based modelling approach for hydromechanical behaviour of unsaturated expansive soils. Comput. Geotech. 2024, 169, 106174. [Google Scholar] [CrossRef]
- Su, M.M.; Yu, Y.; Chen, T.H.; Guo, N.; Yang, Z.X. A thermodynamics-informed neural network for elastoplastic constitutive modeling of granular materials. Comput. Methods Appl. Mech. Eng. 2024, 430, 117246. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Güneş Baydin, A.; Pearlmutter, B.A.; Andreyevich Radul, A.; Mark Siskind, J. Automatic differentiation in machine learning: A survey. J. Mach. Learn. Res. 2018, 18, 1–43. [Google Scholar]
- Ralls, A.M.; Leong, K.; Lu, L.; Liu, S.; Wang, X.; Jiang, Y.; Menezes, P.L. Unraveling the friction and wear mechanisms of surface nanostructured stainless-steel. Wear 2024, 538, 205185. [Google Scholar] [CrossRef]
- Cheng, Y.; Lin, Z.; Xie, S.; Wang, X.; Jiang, Y. Strengthening mechanism of abnormally enhanced fatigue ductility of gradient nanostructured 316L stainless steel. Int. J. Fatigue 2024, 186, 108415. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Cheng, Y.; Wang, Z.; Wang, X. Physics-Informed Neural Networks for Depth-Dependent Constitutive Relationships of Gradient Nanostructured 316L Stainless Steel. Materials 2025, 18, 3532. https://doi.org/10.3390/ma18153532
Li H, Cheng Y, Wang Z, Wang X. Physics-Informed Neural Networks for Depth-Dependent Constitutive Relationships of Gradient Nanostructured 316L Stainless Steel. Materials. 2025; 18(15):3532. https://doi.org/10.3390/ma18153532
Chicago/Turabian StyleLi, Huashu, Yang Cheng, Zheheng Wang, and Xiaogui Wang. 2025. "Physics-Informed Neural Networks for Depth-Dependent Constitutive Relationships of Gradient Nanostructured 316L Stainless Steel" Materials 18, no. 15: 3532. https://doi.org/10.3390/ma18153532
APA StyleLi, H., Cheng, Y., Wang, Z., & Wang, X. (2025). Physics-Informed Neural Networks for Depth-Dependent Constitutive Relationships of Gradient Nanostructured 316L Stainless Steel. Materials, 18(15), 3532. https://doi.org/10.3390/ma18153532




