Study on Axial Compression Performance of CFRP-Aluminum Alloy Laminated Short Tubes
Abstract
1. Introduction
2. Material Properties and Specimen Fabrication
2.1. Constitutive Model of Aluminum Alloy
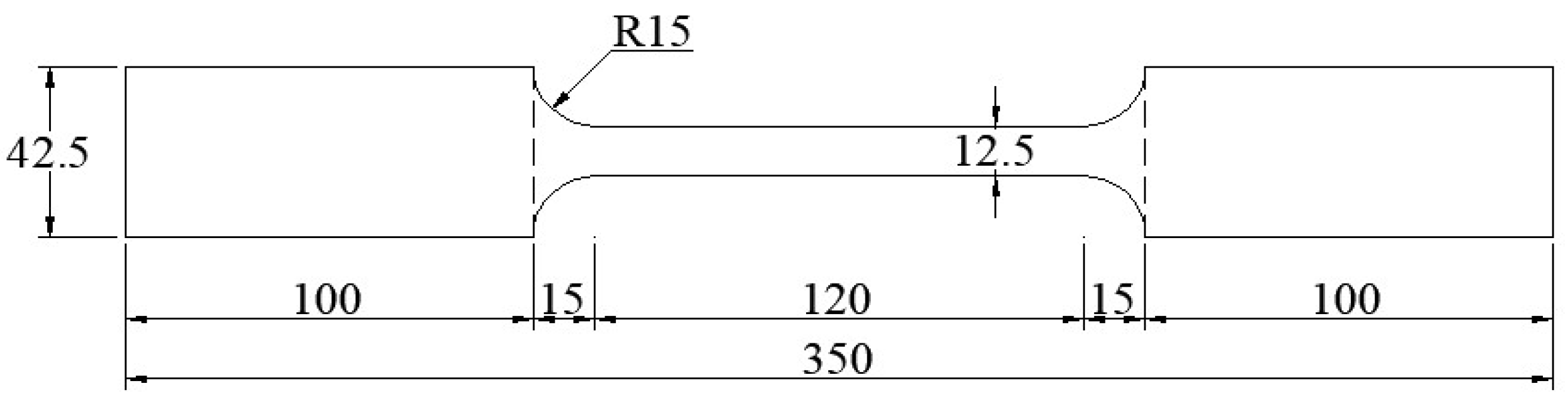
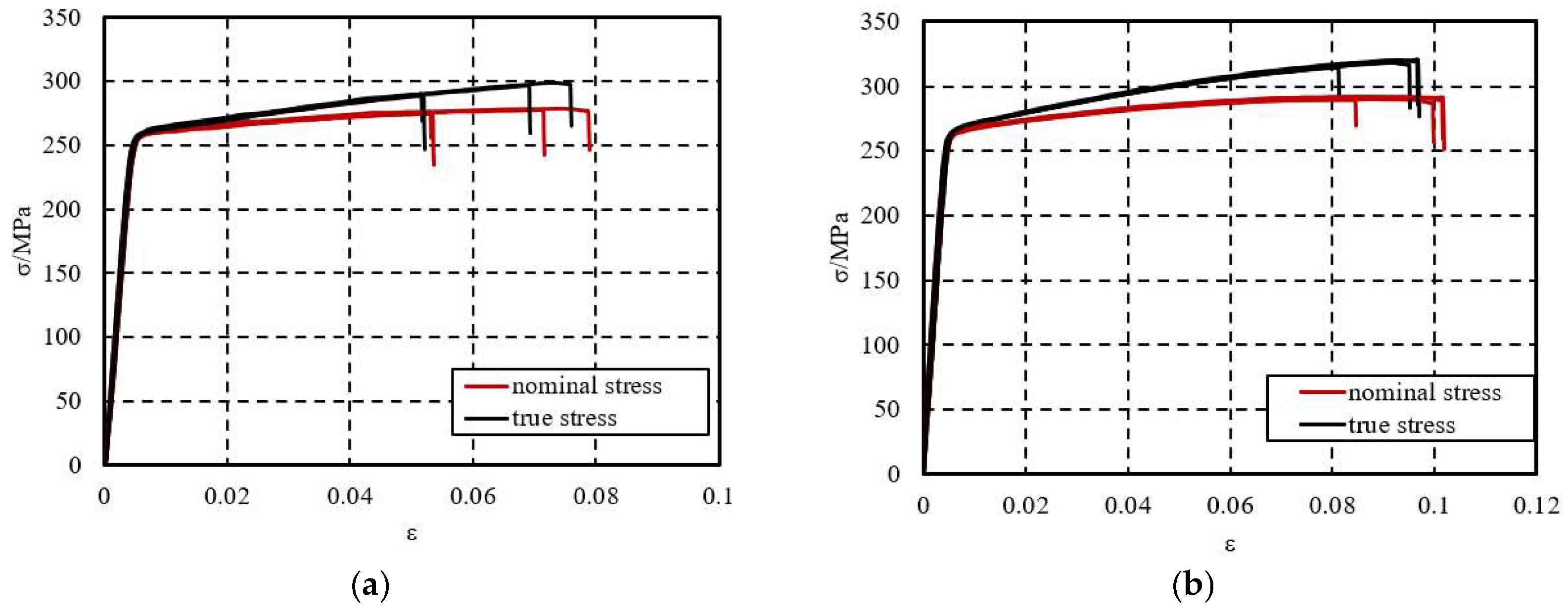
2.1.1. Material Property Test
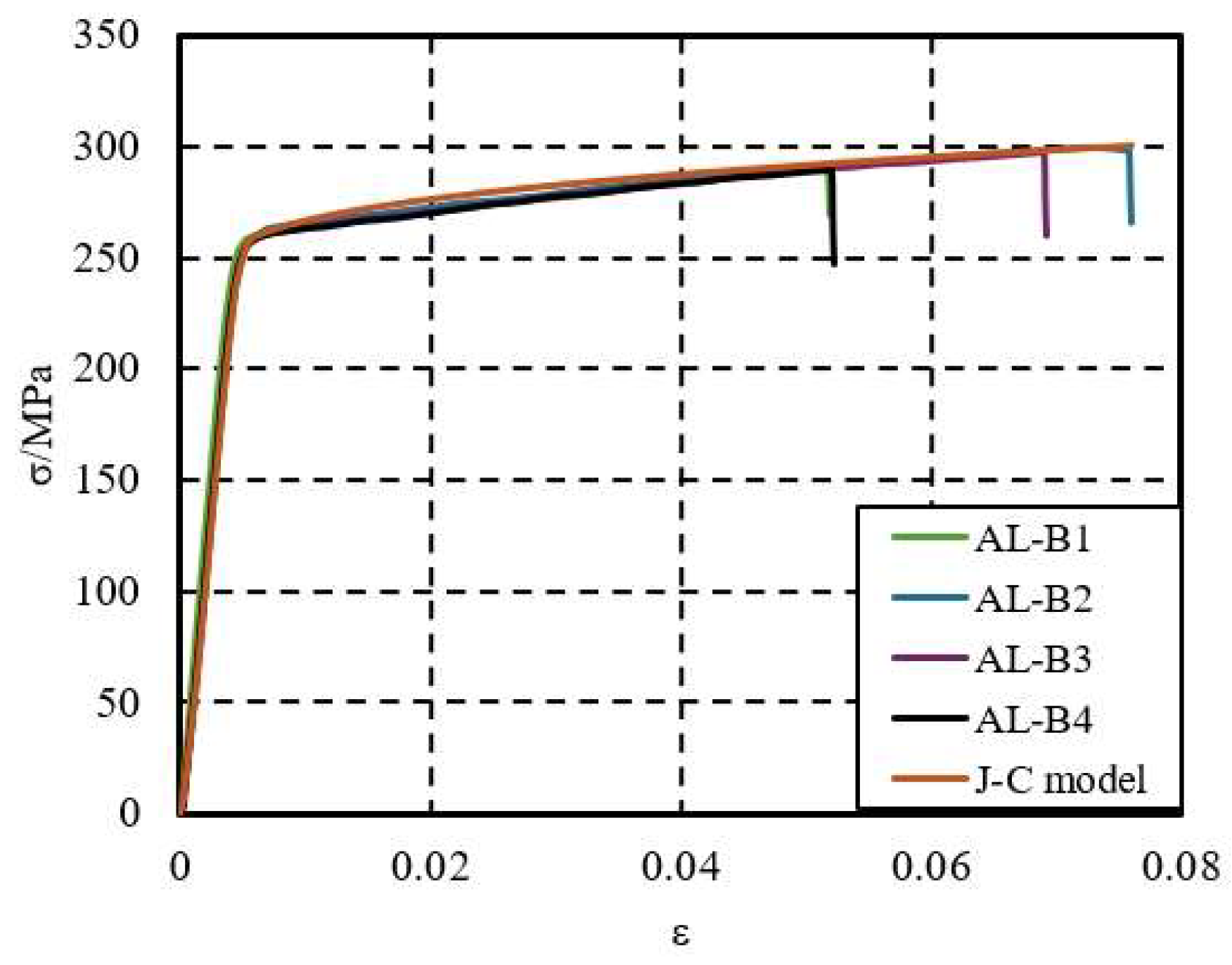
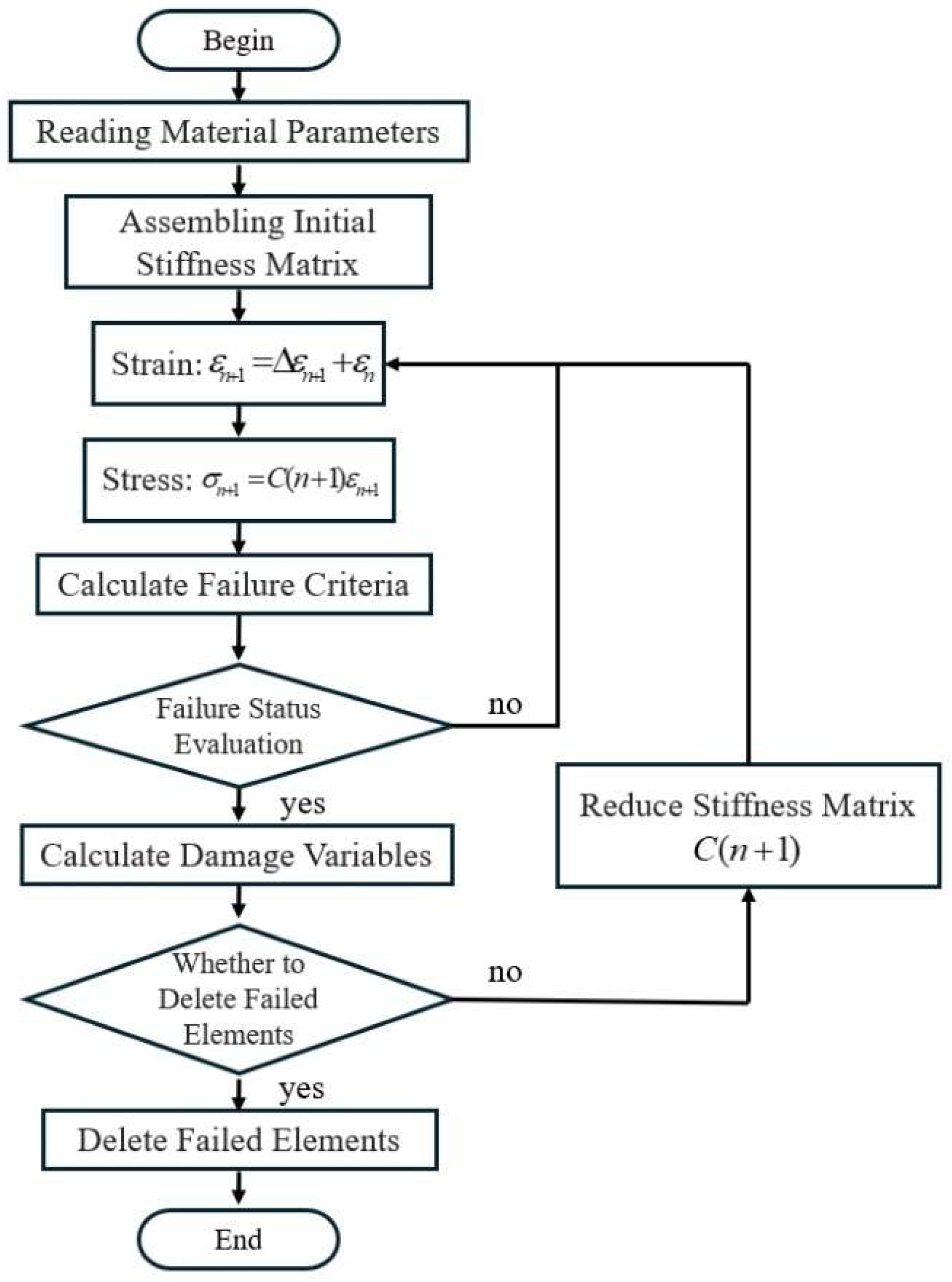
2.1.2. Failure Criteria and Damage Evolution Criteria
- A, B, C, m, n—Material-related constants;
- —Equivalent stress;
- —Equivalent plastic strain;
- —Dimensionless equivalent plastic strain rate;
- —Dimensionless temperature;
- D1~D5—Material performance parameters;
- —Stress triaxiality;
2.2. Constitutive Model of CFRP
2.2.1. Material Properties Test
2.2.2. CFRP Engineering Constants
- E1—Elastic Modulus in the 1 Direction of Composite Material;
- Vf—Fiber Volume Fraction;
- Vm—Matrix Volume Fraction;
- M—Composite material moduli, such as E2, G12, v23;
- Mf—Fiber moduli, such as Ef, Gf, vf;
- Mm—Matrix moduli, such as Em, Gm, vm;
- X1—Strength in the 1 Direction of Composite Material
- Xf—Fiber Strength;
- Xm—Matrix Strength.
2.2.3. Failure Criteria and Damage Evolution Criteria
- X, Y, Z, S—Material strength, where the subscript T denotes tension and C denotes compression;
- , , —Stress components on the fracture surface;
- —The angle between the fracture surface and the cross-section;
- , —Friction coefficient based on the Mohr–Coulomb failure theory;
- —Shear strength on the fracture surface;
- —Material friction angle;
- —Directional stress, where i = j denotes normal stress, and i ≠ j denotes in-plane shear stress.
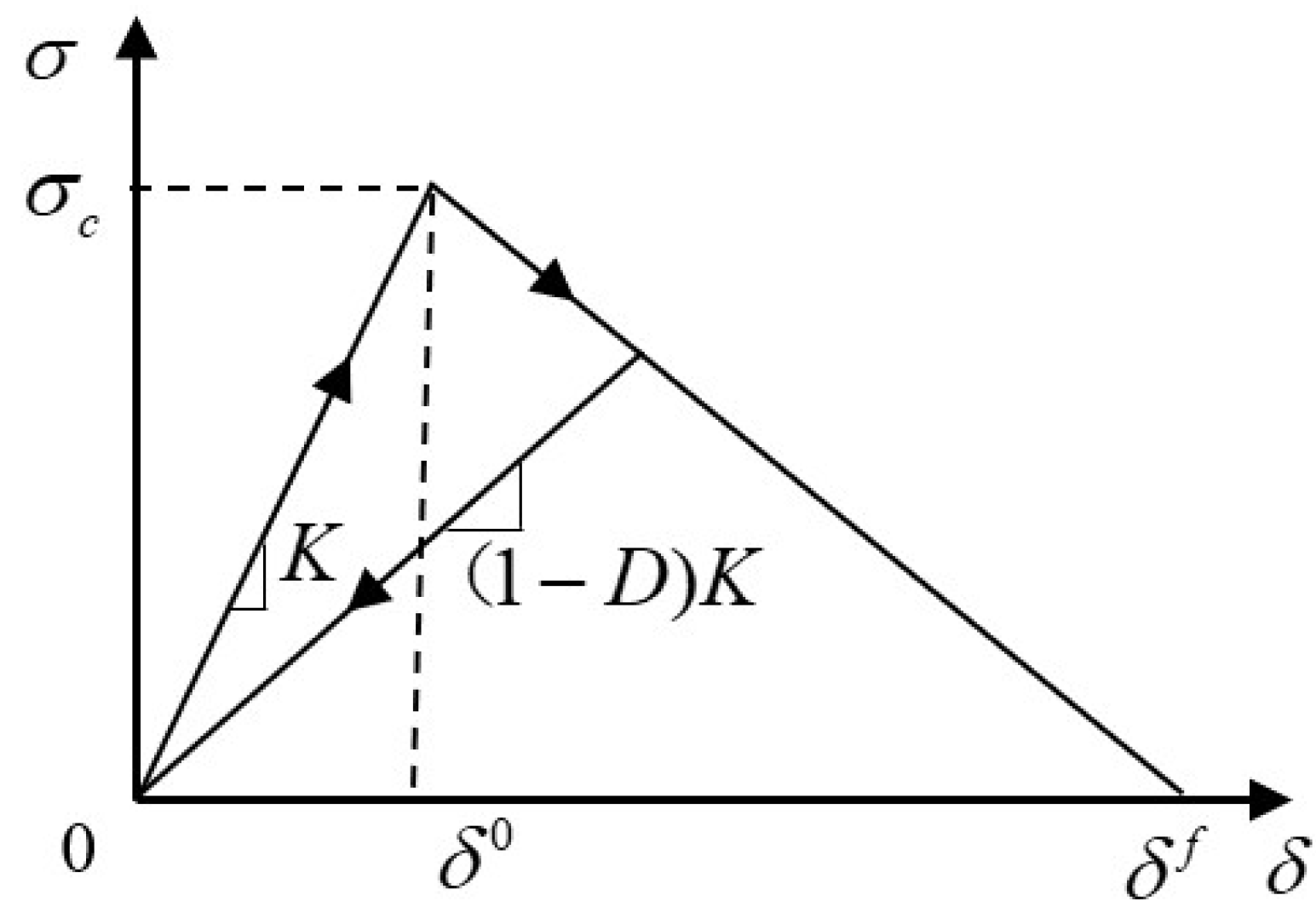
2.3. Interface Constitutive Model
3. Axial Compression Test of Short CFRP-AL Tubes
3.1. Test Plan
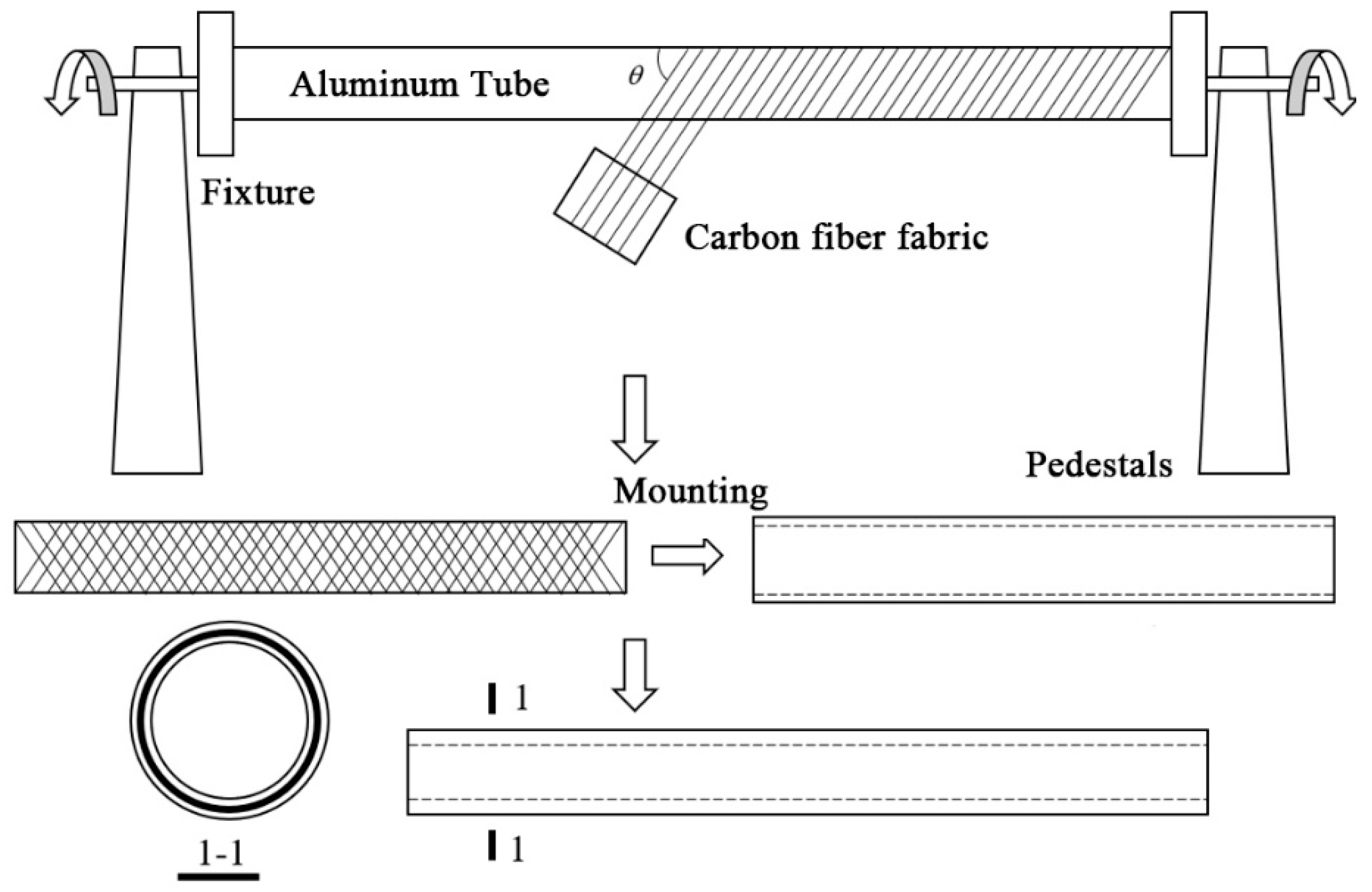
3.1.1. Specimen Fabrication
- Surface Treatment: The aluminum alloy tubes used are 6061-T6 aluminum alloy tubes. The prepared aluminum alloy tubes are cut to the required length. To ensure a certain bonding strength, the metal surface must undergo some surface treatment before bonding [43,44]. Common surface treatments include chemical solvent cleaning and mechanical treatment. For simplicity, acetone solution cleaning is chosen for surface treatment in this study. The outer surface of the inner aluminum alloy tube and the inner surface of the outer aluminum alloy tube are sanded with sandpaper and cleaned with acetone.
- Carbon Fiber Fabric Winding and Epoxy Resin Application: Carbon fiber fabric is manually wound layer by layer onto the outer surface of the inner aluminum alloy tube, followed by the application of epoxy resin. The assembly is slightly heated to enhance the flowability of the epoxy resin.
- Assembly: While the epoxy resin has thorough wettability and good flowability, the carbon fiber-wrapped inner aluminum alloy tube is rotated and assembled into the outer aluminum alloy tube along the fiber angle. During the rotational assembly, the outer aluminum alloy tube exerts some pressure on the inner tube, causing the carbon fiber fabric to tighten and extrude excess epoxy resin, thereby reducing bubbles in the composite material and increasing the fiber volume content.
- Curing and Molding: The assembled composite tube is left to cure naturally at room temperature for 7 days.
- Post-Processing: After curing, the composite tube product is removed and cut to the required dimensions for testing. The edges and burrs of the specimens are polished.
3.1.2. Test Device
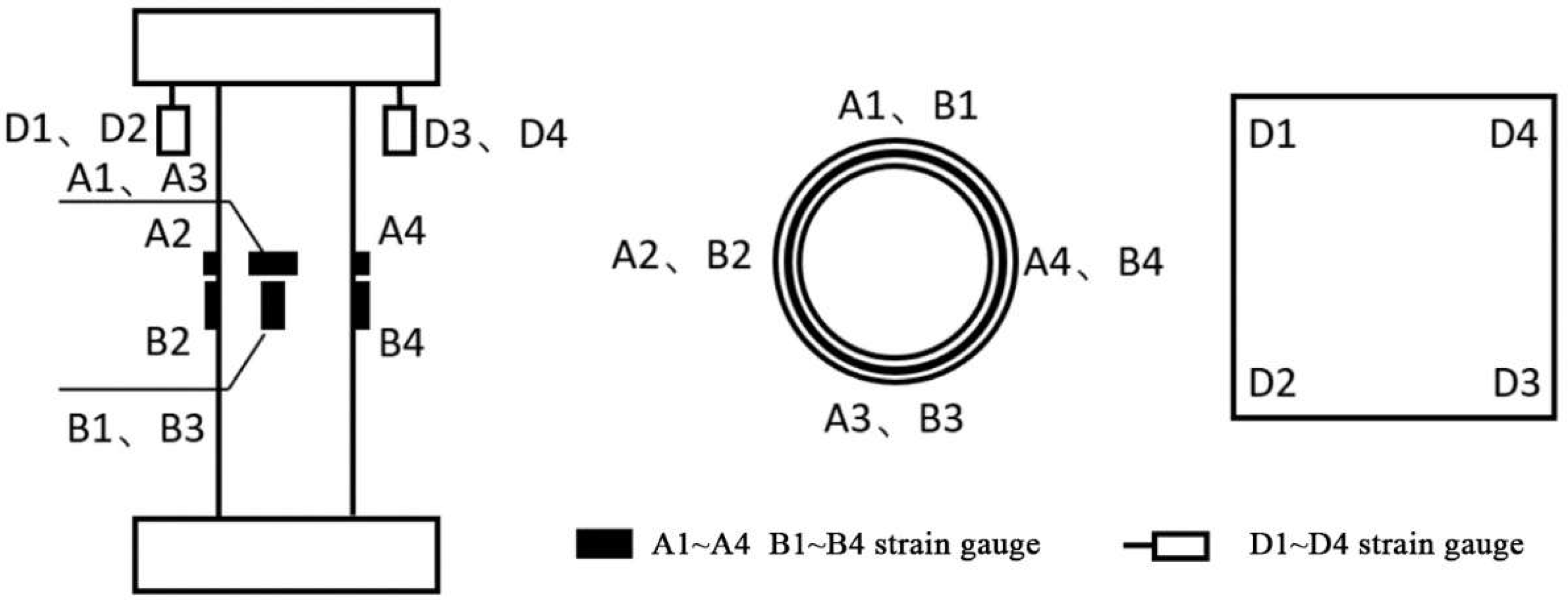
3.1.3. Arrangement of Measurement Points
3.2. Test Results and Analysis
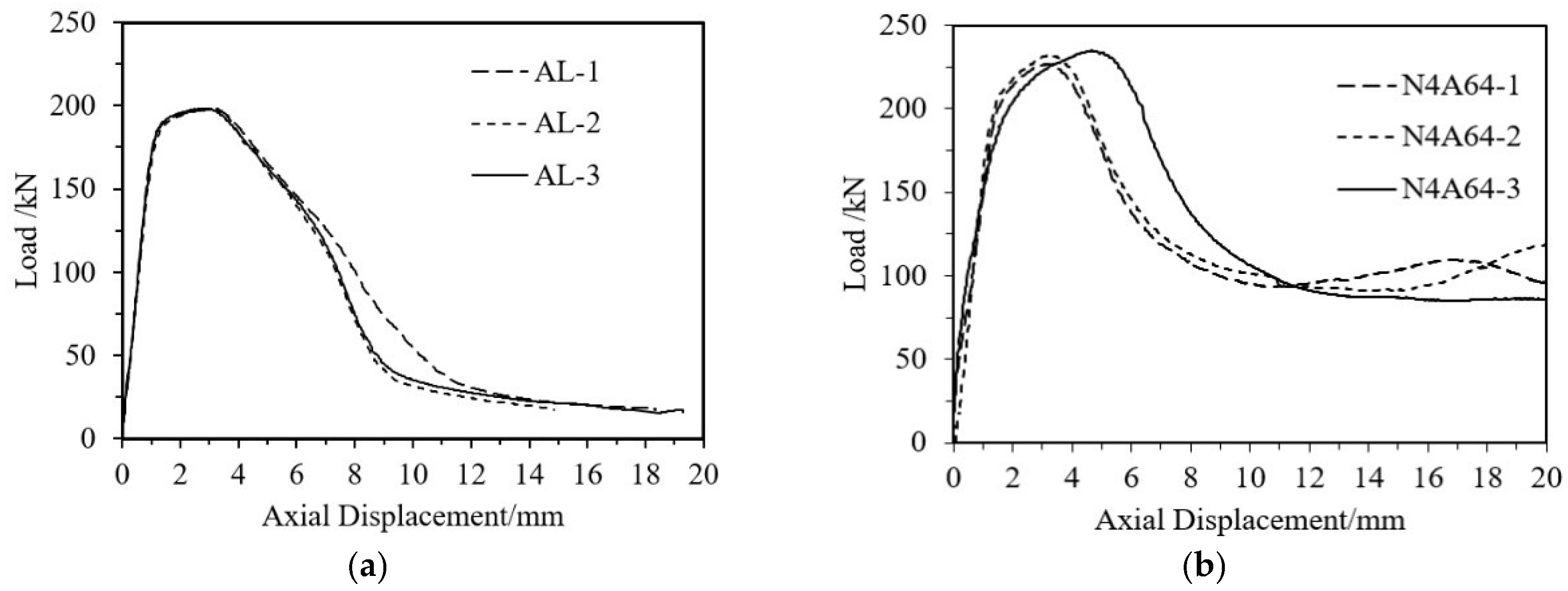
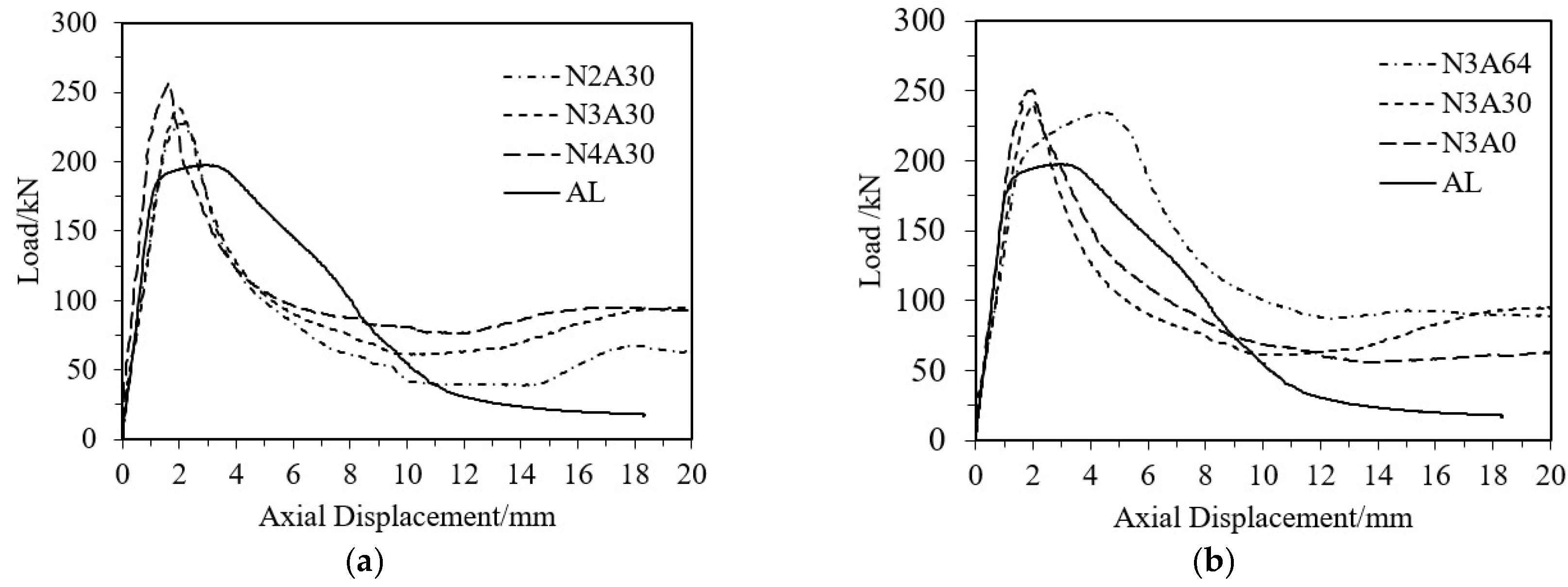
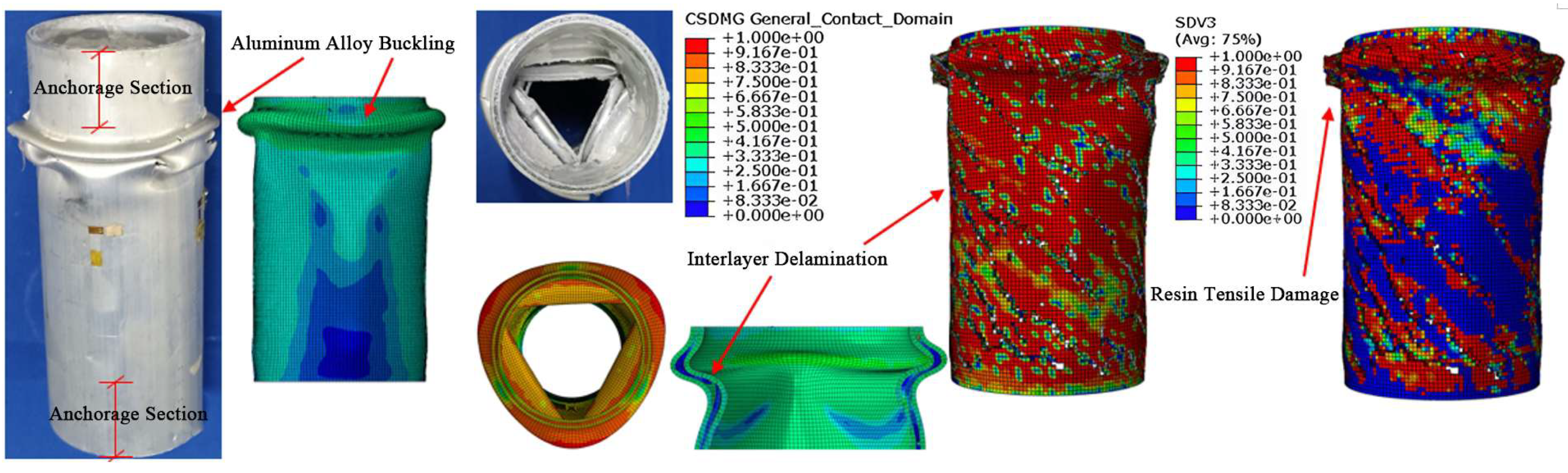
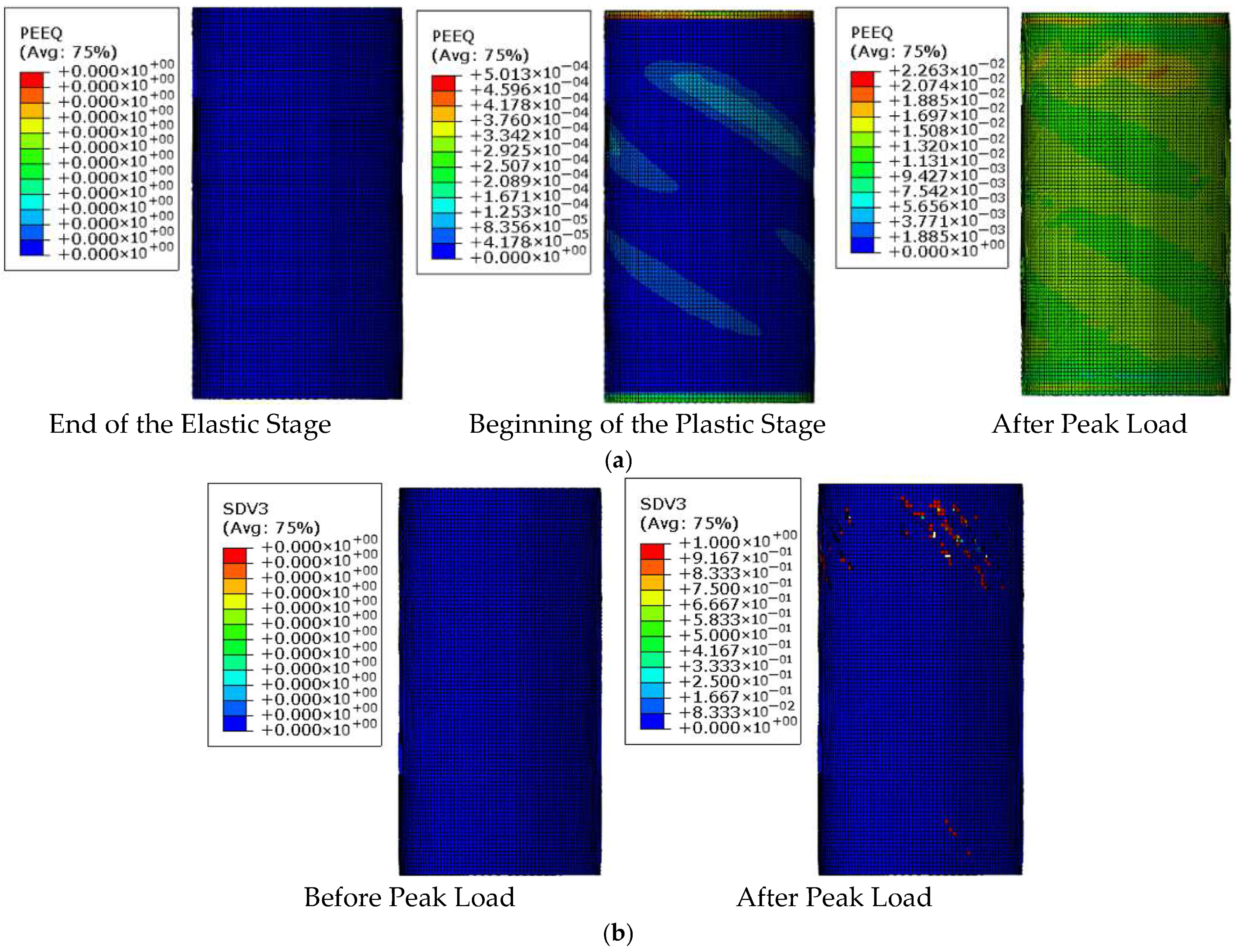
3.2.1. Failure Mode
3.2.2. Ultimate Bearing Capacity
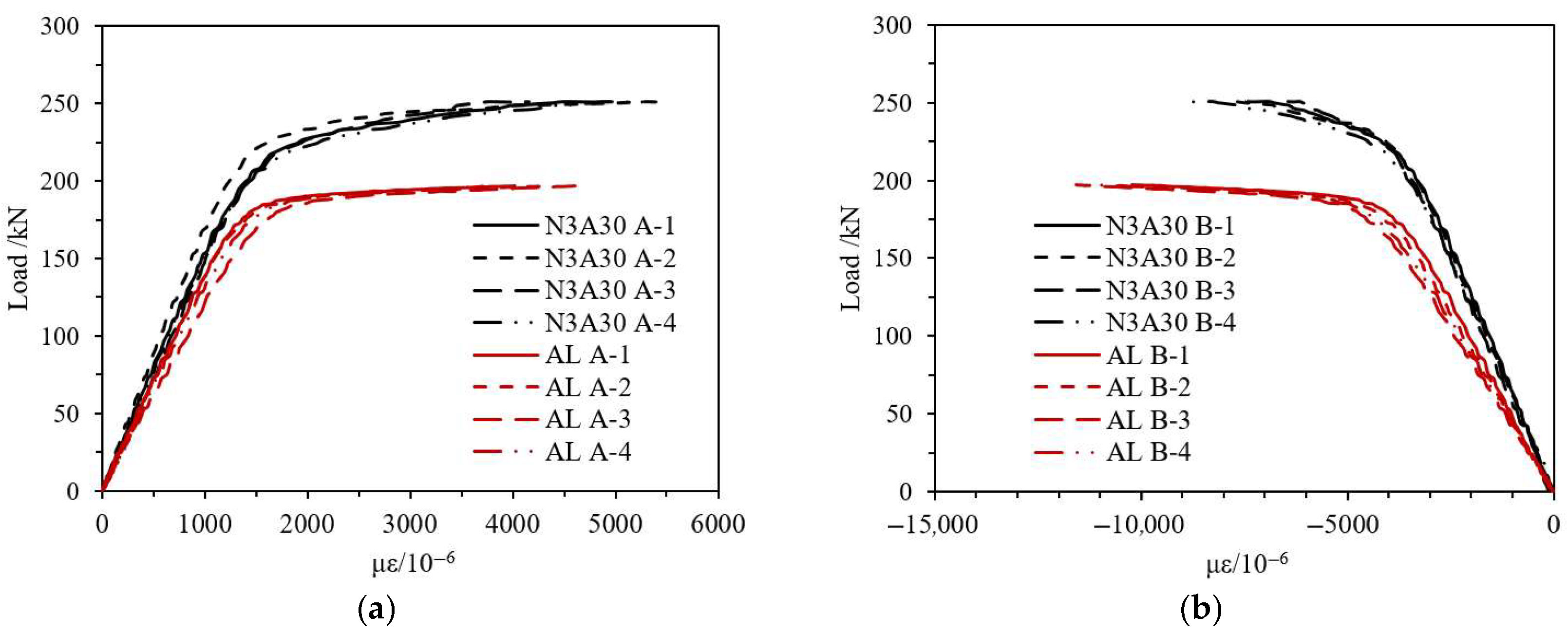
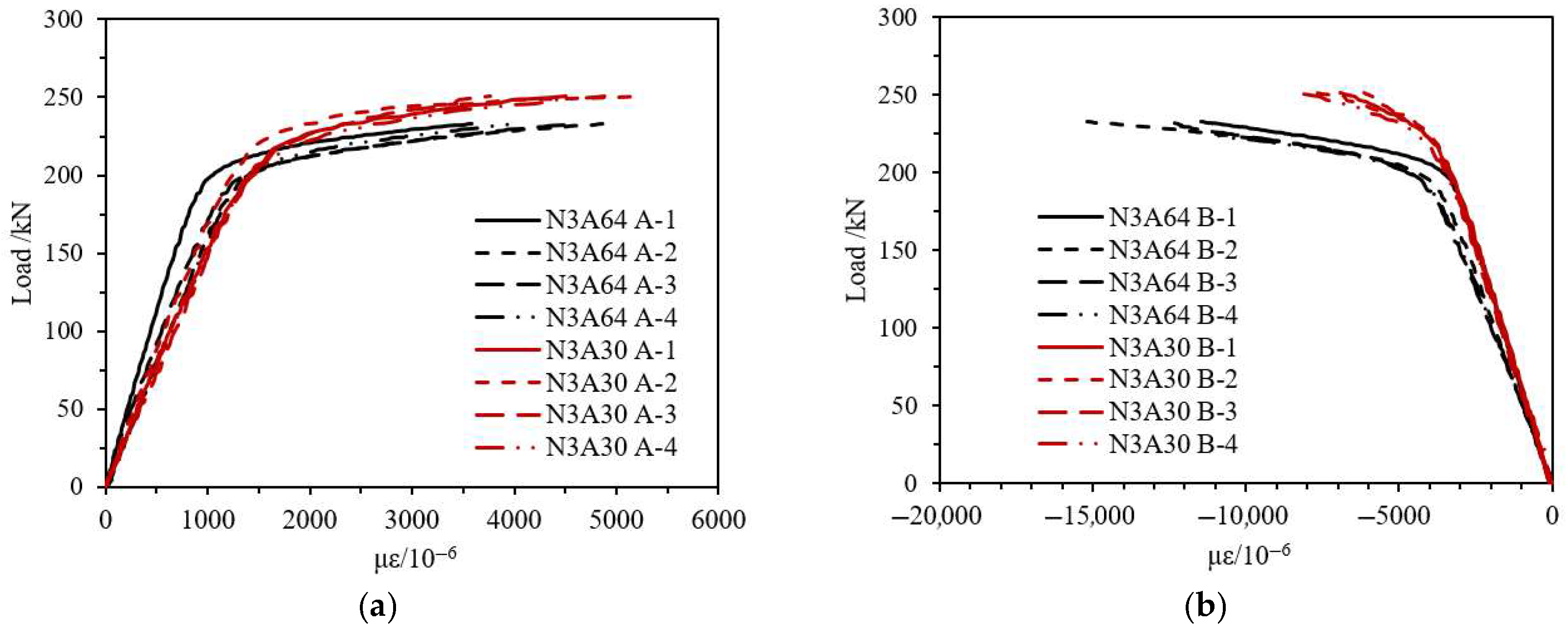
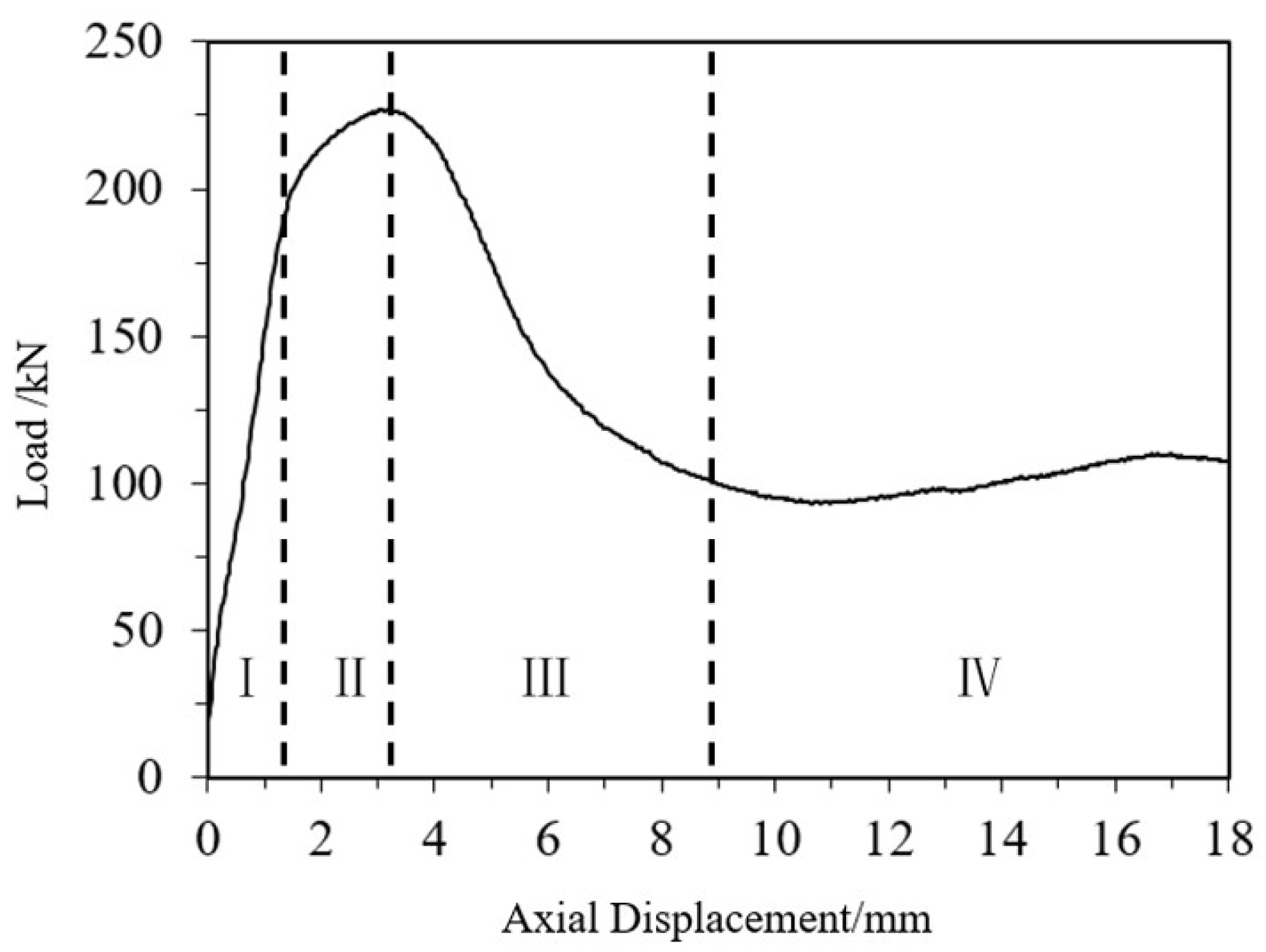
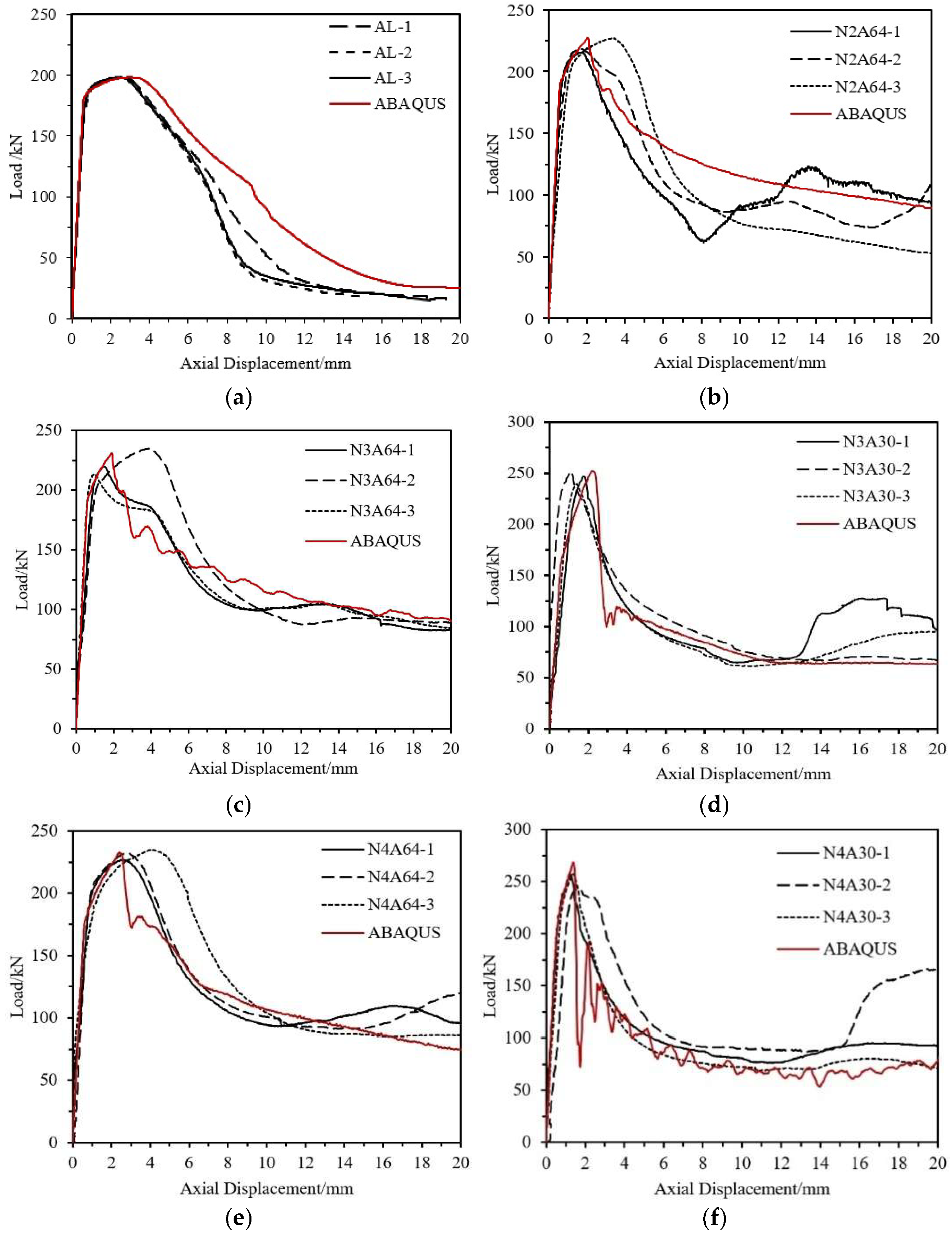
3.2.3. Test Curves
- (1)
- Through the equivalent axial strength of CFRP, it directly increases the ultimate load capacity of the composite specimens;
- (2)
- Through the circumferential confinement effect of CFRP, it limits the initiation and development of crushing deformation after reaching the peak load, thereby enhancing the subsequent load-bearing capacity.
4. Finite Element Analysis
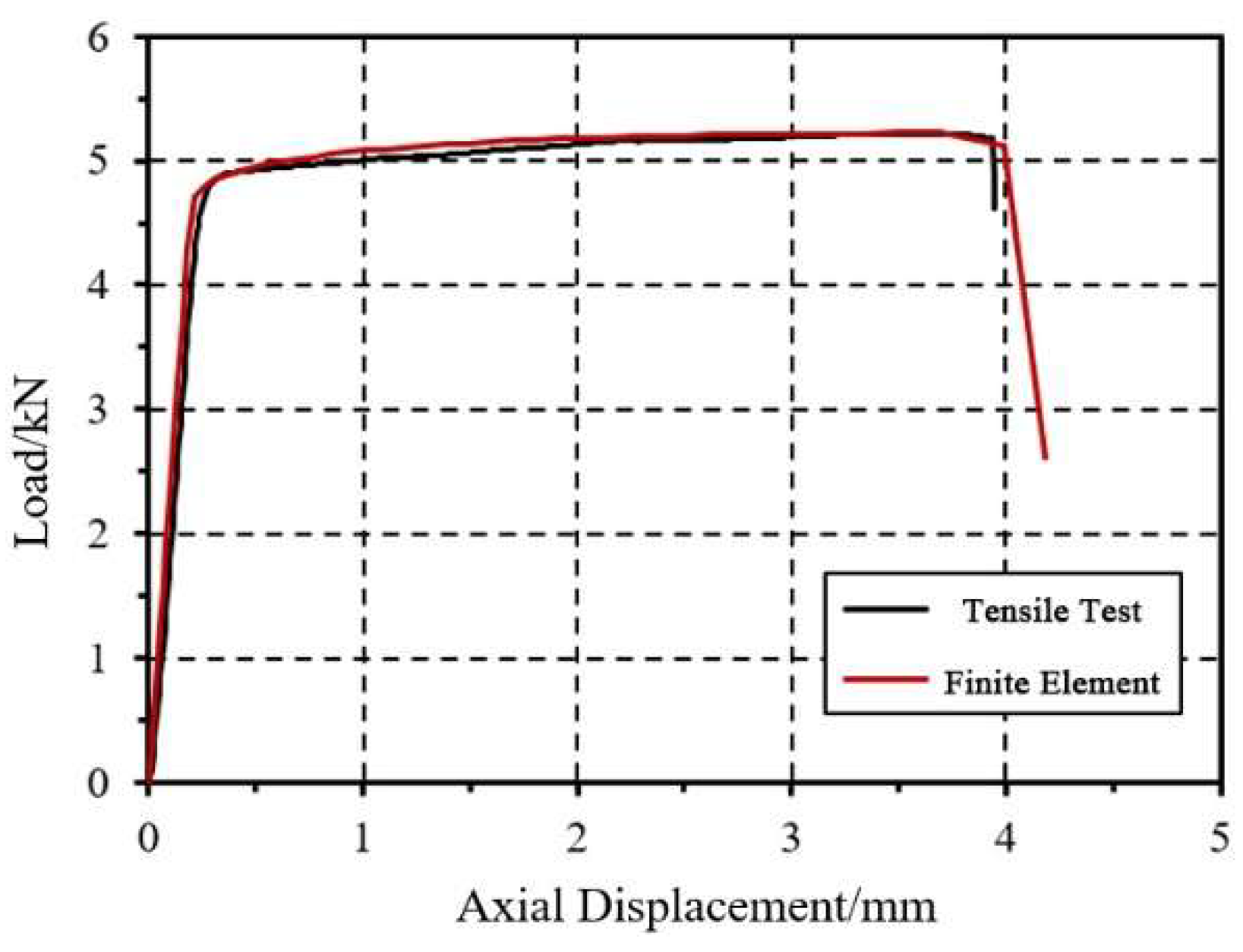
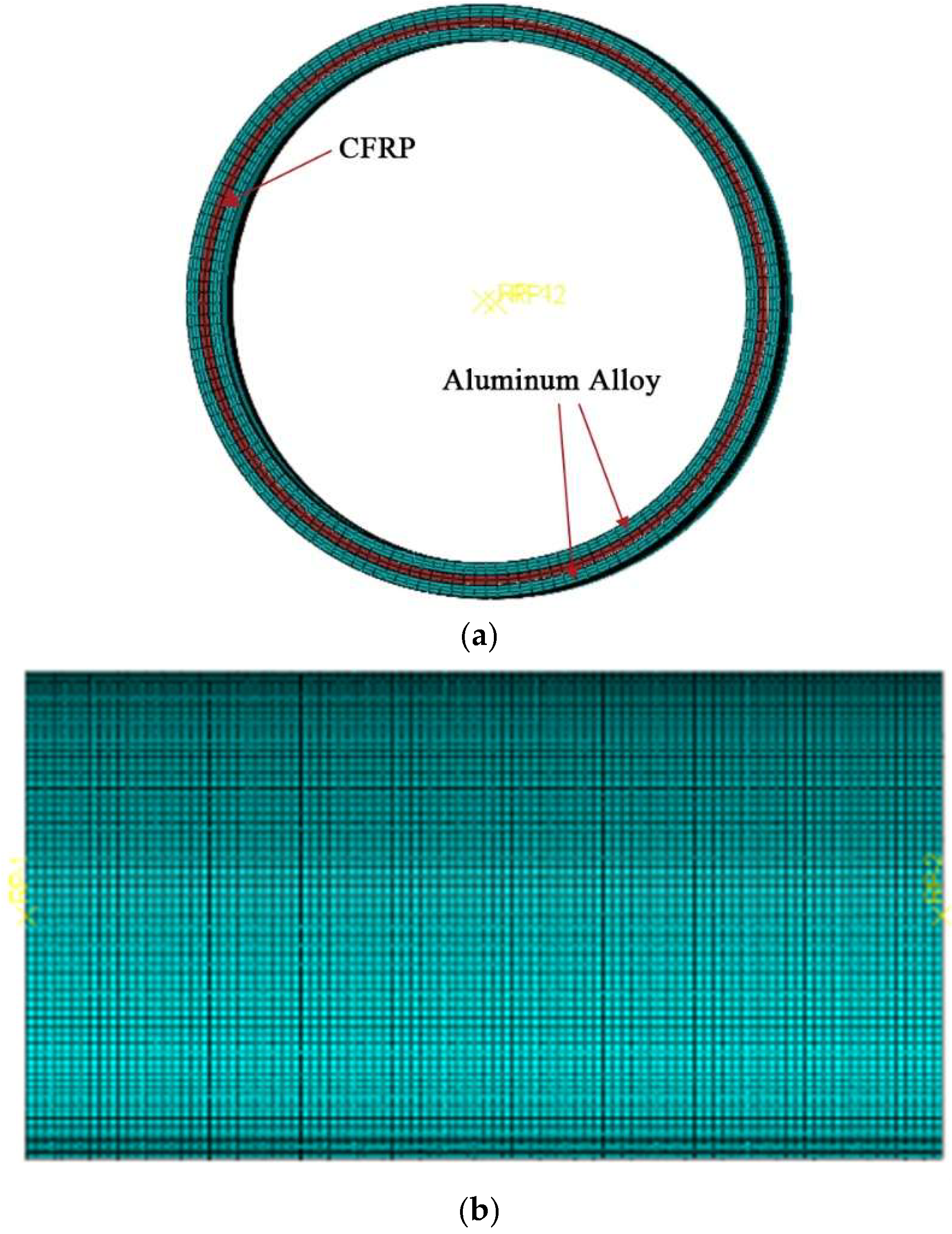
4.1. Finite Element Model
4.2. Finite Element Calculation Results
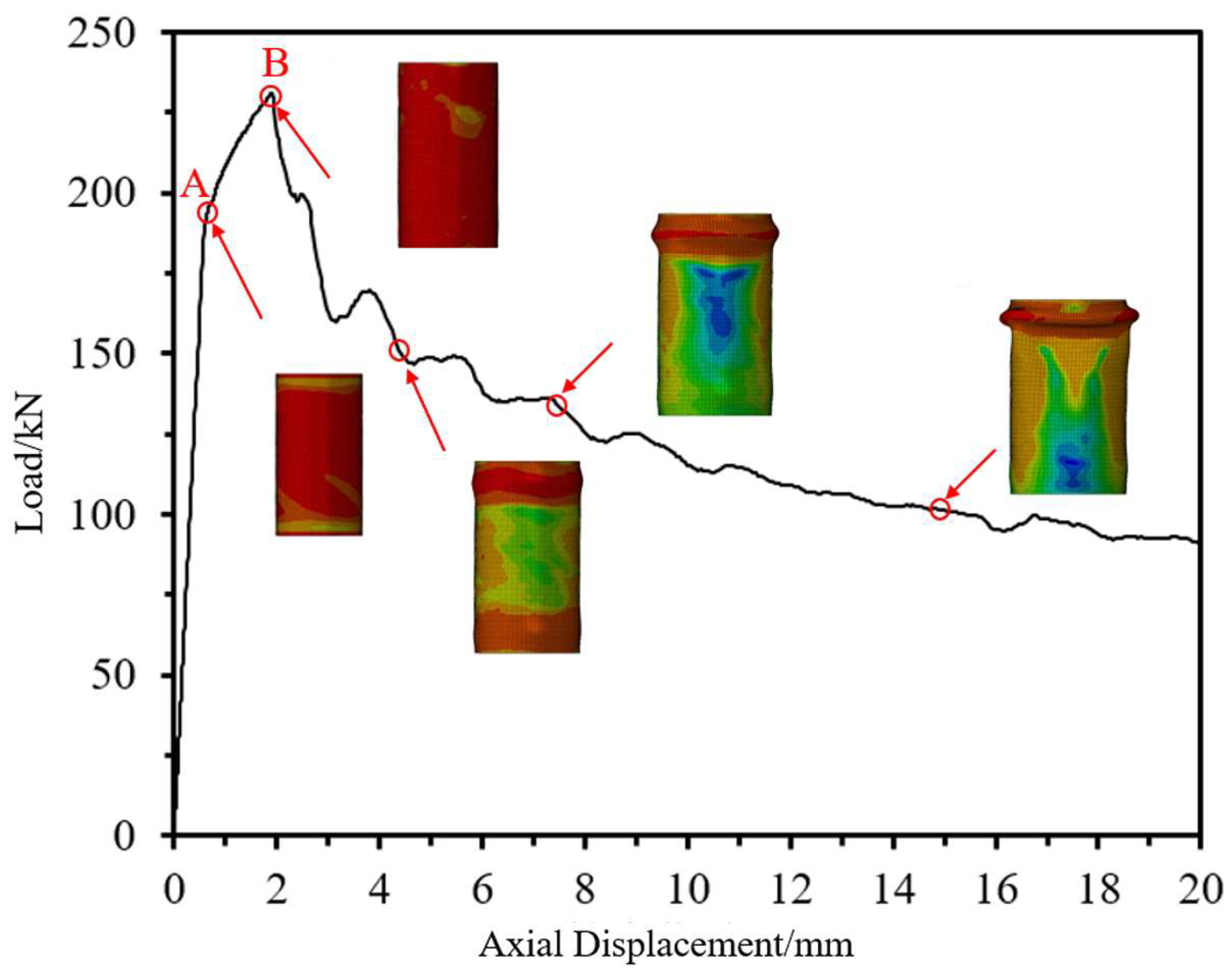
4.3. Mechanism Analysis of CFRP-AL Tubes Under Axial Force
5. Axial Compression Load-Bearing Capacity Formula
5.1. Axial Compression Parameter Analysis of CFRP-AL Tubes
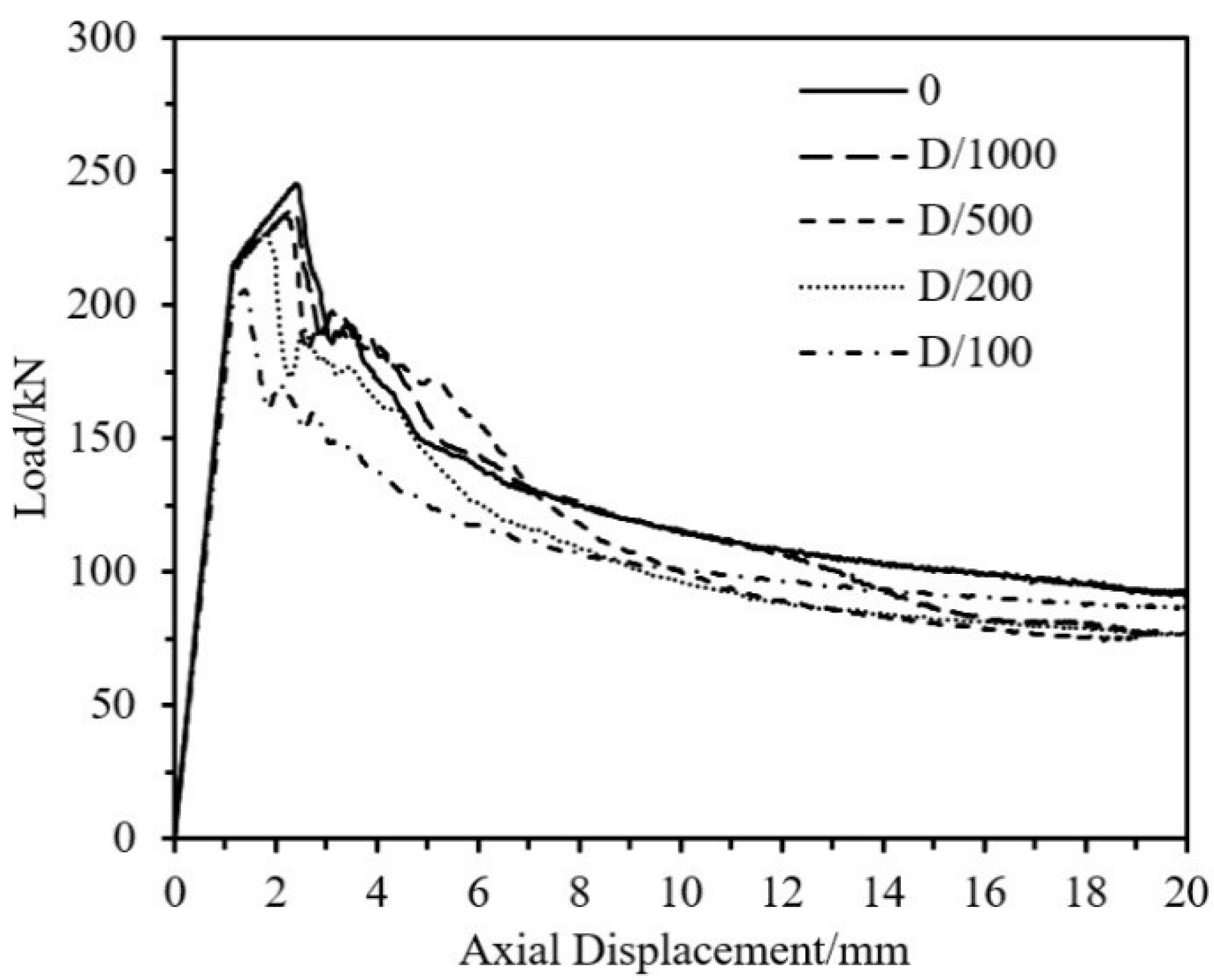
5.1.1. Influence of Initial Imperfections
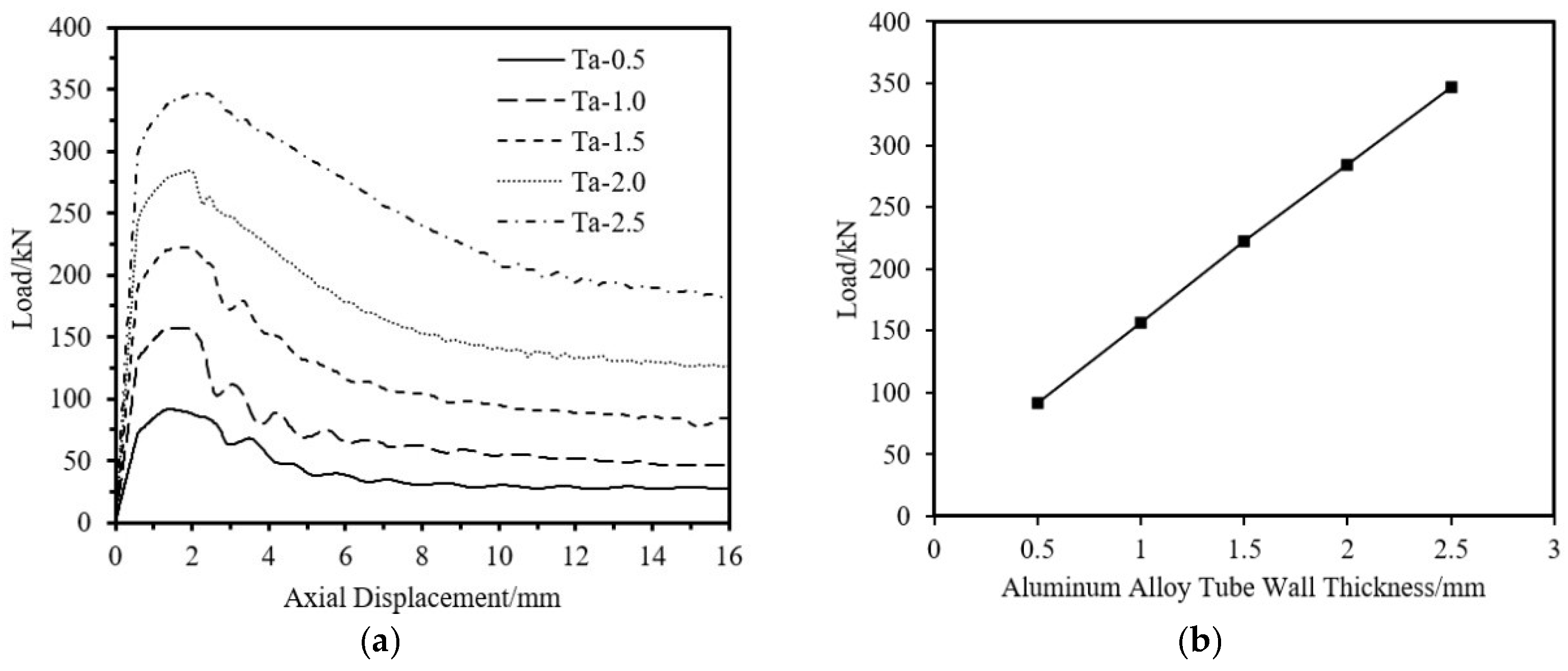
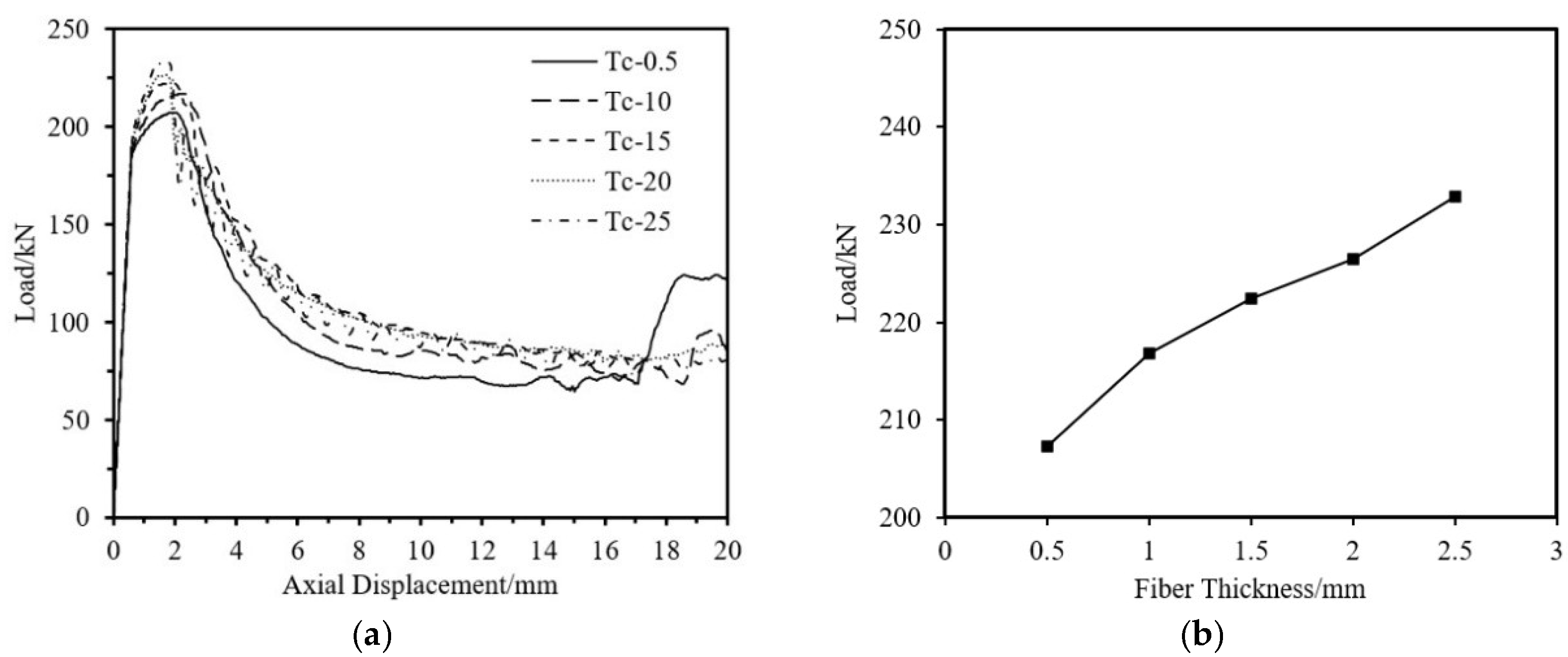
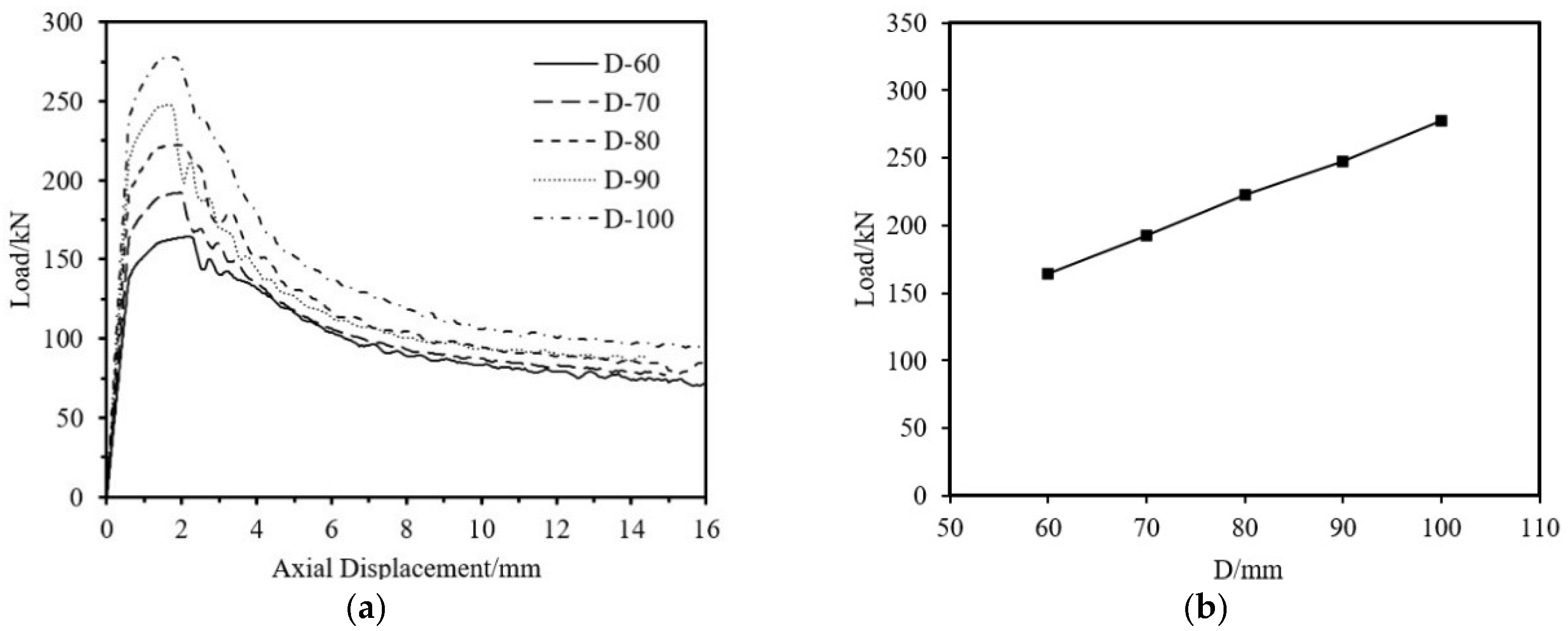
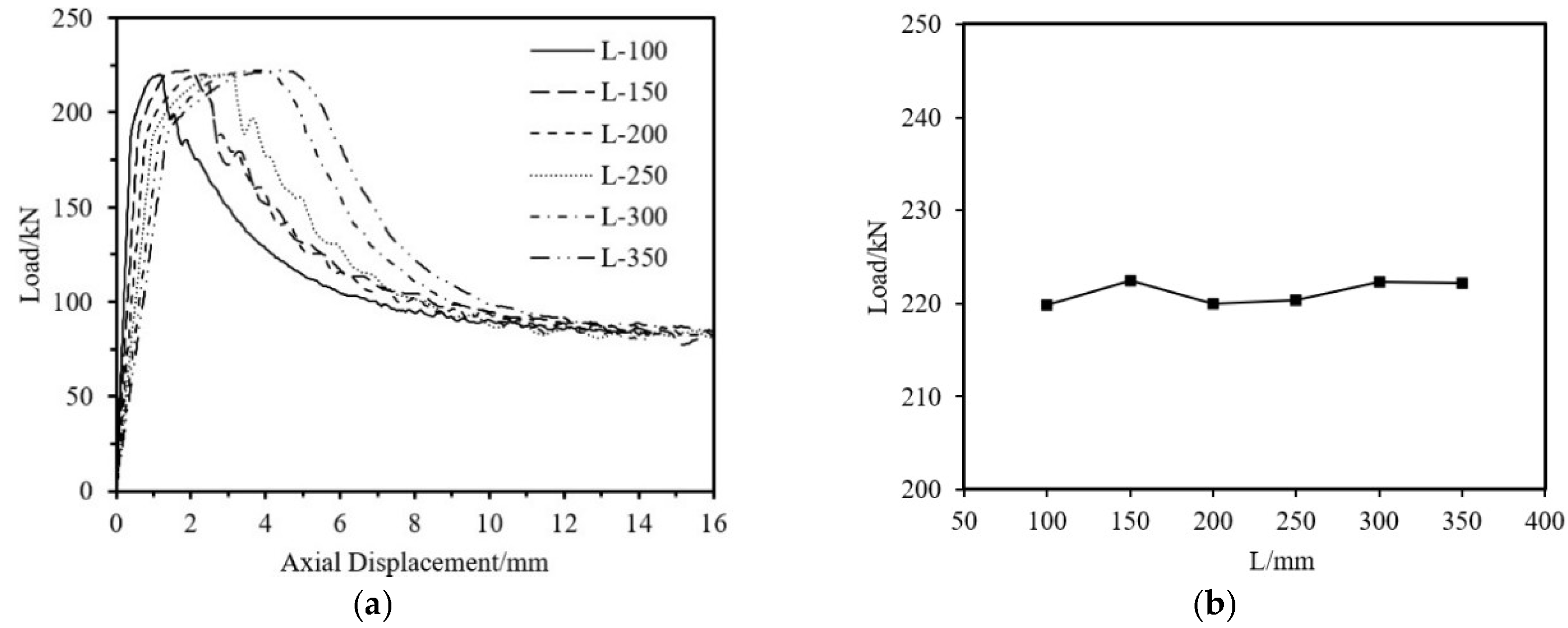
5.1.2. Influence of Component Dimensions
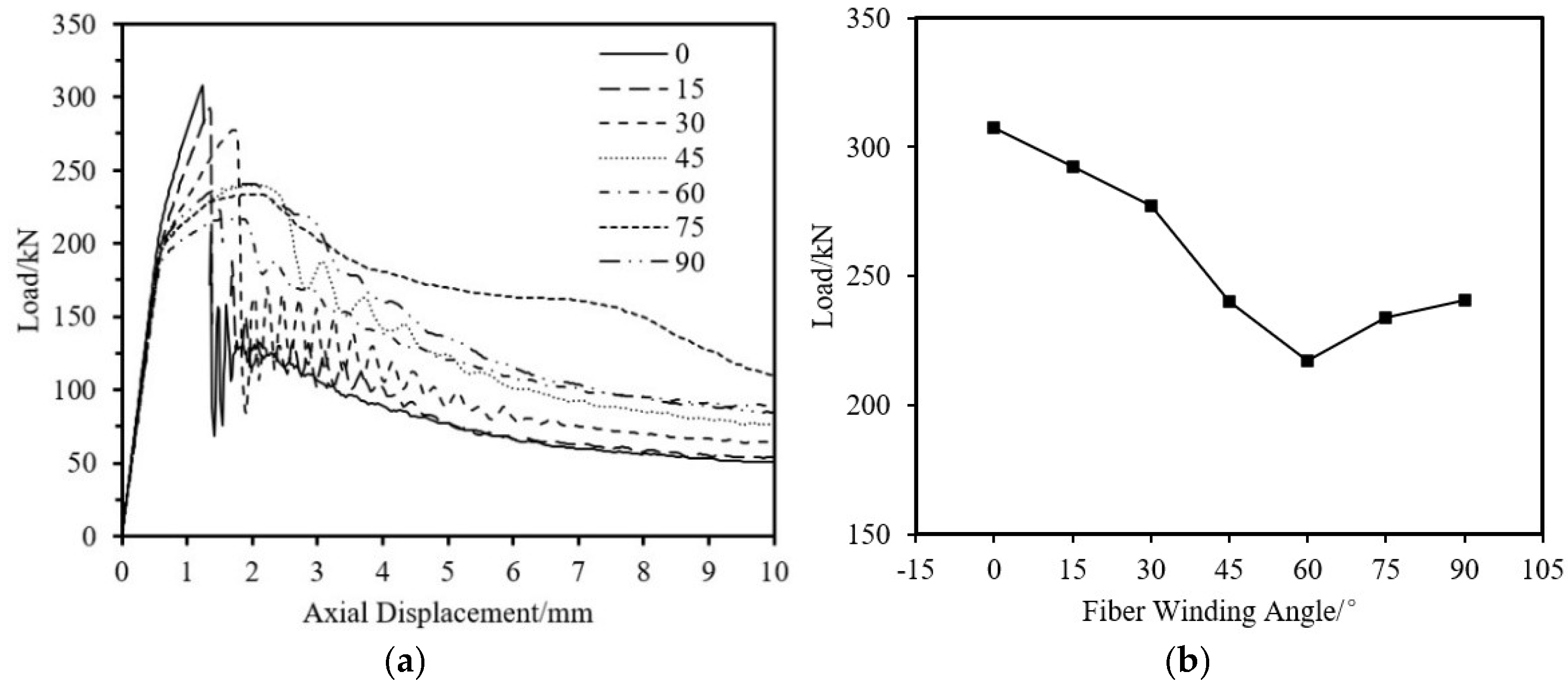
5.1.3. Influence of Fiber Angle
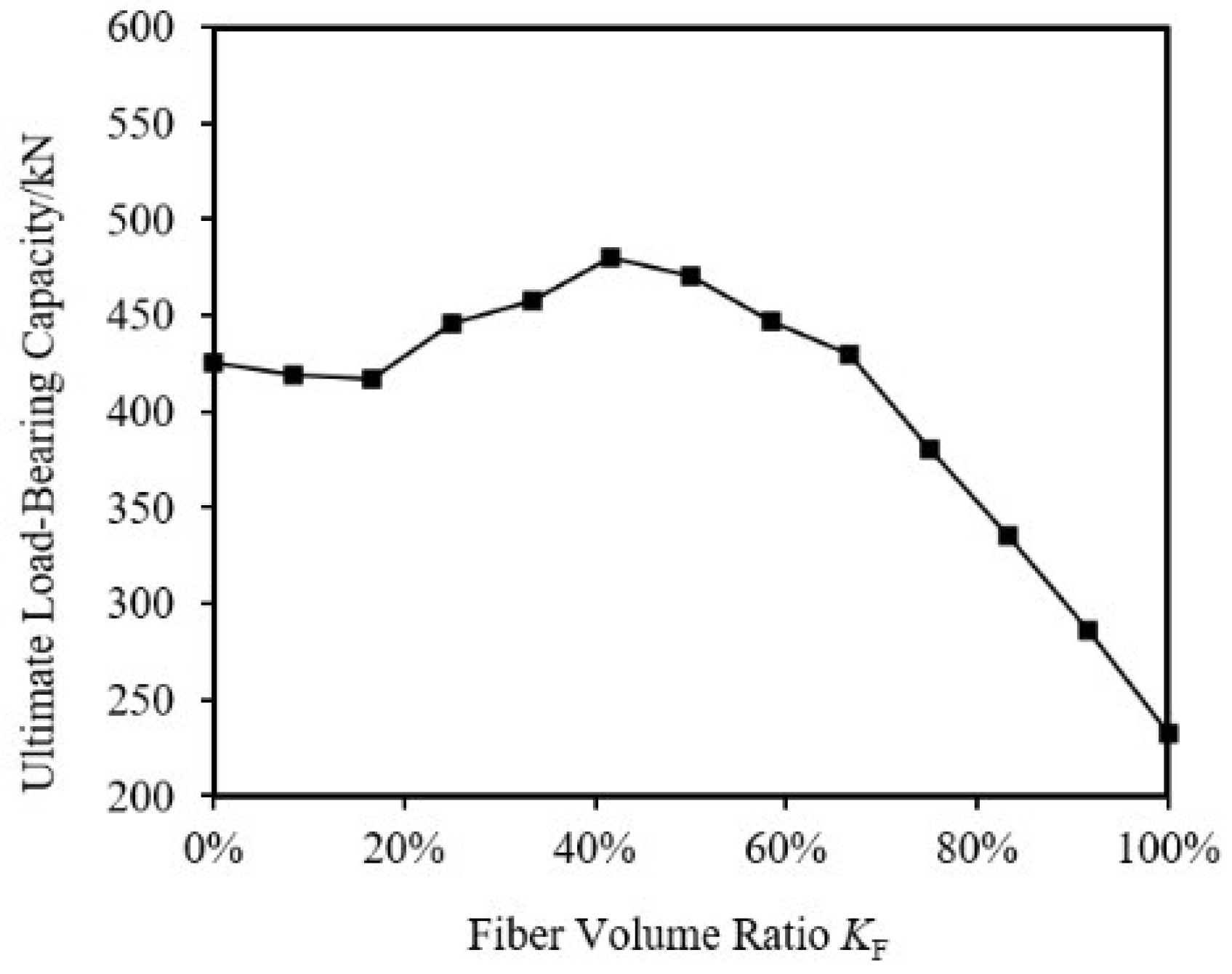
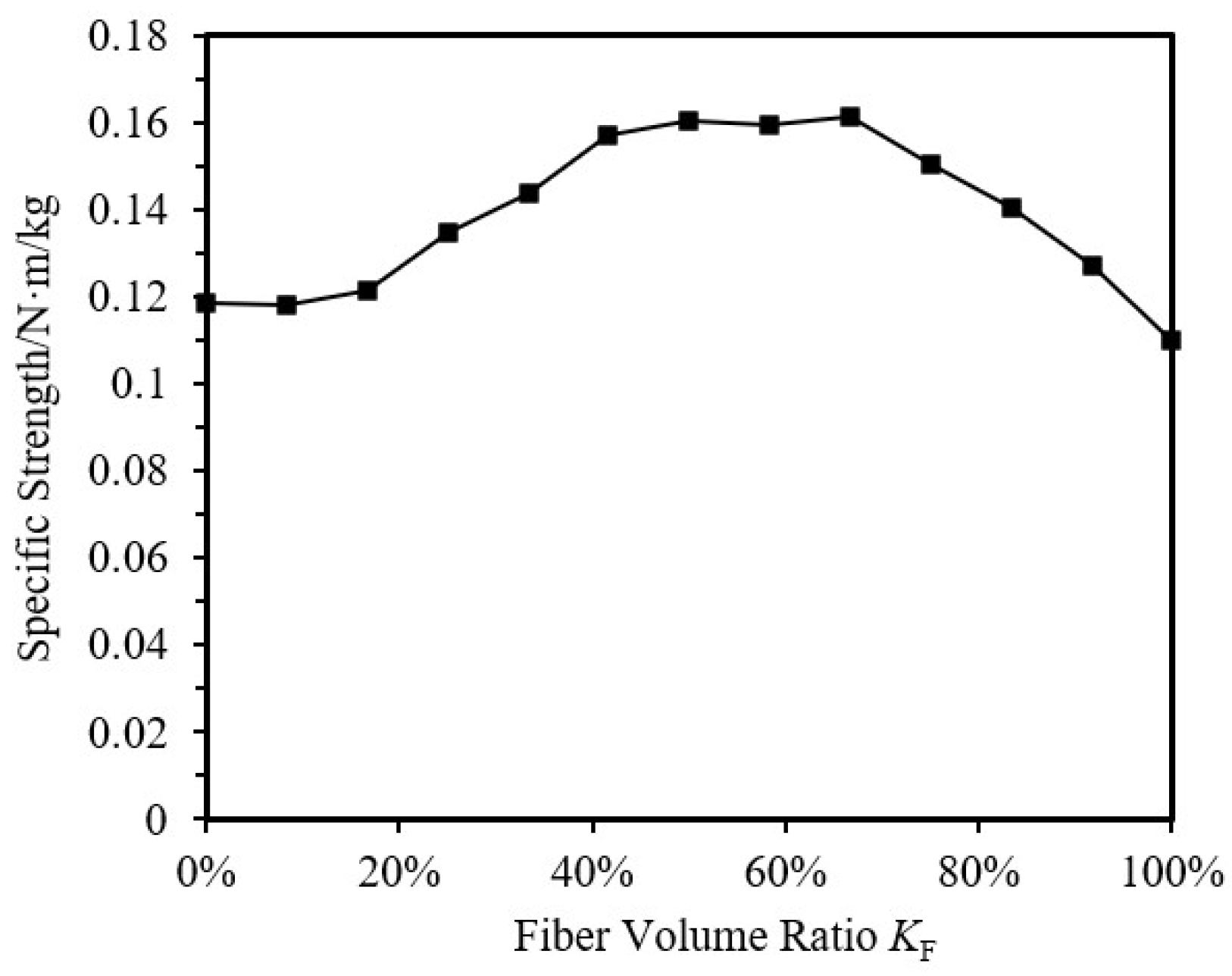
5.1.4. Influence of Fiber Volume Ratio
5.2. Load-Bearing Capacity Formula
- —Axial Elastic Modulus of the i-th Layer of CFRP;
- —Cross-Sectional Area of the i-th Layer of CFRP;
- —Elastic Modulus of Aluminum Alloy;
- —Cross-Sectional Area of the i-th Layer of Aluminum Alloy;
- —Yield Strength of Aluminum Alloy.
6. Conclusions
- The typical failure mode of the specimen is strength failure. Compared with the pure aluminum alloy tube, the ultimate bearing capacity of the CFRP-AL tubes is increased by 11% to 31%.
- The axial compression process of short CFRP-AL tubes can be divided into four stages: elastic stage, plastic deformation stage, buckling stage, and progressive folding load-bearing stage. The role of CFRP in this process is two-fold: firstly, it directly enhances the ultimate load-bearing capacity of the CFRP-AL tubes through equivalent axial strength; secondly, it restricts the initiation and development of folding deformation after peak load through circumferential hoop action. The proportion and magnitude of these two effects are determined by the fiber winding angle and the number of fiber layers.
- Finite element simulations of axial compression specimens were conducted using user material subroutine, considering the effects of initial imperfection, fiber winding angle, fiber thickness, aluminum alloy tube wall thickness, outer diameter, and CFRP volume ratio. The failure patterns of CFRP-AL tubes under axial compression were obtained. The ultimate load-bearing capacity of CFRP-AL tubes first increases and then decreases with the fiber volume ratio KF, reaching its maximum at 41.67%. The ultimate load-bearing capacity of CFRP-AL tubes within the fiber volume ratio range of 25.00% to 66.67% is greater than that of pure aluminum alloy tubes. The specific strength of the tubes first increases and then decreases with KF, and the specific strength of CFRP-AL tubes within the range of 41.67% to 66.67% is relatively high. The specific strength of CFRP-AL tubes is greater than that of pure aluminum alloy tubes and pure CFRP tubes.
- Based on the concept of equivalence and strength theory, a formula for calculating the ultimate load-bearing capacity of short tube strength failure was established. The calculated results are in good agreement with experimental and numerical results. The reliability of the formula has also been confirmed by comparison with other literature.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guo, X.Y.; Wu, Z.D.; Yang, Y.; Bai, J.H.; Zhou, Q.Z.Y. A Study on the Bond-Slip Relationship of the CFRP-Steel Interface of CFRP Strengthened Steel. Materials 2022, 15, 4187. [Google Scholar] [CrossRef] [PubMed]
- Park, J.S.; Kim, J.H.; Park, J.H.; Ko, D.C. Prediction of the Delamination at the Steel and CFRP Interface of Hybrid Composite Part. Materials 2021, 14, 6285. [Google Scholar] [CrossRef] [PubMed]
- Bakar, M.B.C.; Rashid, R.S.M.; Amran, M.; Jaafar, M.S.; Vatin, N.I.; Fediuk, R. Flexural Strength of Concrete Beam Reinforced with CFRP Bars: A Review. Materials 2022, 15, 1144. [Google Scholar] [CrossRef] [PubMed]
- Harris, C.E.; Starnes, J.H.; Shuart, M.J. Design and manufacturing of aerospace composite structures, state-of-the-art assessment. J. Aircr. 2002, 39, 545–560. [Google Scholar] [CrossRef]
- Lee, D.G.; Kim, H.S.; Kim, J.W.; Kim, J.K. Design and manufacture of an automotive hybrid aluminum/composite drive shaft. Compos. Struct. 2004, 63, 87–99. [Google Scholar] [CrossRef]
- Kim, P. A comparative study of the mechanical performance and cost of metal, FRP, and hybrid beams. Appl. Compos. Mater. 1998, 5, 175–187. [Google Scholar] [CrossRef]
- Pantelides, C.P.; Nadauld, J.; Cercone, L. Repair-of cracked aluminum overhead sign structures with glass fiber reinforced polymer composites. J. Compos. Constr. 2003, 7, 118–126. [Google Scholar] [CrossRef]
- Lee, S.H.; Kim, H.J.; Choi, N.S. Bending performance analysis of aluminum-composite hybrid tube beams. In Fracture and Strength of Solids Vi, Pts 1 and 2; Putra, I.S., Suharto, D., Eds.; DTIC: Fort Belvoir, VA, USA, 2006; Volume 306–308, pp. 769–774. [Google Scholar]
- Motavalli, M.; Terrasi, G.P.; Meier, U. On the behaviour of hybrid aluminium/CFRP box beams at low temperatures. Compos. Part A-Appl. Sci. Manuf. 1997, 28, 121–129. [Google Scholar] [CrossRef]
- Triantafillou, T.C.; Kim, P.; Meier, U. Optimization of hybrid aluminum/cfrp box beams. Int. J. Mech. Sci. 1991, 33, 729–739. [Google Scholar] [CrossRef]
- Zhu, G.; Sun, G.; Liu, Q.; Li, G.; Li, Q. On crushing characteristics of different configurations of metal-composites hybrid tubes. Compos. Struct. 2017, 175, 58–69. [Google Scholar] [CrossRef]
- Han, Z.; Li, H.; Xu, X.; Wang, H.; Li, H.; Tao, J. Crushing characteristics of aluminum/CFRP/aluminum hybrid tubes prepared by spinning forming. Compos. Struct. 2020, 249, 112551. [Google Scholar] [CrossRef]
- Mansor, M.A.; Ahmad, Z.; Abdullah, M.R. Crashworthiness capability of thin-walled fibre metal laminate tubes under axial crushing. Eng. Struct. 2022, 252, 113660. [Google Scholar] [CrossRef]
- Nemessányi, C. Brief history of fiber reinforced polymers as structural material. Period. Polytech. Archit. 2023, 54, 193–206. [Google Scholar] [CrossRef]
- Ronagh, H.R.; Eslami, A. Flexural retrofitting of RC buildings using GFRP/CFRP–A comparative study. Compos Part B-Eng. 2013, 46, 188–196. [Google Scholar] [CrossRef]
- Kavitha, S.S.; Joseph, L.; Madhavan, M.K.; Jayanarayanan, K. Comparative study of carbon and glass fiber reinforced polymer composites for the confinement of concrete columns. Mater. Today Proc. 2024, 103, 352–357. [Google Scholar] [CrossRef]
- Ding, G.; Zhang, Y.; Zhu, Y. Experimental and numerical investigation of the flexural behavior of CFRP box girders. Adv. Compos. Lett. 2019, 28, 2633366X19891171. [Google Scholar] [CrossRef]
- Shen, B.; Liu, H.; Lv, S.; Li, Z.; Cheng, W. Progressive Failure Analysis of Laminated CFRP Composites under Three-Point Bending Load. Adv. Mater. Sci. Eng. 2022, 2022, 3047319. [Google Scholar] [CrossRef]
- Zhao, X.L.; Zhang, L. State-of-the-art review on FRP strengthened steel structures. Eng. Struct. 2007, 29, 1808–1823. [Google Scholar] [CrossRef]
- Ritchie, A.; Fam, A.; MacDougall, C. Strengthening Long Steel Columns of S-Sections against Global Buckling around Weak Axis Using CFRP Plates of Various Moduli. J. Compos. Constr. 2015, 19, 04014074. [Google Scholar] [CrossRef]
- Shaat, A.; Fam, A. Finite element analysis of slender HSS columns strengthened with high modulus composites. Steel Compos. Struct. 2007, 7, 19–34. [Google Scholar] [CrossRef]
- Shaat, A.; Fam, A.Z. Slender Steel Columns Strengthened Using High-Modulus CFRP Plates for Buckling Control. J. Compos. Constr. 2009, 13, 2–12. [Google Scholar] [CrossRef]
- Kumar, A.P.; Senthil, R. Axial Behaviour of CFRP-Strengthened Circular Steel Hollow Sections. Arab. J. Sci. Eng. 2016, 41, 3841–3850. [Google Scholar] [CrossRef]
- Kumar, A.P.; Senthil, R. Behavior of CFRP strengthened CHS under axial static and axial cyclic loading. KSCE J. Civ. Eng. 2016, 20, 1493–1500. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, X.; Wang, C. Web crippling of galvanized steel tube strengthened by CFRP sheets. Compos. Part B-Eng. 2016, 84, 200–210. [Google Scholar] [CrossRef]
- Feng, P.; Hu, L.L.; Qian, P.; Ye, L.P. Compressive bearing capacity of CFRP-aluminum alloy hybrid tubes. Compos. Struct. 2016, 140, 749–757. [Google Scholar] [CrossRef]
- Qian, P.; Ye, L.P.; Feng, P. Elasto-plastic buckling behavior of CFRP-aluminum composite pipe under axially compressive load. J. Eng. Mech. 2006, 23, 210–216. (In Chinese) [Google Scholar]
- Qian, P.; Feng, P.; Ye, L.P. Elasto-plastic stability of Keiwitt latticed domes made of carbon fiber reinforced polymer-aluminum alloy composite pipes. J. Tsinghua Univ. (Sci. Technol.) 2007, 47, 1423–1426. [Google Scholar]
- Shin, K.C.; Lee, J.J.; Kim, K.H.; Song, M.C.; Huh, J.S. Axial crush and bending collapse of an aluminum/GFRP hybrid square tube and its energy absorption capability. Compos. Struct. 2002, 57, 279–287. [Google Scholar] [CrossRef]
- Gao, X.Y.; Balendra, T.; Koh, C.G. Buckling strength of slender circular tubular steel braces strengthened by CFRP. Eng. Struct. 2013, 46, 547–556. [Google Scholar] [CrossRef]
- GB/T 228.1-2010; Metallic Materials-Tensile Testing-Part 1: Method of Test at Room Temperature. Standards Press of China: Beijing, China, 2010.
- Johnson, G.R.; Cook, W.H. Fracture Characteristics of Three Metals Subjected to Various Strains, Strain Rates, Temperatures and Pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Schwer, L.E. Aluminum plate perforation: A comparative case study using Lagrange with erosion, multi-material ale, and smooth particle hydrodynamics. In Proceedings of the 7th European LS-DYNA Conference, Salzburg, Austria, 14–15 May 2009. [Google Scholar]
- Zhang, C.Z.; Guo, X.N.; Zong, S.H.; Chen, Y.; Zhu, S.J. Toughness Parameters Calibration of Chinese Structural Aluminum Alloys. J. Hunan Univ. (Nat. Sci.) 2020, 47, 124–133. (In Chinese) [Google Scholar]
- GB/T 3354-2014; Test Method for Tensile Properties of Orientation Fiber Reinforced Polymer Matrix Composite Materials. Standards Press of China: Beijing, China, 2014.
- Jones, R.M. Mechanics of Composite Materials; Taylor & Francis Inc: London, UK, 1999; p. 151. [Google Scholar]
- Li, X.; Ma, D.; Liu, H.; Tan, W.; Gong, X.; Zhang, C.; Li, Y. Assessment of failure criteria and damage evolution methods for composite laminates under low-velocity impact. Compos. Struct. 2019, 207, 727–739. [Google Scholar] [CrossRef]
- Hashin, Z. Failure criteria for unidirectional fiber composites. J. Appl. Mech.-Trans. ASME 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Singh, H.; Namala, K.K.; Mahajan, P. A damage evolution study of E-glass/epoxy composite under low velocity impact. Compos. Part B-Eng. 2015, 76, 235–248. [Google Scholar] [CrossRef]
- Shi, Y.; Swait, T.; Soutis, C. Modelling damage evolution in composite laminates subjected to low velocity impact. Compos. Struct. 2012, 94, 2902–2913. [Google Scholar] [CrossRef]
- Pederson, J. Finite Element Analysis of Carbon Fiber Composite Ripping Using ABAQUS. Master’s Thesis, Clemson University, Clemson, SC, USA, 2006. [Google Scholar]
- Ataş, A.; Soutis, C. Strength prediction of bolted joints in CFRP composite laminates using cohesive zone elements. Compos. Part B-Eng. 2014, 58, 25–34. [Google Scholar] [CrossRef]
- Dehghani, E.; Daneshjoo, F.; Aghakouchak, A.A.; Khaji, N. A new bond-slip model for adhesive in CFRP–steel composite systems. Eng. Struct. 2012, 34, 447–454. [Google Scholar] [CrossRef]
- Lu, X.Z.; Teng, J.G.; Ye, L.P.; Jiang, J.J. Bond-slip models for FRP sheets/plates bonded to concrete. Eng. Struct. 2005, 27, 920–937. [Google Scholar] [CrossRef]
- GB/T 4436-2012; Wrought Aluminum and Aluminum Alloy Tubes-Dimensions and Deviations. Standards Press of China: Beijing, China, 2012.














| Specimen Number | Thicknesses t/mm | Yield Strength σ0.2/MPa | Ultimate Tensile Strength σu/MPa | Modulus of Elasticity E/MPa | Yield Strain εy/με | Fracture Strain εu/με |
|---|---|---|---|---|---|---|
| AL-A1 | 3.0 | 266 | 320 | 64,303 | 6125 | 96,658 |
| AL-A2 | 3.0 | 265 | 314 | 65,714 | 6094 | 83,313 |
| AL-A3 | 3.0 | 266 | 317 | 66,354 | 6135 | 99,955 |
| AL-A4 | 3.0 | 266 | 319 | 63,553 | 6142 | 103,852 |
| avg | - | 266 | 318 | 64,981 | 6124 | 95,945 |
| Specimen Number | Thicknesses t/mm | Yield Strength σ0.2/MPa | Ultimate Tensile Strength σu/MPa | Modulus of Elasticity E/MPa | Yield Strain εy/με | Fracture Strain εu/με |
|---|---|---|---|---|---|---|
| AL-B1 | 1.5 | 259 | 295 | 63,013 | 6211 | 66,523 |
| AL-B2 | 1.5 | 260 | 299 | 63,490 | 6124 | 79,121 |
| AL-B3 | 1.5 | 258 | 297 | 62,792 | 6131 | 87,595 |
| AL-B4 | 1.5 | 258 | 291 | 62,996 | 6109 | 81,042 |
| avg | - | 259 | 296 | 63,073 | 6144 | 78,570 |
| A/MPa | B/MPa | n | C | m |
|---|---|---|---|---|
| 246 | 151 | 0.39 | 0.1 | 1.34 |
| D1 | D2 | D3 | D4 | D5 |
|---|---|---|---|---|
| −0.877 | 1.1 | −0.47 | 0.01 | 1.6 |
| Thickness t/mm | Tensile Strength ft/MPa | Elastic Modulus Ef/GPa | Elongation δt/% |
|---|---|---|---|
| 0.167 | 3543 | 249 | 1.4 |
| Tensile Strength ft/MPa | Compressive Strength fc/MPa | Elastic Modulus E/GPa | Elongation/% |
|---|---|---|---|
| 54.4 | 100.7 | 3.3 | 2.1 |
| E1 /MPa | E2 /MPa | E3 /MPa | v12 | v13 | v23 | G12 /GPa | G13 /GPa | G23 /GPa |
|---|---|---|---|---|---|---|---|---|
| 85,593 | 7982 | 7982 | 0.37 | 0.37 | 0.37 | 2365 | 2365 | 2476 |
| Xt /MPa | Xc /MPa | Yt = Zt/MPa | Yc = Zc/MPa | S12 = S13 /MPa | S23 /MPa | N/mm | N/mm | N/mm | N/mm |
|---|---|---|---|---|---|---|---|---|---|
| 1220 | 870 | 36.2 | 67 | 55 | 55 | 76 | 34 | 0.6 | 2.1 |
| Knn GPa/mm | Kss GPa/mm | Ktt GPa/mm | Tn /MPa | Ts /MPa | Tt /MPa | Gn N/mm | Gs N/mm | Gt N/mm | η |
|---|---|---|---|---|---|---|---|---|---|
| 100 | 100 | 100 | 60 | 80 | 80 | 0.352 | 1.45 | 1.45 | 2 |
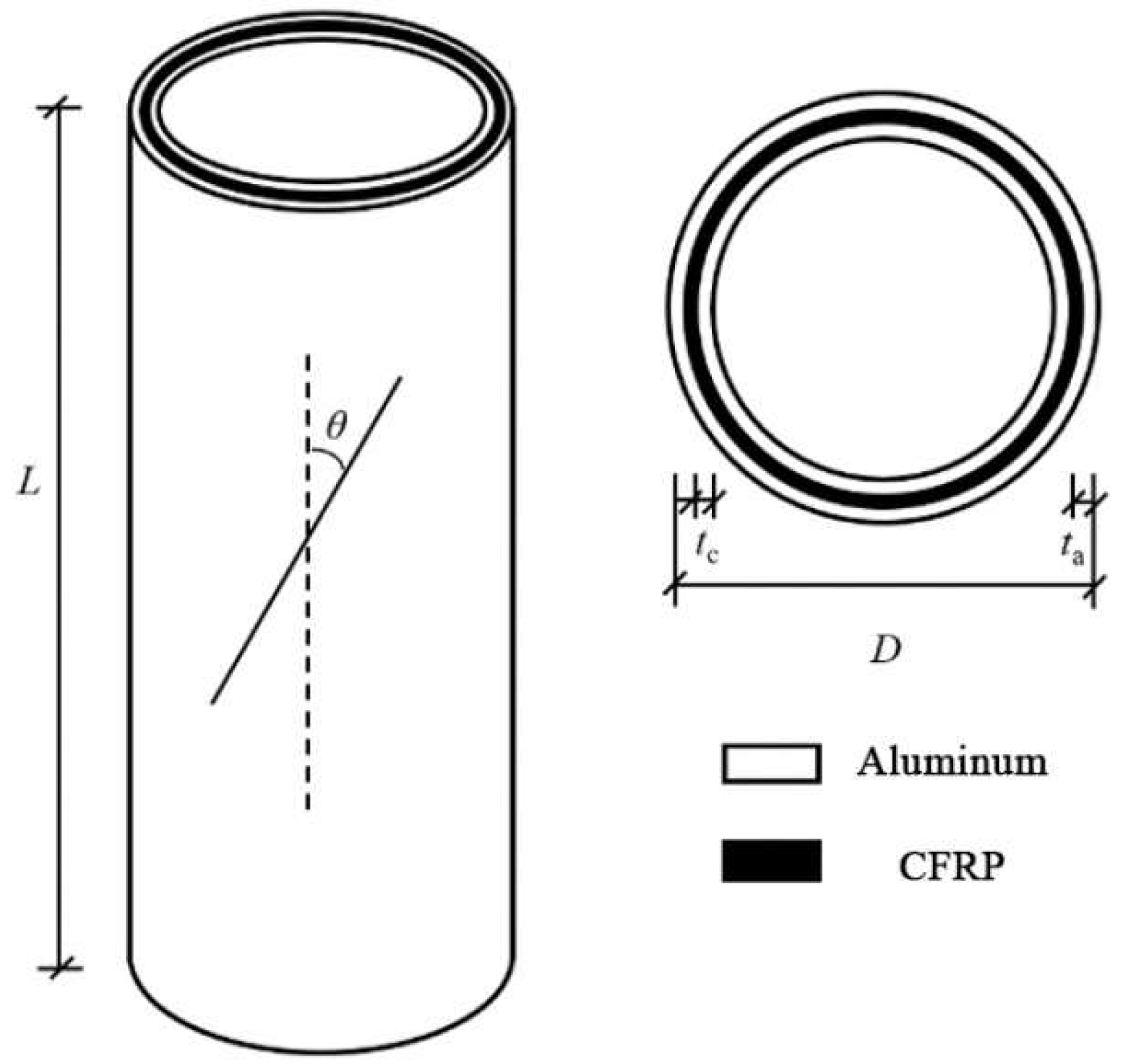
| Specimen Number | L/mm | D/mm | ta/mm | tc/mm | θ/° | n | λ | Specimen Type |
|---|---|---|---|---|---|---|---|---|
| N2A64 | 150 | 80 | 1.5 | 1.0 | 64 | 2 | 5.57 | Composite Tube |
| N2A30 | 150 | 80 | 1.5 | 1.0 | 30 | 2 | 5.57 | Composite Tube |
| N2A0 | 150 | 80 | 1.5 | 1.0 | 0 | 2 | 5.57 | Composite Tube |
| N3A64 | 150 | 80 | 1.5 | 1.5 | 64 | 3 | 5.60 | Composite Tube |
| N3A30 | 150 | 80 | 1.5 | 1.5 | 30 | 3 | 5.60 | Composite Tube |
| N3A0 | 150 | 80 | 1.5 | 1.5 | 0 | 3 | 5.60 | Composite Tube |
| N4A64 | 150 | 80 | 1.5 | 2.0 | 64 | 4 | 5.64 | Composite Tube |
| N4A30 | 150 | 80 | 1.5 | 2.0 | 30 | 4 | 5.64 | Composite Tube |
| N4A0 | 150 | 80 | 1.5 | 2.0 | 0 | 4 | 5.64 | Composite Tube |
| AL | 150 | 76 | 3.0 | - | - | - | 5.81 | Aluminum Alloy Tube |
| Specimen Number | L/mm | D/mm | ta/mm | tc/mm | θ/° | n | λ | Pu,1 /kN | Pu,2 /kN | Pu,3 /kN | Pu,avg /kN | ηs/% |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N2A64 | 150 | 80 | 1.5 | 1.0 | 64 | 2 | 5.57 | 215.66 | 218.26 | 227.28 | 220.40 | 11.26 |
| N2A30 | 150 | 80 | 1.5 | 1.0 | 30 | 2 | 5.57 | 228.13 | 226.8 | 235.22 | 230.05 | 16.14 |
| N2A0 | 150 | 80 | 1.5 | 1.0 | 0 | 2 | 5.57 | 234.68 | 237.97 | 232.53 | 235.06 | 18.67 |
| N3A64 | 150 | 80 | 1.5 | 1.5 | 64 | 3 | 5.60 | 219.69 | 234.89 | 213.53 | 222.70 | 12.43 |
| N3A30 | 150 | 80 | 1.5 | 1.5 | 30 | 3 | 5.60 | 247.18 | 251.07 | 239.52 | 245.92 | 24.15 |
| N3A0 | 150 | 80 | 1.5 | 1.5 | 0 | 3 | 5.60 | 250.23 | 252.58 | 251.17 | 251.33 | 26.88 |
| N4A64 | 150 | 80 | 1.5 | 2.0 | 64 | 4 | 5.64 | 226.7 | 232.03 | 234.94 | 231.22 | 16.73 |
| N4A30 | 150 | 80 | 1.5 | 2.0 | 30 | 4 | 5.64 | 256.84 | 242.58 | 257.24 | 252.22 | 27.33 |
| N4A0 | 150 | 80 | 1.5 | 2.0 | 0 | 4 | 5.64 | 262.98 | 260.75 | 254.12 | 259.28 | 30.89 |
| AL | 150 | 76 | 3.0 | - | - | - | 5.81 | 197.59 | 198.21 | 198.46 | 198.09 | - |
| Specimen Number | L/mm | D/mm | ta/mm | tc/mm | θ/° | n | Initial Imperfection | Ultimate Load/kN |
|---|---|---|---|---|---|---|---|---|
| Imp-0 | 150 | 80 | 1.5 | 1.5 | 64 | 3 | 0 | 244.97 |
| Imp-D/1000 | 150 | 80 | 1.5 | 1.5 | 64 | 3 | D/1000 | 236.45 |
| Imp-D/500 | 150 | 80 | 1.5 | 1.5 | 64 | 3 | D/500 | 232.32 |
| Imp-D/200 | 150 | 80 | 1.5 | 1.5 | 64 | 3 | D/200 | 227.44 |
| Imp-D/100 | 150 | 80 | 1.5 | 1.5 | 64 | 3 | D/100 | 205.74 |
| Specimen Number | L/mm | D/mm | ta/mm | tc/mm | θ/° | Ultimate Load /kN |
|---|---|---|---|---|---|---|
| Ta-0.5 | 150 | 80 | 0.5 | 1.5 | 60 | 91.77 |
| Ta-1.0 | 150 | 80 | 1.0 | 1.5 | 60 | 156.96 |
| Ta-1.5 | 150 | 80 | 1.5 | 1.5 | 60 | 222.41 |
| Ta-2.0 | 150 | 80 | 2.0 | 1.5 | 60 | 283.95 |
| Ta-2.5 | 150 | 80 | 2.5 | 1.5 | 60 | 347.15 |
| Tc-0.5 | 150 | 80 | 1.5 | 0.5 | 60 | 207.31 |
| Tc-1.0 | 150 | 80 | 1.5 | 1.0 | 60 | 216.81 |
| Tc-1.5 | 150 | 80 | 1.5 | 1.5 | 60 | 222.41 |
| Tc-2.0 | 150 | 80 | 1.5 | 2.0 | 60 | 226.47 |
| Tc-2.5 | 150 | 80 | 1.5 | 2.5 | 60 | 232.89 |
| D-60 | 150 | 60 | 1.5 | 1.5 | 60 | 164.26 |
| D-70 | 150 | 70 | 1.5 | 1.5 | 60 | 192.25 |
| D-80 | 150 | 80 | 1.5 | 1.5 | 60 | 222.41 |
| D-90 | 150 | 90 | 1.5 | 1.5 | 60 | 247.67 |
| D-100 | 150 | 100 | 1.5 | 1.5 | 60 | 277.80 |
| L-100 | 100 | 80 | 1.5 | 1.5 | 60 | 219.85 |
| L-150 | 150 | 80 | 1.5 | 1.5 | 60 | 222.41 |
| L-200 | 200 | 80 | 1.5 | 1.5 | 60 | 219.99 |
| L-250 | 250 | 80 | 1.5 | 1.5 | 60 | 220.30 |
| L-300 | 300 | 80 | 1.5 | 1.5 | 60 | 222.28 |
| L-350 | 350 | 80 | 1.5 | 1.5 | 60 | 222.23 |
| Specimen Number | L/mm | D/mm | ta/mm | tc/mm | θ/° | Ultimate Load /kN |
|---|---|---|---|---|---|---|
| θ-0 | 150 | 80 | 1.5 | 1.5 | 0 | 307.72 |
| θ-15 | 150 | 80 | 1.5 | 1.5 | 15 | 292.58 |
| θ-30 | 150 | 80 | 1.5 | 1.5 | 30 | 277.41 |
| θ-45 | 150 | 80 | 1.5 | 1.5 | 45 | 240.19 |
| θ-60 | 150 | 80 | 1.5 | 1.5 | 60 | 217.07 |
| θ-75 | 150 | 80 | 1.5 | 1.5 | 75 | 233.76 |
| θ-90 | 150 | 80 | 1.5 | 1.5 | 90 | 240.92 |
| Specimen Number | L/mm | D/mm | ta/mm | tc/mm | θ/° | n | η | Specimen Type | Ultimate Load/kN |
|---|---|---|---|---|---|---|---|---|---|
| KF-1 | 150 | 80 | 3.0 | - | - | - | 0.00% | Aluminum Alloy Tube | 425.67 |
| KF-2 | 150 | 80 | 2.75 | 0.5 | 30 | 1 | 8.33% | Composite Tube | 418.93 |
| KF-3 | 150 | 80 | 2.5 | 1.0 | 30 | 2 | 16.67% | Composite Tube | 417.09 |
| KF-4 | 150 | 80 | 2.25 | 1.5 | 30 | 3 | 25.00% | Composite Tube | 446.34 |
| KF-5 | 150 | 80 | 2.0 | 2.0 | 30 | 4 | 33.33% | Composite Tube | 457.83 |
| KF-6 | 150 | 80 | 1.75 | 2.5 | 30 | 5 | 41.67% | Composite Tube | 480.51 |
| KF-7 | 150 | 80 | 1.5 | 3.0 | 30 | 6 | 50.00% | Composite Tube | 470.43 |
| KF-8 | 150 | 80 | 1.25 | 3.5 | 30 | 7 | 58.33% | Composite Tube | 446.88 |
| KF-9 | 150 | 80 | 1.0 | 4.0 | 30 | 8 | 66.67% | Composite Tube | 430.12 |
| KF-10 | 150 | 80 | 0.75 | 4.5 | 30 | 9 | 75.00% | Composite Tube | 380.55 |
| KF-11 | 150 | 80 | 0.5 | 5.0 | 30 | 10 | 83.33% | Composite Tube | 335.66 |
| KF-12 | 150 | 80 | 0.25 | 5.5 | 30 | 11 | 91.67% | Composite Tube | 286.17 |
| KF-13 | 150 | 80 | - | 6.0 | 30 | 12 | 100.00% | CFRP Tube | 232.46 |
| Specimen Number | Experimental Average Pu,avg/kN | Numerical Simulation Results Pu,n/kN | Calculated Value Pu/kN | Error with Experimental Value ηs,avg | Error with Numerical Result ηs,n |
|---|---|---|---|---|---|
| N2A64 | 220.40 | 227.65 | 222.39 | 0.90% | −2.31% |
| N2A30 | 230.05 | 236.32 | 234.45 | 1.91% | −0.79% |
| N2A0 | 235.06 | 243.81 | 244.50 | 4.02% | 0.28% |
| N3A64 | 222.70 | 231.00 | 228.93 | 2.80% | −0.90% |
| N3A30 | 245.92 | 252.01 | 246.90 | 0.40% | −2.03% |
| N3A0 | 251.33 | 278.52 | 276.84 | 10.15% | −0.60% |
| N4A64 | 231.22 | 232.50 | 235.36 | 1.79% | 1.23% |
| N4A30 | 252.22 | 267.92 | 259.16 | 2.75% | −3.27% |
| N4A0 | 259.28 | 308.24 | 304.68 | 17.51% | −1.15% |
| AL | 198.09 | 198.29 | 198.14 | 0.03% | −0.08% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, X.; Li, Y.; Wang, L.; Guo, X. Study on Axial Compression Performance of CFRP-Aluminum Alloy Laminated Short Tubes. Materials 2025, 18, 3480. https://doi.org/10.3390/ma18153480
Luo X, Li Y, Wang L, Guo X. Study on Axial Compression Performance of CFRP-Aluminum Alloy Laminated Short Tubes. Materials. 2025; 18(15):3480. https://doi.org/10.3390/ma18153480
Chicago/Turabian StyleLuo, Xiaoqun, Yanheng Li, Li Wang, and Xiaonong Guo. 2025. "Study on Axial Compression Performance of CFRP-Aluminum Alloy Laminated Short Tubes" Materials 18, no. 15: 3480. https://doi.org/10.3390/ma18153480
APA StyleLuo, X., Li, Y., Wang, L., & Guo, X. (2025). Study on Axial Compression Performance of CFRP-Aluminum Alloy Laminated Short Tubes. Materials, 18(15), 3480. https://doi.org/10.3390/ma18153480





