Micromechanical Finite Element Model Investigation of Cracking Behavior and Construction-Related Deficiencies in Asphalt Mixtures
Abstract
1. Introduction
2. Materials and Methods
2.1. Test Materials and Mix Parameters
Material Parameters
2.2. Equipment and Testing Conditions
2.2.1. Dynamic Modulus Test
2.2.2. IDT Test
3. Numerical Simulation Methods and FEM Development
3.1. Theoretical Basis and Fundamental Assumptions
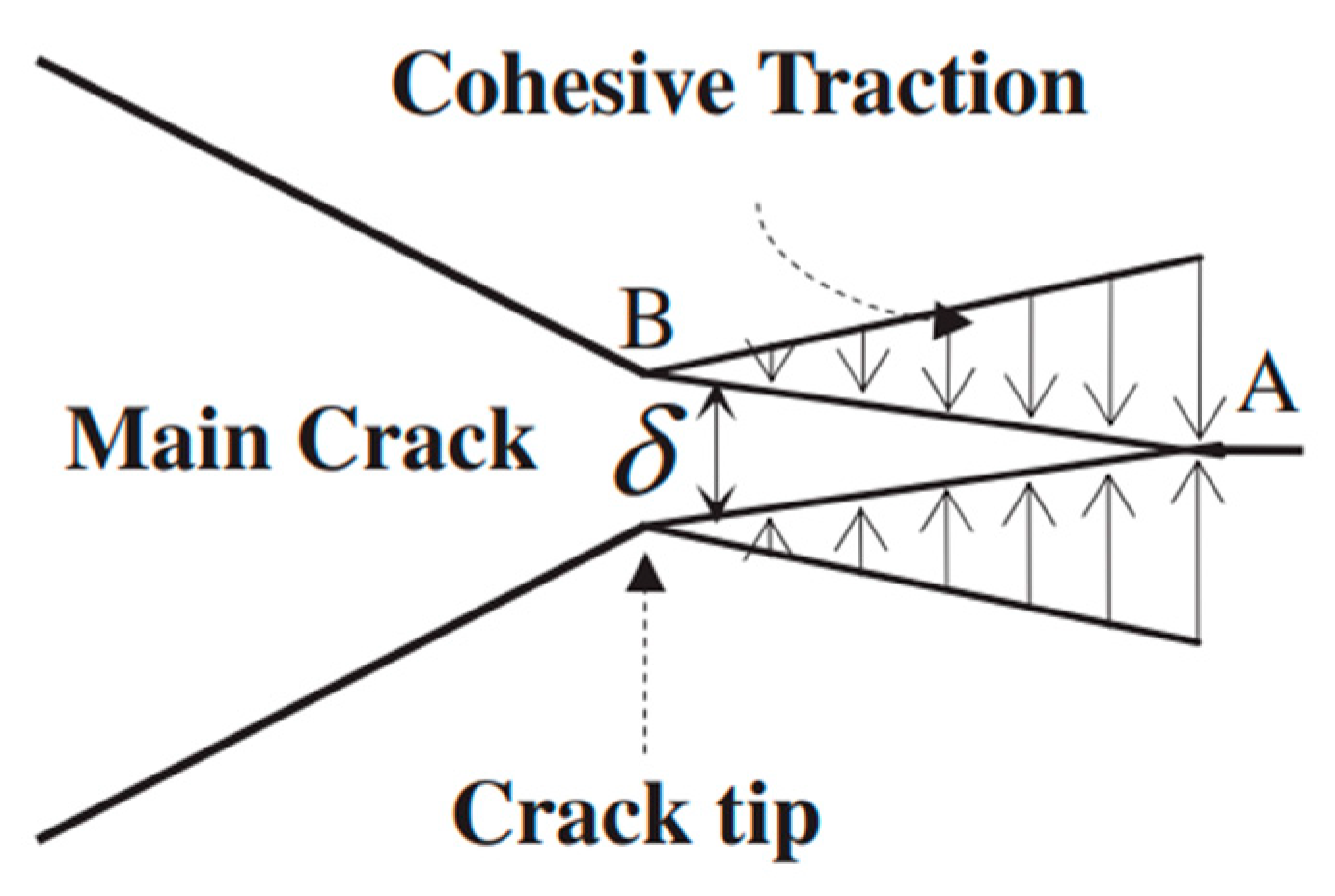
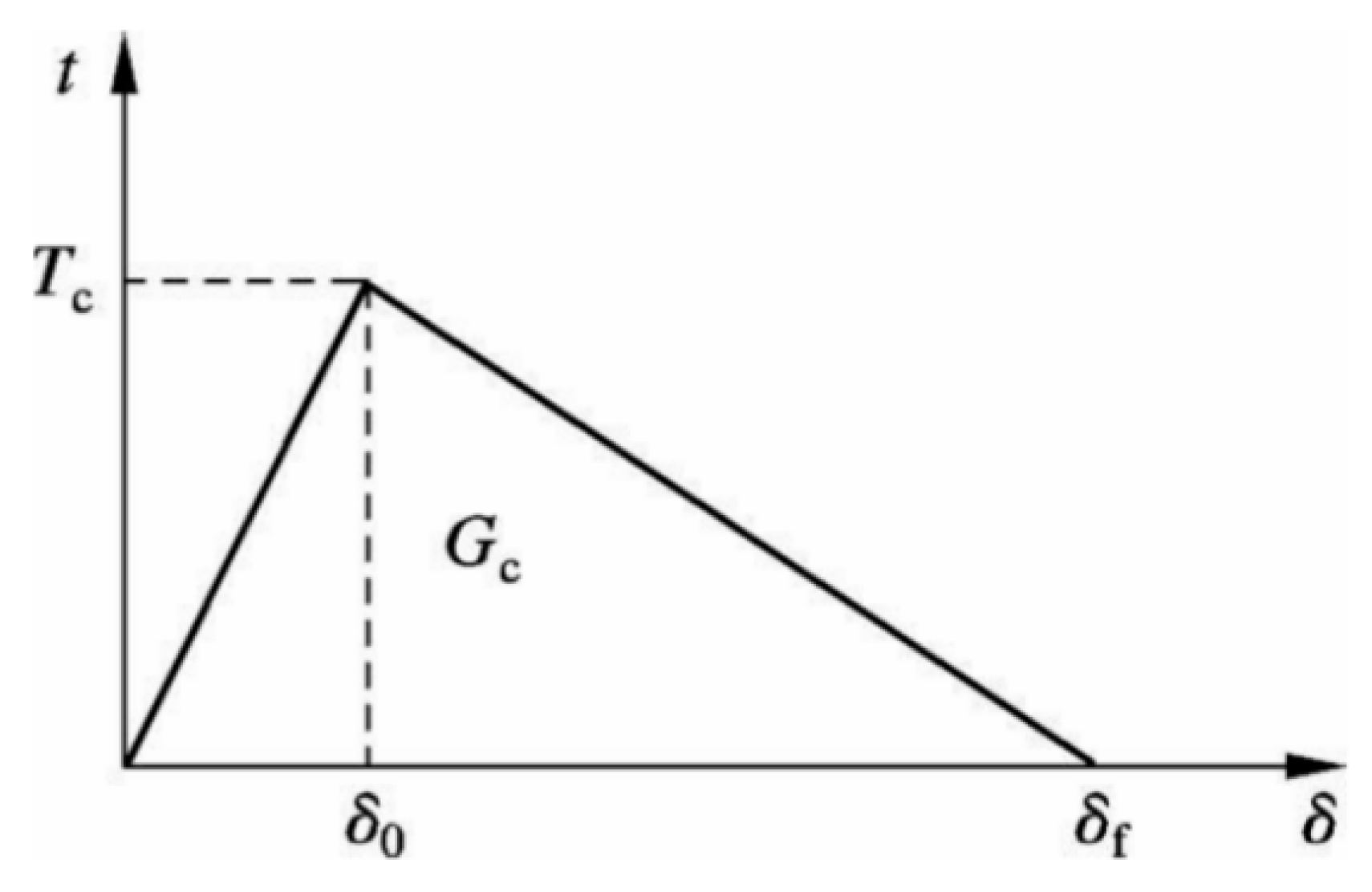
3.1.1. Introduction of CZM
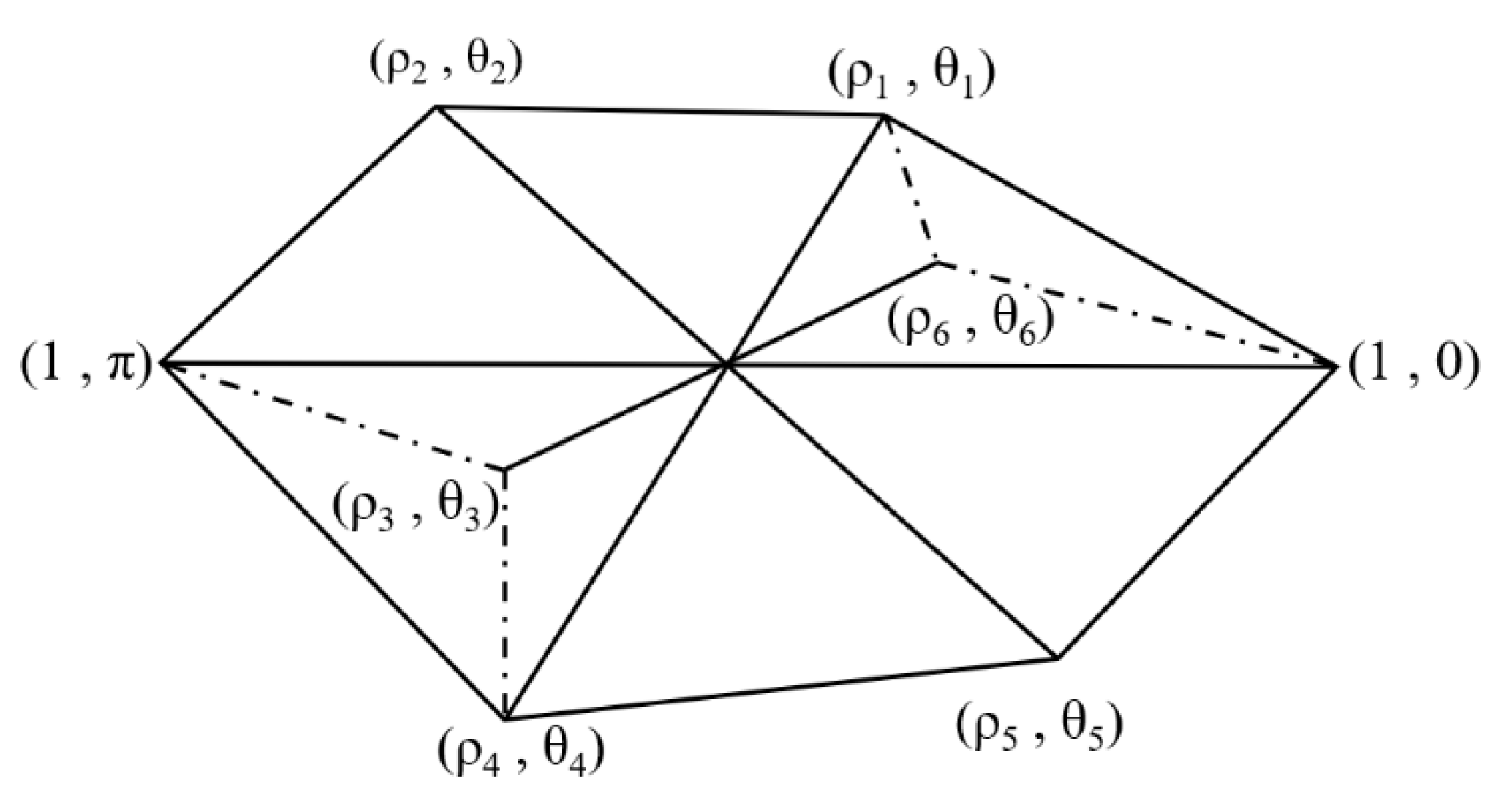
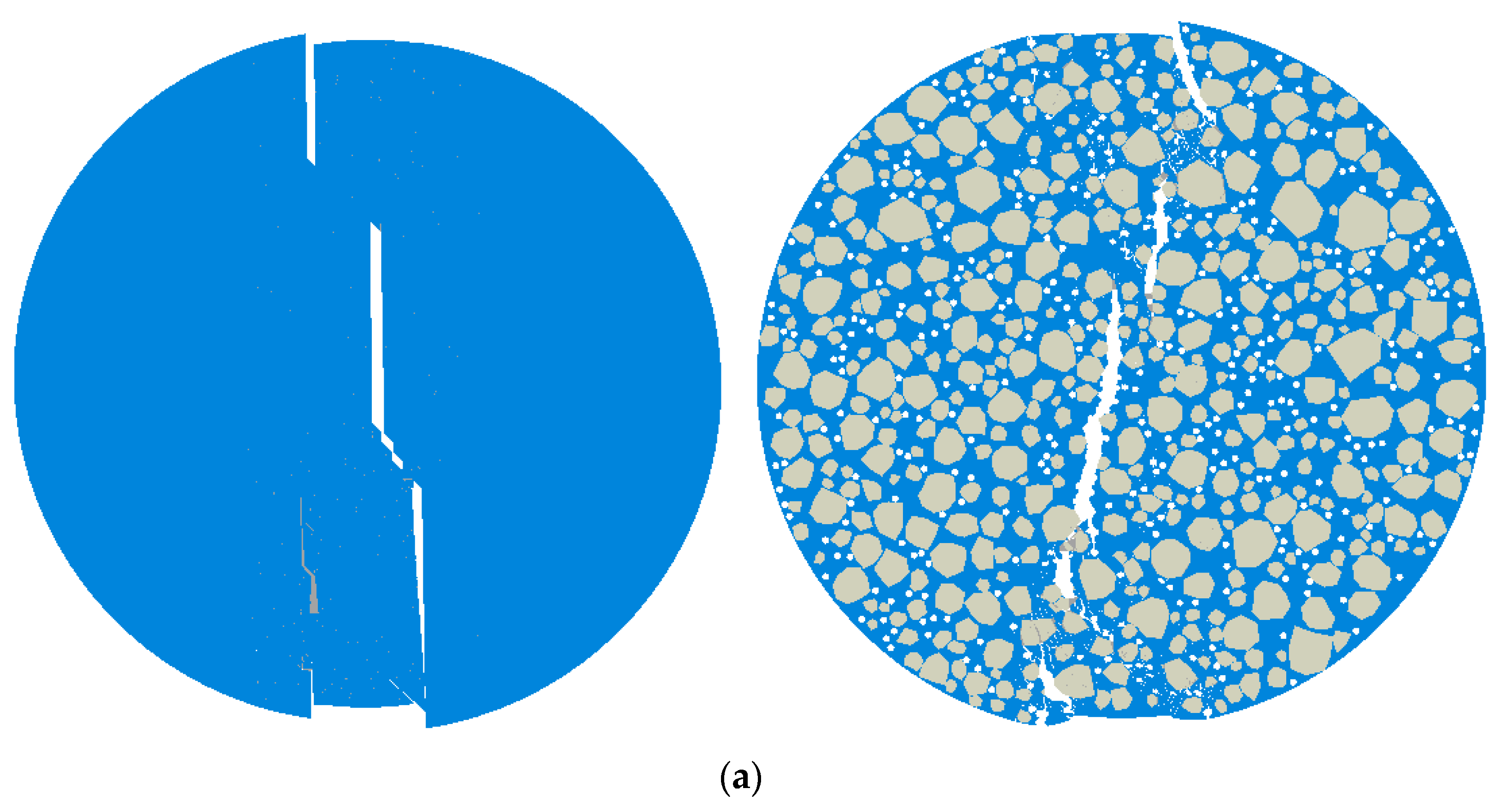
3.1.2. Random Aggregate and Void Generation Theory
3.2. Homogeneous Model Development
3.3. Mesoscopic Model Development
3.3.1. Division of Three-Phase Material Model
3.3.2. Placement of Cohesive Elements in Each Phase
- Coarse Aggregate Region: The coarse aggregate was relatively stiff overall. Therefore, the cohesive element parameters in this region were set higher to reflect its high load-bearing capacity and relatively low ductility.
- Asphalt Mastic Region: Due to the material properties of asphalt mastic, it exhibited pronounced nonlinear behavior. The cohesive elements in this region were designed to reflect lower initial stiffness, higher cracking resistance, and higher plastic deformation possibility.
- Interface Region (Aggregate–Mastic Interface): The interface between the aggregate and mastic represented a weak link in stress transfer within the mixture, prone to interface debonding or crack propagation. The cohesive elements in this region exhibited significantly reduced interface stiffness and fracture toughness compared to the interior of the other two phases.
4. Simulation Results and Quantitative Evaluation
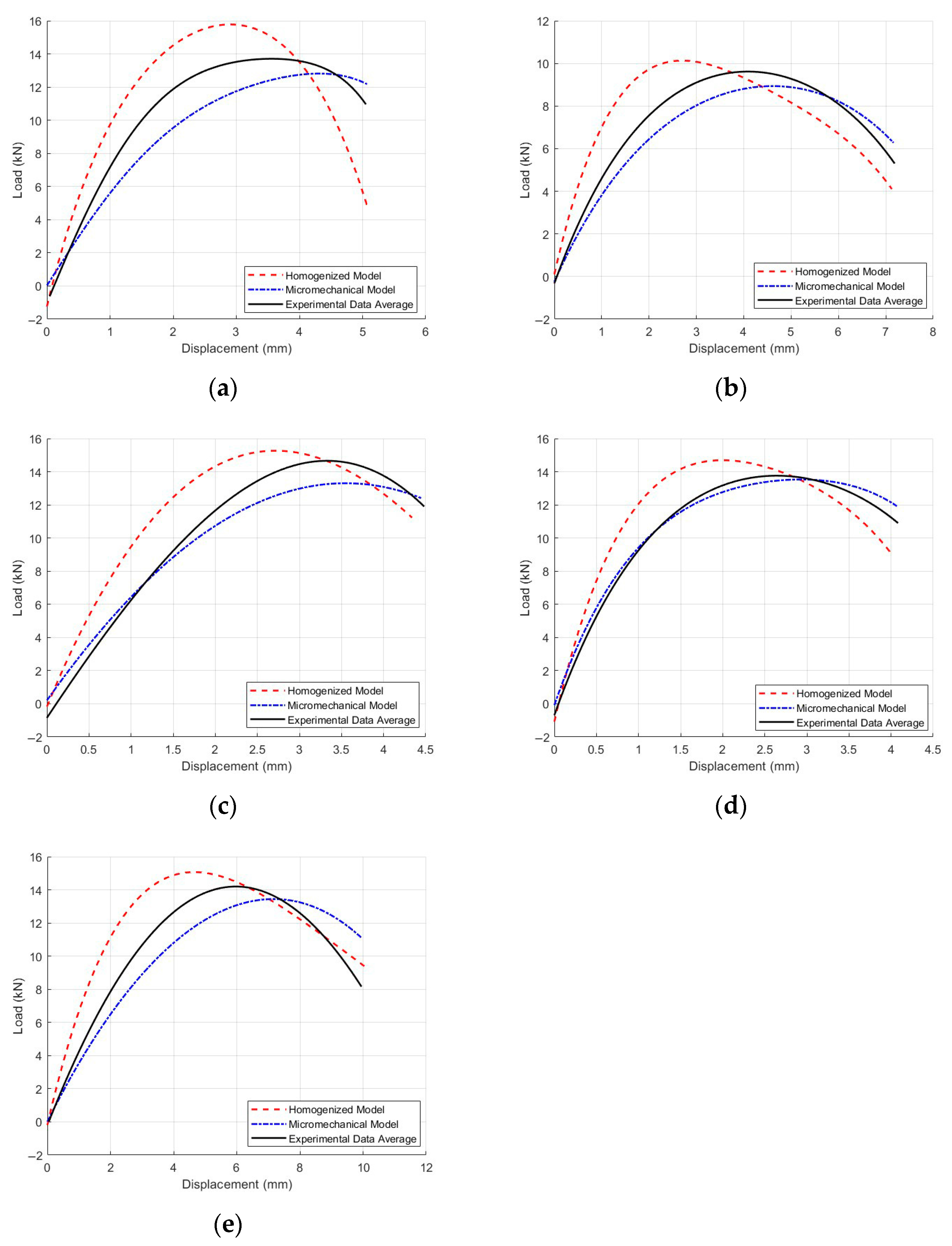
4.1. Comparative Analysis of Load–Displacement Curves
4.2. Quantitative Evaluation Metrics and Error Analysis
4.2.1. Statistical Metrics
4.2.2. Mesh Sensitivity Analysis
4.2.3. Discussion on Error Sources
- Differences in material characterization approaches: The homogeneous model simplifies asphalt mixtures as macroscopically equivalent continuous media, neglecting the distribution and interfacial characteristics of actual constituents, including coarse aggregates, asphalt mortar, and voids. Although this simplification enhances computational efficiency, it inadequately represents the effects of material heterogeneity on crack propagation paths and localized stress concentrations.
- Precision in interface behavior modeling: The mesoscale model achieves superior prediction accuracy through explicit implementation of cohesive elements at aggregate–mortar interfaces and within mortar phases, enabling the precise simulation of interface debonding, micro-crack initiation, and damage evolution processes. In contrast, while CZMs are also employed in homogeneous approaches, their equivalent distribution mechanism fails to capture the preferential interfacial crack propagation observed in actual materials, resulting in deviations from experimental measurements.
- Structural scale and crack evolution paths: The mesoscale framework effectively simulates crack deflection mechanisms influenced by coarse aggregate gradation, spatial distribution, and skeletal structure, thereby accurately reproducing nonlinear phases and fracture processes in experimental curves. Homogeneous models, however, disregard these microstructural mechanisms, exhibiting accelerated stiffness degradation and load reduction during crack propagation stages.
5. Application of Mesoscopic Models
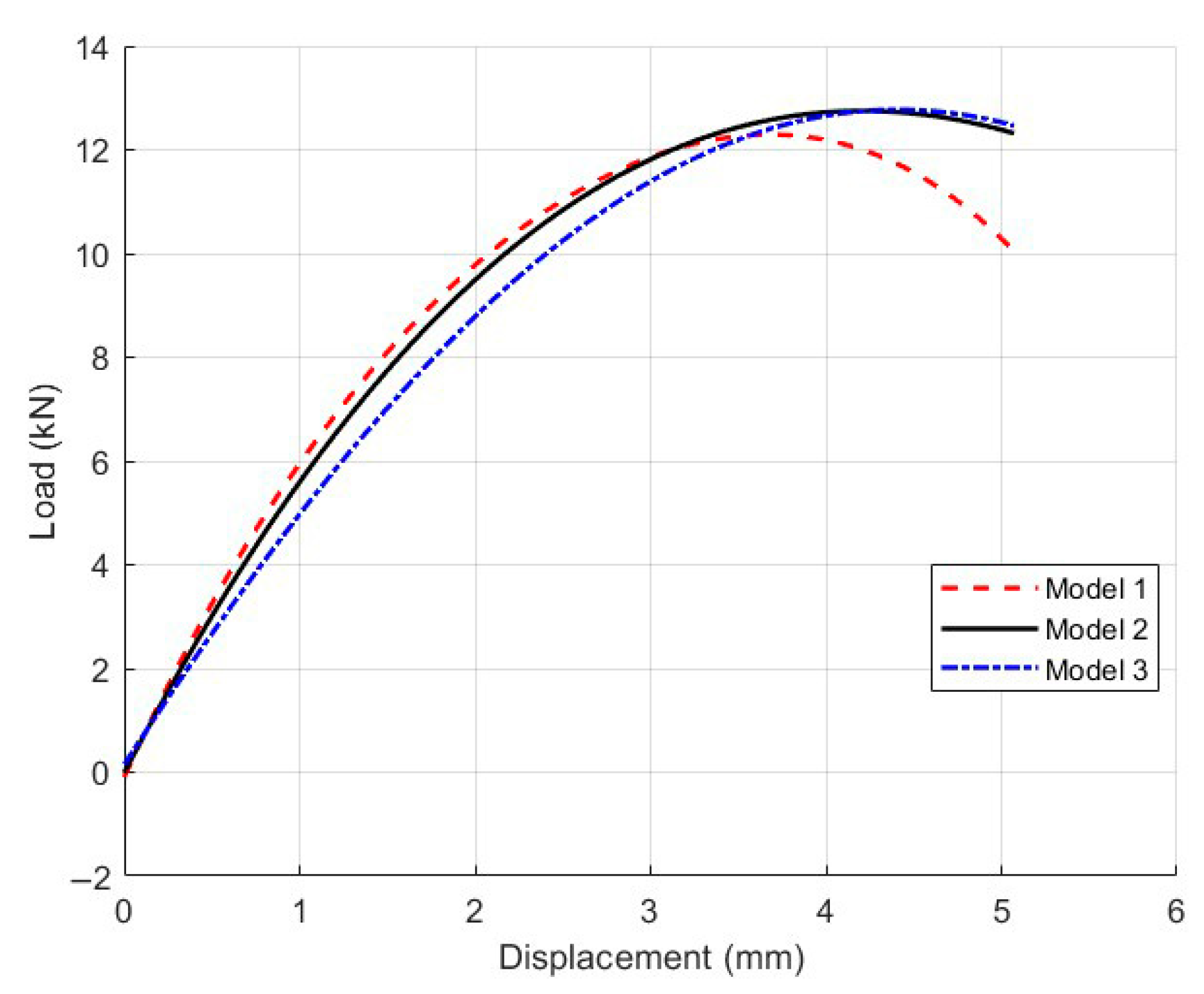
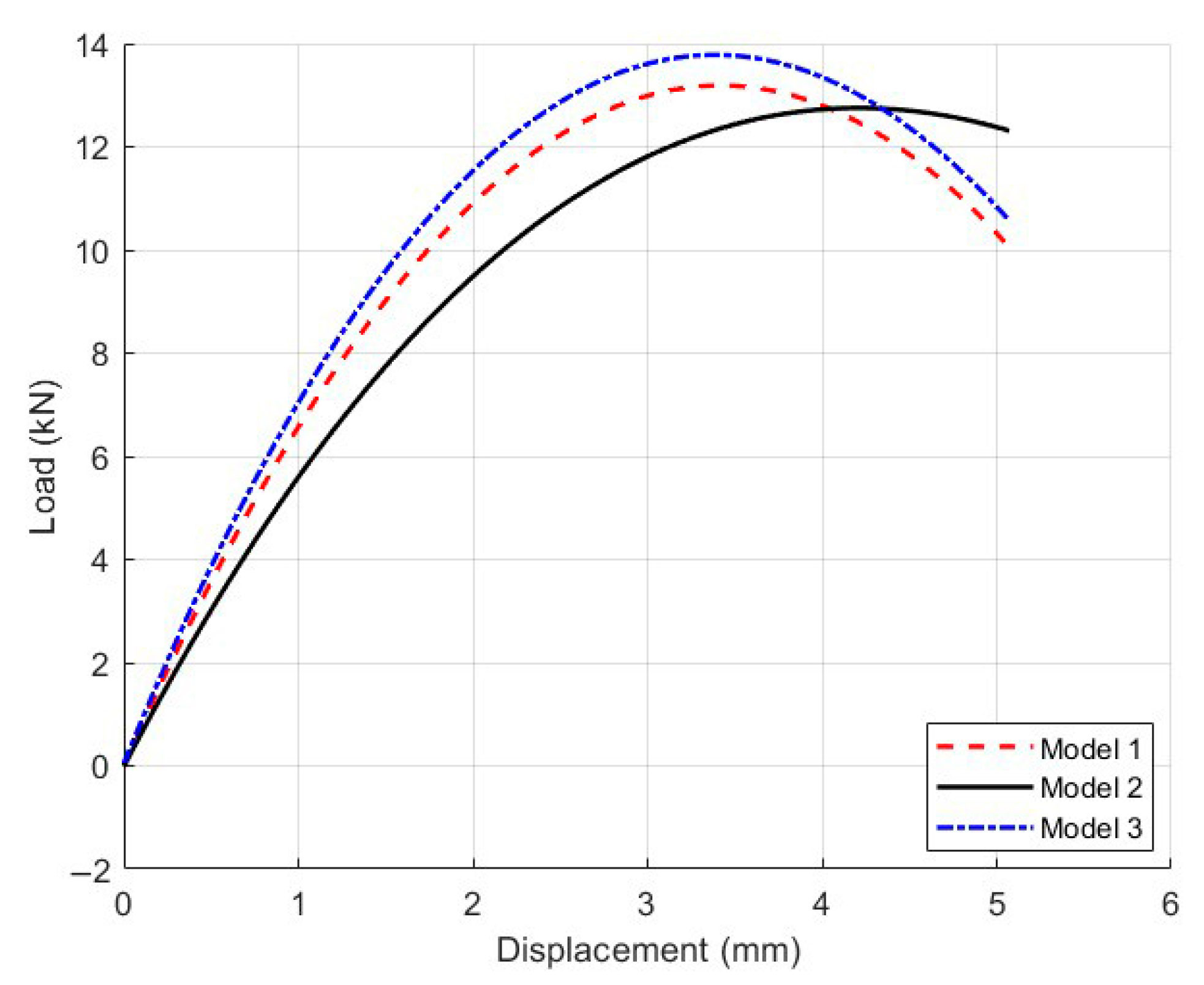
5.1. Influence of Incorrect Compaction Level on Mechanical Response of Mesoscopic Models
5.1.1. Model Parameters and Computational Results
5.1.2. Data Comparison and Analysis of Influencing Factors
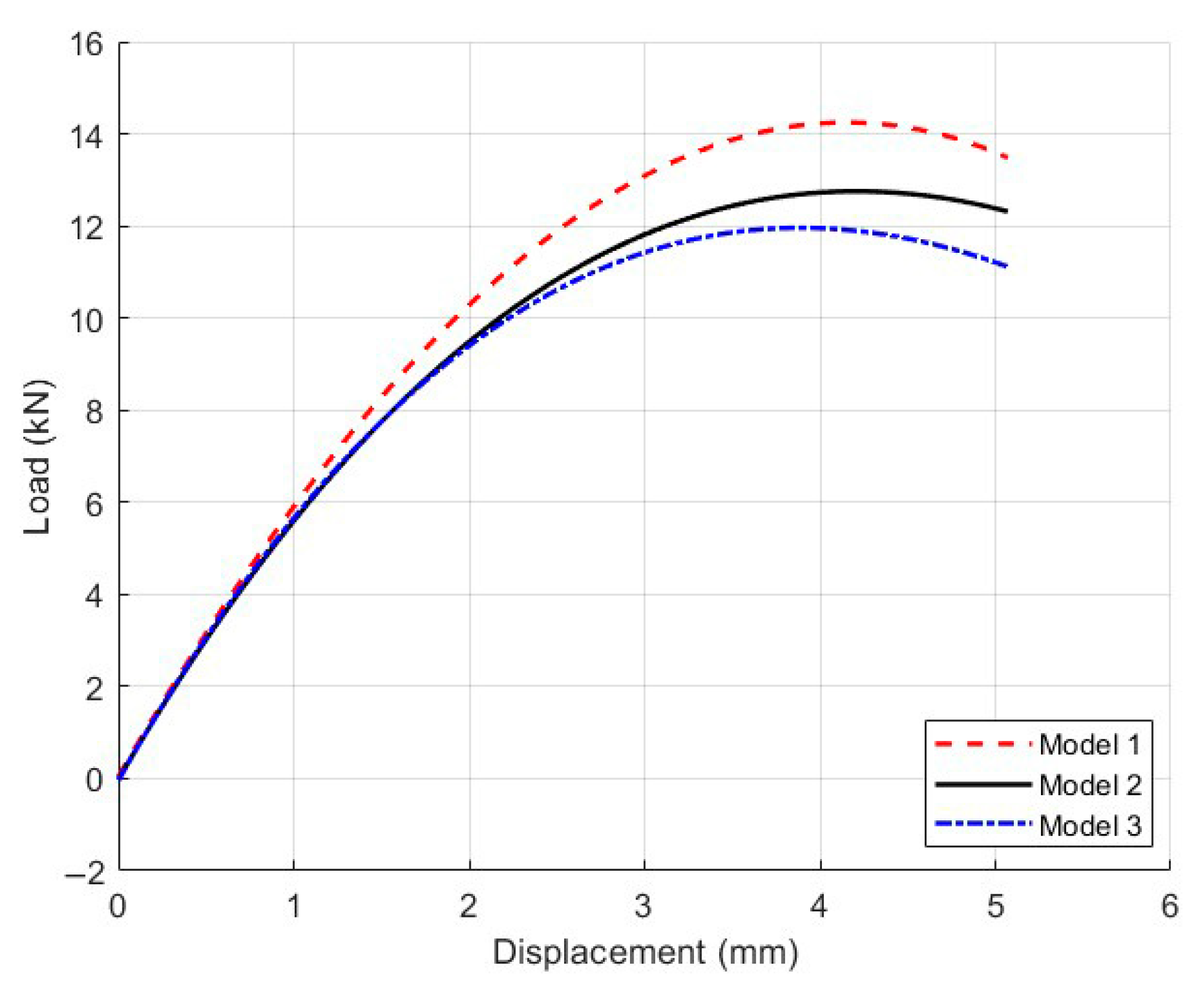
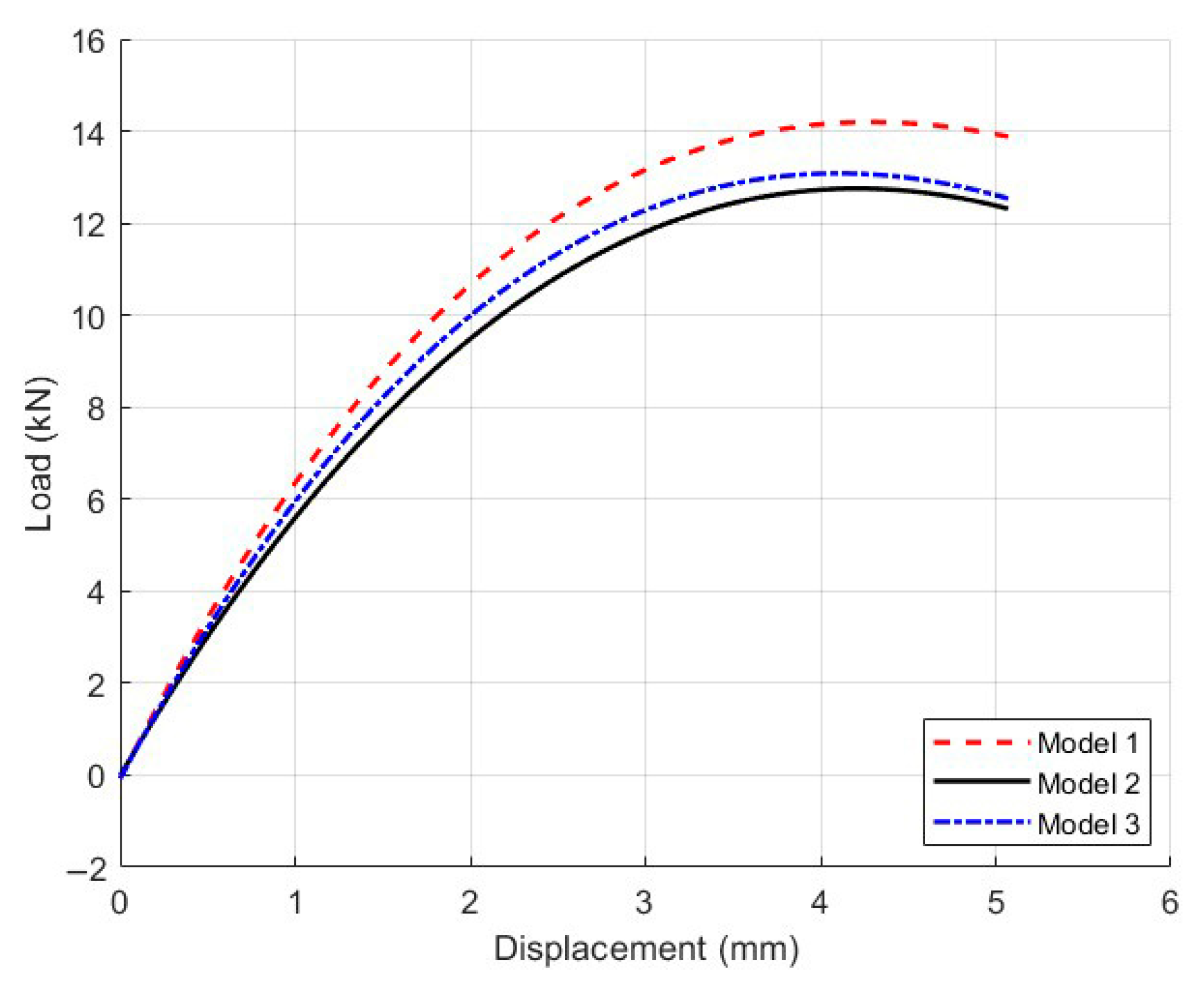
5.2. Influence of Gradation Design Classification on Mechanical Response of Mesoscopic Models
5.2.1. Model Parameters and Computational Results
5.2.2. Data Comparison and Analysis of Influencing Factors
5.3. Influence of Mixing Effort on Mechanical Response of Mesoscopic Models
5.3.1. Model Parameters and Computational Results
5.3.2. Data Comparison and Analysis of Influencing Factors
6. Conclusions
- The micromechanical model achieved significantly better agreement with experimental IDT results, with R2 values ranging from 0.86 to 0.98, compared to 0.66 to 0.77 for the homogenized model.
- It accurately captured crack initiation and propagation paths and better reflected localized damage behavior.
- Simulation of construction deficiencies revealed strong sensitivity in the fracture resistance.
- Increasing air void content from 4% to 10% led to a peak load reduction of up to 35% and stress concentration increases of 25–40%.
- Gap-graded structures accelerated crack coalescence and reduced peak load by 12.5–19.3%.
- In contrast, a dense and uniform aggregate distribution enhanced stress transfer efficiency and improved peak load capacity by 15.4% while also delaying crack propagation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dai, Q.; Ng, K. 2D cohesive zone modeling of crack development in cementitious digital samples with microstructure characterization. Constr. Build. Mater. 2014, 54, 584–595. [Google Scholar] [CrossRef]
- Chen, A.; Airey, G.D.; Thom, N.; Li, Y.; Wan, L. Simulation of Micro-Crack Initiation and Propagation under Repeated Load in Asphalt Concrete Using Zero-Thickness Cohesive Elements. Constr. Build. Mater. 2022, 342, 127934. [Google Scholar] [CrossRef]
- Rahmani, M.; Kim, Y.-R. Coupled thermo-mechanical modeling of reflective cracking in flexible pavements. Int. J. Solids Struct. 2025, 308, 113129. [Google Scholar] [CrossRef]
- Ding, B.; Zou, X.; Peng, Z.; Liu, X. Evaluation of fracture resistance of asphalt mixtures using the single-edge notched beams. Adv. Mater. Sci. Eng. 2018, 2018, 8026798. [Google Scholar] [CrossRef]
- Guo, M.; Motamed, A.; Tan, Y.; Bhasin, A. Investigating the interaction between asphalt binder and fresh and simulated RAP aggregate. Mater. Des. 2016, 105, 25–33. [Google Scholar] [CrossRef]
- Kim, H.; Wagoner, M.P.; Buttlar, W.G. Simulation of fracture behavior in asphalt concrete using a heterogeneous cohesive zone discrete element model. J. Mater. Civ. Eng. 2008, 20, 552–563. [Google Scholar] [CrossRef]
- Liu, P.; Chen, J.; Lu, G.; Wang, D.; Oeser, M.; Leischner, S. Numerical simulation of crack propagation in flexible asphalt pavements based on cohesive zone model developed from asphalt mixtures. Materials 2019, 12, 1278. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Hoff, I.; Liu, G.; Zhang, X.; Barbieri, D.M.; Wang, F. Development of finite element model based on indirect tensile test for various asphalt mixtures. Constr. Build. Mater. 2023, 394, 132085. [Google Scholar] [CrossRef]
- Zhao, Y.; Jiang, L.; Jiang, J.; Ni, F. Accuracy improvement for two-dimensional finite-element modeling while considering asphalt mixture meso-structure characteristics in indirect tensile test simulation. J. Mater. Civ. Eng. 2020, 32, 04020275. [Google Scholar] [CrossRef]
- Wang, H.; Hao, P. Numerical Simulation of Indirect Tensile Test Based on the Microstructure of Asphalt Mixture. J. Mater. Civ. Eng. 2011, 23, 21–29. [Google Scholar] [CrossRef]
- Klimczak, M.; Jaworska, I.; Tekieli, M. 2D digital reconstruction of asphalt concrete microstructure for numerical modeling purposes. Materials 2022, 15, 5553. [Google Scholar] [CrossRef] [PubMed]
- Dong, Z.; Gong, X.; Zhao, L.; Zhang, L. Mesostructural damage simulation of asphalt mixture using microscopic interface contact models. Constr. Build. Mater. 2014, 53, 665–673. [Google Scholar] [CrossRef]
- Yin, A.; Yang, X.; Gao, H.; Zhu, H. Tensile fracture simulation of random heterogeneous asphalt mixture with cohesive crack model. Eng. Fract. Mech. 2012, 92, 40–55. [Google Scholar] [CrossRef]
- López, C.M.; Carol, I.; Aguado, A. Meso-structural study of concrete fracture using interface elements. I: Numerical model and tensile behavior. Mater. Struct. 2008, 41, 583–599. [Google Scholar] [CrossRef]
- Yin, A.; Yang, X.; Zhang, C.; Zeng, G. Three-dimensional heterogeneous fracture simulation of asphalt mixture under uniaxial tension with cohesive crack model. Constr. Build. Mater. 2015, 76, 103–117. [Google Scholar] [CrossRef]
- Guddati, M.N.; Feng, Z.; Kim, Y.R. Towards a micromechanics-based procedure to characterize fatigue performance of asphalt concrete. Transp. Res. Rec. 2002, 1789, 121–128. [Google Scholar] [CrossRef]
- Wei, X.; Sun, Y.; Gong, H.; Li, Y.; Chen, J. Repartitioning-Based Aggregate Generation Method for Fast Modeling 3D Mesostructure of Asphalt Concrete. Comput. Struct. 2023, 281, 107010. [Google Scholar] [CrossRef]
- Wang, F.; Xiao, Y.; Cui, P.; Ma, T.; Kuang, D. Effect of aggregate morphologies and compaction methods on the skeleton structures in asphalt mixtures. Constr. Build. Mater. 2020, 263, 120220. [Google Scholar] [CrossRef]
- Li, J.; Li, P.; Su, J.; Yang, L.; Wu, X. Coarse aggregate movements during compaction and their relation with the densification properties of asphalt mixture. Int. J. Pavement Eng. 2019, 20, 1263–1275. [Google Scholar] [CrossRef]
- Du, J.; Fu, Z. Enhancement effect of aggregates on the low-temperature cracking resistance of asphalt mixtures. Materials 2024, 17, 2865. [Google Scholar] [CrossRef] [PubMed]
- Pouranian, M.R.; Haddock, J.E. Effect of aggregate gradation on asphalt mixture compaction parameters. J. Mater. Civ. Eng. 2020, 32, 04020244. [Google Scholar] [CrossRef]
- Almusawi, A.; Sengoz, B.; Topal, A. Evaluation of mixing and compaction temperatures of polymer modified and warm mix asphalt using different methods. Constr. Build. Mater. 2020, 255, 119357. [Google Scholar] [CrossRef]
- Liu, Q.; Hu, J.; Liu, P.; Wu, J.; Leischner, S.; Oeser, M. Uncertainty analysis of in-situ compaction parameters of asphalt mixture. Constr. Build. Mater. 2021, 279, 122514. [Google Scholar] [CrossRef]
- Hu, M.; Liu, H.; Chen, S. Experimental study on the characteristics of air voids of asphalt mixture under vacuum compaction. IOP Conf. Ser. Earth Environ. Sci. 2021, 719, 032069. [Google Scholar] [CrossRef]
- Castillo, D.; Caro, S.; Darabi, M.; Masad, E. Studying the effect of microstructural properties on the mechanical degradation of asphalt mixtures. Constr. Build. Mater. 2015, 93, 70–83. [Google Scholar] [CrossRef]
- Gajewski, M.D.; Król, J.B. The Influence of Mortar’s Poisson Ratio and Viscous Properties on Effective Stiffness and Anisotropy of Asphalt Mixture. Materials 2022, 15, 8946. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Luo, X.; Luo, R.; Lytton, R.L. Crack initiation in asphalt mixtures under external compressive loads. Constr. Build. Mater. 2014, 72, 94–103. [Google Scholar] [CrossRef]
- Gao, L.; Zhou, Y.; Jiang, J.; Yang, Y.; Kong, H. Mix-mode fracture behavior in asphalt concrete: Asymmetric semi-circular bending testing and random aggregate generation-based modelling. Constr. Build. Mater. 2024, 438, 137225. [Google Scholar] [CrossRef]
- Decky, M.; Papanova, Z.; Juhas, M.; Kudelcikova, M. Evaluation of the Effect of Average Annual Temperatures in Slovakia between 1971 and 2020 on Stresses in Rigid Pavements. Land 2022, 11, 764. [Google Scholar] [CrossRef]
- Coleri, E.; Harvey, J.T.; Yang, K.; Boone, J.M. Development of a Micromechanical Finite Element Model from Computed Tomography Images for Shear Modulus Simulation of Asphalt Mixtures. Constr. Build. Mater. 2012, 30, 783–793. [Google Scholar] [CrossRef]
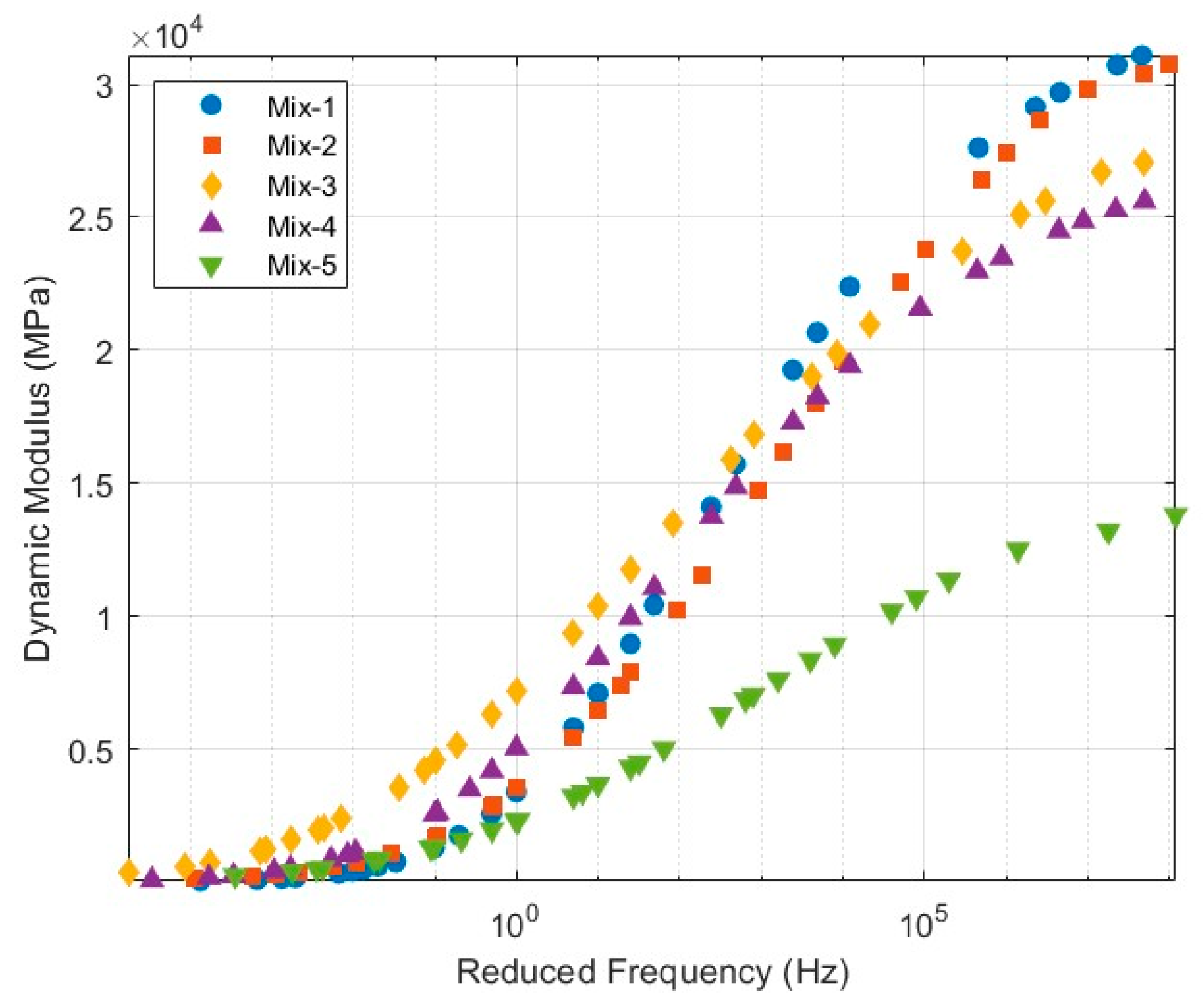



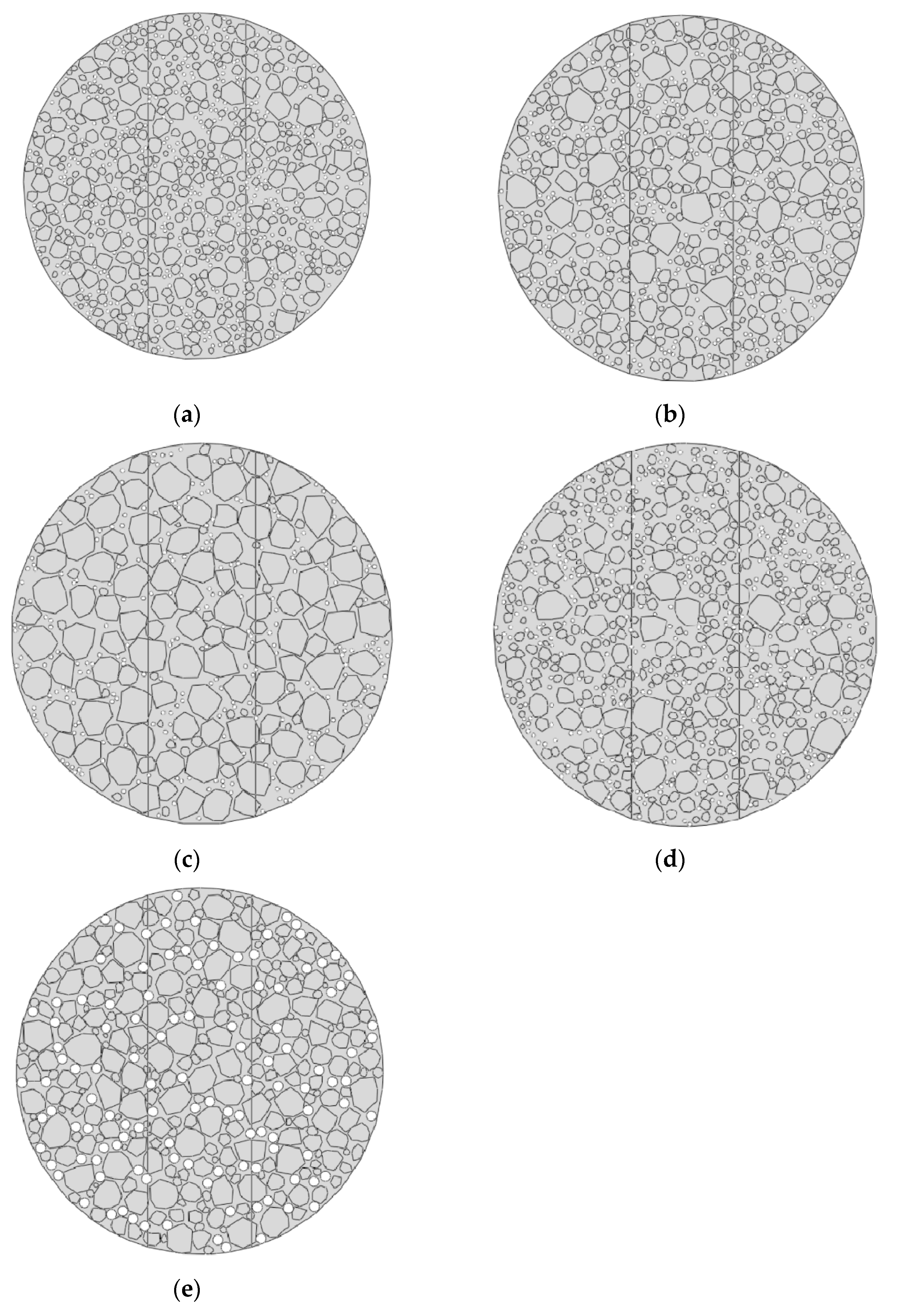

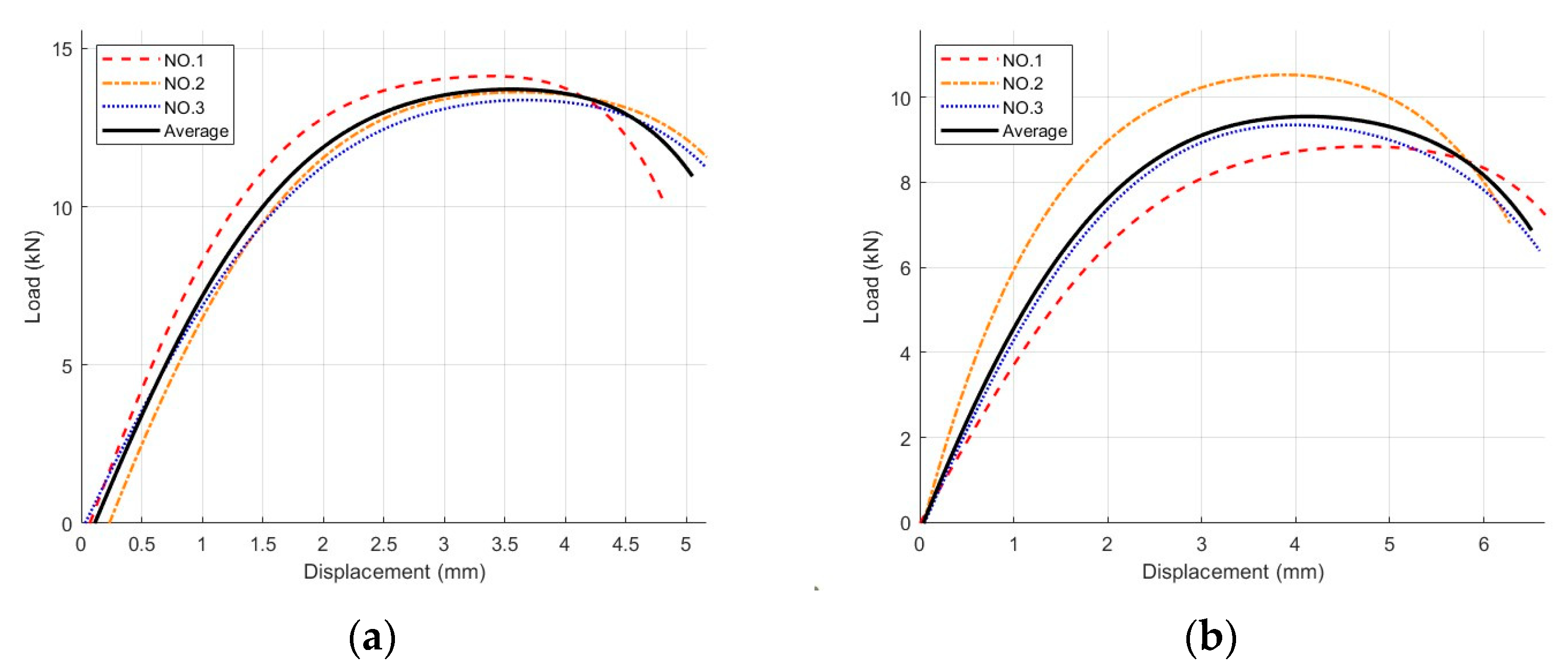
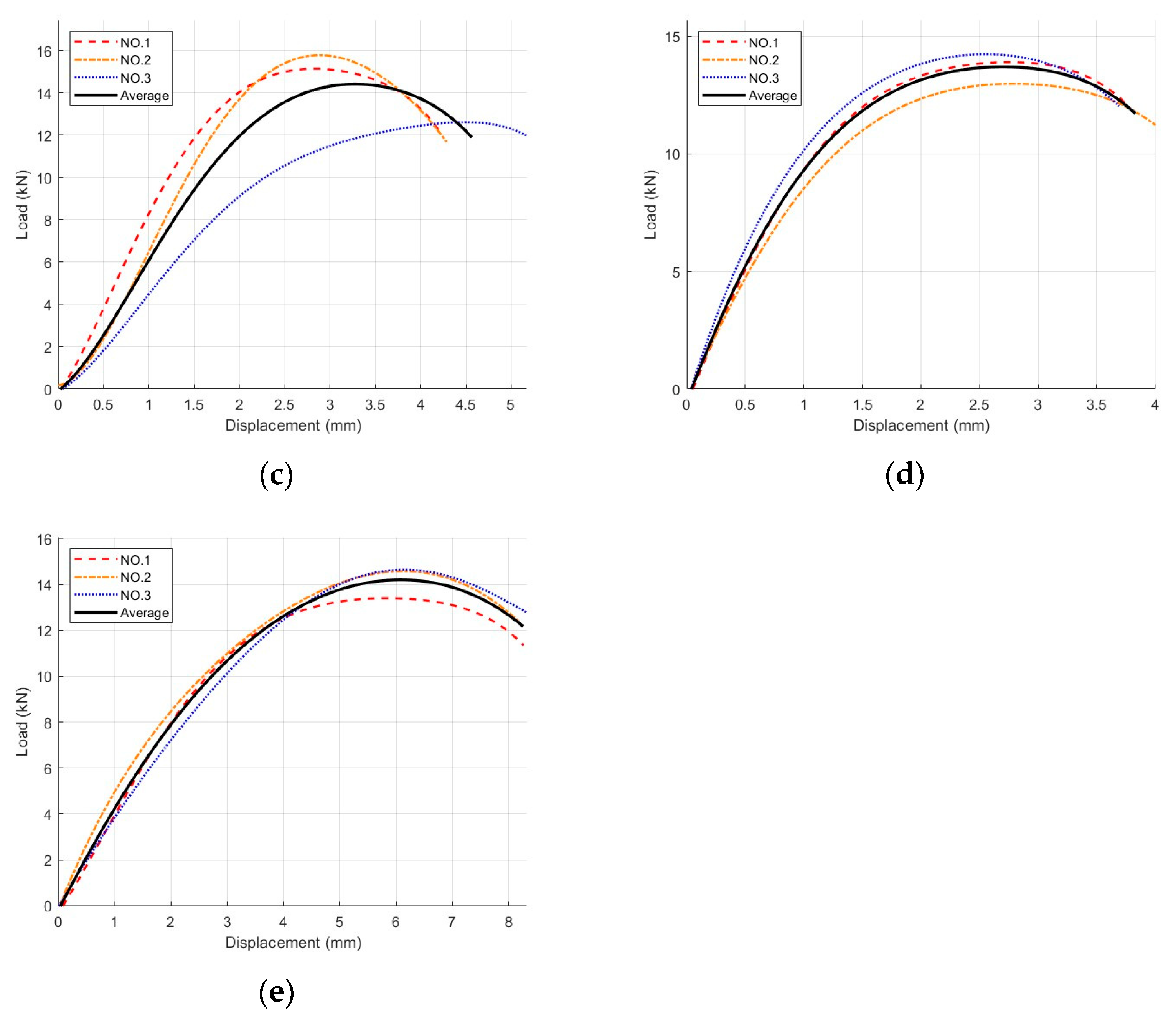

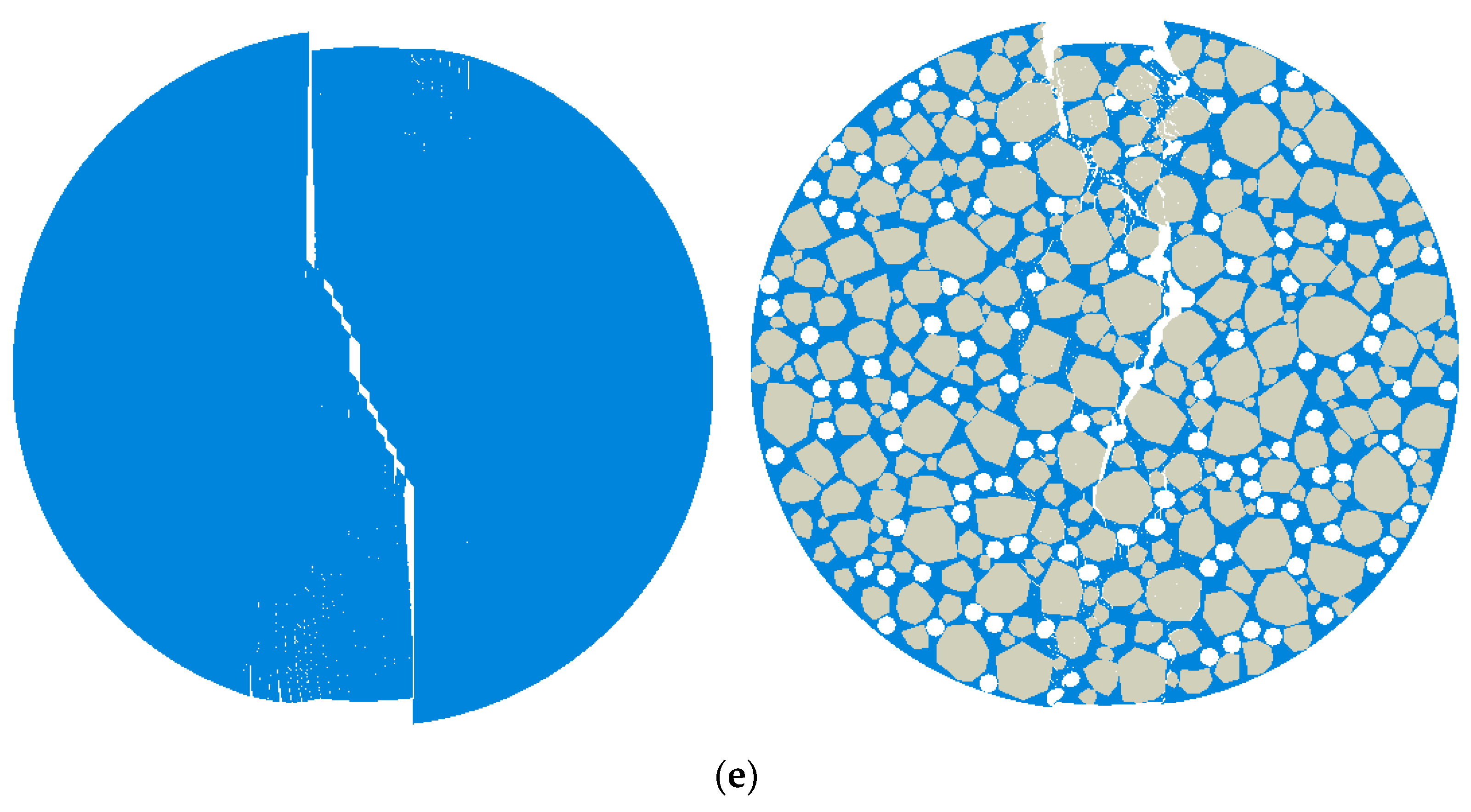







| Asphalt Mixture Designation | Mix-1 | Mix-2 | Mix-3 | Mix-4 | Mix-5 |
|---|---|---|---|---|---|
| Asphalt Content (%) | 5.2 | 4.6 | 6.0 | 5.1 | 6.7 |
| RAP Content (%) | 20.1 | 30.0 | 12.1 | 20.0 | 0 |
| Air Voids (%) | 7.14 | 6.65 | 7.45 | 7.20 | 19.2 |
| Asphalt Mixture Designation | Sieve Size (mm) | 19–16 | 16–9.5 | 9.5–4.75 | 4.75–2.36 | 2.36–0 |
|---|---|---|---|---|---|---|
| Mix-1 | Percent (%) | 0 | 7.5 | 35.5 | 21.8 | 29.4 |
| Mix-2 | Percent (%) | 7.0 | 17.0 | 26.2 | 18.0 | 28.0 |
| Mix-3 | Percent (%) | 0.7 | 76.7 | 7.5 | 4.3 | 7.1 |
| Mix-4 | Percent (%) | 0 | 12.8 | 26.5 | 21.6 | 33.4 |
| Mix-5 | Percent (%) | 0 | 42.0 | 38.9 | 12.8 | 5.1 |
| Material Parameters | Density (kg/m3) | Poisson’s Ratio | Elastic Modulus (MPa) | Cohesive Element Parameters | |||
|---|---|---|---|---|---|---|---|
| Interface Stiffness K (MPa/mm) | Tensile Strength TC (MPa) | Fracture Energy GC (J/m2) | |||||
| Asphalt Mixture Designation | Mix-1 | 2400 | 0.35 | 1296 | 480 | 1.9 | 1850 |
| Mix-2 | 2400 | 0.35 | 1651 | 611 | 1.18 | 1890 | |
| Mix-3 | 2300 | 0.35 | 4543 | 1628 | 2.03 | 2590 | |
| Mix-4 | 2400 | 0.35 | 2670 | 988 | 1.86 | 2190 | |
| Mix-5 | 2200 | 0.35 | 1434 | 531 | 1.79 | 3260 | |
| Asphalt Mixture Designation | Mix-1 | Mix-2 | Mix-3 | Mix-4 | Mix-5 |
|---|---|---|---|---|---|
| Air Voids (%) | 7.14 | 6.65 | 7.45 | 7.20 | 19.2 |
| Air Voids Radius (mm) | 0.80 | 0.77 | 0.82 | 0.80 | 2.06 |
| Material Parameters | Material | Elastic Modulus (MPa) | Poisson’s Ratio | Density (kg/m3) | Cohesive Element Parameters | |||
|---|---|---|---|---|---|---|---|---|
| Interface Stiffness K (MPa/mm) | Tensile Strength TC (MPa) | Fracture Energy GC (J/m2) | ||||||
| Asphalt Mixture Designation | Mix-1 | Aggregate | 55,000 | 0.15 | 2500 | 55,000 | 6.35 | 1250 |
| Mortar | 518 | 0.35 | 2200 | 192 | 1.32 | 1600 | ||
| Interface | 518 | 0.35 | 2200 | 192 | 1.19 | 800 | ||
| Mix-2 | Aggregate | 55,000 | 0.15 | 2500 | 55,000 | 6.35 | 1250 | |
| Mortar | 660 | 0.35 | 2200 | 245 | 0.83 | 1510 | ||
| Interface | 660 | 0.35 | 2200 | 245 | 0.75 | 760 | ||
| Mix-3 | Aggregate | 55,000 | 0.15 | 2500 | 55,000 | 6.35 | 1250 | |
| Mortar | 1817 | 0.35 | 2200 | 673 | 1.42 | 2070 | ||
| Interface | 1817 | 0.35 | 2200 | 673 | 1.28 | 1040 | ||
| Mix-4 | Aggregate | 55,000 | 0.15 | 2500 | 55,000 | 6.35 | 1250 | |
| Mortar | 1068 | 0.35 | 2200 | 395 | 1.3 | 2070 | ||
| Interface | 1068 | 0.35 | 2200 | 395 | 1.17 | 1040 | ||
| Mix-5 | Aggregate | 55,000 | 0.15 | 2500 | 55,000 | 6.35 | 1250 | |
| Mortar | 573 | 0.35 | 2200 | 212 | 1.25 | 2890 | ||
| Interface | 573 | 0.35 | 2200 | 212 | 1.13 | 1450 | ||
| Asphalt Mixture Designation | Model Type | R2 |
|---|---|---|
| Mix-1 | Homogenized Model | 0.6972 |
| Micromechanical Model | 0.9083 | |
| Mix-2 | Homogenized Model | 0.6635 |
| Micromechanical Model | 0.9134 | |
| Mix-3 | Homogenized Model | 0.7728 |
| Micromechanical Model | 0.9612 | |
| Mix-4 | Homogenized Model | 0.7367 |
| Micromechanical Model | 0.9875 | |
| Mix-5 | Homogenized Model | 0.7755 |
| Micromechanical Model | 0.8617 |
| Model Name | Air Voids (%) | Air Voids Radius (mm) |
|---|---|---|
| Model 1 | 4 | 0.65 |
| Model 2 | 7 | 0.79 |
| Model 3 | 10 | 1.00 |
| Model Name | Sieve Size (mm) | 16 | 13.2 | 9.5 | 4.75 | 2.36 |
|---|---|---|---|---|---|---|
| Model 1 | Percent Passing (%) | 100 | 99.2 | - | 57 | 35.2 |
| Model 2 | Percent Passing (%) | 100 | 99.2 | 92.6 | 57 | 35.2 |
| Model 3 | Percent Passing (%) | 100 | 99.2 | 92.6 | - | 35.2 |
| Model Name | Region | Coarse Aggregate Size Groups (mm) and Proportions (%) | |
|---|---|---|---|
| 9.5–4.75 | 4.75–2.36 | ||
| Model 1 | Center | 15.79 | 37.49 |
| Edge | 32.11 | 10.41 | |
| Model 2 | Center | 29.67 | 18.22 |
| Edge | 29.67 | 18.22 | |
| Model 3 | Center | 43.57 | 4.34 |
| Edge | 21.87 | 26.04 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Hou, S.; Yu, H. Micromechanical Finite Element Model Investigation of Cracking Behavior and Construction-Related Deficiencies in Asphalt Mixtures. Materials 2025, 18, 3426. https://doi.org/10.3390/ma18153426
Yang L, Hou S, Yu H. Micromechanical Finite Element Model Investigation of Cracking Behavior and Construction-Related Deficiencies in Asphalt Mixtures. Materials. 2025; 18(15):3426. https://doi.org/10.3390/ma18153426
Chicago/Turabian StyleYang, Liu, Suwei Hou, and Haibo Yu. 2025. "Micromechanical Finite Element Model Investigation of Cracking Behavior and Construction-Related Deficiencies in Asphalt Mixtures" Materials 18, no. 15: 3426. https://doi.org/10.3390/ma18153426
APA StyleYang, L., Hou, S., & Yu, H. (2025). Micromechanical Finite Element Model Investigation of Cracking Behavior and Construction-Related Deficiencies in Asphalt Mixtures. Materials, 18(15), 3426. https://doi.org/10.3390/ma18153426





