Multi-Scale Transient Thermo-Mechanical Coupling Analysis Method for the SiCf/SiC Composite Guide Vane
Abstract
1. Introduction
2. Multi-Scale Analysis Theory
2.1. Asymptotic Expansion Homogenization
2.2. Homogenizations of Thermo-Mechanical Properties
3. Multi-Scale Analysis and Result Validation
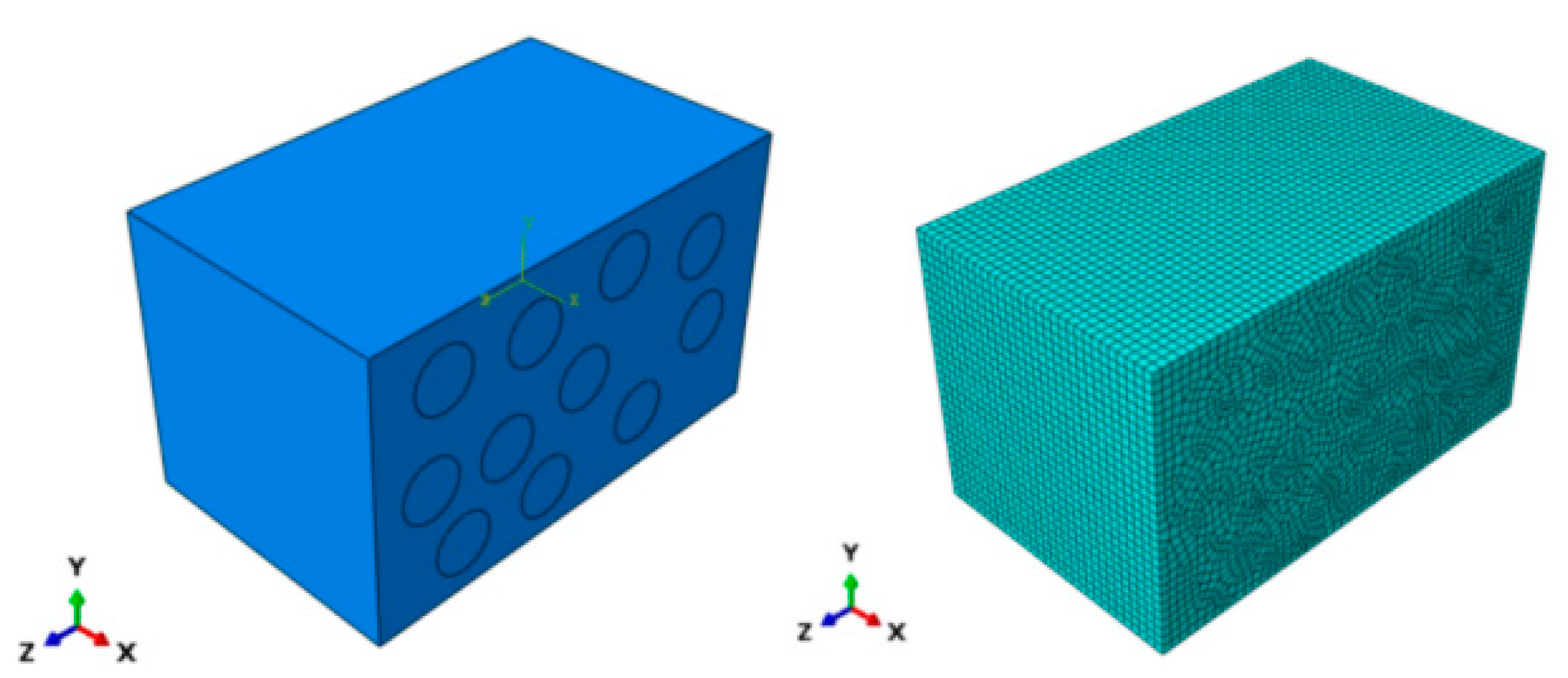
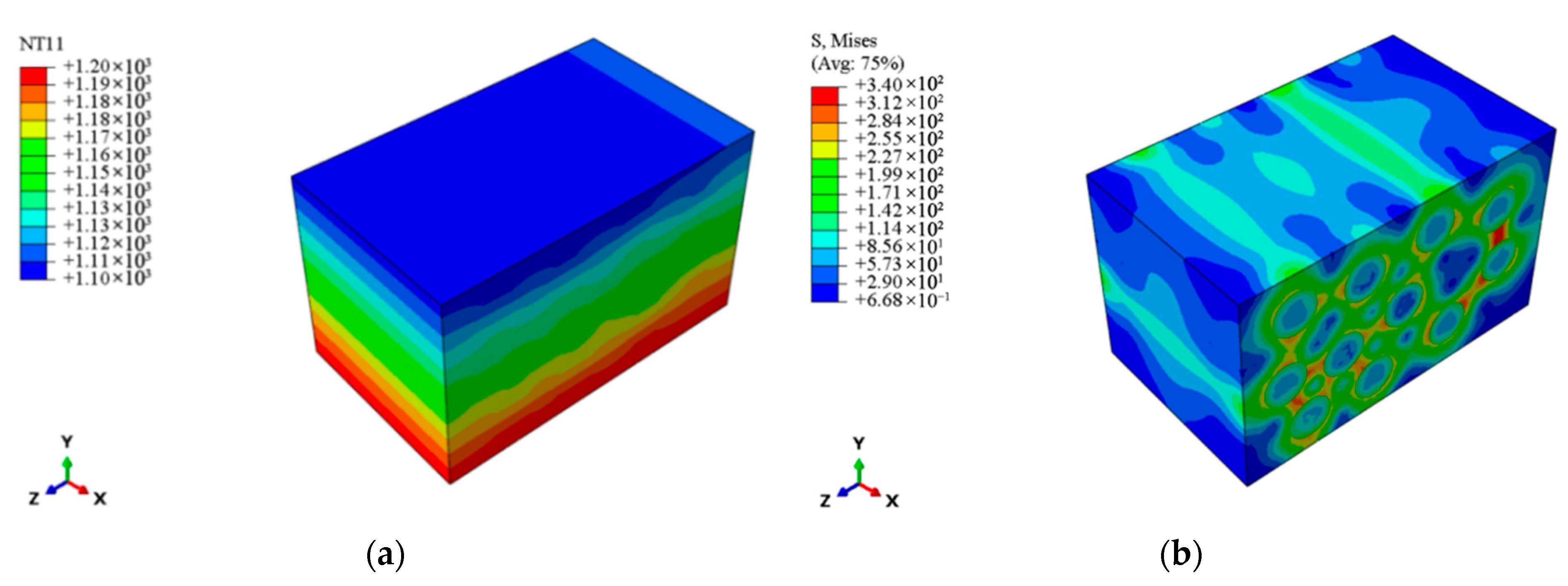
3.1. Multi-Scale Analysis Model
3.2. Revision of Matrix Thermoelastic Properties
3.3. Predictions and Validations of Effective Thermoelastic Properties
3.3.1. Predictions and Validations of Micro-Scale Effective Thermoelastic Properties
3.3.2. Predictions and Validations of Macro-Scale Effective Thermoelastic Properties
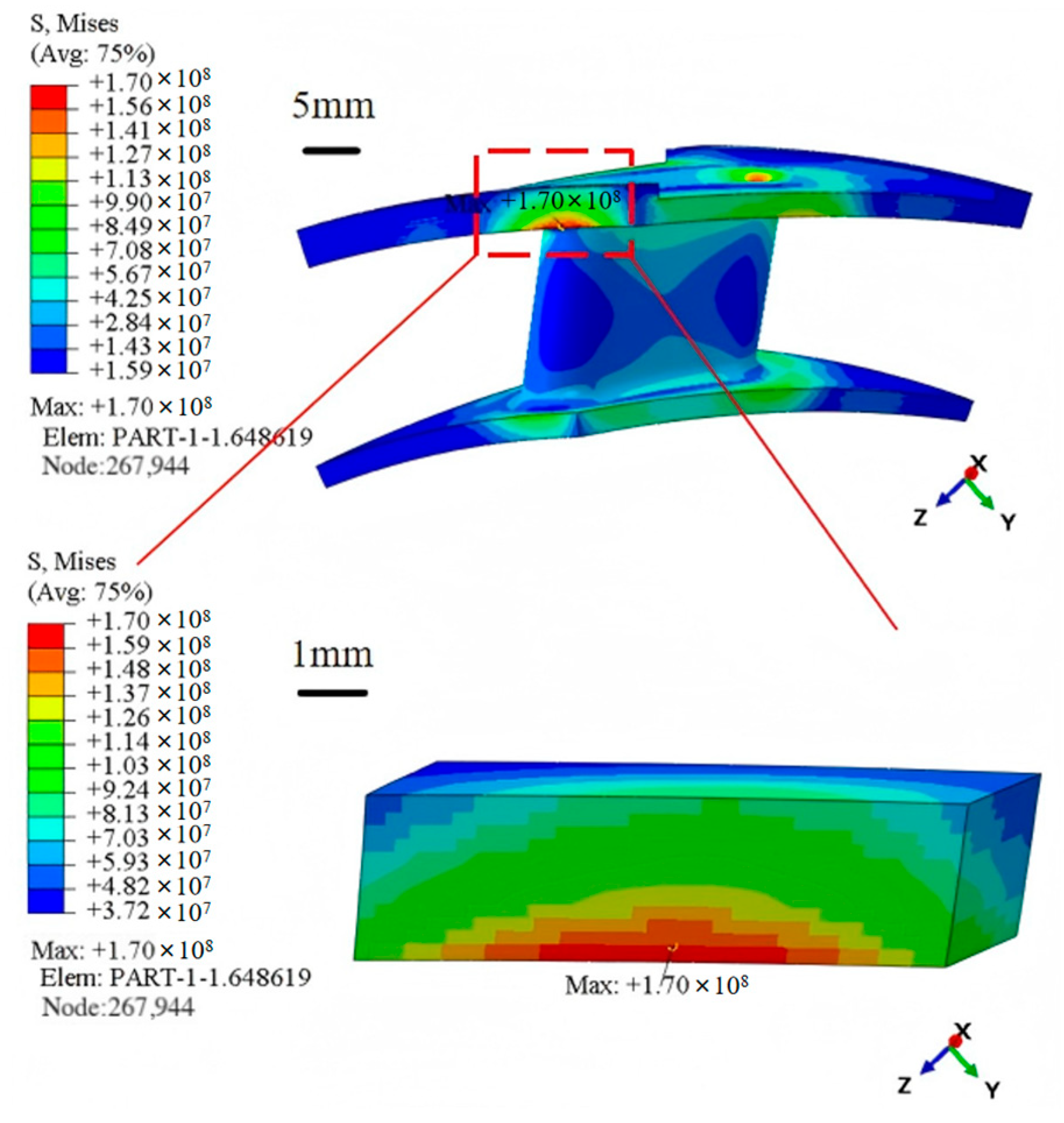
4. Multi-Scale Analysis of Thermal Stress in the Guide Vane
4.1. Macro-Scale Thermal Stress Distribution and Homogenization Method Validation
4.2. Meso-Scale Thermal Stress Analysis
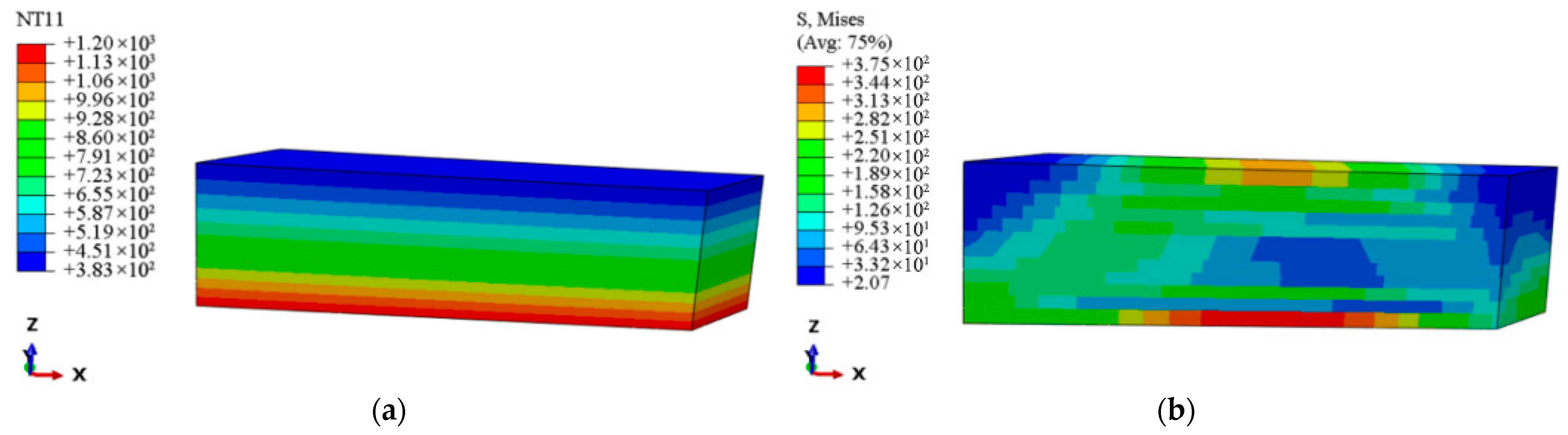
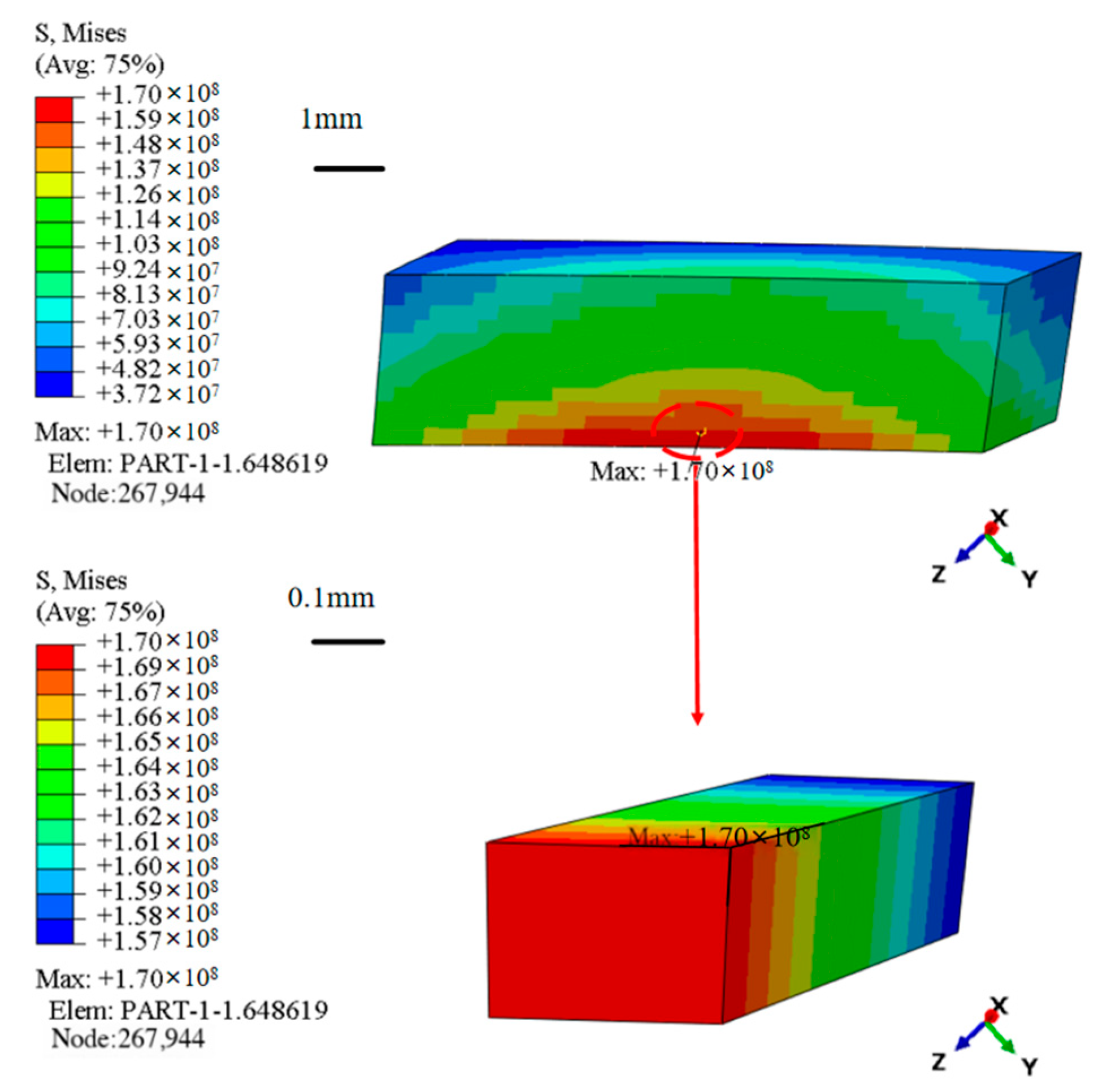
4.3. Micro-Scale Thermal Stress Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Okita, Y.; Mizokami, Y.; Hasegawa, J. Erosion testing of environmental barrier-coated ceramic matrix composite and its behavior on an aero-engine turbine vane under particle-laden hot gas stream. J. Turbomach. 2020, 142, 061001. [Google Scholar] [CrossRef]
- Ohnabe, H.; Masaki, S.; Onozuka, M.; Kaoru, M.; Tadashi, S. Potential application of ceramic matrix composites to aero-engine components. Compos. Part A Appl. Sci. Manuf. 1999, 30, 489–496. [Google Scholar] [CrossRef]
- Liu, X.C.; Guo, X.J.; Xu, Y.L.; Li, L.B.; Zhu, W.; Zeng, Y.Q.; Li, J.; Luo, X.; Hu, X.A. Cyclic thermal shock damage behavior in CVI SiC/SiC high-pressure turbine twin guide vanes. Materials 2021, 14, 6104. [Google Scholar] [CrossRef] [PubMed]
- Huo, S.Y.; Yan, Q.Y.; Gao, X.; You, Y. Ceramic matrix composite turbine vane thermal simulation test and evaluation. Int. J. Turbo 2020, 37, 285–293. [Google Scholar] [CrossRef]
- Zhang, S.; Gao, X.G.; Song, Y.D.; Wang, F.; Zhang, S.R. Fatigue behavior and damage evolution of SiC/SiC composites under high-temperature anaerobic cyclic loading. Ceram. Int. 2021, 47, 29646–29652. [Google Scholar] [CrossRef]
- Ruggles-Wrenn, M.B.; Jones, T.P. Tension–compression fatigue of a SiC/SiC ceramic matrix composite at 1200 ℃ in air and in steam. Int. J. Fatigue 2013, 47, 154–160. [Google Scholar] [CrossRef]
- Ikarashi, Y.; Ogasawara, T.; Aoki, T. Effects of cyclic tensile loading on the rupture behavior of orthogonal 3D woven SiCf/SiC matrix composites at elevated temperatures in air. J. Eur. Ceram. Soc. 2019, 39, 806–812. [Google Scholar] [CrossRef]
- Bhatt, R.T.; Kalluri, S. Tensile creep and fatigue behaviors of SiC/SiC composites in air under thermal gradient conditions. J. Eur. Ceram. Soc. 2025, 45, 117154. [Google Scholar] [CrossRef]
- Xu, Q.; Jin, X.; Liu, L.; Hou, C.; Hu, N.; Chen, J.; Zhao, S.; Marrow, T.J.; Fan, X. Thermal shock and residual strength testing of SiC/SiC composite braided tubes. Exp. Mech. 2023, 63, 955–964. [Google Scholar] [CrossRef]
- Kai, Q.; Xu, X.W.; Mao, C.J.; Bui, T.Q.; Zhang, C. Multiscale damage analysis of through-thickness woven composites under in-plane and out-of-plane loadings: A coupled shell-based model. Compos. Struct. 2025, 358, 118969. [Google Scholar]
- Liu, X.; Shen, X.L.; Gong, L.D.; Li, P. Multi-scale thermoelastic analysis method for 2D SiC/SiC composite turbine guide vanes. Chin. J. Aeronaut. 2018, 31, 117–125. [Google Scholar] [CrossRef]
- Sun, Z.; Shan, Z.D.; Shao, T.M.; Li, J.H.; Wu, X.C. A multiscale modeling for predicting the thermal expansion behaviors of 3D C/SiC composites considering porosity and fiber volume fraction. Ceram. Int. 2021, 47, 7925–7936. [Google Scholar] [CrossRef]
- Liang, S.; Wei, C.; Qiu, B.W.; Zhang, C.; Liao, H.Y.; Ren, X.J.; Zhang, X. Thermo-mechanical response of SiCf/SiC composite cladding: Effect of loss-of-coolant accident duration. Prog. Nucl. Energy 2025, 183, 105681. [Google Scholar] [CrossRef]
- Zhao, X.Y.; Guo, F.; Li, B.B.; Wang, G.N.; Ye, J.R. Multiscale numerical modeling for thermal behavior of plain-woven composites with interfacial and internal defects. Int. J. Heat Mass Transf. 2023, 202, 123711. [Google Scholar] [CrossRef]
- Fang, G.W.; Zheng, M.W.; Chen, M.Z.; Gao, X.G.; Song, Y.D. Stochastic simulation of thermal residual stress in environmental barrier coated 2.5D woven ceramic matrix composites. J. Mater. Eng. Perform. 2024, 33, 4114–4123. [Google Scholar] [CrossRef]
- Singh, R.N.; Wang, H.Y. Thermal shock behavior of fiber-reinforced ceramic matrix composites. Compos. Eng. 1995, 5, 1287–1297. [Google Scholar] [CrossRef]
- Han, J.B.; Wang, R.Q.; Hu, D.Y.; Liu, X.; Zhang, L.; Guo, X.J.; Cho, C.D. Multi-scale analysis and experimental research for turbine guide vanes made of 2D braided SiCf/SiC composites in high-cycle fatigue regime. Int. J. Fatigue 2022, 156, 106697. [Google Scholar] [CrossRef]
- Reynaud, P.; Dalmaz, A.; Tallaron, D.; Rouby, D.; Fantozzi, G. Fatigue behaviour related to interface modification during load cycling in ceramic-matrix fibre composites. Compos. Sci. Technol. 1993, 48, 109–118. [Google Scholar] [CrossRef]
- Wang, S.F.; Zhang, Z. Failure mechanism of turbine guide vane and oxide composition analysis on the surface of failure vane cracks. Eng. Fail. Anal. 2020, 117, 104763. [Google Scholar] [CrossRef]
- Liu, Y.; Qu, Z.; Guo, J.; Zhao, X.M. Numerical study on effective thermal conductivities of plain woven C/SiC composites with considering pores in interlaced woven yarns. Int. J. Heat Mass Tran. 2019, 140, 410–419. [Google Scholar] [CrossRef]
- Dong, K.; Liu, K.; Zhang, Q.; Gu, B.H.; Sun, B.Z. Experimental and numerical analyses on the thermal conductive behaviors of carbon fiber/epoxy plain woven composites. Int. J. Heat Mass Tran. 2016, 102, 501–517. [Google Scholar] [CrossRef]
- Xu, Y.; Ren, S.; Zhang, W. Thermal conductivities of plain woven C/SiC composite: Micromechanical model considering PyC interphase thermal conductance and manufacture-induced voids. Compos. Struct. 2018, 193, 212–223. [Google Scholar] [CrossRef]
- Sun, Z.; Shan, Z.; Huang, H.; Wang, D.; Wang, W.; Liu, J.; Tan, C.; Chen, C. Multi-scale Modeling and Finite Element Analyses of Thermal Conductivity of 3D C/SiC Composites Fabricating by Flexible-Oriented Woven Process. Chin. J. Mech. Eng. 2024, 37, 60. [Google Scholar] [CrossRef]
- Dutra, T.A.; Ferreira, R.T.L.; Resende, H.B.; Guimaraes, A.; Guedes, J.M. A complete implementation methodology for asymptotic homogenized using a finite element commercial software: Preprocessing and postprocessing. Compos. Struct. 2020, 245, 112305. [Google Scholar] [CrossRef]
- Christoff, B.G.; Brito-Santana, H.; Talreja, R.; Tita, V. Development of an abaqus™ plug-in to evaluate the fourth-order elasticity tensor of a periodic material via homogenization by the asymptotic expansion method. Finite Elem. Anal. Des. 2020, 181, 103482. [Google Scholar] [CrossRef]
- GJB 8736-2015; Test Method for Tensile Properties of Continuous Fiber—Reinforced Ceramic Composites at Ambient Temperature. General Armaments Department of the People’s Liberation Army: Beijing, China, 2015.
- GB/T 22588-2008; Determination of Thermal Diffusivity or Thermal Conductivity by the Flash Method. National Standards of People’s Republic of China: Beijing, China, 2008.
- GB/T 16535-2008; Fine Ceramics (Advanced Ceramics, Advanced Technical Ceramics)—Test Method for Linear Thermal Expansion of Monolithic Ceramics by Push-Rod Technique. National Standards of People’s Republic of China: Beijing, China, 2008.
- GB/T 25995-2010; Test Methods for Density and Apparent Porosity of Fine Ceramics. National Standards of People’s Republic of China: Beijing, China, 2010.
- He, Z.P.; Zhang, R.Q.; Fu, D.G.; Li, M.; Chen, Z.K.; Qiu, S.Y. Tensile mechanical behavior of SiC fiber bundle reinforced composites with different interfaces. J. Mater. Eng. 2019, 47, 25–31. [Google Scholar] [CrossRef]
- Zhang, X.D.; Deng, J.K.; Ma, D.Y.; Cao, H.Y.; Zhang, R.Q.; Tang, R. Effective thermal conductivity and microstructure design of fully ceramic microencapsulated fuel pellet based on finite element calculations. J. Lanzhou Univ. Technol. 2022, 48, 9–15. [Google Scholar] [CrossRef]
- Dong, B.; Yu, C.; Deng, C.J.; Zhu, H.X.; Ding, J.; Tang, H. Research progress in thermal conductivity of SiC ceramics. J. Mater. Eng. 2023, 51, 64–75. [Google Scholar] [CrossRef]
- Li, D.Y.; Han, F.; Wang, J.X.; Xu, P.; Zhong, Z.X. Effect of pore-forming agent carbon powder on properties of SiC membrane supports. Membr. Sci. Technol. 2019, 39, 65–72. [Google Scholar] [CrossRef]
- Kiradjiev, K.B.; Halvorsen, S.A.; Gorder, R.A.V.; Howison, S.D. Maxwell-type models for the effective thermal conductivity of a porous material with radiative transfer in the voids. Int. J. Therm. Sci. 2019, 145, 106009. [Google Scholar] [CrossRef]
- Anurag, J.; Burri, A.C.; Sandhyarani, B. Modified Halpin–Tsai model for predicting the mechanical properties of polymer composites reinforced with different cross-sectional fibers. Mater. Today 2023, 91, 14–18. [Google Scholar] [CrossRef]
- Wu, Y.P.; Jia, Q.X.; Yu, D.S.; Zhang, L.Q. Modeling Young’s modulus of rubber–clay nanocomposites using composite theories. Polym. Test. 2004, 23, 903–909. [Google Scholar] [CrossRef]
- Kim, H.S.; Hong, S.I.; Kim, S.J. On the rule of mixtures for predicting the mechanical properties of composites with homogeneously distributed soft and hard particles. J. Mater. Process. Technol. 2021, 112, 109–113. [Google Scholar] [CrossRef]
- Shen, X.L.; Zhang, S.; Liu, X.; Gong, L.D.; Dong, S.J. Prediction of the thermo-mechanical properties of the SiCf/SiC RVE model via FEM and asymptotic homogenization method: Process and implementation details. Arch. Comput. Method Eng. 2021, 28, 3067–3085. [Google Scholar] [CrossRef]
- Liu, H.X.; You, C.; Wu, Q.Y.; Gao, X.G.; Song, Y.D. Thermal stress analysis of CMC turbine guide vane considering thermal-mechanical coupling effect. J. Propul. Technol. 2025, 1–17. Available online: https://www.sciengine.com/doi/pdf/E0A47CFF733341FE9A4D640CA7A16482 (accessed on 11 May 2025).
- Ramos, G.R.; Dos-Santos, T.; Rossi, R. An extension of the hill-mandel principle for transient heat conduction in heterogeneous media with heat generation incorporating finite RVE thermal inertia effects. Int. J. Numer. Methods Eng. 2017, 111, 553–580. [Google Scholar] [CrossRef]
- Ni, Z.; Yu, G.Q.; Chen, Y.C.; Xue, B.C.; Deng, Y.F.; Ma, W.B.; Gao, X.G.; Song, Y.D. Experimental and numerical analysis of CMCs mechanical properties under high-temperature thermal gradient environment. Ceram. Int. 2024, 50, 7132–7149. [Google Scholar] [CrossRef]
- Ding, S.; Zeng, Y.; Jiang, D. Thermal shock resistance of in situ reaction bonded porous silicon carbide ceramics. Mater. Sci. Eng. A 2006, 425, 326–329. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Obara, E.; Wang, S.; Zhu, L.Y.; Li, W.D.; Lin, S.Y.; Han, Z.L.; Luo, C.Y. High-temperature tensile failure mechanism of RTM-made composite T-joints. Def. Technol. 2025, 49, 371–386. [Google Scholar] [CrossRef]

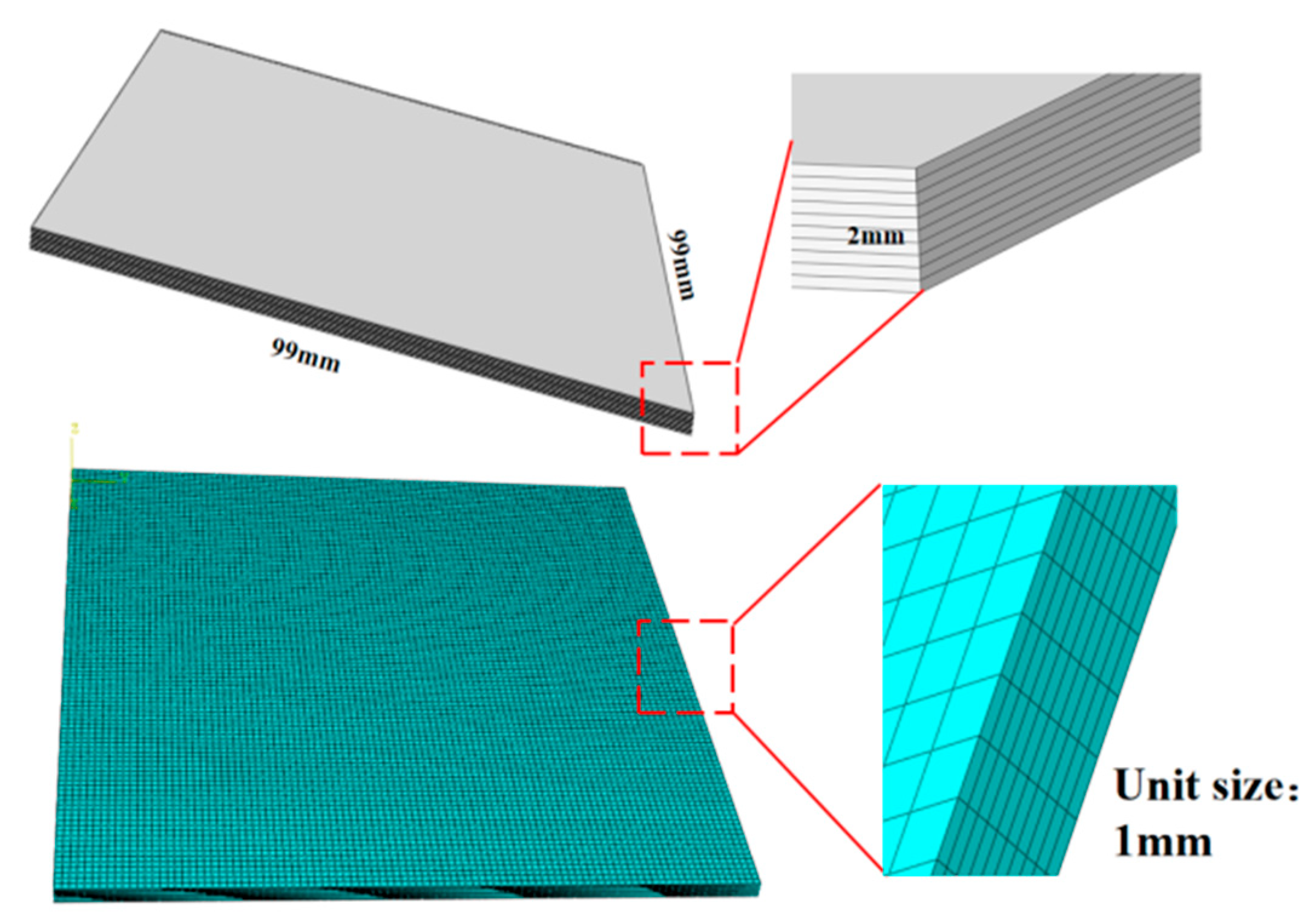
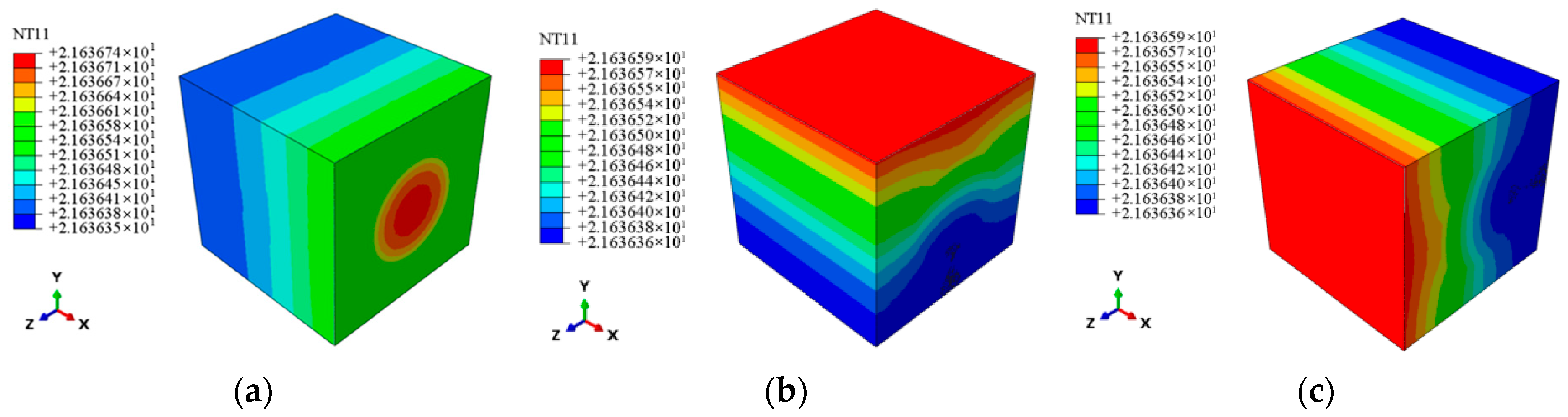
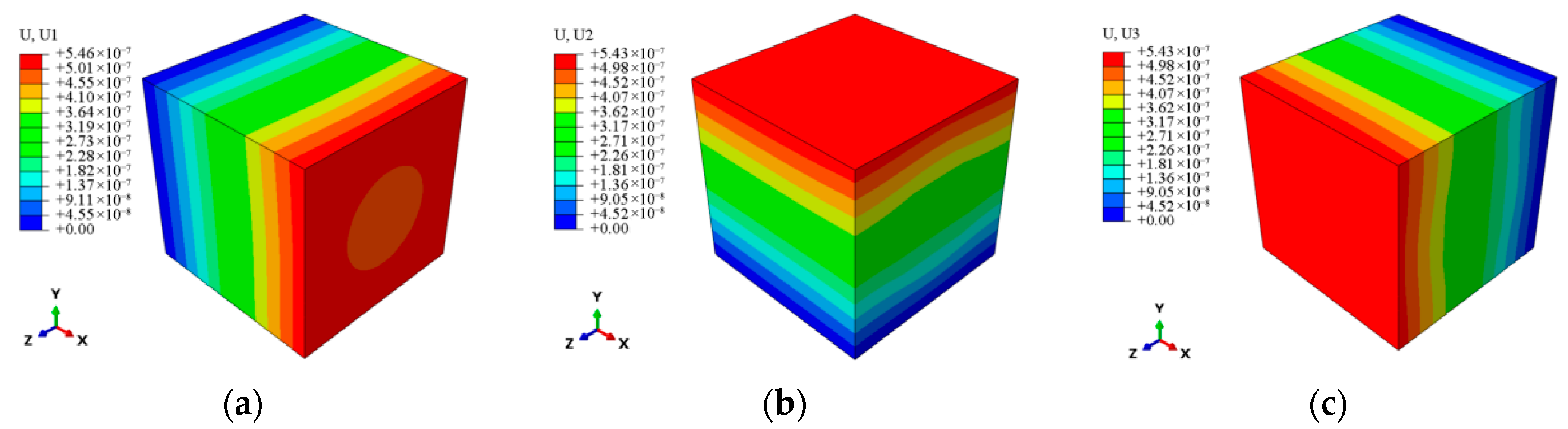
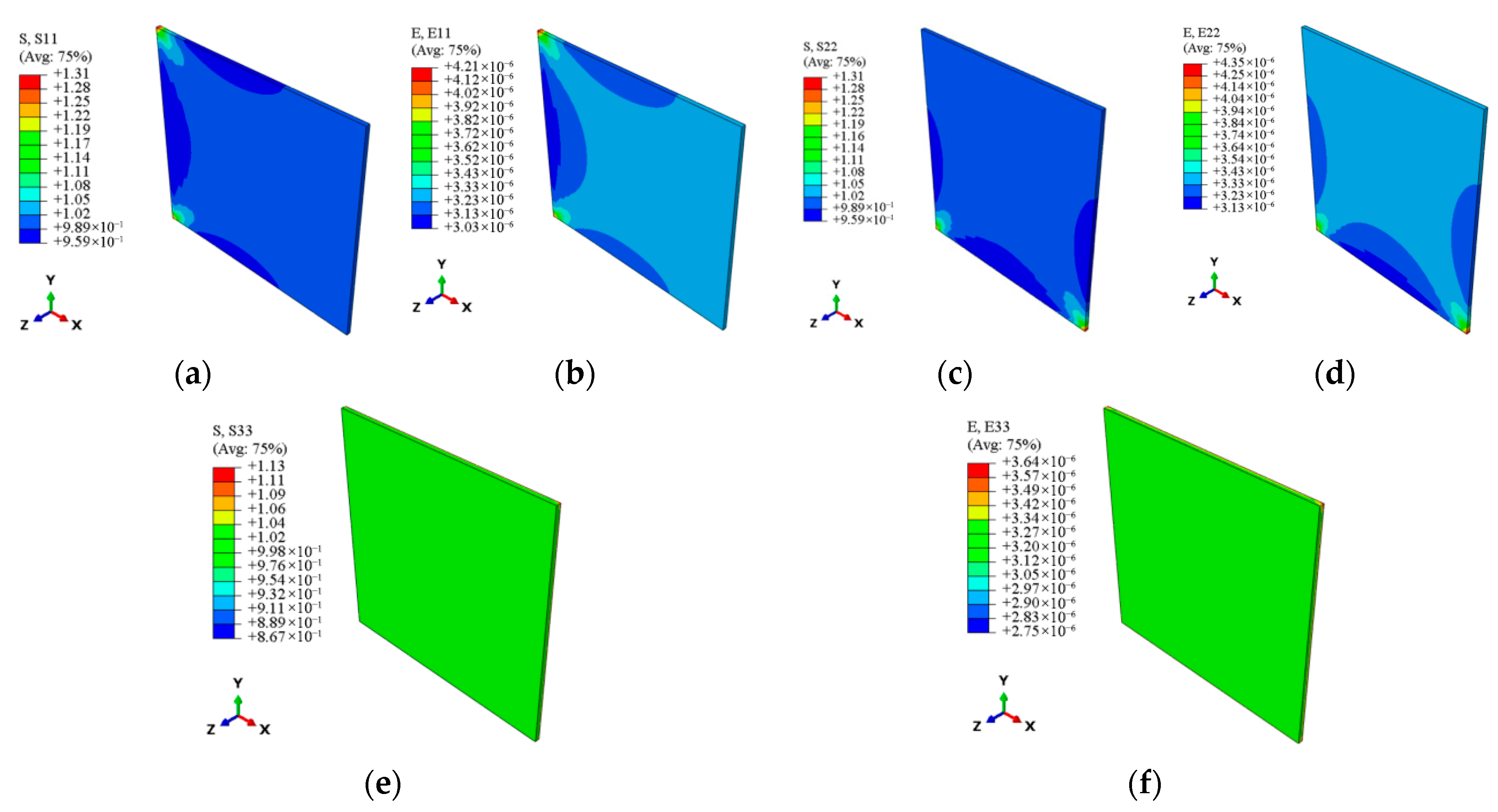
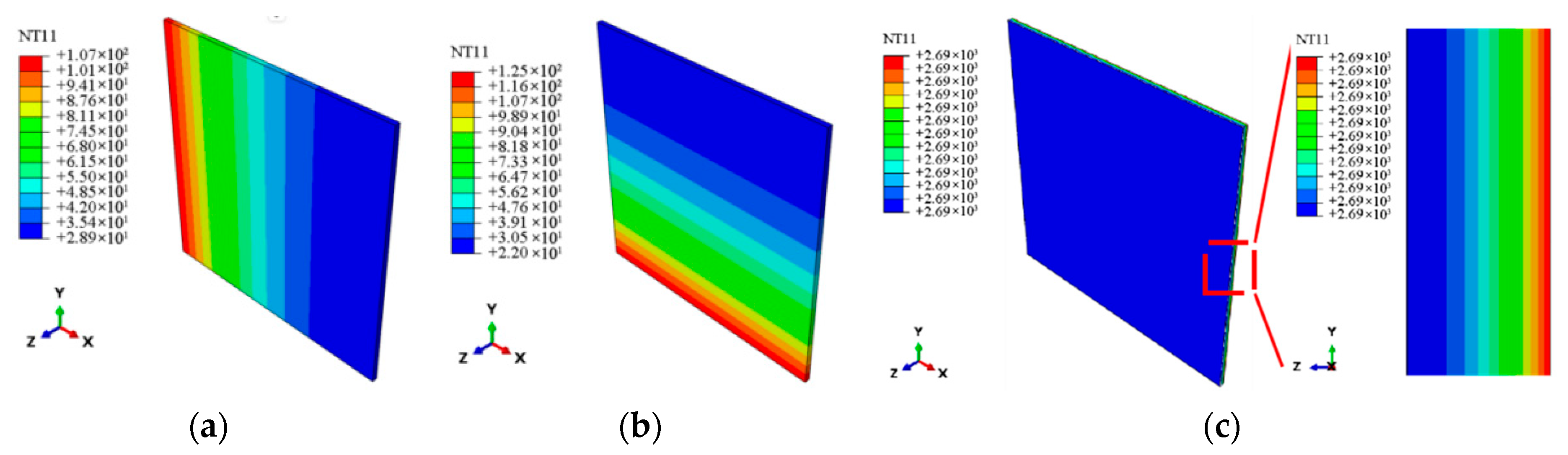
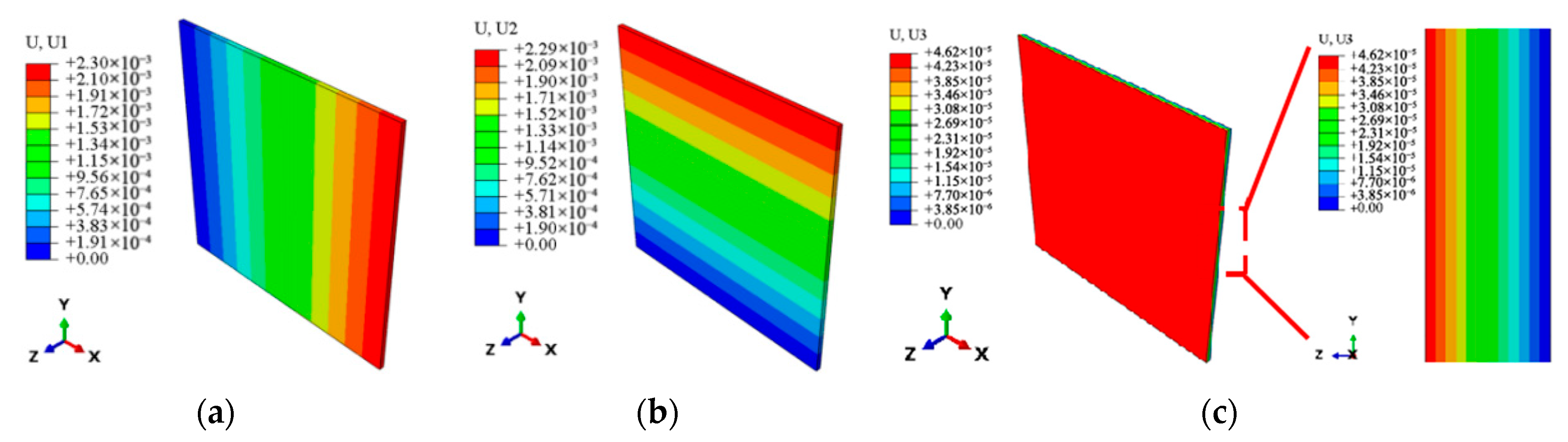

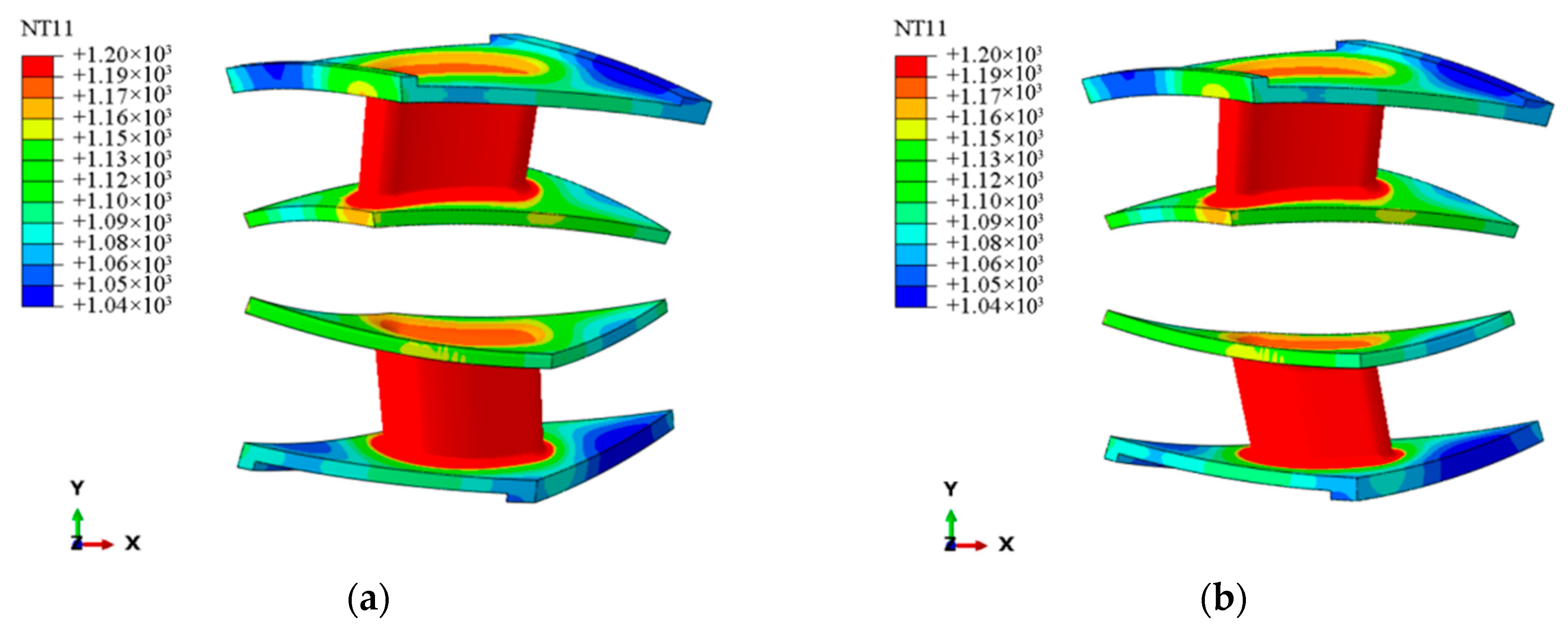
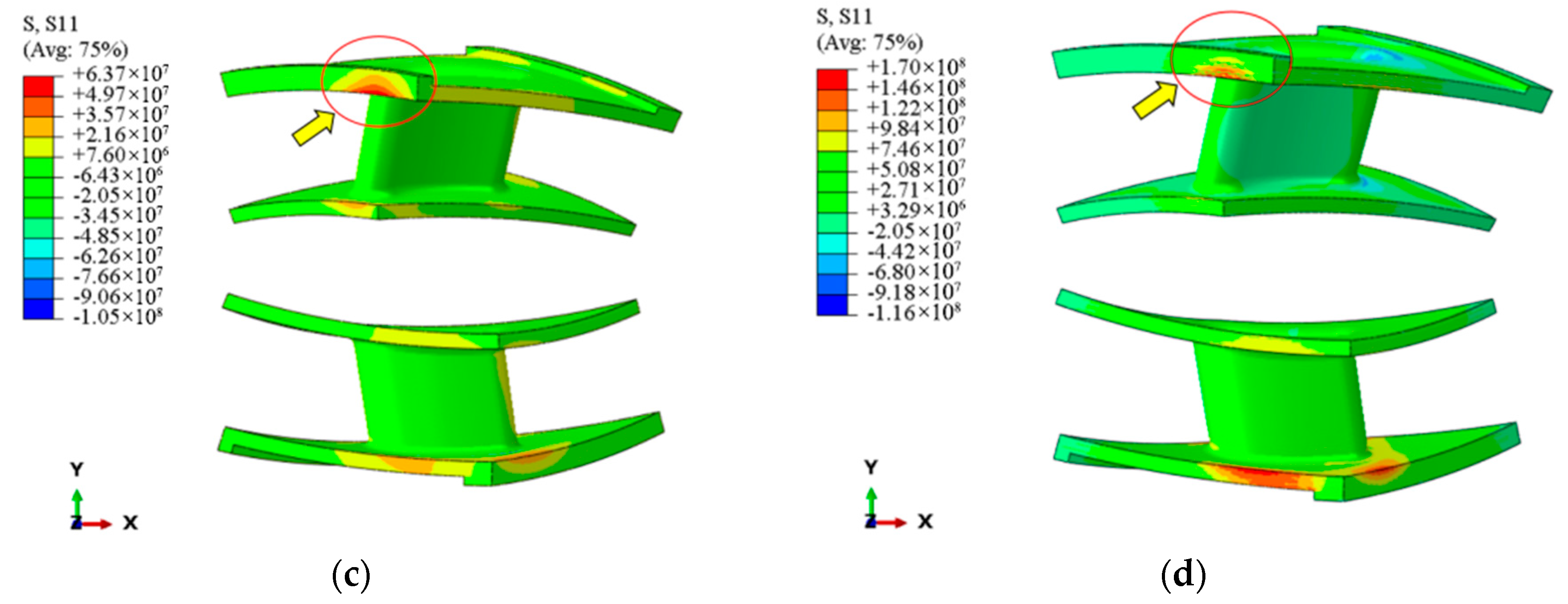

| Property | SiCf/SiC-CMC | SiC Fiber | SiC Matrix (Literature, Excluding Voids) |
|---|---|---|---|
| Tensile modulus | 319.17 GPa | 370 GPa | 350 GPa [30] |
| Density | 2.86 g/cm3 | 3.08 g/cm3 | 3.08 g/cm3 |
| Thermal conductivity k | λ∥ = 65.68 W/(m·K) λ⊥ = 40.78 W/(m·K) | λ∥ = 14.7 W/(m·K) λ⊥ = 11.7 W/(m·K) | 90 W/(m·K) [31] |
| Specific heat capacity C | 0.65 J/(g·K) | 0.71 J/(g·K) | 0.68 J/(g·K) [32] |
| Thermal expansion coefficients α | α∥ = 5.20 × 10−6/K α⊥ = 4.55 × 10−6/K | α∥ = 3.76 × 10−6/K α⊥ = 4.15 × 10−6/K | 4.7 × 10−6/K [33] |
| Property | Revised SiC Matrix | Theoretical SiC Matrix (Including Voids) | Error 1 |
|---|---|---|---|
| Tensile modulus E | 317.31 GPa | 303.12 GPa | 4.68% |
| Density ρ | 2.79 g/cm3 | 2.79 g/cm3 | 0% |
| Thermal conductivities k | 78.03 W/(m·K) | 81.77 W/(m·K) | 4.61% |
| Specific heat capacity C | 0.68 J/(g·K) | 0.63 J/(g·K) | 7.94% |
| Thermal expansion coefficients α | 4.7 × 10−6/K | 5.22 × 10−6/K | 9.96% |
| Stiffness Component (GPa) | ||||||
|---|---|---|---|---|---|---|
| D1111 | D1122 | D2222 | D1133 | D2233 | ||
| 347.19 | 60.44 | 336.15 | 50.55 | 60.71 | ||
| D3333 | D1212 | D1313 | D2323 | - | ||
| 334.67 | 135.40 | 135.38 | 135.32 | - | ||
| Poisson’s ratio | ||||||
| v12 | v13 | v23 | ||||
| 0.147 | 0.152 | 0.149 | ||||
| Predicted Value (GPa) | Experimental Value (GPa) | Error 2 |
|---|---|---|
| E1 = 307.42 | = 319.17 | 3.7% |
| = 297.96 | - | - |
| = 296.40 | - | - |
| = 135.40 | - | - |
| = 135.38 | - | - |
| = 135.32 | - | - |
| Predicted Value W/(m·K) | Experimental Value W/(m·K) | Error 2 |
|---|---|---|
| = 60.25 | = 65.68 | 8.3% |
| = 43.51 | = 40.78 | 6.7% |
| = 43.51 | = 40.78 | 6.7% |
| Predicted Value | Experimental Value | Error 2 |
|---|---|---|
| = 4.75 × 10−6/K | = 5.20 × 10−6/K | 8.6% |
| = 4.62 × 10−6/K | = 4.55 × 10−6/K | 1.5% |
| = 4.62 × 10−6/K | = 4.55 × 10−6/K | 1.5% |
| Thermoelastic Properties | x Axis | y Axis | z Axis |
|---|---|---|---|
| Effective tensile modulus (GPa) | 307.42 | 297.69 | 296.40 |
| Measured tensile modulus (GPa) | 319.17 | - | - |
| Error of tensile modulus | 3.68% | - | - |
| Effective thermal conductivities (w/(m·k)) | 60.25 | 43.51 | 43.51 |
| Measured thermal conductivities (w/(m·k)) | 65.68 | 40.78 | 40.78 |
| Error of thermal conductivity | 8.27% | 6.69% | 6.69% |
| Effective thermal expansion coefficients | 4.75 × 10−6/K | 4.62 × 10−6/K | 4.62 × 10−6/K |
| Measured thermal expansion coefficients | 5.20 × 10−6/K | 4.55 × 10−6/K | 4.55 × 10−6/K |
| Error of thermal expansion coefficients | 8.65% | 1.54% | 1.54% |
| The homogenized mechanical and thermal properties of the blade body | |||||
| E1 | E2 | E3 | G12 | G13 | G23 |
| 302.6 GPa | 302.6 GPa | 296.40 GPa | 135.40 GPa | 135.38 GPa | 135.32 GPa |
| 0.144 | 0.149 | 0.144 | 0.152 | 0.152 | 0.149 |
| 51.88 W/(m·K) | 51.88 W/(m·K) | 43.51 W/(m·K) | |||
| 4.685 × 10−6/K | 4.685 × 10−6/K | 4.62 × 10−6/K | |||
| The homogenized mechanical and thermal properties of the upper/lower edge plate | |||||
| E1 | E2 | E3 | G12 | G13 | G23 |
| 303.7 GPa | 303.7 GPa | 296.40 GPa | 135.36 GPa | 135.36 GPa | 135.32 GPa |
| 0.149 | 0.147 | 0.149 | 0.152 | 0.152 | 0.149 |
| 49.8 W/(m·K) | 49.8 W/(m·K) | 43.51 W/(m·K) | |||
| 4.69 × 10−6/K | 4.69 × 10−6/K | 4.62 × 10−6/K | |||
| The homogenized mechanical and thermal properties of the upper/lower edge plate flange | |||||
| E1 | E2 | E3 | G12 | G13 | G23 |
| 304.5 GPa | 304.5 GPa | 296.4 GPa | 135.38 GPa | 135.38 GPa | 135.32 GPa |
| 0.149 | 0.147 | 0.149 | 0.152 | 0.152 | 0.149 |
| 50.2 W/(m·K) | 50.2 W/(m·K) | 43.51 W/(m·K) | |||
| 4.7 × 10−6/K | 4.7 × 10−6/K | 4.62 × 10−6/K | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Chen, X.; Deng, Y.; Wang, W.; Li, J.; Obara, E.; Han, Z.; Luo, C. Multi-Scale Transient Thermo-Mechanical Coupling Analysis Method for the SiCf/SiC Composite Guide Vane. Materials 2025, 18, 3348. https://doi.org/10.3390/ma18143348
Li M, Chen X, Deng Y, Wang W, Li J, Obara E, Han Z, Luo C. Multi-Scale Transient Thermo-Mechanical Coupling Analysis Method for the SiCf/SiC Composite Guide Vane. Materials. 2025; 18(14):3348. https://doi.org/10.3390/ma18143348
Chicago/Turabian StyleLi, Min, Xue Chen, Yu Deng, Wenjun Wang, Jian Li, Evance Obara, Zhilin Han, and Chuyang Luo. 2025. "Multi-Scale Transient Thermo-Mechanical Coupling Analysis Method for the SiCf/SiC Composite Guide Vane" Materials 18, no. 14: 3348. https://doi.org/10.3390/ma18143348
APA StyleLi, M., Chen, X., Deng, Y., Wang, W., Li, J., Obara, E., Han, Z., & Luo, C. (2025). Multi-Scale Transient Thermo-Mechanical Coupling Analysis Method for the SiCf/SiC Composite Guide Vane. Materials, 18(14), 3348. https://doi.org/10.3390/ma18143348







