In-Plane Vibration Analysis of Rectangular Plates with Elastically Restrained Boundaries Using Differential Quadrature Method of Variational Weak Form
Abstract
1. Introduction
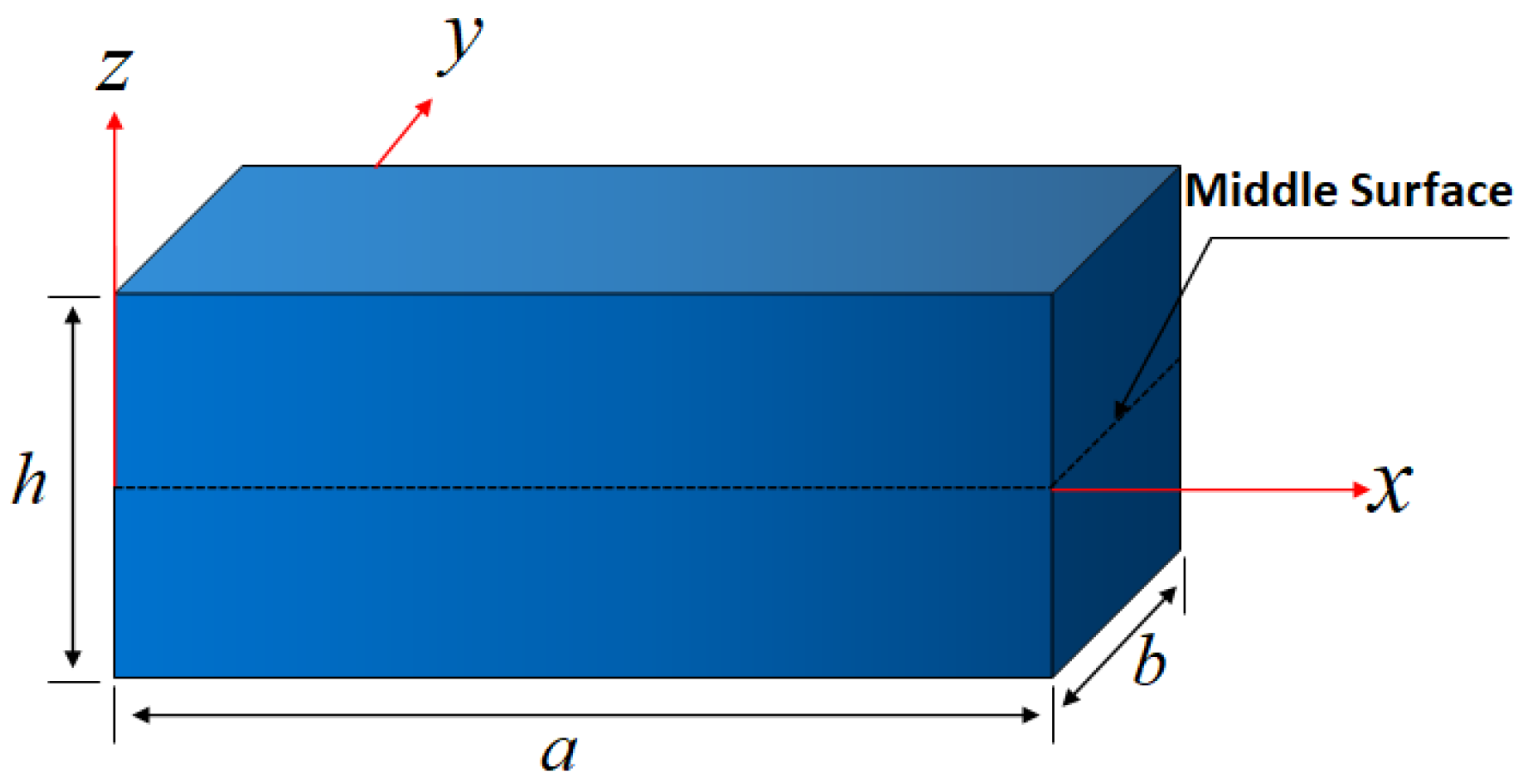
2. Basic Equation
2.1. Establishment of Variational Equations for In-Plane Free Vibration
2.2. Matrixing of Differential and Integral Operators
3. Discretization and Eigenvalue Problem
3.1. Discretization of Weak Form Equations
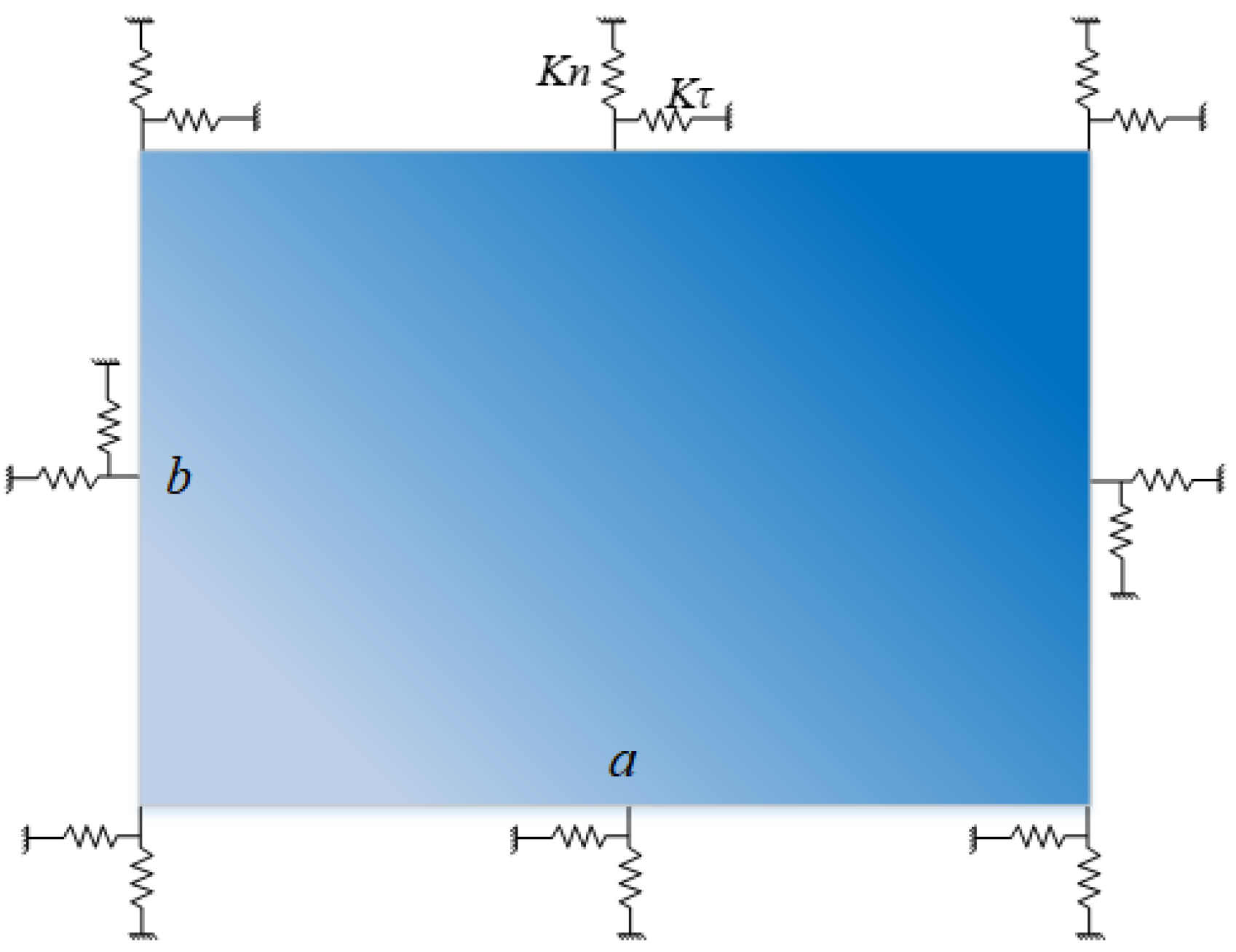
3.2. Discrete Boundary Conditions
4. Numerical Study
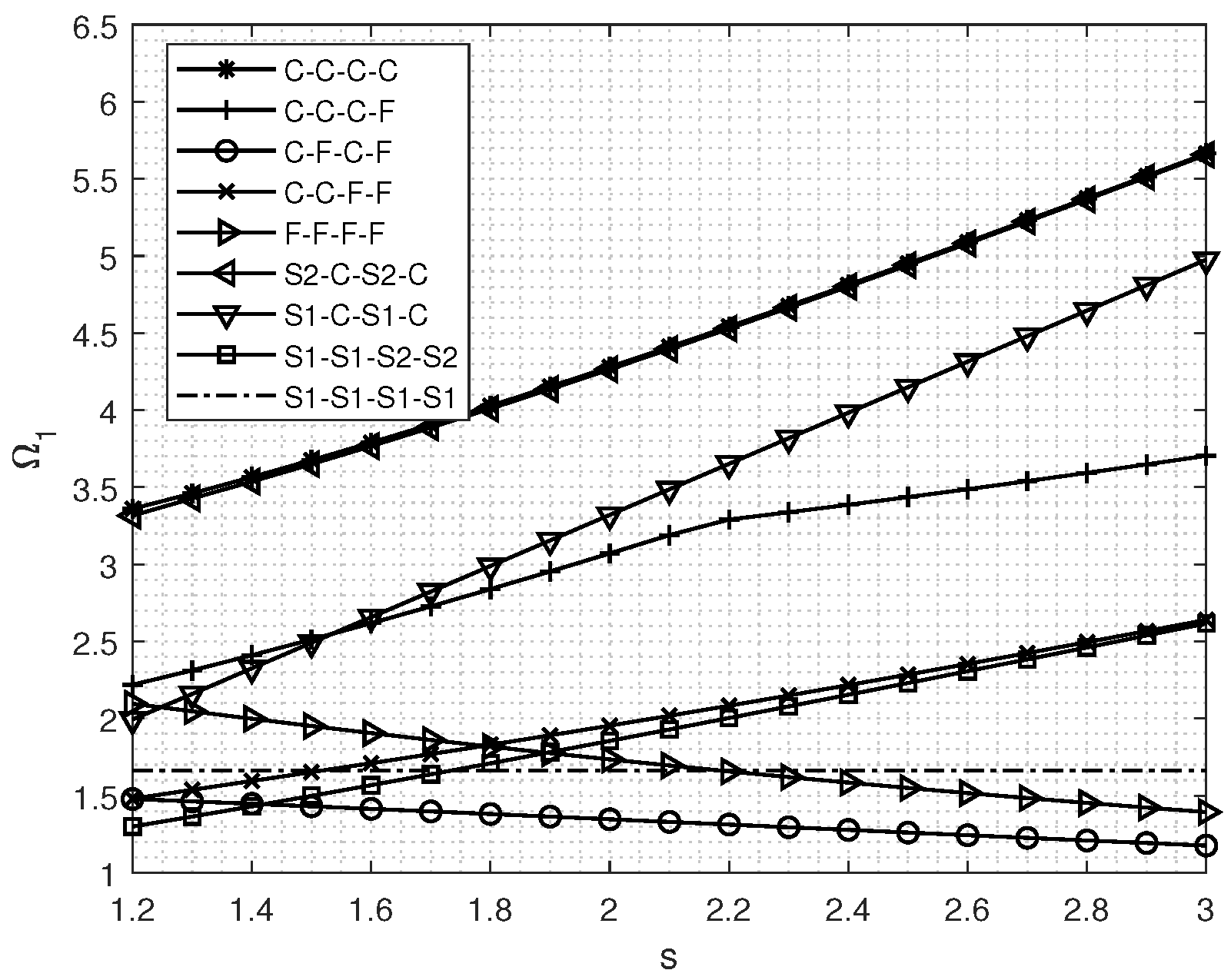
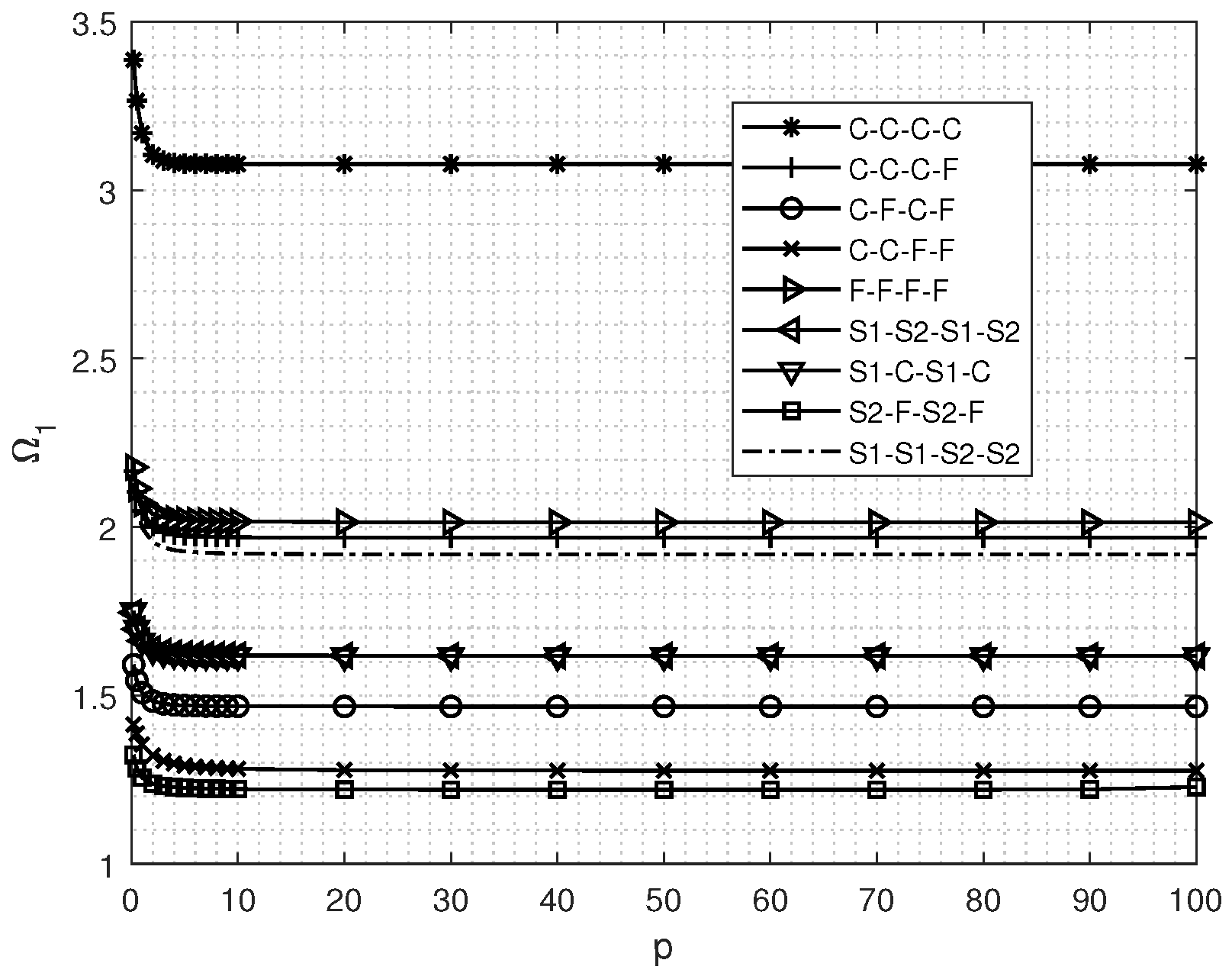
4.1. Results of Vibration Frequency of Unidirectional FGM Rectangular Plates at Different Boundary Confinement and Aspect Ratios
4.2. Results of In-Plane Vibration of Bidirectional FGM Rectangular Plates Under Various Elastic Limits
4.3. In-Plane Vibration Analysis of Free-Vibration Modal Performance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lyon; Richard, H. In-plane contribution to structural noise transmission. Noise Control Eng. J. 1986, 26, 22–27. [Google Scholar] [CrossRef]
- Langley, R.S.; Bercin, A.N. Wave intensity analysis of high frequency vibration. Philos. Trans. R. Soc. Lond. A 1994, 346, 489–499. [Google Scholar]
- Bercin, A.N. An assessment of the effect of in-plane vibration on the energy flow between coupled plates. J. Sound Vib. 1996, 191, 661–680. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Yamada, G.; Honma, S. In-plane vibration of point-supported rectangular plates. J. Sound Vib. 1988, 126, 545–549. [Google Scholar] [CrossRef]
- Shu, C.; Du, H. A generalized approach for implementing general boundary conditions in the GDQ free vibration analysis of plates. Int. J. Solids Struct. 1997, 34, 837–846. [Google Scholar] [CrossRef]
- Fuchs, S.J. Plates with Boundary Conditions of Elastic Support; Transactions of the American Society of Civil Engineers: New York, NY, USA, 1954. [Google Scholar]
- Gutierrez, R.H.; Laura, P.A. In-plane vibrations of thin, elastic, rectangular plates elastically restrained against translation along the edges. J. Sound Vib. 1989, 132, 512–515. [Google Scholar] [CrossRef]
- Bardell, N.S.; Langley, R.S.; Dunsdon, J.M. On the free in-plane vibration of isotropic rectangular plates. J. Sound Vib. 1996, 191, 459–467. [Google Scholar] [CrossRef]
- Farag, N.H.; Pan, J. Free and forced in-plane vibration of rectangular plates. J. Acoust. Soc. Am. 1998, 103, 408–413. [Google Scholar] [CrossRef]
- Farag, N.H.; Pan, J. Modal characteristics of in-plane vibration of rectangular plates. J. Acoust. Soc. Am. 1999, 105, 3295–3310. [Google Scholar] [CrossRef]
- Wang, G.; Wereley, N.M. Free in-plane vibration of rectangular plates. AIAA J. 2002, 40, 953–959. [Google Scholar] [CrossRef]
- Du, J.; Li, W.L.; Jin, G.; Yang, T.; Liu, Z. An analytical method for the in-plane vibration analysis of rectangular plates with elastically restrained edges. J. Sound Vib. 2007, 306, 908–927. [Google Scholar] [CrossRef]
- Du, J.; Liu, Z.; Li, W.L.; Zhang, X. Free in-plane vibration analysis of rectangular plates with elastically point-supported edges. J. Vib. Acoust. 2010, 132, 031002. [Google Scholar] [CrossRef]
- Gorman, D.J. Free in-plane vibration analysis of rectangular plates by the method of superposition. J. Sound Vib. 2004, 272, 831–851. [Google Scholar] [CrossRef]
- Gorman, D.J. Accurate analytical type solutions for the free in-plane vibration of clamped and simply supported rectangular plates. J. Sound Vib. 2004, 276, 311–333. [Google Scholar] [CrossRef]
- Gorman, D.J. Free in-plane vibration analysis of rectangular plates with elastic support normal to the boundaries. J. Sound Vib. 2005, 285, 941–966. [Google Scholar] [CrossRef]
- Gorman, D.J. Exact solutions for the free in-plane vibration of rectangular plates with two opposite edges simply supported. J. Sound Vib. 2006, 294, 131–161. [Google Scholar] [CrossRef]
- Xing, Y.F.; Liu, B. Exact solutions for the free in-plane vibrations of rectangular plates. Int. J. Mech. Sci. 2009, 51, 246–255. [Google Scholar] [CrossRef]
- Dozio, L. Free in-plane vibration analysis of rectangular plates with arbitrary elastic boundaries. Mech. Res. Commun. 2010, 37, 627–635. [Google Scholar] [CrossRef]
- Chen, Y.H.; Jin, G.Y.; Liu, Z.G. Flexural and in-plane vibration analysis of elastically restrained thin rectangular plate with cutout using Chebyshev–Lagrangian method. Int. J. Mech. Sci. 2014, 89, 264–278. [Google Scholar] [CrossRef]
- Shi, D.Y.; Wang, Q.S.; Shi, X.J. A series solution for the in-plane vibration analysis of orthotropic rectangular plates with non-uniform elastic boundary constraints and internal line supports. Arch. Appl. Mech. 2015, 85, 51–73. [Google Scholar] [CrossRef]
- Chen, Z.; Qin, B.; Zhong, R.; Wang, Q. Free in-plane vibration analysis of elastically restrained functionally graded porous plates with porosity distributions in the thickness and in-plane directions. Eur. Phys. J. Plus 2022, 137, 158. [Google Scholar] [CrossRef]
- Guan, X.; Qin, B.; Zhong, R.; Wang, Q. A unified solution for in-plane vibration analysis of composite laminated sector and annular plate with elastic constraints. J. Low Freq. Noise Vib. Act. Control 2021, 40, 1764–1779. [Google Scholar] [CrossRef]
- Liu, T.; Hu, G.; Wang, A.; Wang, Q. A unified formulation for free in-plane vibrations of arbitrarily-shaped straight-sided quadrilateral and triangular thin plates. Appl. Acoust. 2019, 155, 407–422. [Google Scholar] [CrossRef]
- Liu, B.; Xing, Y.; Wang, Z.; Lu, X.; Sun, H. Non-uniform rational Lagrange functions and its applications to isogeometric analysis of in-plane and flexural vibration of thin plates. Comput. Methods Appl. Mech. Eng. 2017, 321, 173–208. [Google Scholar] [CrossRef]
- Xue, Y.; Jin, G.; Ding, H.; Chen, M. Free vibration analysis of in-plane functionally graded plates using a refined plate theory and isogeometric approach. Compos. Struct. 2018, 192, 193–205. [Google Scholar] [CrossRef]
- Chen, M.; Ye, T.; Zhang, J.; Jin, G.; Zhang, Y.; Xue, Y.; Ma, X.; Liu, Z. Isogeometric three-dimensional vibration of variable thickness parallelogram plates with in-plane functionally graded porous materials. Int. J. Mech. Sci. 2020, 169, 105304. [Google Scholar] [CrossRef]
- Hasheminejad, S.M.; Ghaheri, A.; Rezaei, S. Semi-analytic solutions for the free in-plane vibrations of confocal annular elliptic plates with elastically restrained edges. J. Sound Vib. 2012, 331, 434–456. [Google Scholar] [CrossRef]
- Baferani, A.H.; Saidi, A.R.; Ehteshami, H. On free vibration of functionally graded mindlin plate and effect of in-plane displacements. J. Mech. 2013, 29, 373–384. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, D.; Liang, Q.; Ahad, F.E. A unified solution for free in-plane vibration of orthotropic circular, annular and sector plates with general boundary conditions. Appl. Math. Model. 2016, 40, 9228–9253. [Google Scholar] [CrossRef]
- Kamranfard, M.R.; Saidi, A.R.; Naderi, A. Analytical solution for vibration and buckling of annular sectorial porous plates under in-plane uniform compressive loading. Proc. Inst. Mech. Eng. Part-J. Mech. Eng. Sci. 2018, 232, 2211–2228. [Google Scholar] [CrossRef]
- Zhong, R.; Qin, B.; Wang, Q.; Shao, W.; Shuai, C. Prediction of the in-plane vibration behavior of porous annular plate with porosity distributions in the thickness and radial directions. Mech. Adv. Mater. Struct. 2022, 29, 4206–4223. [Google Scholar] [CrossRef]
- Liu, T.; Wang, Q.; Qin, B.; Wang, A. Free in-plane vibration of plates with arbitrary curvilinear geometry: Spectral-Chebyshev model and experimental study. Thin-Walled Struct. 2022, 170, 108628. [Google Scholar] [CrossRef]
- Tornabene, F.; Viscoti, M.; Dimitri, R.; Rosati, L. Dynamic analysis of anisotropic doubly-curved shells with general boundary conditions, variable thickness and arbitrary shape. Compos. Struct. 2023, 309, 116542. [Google Scholar] [CrossRef]
- Hashemi, S.H.; Atashipour, S.R.; Fadaee, M. An exact analytical approach for in-plane and out-of-plane free vibration analysis of thick laminated transversely isotropic plates. Arch. Appl. Mech. 2012, 82, 677–698. [Google Scholar] [CrossRef]
- Lal, R.; Saini, R. On the High-Temperature Free Vibration Analysis of Elastically Supported Functionally Graded Material Plates Under Mechanical In-Plane Force Via GDQR. J. Dyn. Syst. Meas.-Control-Trans. ASME 2019, 141, 101003. [Google Scholar] [CrossRef]
- Pagani, A.; Azzara, R.; Carrera, E. Geometrically nonlinear analysis and vibration of in-plane-loaded variable angle tow composite plates and shells. Acta Mech. 2023, 234, 85–108. [Google Scholar] [CrossRef]
- Pu, Y.; Teng, Z.C.; Zhao, H.Y. DQM Solution for Free Vibration in Rectangular Plate Constrained by Four Edges. Vib. Shock 2016, 35, 55–60. [Google Scholar]
- Pu, Y.; Teng, Z.C.; Zhao, H.Y. In-plane free vibration analysis for rectangular plates with elastically restrained edges by Differential Quadrature Method. J. Vib. Shock 2016, 35, 55–60. [Google Scholar]
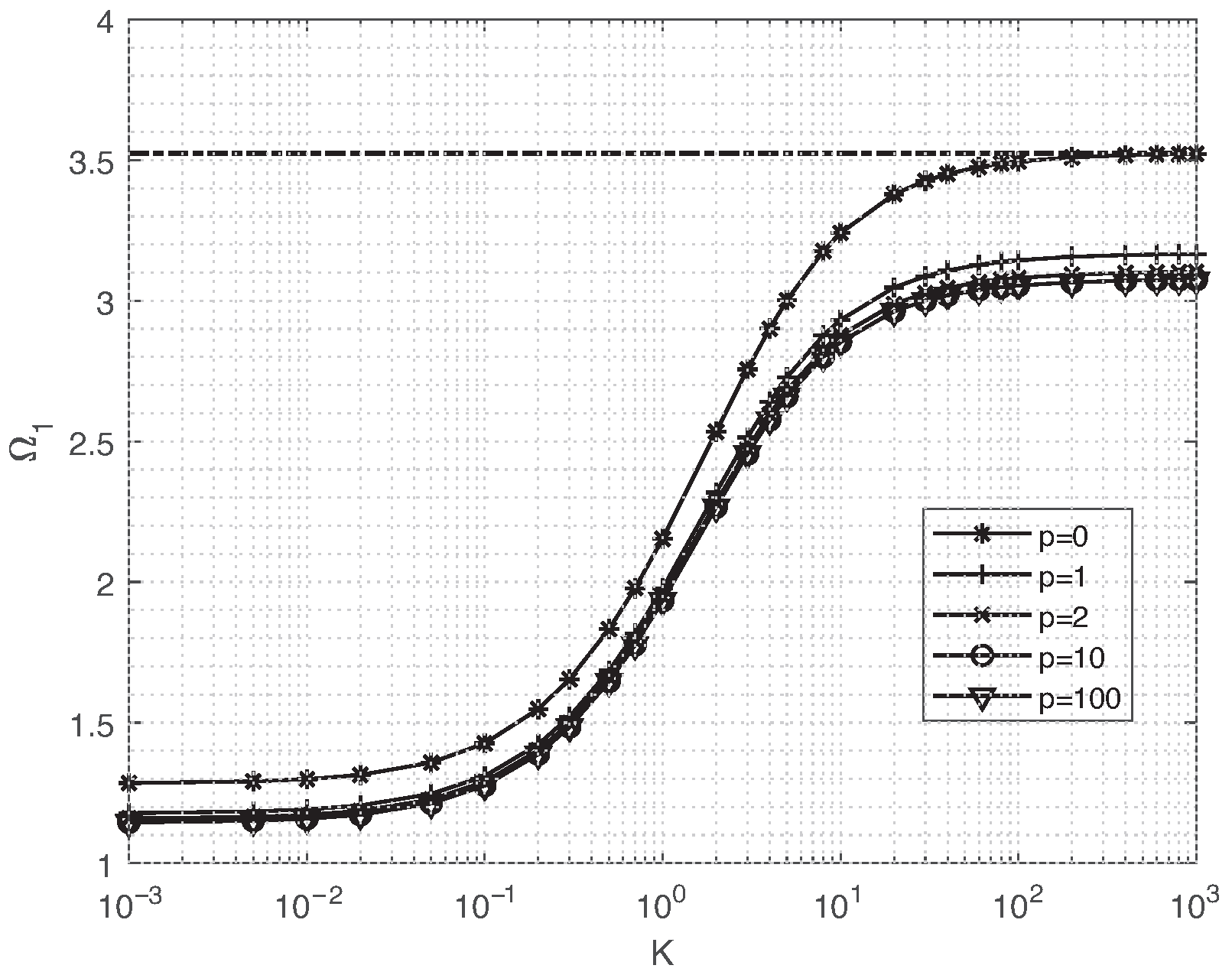
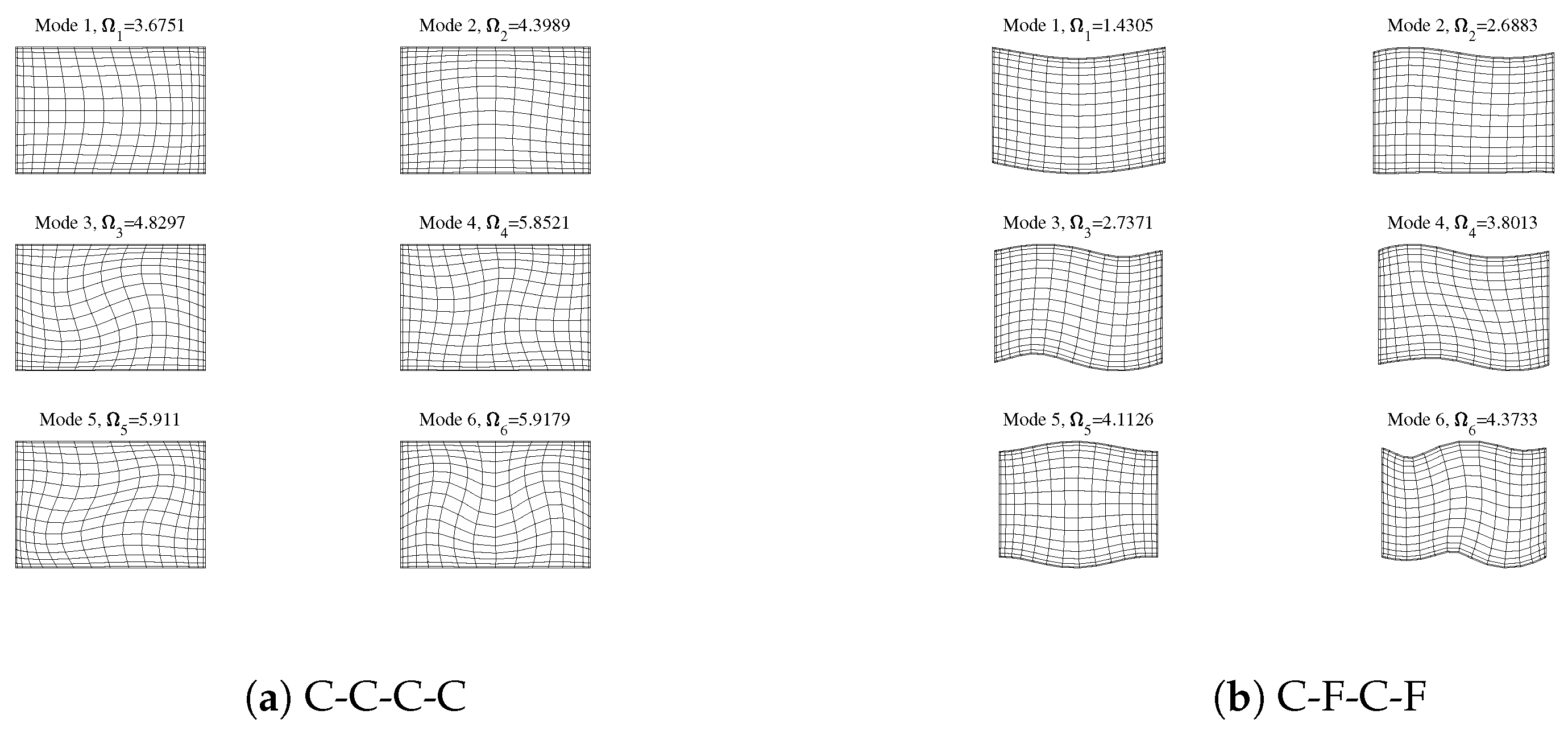

| BCs | s = 1 | s = 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 11 | 15 | 17 | 19 | 21 | 11 | 15 | 17 | 19 | 21 | ||
| CCCC | 1 | 3.2807 | 3.2807 | 3.2807 | 3.2807 | 3.2807 | 4.4134 | 4.4135 | 4.4135 | 4.4135 | 4.4135 |
| 2 | 3.2834 | 3.2835 | 3.2835 | 3.2835 | 3.2835 | 5.8971 | 5.8972 | 5.8972 | 5.8972 | 5.8972 | |
| 3 | 3.8943 | 3.8944 | 3.8944 | 3.8944 | 3.8944 | 6.1845 | 6.1845 | 6.1845 | 6.1845 | 6.1845 | |
| CFCF | 1 | 1.5381 | 1.5493 | 1.5515 | 1.5529 | 1.5538 | 1.3789 | 1.3857 | 1.3871 | 1.3880 | 1.3887 |
| 2 | 2.7594 | 2.7592 | 2.7592 | 2.7591 | 2.7591 | 2.7066 | 2.7166 | 2.7186 | 2.7198 | 2.7206 | |
| 3 | 2.8714 | 2.8783 | 2.8794 | 2.8801 | 2.8805 | 2.7890 | 2.7899 | 2.7901 | 2.7903 | 2.7904 |
| s | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | [39] | 1.5006 | 2.0951 | 2.1034 | 2.8349 | 2.8424 | 3.4721 | 3.5652 | 3.6217 | 3.6497 | 4.0020 |
| Text | 1.5012 | 2.0952 | 2.1042 | 2.8362 | 2.8427 | 3.4728 | 3.5635 | 3.6225 | 3.6251 | 3.9981 | |
| 1 | [39] | 2.1060 | 3.0947 | 3.6158 | 3.6724 | 4.1170 | 4.8536 | 5.2148 | 5.3687 | 5.3981 | 5.5368 |
| Text | 2.1067 | 3.0949 | 3.6173 | 3.6734 | 4.1145 | 4.8550 | 5.2145 | 5.3695 | 5.3903 | 5.5364 | |
| 1.5 | [39] | 2.8427 | 4.1687 | 4.3685 | 4.9492 | 5.2981 | 6.0793 | 6.2028 | 6.3183 | 7.5133 | 7.7688 |
| Text | 2.8435 | 4.1699 | 4.3686 | 4.9482 | 5.2985 | 6.0793 | 6.1833 | 6.3192 | 7.5106 | 7.7709 | |
| 2 | [39] | 3.6315 | 4.7486 | 5.7477 | 6.0733 | 6.7040 | 6.9275 | 6.9539 | 7.8078 | 8.1321 | 8.8012 |
| Text | 3.6323 | 4.7499 | 5.7478 | 6.0723 | 6.6835 | 6.9271 | 6.9554 | 7.8093 | 8.1271 | 8.7985 |
| s | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | [39] | 1.6187 | 1.9707 | 2.2700 | 2.6677 | 2.9090 | 2.9498 | 3.3460 | 3.4689 | 3.6074 | 4.1781 |
| Text | 1.6198 | 1.9713 | 2.2703 | 2.6686 | 2.9079 | 2.9487 | 3.3417 | 3.4439 | 3.6022 | 4.1842 | |
| 1 | [39] | 2.0317 | 2.5129 | 3.1588 | 3.3022 | 3.9736 | 4.6050 | 4.6593 | 4.9507 | 5.0404 | 5.2527 |
| Text | 2.0329 | 2.5145 | 3.1579 | 3.3004 | 3.9681 | 4.6034 | 4.6593 | 4.9452 | 5.0346 | 5.2495 | |
| 1.5 | [39] | 2.4345 | 3.0816 | 3.5348 | 4.4321 | 4.7748 | 4.9049 | 5.5222 | 6.0549 | 6.3252 | 6.7446 |
| Text | 2.4360 | 3.0833 | 3.5333 | 4.4292 | 4.7736 | 4.9001 | 5.5157 | 6.0484 | 6.3171 | 6.7427 | |
| 2 | [39] | 2.8432 | 3.6045 | 3.9840 | 5.0180 | 5.5752 | 5.6825 | 6.3336 | 6.5001 | 6.9714 | 8.0359 |
| Text | 2.8451 | 3.6049 | 3.9836 | 5.0174 | 5.5720 | 5.6784 | 6.3250 | 6.4924 | 6.9639 | 8.0296 |
| s | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | [39] | 1.6187 | 1.9707 | 2.2700 | 2.6677 | 2.9090 | 2.9498 | 3.3460 | 3.4689 | 3.6074 | 4.1781 |
| Text | 1.6198 | 1.9713 | 2.2703 | 2.6686 | 2.9079 | 2.9487 | 3.3417 | 3.4439 | 3.6022 | 4.1842 | |
| 1 | [39] | 2.0317 | 2.5129 | 3.1588 | 3.3022 | 3.9736 | 4.6050 | 4.6593 | 4.9507 | 5.0404 | 5.2527 |
| Text | 2.0329 | 2.5145 | 3.1579 | 3.3004 | 3.9681 | 4.6034 | 4.6593 | 4.9452 | 5.0346 | 5.2495 | |
| 1.5 | [39] | 2.4345 | 3.0816 | 3.5348 | 4.4321 | 4.7748 | 4.9049 | 5.5222 | 6.0549 | 6.3252 | 6.7446 |
| Text | 2.4360 | 3.0833 | 3.5333 | 4.4292 | 4.7736 | 4.9001 | 5.5157 | 6.0484 | 6.3171 | 6.7427 | |
| 2 | [39] | 2.8432 | 3.6045 | 3.9840 | 5.0180 | 5.5752 | 5.6825 | 6.3336 | 6.5001 | 6.9714 | 8.0359 |
| Text | 2.8451 | 3.6049 | 3.9836 | 5.0174 | 5.5720 | 5.6784 | 6.3250 | 6.4924 | 6.9639 | 8.0296 | |
| ∞ | [39] | 1.5537 | 2.7605 | 2.8813 | 3.1023 | 3.4483 | 3.6212 | 4.5904 | 4.6983 | 4.9557 | 5.1334 |
| 1000 | Text | 1.5507 | 2.7588 | 2.8780 | 3.1052 | 3.4445 | 3.6171 | 4.5819 | 4.6971 | 4.9508 | 5.1226 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zhou, W.; Yi, S.; Li, S. In-Plane Vibration Analysis of Rectangular Plates with Elastically Restrained Boundaries Using Differential Quadrature Method of Variational Weak Form. Materials 2025, 18, 3250. https://doi.org/10.3390/ma18143250
Wang X, Zhou W, Yi S, Li S. In-Plane Vibration Analysis of Rectangular Plates with Elastically Restrained Boundaries Using Differential Quadrature Method of Variational Weak Form. Materials. 2025; 18(14):3250. https://doi.org/10.3390/ma18143250
Chicago/Turabian StyleWang, Xianke, Weipeng Zhou, Shichao Yi, and Sen Li. 2025. "In-Plane Vibration Analysis of Rectangular Plates with Elastically Restrained Boundaries Using Differential Quadrature Method of Variational Weak Form" Materials 18, no. 14: 3250. https://doi.org/10.3390/ma18143250
APA StyleWang, X., Zhou, W., Yi, S., & Li, S. (2025). In-Plane Vibration Analysis of Rectangular Plates with Elastically Restrained Boundaries Using Differential Quadrature Method of Variational Weak Form. Materials, 18(14), 3250. https://doi.org/10.3390/ma18143250






