A Novel Method for Determining the Contact Pattern Area in Gear Meshing Based on Computer Processing of Pressure Measurement Film Images
Abstract
1. Introduction
2. Materials and Methods
2.1. Theoretical Basics
2.1.1. General Information of Gear Surface Modeling in CAD System
2.1.2. Determination of Contact Pattern in CAD Environment
2.1.3. FEM Analysis
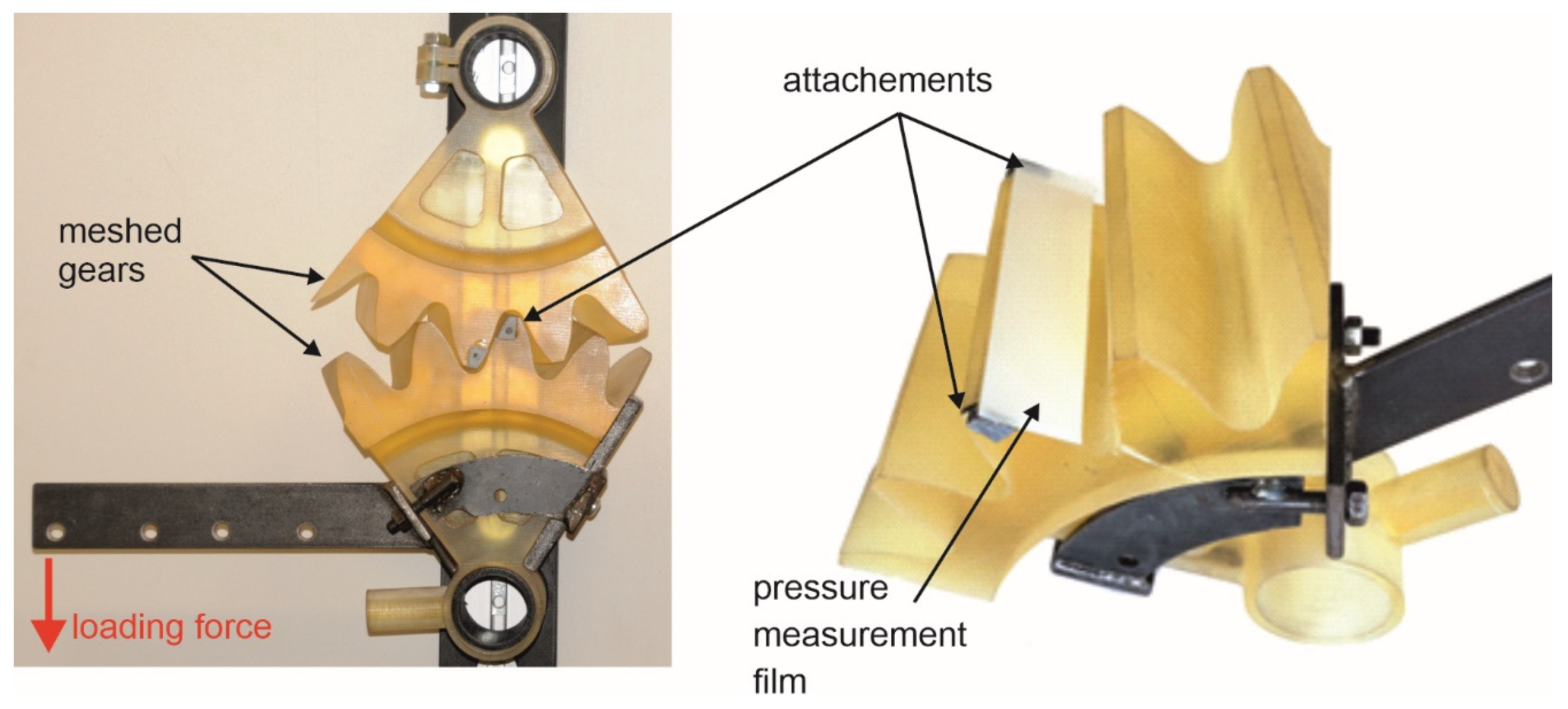
2.1.4. Pressure Measurement by Using Two-Sheet Type Film
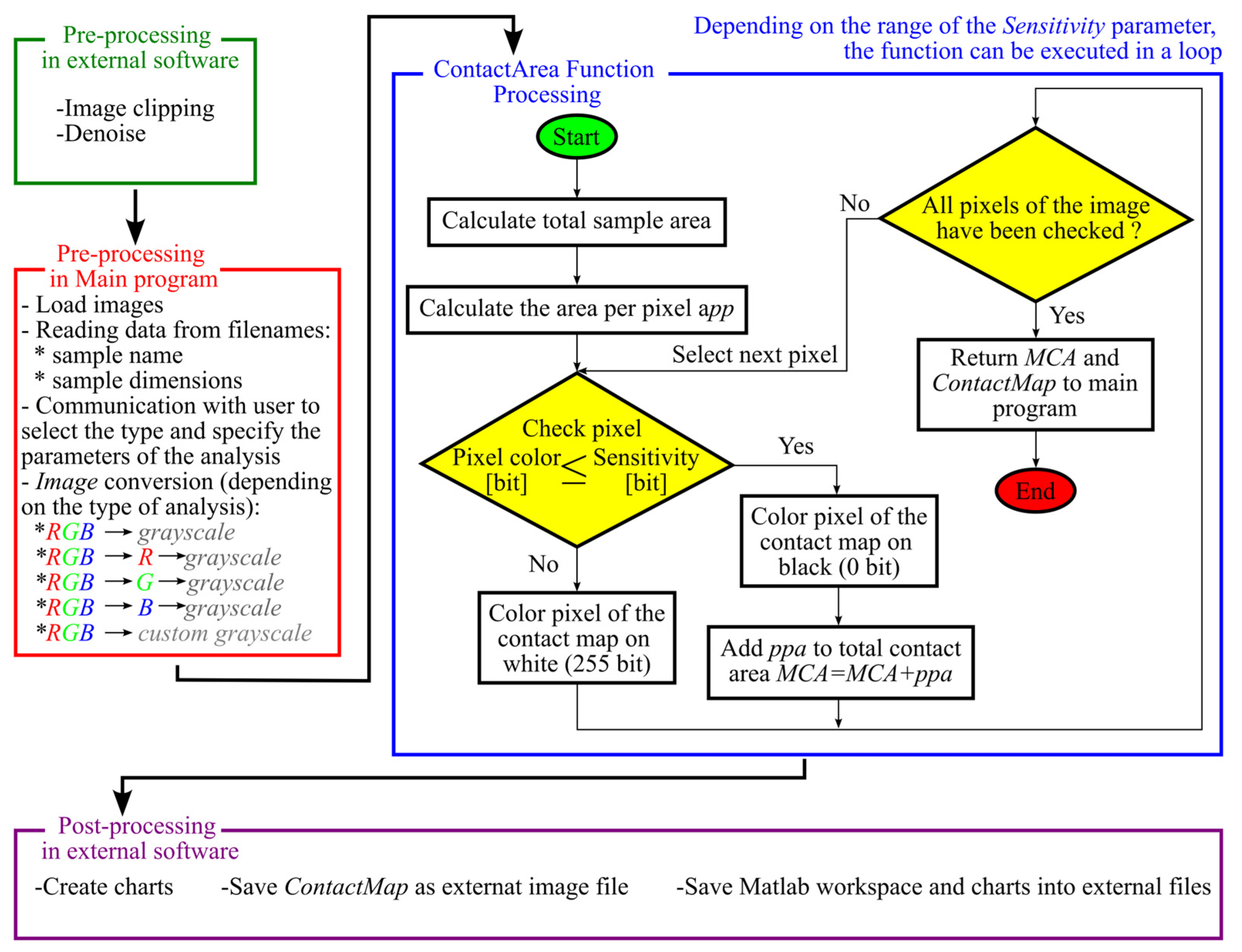
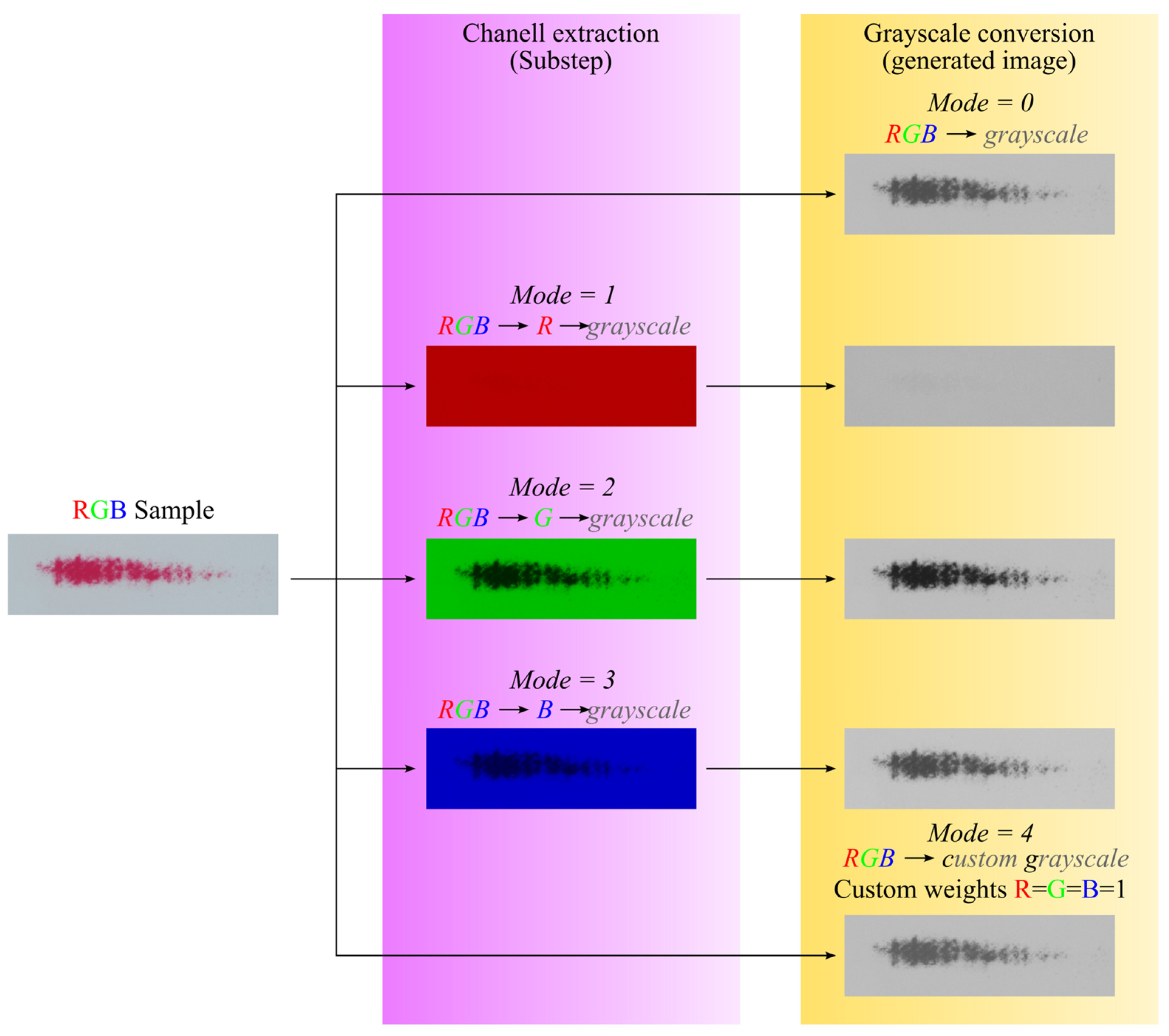
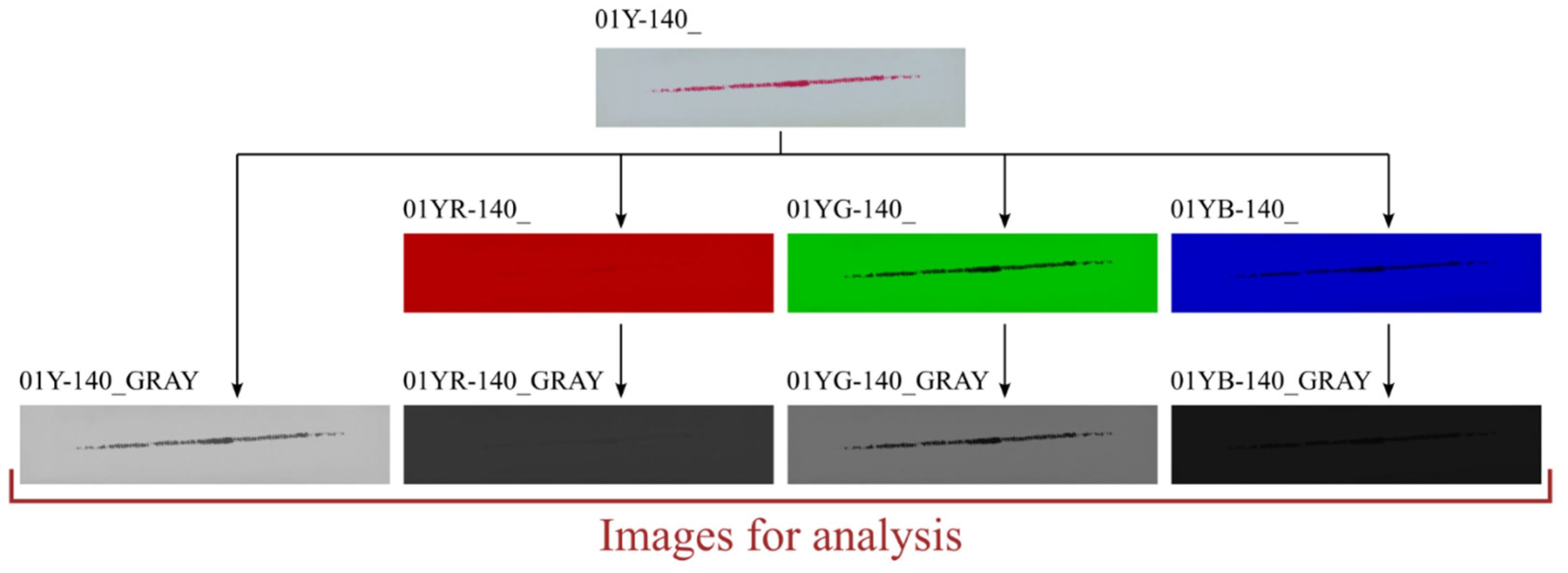
2.1.5. Image Processing—Custom Program for Sample Image Analysis
- Main assumptions
- Automation—the program allows the analysis of multiple samples, with limited user participation. The results of the obtained analysis are automatically saved and catalogued. The role of the user is reduced to the appropriate saving of file names in the working directory of the program, as well as determining the type and key parameters of the analyses performed.
- Modularity—the main program uses specialized subprograms (functions). Each function is used to perform a different type of analysis or perform a specific task. The functions can work independently.
- Description of the functionality of main program and selected subprograms
- red: alphanumeric identification of the sample (it is recommended to use the number itself),
- purple: the actual length of the sample in the horizontal direction, expressed in whole numbers; the length is stated in millimeters,
- blue: hundreds of the horizontal length of the sample; if the length of the sample can be expressed by an integer, this filename can be omitted,
- green: file extension (by default in Microsoft Windows, this part of the file name is invisible),
- black: separators of particular parts of the name.
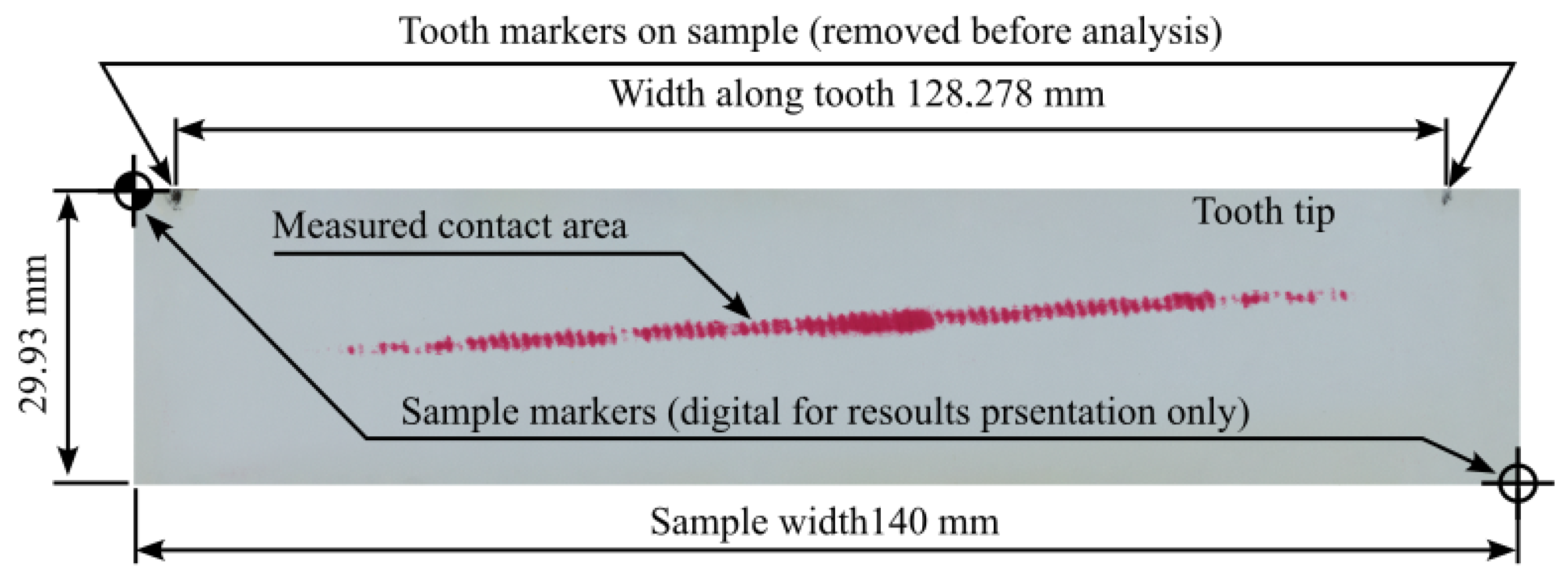
- Image—a file with a color or black-and-white scan of the sample. NOTE: the image should first undergo preprocessing to crop the samples and remove unwanted noise and scanning artifacts,
- l_H—horizontal length of the sample in mm,
- l_V—vertical length of the sample in mm,
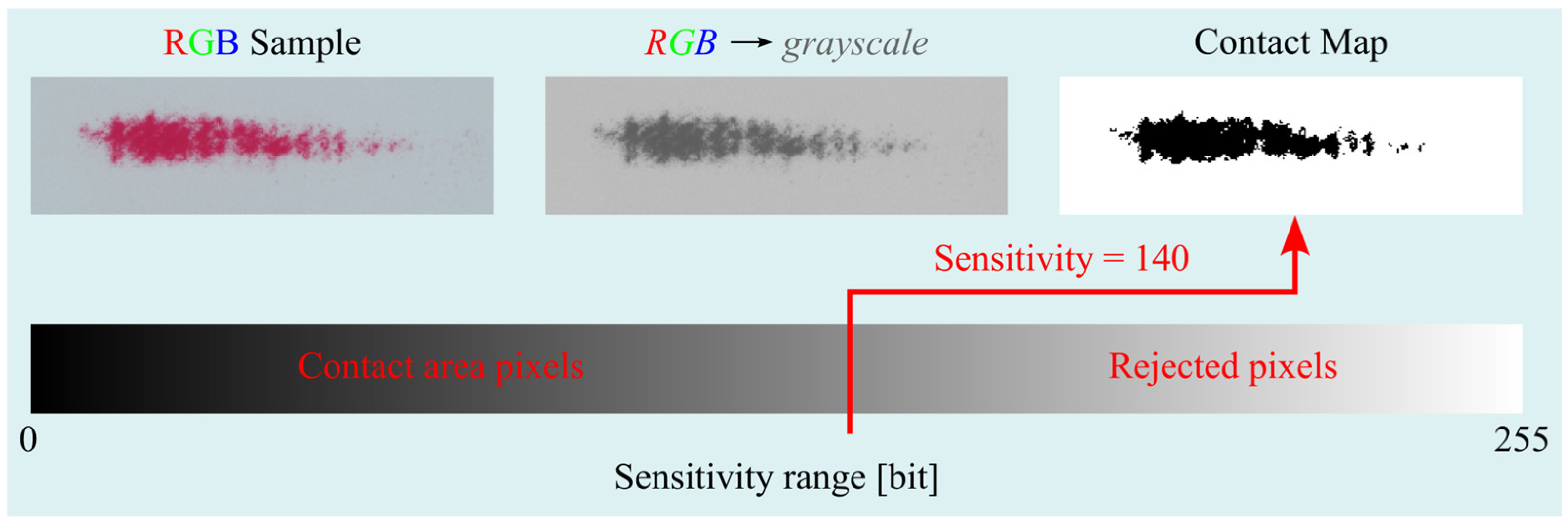
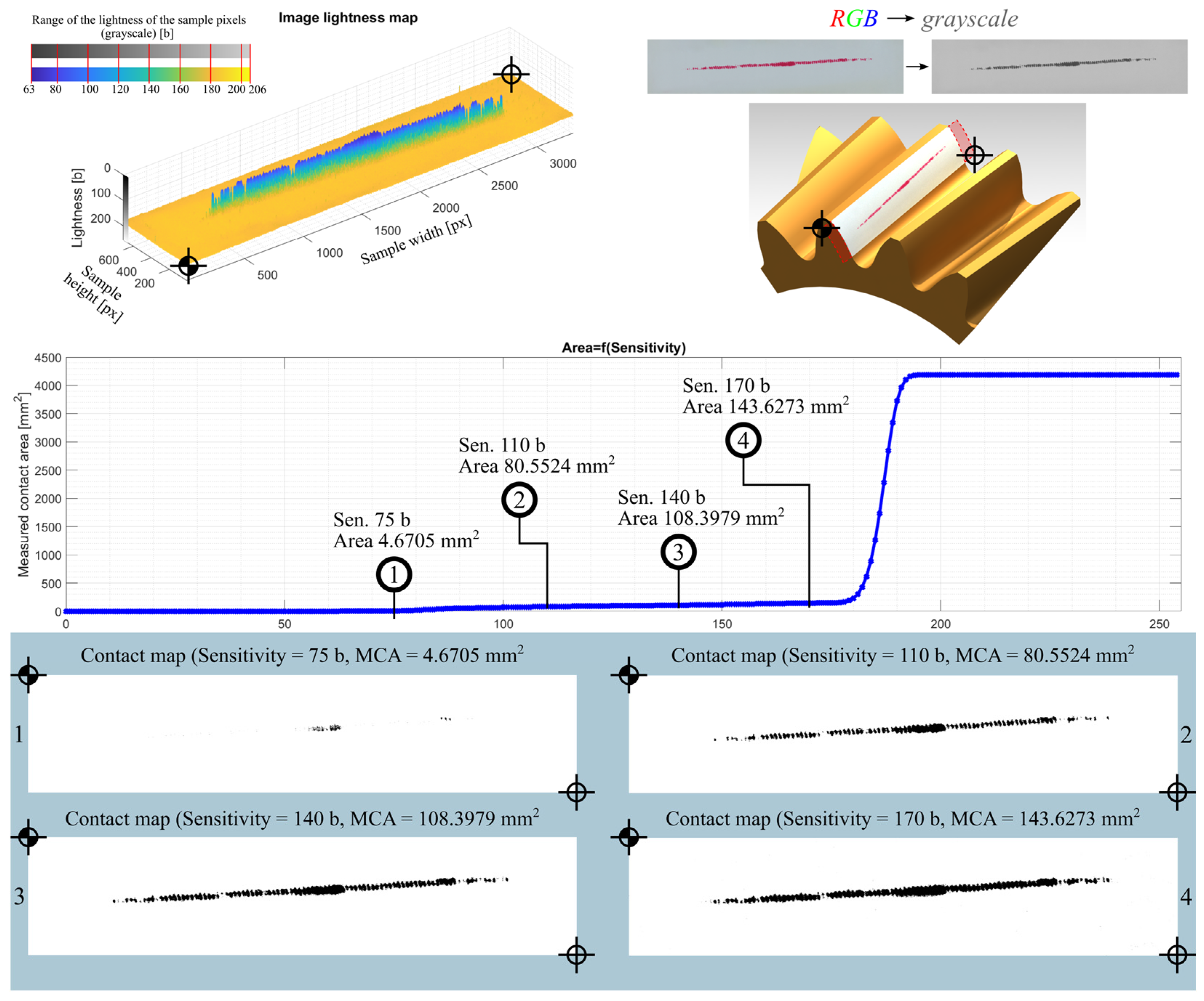
- Sensitivity—sensitivity expressed in bits, ranging from 0 to 255,
- Drawings—control variable taking the value of 0 or 1. The value of 0 means that the function will not display graphs and drawings generated after analyzing a single image, while 1 means that all drawings and graphs will be displayed. When analyzing a large number of files, when this program is called in a loop, it is recommended that this variable take the value 0.
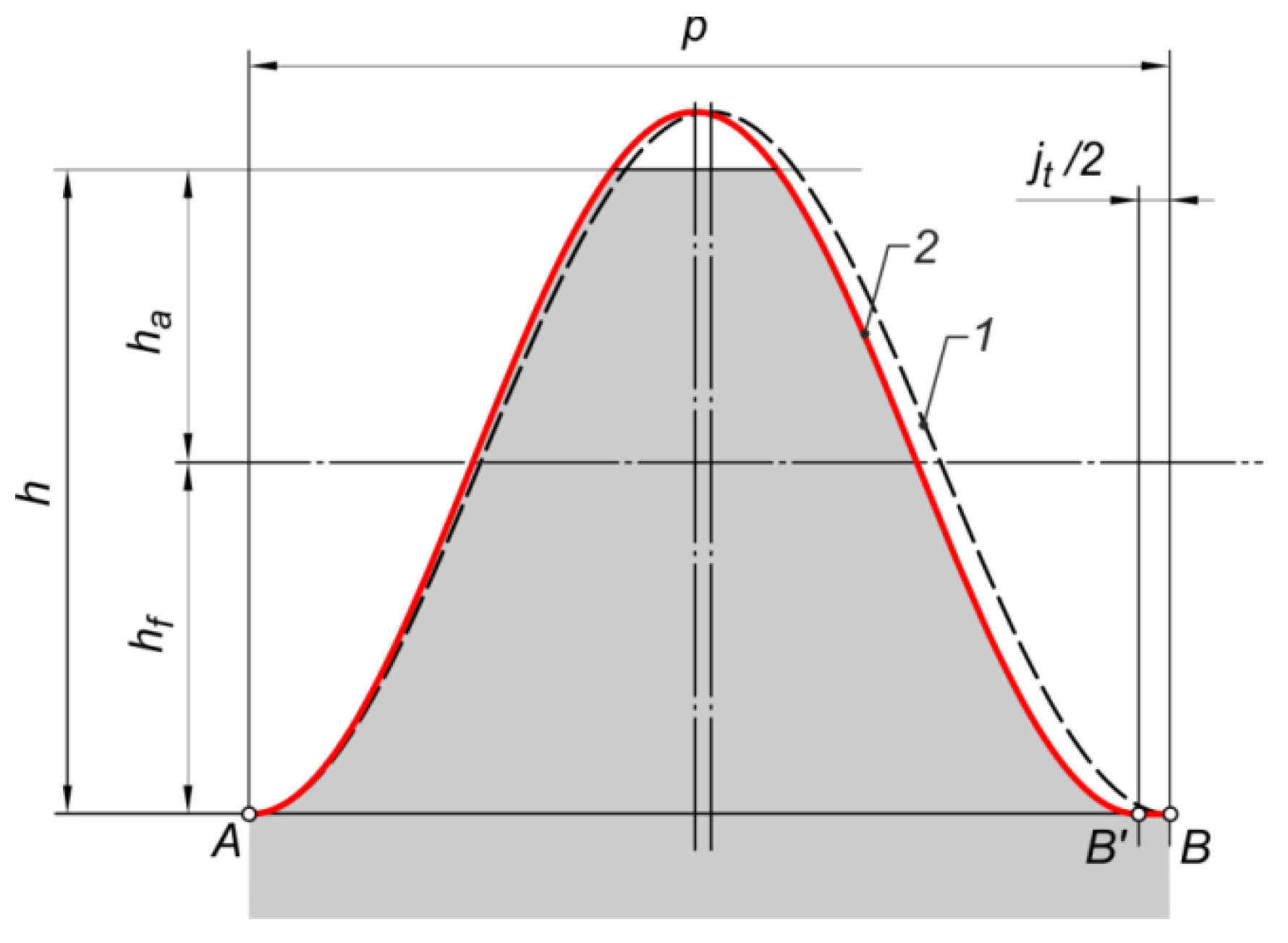
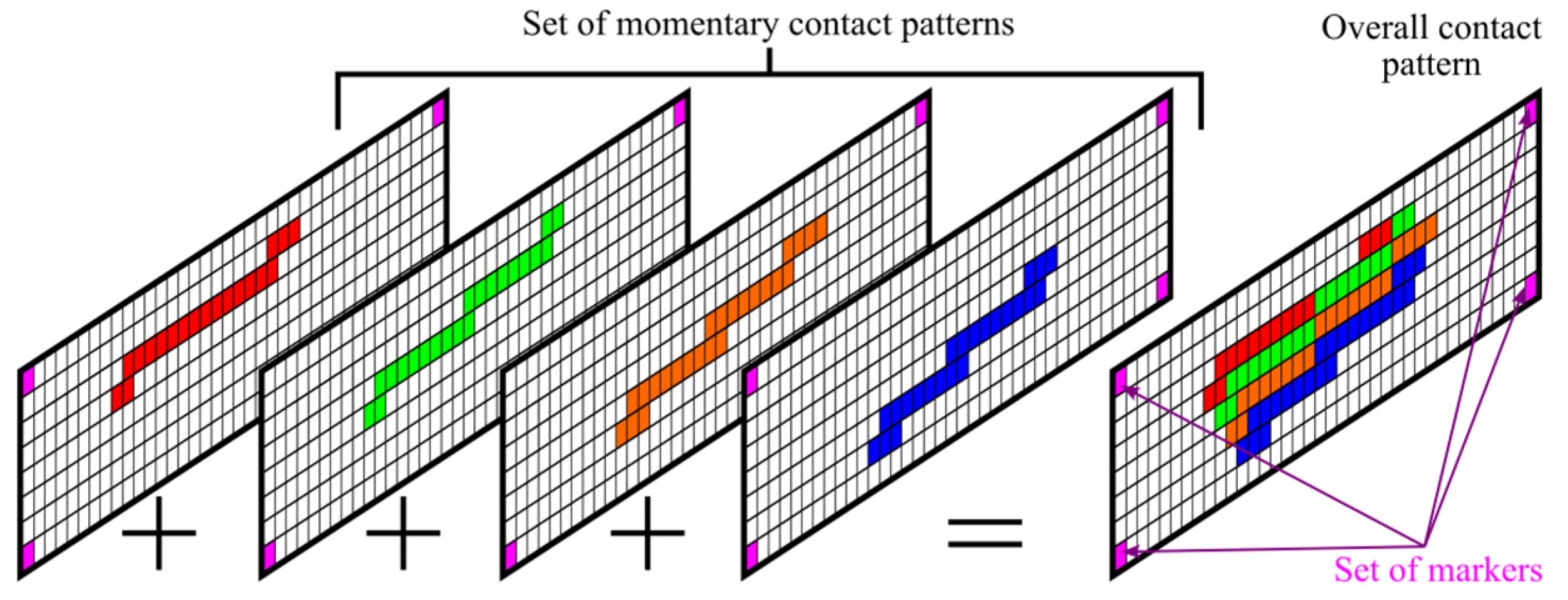
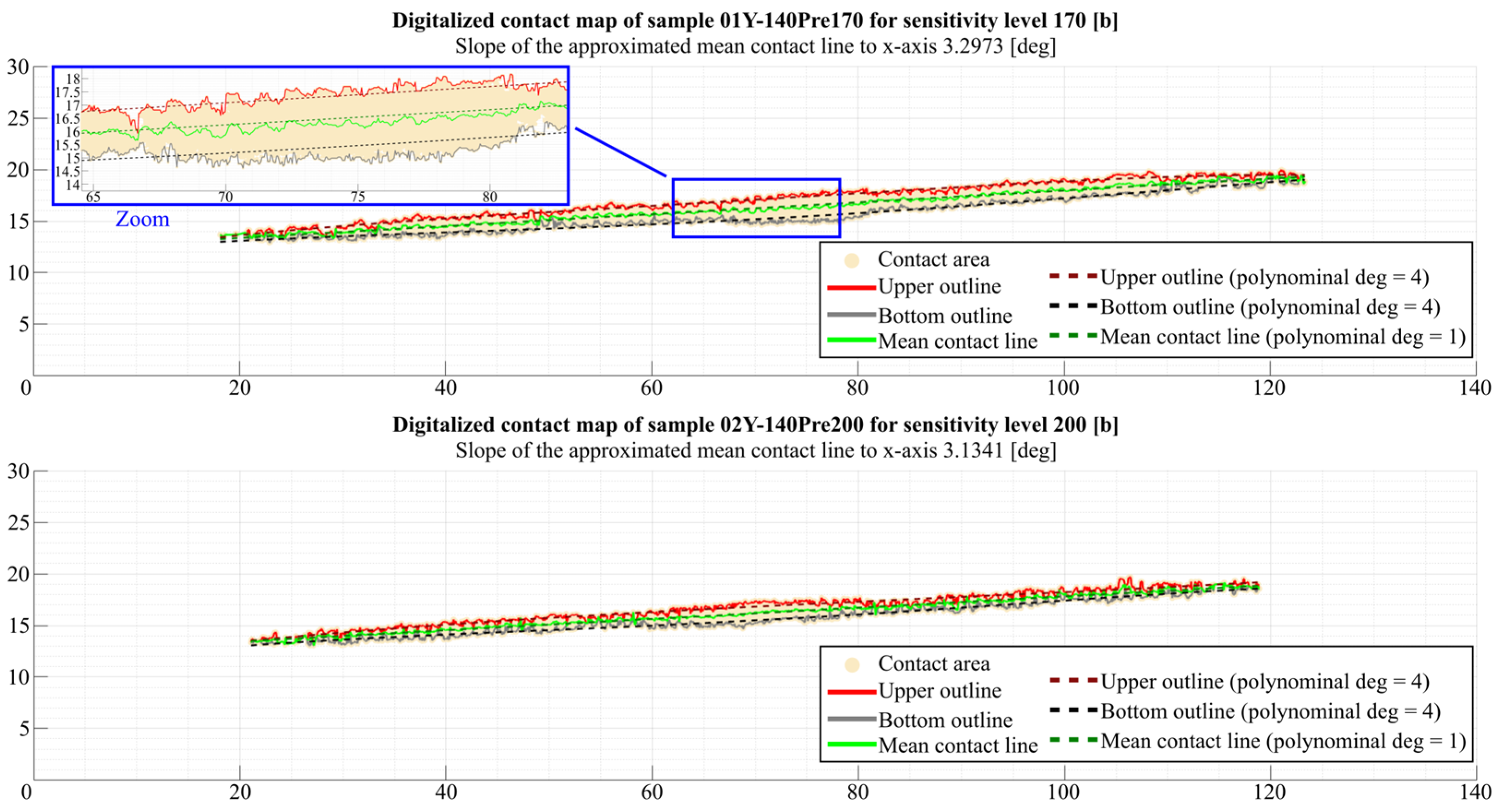
- the curve describing the upper outline line of the contact pattern ,
- a curve describing the bottom outline line of the contact pattern ,
- a curve describing the mean contact line ,
- the user can determine the rate of the polynomial used to describe the above curves ,
- the user can obtain the values of the coefficients standing at the individual expressions of the determined polynomials,
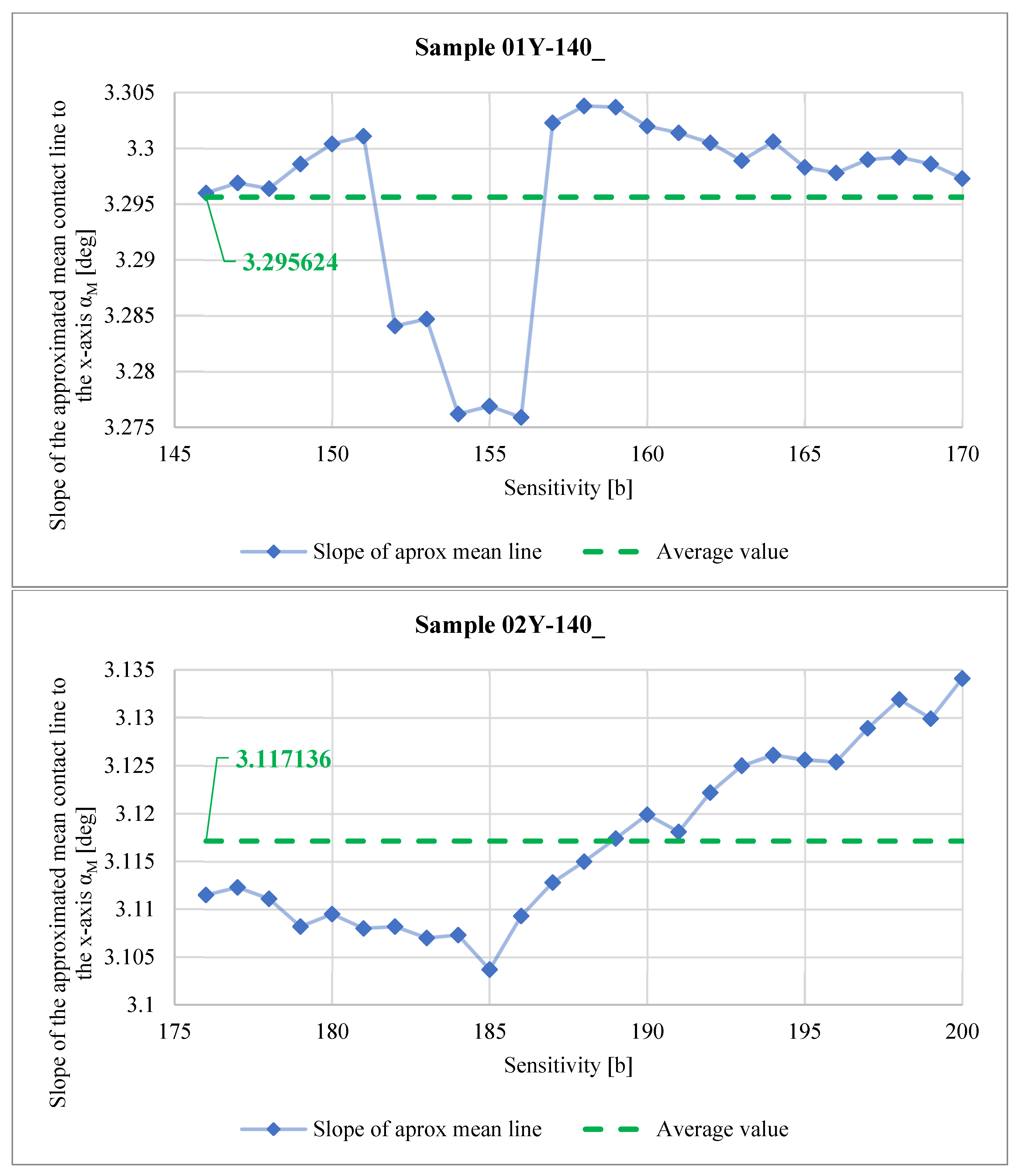
- determination of the angle of slope of the mean contact line to the x-axis (the horizontal edge of the sample) when using a polynomial of degree 1 ,
- determine the length of the momentary contact pattern along the mean contact line ,
- determine the contact area of the contact pattern described by polynomial curves.
- Determine the angle of slope of the mean contact line —for the mean contact line described as the line function (polynomial degree ):
- Determine the length of the momentary contact pattern along the mean contact line with Equation (2):
- -
- and —horizontal coordinates of the first and last pixels/points of the momentary contact pattern, respectively;
- -
- and —vertical coordinates of first and last pixels/points of the momentary contact pattern, respectively, calculated using the equation describing the mean line of the momentary contact pattern .
- Determine the contact area of the contact pattern described by the polynomial curves: —for upper outline and —for bottom outline:
- -
- —degree of upper outline line of the contact pattern
- -
- —degree of bottom outline line of the contact pattern
- After rotating all the curves by the angle , so that the mean line of the contact pattern is horizontal, it is possible to determine a function that allows for a convenient way of determining the change in the contact pattern width as a function of the contact line length.
2.2. Experimental Procedure
2.2.1. Gear Manufacturing
2.2.2. Stand Description
2.2.3. Determination of Gear Tooth Line and Surface Contact
3. Results and Discussion
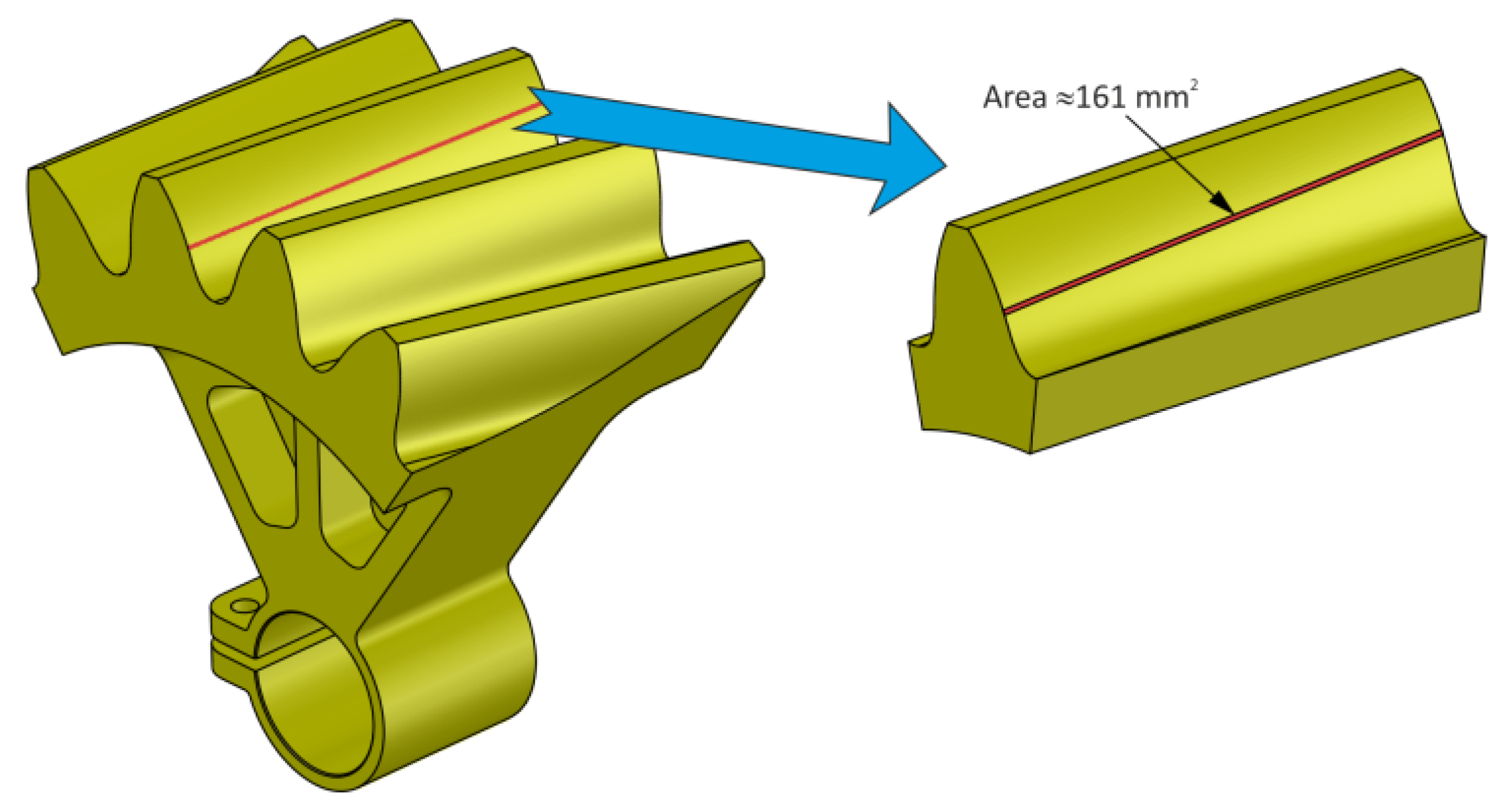
3.1. CAD Analysis of Tooth Contact
3.2. FEM Analysis of Tooth Contact
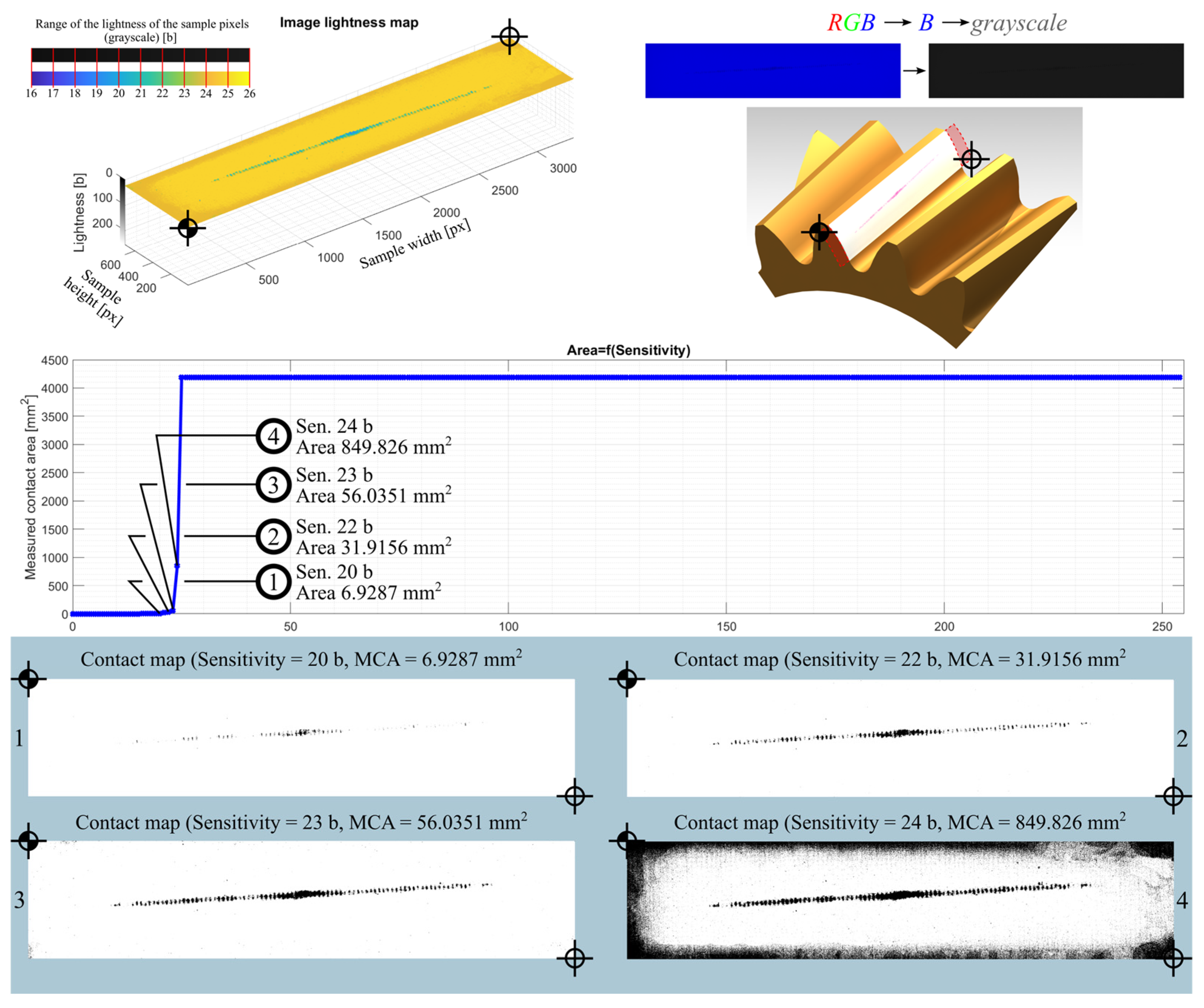
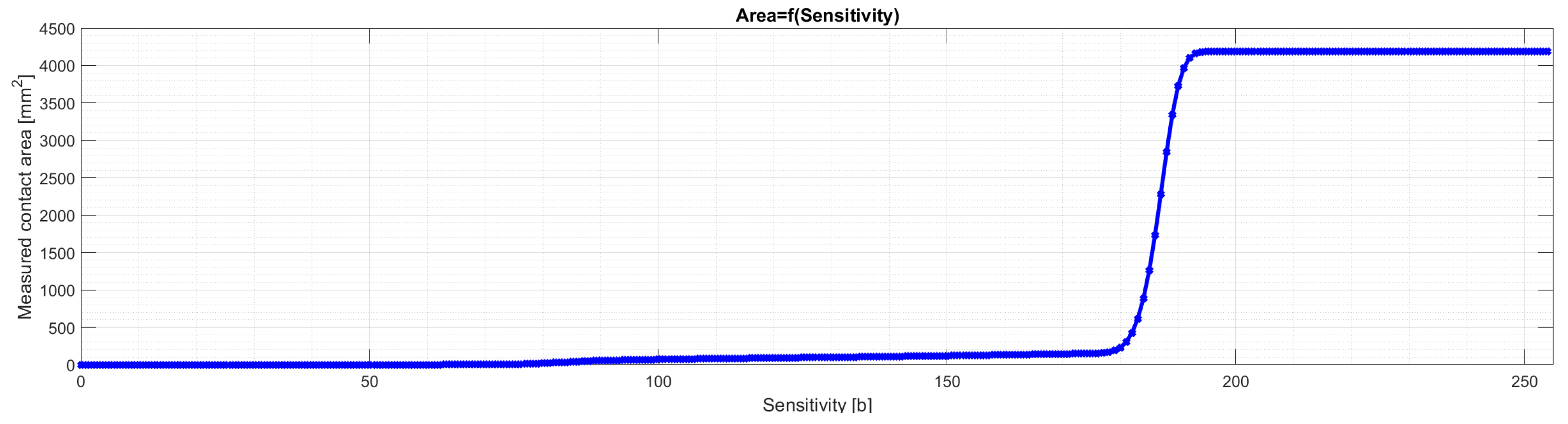
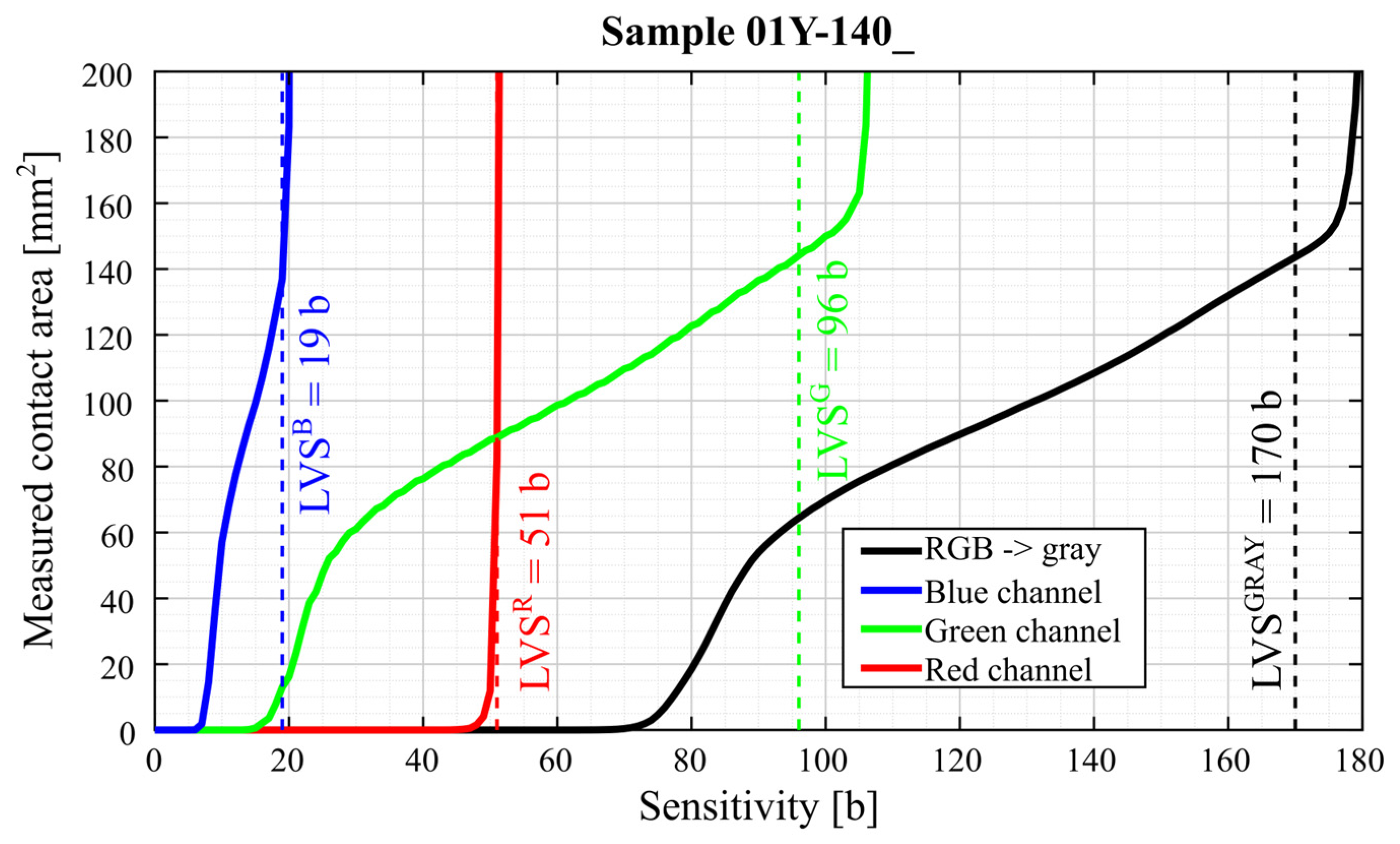
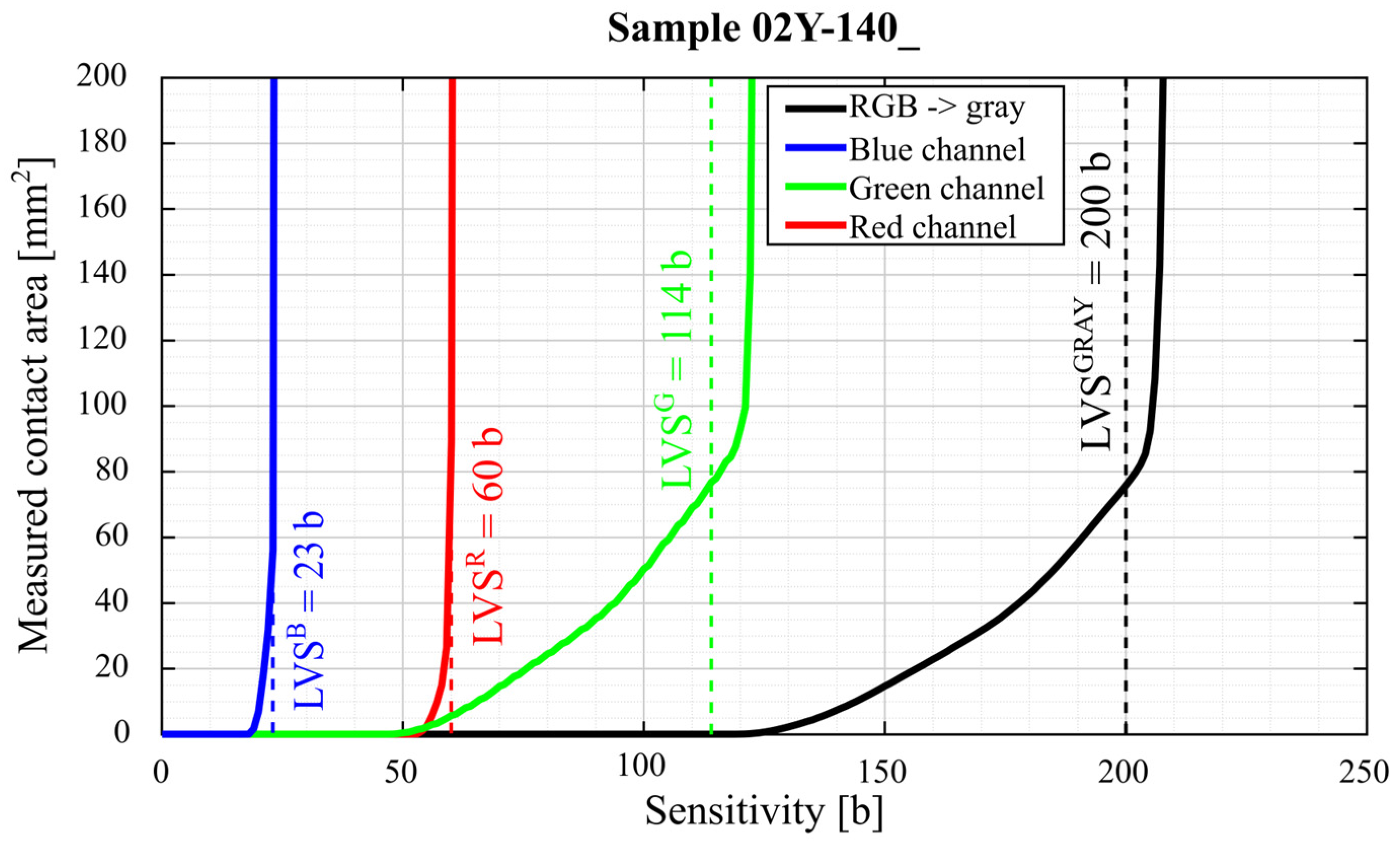
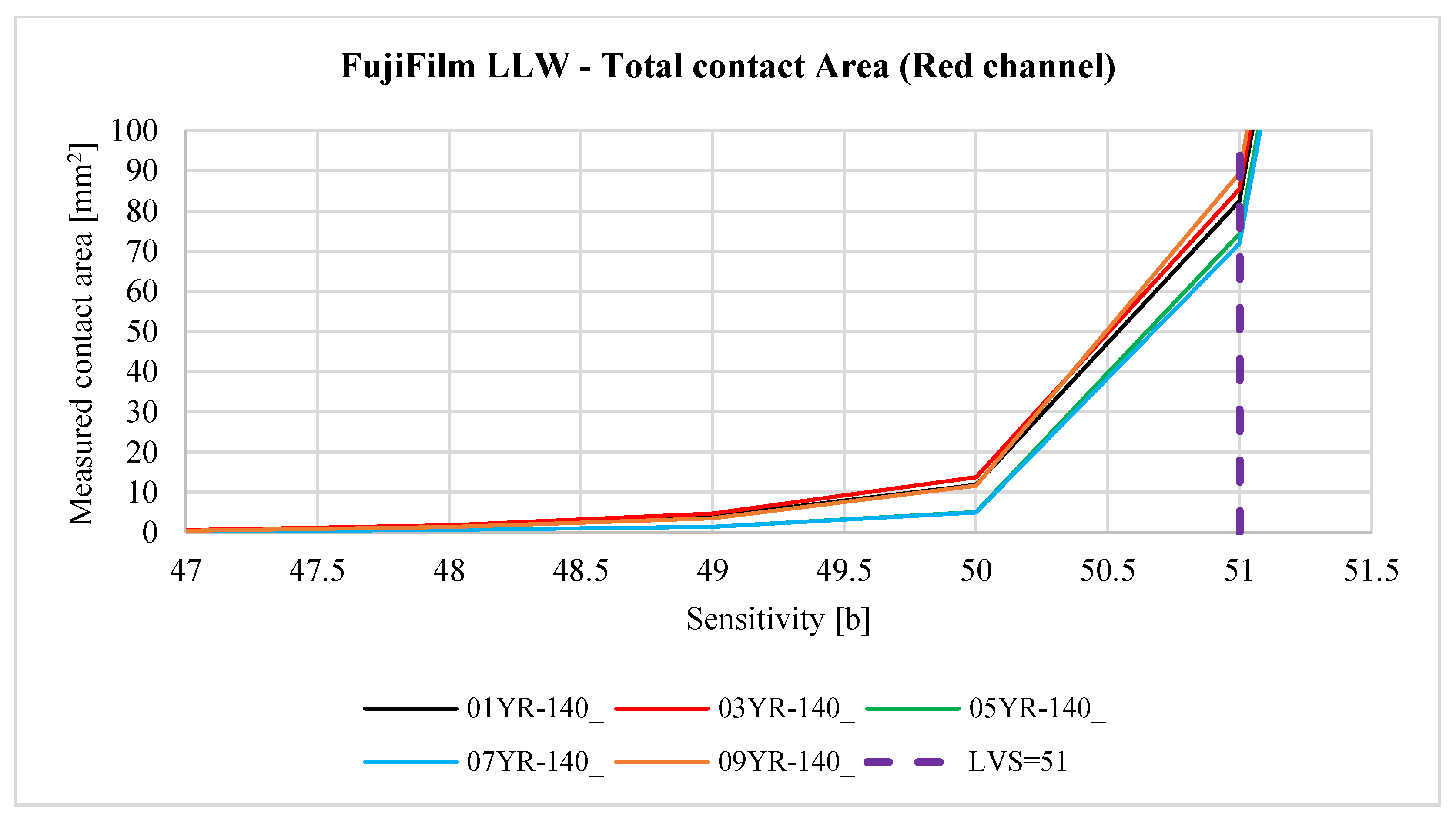
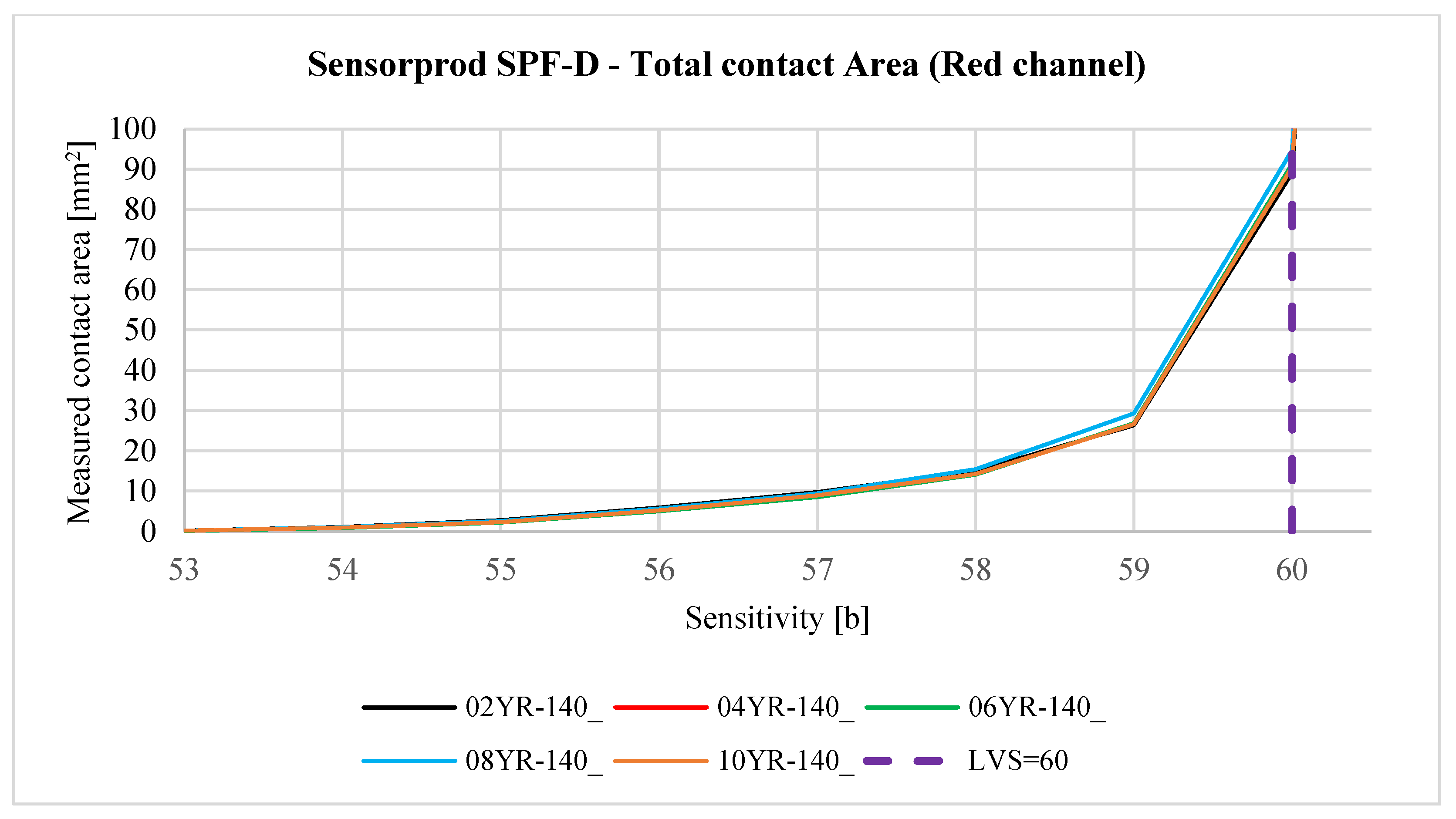
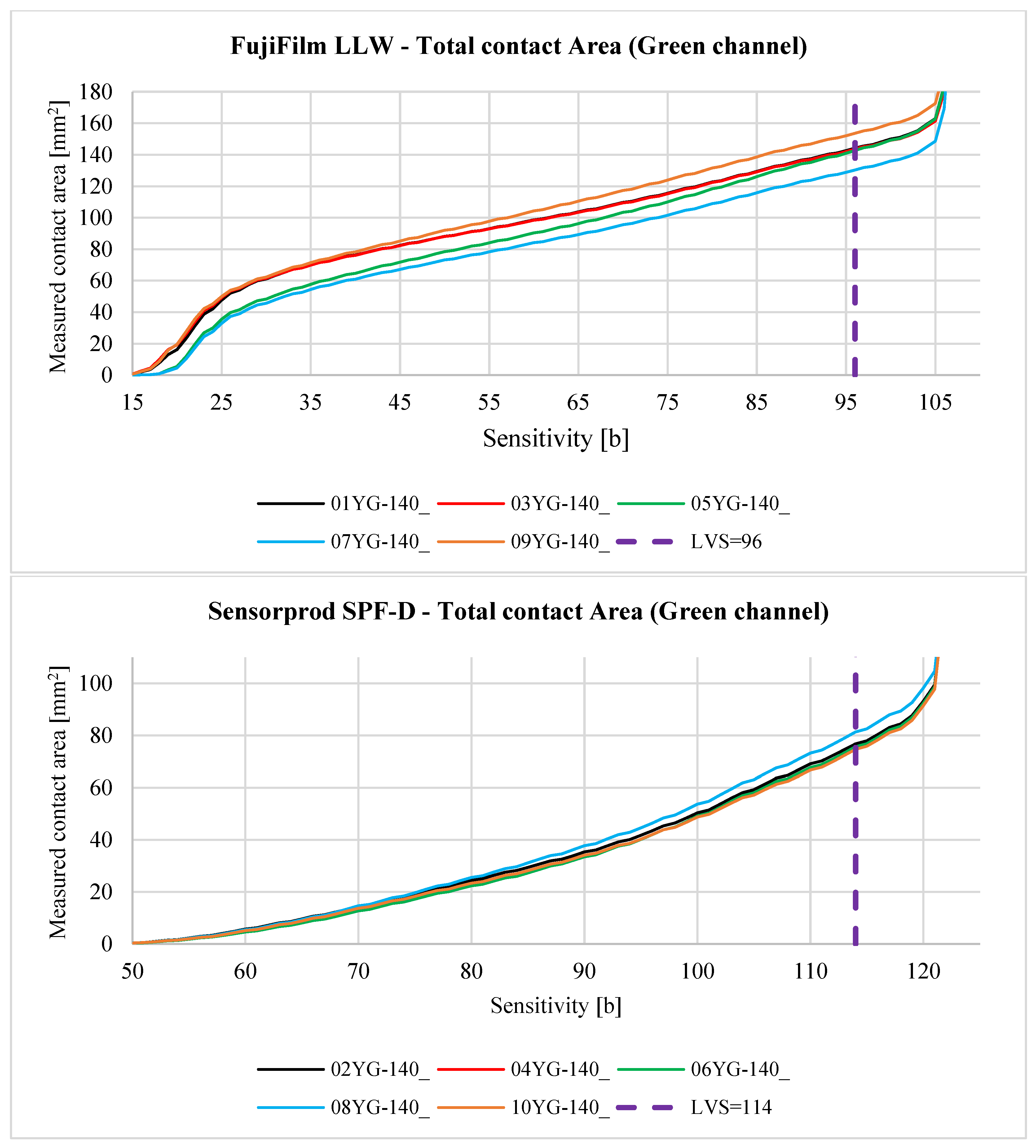
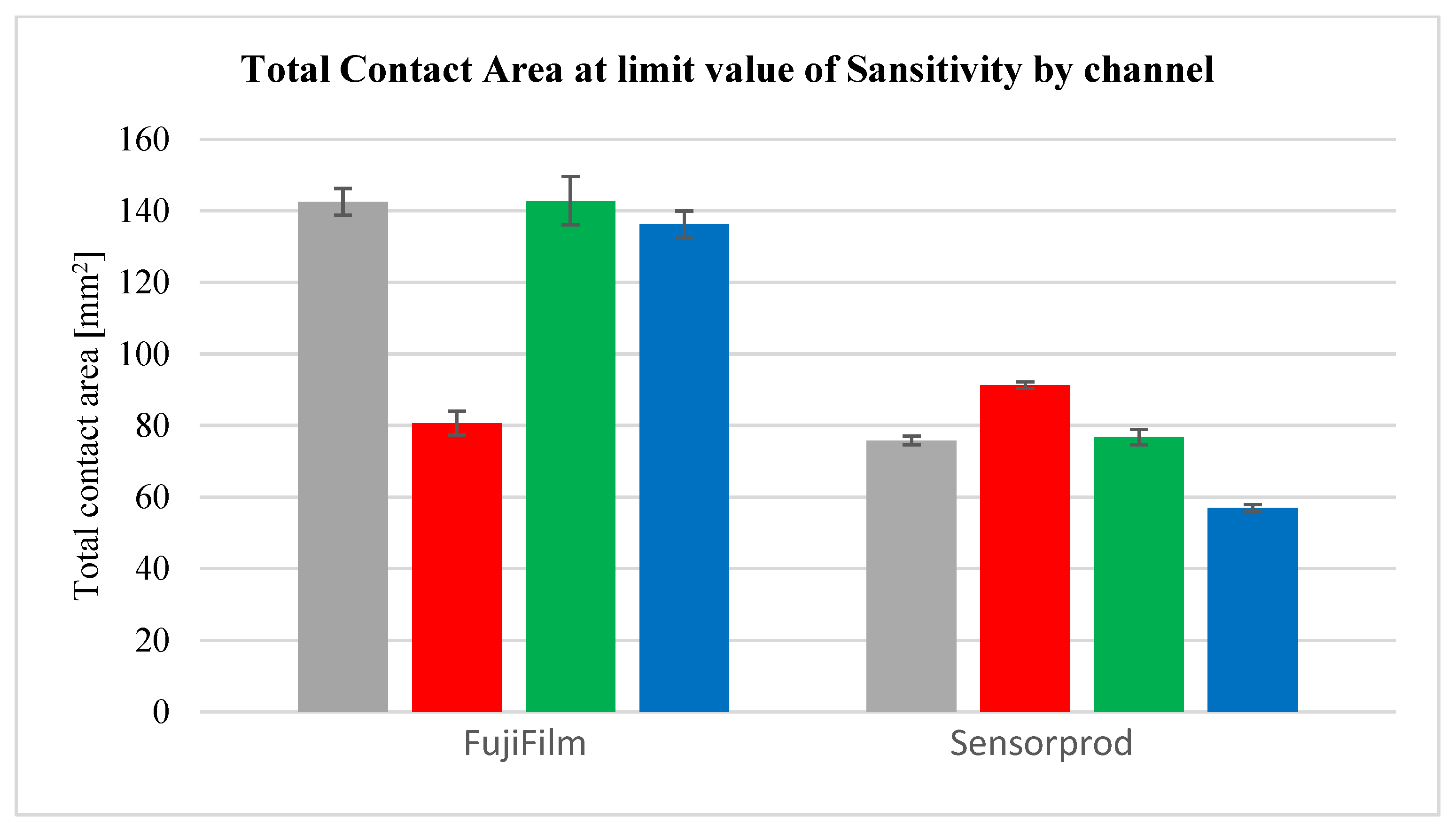
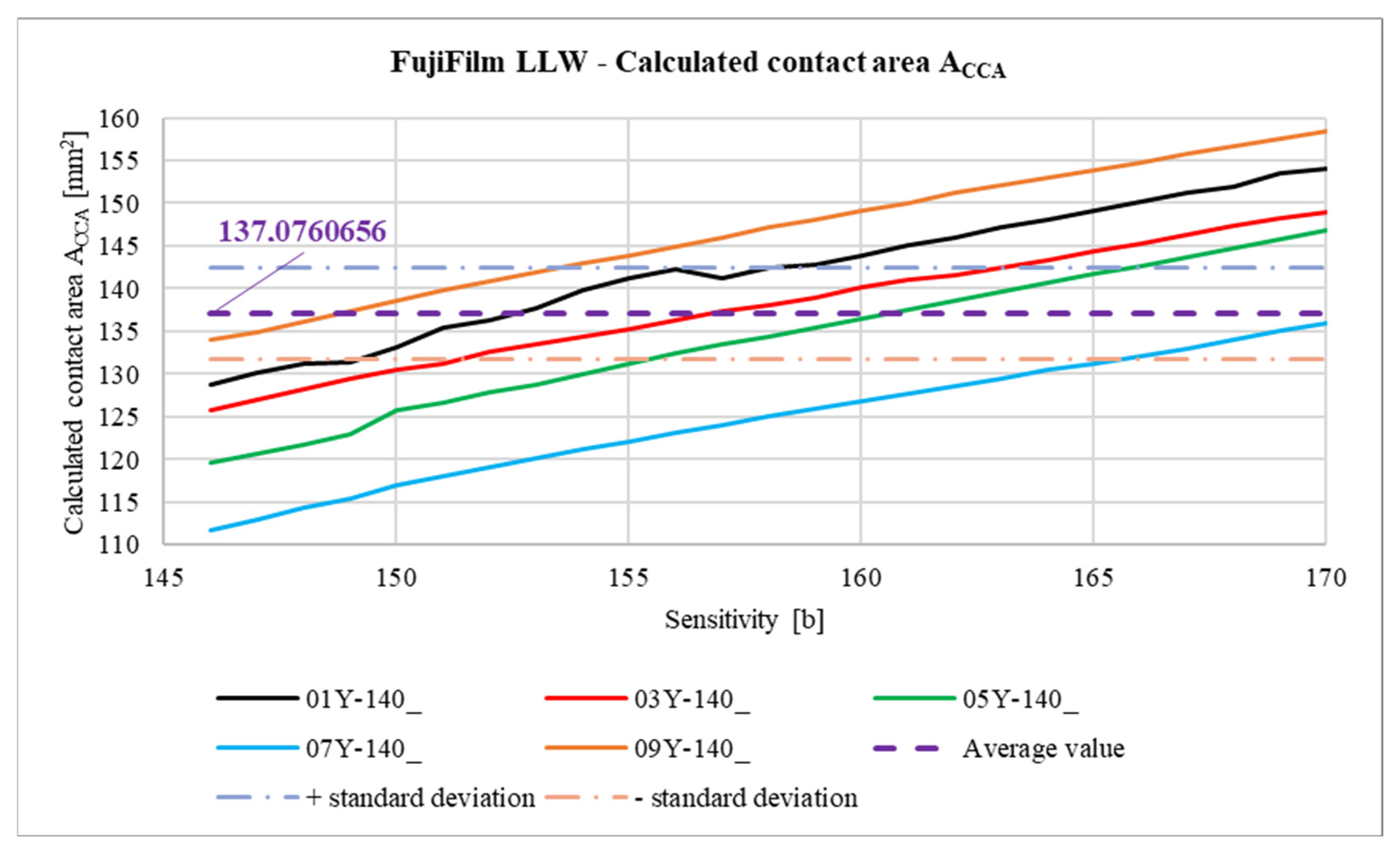
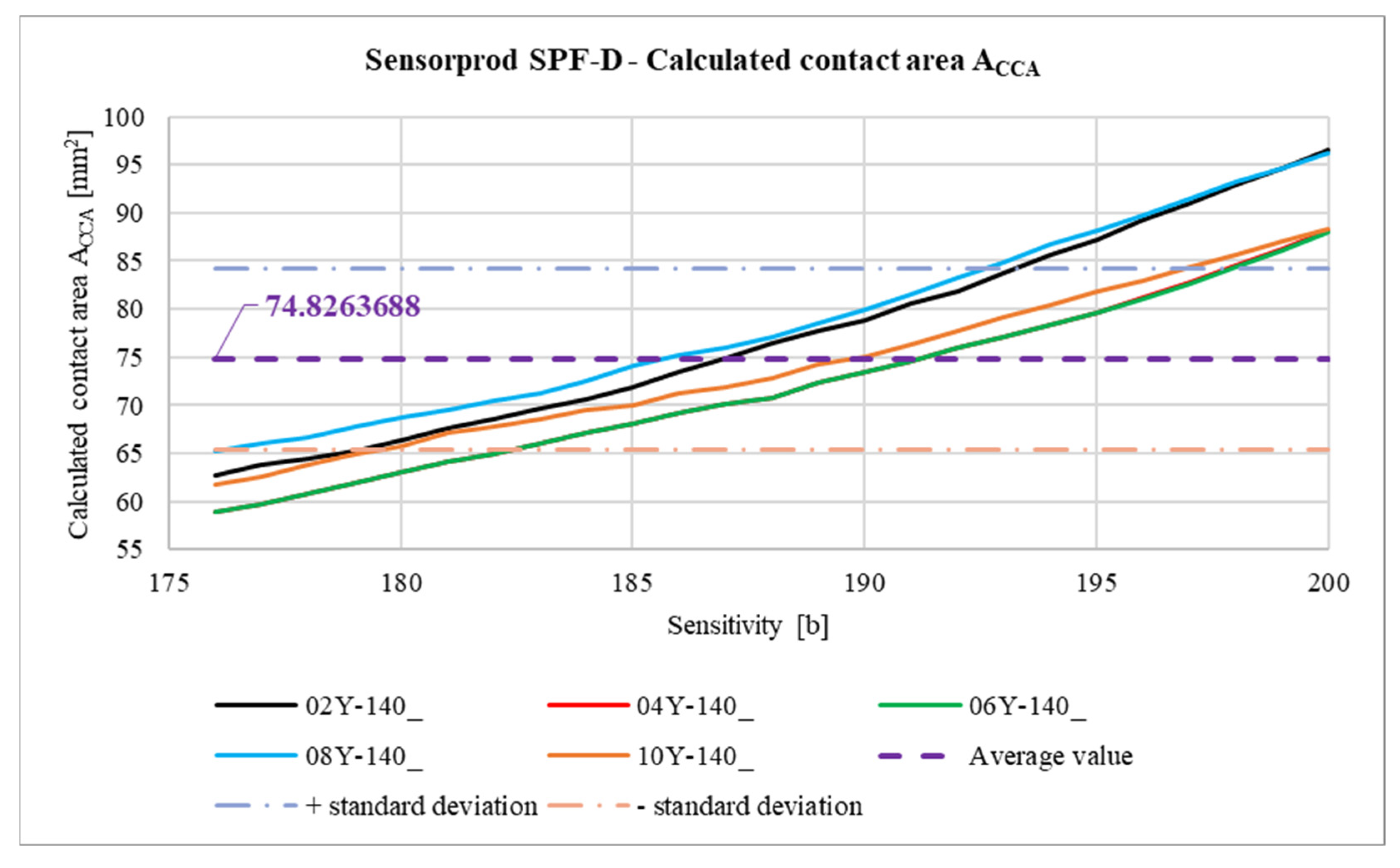
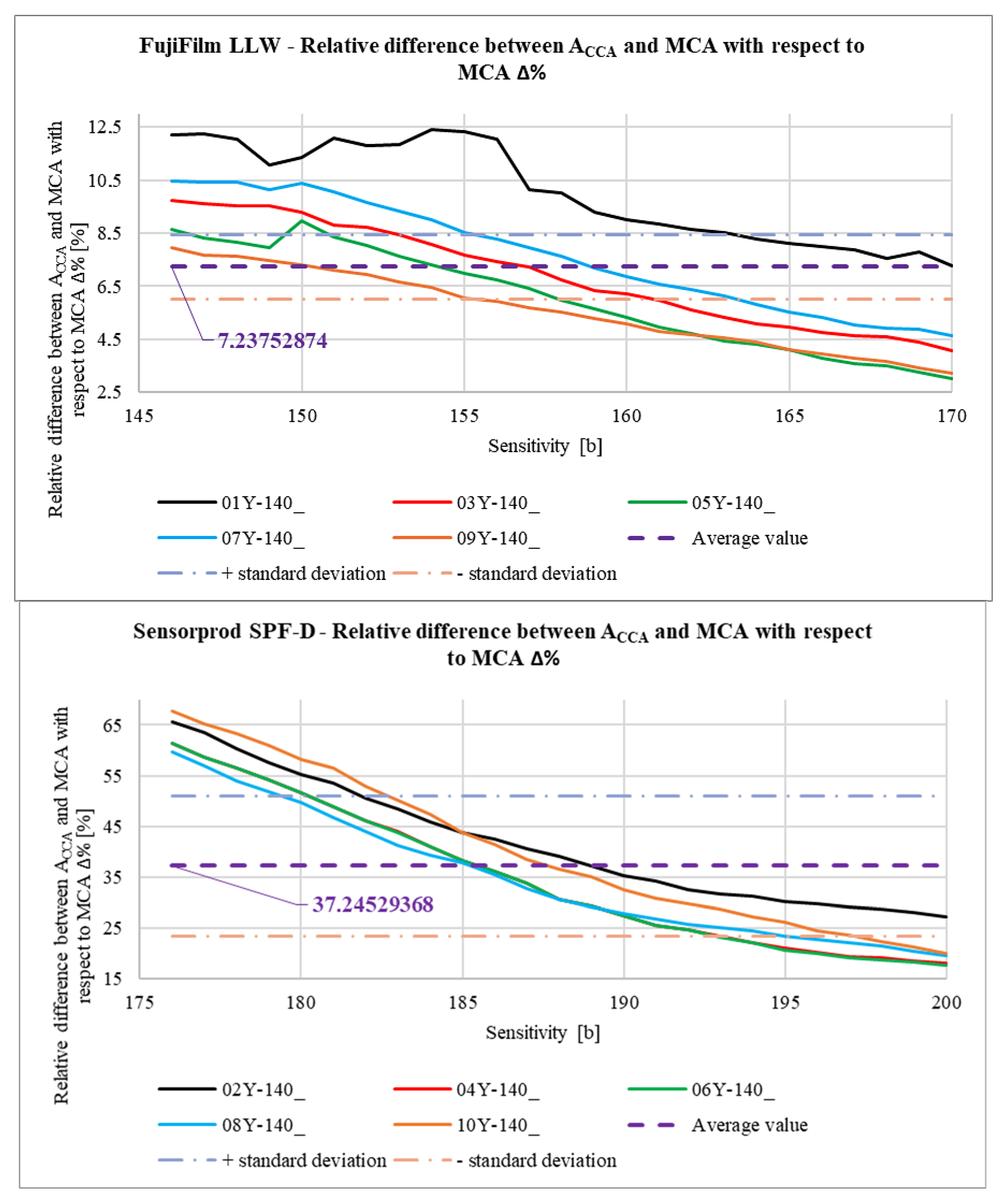
3.3. Image Data Processing
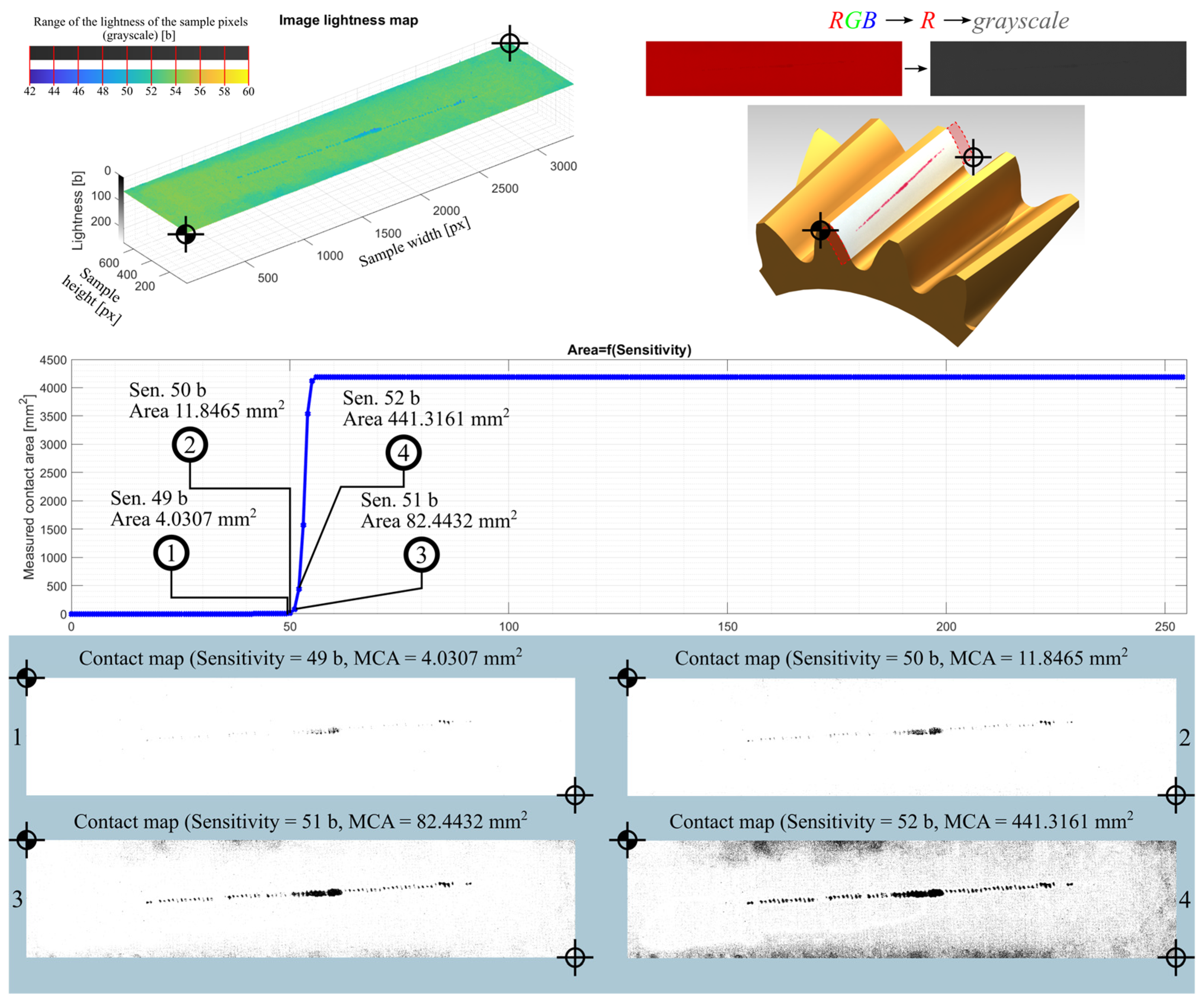
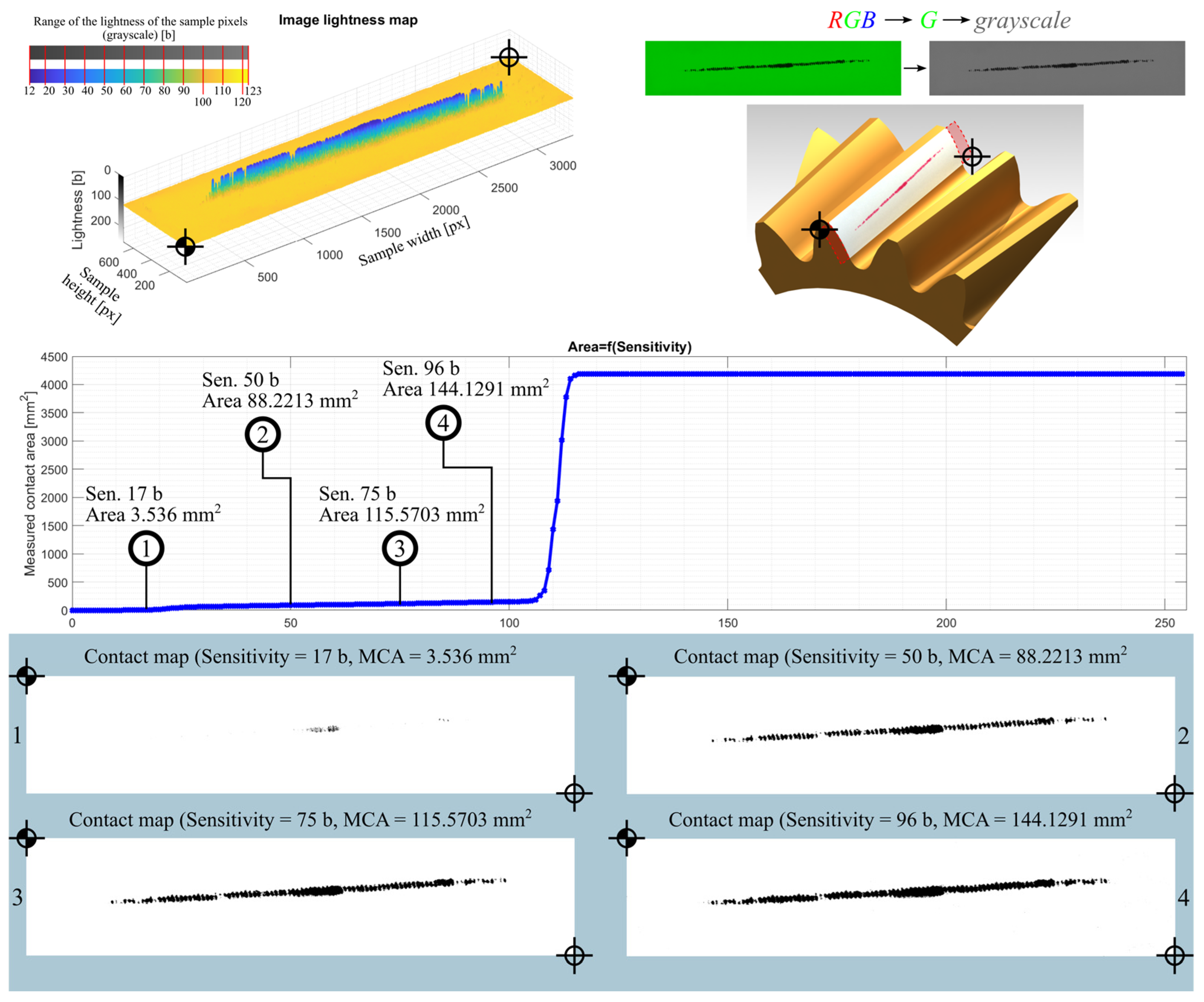
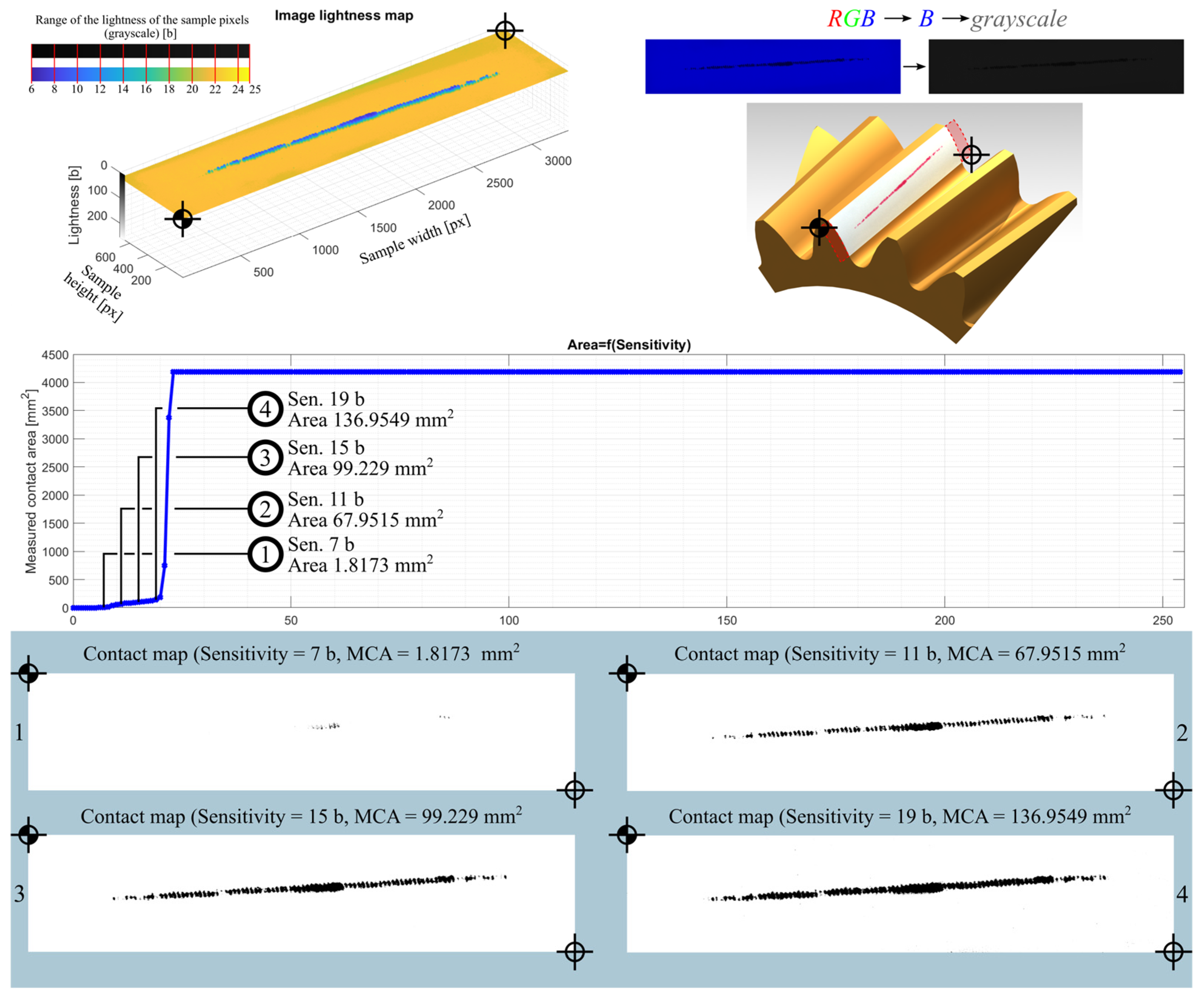
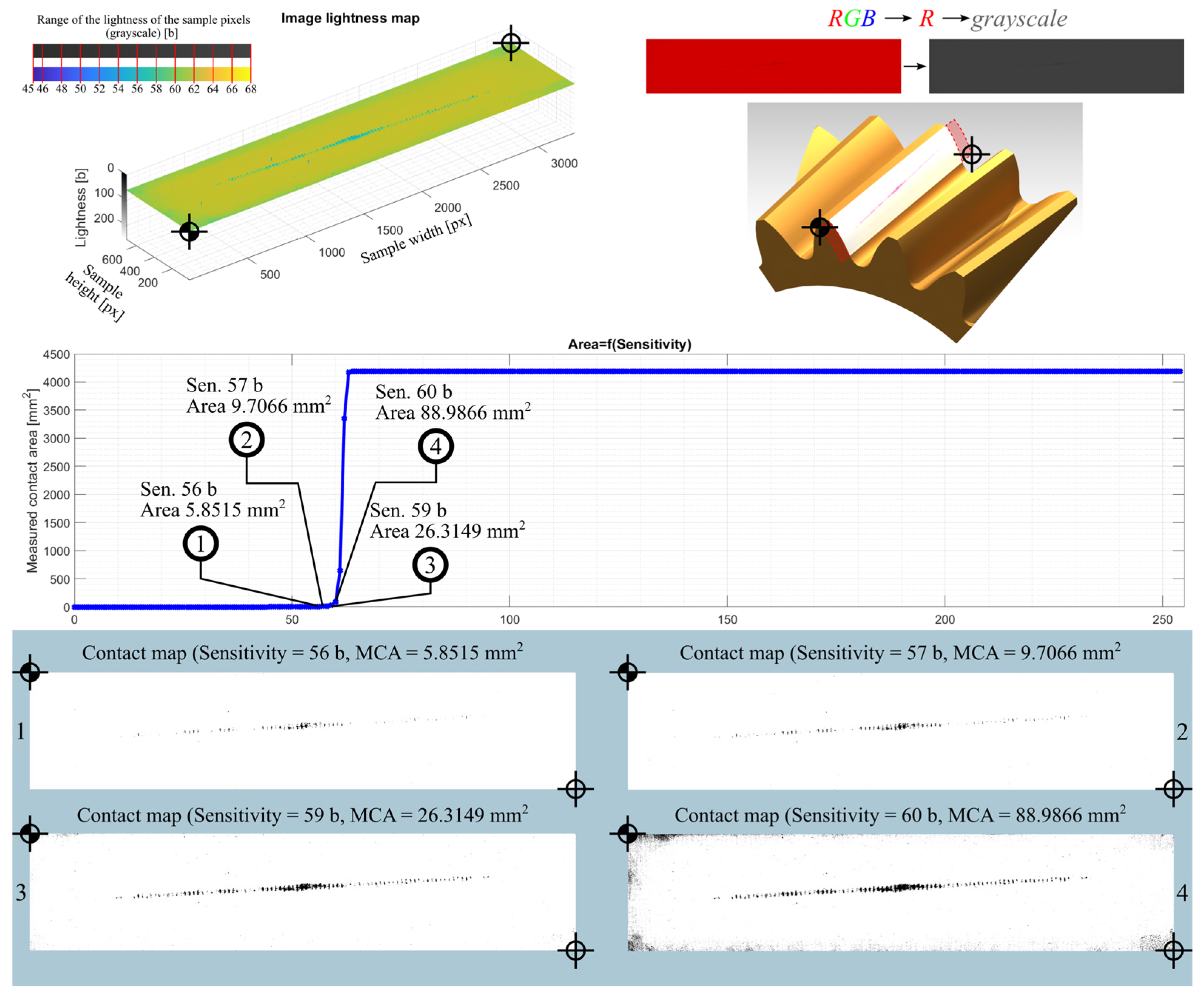
3.3.1. Image Data Processing—Contact Area Measurement
3.3.2. Image Data Processing—Contact Map Analysis
4. Conclusions
- • The results of contact pattern investigations using pressure measurement films are consistent with the analytical and numerical study results.
- • The values obtained for the slope angles of the average contact line determined for both samples are comparable (the relative error is approximately 5%).
- • The pressure measurement films used in the study can be successfully used to study the contact pattern of cylindrical gears, including those with a sinusoidal profile.
- • The method can be used under workshop conditions (without the need for computer analysis of sample scans) to quickly determine the correctness of the gearbox assembly.
- • The results of contact trace investigations using pressure-sensitive films are consistent with the analytical and numerical study results.
- • The developed algorithm for determining the contact pattern with the use of an office optical scanner can replace the need to purchase a dedicated scanner and software from film manufacturers for pressure measurement.
- • Sensorprod films are lighter, which can negatively affect the accuracy of the measurement, as it is easier to lose image detail in the scanning process. In addition, due to the higher lightness of the contact pattern (from about 140 to 220 bits in grayscale), it is much more difficult to distinguish the noise and fine contaminants visible on the sample scan from the actual contact pattern.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| 01 | for i = 1:1:size (ImgeGrayscale,1) % Loop selecting horizontal line of image |
| 02 | |
| 03 | for j = 1:1:size (ImgeGrayscale,2) % Loop selecting vertical line of image |
| 04 | |
| 05 | % Checking pixel lightness |
| 06 | if ImgeGrayscale (i, j) <= Sensitivity % Condition fulfilled |
| 07 | |
| 08 | MCA = MCA + ppa; % Increase the contact area |
| 09 | |
| 10 | ContactMap (i, j) = uint8(0); % Color pixel black (contact detected) |
| 11 | |
| 12 | else % Condition not fulfilled |
| 13 | |
| 14 | ContactMap (i, j) = uint8(255); % Color pixel white (contact not detected) |
| 15 | |
| 16 | end |
| 17 | |
| 18 | end |
| 19 | |
| 20 | end |
Appendix B

References
- Litvin, F.L.; Fuentes, A. Gear Geometry and Applied Theory, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Gutman, Y.; Litvin, F.L. Methods of Synthesis and Analysis for Hypoid Gear-Drives of “Formate” and “Helixform”—Part 1. Calculations for Machine Settings for Member Gear Manufacture of the Formate and Helixform Hypoid Gears. J. Mech. Des. 1981, 103, 83–88. [Google Scholar] [CrossRef]
- Gutman, Y.; Litvin, F.L. Methods of Synthesis and Analysis for Hypoid Gear-Drives of “Formate” and “Helixform”, Part 2. Machine Setting Calculations for the Pinions of Formate and Helixform Gears. J. Mech. Des. 1981, 103, 307–314. [Google Scholar] [CrossRef]
- Gutman, Y.; Litvin, F.L. Methods of Synthesis and Analysis for Hypoid Gear-Drives of “Formate” and “Helixform”, Part 3. Analysis and Optimal Synthesis Methods for Mismatch Gearing and its Application for Hypoid Gears of “Formate” and “Helixform”. J. Mech. Des. 1981, 103, 503–510. [Google Scholar] [CrossRef]
- Radzevich, S.P. Kinematic Geometry of Surface Machining, 1st ed.; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Batsch, M. Tensor based approach for tooth contact analysis of planar and spatial gearing contact. Mech. Mach. Theory 2024, 203, 105828. [Google Scholar] [CrossRef]
- Fudali, P.; Markowski, T.; Pacana, J. Machining Simulation of Novikov Profile Gear Models for Analysis and Computational Calculations. Materials 2025, 18, 1155. [Google Scholar] [CrossRef]
- Batsch, M. Mathematical model and tooth contact analysis of convexo-concave helical bevel Novikov gear mesh. Mech. Mach. Theory 2020, 149, 103842. [Google Scholar] [CrossRef]
- Kawalec, A.; Wiktor, J. Simulation of generation and tooth contact analysis of helical gears with crowned flanks. Proc. Inst. Mech. Eng. J. Eng. Manuf. 2008, 222, 1147–1160. [Google Scholar] [CrossRef]
- Marciniec, A.; Pacana, J.; Pisula, J.; Fudali, P. Comparative analysis of numerical methods for the determination of contact pattern of spiral bevel gears. Aircr. Eng. Aerosp. Technol. 2018, 90, 359–367. [Google Scholar] [CrossRef]
- Pacana, J.; Kozik, M.; Budzik, A. Strength analysis of gears in dual-path gearing by means of FEM. Diagnostyka 2015, 16, 41–46. [Google Scholar]
- Wang, S.; Zhou, Y.; Tang, J.; Tang, K.; Li, Z. Digital tooth contact analysis of face gear drives with an accurate measurement model of face gear tooth surface inspected by CMMs. Mech. Mach. Theory 2022, 167, 104498. [Google Scholar] [CrossRef]
- Argyris, J.; Fuentes, A.; Litvin, F.L. Computerized integrated approach for design and stress analysis of spiral bevel gears. Comput. Methods Appl. Mech. Eng. 2002, 191, 1057–1095. [Google Scholar] [CrossRef]
- Simon, V. Computer simulation of tooth contact analysis of mismatched spiral bevel gears. Mech. Mach. Theory 2007, 42, 365–381. [Google Scholar] [CrossRef]
- Achtmann, J.; Bär, G. Optimized Bearing Ellipses of Hypoid Gears. J. Mech. Des. 2003, 125, 739–745. [Google Scholar] [CrossRef]
- Chen, J.S.; Chen, N.X.; Litvin, F.L. Computerized determination of curvature relations and contact ellipse for conjugate surfaces. Comput. Methods Appl. Mech. Eng. 1995, 125, 151–170. [Google Scholar] [CrossRef]
- Atanasovska, I.; Dimitrijević, D.; Momčilović, D.; Nikolić-Stanojlović, V. Finite Element Model for Stress Analysis and Nonlinear Contact Analysis of Helical Gears. Sci. Tech. Rev. 2009, 59, 61–69. [Google Scholar]
- Cvejić, V.; Nikolić-Stanojević, V. The analysis of contact stress on meshed teeth’s flanks along the path of contact for a tooth pair, Facta Universitatis, Series: Mechanics. Autom. Control Robot. 2003, 3, 1055–1066. [Google Scholar]
- Zhou, C.; Chen, C.; Gui, L.; Fan, Z. A nonlinear multi-point meshing model of spur gears for determining the face load factor. Mech. Mach. Theory 2018, 126, 210–224. [Google Scholar] [CrossRef]
- Binney, D.; Fuentes, A.; Gonzalez-Perez, I.; Litvin, F.L.; Hansen, B.D.; Vecchiato, D. Design, generation and stress analysis of face-gear drive with helical pinion. Comput. Methods Appl. Mech. Eng. 2005, 194, 3870–3901. [Google Scholar] [CrossRef]
- Litvin, F.L.; Aznar, A.F.; Aznar, A.F.; Hayasaka, K. Design, manufacture, stress analysis, and experimental tests of low-noise high endurance spiral bevel gears. Mech. Mach. Theory 2006, 41, 83–118. [Google Scholar] [CrossRef]
- Wu, L.M.; Yang, F. Finite element analysis for gear contact based on UG and ABAQUS. Appl. Mech. Mater. 2013, 442, 229–232. [Google Scholar] [CrossRef]
- Shuting, L. Finite element analyses for contact strength and bending strength of a pair of spur gears with machining errors, assembly errors and tooth modifications. Mech. Mach. Theory 2007, 42, 88–114. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, Y.; Liu, M.; Sun, X. Parameterized high-precision finite element modelling method of 3D helical gears with contact zone refinement. Shock Vib. 2019, 2019, 5809164. [Google Scholar] [CrossRef]
- Mohan, L.V.; Shunmugam, M.S. CAD approach for simulation of generation machining and identification of contact lines. Int. J. Mach. Tools Manuf. 2004, 44, 717–723. [Google Scholar] [CrossRef]
- Bair, B.W.; Chen, C.F.; Sung, M.H.; Wang, J.S. Tooth profile generation and analysis of oval gears with circular-arc teeth. Mech. Mach. Theory 2009, 44, 1306–1317. [Google Scholar] [CrossRef]
- Dimitriou, V.; Antoniadis, A. CAD-based simulation of the hobbing process for the manufacturing of spur and helical gears. Int. J. Adv. Manuf. Technol. 2009, 41, 347–357. [Google Scholar] [CrossRef]
- Markowski, T.; Sobolak, M. Modelowanie I Analiza geometryczna Współpracy Kół Zębatych Z Wykorzystaniem Systemów CAD, W: Przekładnie Zębate O Nietypowym Zazębieniu—Modelowanie, Prototypowanie, Badania Stanowiskowe; Oficyna Wydawnicza Politechniki Rzeszowskiej: Rzeszów, Poland, 2009; pp. 56–79. [Google Scholar]
- Sobolak, M. Discrete digital method of determining the surface topography by tool projection. Arch. Technol. Masz. Autom. 2004, 24, 149–157. [Google Scholar]
- Sobolak, M. Discrete and direct digital methods of simulation of gear generation of face-milled Gleason spiral bevel gears. Zesz. Nauk. Politech. Rzesz. Mech. 2001, 57, 291–300. [Google Scholar]
- Kahraman, A.; Wagaj, P. Influence of Tooth Profile Modification on Helical Gear Durability. J. Mech. Des. 2002, 124, 501–510. [Google Scholar] [CrossRef]
- Batsch, M.; Markowski, T.; Legutko, S.; Krolczyk, G.M. Measurement and mathematical model of convexo-concave Novikov gear mesh. Measurement 2018, 125, 516–526. [Google Scholar] [CrossRef]
- Jagiełowicz, P.E. The direct solid method of geometry analysis of the globoidal worm gear with the rotary teeth. Mechanik 2018, 2, 162–165. [Google Scholar] [CrossRef][Green Version]
- Sobolak, M.; Budzik, G. Experimental method of tooth contact analysis (TCA) with rapid prototyping (RP) use. Rapid Prototyp. J. 2008, 14, 197–201. [Google Scholar] [CrossRef]
- Sobolak, M.; Jagiełowicz, P.E. Using Rapid Prototyping for Prototyping and Research of Polymer Transmissions; Wydawnictwo Politechniki Krakowskiej: Kraków, Poland, 2010; pp. 159–169. [Google Scholar]
- Zarnik, M.S.; Novak, F.; Papa, G. Sensors in proactive maintenance—A case of LTCC pressure sensors. Eksploat. I Niezawodn. Maint. Reliab. 2018, 20, 267–272. [Google Scholar] [CrossRef]
- Schott, A.; Biehl, S.; Bräuer, G.; Herrmann, C. Thin Film Sensor Systems for Use in Smart Production. Future Automot. Prod. Conf. 2021, 2022, 220–231. [Google Scholar] [CrossRef]
- Fukagai, S.; Toyama, T.; Tanaka, T.; Kuzuta, M. Visualization of wheel-rail contact area of running vehicle using film sensor. Proc. Inst. Mech. Eng. J. Rail Rapid Transit 2021, 236, 745–755. [Google Scholar] [CrossRef]
- Sridhar, V.; Chana, K. Development of a Novel Sensor for Gear Teeth Wear and Damage Detection. Int. J. Progn. Health Manag. 2021, 12, 1–8. [Google Scholar] [CrossRef]
- Shi, Z.; Sun, Y.; Yin, X.; Yu, B. Gear pitch rapid measurement by a point laser sensor. Opt. Eng. 2022, 61, 061405. [Google Scholar] [CrossRef]
- Kurasako, A.; Owashi, M.; Sakai, Y.; Mihara, Y.; Ohue, H. Measurement of Contact Pressure Distribution between Spur Gear Teeth using Multi-point Thin-film Sensor. J. Eng. Digit. Technol. 2014, 2, 45–49. [Google Scholar] [CrossRef]
- Mihara, Y.; Ide, Y.; Owashi, M.; Someya, T. Measurement of Contact Pressure between Gear Teeth Using a Thin-Film Sensor. Trans. Jpn. Soc. Mech. Eng. 2011, 77, 3938–3950. [Google Scholar] [CrossRef][Green Version]
- Zhang, Y.; Cui, W.; Deng, J.; Liang, X.; Luo, X.; Wang, X. High Sensitivity Pressure Sensor Using Tandem Wheatstone Bridge for Low Pressures. IEEE Sens. J. 2024, 24, 9498–9505. [Google Scholar] [CrossRef]
- Gardner, E.L.W.; De Luca, A.; Philippe, J.; Dragomirescu, D.; Udrea, F. Thin-Film MOSFET-Based Pressure Sensor. IEEE Sens. Lett. 2019, 3, 1–4. [Google Scholar] [CrossRef]
- Song, L.M.; Qin, M.C.; Li, Z.Y.; Li, D.P. A non-contact gear measurement method based on laser vision. Optoelectron. Lett. 2014, 10, 237–240. [Google Scholar] [CrossRef]
- Bachus, K.N.; DeMarco, A.L.; Judd, K.T.; Horwitz, D.S.; Brodke, D.S. Measuring contact area, force, and pressure for bioengineering applications: Using Fuji Film and TekScan systems. Med. Eng. Phys. 2006, 28, 483–488. [Google Scholar] [CrossRef] [PubMed]
- Ng, T.W.; Yeong, W.K. Inexpensive color evaluation of dye-based pressure-sensitive films for plantar studies. J. Biomech. 2005, 38, 2130–2133. [Google Scholar] [CrossRef]
- Ueki, K.; Moroi, A.; Sotobori, M.; Ishihara, Y.; Marukawa, K.; Iguchi, R.; Kosaka, A.; Ikawa, H.; Nakazawa, R.; Higuchi, M. Evaluation of recovery in lip closing pressure and occlusal force and contact area after orthognathic surgery. J. Cranio-Maxillofac. Surg. 2014, 42, 1148–1153. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, Q.; Zheng, X.; An, N.; Zhou, M.; Niu, L.; Tay, F.R.; Chen, J.; Wang, F. Reliability and validity of two computerised occlusion analysis systems. J. Dent. 2022, 118, 104051. [Google Scholar] [CrossRef] [PubMed]
- Carassiti, M.; Zanzonico, R.; Cecchini, S.; Silvestri, S.; Cataldo, R.; Agro, F.E. Force and pressure distribution using Macintosh and GlideScope laryngoscopes in normal and difficult airways: A manikin study. Br. J. Anaesth. 2012, 108, 146–151. [Google Scholar] [CrossRef]
- Liau, J.-J.; Cheng, C.-K.; Huang, C.-H.; Lo, W.-H. Effect of Fuji pressure sensitive film on actual contact characteristics of artificial tibiofemoral joint. Clin. Biomech. 2002, 17, 698–704. [Google Scholar] [CrossRef]
- Dörner, F.; Körblein, C.; Schindler, C. On the accuracy of the pressure measurement film in Hertzian contact situations similar to wheel-rail contact applications. Wear 2014, 317, 241–245. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, X.; Cai, Y.; Chen, H.; Han, B. Measurement of gas pressure distribution in aerostatic thrust bearings using pressure-sensitive film. Tribol. Int. 2018, 120, 9–15. [Google Scholar] [CrossRef]
- Jin, Y.; Chen, L.; Cheng, C. Thermal behavior of friction discs in dry clutches based on a non-uniform pressure model. Case Stud. Therm. Eng. 2022, 32, 101895. [Google Scholar] [CrossRef]
- Jia, F.; Tian, X.; Zhang, G.; Chen, M.; Ye, J.; Yang, C. Thermal and mechanical investigation of proton exchange membrane fuel cells under combined loading conditions. Appl. Therm. Eng. 2024, 241, 122448. [Google Scholar] [CrossRef]
- Li, Y.; Cui, Y.; Gan, Y.; Zhang, Q. Investigation of the real contact area of tensile fractures with different normal stresses and sizes by using pressure-sensitive films. Eng. Geol. 2023, 314, 107010. [Google Scholar] [CrossRef]
- Gong, G.; Xiong, F.; Shen, L.; Zhang, G.; Cheng, Y.; Tang, Z.C. Fractal contact and asperities coalescence of rock joints under normal loading: Insights from pressure-sensitive film measurement. Int. J. Rock Mech. Min. Sci. 2024, 183, 105908. [Google Scholar] [CrossRef]
- Available online: https://www.fujifilm.com/pl/pl/business/inspection/measurement-film/prescale (accessed on 12 March 2025).
- Wang, T.-M.; Chang, Y.-H.; Yang, T.-C.; Lin, L.-D. Effect of scan delay on measurements of an occlusal pressure sensitive film: An in-vitro study. J. Dent. Sci. 2022, 17, 30–34. [Google Scholar] [CrossRef]
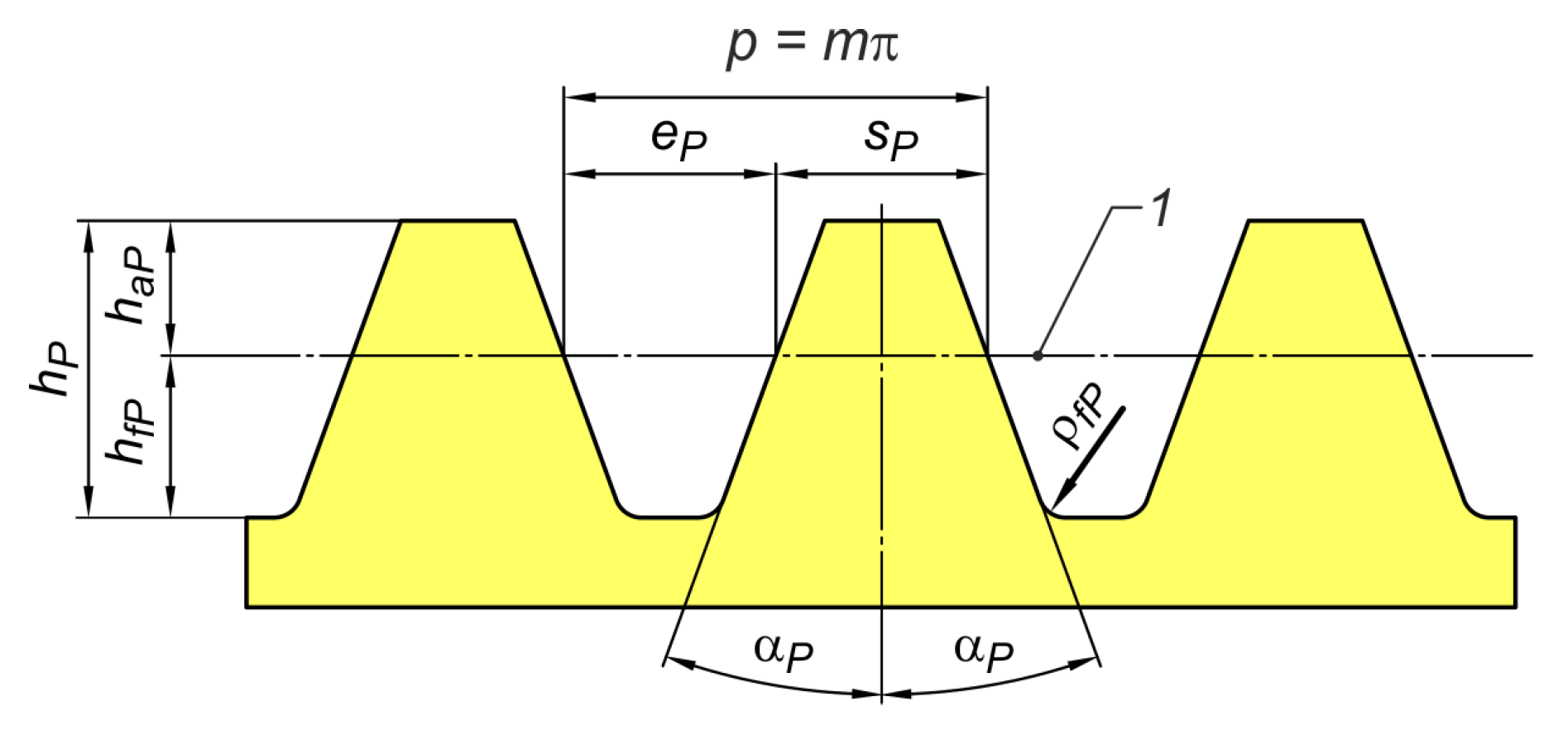
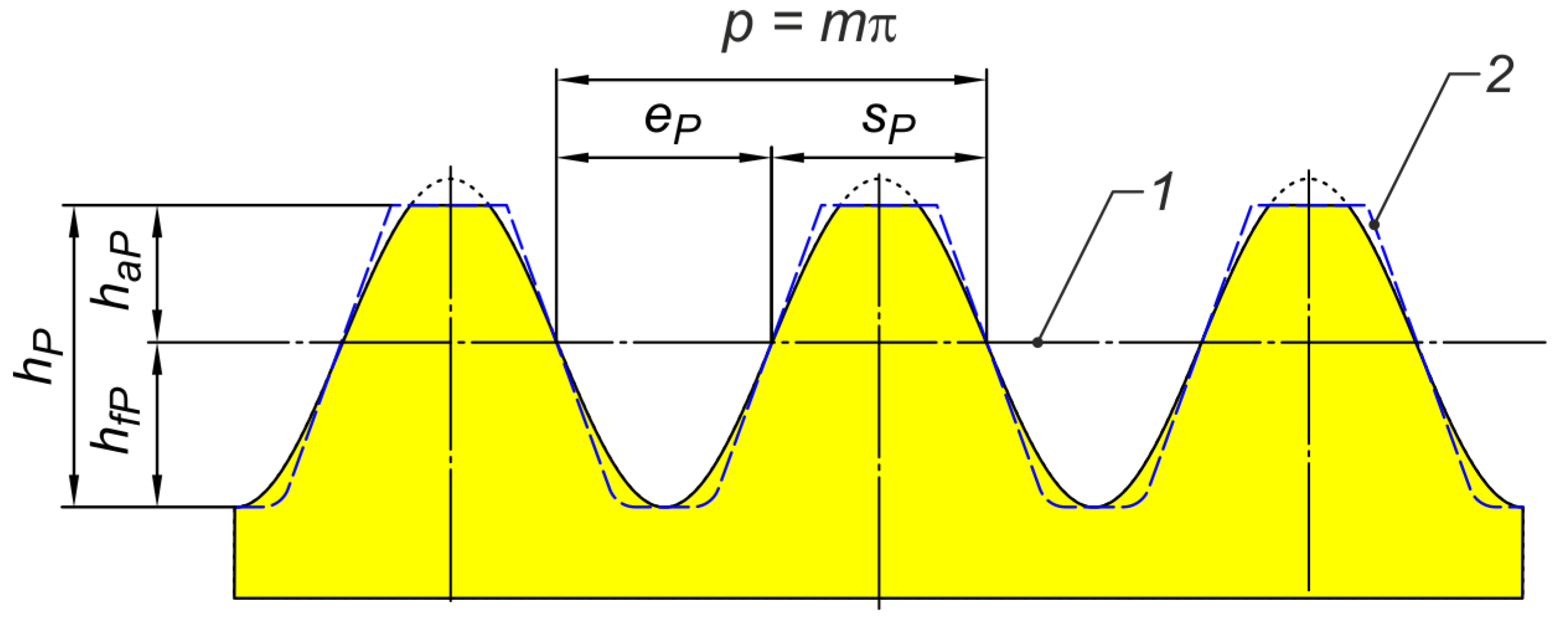
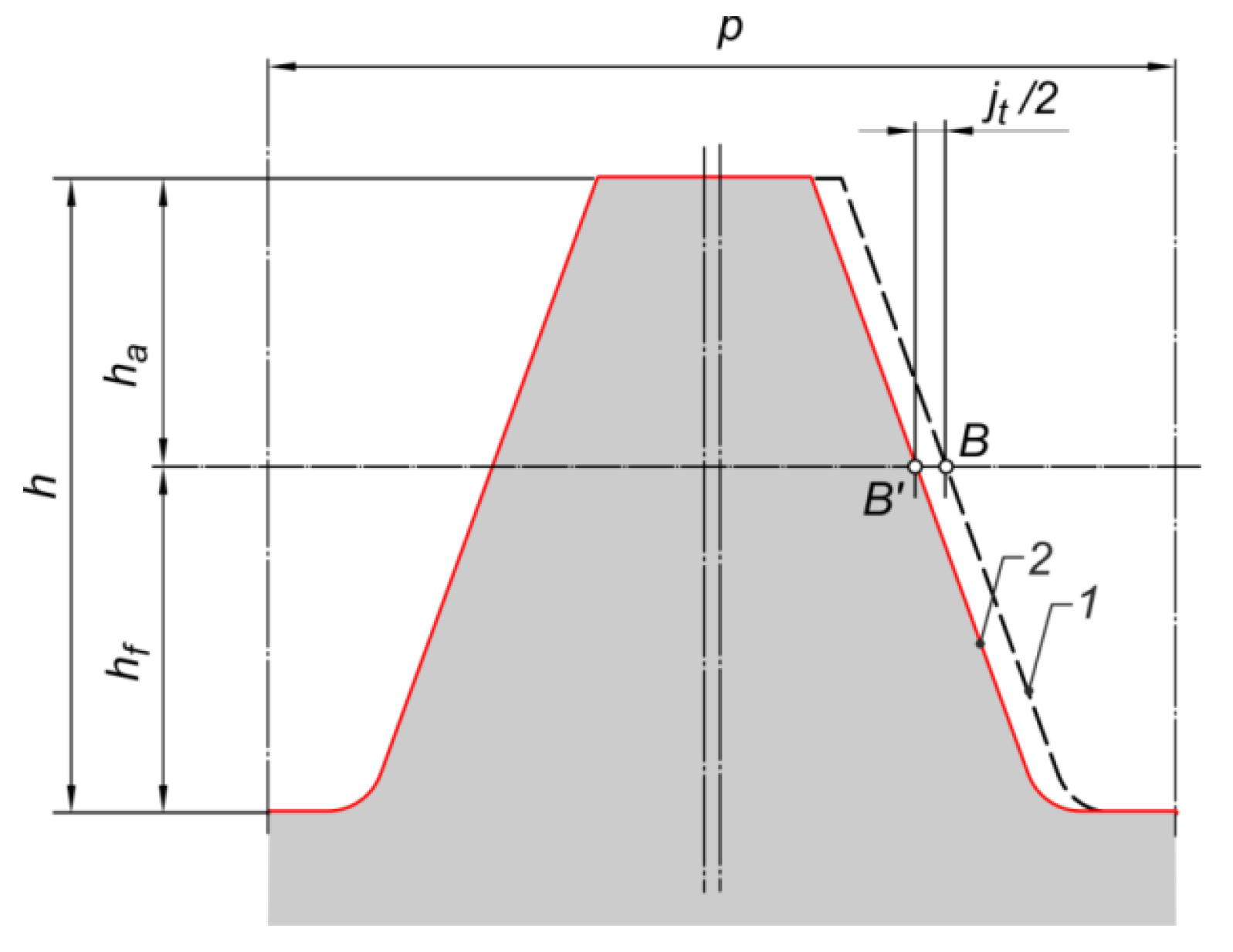
- ISO 53; Cylindrical Gears for General and Heavy Engineering—Standard Basic Rack Tooth Profile. IOS: Geneva, Switzerland, 1998.
- ISO-21771-1; Cylindrical Involute Gears and Gear Pairs: Concepts and Geometry. IOS: Geneva, Switzerland, 2024.
- Sobolak, M. Analiza I Synteza Współpracy Powierzchni Kół Zębatych Metodami Dyskretnymi; Oficyna Wydawnicza Politechniki Rzeszowskiej: Rzeszów, Poland, 2006. [Google Scholar]
- Sanchez-Marin, F.; Iserte, J.L.; Roda-Casanova, V. Numerical tooth contact analysis of gear transmissions through the discretization and adaptive refinement of the contact surfaces. Mech. Mach. Theory 2016, 101, 75–94. [Google Scholar] [CrossRef]
- Ai, Y.; Ye, C.; Liu, J.; Zhou, M. Study on the Evolution Processes of Keyhole and Melt Pool in Different Laser Welding Methods for Dissimilar Materials Based on a Novel Numerical Model. Int. Commun. Heat Mass Transf. 2025, 163, 108629. [Google Scholar] [CrossRef]
- Available online: https://www.sensorprod.com/surface-profiler-film/ (accessed on 12 March 2025).
- Available online: https://www.stratasys.com (accessed on 12 March 2025).
- Batsch, M. Spur gear teeth profile optimization through tensor-based kinematics: Integrating the Reuleaux method with differential evolution. Meccanica 2025, 60, 1053–1077. [Google Scholar] [CrossRef]
- Oishi, A.; Yagawa, G. A surface-to-surface contact search method enhanced by deep learning. Comput. Mech. 2020, 65, 1125–1147. [Google Scholar] [CrossRef]





















| Parameter | Pinion | Gear |
|---|---|---|
| Normal module | ||
| Number of teeth | ||
| Normal pressure angle | ||
| Helix angle | ||
| Face width | ||
| Center distance | ||
| Addendum | ||
| Dedendum | ||
| Circumferential clearance | ||
| Manufacturer’s Label | Value |
|---|---|
| Measurement Range | 0.5–2.5 MPa |
| Operating Temperature | 20–35 °C |
| Humidity Range | 35–80% RH |
| Accuracy | ±10% or less (measured with a densitometer at 23 °C, 65% RH) |
| Type | Two-sheet type |
| Manufacturer’s Label | Value |
|---|---|
| Measurement Range | 350–1400 (2.413–9.652 MPa) |
| Operating Temperature | 5–35 °C (41–95 °F) |
| Humidity Range | 10–90 %RH |
| Gauge (Thickness) | 0.19 mm (7.5 mils) |
| Spatial Resolution | 2.6 µm |
| Accuracy | ±10% |
| Shelf Life | 1 Year |
| Type | Two-sheet type |
| Parameter | Value |
|---|---|
| Modulus of elasticity | 2000 |
| Ultimate tensile strength | 50 |
| Density | 1.185 |
| Elongation at break | 15 |
| Hardness Shore D | 8–3 |
| Sample | Sensitivity [b] | Measured Contact Area |
|---|---|---|
| 01Y-104_ | 75 | 4.6705 |
| 110 | 80.5524 | |
| 140 | 108.3979 | |
| 170 | 143.6273 | |
| 01YR-104_ | 49 | 4.0307 |
| 50 | 11.8465 | |
| 51 | 82.4432 | |
| 52 | 441.3161 | |
| 01YG-104_ | 17 | 3.5360 |
| 50 | 88.2213 | |
| 75 | 115.5703 | |
| 96 | 144.1291 | |
| 01YB-104_ | 7 | 1.8173 |
| 11 | 67.9515 | |
| 15 | 99.2290 | |
| 19 | 136.9549 |
| Sample | Sensitivity [b] | Measured Contact Area |
|---|---|---|
| 02Y-104_ | 140 | 7.3875 |
| 160 | 22.8201 | |
| 180 | 42.6921 | |
| 200 | 75.7529 | |
| 02YR-104_ | 56 | 5.8515 |
| 57 | 9.7066 | |
| 59 | 26.3149 | |
| 60 | 88.9866 | |
| 02YG-104_ | 60 | 5.7261 |
| 80 | 34.4761 | |
| 100 | 50.3825 | |
| 114 | 76.7530 | |
| 02YG-104_ | 20 | 6.9287 |
| 22 | 31.9156 | |
| 23 | 56.0351 | |
| 24 | 849.8260 |
| CAD Method | FEM Method | Experimental Method |
|---|---|---|
 Contact pattern area |  Contact pattern area | FujiFilm LLW Sample 01Y-140_ (at sensitivity 170 b)  Contact pattern area Sensorprod SPF-D  Sample 02Y-140_ (at sensitivity 200 b)  Contact pattern area |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fudali, P.; Jagiełowicz, P.E.; Kalina, A.; Połowniak, P.; Sobolak, M.; Witkowski, W. A Novel Method for Determining the Contact Pattern Area in Gear Meshing Based on Computer Processing of Pressure Measurement Film Images. Materials 2025, 18, 3230. https://doi.org/10.3390/ma18143230
Fudali P, Jagiełowicz PE, Kalina A, Połowniak P, Sobolak M, Witkowski W. A Novel Method for Determining the Contact Pattern Area in Gear Meshing Based on Computer Processing of Pressure Measurement Film Images. Materials. 2025; 18(14):3230. https://doi.org/10.3390/ma18143230
Chicago/Turabian StyleFudali, Paweł, Patrycja Ewa Jagiełowicz, Adam Kalina, Piotr Połowniak, Mariusz Sobolak, and Waldemar Witkowski. 2025. "A Novel Method for Determining the Contact Pattern Area in Gear Meshing Based on Computer Processing of Pressure Measurement Film Images" Materials 18, no. 14: 3230. https://doi.org/10.3390/ma18143230
APA StyleFudali, P., Jagiełowicz, P. E., Kalina, A., Połowniak, P., Sobolak, M., & Witkowski, W. (2025). A Novel Method for Determining the Contact Pattern Area in Gear Meshing Based on Computer Processing of Pressure Measurement Film Images. Materials, 18(14), 3230. https://doi.org/10.3390/ma18143230








