Deposition of Mesoporous Silicon Dioxide Films Using Microwave PECVD
Abstract
1. Introduction
2. Materials and Methods
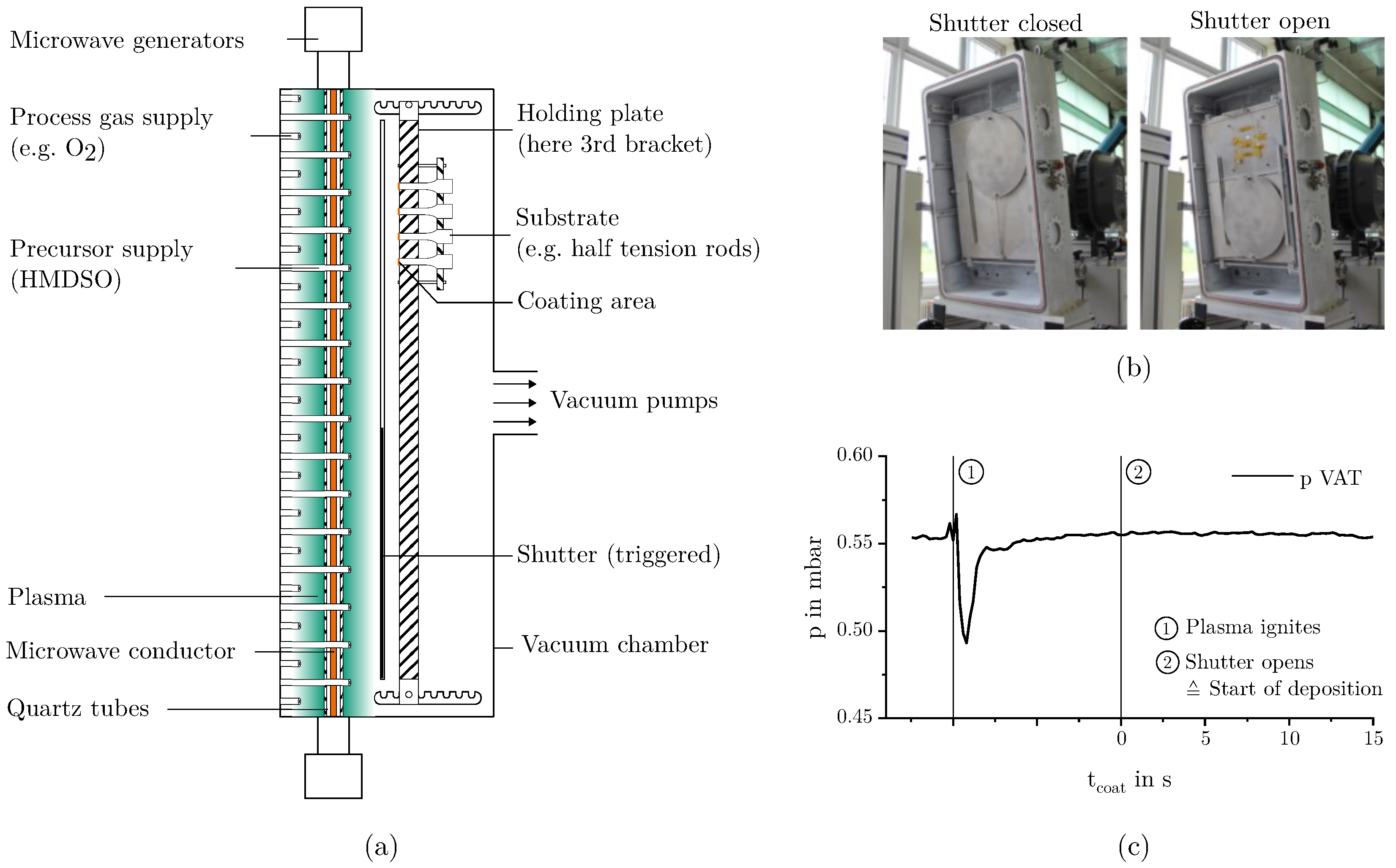
2.1. Deposition of the Mesoporous Silicon Dioxide Films
2.2. Parameter Selection and Experimental Design
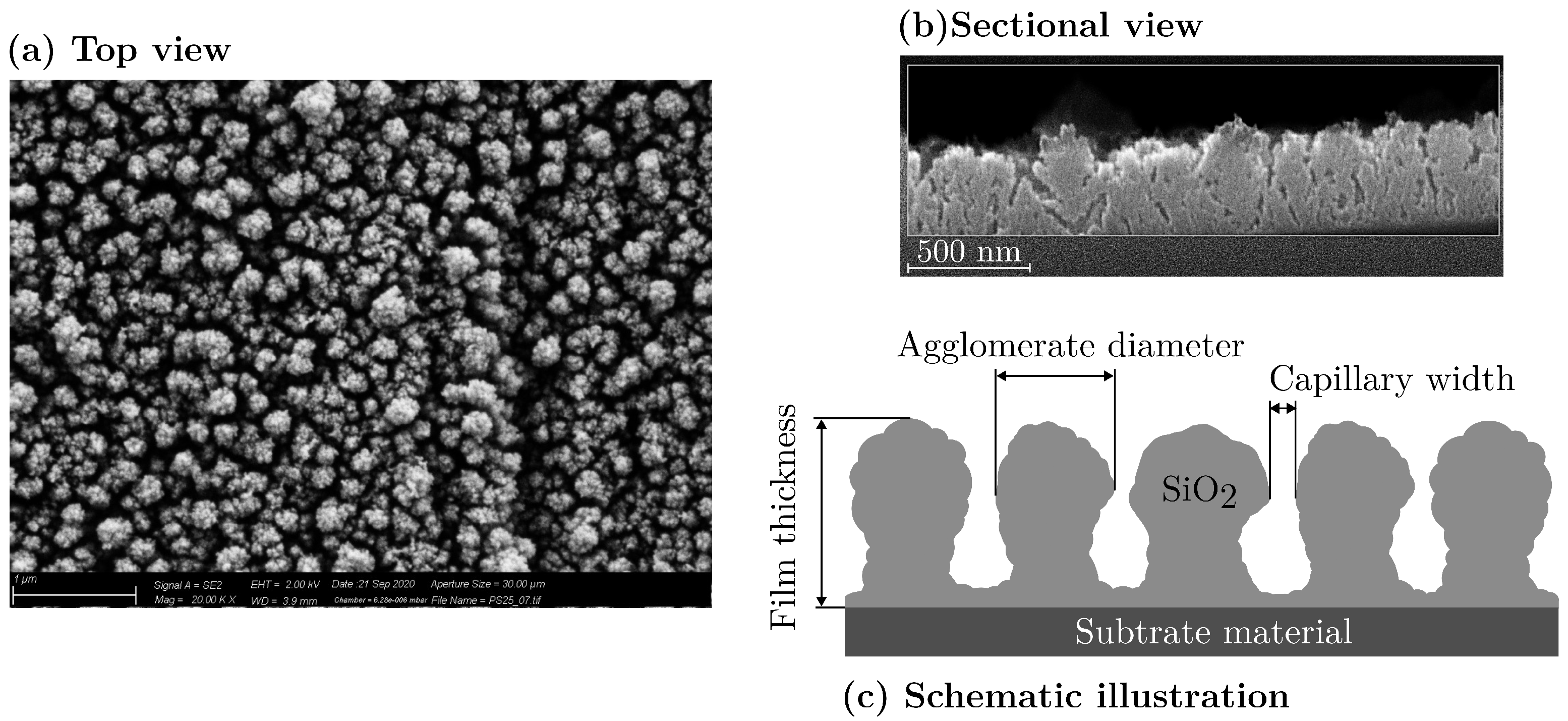
2.3. Characterization of the Deposited Film Morphology
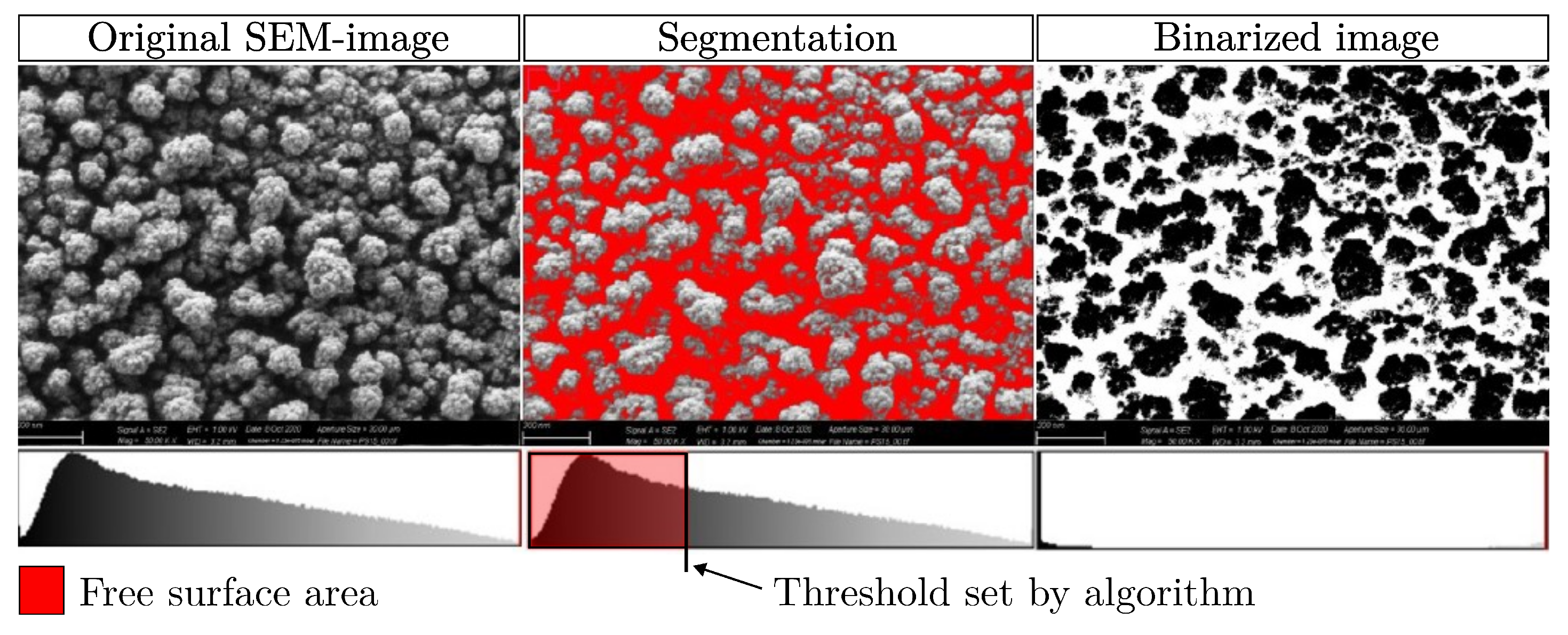
2.3.1. Free Surface Area
2.3.2. Mean Agglomerate Diameter
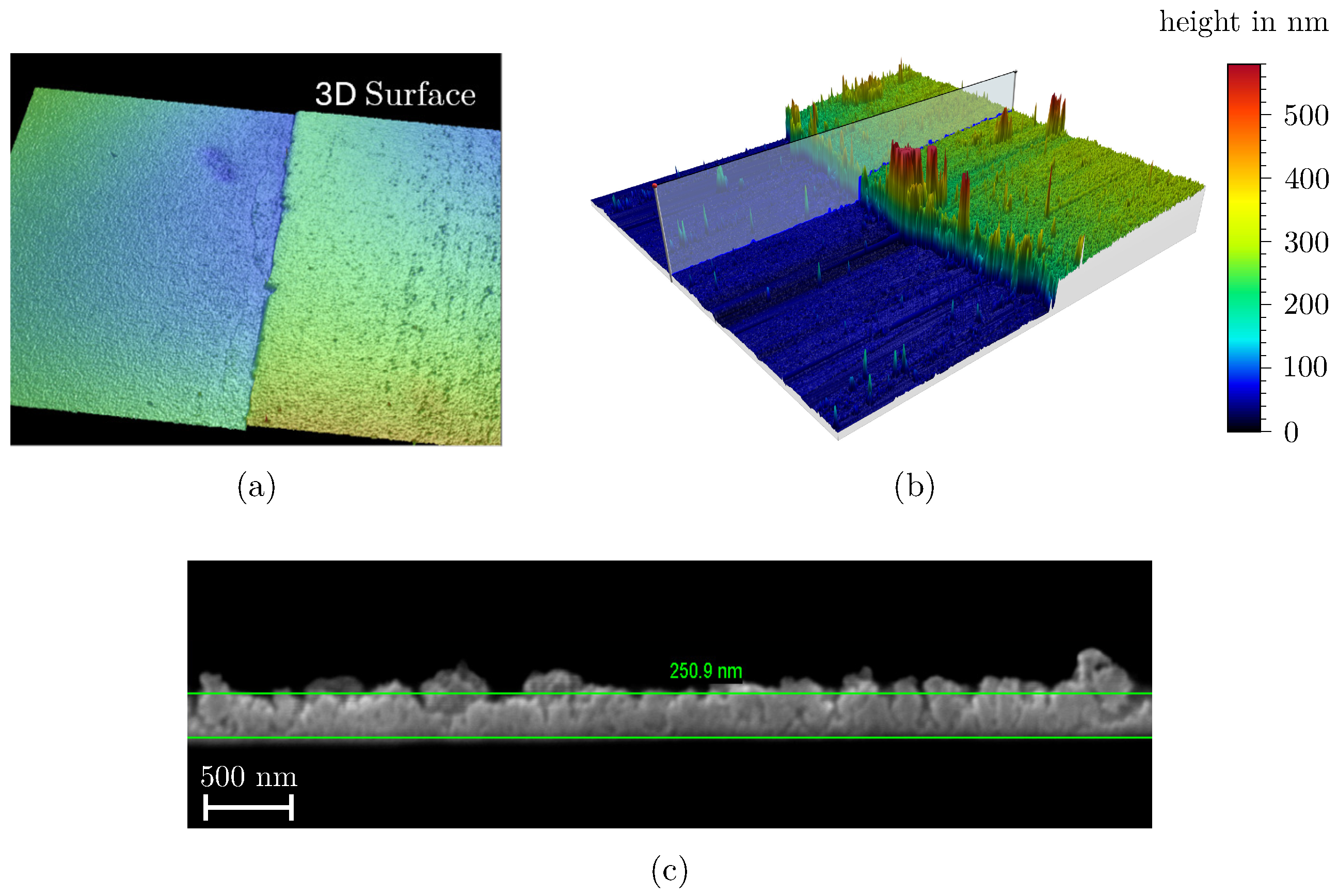
2.3.3. Film Thickness
2.3.4. Mechanical Testing of the Interfacial Tensile Strength
3. Results
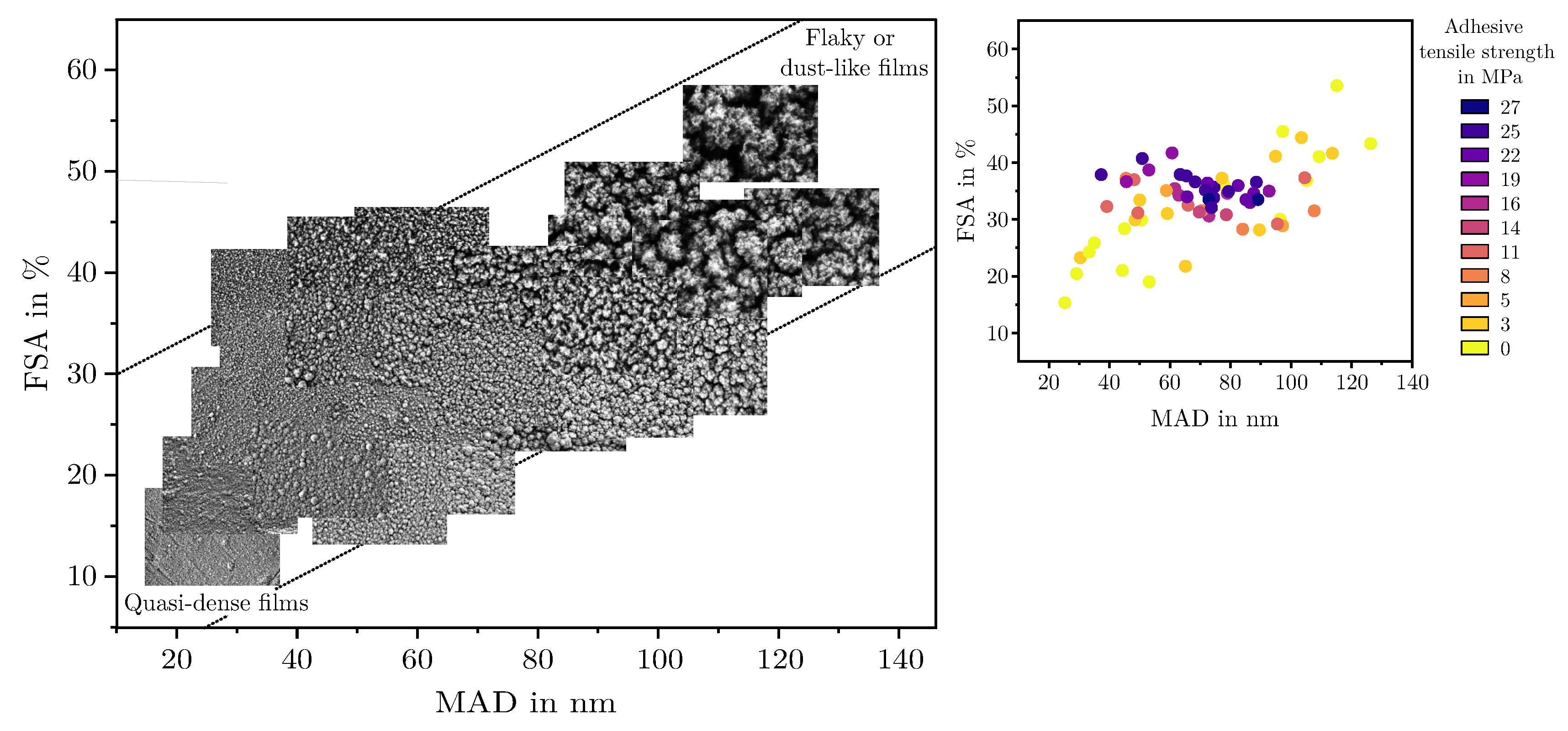
- Quasi-dense films are characterized by a combination of a low MAD, typically below 30 nm, and a FSA of less than 20%. Figure 7a shows a film in the transition region between quasi-dense and mesoporous morphologies. Due to the extremely narrow capillaries between the agglomerates, the structure exhibits a minimal permeability for the polymer melt. Figure 7b illustrates the characteristic fracture pattern of a quasi-dense film. The polymer melt did not infiltrate the porous structure. The image was captured after mechanical testing and reveals that if infiltration occurred at all, it was limited to isolated regions with slightly wider capillaries. On the polymer side of the fracture surface, shown in Figure 7c, it is apparent that the polymer melt spreads only across the surface without penetrating the pore network through capillary action. The interface failed adhesively at the SiO2–polymer boundary, resulting in negligible interfacial strength. The deposition of similar quasi-dense films using microwave plasma-enhanced chemical vapor deposition (PECVD) was first reported by Dreher et al. in 2009 [47]. Subsequent studies by Laux et al. [23] confirmed that such films are not well suited as adhesion-promoting interlayers, particularly in polymer–metal hybrid systems fabricated by injection molding, presumably due to their low porosity and inter-columnar spacing.
- Mesoporous adhesion films exhibit intermediate morphological characteristics with MAD values typically ranging from 30 to 90 nm and the FSA between 25% and 45%. An example of such a mesoporous film is shown in Figure 7d. These structures possess an open-pore network that allows infiltration of the polymer melt during overmolding, which could be also shown in previous studies [16,22,23]. As a result, mixed-mode fracture patterns are commonly observed as can be seen in Figure 7e,f. Depending on local variations in pore size and film thickness, both adhesive and cohesive failure mechanisms can be identified. Residual SiO2 material can be found on one or both sides of the fracture surface, indicating good interlocking at the interface which results in high interfacial adhesion strengths up to 30 MPa for an SiO2–PPS interface.
- Dust-like films, by contrast, typically exhibit MAD greater than 90 nm in combination with a high FSA, as exemplified in Figure 7g. These structures tend to form as flaky or loosely packed dust-like films, and this characteristic becomes more pronounced as both FSA and MAD increase. Due to the weak interconnection between individual agglomerates, these films are referred to as dust-like in the context of this study.When such films are overmolded during injection molding, the polymer melt infiltrates the porous structure. However, due to the low mechanical cohesion within the SiO2 structure, mainly caused by the weak interconnection between individual agglomerates, failure occurs cohesively within the film itself. This behavior is clearly visible in the fracture surfaces shown in Figure 7h,i, where significant residues of SiO2 agglomerates are present on both sides of the fracture interface.
3.1. Results of the Regression Analysis
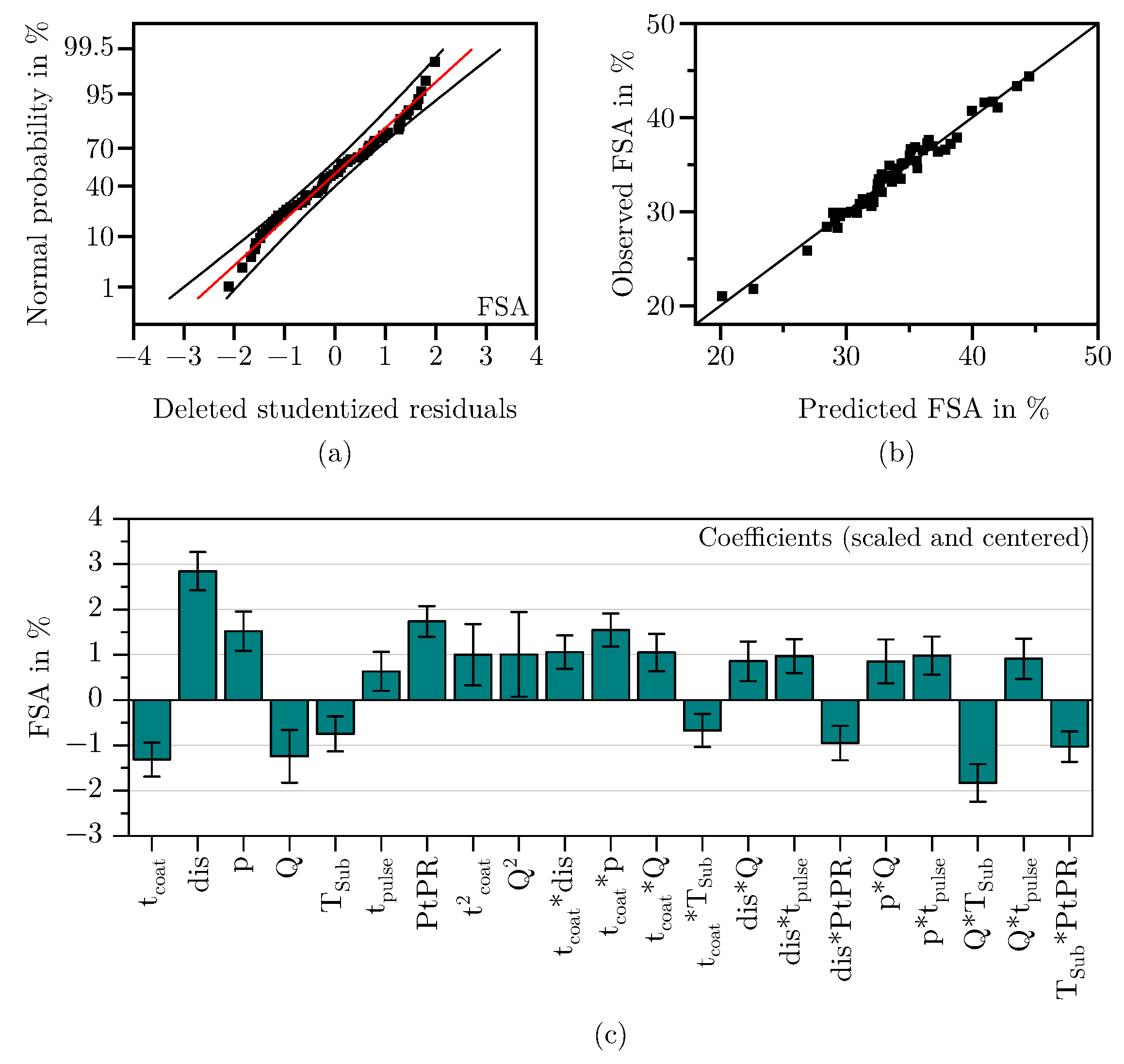
3.1.1. Free Surface Area
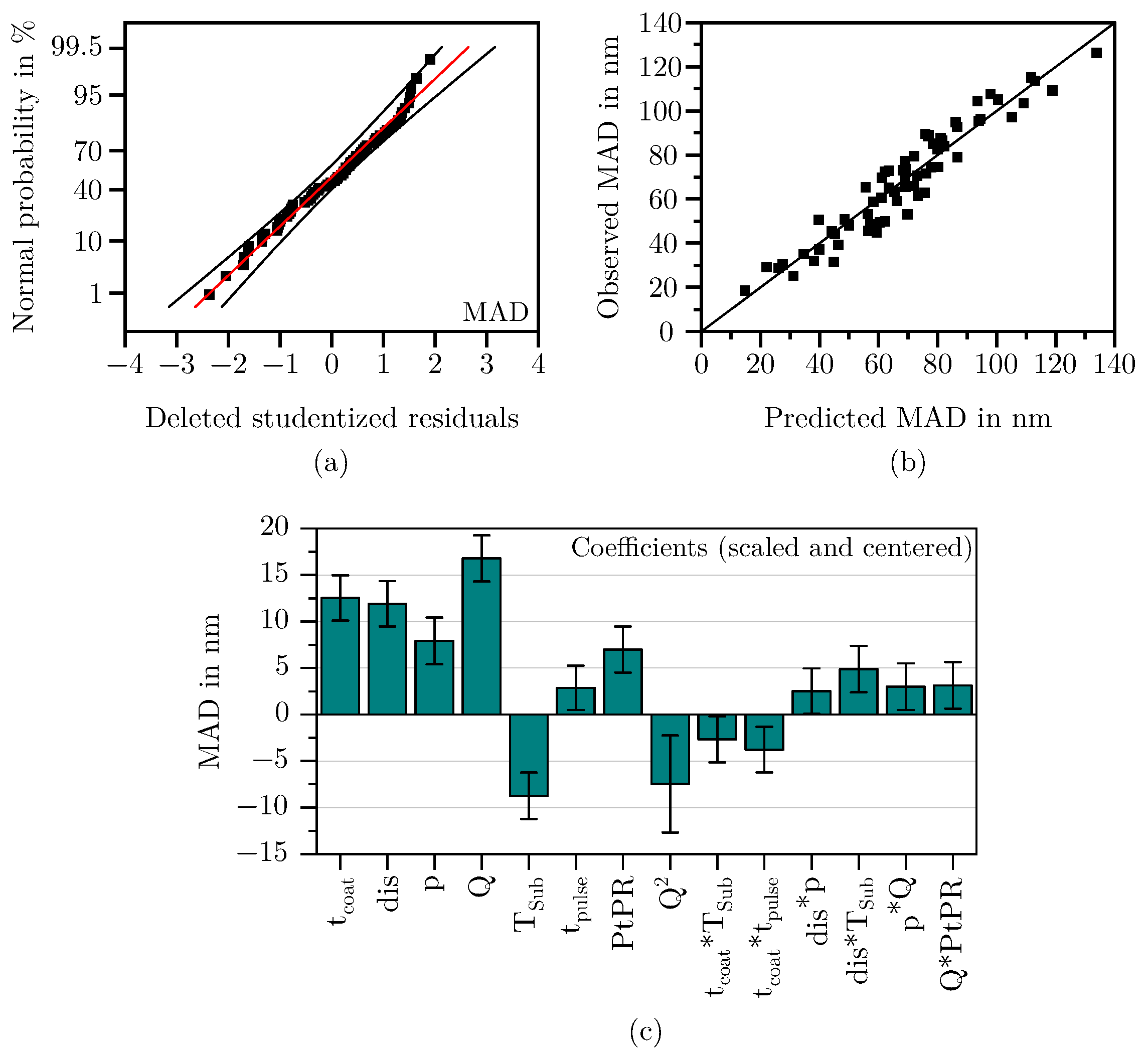
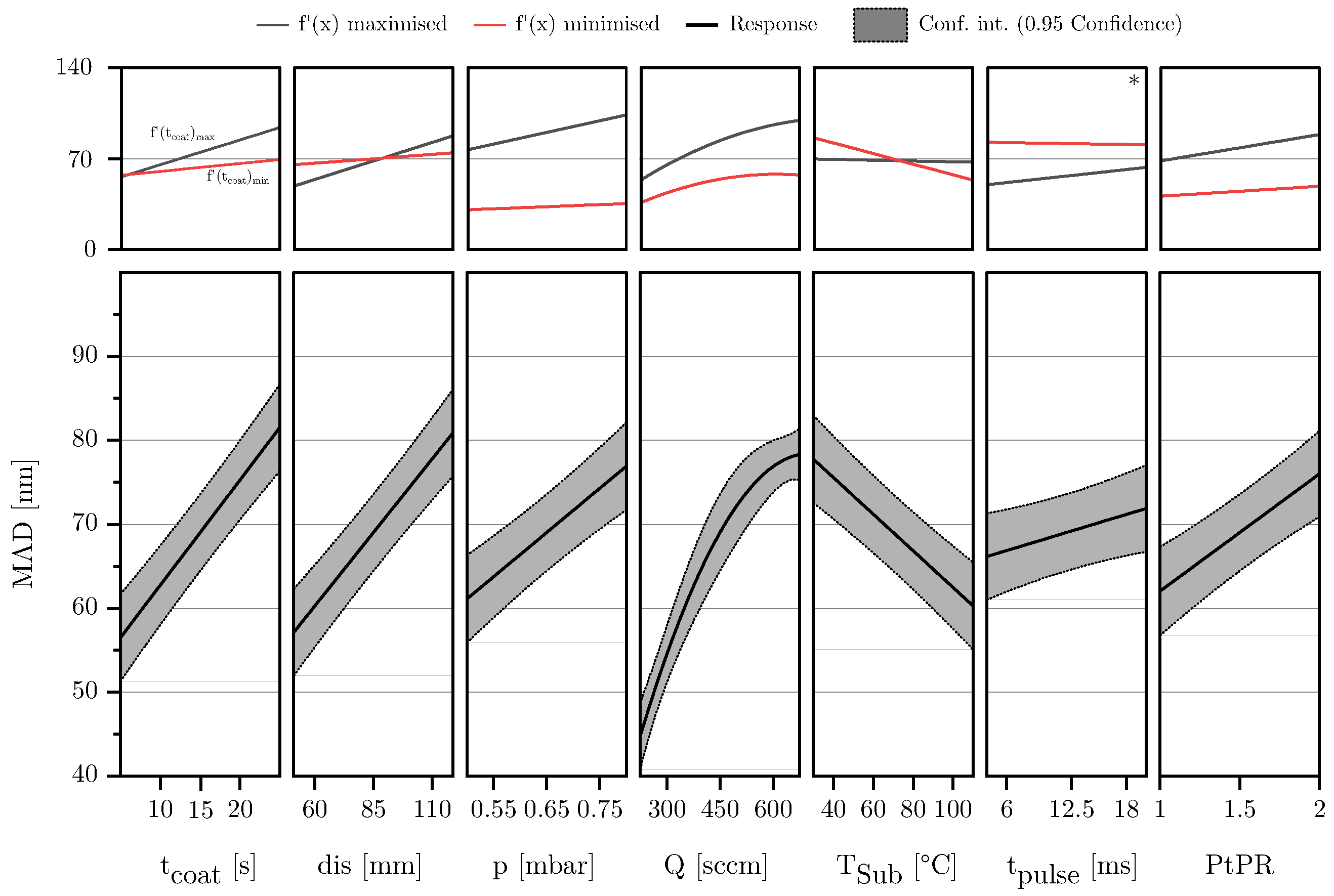
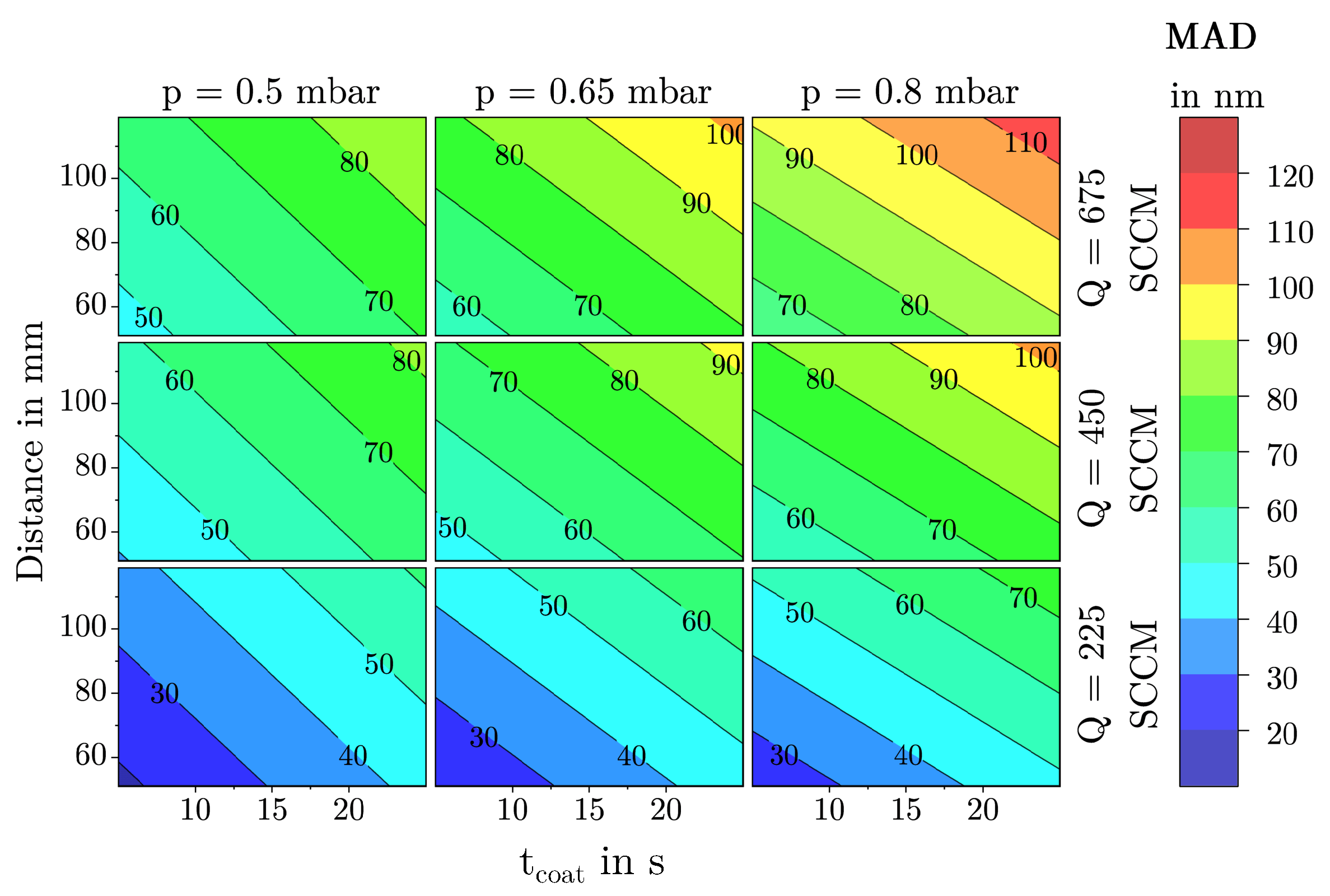
3.1.2. Mean Agglomerate Diameter
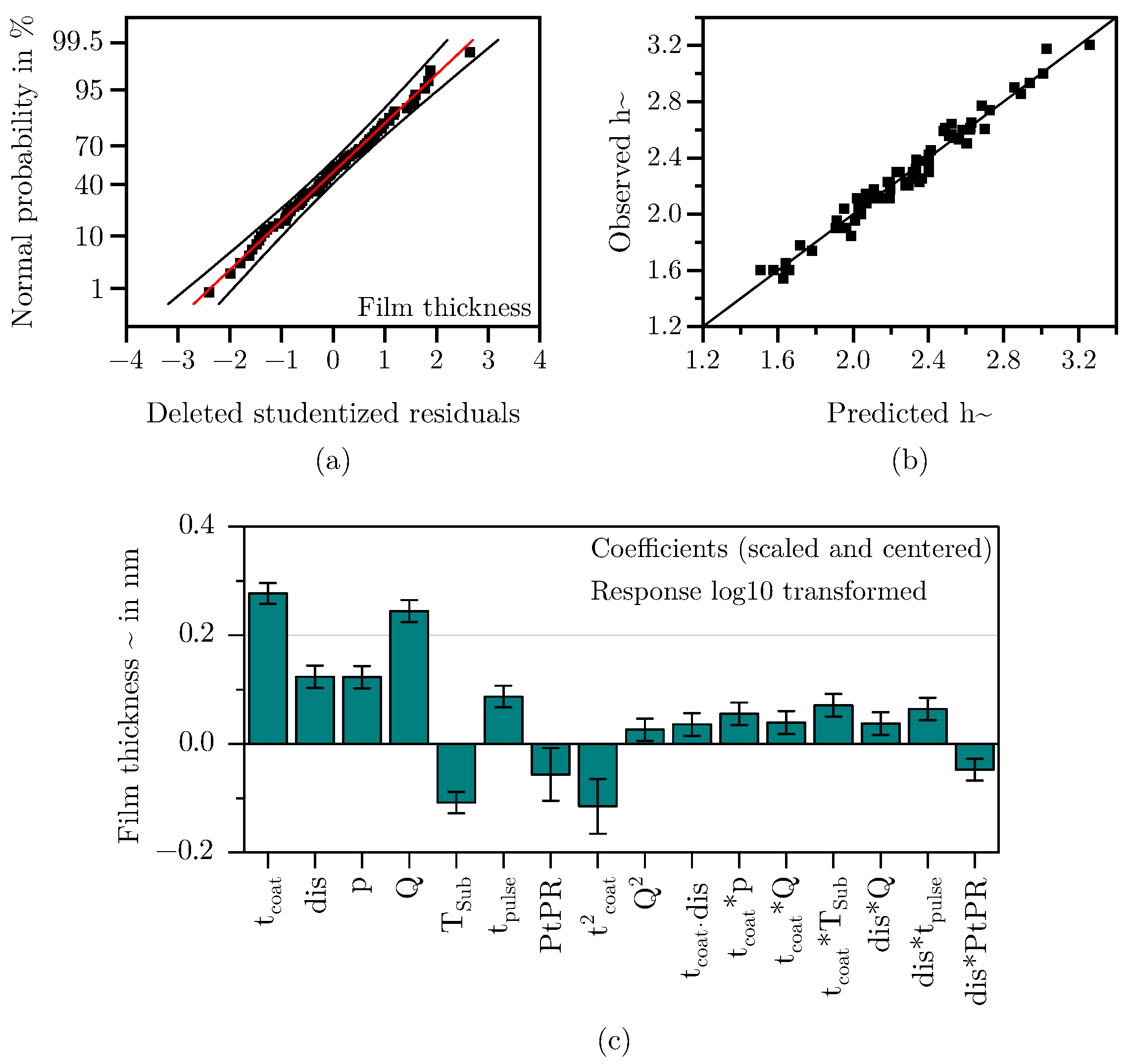
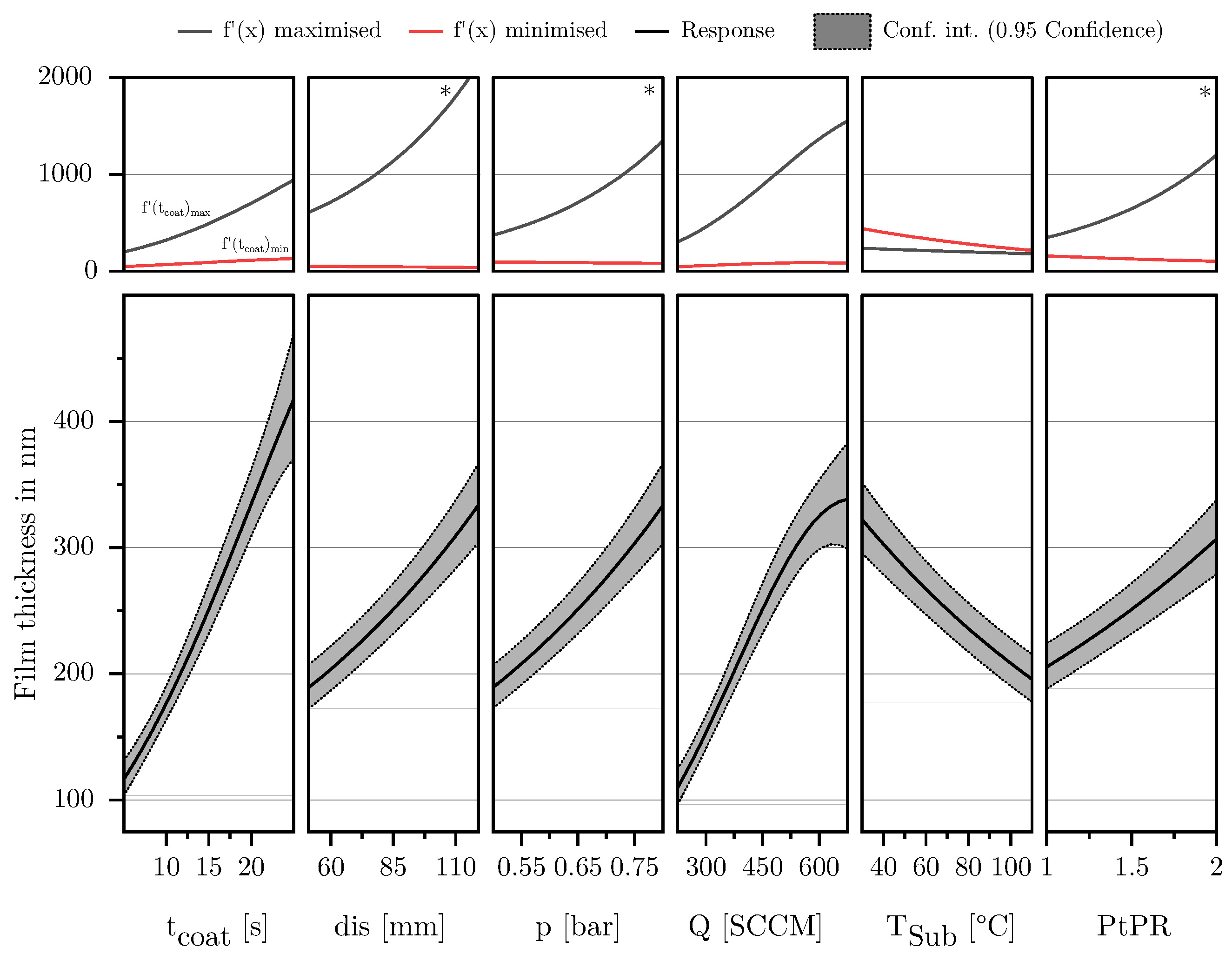
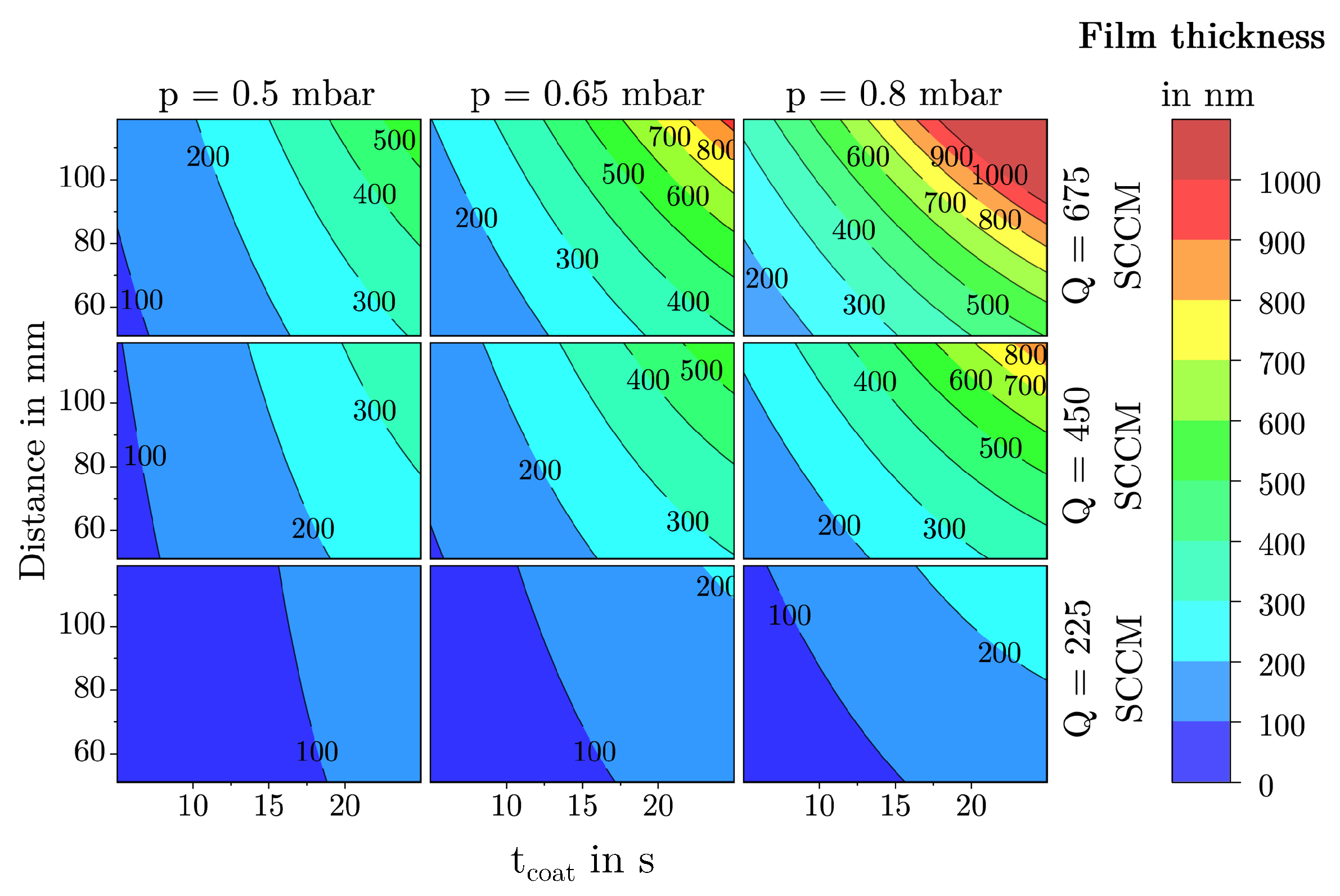
3.1.3. Film Thickness
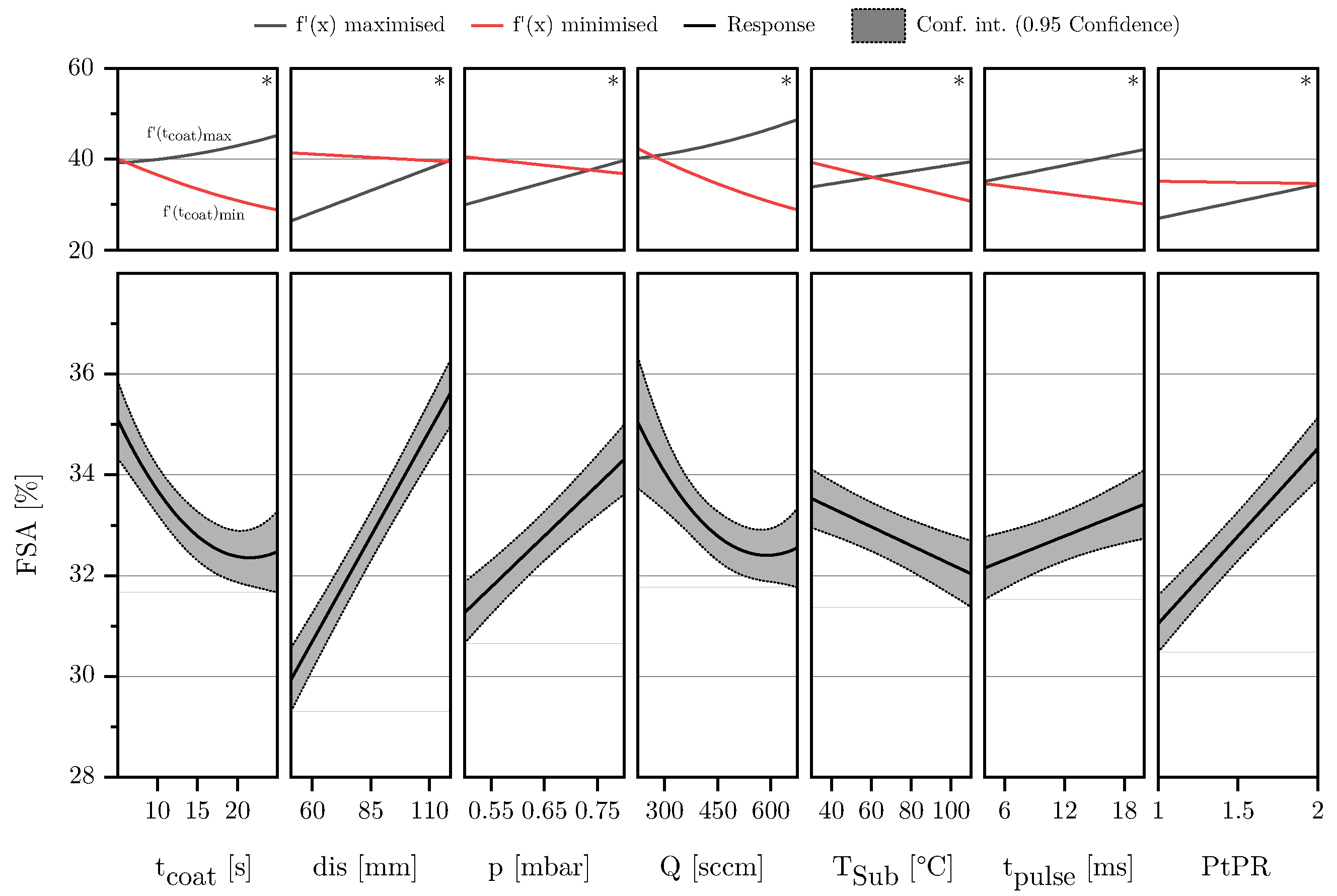
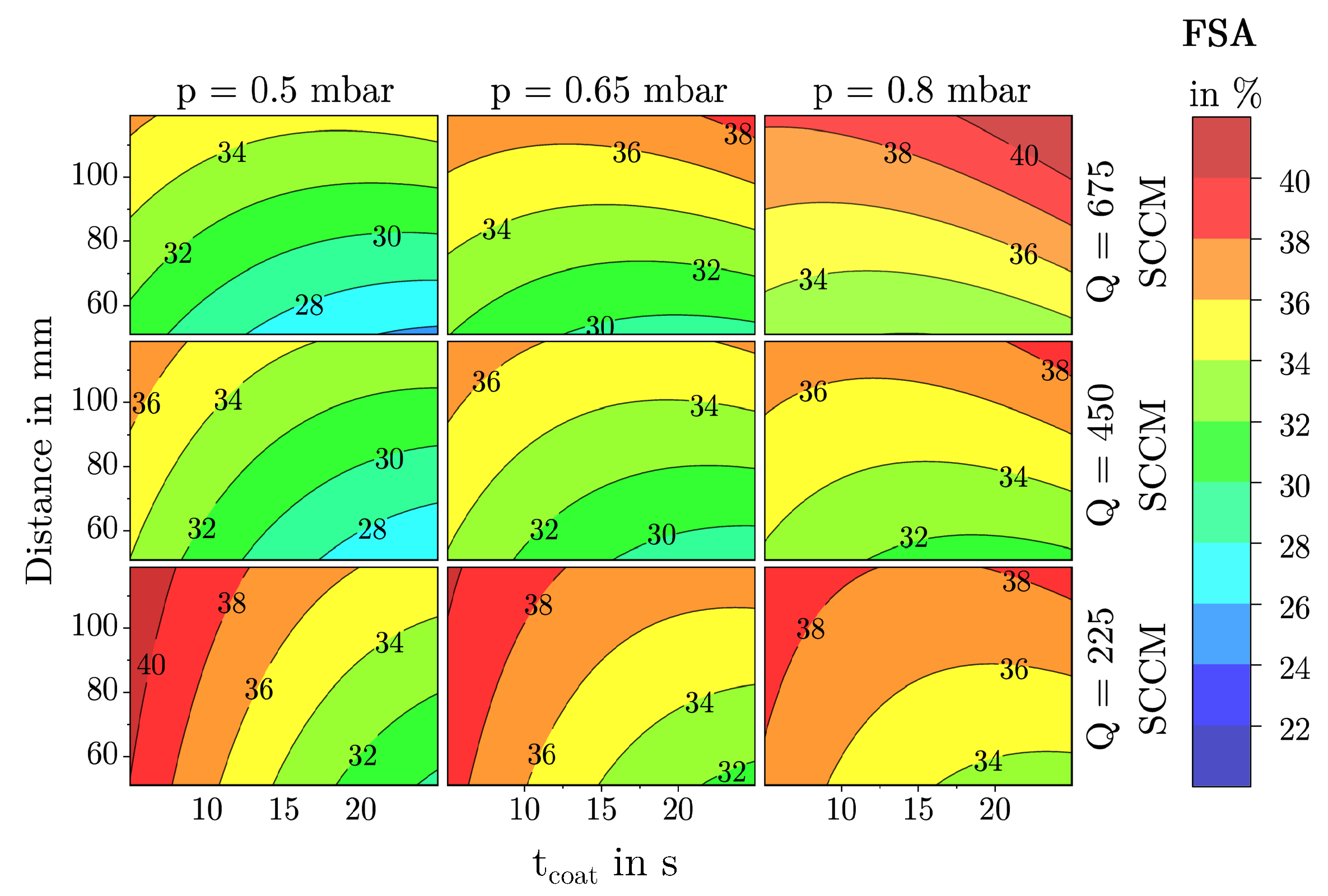
3.2. Description of Characteristic Model Areas Using 4D Contour Plots
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AFM | Atomic force microscopy |
| CCF | Face-centered central composite design |
| here: Distance between precursor feed and substrate | |
| FSA | Free surface area |
| h | Film thickness |
| HMDSO | Hexamethyldisiloxane |
| ICT | Fraunhofer Institute for Chemical Technology |
| MAD | Mean agglomerate diameter |
| MLR | Multiple linear regression |
| p | here: Array pressure |
| PECVD | Plasma-enhanced chemical vapor deposition |
| MPECVD | Microwave plasma-enhanced chemical vapor deposition |
| PID | Proportional–integral–derivative |
| Pause-to-pulse-ratio | |
| Q | Flow rate |
| Q2 | Predictive relevance |
| R | Dynamic range of standard deviation |
| R2 | Coefficient of Determination |
| SCCM | Standard cubic centimeters per minute |
| SED | Secondary electron detector |
| SEM | Scanning electron microscopy |
| SLPM | Standard liter per minute |
| Coating time | |
| Pulse time | |
| Substrate temperature |
References
- Hoshikawa, Y.; Yabe, H.; Nomura, A.; Yamaki, T.; Shimojima, A.; Okubo, T. Mesoporous Silica Nanoparticles with Remarkable Stability and Dispersibility for Antireflective Coatings. Chem. Mater. 2010, 22, 12–14. [Google Scholar] [CrossRef]
- Jin, B.; He, J.; Yao, L.; Zhang, Y.; Li, J. Rational Design and Construction of Well-Organized Macro-Mesoporous SiO2/TiO2 Nanostructure toward Robust High-Performance Self-Cleaning Antireflective Thin Films. ACS Appl. Mater. Interfaces 2017, 9, 17466–17475. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Du, X.; He, J. Self-cleaning antireflective coatings assembled from peculiar mesoporous silica nanoparticles. Langmuir ACS J. Surfaces Colloids 2010, 26, 13528–13534. [Google Scholar] [CrossRef] [PubMed]
- Mizoshita, N.; Ishii, M.; Kato, N.; Tanaka, H. Hierarchical Nanoporous Silica Films for Wear Resistant Antireflection Coatings. ACS Appl. Mater. Interfaces 2015, 7, 19424–19430. [Google Scholar] [CrossRef]
- Shang, Q.; Zhou, Y. Fabrication of transparent superhydrophobic porous silica coating for self-cleaning and anti-fogging. Ceram. Int. 2016, 42, 8706–8712. [Google Scholar] [CrossRef]
- Gomez-Vega, J.M.; Hozumi, A.; Saiz, E.; Tomsia, A.P.; Sugimura, H.; Takai, O. Bioactive glass-mesoporous silica coatings on Ti6Al4V through enameling and triblock-copolymer-templated sol-gel processing. J. Biomed. Mater. Res. 2001, 56, 382–389. [Google Scholar] [CrossRef]
- Gomez-Vega, J.; Iyoshi, M.; Kim, K.; Hozumi, A.; Sugimura, H.; Takai, O. Spin casted mesoporous silica coatings for medical applications. Thin Solid Film. 2001, 398-399, 615–620. [Google Scholar] [CrossRef]
- Aerts, C.A.; Verraedt, E.; Depla, A.; Follens, L.; Froyen, L.; van Humbeeck, J.; Augustijns, P.; van den Mooter, G.; Mellaerts, R.; Martens, J.A. Potential of amorphous microporous silica for ibuprofen controlled release. Int. J. Pharm. 2010, 397, 84–91. [Google Scholar] [CrossRef]
- Qian, K.K.; Bogner, R.H. Application of mesoporous silicon dioxide and silicate in oral amorphous drug delivery systems. J. Pharm. Sci. 2012, 101, 444–463. [Google Scholar] [CrossRef]
- Bearzotti, A.; Bertolo, J.M.; Innocenzi, P.; Falcaro, P.; Traversa, E. Humidity sensors based on mesoporous silica thin films synthesised by block copolymers. J. Eur. Ceram. Soc. 2004, 24, 1969–1972. [Google Scholar] [CrossRef]
- Innocenzi, P.; Martucci, A.; Guglielmi, M.; Bearzotti, A.; Traversa, E.; Pivin, J.C. Mesoporous silica thin films for alcohol sensors. J. Eur. Ceram. Soc. 2001, 21, 1985–1988. [Google Scholar] [CrossRef]
- Zhao, D.; Yang, P.; Melosh, N.; Feng, J.; Chmelka, B.F.; Stucky, G.D. Continuous Mesoporous Silica Films with Highly Ordered Large Pore Structures. Adv. Mater. 1998, 10, 1380–1385. [Google Scholar] [CrossRef]
- Li, Y.; Cai, W.; Cao, B.; Duan, G.; Sun, F.; Li, C.; Jia, L. Two-dimensional hierarchical porous silica film and its tunable superhydrophobicity. Nanotechnology 2006, 17, 238–243. [Google Scholar] [CrossRef]
- Du, X.; Li, X.; He, J. Facile fabrication of hierarchically structured silica coatings from hierarchically mesoporous silica nanoparticles and their excellent superhydrophilicity and superhydrophobicity. ACS Appl. Mater. Interfaces 2010, 2, 2365–2372. [Google Scholar] [CrossRef] [PubMed]
- Gomez-Vega, J.M.; Teshima, K.; Hozumi, A.; Sugimura, H.; Takai, O. Mesoporous silica thin films produced by calcination in oxygen plasma. Surface Coatings Technol. 2003, 169-170, 504–507. [Google Scholar] [CrossRef]
- Emmerich, R.; Dreher, R.; Urban, H.; Graf, M.; Bräuning; Rüdiger; Nauenburg, K.D. Nanoscale Surface Structure for Improving Adhesion. International Patent Application No. PCT/EP2012/072447, 23 May 2013. [Google Scholar]
- Kaiser, M.; Baumgärtner, K.M.; Mattheus, A. Microwave Plasma Sources—Applications in Industry. Contrib. Plasma Phys. 2012, 52, 629–635. [Google Scholar] [CrossRef]
- Liehr, M.; Dieguez-Campo, M. Microwave PECVD for large area coating. Surf. Coatings Technol. 2005, 200, 21–25. [Google Scholar] [CrossRef]
- Wertheimer, M.R.; Moisan, M. Comparison of microwave and lower frequency plasmas for thin film deposition and etching. J. Vac. Sci. Technol. A Vac. Surfaces Film. 1985, 3, 2643–2649. [Google Scholar] [CrossRef]
- Zhao, Y.; Huang, C.; Huang, X.; Huang, H.; Zhao, H.; Wang, S.; Liu, S. Effectiveness of PECVD deposited nano-silicon oxide protective layer for polylactic acid film: Barrier and surface properties. Food Packag. Shelf Life 2020, 25, 100513. [Google Scholar] [CrossRef]
- Walker, M.; Baumgärtner, K.M.; Feichtinger, J.; Kaiser, M.; Schulz, A.; Räuchle, E. Silicon oxide films from the Plasmodul®. Vacuum 2000, 57, 387–397. [Google Scholar] [CrossRef]
- Laux, M.; Beck, B.; Emmerich, R.; Dreher, R.; Henning, F. The effect of an nanoscale surface structure on the interfacial strength of injection molded PPS-metal hybrids. In Proceedings of the The Korean Society for Composite Materials, Spring Conference, Jeju, Republic of Korea, 27–28 April 2017. [Google Scholar]
- Laux, M.; Löhr, Y.; Dreher, R.; Emmerich, R.; Henning, F. Influence of the morphology of nanoporous silicon dioxide based surface coatings on the interfacial strength of injection-moulded polymer-metal hybrids. In Proceedings of the 4th International Conference Hybrid 2020 Materials and Structures, Online, Germany, 28–29 April 2020; pp. 200–205. [Google Scholar]
- ISO 3669:2020; Vacuum Technology—Dimensions of Knife-Edge Flanges. International Organization for Standardization: Geneva, Switzerland, 2020.
- ISO 8037-1:1986; Optics and Optical Instruments—Microscopes—Slides—Part 1: Dimensions, Optical Properties and Marking. International Organization for Standardization: Geneva, Switzerland, 1986.
- He, Z.; Liu, C.; Gao, J.; Li, Z.; Xu, K.; Zhuang, S. Revealing the mechanism of interfacial adhesion enhancement between the SiO2 film and the GaAs substrate via plasma pre-treatments. J. Vac. Sci. Technol. A Vac. Surfaces Film. 2024, 42, 023113. [Google Scholar] [CrossRef]
- do Nascimento, F.; Parada, S.; Moshkalev, S.; Machida, M. Plasma treatment of poly(dimethylsiloxane) surfaces using a compact atmospheric pressure dielectric barrier discharge device for adhesion improvement. Jpn. J. Appl. Phys. 2016, 55, 021602. [Google Scholar] [CrossRef]
- Siebertz, K.; van Bebber, D.; Hochkirchen, T. Statistische Versuchsplanung; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Messier, R.; Giri, A.P.; Roy, R.A. Revised structure zone model for thin film physical structure. J. Vac. Sci. Technol. A Vac. Surfaces Film. 1984, 2, 500–503. [Google Scholar] [CrossRef]
- ZHOU, J.; XU, W.; CHEN, T. An investigation on improving the homogeneity of plasma generated by linear microwave plasma source with a length of 1550 mm. Plasma Sci. Technol. 2021, 23, 025401. [Google Scholar] [CrossRef]
- Carbone, E.; Sadeghi, N.; Vos, E.; Hübner, S.; van Veldhuizen, E.; van Dijk, J.; Nijdam, S.; Kroesen, G. Spatio-temporal dynamics of a pulsed microwave argon plasma: Ignition and afterglow. Plasma Sources Sci. Technol. 2015, 24, 015015. [Google Scholar] [CrossRef]
- Sutter, J.M.; Kalivas, J.H. Comparison of Forward Selection, Backward Elimination, and Generalized Simulated Annealing for Variable Selection. Microchem. J. 1993, 47, 60–66. [Google Scholar] [CrossRef]
- Pires, J.; Martins, F.G.; Sousa, S.; Alvim-Ferraz, M.; Pereira, M.C. Selection and validation of parameters in multiple linear and principal component regressions. Environ. Model. Softw. 2008, 23, 50–55. [Google Scholar] [CrossRef]
- Dunkler, D.; Plischke, M.; Leffondré, K.; Heinze, G. Augmented backward elimination: A pragmatic and purposeful way to develop statistical models. PLoS ONE 2014, 9, e113677. [Google Scholar] [CrossRef]
- Eriksson, L. Multi- and Megavariate Data Analysis: Principles and Appliactions; Umetrics AB: Umea, Sweden, 2001. [Google Scholar]
- Zarraoa, L.; González, M.U.; Paulo, Á.S. Imaging low-dimensional nanostructures by very low voltage scanning electron microscopy: Ultra-shallow topography and depth-tunable material contrast. Sci. Rep. 2019, 9, 16263. [Google Scholar] [CrossRef]
- Joy, D.C.; Joy, C.S. Low voltage scanning electron microscopy. Micron 1996, 27, 247–263. [Google Scholar] [CrossRef]
- Anovitz, L.M.; Cole, D.R. Characterization and Analysis of Porosity and Pore Structures. Rev. Mineral. Geochem. 2015, 80, 61–164. [Google Scholar] [CrossRef]
- Sauvola, J.; Pietikäinen, M. Adaptive document image binarization. Pattern Recognit. 2000, 33, 225–236. [Google Scholar] [CrossRef]
- Niblack, W. An Introduction to Digital Image Processing; Strandberg Publishing Company: Uppsala, Sweden, 1985. [Google Scholar]
- Sankur, B. Survey over image thresholding techniques and quantitative performance evaluation. J. Electron. Imaging 2004, 13, 146. [Google Scholar] [CrossRef]
- Lazzara, G.; Géraud, T. Efficient multiscale Sauvola’s binarization. Int. J. Doc. Anal. Recognit. (IJDAR) 2014, 17, 105–123. [Google Scholar] [CrossRef]
- Kapur, J.N.; Sahoo, P.K.; Wong, A. A new method for gray-level picture thresholding using the entropy of the histogram. Comput. Vis. Graph. Image Process. 1985, 29, 140. [Google Scholar] [CrossRef]
- Klobes, P.; Meyer, K.; Munro, R.G. Porosity and Specific Surface Area Measurements for Solid Materials; National Institute of Standards and Technology, U.S. Department of Commerce: Washington, DC, USA, 2006.
- Thyssenkrupp Materials Services. Datasheet AW-5754 (EN-AW-5754) Aluminum Alloy. Essen: Thyssenkrupp Materials Services, July 2017. Available online: https://datenblaetter.thyssenkrupp.ch/en_aw_5754_0717.pdf (accessed on 20 June 2025).
- ISO 6892-1:2019; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. International Organization for Standardization: Geneva, Switzerland, 2019.
- Dreher, R.; Nauenburg, K.D.; Graf, M.; Emmerich, R.; Bräuning, R. High rate MW-PCVD processes for transparent hard coatings on PC plastic foils: First results and calculations for an up-scaling. In Proceedings of the International Symposium on Plasma Chemistry (ISPC), Bochum, Germany, 26–31 July 2009. [Google Scholar]
- Boylan, G.L.; Cho, B.R. The Normal Probability Plot as a Tool for Understanding Data: A Shape Analysis from the Perspective of Skewness, Kurtosis, and Variability. Qual. Reliab. Eng. Int. 2012, 28, 249–264. [Google Scholar] [CrossRef]
- Borer, B.; Sonnenfeld, A.; Rudolf von Rohr, P. Influence of substrate temperature on morphology of SiOx films deposited on particles by PECVD. Surf. Coatings Technol. 2006, 201, 1757–1762. [Google Scholar] [CrossRef]
- Sartorius Stedim Data Analytics AB. MODDE 12 User Guide; Sartorius: Umea, Schweden, 2017; Available online: https://www.sartorius.com/download/544636/modde-12-user-guide-en-b-00090-sartorius-data.pdf (accessed on 20 June 2025).
- Yasuda, H.; Wang, C.R. Plasma polymerization investigated by the substrate temperature dependence. J. Polym. Sci. Polym. Chem. Ed. 1985, 23, 87–106. [Google Scholar] [CrossRef]





| Parameter | Abbreviation | Unit | Low | Mid | High |
|---|---|---|---|---|---|
| Coating time | s | 5 | 15 | 25 | |
| Distance | dis | mm | 51 | 85 | 119 |
| Chamber pressure | p | mbar | 0.5 | 0.65 | 0.8 |
| Flow rate | Q | SCCM | 225 | 450 | 675 |
| Substrate temperature | °C | 30 | 70 | 110 | |
| Pulse duration | ms | 4 | 12 | 20 | |
| Pause-to-pulse ratio | PtPR | 1 | 1.5 | 2 | |
| Response | |||||
| Free surface area | FSA | percentage | |||
| Mean agglomerate diameter | MAD | nm | |||
| Film thickness | h | nm |
| Parameter | Value | Unit |
|---|---|---|
| Melt temperature | 340 | °C |
| Mold temperature | 155 | °C |
| Dosing volume | 25 | cm3 |
| Injection rate | 60 | cm3/s |
| Switching point | 12 | cm3 |
| Holding pressure | 430 | bar |
| Holding pressure time | 20 | s |
| Total cooling time | 40 | s |
| Film Thickness | FSA | MAD | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Variable | Coeff. SC | p-Value | Coeff. SC | p-Value | Coeff. SC | p-Value | |||
| Constant | 2.39996 | 32.7858 | 69.0311 | ||||||
| 0.277175 | 2.12 × | *** | −1.3126 | 2.26 × | *** | 12.527 | 3.51 × | *** | |
| 0.123398 | 2.13 × | *** | 2.84606 | 4.71 × | *** | 11.904 | 1.82 × | *** | |
| p | 0.122994 | 2.15 × | *** | 1.52006 | 2.01 × | *** | 7.9097 | 5.90 × | *** |
| Q | 0.24465 | 3.99 × | *** | −1.24068 | 1.19 × | *** | 16.7836 | 1.06 × | *** |
| −0.108177 | 6.39 × | *** | −0.746949 | 3.70 × | *** | −8.72345 | 4.25 × | *** | |
| - | 0.633215 | 5.35 × | ** | 2.86518 | 1.93 × | * | |||
| 0.087169 | 2.14 × | *** | 1.73624 | 1.47 × | *** | 6.98881 | 6.00 × | *** | |
| −0.0562705 | 2.39 × | * | 0.999879 | 4.87 × | ** | - | |||
| - | - | - | |||||||
| - | - | - | |||||||
| −0.115093 | 2.65 × | *** | 1.00844 | 3.56 × | * | −7.4682 | 5.82 × | ** | |
| - | - | - | |||||||
| - | - | - | |||||||
| - | - | - | |||||||
| 0.025953 | 1.48 × | * | 1.05831 | 1.04 × | *** | - | |||
| - | 1.54715 | 1.87 × | *** | - | |||||
| 0.035658 | 1.15 × | ** | 1.04961 | 8.32 × | *** | - | |||
| - | −0.671548 | 6.04 × | *** | −2.67023 | 3.51 × | * | |||
| - | - | −3.78306 | 3.26 × | ** | |||||
| - | - | - | |||||||
| 0.055434 | 1.67 × | *** | - | 2.51179 | 4.42 × | * | |||
| 0.039203 | 4.28 × | *** | 0.855687 | 3.17 × | *** | - | |||
| - | - | 4.87852 | 2.63 × | *** | |||||
| - | 0.971383 | 6.37 × | *** | - | |||||
| 0.071159 | 6.51 × | *** | −0.949231 | 1.27 × | *** | - | |||
| 0.037407 | 7.48 × | *** | 0.853839 | 1.01 × | ** | 2.99637 | 2.06 × | * | |
| - | - | - | |||||||
| - | 0.982965 | 3.24 × | *** | - | |||||
| 0.0640944 | 6.40 × | *** | - | - | |||||
| - | −1.83086 | 9.06 × | *** | - | |||||
| - | 0.913311 | 1.86 × | *** | - | |||||
| - | - | 3.13988 | 1.55 × | * | |||||
| - | - | - | |||||||
| −0.0476075 | 1.32 × | *** | −1.02951 | 3.22 × | *** | - | |||
| - | - | - | |||||||
| Q2 | 0.95 | 0.91 | 0.85 | ||||||
| R2 | 0.97 | 0.97 | 0.91 | ||||||
| R2 adj. | 0.96 | 0.96 | 0.88 | ||||||
| Conf. | 0.95 | 0.95 | 0.95 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laux, M.; Dreher, R.; Emmerich, R.; Henning, F. Deposition of Mesoporous Silicon Dioxide Films Using Microwave PECVD. Materials 2025, 18, 3205. https://doi.org/10.3390/ma18133205
Laux M, Dreher R, Emmerich R, Henning F. Deposition of Mesoporous Silicon Dioxide Films Using Microwave PECVD. Materials. 2025; 18(13):3205. https://doi.org/10.3390/ma18133205
Chicago/Turabian StyleLaux, Marcel, Ralf Dreher, Rudolf Emmerich, and Frank Henning. 2025. "Deposition of Mesoporous Silicon Dioxide Films Using Microwave PECVD" Materials 18, no. 13: 3205. https://doi.org/10.3390/ma18133205
APA StyleLaux, M., Dreher, R., Emmerich, R., & Henning, F. (2025). Deposition of Mesoporous Silicon Dioxide Films Using Microwave PECVD. Materials, 18(13), 3205. https://doi.org/10.3390/ma18133205






