Numerical Study of Wear Characteristics of Vertical Shaft Planetary Mixer Blades
Abstract
1. Introduction
2. Models and Methods
2.1. Mixer Model
2.2. Discrete Element Contact Model
2.3. Model of Concrete Aggregate
2.4. Simulation Scheme and Simulation Parameter Setting
3. Results and Discussion
3.1. Preliminary Simulation Analysis
3.2. Effect of Different Factors on Blade Wear
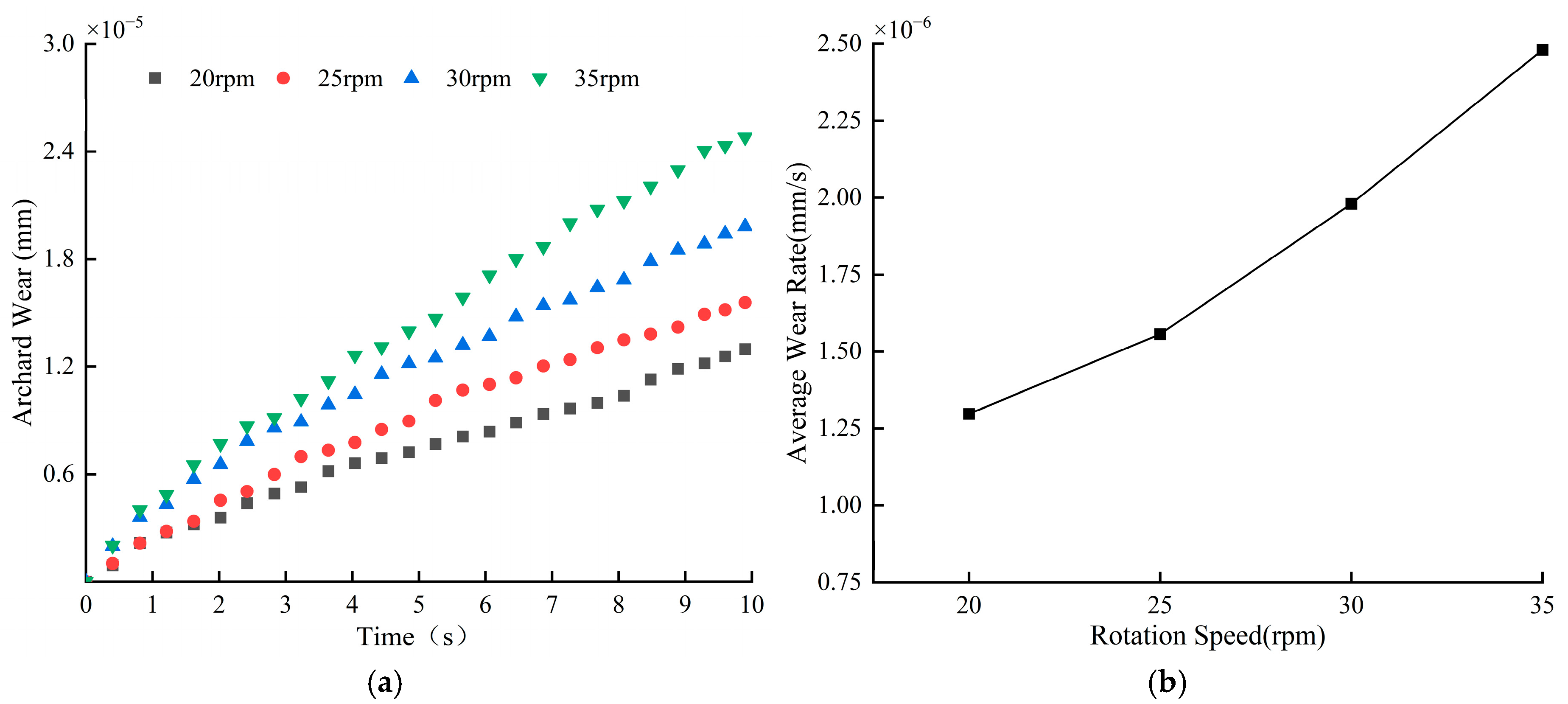
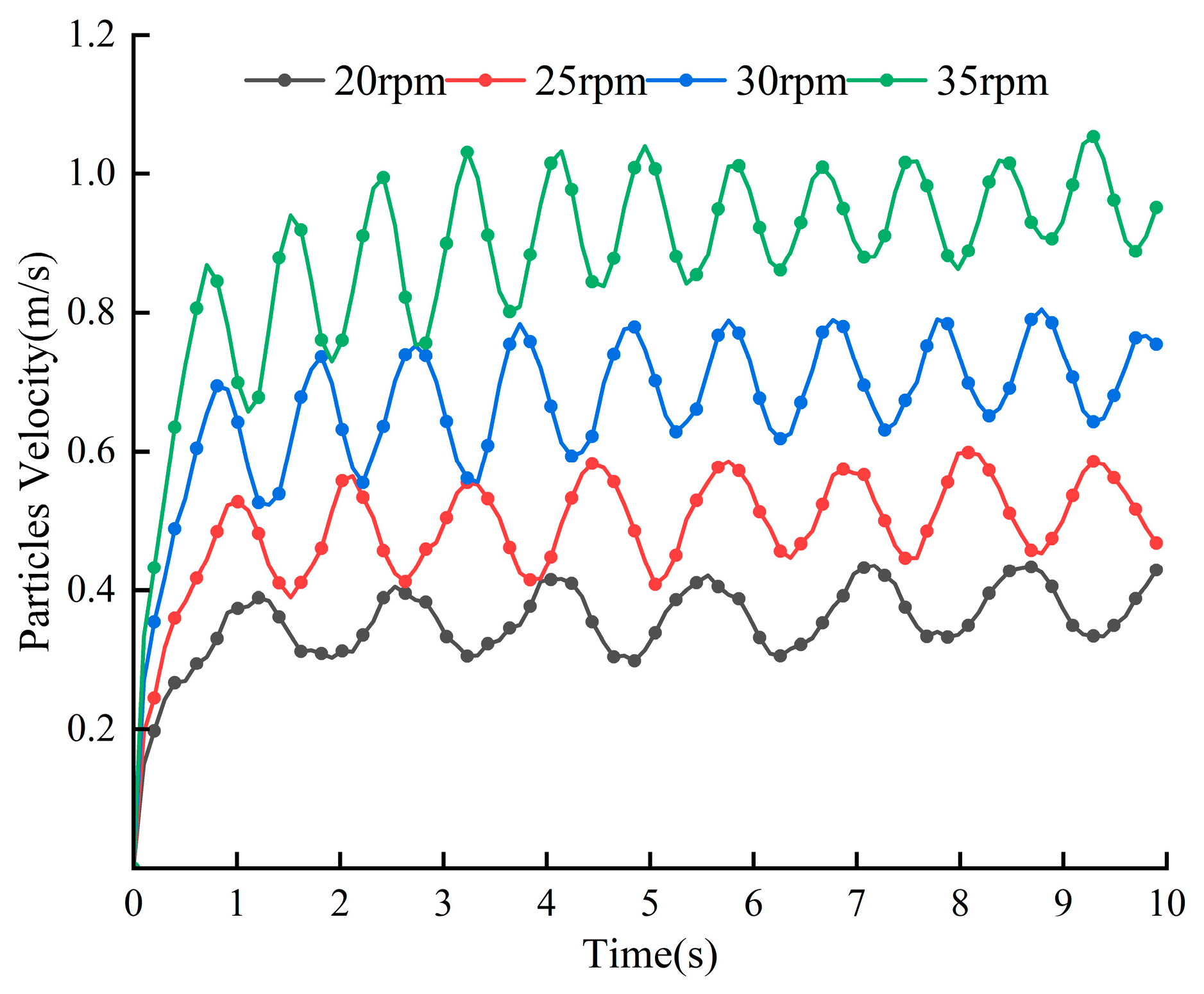
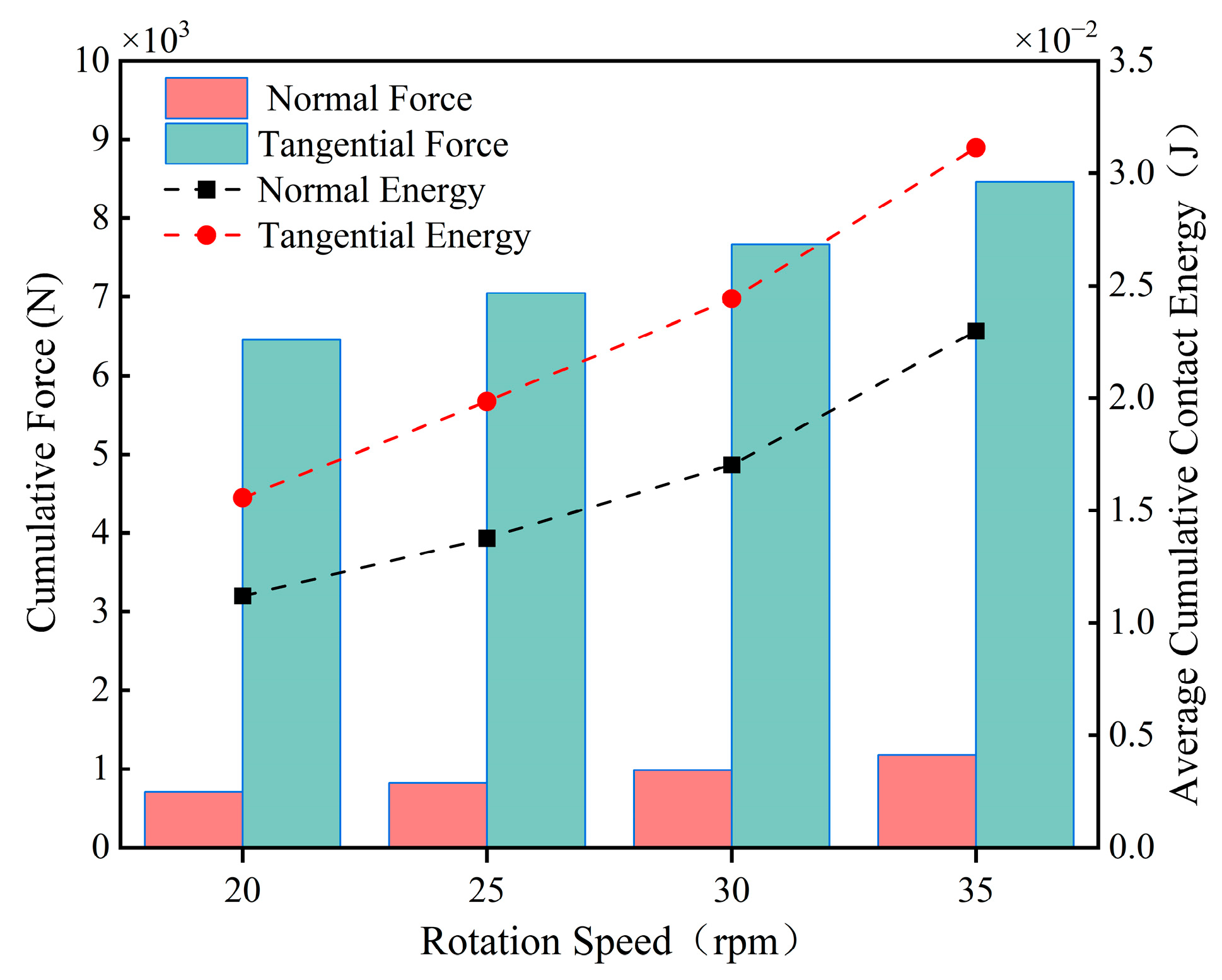
3.2.1. Effect of Mixing Speed on Blade Wear
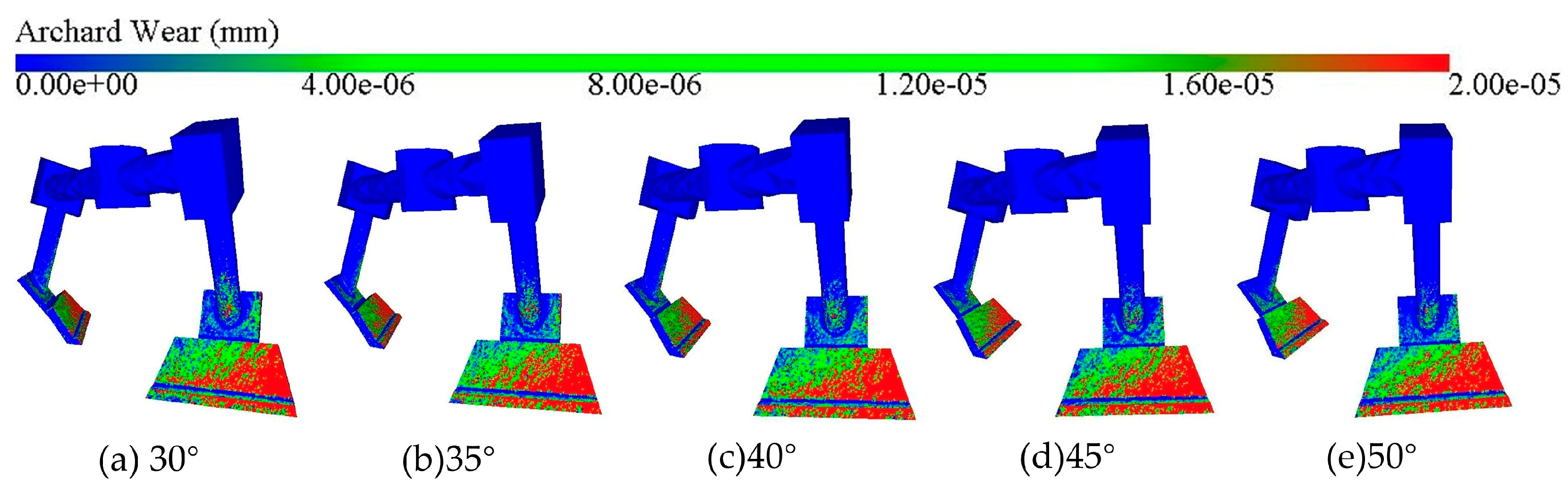
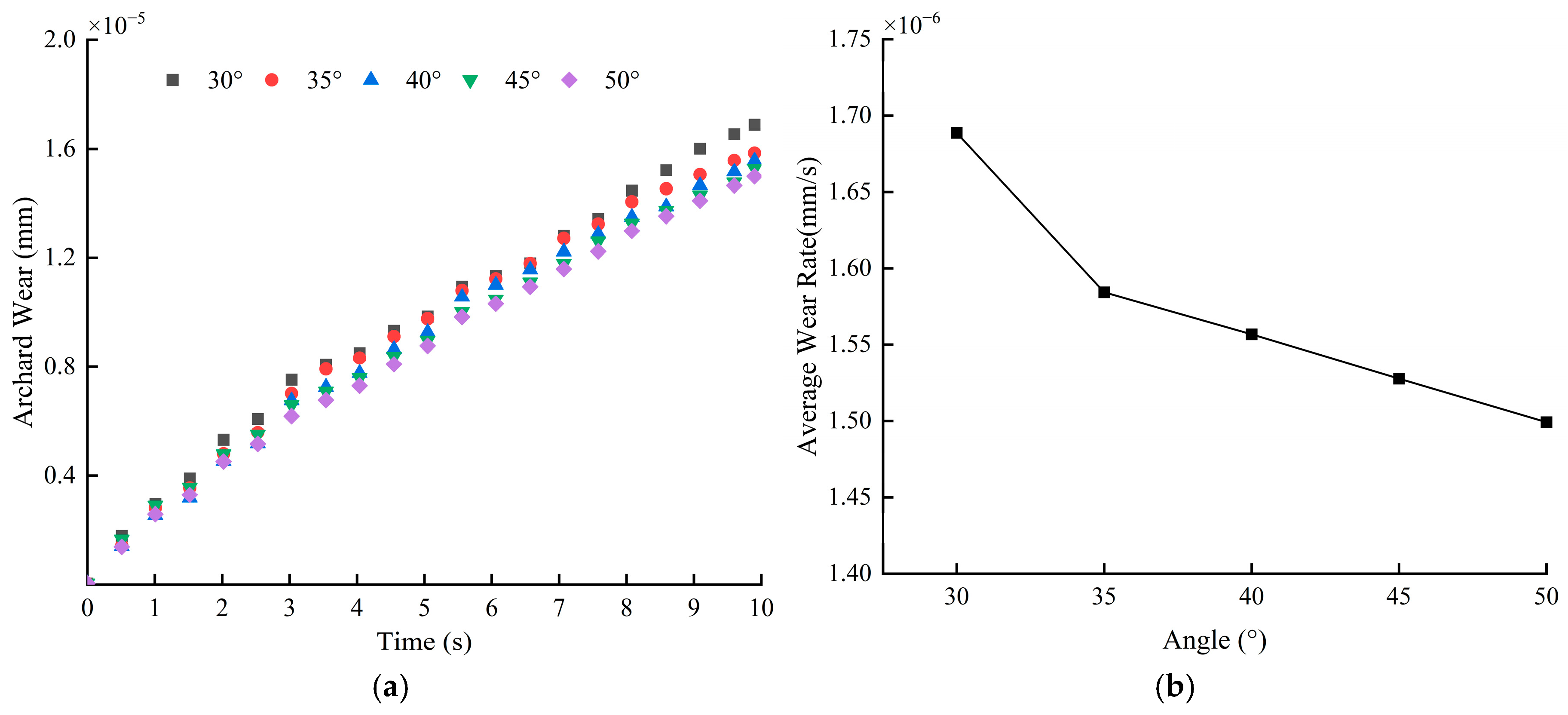
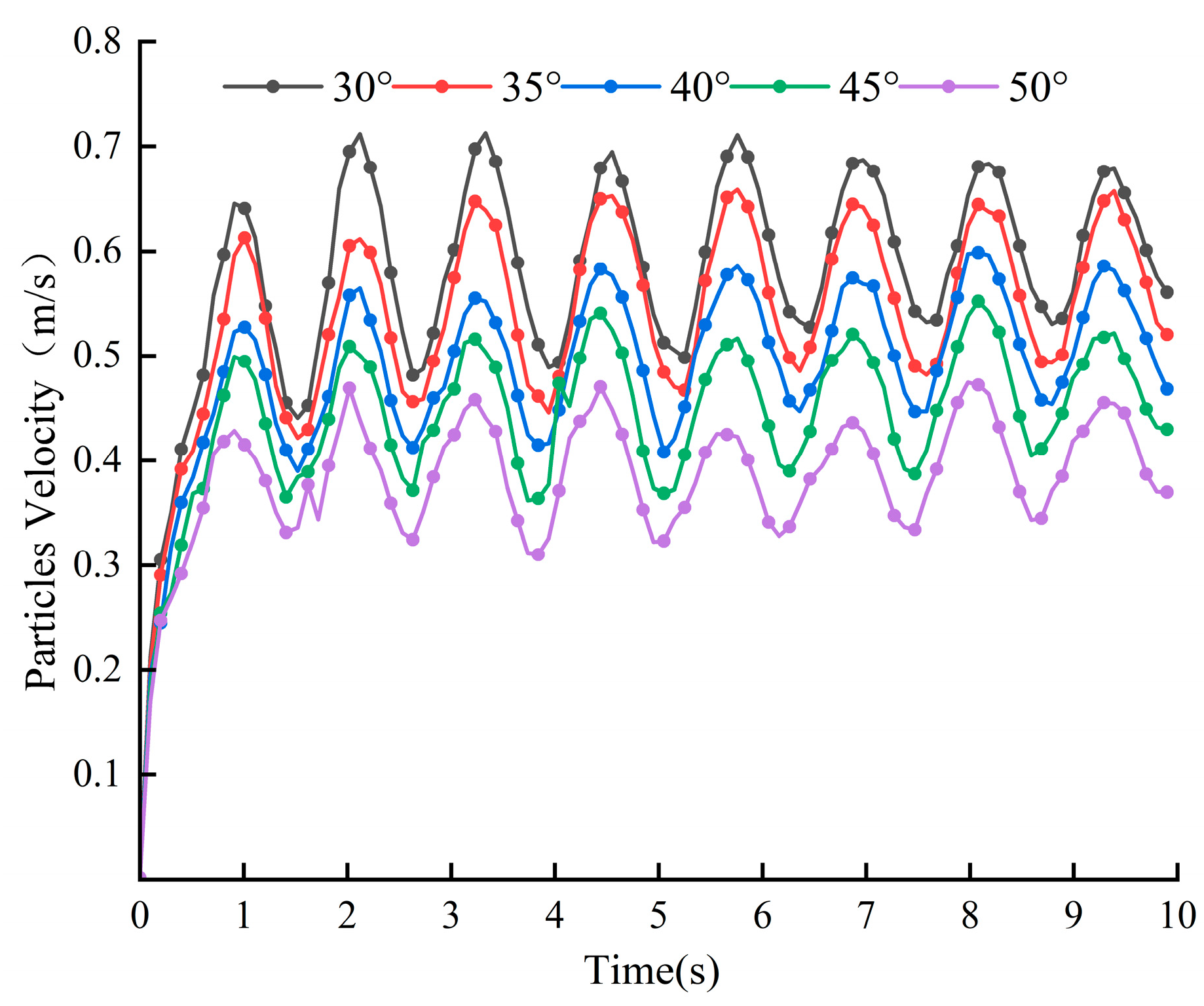
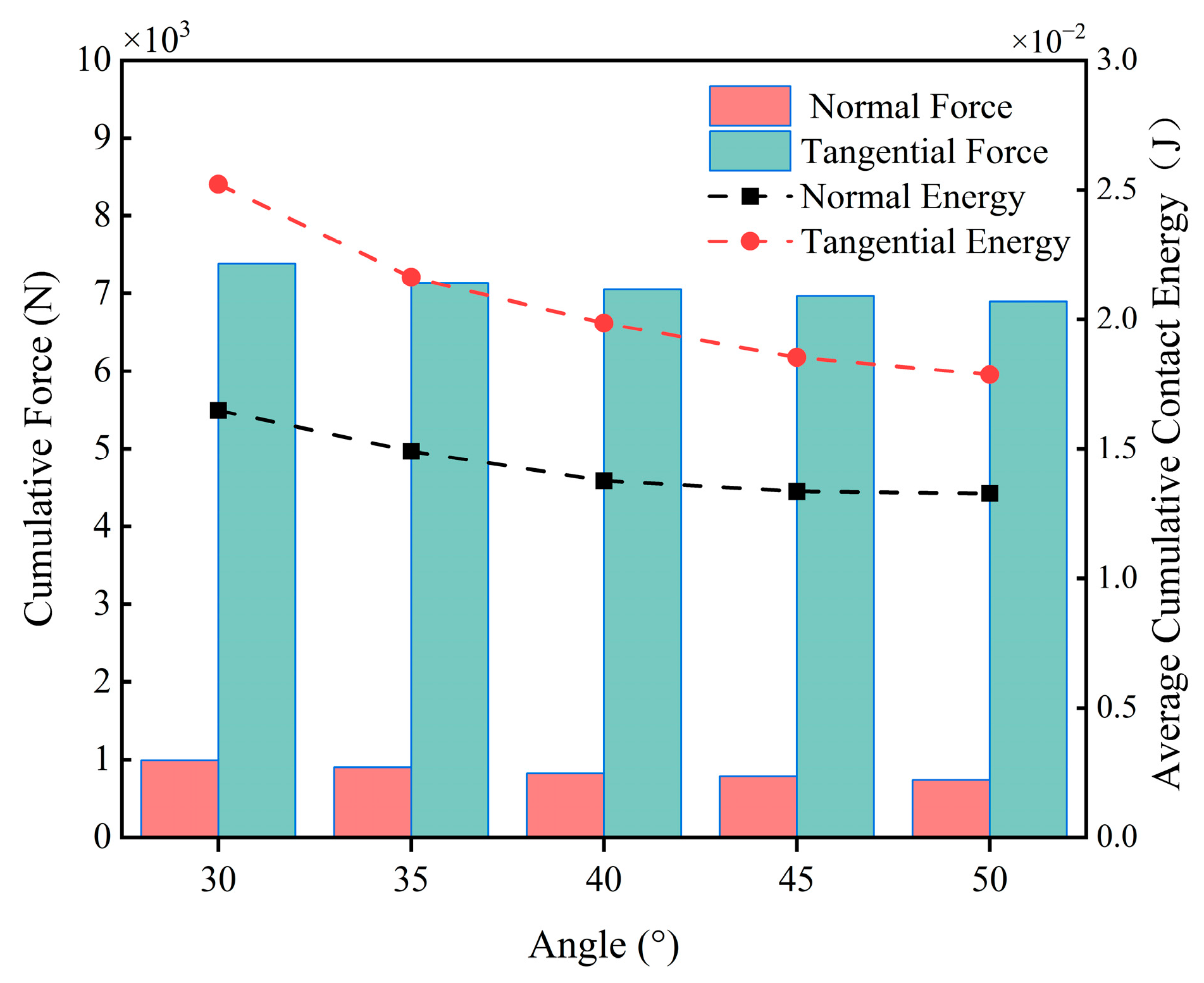
3.2.2. Effect of Blade Angle on Blade Wear
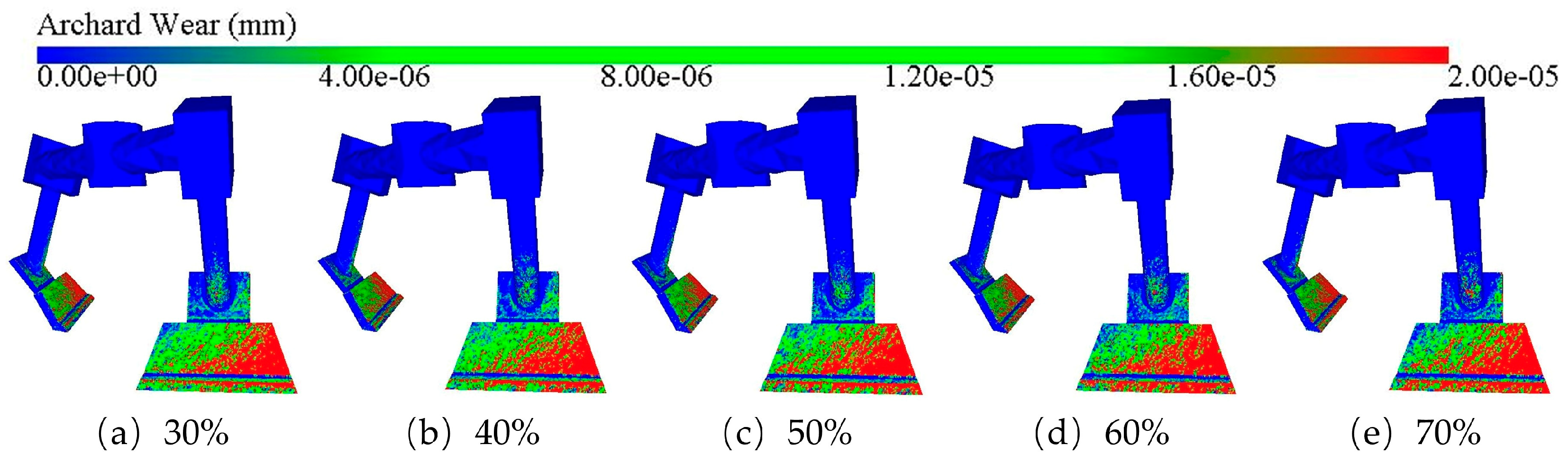
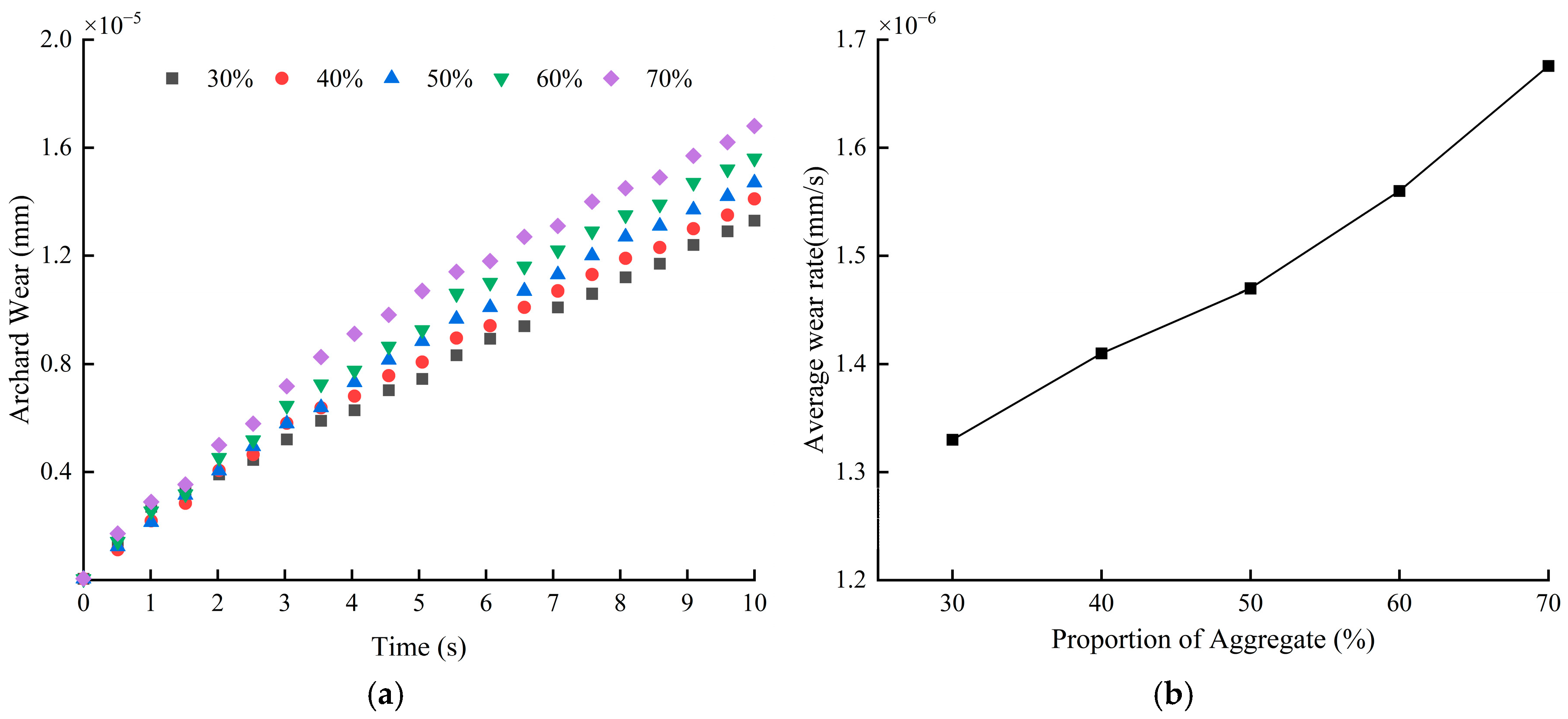
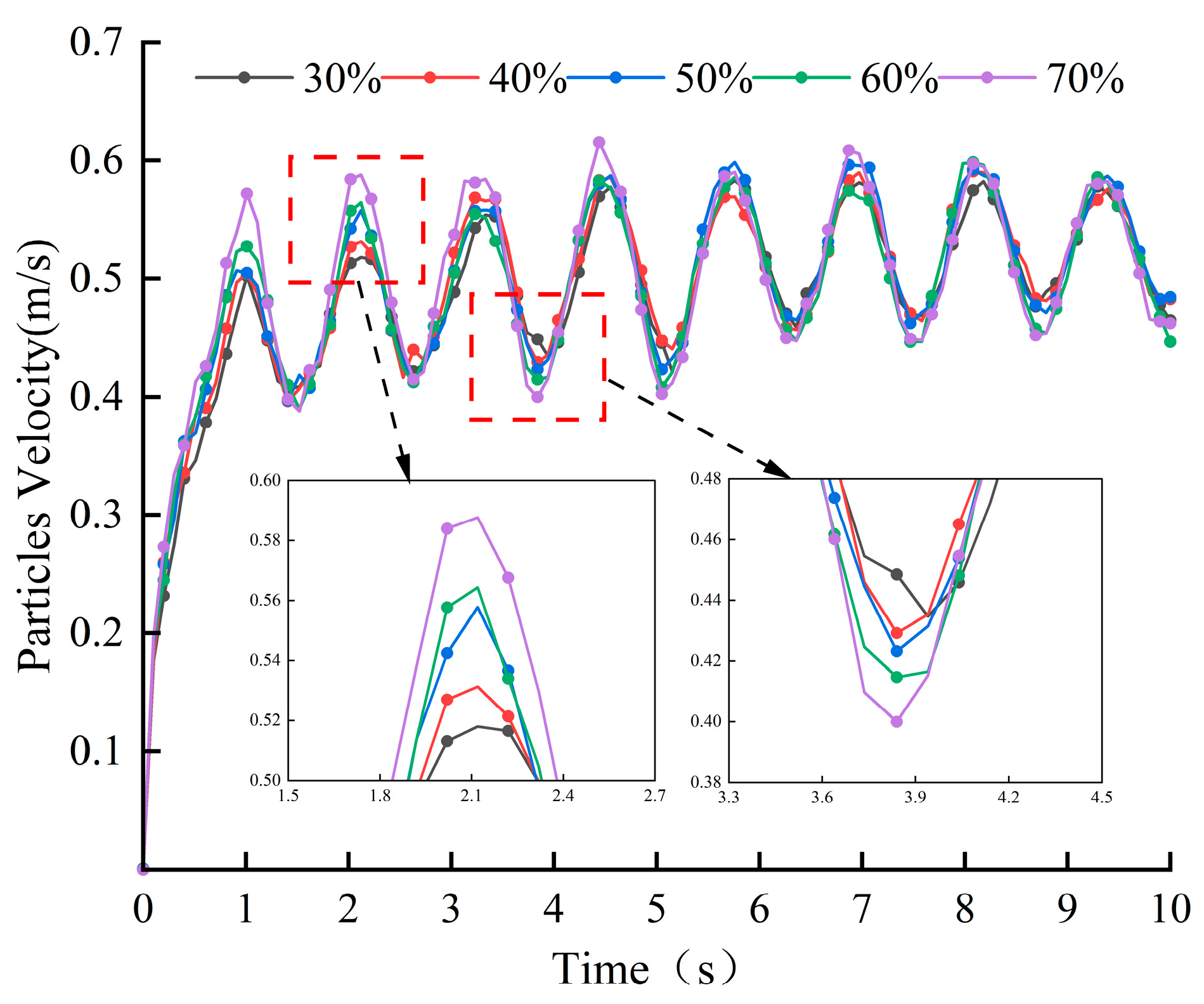
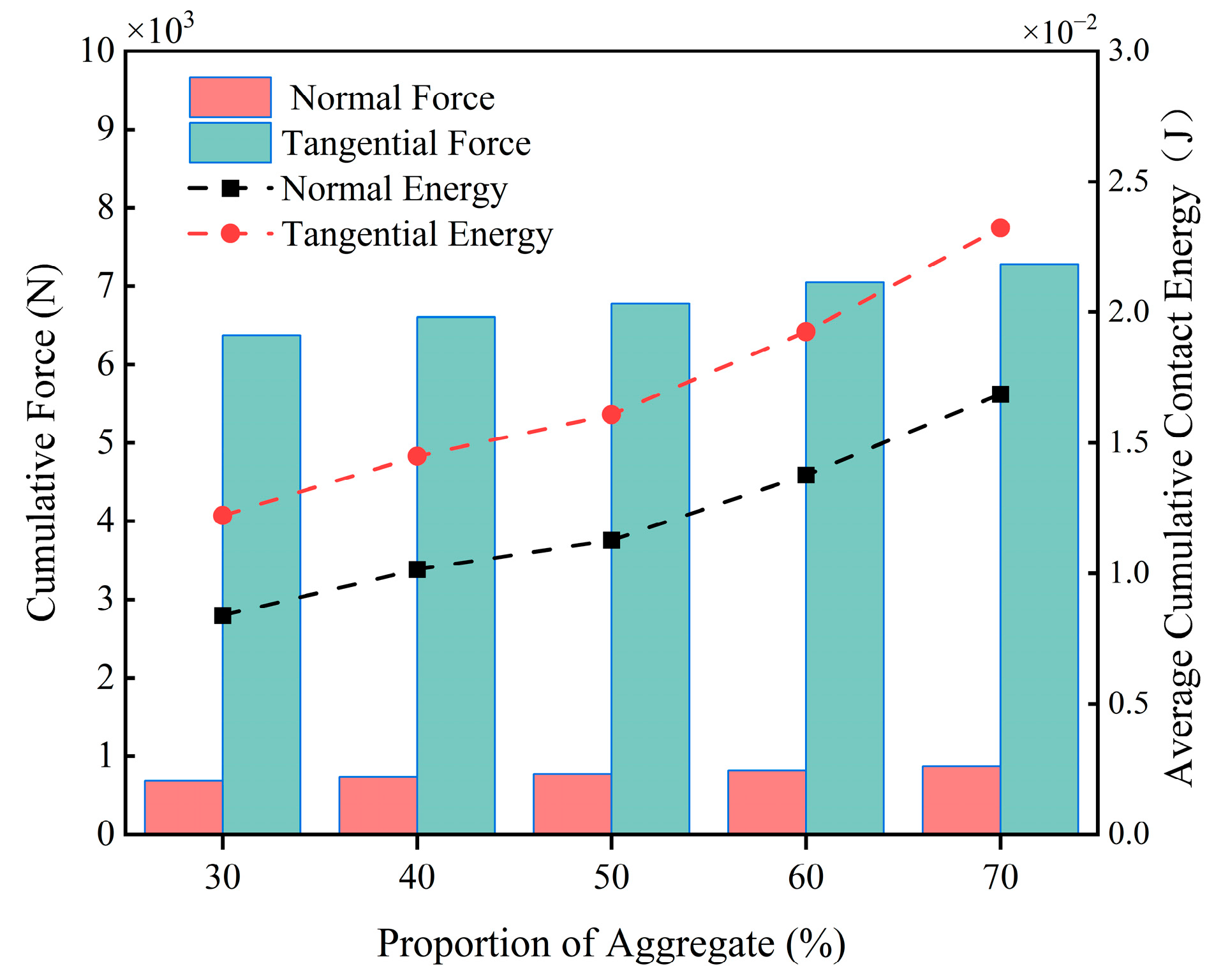
3.2.3. Effect of Aggregate Percentage on Blade Wear
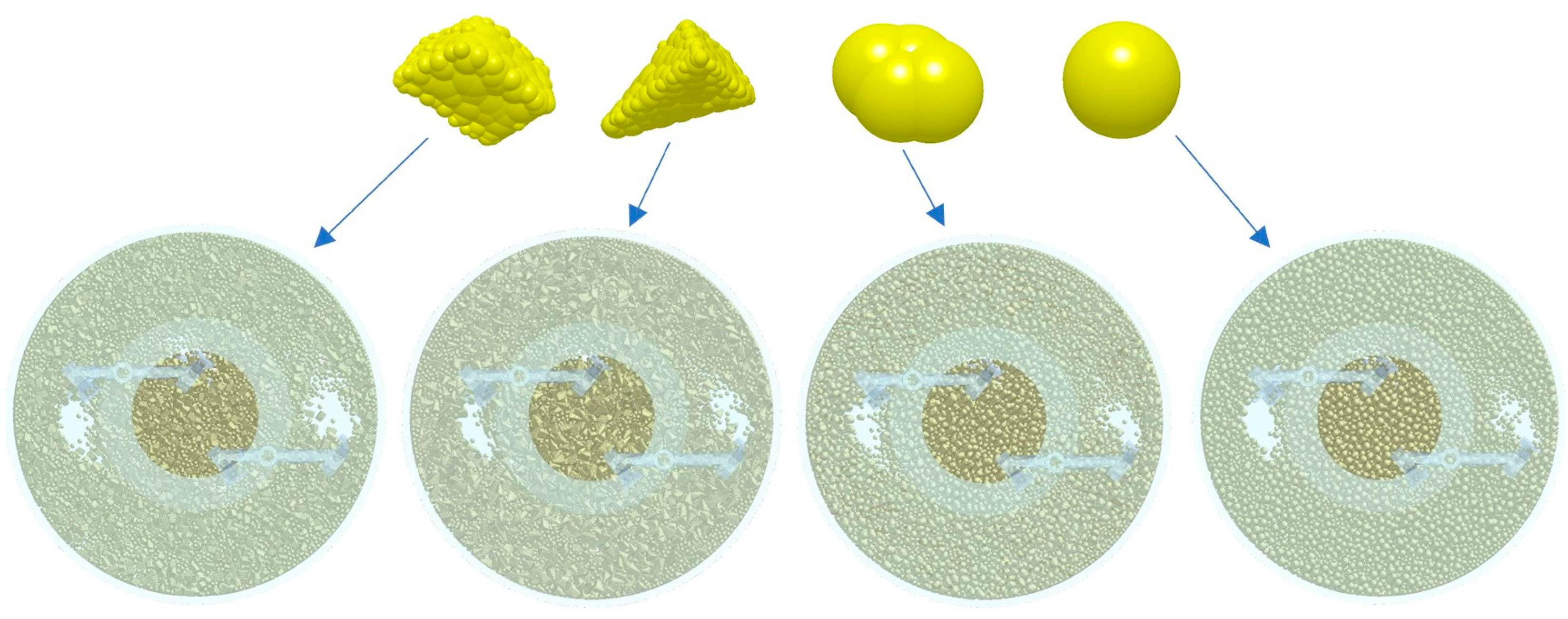
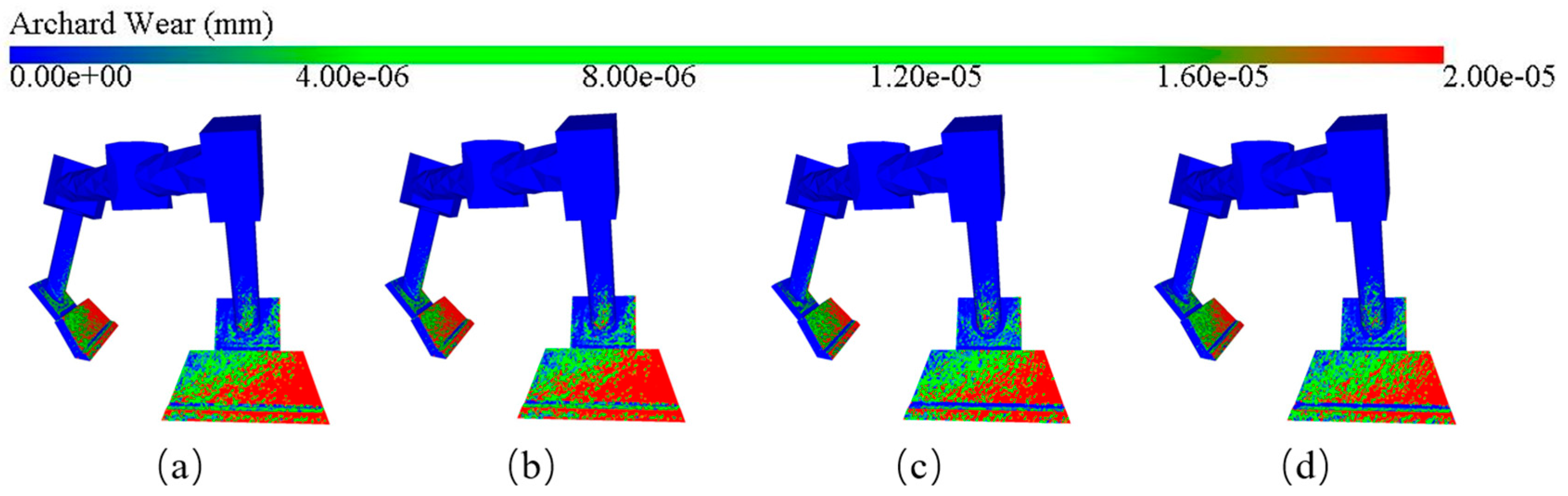
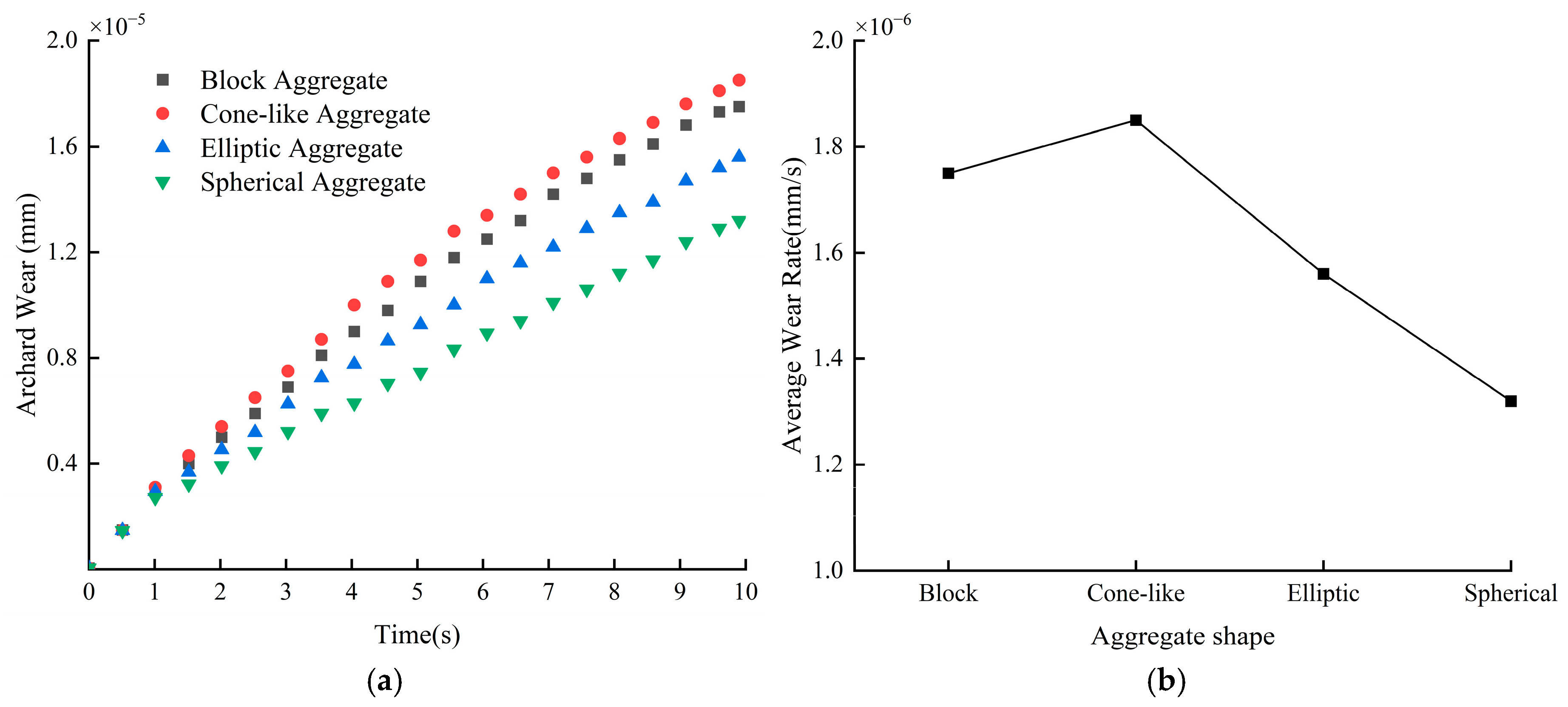
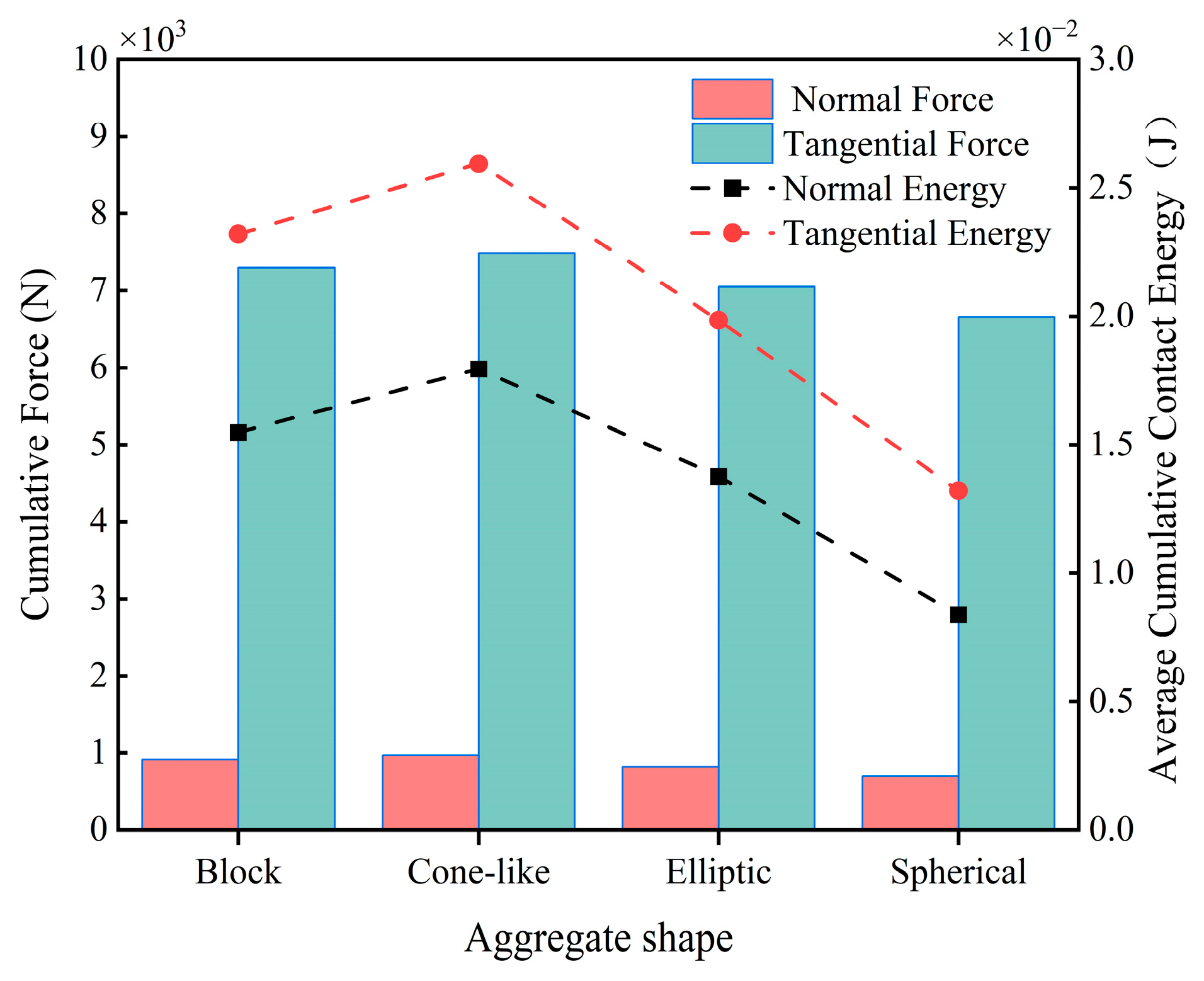
3.2.4. Effect of Aggregate Shape on Blade Wear
4. Conclusions
- (1)
- The type of blade wear is abrasive wear accompanied by impact. The maximum wear location occurs in the outermost middle and lower regions of the blade, which is consistent with the actual spatial distribution of wear.
- (2)
- The blade wear depth increases linearly with the increase in mixing speed. The higher the mixing speed, the more intense the particle movement, the higher the contact frequency of particles with the blade, and the greater the cumulative contact energy and force experienced by the blade, resulting in more severe blade wear.
- (3)
- The depth of blade wear decreases with the increase in blade angle. The larger the blade angle, the slower the particles move, the less contact energy and contact force the blade is subjected to, and the less the blade wears.
- (4)
- The depth of blade wear increases with the increase in the proportion of stone aggregate. Stone aggregate is the main material factor causing blade wear: the larger the proportion of stone aggregate, the larger the impact load of the blade by particle collision, and the more serious the degree of blade wear.
- (5)
- Cone-like stone aggregate has the most serious impact on blade wear, while the impact of spherical aggregate is the lightest. The gravel aggregate is more likely to form a localized high-stress region on the blade surface due to its sharp edges, thus increasing blade wear.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Changwen, M.; Song, M. Development and prospect of concrete technology. Silic. Bull. 2020, 39, 1–11. [Google Scholar] [CrossRef]
- Sarde, B.; Patil, Y. Recent research status on polymer composite used in concrete-An overview. Mater. Today Proc. 2019, 18, 3780–3790. [Google Scholar] [CrossRef]
- Du, J.; Meng, W.; Khayat, K.H.; Bao, Y.; Guo, P.; Lyu, Z.; Abu-Obeidah, A.; Nassif, H.; Wang, H. New development of ultra-high-performance concrete (UHPC). Compos. Part B Eng. 2021, 224, 109220. [Google Scholar] [CrossRef]
- Zhao, J.; Huang, L.; Xie, J. Influence of preparation process on the working performance and compressive strength of ultra-high performance concrete. Concrete 2019, 7, 44–47. [Google Scholar]
- Zhao, K.; Zhao, L.; Liu, S.; Hou, J. Effect of three-step mixing technology based on vibratory mixing on properties of high-strength concrete. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019; Volume 542, p. 012003. [Google Scholar]
- Ping, S.L.; Li, Y.Y.; Gang, L.S. Research on CFD Simulation of the Cement Slurry Mixer. Adv. Mater. Res. 2012, 621, 196–199. [Google Scholar]
- Zheng, J.; Chen, S.; Fu, X.; Fu, G.; Zhong, J.; Chen, B.; Li, Q.; Zhen, Z.; Fu, Y. Digital evaluation of planetary concrete mixer efficiency. Autom. Constr. 2023, 150, 104834. [Google Scholar] [CrossRef]
- Niță, A.; Petrescu, M.G.; Dumitru, T.; Burlacu, A.; Tănase, M.; Laudacescu, E.; Ramadan, I. Experimental research on the wear behavior of materials used in the manufacture of components for cement concrete mixers. Materials 2023, 16, 2326. [Google Scholar] [CrossRef]
- Niță, A.; Laudacescu, E.; Petrescu, M.G.; Dumitru, T.; Burlacu, A.; Bădoiu, D.G.; Tănase, M. Experimental Research Regarding the Effect of Mineral Aggregates on the Wear of Mixing Blades of Concrete Mixers. Materials 2023, 16, 5047. [Google Scholar] [CrossRef]
- Petrescu, M.G.; Popovici, A.-I.; Niță, A.; Isbășoiu, D.; Dumitru, T.; Tănase, M. Modelling Wear Phenomena Specific to Mixer Blades in Concrete Production Plants. Appl. Sci. 2024, 14, 3988. [Google Scholar] [CrossRef]
- Davoodi, F.; Atapour, M.; Ashrafizadeh, F.; Rikhtehgaran, R. Dry Sliding Wear Characteristics of NiP/TiN Duplex Coated Aluminum Alloy and Wear Analysis Using Response Surface Method. J. Mater. Eng. Perform. 2022, 31, 6360–6372. [Google Scholar] [CrossRef]
- Jiang, C.; Fleck, B.A.; Lipsett, M.G. Rapid Wear Modelling in a Slurry Pump Using Soft 3D Impeller Material. Energies 2020, 13, 3264. [Google Scholar] [CrossRef]
- Liu, P.; Han, X.; Sun, D.; Wang, Q. Research progress in molecular dynamics simulation of material friction and wear. Mater. Sci. Technol. 2017, 25, 9. [Google Scholar] [CrossRef]
- Chen, T.; Wang, J. Advances in abrasive grain detection technology for mechanical wear. J. Tribol. 2025, 45, 452–474. [Google Scholar]
- Qu, X.; Chen, J.; Zhou, H.; Zhi, Y. Current status and development trend of research on wear failure of materials and its pre-vention. J. Tribol. 1999, 19, 187–192. [Google Scholar] [CrossRef]
- Cleary, P. Predicting charge motion, power draw, segregation and wear in ball mills using discrete element methods. Miner. Eng. 1998, 11, 1061–1080. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Weerasekara, N.S.; Powell, M.S.; Cleary, P.W.; Tavares, L.; Evertsson, M.; Morrison, R.; Quist, J.; de Carvalho, R. The contribution of DEM to the science of comminution. Powder Technol. 2013, 248, 3–24. [Google Scholar] [CrossRef]
- Li, R.; Duan, G.; Sakai, M. DEM simulations in nuclear engineering: A review of recent progress. J. Nucl. Sci. Technol. 2023, 61, 285–306. [Google Scholar] [CrossRef]
- Siegmann, E.; Jajcevic, D.; Radeke, C.; Strube, D.; Friedrich, K.; Khinast, J.G. Efficient Discrete Element Method Simulation Strategy for Analyzing Large-Scale Agitated Powder Mixers. Chem. Ing. Tech. 2017, 89, 995–1005. [Google Scholar] [CrossRef]
- Zhang, H.; Feng, P.; Ying, W. Abrasive wear and optimal installation angle of concrete double-horizontal shaft mixer stirring blades. SN Appl. Sci. 2020, 2, 1607. [Google Scholar] [CrossRef]
- Teng, Y.; Wu, X.; Yang, S.; Li, S. Numerical study on blade wear of forced mixer based on discrete element method. Mech. Electr. Eng. Technol. 2025, 54, 118–122. [Google Scholar]
- Ryu, S.-H.; Woo, H.-K. Discrete Element Method for Defining the Dynamic Behavior and Abrasion of Gravel in Mixer Trucks during Mixing and Discharging. Korean Soc. Manuf. Process. Eng. 2020, 19, 34–41. [Google Scholar] [CrossRef]
- Moreno-Juez, J.; Tavares, L.M.; Artoni, R.; de Carvalho, R.M.; da Cunha, E.R.; Cazacliu, B. Simulation of the attrition of recycled concrete aggregates during concrete mixing. Materials 2021, 14, 3007. [Google Scholar] [CrossRef]
- Jiang, S.; Hu, D.; Cao, G.; Tan, A. Numerical analysis of mixing cylinder wear in concrete mixer truck. J. Comput. Mech. 2022, 39, 795–802. [Google Scholar]
- Valigi, M.C.; Logozzo, S.; Gasperini, I. Study of wear of planetary concrete mixer blades using a 3D optical scanner. In Proceedings of the ASME 2015 International Mechanical Engineering Congress & Exposition, Houston, TX, USA, 13–19 November 2015; ASME: New York, NY, USA, 2015. [Google Scholar]
- Valigi, M.C.; Logozzo, S.; Rinchi, M. Wear resistance of blades in planetary concrete mixers. Design of a new improved blade shape and 2D validation. Tribol. Int. 2016, 96, 191–201. [Google Scholar] [CrossRef]
- Johnson, K.L.; Kendall, K.; Roberts, A.D. Surface energy and the contact of elastic solids. Proc. R. Soc. A Math. Phys. Eng. Sci. 1971, 324, 301–313. [Google Scholar]
- Zhou, C.; Chen, Z. Mechanical properties of recycled concrete made with different types of coarse aggregate. Constr. Build. Mater. 2017, 134, 497–506. [Google Scholar] [CrossRef]
- Qin, M.; Zhang, G.; Zhang, W.; Li, S. Study on Mechanical Character of C50 Box-beam Concrete with Natural Pebbles. In Proceedings of the 2017 3rd International Forum on Energy, Environment Science and Materials (IFEESM 2017), Shenzhen, China, 25–26 November 2017; Atlantis Press: Beijing, China, 2018; pp. 380–385. [Google Scholar]
- Shen, J.; Wang, B.; Hou, J.; Yao, P. Numerical Study on the Effect of Coarse Aggregate Shape during Concrete Mixing Process. Materials 2024, 17, 1515. [Google Scholar] [CrossRef]


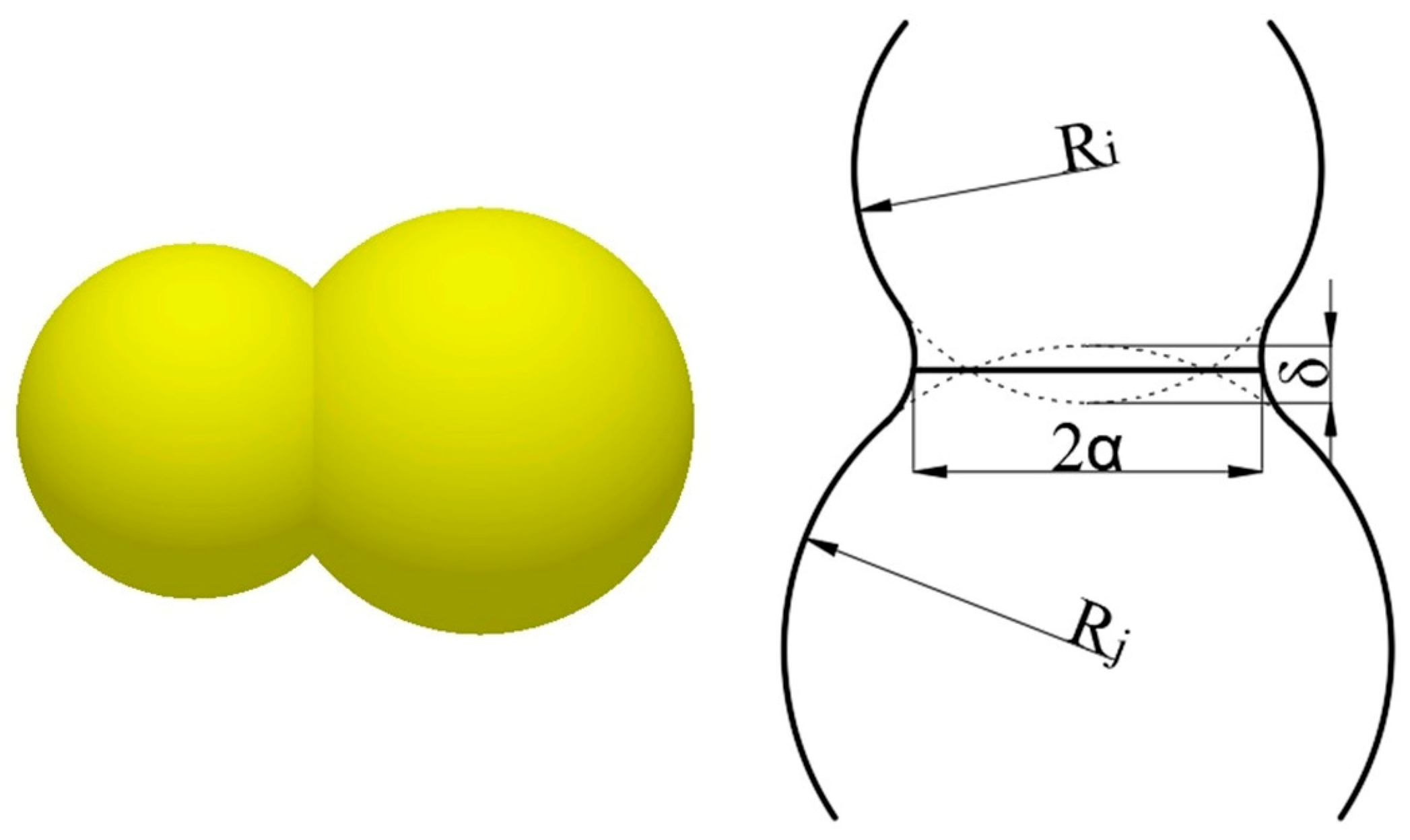


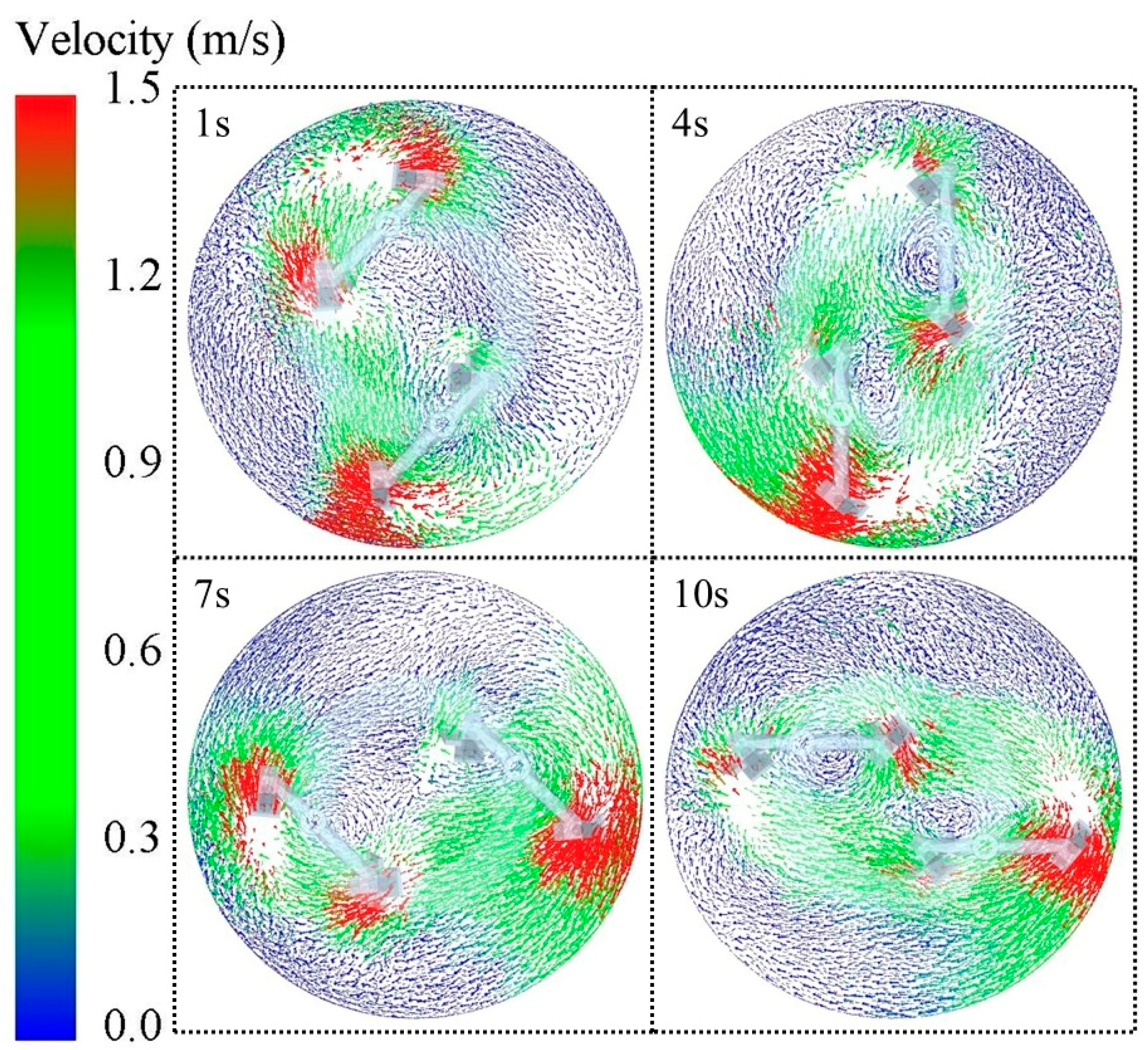
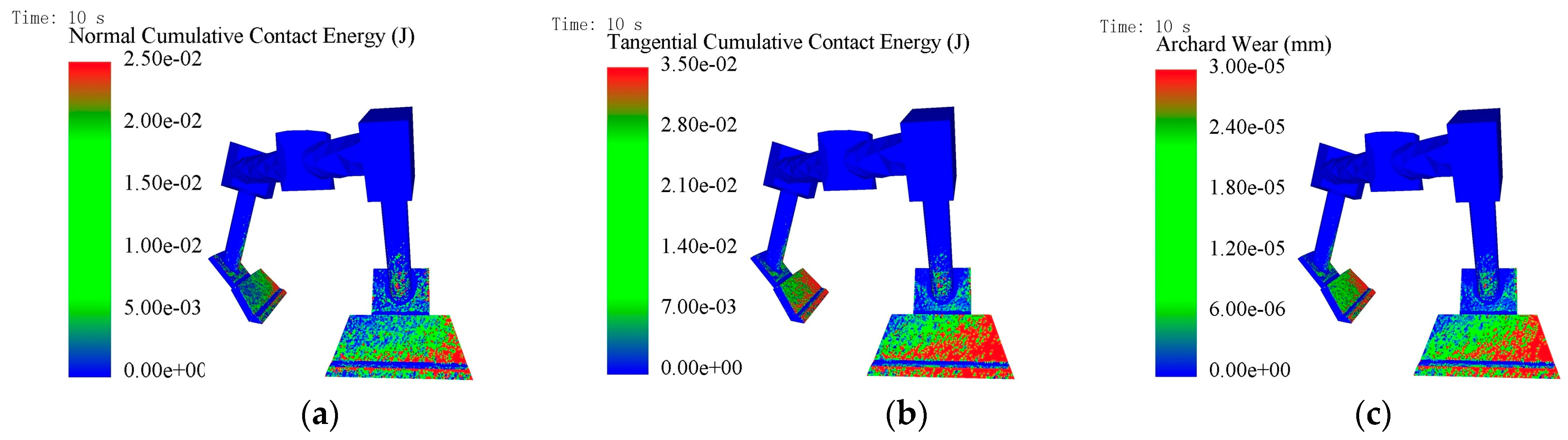

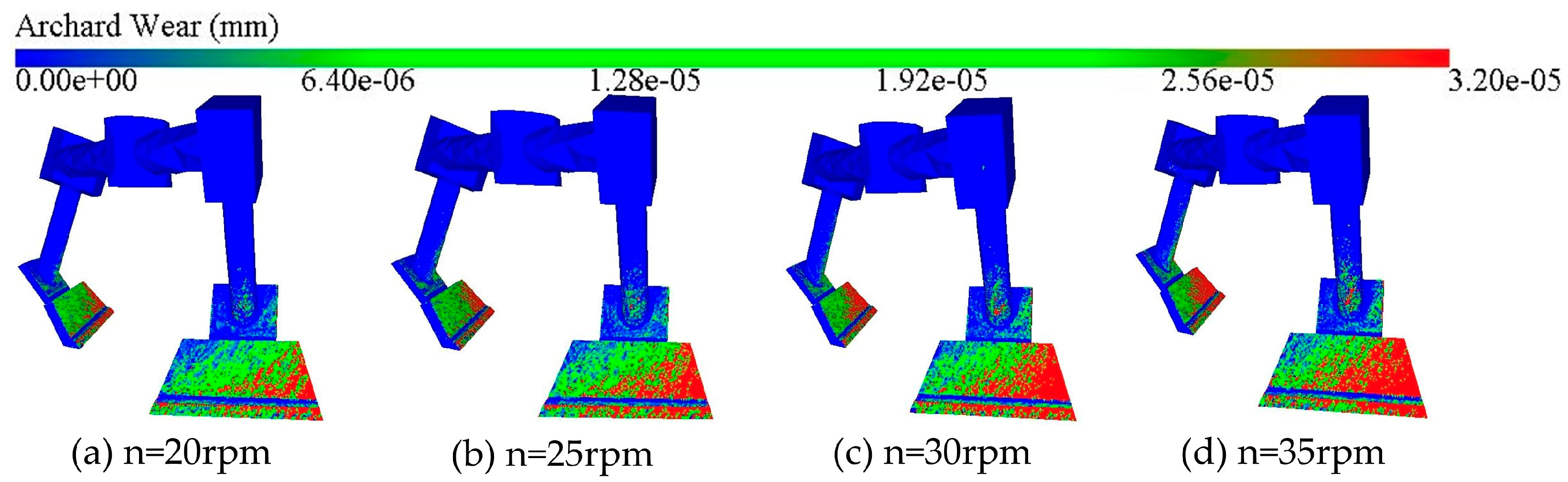

| Material | Poisson’s Ratio | Density (kg/m3) | Shear Modulus (GPa) |
|---|---|---|---|
| Aggregate | 0.35 | 2500 | 20 |
| Mortar | 0.25 | 2000 | 3 |
| Blade | 0.3 | 7850 | 70 |
| Title 1 | Coefficient of Restitution | Coefficient of Static Friction | Coefficient of Rolling Friction | Surface Energy (J/m2) |
|---|---|---|---|---|
| Aggregate–Aggregate | 0.7 | 0.3 | 0.02 | 1 |
| Aggregate–Mortar | 0.8 | 0.35 | 0.015 | 6 |
| Aggregate–Blade | 0.6 | 0.2 | 0.03 | 0.1 |
| Mortar–Mortar | 0.7 | 0.3 | 0.01 | 3 |
| Mortar–Blade | 0.5 | 0.1 | 0.025 | 0.3 |
| Factor | Case | Rotation Speed (rpm) | Blade Angle (°) | Proportion of Aggregate (%) | Aggregate Type |
|---|---|---|---|---|---|
| Rotation speed | 1 | 20 | 40 | 60 | Elliptic |
| 2 | 25 | 40 | 60 | Elliptic | |
| 3 | 30 | 40 | 60 | Elliptic | |
| 4 | 35 | 40 | 60 | Elliptic | |
| Blade angle | 1 | 25 | 30 | 60 | Elliptic |
| 2 | 25 | 35 | 60 | Elliptic | |
| 3 | 25 | 40 | 60 | Elliptic | |
| 4 | 25 | 45 | 60 | Elliptic | |
| 5 | 25 | 50 | 60 | Elliptic | |
| Proportion of aggregate | 1 | 25 | 40 | 30 | Elliptic |
| 2 | 25 | 40 | 40 | Elliptic | |
| 3 | 25 | 40 | 50 | Elliptic | |
| 4 | 25 | 40 | 60 | Elliptic | |
| 5 | 25 | 40 | 70 | Elliptic | |
| Aggregate type | 1 | 25 | 40 | 60 | Block |
| 2 | 25 | 40 | 60 | Cone-like | |
| 3 | 25 | 40 | 60 | Elliptic | |
| 4 | 25 | 40 | 60 | Spherical |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, S.; Zhang, H.; Zeng, Q.; Du, Q.; Liu, X. Numerical Study of Wear Characteristics of Vertical Shaft Planetary Mixer Blades. Materials 2025, 18, 3137. https://doi.org/10.3390/ma18133137
Jiang S, Zhang H, Zeng Q, Du Q, Liu X. Numerical Study of Wear Characteristics of Vertical Shaft Planetary Mixer Blades. Materials. 2025; 18(13):3137. https://doi.org/10.3390/ma18133137
Chicago/Turabian StyleJiang, Shoubo, Hongwei Zhang, Qingliang Zeng, Qian Du, and Xiaopeng Liu. 2025. "Numerical Study of Wear Characteristics of Vertical Shaft Planetary Mixer Blades" Materials 18, no. 13: 3137. https://doi.org/10.3390/ma18133137
APA StyleJiang, S., Zhang, H., Zeng, Q., Du, Q., & Liu, X. (2025). Numerical Study of Wear Characteristics of Vertical Shaft Planetary Mixer Blades. Materials, 18(13), 3137. https://doi.org/10.3390/ma18133137






