Structural Optimization and Performance Analysis of Acoustic Metamaterials with Parallel Unequal Cavities
Abstract
1. Introduction
2. Materials and Methods
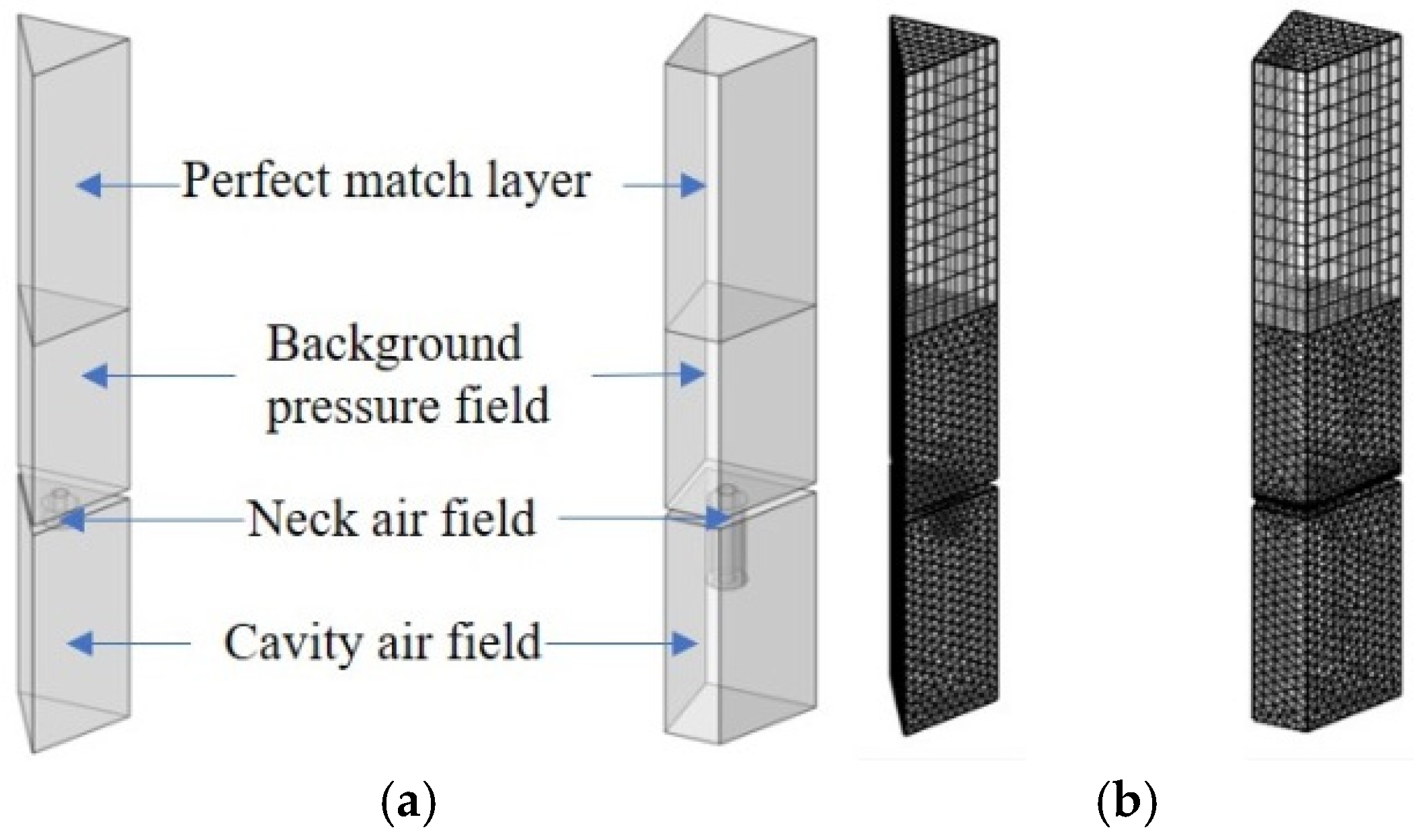
2.1. The Establishment of the Theoretical Model
2.2. Optimization Design
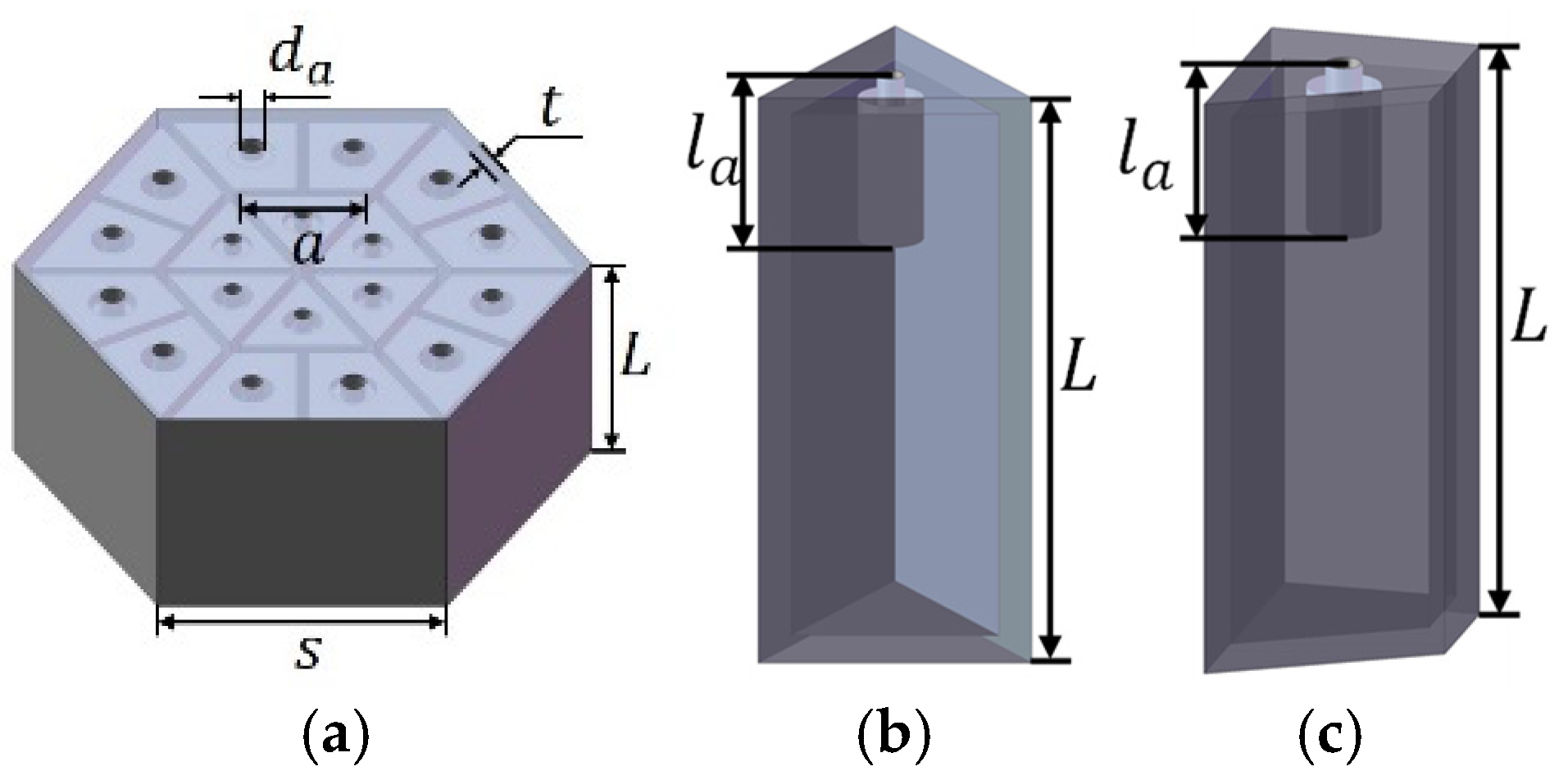
2.2.1. The Design of the Initial Acoustic Metamaterial
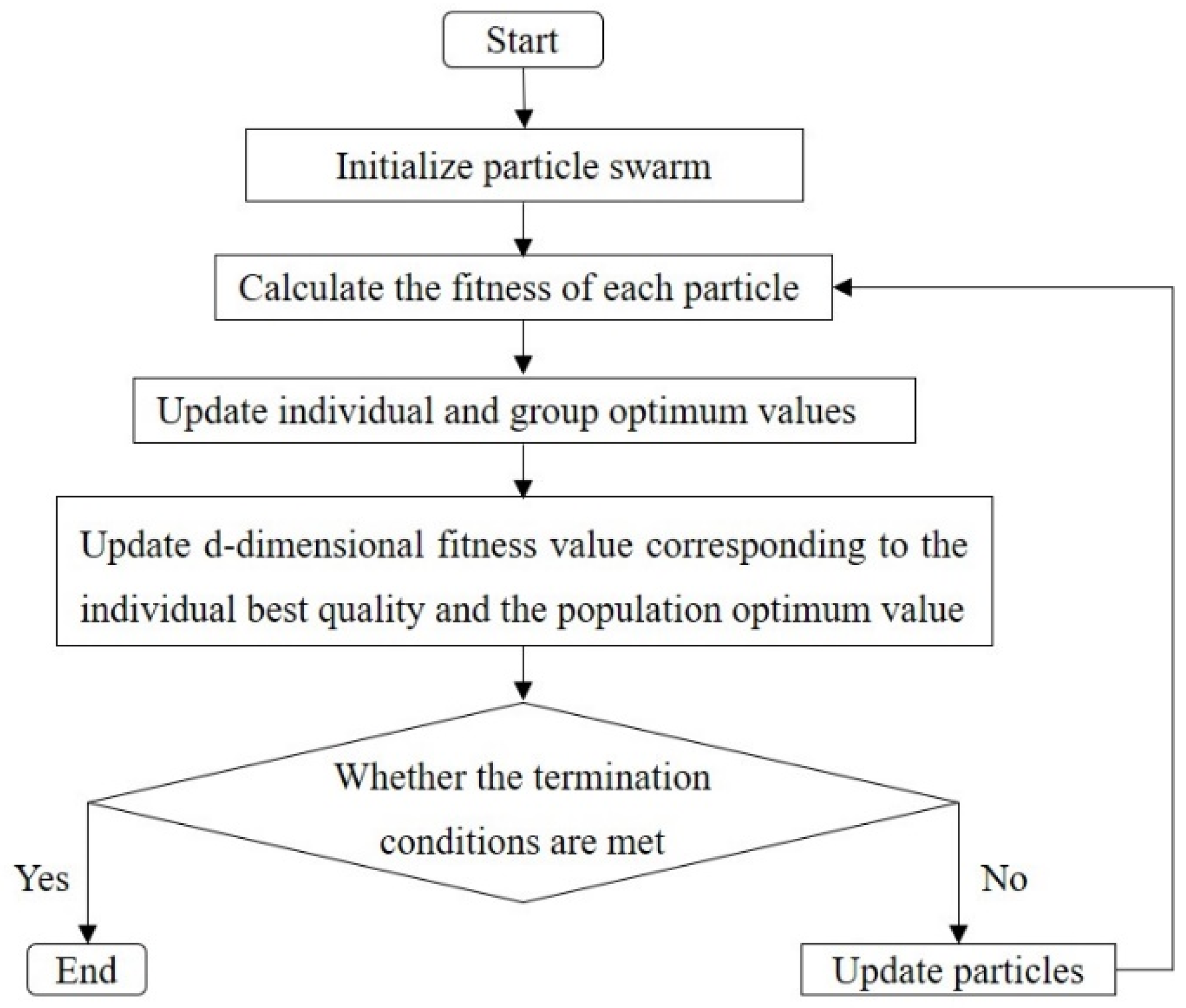
2.2.2. Structural Optimization by the PSO Algorithm
- (1)
- Establishment of the optimization model: With the total value of the sound absorption coefficient in the target frequency domain under the white noise conditions as the objective, the fitness function is defined as follows:
- (2)
- Determination of decision variable and constraints: optimized frequency range is set at 100–900 Hz; plate thickness t is 2 mm. The length of the embedded aperture of the acoustic metamaterial with parallel, unequal cavities is taken as the decision variable, measured in millimeters (mm).
- (3)
- Determination of the operational parameters and termination conditions of the PSO algorithm: population size ; maximum number of iterations ; the weight of self-acceleration ; global acceleration weight ; and the inertia coefficient . The iterations end when the current optimal individual is output, either when all absorption coefficients in the optimized frequency range exceed 0.8 or when the maximum number of iterations is reached.
3. Results and Discussion
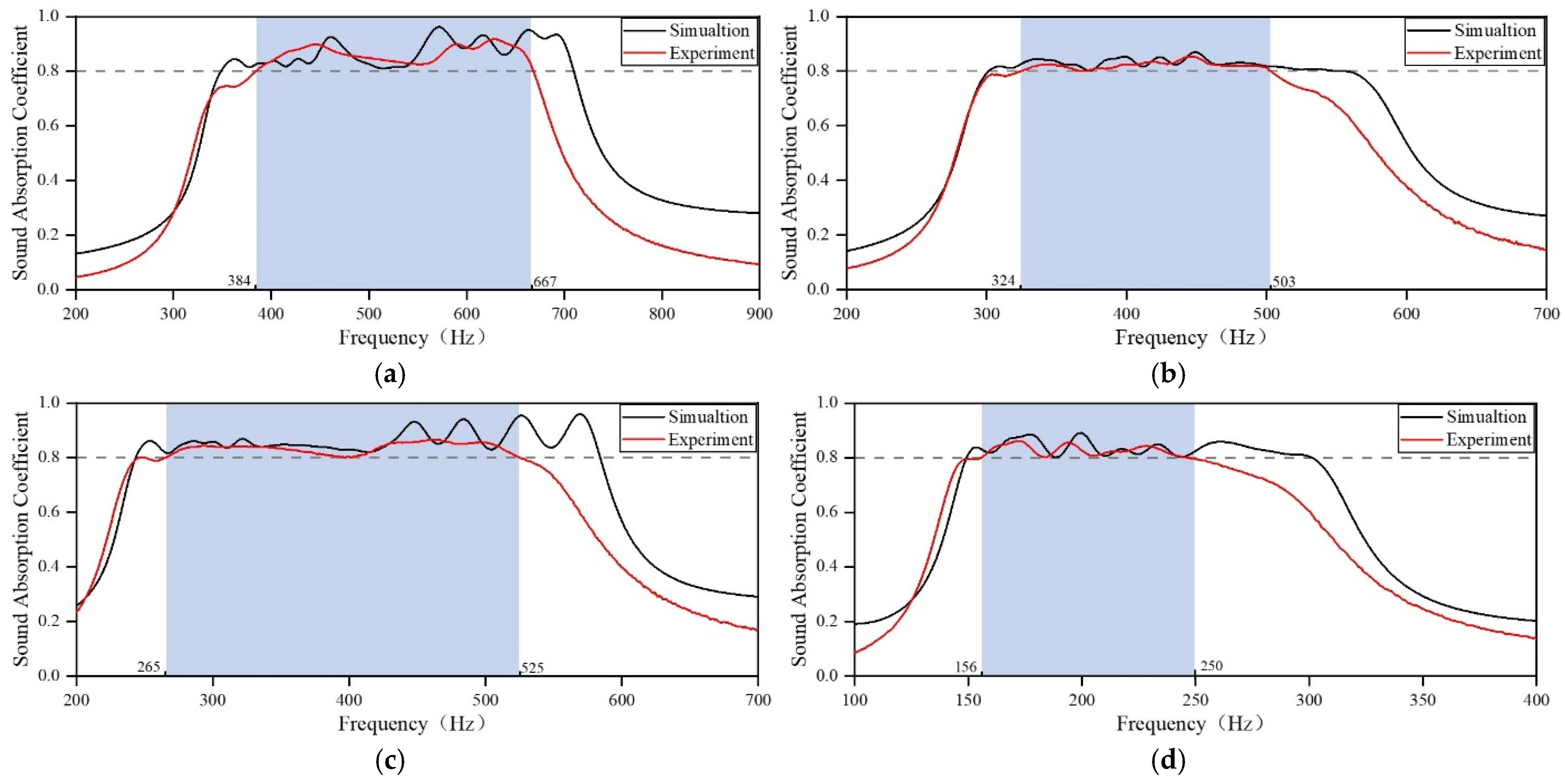
3.1. Experimental Verification
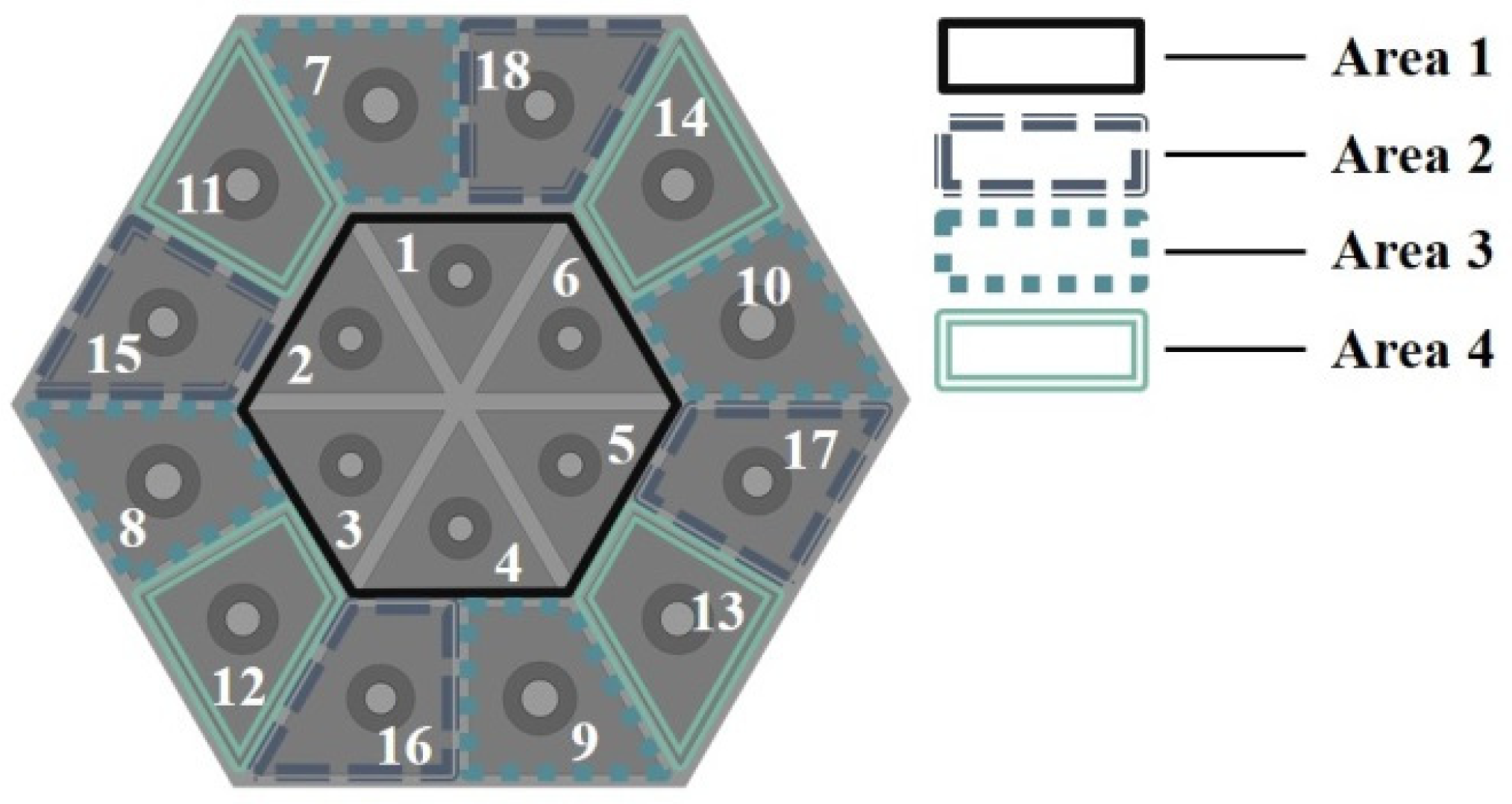
3.2. The Impact of Structural Parameters of Different Regions on the Sound-Absorbing Capacity of the Optimized Structure
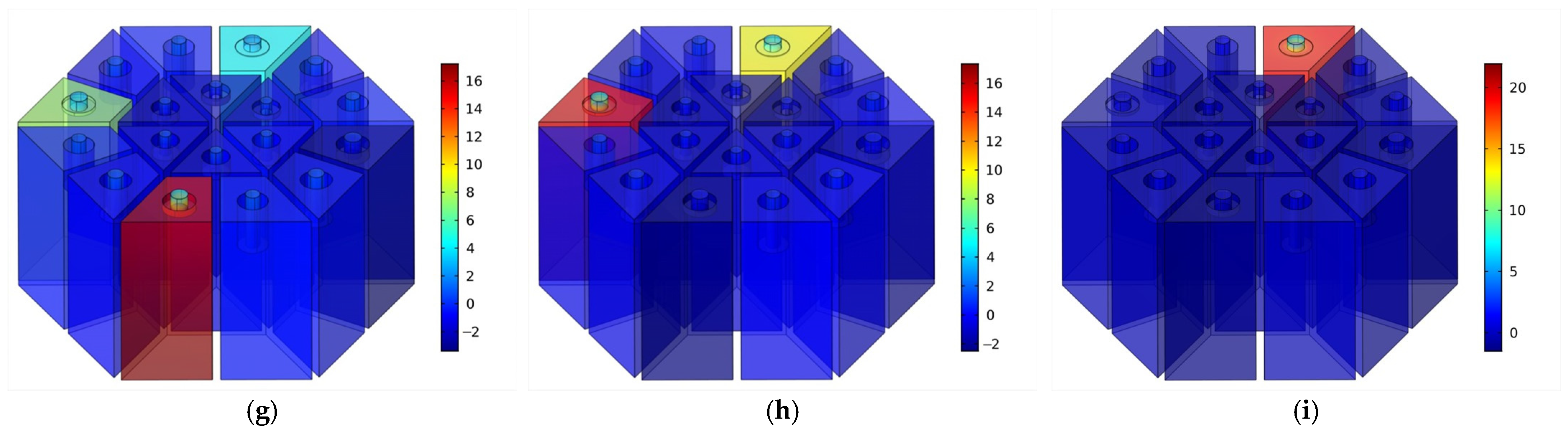
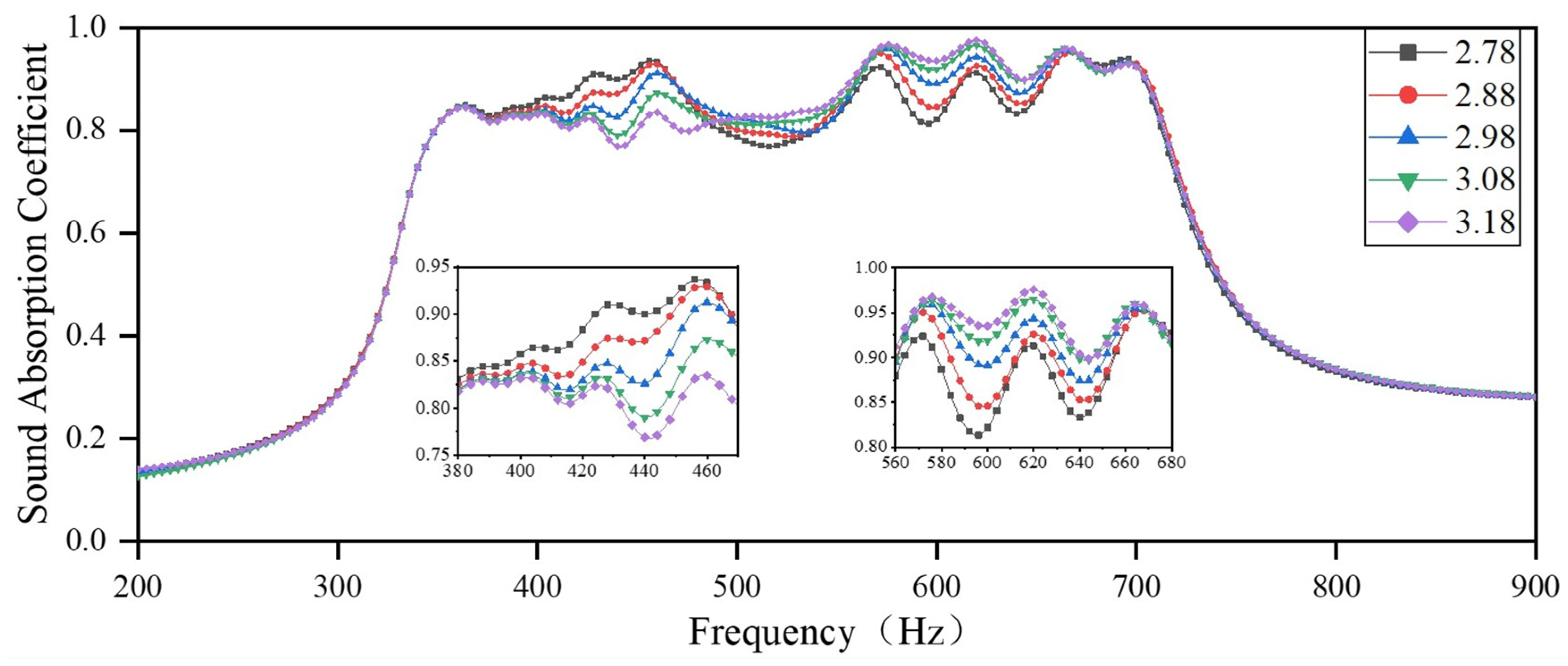
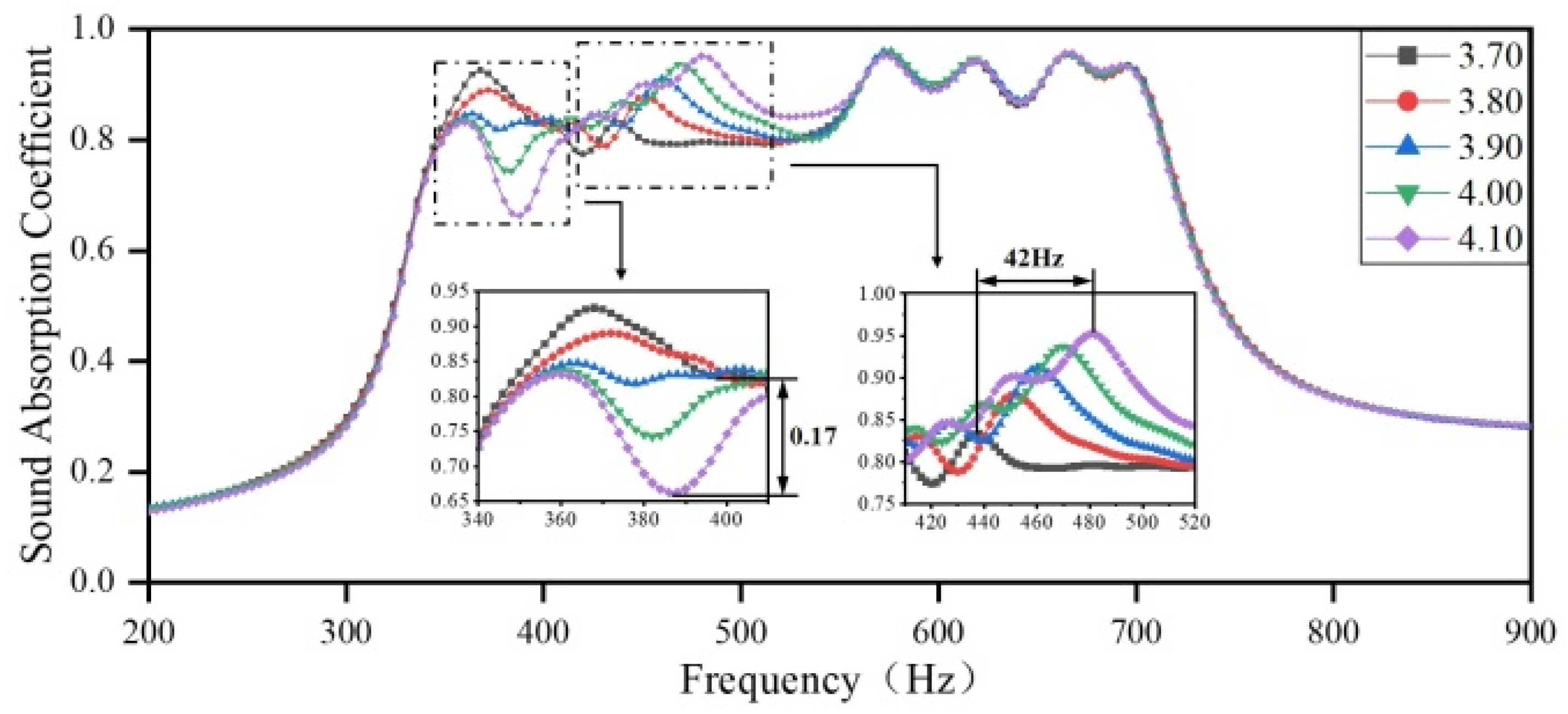
3.2.1. The Impact of Diameters of Apertures in Different Regions on the Sound-Absorbing Capacity
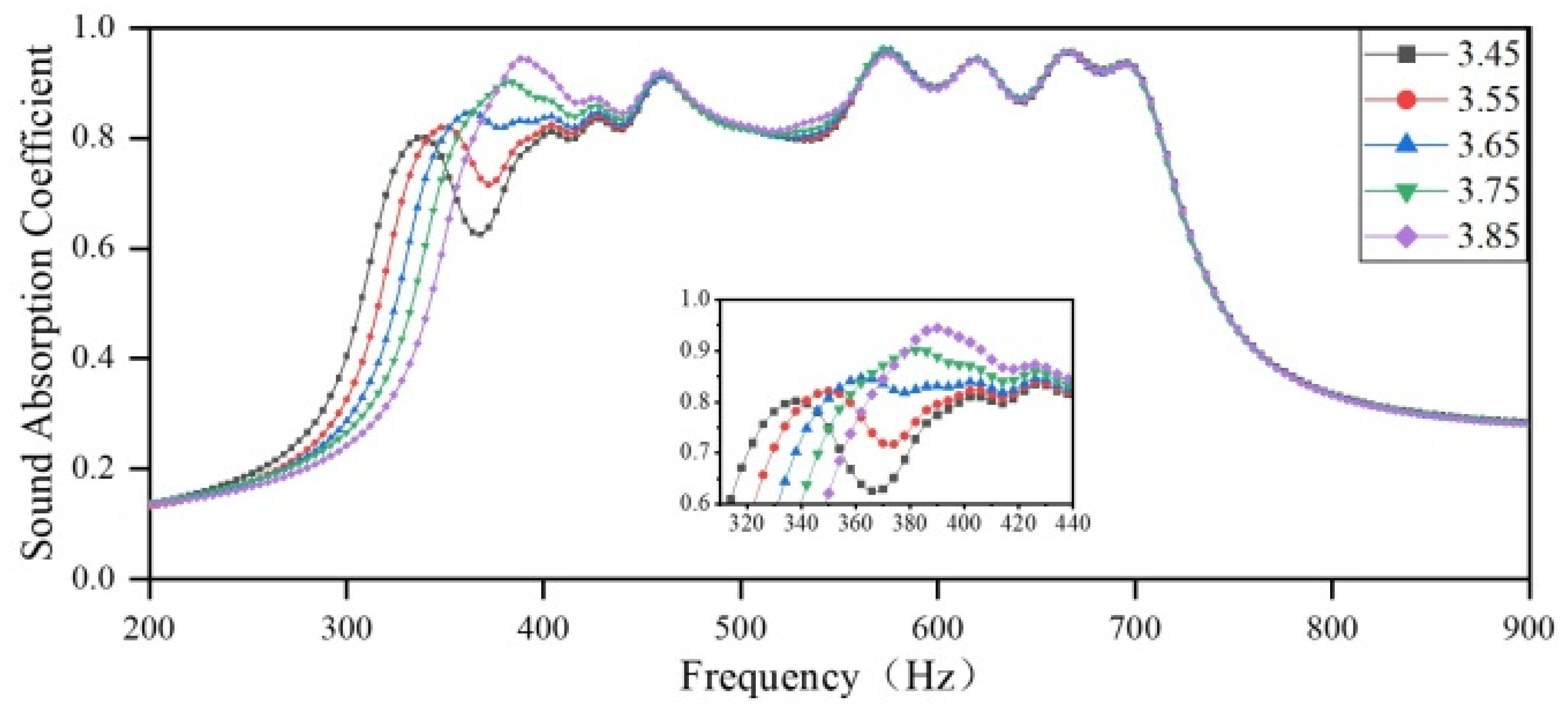
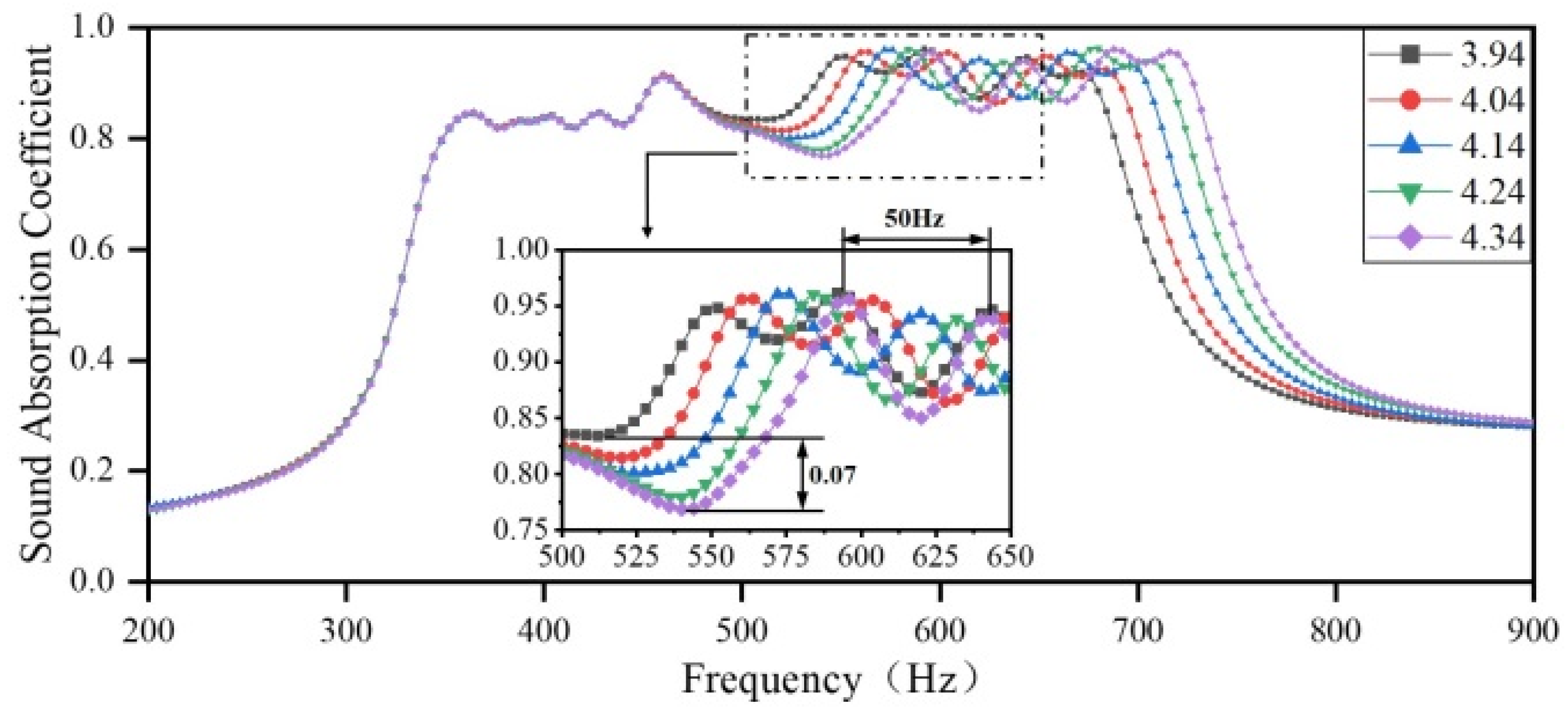
3.2.2. The Impact of the Embedded Aperture Length in Various Regions on the Sound Absorption Coefficient
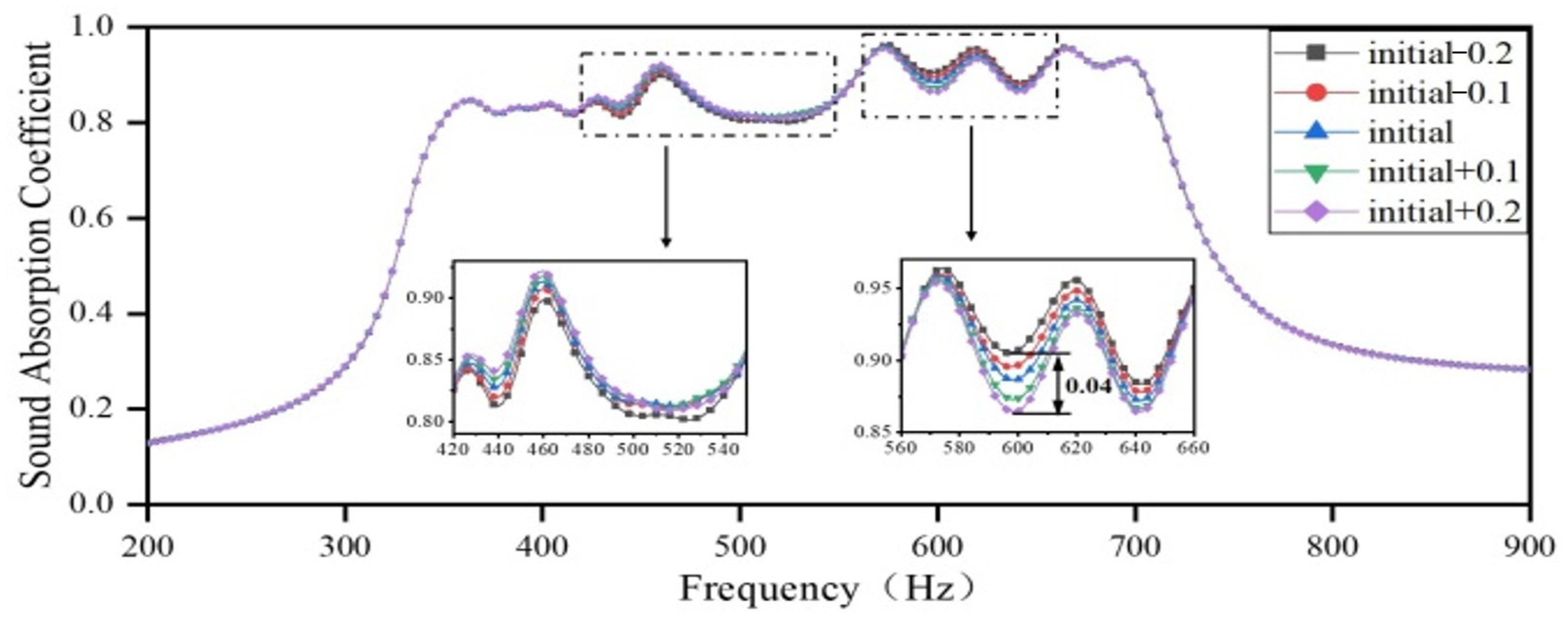
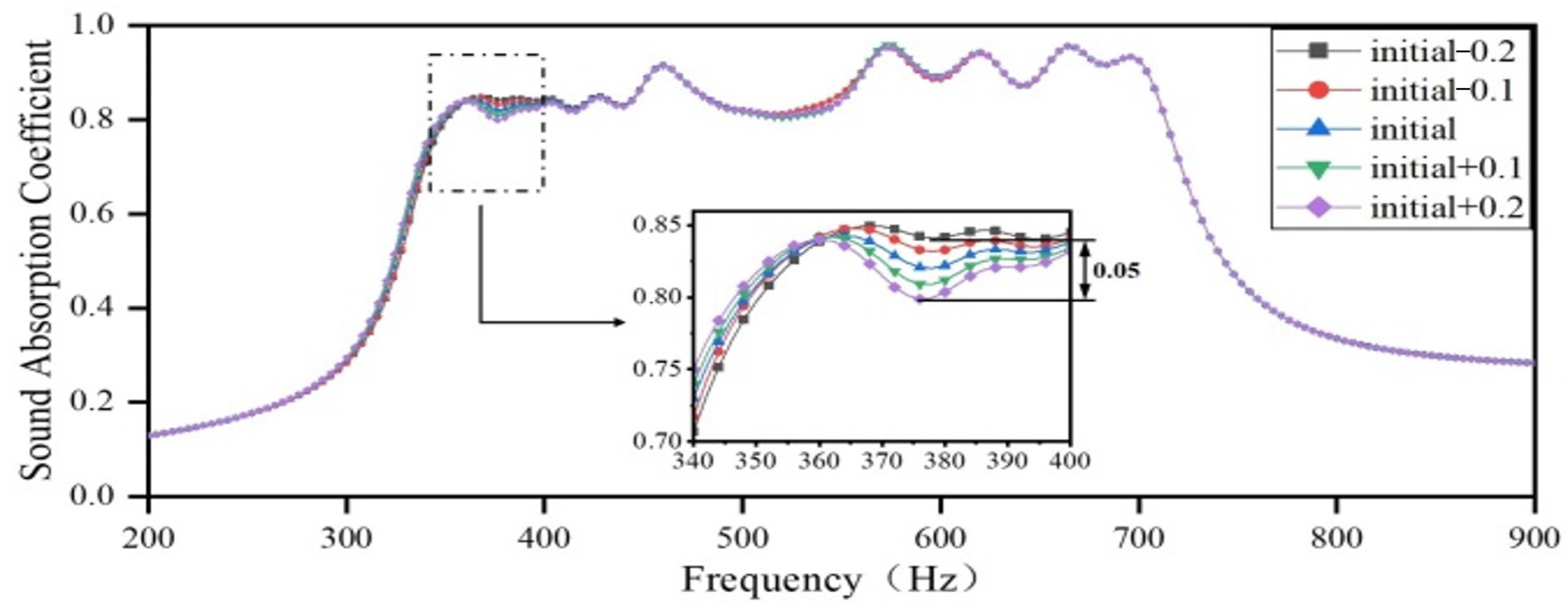
3.2.3. The Impact of the Depth of the Rear Cavity on the Sound Absorption Coefficient
4. Conclusions
- (1)
- The presented acoustic metamaterial with parallel unequal cavities can absorb a low-frequency noise in subwavelength dimensions and has high strength, making it easily manufacturable using additive manufacturing technology. Furthermore, the sound-absorbing bandwidth can be expanded by arranging the unit structures with different sound absorption frequency ranges in arrays. With excellent load-bearing and sound-absorbing capacity, the material has wide application prospects in acoustic engineering and construction.
- (2)
- The resonance frequencies of the individual cavities are designed according to the target sound absorption frequencies, and the initial structural parameters are selected with the aid of finite element analysis, which can largely reduce the burden of optimization. Then, the PSO algorithm adjusts the length of the embedded aperture to achieve a broadband, high-absorption coefficient acoustic metamaterial within the corresponding target frequency range.
- (3)
- The consistency of the experimental results with the optimization results reflects the accuracy and reliability of the design method. According to the presented design method, the acoustic metamaterial with a thickness of only 50 mm achieves an average absorption coefficient of 0.87 from 384 Hz to 667 Hz and an average coefficient of 0.81 from 324 Hz to 503 Hz. The acoustic metamaterial with a thickness of only 70 mm achieves an average absorption coefficient of 0.83 from 265 Hz to 525 Hz. The acoustic metamaterial, with a thickness of 110 mm, achieves an average absorption coefficient of 0.82 from 156 Hz to 250 Hz.
- (4)
- The parameter variation in different regions has varying impacts on the sound-absorbing capacity of the presented acoustic metamaterial. Among them, the change in diameter of the aperture and the small length of the embedded aperture have the most significant influence on the sound absorption coefficient, while variations in the depth of the rear cavity have a minor influence. This can guide the fabrication and processing of subsequent test samples.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, H.; Kwong, J.C.; Copes, R.; Tu, K.; Villeneuve, P.J.; van Donkelaar, A.; Hystad, P.; Martin, R.V.; Murray, B.J.; Jessiman, B.; et al. Living near major roads and the incidence of dementia, Parkinson’s disease, and multiple sclerosis: A population–based cohort study. Lancet 2017, 389, 718–726. [Google Scholar] [CrossRef]
- Munzel, T.; Sorensen, M.; Daiber, A. Transportation noise pollution and cardiovascular disease. Nat. Rev. Cardiol. 2021, 18, 619–636. [Google Scholar] [CrossRef] [PubMed]
- Guha, A.K.; Gokhale, S. Urban workers’ cardiovascular health due to exposure to traffic–originated PM(2.5) and noise pollution in different microenvironments. Sci. Total Environ. 2023, 859 Pt 1, 160268. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Su, J.; Jerrett, M.; Paul, K.C.; Lee, E.; Shih, I.F.; Haan, M.; Ritz, B. Air pollution and traffic noise interact to affect cognitive health in older Mexican Americans. Environ. Int. 2023, 173, 107810. [Google Scholar] [CrossRef]
- Jang, J.Y.; Park, C.S.; Song, K. Lightweight soundproofing membrane acoustic metamaterial for broadband sound insulation. Mech. Syst. Signal Process. 2022, 178, 109270. [Google Scholar] [CrossRef]
- Nguyen, H.; Wu, Q.; Chen, J.; Yu, Y.; Chen, H.; Tracy, S.; Huang, G. A broadband acoustic panel based on double–layer membrane–type metamaterials. Appl. Phys. Lett. 2021, 118, 184101. [Google Scholar] [CrossRef]
- Huang, Y.; Lv, M.; Luo, W.; Zhang, H.; Geng, D.; Li, Q. Sound insulation properties of membrane–type acoustic metamaterials with petal–like split rings. J. Phys. D Appl. Phys. 2022, 55, 045104. [Google Scholar] [CrossRef]
- Sun, Y.; Yuan, X.; Jin, Z.; Hong, G.; Chen, M.; Zhou, M.; Li, W.; Fang, D. An effective method to enhance the underwater sound absorption performance by constructing a membrane–type acoustic metamaterial. J. Phys. D Appl. Phys. 2022, 55, 435302. [Google Scholar] [CrossRef]
- Langfeldt, F.; Cheer, J. Controlling the effective surface mass density of membrane–type acoustic metamaterials using dynamic actuators. J. Acoust. Soc. Am. 2023, 153, 961–971. [Google Scholar] [CrossRef]
- Liu, X.; Liu, M.; Xin, F. Sound absorption of a perforated panel backed with perforated porous material: Energy dissipation of Helmholtz resonator cavity. Mech. Syst. Signal Process. 2023, 185, 109762. [Google Scholar] [CrossRef]
- Yang, X.; Shen, X.; Peng, W.; Zhu, D.; Song, H.; Hu, D.; Shen, C.; Xu, M.; Zhu, N.; Shi, Q. Online tunable sound absorbing acoustic metamaterial with optional aperture and adjustable cavity. Appl. Acoust. 2025, 231, 110556. [Google Scholar] [CrossRef]
- Yang, X.; Shen, X.; Yang, F.; Yin, Z.; Yang, F.; Yang, Q.; Shen, C.; Xu, M.; Wan, J. Acoustic metamaterials of modular nested Helmholtz resonators with multiple tunable absorption peaks. Appl. Acoust. 2023, 213, 109647. [Google Scholar] [CrossRef]
- Gai, X.-L.; Li, X.-H.; Guan, X.-W.; Xing, T.; Cai, Z.-N.; Hu, W.-C. Study on Acoustic Properties of Helmholtz-Type Honeycomb Sandwich Acoustic Metamaterials. Materials 2025, 18, 1600. [Google Scholar] [CrossRef] [PubMed]
- Zuo, G.; Huang, Z.; Ma, F. A tunable sub–wavelength acoustic imaging planar metalens. J. Phys. D Appl. Phys. 2023, 56, 145401. [Google Scholar] [CrossRef]
- Wu, F.; Zhang, X.; Ju, Z.; Zhao, J.; Hu, M.; Gao, M.; Luo, J.; Pu, H. Ultra–Broadband Sound Absorbing Materials Based on Periodic Gradient Impedance Matching. Front. Mater. 2022, 9, 909666. [Google Scholar] [CrossRef]
- Long, H.; Shao, C.; Cheng, Y.; Tao, J.; Liu, X. High absorption asymmetry enabled by a deep–subwavelength ventilated sound absorber. Appl. Phys. Lett. 2021, 118, 263502. [Google Scholar] [CrossRef]
- Guglielmelli, A.; Nemati, S.H.; Vasdekis, A.E.; De Sio, L. Stimuli responsive diffraction gratings in soft–composite materials. J. Phys. D Appl. Phys. 2019, 52, 053001. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Kumar, S.; Singh, S.K.; Bhushan, P.; Sahu, M.; Prakash, O. Ashok chakra–structured meta–structure as a perfect sound absorber for broadband low–frequency sound. Appl. Phys. Lett. 2020, 117, 191901. [Google Scholar] [CrossRef]
- Pavan, G.; Singh, S. Near–perfect sound absorptions in low–frequencies by varying compositions of porous labyrinthine acoustic metamaterial. Appl. Acoust. 2022, 198, 108974. [Google Scholar] [CrossRef]
- Cui, H.; Hu, Z.; Hu, H. Research on the low–frequency sound absorption characteristics of coiled Helmholtz cavity acoustic metamaterials. Adv. Mech. Eng. 2022, 14, 16878132221119996. [Google Scholar] [CrossRef]
- Huang, S.; Fang, X.; Wang, X.; Assouar, B.; Cheng, Q.; Li, Y. Acoustic perfect absorbers via Helmholtz resonators with embedded apertures. J. Acoust. Soc. Am. 2019, 145, 254–262. [Google Scholar] [CrossRef] [PubMed]
- Cheng, B.; Wang, M.; Gao, N.; Hou, H. Machine learning inversion design and application verification of a broadband acoustic filtering structure. Appl. Acoust. 2022, 187, 108522. [Google Scholar] [CrossRef]
- Ren, Z.; Cheng, Y.; Chen, M.; Yuan, X.; Fang, D. A compact multifunctional metastructure for Low–frequency broadband sound absorption and crash energy dissipation. Mater. Des. 2022, 215, 110462. [Google Scholar] [CrossRef]
- Li, H.; Wu, J.; Yan, S.; Mao, Q. Design and study of broadband sound absorbers with partition based on micro–perforated panel and Helmholtz resonator. Appl. Acoust. 2023, 205, 109262. [Google Scholar] [CrossRef]
- Lu, H.-C.; Tseng, H.-Y.; Lin, S.-W. Double–track particle swarm optimizer for nonlinear constrained optimization problems. Inf. Sci. 2023, 622, 587–628. [Google Scholar] [CrossRef]
- Ning, Y.; Li, T.; Du, W.; Yao, C.; Zhang, Y.; Shao, J. Inverse kinematics and planning/control co–design method of redundant manipulator for precision operation: Design and experiments. Robot. Comput. Integr. Manuf. 2023, 80, 102457. [Google Scholar] [CrossRef]
- Huang, Z.; Shao, G.; Zhou, D.; Deng, X.; Qiao, J.; Li, L. 3D printing of high–precision and ferromagnetic functional devices. Int. J. Extrem. Manuf. 2023, 5, 035501. [Google Scholar] [CrossRef]
- Grabulosa, A.; Moughames, J.; Porte, X.; Kadic, M.; Brunner, D. Additive 3D photonic integration that is CMOS compatible. Nanotechnology 2023, 34, 322002. [Google Scholar] [CrossRef]
- Makridis, A.; Okkalidis, N.; Trygoniaris, D.; Kazeli, K.; Angelakeris, M. Composite magnetic 3D–printing filament fabrication protocol opens new perspectives in magnetic hyperthermia. J. Phys. D Appl. Phys. 2023, 56, 285002. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y.; Tao, L.; Wang, T.; Wan, Q. Integrated printing of high–strength, high–shape–retaining polyimide and its composite gradient structures for enhanced tribological properties. Addit. Manuf. 2023, 65, 103440. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, H.; Lian, Z.; Tan, B.; Zheng, Y.; Erdun, E. Numerical simulation for porous hemp plastic composites sound absorption properties. J. Mater. Res. Technol. JmrT 2022, 19, 2458–2469. [Google Scholar] [CrossRef]
- Mo, Z.; Song, G.; Hou, K.; Bolton, J.S. An iterative transfer matrix approach for estimating the sound speed and attenuation constant of air in a standing wave tube. J. Acoust. Soc. Am. 2022, 151, 4016–4027. [Google Scholar] [CrossRef] [PubMed]
- Ryoo, H.; Jeon, W. Broadband sound absorption using multiple hybrid resonances of acoustic metasurfaces. Int. J. Mech. Sci. 2022, 229, 107508. [Google Scholar] [CrossRef]
- Yang, X.; Li, Q.; Shen, X.; Zhou, B.; Wang, N.; Wang, E.; Zhang, X.; Shen, C.; Wang, H.; Jiang, S. Interlayer Parallel Connection of Multiple Helmholtz Resonators for Optional Broadband Low Frequency Sound Absorption. Materials 2025, 18, 682. [Google Scholar] [CrossRef]
- Rafique, F.; Wu, J.H.; Liu, C.R.; Ma, F. Transmission Loss analysis of a simple expansion chamber muffler with extended inlet and outlet combined with inhomogeneous micro–perforated panel (iMPP). Appl. Acoust. 2022, 194, 108808. [Google Scholar] [CrossRef]
- Yang, X.; Wang, E.; Shen, X.; Peng, W.; Zhu, D.; Song, H.; Hu, D.; Shen, C.; Xu, M.; Li, Z.; et al. Multilayer stackable grouped acoustic metamaterial with optional sound absorption performance. J. Appl. Phys. 2025, 137, 123104. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, C. Broadband and low–frequency sound absorption by a slit–perforated multi–layered porous metamaterial. Eng. Struct. 2023, 281, 115743. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, T.; Xin, F.; Zhu, J.; Ding, W. New–parallel connection of the Helmholtz resonator with embedded apertures for low–frequency broadband sound absorption. Jpn. J. Appl. Phys. 2022, 61, 077001. [Google Scholar] [CrossRef]
- Yang, D.; Morgans, A.S. A semi–analytical model for the acoustic impedance of finite length circular holes with mean flow. J. Sound Vib. 2016, 384, 294–311. [Google Scholar] [CrossRef]
- Li, M.; Wu, J.; Wu, B.; Ma, F.; Liu, C.; Yuan, X.; Sun, Y. An ultra–thin low–frequency broadband metasurface with near–zero suppression of aerodynamic acoustic pressure. Appl. Acoust. 2023, 203, 109166. [Google Scholar] [CrossRef]
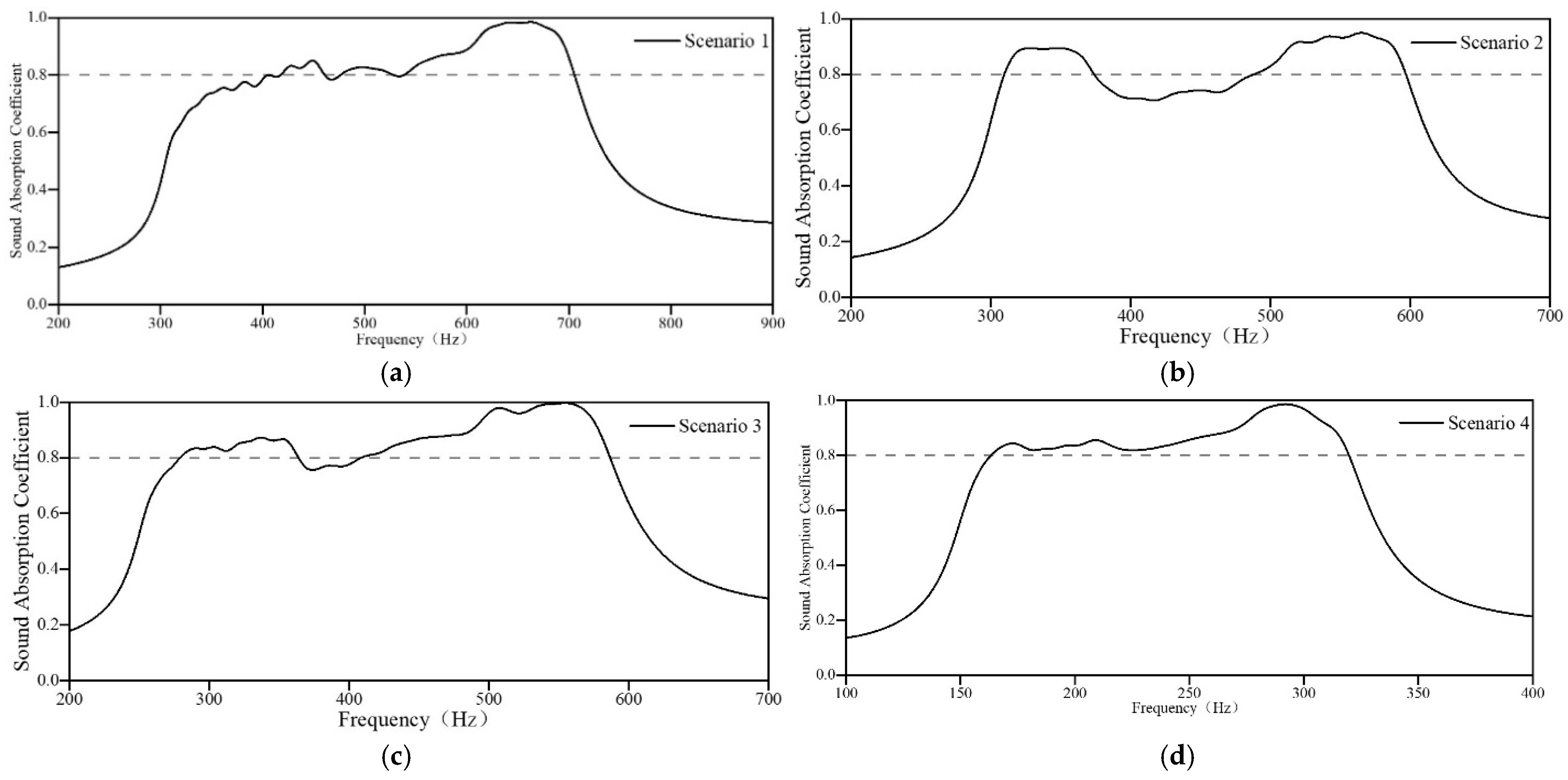
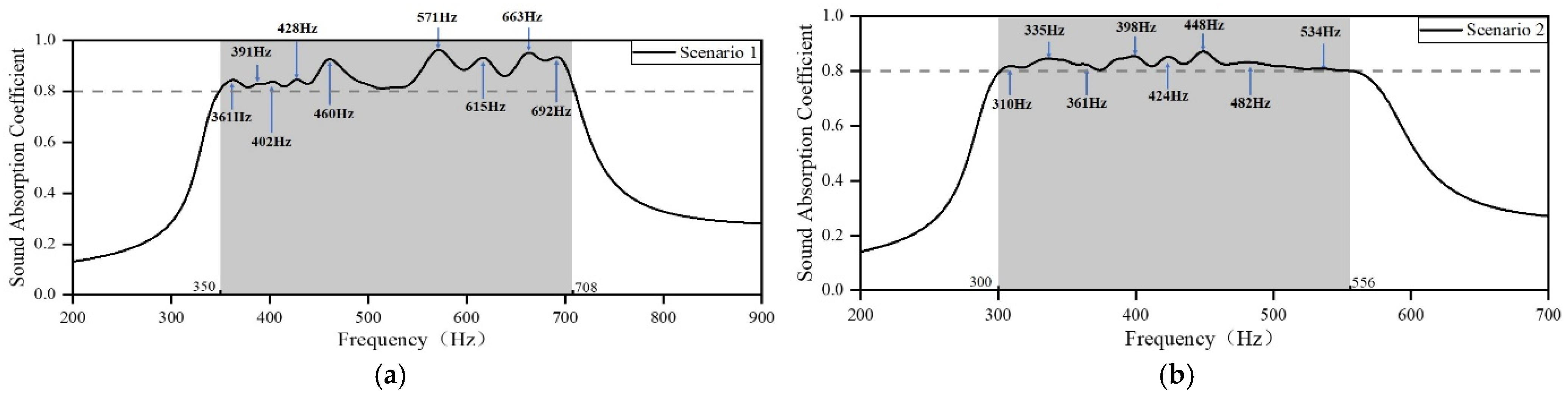
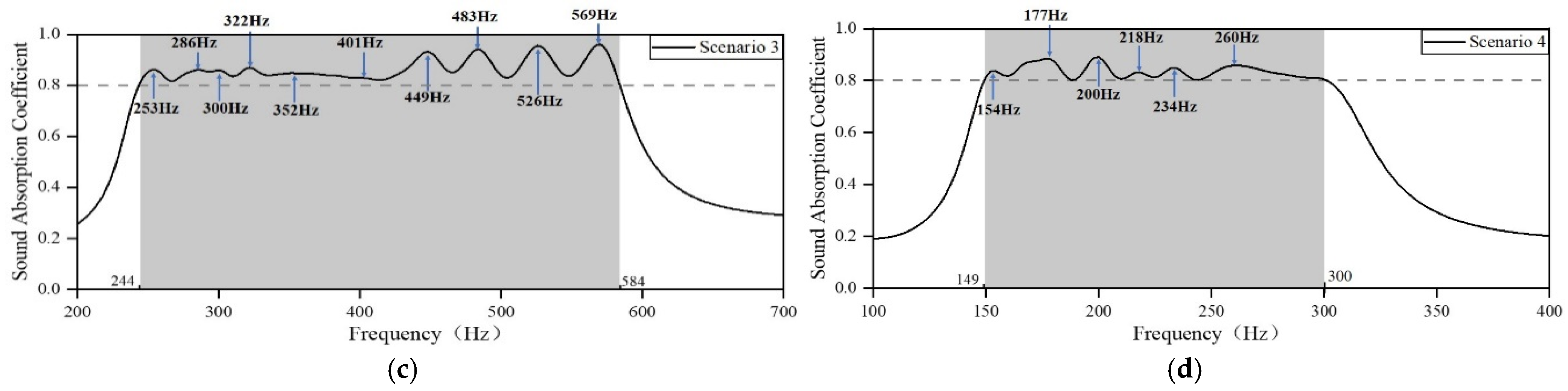

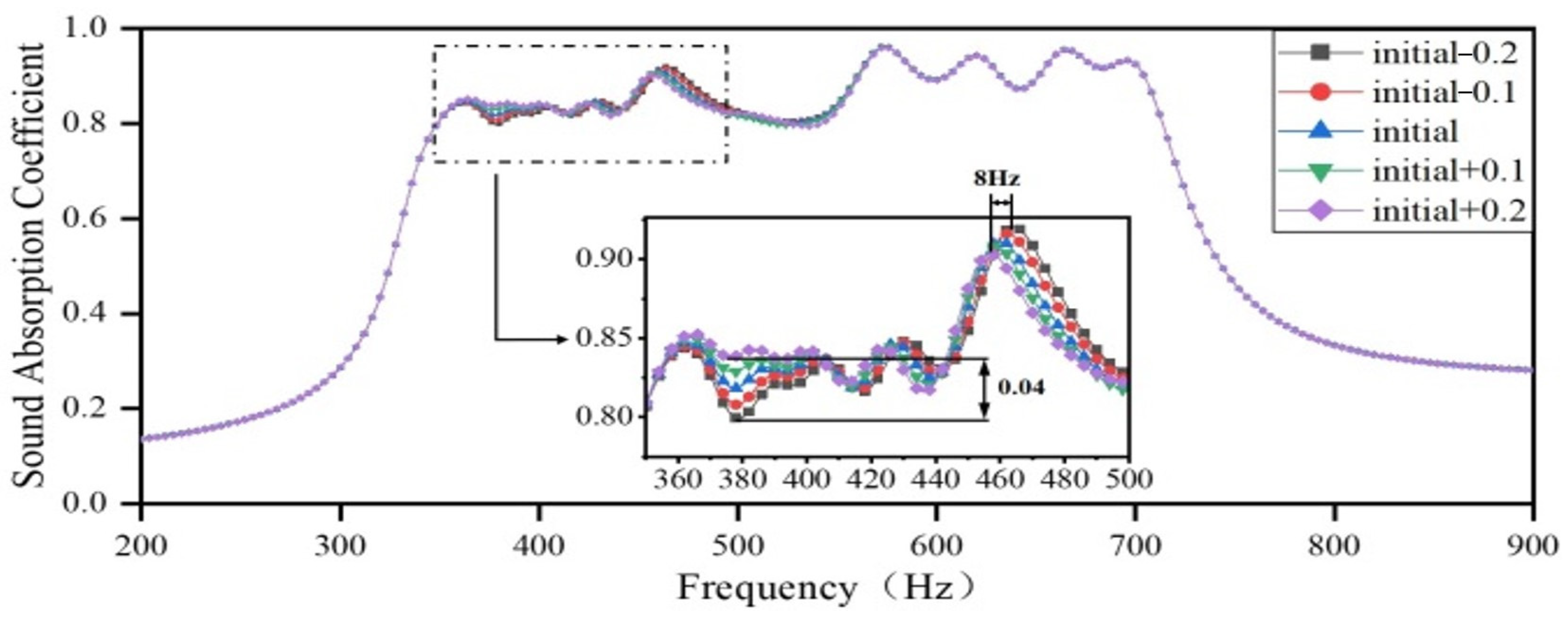
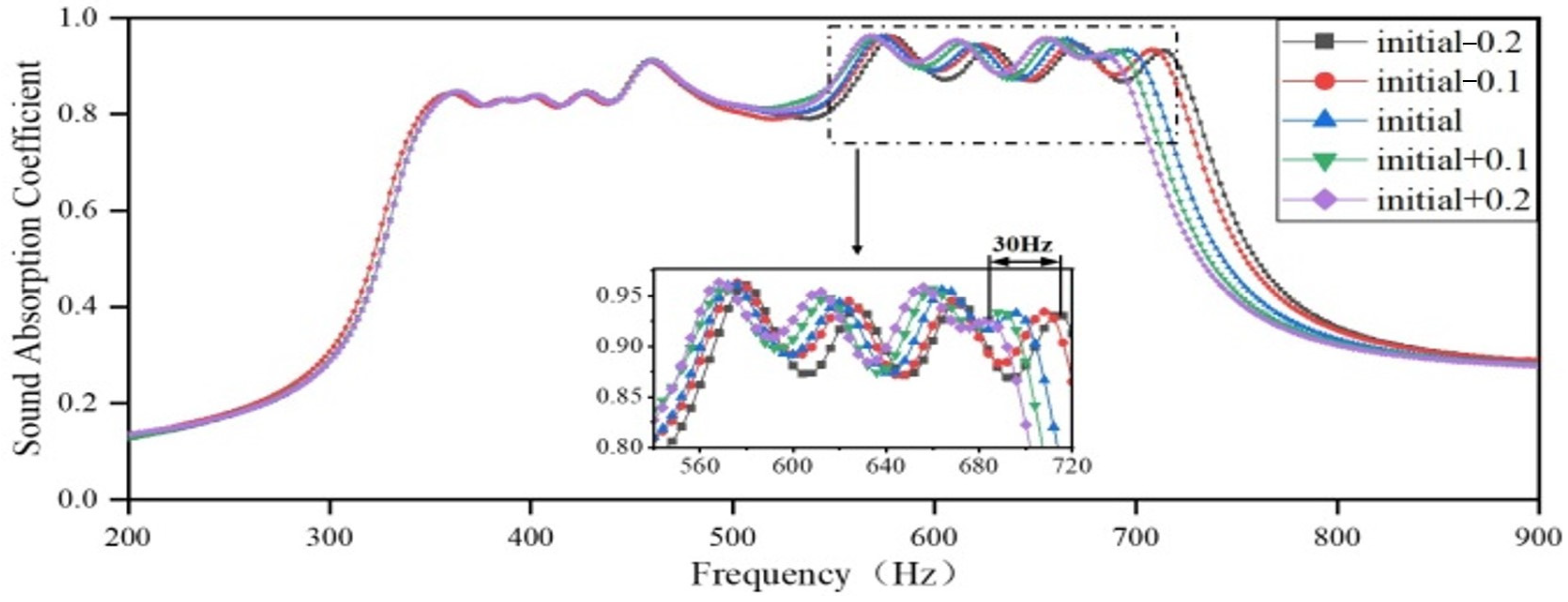
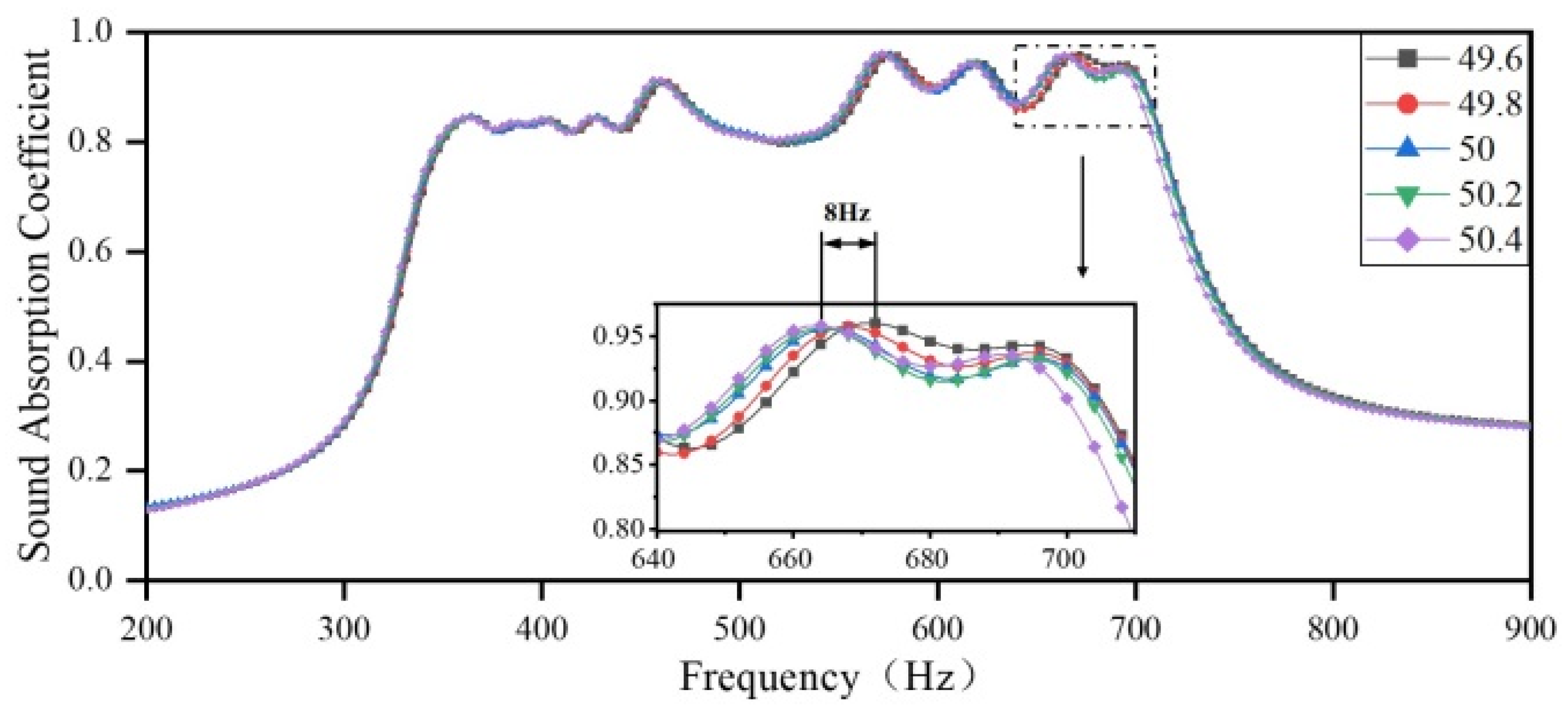
| Scenario | Installable Dimension/mm | Noise Frequency Range/Hz | Target Frequency Range/Hz | Target Sound Absorption Coefficient |
|---|---|---|---|---|
| 1 | 50 | 400–600 | 350–650 | ≥0.8 |
| 2 | 50 | 350–500 | 300–550 | ≥0.8 |
| 3 | 70 | 300–500 | 250–550 | ≥0.8 |
| 4 | 110 | 175–250 | 150–300 | ≥0.8 |
| Region | Thickness/mm | Thickness of Wall/mm | Diameter of Aperture/mm |
|---|---|---|---|
| 1 | 50 | 2 | 2.98 |
| 2 | 3.65 | ||
| 3 | 3.90 | ||
| 4 | 4.14 |
| Region | Serial Number | Resonance Frequency/Hz | |||
|---|---|---|---|---|---|
| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | ||
| 1 | 1 | 450 | 370 | 360 | 210 |
| 2 | 470 | 390 | 380 | 220 | |
| 3 | 490 | 410 | 400 | 230 | |
| 4 | 510 | 430 | 420 | 240 | |
| 5 | 530 | 450 | 440 | 250 | |
| 6 | 550 | 470 | 460 | 260 | |
| 2 | 7 | 305 | 300 | 250 | 150 |
| 8 | 320 | 305 | 260 | 155 | |
| 9 | 335 | 310 | 270 | 160 | |
| 10 | 350 | 315 | 280 | 165 | |
| 3 | 11 | 370 | 325 | 295 | 170 |
| 12 | 390 | 335 | 310 | 180 | |
| 13 | 410 | 345 | 325 | 190 | |
| 14 | 430 | 355 | 340 | 200 | |
| 4 | 15 | 575 | 490 | 475 | 270 |
| 16 | 600 | 510 | 500 | 280 | |
| 17 | 625 | 530 | 525 | 290 | |
| 18 | 650 | 550 | 550 | 300 | |
| Region | Serial Number | Initial Length of the Embedded Aperture/mm | |||
|---|---|---|---|---|---|
| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | ||
| 1 | 1 | 6.765 | 12.125 | 7.228 | 15.965 |
| 2 | 6.100 | 10.532 | 6.002 | 14.214 | |
| 3 | 5.401 | 9.025 | 5.098 | 12.658 | |
| 4 | 4.462 | 7.997 | 4.430 | 11.266 | |
| 5 | 3.917 | 6.765 | 3.829 | 10.211 | |
| 6 | 3.498 | 6.100 | 3.100 | 9.247 | |
| 2 | 7 | 19.213 | 19.998 | 19.150 | 34.489 |
| 8 | 16.990 | 19.213 | 17.348 | 31.964 | |
| 9 | 15.023 | 18.433 | 15.500 | 29.652 | |
| 10 | 13.378 | 17.721 | 14.261 | 27.492 | |
| 3 | 11 | 13.758 | 19.410 | 14.930 | 30.057 |
| 12 | 11.852 | 17.931 | 12.956 | 26.122 | |
| 13 | 10.303 | 16.678 | 11.472 | 23.001 | |
| 14 | 8.952 | 15.395 | 9.995 | 20.002 | |
| 4 | 15 | 3.738 | 6.897 | 3.751 | 10.501 |
| 16 | 3.240 | 6.000 | 2.855 | 9.450 | |
| 17 | 2.719 | 5.200 | 2.310 | 8.633 | |
| 18 | 2.289 | 4.543 | 2.000 | 7.496 | |
| Region | Serial Number | Optimized Length of Embedded Aperture/mm | |||
|---|---|---|---|---|---|
| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | ||
| 1 | 1 | 3.41 | 3.49 | 4.92 | 5.78 |
| 2 | 3.98 | 3.87 | 5.77 | 6.29 | |
| 3 | 4.82 | 4.52 | 6.71 | 7.41 | |
| 4 | 5.55 | 5.21 | 7.62 | 8.52 | |
| 5 | 6.39 | 5.88 | 8.50 | 9.39 | |
| 6 | 7.17 | 6.50 | 9.43 | 10.10 | |
| 2 | 7 | 11.94 | 17.79 | 17.62 | 32.37 |
| 8 | 12.82 | 18.91 | 18.68 | 33.12 | |
| 9 | 13.73 | 20.00 | 19.83 | 33.79 | |
| 10 | 14.55 | 21.15 | 20.95 | 34.51 | |
| 3 | 11 | 8.31 | 15.18 | 12.78 | 28.21 |
| 12 | 10.10 | 17.02 | 15.02 | 28.34 | |
| 13 | 11.67 | 18.61 | 17.01 | 32.85 | |
| 14 | 13.14 | 20.02 | 18.84 | 32.94 | |
| 4 | 15 | 2.21 | 10.67 | 2.05 | 17.81 |
| 16 | 2.89 | 12.51 | 3.19 | 21.16 | |
| 17 | 3.90 | 14.52 | 4.54 | 26.18 | |
| 18 | 5.22 | 15.06 | 5.96 | 26.30 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, T.; Yang, F.; Jiang, C.; Shen, X.; Yang, X.; Peng, W.; Sun, Z.; Wang, E.; Dai, J.; Zhu, J. Structural Optimization and Performance Analysis of Acoustic Metamaterials with Parallel Unequal Cavities. Materials 2025, 18, 3087. https://doi.org/10.3390/ma18133087
Pan T, Yang F, Jiang C, Shen X, Yang X, Peng W, Sun Z, Wang E, Dai J, Zhu J. Structural Optimization and Performance Analysis of Acoustic Metamaterials with Parallel Unequal Cavities. Materials. 2025; 18(13):3087. https://doi.org/10.3390/ma18133087
Chicago/Turabian StylePan, Tengyue, Fei Yang, Chengming Jiang, Xinmin Shen, Xiaocui Yang, Wenqiang Peng, Zhidan Sun, Enshuai Wang, Juying Dai, and Jingwei Zhu. 2025. "Structural Optimization and Performance Analysis of Acoustic Metamaterials with Parallel Unequal Cavities" Materials 18, no. 13: 3087. https://doi.org/10.3390/ma18133087
APA StylePan, T., Yang, F., Jiang, C., Shen, X., Yang, X., Peng, W., Sun, Z., Wang, E., Dai, J., & Zhu, J. (2025). Structural Optimization and Performance Analysis of Acoustic Metamaterials with Parallel Unequal Cavities. Materials, 18(13), 3087. https://doi.org/10.3390/ma18133087









