Partially Disordered Crystal Phases and Glassy Smectic Phases in Liquid Crystal Mixtures
Abstract
1. Introduction
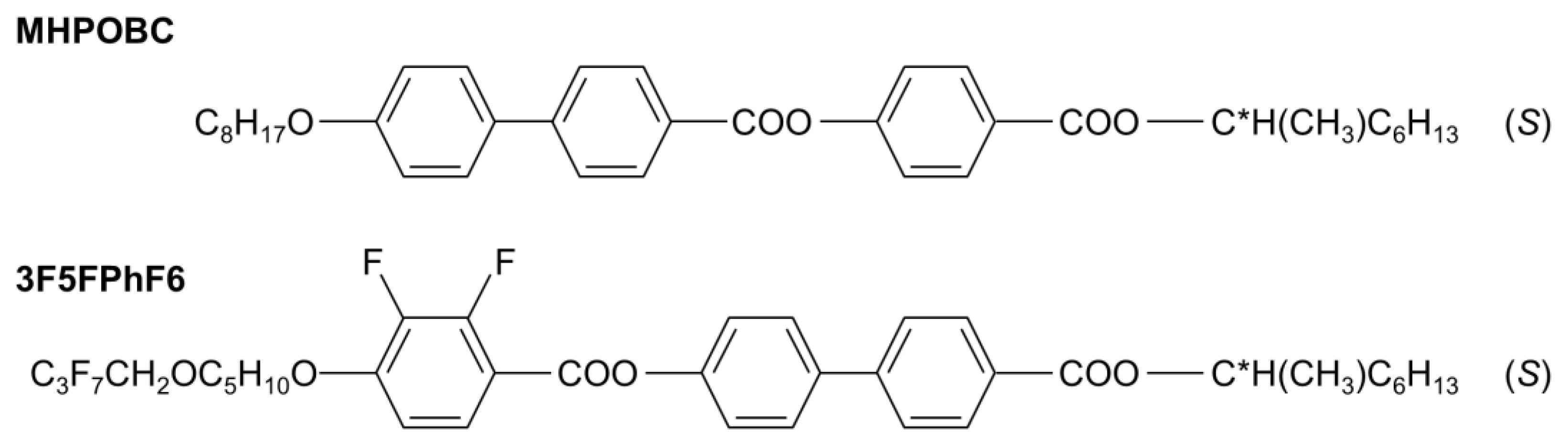
2. Materials and Methods
- MIX5FF6-1, MHPOBC:3F5FPhF6 molar ratio 0.8992(4):0.1008(3);
- MIX5FF6-2, MHPOBC:3F5FPhF6 molar ratio 0.7505(4):0.2495(3);
- MIX5FF6-3, MHPOBC:3F5FPhF6 molar ratio 0.4986(5):0.5014(4).
3. Results and Discussion
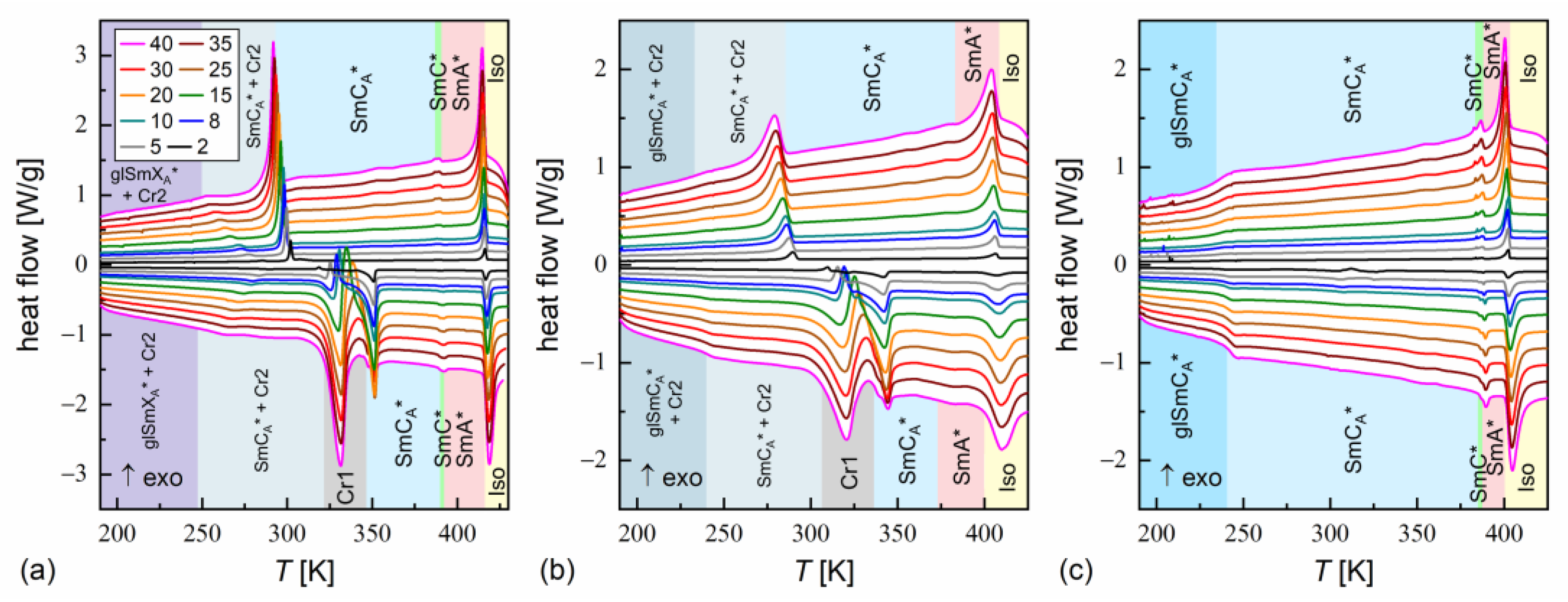
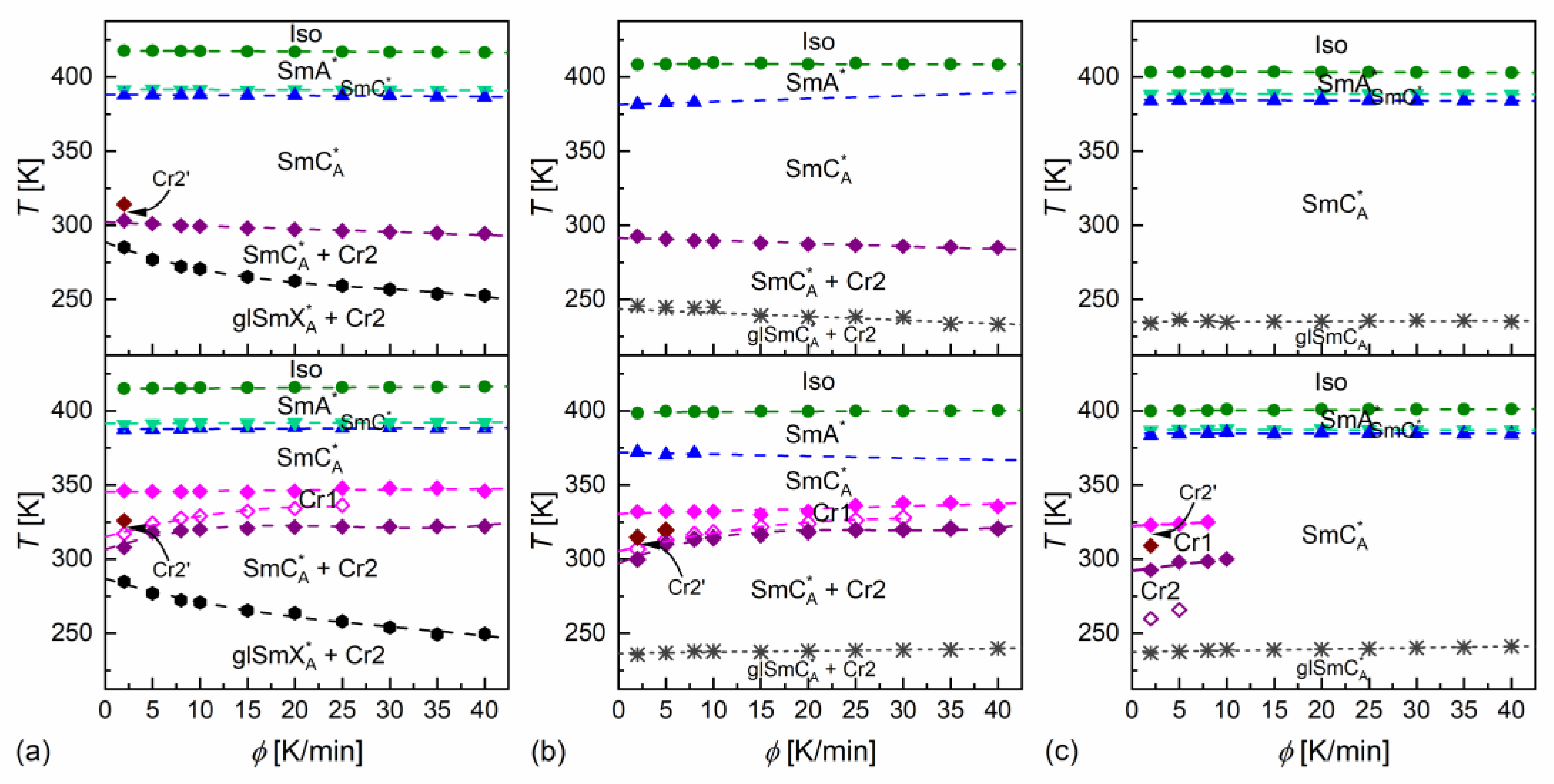
3.1. Phase Sequence
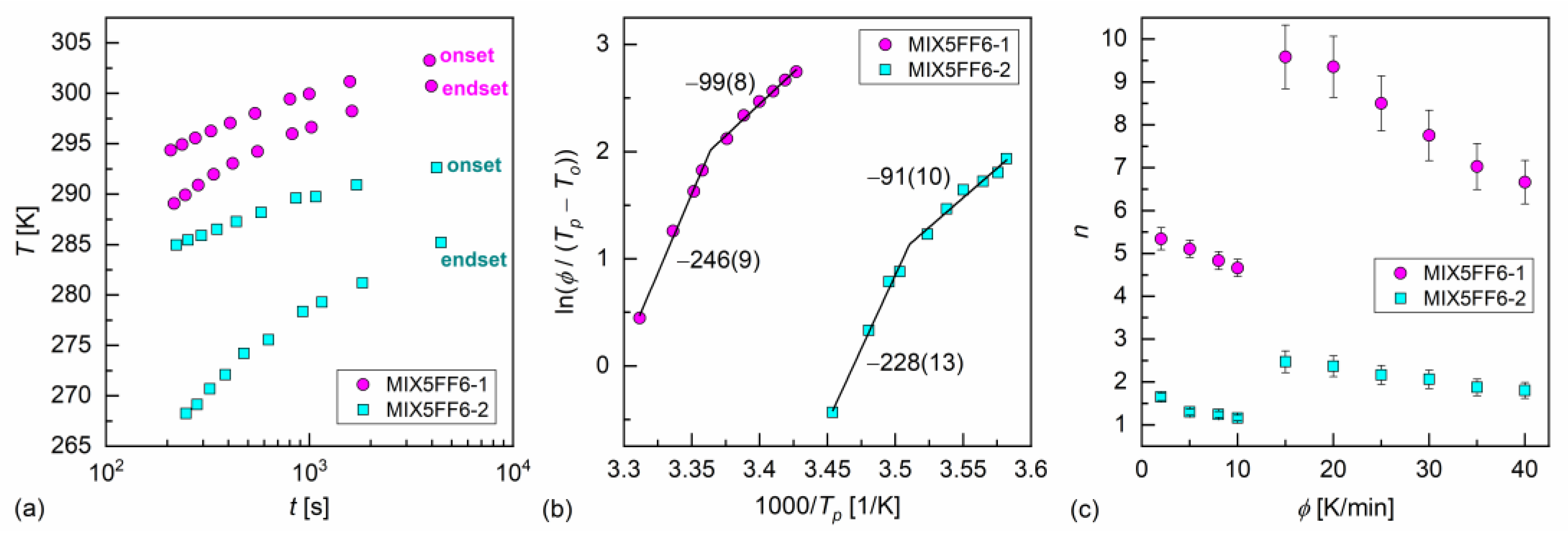
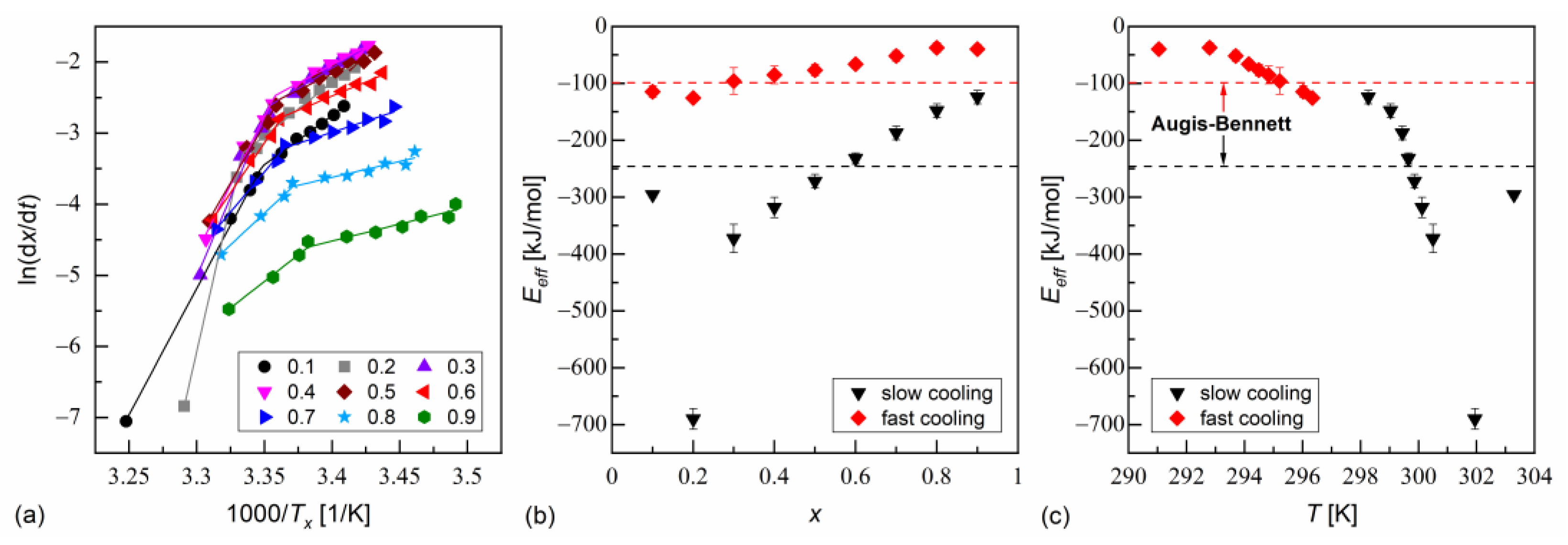
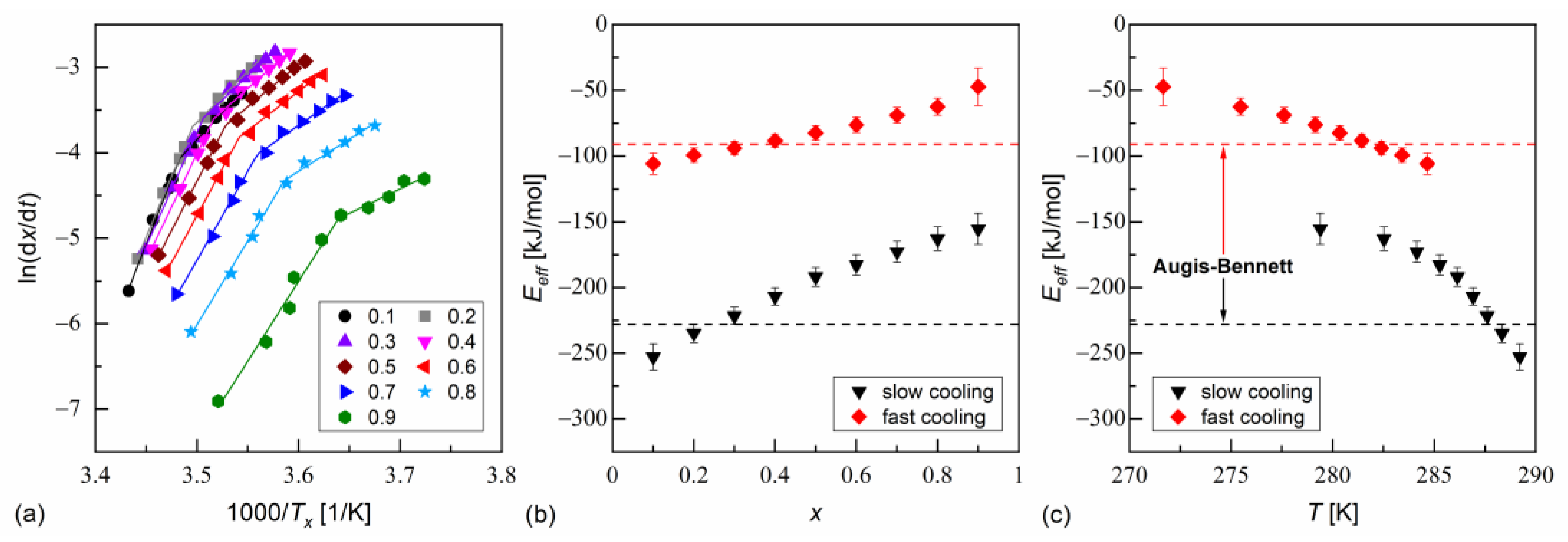
3.2. Crystallization Kinetics
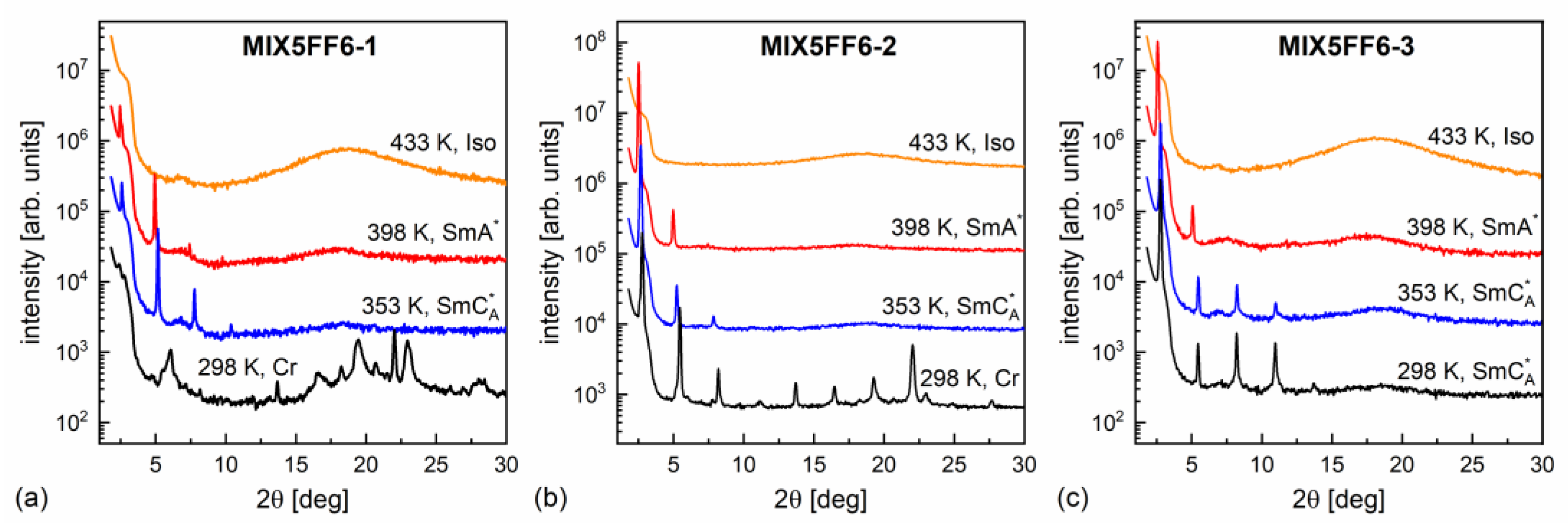
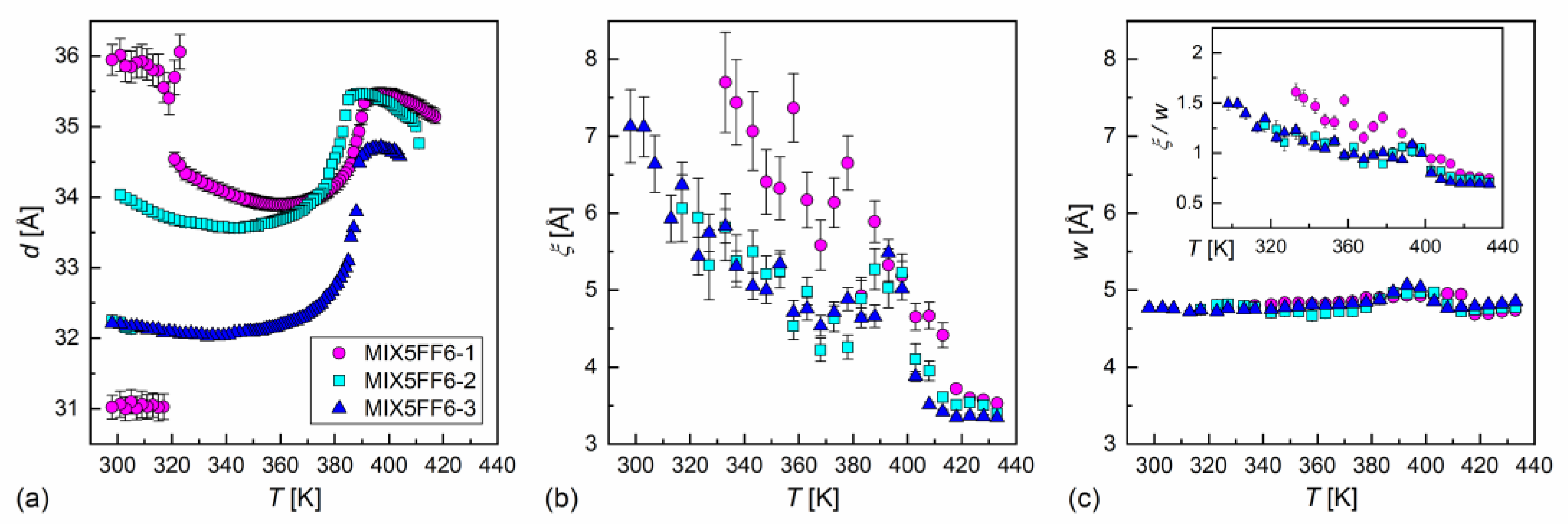
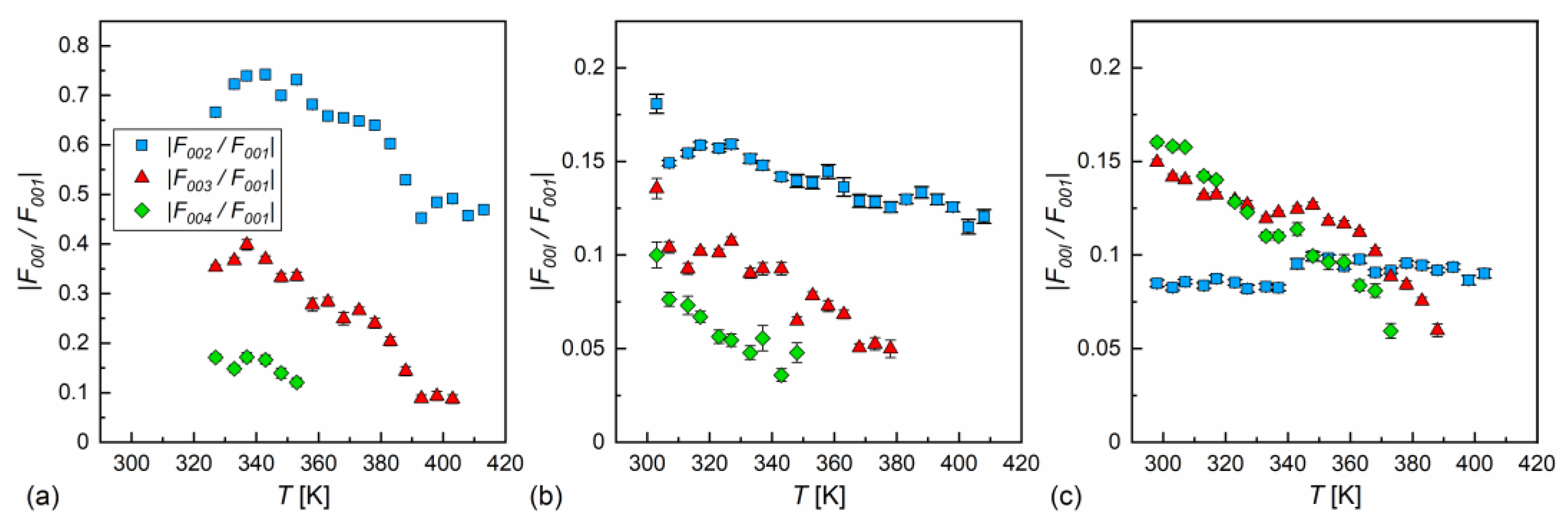
3.3. Structure of Smectic Phases
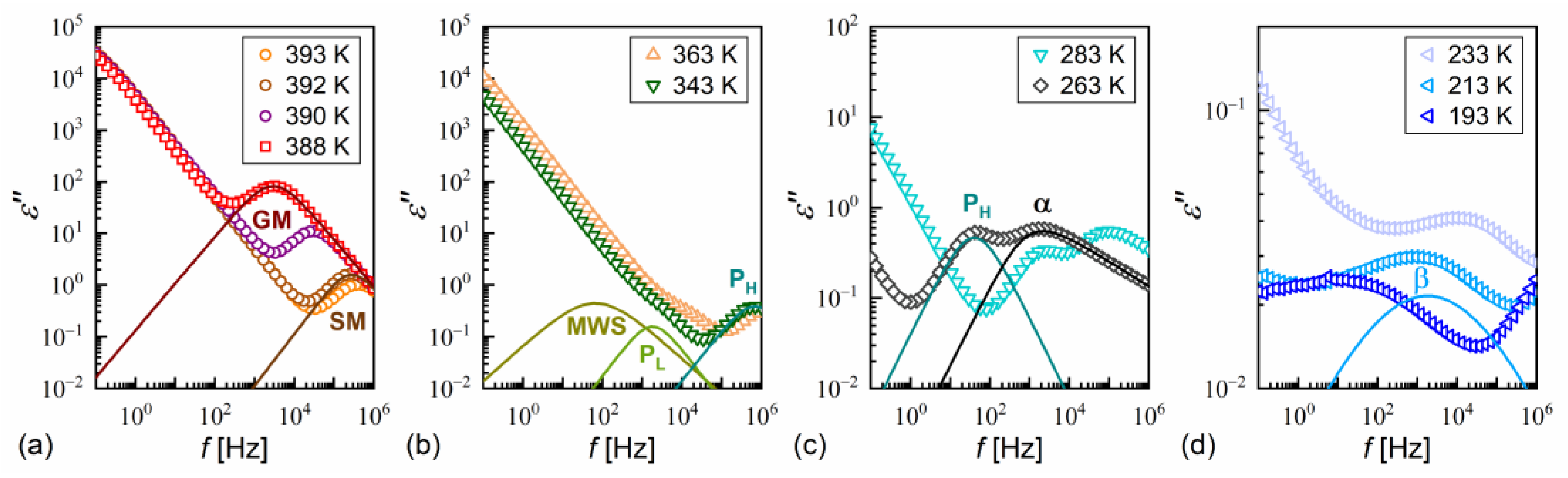
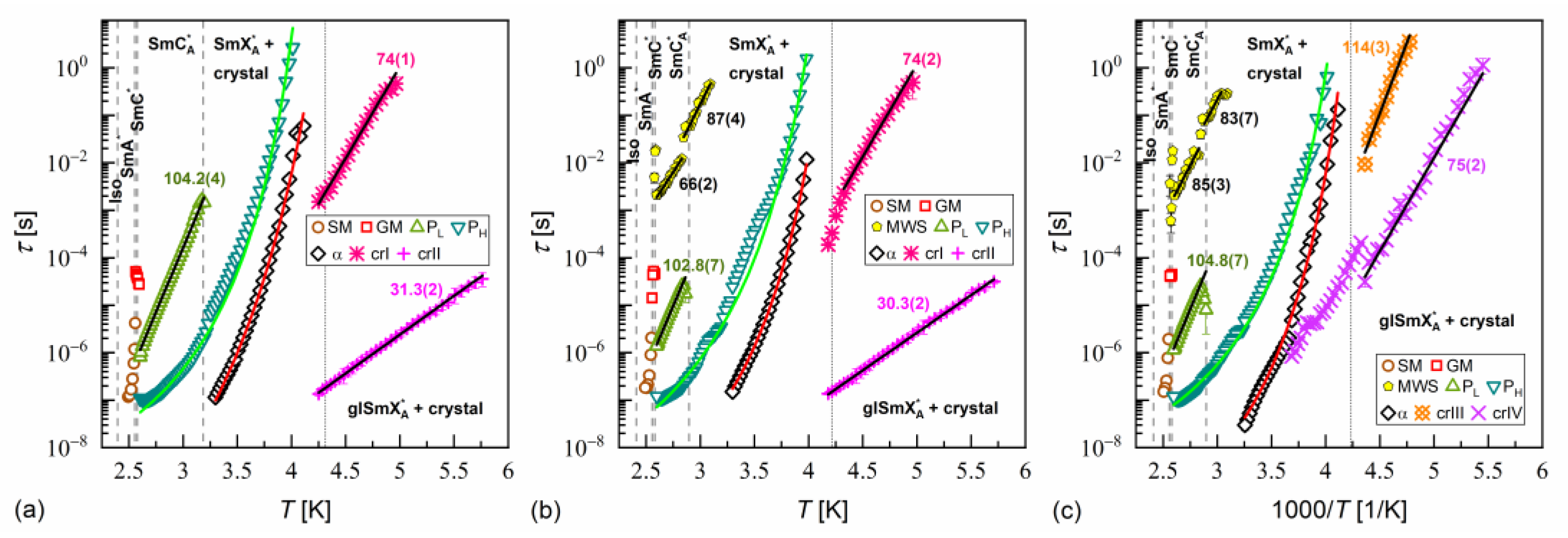
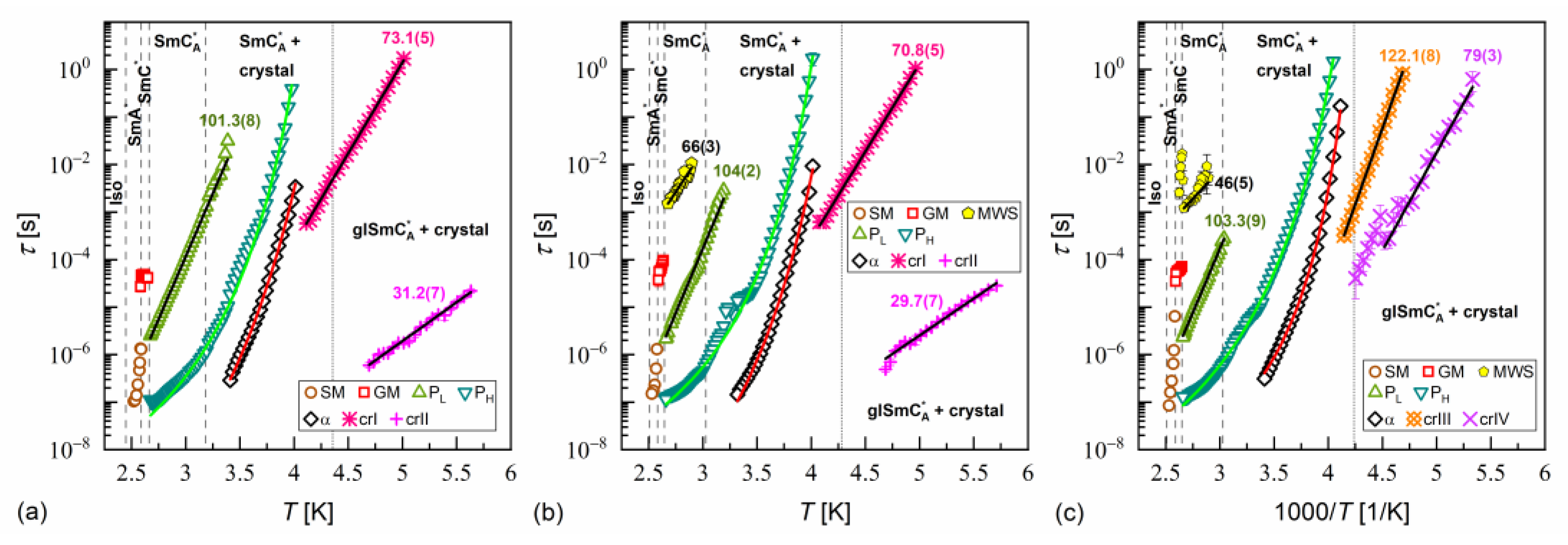
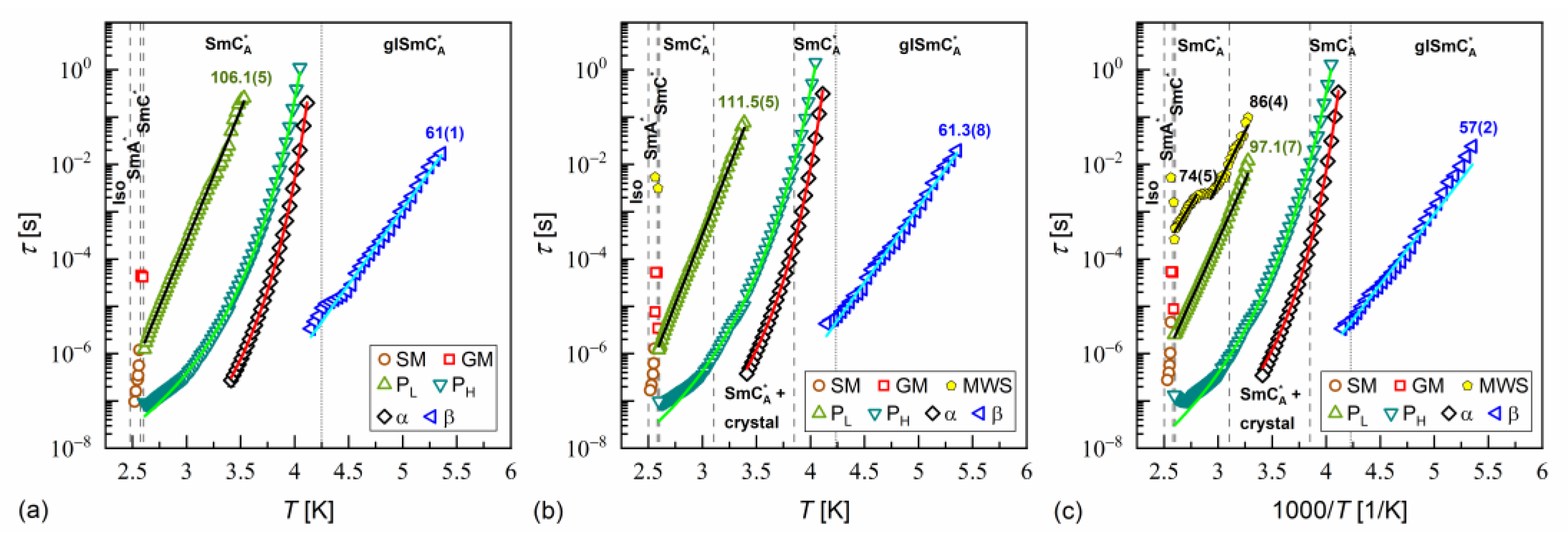
3.4. Dielectric Relaxation Processes
- PL and PH processes (Figure 12b), related to in-phase and anti-phase fluctuations in the phase of the tilt, typical for the SmCA* phase, with a much smaller dielectric increment than for GM and relaxation time increasing with decreasing temperature; the PL process overlapped with rotations around the short molecular axis (s-process) [64,65,66].
- The primary α-process (Figure 12c) had a relaxation time that increased with decreasing temperature, usually in the super-Arrhenius manner, and reached 100 s at the glass transition temperature [32,34]. The α-relaxation has different origins in various substances [32,35,45,68,69] and in the SmCA* phase, it can be related to rotations around the molecular long axis. The dielectric strength of the α-process is comparable to that of the PH process;
- The secondary β-process (Figure 12d) involved a smaller dielectric increment than the α-process and showed an Arrhenius dependence of the relaxation time on temperature, originating either from movements of the rigid molecules (genuine Johari–Goldstein relaxation) or from intramolecular rotation within flexible molecules (pseudo-Johari–Goldstein relaxation) [69].
4. Conclusions
- (1)
- Based on the XRD results, the hexatic SmXA* phase was detected only in MIX5FF6-1, with a continuous increase in the layer spacing during the SmCA* → SmXA* transition and larger correlation length of the intra-layer short-range positional order in the preceding SmCA* phase compared with mixtures with a larger fraction of 3F5FPhF6;
- (2)
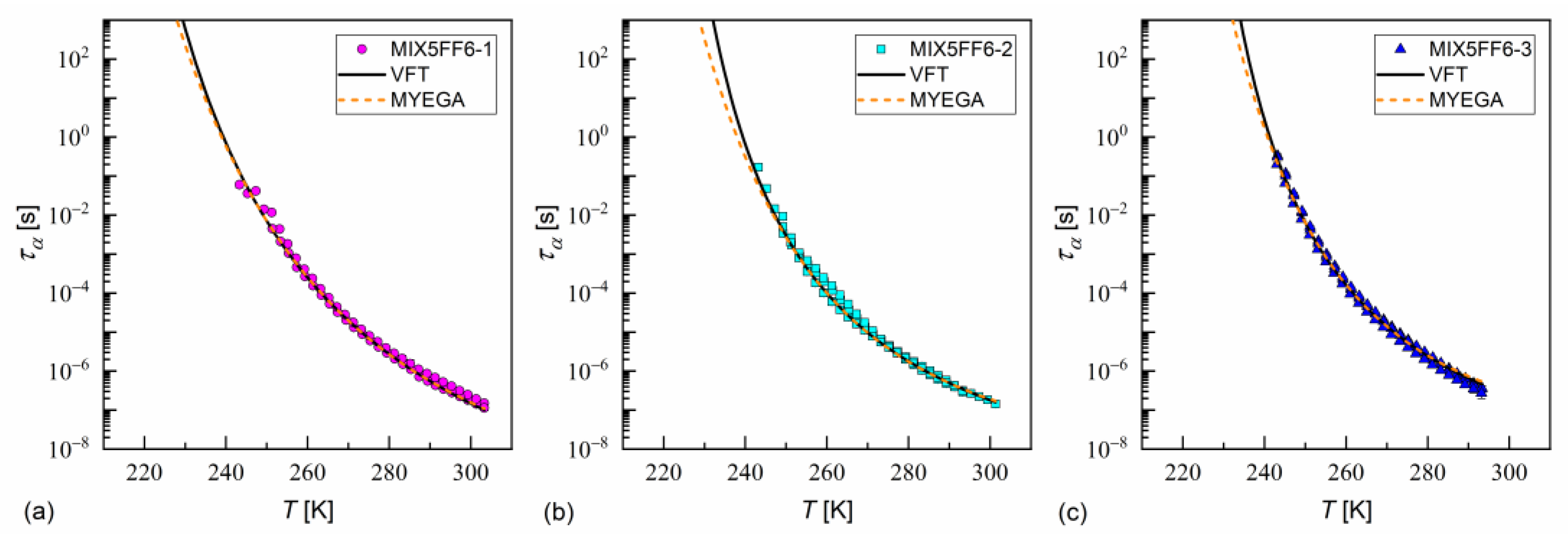
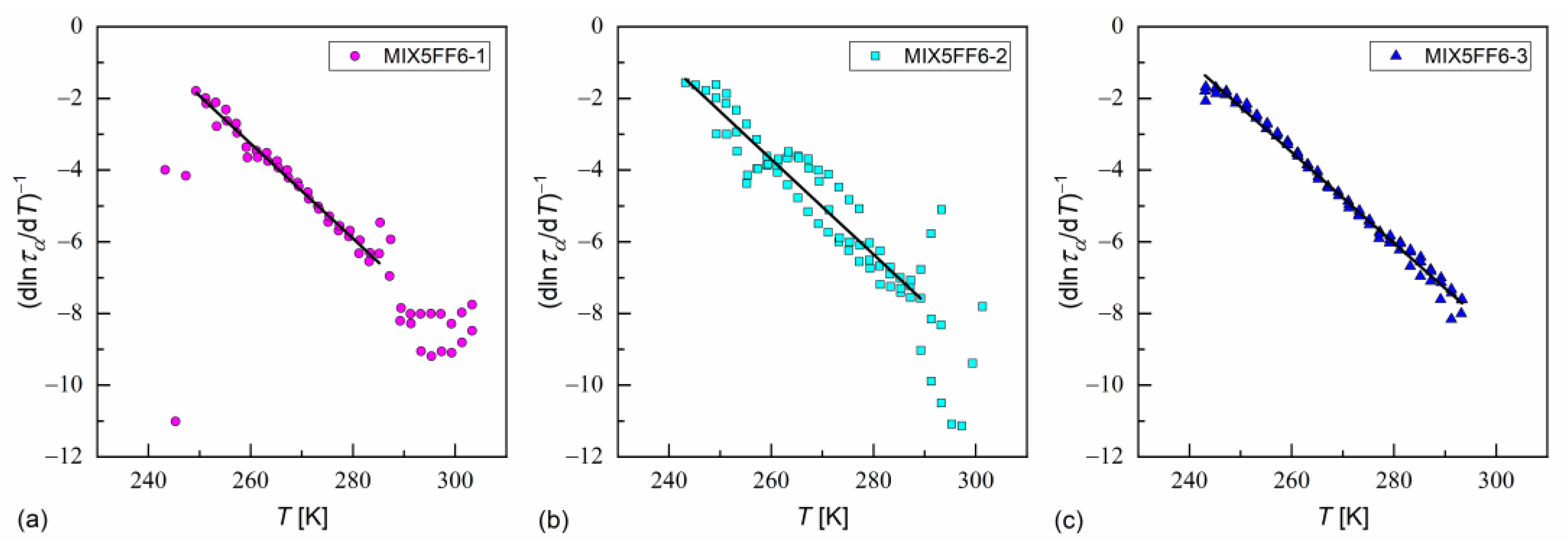
- Only the equimolar MIX5FF6-3 mixture showed good glassforming properties in the smectic state; no crystallization was observed on cooling at 2–40 K/min. The crystal phase appeared only during heating in the process of cold crystallization. The glassforming properties of MIX5FF6-3 were better than pure 3F5FPhF6, where a cooling rate of at least 10 K/min was necessary to avoid partial crystallization [27]. MIX5FF6-1 and MIX5FF6-2, with smaller fractions of 3F5FPhF6, underwent partial melt crystallization on cooling and formed orientationally disordered (ODIC) crystal phases. However, the remaining fraction of SmXA* in MIX5FF6-1 and SmCA* in MIX5FF6-2 underwent glass transition. The glass transition temperatures were similar for all mixtures, 231–236 K, slightly lower than for pure 3F5FPhF6 [27]. MIX5FF6-1, -2, -3 are fragile glassformers, with the fragility index exceeding 50, corresponding to significant deviation of the α-relaxation time from the Arrhenius dependence on temperature. Analysis by the MYEGA model indicated a larger effective activation barrier or smaller number of topological degrees of freedom in MIX5FF6-1, forming glass in the hexatic SmXA* phase, compared with MIX5FF6-2, MIX5FF6-3, and 3F5FPhF6 where glass formed in the SmCA* phase.
- (3)
- Pure SmXA* glass was not obtained in the MHPOBC: 3F5FPhF6 system at moderate cooling rates; MIX5FF6-1 partially crystallized during cooling at 2–40 K/min, and only some fraction of the sample formed the SmXA* glass.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 3F5FPhF6 | (S)-4′-(1-methylheptyloxycarbonyl)biphenyl-4-yl 4-[5-(2,2,3,3,4,4,4-heptafluorobutoxy)pentyl-1-oxy]-2,3-difluorobenzoate |
| BDS | broadband dielectric spectroscopy |
| DOBAMBC | p-decyloxybenzylidene p’-amino 2-methyl butyl cinnamate |
| DSC | differential scanning calorimetry |
| GM | Goldstone mode |
| MHPOBC | (S)-4-[(1-methylheptyloxy)carbonyl]phenyl 4′-octyloxy-4-biphenylcarboxylate |
| MIX5FF6-1 | MHPOBC: 3F5FPhF6 mixture with 0.9: 0.1 molar ratio |
| MIX5FF6-2 | MHPOBC: 3F5FPhF6 mixture with 0.75: 0.25 molar ratio |
| MIX5FF6-3 | MHPOBC: 3F5FPhF6 mixture with 0.5: 0.5 molar ratio |
| MWS | Maxwell–Wagner–Sillars |
| MYEGA | Mauro–Yue–Ellison–Gupta–Allan |
| ODIC | orientationally disordered crystal |
| POM | polarizing optical microscopy |
| SM | soft mode |
| VFT | Vogel–Fulcher–Tammann |
| XRD | X-ray diffraction |
References
- Wunderlich, B.; Grebowicz, J. Thermotropic mesophases and mesophase transitions of linear, flexible macromolecules. In Liquid Crystal Polymers II/III. Advances in Polymer Science; Platé, N.A., Ed.; Springer: Berlin/Heidelberg, Germany, 1984; Volume 60/61. [Google Scholar] [CrossRef]
- Seddon, J.M. Structural studies of Liquid Crystals by X-ray Diffraction. In Handbook of Liquid Crystals; Demus, D., Goodby, J., Gray, G.W., Spiess, H.-W., Vill, V., Eds.; WILEY-VCH Verlag GmbH: Weinheim, Germany, 1998. [Google Scholar]
- Als-Nielsen, J.; Litster, J.D.; Birgeneau, R.J.; Kaplan, M.; Safinya, C.R.; Lindegaard-Andersen, A.; Mathiesen, S. Observation of algebraic decay of positional order in a smectic liquid crystal. Phys. Rev. B 1980, 22, 312–320. [Google Scholar] [CrossRef]
- Žekš, B.; Cepič, M. Modeling of ferroelectric and antiferroelectric liquid crystals. In Relaxation Phenomena. Liquid Crystals, Magnetic Systems, Polymers, High-Tc Superconductors, Metallic Glasses; Haase, W., Wróbel, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar] [CrossRef]
- Lagerwall, J.P.F.; Giesselmann, F. Current Topics in Smectic Liquid Crystal Research. Chem. Phys. Chem. 2006, 7, 20–45. [Google Scholar] [CrossRef]
- De Vries, A.; Ekachai, A.; Spielberg, N. Why the Molecules are Tilted in all Smectic A Phases, and How the Layer Thickness Can be Used to Measure Orientational Disorder. Mol. Cryst. Liq. Cryst. 1979, 49, 143–152. [Google Scholar] [CrossRef]
- Yoon, H.; Agra-Kooijman, D.M.; Ayub, K.; Lemieux, R.P.; Kumar, S. Direct Observation of Diffuse Cone Behavior in de Vries Smectic-A and -C Phases of Organosiloxane Mesogens. Phys. Rev. Lett. 2011, 106, 087801. [Google Scholar] [CrossRef] [PubMed]
- Meyer, R.B.; Liebert, L.; Strzelecki, L.; Keller, P. Ferroelectric liquid crystals. J. Phys. Lett. 1975, 36, 69–71. [Google Scholar] [CrossRef]
- Chandani, A.D.L.; Ouchi, Y.; Takezoe, H.; Fukuda, A.; Terashima, K.; Furukawa, K.; Kishi, A. Novel Phases Exhibiting Tristable Switching. Jpn. J. Appl. Phys. 1989, 28, L1261–L1264. [Google Scholar] [CrossRef]
- Krueger, M.; Giesselmann, F. Laser-light diffraction studies on the electric-field response of the helical director configuration in smectic-C* liquid crystals. J. Appl. Phys. 2007, 101, 094102. [Google Scholar] [CrossRef]
- Żurowska, M.; Dąbrowski, R.; Dziaduszek, J.; Garbat, K.; Filipowicz, M.; Tykarska, M.; Rejmer, W.; Czupryński, K.; Spadło, A.; Bennis, N.; et al. Influence of alkoxy chain length and fluorosubstitution on mesogenic and spectral properties of high tilted antiferroelectric esters. J. Mater. Chem. 2011, 21, 2144–2153. [Google Scholar] [CrossRef]
- Yoshizawa, A. Ferroelectric Smectic Liquid Crystals. Crystals 2024, 14, 350. [Google Scholar] [CrossRef]
- Nepal, S.; Das, B.; Kumar Das, M.; Das Sarkar, M.; Strójwąs, K.; Dmochowska, E.; Czerwiński, M. High tilted antiferroelectric liquid crystals: Polymer-based approach for phase stabilisation and device development. J. Mol. Liq. 2023, 375, 121297. [Google Scholar] [CrossRef]
- Li, J.; Takezoe, H.; Fukuda, A. Novel Temperature Dependences of Helical Pitch in Ferroelectric and Antiferroelectric Chiral Smectic Liquid Crystals. Jpn. J. Appl. Phys. 1991, 30, 532–536. [Google Scholar] [CrossRef]
- Sage, I. Thermochromic liquid crystals. Liq. Cryst. 2011, 38, 1551–1561. [Google Scholar] [CrossRef]
- Chen, S.W. Multifunctional glassy liquid crystals for photonics. J. Soc. Inf. Disp. 2004, 12, 205–211. [Google Scholar] [CrossRef]
- Strachan, G.J.; Górecka, E.; Hobbs, J.; Pociecha, D. Fluorination: Simple Change but Complex Impact on Ferroelectric Nematic and Smectic Liquid Crystal Phases. J. Am. Chem. Soc. 2025, 147, 6058–6066. [Google Scholar] [CrossRef]
- Chachaj-Brekiesz, A.; Górska, N.; Osiecka, N.; Dynarowicz-Łątka, P. Mesophases of non-conventional liquid crystalline molecules. Short-chained alkyl-(F-alkyl)-alkyl semifluorinated alkanes—Comparison with F-alkyl-(alkyl)-F-alkyl triblocks. J. Therm. Anal. Calorim. 2016, 126, 689–697. [Google Scholar] [CrossRef]
- Lopez, E.; Koh, Y.P.; Zapata-Hincapie, J.A.; Simon, S.L. Composition-dependent glass transition temperature in mixtures: Evaluation of configurational entropy models. Polym. Eng. Sci. 2022, 62, 2435–2445. [Google Scholar] [CrossRef]
- Zhang, W.; Froyen, A.A.F.; Schenning, A.P.H.J.; Zhou, G.; Debije, M.G.; de Haan, L.T. Temperature-Responsive Photonic Devices Based on Cholesteric Liquid Crystals. Adv. Photon. Res. 2021, 2, 2100016. [Google Scholar] [CrossRef]
- Zalewski, S. Phase transitions in three-component mixtures containing alkoxybenzoic acids with a chiral material. Phase Trans. 2019, 92, 1102–1109. [Google Scholar] [CrossRef]
- Czerwiec, J.M.; Dąbrowski, R.; Garbat, K.; Marzec, M.; Tykarska, M.; Wawrzyniak, A.; Wróbel, S. Dielectric and electro-optic behaviour of two chiral compounds and their antiferroelectric mixtures. Liq. Cryst. 2012, 39, 1503–1511. [Google Scholar] [CrossRef]
- Betts, R.; Dierking, I. Machine learning classification of polar sub-phases in liquid crystal MHPOBC. Soft Matter 2023, 19, 7502–7512. [Google Scholar] [CrossRef]
- Gorecka, E.; Pociecha, D.; Čepič, M.; Žekš, B.; Dąbrowski, R. Enantiomeric excess dependence of the phase diagram of antiferroelectric liquid crystals. Phys. Rev. E 2002, 65, 061703. [Google Scholar] [CrossRef]
- Ema, K.; Yao, H.; Kawamura, I.; Chan, T.; Garland, C.W. High-resolution calorimetric study of the antiferroelectric liquid crystals methylheptyloxycarbonylphenyl octyloxybiphenyl carboxylate and its octylcarbonylbiphenyl analog. Phys. Rev. E 1993, 47, 1203–1211. [Google Scholar] [CrossRef] [PubMed]
- Lalik, S.; Deptuch, A.; Fryń, P.; Jaworska-Gołąb, T.; Dardas, D.; Pociecha, D.; Urbańska, M.; Tykarska, M.; Marzec, M. Systematic study of the chiral smectic phases of a fluorinated compound. Liq. Cryst. 2019, 46, 2256–2268. [Google Scholar] [CrossRef]
- Deptuch, A.; Juszyńska-Gałązka, E.; Jasiurkowska-Delaporte, M.; Drzewicz, A.; Piwowarczyk, M.; Urbańska, M. Crystallization kinetics in the chiral compound showing the vitrification of the smectic CA* phase for moderate cooling rates. Phase Trans. 2023, 96, 166–185. [Google Scholar] [CrossRef]
- Augis, J.A.; Bennett, J.E. Calculation of the Avrami parameters for heterogeneous solid state reactions using a modification of the Kissinger method. J. Therm. Anal. 1978, 13, 283–292. [Google Scholar] [CrossRef]
- Friedman, H.L. Kinetics of thermal degradation of char-forming plastics from thermogravimetry. Application to a phenolic plastic. J. Polym. Sci. Part C Polym. Symp. 1964, 6, 183–195. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Sbirrazzuoli, N. Isoconversional Kinetic Analysis of Thermally Stimulated Processes in Polymers. Macromol. Rapid Commun. 2006, 27, 1515–1532. [Google Scholar] [CrossRef]
- Rozwadowski, T.; Yamamura, Y.; Saito, K. Interplay between Melt and Cold Crystallization in a Smectic Liquid Crystal, 4-Pentylphenyl 4-(trans-4-Pentylcyclohexyl)benzoate. Cryst. Growth Des. 2021, 21, 2777–2785. [Google Scholar] [CrossRef]
- Böhmer, R.; Ngai, K.L.; Angell, C.A.; Plazek, D.J. Nonexponential relaxations in strong and fragile glass formers. J. Chem. Phys. 1993, 99, 4201–4209. [Google Scholar] [CrossRef]
- Mauro, J.C.; Yue, Y.; Ellison, A.J.; Gupta, P.K.; Allan, D.C. Viscosity of glass-forming liquids. Proc. Natl. Acad. Sci. USA 2009, 106, 19780–19784. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A.; Rzoska, S.J.; Starzonek, S. New scaling paradigm for dynamics in glass-forming systems. Prog. Mater. Sci. 2023, 134, 101074. [Google Scholar] [CrossRef]
- Starzonek, S.; Łoś, J.; Rzoska, S.J.; Drozd-Rzoska, A.; Iglič, A. Are Critical Fluctuations Responsible for Glass Formation? Materials 2024, 17, 3385. [Google Scholar] [CrossRef]
- Tsai, W.-L.; Huang, K.-Y.; Hsueh, C.-I.; Wang, K.-T.; Wen, C.-C.; Lai, H.-M.; Cheng, P.-S. Synthesis and Liquid Crystal Properties of Chiral Compounds Containing the Core Structure of 6-Hydroxynicotinic Acid or 4-Hydroxyphenylacetic Acid. J. Chin. Chem. Soc. 2006, 53, 1385–1390. [Google Scholar] [CrossRef]
- Żurowska, M.; Dąbrowski, R.; Dziaduszek, J.; Czupryński, K.; Skrzypek, K.; Filipowicz, M. Synthesis and Mesomorphic Properties of Chiral Esters Comprising Partially Fluorinated Alkoxyalkoxy Terminal Chains and a 1-methylheptyl Chiral Moiety. Mol. Cryst. Liq. Cryst. 2008, 495, 145/[497]–157/[509]. [Google Scholar] [CrossRef]
- Osiecka, N.; Galewski, Z.; Massalska-Arodź, M. TOApy program for the thermooptical analysis of phase transitions. Thermochim. Acta 2017, 655, 106–111. [Google Scholar] [CrossRef]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef] [PubMed]
- Bearden, J.A. X-Ray Wavelengths. Rev. Mod. Phys. 1967, 39, 78–124. [Google Scholar] [CrossRef]
- Hubbard, C.R. National Bureau of Standards Certificate, Standard Reference Material 675, Low 2θ (Large d-Spacing) Standard for X-Ray Powder Diffraction. Available online: https://tsapps.nist.gov/srmext/certificates/675.pdf (accessed on 11 March 2024).
- Roisnel, T.; Rodríquez-Carvajal, J. WinPLOTR: A Windows Tool for Powder Diffraction Pattern Analysis. Mater. Sci. Forum 2001, 378–381, 118–123. [Google Scholar] [CrossRef]
- Ghanbari, E.; Picken, S.J.; van Esch, J.H. Analysis of differential scanning calorimetry (DSC): Determining the transition temperatures, and enthalpy and heat capacity changes in multicomponent systems by analytical model fitting. J. Therm. Anal. Calorim. 2023, 148, 12393–12409. [Google Scholar] [CrossRef]
- TA Instruments, Overview of Glass Transition Analysis by Differential Scanning Calorimetry. Available online: https://www.tainstruments.com/pdf/literature/TA443.pdf (accessed on 28 January 2025).
- Rozwadowski, T.; Noda, H.; Kolek, Ł.; Ito, M.; Yamamura, Y.; Saitoh, H.; Saito, K. Molecular dynamics and kinetics of isothermal cold crystallization with tunable dimensionality in a molecular glass former, 5′-(2,3-difluorophenyl)-2′-ethoxy-4-pentyloxy-2,3-difluorotolane. Phys. Chem. Chem. Phys. 2023, 25, 724–735. [Google Scholar] [CrossRef]
- Kolek, Ł.; Massalska-Arodź, M.; Majda, D.; Suchodolska, B.; Zalewski, S. Studies of Phase Diagram and Glass Transitions of a Liquid Crystal with Ferro- and Antiferroelectric Phases. Acta Phys. Pol. A 2013, 124, 909–912. [Google Scholar] [CrossRef]
- Dierking, I.; Dominiguez, J.; Harbon, J.; Heaton, J. Classification of liquid crystal textures using convolutional neural networks. Liq. Cryst. 2023, 50, 1526–1540. [Google Scholar] [CrossRef]
- Kim, K.H.; Takanishi, Y.; Ishikawa, K.; Takezoe, H.; Fukuda, A. Phase transitions and conformational changes in an antiferroelectric liquid crystal 4-(1-methylheptyloxycarbonyl)phenyl 4′-octyloxybiphenyl-4-carboxylate (MHPOBC). Liq. Cryst. 1994, 16, 185–202. [Google Scholar] [CrossRef]
- Blaabjerg, L.I.; Lindenberg, E.; Löbmann, K.; Grohganz, H.; Rades, T. Glass Forming Ability of Amorphous Drugs Investigated by Continuous Cooling and Isothermal Transformation. Mol. Pharm. 2016, 13, 3318–3325. [Google Scholar] [CrossRef]
- Yao, B.; Morales Alvarez, V.; Paluch, M.; Fedor, G.; McLaughlin, S.; McGrogan, A.; Swadźba-Kwaśny, M.; Wojnarowska, Z. Crystallization Kinetics of Phosphonium Ionic Liquids: Effect of Cation Alkyl Chain Length and Thermal History. J. Phys. Chem. B 2024, 128, 6610–6621. [Google Scholar] [CrossRef]
- Ediger, M.D.; Harrowell, P.; Yu, L. Crystal growth kinetics exhibit a fragility-dependent decoupling from viscosity. J. Chem. Phys. 2008, 128, 034709. [Google Scholar] [CrossRef]
- Patki, R.; Mezghani, K.; Philips, P.J. Crystallization Kinetics of Polymers. In Physical Properties of Polymers Handbook; Mark, J.E., Ed.; Springer: New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Dołęga, A.; Zieliński, P.M. Kinetics of non-isothermal cold-crystallization of carbamazepine in the glassy state studied by DSC. J. Non-Cryst. Solids 2022, 575, 121198. [Google Scholar] [CrossRef]
- Pagnacco, M.C.; Maksimović, J.P.; Janković, B.Ž. Analysis of transition from low to high iodide and iodine state in the Briggs–Rauscher oscillatory reaction containing malonic acid using Kolmogorov-Johnson-Mehl-Avrami (KJMA) theory. React. Kinet. Mech. Catal. 2018, 123, 61–80. [Google Scholar] [CrossRef]
- Massa, W. Crystal Structure Determination; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]
- Podoliak, N.; Novotná, V.; Glogarová, M.; Hamplová, V.; Kašpar, M.; Bubnov, A.; Kapernaum, N.; Giesselmann, F. Study of de Vries behaviour of the smectic A*-smectic C* phase transition. Phase Trans. 2010, 83, 1026–1036. [Google Scholar] [CrossRef]
- Chruściel, J.; Rudzki, A.; Ossowska-Chruściel, M.D.; Zalewski, S. Studies of de Vries SmA* type phase in chiral thiobenzoates. Phase Trans. 2023, 96, 157–165. [Google Scholar] [CrossRef]
- Budai, J.; Pindak, R.; Davey, S.C.; Goodby, J.W. A structural investigation of the liquid crystal phases of 4-(2′-methylbutyl)phenyl 4′-n-octylbiphenyl-4-carboxylate. J. Phys. Lett. 1984, 45, 1053–1062. [Google Scholar] [CrossRef]
- Deptuch, A.; Górska, N.; Srebro-Hooper, M.; Hooper, J.; Dziurka, M.; Urbańska, M. Investigation of infra-red spectra of three chiral liquid crystalline compounds with different fluorosubstitution of benzene ring. J. Mol. Struc. 2024, 1315, 138907. [Google Scholar] [CrossRef]
- Saito, K.; Miyazawa, T.; Fujiwara, A.; Hishida, M.; Saitoh, H.; Massalska-Arodź, M.; Yamamura, Y. Reassessment of structure of smectic phases: Nano-segregation in smectic E phase in 4-n-alkyl-4′-isothiocyanato-1,1′-biphenyls. J. Chem. Phys. 2013, 139, 114902. [Google Scholar] [CrossRef] [PubMed]
- Davidson, P. Selected Topics in X-Ray Scattering by Liquid-Crystalline Polymers. In Liquid Crystals II. Structure and Bonding; Mingos, D.M.P., Ed.; Springer: Berlin/Heidelberg, Germany, 1999; Volume 95. [Google Scholar] [CrossRef]
- He, B.B. Section 2.5.3.3.4. Lorentz, polarization and absorption corrections. In International Tables for Crystallography; Gilmore, C.J., Kaduk, J.A., Schenk, H., Eds.; Wiley: Hoboken, NJ, USA, 2019; Volume H, pp. 130–131. [Google Scholar]
- Broadband Dielectric Spectroscopy; Kremer, F., Schönhals, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar] [CrossRef]
- Khened, S.M.; Krishna Prasad, S.; Shivkumar, B.; Sadashiva, B.K. Dielectric studies of Goldstone mode and soft mode in the vicinity of the A-C* transition. J. Phys. II 1991, 1, 171–180. [Google Scholar] [CrossRef]
- Fąfara, A.; Ganzke, D.; Haase, W.; Marzec, M.; Wróbel, S.; Czapczyński, C.; Dąbrowski, R. Mean-Field Behavior of the Paraelectric-Ferroelectric Phase Transition of a Fluorinated Compound. Ferroelectrics 2002, 276, 29–36. [Google Scholar] [CrossRef]
- Buivydas, M.; Gouda, F.; Andersson, G.; Lagerwall, S.T.; Stebler, B.; Bömelburg, J.; Heppke, G.; Gestblom, B. Collective and non-collective excitations in antiferroelectric and ferrielectric liquid crystals studied by dielectric relaxation spectroscopy and electro-optic measurements. Liq. Cryst. 1997, 23, 723–739. [Google Scholar] [CrossRef]
- Samet, M.; Levchenko, V.; Boiteux, G.; Seytre, G.; Kallel, A.; Serghei, A. Electrode polarization vs. Maxwell-Wagner-Sillars interfacial polarization in dielectric spectra of materials: Characteristic frequencies and scaling laws. J. Chem. Phys. 2015, 142, 194703. [Google Scholar] [CrossRef]
- Murthy, S.S.N. Experimental study of dielectric relaxation in supercooled alcohols and polyols. Mol. Phys. 1996, 87, 691–709. [Google Scholar] [CrossRef]
- Ngai, K.L.; Paluch, M. Classification of secondary relaxation in glass-formers based on dynamic properties. J. Chem. Phys. 2004, 120, 857–873. [Google Scholar] [CrossRef]
- Havriliak, S.; Negami, S. A complex plane analysis of α-dispersions in some polymer systems. J. Polym. Sci. C Polym. Symp. 1966, 14, 99–117. [Google Scholar] [CrossRef]
- Cole, K.S.; Cole, R.H. Dispersion and Absorption in Dielectrics I. Alternating Current Characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef]
- Deptuch, A.; Lelito, A.; Juszyńska-Gałązka, E.; Jasiurkowska-Delaporte, M.; Urbańska, M. Vitrification of the smectic CA* phase and kinetics of cold crystallization investigated for a fluorinated compound with a chiral centre based on (S)-(+)-3-octanol. Phys. Chem. Chem. Phys. 2023, 25, 12379–12393. [Google Scholar] [CrossRef] [PubMed]
- Wolfram MathWorld, Lambert W-Function. Available online: https://mathworld.wolfram.com/LambertW-Function.html (accessed on 14 April 2025).
- Tanaka, H. Relationship among glass-forming ability, fragility, and short-range bond ordering of liquids. J. Non-Cryst. Solids 2005, 351, 678–690. [Google Scholar] [CrossRef]
- Ossowska-Chruściel, M.D.; Karczmarzyk, Z.; Chruściel, J. The Polymorphism Of 4-N-Pentylphenyl-4″-N-Butyloxythio-Benzoate, (4OS5) in the Crystalline State. Mol. Cryst. Liq. Cryst. 2002, 382, 37–52. [Google Scholar] [CrossRef]
- Hori, K.; Endo, K. Crystal Structure and Polymorphism of Antiferroelectric Mesogen, 4-[(S)-1-Methylheptyloxycarbonyl]phenyl 4′-Octyloxybiphenyl-4-carboxylate (MHPOBC). Bull. Chem. Soc. Jpn. 1993, 66, 46–50. [Google Scholar] [CrossRef]
- Cambridge Crystallographic Data Centre. Entry CCDC 1230059; Cambridge Crystallographic Data Centre: Cambridge, UK, 1993. [Google Scholar]



| Sample | [K] | [K] | [K] | ||
|---|---|---|---|---|---|
| MIX5FF6-1 | −12.7(3) | 1518(95) | 187(3) | 232.3(4) | 76(2) |
| MIX5FF6-2 | −10.4(2) | 786(50) | 207(2) | 234.1(3) | 105(4) |
| MIX5FF6-3 | −10.2(3) | 743(48) | 210(2) | 236.1(2) | 109(3) |
| 3F5FPhF6 [27] | −11.0(2) | 883(50) | 208(1) | 238.0(3) | 105(4) |
| Sample | [K] | [K] | [K] | ||
|---|---|---|---|---|---|
| MIX5FF6-1 | −10.1(2) | 1055(28) | 67(10) | 231.2(6) | 67.1(6) |
| MIX5FF6-2 | −8.5(2) | 1549(33) | 7(2) | 231.4(7) | 80.5(7) |
| MIX5FF6-3 | −7.9(2) | 1882(28) | 1.8(3) | 234.7(9) | 88.9(4) |
| 3F5FPhF6 [27] | −8.71(8) | 1845(25) | 2.5(4) | 238(2) | 94(1) |
| Sample | range [K] | [K] | |
|---|---|---|---|
| MIX5FF6-1 | 249–285 | 235.4(8) | 7.5(2) |
| MIX5FF6-2 | 243–289 | 232(2) | 7.5(4) |
| MIX5FF6-3 | 243–301 | 232.3(5) | 7.9(1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deptuch, A.; Drzewicz, A.; Urbańska, M.; Juszyńska-Gałązka, E. Partially Disordered Crystal Phases and Glassy Smectic Phases in Liquid Crystal Mixtures. Materials 2025, 18, 3085. https://doi.org/10.3390/ma18133085
Deptuch A, Drzewicz A, Urbańska M, Juszyńska-Gałązka E. Partially Disordered Crystal Phases and Glassy Smectic Phases in Liquid Crystal Mixtures. Materials. 2025; 18(13):3085. https://doi.org/10.3390/ma18133085
Chicago/Turabian StyleDeptuch, Aleksandra, Anna Drzewicz, Magdalena Urbańska, and Ewa Juszyńska-Gałązka. 2025. "Partially Disordered Crystal Phases and Glassy Smectic Phases in Liquid Crystal Mixtures" Materials 18, no. 13: 3085. https://doi.org/10.3390/ma18133085
APA StyleDeptuch, A., Drzewicz, A., Urbańska, M., & Juszyńska-Gałązka, E. (2025). Partially Disordered Crystal Phases and Glassy Smectic Phases in Liquid Crystal Mixtures. Materials, 18(13), 3085. https://doi.org/10.3390/ma18133085









