Bending Test and Numerical Simulation of Externally Prestressed Reinforced Concrete Beams on the Side Facade
Abstract
1. Introduction
2. Experimental Program
2.1. Materials and Its Properties
2.2. Component Design and Manufacture
2.3. The Prestressing Application Scheme
2.4. Measurement Point Arrangement and Loading Method
3. Test Results and Analysis
3.1. Analysis of Experimental Phenomena and Failure Modes
3.2. Flexural Capacity
3.3. Load-Reinforcement Strain Curve
4. Finite Element Analysis
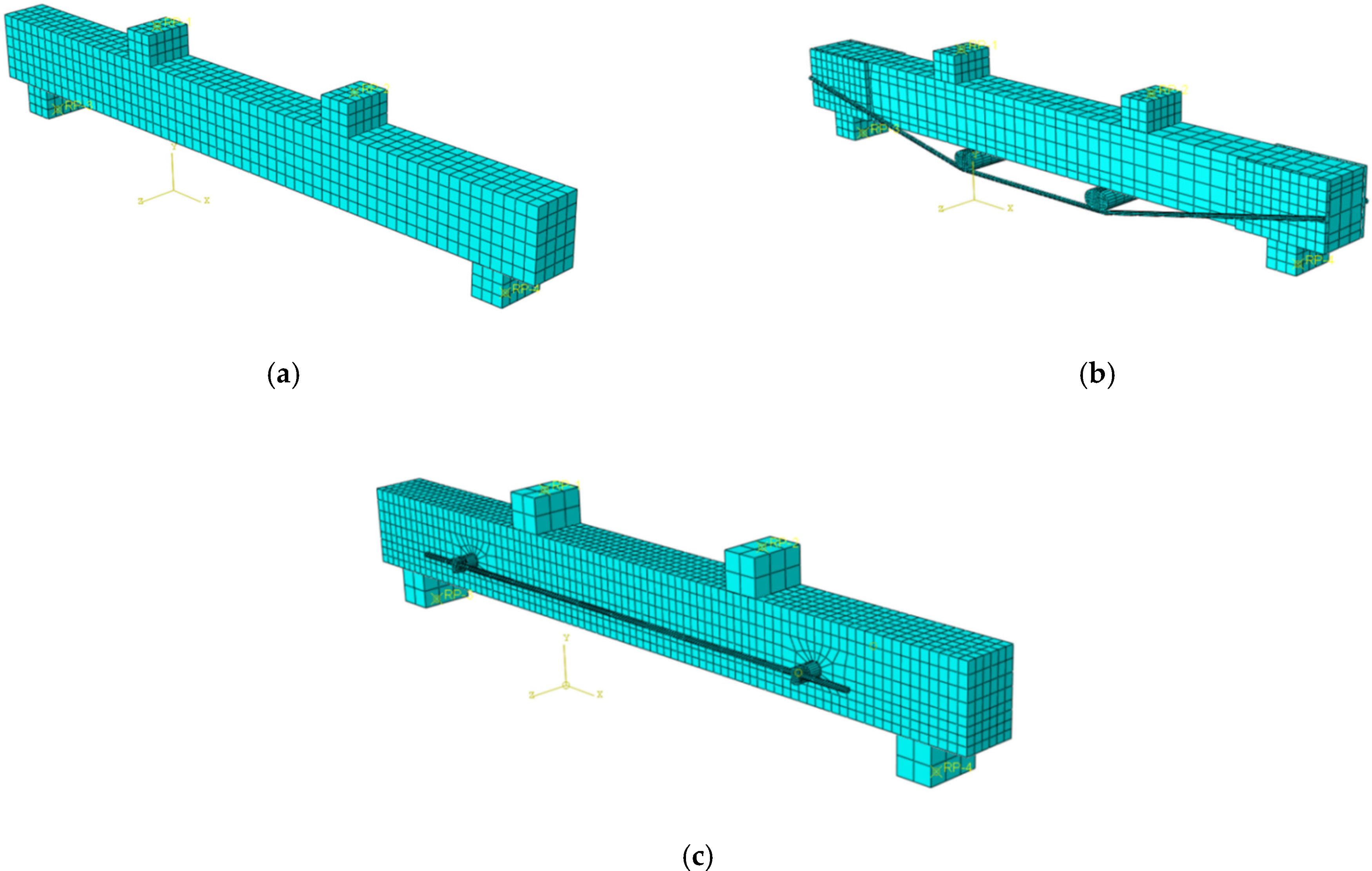
4.1. Establishment of Finite Element Model in ABAQUS
4.1.1. Finite Element Component Design
4.1.2. Initial Prestress Application
4.1.3. Mesh Generation
4.1.4. Definition of Interface Contact and Boundary Conditions
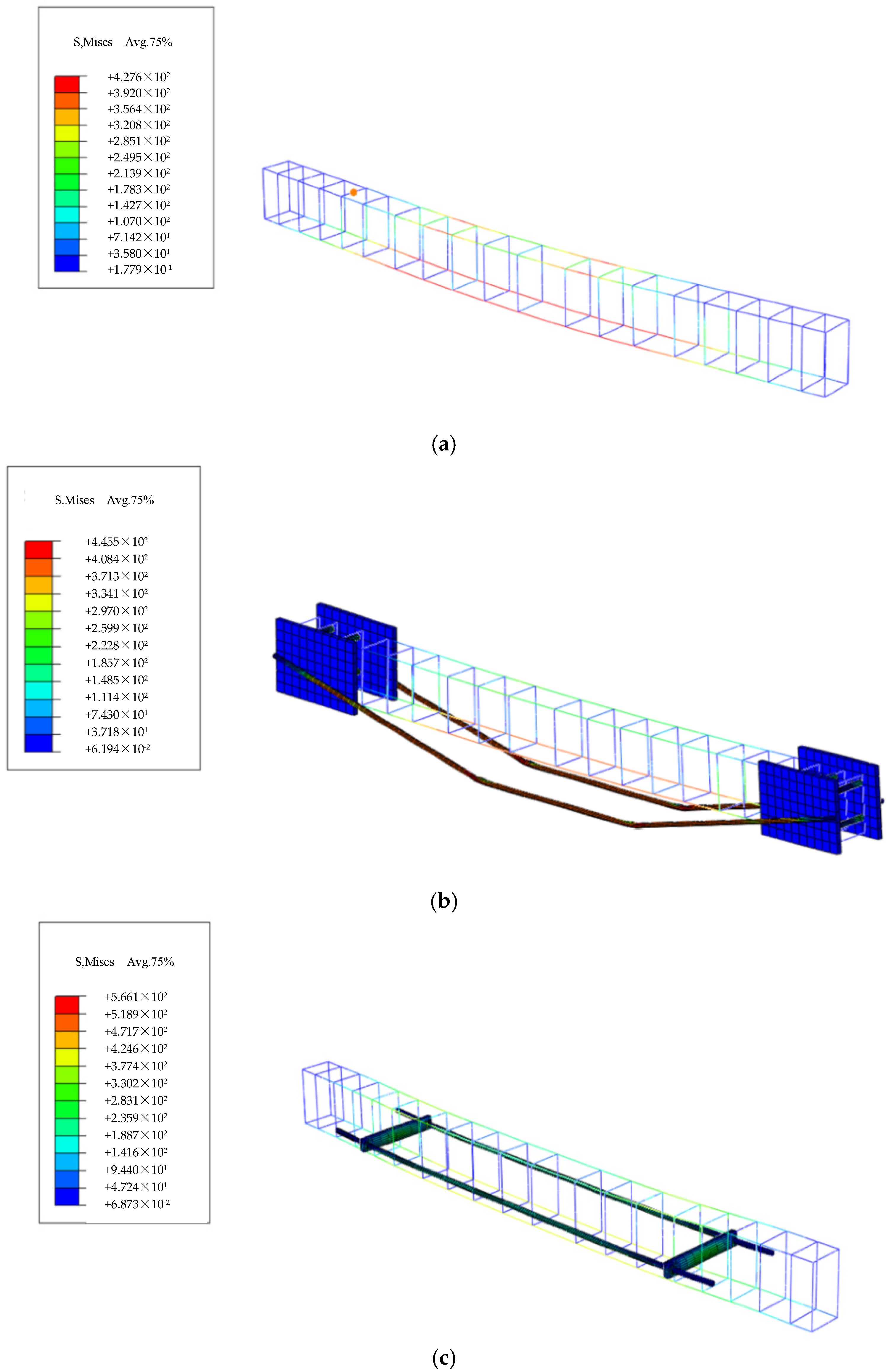
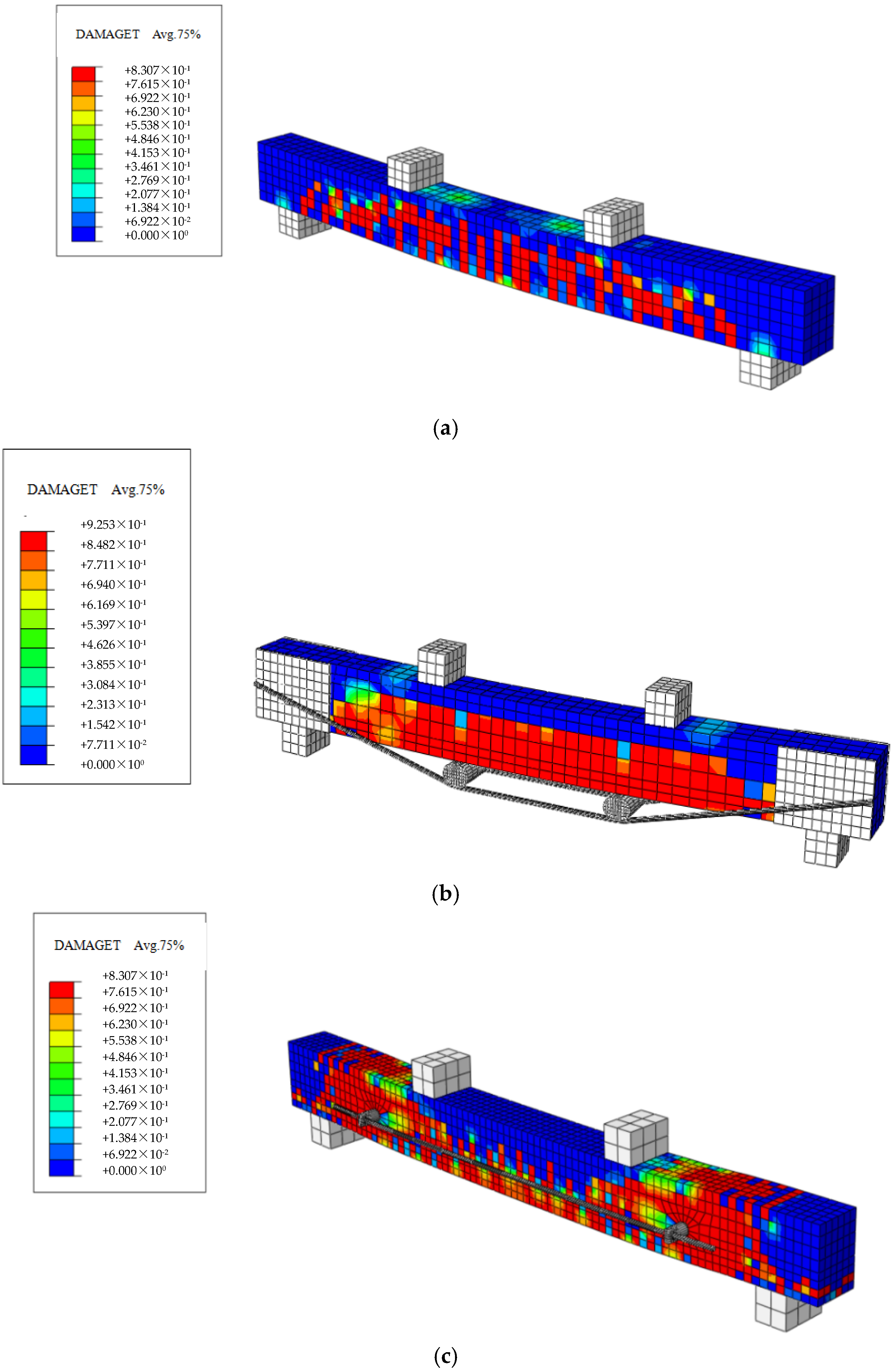
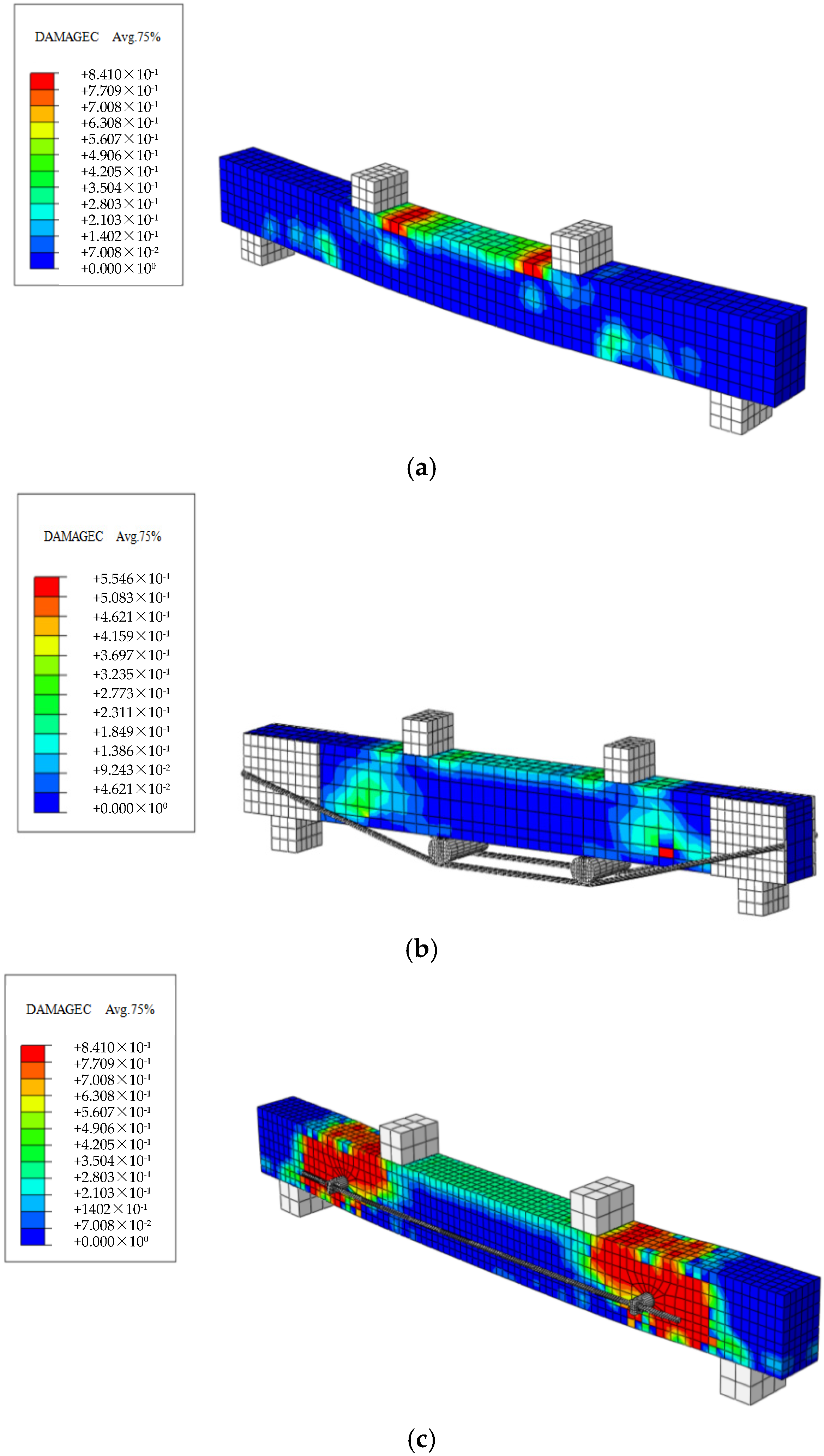
4.2. Post-Processing Analysis
4.3. Comparison of Simulated Values and Experimental Values
5. Conclusions
- (1)
- The external prestressed reinforcement technique can effectively enhance the flexural load-bearing capacity of concrete beams to a certain extent. Compared with the control beam, when initial prestress values of 50 kN, 75 kN, and 100 kN were applied, the ultimate load of the SRB beam increased by 53%, 55%, and 62%, respectively. Additionally, under the conditions of applying initial prestress values of 30 kN, 35 kN, and 40 kN, the ultimate load of the TRB beam increased by 152%, 153%, and 155%, respectively.
- (2)
- The application of the external prestressed reinforcement method to the side facade significantly improved the workability of concrete. When initial prestress values of 50 kN, 75 kN, and 100 kN were applied, the cracking load of the SRB beam increased by 77%, 98%, and 120%, respectively, while the yield load of the SRB beam increased by 55%, 67%, and 85%, respectively. These results demonstrate the fundamental characteristic of prestress in enhancing structural performance.
- (3)
- The reinforcement effect of traditional external prestressing is superior to that of side-facade external prestressing. The traditional external prestressed reinforcement method significantly enhances the working performance of concrete beams. When initial prestress values of 30 kN, 35 kN, and 40 kN were applied, the cracking load of the TRB beam increased by 249%, 265%, and 293%, respectively, while the yield load of the TRB beam increased by 175%, 185%, and 214%, respectively, thereby demonstrating the substantial effectiveness of prestressing. The significant difference in bearing capacity between SRB beams and TRB beams can be attributed to the fact that the traditional external prestressing structural layout is more conducive to achieving the desired prestressing effect. However, the TRB prestressing method is complex to implement, and drilling holes at the ends of concrete beams may introduce safety risks and pose insurmountable challenges.
- (4)
- The ABAQUS finite element software analysis conducted on the three types of concrete beams indicated that the accuracy of the finite element software analysis and calculation met the requirements. The results of modeling and analyzing the test beams showed that the load–deflection curves of the simulation and the test were approximately consistent in their trend, and the ultimate bearing capacity of the simulation was basically consistent with the test results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fang, L. Research on External Prestressing Reinforcement of Continuous Rigid Frame Bridge. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2016. [Google Scholar]
- Liu, L. Experimental Study on Externally Prestressed Reinforced Concrete T-Beam and Box Girder. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2016. [Google Scholar]
- Lee, S.H.; Shin, K.J.; Kang, T.H.K. Flexural strengthening of continuous concrete beams using external prestressed steel bars. PCI J. 2015, 60, 68–86. [Google Scholar] [CrossRef]
- Wang, Y.B.; Mao, M.; Liu, Z.; Zhang, X.; Wu, J. Static test of prestressed concrete beams strengthened with external prestressing. Build. Struct. 2022, 52 (Suppl. S1), 2107–2113. [Google Scholar]
- Qiang, X.H.; Hu, W.; Hu, G.; Jiang, X.; Tang, Y. Theoretical and Numerical Analysis of Reinforced Concrete Beams Strengthened with Externally Prestressed CFRP Tendons. Struct. Eng. 2024, 40, 165–174. [Google Scholar]
- Li, T. Study on Flexural Behavior of Damaged Concrete T-Beams Strengthened by External Prestressing-Truss Combination. Master’s Thesis, Changsha University of Science and Technology, Changsha, China, 2021. [Google Scholar]
- Cao, M.Y. Numerical Simulation and Performance Prediction of Static Load and Fatigue Performance of RC Beams Strengthened with Prestressed CFRP Plates. Master’s Thesis, Dalian University of Technology, Dalian, China, 2021. [Google Scholar]
- Zhou, C.; Wang, W.; Shi, S. Experimental study on shear strengthening of reinforced concrete T-beams with prestressed CFRP sheets. J. Civ. Eng. 2020, 53, 68–76+84. [Google Scholar]
- Shu, S.Y.H. Analysis of Mechanical Properties of Prestressed CFRP Reinforced RC Beams Under Natural Exposure. Master’s Thesis, South China University of Technology, Guangzhou, China, 2021. [Google Scholar]
- Liu, W.H. Study on Mechanical Properties of Concrete Beams Strengthened by Prestressed CFRP Plates with U-Shaped Hoop End Anchor and String Method. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2023. [Google Scholar]
- Wang, H.T.; Zhu, C.; Xiong, H.; Xu, G.; Liu, S. Effect of anchorage method and prestress level on flexural behavior of reinforced concrete beams strengthened with CFRP plates. J. Hohai Univ. (Nat. Sci. Ed.) 2023, 51, 104–110. [Google Scholar]
- Zhang, Z.M.; Yang, Y. Finite element analysis of flexural fatigue performance of reinforced concrete beams strengthened with externally bonded prestressed CFRP sheets. Compos. Mater. Sci. Eng. 2023, 2, 44–53. [Google Scholar] [CrossRef]
- Ren, W.; Huang, P.; Li, X.; Zhao, Y.; Liu, H. Calculation method of optimal prestress of prestressed TRM reinforced concrete beams. Chin. J. Highw. 2022, 35, 311–320. [Google Scholar]
- Li, Y.; Tian, Y. Finite element analysis of flexural behavior of RC beams strengthened with prestressed high strength steel strands. J. Jilin Jianzhu Univ. 2021, 38, 24–28. [Google Scholar]
- John, S.K.; Cascardi, A.; Verre, S.; Nadir, Y. RC-columns subjected to lateral cyclic force with different FRCM-strengthening schemes: Experimental and numerical investigation. Bull. Earthq. Eng. 2025, 23, 1561–1590. [Google Scholar] [CrossRef]
- Cunha, A., Jr.; Yanik, Y.; Olivieri, C.; da Silva, S. Tresca Versus Von Mises: Which Failure Criterion is More Conservative in a Probabilistic Context? J. Appl. Mech. 2024, 91, 111008. [Google Scholar] [CrossRef]
- Tao, J. Study on Shear Behavior of RC Beams Strengthened with Prestressed FRP Grids. Master’s Thesis, Southeast University, Nanjing, China, 2021. [Google Scholar]
- Dong, Z. Experimental Study on Flexural Behavior of Reinforced Concrete Beams Strengthened with Prestressed BFRP Grids. Master’s Thesis, North China University of Technology, Beijing, China, 2021. [Google Scholar]
- Xiao, Y.X. Experimental Study on Static Performance of Prestressed CFRP-Concrete Beams with End Mounted. Master’s Thesis, Changsha University of Science and Technology, Changsha, China, 2022. [Google Scholar]
- Peng, H.; Guo, H.; Zhong, Z.; Shu, M.; Chen, H. Prestressed NSM CFRP Shear Strengthened Reinforced Concrete T-Beam Test. Chin. J. Highw. 2022, 35, 159–168. [Google Scholar]
- Wei, J.J.; Teng, L.; Khayat, K.H. Coupled effect of fiber type and reinforcement ratio on flexural behavior of reinforced beams cast with super workable concrete. Constr. Build. Mater. 2024, 438, 137039. [Google Scholar] [CrossRef]
- Peng, H.; Chou, J.; Wu, P. Experimental study on mechanical behavior of concrete beams strengthened with prestressed carbon fiber composite at the end. J. Build. Struct. 2023, 44, 152–160+203. [Google Scholar]
- Wang, Y.X.; He, M.J.; Li, Z. Flexural behavior of glulam beams reinforced by bonded prestressing tendons. Eng. Struct. 2024, 315, 118436. [Google Scholar] [CrossRef]
- Kirthiga, R.; Elavenil, S. Performance evaluation of pre-damaged reinforced concrete beams strengthened with knitted glass fabric reinforced cementit-ious matrix: Flexure and shear behaviors. Structures 2024, 70, 107744. [Google Scholar] [CrossRef]
- Xiang, A.J. Study on Flexural Behavior of Long-Span Concrete Beams Strengthened by Post-Prestressed Beam Side Composite. Master’s Thesis, Zhejiang University, Hangzhou, China, 2023. [Google Scholar]
- Ren, Z.H.; Zeng, X.T.; Sun, J.B. Using Two-Way pre-stressed semicircular steel plate for construction of reinforced concrete cylinder column. Complexity 2018, 2018, 1481837. [Google Scholar] [CrossRef]
- Ren, Z.H.; Shen, Y.Q.; Zeng, X.T.; Sun, Y.T. Experimental research on axial compression of reinforced concrete short circular columns strengthened with pre-stressed semicircular steel plates. Adv. Civ. Eng. 2021, 2021, 1992084. [Google Scholar] [CrossRef]
- GB/T50081-2019; Standard for Test Methods of Physical and Mechanical Properties of Concrete. China Construction Industry Publishing House: Beijing, China, 2019.
- GB50010-2010; Ministry of Housing and Urban-Rural Development of the People’s Republic of China, General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Code for Design of Concrete Structures. China Construction Industry Press: Beijing, China, 2015.
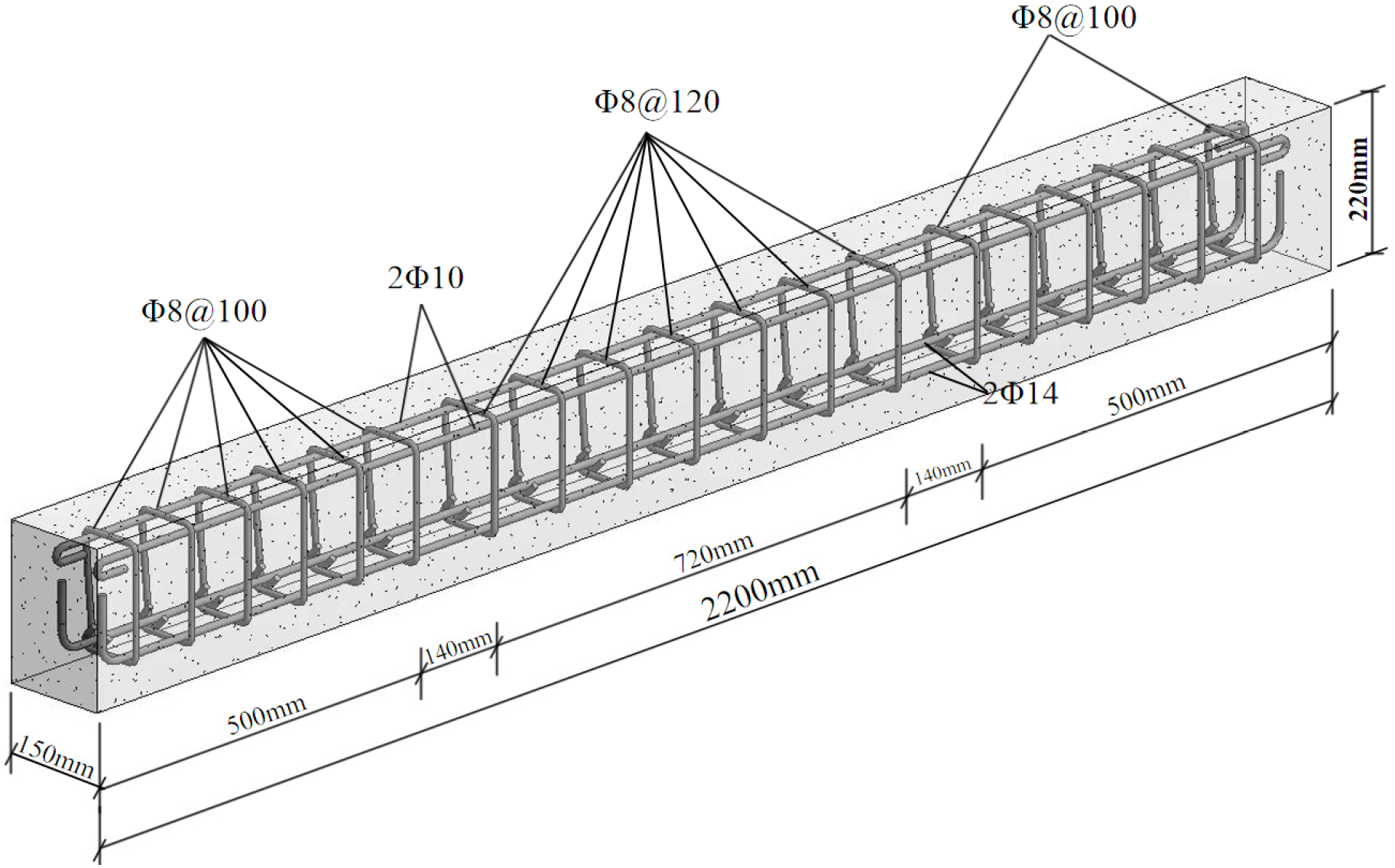




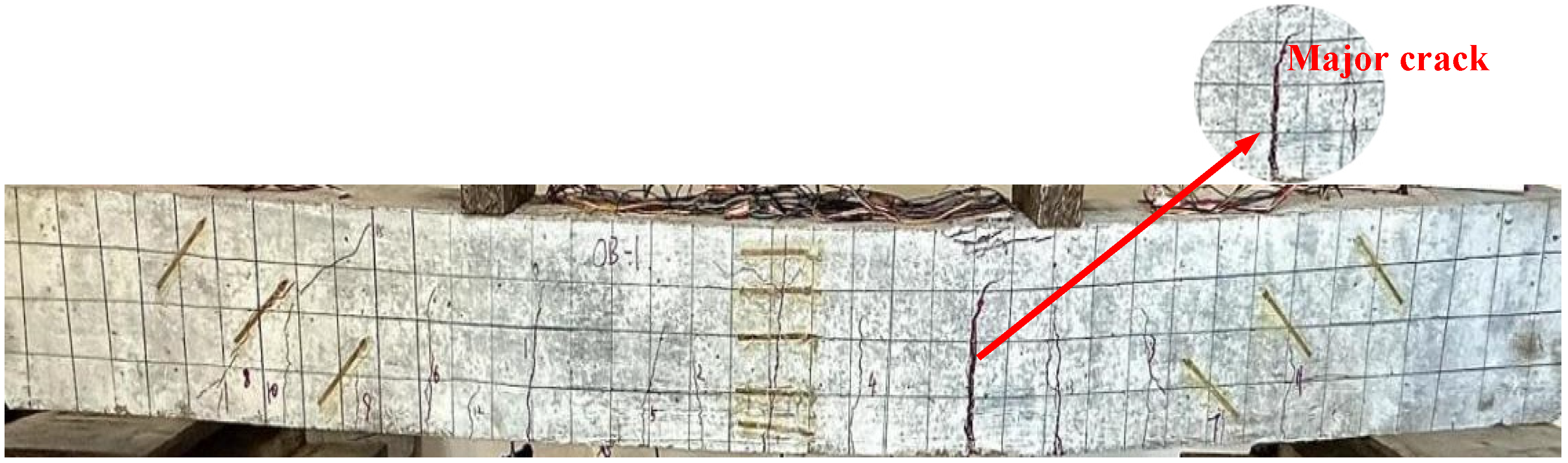






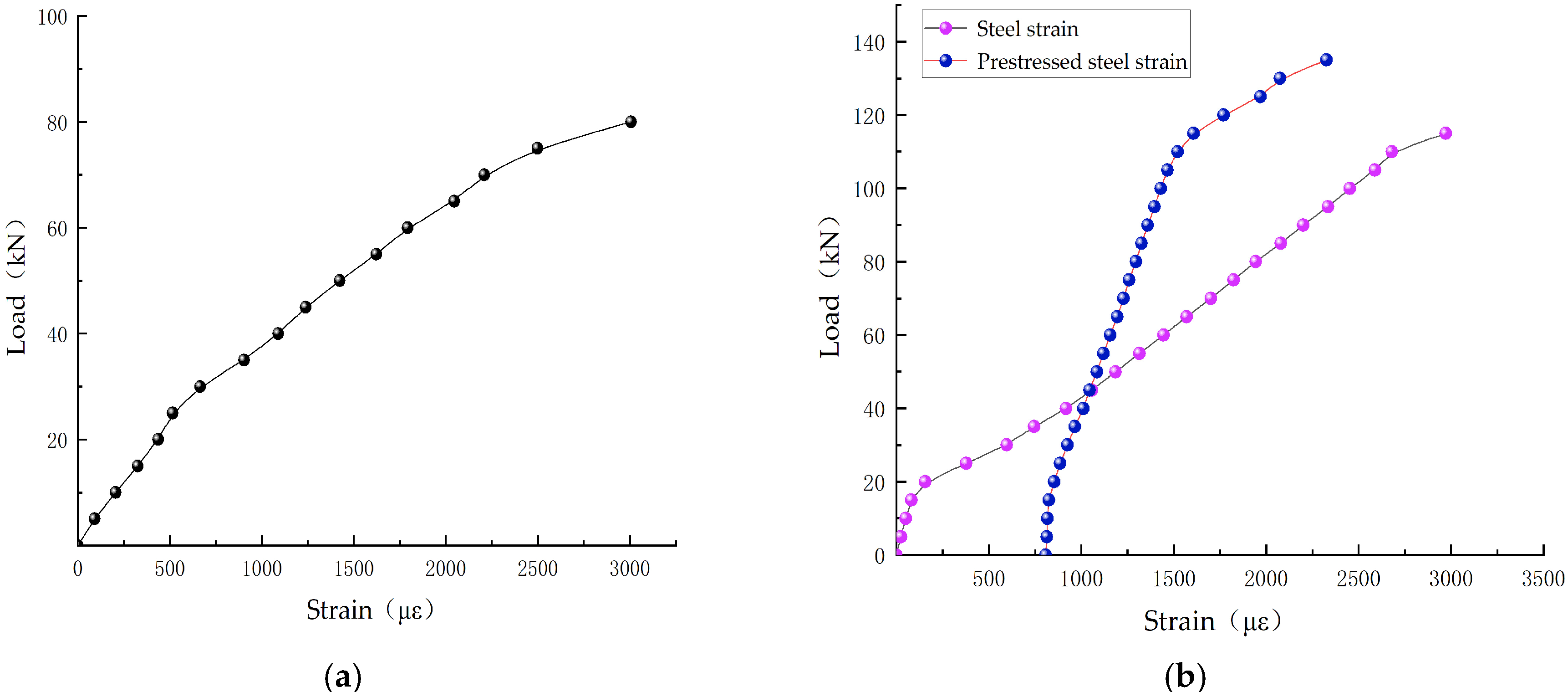
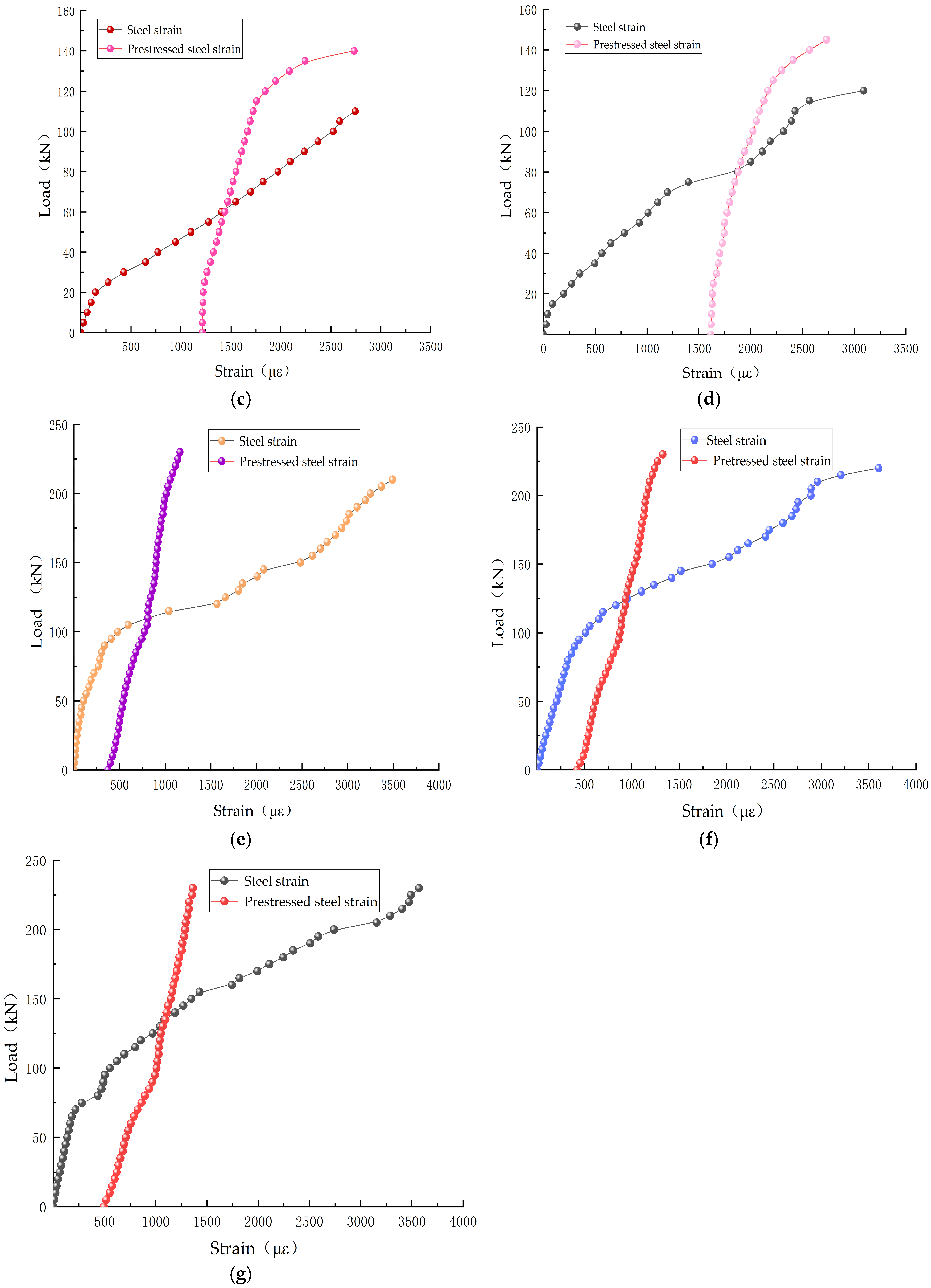

| No. | Cracking Load | Increase Range | Yield Load | Increase Range | Ultimate Load | Increase Range |
|---|---|---|---|---|---|---|
| OB-1 | 20.1 | — | 74.3 | — | 91.3 | — |
| SRB-50-1 | 35.5 | 77% | 115.4 | 55% | 139.2 | 53% |
| SRB-75-1 | 39.8 | 98% | 124.2 | 67% | 141.4 | 55% |
| SRB-100-1 | 44.3 | 120% | 137.6 | 85% | 147.0 | 62% |
| TRB-30-1 | 70.1 | 249% | 204.1 | 175% | 230.0 | 152% |
| TRB-35-2 | 73.4 | 265% | 211.7 | 185% | 231.2 | 153% |
| TRB-40-1 | 78.9 | 293% | 214.5 | 214% | 232.8 | 155% |
| Specimen Identifier | Test Value (kN) | Analog Value (kN) | Tested Values/Simulated Values |
|---|---|---|---|
| OB-1 | 91.3 | 90.2 | 1.01 |
| SRB-50-1 | 139.2 | 127.2 | 1.09 |
| SRB-75-1 | 141.4 | 132.4 | 1.06 |
| SRB-100-1 | 147 | 138.1 | 1.06 |
| TRB-30-1 | 230 | 232.9 | 0.98 |
| TRB-35-2 | 231.2 | 236.6 | 0.97 |
| TRB-40-1 | 232.8 | 240.2 | 0.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Z.; Zhang, K.; Wu, C.; Zhang, Y.; Zeng, X.; Ding, X. Bending Test and Numerical Simulation of Externally Prestressed Reinforced Concrete Beams on the Side Facade. Materials 2025, 18, 3024. https://doi.org/10.3390/ma18133024
Ren Z, Zhang K, Wu C, Zhang Y, Zeng X, Ding X. Bending Test and Numerical Simulation of Externally Prestressed Reinforced Concrete Beams on the Side Facade. Materials. 2025; 18(13):3024. https://doi.org/10.3390/ma18133024
Chicago/Turabian StyleRen, Zhenhua, Ke Zhang, Chengwang Wu, Yi Zhang, Xiantao Zeng, and Xuanming Ding. 2025. "Bending Test and Numerical Simulation of Externally Prestressed Reinforced Concrete Beams on the Side Facade" Materials 18, no. 13: 3024. https://doi.org/10.3390/ma18133024
APA StyleRen, Z., Zhang, K., Wu, C., Zhang, Y., Zeng, X., & Ding, X. (2025). Bending Test and Numerical Simulation of Externally Prestressed Reinforced Concrete Beams on the Side Facade. Materials, 18(13), 3024. https://doi.org/10.3390/ma18133024






