Constitutive Modeling of Rheological Behavior of Cement Paste Based on Material Composition
Abstract
1. Introduction
2. Materials and Methods
2.1. Raw Materials
2.2. Mix Design and Rheological Test Method
3. Experimental Results and Analysis
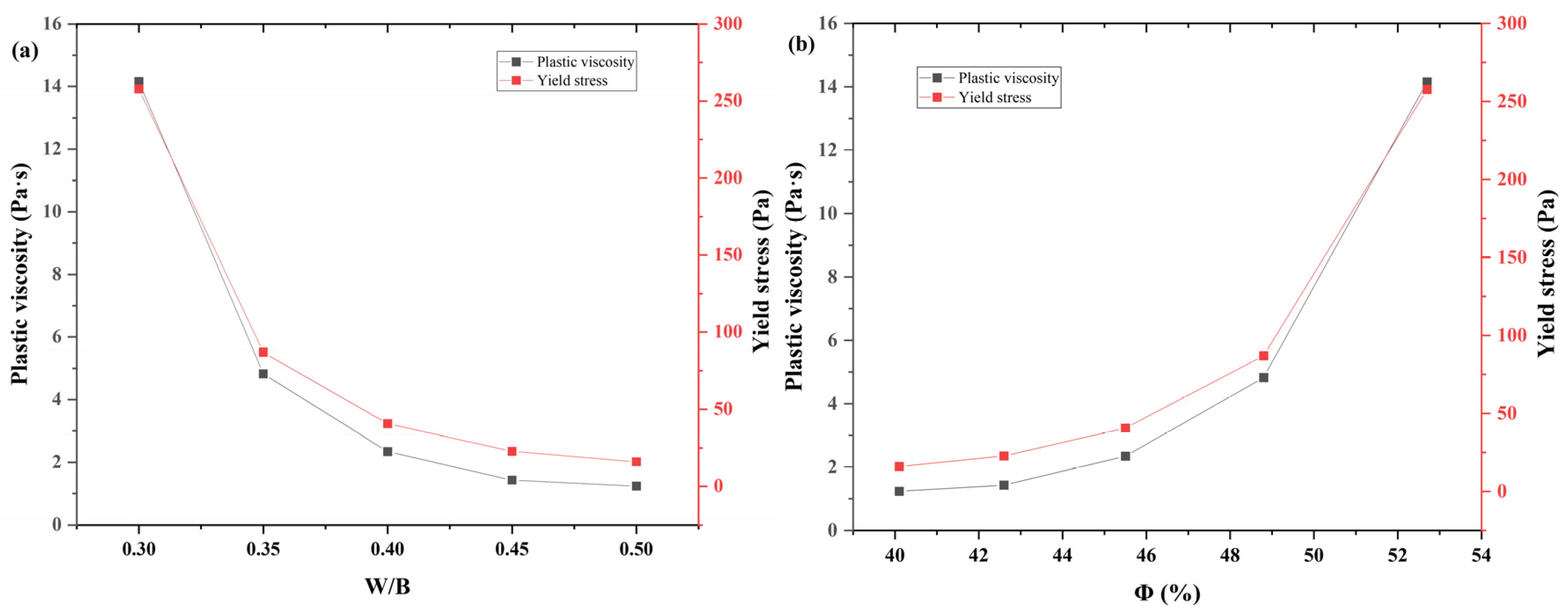
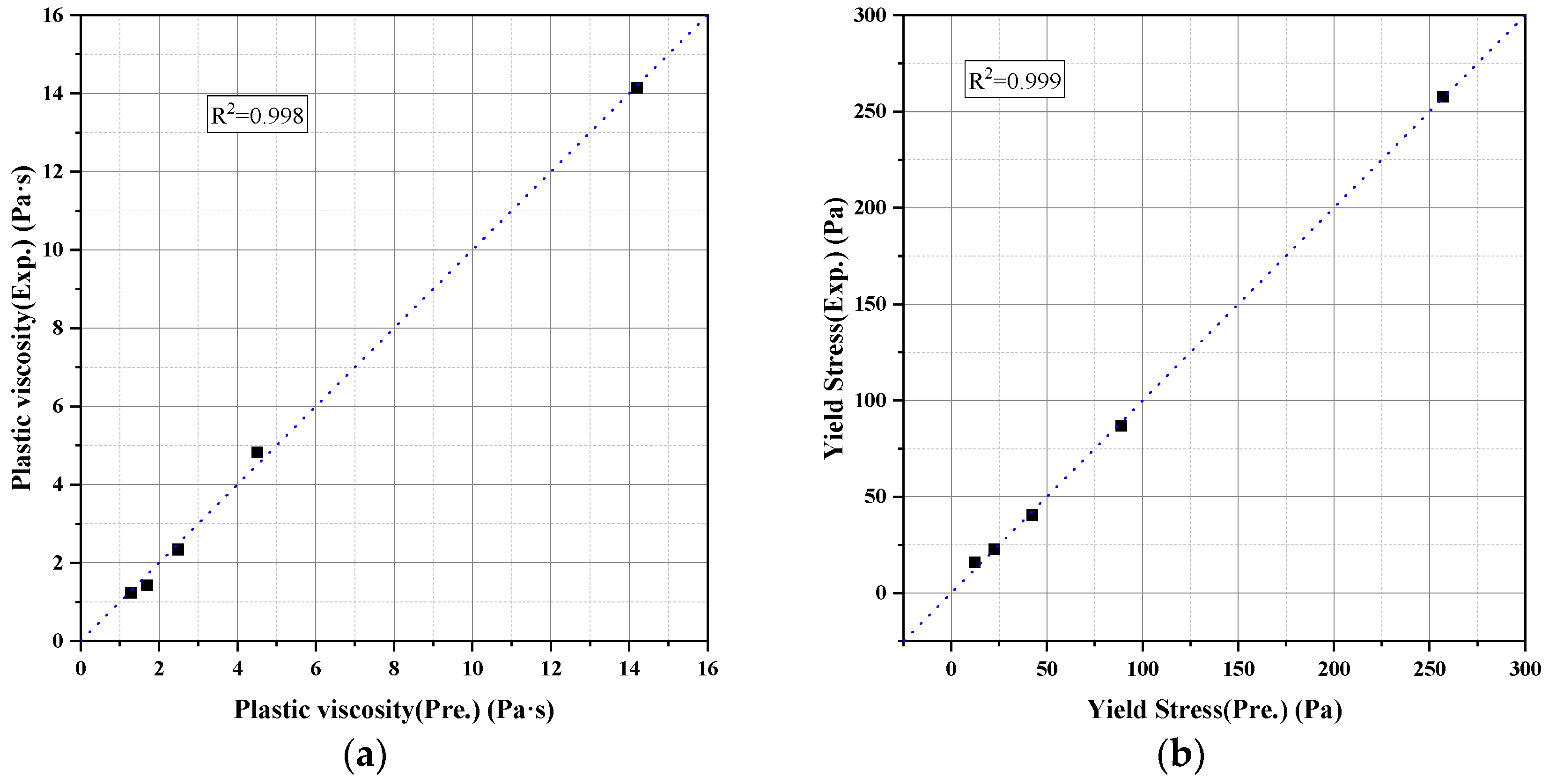
3.1. Effect of Solid Volume Fraction on Rheology
- = 57.9%,
- = 0.164,
- R2 = 0.999 (for viscosity model, Equation (3)).
- = 54.85%,
- = 21.03 Pa,
- R2 = 0.983.
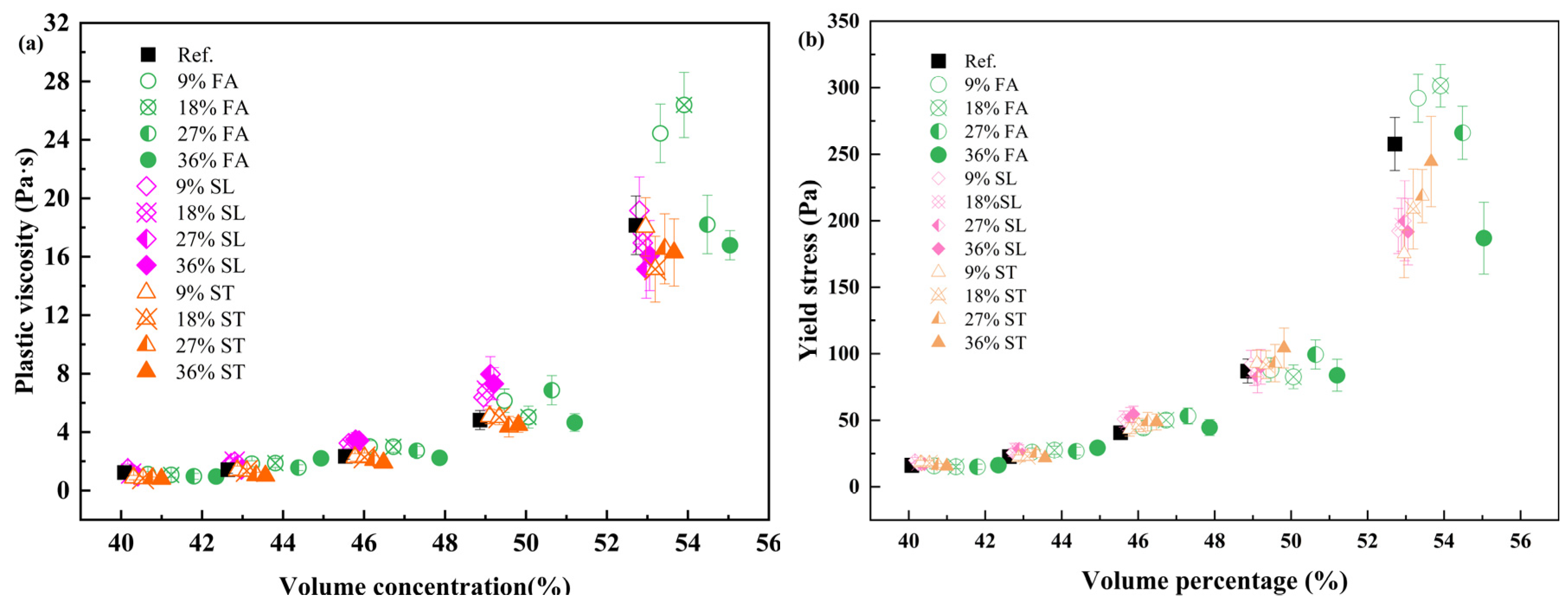
3.2. Effect of Mineral Admixtures on Paste Rheology
3.3. Effect of Superplasticizer on Paste Rheology
4. Conclusions
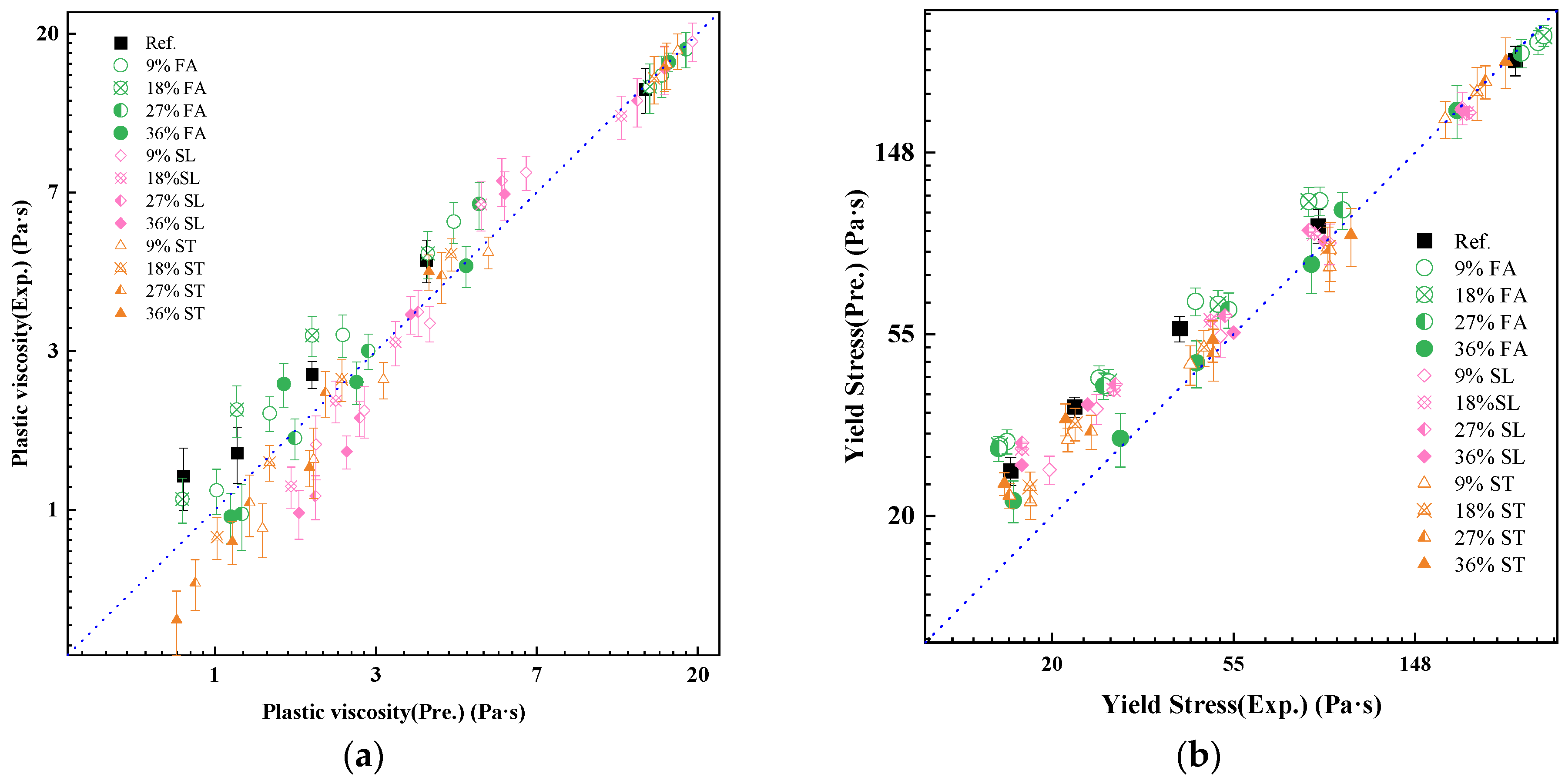
- Solid volume fraction is the dominant factor governing paste rheology.Both plastic viscosity and yield stress increase exponentially as the powder volume fraction approaches the maximum packing limit. A strong nonlinear dependence was observed and accurately captured using modified suspension models. Model fitting for plain cement paste yielded high predictive accuracy (R2 > 0.98) for both viscosity and yield stress, demonstrating a level of predictive capability beyond simple curve-fitting approaches.
- The influence of mineral admixtures on flowability can be fully quantified through three fitted parameters.The rheological impact of fly ash, slag, and limestone powder was successfully modeled by changes in the maximum packing fraction , the yield stress coefficient , and the flow resistance factor . Fly ash significantly enhanced flowability by increasing and reducing interparticle interactions, while slag and limestone exhibited milder effects. All 65 paste formulations were well predicted with R2 > 0.85, highlighting our model’s ability to quantitatively describe the complex interactions of SCMs, a feature typically not addressed by generalized rheological models.
- Superplasticizer action can be simplified as a modulation of virtual packing density.The polycarboxylate-based superplasticizer increased the effective by dispersing flocs and releasing entrapped water. By fixing and , the variation in with dosage allowed the accurate prediction of flow parameters across 16 tested formulations, confirming the model’s robustness in admixture-modified systems. This simplification provides a physically intuitive mechanism for superplasticizer effects, which is a significant advancement over models that treat admixture effects as arbitrary fitting parameters, and offers a pathway to predict their impact without complex direct rheological measurements for every formulation.
- A unified, parameter-efficient model framework was established.Through minimal parameterization, the model bridges raw material characteristics and macroscopic rheological behavior. It enables forward prediction of plastic viscosity and yield stress based on volume concentration and material properties, with clear physical interpretation and practical adaptability. This contrasts sharply with many existing models that rely heavily on empirically derived constants or require extensive, material-specific calibration, making our framework more universally applicable for diverse cementitious systems. By focusing on easily measurable input parameters and the derived , our model bypasses the practical difficulties associated with direct measurement of effective solid volume fractions in real-time, offering a truly predictive and actionable tool.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- ACI PRC-238.1-08; Report on Measurements of Workability and Rheology of Fresh Concrete. American Concrete Institute: Farmington Hills, MI, USA, 2018.
- Roussel, N. Rheology of fresh concrete: From measurements to predictions of casting processes. Mater. Struct. 2007, 40, 1001–1012. [Google Scholar] [CrossRef]
- Nagaraj, A. Rheology of fresh concrete-a review. J. Rehabil. Civ. Eng. 2021, 9, 118–131. [Google Scholar]
- Perrot, A.; Lecompte, T.; Khelifi, H.; Brumaud, C.; Hot, J.; Roussel, N. Yield stress and bleeding of fresh cement pastes. Cem. Concr. Res. 2012, 42, 937–944. [Google Scholar] [CrossRef]
- Mehta, P.K.; Monteiro, P.J. Concrete Microstructure, Properties and Materials; McGraw-Hill Education: New York, NY, USA, 2017. [Google Scholar]
- Kashani, A.R.; Nicolas, R.S.; Qiao, G.G.; van Deventer, J.S.J.; Provis, J.L. Modelling the yield stress of ternary cement–slag–fly ash pastes based on particle size distribution. Powder Technol. 2014, 266, 203–209. [Google Scholar] [CrossRef]
- Scrivener, K.L.; Nonat, A. Hydration of cementitious materials, present and future. Cem. Concr. Res. 2011, 41, 651–665. [Google Scholar] [CrossRef]
- Roussel, N. Understanding the Rheology of Concrete; Woodhead Publishing: Cambridge, UK, 2012. [Google Scholar]
- Du, J.; Zhu, W.W.; Feng, G.; Liang, W.; Cshen, X.G.; Xu, C.F. Rheological Characteristics of Power-law Cement Grouts Based on Time-dependent Behavior of Viscosity. Chem. Eng. Trans. 2016, 51, 1111–1116. [Google Scholar]
- Roussel, N. A thixotropy model for fresh fluid concretes: Theory, validation and applications. Cem. Concr. Res. 2006, 36, 1797–1806. [Google Scholar] [CrossRef]
- Yang, Z.Q.; Hou, K.; Guo, T.T. Study on the Effects of Different Water-Cement Ratios on the Flow Pattern Properties of Cement Grouts. Appl. Mech. Mater. 2011, 71, 1264–1267. [Google Scholar]
- Yang, Z.Q.; Hou, K.; Guo, T.T. Research on Time-Varying Behavior of Cement Grouts of Different Water-Cement Ratios. Appl. Mech. Mater. 2011, 71, 4398–4401. [Google Scholar]
- Marchon, D.; Sulser, U.; Eberhardt, A.; Flatt, R.J. Molecular design of comb-shaped polycarboxylate dispersants for environmentally friendly concrete. Soft Matter 2013, 9, 10719–10728. [Google Scholar] [CrossRef]
- Flatt, R.J. Towards a prediction of superplasticized concrete rheology. Mater. Struct. 2004, 37, 289–300. [Google Scholar] [CrossRef]
- Mehta, P.K.; Burrows, R.W. Building durable structures in the 21st century. Concr. Int. 2001, 23, 57–63. [Google Scholar]
- Ferraris, C.F.; Obla, K.H.; Hill, R.L. The influence of mineral admixtures on the rheology of cement paste and concrete. Cem. Concr. Res. 2001, 31, 245–255. [Google Scholar] [CrossRef]
- Belie, N.D.; Soutsos, M.; Gruyaert, E. Properties of Fresh and Hardened Concrete Containing Supplementary Cementitious Materials: State-of-the-Art Report of the RILEM Technical Committee 238-SCM, Working Group 4; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Ahari, R.; Erdem, T.; Ramyar, K. Effect of various supplementary cementitious materials on rheological properties of self-consolidating concrete. Constr. Build. Mater. 2015, 75, 89–98. [Google Scholar] [CrossRef]
- Robert, C.R.; Sathyan, D.; Anand, K. Effect of superplasticizers on the rheological properties of fly ash incorporated cement paste. Mater. Today Proc. 2018, 5, 23955–23963. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, Y.; Chen, M.; Wang, X.; Ye, C.; Li, X.; Chen, W.; Yang, Y.; Wang, B.; Li, C.; et al. Influence of Coupling Effects between Gravel Soil Porosity and Cement Grout Weight on Diffusion Laws and Morphologies of Penetration Grouting. Appl. Sci. 2022, 12, 7601. [Google Scholar] [CrossRef]
- Krieger, I.; Dougherty, T. A Mechanism for Non Newtonian Flow in Suspensions of Rigid Spheres. J. Rheol. 1959, 3, 137–152. [Google Scholar] [CrossRef]
- Krenzer, K.; Mechtcherine, V.; Palzer, U. Simulating mixing processes of fresh concrete using the discrete element method (DEM) under consideration of water addition and changes in moisture distribution. Cem. Concr. Res. 2019, 115, 274–282. [Google Scholar] [CrossRef]
- GB 175-2007; Common Portland Cements. National Standard of the People’s Republic of China: Beijing, China, 2007.
- GB/T 1596-2017; Fly Ash Used for Cement and Concrete. National Standard of the People’s Republic of China: Beijing, China, 2017.
- GB/T 18046-2008; Ground Granulated Blast Furnace Slag Used for Cement and Concrete. National Standard of the People’s Republic of China: Beijing, China, 2008.
- GB/T 35164-2017; Limestone Powder Used for Cement, Mortar and Concrete. National Standard of the People’s Republic of China: Beijing, China, 2017.
- Li, Y.; Yang, C.; Zhang, Y.; Zheng, J.; Guo, H.; Lu, M. Study on dispersion, adsorption and flow retaining behaviors of cement mortars with TPEG-type polyether kind polycarboxylate superplasticizers. Constr. Build. Mater. 2014, 64, 324–332. [Google Scholar] [CrossRef]
- Huang, H.; Ye, G.; Qian, C.; Schlangen, E. Self-healing in cementitious materials: Materials, methods and service conditions. Mater. Des. 2016, 92, 499–511. [Google Scholar] [CrossRef]
- Roussel, N.; Coussot, P. “Fifty-cent rheometer” for yield stress measurements: From slump to spreading flow. J. Rheol. 2005, 49, 705–718. [Google Scholar] [CrossRef]
- Banfill, P.F.G. Rheology of Fresh Cement and Concrete; Routledge: Abingdon, UK, 1991. [Google Scholar]
- Sha, S.; Wang, M.; Shi, C.; Xiao, Y. Influence of the structures of polycarboxylate superplasticizer on its performance in cement-based materials—A review. Constr. Build. Mater. 2020, 233, 117257. [Google Scholar] [CrossRef]
- Cheung, J.; Jeknavorian, A.; Roberts, L.; Silva, D. Impact of admixtures on the hydration kinetics of Portland cement. Cem. Concr. Res. 2011, 41, 1289–1309. [Google Scholar] [CrossRef]
- Mandal, R.; Panda, S.K.; Nayak, S. Rheology of Concrete: Critical Review, recent Advancements, and future prospectives. Constr. Build. Mater. 2023, 392, 132007. [Google Scholar] [CrossRef]
- Flatt, R.J.; Bowen, P. Yodel: A Yield Stress Model for Suspensions. J. Am. Ceram. Soc. 2006, 89, 1244–1256. [Google Scholar] [CrossRef]
- Wedding, P.; Kantro, D.L. Influence of Water-Reducing Admixtures on Properties of Cement Paste A Miniature Slump Test. Cem. Concr. Aggreg. 1980, 2, 95–102. [Google Scholar]
- Cao, E. Study on the Mechanism of Action of Polycarboxylate Water Reducer on Rheological Properties of Cement Paste System. Ph.D. Thesis, Tsinghua University, Beijing, China, 2011. [Google Scholar]
- Zhang, Y. Early Microstructure and Rheological Properties of Cement-Chemical Admixture-Water Dispersion System. Ph.D. Thesis, Tsinghua University, Beijing, China, 2014. [Google Scholar]
- Fang, L. Characterization of Fresh Cement Paste Microstructure and Its Correlation with Rheological Properties. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2020. [Google Scholar]
- Liu, D.M. Particle packing and rheological property of highly-concentrated ceramic suspensions: φm determination and viscosity prediction. J. Mater. Sci. 2000, 35, 5503–5507. [Google Scholar] [CrossRef]
- Rahman, M.K.; Baluch, M.H.; Malik, M.N.A. Thixotropic behavior of self compacting concrete with different mineral admixtures. Constr. Build. Mater. 2014, 50, 710–717. [Google Scholar] [CrossRef]
- Khatri, R.P.; Sirivivatnanon, V.; Gross, W. Effect of different supplementary cementitious materials on mechanical properties of high performance concrete. Cem. Concr. Res. 1995, 25, 209–220. [Google Scholar] [CrossRef]
- Zhang, J.; Li, D.; Wang, Y. Toward intelligent construction: Prediction of mechanical properties of manufactured-sand concrete using tree-based models. J. Clean. Prod. 2020, 258, 120665. [Google Scholar] [CrossRef]
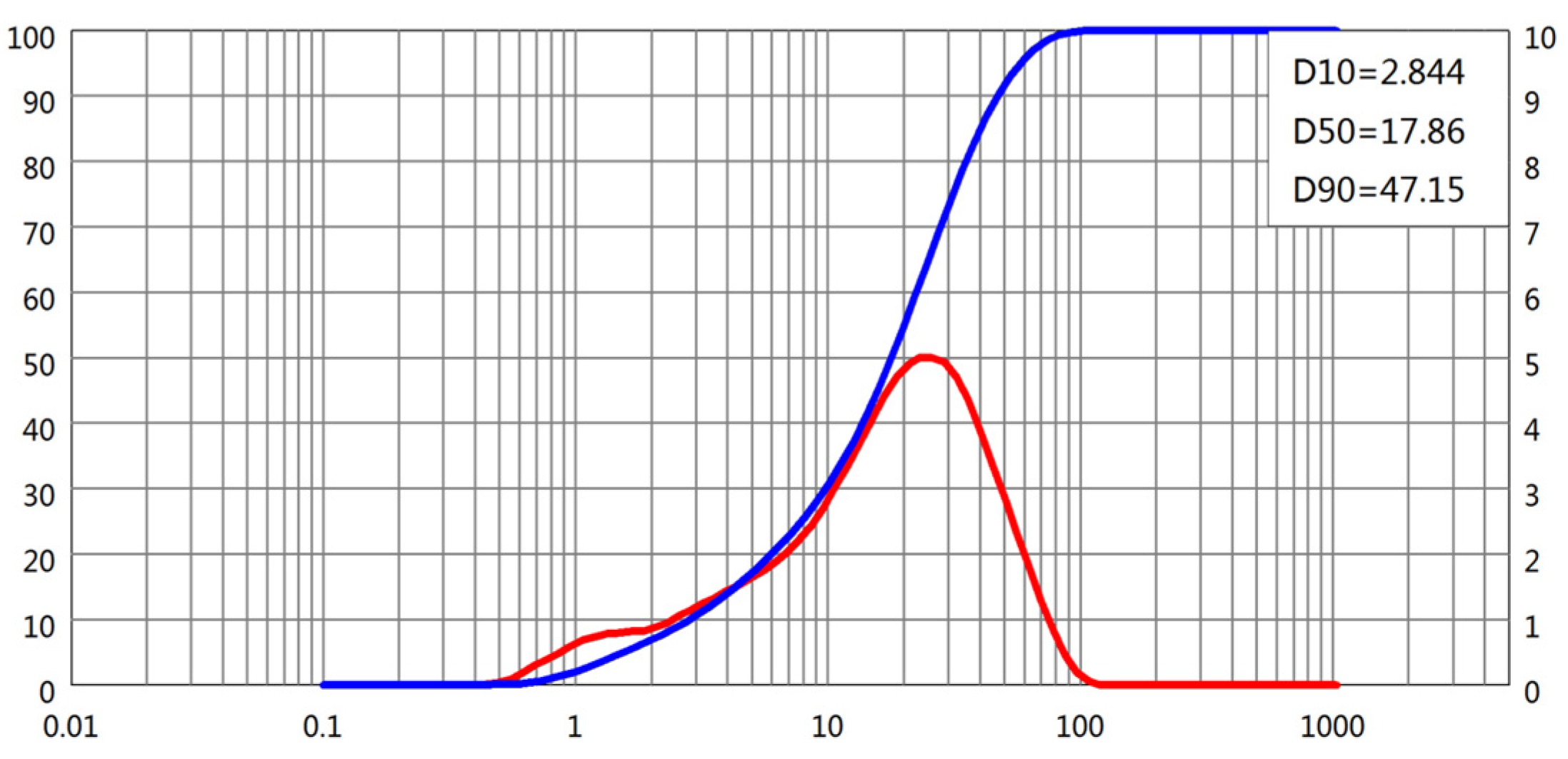
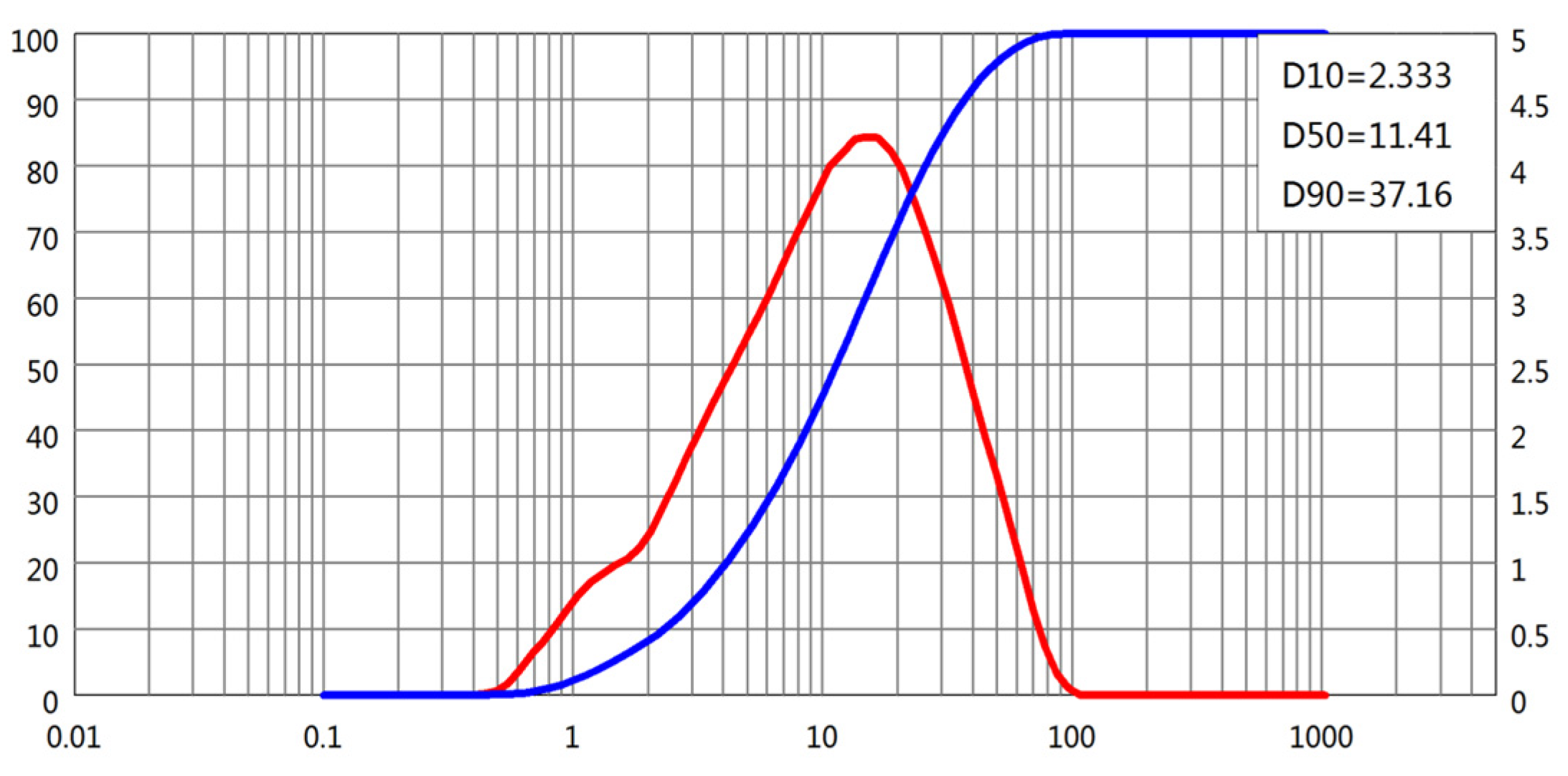






| Blaine (m2/kg) | Density (kg/m3) | Standard Consistency (%) | Initial Set (min) | Final Set (min) | Flexural Strength (MPa) | Compressive Strength (MPa) |
|---|---|---|---|---|---|---|
| 317 | 2990 | 28.4 | 193 | 266 | 9.3 (28 d) | 43.2 (28 d) |
| Material | Density (g/cm3) | Blaine Fineness (m2/kg) | Surface Area per Unit Volume (m2/m3) |
|---|---|---|---|
| Cement (C) | 2.99 | 315.2 | 0.94 |
| Fly ash (FA) | 2.35 | 453.4 | 1.07 |
| Slag powder (SL) | 2.88 | 343.6 | 0.99 |
| Limestone powder (ST) | 2.7 | 311.2 | 0.84 |
| Mix | Cement (g) | Water (g) | w/b | ϕ (%) | Plastic Viscosity (Pa·s) | Yield Stress (Pa) |
|---|---|---|---|---|---|---|
| 1 | 794 | 238 | 0.3 | 52.7 | 14.15 | 25.8 |
| 2 | 735 | 257 | 0.35 | 48.8 | 4.82 | 8.7 |
| 3 | 684 | 273 | 0.4 | 45.5 | 2.34 | 4.1 |
| 4 | 639 | 288 | 0.45 | 42.6 | 1.43 | 2.3 |
| 5 | 600 | 300 | 0.5 | 40.1 | 1.23 | 1.6 |
| (Pa) | R2 (μ) | R2 (τ) | ||
|---|---|---|---|---|
| 57.49% | 40.35 | 0.155 | 0.962 | 0.94 |
| Admixture Type | Replacement | (%) | (Pa) | R2 (μ) | R2 (τ) | |
|---|---|---|---|---|---|---|
| FA | 9% | 58 | 38.4 | 0.156 | 0.98 | 0.87 |
| FA | 18% | 58.3 | 37 | 0.157 | 0.86 | 0.88 |
| FA | 27% | 58.8 | 35.4 | 0.158 | 0.98 | 0.95 |
| FA | 36% | 59.3 | 34 | 0.159 | 0.95 | 0.9 |
| SL | 9% | 57.8 | 39.5 | 0.155 | 0.86 | 0.99 |
| SL | 18% | 58 | 39.1 | 0.155 | 0.86 | 0.99 |
| SL | 27% | 58.3 | 38.4 | 0.155 | 0.86 | 0.98 |
| SL | 36% | 58.4 | 38 | 0.155 | 0.86 | 0.99 |
| ST | 9% | 57.6 | 40.1 | 0.156 | 0.99 | 0.86 |
| ST | 18% | 57.8 | 39.9 | 0.157 | 0.98 | 0.98 |
| ST | 27% | 58 | 39.6 | 0.158 | 0.99 | 0.98 |
| ST | 36% | 58.2 | 39.3 | 0.159 | 0.98 | 0.99 |
| Mix | Vp (L) | Vw (L) | ϕ (%) | SP (%) | Cement (kg/m3) | FA (kg/m3) | Water (kg/m3) | SP (kg/m3) | Yield Stress τ (Pa) | Plastic Viscosity η (Pa·s) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 459 | 533 | 45.80% | 0.80% | 1130 | 234 | 533 | 10.91 | 0.35 | 11.66 |
| 2 | 459 | 531 | 45.90% | 0.90% | 1131 | 234 | 531 | 12.29 | 0.23 | 5.77 |
| 3 | 460 | 530 | 45.90% | 1.00% | 1132 | 234 | 530 | 13.67 | 0.19 | 5.11 |
| 4 | 503 | 493 | 50.20% | 0.40% | 1290 | 256 | 493 | 6.19 | 1.95 | 62.48 |
| 5 | 503 | 490 | 50.30% | 0.50% | 1293 | 257 | 490 | 8.52 | 0.97 | 35.48 |
| 6 | 504 | 489 | 50.30% | 0.60% | 1293 | 257 | 489 | 8.83 | 0.74 | 33.22 |
| 7 | 504 | 489 | 50.40% | 0.60% | 1294 | 257 | 489 | 9.3 | 0.67 | 28.8 |
| 8 | 478 | 517 | 47.80% | 0.40% | 1229 | 244 | 517 | 5.89 | 1.14 | 39.57 |
| 9 | 479 | 515 | 47.90% | 0.50% | 1230 | 244 | 515 | 7.37 | 0.66 | 30.23 |
| 10 | 503 | 491 | 50.30% | 0.50% | 1292 | 257 | 491 | 7.74 | 1.29 | 49.6 |
| 11 | 504 | 487 | 50.40% | 0.70% | 1295 | 257 | 487 | 10.87 | 0.39 | 20.68 |
| 12 | 479 | 516 | 47.90% | 0.40% | 1229 | 244 | 516 | 6.63 | 0.86 | 32.42 |
| 13 | 479 | 516 | 47.90% | 0.50% | 1230 | 244 | 516 | 7.08 | 0.67 | 31.31 |
| 14 | 504 | 488 | 50.40% | 0.60% | 1294 | 257 | 488 | 10.08 | 0.44 | 28.48 |
| 15 | 479 | 514 | 47.90% | 0.50% | 1231 | 244 | 514 | 8.11 | 0.6 | 24.68 |
| 16 | 480 | 513 | 47.90% | 0.60% | 1232 | 245 | 513 | 8.86 | 0.46 | 21.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lian, C.; Zhang, X.; Han, L.; Lin, W.; Wen, W. Constitutive Modeling of Rheological Behavior of Cement Paste Based on Material Composition. Materials 2025, 18, 2983. https://doi.org/10.3390/ma18132983
Lian C, Zhang X, Han L, Lin W, Wen W. Constitutive Modeling of Rheological Behavior of Cement Paste Based on Material Composition. Materials. 2025; 18(13):2983. https://doi.org/10.3390/ma18132983
Chicago/Turabian StyleLian, Chunming, Xiong Zhang, Lu Han, Wenbiao Lin, and Weijun Wen. 2025. "Constitutive Modeling of Rheological Behavior of Cement Paste Based on Material Composition" Materials 18, no. 13: 2983. https://doi.org/10.3390/ma18132983
APA StyleLian, C., Zhang, X., Han, L., Lin, W., & Wen, W. (2025). Constitutive Modeling of Rheological Behavior of Cement Paste Based on Material Composition. Materials, 18(13), 2983. https://doi.org/10.3390/ma18132983





