Epoxy Adhesive Materials as Protective Coatings: Strength Property Analysis Using Machine Learning Algorithms
Abstract
1. Introduction
- the effect of resin type, curing agent type, and filler concentration and type on mechanical properties;
- evaluation of microstructure using scanning electron microscopy (SEM);
- construction and validation of regression models that enable prediction of strength parameters based on material composition.
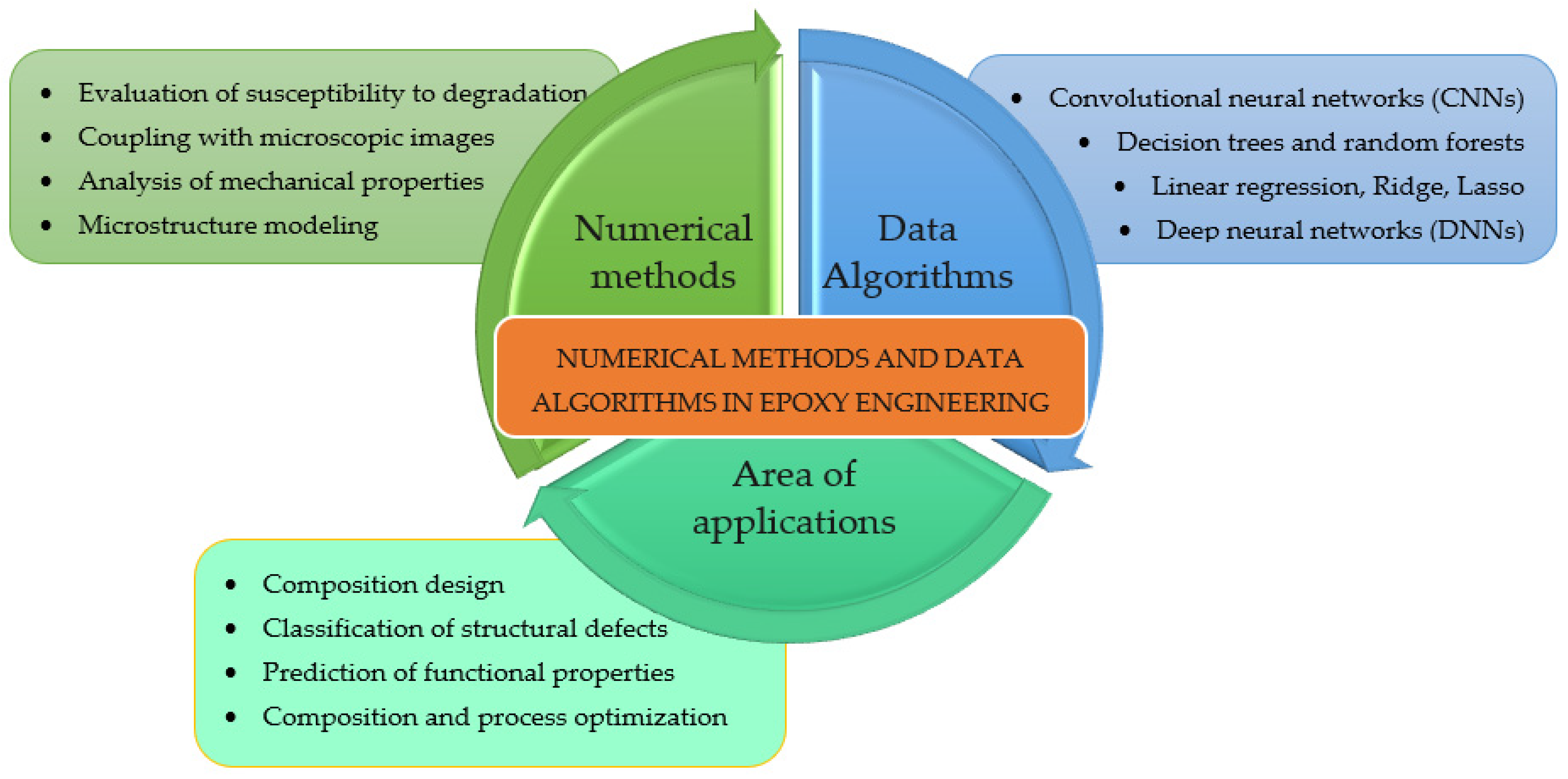
2. Numerical Methods and Data Algorithms in Epoxy Materials Engineering
3. Materials and Methods
3.1. Materials and Their Properties
3.2. Preparing Samples for Testing
- Weighing the specified amount of resin;
- Adding a filler (for modified compositions) to the epoxy resin in the appropriate amount;
- Mechanical stirring of the composition components for a period of 3 min at a speed of 460 rpm;
- Adding curing agent to the resin mixed with the filler in appropriate amounts;
- Mechanical mixing of the components of the composition at a speed of 460 rpm for a period of 3 min;
- Venting the epoxy composition over a period of 3 min.
3.3. Material Testing
3.4. Machine Learning Approach
4. Results and Discussion
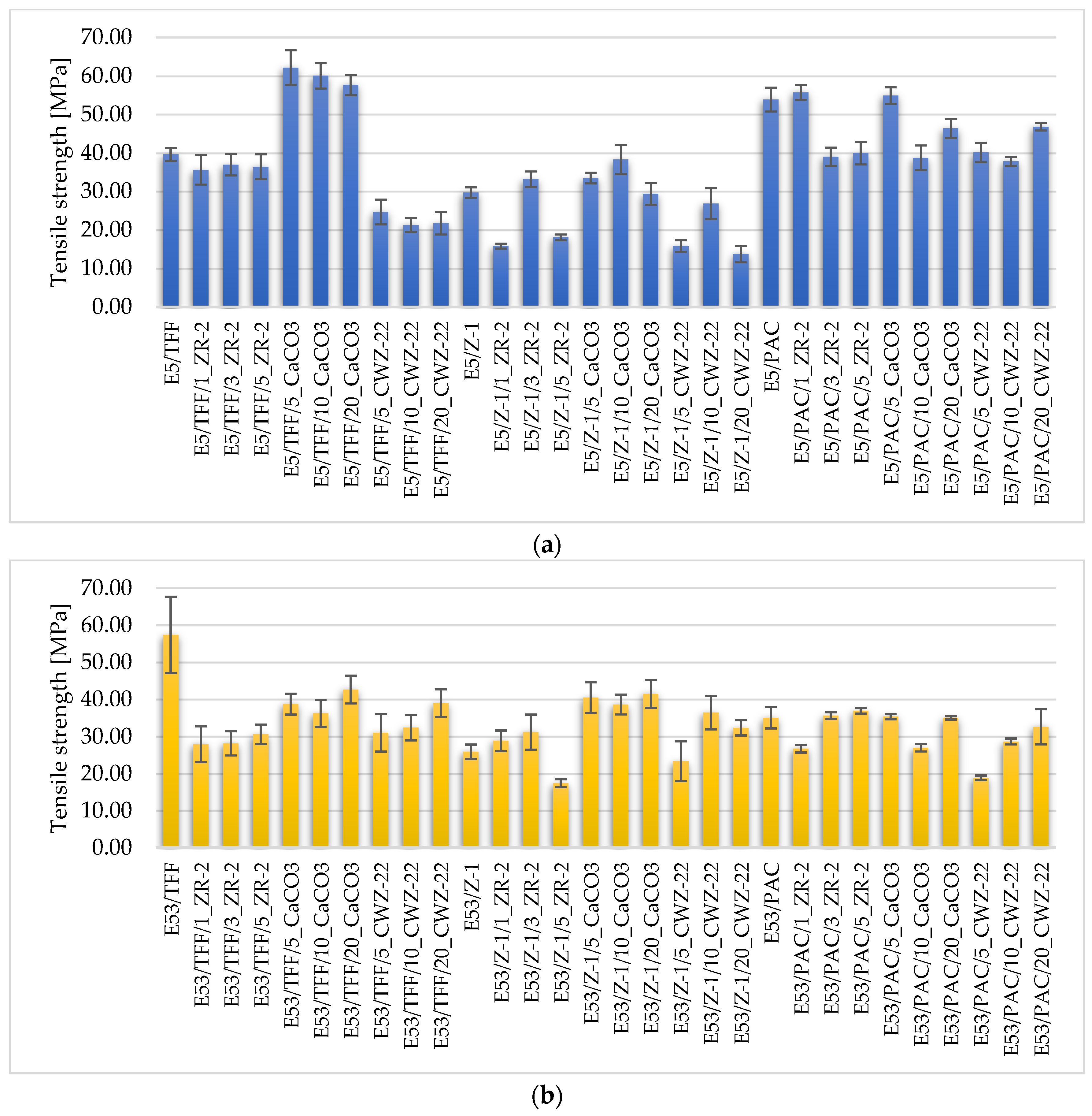
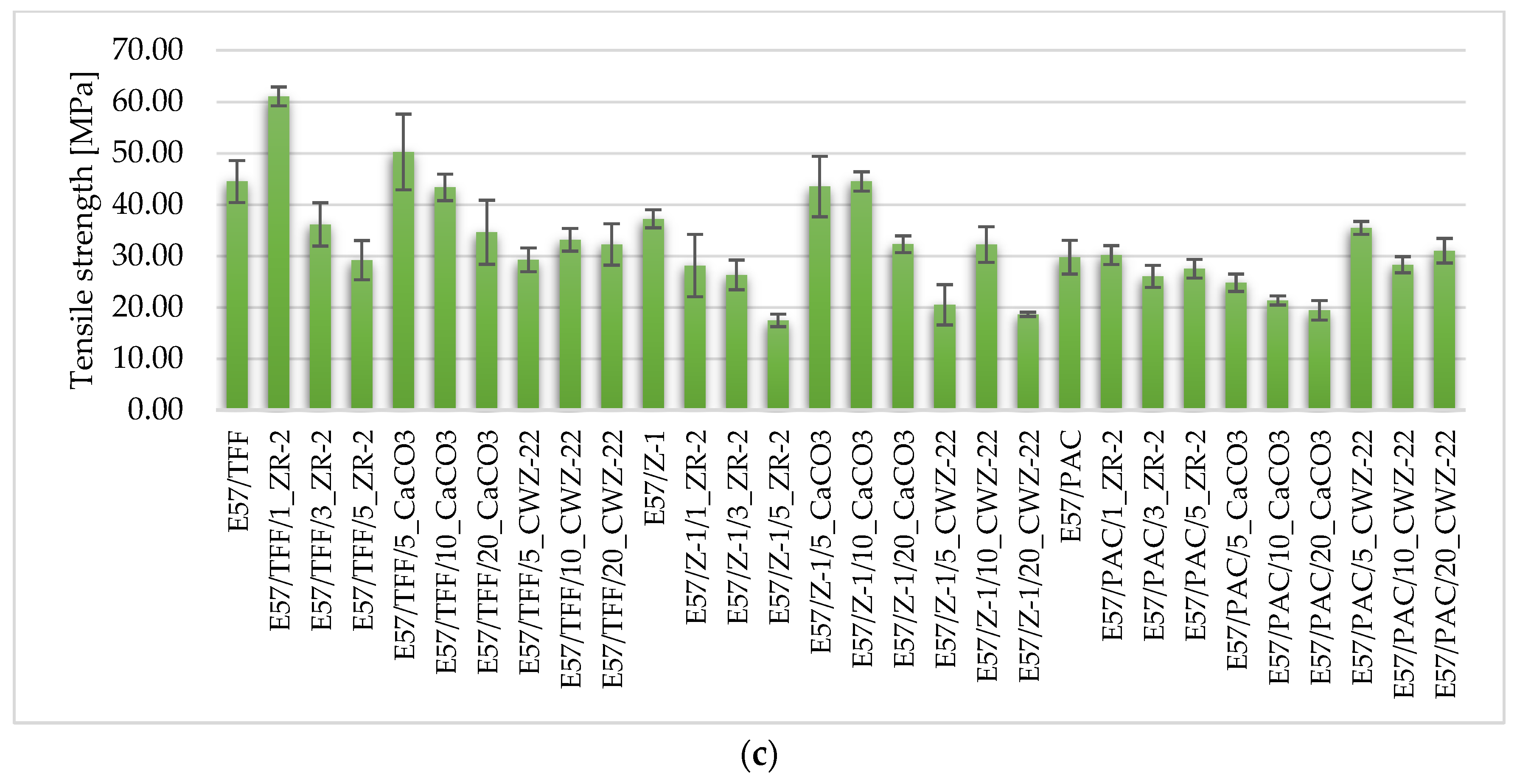
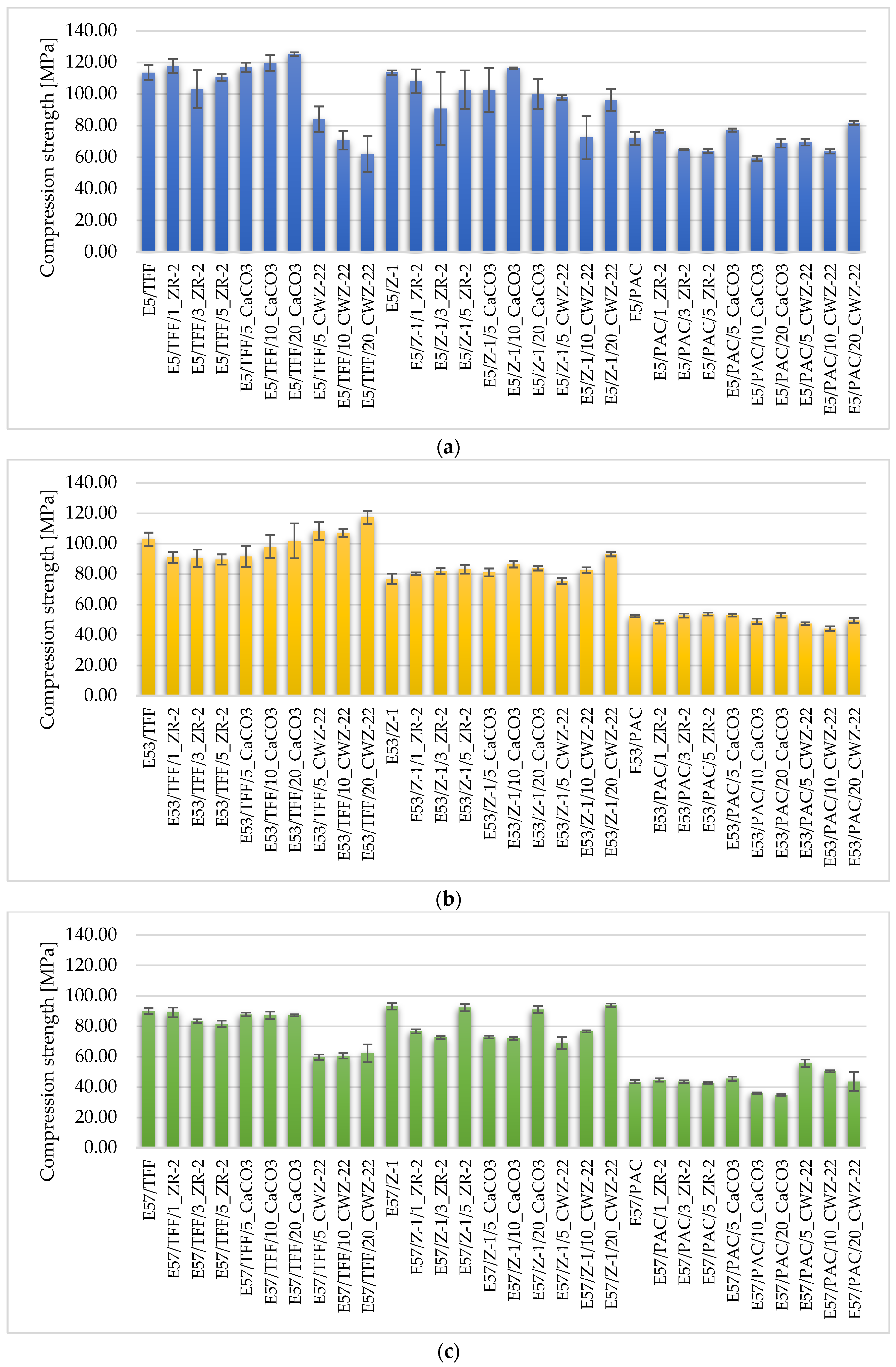
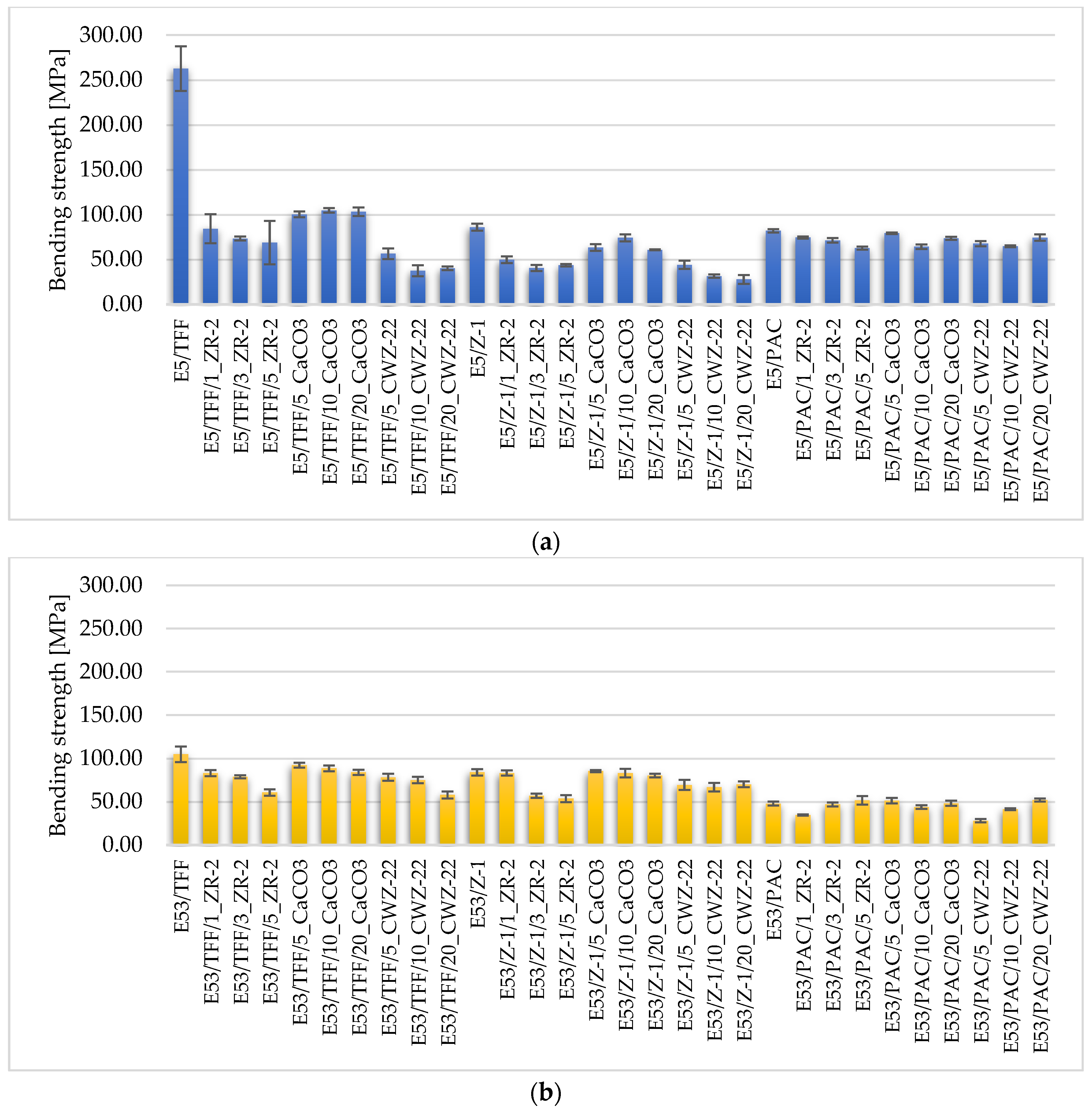
4.1. Strength Test Results
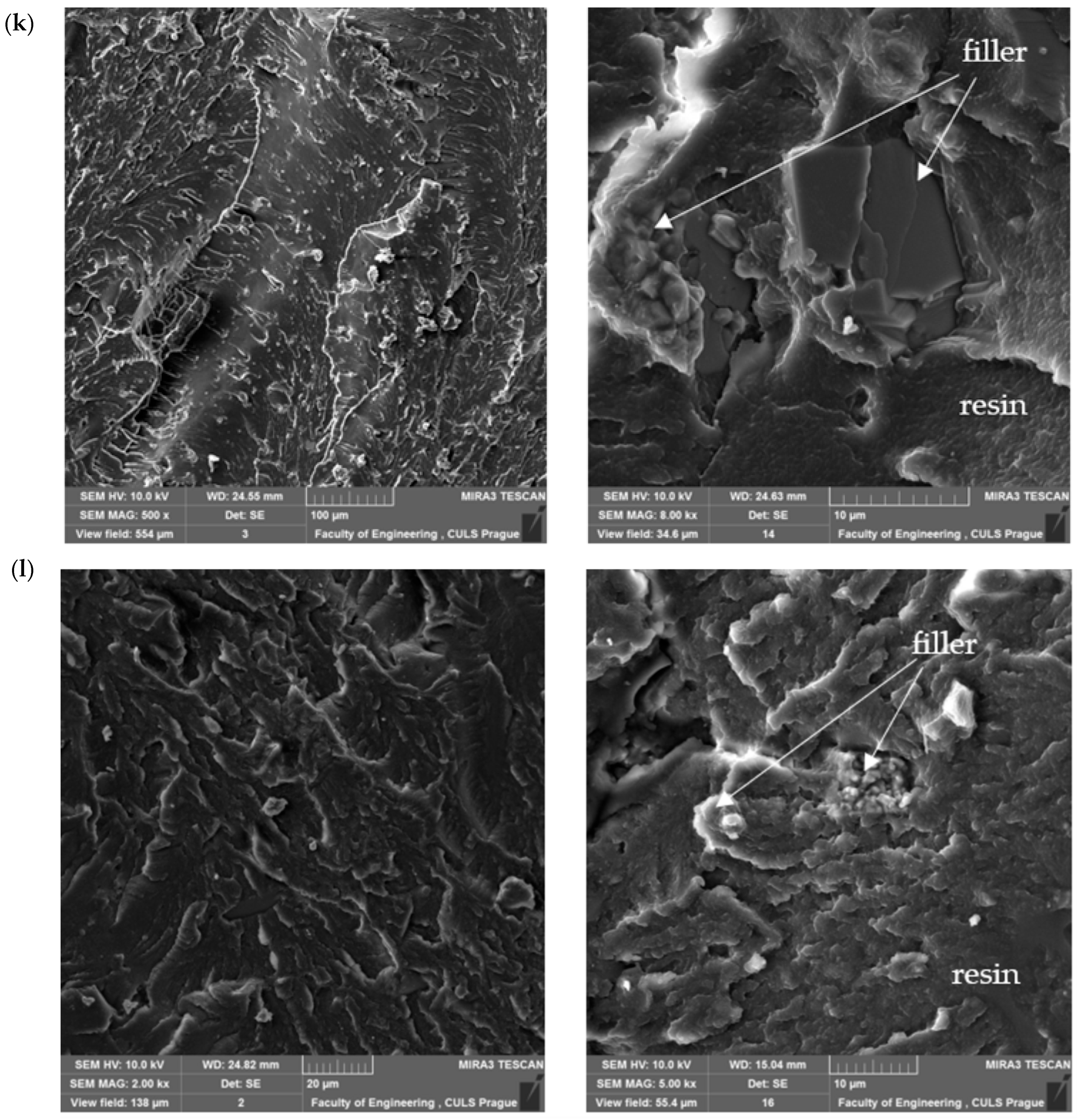
4.2. SEM Analysis of Microstructure
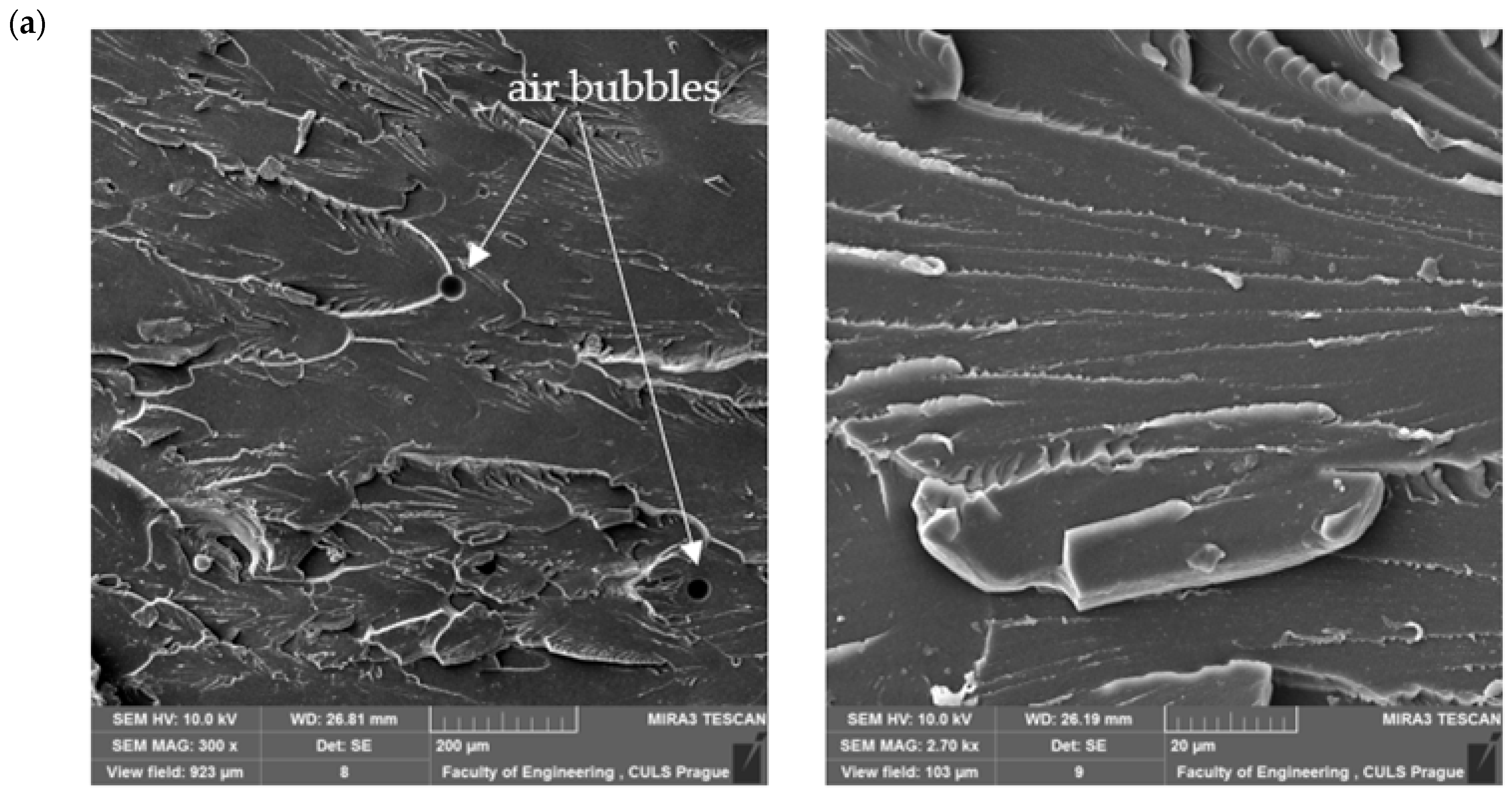
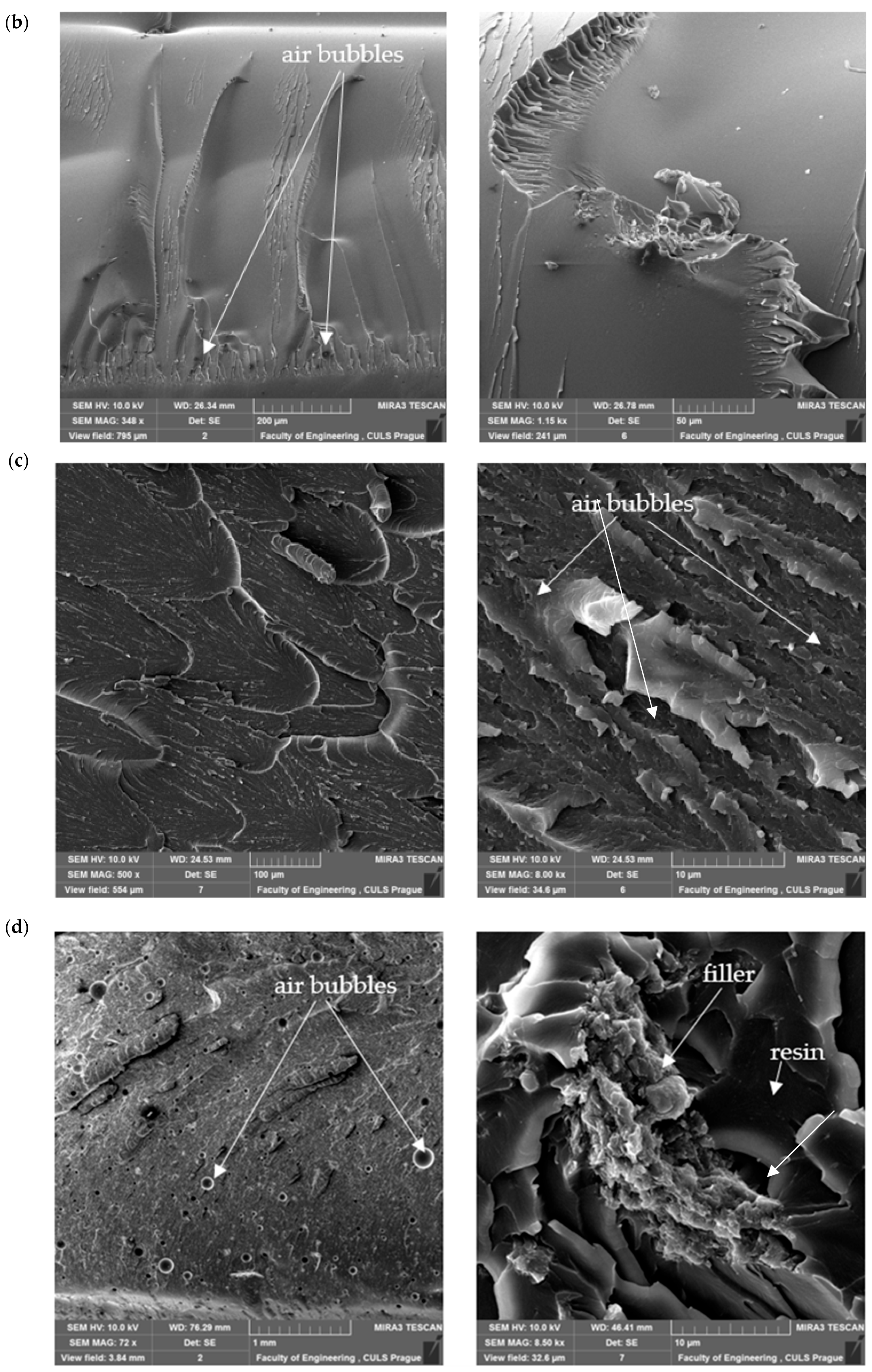
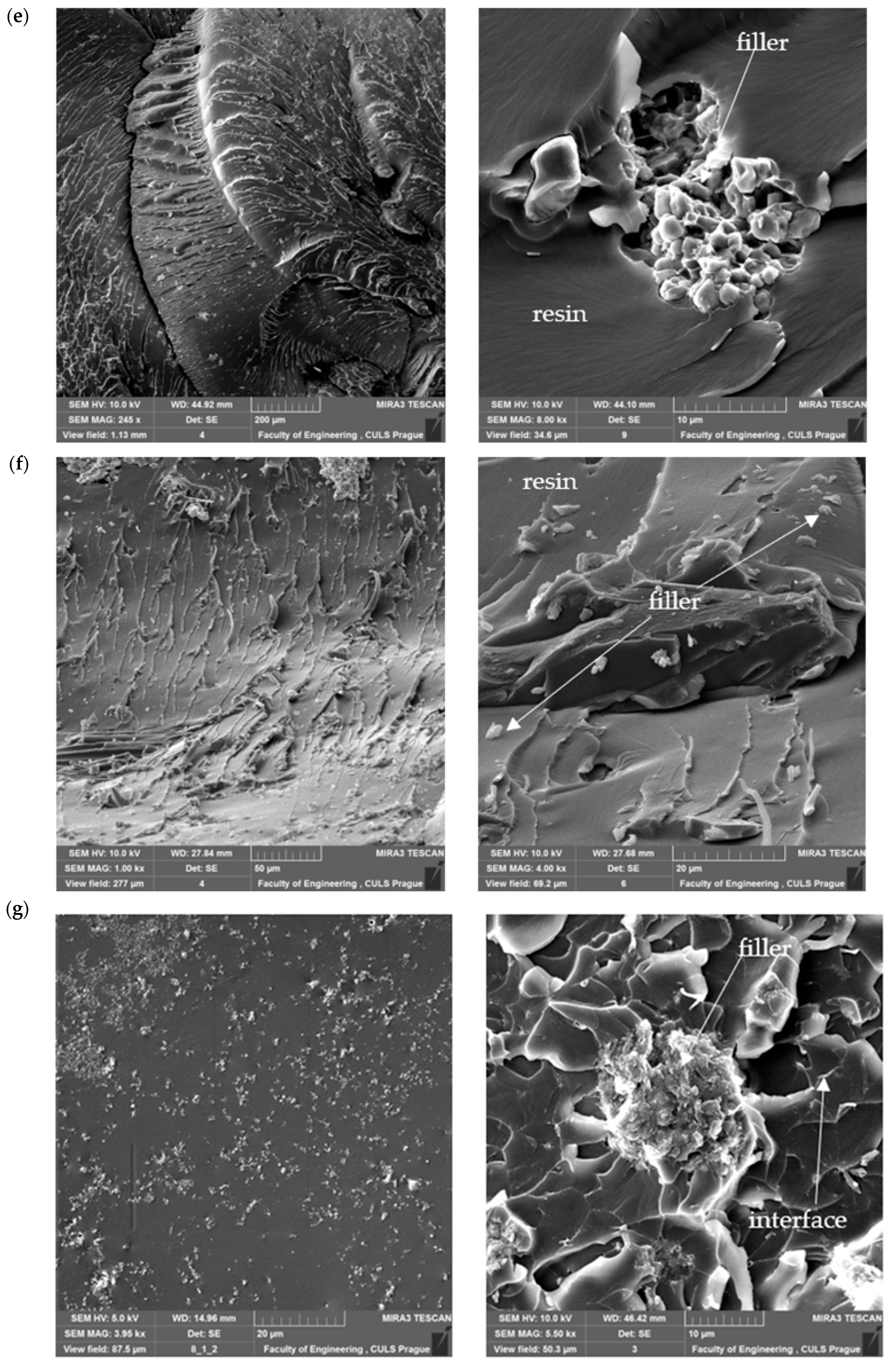
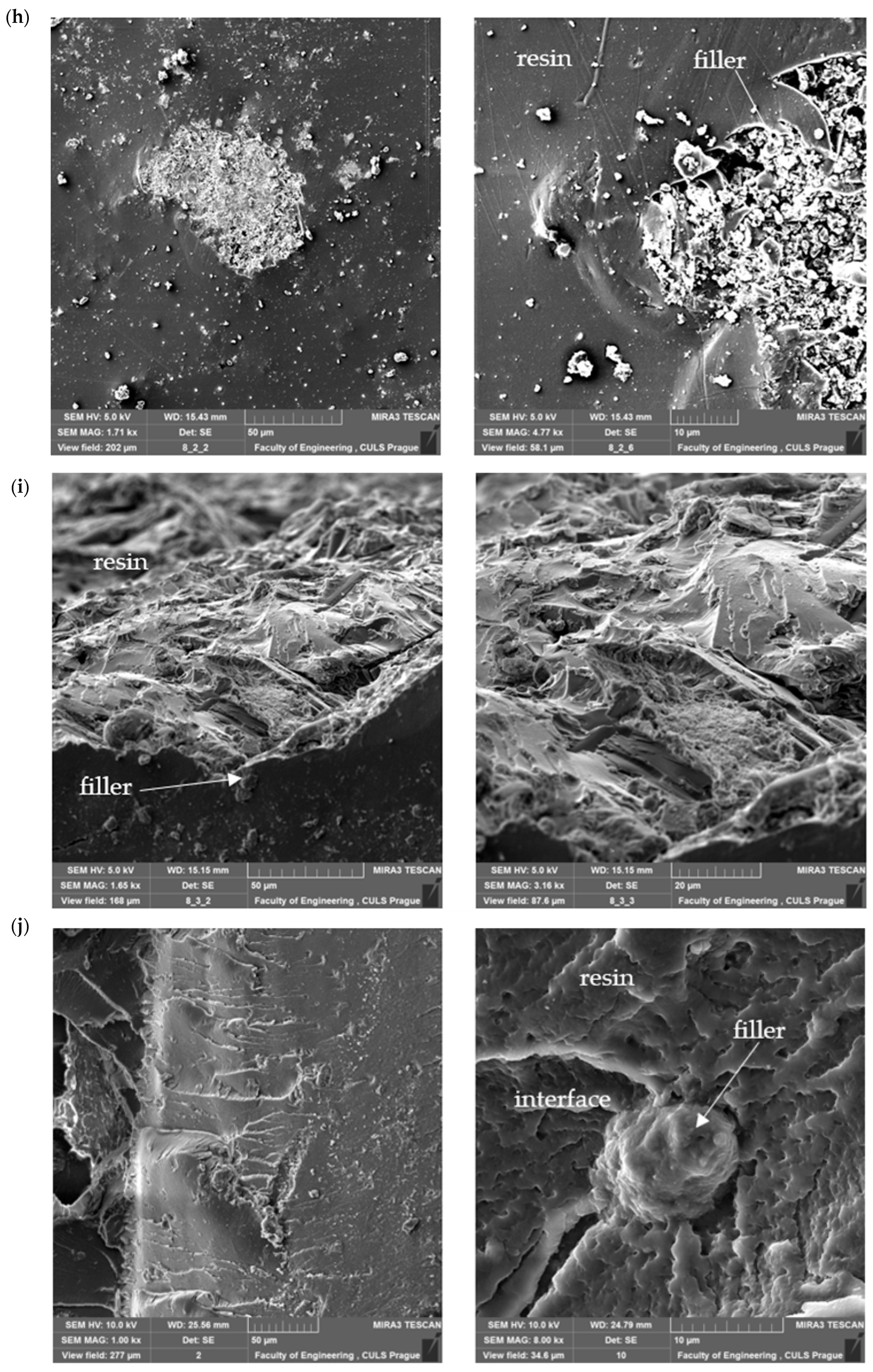
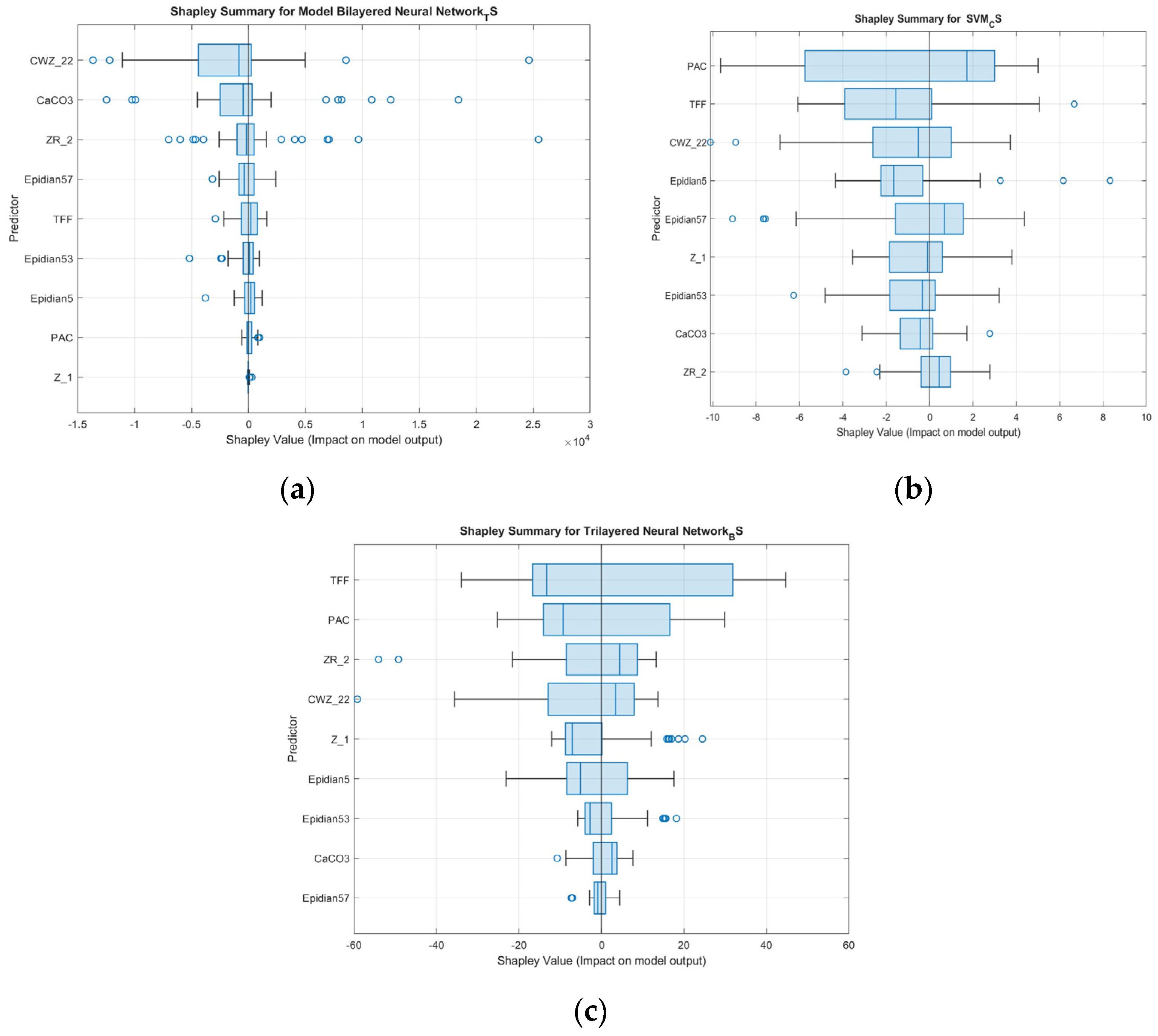
5. Prediction Results Analysis
- TFF is the only variable that is consistently important across all three models. It is particularly dominant in the bending strength model, where it has the highest and most stable positive average impact. This suggests that TFF plays a versatile role, influencing a range of mechanical properties, which is likely due to its structural or adhesive characteristics in the composite.
- PAC is highly influential for compression and bending strength but almost irrelevant for tensile strength. Its behavior is variable and sometimes bidirectional, indicating that its role depends heavily on its interaction with the other components of the formulation.
- CWZ-22 has the greatest impact on tensile strength prediction, with reduced relevance in compression and bending. This suggests that its contribution may relate to stiffness or network formation under tensile loads.
- ZR-2 is important for tensile and bending strength but not compression, mirroring the pattern observed for CWZ-22.
- CaCO3 is a key predictor only in the tensile model, highlighting its specific role in enhancing tensile resistance, likely through particle reinforcement or matrix modification.
- Z1, Epidian 53, Epidian 5, and Epidian 57 remain minor contributors across all tasks, though some exhibit small but variable influences, especially in specific samples.
6. Conclusions
- For tensile strength, a 2-layer neural network model achieved an R2 = 0.64, an RMSE = 4483.5, and a MAPE = 1494.2%.
- For compression strength, an SVM model achieved an R2 = 0.93, an RMSE = 6.42, and a MAPE = 5.0%.
- The most accurate model for bending strength was a 3-layer neural network, which obtained an R2 = 0.95, an RMSE = 6.62, and a MAPE = 7.1%.
- TFF was the most consistent predictor across all models, particularly in bending.
- PAC significantly influenced compression and bending strength but had little effect on tensile strength.
- CWZ-22 and CaCO3 were key drivers of tensile strength.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Curtarolo, S.; Setyawan, W.; Hart, G.L.W.; Jahnatek, M.; Chepulskii, R.V.; Taylor, R.H.; Wang, S.; Xue, J.; Yang, K.; Levy, O.; et al. AFLOW: An Automatic Framework for High-Throughput Materials Discovery. Comput. Mater. Sci. 2012, 58, 218–226. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A Materials Genome Approach to Accelerating Materials Innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef]
- Taub, A.I.; Luo, A.A. Advanced Lightweight Materials and Manufacturing Processes for Automotive Applications. MRS Bull. 2015, 40, 1045–1054. [Google Scholar] [CrossRef]
- Karthikeyan, N.; Naveen, J. Progress in Adhesive-Bonded Composite Joints: A Comprehensive Review. J. Reinf. Plast. Compos. 2024, 07316844241248236. [Google Scholar] [CrossRef]
- Fekiač, J.J.; Krbata, M.; Kohutiar, M.; Janík, R.; Kakošová, L.; Breznická, A.; Eckert, M.; Mikuš, P. Comprehensive Review: Optimization of Epoxy Composites, Mechanical Properties, & Technological Trends. Polymers 2025, 17, 271. [Google Scholar] [CrossRef]
- Szewczak, A. Impact of Epoxy Resin Modification on Their Strength Parameters. Bud. Archit. 2020, 18, 041–050. [Google Scholar] [CrossRef]
- Kudžma, A.; Stonys, R.; Kilikevičius, A.; Višniakov, N.; Antonovič, V.; Škamat, J. Effect of Low Oxidation Graphene Oxide on Physical, Dynamic and Mechanical Properties of MCC Type Refractory Castable. In Proceedings of the 24th International Conference on Composite Structures (ICCS-24), Porto, Portugal, 14–16 June 2021. [Google Scholar]
- Ahmad Temizi, M.A.; Meor Ahmad, M.I.; Khamis, N.K.; Ahmad Samsudin, M.Y. Merit Technologies Sdn. Bhd, Jalan PJU 3/45, Sunway Damansara, 47810 Petaling Jaya, Selangor Study of Mechanical and Thermal Properties for Epoxy Grouts Subjected to Seawater Conditioning at Elevated Temperature: Tensile Test and Compressive Test. J. Kejuruter. 2022, 34, 1017–1025. [Google Scholar] [CrossRef]
- Yan, H.; Tan, J.; Chen, H.; He, T.; Zeng, D.; Zhang, L. Machine Learning-Based Prediction of Tribological Properties of Epoxy Composite Coating. Polymers 2025, 17, 282. [Google Scholar] [CrossRef]
- Jang, H.; Ryu, D.; Lee, W.; Park, G.; Kim, J. Machine Learning-Based Epoxy Resin Property Prediction. Mol. Syst. Des. Eng. 2024, 9, 959–968. [Google Scholar] [CrossRef]
- Berladir, K.; Antosz, K.; Ivanov, V.; Mitaľová, Z. Machine Learning-Driven Prediction of Composite Materials Properties Based on Experimental Testing Data. Polymers 2025, 17, 694. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, T.; Sun, W. Construction of Biocompatible Bilayered Light-driven Actuator Composed of rGO/PNIPAM and PEGDA Hydrogel. J. Appl. Polym. Sci. 2020, 137, 49375. [Google Scholar] [CrossRef]
- Foroutani, K.; Ghasemi, S.M.; Pourabbas, B. Ordered Isoporous Membranes from Ionic Diblock Copolymers via SNIPS: Optimizing Effective Factors with a Structural Survey. Prog. Org. Coat. 2021, 161, 106554. [Google Scholar] [CrossRef]
- Rudawska, A. Epoxy Adhesives. In Handbook of Adhesive Technology; CRS Press Taylor & Frances Group: Boca Raton, FL, USA, 2018; pp. 415–442. [Google Scholar]
- Ma, X.; Zhang, Y.; Wang, X. Machine Learning for Composite Materials. MRS Commun. 2020, 10, 551–556. [Google Scholar] [CrossRef]
- Raccuglia, P.; Elbert, K.C.; Adler, P.D.F.; Falk, C.; Wenny, M.B.; Mollo, A.; Zeller, M.; Friedler, S.A.; Schrier, J.; Norquist, A.J. Machine-Learning-Assisted Materials Discovery Using Failed Experiments. Nature 2016, 533, 73–76. [Google Scholar] [CrossRef]
- Ramprasad, R.; Batra, R.; Pilania, G.; Mannodi-Kanakkithodi, A.; Kim, C. Machine Learning in Materials Informatics: Recent Applications and Prospects. Npj Comput. Mater. 2017, 3, 54. [Google Scholar] [CrossRef]
- Xie, T.; Grossman, J.C. Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties. Phys. Rev. Lett. 2018, 120, 145301. [Google Scholar] [CrossRef]
- Czub, P.; Penczek, P. Epoxy Resin Chemistry and Technology; Wydawnictwa Naukowo-Techniczne: Warszawa, Poland, 2002; ISBN 978-83-204-2611-3. [Google Scholar]
- Królikowski, W.; Rosłaniec, Z. Polymer Nanocomposites. Kompozyty 2004, 9, 3–16. [Google Scholar]
- BN-89 6376-02–Industry Standard; Epoxy Resins Epidian 1, 2, 3, 4, 5, 6. Zakłady Chemiczne Organika-Sarzyna: Nowa Sarzyna, Poland, 2013; Access Location: Library of Lublin University of Technology. (In Polish)
- BN-73 6376-01–Industry Standard; Epoxy Resins Epidian 51 i 53. Institution Developing the Standard—Zakłady Chemiczne in Oświęcim. Zakłady Chemiczne Organika-Sarzyna: Nowa Sarzyna, Poland, 1974. Available online: https://bcpw.bg.pw.edu.pl/dlibra/publication/12442/edition/11925?language=pl (accessed on 13 June 2025). (In Polish)
- Information Catalogue of Ciech, S.A. Available online: https://www.zywicesarzyna.pl/ (accessed on 13 June 2025).
- Bereska, B.; Iłowska, J.; Czaja, K.; Bereska, A. Curing Agents for Epoxy Resins. Przem. Chem. 2014, 93, 443–448. [Google Scholar]
- Material Safety Data Sheet for Montmorillonite ZR-2 NanoBent. Available online: https://www.sorbentsystems.com/pdf/montmorillonitemsds.pdf?srsltid=AfmBOoqAlBCRt_AwRrrYWB-6NSwXF4a6tyuSBUSKVk-MzVitPNQECEwP (accessed on 13 June 2025).
- Safety Data Sheet for CaCO3. Available online: https://www.carlroth.com/medias/SDB-P013-MT-EN.pdf?context=bWFzdGVyfHNlY3VyaXR5RGF0YXNoZWV0c3wyNDQ1NDh8YXBwbGljYXRpb24vcGRmfGFEWmhMMmhpTnk4NU1UYzJORGMwTlRVd016QXlMMU5FUWw5UU1ERXpYMDFVWDBWT0xuQmtaZ3xhMzc2MjBhZDhhMjgxMDExZDk2NDY2NDRmYTk5NjY5NGJmYmUxN2RiN2JkMWRlYWIwMWJmOWZkNGExMGFiZGY3 (accessed on 13 June 2025).
- Characteristics Sheet of CWZ-22 Activated Carbon. Available online: https://mass-zone.eu/en/stanlab-activated-carbon-dust-cwz-22-1kg-p-8886.html (accessed on 13 June 2025).
- Dickens, B. Model-Free Estimation of Outdoor Performance of a Model Epoxy Coating System Using Accelerated Test Laboratory Data. J. Coat. Technol. Res. 2009, 6, 419–428. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, K.; Lu, X.; Lam, Y.C. A Review on the Mechanical Methods for Evaluating Coating Adhesion. Acta Mech. 2014, 225, 431–452. [Google Scholar] [CrossRef]
- Ye, D.; Xu, Z.; Liu, H.; Zhang, Z.; Wang, P.; Wu, Y.; Yin, C. Terahertz Non-Destructive Testing of Porosity in Multi-Layer Thermal Barrier Coatings Based on Small-Sample Data. Coatings 2024, 14, 1357. [Google Scholar] [CrossRef]
- PN-EN ISO 527-1-Plastics; Determination of Mechanical Properties in Static Tension. Europe. ISO: Geneva, Switzerland, 2012. (In Polish)
- ISO 604-Plastics; Determination of Properties in Compression. Europe. ISO: Geneva, Switzerland, 2006.
- DIN-EN ISO 178-Plastics; Determination of Flexural Properties. Europe. ISO: Geneva, Switzerland, 2019.
- Hastie, T.; Tibsgirani, R.; Friedman, J. The Elements of Statistical Learning; Springer: New York, NY, USA, 2009. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R.; Taylor, J. An Introduction to Statistical Learning; Springer Texts in Statistics; Springer: Cham, Switzerland, 2013; ISBN 978-3-031-38746-3. [Google Scholar]
- Antosz, K.; Kozłowski, E.; Sęp, J.; Prucnal, S. Application of Machine Learning to the Prediction of Surface Roughness in the Milling Process on the Basis of Sensor Signals. Materials 2025, 18, 148. [Google Scholar] [CrossRef] [PubMed]
- Thomson, W. The Shapley Value, a Crown Jewel of Cooperative Game Theory. In Handbook of the Shapley Value; Fragnelli, V., Sanchez-Soriano, J., Eds.; Series in Operations Research; Chapman and Hall/CRC: Boca Raton, FL, USA, 2019; pp. 1–15. ISBN 978-1-351-24141-0. [Google Scholar]
- Nwoye, I.; Obelle, M.C.; Nwakpa, S.O.; Onyia, C.W.; Obuekwe, I.; Idenyi, N.E. Predictability of the Impact Strength of CaCO 3 -Epoxy Resin Composite Based on CaCO 3 Input Concentration and Sustained Stress at Impact. Int. J. Mater. Lifetime 2015, 2, 6–12. [Google Scholar]
- Park, S.-J. Interface Science and Composites; Issn Ser; Elsevier Science & Technology: San Diego, CA, USA, 2011; ISBN 978-0-08-096348-8. [Google Scholar]
- Miturska, I.; Rudawska, A.; Müller, M.; Valášek, P. The Influence of Modification with Natural Fillers on the Mechanical Properties of Epoxy Adhesive Compositions after Storage Time. Materials 2020, 13, 291. [Google Scholar] [CrossRef]
- Miturska, I.; Rudawska, A.; Müller, M.; Hromasová, M. The Influence of Mixing Methods of Epoxy Composition Ingredients on Selected Mechanical Properties of Modified Epoxy Construction Materials. Materials 2021, 14, 411. [Google Scholar] [CrossRef]
- Yang, G.; Heo, Y.-J.; Park, S.-J. Effect of Morphology of Calcium Carbonate on Toughness Behavior and Thermal Stability of Epoxy-Based Composites. Processes 2019, 7, 178. [Google Scholar] [CrossRef]
- Rudawska, A.; Frigione, M. Aging Effects of Aqueous Environment on Mechanical Properties of Calcium Carbonate-Modified Epoxy Resin. Polymers 2020, 12, 2541. [Google Scholar] [CrossRef]
- Shivamurthy, B.; Murthy, K.; Joseph, P.C.; Rishi, K.; Bhat, K.U.; Anandhan, S. Mechanical Properties and Sliding Wear Behavior of Jatropha Seed Cake Waste/Epoxy Composites. J. Mater. Cycles Waste Manag. 2015, 17, 144–156. [Google Scholar] [CrossRef]
- Yu, D.; Wang, J.; Tian, J.; Xu, X.; Dai, J.; Wang, X. Preparation and Characterization of TiO2/ZnO Composite Coating on Carbon Steel Surface and Its Anticorrosive Behavior in Seawater. Compos. Part. B Eng. 2013, 46, 135–144. [Google Scholar] [CrossRef]
- Fu, J.; Kamali-Bernard, S.; Bernard, F.; Cornen, M. Comparison of Mechanical Properties of C-S-H and Portlandite between Nano-Indentation Experiments and a Modeling Approach Using Various Simulation Techniques. Compos. Part. B Eng. 2018, 151, 127–138. [Google Scholar] [CrossRef]




| Properties | Epidian 5 Epoxy Resin | Epidian 53 Epoxy Resin | Epidian 57 Epoxy Resin |
|---|---|---|---|
| Epoxy number | 0.48–0.52 mol/100 g | ≥0.41 mol/100 g | ≥0.40 mol/100 g |
| pH value | ok. 7 | ok. 7 | ok. 7 |
| Viscosity at 25 °C | 20,000–30,000 mPa·s | 900–1500 mPa·s | 13,000–19,000 mPa·s |
| Density in 20 °C | 1.16 g/cm3 | 1.11–1.15 g/cm3 | 1.14–1.17 g/cm3 |
| Flash temperature | 266 °C | 58 °C | 134 °C |
| Temperature auto-ignition | 490 °C | 460 °C | 455 °C |
| Melting point | 30–50 °C | Not applicable | Not applicable |
| Initial boiling point | not marked—distribution | 141 °C | >215 °C does not boil |
| Properties | Mannich’s Principle (TFF Curing Agent) | Amine Curing Agent (Z-1 Curing Agent) | Polyamide Curing Agent (PAC Curing Agent) |
|---|---|---|---|
| Viscosity at 25 °C | max. 10,000 mPa·s | 20–30 mPa·s | 10,000–25,000 mPa·s |
| Density in 20 °C | 1.15–1.20 g/cm3 | 0.978–0.983 g/cm3 | 1.10–1.20 g/cm3 |
| Amine number | 500–700 mg KOH/g | min. 1100 mg KOH/g | 290–360 mg KOH/g |
| Gelation time (example for composition with Epidian 5 at 20 °C, for 100 g sample) | 17 min | 33 min | 180 min |
| Epoxy Resin | Curing Agent (Parts by Weight per 100 Parts by Weight of Epoxy Resin) | ||
|---|---|---|---|
| TFF Epoxy Resin | Z-1 Epoxy Resin | PAC Epoxy Resin | |
| Epidian 5 (E5) | 26 part-weight. | 12 part-weight. | 80 part-weight. |
| Epidian 53 (E53) | 22 part-weight. | 10 part-weight. | 80 part-weight. |
| Epidian 57 (E57) | 22 part-weight. | 10 part-weight. | 80 part-weight. |
| Properties | ZR2 NanoBent |
|---|---|
| Form | cream-colored lamellar powder |
| Water content | ≤3.0% weights |
| Roasting loss at 650 °C | 25–30% weights |
| Swelling in Xylene | >20% volume |
| Vapor sorption of white spirit 48 h | >20% weights |
| Bulk density | <0.5 g/cm3 |
| CEC ion exchange capacity of bentonite raw material | min. 80 mmol/100 g dry bentonite raw material |
| Properties | CaCO3 Calcium Carbonate |
|---|---|
| Form | light gray solid of various sizes: lumps or fine powder |
| Fragrance | odorless |
| pH | 9.2 (at 25 °C) |
| Melting point | >450 °C (decomposition temperature—825 °C) |
| Flammability | non-flammable |
| Explosive limits | non-explosive (free of any chemical structures associated with explosive properties) |
| Relative density | 2.711 g/cm3 (at 20 °C) |
| Solubility in water | 14 mg/dm3 (at 25 °C) |
| Viscosity | not applicable (solid with melting point > 450 °C) |
| Explosive properties | non-explosive (free of any chemical structures associated with explosive properties) |
| Oxidizing properties | non-oxidizing (based on chemical structure, the substance does not contain excess oxygen or any structural group tending to react exothermically with combustible material) |
| Decomposition temperature | 825 °C |
| Bulk density | (0.7–1.4)·106 g/m3 (at 20 °C) |
| Electrostatic properties | the substance does not generate electrostatic charges |
| Properties | CWZ-22 Activated Carbon |
|---|---|
| Form | solid, dusty black color |
| Fragrance | odorless |
| pH | about 6 (50 g/L H2O as suspension, 20 °C) |
| Melting point | no data, sublimation about 3700 °C |
| Explosive limits | no data |
| Relative density | about 2 g/cm3 |
| Solubility in water | in water: insoluble in organic solvents: no data |
| Bulk density | about 400·103 g/m3 |
| No | Epoxy Resin | Curing Agent | Filler | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Epidian 5 | Epidian 53 | Epidian 57 | TFF | Z-1 | PAC | ZR-2 | CaCO3 | CWZ-22 | |
| 1 | 100 | 0 | 0 | 26 | 0 | 0 | 0 | 0 | 0 |
| 2 | 100 | 0 | 0 | 26 | 0 | 0 | 1 | 0 | 0 |
| 3 | 100 | 0 | 0 | 26 | 0 | 0 | 3 | 0 | 0 |
| 4 | 100 | 0 | 0 | 26 | 0 | 0 | 5 | 0 | 0 |
| 5 | 100 | 0 | 0 | 26 | 0 | 0 | 0 | 5 | 0 |
| 6 | 100 | 0 | 0 | 26 | 0 | 0 | 0 | 10 | 0 |
| 7 | 100 | 0 | 0 | 26 | 0 | 0 | 0 | 20 | 0 |
| 8 | 100 | 0 | 0 | 26 | 0 | 0 | 0 | 0 | 5 |
| 9 | 100 | 0 | 0 | 26 | 0 | 0 | 0 | 0 | 10 |
| 10 | 100 | 0 | 0 | 26 | 0 | 0 | 0 | 0 | 20 |
| 11 | 100 | 0 | 0 | 0 | 12 | 0 | 0 | 0 | 0 |
| 12 | 100 | 0 | 0 | 0 | 12 | 0 | 1 | 0 | 0 |
| 13 | 100 | 0 | 0 | 0 | 12 | 0 | 3 | 0 | 0 |
| 14 | 100 | 0 | 0 | 0 | 12 | 0 | 5 | 0 | 0 |
| 15 | 100 | 0 | 0 | 0 | 12 | 0 | 0 | 5 | 0 |
| 16 | 100 | 0 | 0 | 0 | 12 | 0 | 0 | 10 | 0 |
| 17 | 100 | 0 | 0 | 0 | 12 | 0 | 0 | 20 | 0 |
| 18 | 100 | 0 | 0 | 0 | 12 | 0 | 0 | 0 | 5 |
| 19 | 100 | 0 | 0 | 0 | 12 | 0 | 0 | 0 | 10 |
| 20 | 100 | 0 | 0 | 0 | 12 | 0 | 0 | 0 | 20 |
| 21 | 100 | 0 | 0 | 0 | 0 | 80 | 0 | 0 | 0 |
| 22 | 100 | 0 | 0 | 0 | 0 | 80 | 1 | 0 | 0 |
| 23 | 100 | 0 | 0 | 0 | 0 | 80 | 3 | 0 | 0 |
| 24 | 100 | 0 | 0 | 0 | 0 | 80 | 5 | 0 | 0 |
| 25 | 100 | 0 | 0 | 0 | 0 | 80 | 0 | 5 | 0 |
| 26 | 100 | 0 | 0 | 0 | 0 | 80 | 0 | 10 | 0 |
| 27 | 100 | 0 | 0 | 0 | 0 | 80 | 0 | 20 | 0 |
| 28 | 100 | 0 | 0 | 0 | 0 | 80 | 0 | 0 | 5 |
| 29 | 100 | 0 | 0 | 0 | 0 | 80 | 0 | 0 | 10 |
| 30 | 100 | 0 | 0 | 0 | 0 | 80 | 0 | 0 | 20 |
| No | Epoxy Resin | Curing Agent | Filler | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Epidian 5 | Epidian 53 | Epidian 57 | TFF | Z-1 | PAC | ZR-2 | CaCO3 | CWZ-22 | |
| 1 | 0 | 100 | 0 | 22 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 100 | 0 | 22 | 0 | 0 | 1 | 0 | 0 |
| 3 | 0 | 100 | 0 | 22 | 0 | 0 | 3 | 0 | 0 |
| 4 | 0 | 100 | 0 | 22 | 0 | 0 | 5 | 0 | 0 |
| 5 | 0 | 100 | 0 | 22 | 0 | 0 | 0 | 5 | 0 |
| 6 | 0 | 100 | 0 | 22 | 0 | 0 | 0 | 10 | 0 |
| 7 | 0 | 100 | 0 | 22 | 0 | 0 | 0 | 20 | 0 |
| 8 | 0 | 100 | 0 | 22 | 0 | 0 | 0 | 0 | 5 |
| 9 | 0 | 100 | 0 | 22 | 0 | 0 | 0 | 0 | 10 |
| 10 | 0 | 100 | 0 | 22 | 0 | 0 | 0 | 0 | 20 |
| 11 | 0 | 100 | 0 | 0 | 10 | 0 | 0 | 0 | 0 |
| 12 | 0 | 100 | 0 | 0 | 10 | 0 | 1 | 0 | 0 |
| 13 | 0 | 100 | 0 | 0 | 10 | 0 | 3 | 0 | 0 |
| 14 | 0 | 100 | 0 | 0 | 10 | 0 | 5 | 0 | 0 |
| 15 | 0 | 100 | 0 | 0 | 10 | 0 | 0 | 5 | 0 |
| 16 | 0 | 100 | 0 | 0 | 10 | 0 | 0 | 10 | 0 |
| 17 | 0 | 100 | 0 | 0 | 10 | 0 | 0 | 20 | 0 |
| 18 | 0 | 100 | 0 | 0 | 10 | 0 | 0 | 0 | 5 |
| 19 | 0 | 100 | 0 | 0 | 10 | 0 | 0 | 0 | 10 |
| 20 | 0 | 100 | 0 | 0 | 10 | 0 | 0 | 0 | 20 |
| 21 | 0 | 100 | 0 | 0 | 0 | 80 | 0 | 0 | 0 |
| 22 | 0 | 100 | 0 | 0 | 0 | 80 | 1 | 0 | 0 |
| 23 | 0 | 100 | 0 | 0 | 0 | 80 | 3 | 0 | 0 |
| 24 | 0 | 100 | 0 | 0 | 0 | 80 | 5 | 0 | 0 |
| 25 | 0 | 100 | 0 | 0 | 0 | 80 | 0 | 5 | 0 |
| 26 | 0 | 100 | 0 | 0 | 0 | 80 | 0 | 10 | 0 |
| 27 | 0 | 100 | 0 | 0 | 0 | 80 | 0 | 20 | 0 |
| 28 | 0 | 100 | 0 | 0 | 0 | 80 | 0 | 0 | 5 |
| 29 | 0 | 100 | 0 | 0 | 0 | 80 | 0 | 0 | 10 |
| 30 | 0 | 100 | 0 | 0 | 0 | 80 | 0 | 0 | 20 |
| No | Epoxy Resin | Curing Agent | Filler | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Epidian 5 | Epidian 53 | Epidian 57 | TFF | Z-1 | PAC | ZR-2 | CaCO3 | CWZ-22 | |
| 1 | 0 | 0 | 100 | 22 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 100 | 22 | 0 | 0 | 1 | 0 | 0 |
| 3 | 0 | 0 | 100 | 22 | 0 | 0 | 3 | 0 | 0 |
| 4 | 0 | 0 | 100 | 22 | 0 | 0 | 5 | 0 | 0 |
| 5 | 0 | 0 | 100 | 22 | 0 | 0 | 0 | 5 | 0 |
| 6 | 0 | 0 | 100 | 22 | 0 | 0 | 0 | 10 | 0 |
| 7 | 0 | 0 | 100 | 22 | 0 | 0 | 0 | 20 | 0 |
| 8 | 0 | 0 | 100 | 22 | 0 | 0 | 0 | 0 | 5 |
| 9 | 0 | 0 | 100 | 22 | 0 | 0 | 0 | 0 | 10 |
| 10 | 0 | 0 | 100 | 22 | 0 | 0 | 0 | 0 | 20 |
| 11 | 0 | 0 | 100 | 0 | 10 | 0 | 0 | 0 | 0 |
| 12 | 0 | 0 | 100 | 0 | 10 | 0 | 1 | 0 | 0 |
| 13 | 0 | 0 | 100 | 0 | 10 | 0 | 3 | 0 | 0 |
| 14 | 0 | 0 | 100 | 0 | 10 | 0 | 5 | 0 | 0 |
| 15 | 0 | 0 | 100 | 0 | 10 | 0 | 0 | 5 | 0 |
| 16 | 0 | 0 | 100 | 0 | 10 | 0 | 0 | 10 | 0 |
| 17 | 0 | 0 | 100 | 0 | 10 | 0 | 0 | 20 | 0 |
| 18 | 0 | 0 | 100 | 0 | 10 | 0 | 0 | 0 | 5 |
| 19 | 0 | 0 | 100 | 0 | 10 | 0 | 0 | 0 | 10 |
| 20 | 0 | 0 | 100 | 0 | 10 | 0 | 0 | 0 | 20 |
| 21 | 0 | 0 | 100 | 0 | 0 | 80 | 0 | 0 | 0 |
| 22 | 0 | 0 | 100 | 0 | 0 | 80 | 1 | 0 | 0 |
| 23 | 0 | 0 | 100 | 0 | 0 | 80 | 3 | 0 | 0 |
| 24 | 0 | 0 | 100 | 0 | 0 | 80 | 5 | 0 | 0 |
| 25 | 0 | 0 | 100 | 0 | 0 | 80 | 0 | 5 | 0 |
| 26 | 0 | 0 | 100 | 0 | 0 | 80 | 0 | 10 | 0 |
| 27 | 0 | 0 | 100 | 0 | 0 | 80 | 0 | 20 | 0 |
| 28 | 0 | 0 | 100 | 0 | 0 | 80 | 0 | 0 | 5 |
| 29 | 0 | 0 | 100 | 0 | 0 | 80 | 0 | 0 | 10 |
| 30 | 0 | 0 | 100 | 0 | 0 | 80 | 0 | 0 | 20 |
| Model Hyperparameters | Neural Network Model for Tensile Strength [MPa] | SVM Model for Compression Strength [MPa] | Neural Network Model Bending Strength [MPa] |
|---|---|---|---|
| Prediction speed (obs/s) | 73,000 | 23,000 | 67,000 |
| Training time (s) | 2.5936 | 2.6161 | 1.51 |
| Layers | 2 | N/A | 3 |
| Layer sizes | 10-10 | N/A | 10-10-10 |
| Activation | ReLU | N/A | ReLU |
| Regularization | λ = 0 | kernel scale (RBF kernel) = 0.75 (γ ≈ 0.889); box constraint C ≈ 100 (auto); epsilon ≈ 2.5 MPa (auto) | λ = 0 |
| Standardize data | Yes | Yes | Yes |
| Model Results | Neural Network Model for Tensile Strength [MPa] | SVM Model for Compression Strength [MPa] | Neural Network Model for Bending Strength [MPa] |
|---|---|---|---|
| R-Squared (Validation) | 0.64 | 0.93 | 0.95 |
| RMSE (Validation) | 4483.5 | 6.4227 | 6.6236 |
| MSE (Validation) | 20,102,000.0 | 41.251 | 43.872 |
| MAE (Validation) | 694.66 | 3.8083 | 4.317 |
| MAPE (Validation) | 1494.2% | 5.0% | 7.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miturska-Barańska, I.; Antosz, K. Epoxy Adhesive Materials as Protective Coatings: Strength Property Analysis Using Machine Learning Algorithms. Materials 2025, 18, 2803. https://doi.org/10.3390/ma18122803
Miturska-Barańska I, Antosz K. Epoxy Adhesive Materials as Protective Coatings: Strength Property Analysis Using Machine Learning Algorithms. Materials. 2025; 18(12):2803. https://doi.org/10.3390/ma18122803
Chicago/Turabian StyleMiturska-Barańska, Izabela, and Katarzyna Antosz. 2025. "Epoxy Adhesive Materials as Protective Coatings: Strength Property Analysis Using Machine Learning Algorithms" Materials 18, no. 12: 2803. https://doi.org/10.3390/ma18122803
APA StyleMiturska-Barańska, I., & Antosz, K. (2025). Epoxy Adhesive Materials as Protective Coatings: Strength Property Analysis Using Machine Learning Algorithms. Materials, 18(12), 2803. https://doi.org/10.3390/ma18122803







