Theoretical Analysis of Low-Frequency Sound Absorption Owing to the Vibration of Lightweight Powder Using a 1D Beam Model
Abstract
1. Introduction
2. Measurement Overview and Preliminary Investigation
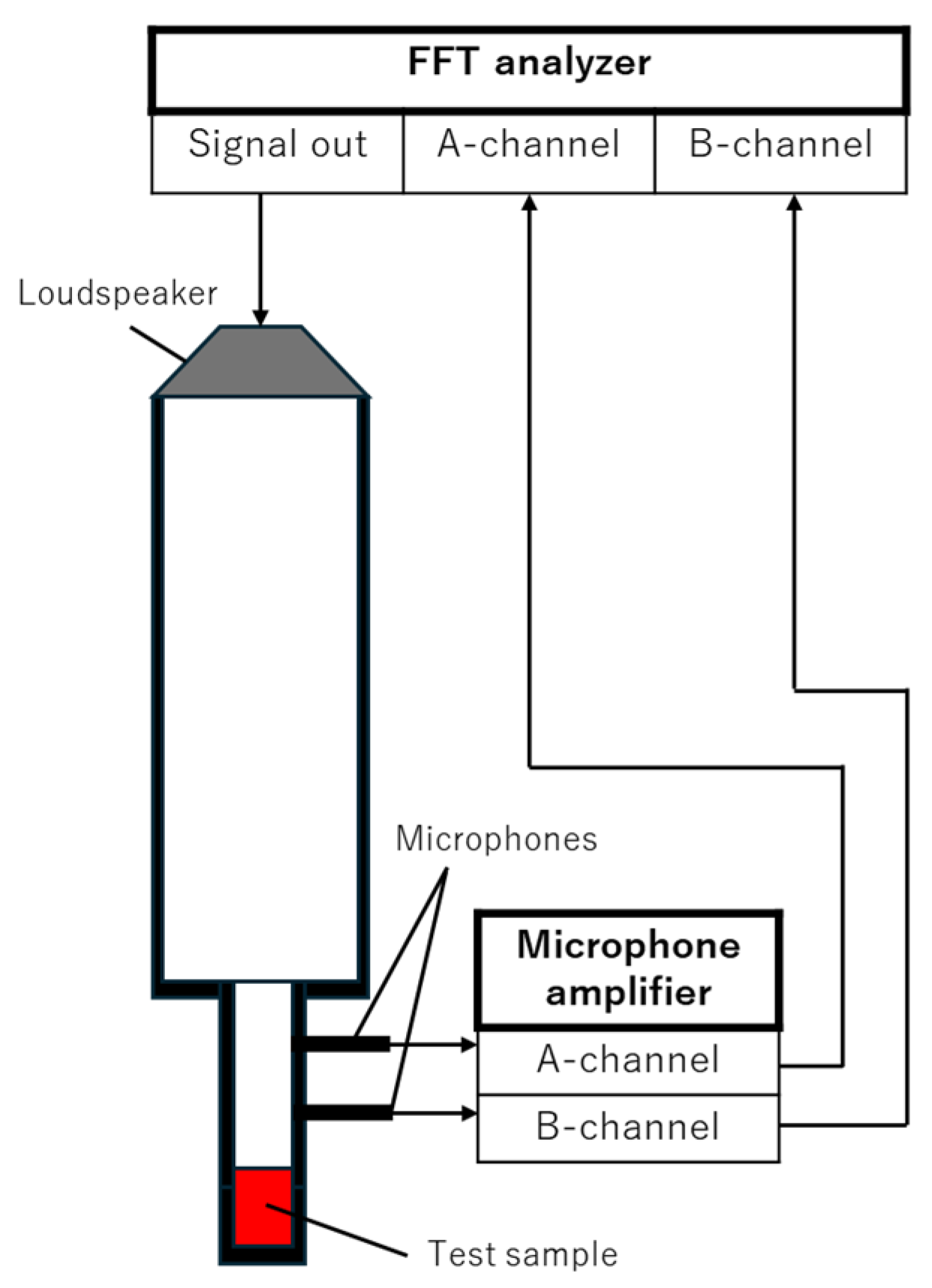
2.1. Measurement Apparatus and Samples
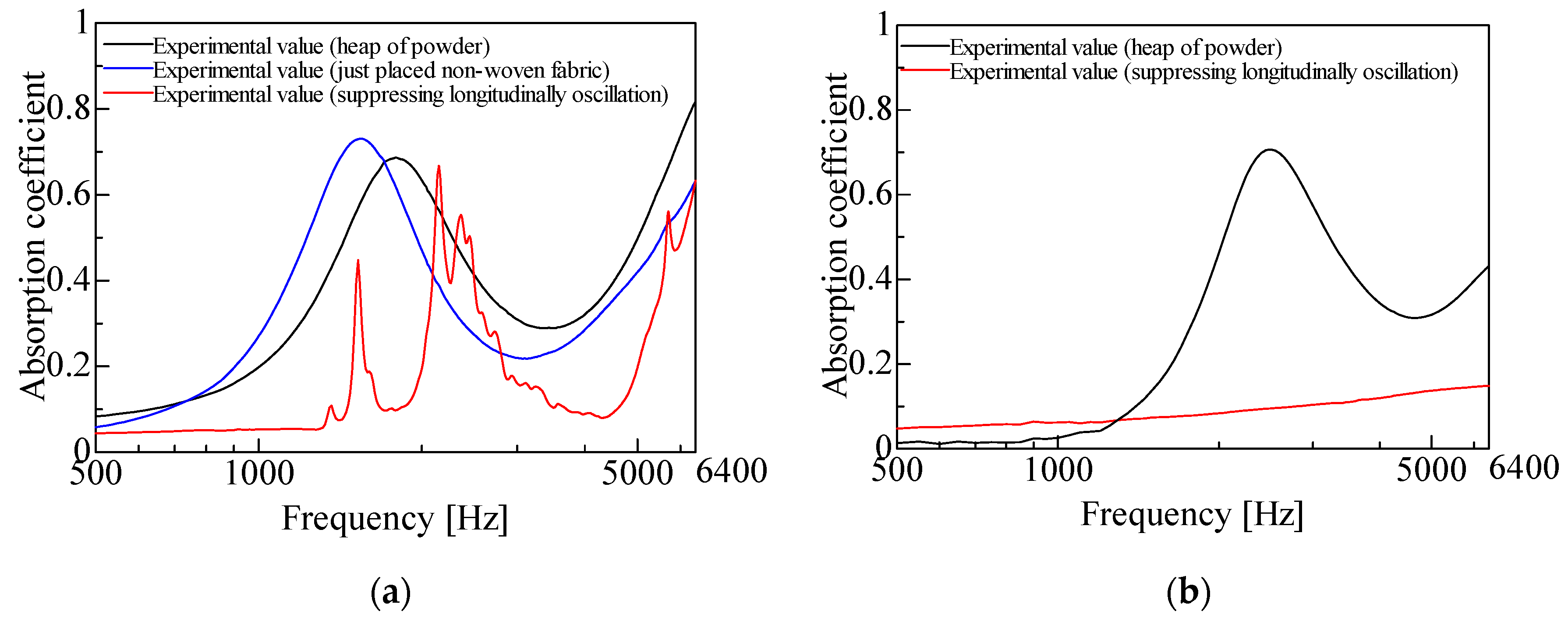
2.2. Demonstration of Sound Absorption Due to Longitudinal Vibration
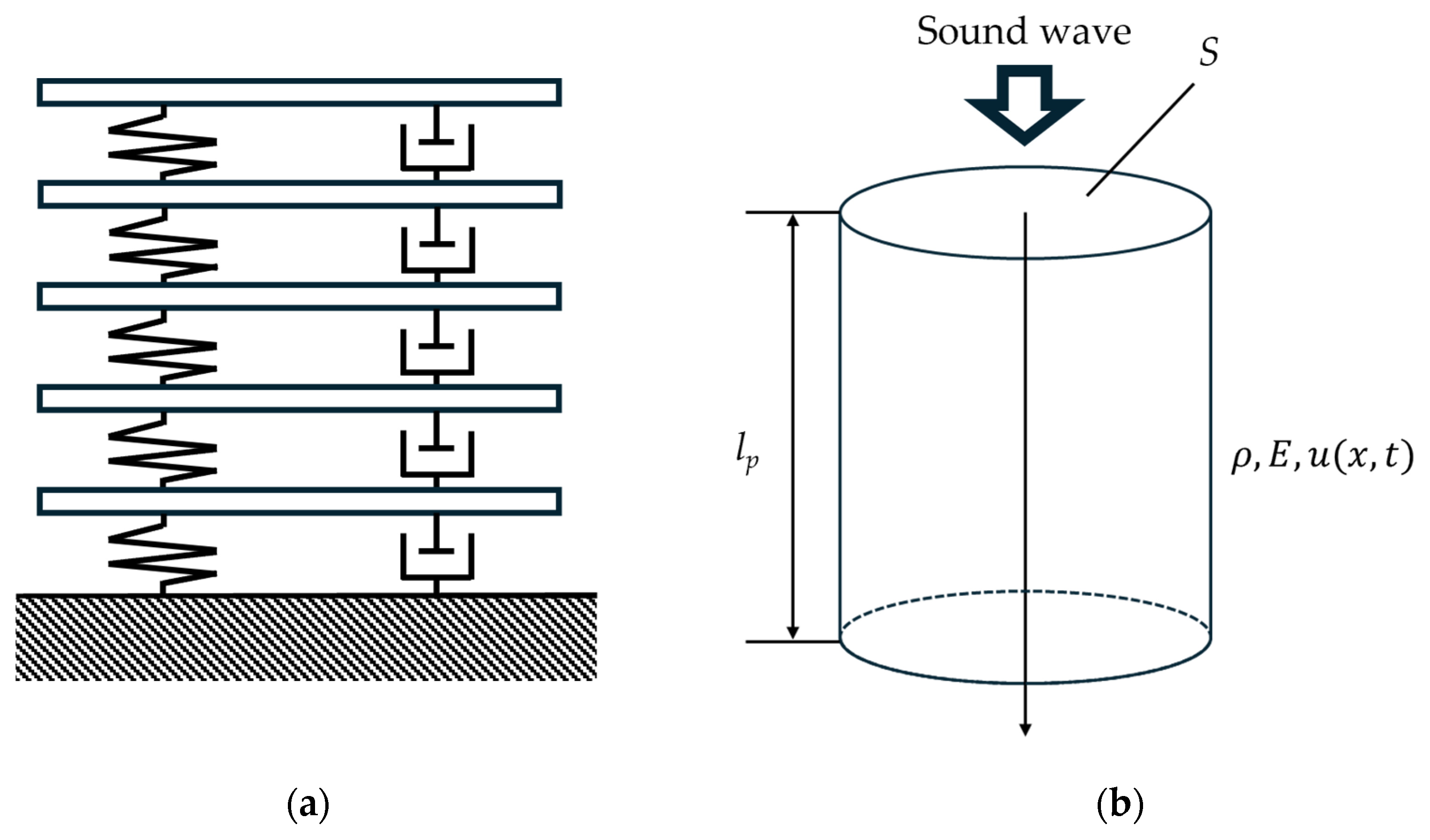
3. Theoretical Analysis
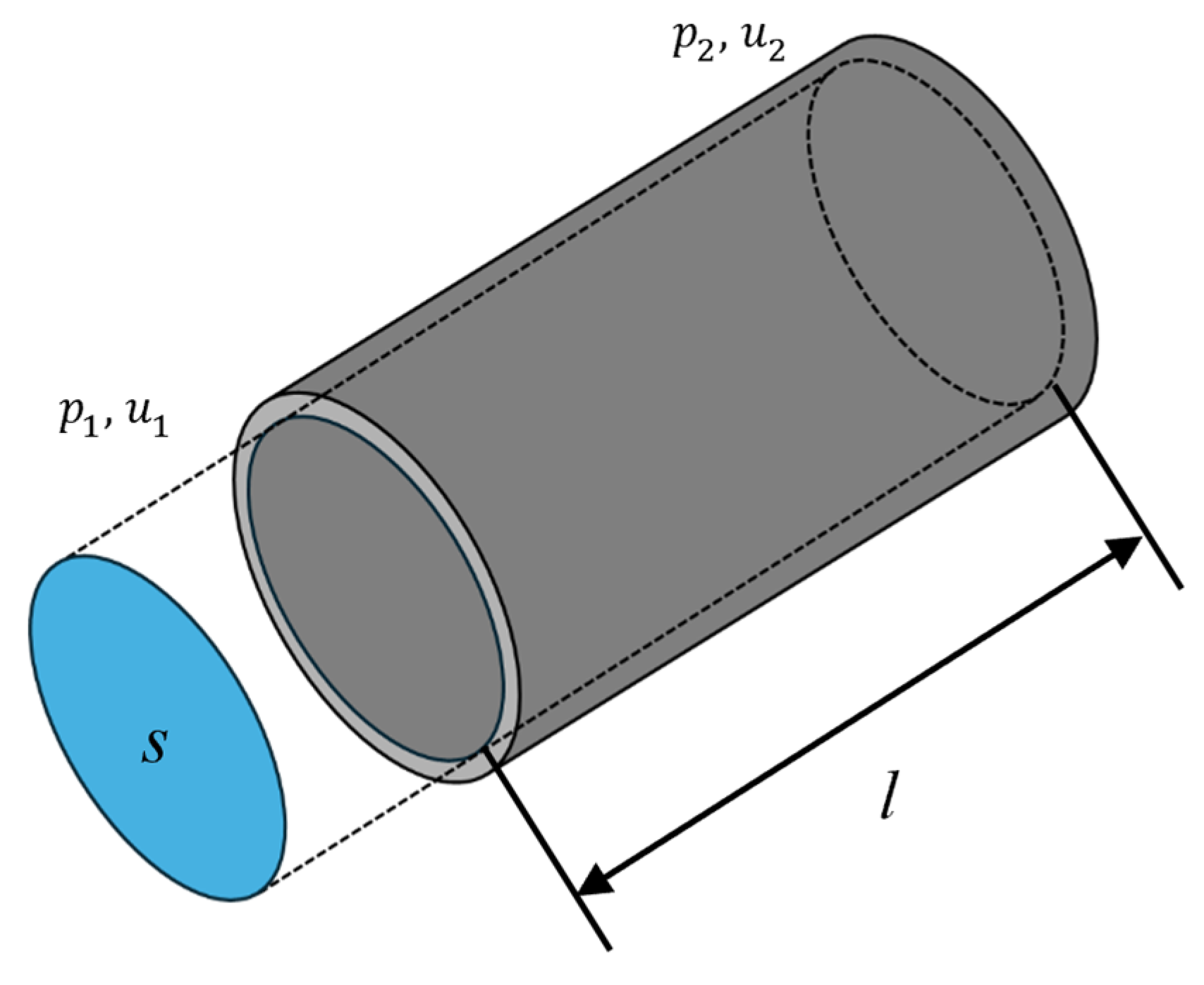
3.1. Transfer Matrix Method
3.2. Characteristic Impedance and Propagation Constants of Powder Layers
3.3. Characteristic Impedance and Propagation Constants of Nonwoven Fabrics
3.4. Characteristic Impedance and Propagation Constants of the Air Space
3.5. Cascade Connection of Four-Terminal Networks in Equivalent Circuits
3.6. SAC Calculation
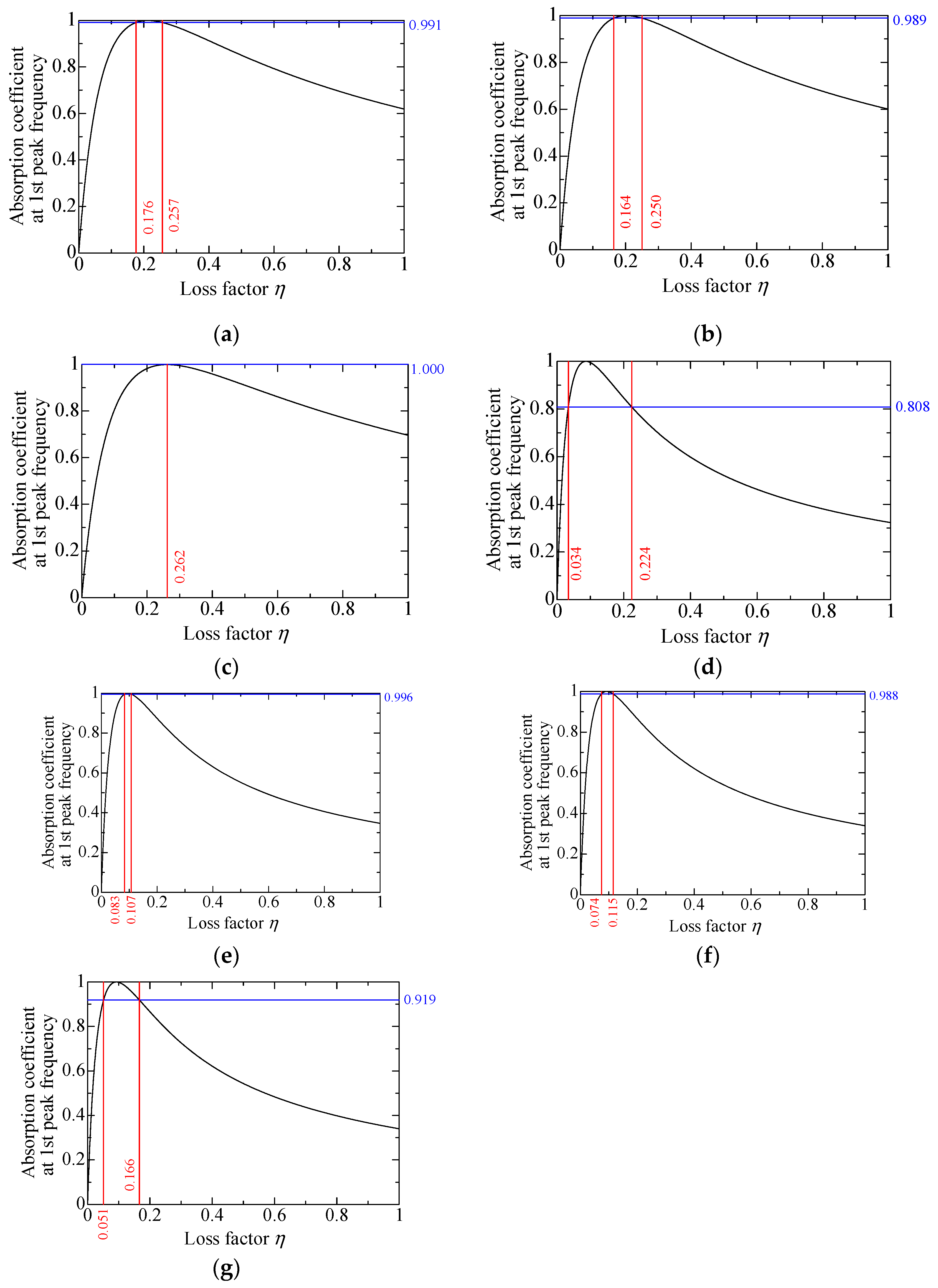
3.7. Determination of the Loss Factor
4. Verification of the Transfer Matrix of the Powder Layer
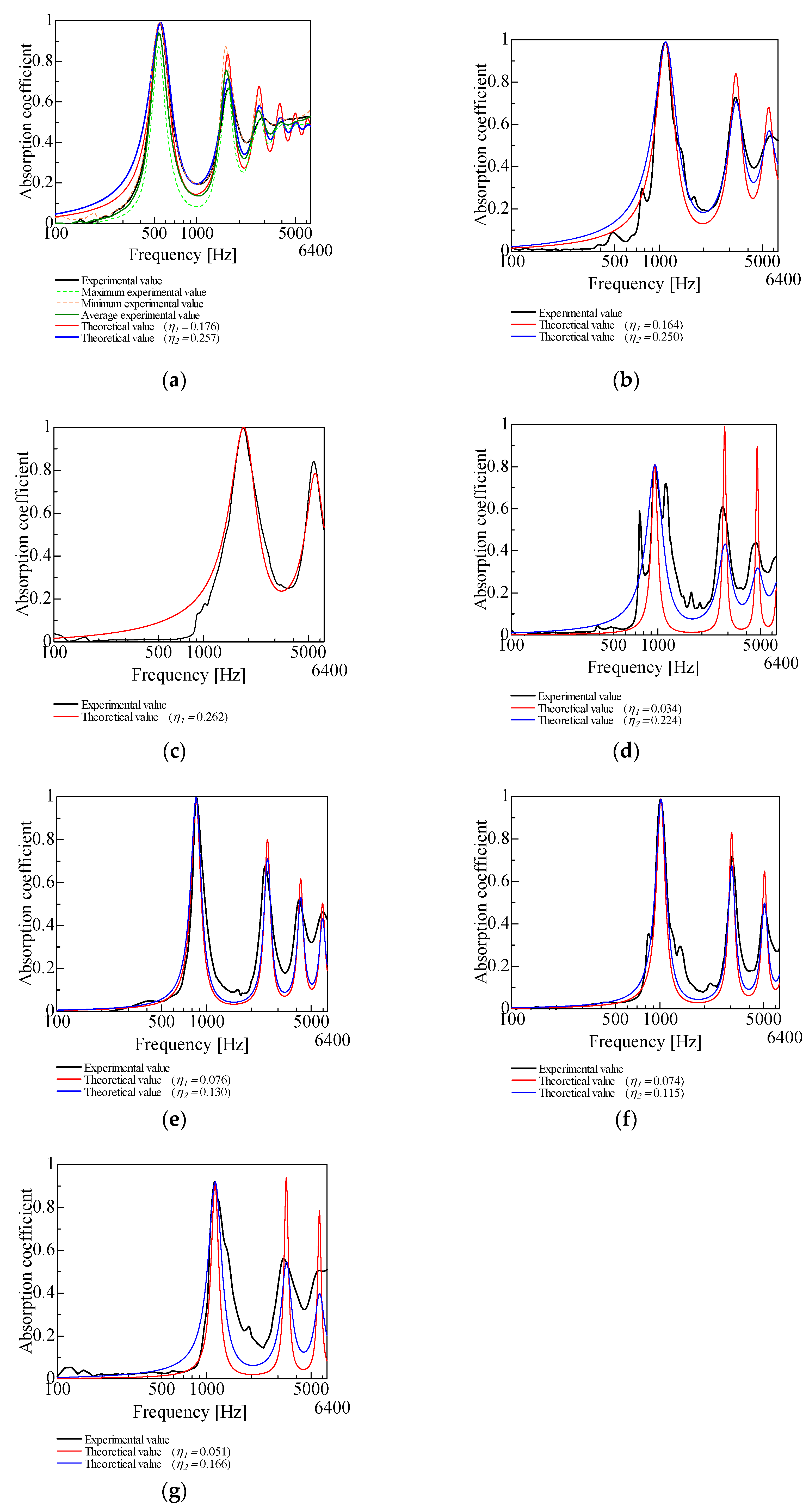
4.1. Comparison of the Experimental and Theoretical Values of the SAC in the Powder Layer Alone
4.2. Comparison of Experimental and Theoretical Values for the SAC with a Back Air Space
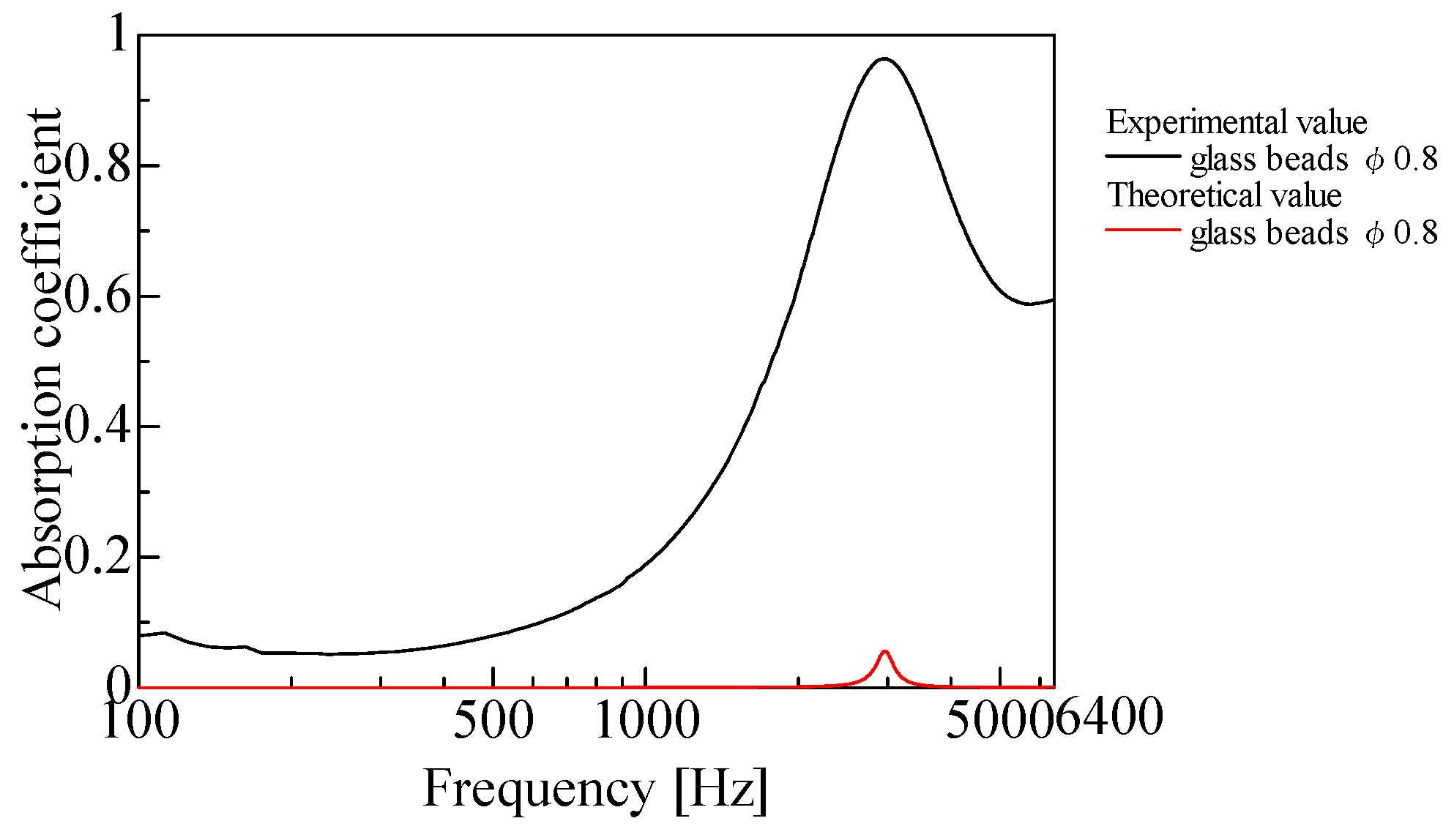
4.3. Powders to Which This Method Can Be Applied
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SAC | Sound absorption coefficient |
| SAM | Sound-absorbing materials |
| 5-DOF | Five degrees of freedom |
References
- Okudaira, Y.; Kurihara, Y.; Ando, H.; Satoh, M.; Miyanami, K. Sound absorption measurements for evaluating dynamic physical properties of a powder bed. Powder Technol. 1993, 77, 39–48. [Google Scholar] [CrossRef]
- Falegnami, A.; Tomassi, A.; Gunella, C.; Amalfitano, S.; Corbelli, G.; Armonaite, K.; Fornaro, C.; Giorgi, L.; Pollini, A.; Caforio, A.; et al. Defining conceptual artefacts to manage and design simplicities in complex adaptive systems. Heliyon 2024, 10, e41033. [Google Scholar] [CrossRef] [PubMed]
- Okudaira, Y.; Kurihara, Y.; Ando, H.; Satoh, M.; Miyanami, K. Sound Absorption Characteristics of Powder Beds Comprised of Binary Powder Mixtures. J. Jpn. Soc. Powder Powder Metall. 1995, 42, 239–244. [Google Scholar] [CrossRef]
- Sakamoto, S.; Yamaguchi, K.; Ii, K.; Takakura, R.; Nakamura, Y.; Suzuki, R. Theoretical and experiment analysis on the sound absorption characteristics of a layer of fine lightweight powder. J. Acoust. Soc. Am. 2019, 146, 2253–2262. [Google Scholar] [CrossRef] [PubMed]
- Sakamoto, S.; Takakura, R.; Suzuki, R.; Katayama, I.; Saito, R.; Suzuki, K. Theoretical and experimental analyses of acoustic characteristics of fine-grain powder considering longitudinal vibration and boundary layer viscosity. J. Acoust. Soc. Am. 2021, 149, 1030–1040. [Google Scholar] [CrossRef] [PubMed]
- Sakamoto, S.; Saito, R.; Jindai, K.; Ikeda, K. Conditions for sound absorption caused by longitudinal vibration of lightweight powder. Noise Control Eng. J. 2024, 72, 402–411. [Google Scholar] [CrossRef]
- Sakamoto, S.; Jindai, K.; Ikeda, K.; Kawakami, Y.; Soeta, H. Predicting Lightweight Powders with Useful Sound Absorption Characteristics from Their Specifications. Appl. Sci. 2024, 14, 9765. [Google Scholar] [CrossRef]
- Palacio, O.; Malfait, W.J.; Michel, S.; Barbezat, M.; Mazrouei-Sebdani, Z. Vibration and structure-borne sound isolation properties of silica aerogels. Constr. Build. Mater. 2023, 399, 132568. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid. I. Low-Frequency Range. J. Acoust. Soc. Am. 1956, 28, 168–178. [Google Scholar] [CrossRef]
- Tsuruha, T.; Yamada, Y.; Otani, M.; Takano, Y. Effect of casing on sound absorption characteristics of fine spherical granular material. J. Acoust. Soc. Am. 2020, 147, 3418–3428. [Google Scholar] [CrossRef] [PubMed]
- Sakamoto, S.; Ikeda, K.; Kawakami, Y.; Soeta, H. Estimation of transfer matrix by applying the theoretical acoustic incident impedance of a lightweight powder layer to the two-thickness method. Noise Control Eng. J. 2025, 73, 9. [Google Scholar] [CrossRef]
- Saiki, S.; Matsumura, T.; Fujise, A. Speaker System. European Patent EP 2003924A1, 25 April 2012. [Google Scholar]
- ISO 10534-2; Acoustics—Determination of Acoustic Properties in Impedance Tubes—Part 2: Two-Microphone Technique for Normal Sound Absorption Coefficient and Normal Surface Impedance. International Organization for Standardization: Geneva, Switzerland, 2023.
- Merkus, H.G. Particle Size Measurements: Fundamentals, Practice, Quality; Springer Science and Business Media: New York, NY, USA, 2019; p. 15. [Google Scholar]
- Lahe, A.; Braunbrück, A.; Klauson, A. Modified transfer matrix method for steady-state forced vibration: A system of bar elements. Proc. Est. Acad. Sci. 2020, 69, 143–161. [Google Scholar] [CrossRef]
- Ceauşu, V.; Craifaleanu, A.; Dragomirescu, C. Transfer matrix method for forced vibrations of bars. UPB Sci. Bull. Ser. D Mech. Eng. 2010, 72, 35–42. [Google Scholar]
- Sugi, C. Resonant Frequencies and Equivalent Mass Coefficients of Longitudinally Vibrating Composite Bars; Faculty of Engineering, Yamanashi University: Yamanashi, Japan, 1964; Volume 14, pp. 101–109, (In Japanese). [Google Scholar] [CrossRef]
- Laganà, F.; Prattico, D.; De Carlo, D.; Oliva, G.; Pullano, S.A.; Calcagno, S. Engineering Biomedical Problems to Detect Carcinomas: A Tomographic Impedance Approach. Eng 2024, 5, 1594–1614. [Google Scholar] [CrossRef]
- Delany, M.E.; Bazley, E.N. Acoustic Properties of Fibrous Absorbent Materials. Appl. Acoust. 1970, 3, 105–116. [Google Scholar] [CrossRef]
- Miki, Y. Acoustical properties of porous materials—Modifications of Delany-Bazley models. J. Acoust. Soc. Jpn. 1990, 11, 19–24. [Google Scholar] [CrossRef]
- Komatsu, T. Improvement of the Delany-Bazley and Miki models for fibrous sound-absorbing materials. Acoust. Sci. Technol. 2008, 29, 121–129. [Google Scholar] [CrossRef]








| Bulk Density ρ [g/cm3] | First Peak Frequency [Hz] | Feret Diameter [μm] | |
|---|---|---|---|
| Granulated silica (Featherfield Co., Ltd., Hiroshima, Japan) | 0.0568 | 550 | 43 |
| Hollow plastic beads A (Expancel® 920DE40d30) (Japan Fillite Co., Ltd., Osaka, Japan) | 0.0298 | 1100 | 42 |
| Hollow plastic beads B (matsumoto micro sphere® F–80DE) (Matsumoto Yushi-Seiyaku Co., Ltd., Osaka, Japan) | 0.0139 | 1837.5 | 110 |
| Hollow glass beads (Hobbico, Inc., Champaign, IL, USA) | 0.0800 | 950 | 29 |
| Calcium-carbonate-coated hollow plastic beads A (EMC–40(B)) (Japan Fillite Co., Ltd., Osaka, Japan) | 0.082 | 850 | 53 |
| Calcium-carbonate-coated hollow plastic beads B (EMC–80(B)) (Japan Fillite Co., Ltd., Osaka, Japan) | 0.0707 | 1012.5 | 70 |
| Calcium-carbonate-coated hollow plastic beads C (EMC–120()) (Japan Fillite Co., Ltd., Osaka, Japan) | 0.0628 | 1137.5 | 120 |
| Experimental Value of the Absorption Coefficient at First Peak Frequency | |||
|---|---|---|---|
| Granulated silica | 0.991 | 0.176 | 0.257 |
| Hollow plastic beads A (Expancel® 920DE40d30) | 0.989 | 0.164 | 0.250 |
| Hollow plastic beads B (Matsumoto micro sphere® F–80DE) | 1.000 | 0.262 | |
| Hollow glass beads | 0.808 | 0.034 | 0.224 |
| Calcium-carbonate-coated hollow plastic beads A (EMC–40(B)) | 0.996 | 0.083 | 0.107 |
| Calcium-carbonate-coated hollow plastic beads B (EMC–80(B)) | 0.988 | 0.074 | 0.115 |
| Calcium-carbonate-coated hollow plastic beads C (EMC–120(α)) | 0.919 | 0.051 | 0.166 |
| (Experimental) [Hz] | (Theoretical) [Hz] | Percent Error [%] | |
|---|---|---|---|
| Granulated silica | 550 | 555 | 0.90 |
| Hollow plastic beads A (Expancel® 920DE40d30) | 1100 | 1107.5 | 0.68 |
| Hollow plastic beads B (Matsumoto micro sphere® F–80DE) | 1837.5 | 1852.5 | 0.81 |
| Hollow glass beads | 950 | 955 | 0.52 |
| Calcium-carbonate-coated hollow plastic beads A (EMC–40(B)) | 850 | 850 | 0.00 |
| Calcium-carbonate-coated hollow plastic beads B (EMC–80(B)) | 1012.5 | 1012.5 | 0.00 |
| Calcium-carbonate-coated hollow plastic beads C (EMC–120(α)) | 1137.5 | 1142.5 | 0.44 |
| (Experimental) [Hz] | (Theoretical) [Hz] | Percent Error [%] | |
|---|---|---|---|
| Granulated silica | 375 | 330 | 12.0 |
| Hollow plastic beads A (Expancel® 920DE40d30) | 512.5 | 502.5 | 1.95 |
| Hollow plastic beads B (Matsumoto micro sphere® F–80DE) | 775 | 755 | 2.58 |
| Hollow glass beads | 387.5 | 320 | 17.4 |
| Calcium-carbonate-coated hollow plastic beads A (EMC–40(B)) | 362.5 | 312.5 | 13.8 |
| Calcium-carbonate-coated hollow plastic beads B (EMC–80(B)) | 387.5 | 340 | 12.3 |
| Calcium-carbonate-coated hollow plastic beads C (EMC–120(α)) | 400 | 365 | 8.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakamoto, S.; Kawakami, Y.; Soeta, H.; Kubo, Y. Theoretical Analysis of Low-Frequency Sound Absorption Owing to the Vibration of Lightweight Powder Using a 1D Beam Model. Materials 2025, 18, 2611. https://doi.org/10.3390/ma18112611
Sakamoto S, Kawakami Y, Soeta H, Kubo Y. Theoretical Analysis of Low-Frequency Sound Absorption Owing to the Vibration of Lightweight Powder Using a 1D Beam Model. Materials. 2025; 18(11):2611. https://doi.org/10.3390/ma18112611
Chicago/Turabian StyleSakamoto, Shuichi, Yuya Kawakami, Hiroaki Soeta, and Yosuke Kubo. 2025. "Theoretical Analysis of Low-Frequency Sound Absorption Owing to the Vibration of Lightweight Powder Using a 1D Beam Model" Materials 18, no. 11: 2611. https://doi.org/10.3390/ma18112611
APA StyleSakamoto, S., Kawakami, Y., Soeta, H., & Kubo, Y. (2025). Theoretical Analysis of Low-Frequency Sound Absorption Owing to the Vibration of Lightweight Powder Using a 1D Beam Model. Materials, 18(11), 2611. https://doi.org/10.3390/ma18112611






