Rutting Behavior of Dual-Layer Asphalt Pavements Subjected to Variable Temperature
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Asphalt
2.1.2. Aggregate
2.1.3. Gradation of the Asphalt Mixture
2.2. Specimen Preparation Method
- (1)
- Bottom-layer preparation: According to the mold volume and maximum dry density of the asphalt mixture, the mass of the asphalt mixture in the loose state was determined. Then, the mixture was poured into the bottom-layer mold and compacted to the mold height using a roller compactor. The formula used to determine the mass of the asphalt mixture in the loose state is presented as Equation (1):where ml is the mass of the asphalt mixture in the loose state, ρd,max is the maximum dry density of the asphalt mixture, and V is the mold volume.
- (2)
- Tack-coat application: After the bottom layer cooled, the tack coat was uniformly applied to it at an application rate of 0.45 kg/m2. In order to fully penetrate and cure the tack coat, the surface-layer mold was positioned after a two-hour curing period for the tack coat.
- (3)
- Surface-layer preparation: The mass of the asphalt mixture in the loose state was determined using Equation (1). Then, the asphalt mixture was poured into the surface-layer mold and compacted to the mold height using a roller compactor.
2.3. Rutting Test Method
2.4. Field Measurement Method
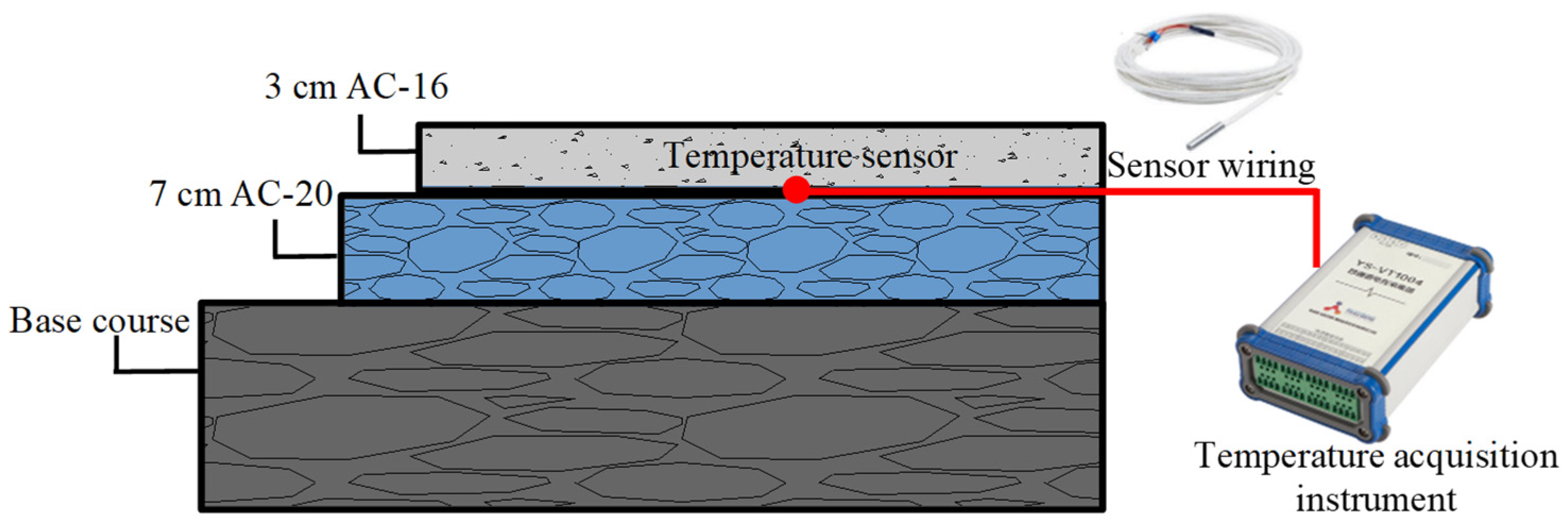
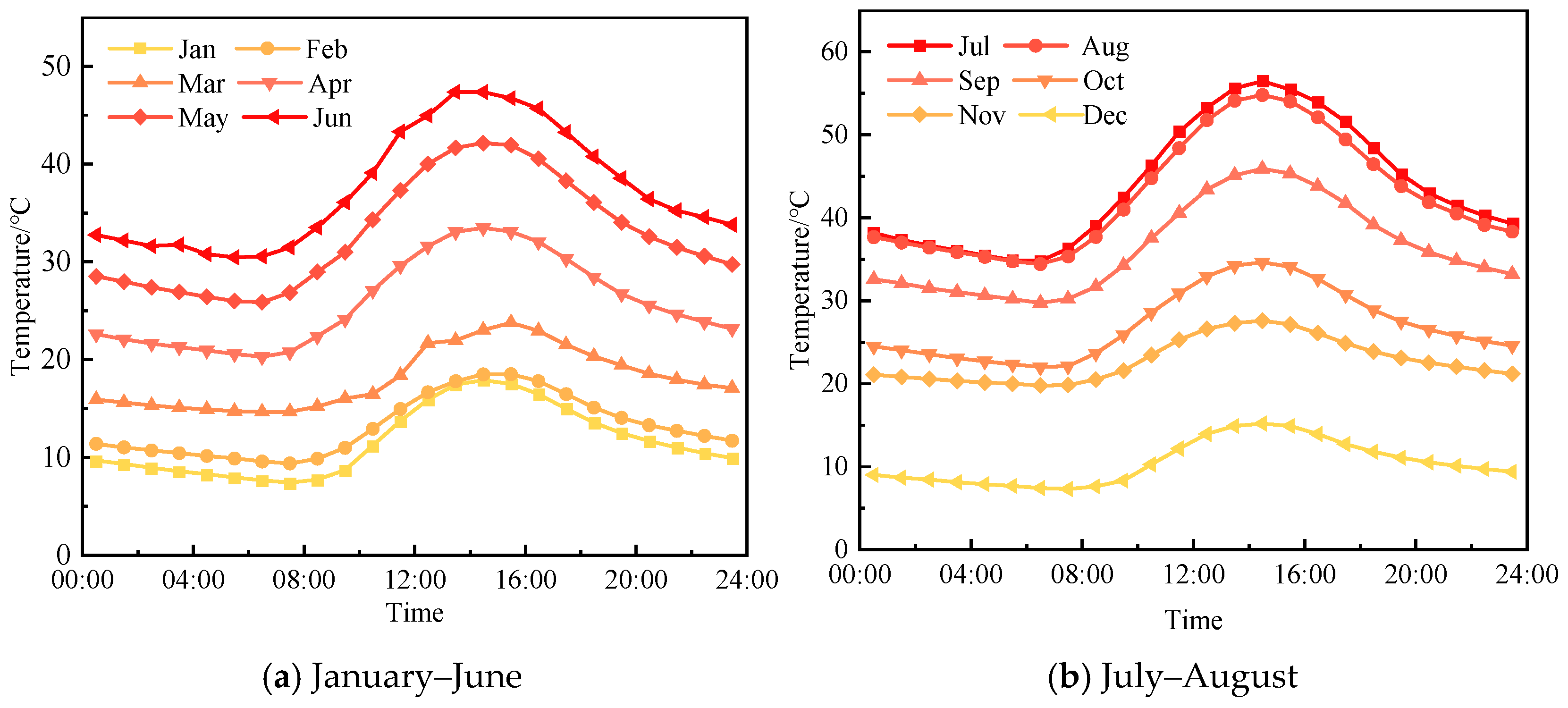
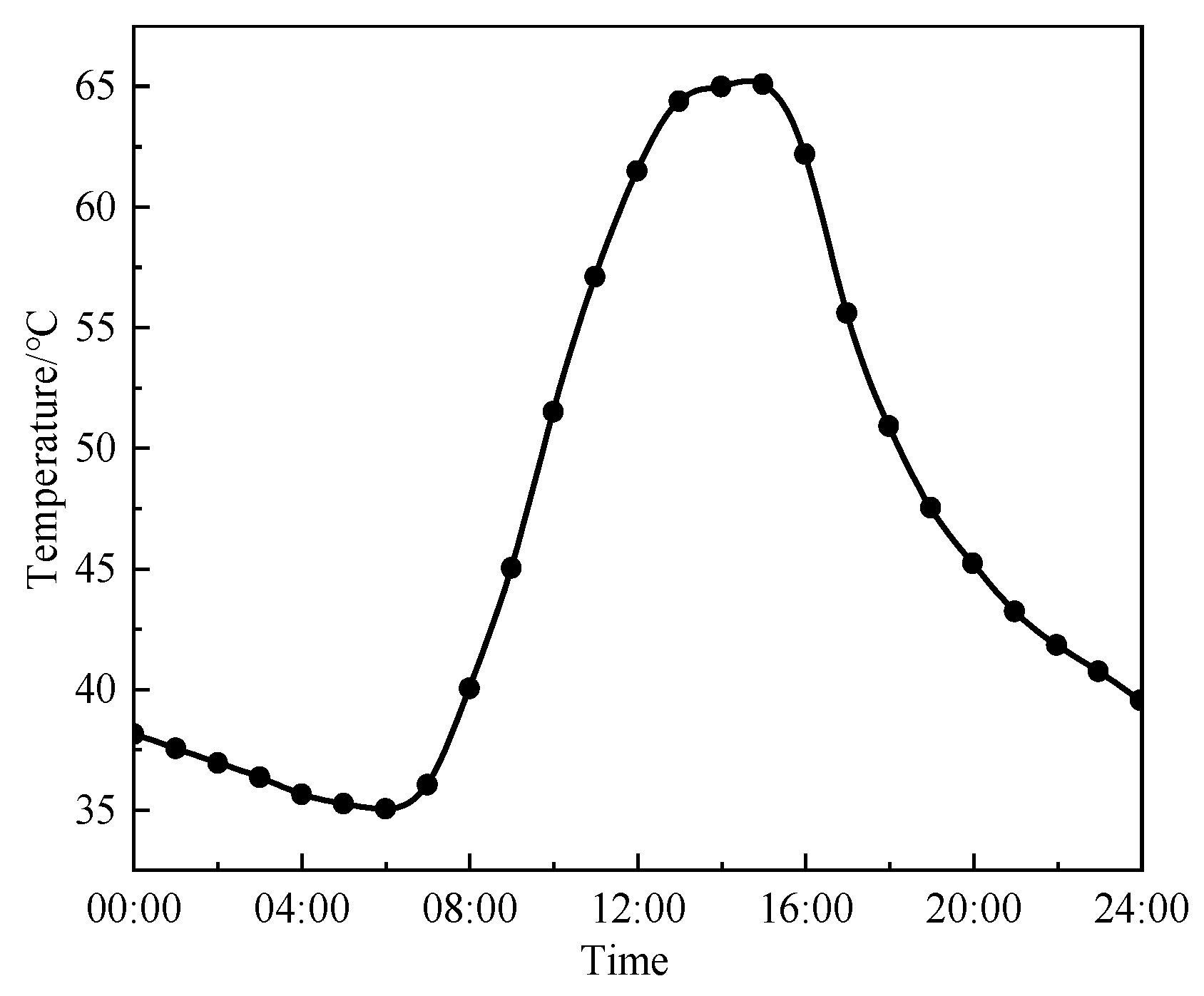
2.4.1. Pavement Temperature Measurement
2.4.2. Rutting Deformation Measurement
3. Results and Discussion
3.1. The Effect of Temperature Variation on Rutting Development
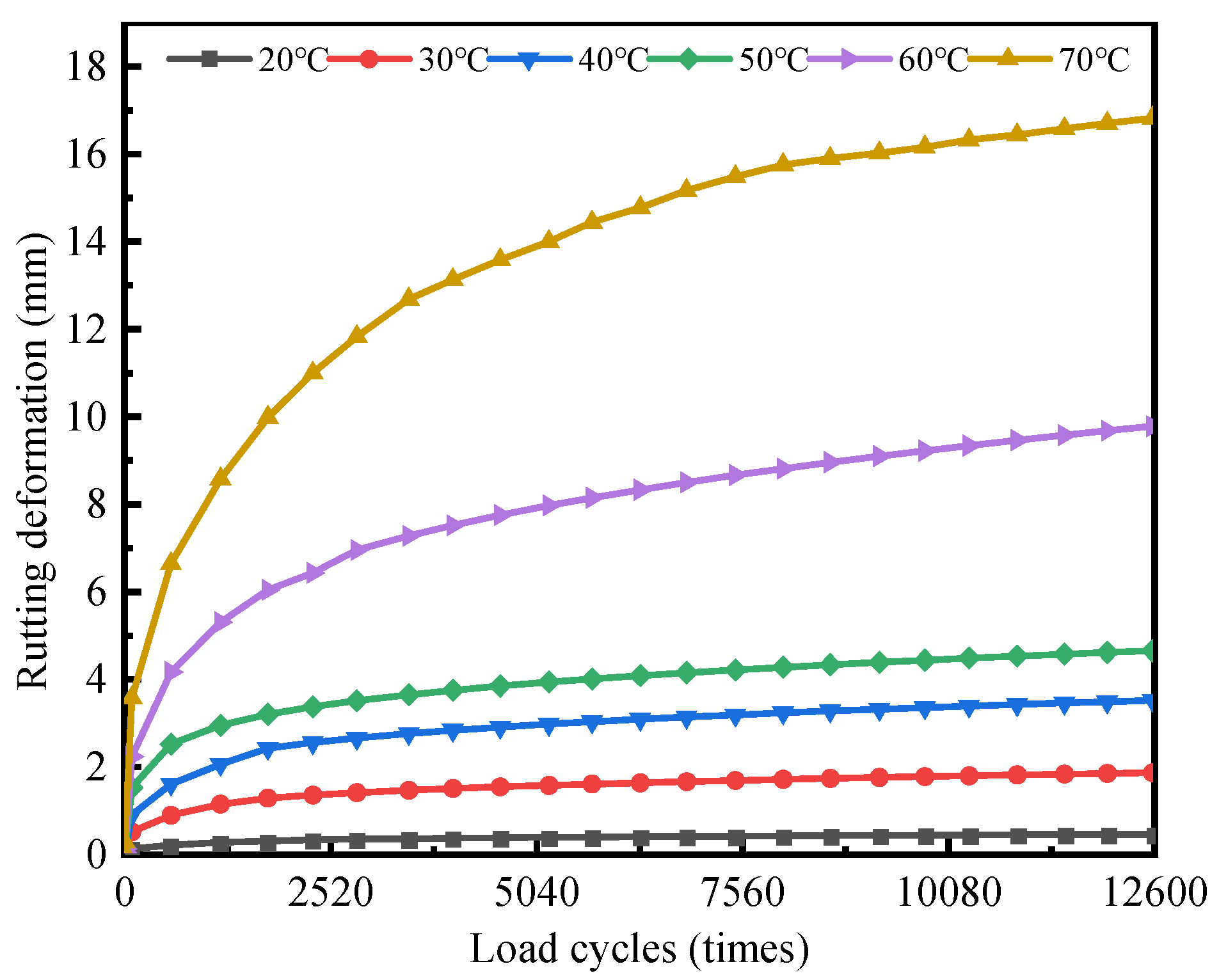
3.1.1. Constant Temperature State
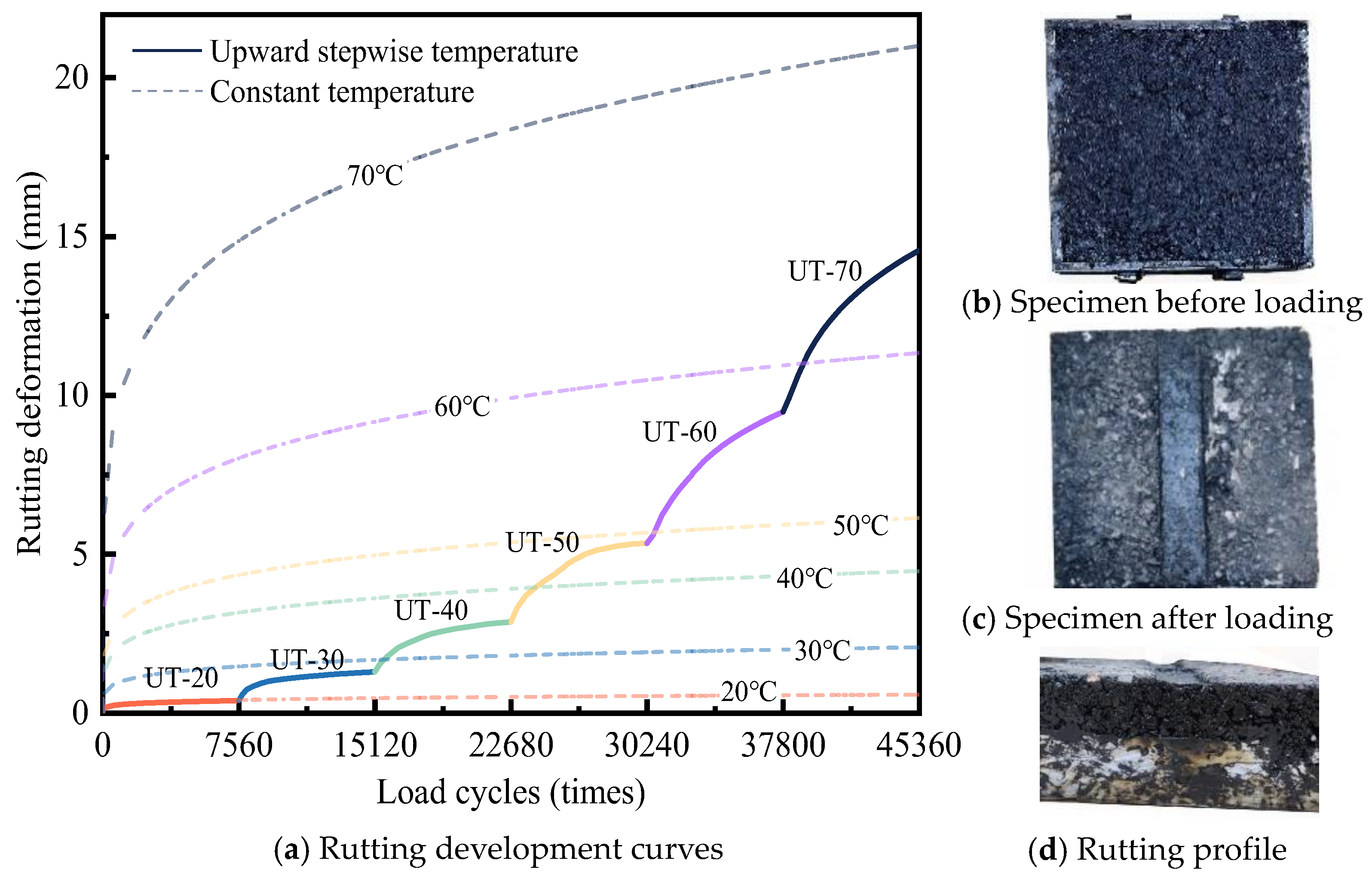
3.1.2. Increasing Temperature State
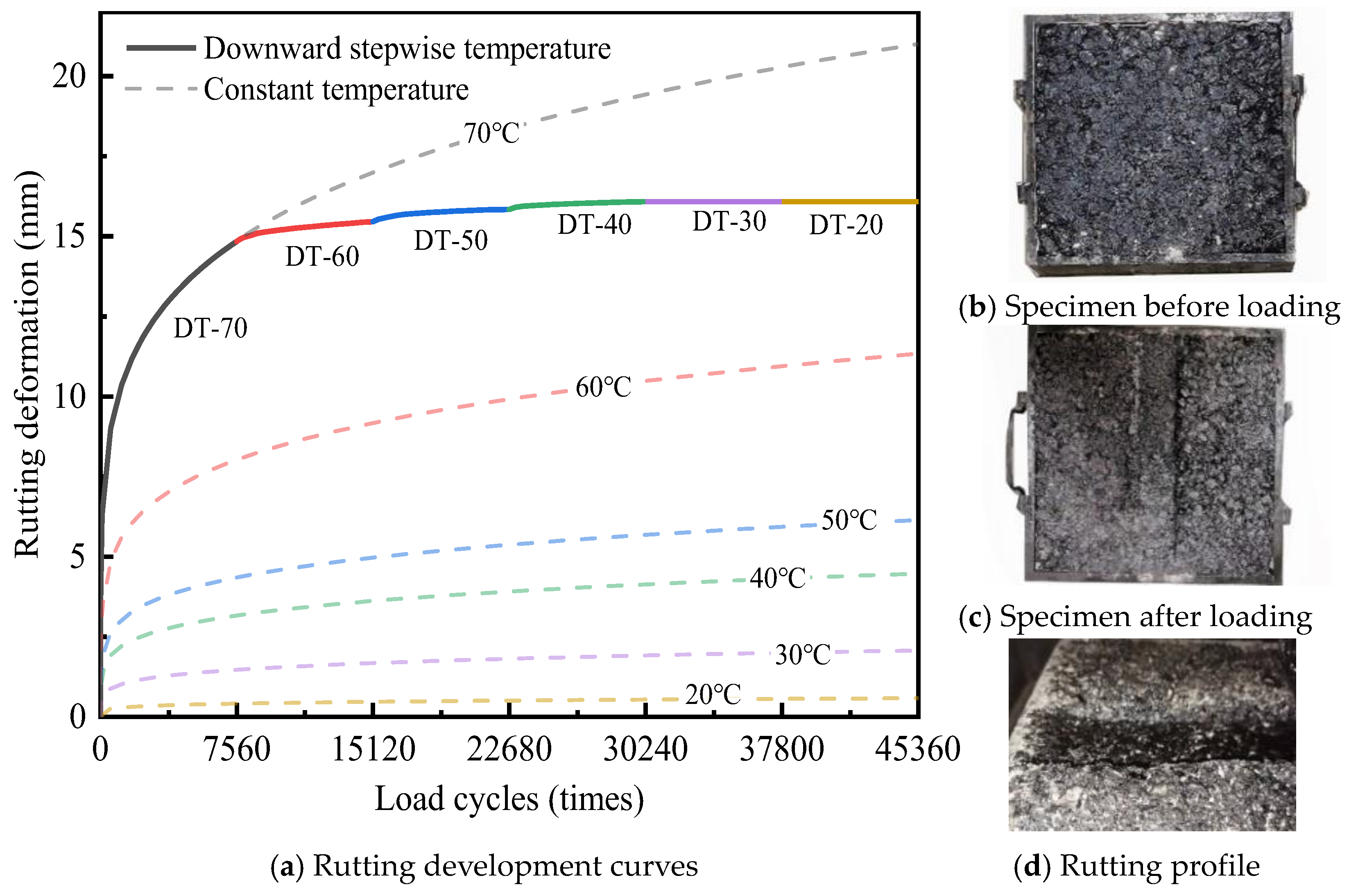
3.1.3. Decreasing Temperature State
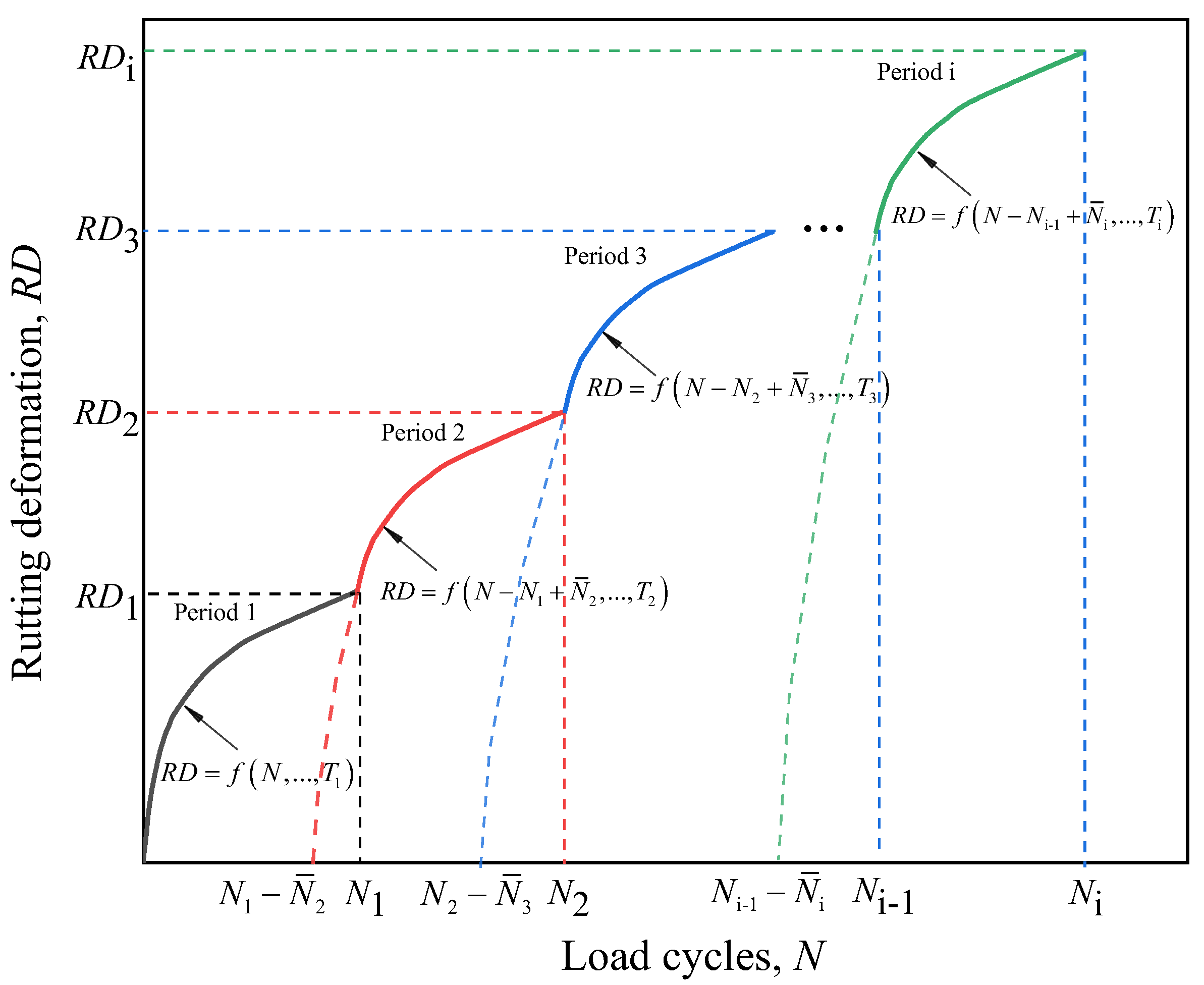
3.2. Rutting Development Regularity Under Variable Temperature
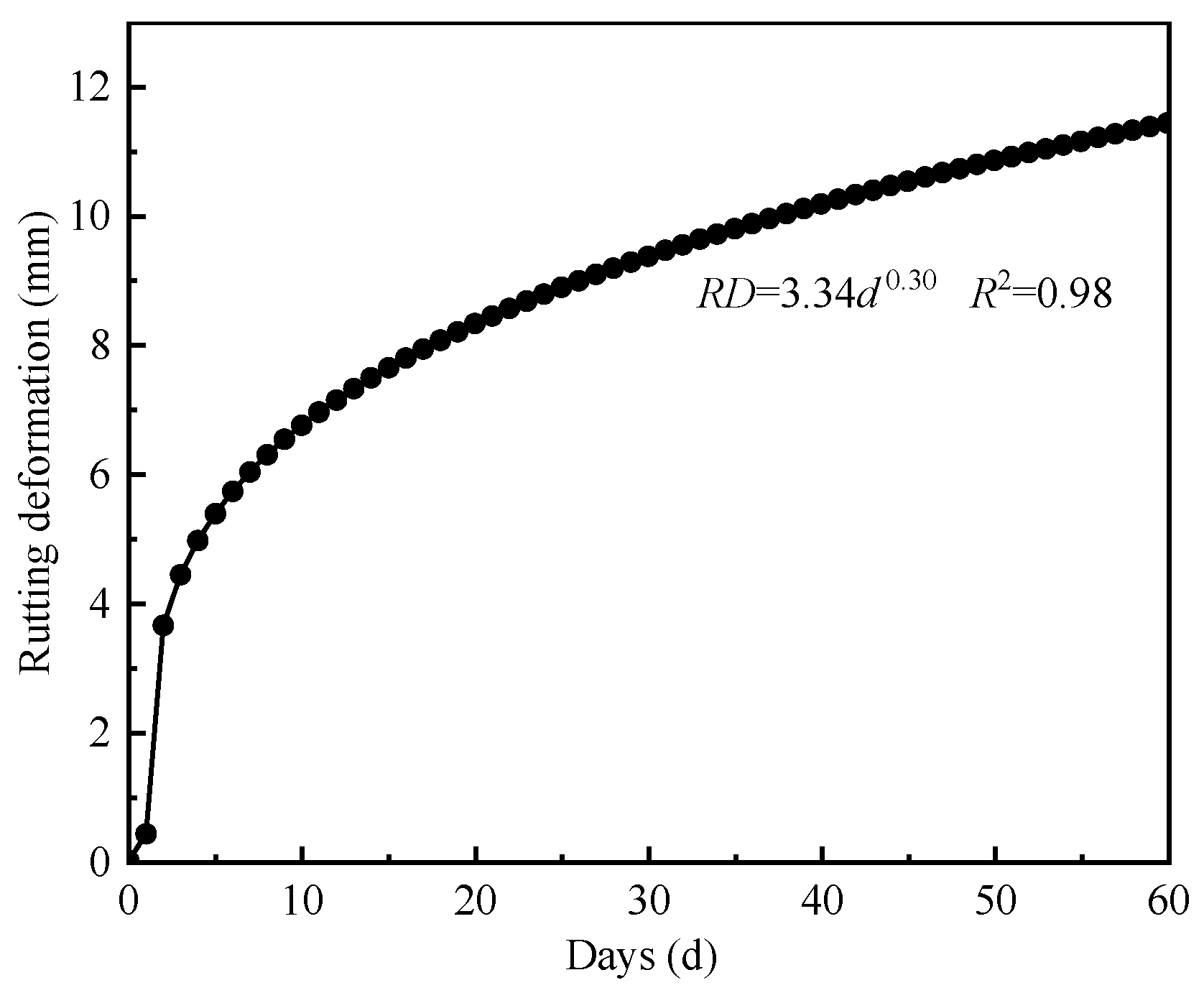
3.2.1. Rutting Test Result Under Variable Temperatures
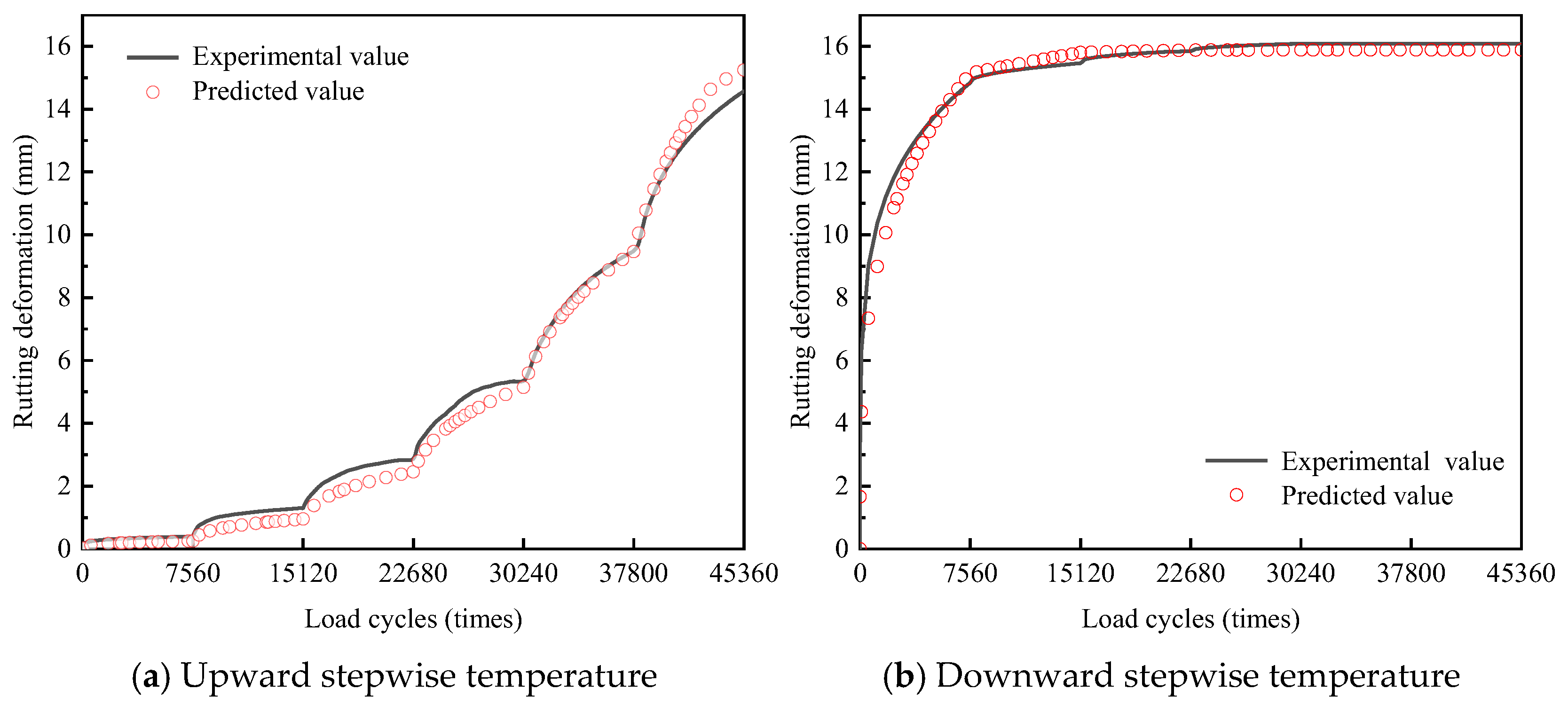
3.2.2. Verification of the Rutting Development Regularity
3.3. Rutting Performance Evaluation of the DLAP
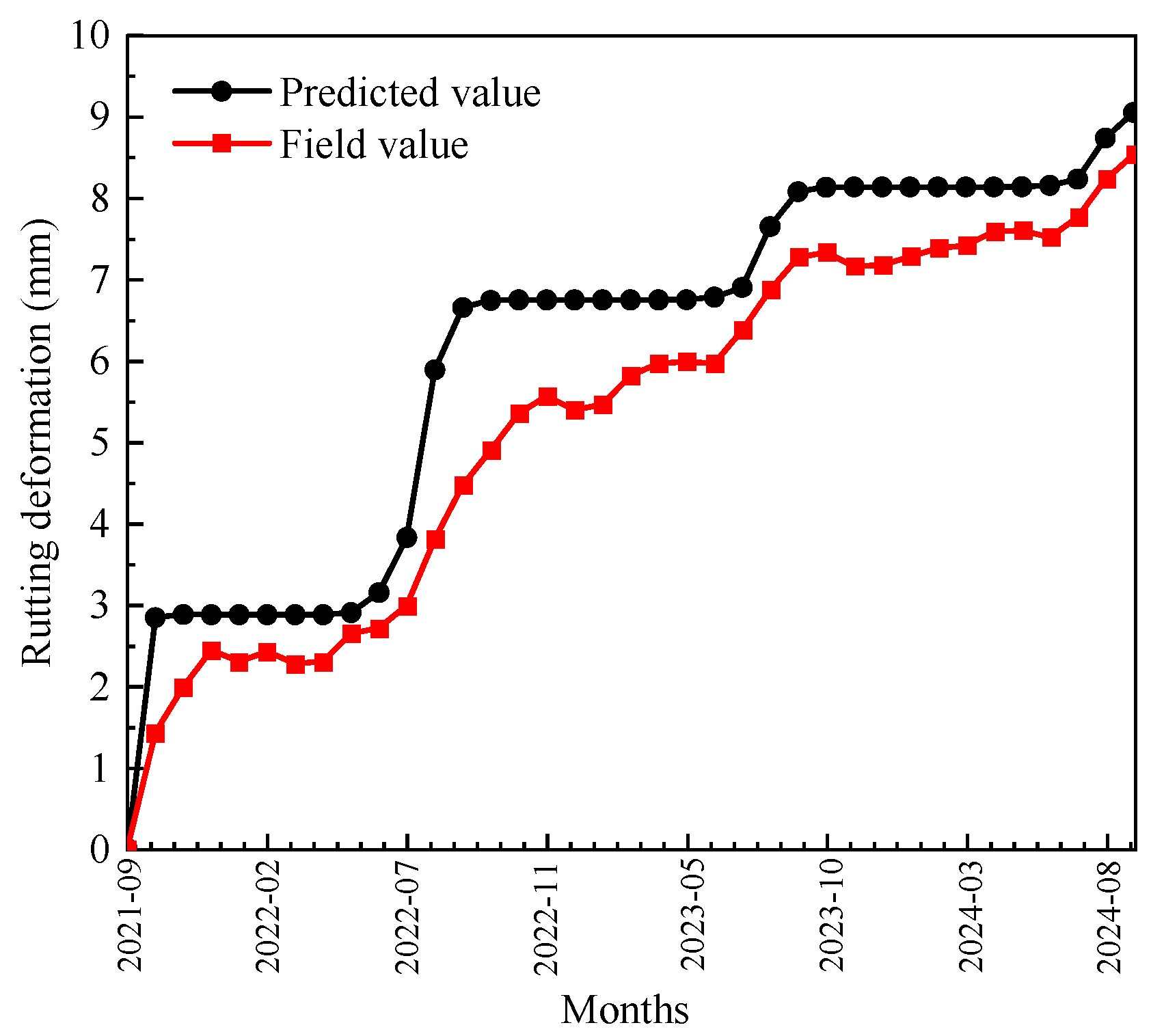
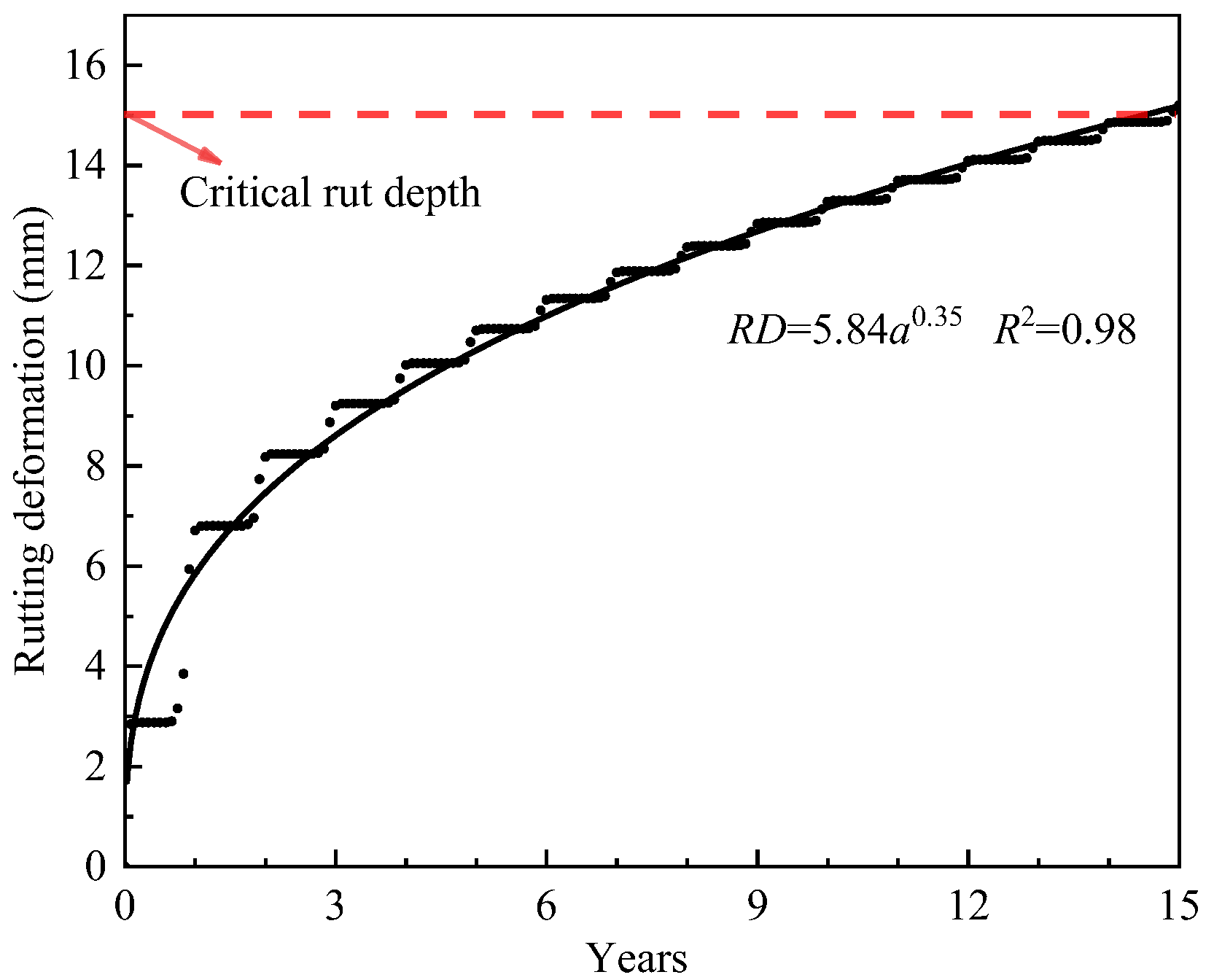
3.3.1. Rutting Performance Under Actual Service Conditions
3.3.2. Rutting Performance Under Extreme Heat Conditions
4. Conclusions
- (1)
- The rutting deformation of DLAP exhibits a stepwise variation under variable temperature conditions, and the rutting development of DLAP demonstrates significant temperature dependence. When the temperature exceeds 50 °C, rutting deformation becomes uncontrollable and increases continuously at a high growth rate. It can be seen that the sensitive temperature for the high-temperature performance of DLAP is 50 °C. Therefore, the high-temperature performance of DLAP at 50 °C should be emphasized in the design of pavement materials.
- (2)
- A time-hardening model was developed to predict the rutting deformation of DLAP under variable temperature based on stepwise temperature-controlled rutting test results. The prediction accuracy of the model was validated through field experiments. Stepwise temperature-controlled rutting tests on multilayer rutting specimens could offer an effective approach for estimating asphalt-pavement rutting deformation under variable temperature.
- (3)
- The annual temperature variation of DLAP was collected on-site to evaluate its rutting performance. Under actual service conditions, the rutting development of DLAP can still be effectively described by the power-law function. The DLAP demonstrates satisfactory rutting resistance, which showing strong adaptability to the traffic loads and temperature conditions of the engineering practice.
- (4)
- This study investigated the rutting performance of DLAP under variable temperature, achieving some preliminary results. However, the boundary conditions, loading conditions, and temperature gradients used in the rutting test differ from actual asphalt pavements. This discrepancy may limit the generalizability of the results. In future research, we will focus on the effect of temperature gradients and sensitive temperature ranges on the rutting deformation of rutting specimens in laboratory tests with high temperature, which will in turn modify the existing model and enhance its applicability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Formulation of the Rutting Development Regularity
References
- Zhu, J.; Sun, L.; Wang, Y.; Li, H.; Liu, L. Development and calibration of shear-based rutting model for asphalt concrete layers. Int. J. Pavement Eng. 2017, 18, 937–944. [Google Scholar] [CrossRef]
- Li, X.; Sha, A.; Jiao, W.; Cao, Y.; Song, R. Strain response and creep behavior of asphalt mixture based on multi-damage fractional visco-elasto-plastic constitutive model. Constr. Build. Mater. 2025, 472, 140834. [Google Scholar] [CrossRef]
- Tian, T.; Jiang, Y.; Yi, Y.; Nie, C. The splitting fatigue properties of ultra-large particle size asphalt mixture under the coupling effect of temperature and load. Eng. Fract. Mech. 2025, 319, 110990. [Google Scholar] [CrossRef]
- Kim, W.J.; Le, V.P.; Lee, H.J.; Phan, H.T. Calibration and validation of a rutting model based on shear stress to strength ratio for asphalt pavements. Constr. Build. Mater. 2017, 149, 327–337. [Google Scholar] [CrossRef]
- Sinanmis, R.; Woods, L. Traffic channelisation and pavement deterioration: An investigation of the role of lateral wander on asphalt pavement rutting. Int. J. Pavement Eng. 2022, 24, 2118272. [Google Scholar] [CrossRef]
- Mamlouk, M.; Vinayakamurthy, M.; Underwood, B.S.; Kaloush, K.E. Effects of the international roughness index and rut depth on crash rates. Transp. Res. Rec. 2018, 2672, 418–429. [Google Scholar] [CrossRef]
- Liu, T.; Yang, S.; Jiang, X.; Liao, B.; Castillo-Camarena, E.A. Adaptation measures for asphalt pavements to climate change in China. J. Clean. Prod. 2023, 415, 137861. [Google Scholar] [CrossRef]
- Ekmekci, M.; Sinanmis, R.; Woods, L. Predictive modeling for highway pavement rutting: A comparative analysis of auto-machine learning and structural equation models. Transp. Res. Rec. 2024, 2678, 724–737. [Google Scholar] [CrossRef]
- Du, Y.; Chen, J.; Han, Z.; Liu, W. A review on solutions for improving rutting resistance of asphalt pavement and test methods. Constr. Build. Mater. 2018, 168, 893–905. [Google Scholar] [CrossRef]
- Li, N.; Zhan, H.; Yu, X.; Tang, W.; Yu, H.; Dong, F. Research on the high temperature performance of asphalt pavement based on field cores with different rutting development levels. Mater. Struct. 2021, 54, 70. [Google Scholar] [CrossRef]
- Coleri, E.; Harvey, J.T.; Yang, K.; Boone, J.M. A micromechanical approach to investigate asphalt concrete rutting mechanisms. Constr. Build. Mater. 2012, 30, 36–49. [Google Scholar] [CrossRef]
- Büchner, J.; Wistuba, M.P. Assessing creep properties of asphalt binder, asphalt mastic and asphalt mixture. Road Mater. Pavement Des. 2022, 23 (Suppl. S1), 116–130. [Google Scholar] [CrossRef]
- Fang, H.; Liu, Q.; Mo, L.; Javilla, B.; Shu, B.; Wu, S. Characterization of three-stage rutting development of asphalt mixtures. Constr. Build. Mater. 2017, 154, 340–348. [Google Scholar] [CrossRef]
- Tian, Y.; Lee, J.; Nantung, T.; Haddock, J.E. Development of a mid-depth profile monitoring system for accelerated pavement testing. Constr. Build. Mater. 2017, 140, 1–9. [Google Scholar] [CrossRef]
- Jiang, J.; Ni, F.; Yao, L.; Dong, Q. Developing a load-temperature master curve for the permanent deformation of asphalt mixtures by the power function model. Road Mater. Pavement Des. 2020, 21, 1359–1373. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, E.; Li, N.; Wang, L.; Si, C.; Wang, C. Micromechanical analysis of the rutting evolution of asphalt pavement under temperature–stress coupling based on the discrete element method. Constr. Build. Mater. 2022, 325, 126800. [Google Scholar] [CrossRef]
- Shi, S.; Tong, J.; Chen, F.; Hu, J.; Ma, T. Towards an improved prediction of asphalt pavement rutting through thermal-mechanical coupled constitutive modelling. Int. J. Pavement Eng. 2023, 24, 2192495. [Google Scholar] [CrossRef]
- Deng, Y.; Shi, X.; Zhang, Y.; Chen, J. Numerical modelling of rutting performance of asphalt concrete pavement containing phase change material. Eng. Comput. 2023, 39, 1167–1182. [Google Scholar] [CrossRef]
- Wang, H.; Fan, Z.; Zhang, J. Development of a full-depth wheel tracking test for asphalt pavement structure: Methods and performance evaluation. Adv. Mater. Sci. Eng. 2016, 2016, 1737013. [Google Scholar] [CrossRef]
- Du, Y.F.; Qin, S.; Wang, S.Y. Bidirectional heat induced structure of asphalt pavement for reducing pavement temperature. Appl. Therm. Eng. 2015, 75, 298–306. [Google Scholar]
- Nian, T.; Li, S.; Li, P.; Li, J.; Han, Z.; Xue, S. Mechanical response of interlayer structural shear performance of asphalt pavement with functional layer considering interlayer contact state. Case Stud. Constr. Mater. 2023, 18, e01934. [Google Scholar] [CrossRef]
- Jelagin, D.; Olsson, E.; Raab, C.; Partl, M.N. Experimental and numerical modelling of shear bonding between asphalt layers. Road Mater. Pavement Des. 2023, 24 (Suppl. S1), 176–191. [Google Scholar] [CrossRef]
- Li, Q.; Ni, F.; Gao, L.; Yuan, Q.; Xiao, Y. Evaluating the rutting resistance of asphalt mixtures using an advanced repeated load permanent deformation test under field conditions. Constr. Build. Mater. 2014, 61, 241–251. [Google Scholar] [CrossRef]
- JTG 3432-2024; Ministry of Transport of the People’s Republic of China. Test Methods of Aggregate for Highway Engineering. China Communications Press: Beijing, China, 2024.
- JTG F40-2004; Ministry of Transport of the People’s Republic of China. Technical Specifications for Construction of Highway Asphalt Pavements. China Communications Press: Beijing, China, 2004.
- JTG E20-2011; Ministry of Transport of the People’s Republic of China. Standard Test Methods of Bitumen and Bituminous Mixtures for Highway Engineering. China Communications Press: Beijing, China, 2011.
- JTG D50-2017; Ministry of Transport of the People’s Republic of China. Specifications for Design of Highway Asphalt Pavement. China Communications Press: Beijing, China, 2017.
- Jiang, Y.; Zhang, Y.; Deng, C.; Yi, Y.; Tian, T.; Yuan, K. High-temperature rutting resistance of inverted asphalt pavement structure. Adv. Civ. Eng. 2020, 2020, 1–10. [Google Scholar] [CrossRef]
- Li, Q.; Yang, H.; Ni, F.; Ma, X.; Luo, L. Cause analysis on permanent deformation for asphalt pavements using field cores. Constr. Build. Mater. 2015, 100, 40–51. [Google Scholar] [CrossRef]
- Xing, C.; Tang, S.; Chang, Z.; Han, Z.; Li, H.; Zhu, B. A comprehensive review on the plant-mixed cold recycling technology of emulsified asphalt: Raw materials and factors affecting performances. Constr. Build. Mater. 2024, 439, 137344. [Google Scholar] [CrossRef]
- Ren, J.; Liu, Z.; Xue, J.; Xu, Y. Influence of the mesoscopic viscoelastic contact model on characterizing the rheological behavior of asphalt concrete in the DEM simulation. Adv. Civ. Eng. 2020, 2020, 5248267. [Google Scholar] [CrossRef]
- Javilla, B.; Mo, L.; Hao, F.; Shu, B.; Wu, S. Multi-stress loading effect on rutting performance of asphalt mixtures based on wheel tracking testing. Constr. Build. Mater. 2017, 148, 1–9. [Google Scholar] [CrossRef]
- Pouranian, M.R.; Imaninasab, R.; Shishehbor, M. The effect of temperature and stress level on the rutting performance of modified stone matrix asphalt. Road Mater. Pavement Des. 2020, 21, 1386–1398. [Google Scholar] [CrossRef]
- Suh, Y.-C.; Cho, N.-H. Development of a rutting performance model for asphalt concrete pavement based on test road and accelerated pavement test data. KSCE J. Civ. Eng. 2014, 18, 165–171. [Google Scholar] [CrossRef]
- Jäntschi, L. Structure-property relationships for solubility of monosaccharides. Appl. Water Sci. 2019, 9, 38. [Google Scholar] [CrossRef]
- Rahman, M.S.; Erlingsson, S. Predicting permanent deformation behaviour of unbound granular materials. Int. J. Pavement Eng. 2014, 16, 587–601. [Google Scholar] [CrossRef]
- Erlingsson, S.; Rahman, M.S. Evaluation of permanent deformation characteristics of unbound granular materials by means of multistage repeated-load triaxial tests. Transp. Res. Rec. 2013, 2369, 11–19. [Google Scholar] [CrossRef]

| Asphalt | Penetration Index (0.1 mm) | Ductility (cm) | Soft Point (°C) | Relative Density | Dissolvability Intrichloro Ethylene (%) |
|---|---|---|---|---|---|
| 70# petroleum asphalt | 69 | 37 | 48.6 | 1.045 | 99.5 |
| SBS-modified asphalt | 65 | 70 | 85.0 | 1.035 | 99.6 |
| Aggregate | Mineral Type | Technical Properties |
|---|---|---|
| Coarse aggregate | Amphibolite | Apparent density: 2.835 g/cm3; Crush value: 14.4%; Los Angeles attrition loss: 18.8%; Flakiness index: 6.3% |
| Fine aggregate | Limestone | Apparent density: 2.742 g/cm3; Methylene blue value: 3.1 g/kg; Sand equivalent: 82.3%; Angularity: 38.7 s |
| Mineral powder | Limestone | Apparent density: 2.717 g/cm3; Hydrophilic coefficient: 0.6; Plasticity index: 3.6%; Water content: 0.4% |
| Mixture Types | Mass Percentage Passing (%) for the Sieve Size (mm) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 26.5 | 19 | 16 | 13.2 | 9.5 | 4.75 | 2.36 | 1.18 | 0.6 | 0.3 | 0.15 | 0.075 | |
| AC-16 | - | 100 | 94.3 | 88.2 | 70.3 | 45.0 | 33.2 | 22.7 | 16.1 | 9.9 | 7.3 | 5.8 |
| AC-20 | 100 | 92.2 | 83.4 | 73.3 | 60.9 | 41.1 | 31.4 | 21.7 | 15.1 | 9.1 | 6.6 | 5.0 |
| Mixture Types | VV (%) | VFA (%) | VMA (%) | MS (kN) | FL (mm) | OAC (%) |
|---|---|---|---|---|---|---|
| AC-16 | 3.4 | 73.2 | 14.2 | 13.3 | 3.3 | 4.5 |
| AC-20 | 4.1 | 71.4 | 14.6 | 14.4 | 2.7 | 4.2 |
| Regression Equation | Temperature Interval | Regression Parameter of A | Regression Parameter of B | R2 | ||
|---|---|---|---|---|---|---|
| Value | Standard Error | Value | Standard Error | |||
| RD = ANB | UT-20 | 0.070 | 0.016 | 0.193 | 0.001 | 0.99 |
| UT-30 | 0.226 | 0.008 | 0.196 | 0.004 | 0.99 | |
| UT-40 | 0.516 | 0.016 | 0.194 | 0.004 | 0.99 | |
| UT-50 | 1.121 | 0.056 | 0.177 | 0.006 | 0.97 | |
| UT-60 | 1.744 | 0.069 | 0.188 | 0.005 | 0.99 | |
| UT-70 | 4.280 | 0.132 | 0.136 | 0.004 | 0.98 | |
| Regression Equation | Temperature Interval | Regression Parameter of A | Regression Parameter of B | R2 | ||
|---|---|---|---|---|---|---|
| Value | Standard Error | Value | Standard Error | |||
| RD = ANB | DT-70 | 2.648 | 0.001 | 0.193 | 6.34 × 10−6 | 0.99 |
| DT-60 | 14.041 | 0.051 | 0.010 | 4.45 × 10−4 | 0.96 | |
| DT-50 | 14.946 | 0.018 | 0.006 | 1.53 × 10−4 | 0.99 | |
| DT-40 | 15.548 | 0.016 | 0.004 | 1.34 × 10−4 | 0.97 | |
| DT-30 | / | / | / | / | / | |
| DT-20 | / | / | / | / | / | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, Y.; Jiang, Y.; Bai, C.; Zhang, H.; Liang, Y.; Lou, W.; Chen, Z. Rutting Behavior of Dual-Layer Asphalt Pavements Subjected to Variable Temperature. Materials 2025, 18, 2603. https://doi.org/10.3390/ma18112603
Tan Y, Jiang Y, Bai C, Zhang H, Liang Y, Lou W, Chen Z. Rutting Behavior of Dual-Layer Asphalt Pavements Subjected to Variable Temperature. Materials. 2025; 18(11):2603. https://doi.org/10.3390/ma18112603
Chicago/Turabian StyleTan, Ya, Yingjun Jiang, Chenfan Bai, Hongjiang Zhang, Yingchao Liang, Wenhui Lou, and Zhejiang Chen. 2025. "Rutting Behavior of Dual-Layer Asphalt Pavements Subjected to Variable Temperature" Materials 18, no. 11: 2603. https://doi.org/10.3390/ma18112603
APA StyleTan, Y., Jiang, Y., Bai, C., Zhang, H., Liang, Y., Lou, W., & Chen, Z. (2025). Rutting Behavior of Dual-Layer Asphalt Pavements Subjected to Variable Temperature. Materials, 18(11), 2603. https://doi.org/10.3390/ma18112603






