High-Cycle Fatigue Life Prediction of Additive Manufacturing Inconel 718 Alloy via Machine Learning
Abstract
1. Introduction
2. Materials and Methods
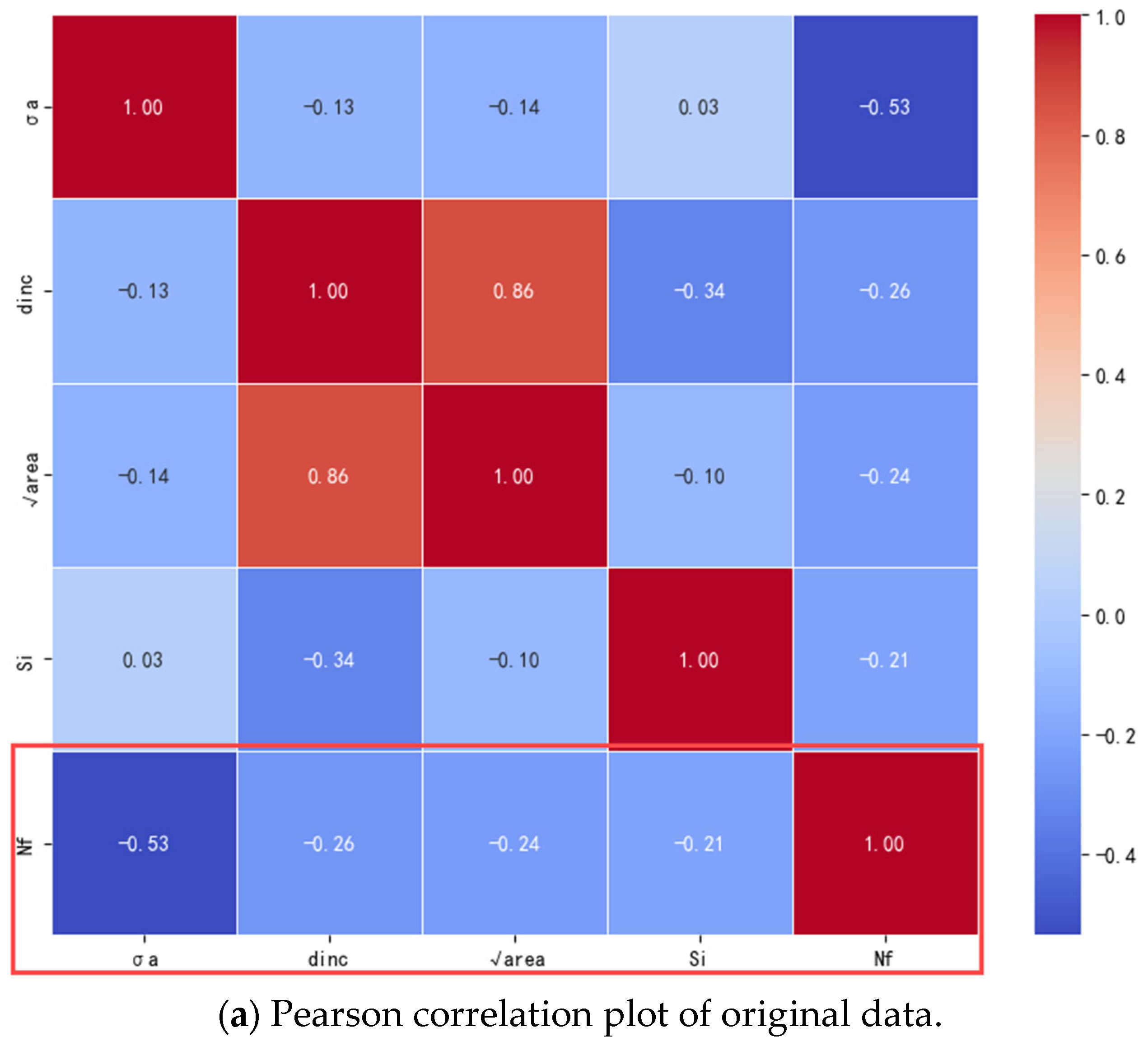
2.1. Original Dataset Construction
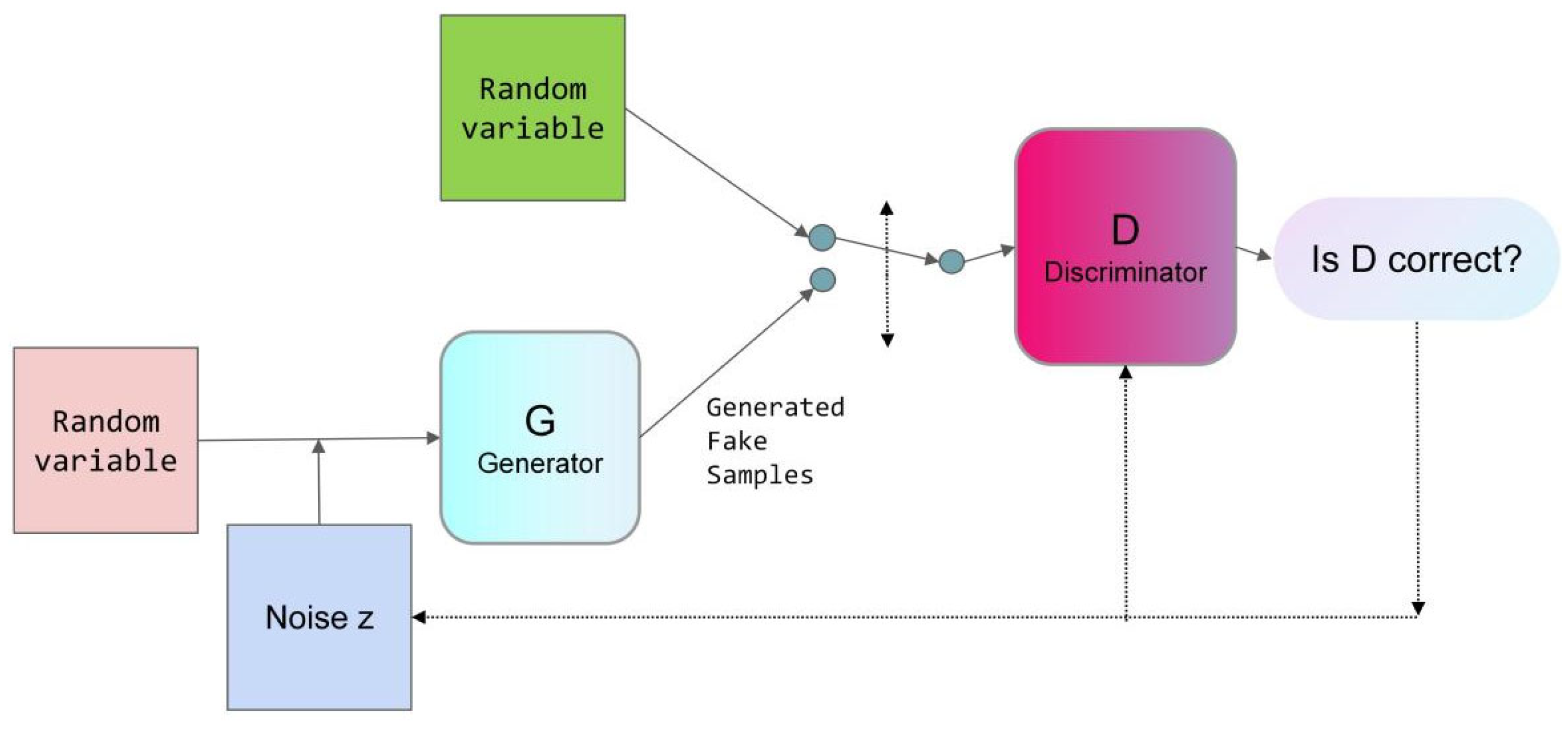
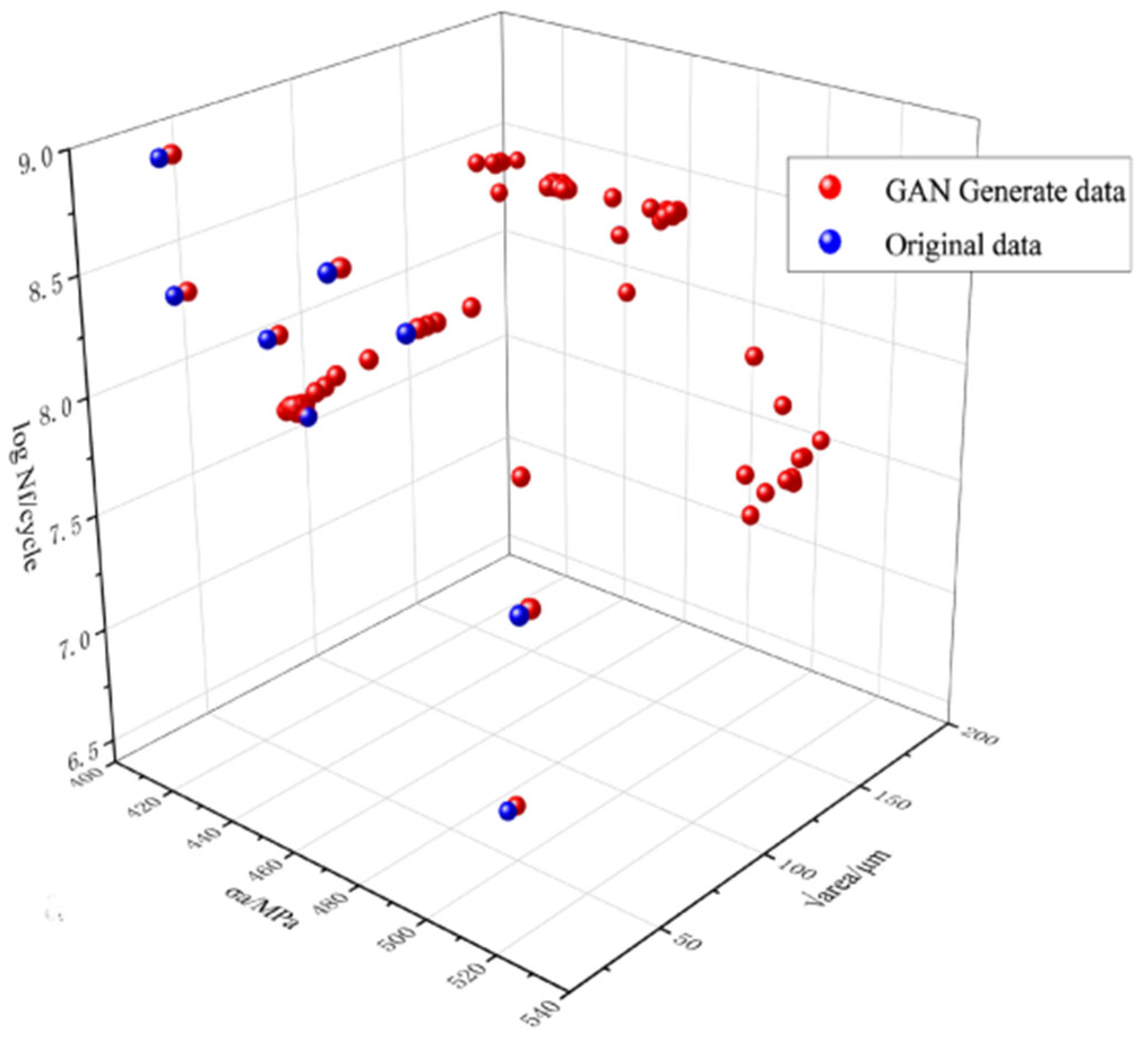
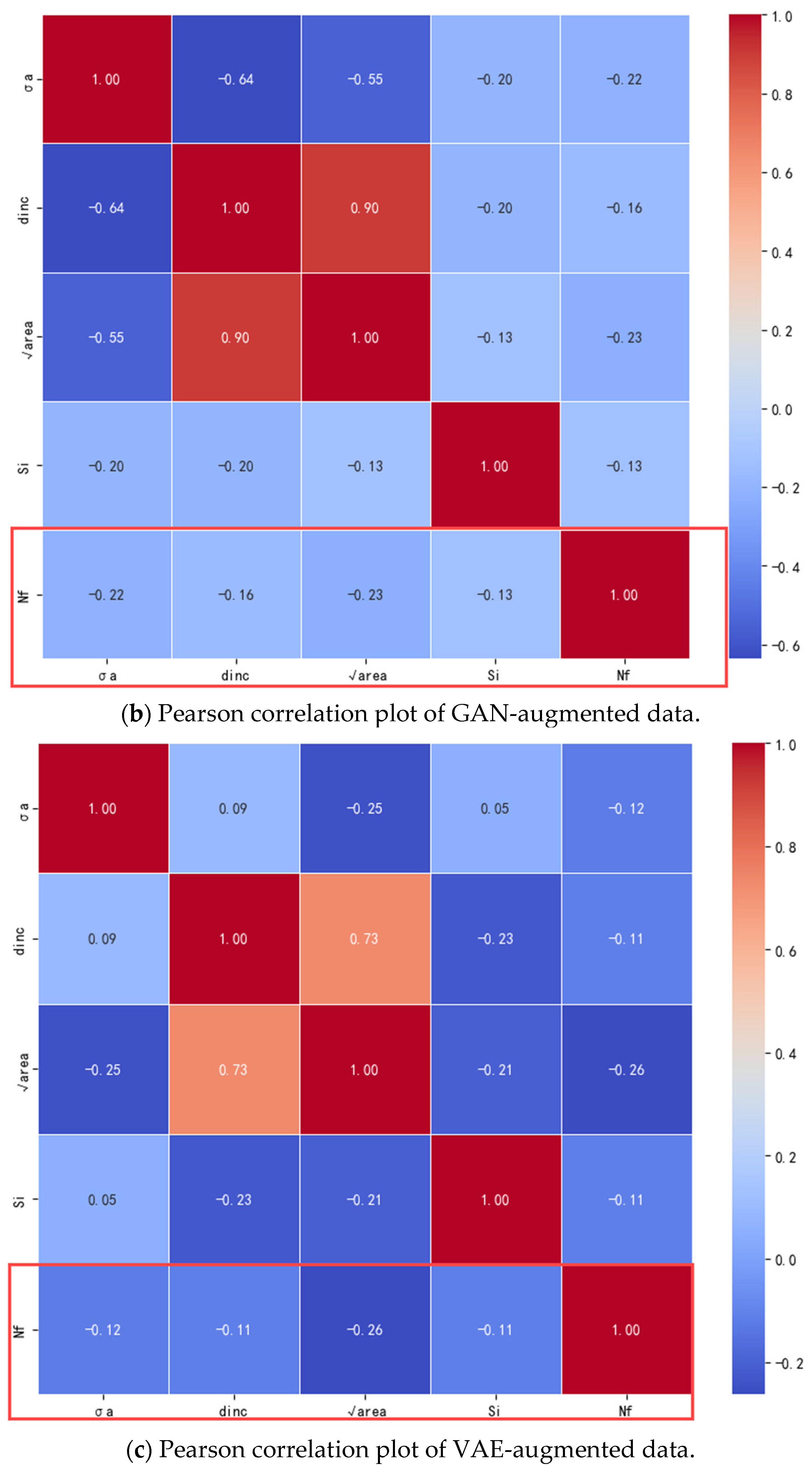
2.2. Generative Adversarial Network (GAN) Data Expansion
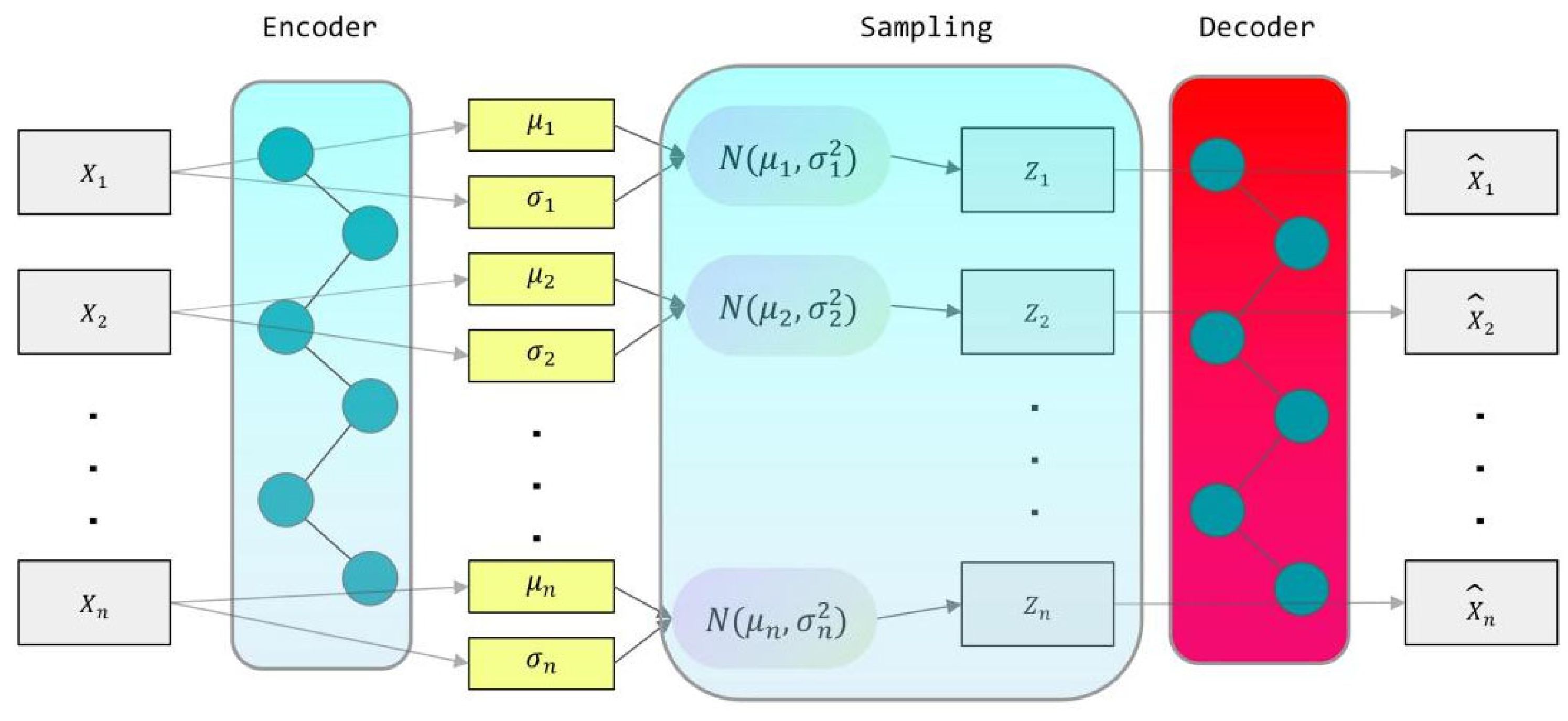
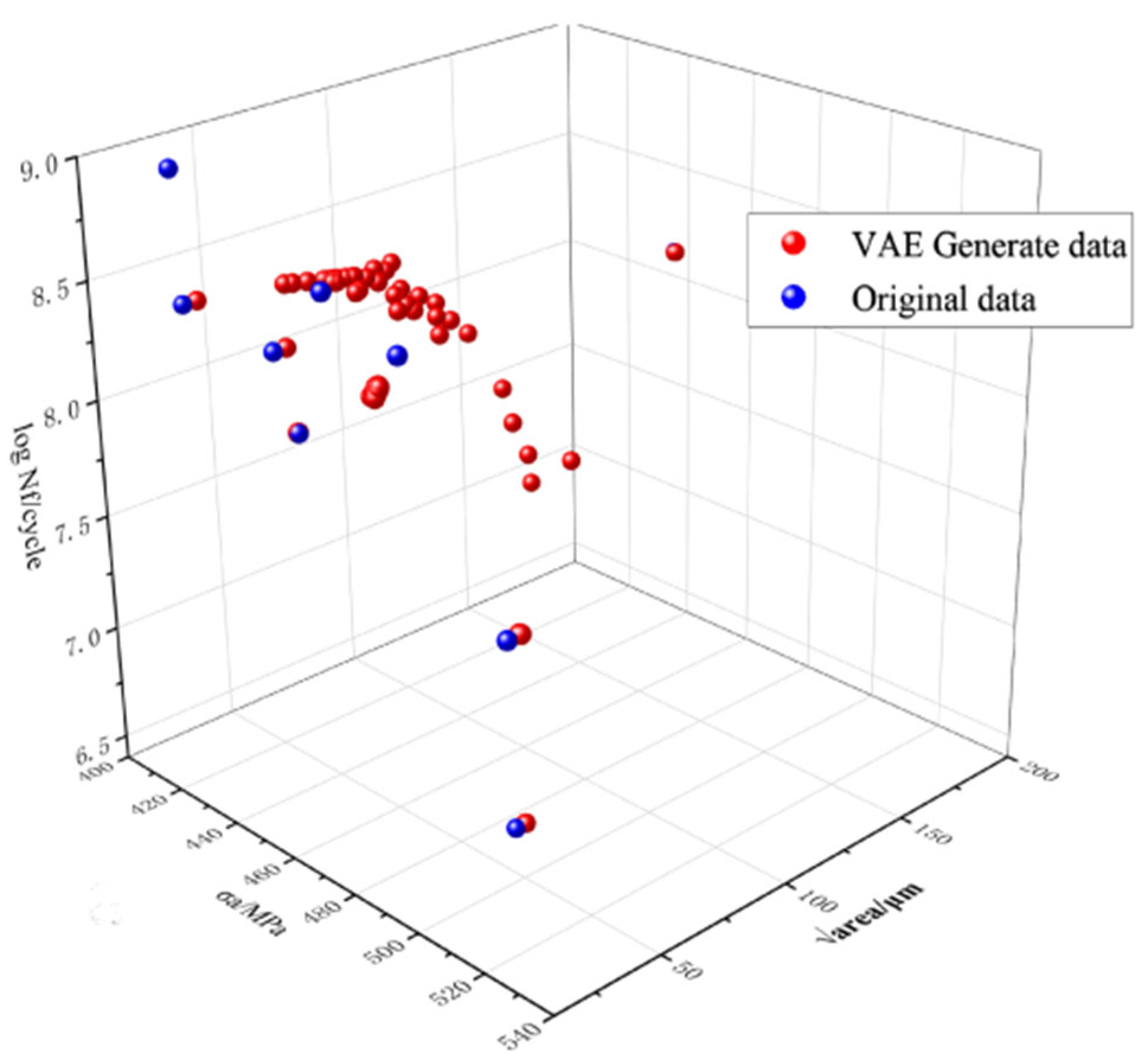
2.3. Variational Auto-Encoder (VAE) Data Expansion
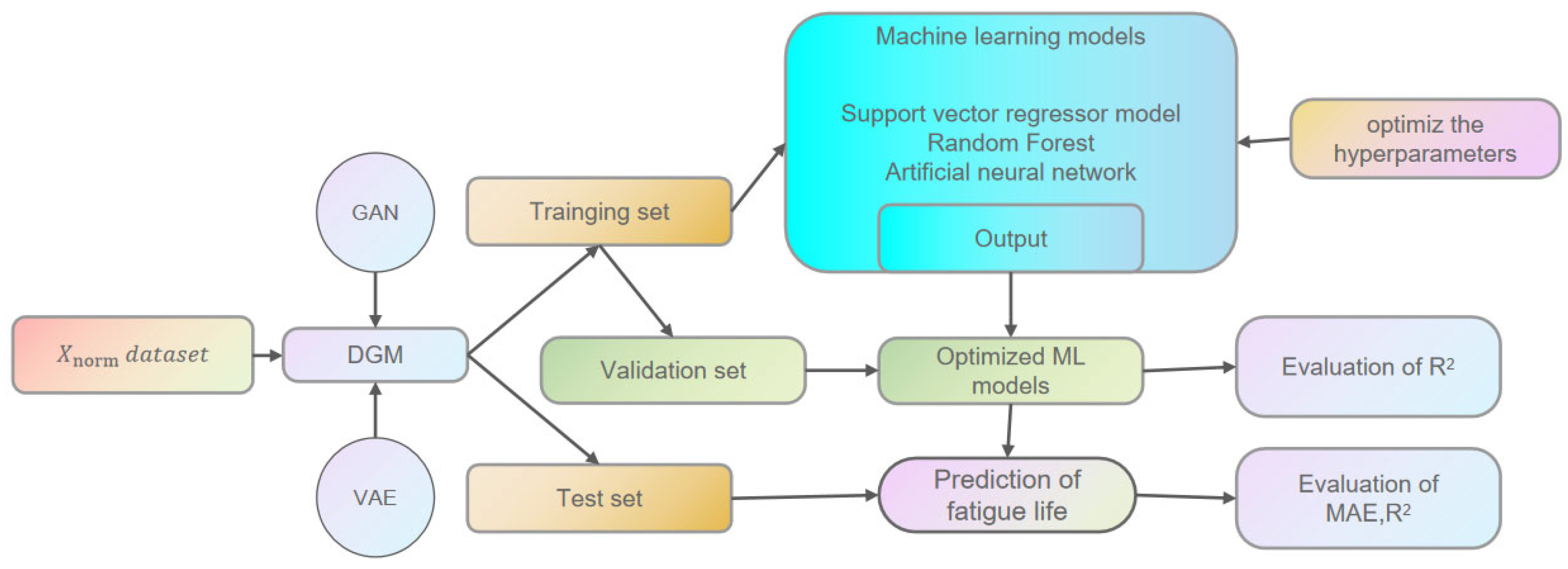
3. Development of Machine Learning Models
3.1. Data Usability
3.2. Data Preprocessing
3.3. Machine Learning Models
3.3.1. Support Vector Regression Model
3.3.2. Random Forest Model
3.3.3. Artificial Neural Network
3.3.4. Model Evaluation Criteria
3.4. Hyperparameter Optimization
4. Results and Discussion
4.1. Parameter Configuration and Training Set Performance of the ML Model
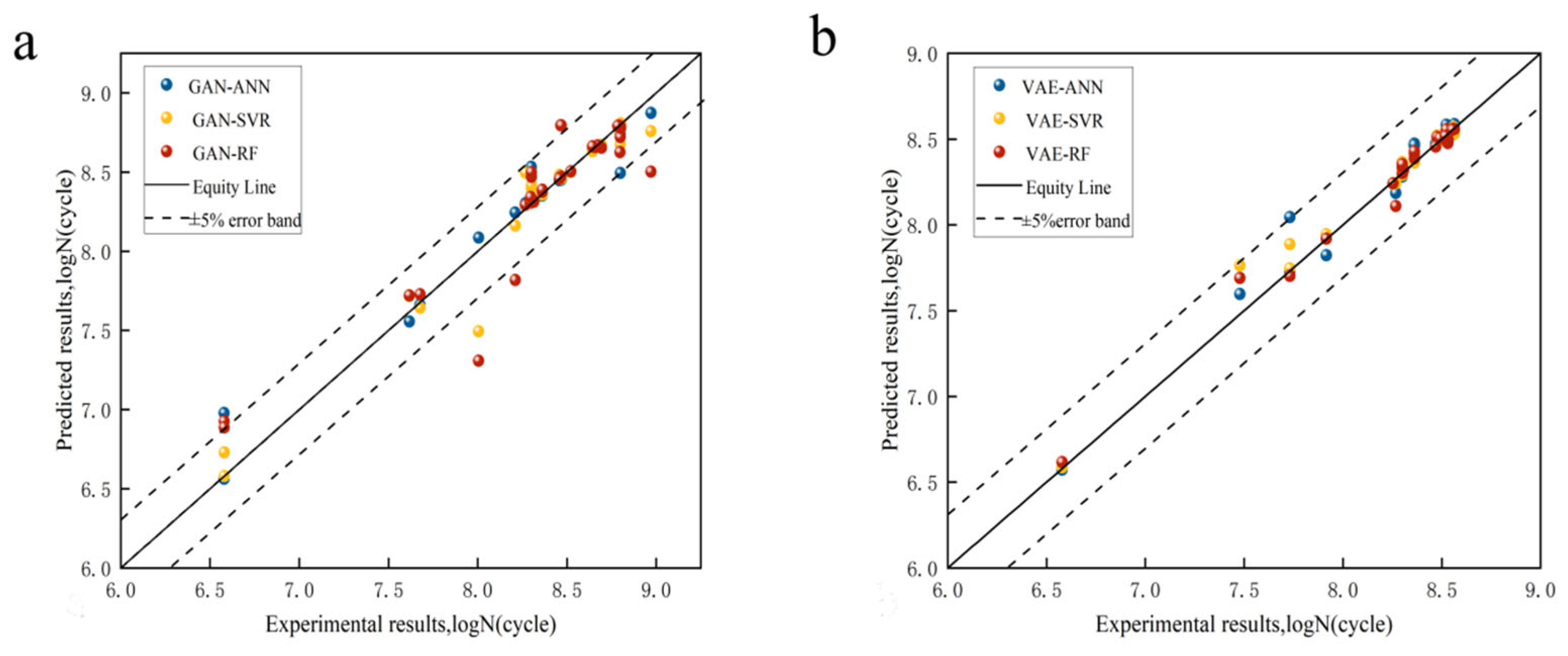
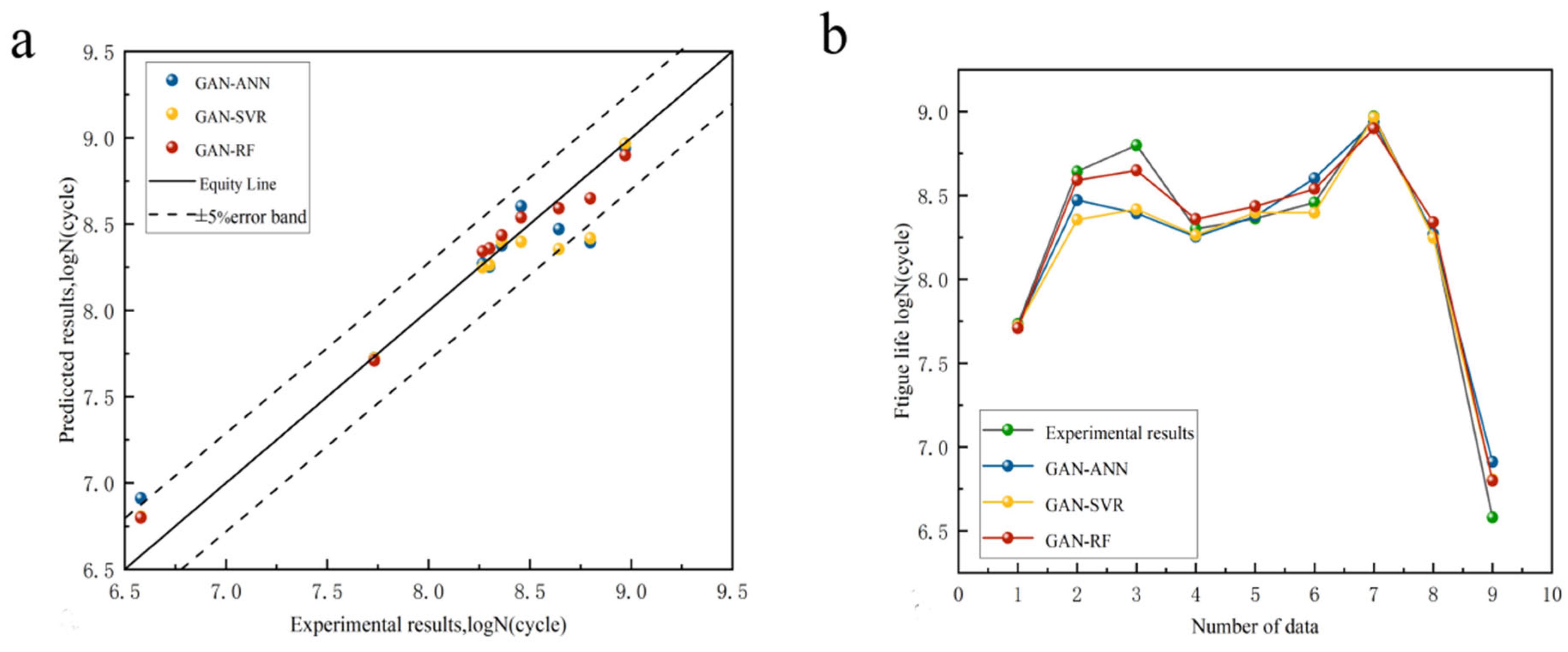
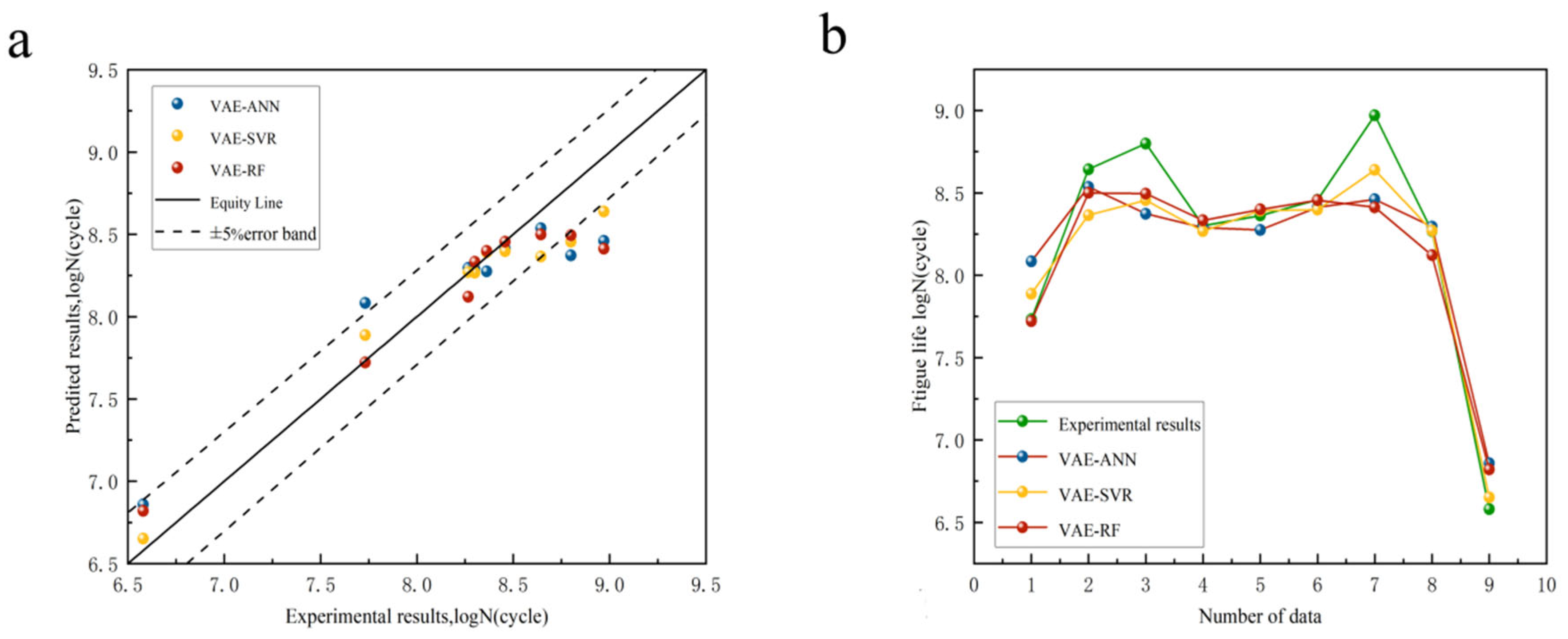
4.2. Fatigue Life Prediction
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gong, G.; Ye, J.; Chi, Y.; Zhao, Z.; Wang, Z.; Xia, G.; Du, X.; Tian, H.; Yu, H.; Chen, C. Research status of laser additive manufacturing for metal: A review. J. Mater. Res. Technol. 2021, 15, 855–884. [Google Scholar] [CrossRef]
- Armstrong, M.; Mehrabi, H.; Naveed, N. An overview of modern metal additive manufacturing technology. J. Manuf. Process. 2022, 84, 1001–1029. [Google Scholar] [CrossRef]
- Lu, J.; Zhuo, L. Additive manufacturing of titanium alloys via selective laser melting: Fabrication, microstructure, post-processing, performance and prospect. Int. J. Refract. Met. Hard Mater. 2023, 111, 106110. [Google Scholar] [CrossRef]
- Kanishka, K.; Acherjee, B. Revolutionizing manufacturing: A comprehensive overview of additive manufacturing processes, materials, developments, and challenges. J. Manuf. Process. 2023, 107, 574–619. [Google Scholar] [CrossRef]
- Qin, Z.; Li, B.; Chen, C.; Chen, T.; Chen, R.; Zhang, H.; Xue, H.; Yao, C.; Tan, L. Crack initiation mechanisms and life prediction of GH4169 superalloy in the high cycle and very high cycle fatigue regime. cycle and very high cycle fatigue regime. J. Mater. Res. Technol. 2023, 26, 720–736. [Google Scholar] [CrossRef]
- Derrick, C.; Fatemi, A. Correlations of fatigue strength of additively manufactured metals with hardness and defect size. Int. J. Fatigue 2022, 162, 106920. [Google Scholar] [CrossRef]
- Sanaei, N.; Fatemi, A. Defects in additive manufactured metals and their effect on fatigue performance: A state-of-the-art review. Prog. Mater. Sci. 2021, 117, 100724. [Google Scholar] [CrossRef]
- Mayer, H.; Haydn, W.; Schuller, R.; Issler, S.; Furtner, B.; Bacher-Höchst, M. Very high cycle fatigue properties of bainitic high carbon-chromium steel. Int. J. Fatigue 2009, 31, 242–249. [Google Scholar] [CrossRef]
- Mayer, H.; Haydn, W.; Schuller, R.; Issler, S.; Bacher-Höchst, M. Very high cycle fatigue properties of bainitic high carbon–chromium steel under variable amplitude conditions. Int. J. Fatigue 2009, 31, 1300–1308. [Google Scholar] [CrossRef]
- Zhu, M.-L.; Jin, L.; Xuan, F.-Z. Fatigue life and mechanistic modeling of interior micro-defect induced cracking in high cycle and very high cycle regimes. Acta Mater. 2018, 157, 259–275. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Bathias, C.; Kawagoishi, N.; Chen, Q. Effect of inclusion on subsurface crack initiation and gigacycle fatigue strength. Int. J. Fatigue 2002, 24, 1269–1274. [Google Scholar] [CrossRef]
- Murakami, Y.; Kodama, S.; Konuma, S. Quantitative evaluation of effects of non-metallic inclusions on fatigue strength of high strength steels. I: Basic fatigue mechanism and evaluation of correlation between the fatigue fracture stress and the size and location of non-metallic inclusions. Int. J. Fatigue 1989, 11, 291–298. [Google Scholar] [CrossRef]
- Fan, J.-L.; Zhu, G.; Zhu, M.-L.; Xuan, F.-Z. A data-physics integrated approach to life prediction in very high cycle fatigue regime. Int. J. Fatigue 2023, 176, 107917. [Google Scholar] [CrossRef]
- Peng, X.; Wu, S.; Qian, W.; Bao, J.; Hu, Y.; Zhan, Z.; Guo, G.; Withers, P.J. The potency of defects on fatigue of additively manufactured metals. Int. J. Mech. Sci. 2022, 221, 107185. [Google Scholar] [CrossRef]
- Luo, Y.W.; Zhang, B.; Feng, X.; Song, Z.M.; Qi, X.B.; Li, C.P.; Chen, G.F.; Zhang, G.P. Pore-affected fatigue life scattering and prediction of additively manufactured Inconel 718: An investigation based on miniature specimen testing and machine learning approach. Mater. Sci. Eng. A 2021, 802, 140693. [Google Scholar] [CrossRef]
- Liu, Y.-K.; Fan, J.-L.; Zhu, G.; Zhu, M.-L.; Xuan, F.-Z. Data-driven approach to very high cycle fatigue life prediction. Eng. Fract. Mech. 2023, 292, 109630. [Google Scholar] [CrossRef]
- Niu, S.; Peng, Y.; Li, B.; Wang, X. A transformed-feature-space data augmentation method for defect segmentation. Comput. Ind. 2023, 147, 103860. [Google Scholar] [CrossRef]
- Shi, L.; Yang, X.; Chang, X.; Wu, J.; Sun, H. An improved density peaks clustering algorithm based on k nearest neighbors and turning point for evaluating the severity of railway accidents. Reliab. Eng. Syst. Saf. 2023, 233, 109132. [Google Scholar] [CrossRef]
- Zhan, Z.; Hu, W.; Meng, Q. Data-driven fatigue life prediction in additive manufactured titanium alloy: A damage mechanics based machine learning framework. Eng. Fract. Mech. 2021, 252, 107850. [Google Scholar] [CrossRef]
- Tran, L.; Yin, X.; Liu, X. Representation Learning by Rotating Your Faces. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 3007–3021. [Google Scholar] [CrossRef]
- Qiao, T.; Zhang, J.; Xu, D.; Tao, D. MirrorGAN: Learning Text-To-Image Generation by Redescription. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15 June 2019; pp. 1505–1514. [Google Scholar]
- Yu, J.; Guo, Z. Remaining useful life prediction of planet bearings based on conditional deep recurrent generative adversarial network and action discovery. J. Mech. Sci. Technol. 2021, 35, 21–30. [Google Scholar] [CrossRef]
- Wang, X.; Xu, L.; Zhao, L.; Ren, W.; Li, Q.; Han, Y. Machine learning method for estimating the defect-related mechanical properties of additive manufactured alloys. Eng. Fract. Mech. 2023, 291, 109559. [Google Scholar] [CrossRef]
- He, G.; Zhao, Y.; Yan, C. Application of tabular data synthesis using generative adversarial networks on machine learning-based multiaxial fatigue life prediction. Int. J. Press. Vessel. Pip. 2022, 199, 104779. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the 27th International Conference on Neural Information Processing Systems, Bangkok, Thailand, 23–27 November 2020; MIT Press: Montreal, QC, Canada, 2014; Volume 2, pp. 2672–2680. [Google Scholar]
- Xu, X.; Zhang, T.; Su, Y. Temporal variations and trend of ground-level ozone based on long-term measurements in Windsor, Canada. Atmos. Chem. Phys. 2019, 19, 7335–7345. [Google Scholar] [CrossRef]
- Patki, R.N.; Veeramachaneni, K. The Synthetic Data Vault, 2016. Available online: https://ieeexplore.ieee.org/document/7796926 (accessed on 21 May 2022).
- Choi, E.; Biswal, S.; Malin, B.; Duke, J.; Stewart, W.; Sun, J. Generating Multi-Label Discrete Patient Records Using Generative Adversarial Networks. arXiv 2017, arXiv:1703.06490. [Google Scholar]
- Xu, L.; Veeramachaneni, K. Synthesising Tabular Data Using Generative Adversarial Networks. arXiv 2018, arXiv:1811.11264. [Google Scholar]
- Kingma, D.P. Max Welling. Auto-Encoding Variational Bayes. arXiv 2022, arXiv:1312.6114. [Google Scholar]
- Yan, N.; Han, X.; Yu, Y.; You, M.; Peng, W. Ultra-high circumferential fatigue properties of Inconel718 nickel-based high-temperature alloy. Mech. Eng. Mater. 2016, 40, 9–12. [Google Scholar]
- Wang, L.; Liu, Y.; Chen, G.; Liu, J. High-temperature low-week fatigue damage mechanism of Inconel718 nickel-based high-temperature alloy. Mech. Eng. Mater. 2019, 43, 45–49. [Google Scholar]
- Yao, L.; Zhang, X.; Liu, F.; Tu, M.C. High-temperature low-frequency fatigue properties of Inconel718 nickel-based high-temperature alloy. Mech. Eng. Mater. 2016, 40, 25–29, 64. [Google Scholar]
- Song, Z. Study on Ultra-High Circumferential Fatigue Fracture Mechanism of Inconel 718 Nickel-Based High Temperature Alloy Based on SLM Forming; Taiyuan University of Science and Technology: Taiyuan, China, 2021. [Google Scholar]
- Horňas, J.; Běhal, J.; Homola, P.; Doubrava, R.; Holzleitner, M.; Senck, S. A machine learning based approach with an augmented dataset for fatigue life prediction of additively manufactured Ti-6Al-4V samples. Eng. Fract. Mech. 2023, 293, 109709. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Vandewalle, J.; De Moor, B. Optimal control by least squares support vector machines. Neural Netw. 2001, 14, 23–35. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Li, B.; Xuan, F.-Z. Fatigue-life prediction of additively manufactured metals by continuous damage mechanics (CDM)-informed machine learning with sensitive features. Int. J. Fatigue 2022, 164, 107147. [Google Scholar] [CrossRef]
- Zhang, G.; Su, B.; Liao, W.; Wang, X.; Zou, J.; Yuan, R.; Li, J. Prediction of fatigue life of powder metallurgy superalloy disk via machine learning. Foundry Technol. 2022, 43, 519–524. [Google Scholar]
- Rodriguez-Galiano, V.; Sanchez-Castillo, M.; Chica-Olmo, M.; Chica-Rivas, M. Machine learning predictive models for mineral prospectivity: An evaluation of neural networks, random forest, regression trees and support vector machines. Ore Geol. Rev. 2015, 71, 804–818. [Google Scholar] [CrossRef]
- Zhang, X.-C.; Gong, J.-G.; Xuan, F.-Z. A deep learning based life prediction method for components under creep, fatigue and creep-fatigue conditions. Int. J. Fatigue 2021, 148, 106236. [Google Scholar] [CrossRef]
- Fathalla, E.; Tanaka, Y.; Maekawa, K. Remaining fatigue life assessment of in-service road bridge decks based upon artificial neural networks. Eng. Struct. 2018, 171, 602–616. [Google Scholar] [CrossRef]
- Kang, S.; Cho, S. Approximating support vector machine with artificial neural network for fast prediction. Expert Syst. Appl. 2014, 41, 4989–4995. [Google Scholar] [CrossRef]

| Ni | Nb | Mo | Ti | Al | Cr | C | Fe |
|---|---|---|---|---|---|---|---|
| 53.00 | 5.30 | 3.00 | 1.00 | 0.50 | 19.00 | 0.05 | Balance |
| 522 | 21.00 | 8.00 | 18.61 | 0.34 | 5.4 × 107 |
| 493 | 21.00 | 3.00 | 18.61 | 0.29 | 4.4 × 108 |
| 474 | 17.00 | 3.00 | 15.06 | 0.29 | 6.3 × 108 |
| 474 | 6.00 | 6.00 | 5.31 | 0.27 | 2 × 108 |
| 444 | 32.85 | 128.57 | 29.11 | 0.34 | 2.3 × 108 |
| 420 | 25.45 | 15.90 | 22.55 | 0.31 | 2.87 × 108 |
| 415 | 28.81 | 141.30 | 25.53 | 0.27 | 9.35 × 108 |
| 452 | 200.00 | 430.76 | 177.24 | 0.29 | 1.85 × 108 |
| 496 | 58.33 | 333.32 | 51.69 | 0.25 | 3.8 × 106 |
| ML Model | Tuning Entity | Range | No. of Values |
|---|---|---|---|
| SVR | K | [‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’] | 4 |
| C | [10, 20, ……, 140, 150] | 15 | |
| ε | [0.001, 0.01, 0.1, 1, 10] | 5 | |
| γ | [0.001, 0.01, 0.1, 1, 10] | 5 | |
| RF | n_estimators | [50, 100, 150, 200, 500] | 5 |
| max_depth | [None, 10, 20, 30, 40, 50] | 6 | |
| min_samples_split | [1, 2, 4, 6, 8, 10, 16] | 6 | |
| min_samples_leaf | [1, 2, 4] | 6 | |
| ANN | hidden_layer_sizes | [(i, j, k)] i ϵ [20, 30, …, 70, 80] j ϵ [0, 10, 20, 40] k ϵ [0, 10, 15, 20] | (7, 5, 4) |
| activation | [identity, RELU, sigmoid, tanh] | 4 | |
| solver | [adam, lbfgs, sgd] | 3 | |
| max_iter | [10, 50, 100, 500, 1000, 5000] | 6 |
| ML Model | Tuning Entity | Value |
|---|---|---|
| GAN-SVR | K | RBF |
| C | 100 | |
| ε | 0.01 | |
| γ | 1 | |
| GAN-RF | 100 | |
| 20 | ||
| 1 | ||
| 2 | ||
| GAN-ANN | hidden_layer_sizes. | (20, 20, 5) |
| activation. | [tanh] | |
| solver. | [lbfgs] | |
| max_iter. | 500 |
| ML Model | Tuning Entity | Value |
|---|---|---|
| VAE-SVR | K | RBF |
| C | 20 | |
| ε | 0.01 | |
| γ | 1 | |
| VAE-RF | 100 | |
| 20 | ||
| 1 | ||
| 2 | ||
| VAE-ANN | hidden_layer_sizes. | (80, 10, 20) |
| activation. | [tanh] | |
| solver. | [lbfgs] | |
| max_iter. | 100 |
| ML Model | R2 |
|---|---|
| GAN-SVR | 0.958 |
| GAN-RF | 0.864 |
| GAN-ANN | 0.965 |
| VAE-SVR | 0.979 |
| VAE-RF | 0.968 |
| VAE-ANN | 0.923 |
| ML Model | R2 | MAE (Per Cent) |
|---|---|---|
| GAN-SVR | 0.929 | 1.46 |
| GAN-RF | 0.975 | 1.13 |
| GAN-ANN | 0.919 | 1.62 |
| VAE-SVR | 0.865 | 2.00 |
| VAE-RF | 0.879 | 2.01 |
| VAE-ANN | 0.861 | 2.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Z.; Peng, J.; Zhu, L.; Deng, C.; Zhao, Y.; Guo, Q.; Zhu, A. High-Cycle Fatigue Life Prediction of Additive Manufacturing Inconel 718 Alloy via Machine Learning. Materials 2025, 18, 2604. https://doi.org/10.3390/ma18112604
Song Z, Peng J, Zhu L, Deng C, Zhao Y, Guo Q, Zhu A. High-Cycle Fatigue Life Prediction of Additive Manufacturing Inconel 718 Alloy via Machine Learning. Materials. 2025; 18(11):2604. https://doi.org/10.3390/ma18112604
Chicago/Turabian StyleSong, Zongxian, Jinling Peng, Lina Zhu, Caiyan Deng, Yangyang Zhao, Qingya Guo, and Angran Zhu. 2025. "High-Cycle Fatigue Life Prediction of Additive Manufacturing Inconel 718 Alloy via Machine Learning" Materials 18, no. 11: 2604. https://doi.org/10.3390/ma18112604
APA StyleSong, Z., Peng, J., Zhu, L., Deng, C., Zhao, Y., Guo, Q., & Zhu, A. (2025). High-Cycle Fatigue Life Prediction of Additive Manufacturing Inconel 718 Alloy via Machine Learning. Materials, 18(11), 2604. https://doi.org/10.3390/ma18112604






