Enhanced Thermoelectric Properties of Phosphorene via Quantum Size Effects and Relaxation Time Tuning
Abstract
1. Introduction
2. Computational Details
3. Results and Discussion
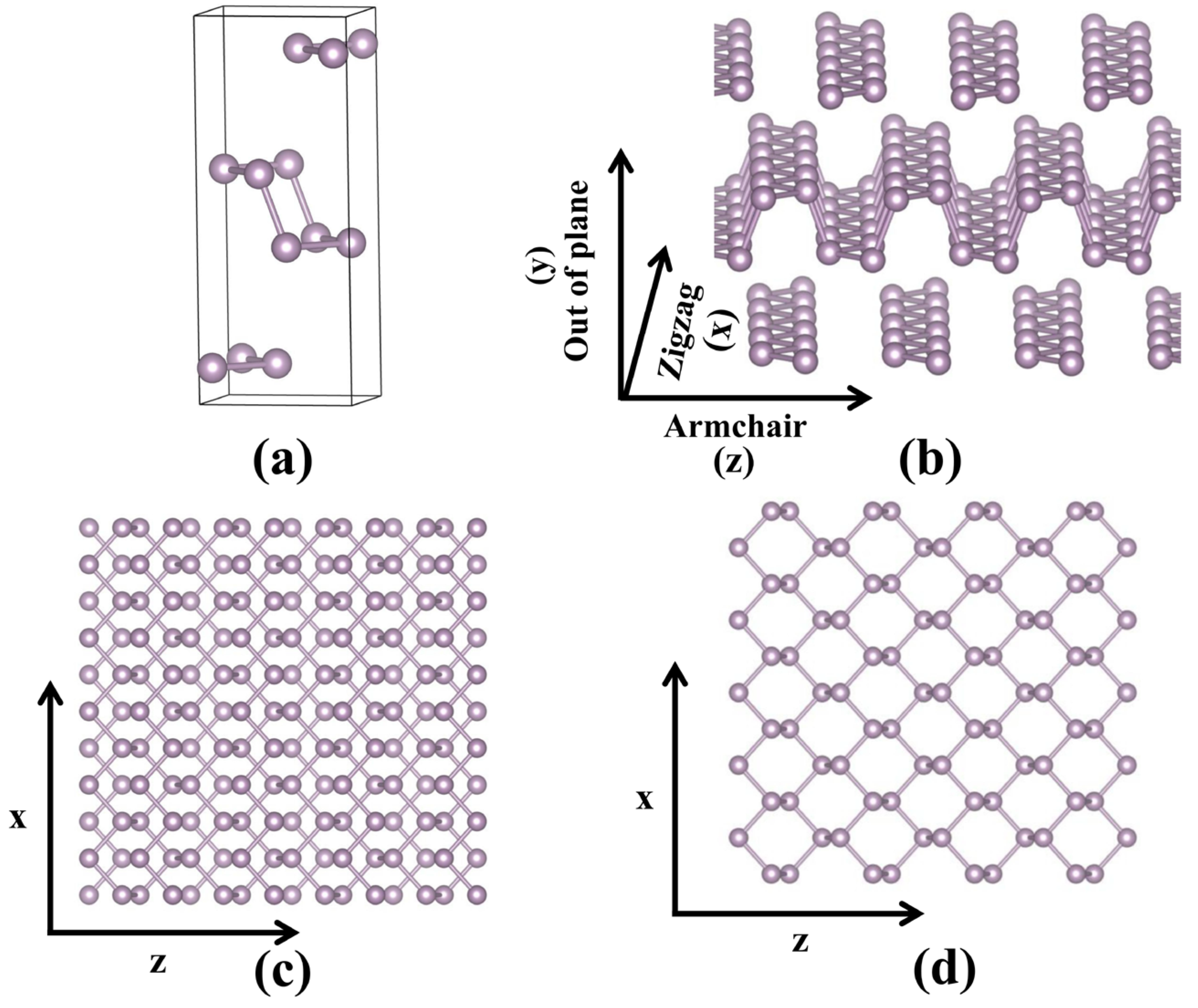
3.1. Crystal Structure and Electronic Properties
3.2. Transport Coefficients
3.3. Thermoelectric Figure of Merit
3.4. Further Optimized ZT Values of Phosphorene
4. Summary
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hromadová, L.; Martoňák, R.; Tosatti, E. Structure change, layer sliding, and metallization in high-pressure MoS2. Phys. Rev. B 2013, 87, 144105. [Google Scholar] [CrossRef]
- Tan, G.; Zhao, L.D.; Kanatzidis, M.G. Rationally Designing High-Performance Bulk Thermoelectric Materials. Chem. Rev. 2016, 116, 12123–12149. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.; Zhao, L.D. Seeking new, highly effective thermoelectrics. Science 2020, 367, 1196–1197. [Google Scholar] [CrossRef] [PubMed]
- Nolas, G.S.; Sharp, J.W.; Goldsmid, H.J. Thermoelectrics—Basic Principles and New Materials Developments; Springer Science & Business Media: Berlin, Germany, 2001. [Google Scholar]
- Zhou, W.X.; Cheng, Y.; Chen, K.Q.; Xie, G.; Wang, T.; Zhang, G. Thermal Conductivity of Amorphous Materials. Adv. Funct. Mater. 2019, 30, 1903829. [Google Scholar] [CrossRef]
- Sales, B.C.; Mandrus, D.; Williams, R.K. Filled Skutterudite Antimonides: A New Class of Thermoelectric Materials. Science 1996, 272, 1325–1328. [Google Scholar] [CrossRef]
- Heremans, J.P.; Jovovic, V.; Toberer, E.S.; Saramat, A.; Kurosaki, K.; Charoenphakdee, A.; Yamanaka, S.; Snyder, G.J. Enhancement of Thermoelectric Efficiency in PbTe by Distortion of the Electronic Density of States. Science 2008, 321, 554–557. [Google Scholar] [CrossRef]
- Pei, Y.; Shi, X.; LaLonde, A.; Wang, H.; Chen, L.; Snyder, G.J. Convergence of electronic bands for high performance bulk thermoelectrics. Nature 2011, 473, 66–69. [Google Scholar] [CrossRef]
- Liu, W.; Tan, X.; Yin, K.; Liu, H.; Tang, X.; Shi, J.; Zhang, Q.; Uher, C. Convergence of Conduction Bands as a Means of Enhancing Thermoelectric Performance of n-Type Mg2 Si1-x Snx Solid Solutions. Phys. Rev. Lett. 2012, 108, 166601. [Google Scholar] [CrossRef]
- Biswas, K.; He, J.; Blum, I.D.; Wu, C.I.; Hogan, T.P.; Seidman, D.N.; Dravid, V.P.; Kanatzidis, M.G. High-performance bulk thermoelectrics with all-scale hierarchical architectures. Nature 2012, 489, 414–418. [Google Scholar] [CrossRef]
- Zhao, L.; He, J.; Bérardan, D.; Lin, Y.; Li, J.-F.; Nan, C.W.; Dragoe, N. BiCuSeO Oxyselenides: New Promising Thermoelectric Materials. Energy Environ. Sci. 2014, 7, 2900–2924. [Google Scholar] [CrossRef]
- Morelli, D.T.; Jovovic, V.; Heremans, J.P. Intrinsically Minimal Thermal Conductivity in Cubic I-V-VI2 Semiconductors. Phys. Rev. Lett. 2008, 101, 035901. [Google Scholar] [CrossRef] [PubMed]
- Venkatasubramanian, R.; Siivola, E.; Colpitts, T.; O’Quinn, B. Thin-film thermoelectric devices with high room-temperature figures of merit. Nature 2001, 413, 597–602. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Gibbs, Z.M.; Agapito, L.A.; Li, G.; Kim, H.-S.; Nardelli, M.B.; Curtarolo, S.; Snyder, G.J. Convergence of multi-valley bands as the electronic origin of high thermoelectric performance in CoSb3 skutterudites. Nat. Mater. 2015, 14, 1223–1228. [Google Scholar] [CrossRef]
- Hsu, K.F.; Loo, S.; Guo, F.; Chen, W.; Dyck, J.S.; Uher, C.; Hogan, T.; Polychroniadis, E.K.; Kanatzidis, M.G. Cubic AgPbm SbTe2+m: Bulk Thermoelectric Materials with High Figure of Merit. Science 2004, 303, 818–821. [Google Scholar] [CrossRef]
- Fei, R.; Faghaninia, A.; Soklaski, R.; Yan, J.-A.; Lo, C.; Yang, L. Enhanced Thermoelectric Efficiency via Orthogonal Electrical and Thermal Conductances in Phosphorene. Nano Lett. 2014, 14, 6393–6399. [Google Scholar] [CrossRef]
- Lv, H.Y.; Lu, W.J.; Shao, D.F.; Sun, Y.P. Enhanced thermoelectric performance of phosphorene by strain-induced band convergence. Phys. Rev. B 2014, 90, 085433. [Google Scholar] [CrossRef]
- Lv, H.-y.; Lu, W.J.; Shao, D.-F.; Sun, Y.P. Large thermoelectric power factors in black phosphorus and phosphorene. arXiv 2014. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, H.J.; Cheng, L.; Wei, J.; Liang, J.H.; Fan, D.D.; Jiang, P.H.; Sun, L.; Shi, J. High thermoelectric performance can be achieved in black phosphorus. J. Mater. Chem. C 2016, 4, 991–998. [Google Scholar] [CrossRef]
- Jang, H.; Wood, J.D.; Ryder, C.R.; Hersam, M.C.; Cahill, D.G. Anisotropic Thermal Conductivity of Exfoliated Black Phosphorus. Adv. Mater. 2016, 27, 8017–8022. [Google Scholar] [CrossRef]
- Duan, S.; Cui, Y.; Chen, X.; Yi, W.; Liu, Y.; Liu, X. Ultrahigh Thermoelectric Performance Realized in Black Phosphorus System by Favorable Band Engineering through Group VA Doping. Adv. Funct. Mater. 2019, 29, 1904346. [Google Scholar] [CrossRef]
- Liu, H.; Neal, A.T.; Zhu, Z.; Luo, Z.; Xu, X.; Tománek, D.; Ye, P.D. Phosphorene: An Unexplored 2D Semiconductor with a High Hole Mobility. ACS Nano 2014, 8, 4033–4041. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.; Lee, S.; Yoon, J.-Y.; Cheon, J.; Jeong, H.Y.; Kim, K. Fabrication and Imaging of Monolayer Phosphorene with Preferred Edge Configurations via Graphene-Assisted Layer-by-Layer Thinning. Nano Lett. 2020, 20, 559–566. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B Condens. Matter 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Payne, M.C.; Teter, M.P.; Allan, D.C.; Arias, T.A.; Joannopoulos, J.D. Iterative minimization techniques for ab initio total-energy calculations: Molecular dynamics and conjugate gradients. Rev. Mod. Phys. 1992, 64, 1045. [Google Scholar] [CrossRef]
- Madsen, G.K.H.; Singh, D.J. BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 2006, 175, 67–71. [Google Scholar] [CrossRef]
- Bardeen, J.; Shockley, W. Deformation Potentials and Mobilities in Non-Polar Crystals. Phys. Rev. 1950, 80, 72–80. [Google Scholar] [CrossRef]
- Qiao, J.; Kong, X.; Hu, Z.-X.; Yang, F.; Ji, W. High-mobility transport anisotropy and linear dichroism in few-layer black phosphorus. Nat. Commun. 2014, 5, 4475. [Google Scholar] [CrossRef]
- Xi, J.; Long, M.; Tang, L.; Wang, D.; Shuai, Z. First-principles prediction of charge mobility in carbon and organic nanomaterials. Nanoscale 2012, 4, 4348–4369. [Google Scholar] [CrossRef]
- Ashcroft, N.W.; Mermin, N.D.; Smoluchowski, R. Solid State Physics. Phys. Today 1977, 30, 61–65. [Google Scholar] [CrossRef]
- Lv, H.Y.; Liu, H.J.; Shi, J.; Tang, X.F.; Uher, C. Optimized thermoelectric performance of Bi2Te3 nanowires. J. Mater. Chem. A 2013, 1, 6831–6838. [Google Scholar] [CrossRef]
- Togo, A.; Oba, F.; Tanaka, I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B 2008, 78, 134106. [Google Scholar] [CrossRef]
- Li, W.; Carrete, J.A.; Katcho, N.; Mingo, N. ShengBTE: A solver of the Boltzmann transport equation for phonons. Comput. Phys. Commun. 2014, 185, 1747–1758. [Google Scholar] [CrossRef]
- Cartz, L.; Srinivasa, S.R.; Riedner, R.J.; Jorgensen, J.D.; Worlton, T.G. Effect of pressure on bonding in black phosphorus. J. Chem. Phys. 2008, 71, 1718–1721. [Google Scholar] [CrossRef]
- Cui, Y.-F.; Duan, S.; Chen, X.; Yang, M.-M.; Yang, B.-C.; Yi, W.-C.; Liu, X.-B. Prediction of enhanced thermoelectric performance in two-dimensional black phosphorus nanosheets. Vacuum 2021, 183, 109790. [Google Scholar] [CrossRef]
- Yang, J.; Yang, G.; Zhang, G.; Wang, Y.X. Low effective mass leading to an improved ZT value by 32% for n-type BiCuSeO: A first-principles study. J. Mater. Chem. A 2014, 2, 13923–13931. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, G.; Hou, Z.; Yang, B.; Zhang, X.; Liu, E.; Xi, X.; Liu, Z.; Zeng, Z.; Wang, W.; et al. Large anisotropic thermal transport properties observed in bulk single crystal black phosphorus. Appl. Phys. Lett. 2016, 108, 092102. [Google Scholar] [CrossRef]
- Cutler, M.; Leavy, J.F.; Fitzpatrick, R.L. Electronic Transport in Semimetallic Cerium Sulfide. Phys. Rev. 1964, 133, A1143–A1152. [Google Scholar] [CrossRef]
- Qin, G.; Yan, Q.B.; Qin, Z.; Yue, S.Y.; Hu, M.; Su, G. Anisotropic intrinsic lattice thermal conductivity of phosphorene from first principles. Phys. Chem. Chem. Phys. 2015, 17, 4854–4858. [Google Scholar] [CrossRef]
- Mamori, H.; Mouatassim, H.; Zaari, H.; Benyoussef, A.; El Kenz, A.; Taleb, A.; Caballero-Briones, F.; Mounkachi, O. A DFT study for improving the thermoelectric efficiency in AB bilayer phosphorene using uniaxial strain. Comput. Mater. Sci. 2024, 244, 113182. [Google Scholar] [CrossRef]
- Zhang, W.; Li, F.; Hu, J.; Zhang, P.; Yin, J.; Tang, X.; Jiang, Y.; Wu, B.; Ding, Y. Strain engineering on transmission carriers of monolayer phosphorene. J. Phys. Condens. Matter 2017, 29, 465501. [Google Scholar] [CrossRef] [PubMed]
- Pandit, A.; Hamad, B. Thermoelectric and lattice dynamics properties of layered MX (M = Sn, Pb; X = S, Te) compounds. Appl. Surf. Sci. 2021, 538, 147911. [Google Scholar] [CrossRef]
- Song, J.; Sun, M. Modulating Thermoelectric Properties of the MoSe2/WSe2 Superlattice Heterostructure by Twist Angles. ACS Appl. Mater. Interfaces 2024, 16, 3325–3333. [Google Scholar] [CrossRef] [PubMed]










| Materials | Reference | a (Å) | b (Å) | c (Å) |
|---|---|---|---|---|
| Phosphorus | Experiment [35] | 3.31 | 10.47 | 4.37 |
| This work | 3.31 | 11.30 | 4.56 | |
| Phosphorene | This work | 3.30 | 4.62 |
| Carrier Type | m* (me) | C3D (J/m3) | |E1| (eV) | (fs) |
|---|---|---|---|---|
| e (Zigzag) | 1.27 | 87.90 | 5.91 | 61.32 |
| h (Zigzag) | 1.42 | 87.90 | 1.36 | 979.44 |
| e (Armchair) | 0.16 | 21.23 | 2.91 | 1332.75 |
| h (Armchair) | 0.15 | 21.23 | 4.78 | 582.58 |
| e (Out of plane) | 0.21 | 6.58 | 7.05 | 47.72 |
| h (Out of plane) | 0.44 | 6.58 | 9.20 | 9.29 |
| Carrier Type | m* (me) | C2D (J/m2) | |E1| (eV) | (fs) |
|---|---|---|---|---|
| e (Zigzag) | 1.24 | 51.56 | 5.29 | 11.99 |
| h (Zigzag) | 2.94 | 51.56 | 0.28 | 1735.37 |
| e (Armchair) | 0.18 | 12.18 | 1.44 | 261.83 |
| h (Armchair) | 0.17 | 12.18 | 2.7 | 80.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Zhang, C.; Ge, G.; Yang, G.; Yang, J. Enhanced Thermoelectric Properties of Phosphorene via Quantum Size Effects and Relaxation Time Tuning. Materials 2025, 18, 2506. https://doi.org/10.3390/ma18112506
Sun Z, Zhang C, Ge G, Yang G, Yang J. Enhanced Thermoelectric Properties of Phosphorene via Quantum Size Effects and Relaxation Time Tuning. Materials. 2025; 18(11):2506. https://doi.org/10.3390/ma18112506
Chicago/Turabian StyleSun, Zhiqian, Chenkai Zhang, Guixian Ge, Gui Yang, and Jueming Yang. 2025. "Enhanced Thermoelectric Properties of Phosphorene via Quantum Size Effects and Relaxation Time Tuning" Materials 18, no. 11: 2506. https://doi.org/10.3390/ma18112506
APA StyleSun, Z., Zhang, C., Ge, G., Yang, G., & Yang, J. (2025). Enhanced Thermoelectric Properties of Phosphorene via Quantum Size Effects and Relaxation Time Tuning. Materials, 18(11), 2506. https://doi.org/10.3390/ma18112506





