Construction and Application of a Quantitative Perforation Erosion Model Based on Field Experiments
Abstract
1. Introduction
2. Field-Scale Perforation Erosion Experiments
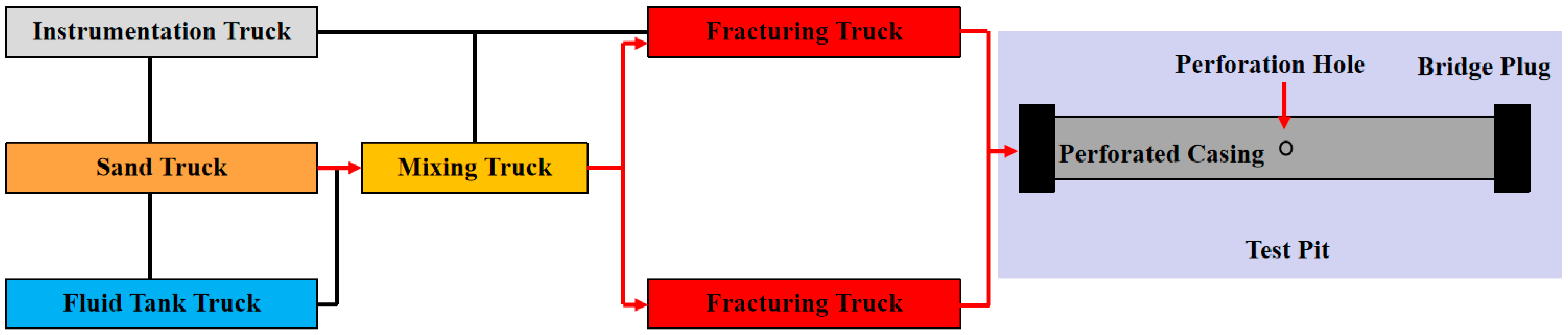
2.1. Design of the Field-Scale High-Intensity Perforation Erosion System
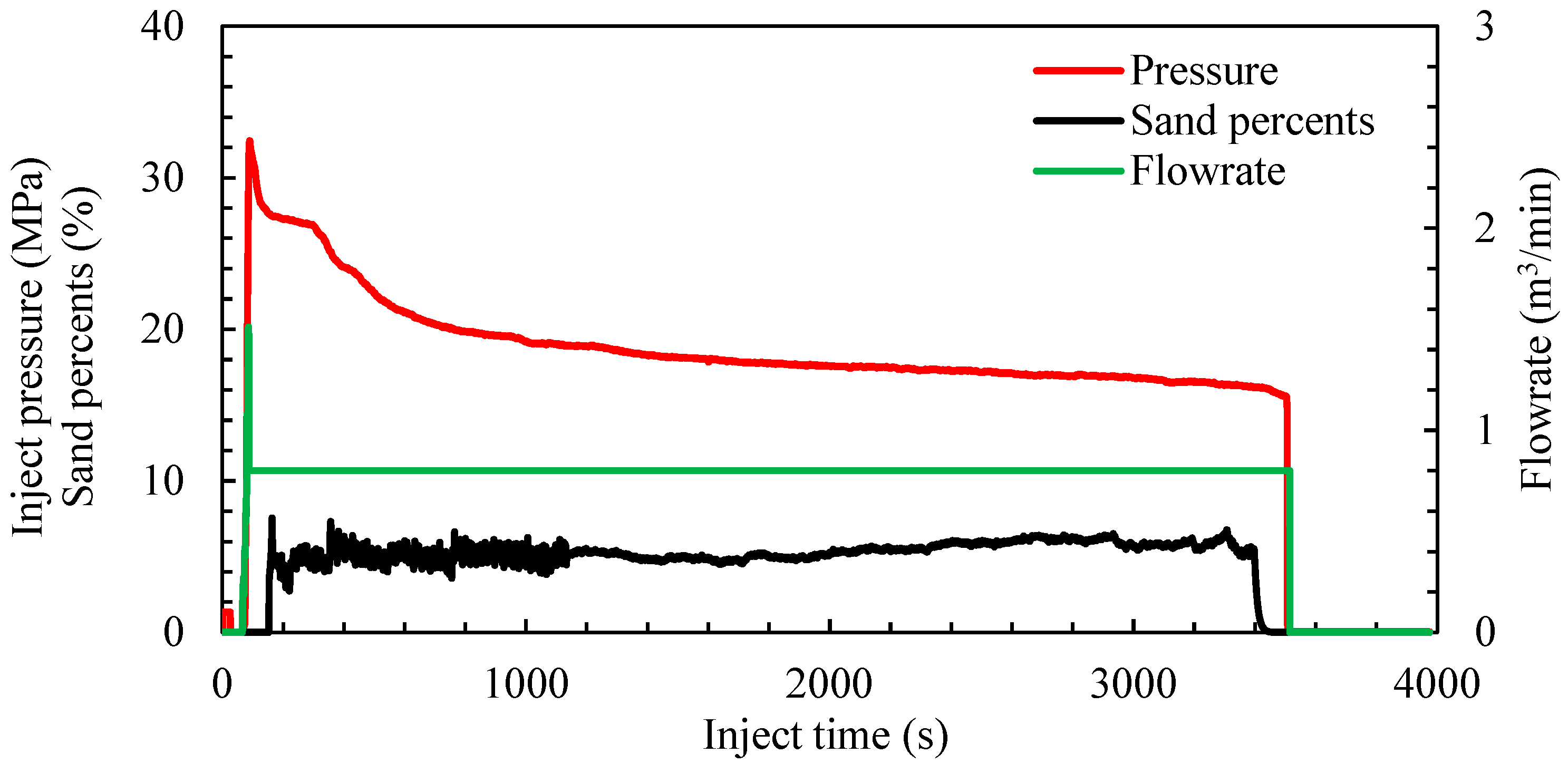
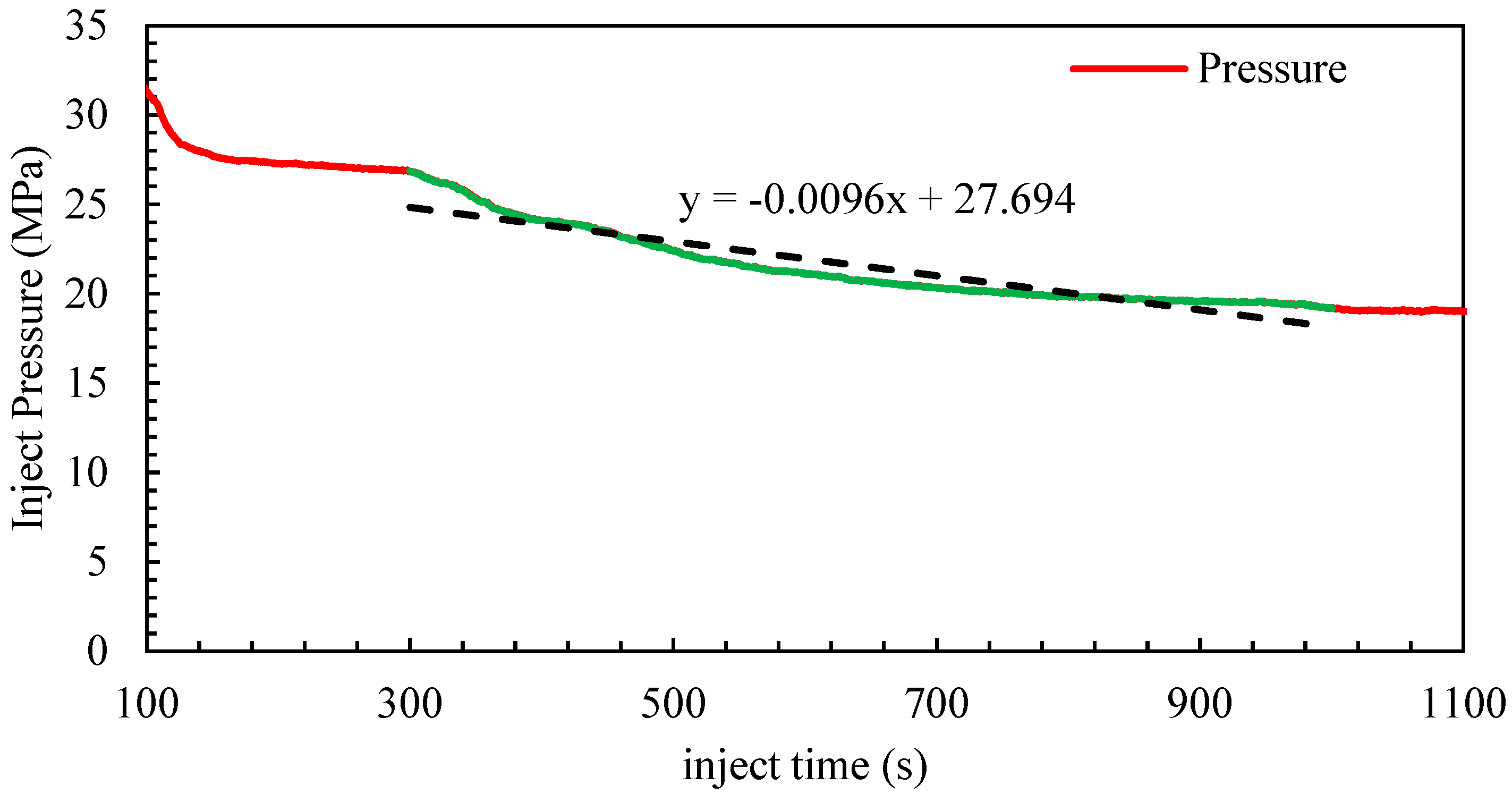
2.2. Experimental Methods and Procedures
3. Perforation Erosion Model
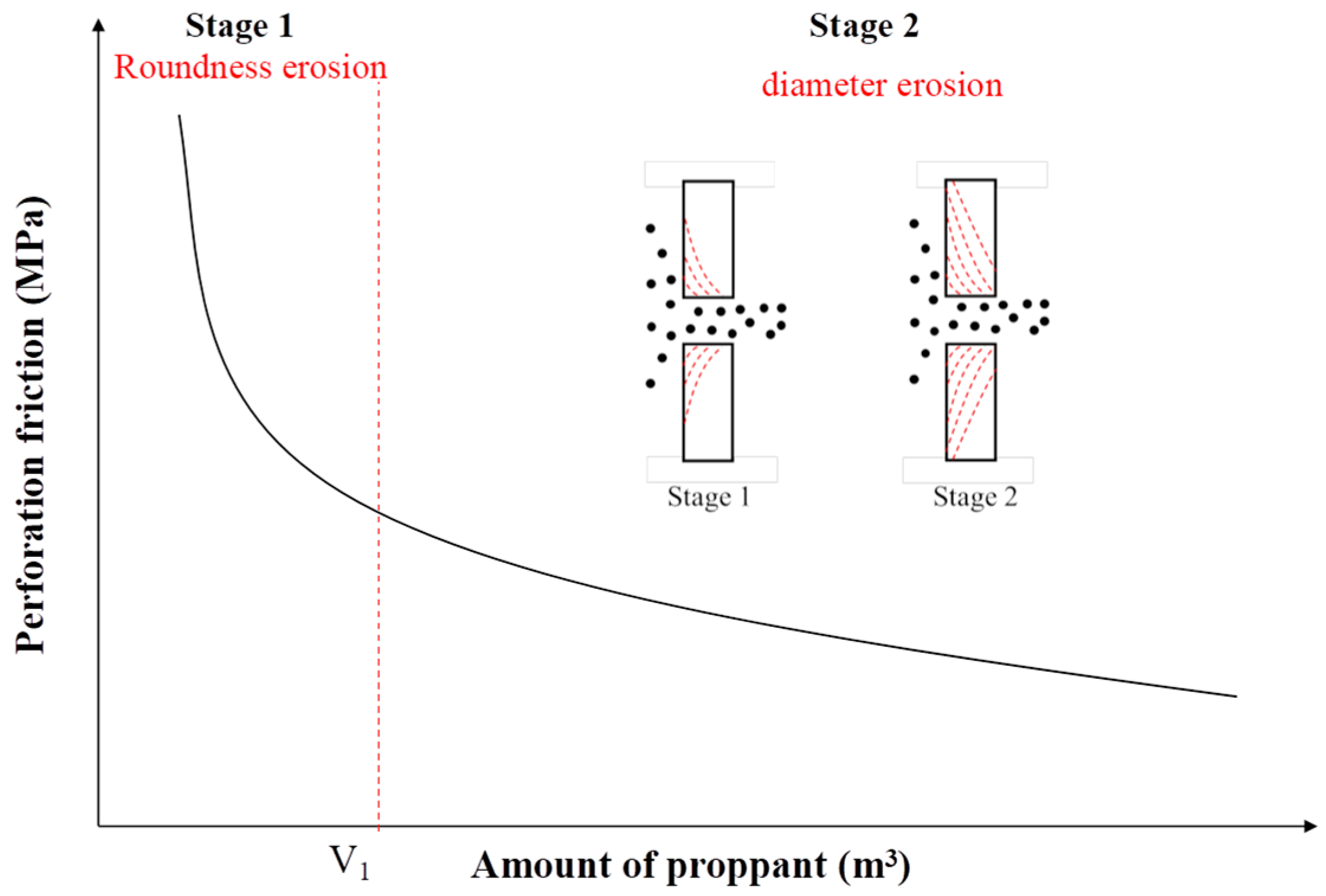
3.1. Construction of the Perforation Erosion Prediction Model
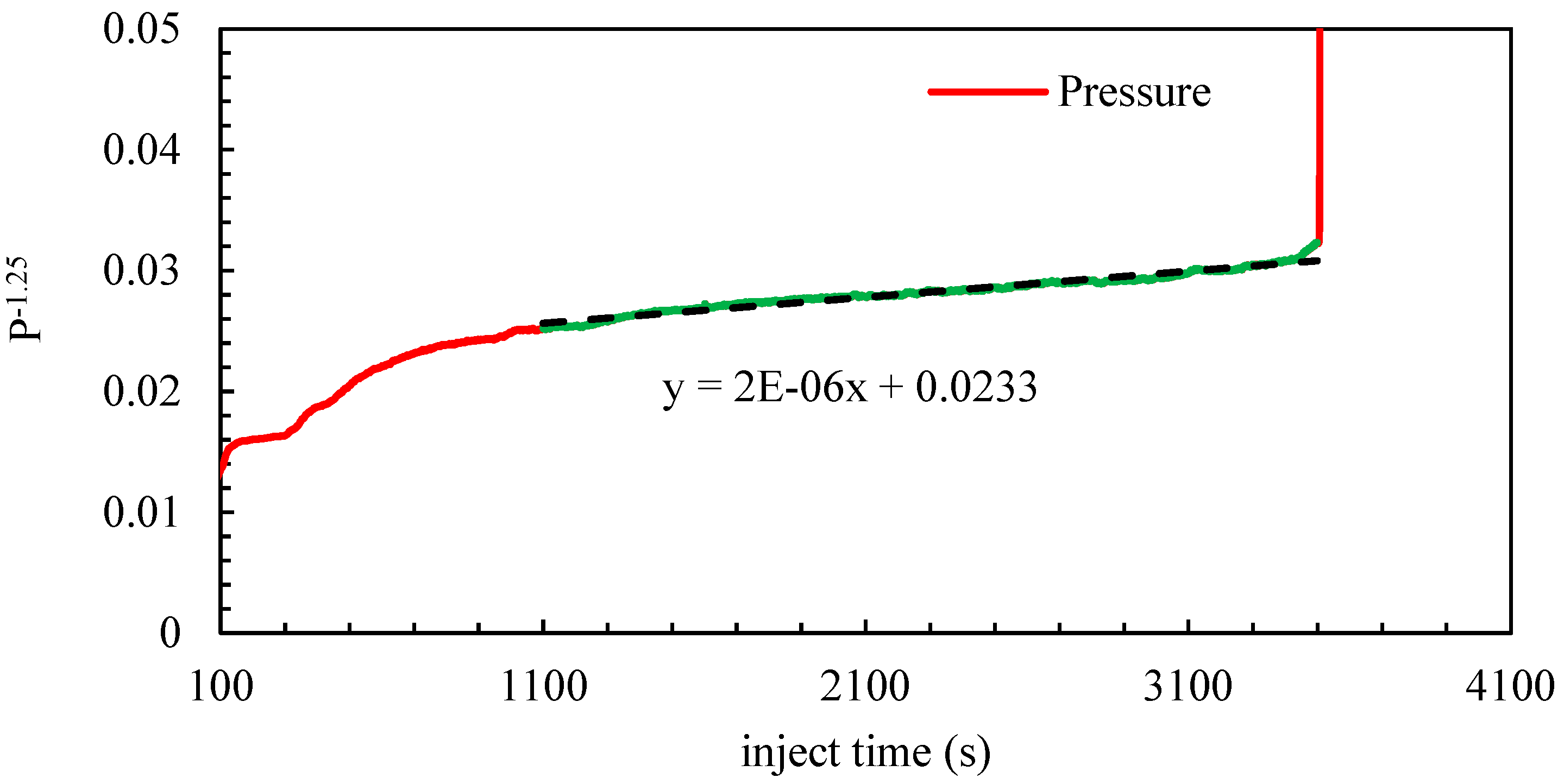
3.2. Calculation of α and β Based on Experimental Data
4. Quantitative Characteristics of Perforation Erosion
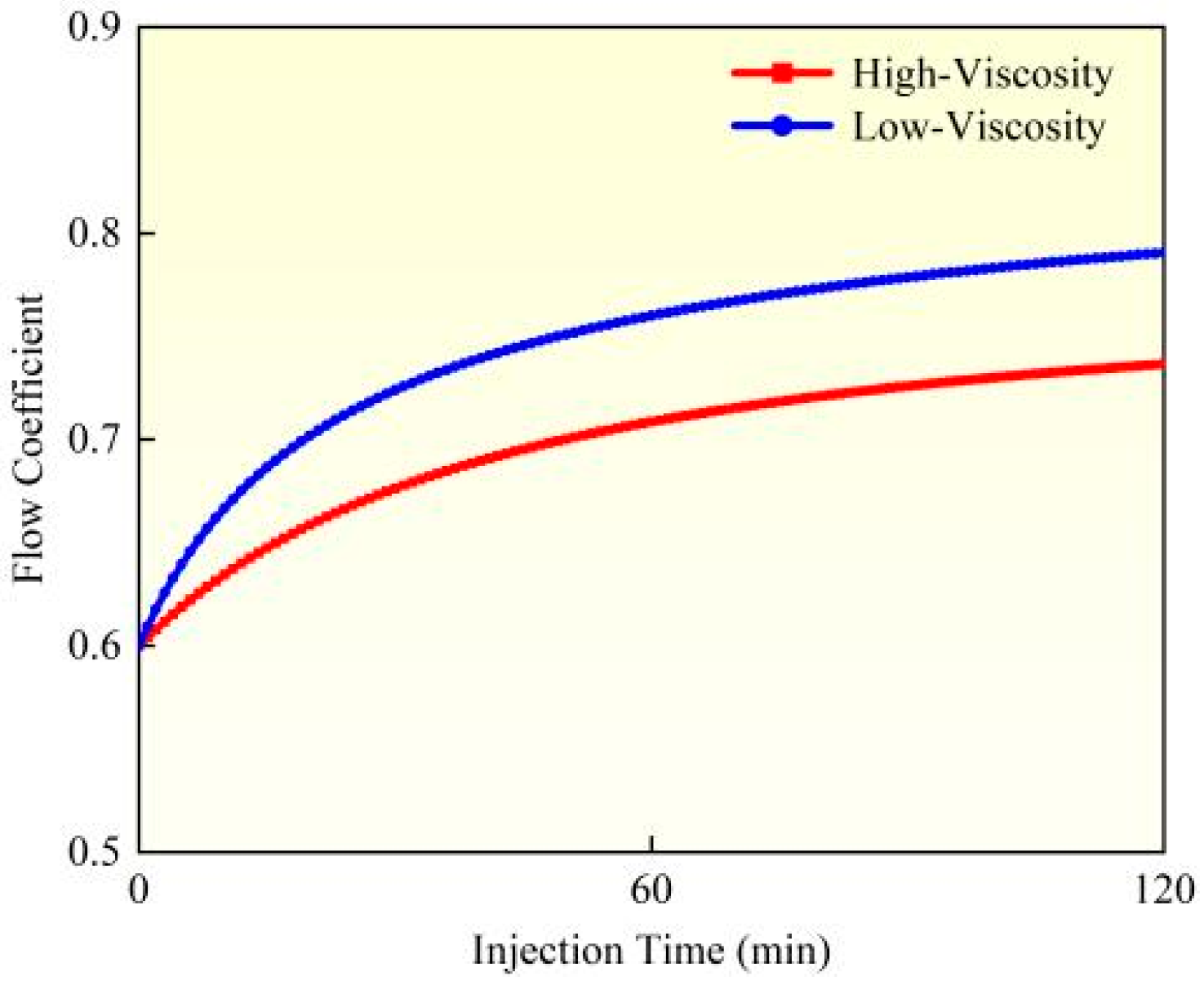
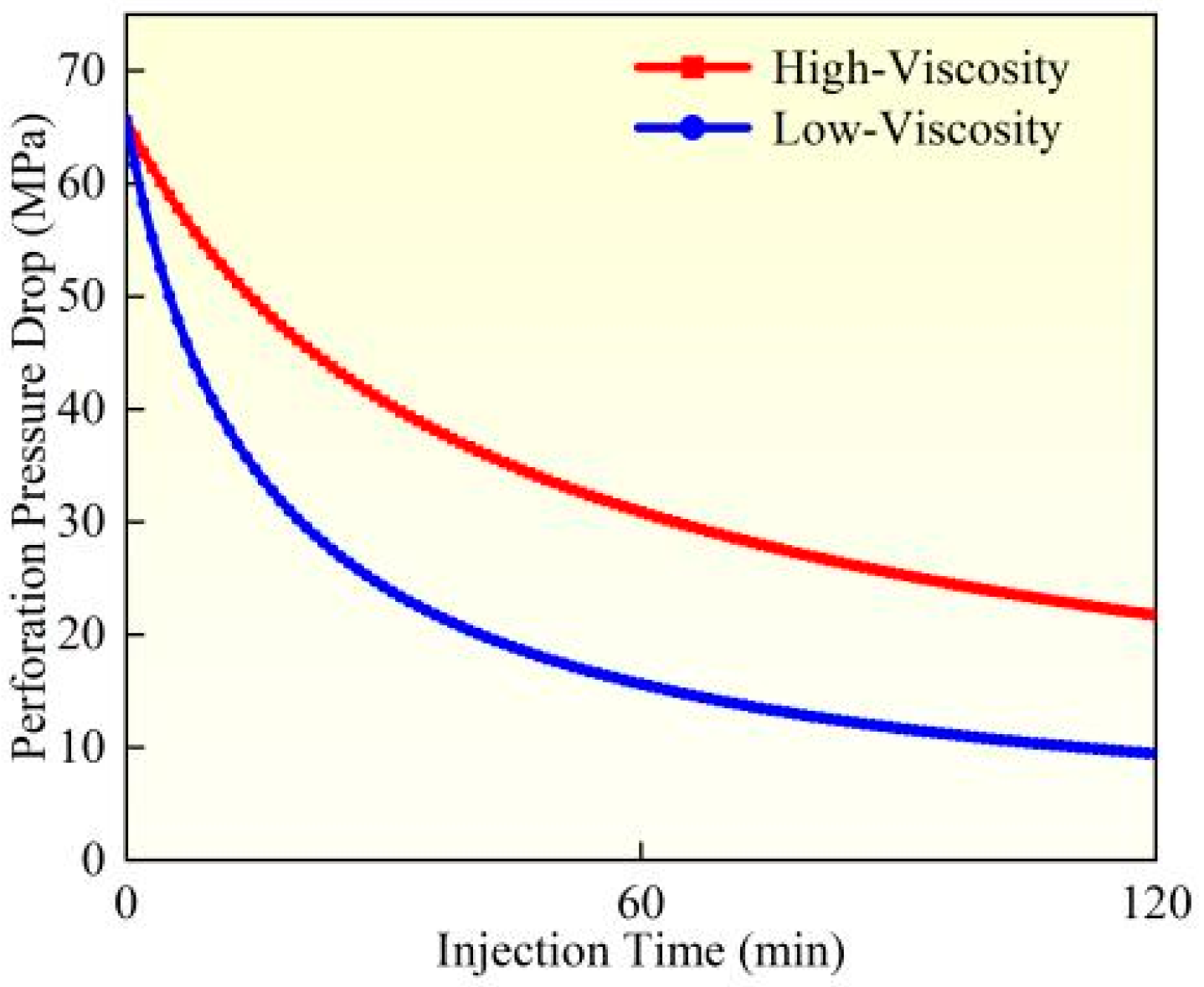
4.1. Perforation Erosion Under Different Fluid Viscosities
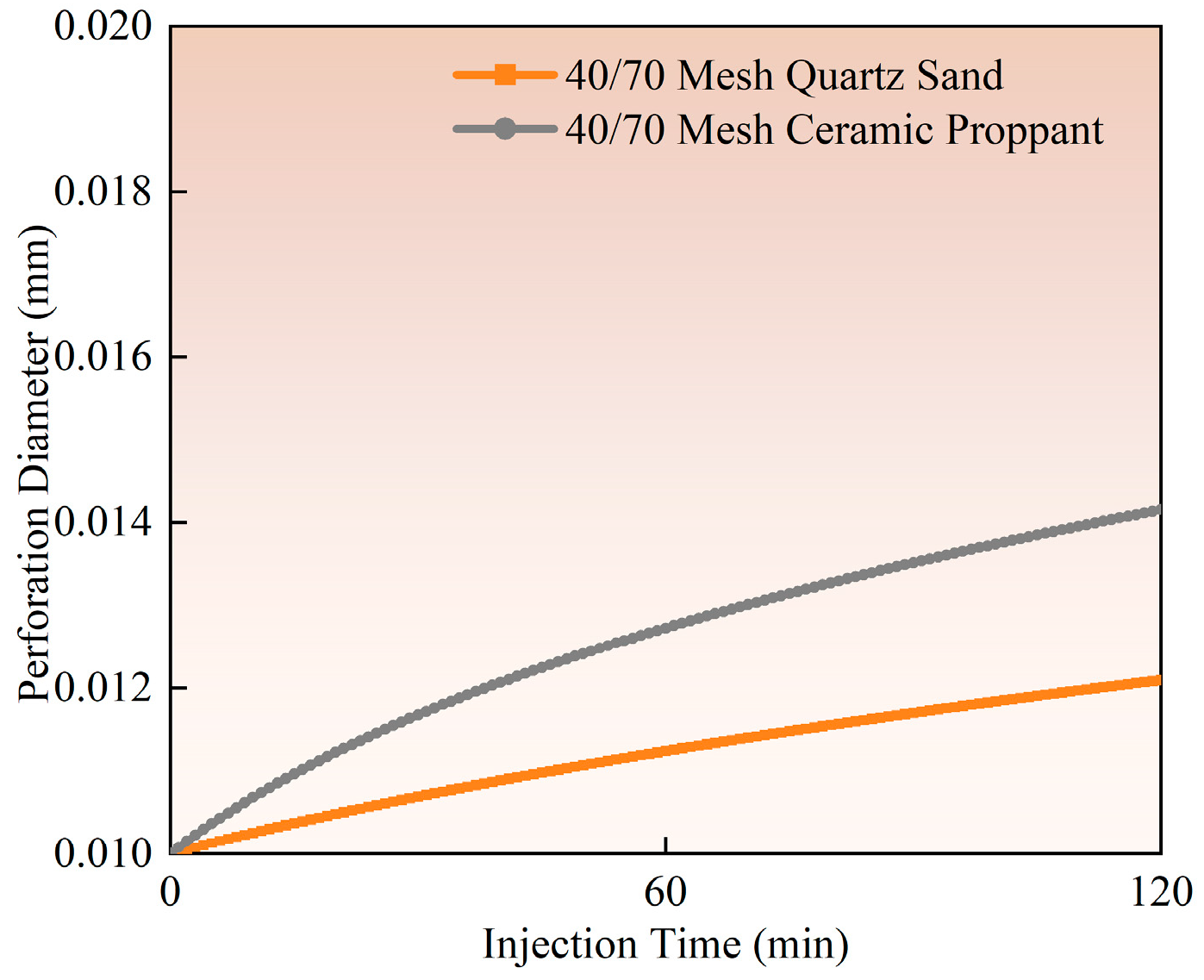
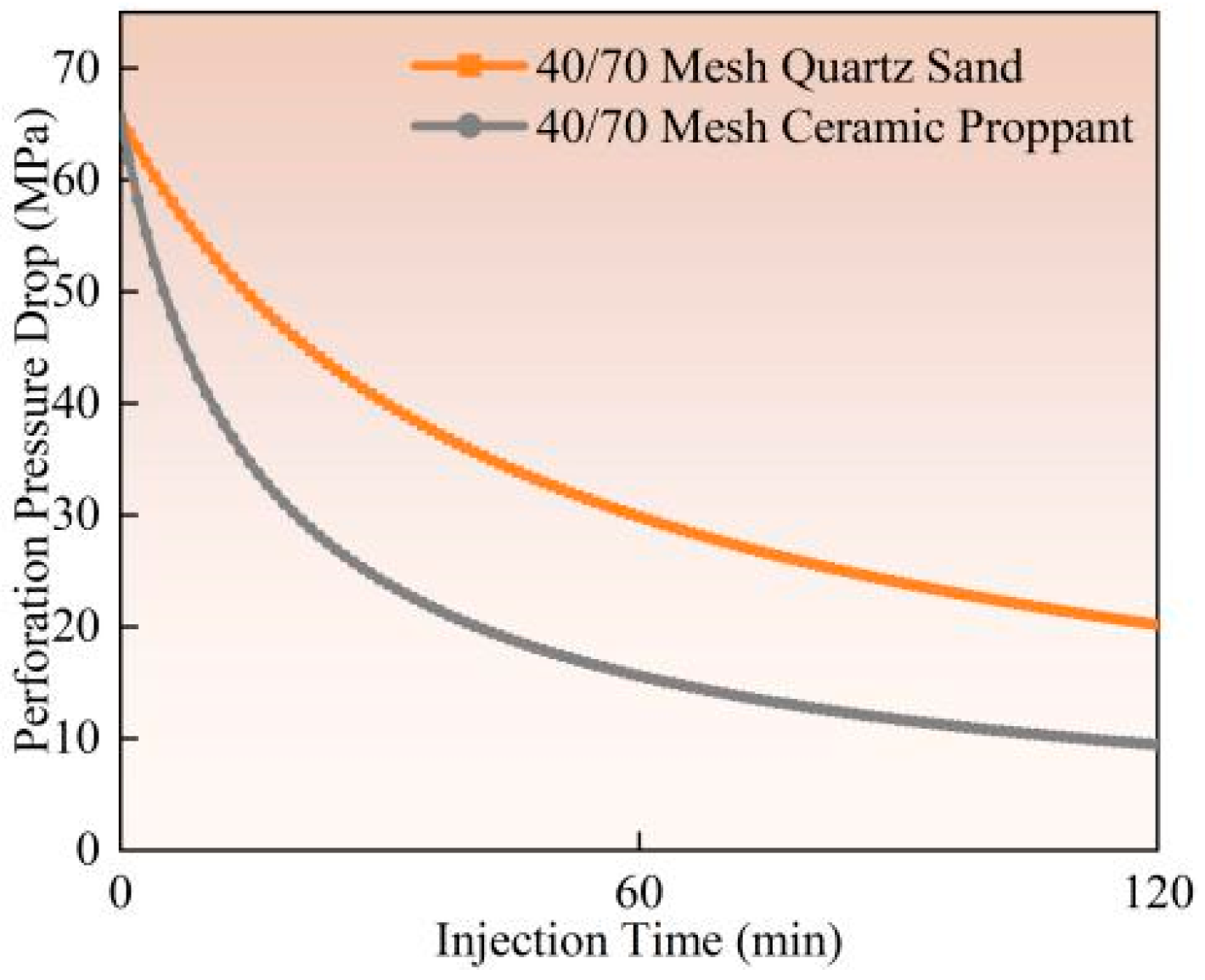
4.2. Perforation Erosion Under Different Proppant Types
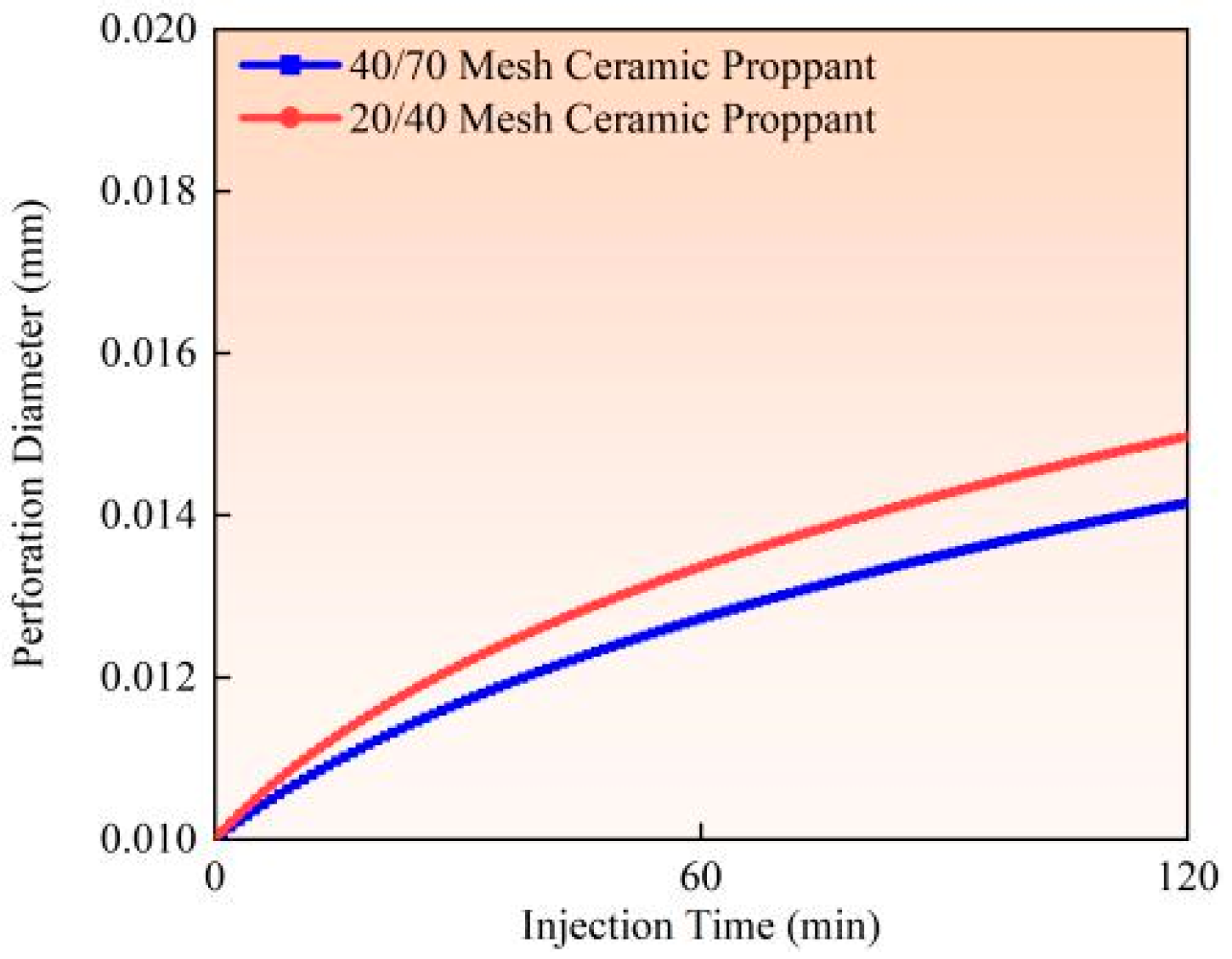
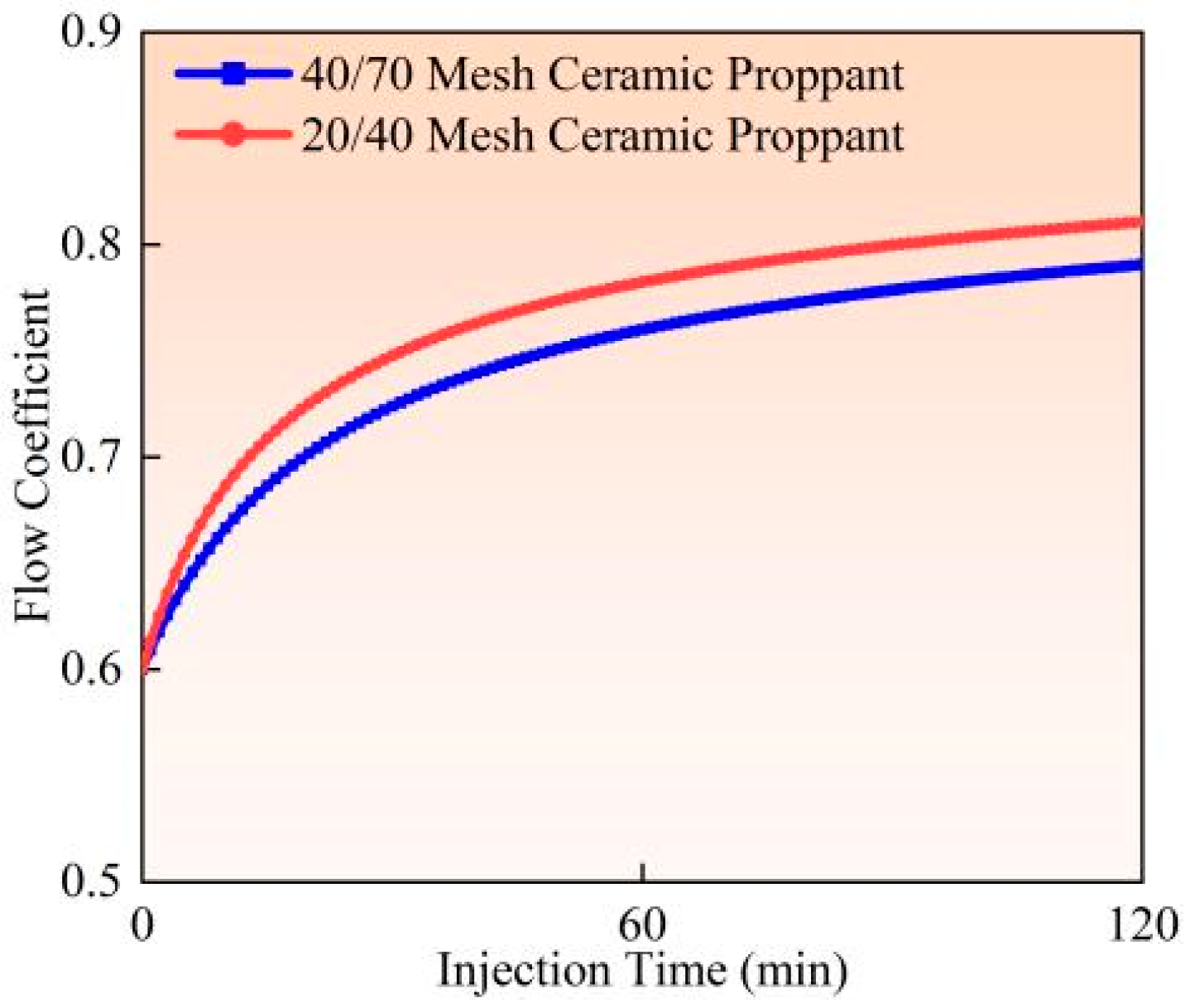
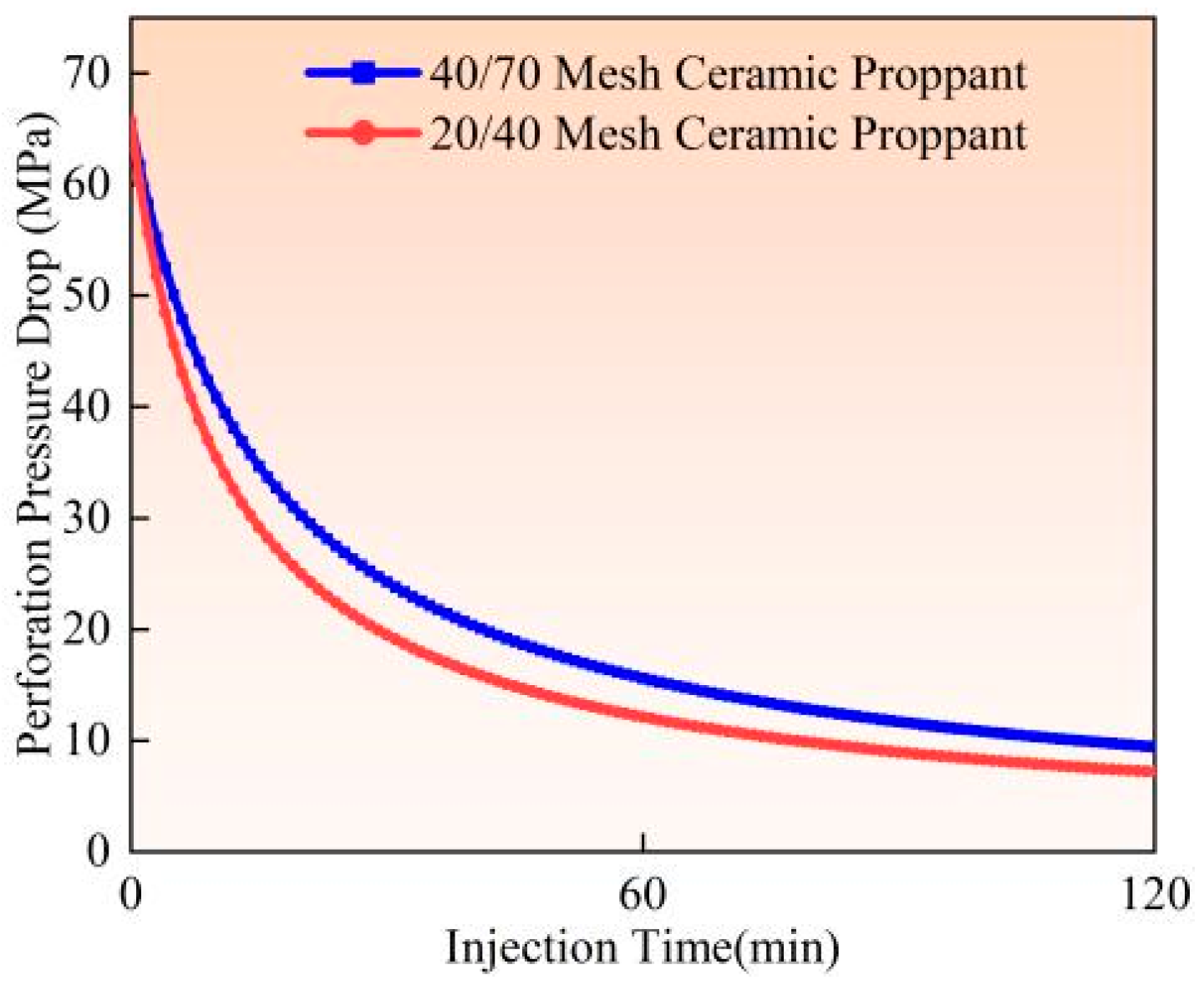
4.3. Perforation Erosion Under Different Proppant Sizes
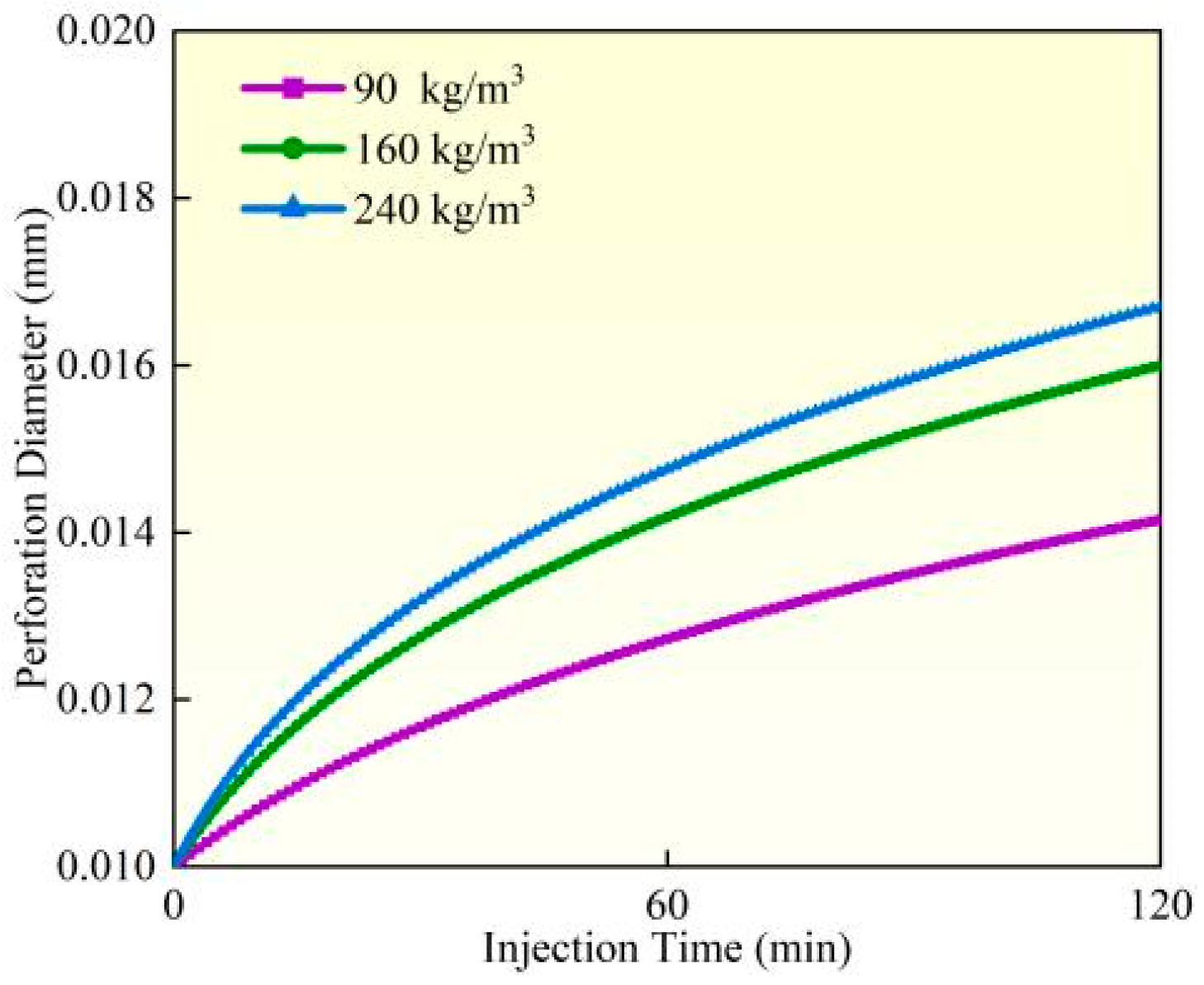
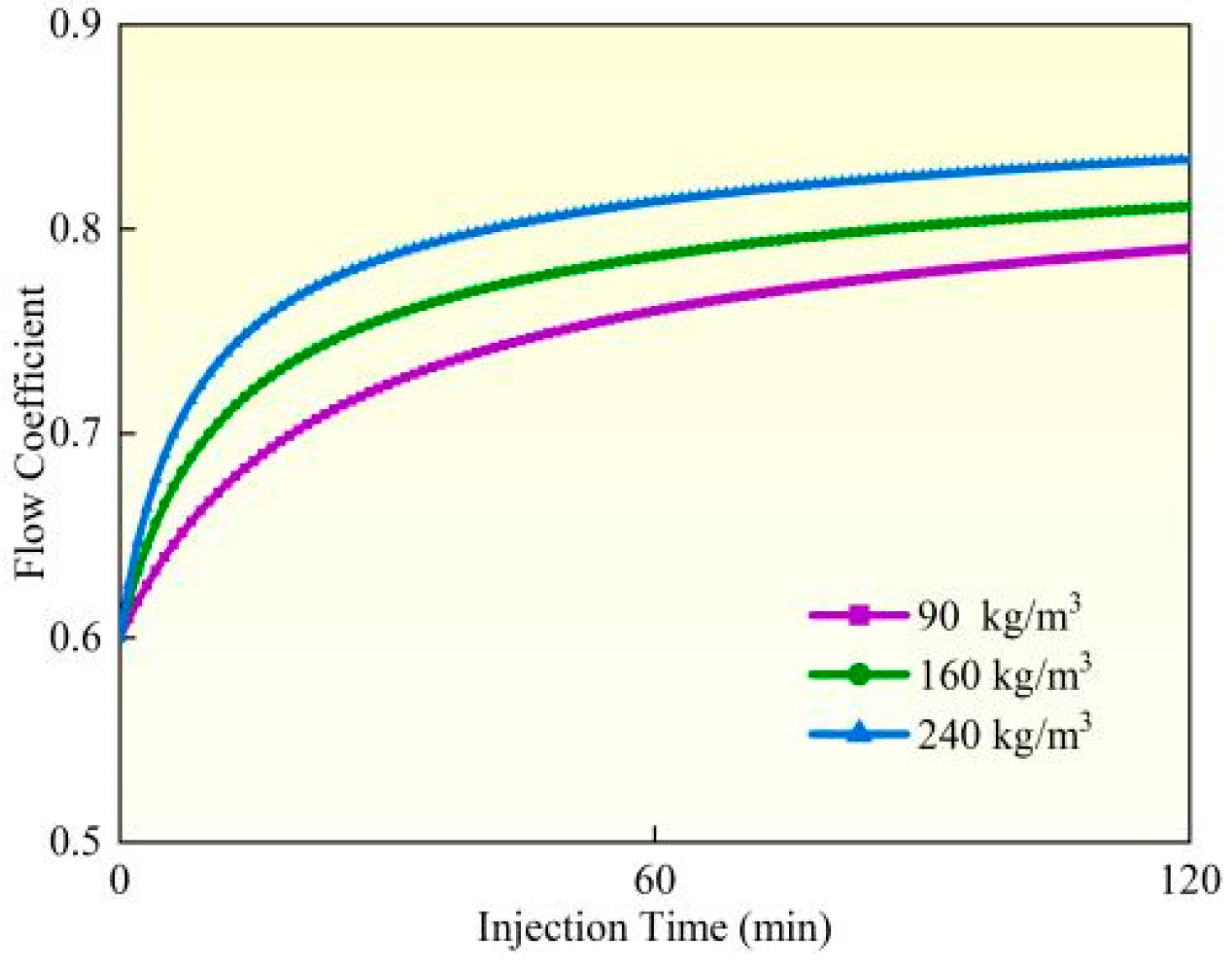
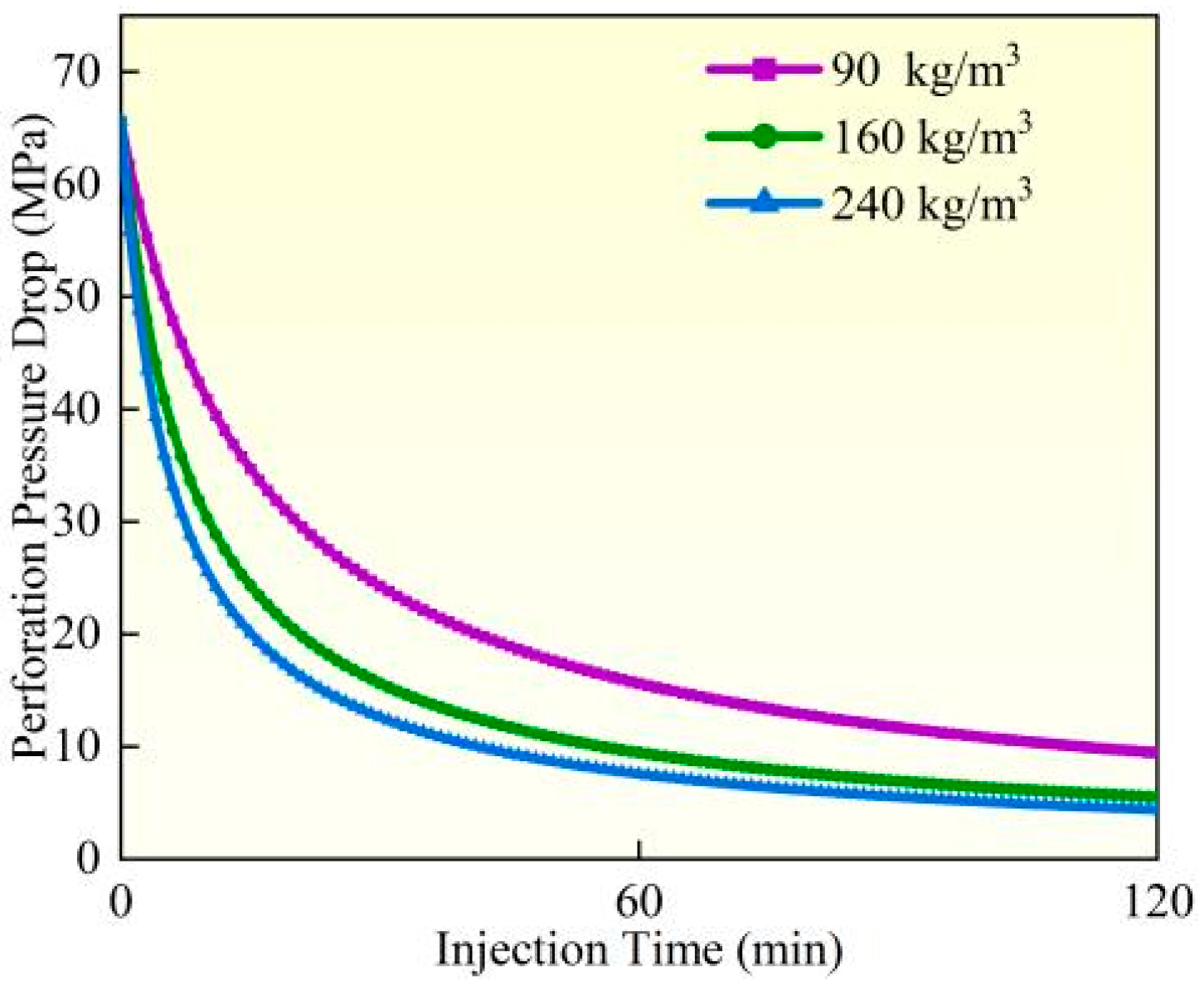
4.4. Perforation Erosion Under Different Sand Concentrations
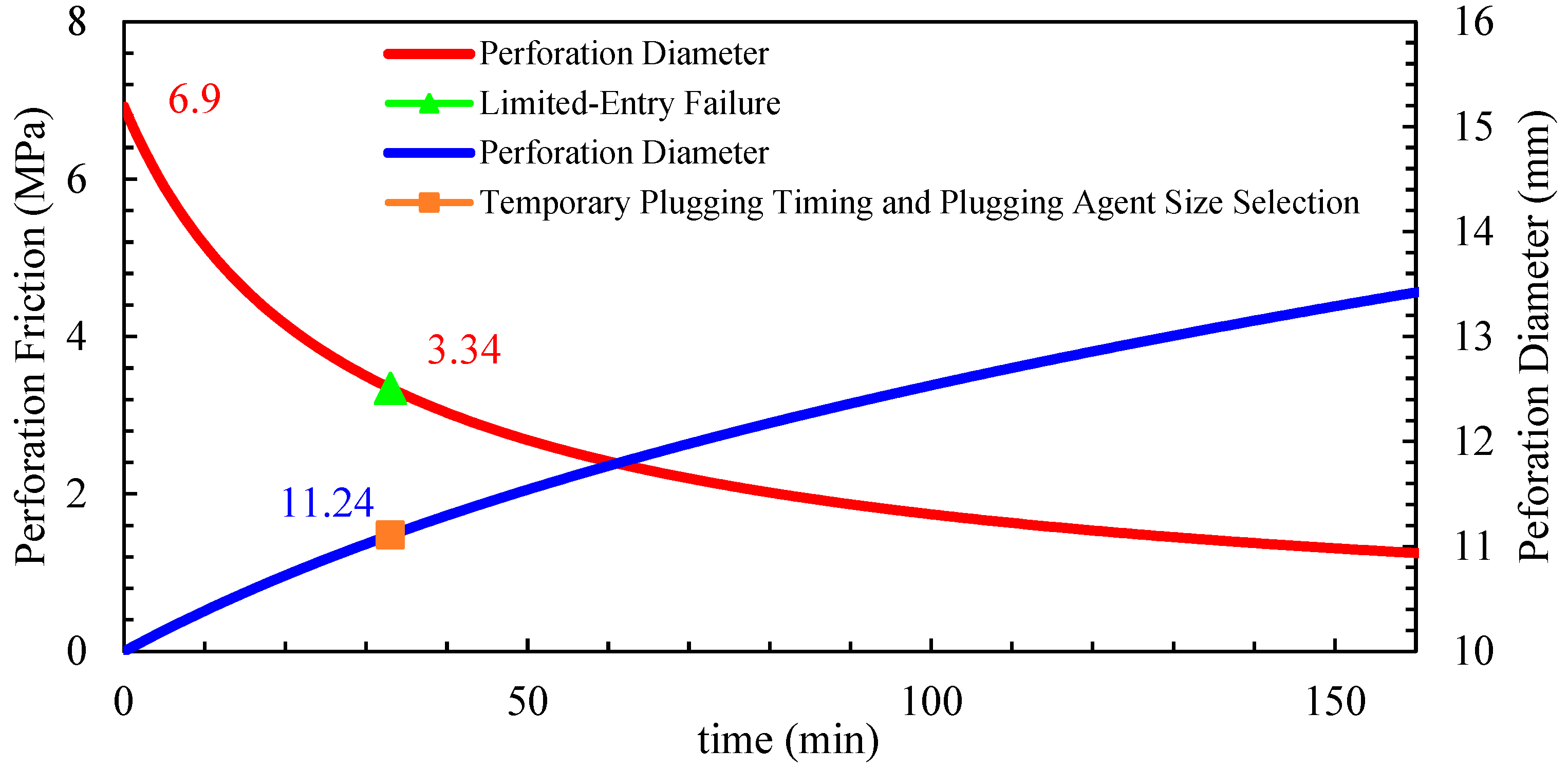
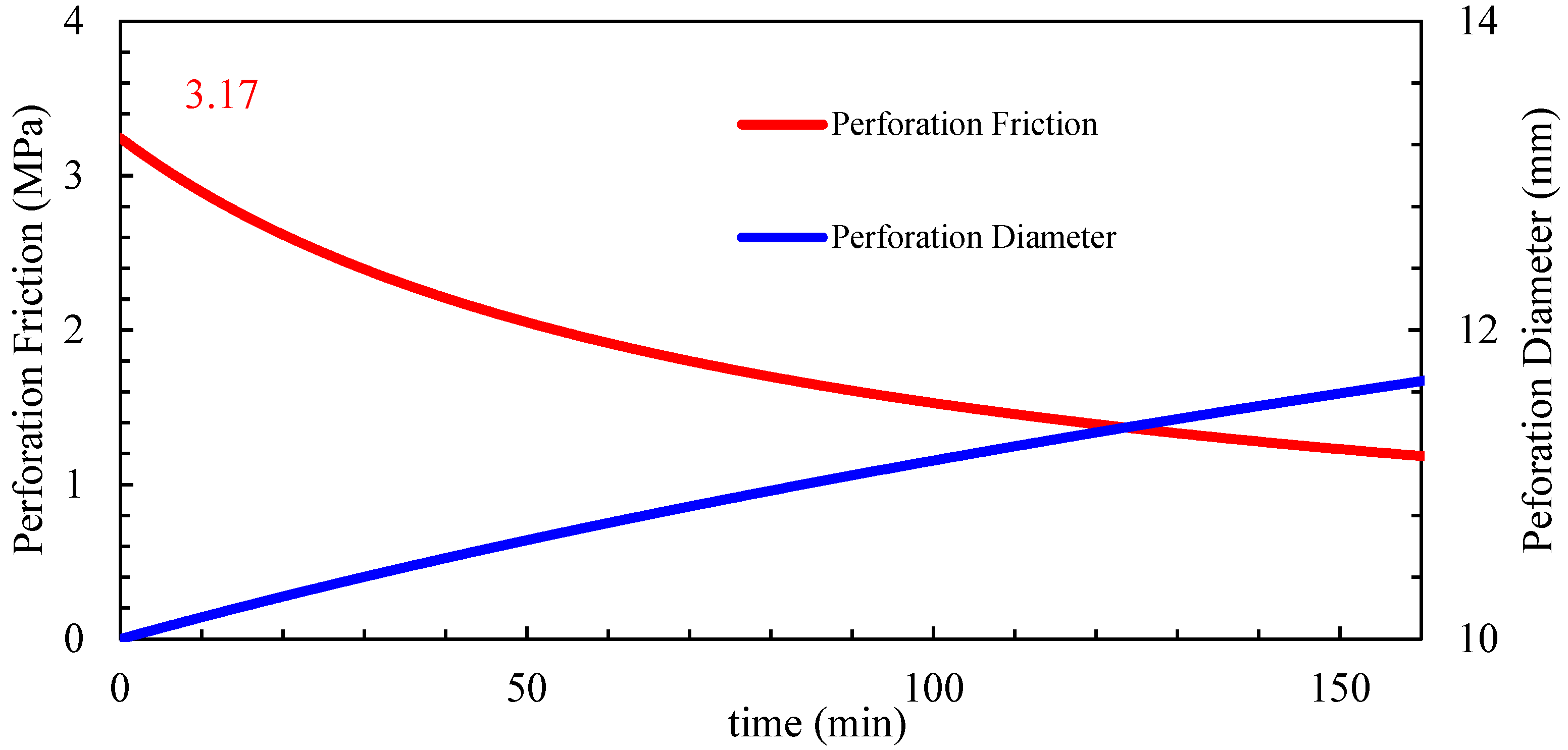
5. Application Case Study of Perforation Erosion Model
5.1. Application Methodology of the Perforation Erosion Model
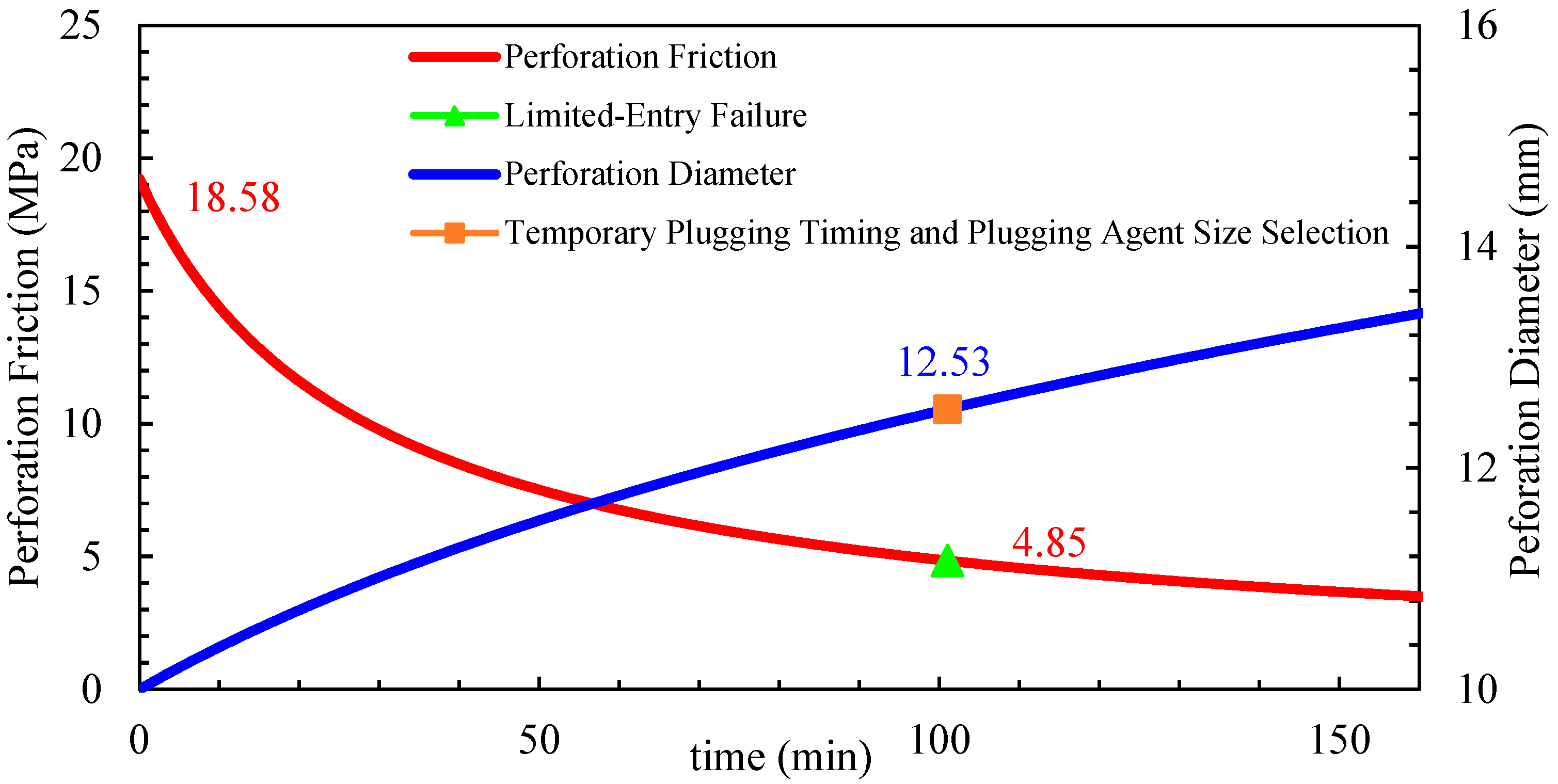
5.2. Field Application and Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhuo, R.; Ma, X.; Li, J.; Ren, L.; Cheng, N.; Ma, J.; Zhang, S. Influence of limited-entry fracturing on perforation erosion in horizontal wells. Drill. Prod. Technol. 2023, 46, 77–82. [Google Scholar]
- Li, G.; Lei, Z.; Dong, W.; Wang, H.; Zheng, X.; Tan, J. Progress, challenges, and prospects of unconventional oil and gas development in China. China Pet. Explor. 2022, 27, 1–11. [Google Scholar]
- Zhao, J.; Ren, L.; Jiang, T.; Hu, D.; Wu, L.; Wu, J.; Yin, C.; Li, Y.; Hu, Y.; Lin, R.; et al. A decade of shale gas fracturing in China: Review and outlook. Nat. Gas Ind. 2021, 41, 121–142. [Google Scholar]
- Wu, Q.; Xu, Y.; Zhang, S.; Wang, T.; Guan, B. Core theories and key optimization designs of volumetric fracturing technology for unconventional reservoirs. Acta Pet. Sin. 2014, 35, 706–714. [Google Scholar]
- Zou, C.; Yang, Z.; Zhu, R.; Zhang, G.; Hou, L.; Wu, S.; Tao, S.; Yuan, X.; Dong, D.; Wang, Y.; et al. Progress in exploration, development, and theoretical technologies of unconventional oil and gas in China. Acta Geol. Sin. 2015, 89, 979–1007. [Google Scholar]
- Zhang, J.; Lu, Z.; Shi, S. Large-scale field experimental study on casing perforation erosion during fracturing. Drill. Prod. Technol. 2023, 46, 85–91. [Google Scholar]
- Liu, Y.; Qin, L.; Wang, Z.; Dou, Y. Numerical simulation of perforation erosion during casing fracturing. Pet. Mach. 2015, 43, 66–69. [Google Scholar]
- Zhang, S.; Zeng, D.; Pan, Y.; Tian, G.; Yu, H.; Shi, S. Research progress on the erosion of fracturing strings during large-scale sand fracturing. Xinjiang Oil Gas 2022, 18, 65–72. [Google Scholar]
- Huang, G.; Hu, X.; Zhou, F.; Li, X.; Dong, E.; Li, Z. A new multi-cluster fracturing simulation model coupled with perforation erosion: Based on the continuous–discontinuous method. Rock Mech. Rock Eng. 2023, 56, 3887–3901. [Google Scholar] [CrossRef]
- Hu, X.; Li, X.; Zhou, F.; Bai, Y.; Chen, C.; Zhang, P. Simulation study on proppant transport in a horizontal wellbore considering perforation erosion. Geoenergy Sci. Eng. 2023, 231, 212282. [Google Scholar] [CrossRef]
- Li, Z.; Li, Z.; Cheng, J.; Cui, L. Experimental study on erosion and hole enlargement by high-speed jet flow. Shandong Chem. Ind. 2022, 51, 1–4. [Google Scholar]
- Wu, B.; Zhou, F.; Wang, M.; Lv, Z.; Li, M.; Wang, B.; Guo, X.; Zhang, J. Field-Scale Experimental Study on the Perforation Erosion in Horizontal Wellbore under Real Fracturing Conditions. Processes 2022, 10, 1058. [Google Scholar] [CrossRef]
- Wang, B.; Gu, X.; Li, W.; Zhang, G.; Ge, H.; Zhou, F. Experimental study on plugging law of irregular perforations under strong erosion. J. Xi’an Shiyou Univ. Nat. Sci. Ed. 2023, 38, 46–53. [Google Scholar]
- Zang, C.; Jiang, H.; Shi, S.; Li, J.; Zou, Y.; Zhang, S.; Tian, G.; Yang, P. Analysis of uniform fracture initiation in multi-cluster fracturing based on perforation imaging monitoring: A case study of the tight conglomerate in Mahu Sag, unggar Basin. Pet. Explor. Dev. 2022, 49, 394–402. [Google Scholar] [CrossRef]
- Xu, G. Numerical simulation study on hydraulic jet erosion of coiled tubing. Oil Field Equip. 2016, 45, 12–15. [Google Scholar]
- Guo, X.; Cheng, L.; Zhang, J.; Li, H.; Li, Y. Numerical simulation study of hole erosion under directional perforating conditions. Xinjiang Oil Gas 2022, 18, 56–61. [Google Scholar]
- Eckdahl, R.; Vigrass, A.; Singh, A.; Liu, X.; Chrusch, L. Assessment of limited entry cluster distribution effectiveness and impactful variables using perforation erosion measurements. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 4–6 February 2022. [Google Scholar]
- Cramer, D.; Friehauf, K.; Roberts, G.; Whittaker, J. Integrating DAS, treatment pressure analysis and video-based perforation imaging to evaluate limited entry treatment effectiveness. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 4–6 February 2019. [Google Scholar]
- Roberts, G.; Whittaker, J.; McDonald, J.; Paxson, T. Proppant Distribution Observations from 20,000+ Perforation Erosion Measurements. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 4–6 February 2020. [Google Scholar]
- Long, G.; Liu, S.; Xu, G.; Wong, S.-W.; Chen, H.; Xiao, B. A perforation-erosion model for hydraulic-fracturing applications. SPE Prod. Oper. 2018, 33, 770–783. [Google Scholar] [CrossRef]
- Wang, F.; Li, J.; Xiang, Z.; Chen, R.; Zhao, Y.; Mou, Y. Simulation and countermeasures of casing erosion at downhole decoupled sandblaster during fracturing. Xinjiang Oil Gas 2023, 19, 57–65. [Google Scholar]
- Wang, Y.; Lu, Y.; Li, Y.; Wang, X.; Yan, X.; Zhang, Z. Progress and application of fracturing technology in unconventional reservoirs. Acta Pet. Sin. 2012, 33 (Suppl. S1), 149–158. [Google Scholar]
- Zhou, T.; Zhang, S.; Chen, M.; Huang, Z. Competitive propagation and control of multi-cluster fractures in horizontal wells. Sci. Sin. Technol. 2019, 49, 469–478. [Google Scholar] [CrossRef]
- Zhou, F.; Su, H.; Liang, X.; Meng, L.; Yuan, L.; Li, X.; Liang, T. Integrated technology of efficient fracture network stimulation and enhanced oil recovery in tight oil reservoirs. Pet. Explor. Dev. 2019, 46, 1007–1014. [Google Scholar] [CrossRef]
- Crump, J.B.; Conway, M.W. Effects of perforation-entry friction on bottom hole treating analysis. J. Pet. Technol. 1988, 40, 1041–1048. [Google Scholar] [CrossRef]
- Stephen, R.; Thomas, L.; Tim, L.; Kacper, W.; Andrew, E.; Blake, H.; Michael, O. Acoustic imaging of perforation erosion in hydraulically fractured wells for optimizing cluster efficiency. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 4–6 February 2020. [Google Scholar]



| Experiment | Flow Rate (m³/min) | Proppant Concentration (kg/m³) | Proppant Size and Type | Erosion Coefficient (α) | Erosion Coefficient (β) |
|---|---|---|---|---|---|
| 1 | 0.9 (High Viscosity) | 90 | 40/70 Mesh Quartz Sand | 1.17 × 10−13 | 9.01 × 10−11 |
| 2 | 0.9 | 90 | 40/70 Mesh Ceramic | 1.34 × 10−13 | 5.66 × 10−11 |
| 3 | 0.9 | 90 | 40/70 Mesh Quartz Sand | 3.96 × 10−13 | 1.43 × 10−10 |
| 160 | 4.51 × 10−13 | 1.60 × 10−10 | |||
| 240 | 3.80 × 10−13 | 1.68 × 10−10 | |||
| 4 | 0.9 | 160 | 20/40 Mesh Quartz Sand | 3.10 × 10−13 | 1.16 × 10−10 |
| Perforations per Cluster | Clusters per Stage | Perforations per Stage | Fracturing Stages |
|---|---|---|---|
| 3 | 6 | 18 | Stages 7, 10, 13 |
| 5 | 6 | 30 | Stages 8, 11, 14 |
| 8 | 6 | 48 | Stages 9, 12, 15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Li, H.; Zhang, E.; Ma, J.; Shang, Z.; Liu, X. Construction and Application of a Quantitative Perforation Erosion Model Based on Field Experiments. Materials 2025, 18, 2507. https://doi.org/10.3390/ma18112507
Wang B, Li H, Zhang E, Ma J, Shang Z, Liu X. Construction and Application of a Quantitative Perforation Erosion Model Based on Field Experiments. Materials. 2025; 18(11):2507. https://doi.org/10.3390/ma18112507
Chicago/Turabian StyleWang, Bo, Huan Li, Enyu Zhang, Jinglong Ma, Zichen Shang, and Xiongfei Liu. 2025. "Construction and Application of a Quantitative Perforation Erosion Model Based on Field Experiments" Materials 18, no. 11: 2507. https://doi.org/10.3390/ma18112507
APA StyleWang, B., Li, H., Zhang, E., Ma, J., Shang, Z., & Liu, X. (2025). Construction and Application of a Quantitative Perforation Erosion Model Based on Field Experiments. Materials, 18(11), 2507. https://doi.org/10.3390/ma18112507







