Seismic Performance of Recycled Aggregate Concrete-Filled Steel Tube Column–Composite Beam Frames with Column-End Stirrup Confinement
Abstract
1. Introduction
2. Finite Element Model
2.1. Overview of Example
2.2. Finite Element Model Establishment
2.3. Material Constitutive Models
2.4. Boundary Conditions and Seismic Wave Input
2.5. Frequency and Vibration Mode Analysis
3. Structural Response Analysis
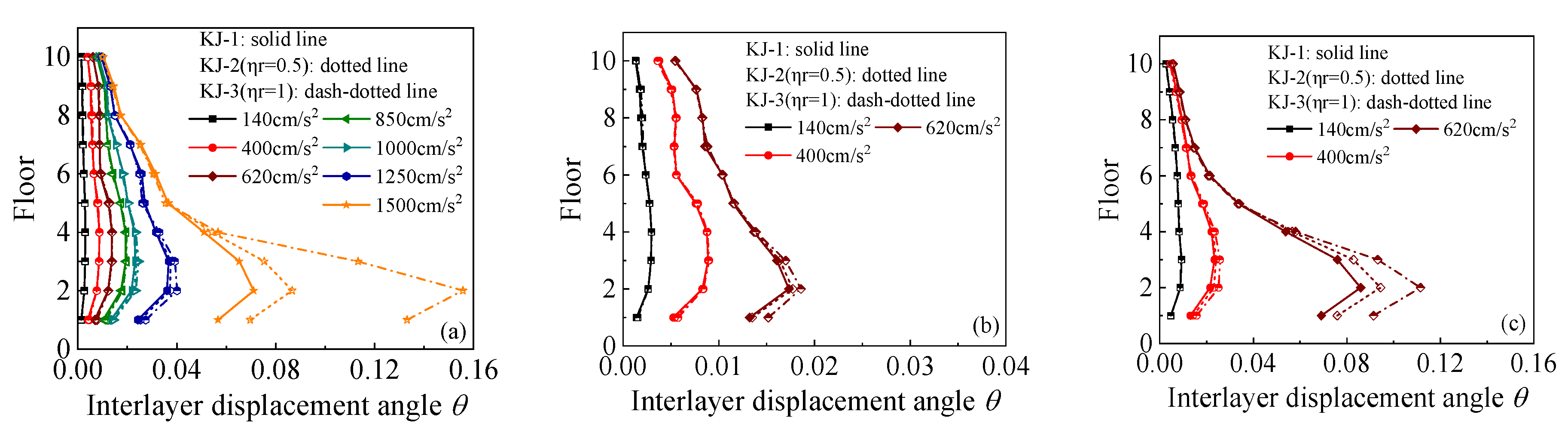
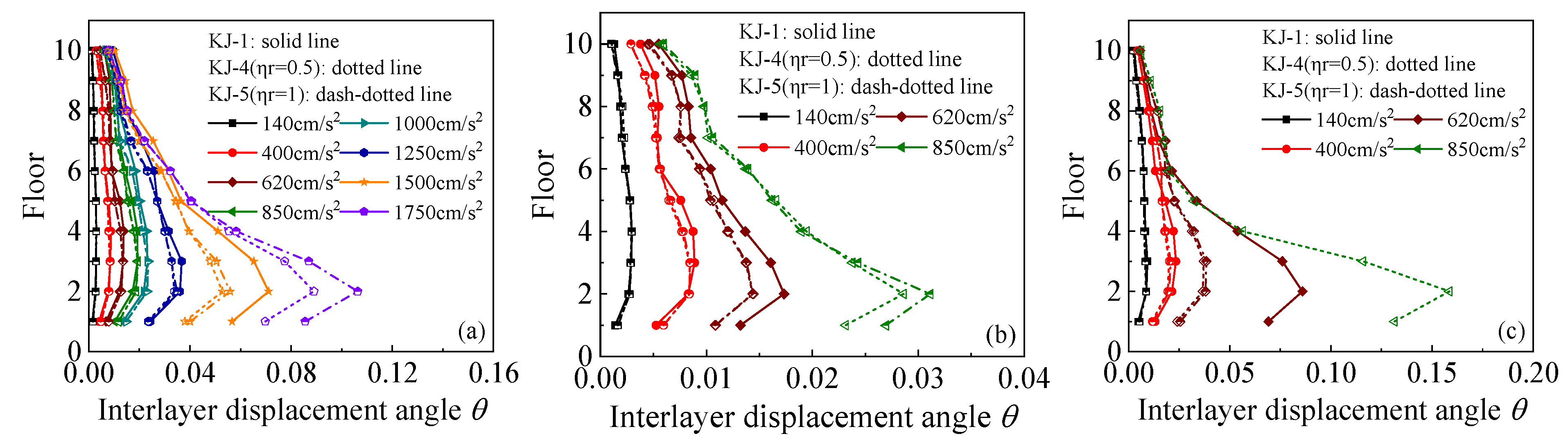
3.1. Ultimate Seismic Capacity and Interlayer Displacement Angle
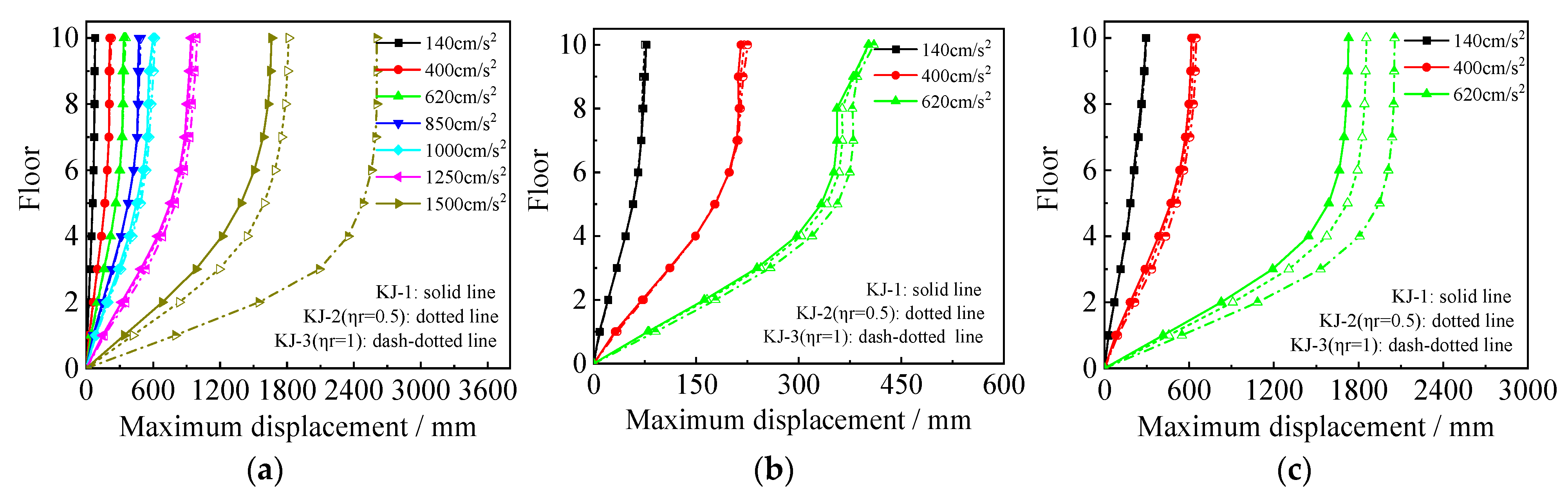
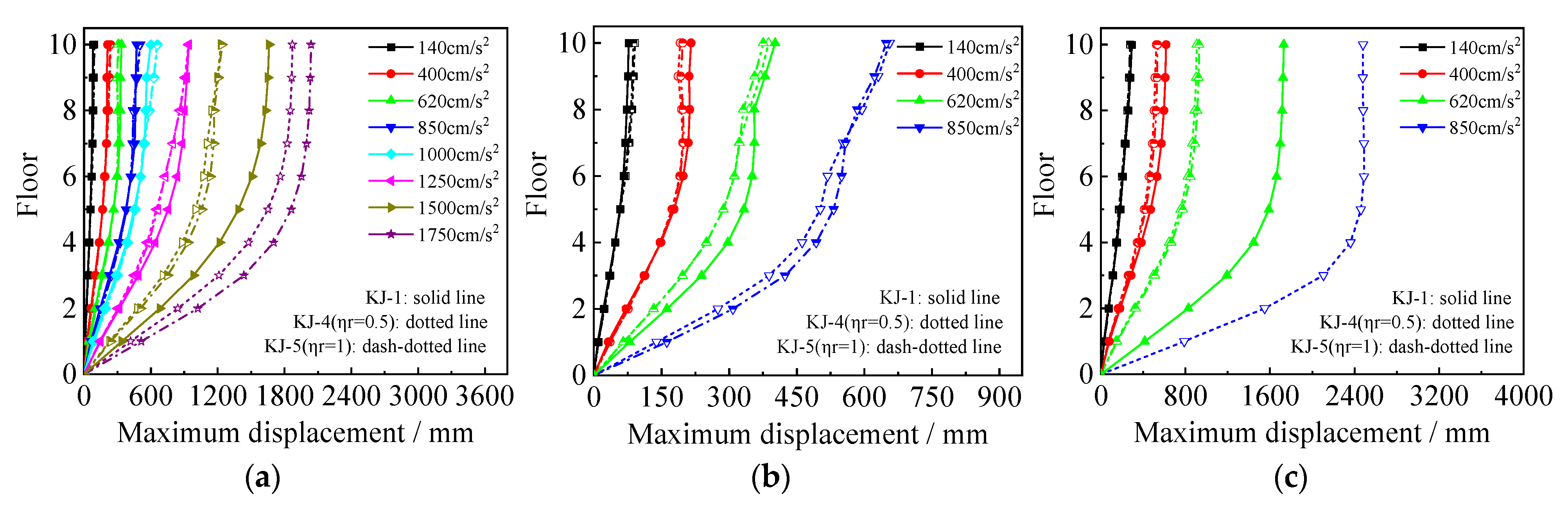
3.2. Maximum Lateral Displacements
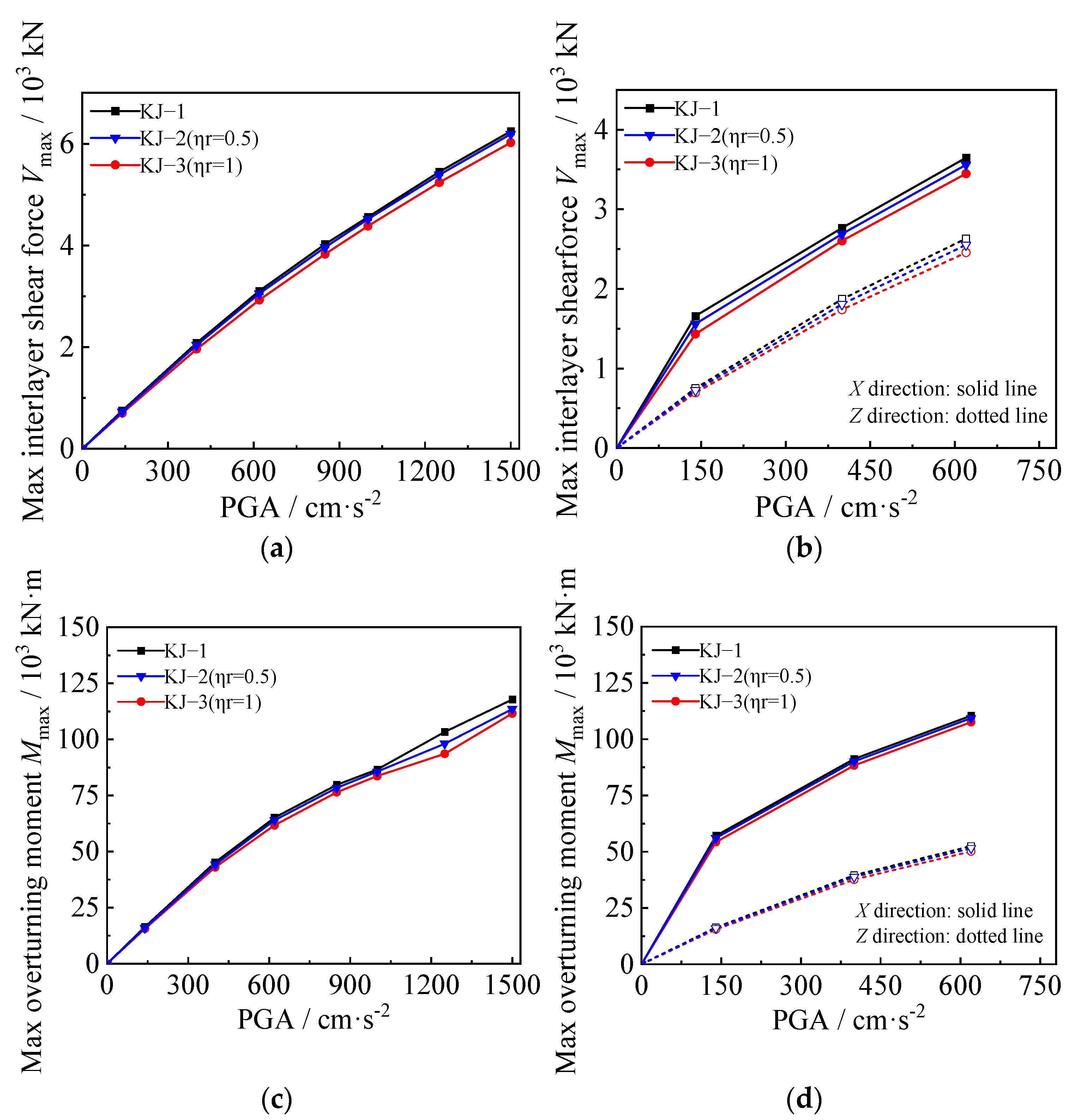
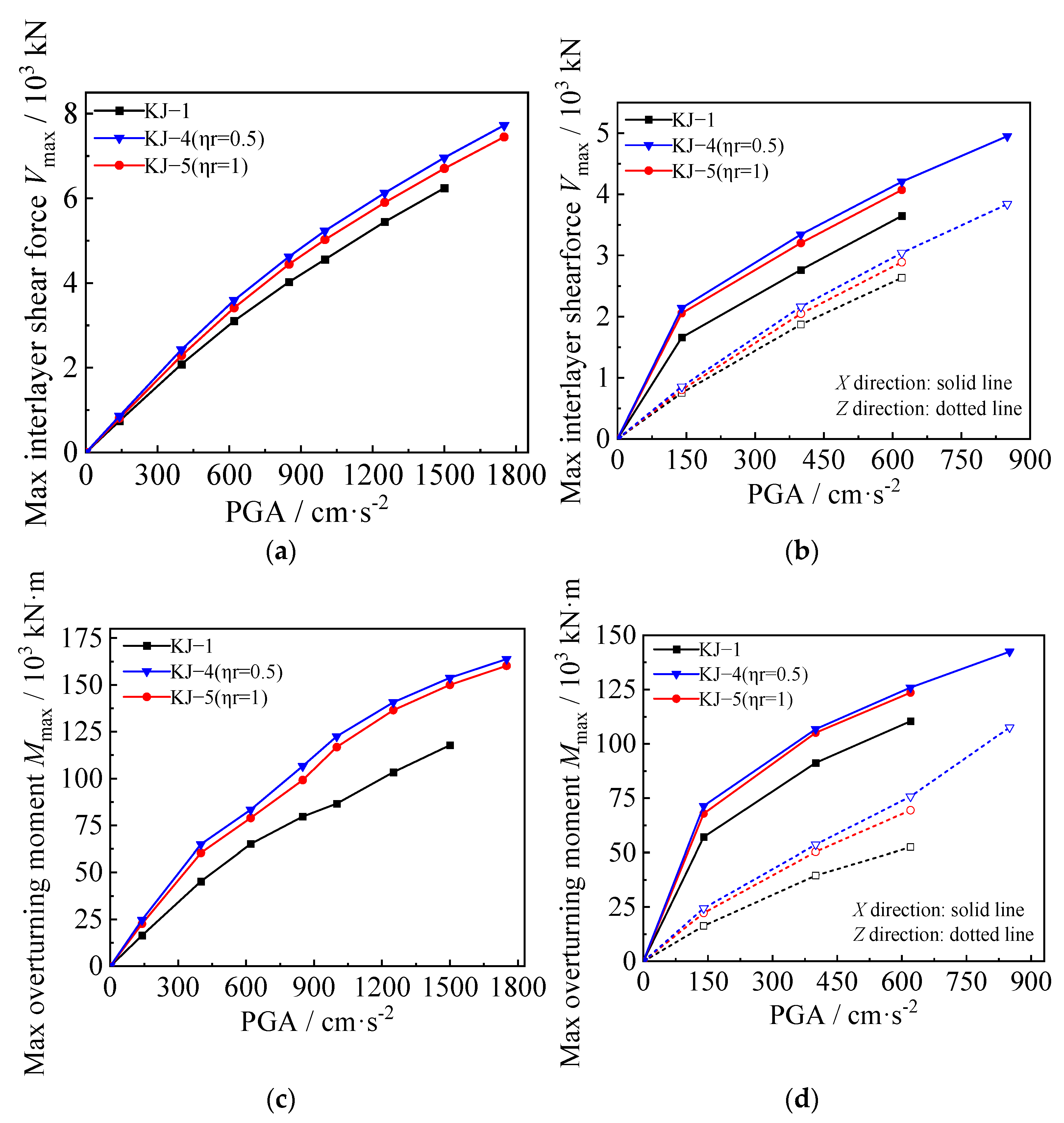
3.3. Maximum Interlayer Shear Force and Overturning Moment
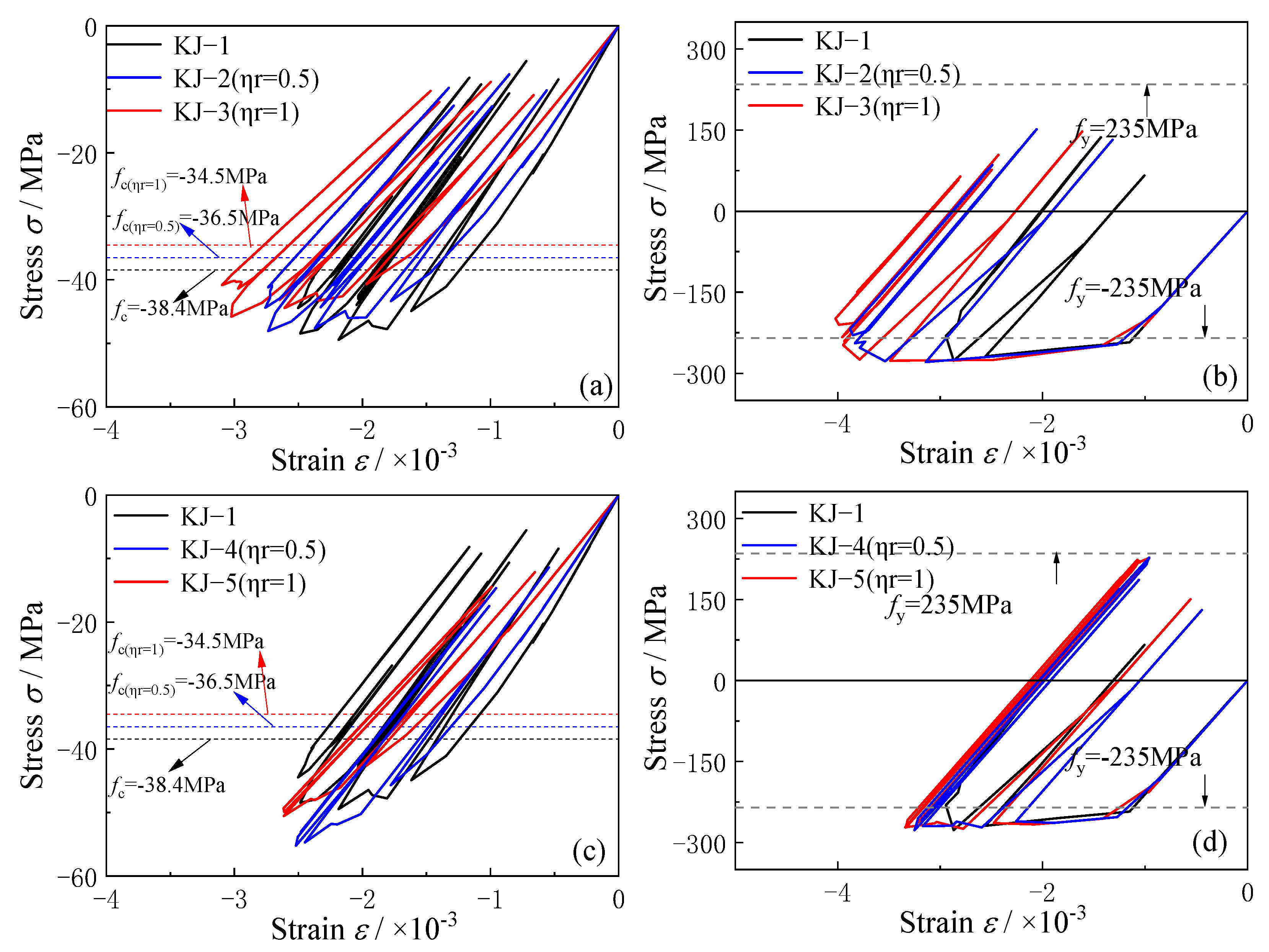
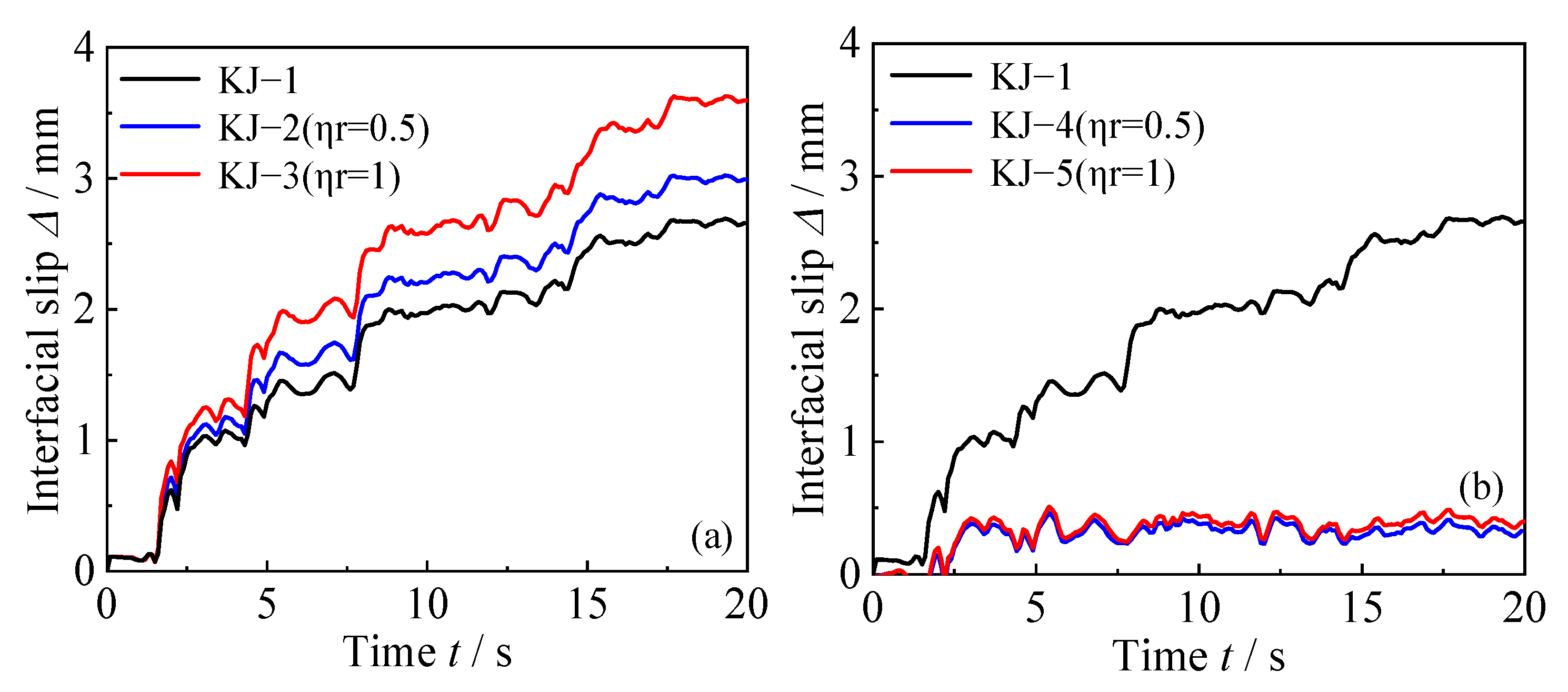
3.4. Stress–Strain Curve and Interface Slip
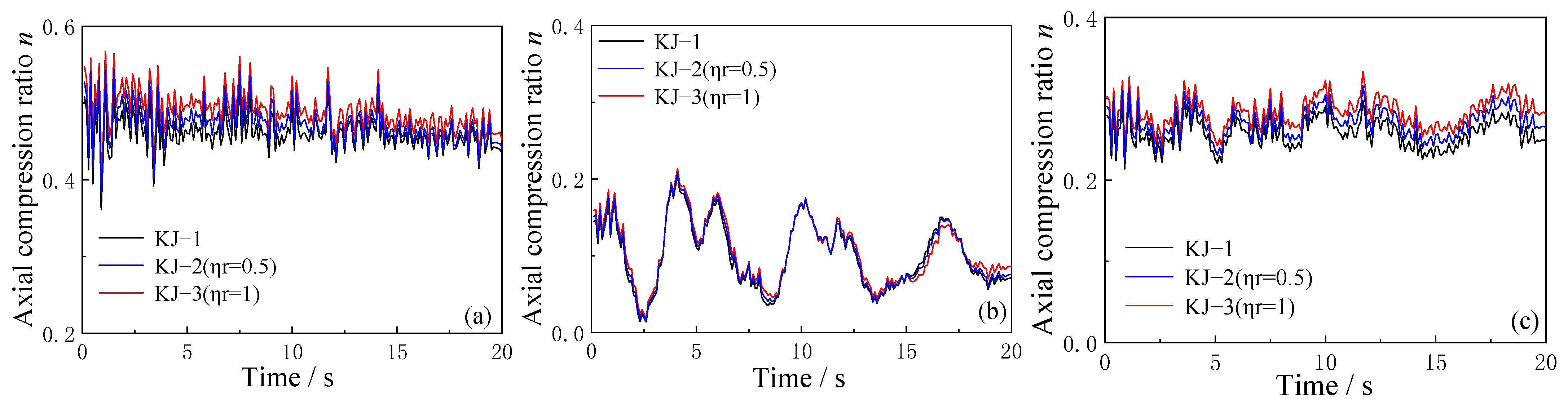
3.5. Axial Compression Ratio Time History Curve
4. Structural Plastic Energy Dissipation and Stiffness Damage
4.1. Structural Plastic Energy Dissipation
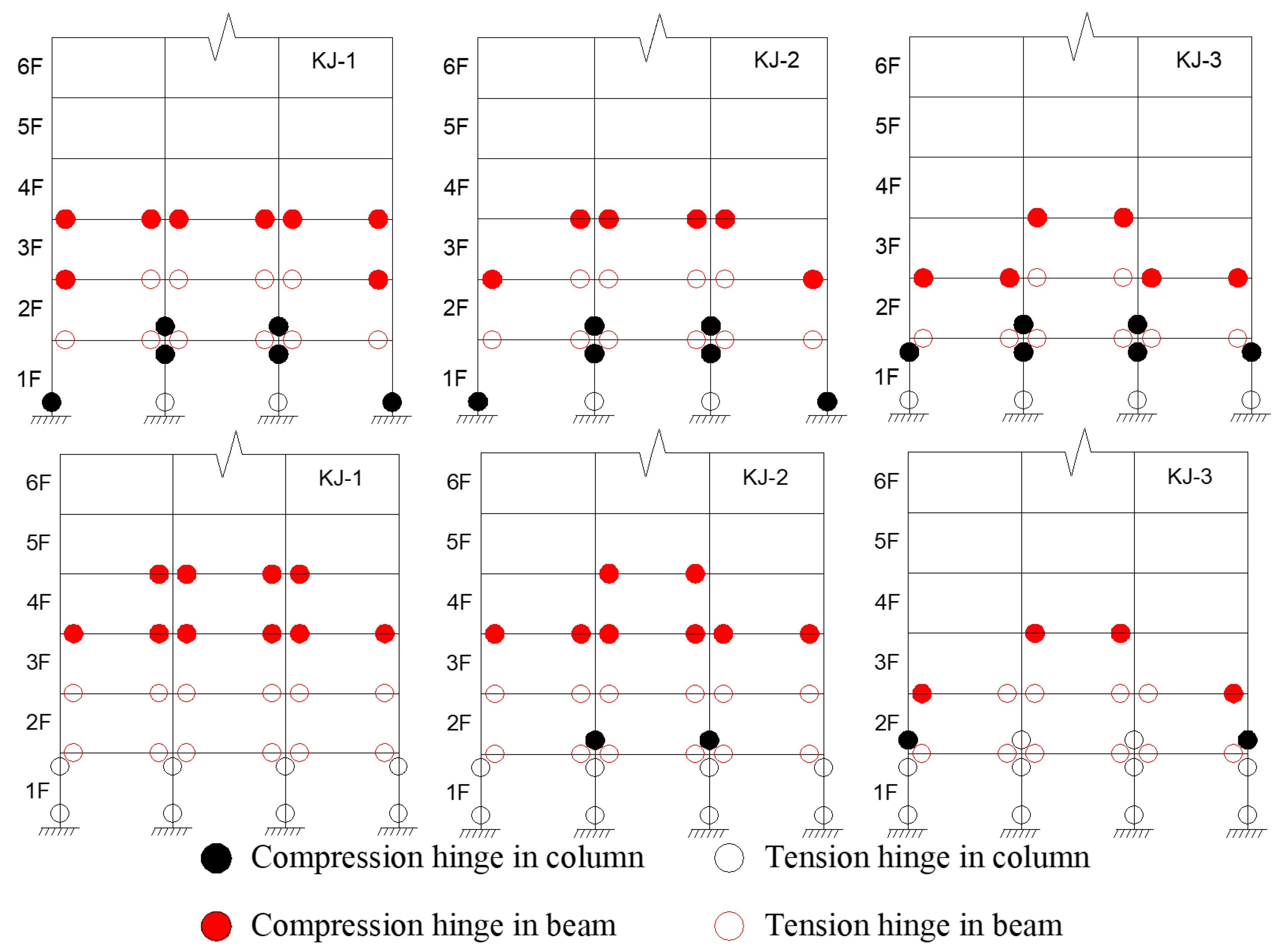
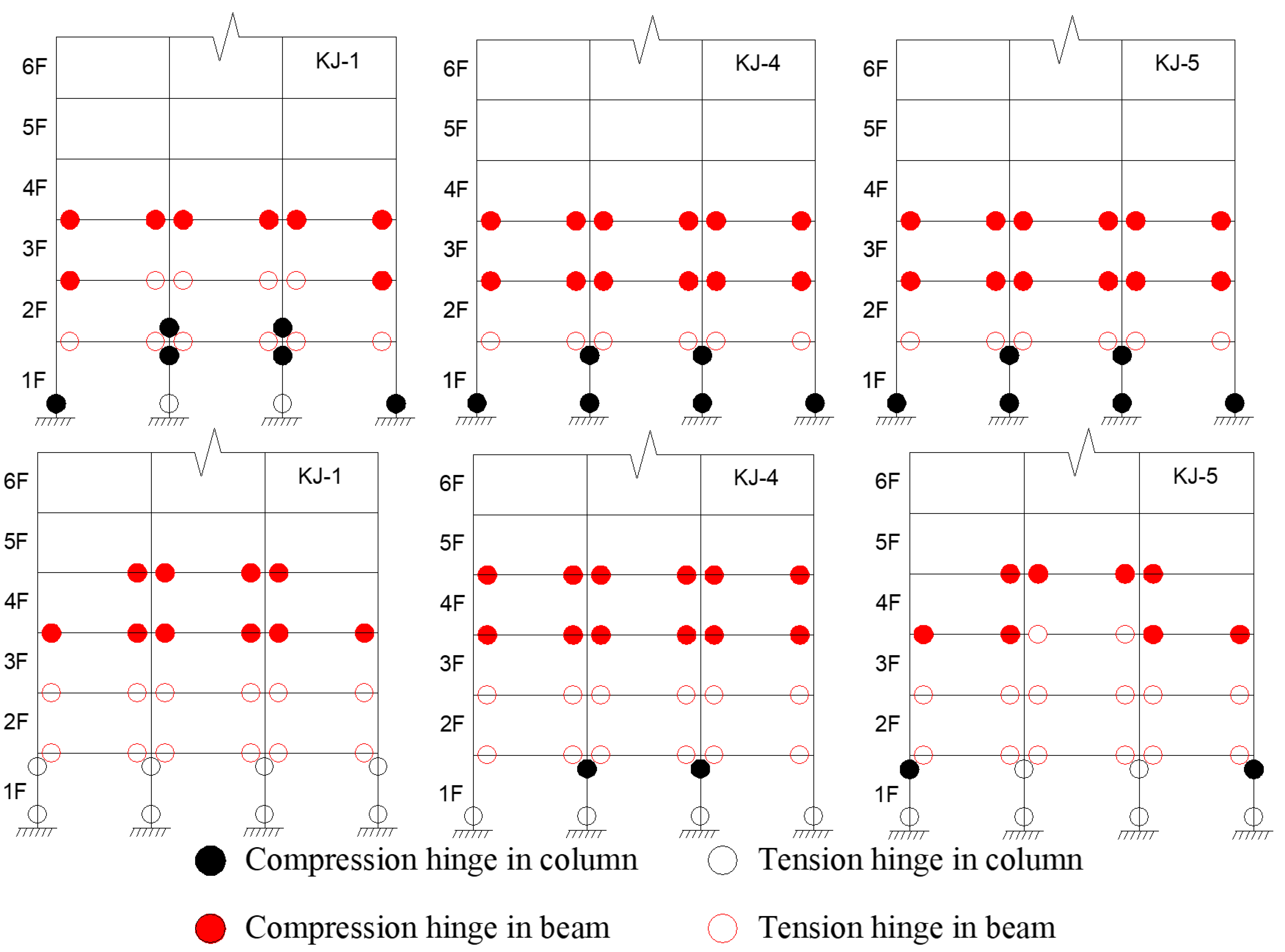
4.2. Development of Structural Plastic Hinge
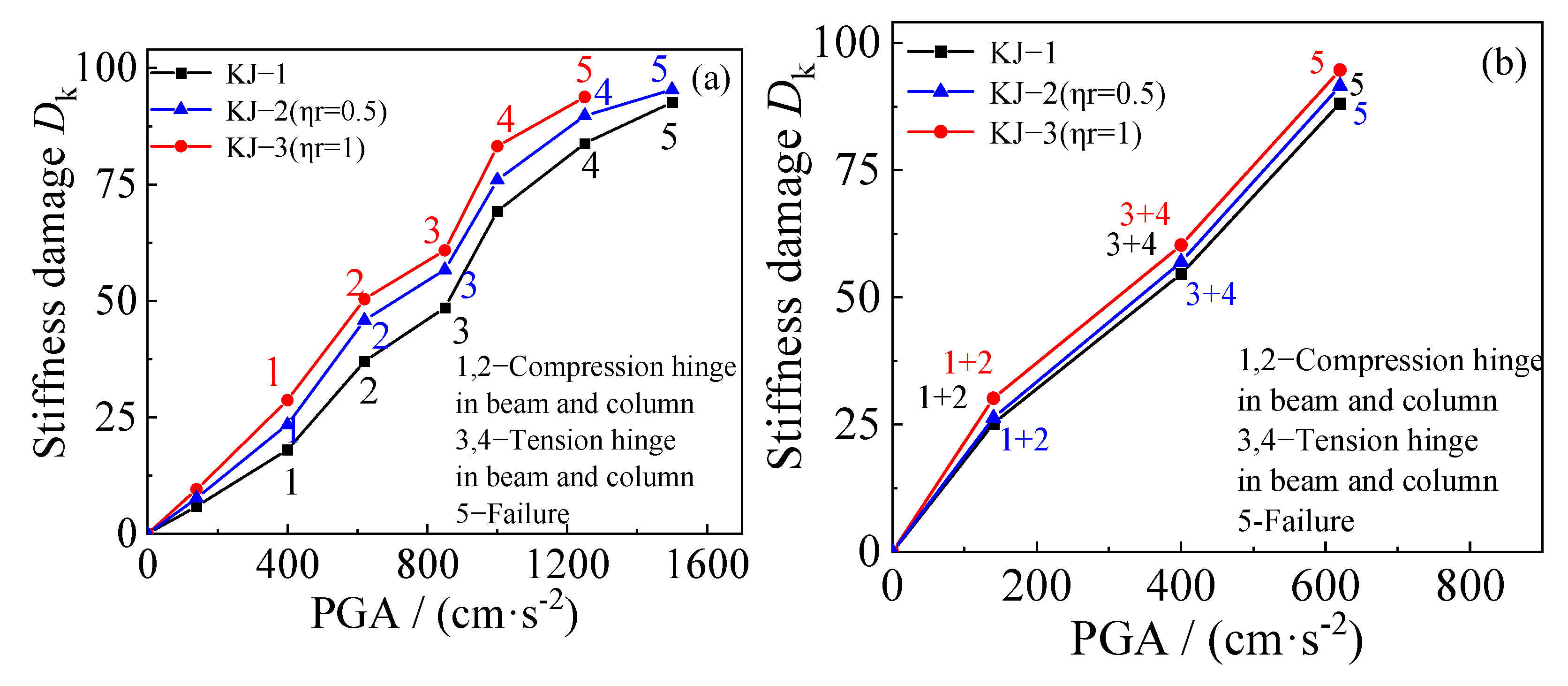
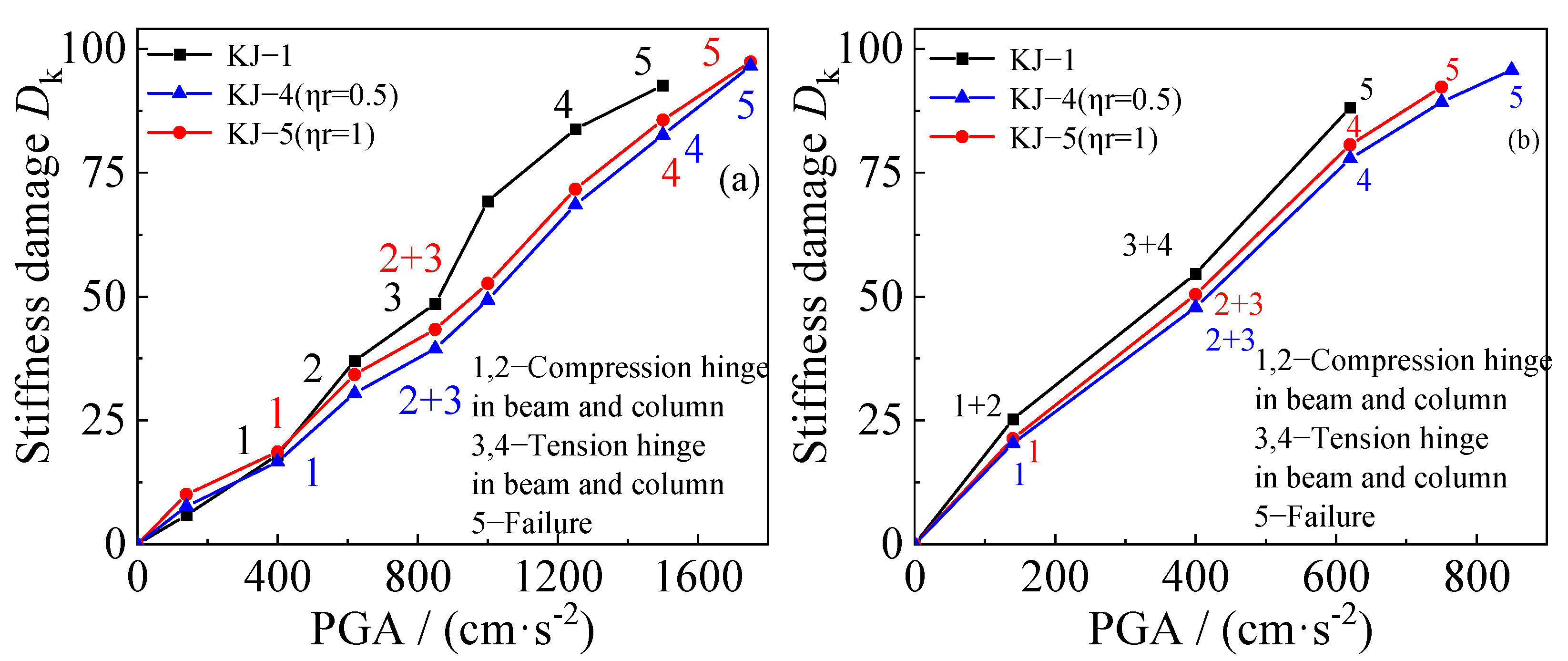
4.3. Stiffness Damage
5. Conclusions
- (1)
- Recycled aggregate replacement leads to a decrease in the structure’s natural frequency, an increase in the interlayer displacement angle, a decrease in the interlayer shear force and bending moment that the structure is subjected to, more interface slip between the core concrete and the steel tube, reduced plastic energy dissipation, and increased stiffness damage. The higher the recycled aggregate replacement ratio, the more significant the effect on seismic performance.
- (2)
- Column-end stirrup-confined reinforcement reduces interface slip between the concrete column and the steel tube by directly restraining the core concrete. It enhances the energy dissipation capacity of the CFST column, increases the total plastic energy dissipation of the structure, and reduces the energy dissipation ratio of the CFST column. Additionally, it increases the number of plastic hinges at the beam end and reduces the number of plastic hinges at the column end, delaying the formation of a “compression hinge” and extending the transition to a “tension hinge”.
- (3)
- The stirrup-confined recycled concrete frame exhibits a higher natural frequency, smaller interlayer displacement angle, lower stiffness damage, and better overall seismic performance than conventional concrete frames. This demonstrates that column-end stirrup-confined reinforcement can effectively mitigate the adverse effects of recycled aggregate replacement on seismic performance.
- (4)
- Although recycled concrete exhibits lower material and mechanical properties compared to conventional concrete, its seismic performance can be significantly enhanced sometimes even surpassing that of traditional composite frames through effective column-end stirrup reinforcement. This suggests that recycled concrete is a promising alter-native for conventional concrete in seismic applications. However, the seismic performance of recycled concrete structures is influenced by factors such as the quality of recycled aggregates, construction processes, and reinforcement design. Future research should focus on optimizing the use of different recycled aggregate ratios, improving construction quality control, and refining reinforcement strategies. These efforts will provide crucial insights to ensure the practical application of recycled concrete in real-world engineering projects.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFST | Concrete-filled steel tubular |
| RAC-FST | Recycled aggregate concrete-filled steel tubular |
| CFRP | Carbon fiber-reinforced polymer |
| FRP | Fiber-reinforced polymer |
| ϕ | Stirrup diameter |
| bf | Width of steel beam flange |
| fc | Axial compressive strength of concrete |
| fy | Yield strength of the steel tube |
| fcu | Concrete cube strength |
| ηr | Replacement rate |
| ε | Strain |
| PGA | Peak ground acceleration |
References
- Xiao, J.; Li, W.; Fan, Y.; Huang, X. An overview of study on recycled aggregate concrete in China (1996–2011). Constr. Build. Mater. 2012, 31, 364–383. [Google Scholar] [CrossRef]
- Xu, Y.; Ding, F.; Lyu, F.; Wang, L.; Yu, Z. Study on dynamic performance of CFST column-composite beam frame structural system under strong earthquake. J. Build. Eng. 2024, 94, 109970. [Google Scholar] [CrossRef]
- Günçan, N.F. Using waste concrete as aggregate. Cem. Concr. Res. 1995, 25, 1385–1390. [Google Scholar]
- Rahal, K. Mechanical properties of concrete with recycled coarse aggregate. Build. Environ. 2007, 42, 407–415. [Google Scholar] [CrossRef]
- Evangelista, L.; De Brito, J. Mechanical behaviour of concrete made with fine recycled concrete aggregates. Cem. Concr. Compos. 2007, 29, 397–401. [Google Scholar] [CrossRef]
- Xiao, J.; Li, J.; Zhang, C. Mechanical properties of recycled aggregate concrete under uniaxial loading. Cem. Concr. Res. 2005, 35, 1187–1194. [Google Scholar] [CrossRef]
- Etxeberria, M.; Vázquez, E.; Mari, A.; Barra, M. Influence of amount of recycled coarse aggregates and production process on properties of recycled aggregate concrete. Cem. Concr. Res. 2007, 37, 735–742. [Google Scholar] [CrossRef]
- Liu, B.; Feng, C.; Deng, Z. Shear behavior of three types of recycled aggregate concrete. Constr. Build. Mater. 2019, 217, 557–572. [Google Scholar] [CrossRef]
- Ding, F.; Fang, C.; Gong, Y.; Yu, Z.; Hu, L. Unified calculation method of uniaxial mechanical performance index of recycled concrete. J. Archit. Civ. Eng. 2014, 31, 16–22. [Google Scholar]
- Choi, W.C.; Yun, H.D. Compressive behavior of reinforced concrete columns with recycled aggregate under uniaxial loading. Eng. Struct. 2012, 41, 285–293. [Google Scholar] [CrossRef]
- Ma, H.; Xue, J.; Zhang, X.; Luo, D. Seismic performance of steel-reinforced recycled concrete columns under low cyclic loads. Constr. Build. Mater. 2013, 48, 229–237. [Google Scholar] [CrossRef]
- Tang, Y.; Li, L.; Feng, W.; Liu, F.; Liao, B. Seismic performance of recycled aggregate concrete–filled steel tube columns. J. Constr. Steel Res. 2017, 133, 112–124. [Google Scholar] [CrossRef]
- Yang, Y.; Han, L. Experimental behaviour of recycled aggregate concrete filled steel tubular columns. J. Constr. Steel Res. 2006, 62, 1310–1324. [Google Scholar] [CrossRef]
- Xiao, J.; Sun, Y.; Falkner, H. Seismic performance of frame structures with recycled aggregate concrete. Eng. Struct. 2006, 28, 1–8. [Google Scholar] [CrossRef]
- Xiao, J.; Wang, C.; Li, J. Shake-table model tests on recycled aggregate concrete frame structure. ACI Struct. J. 2012, 109, 777–786. [Google Scholar]
- Han, L.; Li, W.; Bjorhovde, R. Developments and advanced applications of concrete-filled steel tubular (CFST) structures: Members. J. Constr. Steel Res. 2014, 100, 211–228. [Google Scholar] [CrossRef]
- Han, L.; Li, W.; Yang, Y. Seismic behaviour of concrete-filled steel tubular frame to RC shear wall high-rise mixed structures. J. Constr. Steel Res. 2009, 65, 1249–1260. [Google Scholar] [CrossRef]
- Ding, F.; Yin, G.; Jiang, L.; Bai, Y. Composite frame of circular CFST column to steel-concrete composite beam under lateral cyclic loading. Thin-Walled Struct. 2018, 122, 137–146. [Google Scholar] [CrossRef]
- Nie, J.; Qin, K.; Cai, C.S. Seismic behavior of connections composed of CFSSTCs and steel–concrete composite beams—Experimental study. J. Constr. Steel Res. 2008, 64, 1178–1191. [Google Scholar] [CrossRef]
- Laterza, M.; D’Amato, M.; Thanthirige, L.P.; Braga, F.; Gigliotti, R. Comparisons of codal detailing rules for curvature ductility and numerical investigations. Open Constr. Build. Technol. J. 2014, 8, 132–141. [Google Scholar] [CrossRef]
- Mao, X.; Xiao, Y. Seismic behavior of confined square CFT columns. Eng. Struct. 2006, 28, 1378–1386. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, C.; Lu, X. Experimental study of hysteretic behaviour for concrete-filled square thin-walled steel tubular columns. J. Constr. Steel Res. 2007, 63, 317–325. [Google Scholar] [CrossRef]
- Hsu, H.; Yu, H. Seismic performance of concrete-filled tubes with restrained plastic hinge zones. J. Constr. Steel Res. 2003, 59, 587–608. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, J.; Long, Y. Hysteretic behavior of square CFT columns with binding bars. J. Constr. Steel Res. 2017, 131, 162–175. [Google Scholar] [CrossRef]
- Han, L.; Ren, Q.; Li, W. Tests on stub stainless steel–concrete–carbon steel double-skin tubular (DST) columns. J. Constr. Steel Res. 2011, 67, 437–452. [Google Scholar] [CrossRef]
- Chaallal, O.; Shahawy, M.; Hassan, M. Performance of axially loaded short rectangular columns strengthened with carbon fiber-reinforced polymer wrap. J. Compos. Constr. 2003, 7, 200–208. [Google Scholar] [CrossRef]
- Xiao, Y.; He, W.; Choi, K. Confined concrete-filled tubular columns. J. Struct. Eng. 2005, 131, 488–497. [Google Scholar] [CrossRef]
- Chen, Z.; Dong, S.; Du, Y. Experimental study and numerical analysis on seismic performance of FRP confined high-strength rectangular concrete-filled steel tube columns. Thin-Walled Struct. 2021, 162, 107560. [Google Scholar] [CrossRef]
- Feng, P.; Cheng, S.; Bai, Y.; Ye, L. Mechanical behavior of concrete-filled square steel tube with FRP-confined concrete core subjected to axial compression. Compos. Struct. 2015, 123, 312–324. [Google Scholar] [CrossRef]
- Ding, F.; Xu, Y.; Wang, L.; Yin, G.; Yu, Z. Pseudo-static tests of stirrup-confined square CFST two-story two-span composite frame structure. Eng. Mech. 2023, 40, 58–70. [Google Scholar]
- Zhang, J.; Liu, P.; He, C.; Ding, F.; Hu, M.; Shen, J.; Lin, Q.; Liu, X.; Yang, J.; Qiu, Y.; et al. Torsional behavior of I-steel–concrete composite beam considering the composite effects. Struct. Concr. 2022, 23, 1151–1175. [Google Scholar] [CrossRef]
- Ding, F.; Wu, X.; Xiang, P.; Yu, Z. New damage ratio strength criterion for concrete and lightweight aggregate concrete. ACI Struct. J. 2021, 118, 165–178. [Google Scholar]
- Zhang, S.; Ding, F.; Cai, Y.; Lyu, F.; Wang, L.; Wang, H. Numerical investigation in the performance of welded multi-cavity double steel plate-concrete composite shear wall under cyclic loading. J. Build. Eng. 2025, 105, 112477. [Google Scholar]
- Xu, Q.; Sun, H.; Ding, F.; Lyu, F. Analysis of ultimate seismic performance of thin-walled concrete-filled steel tube bridge piers under dynamic load. Eng. Struct. 2023, 292, 116544. [Google Scholar] [CrossRef]
- GB 50009-2012; Load Code for the Design of Building Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2012.
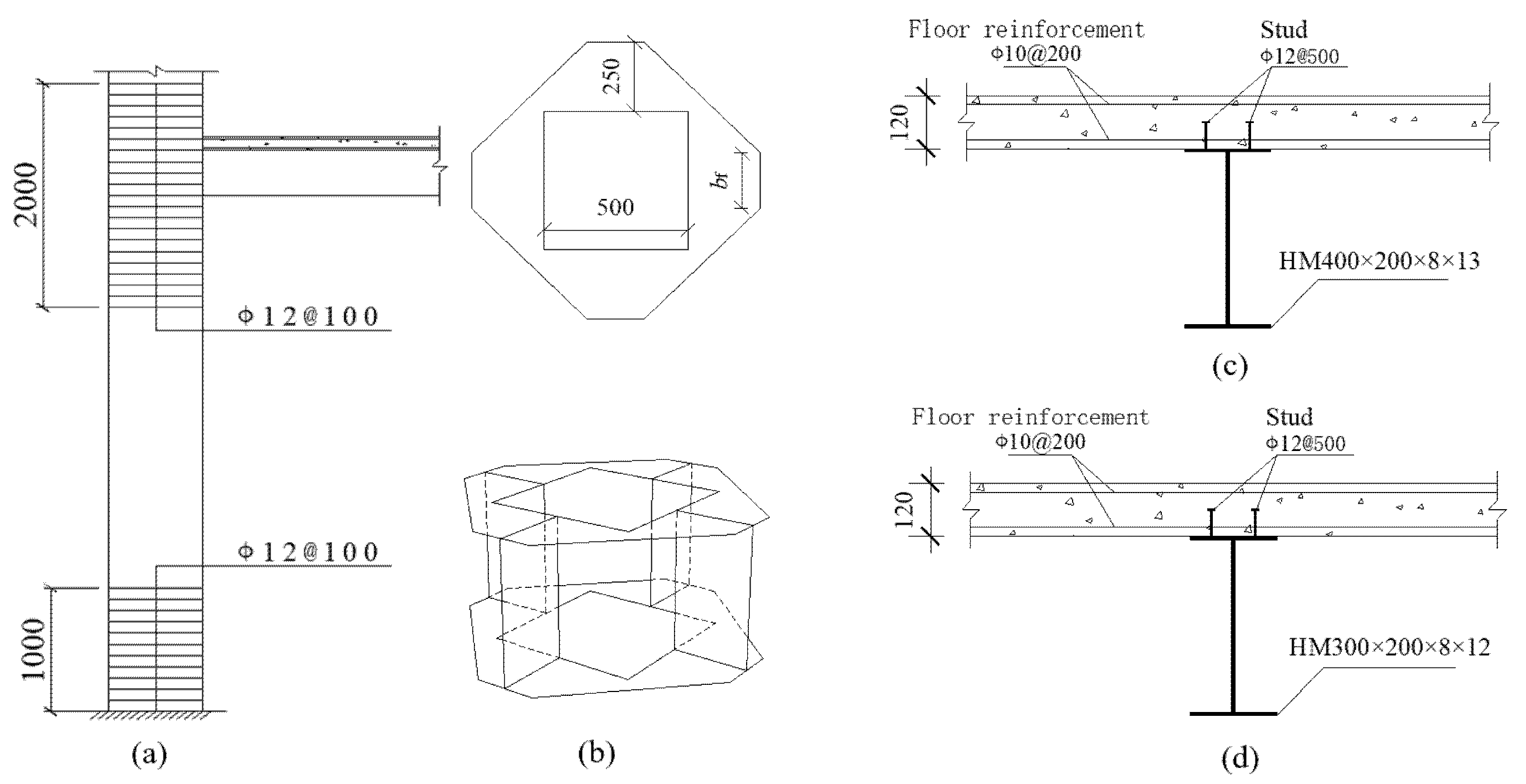
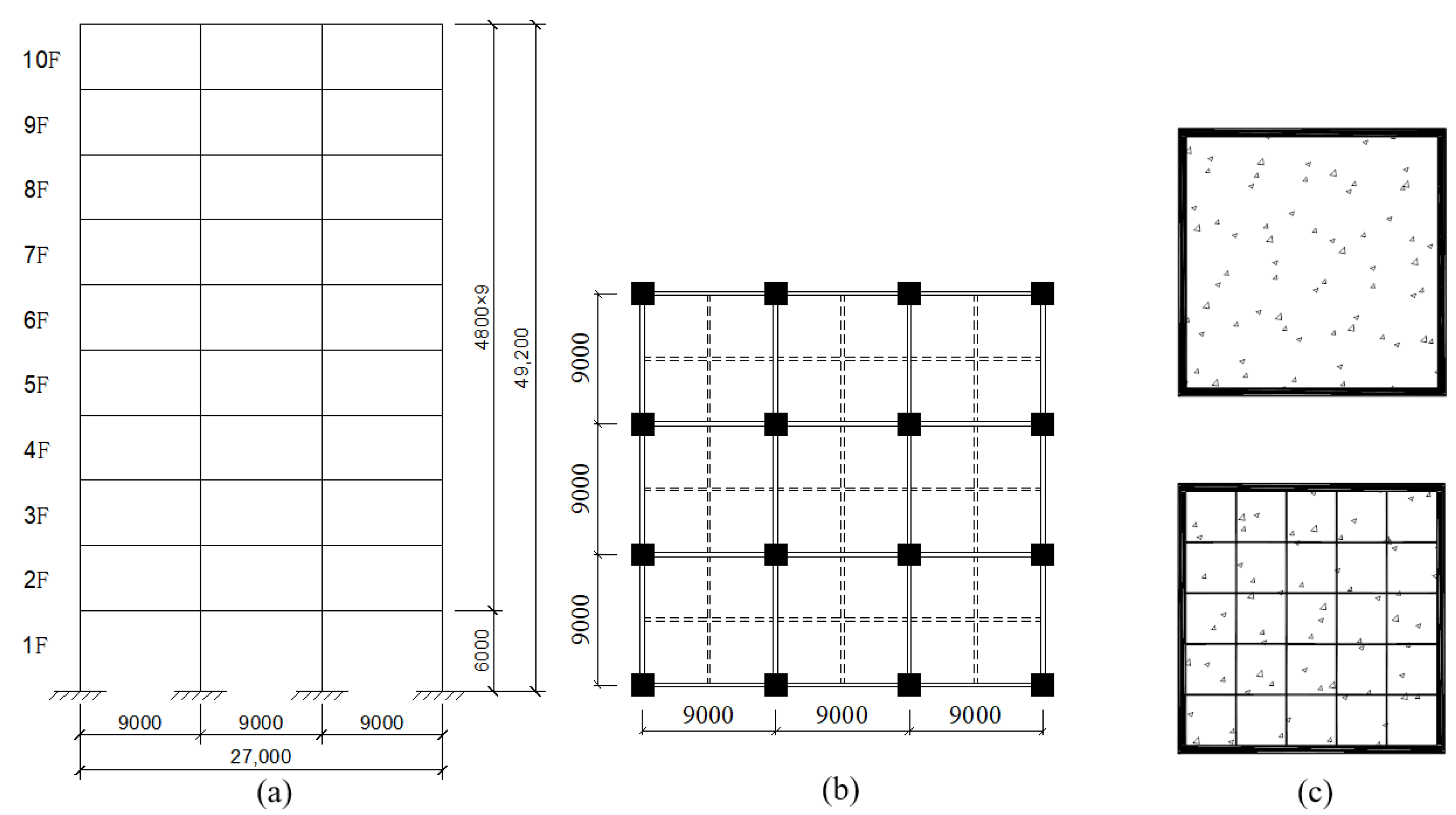
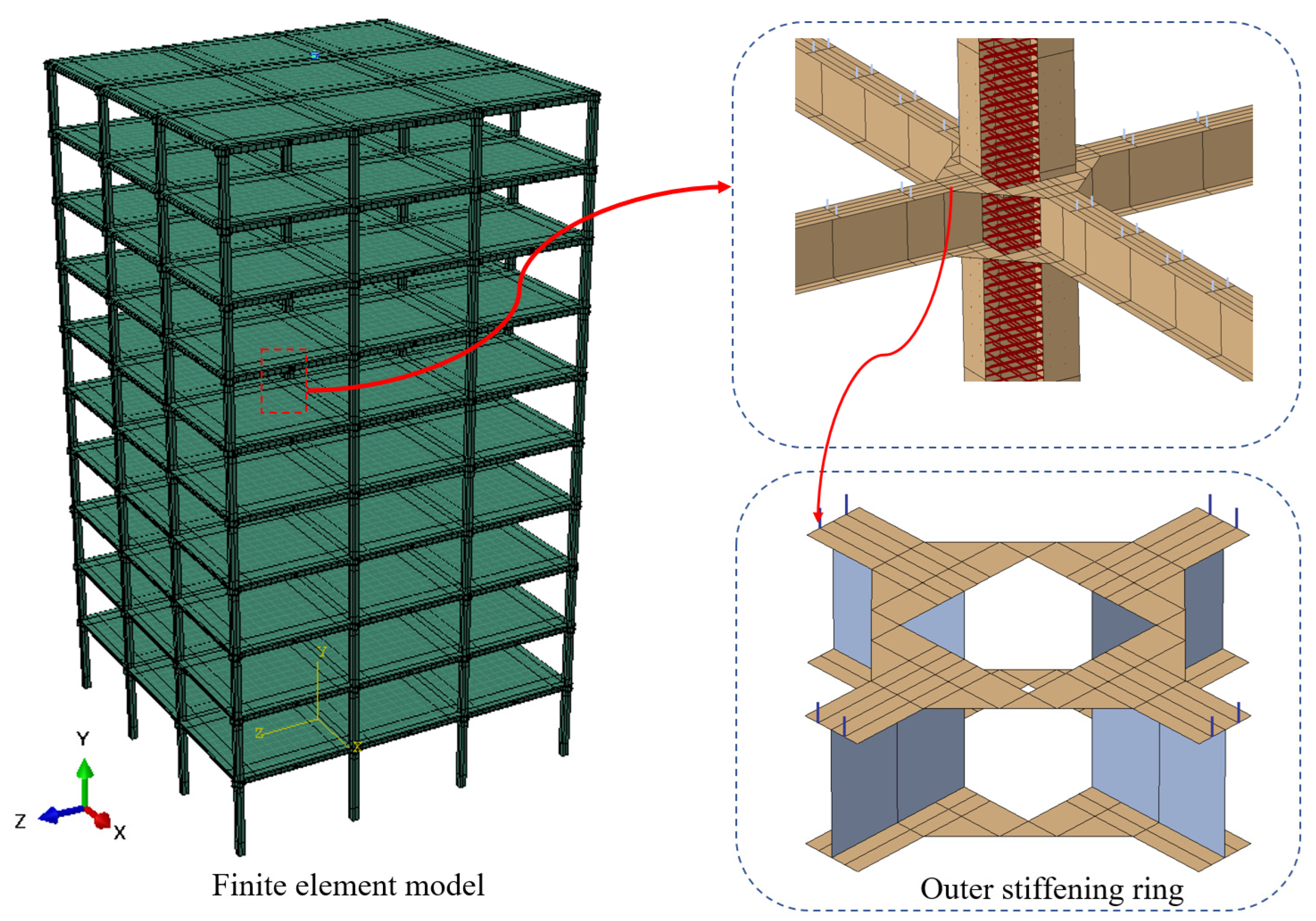
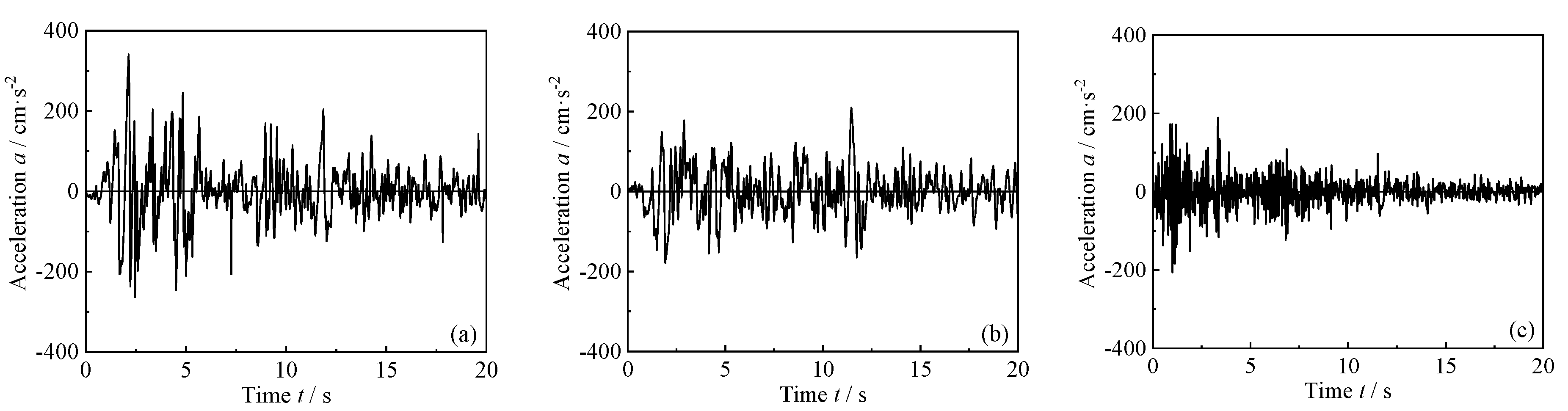



| Model Case | Column-End Stirrup Confined | Seismic Wave Direction | Recycled Aggregate Replacement Ratio/% |
|---|---|---|---|
| KJ-1 | No | N–S; N–S, E–W, U–D | 0 |
| KJ-2 | No | N–S; N–S, E–W, U–D | 50 |
| KJ-3 | No | N–S; N–S, E–W, U–D | 100 |
| KJ-4 | Yes | N–S; N–S, E–W, U–D | 50 |
| KJ-5 | Yes | N–S; N–S, E–W, U–D | 100 |
| Material | Recycled Aggregate Replacement Ratio/% | Elastic Modulus/MPa | Poisson’s Ratio | Strength Grade |
|---|---|---|---|---|
| Concrete | 0 | 34,998 | 0.2 | C50 |
| Concrete | 50 | 29,748 | 0.2 | C50 |
| Concrete | 100 | 24,498 | 0.2 | C50 |
| Steel bar | 2.06 × 105 | 0.285 | HRB400 | |
| Stud | 2.06 × 105 | 0.285 | ML15 | |
| Steel tube | 2.06 × 105 | 0.285 | Q235 | |
| Steel beam | 2.06 × 105 | 0.285 | Q235 |
| Force Mode | Compression | Tension |
|---|---|---|
| Conventional concrete | fc = 0.4fcu7/6, Ec = 9500fcu1/3, εc = 291fcu7/15 × 10−6; A1 = 6.9fcu−11/30, B1 = 1.67(A1 − 1)2; | ft = 0.24fcu2/3, εt = 33fcu1/3 × 10−6, A2 = 1.3, B2 = 0.15, α2 = 0.8 |
| Recycled aggregate concrete | fc = 0.4fcu7/6(1 − 0.1ηr), Ec = 9500fcu1/3(1 − 0.3ηr), εc = (1 + 0.2ηr)291fcu7/15 × 10−6, A1 = 6.9fcu−11/30(1 − 0.3ηr)(1 + 0.2ηr)/(1 − 0.1ηr), B1 = 1.67(A1 − 1)2 | ft = 0.24fcu2/3(1 − 0.1ηr), εt = 33fcu1/3 × 10−6(1 + 0.1ηr), A2 = 1.3(1 − 0.3ηr)(1 + 0.1ηr)/(1 − 0.1ηr), B2 = 1.67(A2 − 1)2, α2 = 0.8 |
| Model No. | KJ-1/Hz | KJ-2 (ηr = 0.5)/Hz | Rate of Decrease/% | KJ-3 (ηr = 1)/Hz | Rate of Decrease | Vibration Modes |
|---|---|---|---|---|---|---|
| 1 | 0.233 | 0.228 | 2.15 | 0.222 | 4.72% | Translational vibration |
| 2 | 0.258 | 0.252 | 2.33 | 0.244 | 5.43% | Translational vibration |
| 3 | 0.299 | 0.291 | 2.68 | 0.283 | 5.35% | Torsional vibration |
| 4 | 0.735 | 0.717 | 2.48 | 0.696 | 5.31% | Bending vibration |
| 5 | 0.807 | 0.785 | 2.73 | 0.76 | 5.82% | Bending vibration |
| 6 | 0.936 | 0.91 | 2.78 | 0.881 | 5.88% | Torsional vibration |
| Model No. | KJ-1/Hz | KJ-4 (ηr = 0.5)/Hz | Rate of Increase/% | KJ-3 (ηr = 1)/Hz | Rate of Increase | Vibration Modes |
|---|---|---|---|---|---|---|
| 1 | 0.233 | 0.249 | 6.87% | 0.243 | 4.29% | Translational vibration |
| 2 | 0.258 | 0.256 | −0.78% | 0.248 | −3.88% | Translational vibration |
| 3 | 0.299 | 0.306 | 2.34% | 0.297 | −0.67% | Torsional vibration |
| 4 | 0.735 | 0.78 | 6.12% | 0.757 | 2.99% | Bending vibration |
| 5 | 0.807 | 0.8 | −0.87% | 0.773 | −4.21% | Bending vibration |
| 6 | 0.936 | 0.955 | 2.03% | 0.925 | −1.17% | Torsional vibration |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Chen, X.; Xu, H.; Hui, B.; Huang, J.; Wang, L.; Sadat, S.I.; Ding, F. Seismic Performance of Recycled Aggregate Concrete-Filled Steel Tube Column–Composite Beam Frames with Column-End Stirrup Confinement. Materials 2025, 18, 2458. https://doi.org/10.3390/ma18112458
Yang Z, Chen X, Xu H, Hui B, Huang J, Wang L, Sadat SI, Ding F. Seismic Performance of Recycled Aggregate Concrete-Filled Steel Tube Column–Composite Beam Frames with Column-End Stirrup Confinement. Materials. 2025; 18(11):2458. https://doi.org/10.3390/ma18112458
Chicago/Turabian StyleYang, Zhi, Xingnian Chen, Hongchang Xu, Baoye Hui, Jia Huang, Liping Wang, Said Ikram Sadat, and Faxing Ding. 2025. "Seismic Performance of Recycled Aggregate Concrete-Filled Steel Tube Column–Composite Beam Frames with Column-End Stirrup Confinement" Materials 18, no. 11: 2458. https://doi.org/10.3390/ma18112458
APA StyleYang, Z., Chen, X., Xu, H., Hui, B., Huang, J., Wang, L., Sadat, S. I., & Ding, F. (2025). Seismic Performance of Recycled Aggregate Concrete-Filled Steel Tube Column–Composite Beam Frames with Column-End Stirrup Confinement. Materials, 18(11), 2458. https://doi.org/10.3390/ma18112458







