Abstract
The Curie temperature (Tc) of LaMnO3-based perovskites is one of the most important properties associated with their magnetic and spintronic applications. The search for new perovskites with even higher Tc is a challenging problem in material design. Through the systematic optimization of support vector regression (SVR) architecture, we establish a predictive framework for determining the Curie temperature (Tc) of doped LaMnO3 perovskites, leveraging fundamental atomic descriptors. The correlation coefficient (R) between the predicted and experimental Curie temperatures demonstrated high values of 0.9111 when evaluated through the leave-one-out cross-validation (LOOCV) approach, while maintaining a robust correlation of 0.8385 on the independent test set. The subsequent high-throughput screening of perovskite compounds exhibiting higher Curie temperatures was implemented via our online computation platform for materials data mining (OCPMDM), enabling the rapid identification of candidate materials through systematic screening protocols. The findings demonstrate that machine learning exhibits significant efficacy and cost-effectiveness in identifying lanthanum manganite perovskites with elevated Tc, as validated through comparative computational and empirical analyses. Furthermore, a web-based computational infrastructure is implemented for the global dissemination of the predictive framework, enabling the open-access deployment of the validated machine learning model.
1. Introduction
Perovskite exhibits broad applicability in fields such as hydrogen generation via photocatalytic water splitting and photovoltaic devices, attributed to its exceptional ferroelectric behavior, versatile physicochemical functionalities, and facile structural tailorability [1,2]. Nevertheless, the exploration of perovskite-based functionalities is largely limited by the insufficiently high Curie temperatures (Tc) of existing materials. Tc is the temperature at which a system undergoes a phase transition from ferromagnetic to paramagnetic, or the temperature at which transition from ferroelectric to paraelectric ordering takes place. Enhancing the Curie temperature of perovskite materials remains a critical challenge requiring further investigation in this research field [3,4,5].
With the constant advancement of the Materials Genome Initiative (MGI), an increasing number of data mining models have been reported to facilitate the acceleration of material design and optimization. An increasing number of researchers are contributing to the rational design and property customization of advanced materials through the strategic manipulation of material “genes”. These genes are atomic-scale descriptors that include composition, structural characteristics, defect states, and synthesis parameters, all of which influence macroscopic functionalities. Data-driven material design also establishes a multidisciplinary framework that synergistically couples computational datasets with experimental validation through the integration of high-throughput computational screening and multiscale simulation techniques. This paradigm transition replaces conventional empirical trial-and-error approaches with a rational design strategy, enabling cost-effectiveness, efficiency, and accelerated development timelines. The systematic convergence of these methodologies facilitates the rapid exploration of material property landscapes, thereby substantially lowering research and development expenditures and the time-to-market for advanced functional materials. Sun et al. developed a data-driven surrogate model to predict the solar array output power in stratospheric airships, which achieved a remarkable improvement in prediction accuracy by 98.65% compared to conventional numerical simulations, while demonstrating a 10-million-fold increase in computational efficiency [6]. Li et al. reported an enhanced performance in inverted perovskite solar cells through chemical interface engineering, achieving an impressive power conversion efficiency (PCE) of 25% [7].
As the typical colossal magnetoresistive perovskites, the search for new lanthanum manganite (LaMnO3)-based perovskites with a higher Tc is a challenging problem for emerging spintronics. Herein, we develop a machine learning model to screen doped LaMnO3 perovskites with a high temperature performance. The structural configuration of the ABO3-type perovskites examined in this study is schematically represented in Figure 1, demonstrating the characteristic cation occupancy where the A-site is predominantly occupied by rare-earth/alkaline-earth species (e.g., La3+, Sr2+), and the B-site by transition metal cations (e.g., Mn3+). The A and B lattice positions in the A-type antiferromagnetic [8] insulator LaMnO3 permit cation substitution to modulate its functional properties. For instance, the substitution of some La3+ by divalent cations like Sr2+ or Ca2+ induces significant electronic effects, which form the basis of enormous complex phenomena, including colossal magnetoresistance.
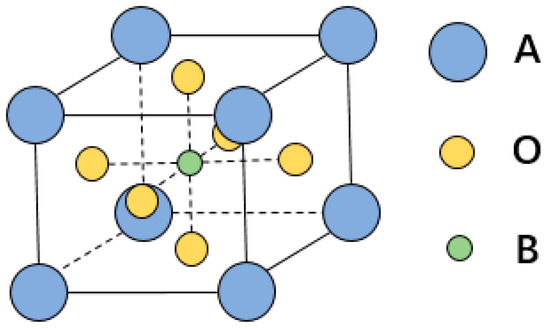
Figure 1.
The crystal structure of ABO3 perovskite where the A-site cation is usually a rare-earth/alkaline-earth element like La3+ and Sr2+, while the B-site cation is a transition metal element such as Mn3+.
It should be noted that many theoretical and experimental researchers might criticize machine learning models, because these algorithms are often utilized as a black box in most case studies. In this work, we will not discuss the validity of the criticism and possible approaches to this challenge. Nevertheless, we have provided our developed models by allowing anyone to use the tool online easily, as it is accessible via a public website. Thus, we hope that it will guide future experiments to accelerate the search for lanthanum manganite perovskites with a higher Tc.
2. Methods
2.1. The Flowchart of Materials Data Mining
Figure 2 illustrates the six steps of material data mining undertaken in this study. To develop a robust machine learning model for assisting the design of lanthanum manganite perovskite materials with an elevated critical temperature (Tc), the following six-step protocol should be implemented: (i) Data preparation involves the compilation of a rigorously validated benchmark dataset to facilitate the training and testing of computational models; (ii) Feature selection requires us to choose the optimal subset from the initial features as the descriptors of the model; (iii) Model selection demonstrates the establishment of a statistical optimization framework that systematically captures the underlying correlations between the response variables and the prediction space; (iv) Hyper-parameter optimization suggests how to adjust the parameters adopted in a model so that the model can perform well; (v) Model Validation refers to the process of assessing the predictive accuracy of a developed model through cross-validation tests and independent tests; (vi) Model Application establishes a workflow integrating predictive modeling with material design, culminating in the deployment of an automated web platform that enables the accelerated discovery of candidate materials through cloud-based computational screening. Below, we detail the contents of the six steps mentioned above.
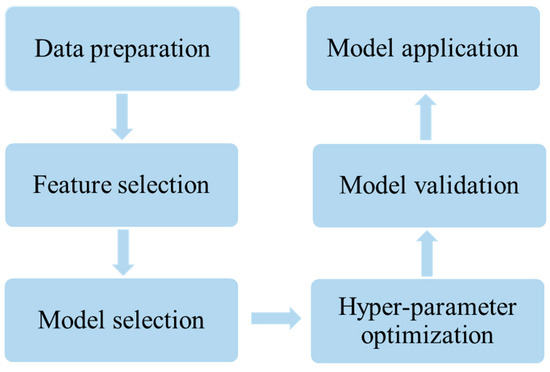
Figure 2.
The flowchart of the six steps undertaken during material data mining in this work.
2.2. Data Preparation
We collected 66 example compounds of LaxMyNzR1-x-y-zMnnQ1-nO3 perovskites (M, N, R, and Q are dopant metal cations) with a Tc ranging between 160 K and 380 K from the literature (see Table S1 in the Supplementary Materials) [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. The dataset was divided into two subsets in a random way: 53 samples for the training and the leave-one-out cross-validation (LOOCV) set, and 13 samples for the test set. In addition, we collected 21 atomic parameters as the initial features quoted from Lange’s Handbook of Chemistry (16th ed.) [25], as tabulated in Table 1.

Table 1.
The 21 atomic parameters used as the initial features of the dataset.
2.3. Machine Learning Methods
2.3.1. Gradient Boosting Regression (GBR)
Gradient boosting is an integrated learning algorithm that is based on the idea of adding new trees to the ensemble in order [26]. It can avoid the problem of overfitting with good accuracy. At each iteration, GBR minimizes the loss function by recovering the error of the previous ensemble trees while performing prediction in the next tree [27]. Thus, the error will keep decreasing. GBR has several advantages, such as excellent adaptability to high-dimensional mixed types of input values, including numerical and categorical variables and robustness against irrelevant input variables, which means that we do not need to input the missing values because the model can handle it automatically. In addition, the model does not need to be retrained from the very beginning when new data are available, therefore improving the calculation efficiency greatly. Because of these multiple advantages, GBR has been widely used in many research fields [28,29,30].
2.3.2. Decision Tree Regression (DTR)
Decision tree is a data analytic technique that explores the potential complex interactions within data by creating binary segmentations of individuals into sub-groups [31]. The membership of a subgroup is derived from the response to a set of measurement/prediction variables. Individuals are initially grouped based on similar scores for one predictor, and then divided into different subgroups based on further predictors [32]. And the position of the variables is determined hierarchically by locating the most important variables at the root of the tree [33]. Decision tree has many advantages. For example, it does not need to assume the distribution of exploratory variables; it is not affected by the high correlation between independent variables; and the most important variables that explain the dependent variables are included in the decision tree, while the unimportant variables are excluded [34]. There are various decision tree methods, including chi-squared automatic interaction detection (CHAID), the classification and regression tree (CART), and exclusive CHAID. Although decision tree was originally developed for large datasets, it may also provide accurate predictions for small datasets.
2.3.3. Random Forest Regression (RFR)
The random forest algorithm, initially proposed by Breiman and rooted in decision tree architectures, exhibits enhanced generalization capabilities as an ensemble learning methodology [35]. RFR constitutes an ensemble of unpruned regression trees constructed through the bootstrap sampling of training data with random feature selection during tree construction, ultimately aggregating predictions through mean averaging across all constituent trees in the regression framework [36]. In other words, random forest aims to find a consensus among the imperfect trees rather than a perfect one which may result in overfitting. This algorithm is well suited to dealing with high-dimensional datasets, avoiding overfitting and allowing an averaging effect across all the single models [37,38].
2.3.4. Support Vector Regression (SVR)
Support vector machine (SVM) was initially introduced by Vapnik in 1964, and is grounded in the framework of statistical learning theory (SLT) [39]. This supervised learning algorithm employs risk minimization principles by strategically balancing empirical risk and expected risk, thereby deriving globally optimal solutions through the convex optimization of the regularized loss function. SVM, encompassing support vector classification (SVC) and support vector regression (SVR), has been widely utilized to address nonlinear classification and regression challenges owing to its demonstrated robustness in handling small-scale datasets characterized by high-dimensional feature spaces [40,41,42].
Given the training data {(xi, yi), i = 1, 2, … l}, x ∈ Rn, y ∈ R, the regression function is defined as the following linear relationship:
where w and b are the coefficients to be adjusted. The optimal regression function can be obtained by calculating the minimum value of the following formula:
where C is the regularization constant, which adjusts the trade-off between the model complexity and training errors. and are the upper and lower limits of slack variables. Vapnik put forward the ɛ-insensitive loss function:
This function aims to determine an optimal hyperplane that maximizes the margin of separation between two linearly separable subsets within the training dataset. The solution can be obtained by the following quadratic programming optimization problem shown in Equation (4)
The constraints of this optimization problem are as follows:
where and are the Lagrangian coefficients. By solving the above-described optimization problem, the coefficients of Equation (1) can be found as follows:
For the nonlinear relationship between the input and output, the kernel function (K) is introduced to map the original input into the feature space nonlinearly; thus, SVR can be used for more complicated nonlinear regression problems. Within the feature space, the kernel function is formally expressed as follows:
The predominantly employed kernel functions encompass the Gaussian radial basis function (RBF) and polynomial kernels. In this study, the RBF is utilized in the SVR model as follows:
2.4. Computational Software
The material data mining was carried out by using the ExpMiner software package (http://materials-data-mining.com/home/static/download/ExpMiner_setup.msi (15 May 2025)) and the Online Computational Platform of Material Data Mining (OCPMDM) developed in our laboratory [43,44]. ExpMiner can be freely downloaded from the website of the Laboratory of Materials Data Mining in Shanghai University (http://materials-data-mining.com/home/static/download/ExpMiner_setup.msi (accessed on 15 May 2025)), and the OCPMDM can be accessed online at http://materials-data-mining.com/ocpmdm/ (accessed on 15 May 2025).
3. Results and Discussion
3.1. Feature Selection
For any machine learning model, feature selection is very critical because it is difficult to eliminate unnecessary features to improve the prediction performance. The success of a model is determined by the key features selected from a great deal of candidate features. Proper feature selection can not only reduce the dimension of the feature space without redundancy, but also shorten the training time, and further improve the precision and performance of the model [45].
In this work, GA (Genetic Algorithm) [46] combined with SVR, FR (Forward Regression) and BR (Backward Regression) was adopted to select the key features, respectively. The GA approach simulates the natural selection of Darwin’s biological evolution and the biological evolution process of the genetic mechanism. It is a kind of randomization search method derived from the evolution law of biology (survival of the fittest). Compared with other algorithms, GA can move from the local optima present on the response surface and realize a wide variety of optimizations without requiring knowledge or a gradient about the response surface to be present. FR and BR are two classical methods used for independent variable screening, whose principles are simple but effective. Forward selection is performed to keep one variable at the beginning, and then other variables are added step by step [47]. Meanwhile, the contribution of variables to the model is observed, keeping the variables with a significant contribution and eliminating the ones with a small contribution until the model reaches an optimal level. On the contrary, the backward selection is performed to adopt all the variables at the beginning, and then gradually eliminate the variables that have no significant contribution to the model until all the variables in the model have a significant contribution.
In order to evaluate the feature selection, the root mean square error (RMSE) was employed as the goodness-of-fit measure. The RMSE is defined as follows:
where and are the experimental and predicted values of sample , respectively, and is the number of samples. A statistically significant inverse relationship is observed between RMSE magnitudes and the optimality of the feature set, where diminished RMSE values systematically correspond to an enhanced predictive performance in computational modeling frameworks.
A total of 21 initial features (all are listed in Table S1 in the Supplementary Materials) such as the tolerance factor, atomic radius and molecular mass were chosen to describe the perovskites. To mitigate the redundancy and interdependence among the 21 features, their Pearson correlation coefficients were computed and are presented in Figure 3a. After checking the correlation coefficients between pairs of features, it was found that four features could be deleted because their correlation coefficients with the other features were more than 0.9. As shown in Figure 3b, the decorrelation process resulted in a reduction in the selected feature set from 21 to 17.
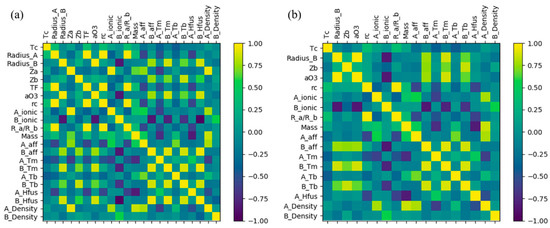
Figure 3.
Pearson correlation coefficient heat map of (a) 21 initial features and (b) 17 selected features after deleting the features with co-linearity. The color-coded bar adjacent to the figure represents correlation coefficients, with yellow denoting positive correlations and blue signifying negative correlations.
Then, GA combined with SVR, BR and FR was employed to filter the features. According to the LOOCV results, FR outperformed the other two algorithms, as shown in Table 2. Thus, the seven features from the forward method based on the LOOCV results obtained by using SVR were selected to establish the model as the optimal subset of initial features.

Table 2.
The results of feature selection when using different algorithms.
3.2. Model Selection
The development of an optimal model that achieves a balance between overfitting and underfitting is critical in data mining. Here, the operational validation of different machine learning models was executed through LOOCV procedures, employing correlation coefficient R as the key performance indicator for predictive consistency measurement. In this work, four algorithms, namely, SVR, GBR, RFR and DTR, were used to predict the Tc of perovskites, whose results are shown in Table 3 and Figure 4. Comparative analyses showed that SVR outperformed the other models based on the R, RMSE and MRE (mean relative error) of LOOCV tests. Thus, the SVR algorithm was selected to construct the prediction model. The MRE is defined as follows:
where and denote the experimental and predicted values of sample , respectively, and represents the total sample count.

Table 3.
The results of the LOOCV validations when using different algorithms, including SVR, GBR, RFR and DTR.
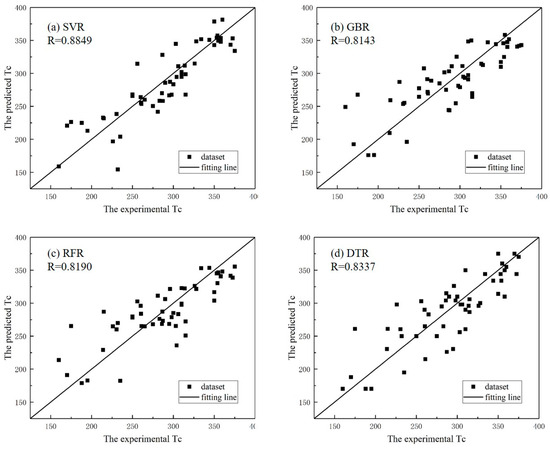
Figure 4.
The experimental versus the predicted Tc of the LOOCV results when using (a) SVR, (b) GBR, (c) RFR and (d) DTR models.
3.3. Hyper-Parameter Optimization
The model selection identified Support Vector Regression (SVR) as the optimal candidate, demonstrating statistical superiority, with the highest R = 0.8849 and lowest RMSE (26.50) compared to other algorithms. To improve its generalization ability, the SVR model using the Gaussian radial basis function (RBF) was further optimized based on the hyper-parameter optimization. The optimal model performance was achieved with parameter values of C = 32, .06, and .0, as illustrated in Figure 5.
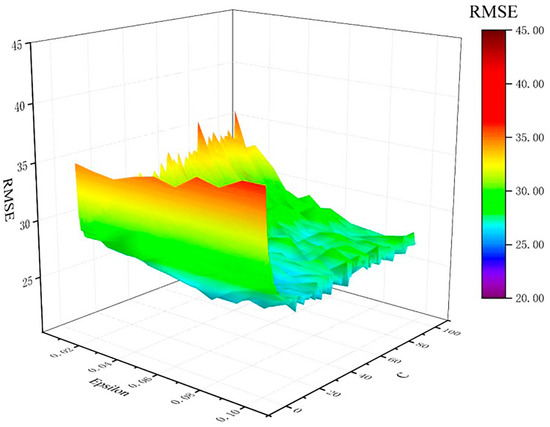
Figure 5.
RMSE of LOOCV vs. and C adopted in the SVR model.
3.4. Model Validation
To validate the generalization capability of the SVR model, LOOCV was employed to assess the predictive robustness of the developed framework, thereby ensuring the rigorous evaluation of its extrapolation performance. Figure 6 shows the plots of the predicted values versus the experimental values of Tc for lanthanum manganite perovskites based on the LOOCV of the training set. It is observed that the predicted values lie near the actual line (y = x), with R and RMSE values equal to 0.9119 and 23.22 (K), respectively, as shown in Table 4. The MAE is defined as follows:
where and are the experimental and predicted values of sample , respectively, and is the number of samples.
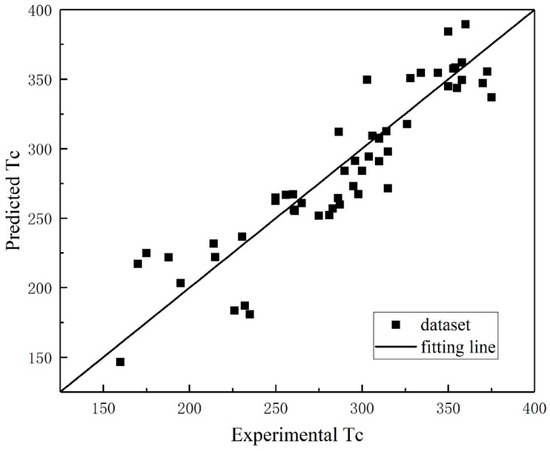
Figure 6.
The experimental versus the predicted Tc based on the LOOCV results.

Table 4.
The LOOCV validation results of the training dataset.
To further confirm the generalization performance of the SVR model, the Curie temperatures of the 13 samples in the independent test set were predicted by using the trained model. Figure 7 illustrates the experimental and predicted Tc values of the training and test datasets, respectively. The R of the independent test is 0.8385, which is shown in Table 5.
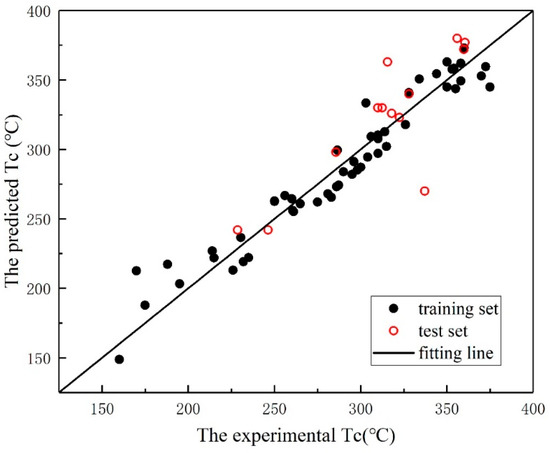
Figure 7.
The experimental versus the predicted Tc of perovskites when using SVR.

Table 5.
The results of the independent test.
From the above results, it can be concluded that the SVR model established in this work would be able to predict the Tc of lanthanum manganite perovskites.
3.5. Sensitivity Analysis
Sensitivity analysis has been extensively applied across various data mining domains to investigate the variation in the target variable with respect to an individual feature, while maintaining other features constant at sensitivity points. The SVR model available here shows that some parameters are significant with regard to the Tc of perovskites. Figure 8 delineates the sensitivity assessment for each feature in the optimized subset.
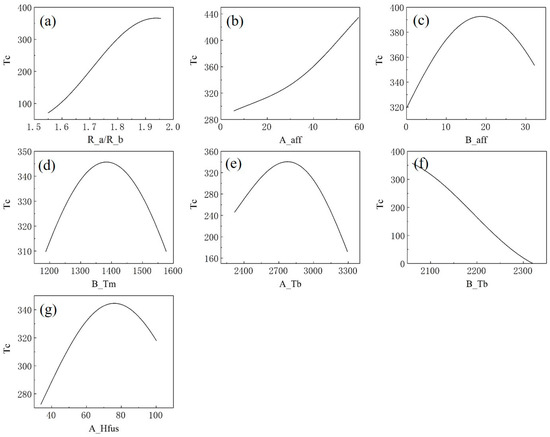
Figure 8.
Sensitivity analyses with (a) the ratio of the atomic radius of the A and B positions (R_a/R_b), (b) the electron affinity of the A position (A_aff), (c) the electron affinity of the B position (B_aff), (d) the melting point of the B position (B_Tm), (e) the normal boiling point of the A position (A_Tb), (f) the normal boiling point of the B position (B_Tb), (g) the enthalpy of fusion at the melting point of the A position (A_Hfus). The sensitivity point is set at the average values of features of samples with a higher Tc.
Figure 8a,b show that the Tc goes up with the increase in R_a/R_b and A_aff, respectively. Figure 8c–e,g demonstrate that B_aff, B_Tm, A_Tb and A_Hfus have parabolic relationships with Tc, with a maximum Tc equal to 392.7, 345.7, 340.5 and 342.6, respectively. In Figure 8f, B_Tb is negatively correlated with Tc.
3.6. Model Application
3.6.1. High-Throughput Screening of New Lanthanum Manganite Perovskites
In order to discover new perovskites with a higher Tc, the established model for predicting Tc was used on OCPMDM to screen out the targeted perovskites among various candidates. The screening was performed according to the following rules:
- (1)
- The A site is doped with no more than two different doping ions, while the B site is doped with no more than one doping ion.
- (2)
- The A site compositional configuration follows a ternary doping scheme:
- Primary occupant: La with stoichiometric ratios spanning 0.5–1.0 in 0.02 increments.
- Secondary dopant: Sr, Ag, Ca, Pb, or Ba allocated within the 0.0–0.5 range (0.02 step resolution).
- Tertiary constituent: Nd, Ba, Ag, Ca, or Dy occupying residual stoichiometric fractions.
- (3)
- The B-site doping architecture adopts a two-component system:
- Primary constituent: Mn with stoichiometric fractions ranging 0.9–1.0 in 0.02 incremental steps.
- Secondary dopant: Fe or Cr occupying the complementary stoichiometric proportion.
Thus, in total, 99,900 candidates were obtained fir screening. It was found that the highest Tc (391.7 K) of the candidate sample was La0.54Ag0.14Ba0.32MnO3, which has a tolerance factor of 0.89 and exceeds the highest Tc in the training data set (375 K). We hope that the perovskite with a predicted high Tc (391.7 K) will be experimentally verified soon in the laboratory.
3.6.2. Online Web Server Accessible in Public
To facilitate the application of the developed SVR model in perovskite design, a web-based computational platform was implemented to predict the Tc of lanthanum manganite perovskites, leveraging the predictive framework established in this study. Figure 9 shows the interface of the online server for utilizing our model. Once the chemical formula of perovskite is input and the Predict button is pressed, the Curie temperature predicted by the model available in this paper can be obtained. In addition, users can also add the model description, model creator and paper DOI for the work. The online server is accessible via the following URL: http://materials-data-mining.com/ocpmdm/material_api/negr5q1xunlmjagj (accessed on 15 May 2025).
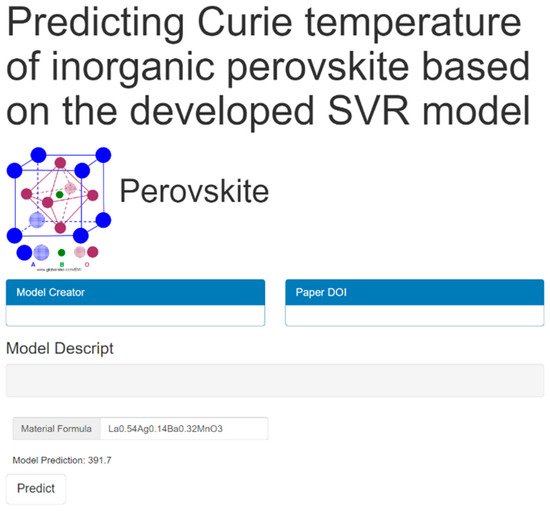
Figure 9.
The interface of the online web server accessible to the public.
4. Conclusions
Based on the data collected from the published references, we developed an SVR machine learning model to predict the Curie temperature of lanthanum manganite perovskites by using atomic parameters as inputs. The machine learning model showed a good performance when predicting Tc in a fast and easy way. Based on the high-throughput screening of visual candidates, we discovered the specific perovskite compound (La0.54Ag0.14Ba0.32MnO3) with a higher Curie temperature than the highest one in the training set. It is thought that other properties of materials could be optimized using the reliable data collected and the QSPR model constructed at a low cost [48,49]. As demonstrated in various publications [50,51,52,53,54], the Curie temperature of lanthanum manganite perovskites is affected by many factors such as the types and proportions of doping ions, their morphology, the experimental conditions and so on, which may lead to the deviation of the model established in this paper. Consequently, subsequent research phases will prioritize methodological refinement, including the reporting of more samples and the factors available for improving the prediction accuracy of the model in material design.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/ma18112437/s1, Table S1: The dataset for modeling.
Author Contributions
Methodology, X.J.; software, L.T.; validation, W.W.; investigation, L.T.; data curation, W.W.; writing—original draft preparation, L.T.; writing—review and editing, X.J., Z.X. and W.L.; supervision, Z.X., W.Z. and W.L.; project administration, W.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Major Science and Technology Projects of Yunnan Precious Metals Laboratory (No. YPML-2023050205), Yunnan Precious Metals Laboratory Science and Technology Plan Project (No. YPML-2023050208, YPML-2023050280).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are openly available in the Supplementary Materials.
Conflicts of Interest
Author Wenyan Zhou was employed by the company Sino-Platinum Metals Semiconductor Materials (Yunnan) Co., Ltd. and Yunnan Precious Metals Laboratory Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Yan, R.; Zou, Y.; Du, C.; Yu, H.; Jiang, J.; Cao, J.; Yu, G.; Dong, W.; Peng, H.; Yang, Y.; et al. Research progress of polarized perovskite type ferroelectric materials for photocatalytic hydrogen production. J. Energy Chem. 2025, 107, 87–102. [Google Scholar] [CrossRef]
- Li, Q.; Zheng, Y.; Wang, H.; Liu, X.; Lin, M.; Sui, X.; Leng, X.; Liu, D.; Wei, Z.; Song, M.; et al. Graphene-polymer reinforcement of perovskite lattices for durable solar cells. Science 2025, 387, 1069–1077. [Google Scholar] [CrossRef]
- Xu, H.; Guo, W.; Liu, Y.; Ma, Y.; Fan, Q.; Tang, L.; Li, W.; Ni, H.; Luo, J.; Sun, Z. Customizing Room-Temperature Perovskite Ferroelectrics toward the Multichannel Domain Manipulation. Angew. Chem. Int. Ed. 2025, e202501238. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, S.; Wang, X.; Ye, X.; Qin, S.; Shen, X.; Lu, D.; Dai, J.; Cao, Y.; Chen, K.; et al. Realization of a Half Metal with a Record-High Curie Temperature in Perovskite Oxides. Adv. Mater. 2022, 34, e2200626. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.; Jiang, H.; Peng, Y.; Zhang, X.; Chen, S.; Liu, X.; Luo, J. High-Curie Temperature Multilayered Hybrid Double Perovskite Photoferroelectrics Induced by Aromatic Cation Alloying. J. Am. Chem. Soc 2021, 143, 15900–15906. [Google Scholar] [CrossRef]
- Sun, K.; Liu, S.; Gao, Y.; Du, H.; Cheng, D.; Wang, Z. Output power prediction of stratospheric airship solar array based on surrogate model under global wind field. Chin. J. Aeronaut. 2025, 38, 103244. [Google Scholar] [CrossRef]
- Li, K.; Zhu, Y.; Chang, X.; Zhou, M.; Yu, X.; Zhao, X.; Wang, T.; Cai, Z.; Zhu, X.; Wang, H.; et al. Self-Induced Bi-interfacial Modification via Fluoropyridinic Acid For High-Performance Inverted Perovskite Solar Cells. Adv. Energy Mater. 2024, 15, 613. [Google Scholar] [CrossRef]
- Yang, Y.; Xiang, H.; Zhao, H.; Stroppa, A.; Zhang, J.; Cao, S.; Íñiguez, J.; Bellaiche, L.; Ren, W. Improper ferroelectricity at antiferromagnetic domain walls of perovskite oxides. Phys. Rev. B 2017, 96, 104431. [Google Scholar] [CrossRef]
- Abassi, M.; Dhahri, N.; Dhahri, J.; Hlil, E.K. Structural and large magnetocaloric properties of La0.67-xYxBa0.23Ca0.1MnO3 perovskites (0< = × < = 0.15). Physica B Condens. Matter 2014, 449, 138–143. [Google Scholar] [CrossRef]
- Anwar, M.S.; Ahmed, F.; Koo, B.H. Structural distortion effect on the magnetization and magnetocaloric effect in Pr modified La0.65Sr0.35MnO3 manganite. J. Alloys Compd. 2014, 617, 893–898. [Google Scholar] [CrossRef]
- Anwar, M.S.; Ahmed, F.; Koo, B.H. Influence of Ce addition on the structural, magnetic, and magnetocaloric properties in La0.7-xCexSr0.3MnO3 (0 < = × < = 0.3) ceramic compound. Ceram. Int. 2015, 41, 5821–5829. [Google Scholar] [CrossRef]
- Arayedh, B.; Kallel, S.; Kallel, N.; Peña, O. Influence of non-magnetic and magnetic ions on the MagnetoCaloric properties of La0.7Sr0.3Mn0.9M0.1O3 doped in the Mn sites by M = Cr, Sn, Ti. J. Magn. Magn. Mater. 2014, 361, 68–73. [Google Scholar] [CrossRef]
- Chau, N.; Nhat, H.N.; Luong, N.H.; Minh, D.L.; Tho, N.D.; Chau, N.N. Structure, magnetic, magnetocaloric and magnetoresistance properties of La1-xPbxMnO3 perovskite. Physica B Condens. Matter 2003, 327, 270–278. [Google Scholar] [CrossRef]
- Debnath, J.C.; Zeng, R.; Kim, J.H.; Dou, S.X. Large magnetic entropy change near room temperature in La0.7(Ca0.27Ag0.03)MnO3 perovskite. J. Alloys Compd. 2011, 509, 3699–3704. [Google Scholar] [CrossRef]
- Dhahri, J.; Dhahri, A.; Oummezzine, M.; Hlil, E.K. Effect of substitution of Fe for Mn on the structural, magnetic properties and magnetocaloric effect of LaNdSrCaMnO3. J. Magn. Magn. Mater. 2015, 378, 353–357. [Google Scholar] [CrossRef]
- Ghodhbane, S.; Tka, E.; Dhahri, J.; Hlil, E.K. A large magnetic entropy change near room temperature in La0.8Ba0.1Ca0.1Mn0.97Fe0.03O3 perovskite. J. Alloys Compd. 2014, 600, 172–177. [Google Scholar] [CrossRef]
- Kallel, N.; Kallel, S.; Hagaza, A.; Oumezzine, M. Magnetocaloric properties in the Cr-doped La0.7Sr0.3MnO3 manganites. Physica B Condens. Matter 2009, 404, 285–288. [Google Scholar] [CrossRef]
- Koubaa, M.; Koubaa, W.C.-R.; Cheikhrouhou, A. Magnetocaloric effect and magnetic properties of La0.75Ba0.1M0.15MnO3 (M = Na, Ag and K) perovskite manganites. J. Alloys Compd. 2009, 479, 65–70. [Google Scholar] [CrossRef]
- Koubaa, W.C.-R.; Koubaa, M.; Cheikhrouhou, A. Structural, magnetotransport, and magnetocaloric properties of La0.7Sr0.3-xAgxMnO3 perovskite manganites. J. Alloys Compd. 2008, 453, 42–48. [Google Scholar] [CrossRef]
- Li, B.H.; Xian-Yu, W.X.; Wan, X.; Zhang, J.; Shen, B.G. Colossal magnetoresistance effects and magnetic properties of La0.7Sr0.3MxMn1−xO3(M = Cr,Fe). Acta Phys. Sin. 2000, 49, 1366–1370. [Google Scholar]
- Phan, M.H.; Tian, S.B.; Hoang, D.Q.; Yu, S.C.; Nguyen, C.; Ulyanov, A.N. Large magnetic-entropy change above 300 K in CMR materials. J. Magn. Magn. Mater. 2003, 258, 309–311. [Google Scholar] [CrossRef]
- Sankarrajan, S.; Sakthipandi, K.; Manivasakan, P.; Thyagarajan, K.; Rajendran, V. On-line phase transition in La1-xSrxMnO3 (0.28 < = x < = 0.36) perovskites through ultrasonic studies. Phase Transit. 2011, 84, 657–672. [Google Scholar] [CrossRef]
- Zhang, D.; Du, Y. Relation between structure and Curie-temperature of peroviskite with colossal magnetoresistance effect. J. Funct. Mater. 2002, 33, 495–496, 499. [Google Scholar]
- Zhao, J.; Li, L.; Wang, G. Magnetocaloric Properties in (La0.57Dy0.1)Sr0.33MnO3 Poly-crystalline Nanoparticles. Rare Met. Mater. Eng. 2009, 38, 1707–1710. [Google Scholar]
- James Speight, P.D. Lange’s Handbook of Chemistry, 16th ed.; McGraw-Hill Education: New York, NY, USA, 2005. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Math. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Wu, T.; Wang, J. Global discovery of stable and non-toxic hybrid organic-inorganic perovskites for photovoltaic systems by combining machine learning method with first principle calculations. Nano Energy 2019, 66, 104070. [Google Scholar] [CrossRef]
- Witman, M.; Ling, S.; Grant, D.M.; Walker, G.S.; Agarwal, S.; Stavila, V.; Allendorf, M.D. Extracting an Empirical Intermetallic Hydride Design Principle from Limited Data via Interpretable Machine Learning. J. Phys. Chem. Lett. 2020, 11, 40–47. [Google Scholar] [CrossRef]
- Im, J.; Lee, S.; Ko, T.-W.; Kim, H.W.; Hyon, Y.; Chang, H. Identifying Pb-free perovskites for solar cells by machine learning. npj Comput. Mater. 2019, 5, 37. [Google Scholar] [CrossRef]
- Breiman, L. Classification and Regression Trees; Routledge: London, UK, 2017. [Google Scholar]
- Pilania, G.; Liu, X.-Y.; Wang, Z. Data-enabled structure–property mappings for lanthanide-activated inorganic scintillators. J. Mater. Sci. 2019, 54, 8361–8380. [Google Scholar] [CrossRef]
- Meredig, B.; Agrawal, A.; Kirklin, S.; Saal, J.E.; Doak, J.W.; Thompson, A.; Zhang, K.; Choudhary, A.; Wolverton, C. Combinatorial screening for new materials in unconstrained composition space with machine learning. Phys. Rev. B 2014, 89, 094104. [Google Scholar] [CrossRef]
- Zeng, Y.; Li, Q.; Bai, K. Prediction of interstitial diffusion activation energies of nitrogen, oxygen, boron and carbon in bcc, fcc, and hcp metals using machine learning. Comput. Mater. Sci. 2018, 144, 232–247. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Stanev, V.; Oses, C.; Kusne, A.G.; Rodriguez, E.; Paglione, J.; Curtarolo, S.; Takeuchi, I. Machine learning modeling of superconducting critical temperature. npj Comput. Mater. 2018, 4, 29. [Google Scholar] [CrossRef]
- Harikrishna, S.; Weining, R.; Alessandro, T.; Haibo, M. Toward Predicting Efficiency of Organic Solar Cells via Machine Learning and Improved Descriptors. Adv. Energy Mater. 2018, 8, 1801032. [Google Scholar] [CrossRef]
- Zhu, Q.; Xu, P.; Ji, X.; Shao, M.; Duan, Z.; Lu, W. Discovery and verification of two-dimensional organic–inorganic hybrid perovskites via diagrammatic machine learning model. Mater. Des. 2024, 238, 112642. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 2000. [Google Scholar]
- Möller, J.J.; Körner, W.; Krugel, G.; Urban, D.F.; Elsässer, C. Compositional optimization of hard-magnetic phases with machine-learning models. Acta Mater. 2018, 153, 53–61. [Google Scholar] [CrossRef]
- Balachandran, P.V.; Kowalski, B.; Sehirlioglu, A.; Lookman, T. Experimental search for high-temperature ferroelectric perovskites guided by two-step machine learning. Nat. Commun. 2018, 9, 1668. [Google Scholar] [CrossRef]
- Che, H.; Lu, T.; Cai, S.; Li, M.; Lu, W. Inverse Design of Low-Resistivity Ternary Gold Alloys via Interpretable Machine Learning and Proactive Search Progress. Materials 2024, 17, 3614. [Google Scholar] [CrossRef]
- Zhang, Q.; Chang, D.; Zhai, X.; Lu, W. OCPMDM: Online computation platform for materials data mining. Chemom. Intell. Lab. Syst. 2018, 177, 26–34. [Google Scholar] [CrossRef]
- Chang, D.; Xu, P.; Ji, X.; Li, M.; Lu, W. Application of Online Computational Platform of Materials Data Mining (OCPMDM) in Search for ABO3 Perovskites with Multi-Properties. Sci. Adv. Mater. 2023, 15, 1014–1025. [Google Scholar] [CrossRef]
- Tao, Q.; Xu, P.; Li, M.; Lu, W. Machine learning for perovskite materials design and discovery. npj. Comput. Mater. 2021, 7, 23. [Google Scholar] [CrossRef]
- Browning, N.J.; Ramakrishnan, R.; von Lilienfeld, O.A.; Roethlisberger, U. Genetic Optimization of Training Sets for Improved Machine Learning Models of Molecular Properties. J. Phys. Chem. Lett. 2017, 8, 1351–1359. [Google Scholar] [CrossRef]
- Wang, H. Forward Regression for Ultra-High Dimensional Variable Screening. J. Am. Stat. Assoc. 2009, 104, 1512–1524. [Google Scholar] [CrossRef]
- Ramprasad, R.; Batra, R.; Pilania, G.; Mannodi-Kanakkithodi, A.; Kim, C. Machine learning in materials informatics: Recent applications and prospects. npj Comput. Mater. 2017, 3, 54. [Google Scholar] [CrossRef]
- Butler, K.T.; Davies, D.W.; Cartwright, H.; Isayev, O.; Walsh, A. Machine learning for molecular and materials science. Nature 2018, 559, 547–555. [Google Scholar] [CrossRef]
- Taboada-Moreno, C.A.; Sánchez-De Jesús, F.; Pedro-García, F.; Cortés-Escobedo, C.A.; Betancourt-Cantera, J.A.; Ramírez-Cardona, M.; Bolarín-Miró, A.M. Large magnetocaloric effect near to room temperature in Sr doped La0.7Ca0.3MnO3. J. Magn. Magn. Mater. 2020, 496, 165887. [Google Scholar] [CrossRef]
- Shreekala, R.; Rajeswari, M.; Srivastava, R.C.; Ghosh, K.; Eom, C.B. Ferromagnetism at room temperature in La0.8Ca0.2MnO3 thin films. Appl. Phys. Lett. 1999, 74, 1886–1888. [Google Scholar] [CrossRef]
- Schiffer, P.; Ramirez, A.P.; Bao, W.; Cheong, S.W. Low Temperature Magnetoresistance and the Magnetic Phase Diagram of La1−xCaxMnO3. Phys. Rev. Lett. 1995, 75, 3336–3339. [Google Scholar] [CrossRef]
- Prellier, W.; Rajeswari, M.; Venkatesan, T.; Greene, R.L. Effects of annealing and strain on La1−xCaxMnO3 thin films: A phase diagram in the ferromagnetic region. Appl. Phys. Lett. 1999, 75, 1446–1448. [Google Scholar] [CrossRef]
- Fontcuberta, J.; Laukhin, V.; Obradors, X. Local disorder effects on the pressure dependence of the metal-insulator transition in manganese perovskites. Appl. Phys. Lett. 1998, 72, 2607–2609. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).