Crystal Plasticity Modeling of Strain Hardening Induced by Coherent Precipitates in Inconel 718 Superalloy
Abstract
1. Introduction
2. Material Preparation and Microstructural Characterization
3. Modeling Methods
3.1. Crystal Plasticity-Based Micromechanical Finite Element Models
3.2. Constitutive Formulation
3.3. Calibration of the CPFE Model Assisted by Experimental Data and MD Simulations
4. Results
4.1. Multiscale Stress–Strain Response
4.2. The Distribution and Evolution of the SSD and GND Dislocation Density
4.3. Dislocation Shearing Effect
4.4. Length-Scale Dependence of the Unit Cell Model
5. Discussion
6. Concluding Remarks
- The length-scale dependent crystal plasticity modeling results reveal distinct behaviors of the three variants, which significantly influence the deformation process in the phase and lead to pronounced strain and stress heterogeneity. Specifically, the [100] and [001] variants exhibit higher stress partitioning compared with the [010] variant under uniaxial [010] tensile loading, enabling them to accommodate dislocation shearing more effectively. This behavior reduces strain localization and dislocation density in the adjacent phase, highlighting the critical role of variant-specific interactions in governing deformation mechanisms.
- During plastic deformation, the dislocation density, especially at phase boundaries, shows a notable increase. Through the CPFE model, the length scale effect was systematically measured. The results quantitatively indicate that a reduction in precipitate size corresponds to a significant enhancement in strain hardening. For example, a precipitate significantly influences the evolution of the GND density, although a relatively weak length-scale effect was observed on the stress partitioning among the three precipitate variants. The flow stress difference between the largest and smallest size of the precipitate currently is about 100 MPa at 5% applied strain.
- This study provides critical information on the micromechanical behavior of precipitates in nickel-based superalloys, particularly IN718, elucidating the interaction between precipitate size, variant-specific deformation, and strain hardening. The findings underscore the importance of tailoring precipitate morphology and distribution to optimize mechanical performance in high-temperature applications. These results offer practical guidance for the design and processing of advanced alloys, enabling improved control over their deformation and strengthening mechanisms under service conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IN718 | Inconel 718 |
| CP | Crystal plasticity |
| MD | Molecular dynamics |
| CRSS | Critical resolved shear stress |
| EBSD | Electron backscatter diffraction |
| FE | Finite element |
| CPFE | Crystal plasticity finite element |
| SSD | Statistically stored dislocation |
| GND | Geometrically necessary dislocation |
References
- Hall, E. The deformation and ageing of mild steel: III discussion of results. Proc. Phys. Soc. Sect. B 1951, 64, 747. [Google Scholar] [CrossRef]
- Decker, R. The evolution of wrought age-hardenable superalloys. JOM 2006, 58, 32–36. [Google Scholar] [CrossRef]
- Reed, R.C. The Superalloys: Fundamentals and Applications; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Nageswara Rao, M. Factors influencing the notch rupture life of superalloy 718. Trans. Indian Inst. Met. 2010, 63, 363–367. [Google Scholar] [CrossRef]
- Bridges, D.; Xu, R.; Hu, A. Microstructure and mechanical properties of Ni nanoparticle-bonded Inconel 718. Mater. Des. 2019, 174, 107784. [Google Scholar] [CrossRef]
- Bai, P.; Huo, P.; Wang, J.; Yang, C.; Zhao, Z.; Zhang, Z.; Wang, L.; Du, W.; Qu, H. Microstructural evolution and mechanical properties of Inconel 718 alloy manufactured by selective laser melting after solution and double aging treatments. J. Alloy. Compd. 2022, 911, 164988. [Google Scholar] [CrossRef]
- Holfelder, P.; Brenner, F.; Rund, M.; Witte, A.; Junghans, S.; Seyfert, C.; Richter, M.; Dell, H.; Koukolikova, M.; Gese, H.; et al. Finite element simulation of plasticity and fracture for Inconel 718 deposited by laser powder bed fusion—Chances, use and challenges. Addit. Manuf. 2022, 56, 102888. [Google Scholar] [CrossRef]
- Oblak, J.; Paulonis, D.; Duvall, D. Coherency strengthening in Ni base alloys hardened by DO22 γ′ precipitates. Metall. Trans. 1974, 5, 143–153. [Google Scholar] [CrossRef]
- Han, Y.f.; Deb, P.; Chaturvedi, M. Coarsening behaviour of γ″-and γ′-particles in Inconel alloy 718. Met. Sci. 1982, 16, 555–562. [Google Scholar] [CrossRef]
- Sundararaman, M.; Mukhopadhyay, P.; Banerjee, S. Deformation behaviour of γ″ strengthened inconel 718. Acta Metall. 1988, 36, 847–864. [Google Scholar] [CrossRef]
- Qin, H.; Bi, Z.; Yu, H.; Feng, G.; Zhang, R.; Guo, X.; Chi, H.; Du, J.; Zhang, J. Assessment of the stress-oriented precipitation hardening designed by interior residual stress during ageing in IN718 superalloy. Mater. Sci. Eng. A 2018, 728, 183–195. [Google Scholar] [CrossRef]
- Zhang, D.; Guan, Z.; Qian, W.; Ye, Y.; Dai, F.; Hua, Y.; Cai, J. The effect of heterogeneous precipitation behavior on the mechanical properties of IN718 superalloy after laser shock peening and heat treatment processes. J. Manuf. Process. 2023, 99, 755–764. [Google Scholar] [CrossRef]
- Yuan, G.J.; Chen, H.; Li, D.F.; Gong, C.Y.; Zhang, X.C.; Tu, S.T. The effect of δ phase on the microplasticity evolution of a heat-treated nickel base superalloy. Mech. Mater. 2020, 148, 103520. [Google Scholar] [CrossRef]
- Rielli, V.V.; Godor, F.; Gruber, C.; Stanojevic, A.; Oberwinkler, B.; Primig, S. Effects of processing heterogeneities on the micro-to nanostructure strengthening mechanisms of an alloy 718 turbine disk. Mater. Des. 2021, 212, 110295. [Google Scholar] [CrossRef]
- Adomako, N.K.; Haghdadi, N.; Primig, S. Electron and laser-based additive manufacturing of Ni-based superalloys: A review of heterogeneities in microstructure and mechanical properties. Mater. Des. 2022, 223, 111245. [Google Scholar] [CrossRef]
- Merrick, H. The low cycle fatigue of three wrought nickel-base alloys. Metall. Trans. 1974, 5, 891–897. [Google Scholar] [CrossRef]
- Chaturvedi, M.; Han, Y.f. Strengthening mechanisms in Inconel 718 superalloy. Met. Sci. 1983, 17, 145–149. [Google Scholar] [CrossRef]
- Fisk, M.; Ion, J.C.; Lindgren, L.E. Flow stress model for IN718 accounting for evolution of strengthening precipitates during thermal treatment. Comput. Mater. Sci. 2014, 82, 531–539. [Google Scholar] [CrossRef]
- McAllister, D.; Lv, D.; Peterson, B.; Deutchman, H.; Wang, Y.; Mills, M. Lower temperature deformation mechanisms in a γ″-strengthened Ni-base superalloy. Scr. Mater. 2016, 115, 108–112. [Google Scholar] [CrossRef]
- Eghtesad, A.; Knezevic, M. A full-field crystal plasticity model including the effects of precipitates: Application to monotonic, load reversal, and low-cycle fatigue behavior of Inconel 718. Mater. Sci. Eng. A 2021, 803, 140478. [Google Scholar] [CrossRef]
- Holmberg-Kasa, J.; Olsson, P.A.T.; Fisk, M. Investigating Elastic Deformation of Ordered Precipitates by Ab Initio-Informed Phase-Field Crystal Modeling. Metals 2024, 14, 1399. [Google Scholar] [CrossRef]
- Han, Y.; Chaturvedi, M. A study of back stress during creep deformation of a superalloy inconel 718. Mater. Sci. Eng. 1987, 85, 59–65. [Google Scholar] [CrossRef]
- Kurdi, A.; Aldoshan, A.; Alshabouna, F.; Alodadi, A.; Degnah, A.; Alnaser, H.; Tabbakh, T.; Basak, A.K. Investigation into the Microstructure and Hardness of Additively Manufactured (3D-Printed) Inconel 718 Alloy. Materials 2023, 16, 2383. [Google Scholar] [CrossRef] [PubMed]
- Meng, G.; Gong, Y.; Zhang, J.; Zhao, J. The microstructural evolution and mechanical response of laser direct energy deposition Inconel 718 alloy based on simulation and experimental methods. Eng. Fail. Anal. 2024, 161, 108334. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, C.; Lin, X.; Zhao, H.; Yang, H.; Huang, W. Deformation behavior of selective laser-melted Inconel 718 superalloy. Mater. Charact. 2024, 216, 114180. [Google Scholar] [CrossRef]
- Bacon, D.J.; Osetsky, Y.N. Hardening due to copper precipitates in α-iron studied by atomic-scale modelling. J. Nucl. Mater. 2004, 329, 1233–1237. [Google Scholar] [CrossRef]
- Osetsky, Y.N.; Pharr, G.M.; Morris, J.R. Two modes of screw dislocation glide in fcc single-phase concentrated alloys. Acta Mater. 2019, 164, 741–748. [Google Scholar] [CrossRef]
- Antillon, E.; Woodward, C.; Rao, S.; Akdim, B.; Parthasarathy, T. A molecular dynamics technique for determining energy landscapes as a dislocation percolates through a field of solutes. Acta Mater. 2019, 166, 658–676. [Google Scholar] [CrossRef]
- Vaida, A.; Guénoléb, J.; Prakashc, A.; Korte-Kerzelb, S.; Bitzeka, E. Atomistic Simulations of Basal Dislocations Interacting with Mg17Al12 Precipitates in Mg. Materialia 2019, 7, 100355. [Google Scholar] [CrossRef]
- Li, J.; Chen, H.; Fang, Q.; Jiang, C.; Liu, Y.; Liaw, P.K. Unraveling the dislocation–precipitate interactions in high-entropy alloys. Int. J. Plast. 2020, 133, 102819. [Google Scholar] [CrossRef]
- Esteban-Manzanares, G.; Alizadeh, R.; Papadimitriou, I.; Dickel, D.; Barrett, C.; LLorca, J. Atomistic simulations of the interaction of basal dislocations with MgZn2 precipitates in Mg alloys. Mater. Sci. Eng. A 2020, 788, 139555. [Google Scholar] [CrossRef]
- Li, J.; Fang, Q.; Liu, B.; Liu, Y. The effects of pore and second-phase particle on the mechanical properties of machining copper matrix from molecular dynamic simulation. Appl. Surf. Sci. 2016, 384, 419–431. [Google Scholar] [CrossRef]
- Meissonnier, F.; Busso, E.; O’Dowd, N. Finite element implementation of a generalised non-local rate-dependent crystallographic formulation for finite strains. Int. J. Plast. 2001, 17, 601–640. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.D.; Bieler, T.R.; Raabe, D. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Ghorbanpour, S.; Zecevic, M.; Kumar, A.; Jahedi, M.; Bicknell, J.; Jorgensen, L.; Beyerlein, I.J.; Knezevic, M. A crystal plasticity model incorporating the effects of precipitates in superalloys: Application to tensile, compressive, and cyclic deformation of Inconel 718. Int. J. Plast. 2017, 99, 162–185. [Google Scholar] [CrossRef]
- Cruzado, A.; Lucarini, S.; LLorca, J.; Segurado, J. Crystal plasticity simulation of the effect of grain size on the fatigue behavior of polycrystalline Inconel 718. Int. J. Fatigue 2018, 113, 236–245. [Google Scholar] [CrossRef]
- Agaram, S.; Kanjarla, A.K.; Bhuvaraghan, B.; Srinivasan, S.M. Dislocation density based crystal plasticity model incorporating the effect of precipitates in IN718 under monotonic and cyclic deformation. Int. J. Plast. 2021, 141, 102990. [Google Scholar] [CrossRef]
- le Graverend, J.B. Crystal-plasticity modeling of monotonic and cyclic softening in inconel 718 superalloy. Int. J. Mech. Sci. 2023, 239, 107871. [Google Scholar] [CrossRef]
- Lai, R.; Zhao, J.; Lei, L.; Shi, L.; Wu, S.; Zhang, X. Revealing the tensile anisotropic mechanisms of additive manufactured IN718 alloy based on crystal plasticity modeling. Comput. Mater. Sci. 2025, 251, 113735. [Google Scholar] [CrossRef]
- Zhu, K.Y.; Dai, S.; Zou, S.H.; Yu, Y.J.; Deng, Z.C. Experimental study and crystal plasticity modeling of additive manufacturing IN718 superalloy considering negative strain rate sensitivity behavior. Eur. J. Mech.—A/Solids 2024, 106, 105304. [Google Scholar] [CrossRef]
- Knezevic, M.; Ghorbanpour, S. Modeling Tensile, Compressive, and Cyclic Response of Inconel 718 Using a Crystal Plasticity Model Incorporating the Effects of Precipitates. In Proceedings of the 9th International Symposium on Superalloy 718 & Derivatives: Energy, Aerospace, and Industrial Applications; Springer: New York, NY, USA, 2018; pp. 655–668. [Google Scholar]
- Ghorbanpour, S.; Alam, M.E.; Ferreri, N.C.; Kumar, A.; McWilliams, B.A.; Vogel, S.C.; Bicknell, J.; Beyerlein, I.J.; Knezevic, M. Experimental characterization and crystal plasticity modeling of anisotropy, tension-compression asymmetry, and texture evolution of additively manufactured Inconel 718 at room and elevated temperatures. Int. J. Plast. 2020, 125, 63–79. [Google Scholar] [CrossRef]
- Li, D.F.; Golden, B.J.; O’Dowd, N.P. Multiscale modelling of mechanical response in a martensitic steel: A micromechanical and length-scale-dependent framework for precipitate hardening. Acta Mater. 2014, 80, 445–456. [Google Scholar] [CrossRef]
- Jiang, W.; Xu, P.; Li, Y.; Wang, H.; Cai, Z.; Li, J.; Liang, Y.; Liang, Y. Effect of a gradient structure on the mechanical performance of Inconel 718 Ni-based superalloy at elevated temperatures. J. Mater. Res. Technol. 2023, 23, 2031–2042. [Google Scholar] [CrossRef]
- Toursangsaraki, M.; Du, D.; Wang, H.; Dong, A. Crystal plasticity quantification of anisotropic tensile and fatigue properties in laser powder bed fused Inconel 718 superalloy. Addit. Manuf. 2024, 89, 104300. [Google Scholar] [CrossRef]
- Wan, C.F.; Sun, L.G.; Qin, H.L.; Bi, Z.N.; Li, D.F. A Molecular Dynamics Study on the Dislocation-Precipitate Interaction in a Nickel Based Superalloy during the Tensile Deformation. Materials 2023, 16, 6140. [Google Scholar] [CrossRef]
- Russakova, A.; Zhilkashinova, A.; Alontseva, D.; Abilev, M.; Khozhanov, A.; Zhilkashinova, A. Effect of the Dislocation Substructure Parameters of Hadfield Steel on Its Strain Hardening. Materials 2023, 16, 1717. [Google Scholar] [CrossRef]
- Wu, P.; Song, K.; Liu, F. Effect of Coherent Nanoprecipitate on Strain Hardening of Al Alloys: Breaking through the Strength-Ductility Trade-Off. Materials 2024, 17, 4197. [Google Scholar] [CrossRef]
- Jinhui, D.; Xudong, L.; Qun, D.; Ying, L. Effect of solution treatment on the microstructure and mechanical properties of IN718 alloy. Rare Met. Mater. Eng. 2017, 46, 2359–2365. [Google Scholar] [CrossRef]
- Qin, H.; Bi, Z.; Li, D.; Zhang, R.; Lee, T.L.; Feng, G.; Dong, H.; Du, J.; Zhang, J. Study of precipitation-assisted stress relaxation and creep behavior during the ageing of a nickel-iron superalloy. Mater. Sci. Eng. A 2019, 742, 493–500. [Google Scholar] [CrossRef]
- Li, D.F.; Barrett, R.A.; O’Donoghue, P.E.; O’Dowd, N.P.; Leen, S.B. A multi-scale crystal plasticity model for cyclic plasticity and low-cycle fatigue in a precipitate-strengthened steel at elevated temperature. J. Mech. Phys. Solids 2017, 101, 44–62. [Google Scholar] [CrossRef]
- Lee, E.H. Elastic-plastic deformation at finite strains. J. Appl. Mech. 1969, 36, 1–6. [Google Scholar] [CrossRef]
- Asaro, R.J.; Rice, J. Strain localization in ductile single crystals. J. Mech. Phys. Solids 1977, 25, 309–338. [Google Scholar] [CrossRef]
- Li, D.F.; O’Dowd, N.P. On the evolution of lattice deformation in austenitic stainless steels—The role of work hardening at finite strains. J. Mech. Phys. Solids 2011, 59, 2421–2441. [Google Scholar] [CrossRef]
- Busso, E.P.; McClintock, F.A. A dislocation mechanics-based crystallographic model of a B2-type intermetallic alloy. Int. J. Plast. 1996, 12, 1–28. [Google Scholar] [CrossRef]
- Cheong, K.; Busso, E.; Arsenlis, A. A study of microstructural length scale effects on the behaviour of FCC polycrystals using strain gradient concepts. Int. J. Plast. 2005, 21, 1797–1814. [Google Scholar] [CrossRef]
- Zhang, R.; Qin, H.; Bi, Z.; Li, J.; Paul, S.; Lee, T.; Nenchev, B.; Zhang, J.; Kabra, S.; Kelleher, J.; et al. Using variant selection to facilitate accurate fitting of γ″ peaks in neutron diffraction. Metall. Mater. Trans. A 2019, 50, 5421–5432. [Google Scholar] [CrossRef]
- Gnäupel-Herold, T.; Brand, P.C.; Prask, H.J. Calculation of single-crystal elastic constants for cubic crystal symmetry from powder diffraction data. J. Appl. Crystallogr. 1998, 31, 929–935. [Google Scholar] [CrossRef]
- Weinberger, C.R.; Boyce, B.L.; Battaile, C.C. Slip planes in bcc transition metals. Int. Mater. Rev. 2013, 58, 296–314. [Google Scholar] [CrossRef]
- Li, D.F.; Davies, C.M.; Zhang, S.Y.; Dickinson, C.; O’Dowd, N.P. The effect of prior deformation on subsequent microplasticity and damage evolution in an austenitic stainless steel at elevated temperature. Acta Mater. 2013, 61, 3575–3584. [Google Scholar] [CrossRef]
- Cruzado, A.; Gan, B.; Chang, H.; Ostolaza, K.; Linaza, A.; Milenkovic, S.; Molina-Aldareguia, J.; Llorca, J.; Segurado, J. Microtesting and Crystal Plasticity Modelling of IN718 Superalloy Grains. In Proceedings of the 8th International Symposium on Superalloy, Pittsburgh, PA, USA, 28 September–1 October 2014; Volume 718. [Google Scholar]
- Cheong, K.S.; Busso, E.P. Effects of lattice misorientations on strain heterogeneities in FCC polycrystals. J. Mech. Phys. Solids 2006, 54, 671–689. [Google Scholar] [CrossRef]
- Society, C.M. China Superalloys Handbook; China Standard Press: Beijing, China, 2012. [Google Scholar]
- Orowan, E. Fracture and strength of solids. Rep. Prog. Phys. 1949, 12, 185. [Google Scholar] [CrossRef]
- Voyiadjis, G.; Yaghoobi, M. Size Effects in Plasticity: From Macro to Nano; Academic Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Qin, H.; Bi, Z.; Zhang, R.; Lee, T.L.; Yu, H.; Chi, H.; Li, D.; Dong, H.; Du, J.; Zhang, J. Stress-Induced Variant Selection of γ″ Phase in Inconel 718 During Service: Mechanism and Effects on Mechanical Behavior. In Proceedings of the 14th International Symposium on Superalloys (Superalloys 2020), Seven Springs, PA, USA, 13–17 September 2020; Springer: Cham, Switzerland, 2020; pp. 713–725. [Google Scholar]
- Lv, D.; McAllister, D.; Mills, M.; Wang, Y. Deformation mechanisms of D022 ordered intermetallic phase in superalloys. Acta Mater. 2016, 118, 350–361. [Google Scholar] [CrossRef]
- Ashby, M. The deformation of plastically non-homogeneous materials. Philos. Mag. A J. Theor. Exp. Appl. Phys. 1970, 21, 399–424. [Google Scholar] [CrossRef]
- Hughes, D.; Hansen, N.; Bammann, D. Geometrically necessary boundaries, incidental dislocation boundaries and geometrically necessary dislocations. Scr. Mater. 2003, 48, 147–153. [Google Scholar] [CrossRef]
- Dunne, F.; Kiwanuka, R.; Wilkinson, A. Crystal plasticity analysis of micro-deformation, lattice rotation and geometrically necessary dislocation density. Proc. R. Soc. A Math. Phys. Eng. Sci. 2012, 468, 2509–2531. [Google Scholar] [CrossRef]
- Busso, E.; Meissonnier, F.; O’dowd, N. Gradient-dependent deformation of two-phase single crystals. J. Mech. Phys. Solids 2000, 48, 2333–2361. [Google Scholar] [CrossRef]
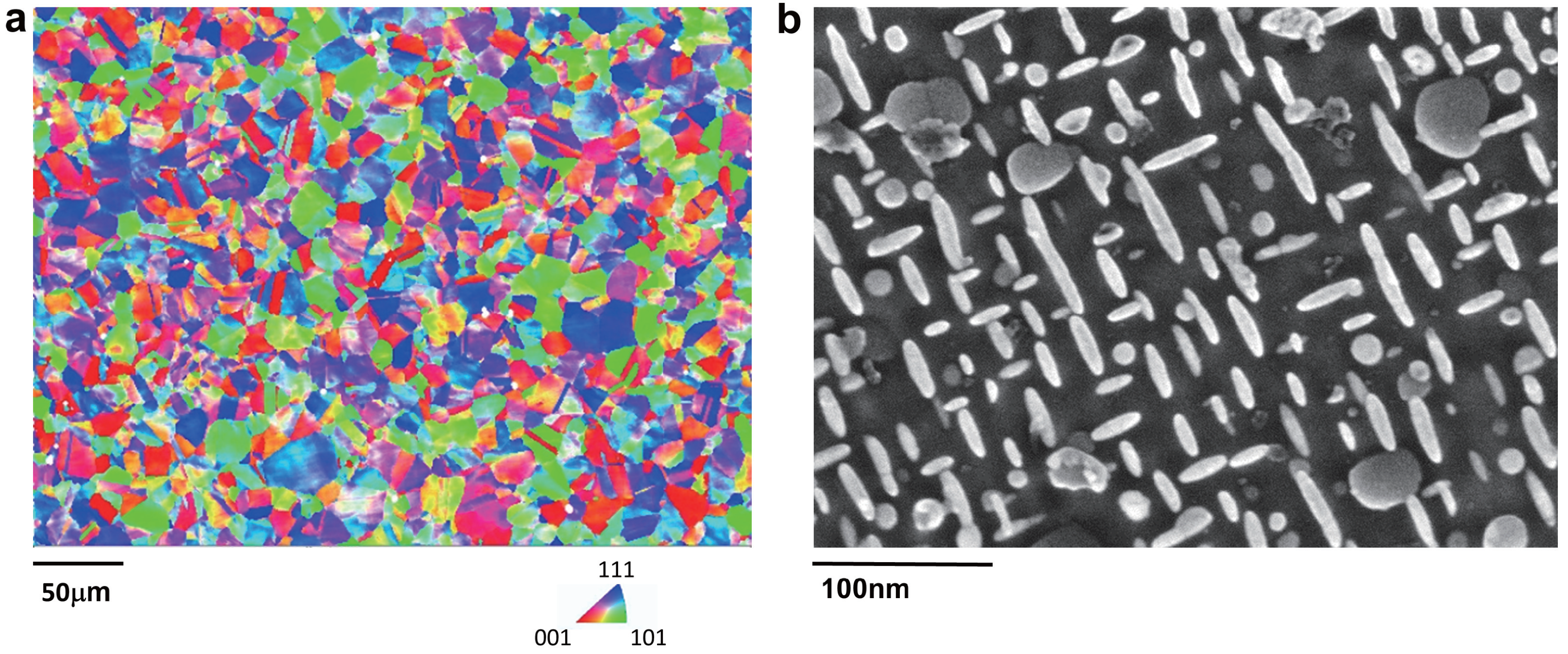
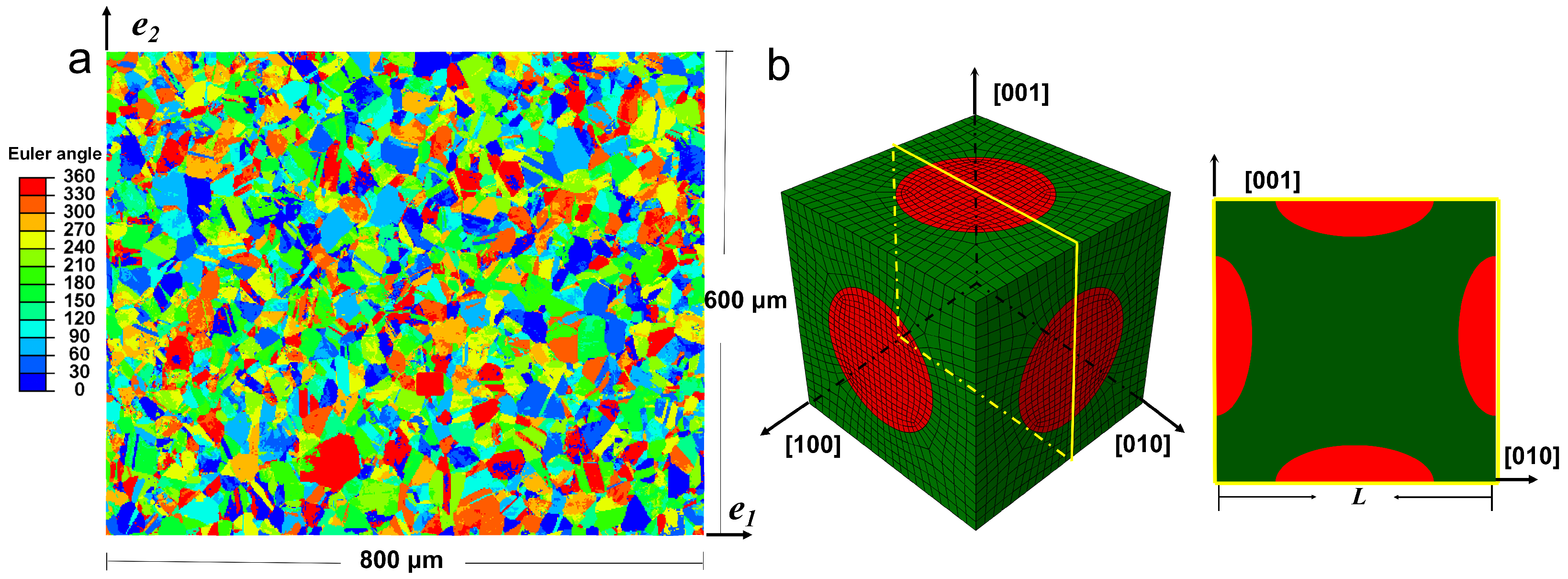

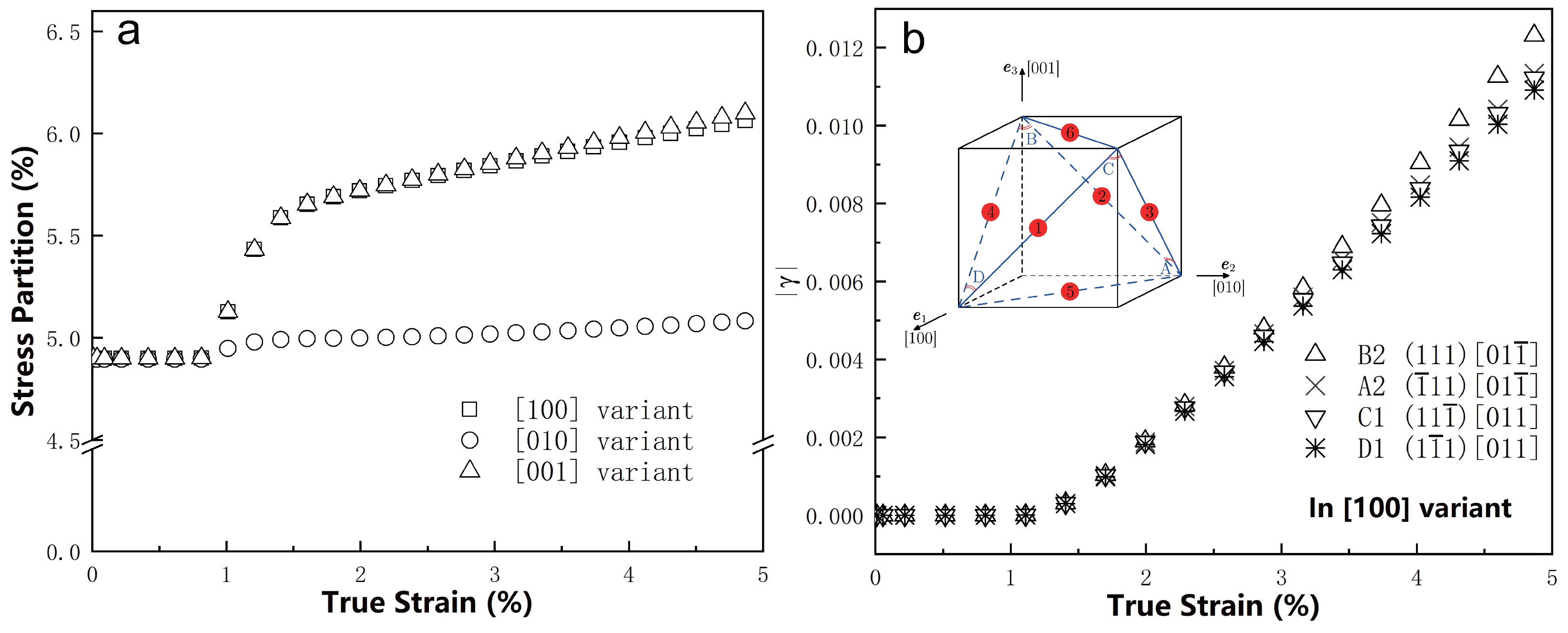
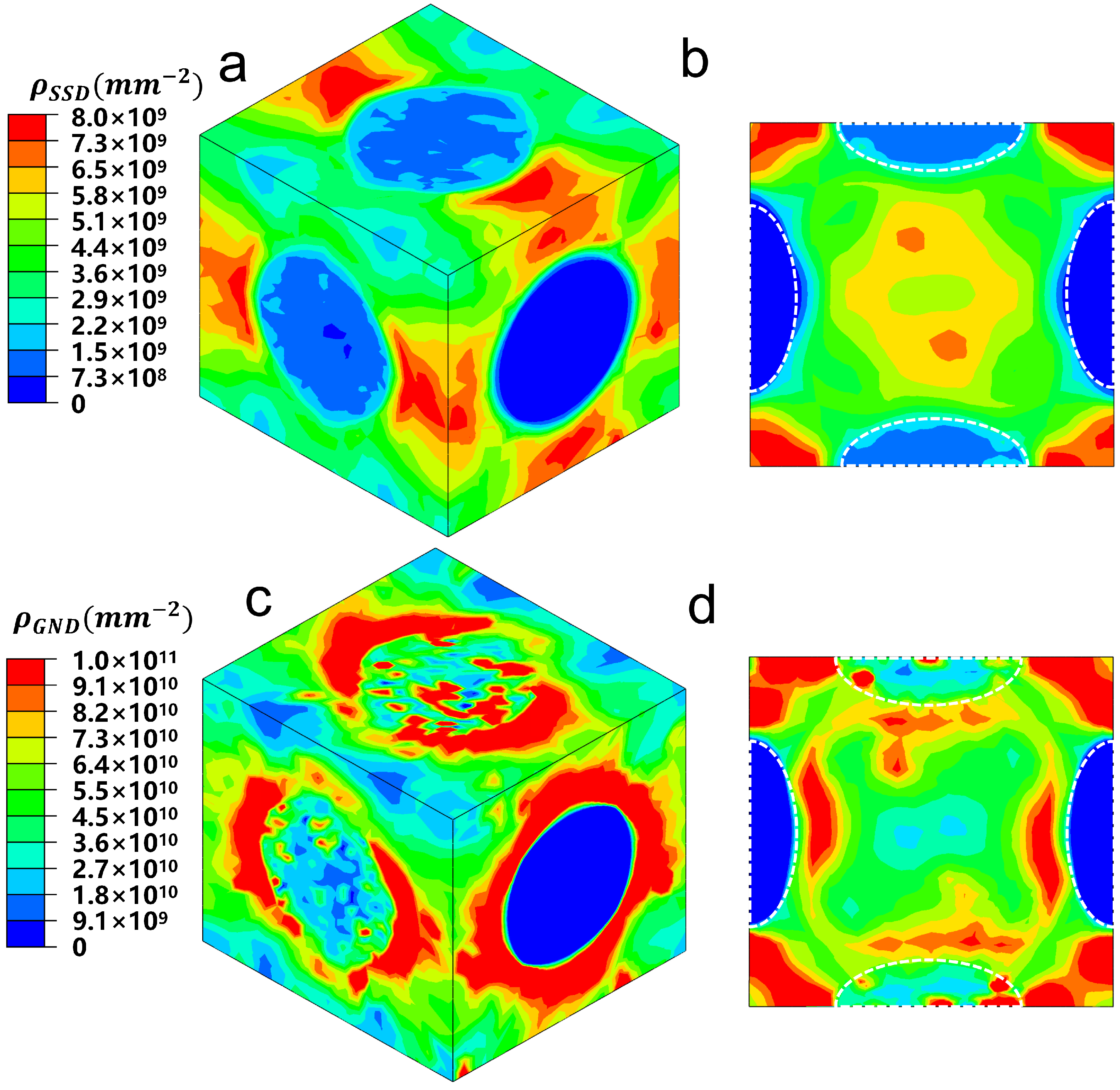
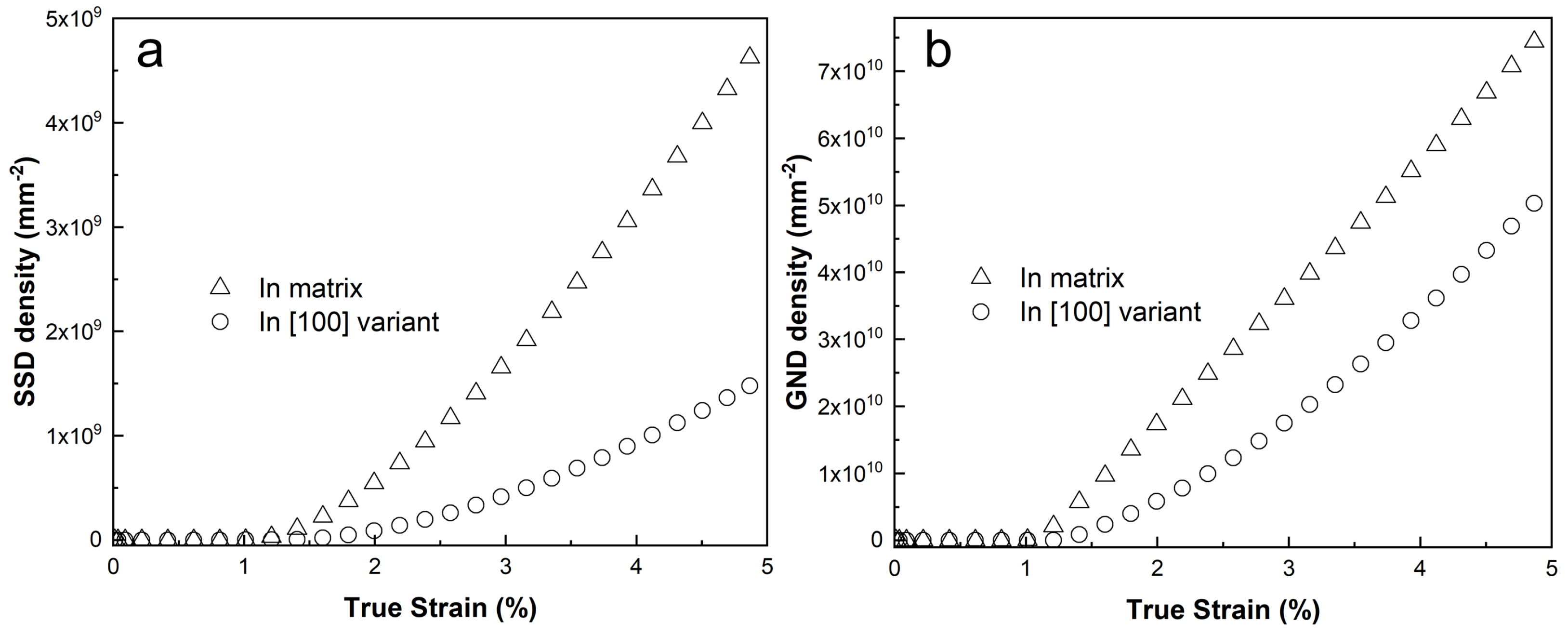
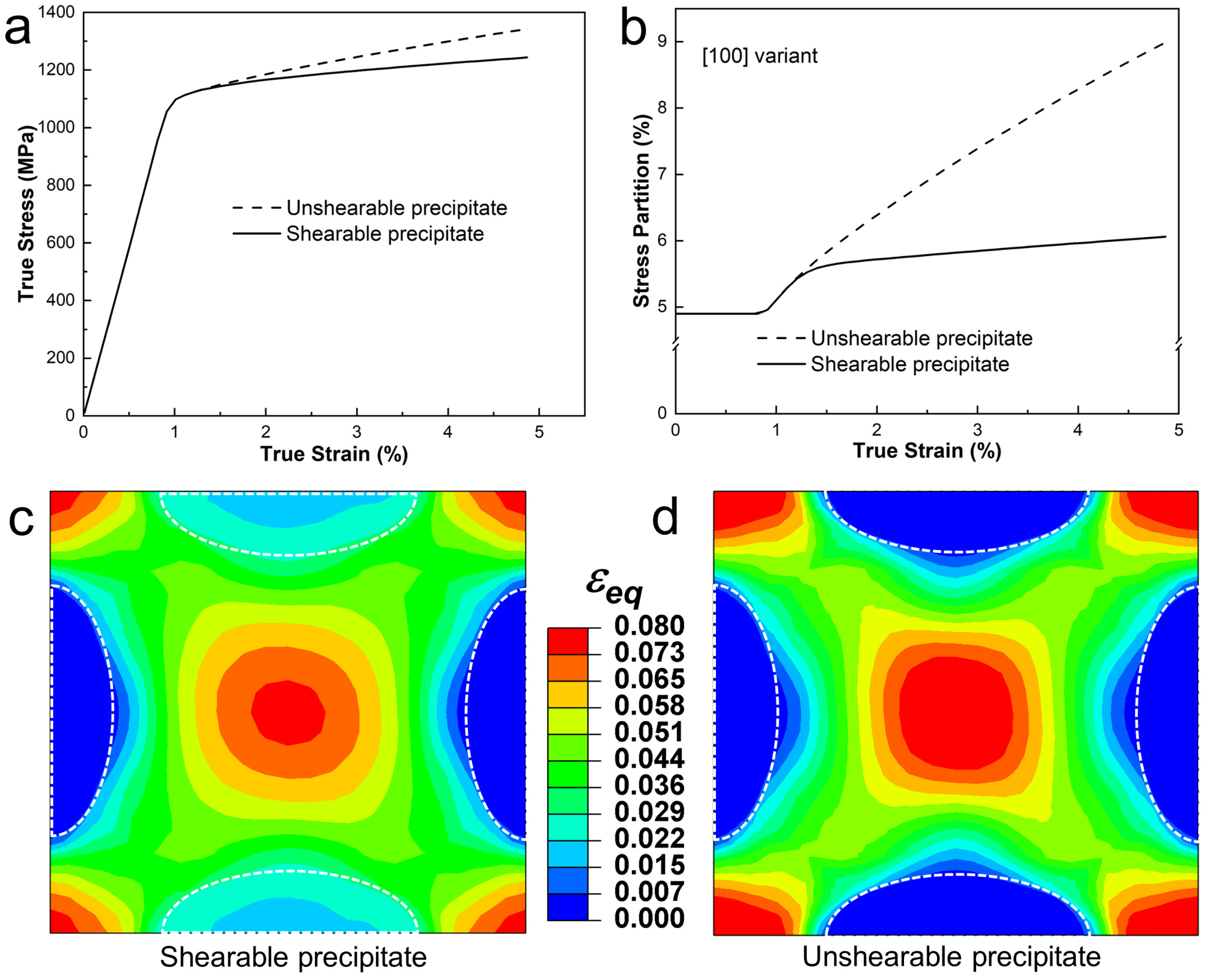
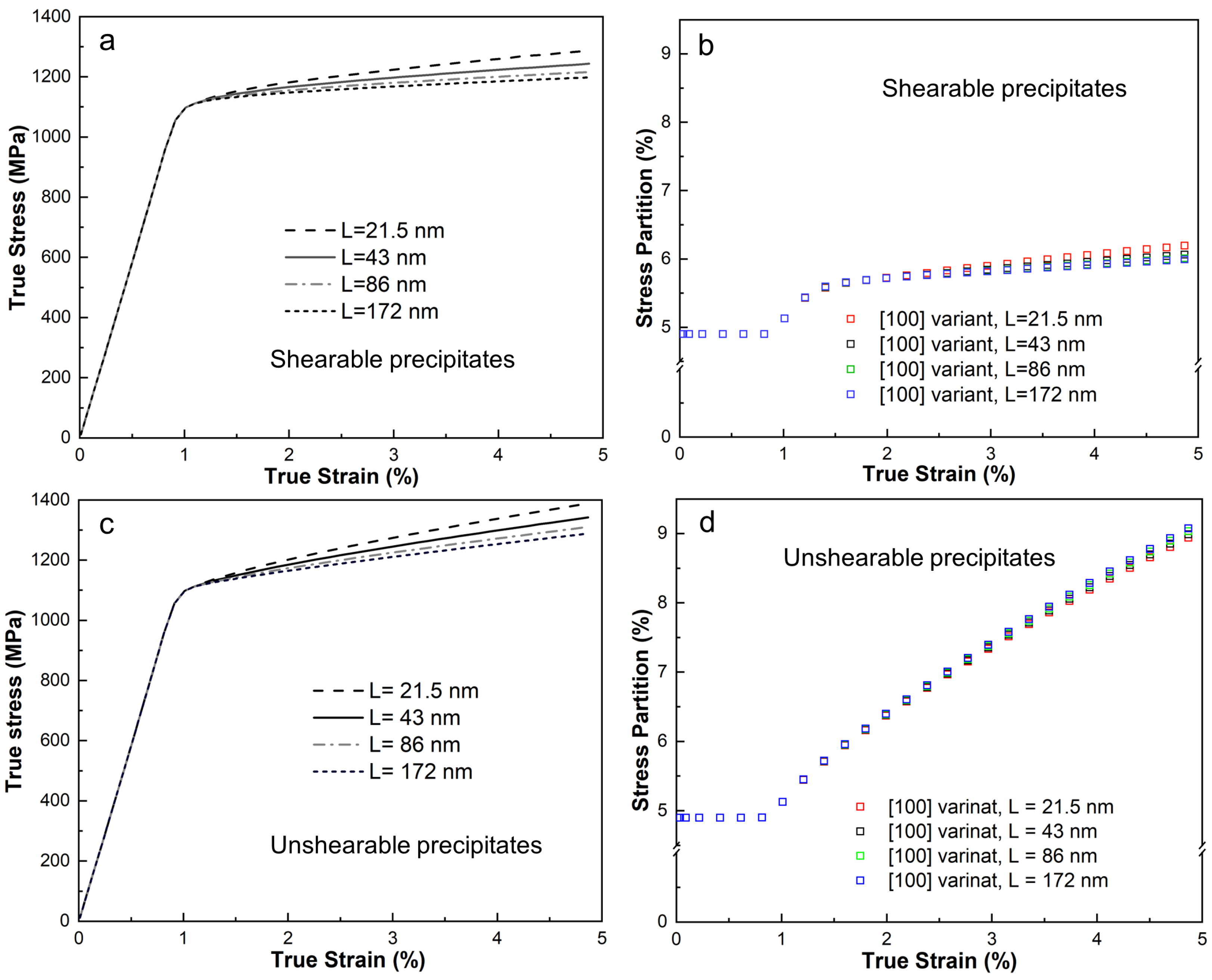

| Ni | Cr | Fe | Nb | Mo | Ti | Al | C |
|---|---|---|---|---|---|---|---|
| Balance | 18.05 | 18.00 | 5.42 | 2.90 | 0.91 | 0.48 | 0.02 |
| Elastic Constants | Flow Rule | Hardening Laws |
|---|---|---|
| = 235.5 GPa | , nm | |
| = 153.1 GPa | , | |
| = 125.4 GPa | nm, | |
| kJ/mol | ||
| MPa |
| Phase | Phase | Homogenized Crystal | |
|---|---|---|---|
| (MPa) | 900 | 700 | 700 |
| Mechanisms | Shearing and Bypassing | Bypassing | ||
|---|---|---|---|---|
| With SG | Without SG | With SG | Without SG | |
| Stress at (MPa) | 1243 | 1154 | 1342 | 1234 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, C.; Wang, B. Crystal Plasticity Modeling of Strain Hardening Induced by Coherent Precipitates in Inconel 718 Superalloy. Materials 2025, 18, 2436. https://doi.org/10.3390/ma18112436
Wan C, Wang B. Crystal Plasticity Modeling of Strain Hardening Induced by Coherent Precipitates in Inconel 718 Superalloy. Materials. 2025; 18(11):2436. https://doi.org/10.3390/ma18112436
Chicago/Turabian StyleWan, Changfeng, and Biao Wang. 2025. "Crystal Plasticity Modeling of Strain Hardening Induced by Coherent Precipitates in Inconel 718 Superalloy" Materials 18, no. 11: 2436. https://doi.org/10.3390/ma18112436
APA StyleWan, C., & Wang, B. (2025). Crystal Plasticity Modeling of Strain Hardening Induced by Coherent Precipitates in Inconel 718 Superalloy. Materials, 18(11), 2436. https://doi.org/10.3390/ma18112436






