Study on Flexural Performance of Recycled Aggregate Concrete Beams Incorporating Glazed Hollow Beads
Abstract
1. Introduction
2. Experimental Program
2.1. Design of Specimens
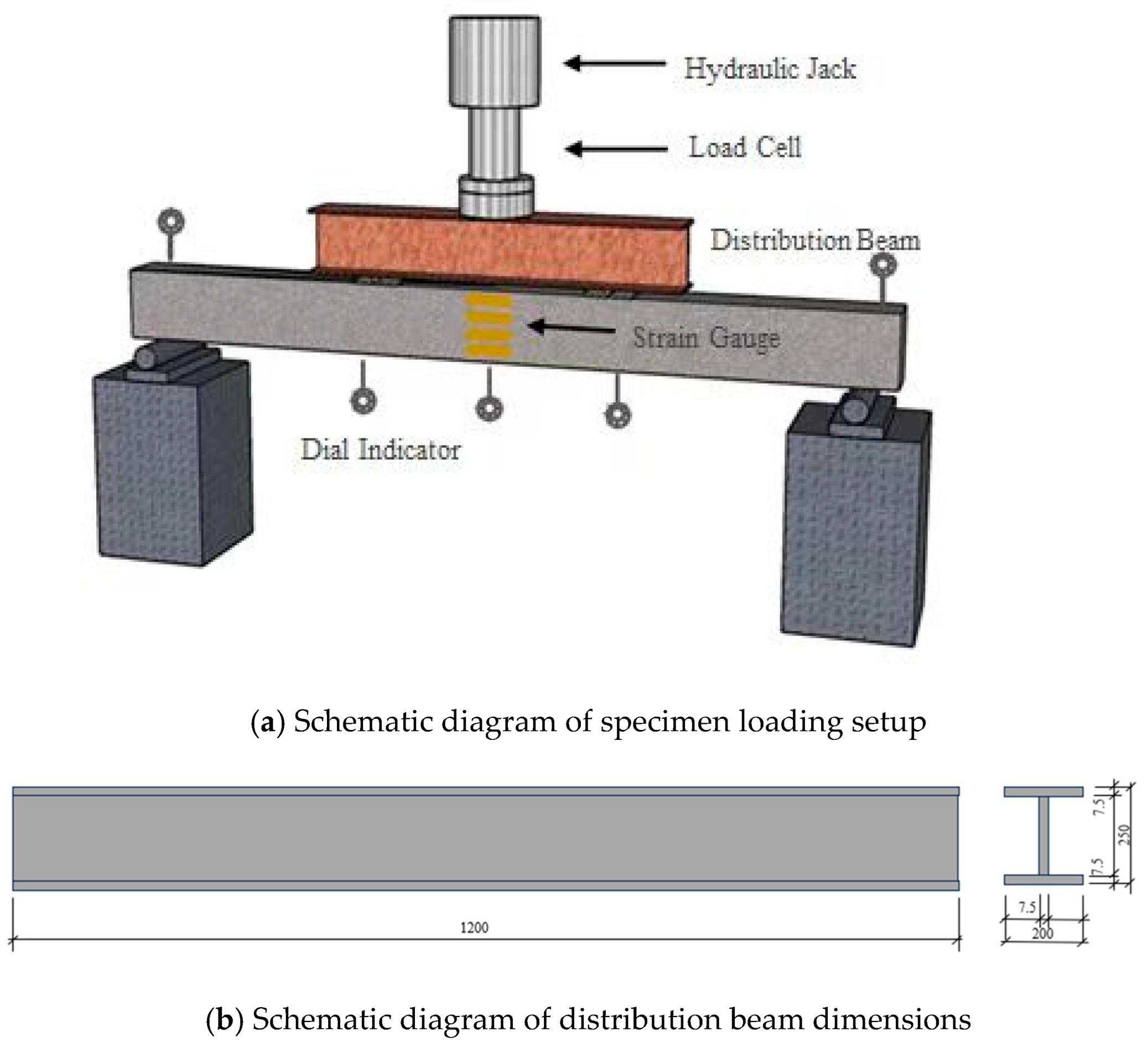
2.2. Experimental Loading and Measurement
2.2.1. Loading Protocol
2.2.2. Measurement Instruments
2.3. Material Properties
3. Experimental Results and Discussion
3.1. Failure Mode
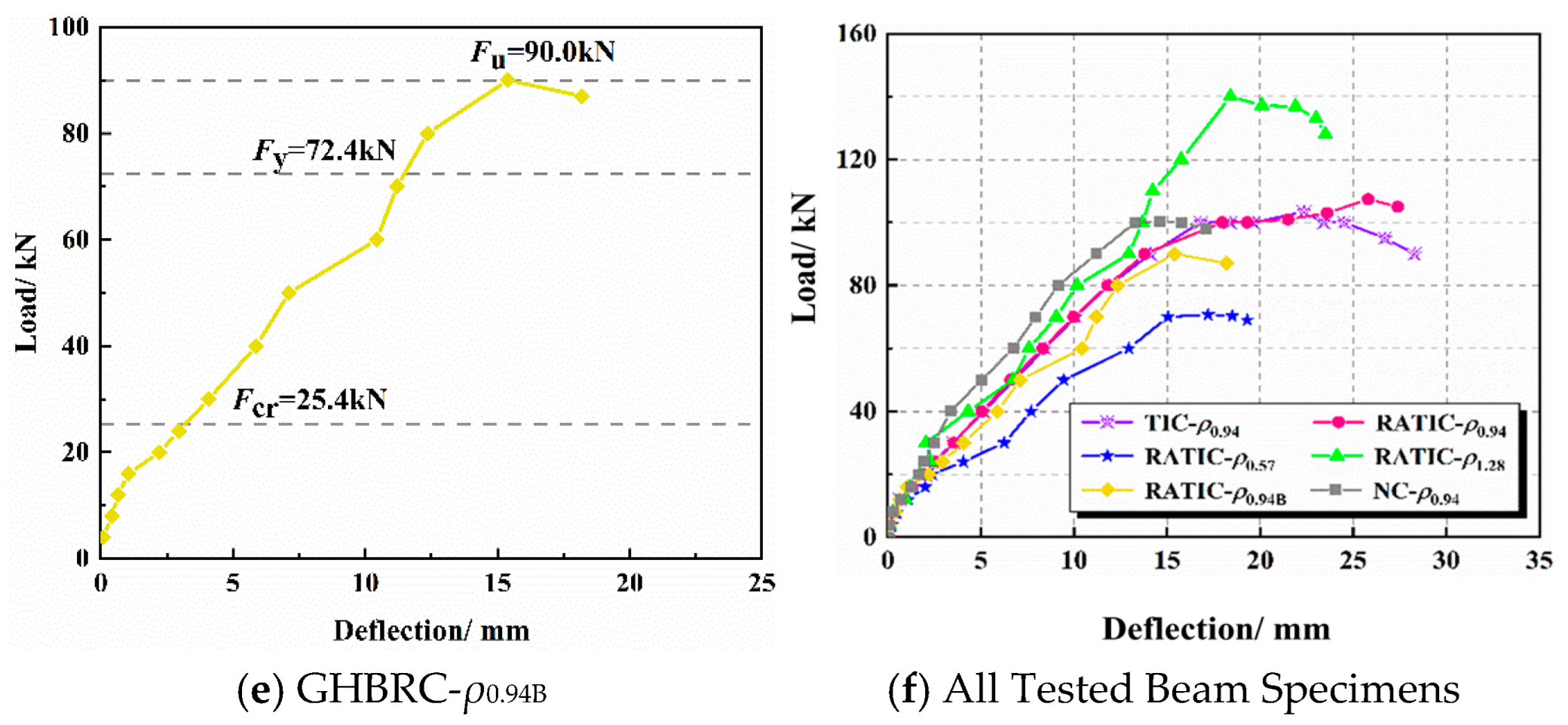
3.2. Deflection Behavior
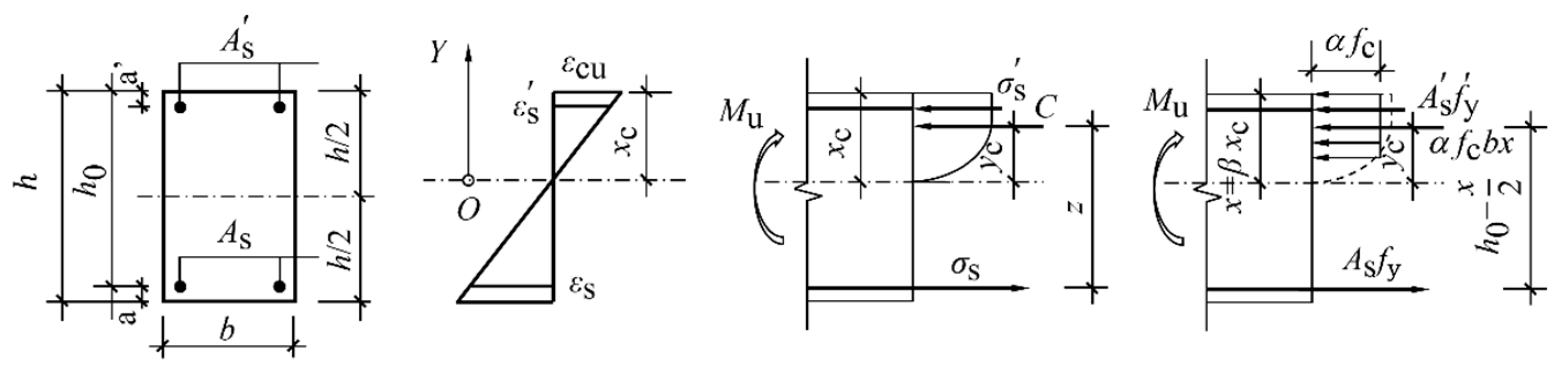
4. Flexural Bearing Capacity of Cross-Section
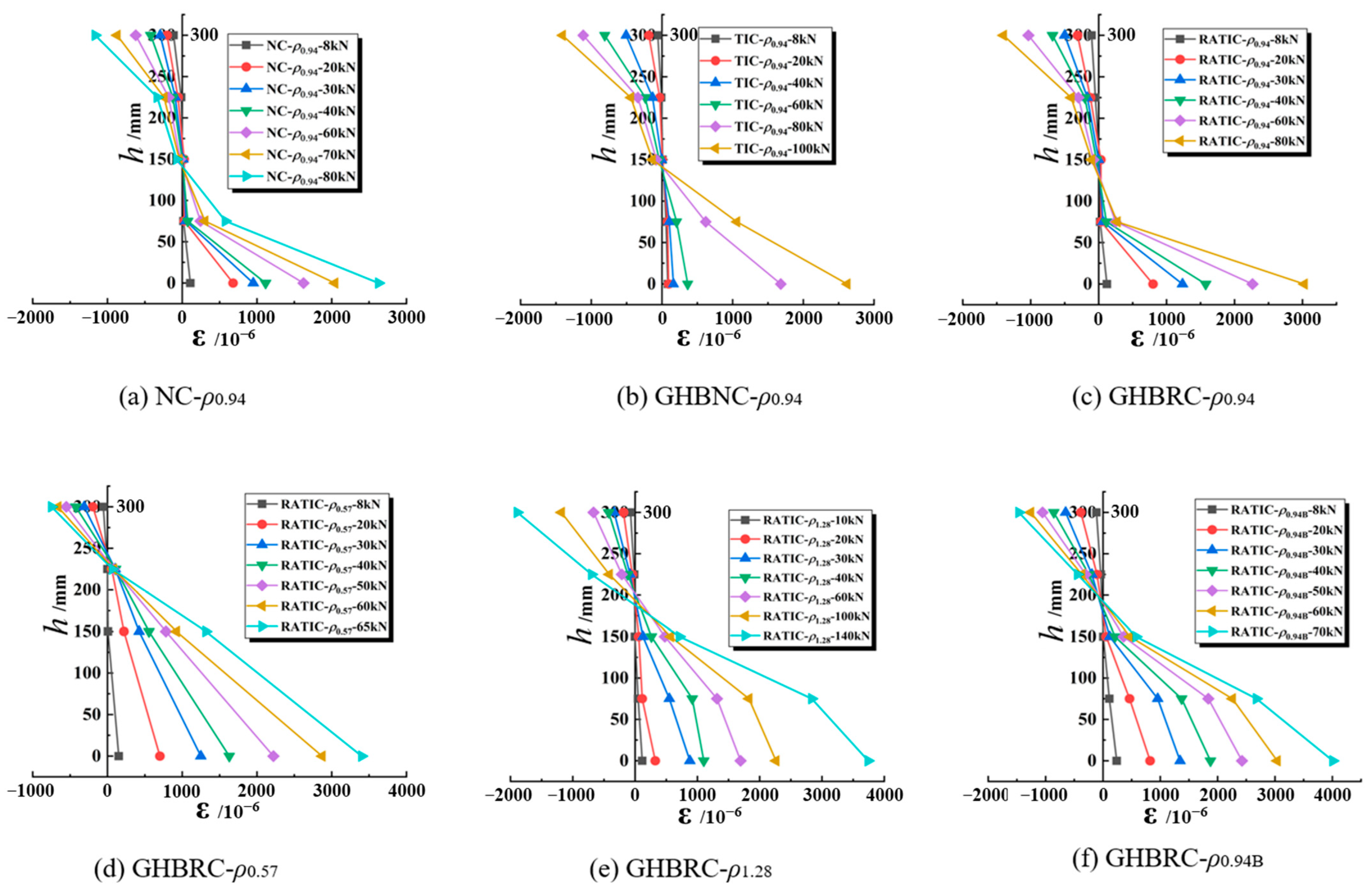
4.1. Applicability of Plane Section Assumption
4.2. Analysis of Flexural Capacity of Normal Sections
4.2.1. Basic Assumptions
4.2.2. Analytical Formula for Flexural Capacity of Normal Sections
5. Mid-Span Deflection Calculation Model
5.1. Mid-Span Deflection Analysis
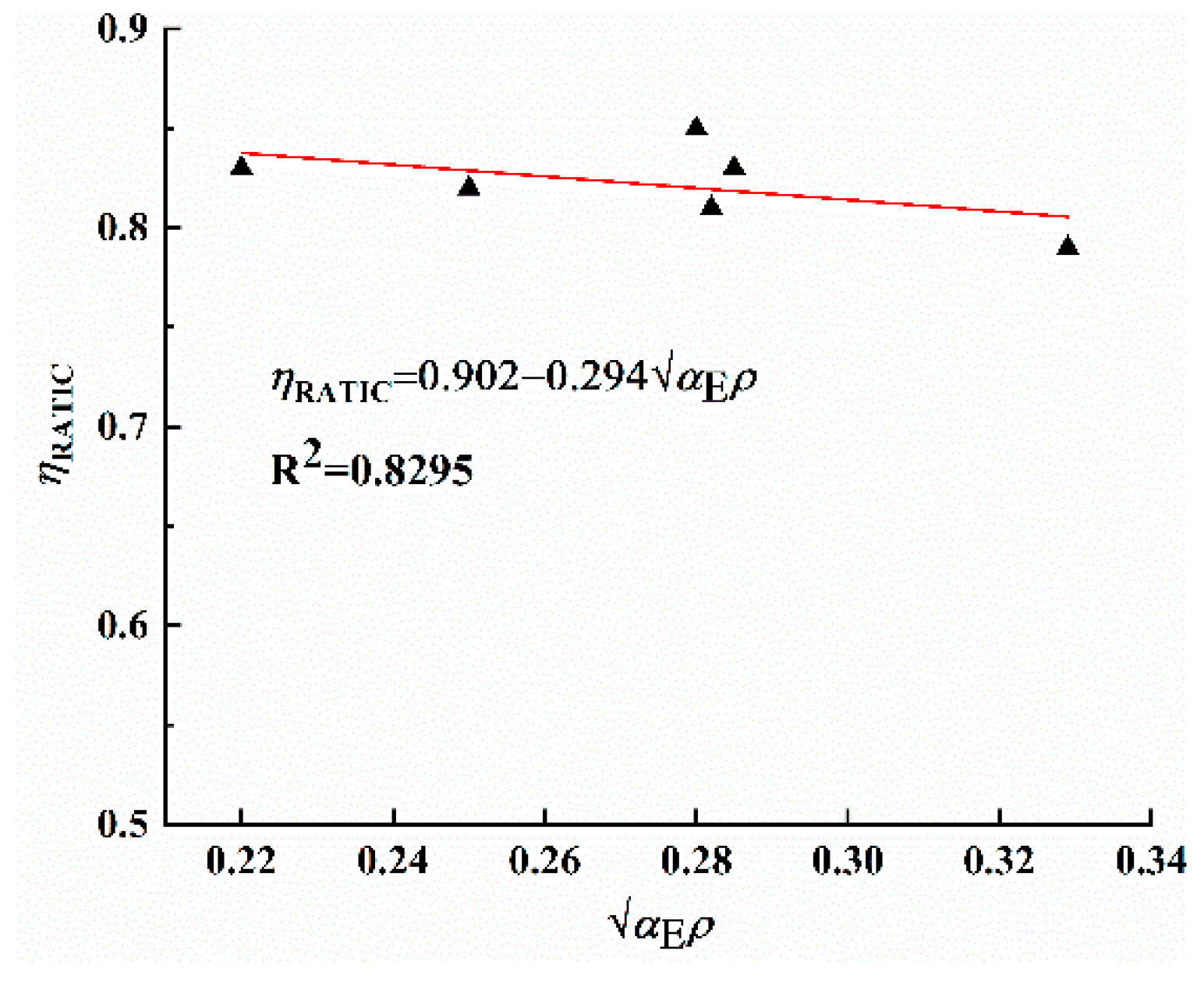
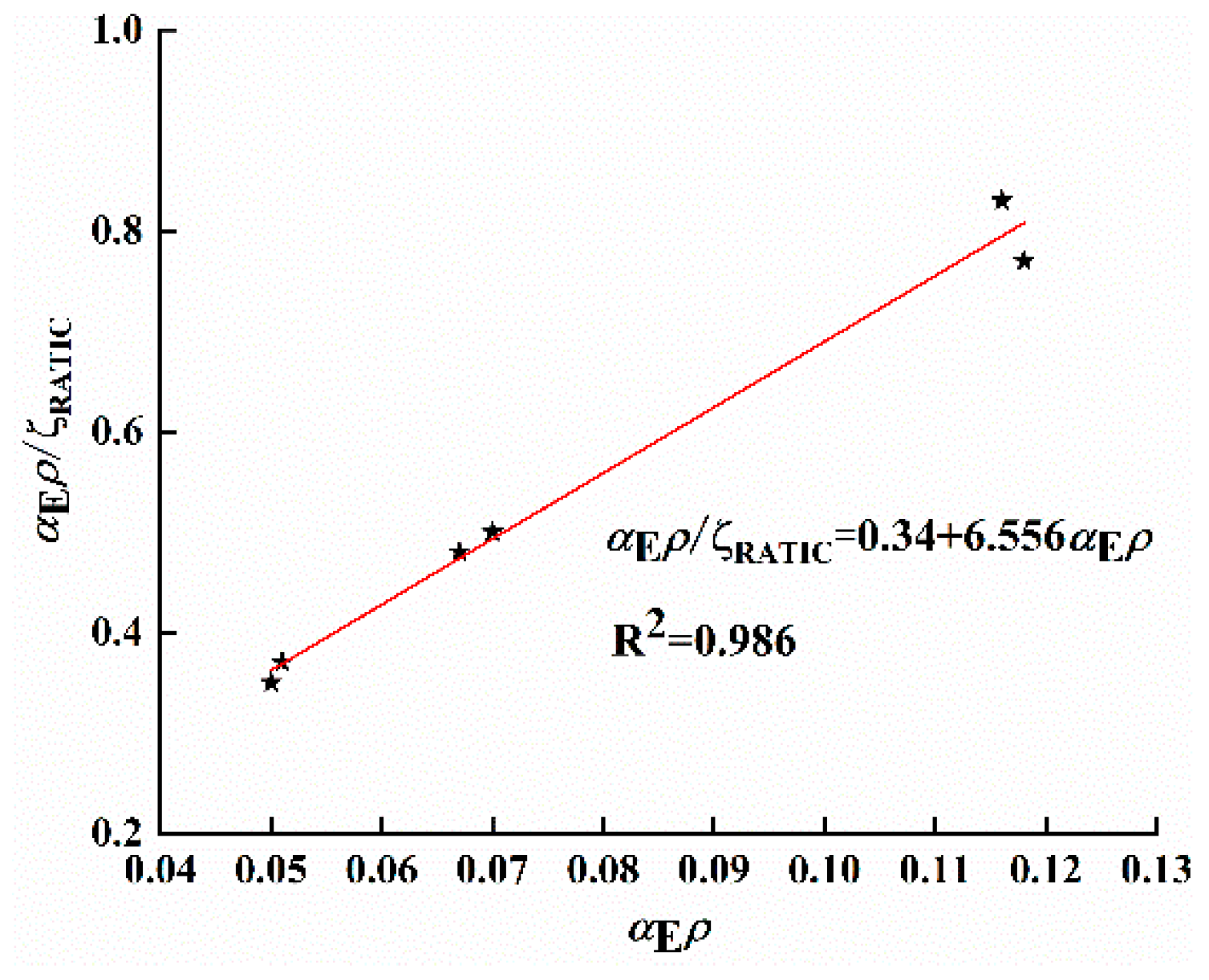
5.1.1. Internal Lever Arm Coefficient
5.1.2. The Strain Non-Uniformity Coefficient of Reinforcing Steel
5.1.3. The Cross-Sectional Elastoplastic Moment Resistance Coefficient
5.2. Mid-Span Deflection Calculation
6. Conclusions and Remarks
- (1)
- The failure modes of GHBRC beams exhibit close resemblance to those of conventional concrete beams. The concrete strain distribution at mid-span demonstrates uniform variation along beam depth, adhering to the plane section assumption. This confirms the applicability of existing theoretical frameworks for conventional concrete beam analysis to GHBRC systems. Furthermore, the load-response progression observed in flexural tests of GHBRC beams is characterized by three distinct phases identical to conventional concrete behavior: elastic phase (pre-cracking), cracking propagation phase, and reinforcement yielding phase.
- (2)
- The incorporation of glazed hollow bead aggregates induces a “gas-spring” mechanism within the concrete matrix, resulting in 35% greater ultimate mid-span deflection (and enhanced ductility in recycled concrete beams. Experimental data demonstrate an inverse correlation between reinforcement ratio and deformation characteristics: specimens GHBRC-ρ1.28 and GHBRC-ρ0.94 exhibit 19% and 22% reduced ultimate deflections, respectively, compared to GHBRC-ρ0.57. Consequently, strategic enhancement of the reinforcement ratio within the under-reinforced beam design range proves effective in controlling the deflection of thermal-insulating recycled concrete beams.
- (3)
- Four fundamental postulates are established for GHBRC beams, through which the constitutive relationship between the rectangular stress block equivalence factor and aggregate composition ratios is derived. This formulation validates the rationality of flexural capacity calculation models, with experimental results demonstrating 3.1% higher ultimate flexural capacity compared to conventional concrete beams at equivalent reinforcement ratios. The quantified mechanical enhancement, coupled with its inherent thermal insulation properties, confirms the structural GHBRC in load-bearing applications while satisfying energy efficiency requirements.
- (4)
- The three critical parameters governing short-term stiffness calculation were established through multivariate regression analysis, culminating in the formulation for GHBRC beams. Implementation of this equation enables the precise determination of mid-span deflection under incremental loading stages. Comparative analysis reveals strong agreement between the computational results and the experimental measurements. This validation confirms the robust applicability of the derived stiffness formulation for GHBRC beam systems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Luo, W.; Wang, J.; Wang, Y.; Xu, Y.; Xiao, J. A review of life cycle assessment of recycled aggregate concrete. Constr. Build. Mater. 2019, 209, 115–125. [Google Scholar] [CrossRef]
- Estanqueiro, B.; Dinis Silvestre, J.; de Brito, J.; Duarte Pinheiro, M. Environmental life cycle assessment of coarse natural and recycled aggregates for concrete. Eur. J. Environ. Civ. Eng. 2018, 22, 429–449. [Google Scholar] [CrossRef]
- Ma, Z.; Shen, J.; Wang, C.; Wu, H. Characterization of sustainable mortar containing high-quality recycled manufactured sand crushed from recycled coarse aggregate. Cem. Concr. Compos. 2022, 132, 104629. [Google Scholar] [CrossRef]
- Wang, B.; Yan, L.; Fu, Q.; Kasal, B. A comprehensive review on recycled aggregate and recycled aggregate concrete. Resour. Conserv. Recycl. 2021, 171, 105565. [Google Scholar] [CrossRef]
- Shi, C.; Li, Y.; Zhang, J.; Li, W.; Chong, L.; Xie, Z. Performance enhancement of recycled concrete aggregate—A review. J. Clean. Prod. 2016, 112, 466–472. [Google Scholar] [CrossRef]
- Hu, J.; Wang, Z.; Kim, Y. Feasibility study of using fine recycled concrete aggregate in producing self-consolidation concrete. J. Sustain. Cem.-Based Mater. 2013, 2, 20–34. [Google Scholar] [CrossRef]
- Xiao, J. Research on multimedia video technology based on the DR-DVC algorithm. Int. J. Comput. Sci. Math. 2022, 16, 327–339. [Google Scholar] [CrossRef]
- Cheng, J.; Yi, J.; Dai, S.; Xiong, Y. Can low-carbon city construction facilitate green growth? Evidence from China’s pilot low-carbon city initiative. J. Clean. Prod. 2019, 231, 1158–1170. [Google Scholar] [CrossRef]
- Tu, J.; Wang, Y.; Zhou, M.; Zhang, Y. Heat transfer mechanism of glazed hollow bead insulation concrete. J. Build. Eng. 2021, 40, 102629. [Google Scholar] [CrossRef]
- Zhu, L.; Dai, J.; Bai, G.; Zhang, F. Study on thermal properties of recycled aggregate concrete and recycled concrete blocks. Constr. Build. Mater. 2015, 94, 620–628. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Y.; Tu, J.; Wang, W. Effects of glazed hollow beads on the drying shrinkage value and trend of recycled aggregate concrete. J. Build. Eng. 2023, 68, 106021. [Google Scholar] [CrossRef]
- Du, S.; Liang, B.; Zhang, Y.; Lei, C.; Wang, C.; Jin, Z.; Li, B.; Li, X.; Liu, Y. Mechanical properties and damage characteristics analysis on recycled aggregate concrete with glazed hollow beads after high temperatures by acoustic emission method. J. Build. Eng. 2024, 90, 109429. [Google Scholar] [CrossRef]
- Wang, X.; Wang, W.; Liu, Y.; Duan, P.; Liang, X.; Zhang, H.; Ge, Z. Enhancing chloride ion permeability resistance of recycled aggregate concrete through internal curing with glazed hollow beads. Constr. Build. Mater. 2024, 438, 137293. [Google Scholar] [CrossRef]
- Du, S.; Zhang, Y.; Zhang, J.; Selyutina, N.; Smirnov, I.; Ma, G.; Zhang, X.; Li, B.; Miao, Y.; Liu, Y. Study on pore characteristics of recycled aggregate concrete mixed with glazed hollow beads at high temperatures based on 3-D reconstruction of computed tomography images. Constr. Build. Mater. 2022, 323, 126564. [Google Scholar] [CrossRef]
- Miao, Y.; Lei, C.; Zhang, Y.; Selyutina, N.; Smirnov, I.; Ma, G.; Liu, Y.; Lu, Z. Micro/meso-scale damage analysis of recycled aggregate concrete mixed with glazed hollow beads after high temperatures based on 2D CT images. Constr. Build. Mater. 2023, 365, 130063. [Google Scholar] [CrossRef]
- Song, B.; Xu, X.; Shangguan, Y.; Wang, Q.; Yao, L.; Guo, L.; Lei, H. Experimental and numerical investigation of square glazed hollow beads recycled aggregate concrete-filled double-skin steel tubular (GRCFDST) short columns under axial compression. Constr. Build. Mater. 2025, 466, 140254. [Google Scholar] [CrossRef]
- Bai, W.H.; Sun, B.X. Experimental study on flexural behavior of recycled coarse aggregate concrete beam. Appl. Mech. Mater. 2010, 29, 543–548. [Google Scholar] [CrossRef]
- Fathifazl, G.; Razaqpur, A.G.; Isgor, O.B.; Abbas, A.; Fournier, B.; Foo, S. Flexural performance of steel-reinforced recycled concrete beams. ACI Struct. J. 2009, 106, 858–867. [Google Scholar]
- Ajdukiewicz, A.B.; Kliszczewicz, A. Behavior of RC beams from recycled aggregate concrete. In Proceedings of the ACI Fifth International Conference on “Innovation and Design with Emphasis on Seismic, Wind and Environmental Loading, Quality Control and Innovation in Materials/Hot Weather Concreting”, Cancun, Mexico, 10–13 December 2002; pp. 10–13. [Google Scholar]
- Sojobi, A.O.; Liew, K.M. Flexural behaviour and efficiency of CFRP-laminate reinforced recycled concrete beams: Optimization using linear weighted sum method. Compos. Struct. 2021, 260, 113259. [Google Scholar] [CrossRef]
- Dawood, M.H.; Al-Asadi, A.K. Mechanical properties and flexural behaviour of reinforced concrete beams containing recycled concrete aggregate. Sci. Rev. Eng. Environ. Sci. (SREES) 2022, 31, 259–269. [Google Scholar] [CrossRef]
- Avram, S.E.; Barbu Tudoran, L.; Cuc, S.; Borodi, G.; Birle, B.V.; Petean, I. Conditioning influence of kaolinite matrices on flexural strength of raw pressed slurry collected from ceramic tile production wastewater. J. Compos. Sci. 2024, 8, 219. [Google Scholar] [CrossRef]
- Mukai, T.; Kikuchi, M. Properties of reinforced concrete beams containing recycled aggregate. In Demolition Reuse Conc Mason V2; CRC Press: Boca Raton, FL, USA, 2023; pp. 670–679. [Google Scholar]
- Wang, X.; Wang, W.; Huang, J.; Wang, Z.; Ma, S.; Liu, Y. Relationship between internal humidity and drying shrinkage of recycled aggregate thermal insulation concrete considering recycled aggregate content. Constr. Build. Mater. 2022, 355, 129224. [Google Scholar] [CrossRef]
- Mechtcherine, V.; Dudziak, L.; Hempel, S. Creep, Shrinkage and Durability Mechanics of Concrete and Concrete Structures. In Proceedings of the 8th International Conference on Creep, Shrinkage and Durability Mechanics of Concrete and Concrete Structures, Ise-Shima, Japan, 30 September–2 October 2008; pp. 847–853. [Google Scholar]
- Zhang, Y.; Ma, G.; Wang, Z.; Niu, Z.; Liu, Y.; Li, Z. Shear behavior of reinforced glazed hollow bead insulation concrete beams. Constr. Build. Mater. 2018, 174, 81–95. [Google Scholar] [CrossRef]
- Teng, S.; Kong, F.; Poh, S. Shear strength of reinforced and prestressed concrete deep beams. Part 1: Current design methods and a proposed equation. Proc. Inst. Civ. Eng.-Struct. Build. 1998, 128, 112–123. [Google Scholar] [CrossRef]
- ACI Committee 318 Building Code Requirements for Reinforced Concrete (ACI 318-71). ACI J. Proc. 1972, 68. [CrossRef]
- Yang, K.-H.; Ashour, A.; Song, J.-K. Shear capacity of reinforced concrete beams using neural network. Int. J. Concr. Struct. Mater. 2007, 1, 63–73. [Google Scholar]
- Vahidi, E.; Malekabadi, M. GRC and Sustainable Building Design; GRC: Istanbul, Turkey, 2011. [Google Scholar]
- Wu, Y.-F. The structural behavior and design methodology for a new building system consisting of glass fiber reinforced gypsum panels. Constr. Build. Mater. 2009, 23, 2905–2913. [Google Scholar] [CrossRef]
- Helal, J.; Stephan, A.; Crawford, R.H. The influence of structural design methods on the embodied greenhouse gas emissions of structural systems for tall buildings. Structures 2020, 24, 650–665. [Google Scholar] [CrossRef]
- Vu, N.S.; Li, B.; Beyer, K. Effective stiffness of reinforced concrete coupling beams. Eng. Struct. 2014, 76, 371–382. [Google Scholar]
- Standard GB/T 25177; Recycled Coarse Aggregate For Concrete. Standardization Administration of China: Beijing, China, 2010.
- Lam, L.; Teng, J. Stress–strain model for FRP-confined concrete under cyclic axial compression. Eng. Struct. 2009, 31, 308–321. [Google Scholar] [CrossRef]
- Chen, X.; Hao, H.; de Brito, J.; Liu, G.; Wang, J. Discussion of the implementation of water compensation methods for recycled aggregate concrete: A critical review. Cem. Concr. Compos. 2025, 161, 106080. [Google Scholar] [CrossRef]
- Gu, X.; Guo, H.; Zhou, B.; Zhang, W.; Jiang, C. Corrosion non-uniformity of steel bars and reliability of corroded RC beams. Eng. Struct. 2018, 167, 188–202. [Google Scholar] [CrossRef]
- Tai, K.X.; Zhang, Z.A.; Ding, D.J. Construction of concrete filled steel tube arch bridges in China. Indian Concr. J. 2007, 81, 41. [Google Scholar]
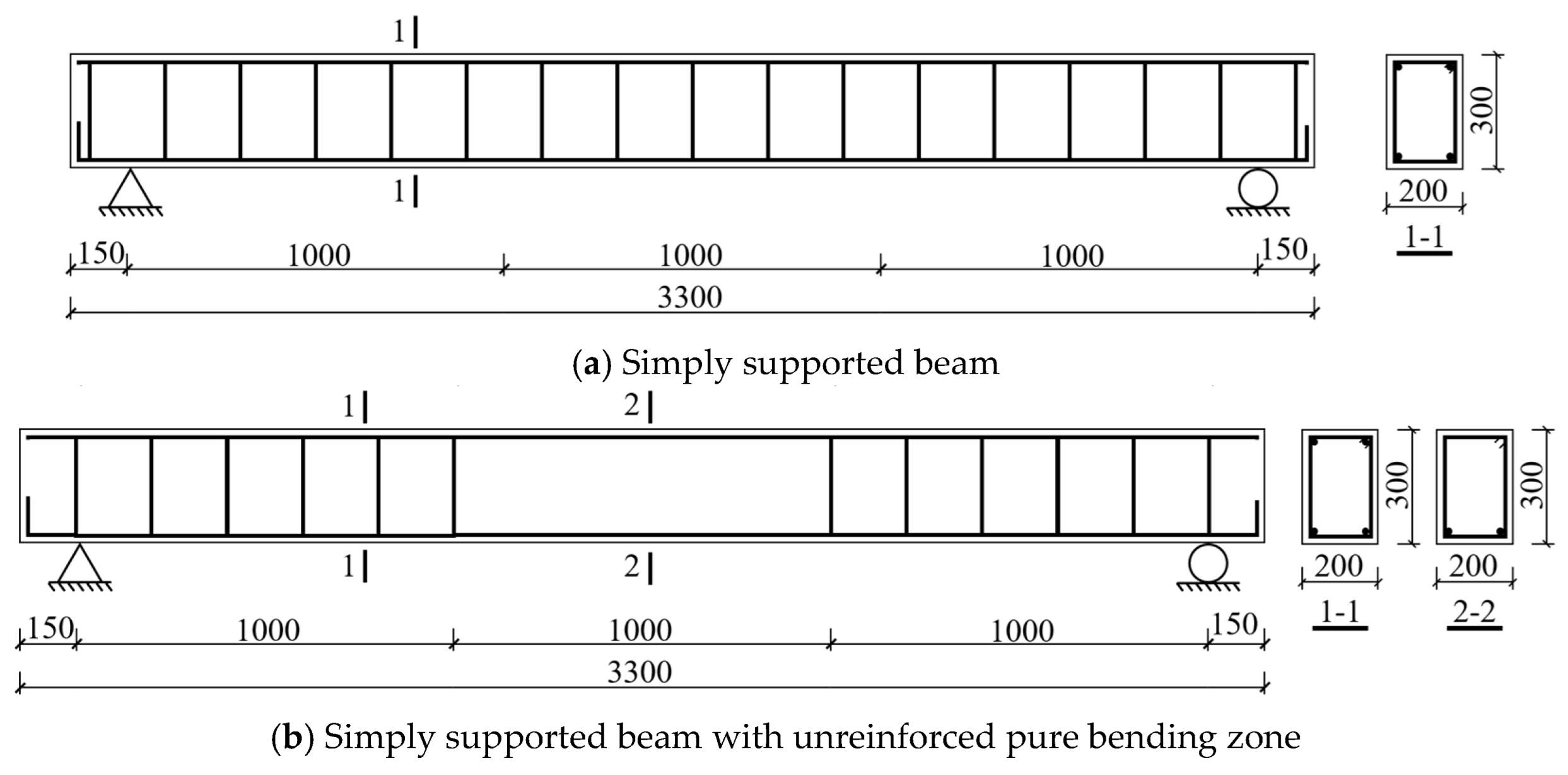







| Specimen Label | b × h × l (mm) | Reinforcement Details | |||
|---|---|---|---|---|---|
| Tensile Reinforcement | Stirrups | Spacer Bars | |||
| Reinforcement Ratio | Reinforcement Arrangement | ||||
| 200 × 300 × 3300 | 0.94% | 2C18 | Φ6@200 | 2C12 | |
| 200 × 300 × 3300 | 0.94% | 2C18 | Φ6@200 | 2C12 | |
| 200 × 300 × 3300 | 0.57% | 2C14 | Φ6@200 | 2C12 | |
| 200 × 300 × 3300 | 0.94% | 2C18 | Φ6@200 | 2C12 | |
| 200 × 300 × 3300 | 0.94% | 2C18 | Φ6@200 | - | |
| 200 × 300 × 3300 | 1.28% | 2C22 | Φ6@200 | 2C12 | |
| Classification | Relevant Ratios | Partial Composition (kg/m3) | ||||||
|---|---|---|---|---|---|---|---|---|
| Water/ Binder | NCA/ Water | RCA/ Cement | Sand/ Cement | Cement | Glazed Hollow Beads | Silica Fume | Water-Reducing Admixture | |
| NC | 0.52 | 2.50 | 0 | 1.07 | 484 | 0 | 36 | 5.70 |
| GHBNC | 0.52 | 2.50 | 0 | 1.07 | 484 | 169 | 36 | 5.70 |
| GHBRC | 0.52 | 1.25 | 1.20 | 1.07 | 484 | 169 | 36 | 5.70 |
| Classification | Ρ (kg/m3) | fc (MPa) | Ec (104 N/mm4) | λ (W/(m⸱K)) |
|---|---|---|---|---|
| NC | 2500 ± 26.4 | 37.5 ± 0.36 | 3.01 ± 0.03 | 1.74 ± 0.02 |
| GHBNC | 1800 ± 36.1 | 36.2 ± 0.20 | 2.63 ± 0.04 | 0.40 ± 0.01 |
| GHBRC | 1730 ± 34.6 | 34.2 ± 0.26 | 2.36 ± 0.02 | 0.56 ± 0.02 |
| NC | GHBNC | GHBRC | |
|---|---|---|---|
| 1.0 | 0.996 | 0.989 | |
| 0.798 | 0.793 | 0.785 |
| Specimens | Flexural Capacity (kN) | Mu,test/MU | |
|---|---|---|---|
| Mu,test | MU | ||
| NC-ρ0.94 | 100.3 ± 0.95 | 98.3 | 1.02 ± 0.01 |
| GHBNC-ρ0.94 | 103.4 ± 1.79 | 104.4 | 0.99 ± 0.02 |
| GHBRC-ρ0.94 | 107.5 ± 2.76 | 104.2 | 1.03 ± 0.03 |
| GHBRC-ρ0.57 | 70.7 ± 0.70 | 72.8 | 0.97 ± 0.01 |
| GHBRC-ρ1.28 | 138.4 ± 5.14 | 142.6 | 0.97 ± 0.04 |
| GHBRC-ρ0.94B | 93.4 ± 2.49 | 94.3 | 0.99 ± 0.03 |
| Speciments | Load (kN) | FGHBRC (mm) | Test/Equation (16) | |
|---|---|---|---|---|
| Test | Equation (16) | |||
| 30 | 2.48 ± 0.05 | 2.70 | 0.92 ± 0.02 | |
| NC-ρ0.94 | 60 | 6.75 ± 0.19 | 7.03 | 0.96 ± 0.03 |
| 90 | 11.20 ± 0.12 | 11.79 | 0.95 ± 0.01 | |
| 30 | 3.51 ± 0.13 | 3.58 | 0.98 ± 0.04 | |
| GHBNC-ρ0.94 | 60 | 8.45 ± 0.24 | 9.29 | 0.91 ± 0.03 |
| 90 | 14.10 ± 0.26 | 15.00 | 0.94 ± 0.02 | |
| 30 | 3.56 ± 0.04 | 3.83 | 0.93 ± 0.01 | |
| GHBRC-ρ0.94 | 60 | 8.33 ± 0.34 | 8.50 | 0.98 ± 0.04 |
| 90 | 13.79 ± 0.15 | 14.36 | 0.96 ± 0.01 | |
| 30 | 6.26 ± 0.19 | 6.96 | 0.90 ± 0.03 | |
| GHBRC-ρ0.57 | 60 | 12.04 ± 0.47 | 13.07 | 0.92 ± 0.04 |
| 70 | 15.05 ± 0.16 | 15.68 | 0.96 ± 0.01 | |
| 30 | 2.05 ± 0.10 | 2.09 | 0.98 ± 0.05 | |
| GHBRC-ρ1.28 | 60 | 7.58 ± 0.19 | 7.43 | 1.02 ± 0.03 |
| 90 | 12.94 ± 0.13 | 12.81 | 1.01 ± 0.01 | |
| 30 | 4.08 ± 0.14 | 4.00 | 1.02 ± 0.04 | |
| GHBRC-ρ0.94B | 60 | 10.43 ± 0.31 | 11.46 | 0.91 ± 0.03 |
| 90 | 15.40 ± 0.57 | 15.71 | 0.98 ± 0.04 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, J.; Liu, Y.; Li, X.; Wang, Z. Study on Flexural Performance of Recycled Aggregate Concrete Beams Incorporating Glazed Hollow Beads. Materials 2025, 18, 2435. https://doi.org/10.3390/ma18112435
Hou J, Liu Y, Li X, Wang Z. Study on Flexural Performance of Recycled Aggregate Concrete Beams Incorporating Glazed Hollow Beads. Materials. 2025; 18(11):2435. https://doi.org/10.3390/ma18112435
Chicago/Turabian StyleHou, Jingguang, Yuanzhen Liu, Xiangzheng Li, and Zhaoxu Wang. 2025. "Study on Flexural Performance of Recycled Aggregate Concrete Beams Incorporating Glazed Hollow Beads" Materials 18, no. 11: 2435. https://doi.org/10.3390/ma18112435
APA StyleHou, J., Liu, Y., Li, X., & Wang, Z. (2025). Study on Flexural Performance of Recycled Aggregate Concrete Beams Incorporating Glazed Hollow Beads. Materials, 18(11), 2435. https://doi.org/10.3390/ma18112435






