Toughening Effect of Micro-Cracks on Low-Temperature Crack Propagation in Asphalt Concrete
Abstract
1. Introduction
2. Modulus Damage Model of Asphalt Concrete
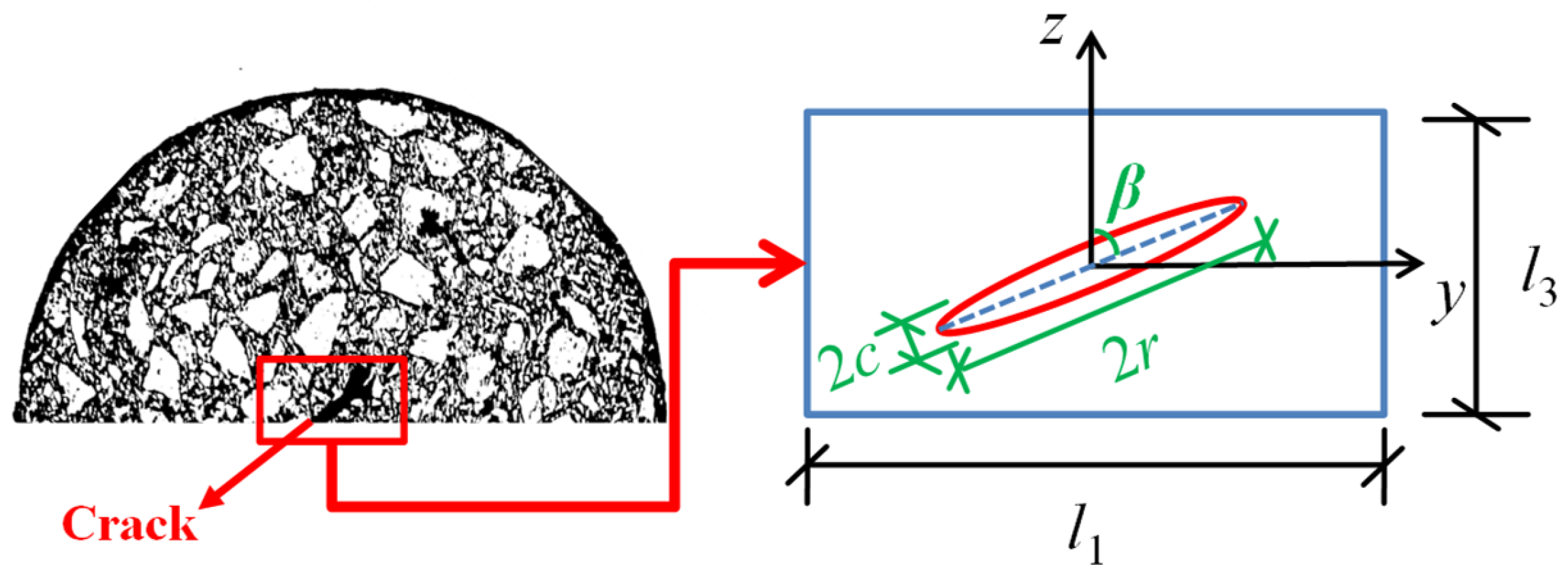
2.1. Modulus Damage Model Based on Main Crack Configuration Characteristics
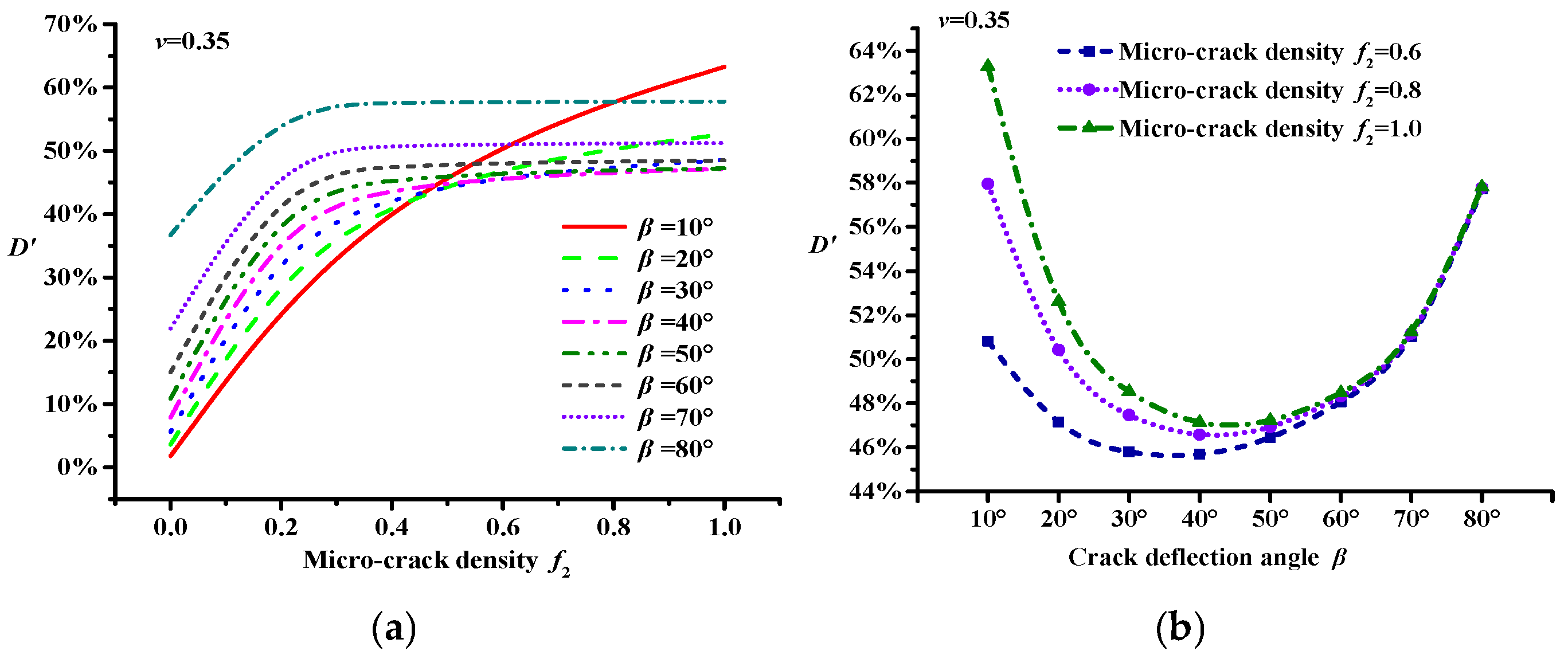
2.2. Toughening Effect of Micro-Cracks
- Micro-crack closure and crack surface friction are neglected.
- The micro-crack distribution is random.
- Only weak interactions exist between neighboring micro-cracks.
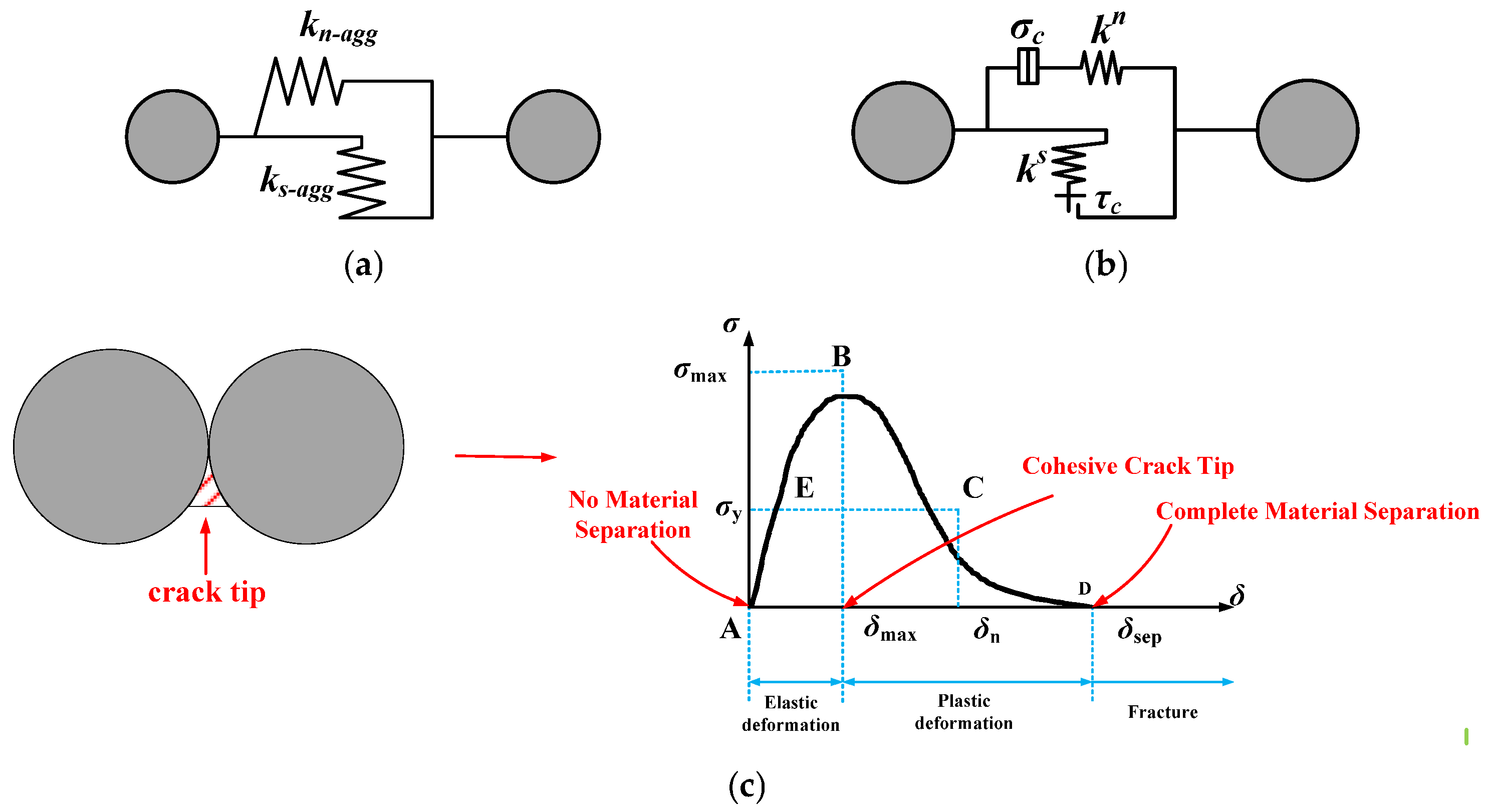
3. Mesoscopic Damage Model of Asphalt Concrete
3.1. Meso-Parameter of Asphalt Concrete
3.2. Construction of Micro-Cracks and Main Crack
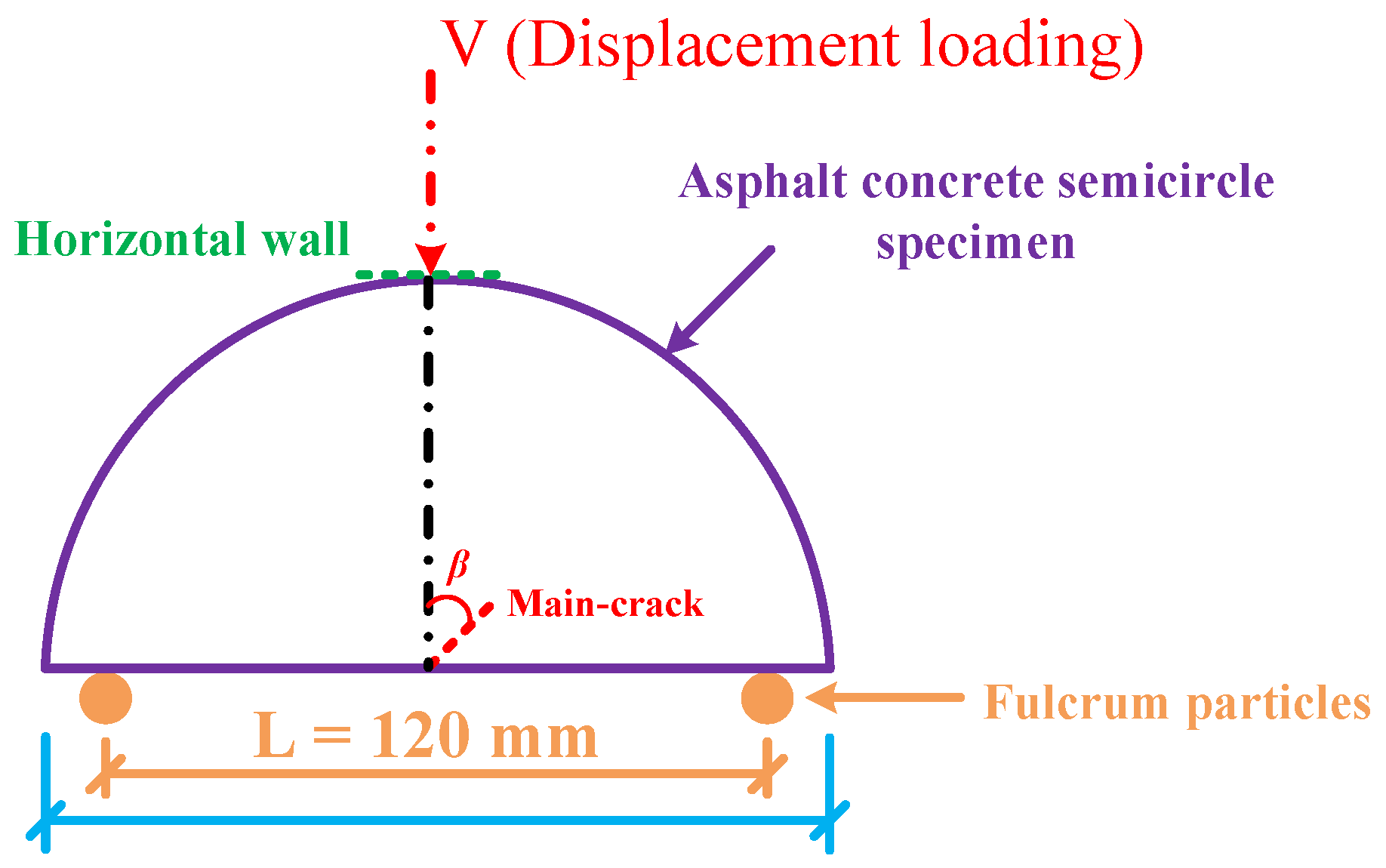
3.3. Virtual SCB Test
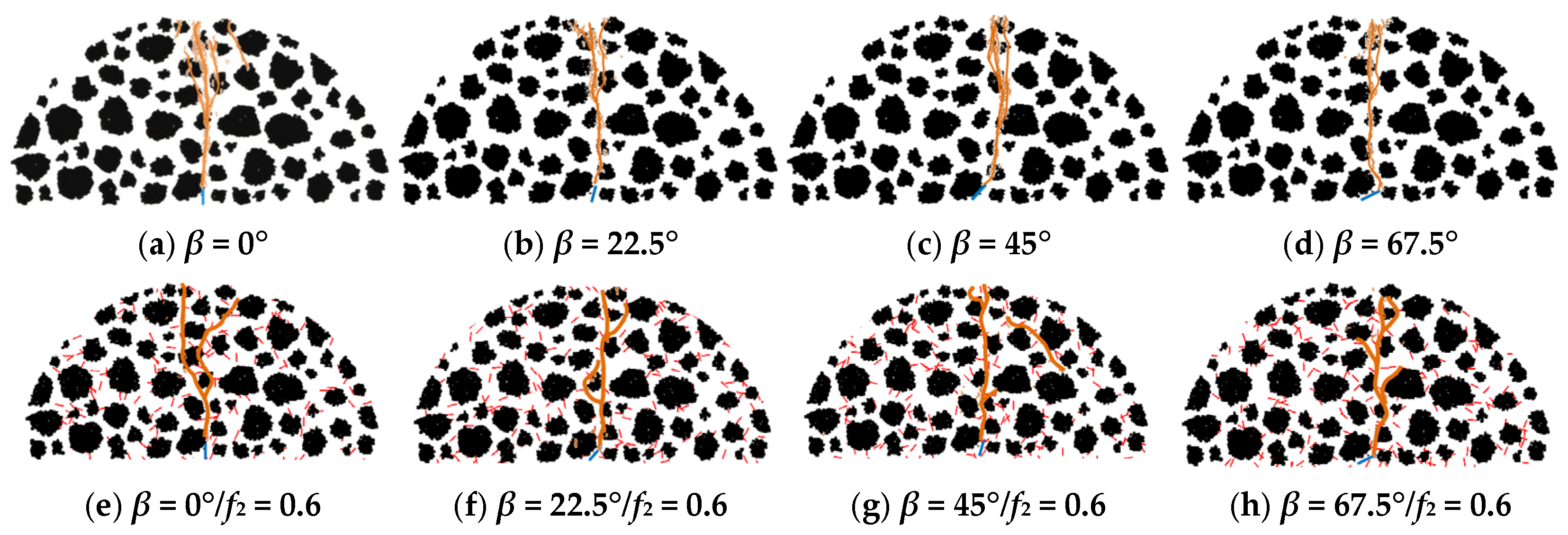
4. Crack Propagation Characteristics Under the Toughening Effect of Micro-Cracks
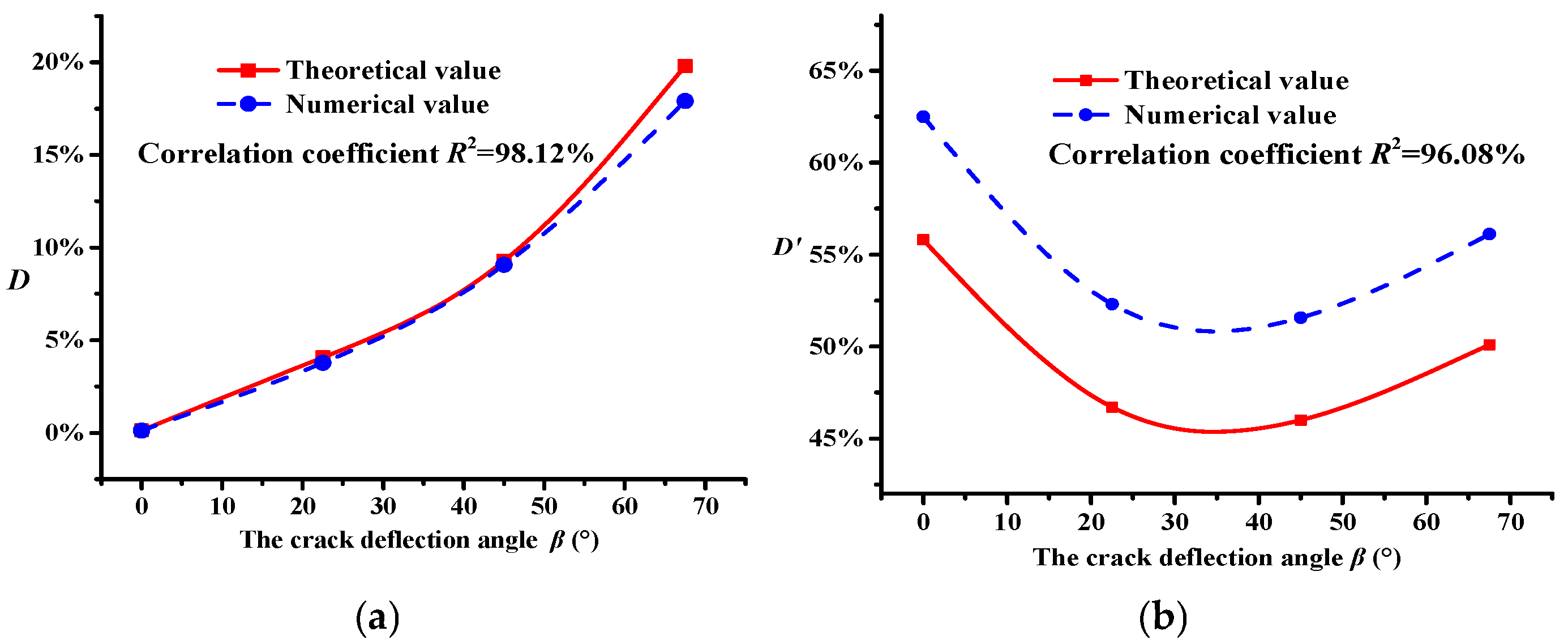
4.1. Modulus Damage of Asphalt Concrete
4.2. Dynamic Parameters in the Main Crack Propagation Process
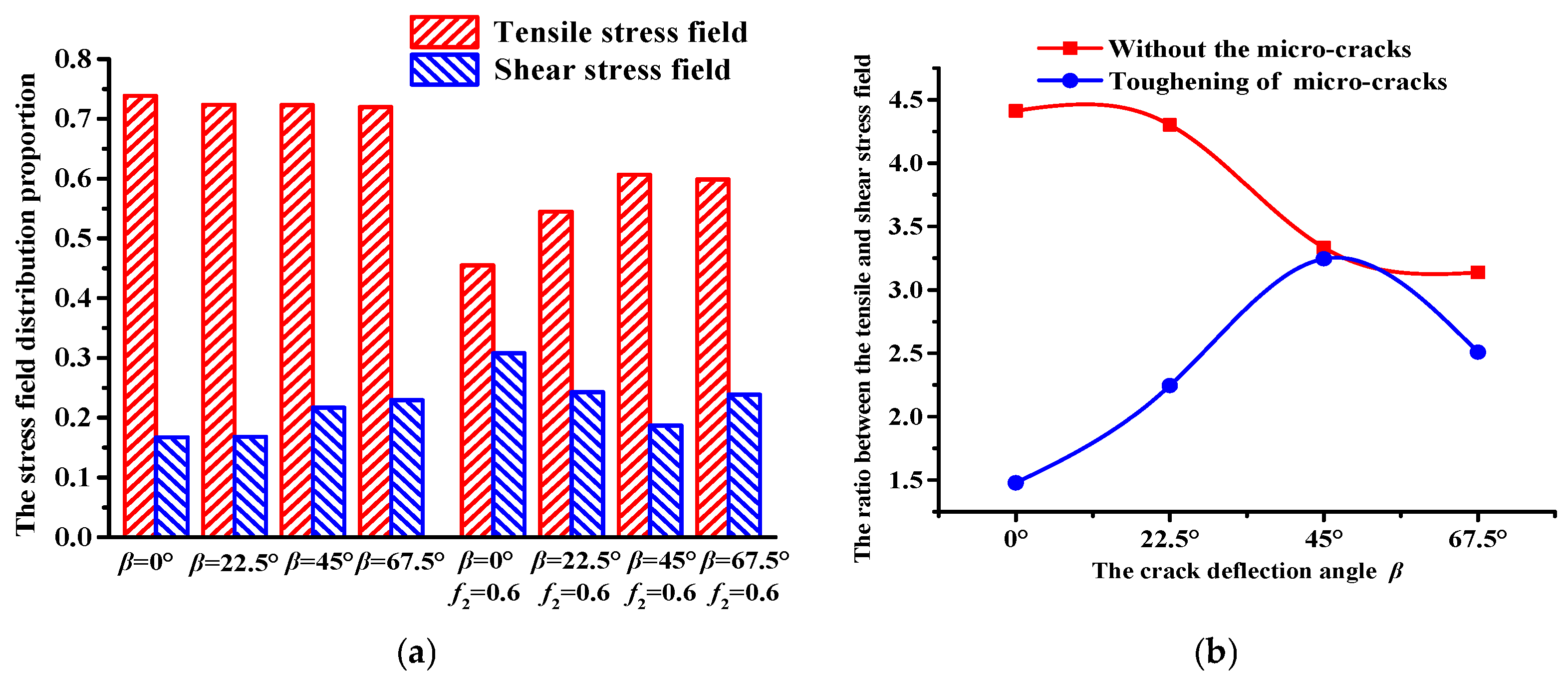
4.3. Stress Field Distribution
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| DEM | Discrete Element Method |
| SCB | Semi-Circular Bending |
| FEM | Finite Element Method |
| RVE | Representative Volume Element |
| β | Crack deflection angle |
| 2c | Crack thickness |
| 2r | Crack length |
| D | Modulus damage variable |
| E | Modulus of the asphalt concrete without the main crack |
| ET | Effective modulus of the asphalt concrete with the main crack |
| f0 | Volume fractions of the asphalt concrete |
| f1 | Volume fractions of the main crack |
| ν | Poisson ratio |
| α | Shape ratio of the main crack |
| p | Area fraction |
| D′ | Modulus damage variable under the toughening effect of the micro-cracks |
| E′ | Effective modulus of asphalt concrete with micro-cracks and a main crack |
| f2 | Micro-crack density |
| PPA | Polyphosphoric acid |
| SBS | Styrene butadiene styrene |
| PG | Performance grade |
| Kn-agg | Normal stiffness of the aggregates |
| Ks-agg | Tangential stiffness of the aggregates |
| Es | Dynamic modulus of the aggregates |
| νs | Poisson ratio of the aggregates |
| R | Radius of an aggregate particle |
| kn | Internal normal stiffnesses of the asphalt mortar |
| ks | Tangential stiffnesses of the asphalt mortar |
| Ea | Dynamic modulus of the asphalt mortar |
| νa | Poisson ratio of the asphalt mortar |
| Normal contact forces | |
| Tangential contact forces | |
| σmax | Maximum contact force |
| φ | Angle between the direction of the contact force and the connecting line to the particle center. |
| PFC2D | Particle flow code |
References
- Du, J.; Wang, J.; Fu, Z. Influence of Interaction between Microcracks and Macrocracks on Crack Propagation of Asphalt Concrete. Materials 2024, 17, 2877. [Google Scholar] [CrossRef] [PubMed]
- Gong, S.X. On the main crack-microcrack interaction under mode III loading. Eng. Fract. Mech. 1995, 51, 753–762. [Google Scholar] [CrossRef]
- Li, X.; Sheng, Y.; Yang, H.; Jiang, X. Micromechanisms of a macrocrack propagation behavior affected by short to long fatigue microcracks. Mech. Adv. Mater. Struct. 2022, 29, 2726–2739. [Google Scholar] [CrossRef]
- Petrova, V.E. Interaction between a main crack and inclusions of a given orientation. Mech. Compos. Mater. 1988, 24, 288–294. [Google Scholar] [CrossRef]
- Tamuzs, V.; Petrova, V. Modified model of macro–microcrack interaction. Theor. Appl. Fract. Mech. 1999, 32, 111–117. [Google Scholar] [CrossRef]
- Petrova, V.; Tamuzs, V.; Romalis, N. A Survey of Macro-Microcrack Interaction Problems. ASME Appl. Mech. Rev. 2000, 53, 117–146. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Jiang, X. Influence of a micro-crack on the finite macro-crack. Eng. Fract. Mech. 2017, 177, 95–103. [Google Scholar] [CrossRef]
- Li, X.; Xu, L.; Yang, H.; Jiang, X. Effect of micro-cracks on plastic zone ahead of the macro-crack tip. J. Mater. Sci. 2017, 52, 13490–13503. [Google Scholar] [CrossRef]
- Xia, X.Z.; Zhang, Q.; Qiao, P.Z.; Li, L.J. Interaction between cracks and effect of microcrack zone on main crack tip. Appl. Math. Mech. 2010, 31, 67–76. [Google Scholar] [CrossRef]
- Huang, F.; Yi, Z.; Yang, Q.; Ma, Y.; He, X.; Zhao, C.; Gu, J.; Li, Y. Elastic-plastic analysis of the crack surface vicinity under a pair of anti-plane forces applied at an arbitrary point on the crack surface. AIP Adv. 2018, 8, 105033. [Google Scholar] [CrossRef]
- Jiang, Z.D.; Petit, J.; Bezine, G. Fatigue propagation of two parallel cracks. Eng. Fract. Mech. 1990, 37, 1139–1144. [Google Scholar] [CrossRef]
- Jiang, Z.D.; Petit, J.; Bezine, G. An investigation of stress intensity factors for two unequal parallel cracks in a finite width plate. Eng. Fract. Mech. 1992, 42, 129–138. [Google Scholar] [CrossRef]
- Renshaw, C.E.; Schulson, E.M. Universal behaviour in compressive failure of brittle materials. Nature 2001, 412, 897–900. [Google Scholar] [CrossRef]
- Li, Y.P.; Yang, C.H. Approximate analysis of interaction of closely spaced cracks. J. Mech. Mater. Struct. 2006, 1, 147–162. [Google Scholar] [CrossRef][Green Version]
- Zhao, J.; Wang, W. Numerical simulation and experiment of interaction and influence on two colinear and offset cracks by FRANC2D Software. Press. Vessel. Pip. Conf. 2011, 44519, 453–458. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.; Xu, D.; Zeng, Q.; Zhuang, Z. Extended finite element method analysis for shielding and amplification effect of a main crack interacted with a group of nearby parallel microcracks. Int. J. Damage Mech. 2016, 25, 4–25. [Google Scholar] [CrossRef]
- Mishra, P.K.; Das, S. Interaction between interfacial collinear Griffith cracks in composite media under thermal loading. Z. Naturforschung A 2016, 71, 465–473. [Google Scholar] [CrossRef]
- Aliha, M.R.M.; Sarbijan, M.J.; Bahmani, A. Fracture toughness determination of modified HMA mixtures with two novel disc shape configurations. Constr. Build. Mater. 2017, 155, 789–799. [Google Scholar] [CrossRef]
- Eghbali, M.R.; Tafti, M.F.; Aliha, M.R.M.; Motamedi, H. The effect of ENDB specimen geometry on mode I fracture toughness and fracture energy of HMA and SMA mixtures at low temperatures. Eng. Fract. Mech. 2019, 216, 106496. [Google Scholar] [CrossRef]
- Najjar, S.; Moghaddam, A.M.; Sahaf, A.; Aliha, M.R.M. Low temperature fracture resistance of cement emulsified asphalt mortar under mixed mode I/III loading. Theor. Appl. Fract. Mech. 2020, 110, 102800. [Google Scholar] [CrossRef]
- Gao, L.; Kong, H.; Deng, X.; Wang, Z. Multi-scale finite element simulation of asphalt mixture anti-cracking performance. Theor. Appl. Fract. Mech. 2022, 121, 103490. [Google Scholar] [CrossRef]
- Szydłowski, C.; Smakosz, Ł.; Stienss, M.; Górski, J. The use of a two-phase Monte Carlo material model to reflect the dispersion of asphalt concrete fracture parameters. Theor. Appl. Fract. Mech. 2022, 119, 103326. [Google Scholar] [CrossRef]
- Pirmohammad, S.; Momeni, R.; Khanghahi, S.H. Effect of SCB specimen size on mode I fracture parameters of asphalt concrete at low and intermediate temperatures. Theor. Appl. Fract. Mech. 2024, 130, 104314. [Google Scholar] [CrossRef]
- Daud, R.; Ariffin, A.K.; Abdullah, S.; Ismail, A.E. Computation of mixed mode stress intensity factor for parallel edge cracks. Appl. Mech. Mater. 2011, 52, 1326–1331. [Google Scholar] [CrossRef]
- Jin, H.J.; Wu, S.J. A new driving force parameter for fatigue growth of multiple cracks. Int. J. Fatigue 2017, 96, 10–16. [Google Scholar] [CrossRef]
- Kamaya, M.; Miyokawa, E.; Kikuchi, M. Growth prediction of two interacting surface cracks of dissimilar sizes. Eng. Fract. Mech. 2010, 77, 3120–3131. [Google Scholar] [CrossRef]
- Xu, L.; Zhao, L.; Jing, H.; Han, Y. Evaluation of multiple cracks interaction effect subjected to biaxial tension under creep regime. Int. J. Mech. Sci. 2017, 122, 203–214. [Google Scholar] [CrossRef]
- Zhu, D.J. Stress intensity factor and interaction analysis of offset parallel cracks in brittle solids. Eur. J. Mech.-A/Solids 2021, 85, 104119. [Google Scholar] [CrossRef]
- Candaş, A.; Oterkus, E.; İmrak, C.E. Dynamic crack propagation and its interaction with micro-cracks in an impact problem. J. Eng. Mater. Technol. 2021, 143, 011003. [Google Scholar] [CrossRef]
- Alam, S.Y.; Loukili, A. Effect of micro-macro crack interaction on softening behaviour of concrete fracture. Int. J. Solids Struct. 2020, 182, 34–45. [Google Scholar] [CrossRef]
- Yuan, F.; Cheng, L.; Shao, X.; Dong, Z.; Zhang, L.; Wu, G.; He, X. Full-field measurement and fracture and fatigue characterizations of asphalt concrete based on the SCB test and stereo-DIC. Eng. Fract. Mech. 2020, 235, 107127. [Google Scholar] [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1957, 241, 376–396. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Kassem, E.; Grasley, Z.C.; Masad, E. Viscoelastic Poisson’s ratio of asphalt mixtures. Int. J. Geomech. 2013, 13, 162–169. [Google Scholar] [CrossRef]
- Aurangzeb, Q.; Ozer, H.; Al-Qadi, I.L.; Hilton, H.H. Viscoelastic and Poisson’s ratio characterization of asphalt materials: Critical review and numerical simulations. Mater. Struct. 2017, 50, 49. [Google Scholar] [CrossRef]
- Feng, X.Q.; Li, J.Y.; Yu, S.W. A simple method for calculating interaction of numerous microcracks and its applications. Int. J. Solids Struct. 2003, 40, 447–464. [Google Scholar] [CrossRef]
- Yang, W. Macro and Micro Fracture Mechanics; National Defense Industry: Beijing, China, 1995. (In Chinese) [Google Scholar]
- Budiansky, B.; O’Connell, R.J. Elastic moduli of a cracked solid. Int. J. Solids Struct. 1976, 12, 81–97. [Google Scholar] [CrossRef]
- Lai, Y.; Zhang, Y.-X. Methods of Rock Crack Density Determination and Their Application. J. Civil Archit. Environ. Eng. 2009, 31, 51–56. [Google Scholar] [CrossRef]
- Du, J.H.; Fu, Z. Influence of crack configurations of asphalt mortar on the loading response characteristics of cracks under low-temperature conditions. Eng. Fract. Mech. 2024, 309, 110386. [Google Scholar] [CrossRef]
- Kim, H.; Wagoner, M.P.; Buttlar, W.G. Simulation of fracture behavior in asphalt concrete using a heterogeneous cohesive zone discrete element model. J. Mater. Civil Eng. 2008, 20, 552–563. [Google Scholar] [CrossRef]
- Liu, Y.; Dai, Q.; You, Z. Viscoelastic model for discrete element simulation of asphalt mixtures. J. Eng. Mech. 2009, 135, 324–333. [Google Scholar] [CrossRef]
- You, Z.; Adhikari, S.; Dai, Q. Three-dimensional discrete element models for asphalt mixtures. J. Eng. Mech. 2008, 134, 1053–1063. [Google Scholar] [CrossRef]
- Wang, L.B. Mechanics of Asphalt: Microstructure and Micromechanics; McGraw-Hill Professional: New York, NY, USA, 2012. [Google Scholar]
- Leng, Y. Test Study on Asphalt Concrete Mixture Material Design and Comprehensive Performance of High-Speed Railway Surface Layer of Foundation Bed Reinforced by Asphalt Concrete at Seasonal Frozen Region; Southwest Jiaotong University: Chengdu, China, 2015. (In Chinese) [Google Scholar]
- Du, J.; Ren, D.; Ai, C.; Zhang, J.; Qiu, Y. Effect of aggregate gradation on crack propagation in asphalt mixtures at low temperatures based on the Eshelby equivalent inclusion theory. Constr. Build. Mater. 2021, 290, 123181. [Google Scholar] [CrossRef]



| Aperture size (mm) | 16.0 | 13.2 | 9.5 | 4.75 | 2.36 | 1.18 | 0.60 | 0.30 | 0.15 | 0.075 |
| Passing ratio (%) | 100.0 | 97.5 | 84.0 | 62.5 | 42.5 | 32.0 | 24.0 | 15.5 | 11.0 | 6.0 |
| Oil–Stone Ratio (%) | Gross Volumetric Density (g/cm3) | Marshall Stability (kN) | Porosity (%) | Flow Value (mm) | Void Filled with Asphalt (VFA) (%) | Maximum Theoretical Density (g/cm3) |
| 6.27 | 2.547 | 12.48 | 2.1 | 4.34 | 76.2 | 2.610 |
| Particle Contact | Meso-Parameters | |
|---|---|---|
| Aggregate | Dynamic modulus (GPa) | 55.5 |
| Tensile strength σ (MPa) | 27.6 | |
| Poisson’s ratio νs | 0.23 | |
| Normal stiffness kn (MPa) | 222 | |
| Tangential stiffness ks (MPa) | 90.24 | |
| Asphalt concrete | Void ratio (%) | 2.1 |
| Particle density (kg∙m−3) | 2582 | |
| Asphalt mortar | Interparticle contact modulus Ec (GPa) | 0.832 |
| Particle normal to the tangential stiffness ratio kn/ks | 1 | |
| Parallel bond modulus (GPa) | 0.596 | |
| Parallel bond normal to tangential stiffness ratio knc/ksc | 0.667/0.133 | |
| Interparticle friction coefficient fs | 0.5 | |
| Average normal strength of parallel bond σc (MPa) | 3.553 | |
| Standard deviation of parallel bond normal strength (MPa) | 1 | |
| Average tangential strength of parallel bond τc (MPa) | 3.553 | |
| Standard deviation of the parallel bond tangential strength (MPa) | 1 | |
| Micro-Crack Density f2 | Crack Deflection Angle β | Crack Incubation Stage | Crack Propagation Stage | Macro-Crack Formation Stage | |||
|---|---|---|---|---|---|---|---|
| Crack Number (Items) | ∆1 | Crack Number (Items) | ∆2 | Crack Number (Items) | ∆3 | ||
| 0.0 | 0° | 1 | 4.401 | 36 | 0.253 | 593 | 0.030 |
| 22.5° | 1 | 4.398 | 33 | 0.240 | 462 | 0.023 | |
| 45° | 1 | 4.395 | 26 | 0.215 | 446 | 0.020 | |
| 67.5° | 1 | 4.380 | 14 | 0.145 | 388 | 0.020 | |
| 0.6 | 0° | 1 | 4.346 | 11 | 0.306 | 131 | 0.033 |
| 22.5° | 1 | 4.285 | 12 | 0.356 | 137 | 0.037 | |
| 45° | 1 | 4.210 | 14 | 0.700 | 144 | 0.040 | |
| 67.5° | 1 | 4.110 | 13 | 0.546 | 135 | 0.032 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, J.; Dai, X.; Liu, Q.; Fu, Z. Toughening Effect of Micro-Cracks on Low-Temperature Crack Propagation in Asphalt Concrete. Materials 2025, 18, 2429. https://doi.org/10.3390/ma18112429
Du J, Dai X, Liu Q, Fu Z. Toughening Effect of Micro-Cracks on Low-Temperature Crack Propagation in Asphalt Concrete. Materials. 2025; 18(11):2429. https://doi.org/10.3390/ma18112429
Chicago/Turabian StyleDu, Jianhuan, Xianxing Dai, Qingyang Liu, and Zhu Fu. 2025. "Toughening Effect of Micro-Cracks on Low-Temperature Crack Propagation in Asphalt Concrete" Materials 18, no. 11: 2429. https://doi.org/10.3390/ma18112429
APA StyleDu, J., Dai, X., Liu, Q., & Fu, Z. (2025). Toughening Effect of Micro-Cracks on Low-Temperature Crack Propagation in Asphalt Concrete. Materials, 18(11), 2429. https://doi.org/10.3390/ma18112429





