Numerical Analysis on Optimal Adhesive Thickness in CFRP Single-Lap Joints Considering Material Properties
Highlights
- FE analysis reveals thickness-dependent damage mechanisms in CFRP joints.
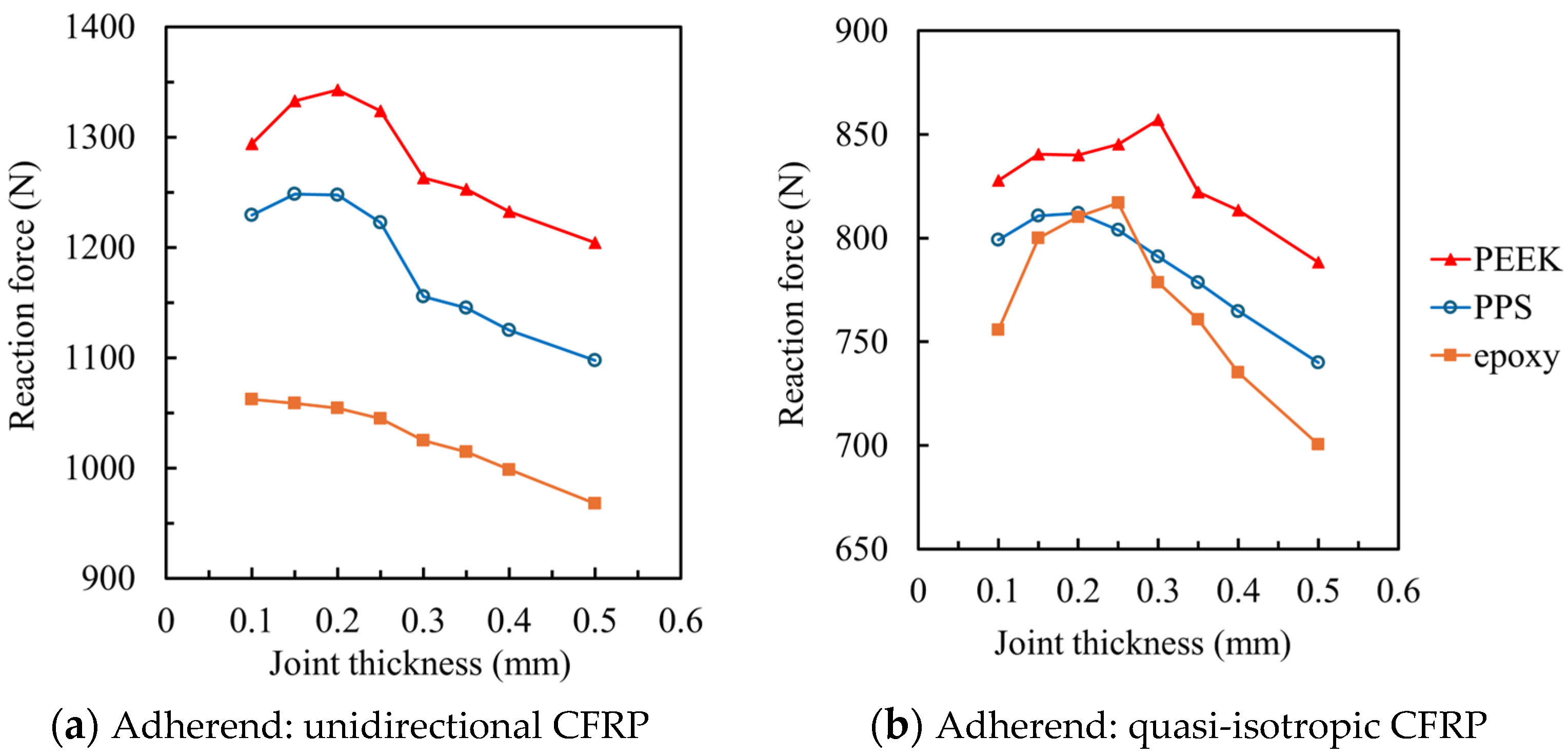
- Optimal adhesive thickness ranges between 0.1 and 0.3 mm depending on material.
- Both overly thick and thin layers reduce joint strength significantly.
- Peel stress dominates failure initiation near adhesive edge regions.
Abstract
1. Introduction
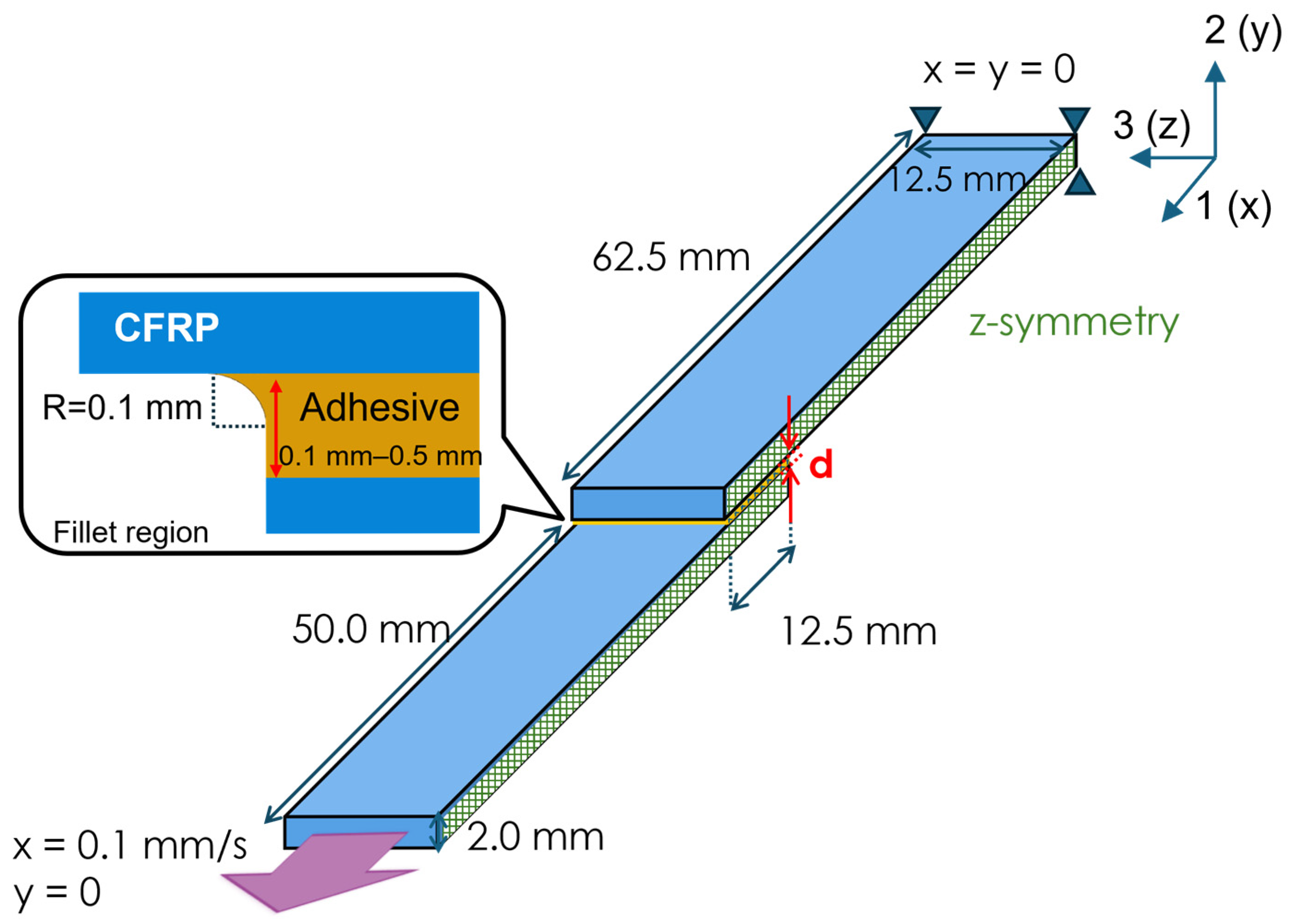
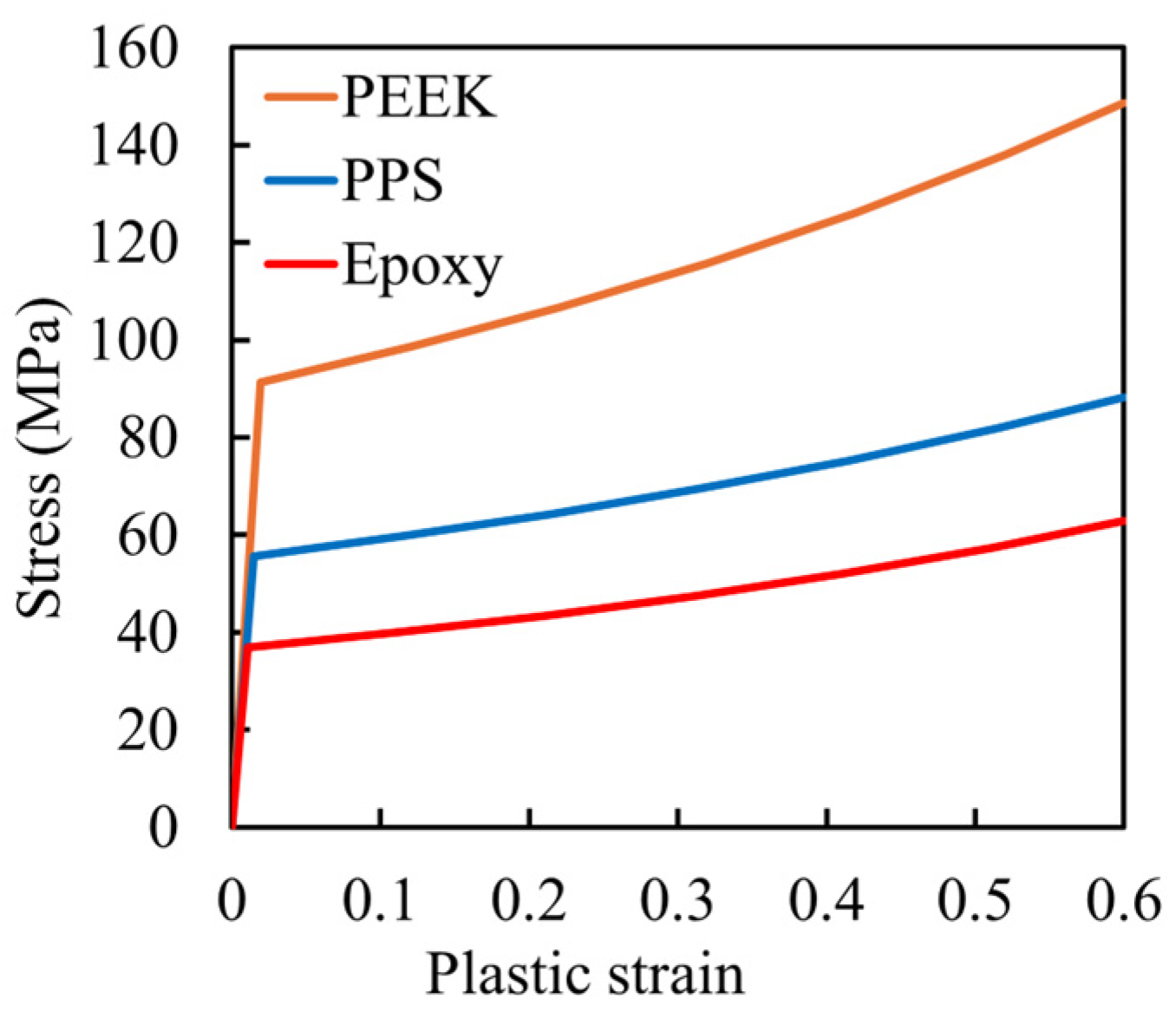
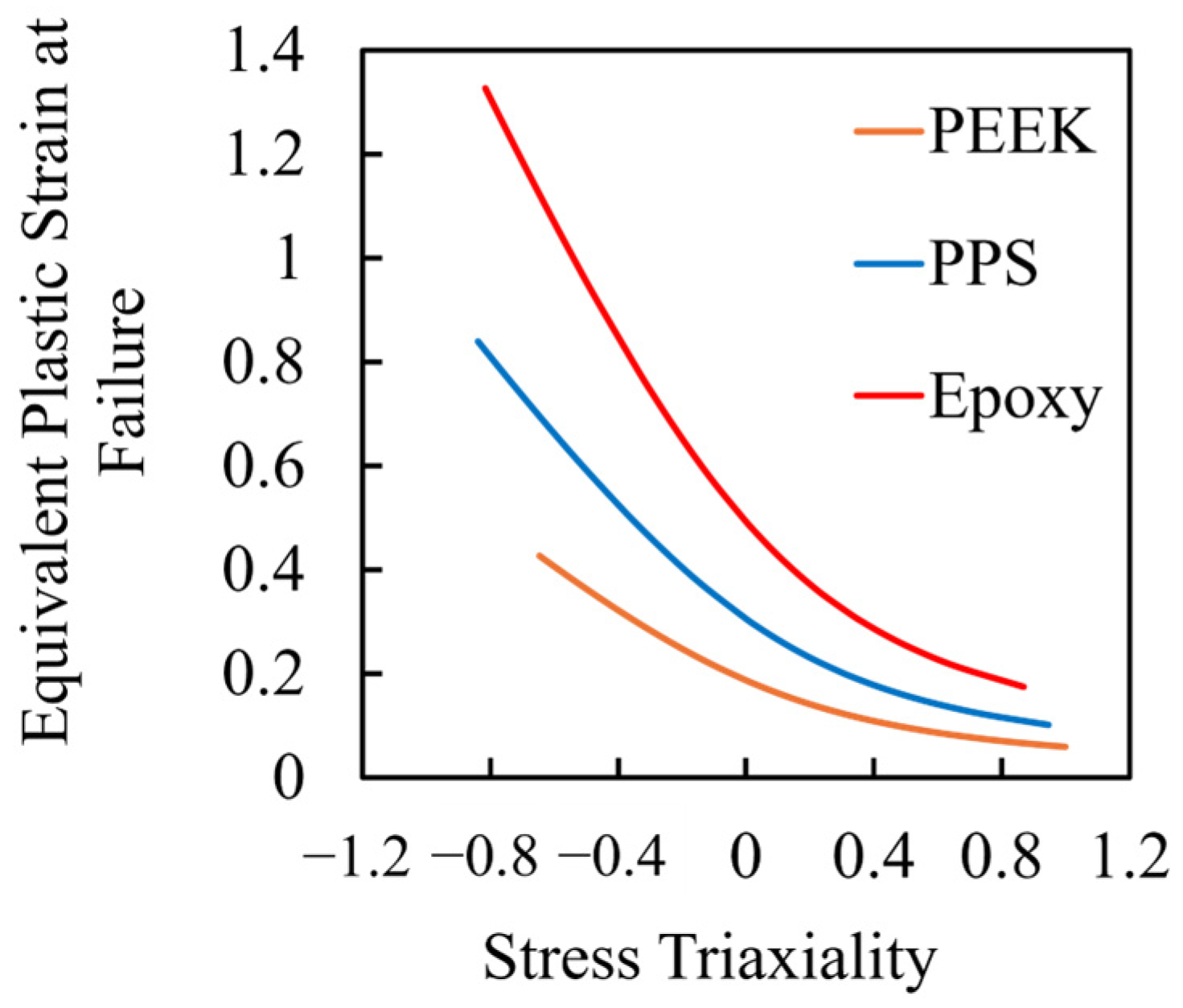
2. Methods
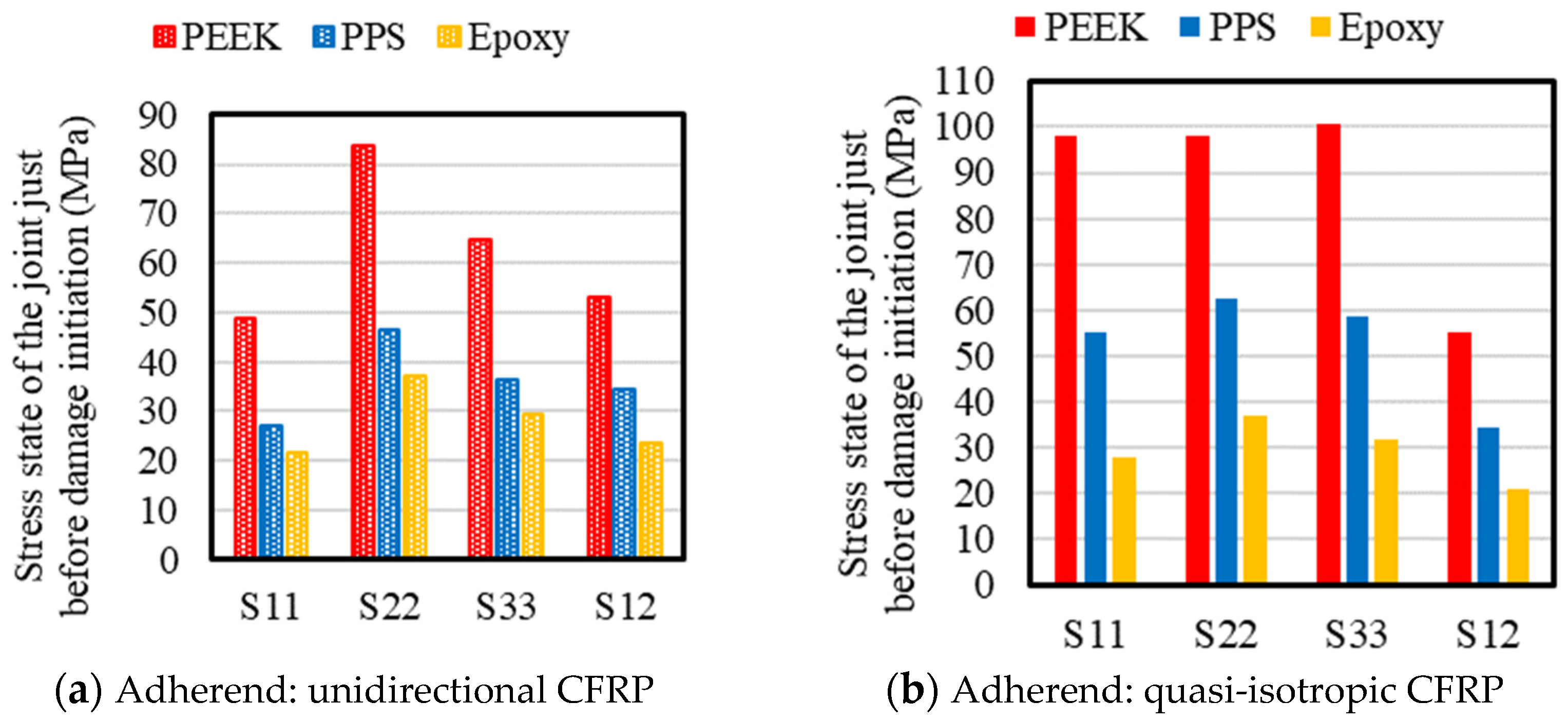
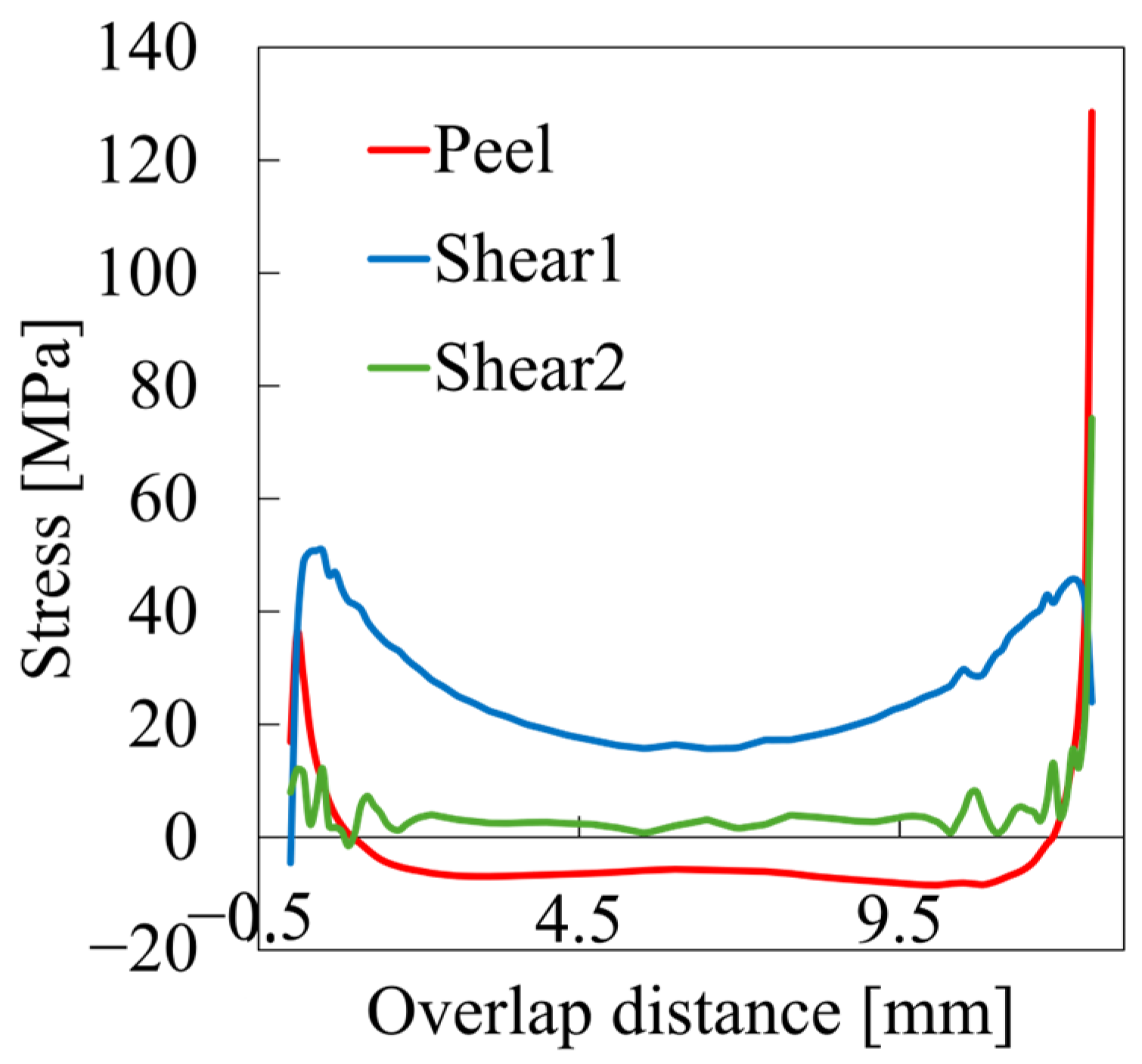
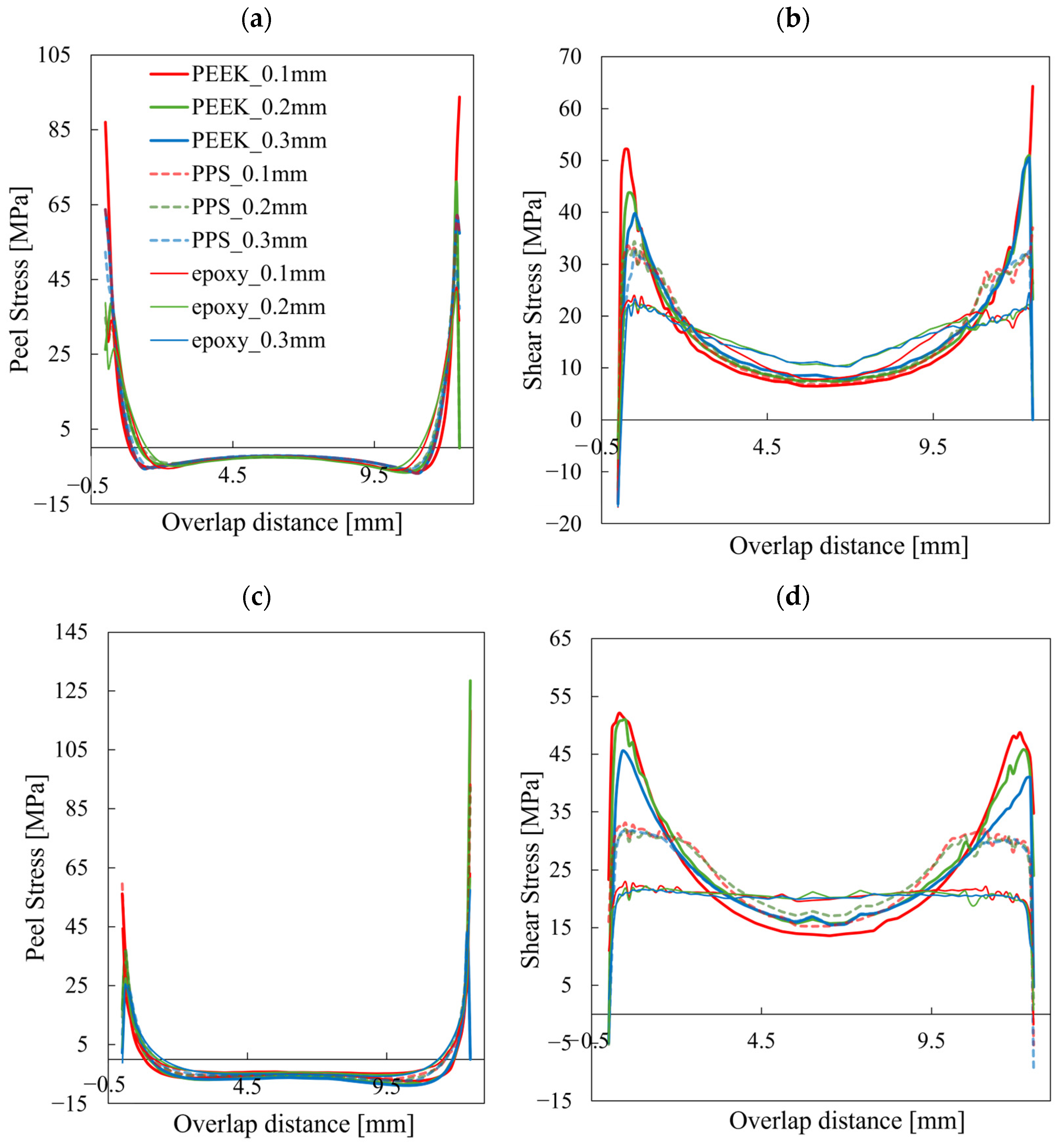
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Redmann, A.; Damodaran, V.; Tischer, F.; Prabhakar, P.; Osswald, T.A. Evaluation of single-lap and block shear test methods in adhesively bonded composite joints. J. Compos. Sci. 2021, 5, 27. [Google Scholar] [CrossRef]
- O’Brien, T.K.; Martin, R.H. Round robin testing for mode I interlaminar fracture toughness of composite materials. Compos. Technol. Res. 1993, 15, 269–281. [Google Scholar] [CrossRef]
- Terasaki, N.; Fujio, Y.; Sakata, Y.; Horiuchi, S.; Akiyama, H. Visualization of crack propagation for assisting double cantilever beam test through mechanoluminescence. J. Adhes. 2018, 94, 867–879. [Google Scholar] [CrossRef]
- Tam, L.; Pilliar, R. Effects of dentin surface treatments on the fracture toughness and tensile bond strength of a dentin-composite adhesive interface. J. Dent. Res. 1994, 73, 1530–1538. [Google Scholar] [CrossRef]
- Da Silva, L.F.; Critchlow, G.; Figueiredo, M. Parametric study of adhesively bonded single lap joints by the Taguchi method. J. Adhes. Sci. Technol. 2008, 22, 1477–1494. [Google Scholar] [CrossRef]
- Aydin, M.D.; Özel, A.; Temiz, Ş. The effect of adherend thickness on the failure of adhesively-bonded single-lap joints. J. Adhes. Sci. Technol. 2005, 19, 705–718. [Google Scholar] [CrossRef]
- Akkasali, N.K.; Biswas, S.; Sen, S.; Anitha, S. A state-of-the-art review on adhesively bonded joints of similar and dissimilar materials. J. Adhes. Sci. Technol. 2024, 38, 4317–4371. [Google Scholar] [CrossRef]
- Bidadi, J.; Saeidi Googarchin, H.; Akhavan-Safar, A.; Carbas, R.J.; da Silva, L.F. Characterization of bending strength in similar and dissimilar carbon-fiber-reinforced polymer/aluminum single-lap adhesive joints. Appl. Sci. 2023, 13, 12879. [Google Scholar] [CrossRef]
- Nallamuthu, R.; Vellayaraj, A.; Chelliah, S.K.; Bose, P.; Thirugnanasamabandam, A. A comprehensive investigation on tensile behavior of surface-modified Kevlar hybrid nanocomposites for similar and dissimilar joints. Polym. Compos. 2024, 45, 8076–8090. [Google Scholar] [CrossRef]
- Demiral, M.; Kadioglu, F. Damage characteristics of a step lap joint exposed to flexural loading for its different configurations. Polymers 2023, 15, 2458. [Google Scholar] [CrossRef]
- Santos, M.; Santos, J. Adhesive single-lap joint evaluation using ultrasound guided waves. Appl. Sci. 2023, 13, 6523. [Google Scholar] [CrossRef]
- Koyanagi, J.; Takamura, M.; Wakayama, K.; Uehara, K.; Takeda, S. Numerical simulation of ultrasonic welding for CFRP using energy director. Adv. Compos. Mater. 2022, 31, 428–441. [Google Scholar] [CrossRef]
- Fernández-Cañadas, L.M.; Ivañez, I.; Sanchez-Saez, S.; Barbero, E.J. Effect of adhesive thickness and overlap on the behavior of composite single-lap joints. Mech. Adv. Mater. Struct. 2021, 28, 1111–1120. [Google Scholar] [CrossRef]
- Da Silva, L.F.; Öchsner, A.; Adams, R.D. Handbook of Adhesion Technology; Springer International Publishing: Berlin, Germany, 2011. [Google Scholar]
- Sadık, A.; Karabudak, F. Strength analysis in Bonded, bolted and bolted-Bonded joints, single lap joints, Metal/Composite Plates. Appl. Sci. 2023, 13, 10476. [Google Scholar] [CrossRef]
- Zhao, L.; Xin, A.; Liu, F.; Zhang, J.; Hu, N. Secondary bending effects in progressively damaged single-lap, single-bolt composite joints. Results Phys. 2016, 6, 704–711. [Google Scholar] [CrossRef]
- Luo, H.; Yan, Y.; Zhang, T.; Liang, Z. Progressive failure and experimental study of adhesively bonded composite single-lap joints subjected to axial tensile loads. J. Adhes. Sci. Technol. 2016, 30, 894–914. [Google Scholar] [CrossRef]
- Tong, L. Bond strength for adhesive-bonded single-lap joints. Acta Mech. 1996, 117, 101–113. [Google Scholar] [CrossRef]
- Liao, L.; Kobayashi, T.; Sawa, T.; Goda, Y. 3-D FEM stress analysis and strength evaluation of single-lap adhesive joints subjected to impact tensile loads. Int. J. Adhes. Adhes. 2011, 31, 612–619. [Google Scholar] [CrossRef]
- Damghani, M.; Khan, M.S.; Atkinson, G.A. Experimental study of bonded, bolted, and hybrid bonded-bolted single lap shear joints with woven CFRP adherends. Compos. Struct. 2024, 334, 117989. [Google Scholar] [CrossRef]
- Takamura, M.; Isozaki, M.; Takeda, S.; Oya, Y.; Koyanagi, J. Evaluation of true bonding strength for adhesive bonded carbon fiber-reinforced plastics. Materials 2024, 17, 394. [Google Scholar] [CrossRef]
- Takamura, M.; Uehara, K.; Koyanagi, J.; Takeda, S. Multi-Timescale simulations of temperature elevation for ultrasonic welding of CFRP with energy director. J. Multiscale Model. 2021, 12, 2143003. [Google Scholar] [CrossRef]
- Chu, C.-W.; Zhang, Y.; Obayashi, K.; Kojio, K.; Takahara, A. Single-lap joints bonded with epoxy nanocomposite adhesives: Effect of organoclay reinforcement on adhesion and fatigue behaviors. ACS Appl. Polym. Mater. 2021, 3, 3428–3437. [Google Scholar] [CrossRef]
- Li, Y.; Deng, H.; Takamura, M.; Koyanagi, J. Durability analysis of CFRP adhesive joints: A study based on entropy damage modeling using FEM. Materials 2023, 16, 6821. [Google Scholar] [CrossRef]
- Ghasemvand, M.; Behjat, B.; Ebrahimi, S. Experimental investigation of the effects of adhesive defects on the strength and creep behavior of single-lap adhesive joints at various temperatures. J. Adhes. 2023, 99, 1227–1243. [Google Scholar] [CrossRef]
- Diharjo, K.; Anwar, M.; Tarigan, R.A.P.; Rivai, A. Effect of adhesive thickness and surface treatment on shear strength on single lap joint Al/CFRP using adhesive of epoxy/Al fine powder. AIP Conf. Proc. 2016, 1710, 30030. [Google Scholar] [CrossRef]
- Yang, K.; Feng, H.; Li, P.; Ji, S.; Lv, Z.; Liu, Z. The effects of environments and adhesive layer thickness on the failure modes of composite material bonded joints. Sci. Rep. 2024, 14, 22776. [Google Scholar] [CrossRef]
- Banea, M.D.; da Silva, L.F.M.; Campilho, R.D. The effect of adhesive thickness on the mechanical behavior of a structural polyurethane adhesive. J. Adhes. 2015, 91, 331–346. [Google Scholar] [CrossRef]
- Grant, L.; Adams, R.D.; da Silva, L.F. Experimental and numerical analysis of single-lap joints for the automotive industry. Int. J. Adhes. Adhes. 2009, 29, 405–413. [Google Scholar] [CrossRef]
- Oshima, S.; Koyanagi, J. Review on Damage and Failure in Adhesively Bonded Composite Joints: A Microscopic Aspect. Polymers 2025, 17, 377. [Google Scholar] [CrossRef]
- Siraj, N.; Hashmi, S.A.R.; Verma, S. State-of-the-art review on the high-performance poly (ether ether ketone) composites for mechanical, tribological and bioactive characteristics. Polym. Adv. Technol. 2022, 33, 3049–3077. [Google Scholar] [CrossRef]
- Iwamoto, S.; Oya, Y.; Koyanagi, J. Evaluation of microscopic damage of PEEK polymers under cyclic loadings using molecular dynamics simulations. Polymers 2022, 14, 4955. [Google Scholar] [CrossRef] [PubMed]
- ISO 4587:2003; Adhesives—Determination of Tensile Lap-Shear Strength of Rigid-to-Rigid Bonded Assemblies. International Organization for Standardization: Geneva, Switzerland, 2003.
- Morimoto, T.; Sugimoto, S.; Katoh, H.; Hara, E.; Yasuoka, T.; Iwahori, Y.; Ogasawara, T.; Ito, S. JAXA advanced composites database. In JAXA Research and Development Memorandum; JAXA-RM-14-004; JAXA: Tokyo, Japan, 2015. [Google Scholar]
- Rae, P.; Brown, E.; Orler, E. The mechanical properties of poly (ether-ether-ketone)(PEEK) with emphasis on the large compressive strain response. Polymer 2007, 48, 598–615. [Google Scholar] [CrossRef]
- Das, A.; Chatham, C.A.; Fallon, J.J.; Zawaski, C.E.; Gilmer, E.L.; Williams, C.B.; Bortner, M.J. Current understanding and challenges in high temperature additive manufacturing of engineering thermoplastic polymers. Addit. Manuf. 2020, 34, 101218. [Google Scholar] [CrossRef]
- Zuo, P.; Tcharkhtchi, A.; Shirinbayan, M.; Fitoussi, J.; Bakir, F. Overall investigation of poly (phenylene sulfide) from synthesis and process to applications—A review. Macromol. Mater. Eng. 2019, 304, 1800686. [Google Scholar] [CrossRef]
- Afendi, M.; Teramoto, T. Fracture toughness test of epoxy adhesive dissimilar joint with various adhesive thicknesses. J. Solid Mech. Mater. Eng. 2010, 4, 999–1010. [Google Scholar] [CrossRef][Green Version]
- Christensen, R.M. A comprehensive theory of yielding and failure for isotropic materials. J. Eng. Mater. Technol. 2007, 129, 173–181. [Google Scholar] [CrossRef]
- Da Silva, L.F.; Rodrigues, T.; Figueiredo, M.; De Moura, M.; Chousal, J. Effect of adhesive type and thickness on the lap shear strength. J. Adhes. 2006, 82, 1091–1115. [Google Scholar] [CrossRef]
- Rośkowicz, M.; Godzimirski, J.; Komorek, A.; Jasztal, M. The effect of adhesive layer thickness on joint static strength. Materials 2021, 14, 1499. [Google Scholar] [CrossRef]
- Pires, V.D.; Ribeiro, F.C.; Carbas, R.J.; Marques, E.A.; da Silva, L.F. The reduction of stress concentrations in adhesive joints with the use of curved aluminum adherends. Mech. Adv. Mater. Struct. 2024, 31, 10962–10973. [Google Scholar] [CrossRef]


| Young’s Modulus [MPa] | Poisson’s Ratio | Density [g/cm3] | Specific Heat [J/(kg·K)] | Thermal Conductivity [W/(m·K)] | Thermal Expansion Coefficient Vertical [1/K] | Thermal Expansion Coefficient Shear1 [1/K] | Thermal Expansion Coefficient Shear2 [1/K] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E1 | E2 | E3 | G12 | G13 | G23 | ||||||||||
| Quasi-isotropic | 56,800 | 8210 | 56,800 | 3000 | 4360 | 3000 | 0.35 | 0.25 | 0.35 | 1.24 | 1408 | 0.72 | 1.0 × 10−7 | 4.5 × 10−5 | 1.0 × 10−7 |
| unidirectional | 152,000 | 8210 | 8210 | 4360 | 4360 | 3000 | 0.25 | 0.25 | 0.35 | 1.24 | 1408 | 0.72 | 1.0 × 10−7 | 4.5 × 10−5 | 4.5 × 10−5 |
| Young’s Modulus [MPa] | Poisson’s Ratio | Tensile Strength [MPa] | Compressive Strength [MPa] | Density [t/mm3] | Specific Heat [mJ/t·K] | Thermal Conductivity [W/(m·K)] | Thermal Expansion Coefficient [1/K] | Yield Stress [MPa] | |
|---|---|---|---|---|---|---|---|---|---|
| PEEK [35] | 4600 | 0.370 | 100 | 250 | 1.30 × 10−9 | 1.00 × 109 | 0.240 | 5.00 × 10−5 | 90 |
| PPS [36,37] | 3697 | 0.350 | 64 | 160 | 1.35 × 10−9 | 1.00 × 109 | 0.290 | 4.90 × 10−5 | 55 |
| Epoxy [38] | 3400 | 0.396 | 48 | 120 | 1.23 × 10−9 | 1.06 × 109 | 0.168 | 6.00 × 10−5 | 36.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takamura, M.; Isozaki, M.; Takeda, S.-i.; Koyanagi, J. Numerical Analysis on Optimal Adhesive Thickness in CFRP Single-Lap Joints Considering Material Properties. Materials 2025, 18, 2423. https://doi.org/10.3390/ma18112423
Takamura M, Isozaki M, Takeda S-i, Koyanagi J. Numerical Analysis on Optimal Adhesive Thickness in CFRP Single-Lap Joints Considering Material Properties. Materials. 2025; 18(11):2423. https://doi.org/10.3390/ma18112423
Chicago/Turabian StyleTakamura, Maruri, Minori Isozaki, Shin-ichi Takeda, and Jun Koyanagi. 2025. "Numerical Analysis on Optimal Adhesive Thickness in CFRP Single-Lap Joints Considering Material Properties" Materials 18, no. 11: 2423. https://doi.org/10.3390/ma18112423
APA StyleTakamura, M., Isozaki, M., Takeda, S.-i., & Koyanagi, J. (2025). Numerical Analysis on Optimal Adhesive Thickness in CFRP Single-Lap Joints Considering Material Properties. Materials, 18(11), 2423. https://doi.org/10.3390/ma18112423








