In Situ Investigation of the Mechanical Property Anisotropy of TC11 Forgings Through Electron Backscatter Diffraction
Abstract
1. Introduction
2. Materials and Methods
2.1. Material
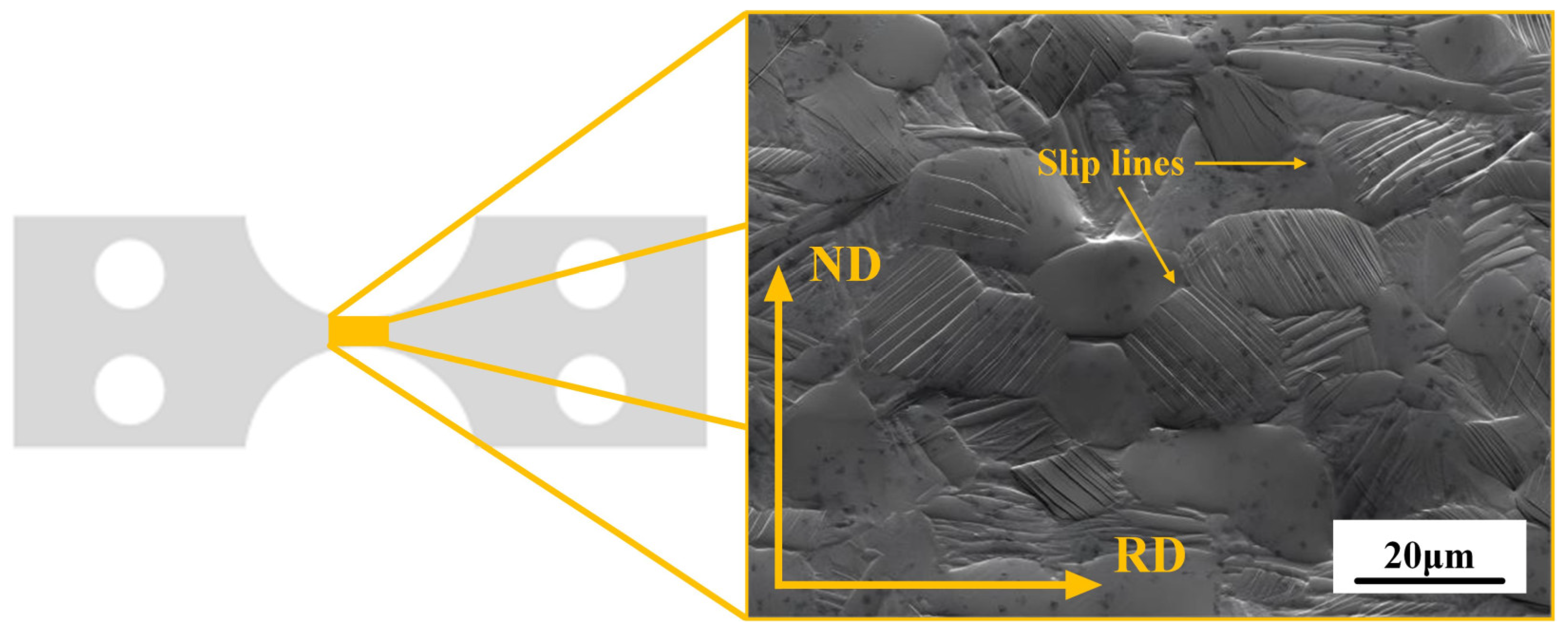
2.2. Specific Surface Preparation and Conditions for the EBSD Measurements of the Micro Tensile Samples
2.3. In Situ Tensile Test
2.4. Determination of the Activated Slip System
3. Results
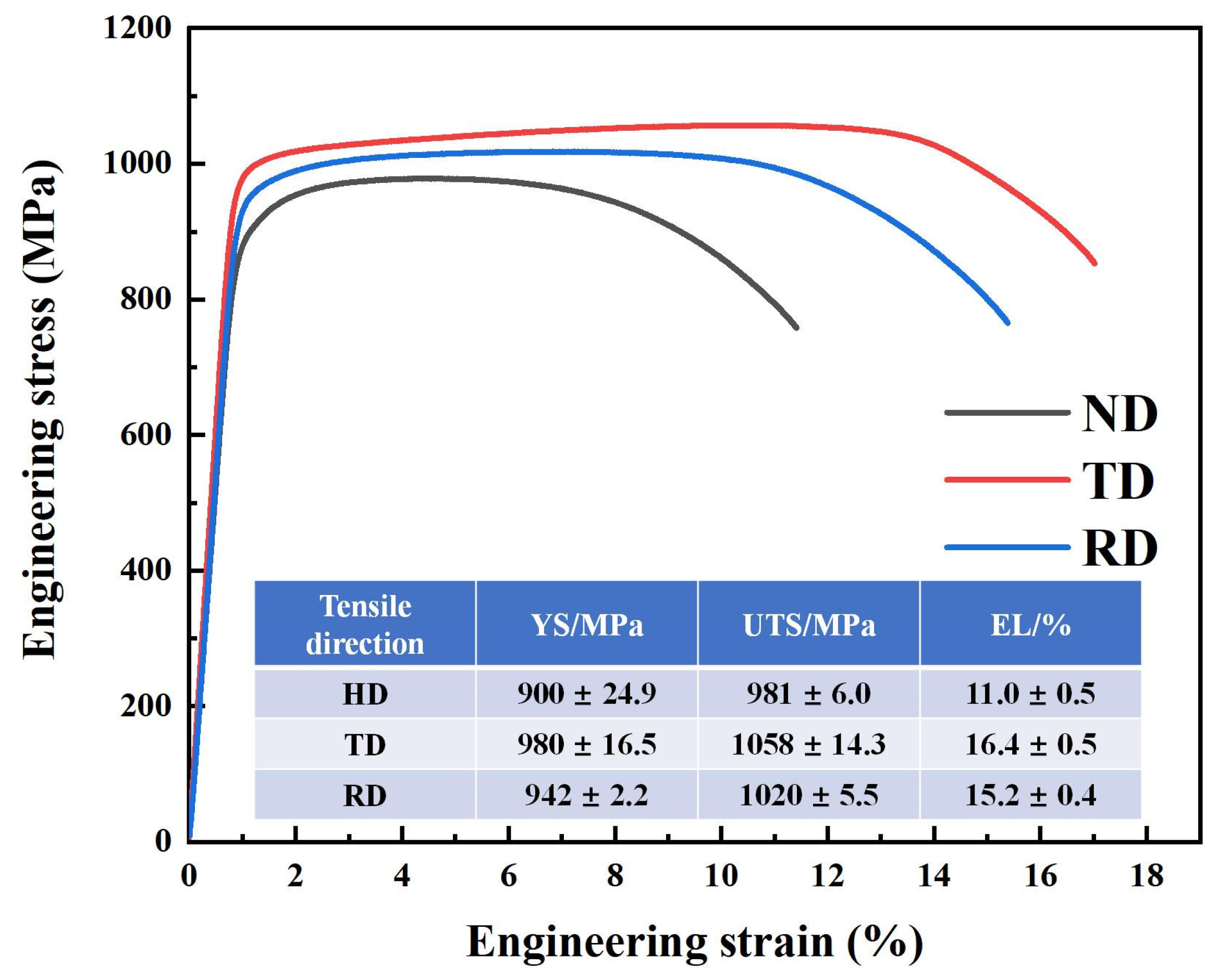
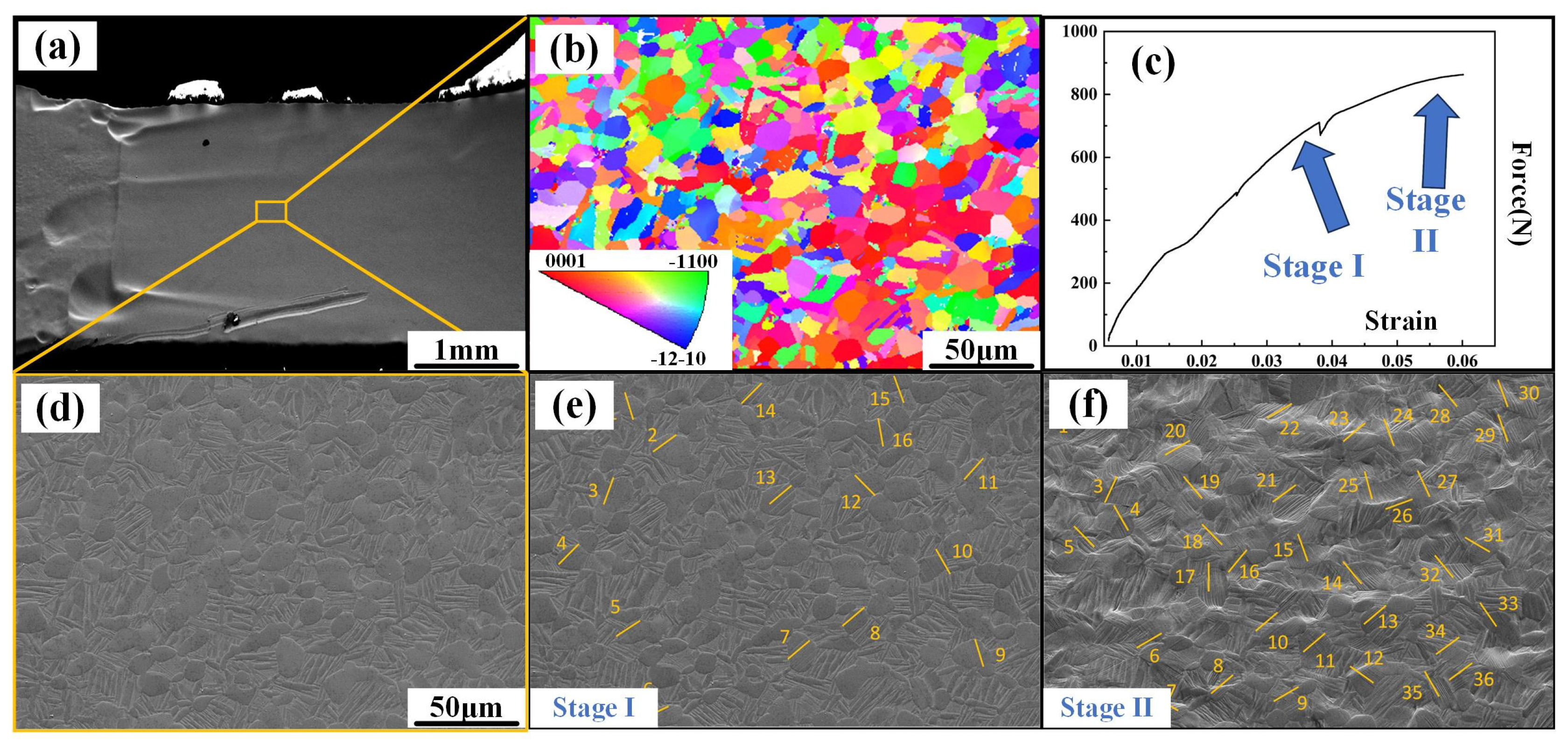
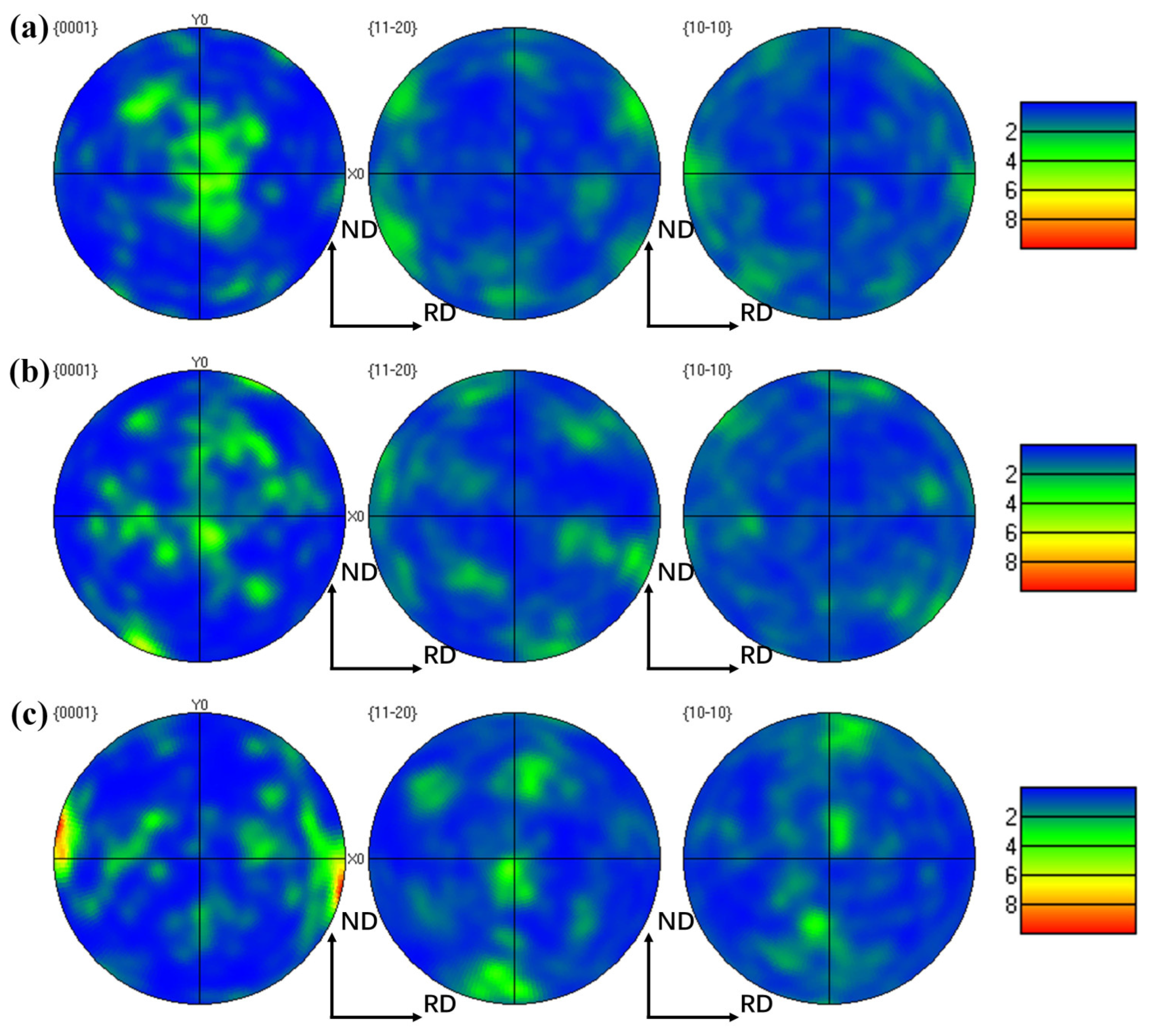
3.1. Microstructure and Mechanical Properties of the Specimen Before In Situ Tensile Test
3.2. In Situ Tensile Test
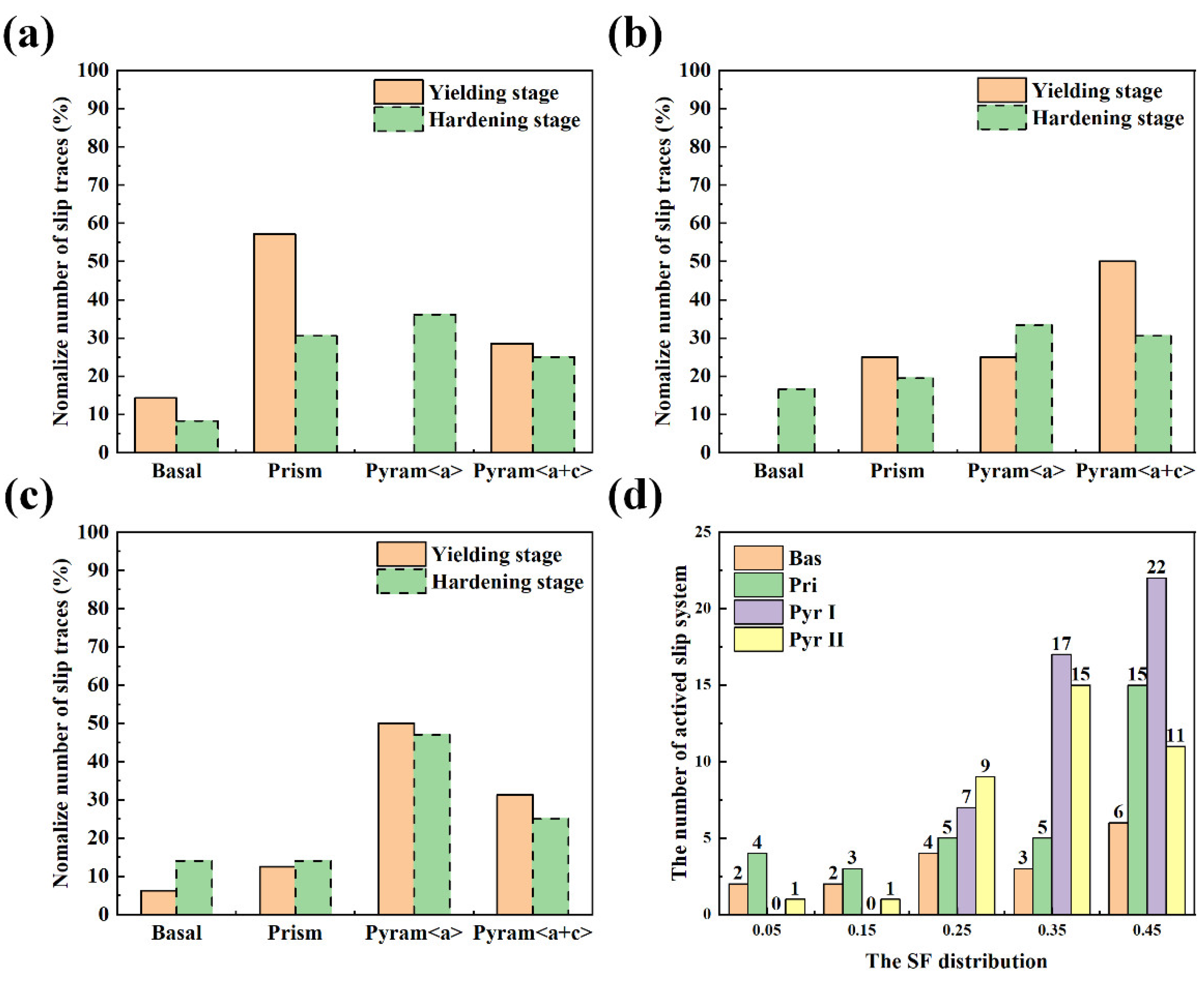
4. Discussion
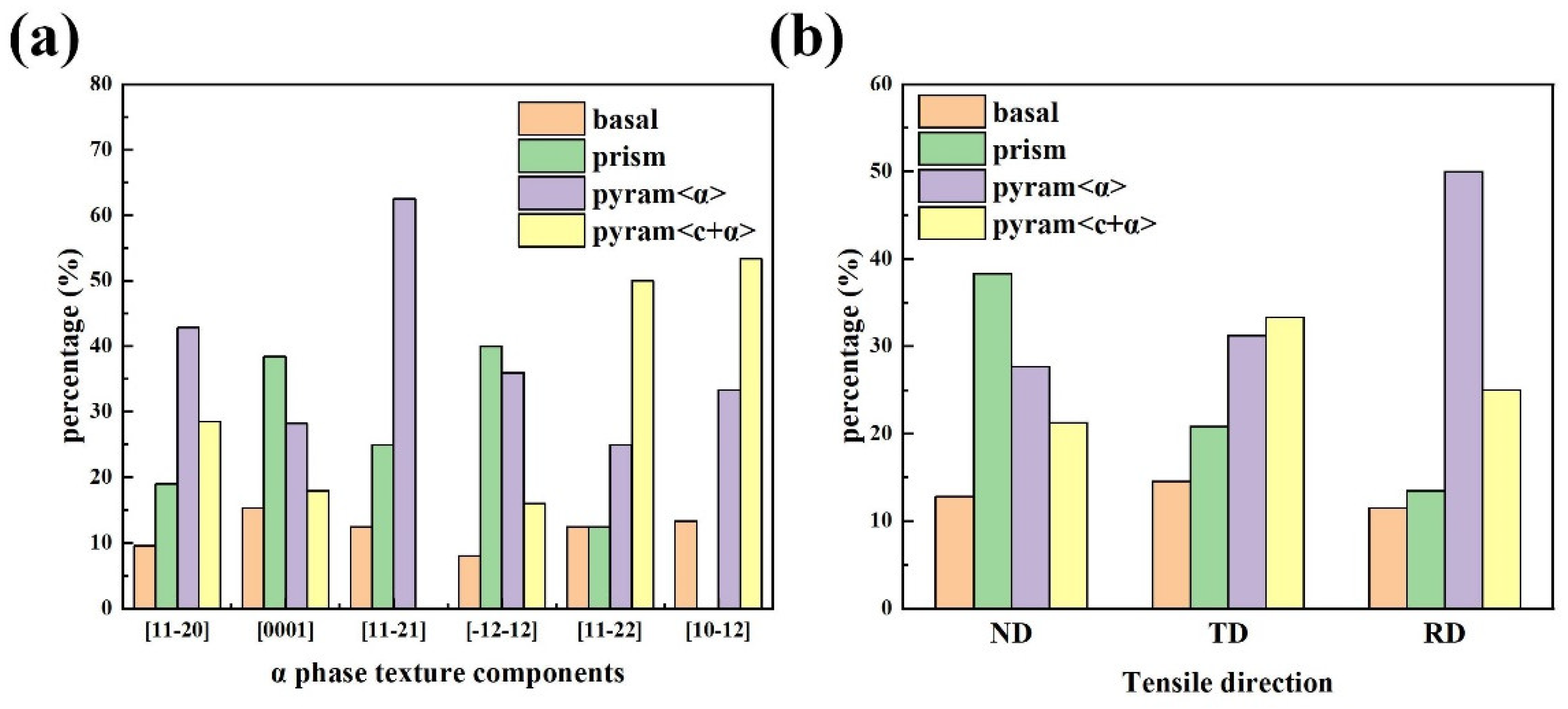
4.1. Estimation and Analysis of the CRSS Ratio for the α Phase
4.2. Determination of the Resistance Coefficient
4.3. Influence of Texture and Slip Systems on the Mechanical Properties
5. Conclusions
6. Limitations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chai, Z.; Yi, W. Hot deformation behavior and microstructure evolution of TC11 dual-phase titanium alloy. Mater. Sci. Eng. A 2024, 898, 146331. [Google Scholar] [CrossRef]
- Wang, K.; Zeng, W. Prediction of dynamic globularization of Ti-17 titanium alloy with initial lamellar microstructure during hot compression. Mater. Sci. Eng. A 2010, 527, 6193–6199. [Google Scholar] [CrossRef]
- Li, A.B.; Huang, L.J. Hot working ofTi6A13Mo-2Zr0.3Sialloy with lamellar a+β starting stcture using prcessing map. Mater. Des. 2009, 30, 1625–1631. [Google Scholar] [CrossRef]
- Chen, H.; Cao, C. Hot defomation mechanism and microstucure evolution of TCll titanium alloy in β field. Trans. Nonferrous Met. Soc. China 2008, 18, 1021–1027. [Google Scholar] [CrossRef]
- Kang, L.; Yang, C. A review on high-strength titanium alloys: Microstructure, strengthening, and properties. Adv. Eng. Mater. 2019, 21, 1801359. [Google Scholar] [CrossRef]
- Chen, G.; Huo, Y.; Lin, J. Crystal plasticity finite element method investigation of normal tensile deformation anisotropy in rolled pure titanium sheet. Thin-Walled Struct. 2024, 200, 111904. [Google Scholar] [CrossRef]
- Ahmadikia, B.; Paraskevas, O. Christos Thrampoulidis, Data-driven texture design for reducing elastic and plastic anisotropy in titanium alloys. Acta Mater. 2024, 265, 119585. [Google Scholar] [CrossRef]
- Kim, J.; Kang, J. Micromechanical analysis of anisotropy and asymmetry in pure titanium using electron backscatter diffraction and crystal plasticity finite element modeling. J. Mater. Res. Technol. 2023, 27, 4088–4108. [Google Scholar] [CrossRef]
- Li, W.; Li, S.; Yu, H. Research on the anisotropy of plastic behavior and deformation mechanism of textured pure titanium. Mater. Charact. 2022, 194, 112483. [Google Scholar] [CrossRef]
- Wu, J.; Wang, B.; Liu, W. Mechanical Properties and Planar Anisotropy of TC1 Titanium Alloy Sheet. Rare Met. Mater. Eng. 2017, 46, 363–369. [Google Scholar] [CrossRef]
- Banerjee, D.; Pilchak, A.; Williams, J. Processing, Structure, texture and microtexture in titanium alloys. Mater. Sci. Forum 2012, 710, 66–84. [Google Scholar] [CrossRef]
- Weiss, S.; Semiatin, S.L. Thermomechanical processing of beta titanium alloys—An overview. Mater. Sci. Eng 1998, 243, 46–65. [Google Scholar] [CrossRef]
- Davies, P. An Investigation of Microstructure and Texture Evolution in the Near-α Titanium Alloy Timetal 834. Ph.D. Thesis, University of Sheffield, Sheffield, UK, 2009. [Google Scholar]
- Germain, L.; Gey, N.; Humbert, M. An automated method to analyze separately the microtextures of primary alpha p grains and the secondary alpha s inherited colonies in bimodal titanium alloys. Mater. Charact. 2005, 54, 216–222. [Google Scholar] [CrossRef]
- Thomas, M.; Wynne, B.; Rainforth, W. An alternative method to separate and analyse the microtextures and microstructures of primary alpha grains and transformed beta grains in near-α titanium alloy Timetal 834. Mater. Charact. 2005, 55, 388–394. [Google Scholar] [CrossRef]
- Salem, A.; Glavicic, M.; Semiatin, S. A coupled EBSD/EDS method to determine the primary- and secondary-alpha textures in titanium alloys with duplex microstructures. Mater. Sci. Eng. 2008, 494, 350–359. [Google Scholar] [CrossRef]
- Bache, M.; Evans, W.; Davies, H. Electron back scattered diffraction (EBSD) analysis of quasi-cleavage and hydrogen induced fractures under cyclic and dwell loading in titanium alloys. J. Mater. Sci. 1997, 32, 3435–3442. [Google Scholar] [CrossRef]
- Semiatin, S.; Bieler, Y. Effect of texture and slip mode on the anisotropy of plastic flow and flow softening during hot working of Ti-6Al-4V. Mater. Trans. 2001, 32, 1787–1799. [Google Scholar] [CrossRef]
- Lei, Z.; Gao, P. Analysis of anisotropy mechanism in the mechanical property of titanium alloy tube formed through hot flow forming. J. Mater. Sci. Technol. 2021, 86, 77–90. [Google Scholar] [CrossRef]
- Yi, S.; Davies, C.; Brokmeier, H. Deformation and texture evolution in AZ31 magnesium alloy during uniaxial loading. Acta Mater. 2006, 54, 549–562. [Google Scholar] [CrossRef]
- He, S.; Zeng, W.; Xu, J. Analysis of anisotropy mechanism in relation with slip activity in near A titanium alloy pipe after pilger cold rolling. J. Alloys Compd. 2022, 909, 164785. [Google Scholar] [CrossRef]
- Zhang, P.; Zeng, W.; Zhang, F. In-situ investigation of tensile anisotropy mechanism in an advanced Ti2AlNb-based alloy associated with CRSS ratio and damage model. Mater. Sci. Eng. 2024, 890, 145894. [Google Scholar] [CrossRef]
- Jia, R.; Zeng, W.; Zhao, Z. In situ EBSD/HR-DIC-based investigation on anisotropy mechanism of a near α titanium plate with strong transverse texture. Mater. Sci. Eng. 2023, 867, 144743. [Google Scholar] [CrossRef]
- Bridier, F.; Villechaise, P. Analysis of the different slip systems activated by tension in a α/β titanium alloy in relation with local crystallographic orientation. Acta Mater. 2005, 53, 555–567. [Google Scholar] [CrossRef]
- Baniasadi, H.; Äkräs, L.; Madani, Z.; Silvenius, F.; Fazeli, M.; Lipponen, S.; Vapaavuori, J.; Seppälä, J. Development and characterization of polylactic acid/starch biocomposites—From melt blending to preliminary life cycle assessment. Int. J. Biol. Macromol. 2024, 279, 135173. [Google Scholar] [CrossRef] [PubMed]
- Long, W.; Ou, M.G.; Mao, X.Q.; Liang, Y.-L. In situ deformation behavior of TC21 titanium alloy with different α morphologies (equiaxed/lamellar). Rare Met. 2021, 40, 1173–1181. [Google Scholar] [CrossRef]
- Zhang, S.; Zeng, W. In-situ SEM study of tensile deformation of a near-βtitanium alloy. Mater. Sci. Eng. 2017, 708, 574–581. [Google Scholar] [CrossRef]
- Xia, Y. Superior strength-ductility synergy of layered aluminum under uniaxial tensile loading: The roles of local stress state and local strain state. Int. J. Plast. 2022, 152, 103240. [Google Scholar] [CrossRef]
- Hull, D.; Bacon, D. Introduction to Dislocations, 5th ed.; Elsevier Ltd.: Amsterdam, The Netherlands, 2011; Available online: https://www.sciencedirect.com/book/9780080966724/introduction-to-dislocations (accessed on 1 April 2024).
- Zhang, Y.; Han, Y. Structural Intermetallics; National Defense Industry Press: Beijing, China, 2001. [Google Scholar]
- Inui, H.; Toda, Y.; Yamaguchi, M. Plastic deformation of single crystals of a DO19 compound with an off-stoichiometric composition (Ti-36.5at.% Al) at room temperature. Philos. Mag. A 1993, 67, 1315–1332. [Google Scholar] [CrossRef]
- Umakoshi, Y.; Nakano, T.; Takenaka, T.; Sumimoto, K.; Yamane, T. Orientation and temperature dependence of yield stress and slip geometry of Ti3Al and Ti3Al-V single crystals. Acta Mater. 1993, 41, 1149–1154. [Google Scholar] [CrossRef]
- Gong, J.; Wilkinson, A. Anisotropy in the plastic flow properties of single-crystal α titanium determined from micro-cantilever beams. Acta Mater. 2009, 57, 5693–5705. [Google Scholar] [CrossRef]
- H’emery, S.; Villechaise, P. Microplasticity at room temperature in α/β titanium alloys. Mater. Trans. A 2020, 51, 4931–4969. [Google Scholar] [CrossRef]
- Kishida, K.; Yoshikawa, J. C-axis tensile deformation of Ti3Al with the DO19 structure at room temperature. Acta Mater. 1999, 47, 3405–3410. [Google Scholar] [CrossRef]
- Séchepée, I.; Dubray, C.; Velay, V.; Matsumoto, H. Effects of grain size and β fraction on the deformation modes of a Ti-6Al-2Sn-4Zr-2Mo-Si alloy with equiaxed (α + β) microstructures: Slip trace analysis and multiscale simulation of polycrystal plasticity. J. Alloys Compd. 2024, 981, 173722. [Google Scholar] [CrossRef]
- Venkataramani, G.; Deka, D.; Ghosh, S. Crystal plasticity based FE model for understanding microstructural effects on creep and dwell fatigue in Ti-6242. J. Eng. Mater. Technol. 2006, 128, 356–365. [Google Scholar] [CrossRef]
- Mayeur, J.R.; McDowell, D.L. A three-dimensional crystal plasticity model for duplex Ti-6Al-4V. Int. J. Plast. 2007, 23, 1457–1485. [Google Scholar] [CrossRef]
- Benmessaoud, F.; Cheikh, M.; Velay, V.; Vidal, V.; Matsumoto, H. Role of grain size and crystallographic texture on tensile behavior induced by sliding mechanism in Ti-6Al-4V alloy. Mater. Sci. Eng. A 2020, 774, 138835. [Google Scholar] [CrossRef]
- Zhang, H.R.; Niu, H.Z.; Zang, M.C.; Tan, H.; Zhang, D.L. β-transformed domains enhanced tensile properties and the related deformation behavior of a near alpha titanium alloy. Mater. Sci. Eng. A 2021, 141902. [Google Scholar] [CrossRef]
- Zang, M.C.; Niu, H.Z.; Liu, S.; Zhang, H.R.; Zhang, D.L. Achieving high tensile strength-ductility synergy of a fully-lamellar structured near alpha titanium alloy at extra-low temperatures. J. Alloys Compd. 2022, 923, 166363. [Google Scholar] [CrossRef]
- Dick, T.; Cailletaud, G. Fretting modelling with a crystal plasticity model of Ti6Al4V. Comput. Mater. Sci. 2006, 38, 113–125. [Google Scholar] [CrossRef]
- Chong, Y.; Deng, G.; Gao, S.; Yi, J.; Shibata, A.; Tsuji, N. Yielding nature and Hall-Petch relationships in Ti-6Al-4V alloy with fully equiaxed and bimodal microstructures. Scr. Mater. 2019, 172, 77–82. [Google Scholar] [CrossRef]
- Bridier, F.; McDowell, D.L.; Villechaise, P.; Mendez, J. Crystal plasticity modeling of slip activity in Ti-6Al-4V under high cycle fatigue loading. Int. J. Plast. 2009, 25, 1066–1082. [Google Scholar] [CrossRef]
- Hasija, V.; Ghosh, S.; Mills, M.J.; Joseph, D.S. Deformation and creep modeling in polycrystalline Ti-6Al alloys. Acta Mater. 2003, 51, 4533–4549. [Google Scholar] [CrossRef]
- Williams, J.C.; Baggerly, R.G.; Paton, N.E. Deformation behavior of HCP Ti-Al alloy single crystals. Metall. Mater. Trans. A. 2002, 33, 837–850. [Google Scholar] [CrossRef]
- Zhang, W.; Gao, Y.; Xia, Y. Indentation Schmid factor and incipient plasticity by nanoindentation pop-in tests in hexagonal close-packed single crystals. Acta Mater. 2017, 134, 53–65. [Google Scholar] [CrossRef]
- Germain, L.; Gey, N.; Humber, M. Texture heterogeneities induced by subtransus processing of near α titanium alloys. Acta Mater. 2008, 56, 4298–4308. [Google Scholar] [CrossRef]
- Zhang, P.; Zeng, W.; Ma, H. Research on tensile anisotropy of Ti-22Al-25Nb alloy isothermally forged in B2 phase region related with texture and variant selection. Mater. Charact. 2023, 201, 112899. [Google Scholar] [CrossRef]
- Lei, L.; Zhao, Q.; Wu, C. Variant selection, coarsening behavior of α phase and associated tensile properties in an α + β titanium alloy. J. Mater. Sci. Technol. 2022, 99, 101–113. [Google Scholar] [CrossRef]



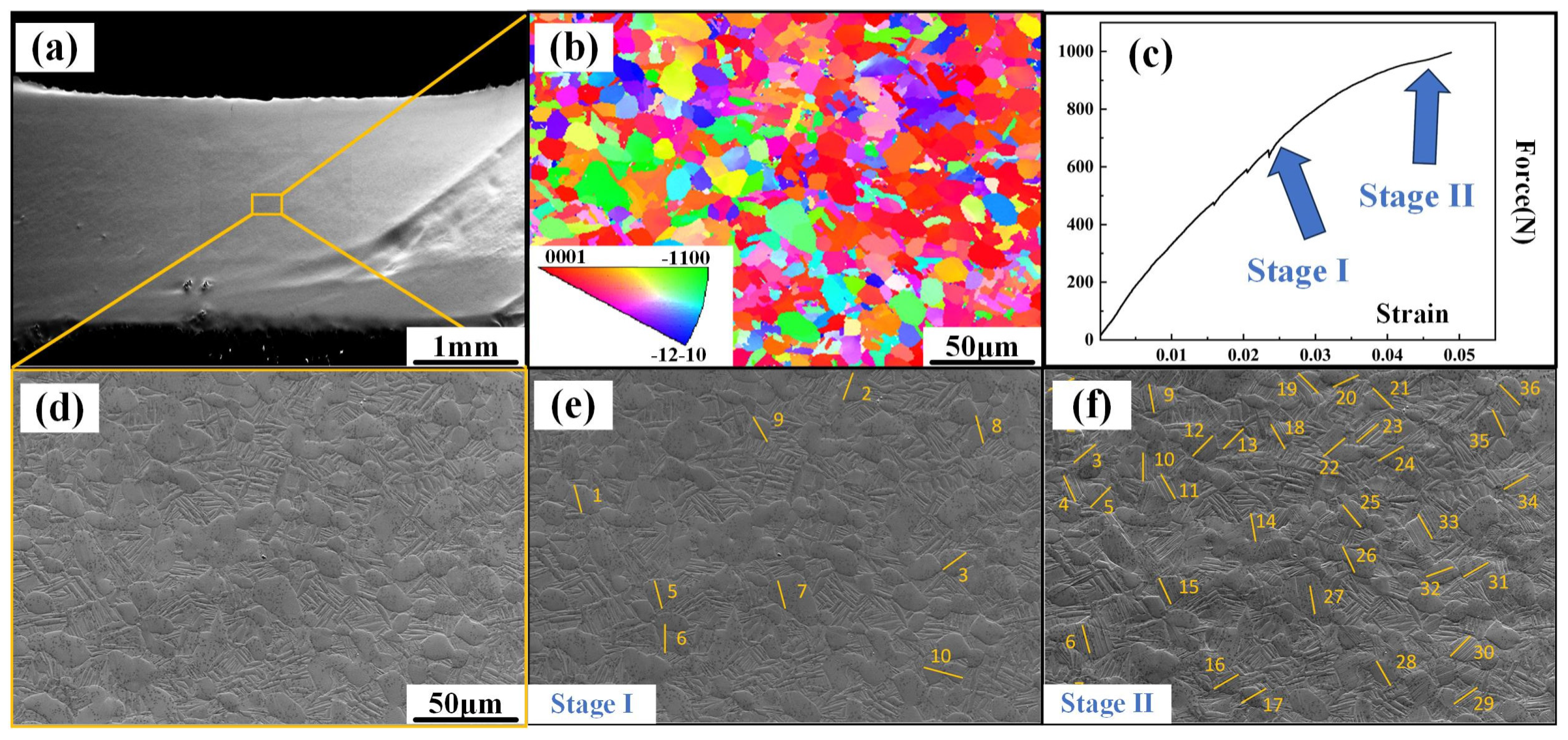

| Grain | Slip Plane and Direction | Activated System | SF | |
|---|---|---|---|---|
| Stage I | 1 | () [] | Prismatic <a> | 0.41 |
| 2 | (0001) [1] | Basal <a> | 0.28 | |
| 3 | (] | Pyramidal slip <c + a> | 0.33 | |
| 4 | () [11] | Prismatic <a> | 0.35 | |
| 5 | () [11] | Prismatic <a> | 0.40 | |
| 6 | (] | Prismatic <a> | 0.38 | |
| 7 | (] | Pyramidal slip <c + a> | 0.36 | |
| 8 | () [11] | Prismatic <a> | 0.42 | |
| 9 | (] | Pyramidal slip <c + a> | 0.32 | |
| 10 | (] | Prismatic <a> | 0.41 | |
| Stage II | 1 | (0) [11] | Pyramidal slip <a> | 0.35 |
| 2 | (] | Pyramidal slip <c + a> | 0.19 | |
| 3 | (] | Pyramidal slip <c + a> | 0.26 | |
| 4 | (] | Pyramidal slip <a> | 0.36 | |
| 5 | () [11] | Prismatic <a> | 0.37 | |
| 6 | (] | Pyramidal slip <a> | 0.45 | |
| 7 | (] | Pyramidal slip <c + a> | 0.37 | |
| 8 | (] | Pyramidal slip <c + a> | 0.24 | |
| 9 | () [11] | Pyramidal slip <a> | 0.33 | |
| 10 | (] | Prismatic <a> | 0.49 | |
| 11 | (0001) [1] | Basal <a> | 0.45 | |
| 12 | () [11] | Prismatic <a> | 0.32 | |
| 13 | () [11] | Prismatic <a> | 0.28 | |
| 14 | (] | Prismatic <a> | 0.47 | |
| 15 | (0001) [11] | Basal <a> | 0.41 | |
| 16 | (] | Prismatic <a> | 0.06 | |
| 17 | (] | Prismatic <a> | 0.06 | |
| 18 | (] | Prismatic <a> | 0.16 | |
| 19 | () [11] | Pyramidal slip < a> | 0.45 | |
| 20 | () [11] | Pyramidal slip <a> | 0.44 | |
| 21 | (] | Prismatic <a> | 0.40 | |
| 22 | (] | Pyramidal < slip c + a> | 0.27 | |
| 23 | () [11] | Pyramidal slip <a> | 0.38 | |
| 24 | (] | Pyramidal slip <a> | 0.28 | |
| 25 | (] | Pyramidal slip <c + a> | 0.37 | |
| 26 | () [11] | Pyramidal slip <a> | 0.44 | |
| 27 | (] | Prismatic <a> | 0.47 | |
| 28 | () [11] | Pyramidal slip <a> | 0.41 | |
| 29 | (] | Pyramidal slip <c + a> | 0.31 | |
| 30 | () [11] | Pyramidal slip <a> | 0.47 | |
| 31 | (] | Prismatic <a> | 0.07 | |
| 32 | (] | Prismatic <a> | 0.02 | |
| 33 | (] | Pyramidal slip <a> | 0.35 | |
| 34 | (] | Pyramidal slip <c + a> | 0.38 | |
| 35 | (] | Pyramidal slip <c + a> | 0.39 | |
| 36 | () [11] | Pyramidal slip <a> | 0.33 |
| Grain | Slip Plane and Direction | Activated System | SF | |
|---|---|---|---|---|
| Stage I | 1 | () [11] | Pyramidal slip <a> | 0.32 |
| 2 | (] | Pyramidal slip <a> | 0.46 | |
| 3 | (] | Prismatic <a> | 0.31 | |
| 4 | (] | Pyramidal slip <a> | 0.25 | |
| 5 | (] | Pyramidal slip <a> | 0.46 | |
| 6 | (] | Pyramidal slip <a> | 0.24 | |
| 7 | () [1] | Pyramidal slip <a> | 0.42 | |
| 8 | (] | Pyramidal slip <c + a> | 0.27 | |
| 9 | () [11] | Prismatic <a> | 0.29 | |
| 10 | (0001) [1] | Basal <a> | 0.42 | |
| 11 | () [1] | Pyramidal slip <c + a> | 0.27 | |
| 12 | (] | Pyramidal slip <a> | 0.28 | |
| 13 | () [1] | Pyramidal slip <a> | 0.40 | |
| 14 | () [1] | Pyramidal slip <c + a> | 0.50 | |
| 15 | (] | Pyramidal slip <c + a> | 0.37 | |
| 16 | (] | Pyramidal slip <c + a> | 0.37 | |
| Stage II | 1 | (] | Pyramidal slip <c + a> | 0.21 |
| 2 | (] | Pyramidal slip <c + a> | 0.42 | |
| 3 | (] | Prismatic <a> | 0.41 | |
| 4 | () [11] | Pyramidal slip <a> | 0.45 | |
| 5 | (] | Pyramidal slip <a> | 0.42 | |
| 6 | (] | Pyramidal slip <a> | 0.46 | |
| 7 | (0001) [1] | Basal <a> | 0.21 | |
| 8 | (] | Pyramidal slip <c + a> | 0.50 | |
| 9 | (] | Pyramidal slip <a> | 0.44 | |
| 10 | (] | Pyramidal slip <c + a> | 0.31 | |
| 11 | (] | Pyramidal slip <a> | 0.44 | |
| 12 | (] | Pyramidal slip <c + a> | 0.01 | |
| 13 | (] | Pyramidal slip <a> | 0.29 | |
| 14 | () [1] | Pyramidal slip <a> | 0.37 | |
| 15 | () [11] | Pyramidal slip <a> | 0.38 | |
| 16 | () [11] | Pyramidal slip <a> | 0.45 | |
| 17 | (0001) [1] | Basal <a> | 0.02 | |
| 18 | (0001) [1] | Basal <a> | 0.07 | |
| 19 | () [11] | Pyramidal slip <a> | 0.33 | |
| 20 | () [11] | Prismatic <a> | 0.50 | |
| 21 | () [1] | Pyramidal slip <a> | 0.38 | |
| 22 | (] | Pyramidal slip <a> | 0.36 | |
| 23 | () [1] | Pyramidal slip <a> | 0.35 | |
| 24 | () [11] | Prismatic <a> | 0.34 | |
| 25 | () [11] | Prismatic <a> | 0.26 | |
| 26 | () [11] | Pyramidal slip <a> | 0.25 | |
| 27 | (0001) [1] | Basal <a> | 0.35 | |
| 28 | () [11] | Pyramidal slip <a> | 0.25 | |
| 29 | (] | Pyramidal slip <c + a> | 0.44 | |
| 30 | () [11] | Pyramidal <a> slip | 0.30 | |
| 31 | (] | Prismatic <a> | 0.29 | |
| 32 | (] | Pyramidal slip <c + a> | 0.32 | |
| 33 | (0001) [1] | Basal <a> | 0.49 | |
| 34 | (] | Pyramidal slip <a> | 0.16 | |
| 35 | () [1] | Pyramidal slip <a> | 0.35 | |
| 36 | (] | Pyramidal slip <c + a> | 0.39 |
| Grain | Slip Plane and Direction | Activated System | SF | |
|---|---|---|---|---|
| Stage I | 1 | (] | Pyramidal slip <c + a> | 0.47 |
| 2 | () [11] | Prismatic <a> | 0.42 | |
| 3 | (0001) [] | Basal <a> | 0.31 | |
| 4 | () [11] | Prismatic <a> | 0.41 | |
| 5 | () [11] | Prismatic <a> | 0.50 | |
| 6 | (] | Pyramidal slip <c + a> | 0.25 | |
| 7 | (] | Pyramidal slip <c + a> | 0.39 | |
| 8 | (] | Pyramidal slip <c + a> | 0.44 | |
| 9 | () [11] | Pyramidal slip <c + a> | 0.50 | |
| 10 | () [11] | Pyramidal slip <a> | 0.40 | |
| 11 | () [1] | Pyramidal slip <a> | 0.38 | |
| 12 | () [1] | Pyramidal slip <a> | 0.34 | |
| Stage II | 1 | (0) [11] | Pyramidal slip <a> | 0.42 |
| 2 | (0001) [11] | Basal <a> | 0.30 | |
| 3 | (0001) [11] | Basal <a> | 0.45 | |
| 4 | (0001) [] | Basal <a> | 0.21 | |
| 5 | (] | Pyramidal slip <a> | 0.42 | |
| 6 | () [11] | Prismatic <a> | 0.44 | |
| 7 | () [11] | Pyramidal slip <c + a> | 0.49 | |
| 8 | () [11] | Pyramidal slip <a> | 0.31 | |
| 9 | () [11] | Prismatic <a> | 0.35 | |
| 10 | (] | Pyramidal slip <c + a> | 0.31 | |
| 11 | () [11] | Pyramidal slip <a> | 0.45 | |
| 12 | (] | Pyramidal slip <c + a> | 0.46 | |
| 13 | () [1] | Pyramidal slip <c + a> | 0.41 | |
| 14 | () [11] | Pyramidal slip <a> | 0.48 | |
| 15 | (0001) [] | Basal <a> | 0.41 | |
| 16 | (0] | Prismatic <a> | 0.42 | |
| 17 | (] | Pyramidal slip <c + a> | 0.33 | |
| 18 | (] | Pyramidal slip <c + a> | 0.23 | |
| 19 | (] | Pyramidal slip <a> | 0.40 | |
| 20 | (0001) [] | Basal <a> | 0.41 | |
| 21 | (] | Pyramidal slip <c + a> | 0.38 | |
| 22 | (0] | Prismatic <a> | 0.28 | |
| 23 | (] | Pyramidal slip <a> | 0.34 | |
| 24 | (] | Prismatic <a> | 0.46 | |
| 25 | (] | Prismatic <a> | 0.45 | |
| 26 | () [11] | Prismatic <a> | 0.41 | |
| 27 | (0001) [] | Basal <a> | 0.28 | |
| 28 | () [11] | Pyramidal slip <a> | 0.45 | |
| 29 | (] | Pyramidal slip <c + a> | 0.21 | |
| 30 | (] | Pyramidal slip <c + a> | 0.49 | |
| 31 | () [11] | Pyramidal slip <c + a> | 0.39 | |
| 32 | (] | Pyramidal slip <a> | 0.35 | |
| 33 | (] | Pyramidal slip <a> | 0.33 | |
| 34 | (] | Pyramidal slip <c + a> | 0.47 | |
| 35 | (] | Pyramidal slip <a> | 0.35 | |
| 36 | () [1] | Pyramidal slip <a> | 0.33 |
| Favorable Slip Systems | Yielding Stage | Hardening Stage |
|---|---|---|
| ND | Basal <a> slips, prismatic <a> slips, Pyramidal < c + a> slips | Pyramidal < a> slips |
| RD | prismatic <a> slips, Pyramidal < a> slips, Pyramidal < c + a> slips | Basal < a> slips |
| TD | Basal < a> slips, prismatic <a> slips, Pyramidal < a> slips Pyramidal < c + a> slips | No newly activated slip system |
| Alloy Used | Basal <a> | Pyramidal <c + a> | Reference |
|---|---|---|---|
| Ti-6242S | 0.82–1.2 | 4.08–5.78 | [36] |
| Ti-6242S | 1.06 | 1.80 | [37] |
| Ti-6Al-4V | 1–1.5 | 3.0–3.5 | [38] |
| Ti-6Al-4V | 1.33–1.41 | 2.72–3.41 | [39] |
| Ti-6Al-4V | 0.93–1.3 | 1.1–1.6 | [40] |
| Ti-6Al-4V | 1.43 | 4.23 | [41] |
| Ti-6Al-4V | 0.93 | 1.80 | [42] |
| Ti-6Al-4V | 1.13 | 1.61 | [43] |
| Ti-6Al-4V | 1.14 | 1.59 | [44] |
| Ti-6Al | 1.01 | 2.64 | [45] |
| Ti-6Al | 0.95 | 3.85 | [46] |
| Direction | χ | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| ND° | 0.24 | 0.45 | 0.22 | 0.38 | 0.17 | 0.42 | 0.25 | 0.16 | 0.58 |
| TD° | 0.32 | 0.17 | 0.41 | 0.28 | 0.15 | 0.16 | 0.28 | 0.41 | 0.76 |
| RD° | 0.48 | 0.31 | 0.29 | 0.33 | 0.21 | 0.15 | 0.39 | 0.25 | 0.73 |
| Slip System | ] | [0001] | ] | ] | ] | ] |
|---|---|---|---|---|---|---|
| Bas | 0.35 | 0.29 | 0.35 | 0.31 | 0.31 | 0.14 |
| Pri | 0.31 | 0.41 | 0.45 | 0.43 | 0.28 | 0 |
| Pyr I | 0.38 | 0.37 | 0.47 | 0.37 | 0.34 | 0.36 |
| Pyr II | 0.34 | 0.40 | 0 | 0.32 | 0.41 | 0.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Li, K.; Yuan, W. In Situ Investigation of the Mechanical Property Anisotropy of TC11 Forgings Through Electron Backscatter Diffraction. Materials 2025, 18, 2384. https://doi.org/10.3390/ma18102384
Li Q, Li K, Yuan W. In Situ Investigation of the Mechanical Property Anisotropy of TC11 Forgings Through Electron Backscatter Diffraction. Materials. 2025; 18(10):2384. https://doi.org/10.3390/ma18102384
Chicago/Turabian StyleLi, Qineng, Ke Li, and Wuhua Yuan. 2025. "In Situ Investigation of the Mechanical Property Anisotropy of TC11 Forgings Through Electron Backscatter Diffraction" Materials 18, no. 10: 2384. https://doi.org/10.3390/ma18102384
APA StyleLi, Q., Li, K., & Yuan, W. (2025). In Situ Investigation of the Mechanical Property Anisotropy of TC11 Forgings Through Electron Backscatter Diffraction. Materials, 18(10), 2384. https://doi.org/10.3390/ma18102384






