Effect of Non-Uniform Temperature Field on Sintering Performance of Conductive Silver Paste in Laser Sintering
Abstract
1. Introduction
2. Influence of Process Parameters on Sintering Performance
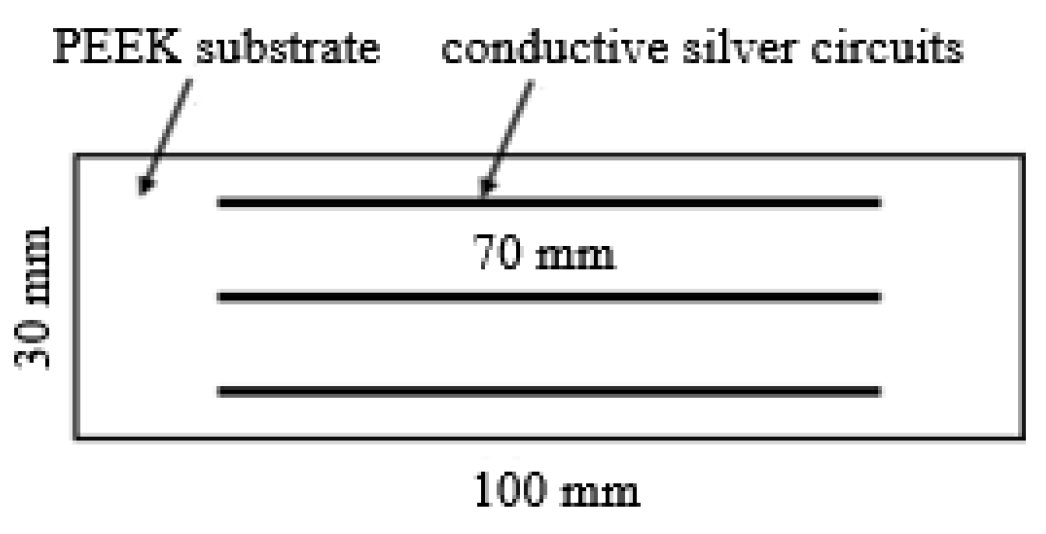
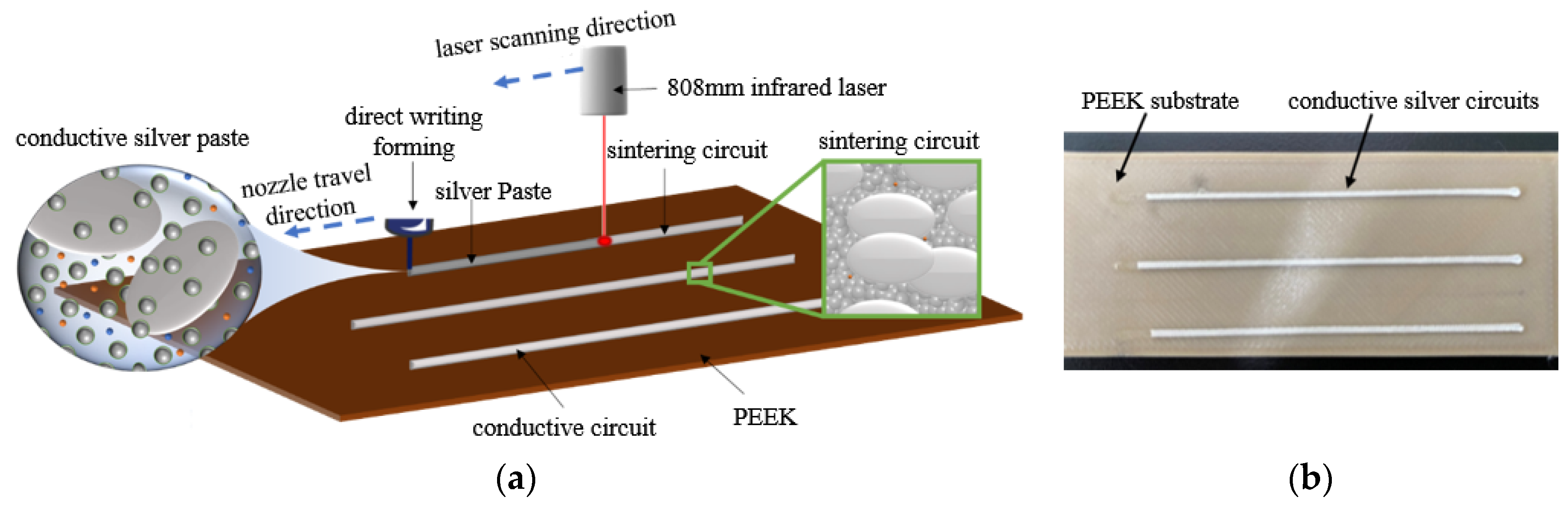
2.1. Experimental Design
2.2. Characterization Methods
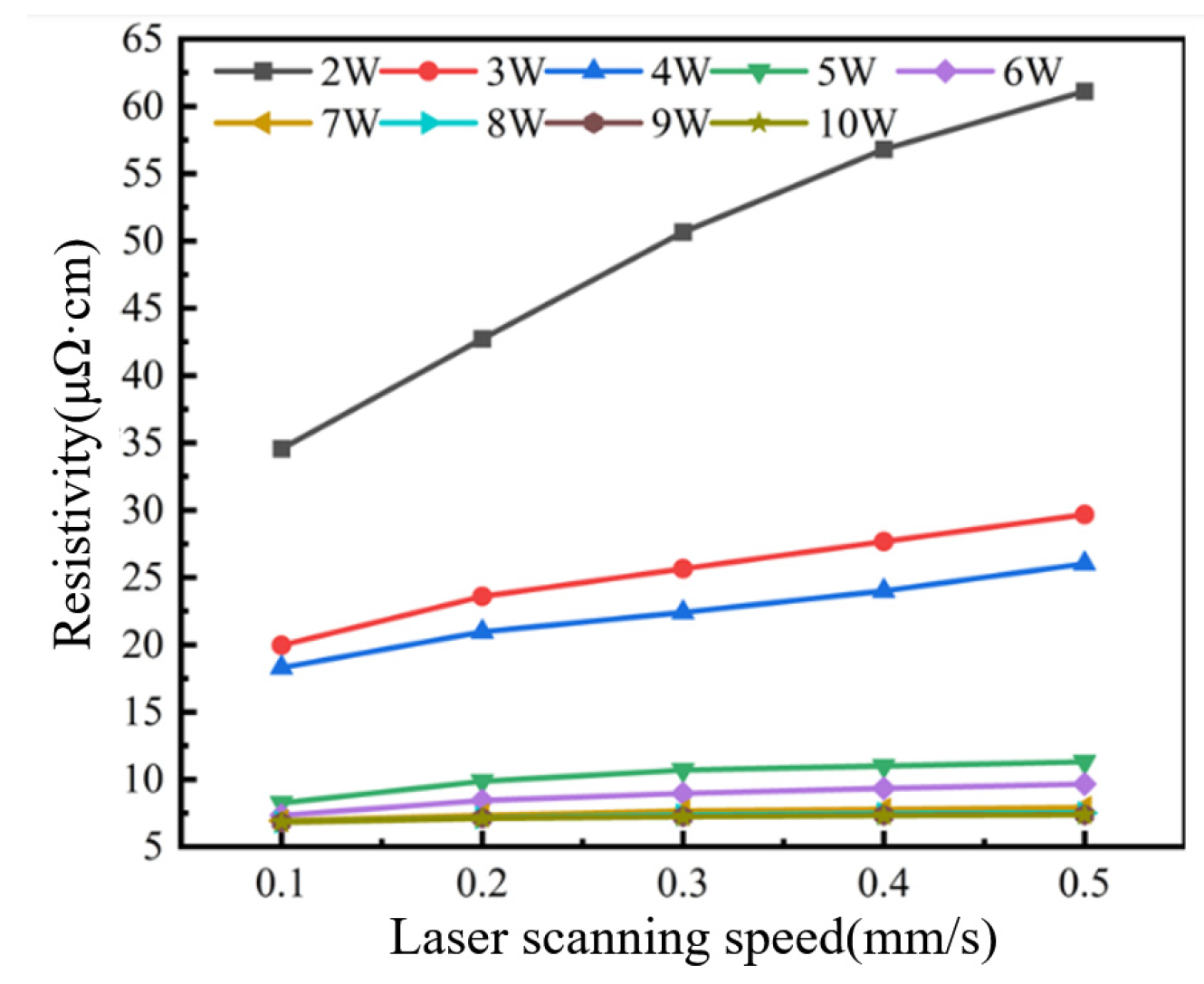
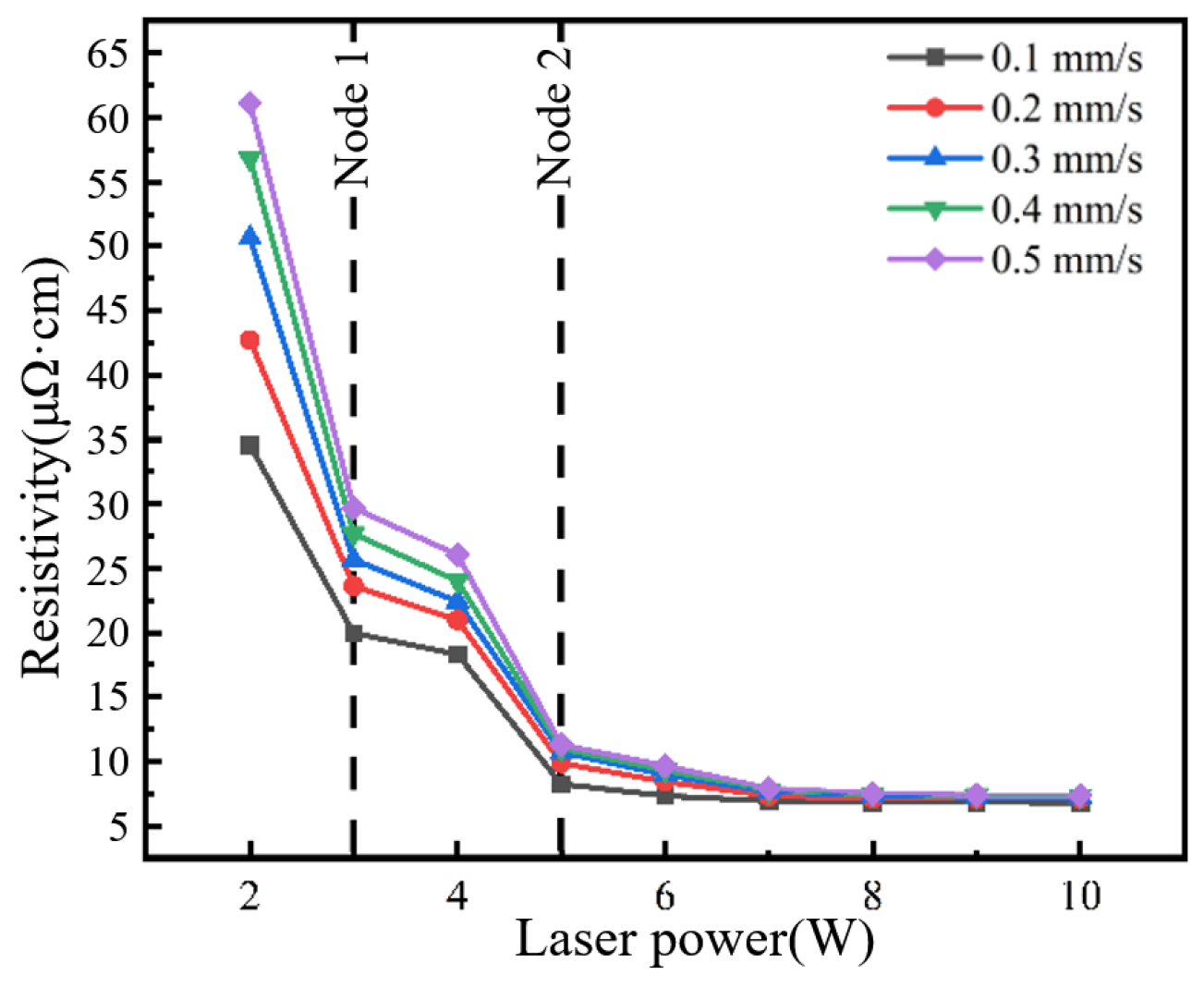
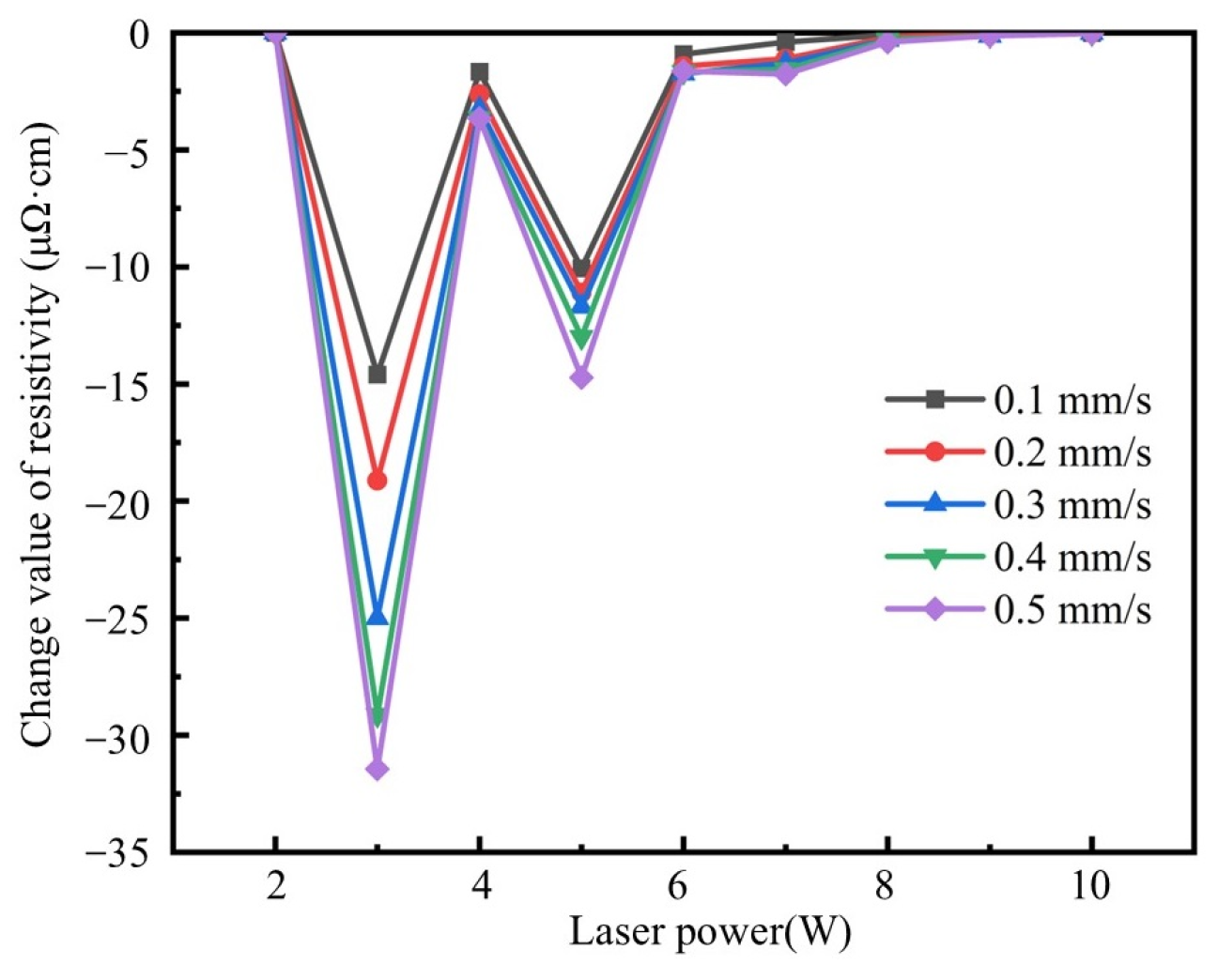
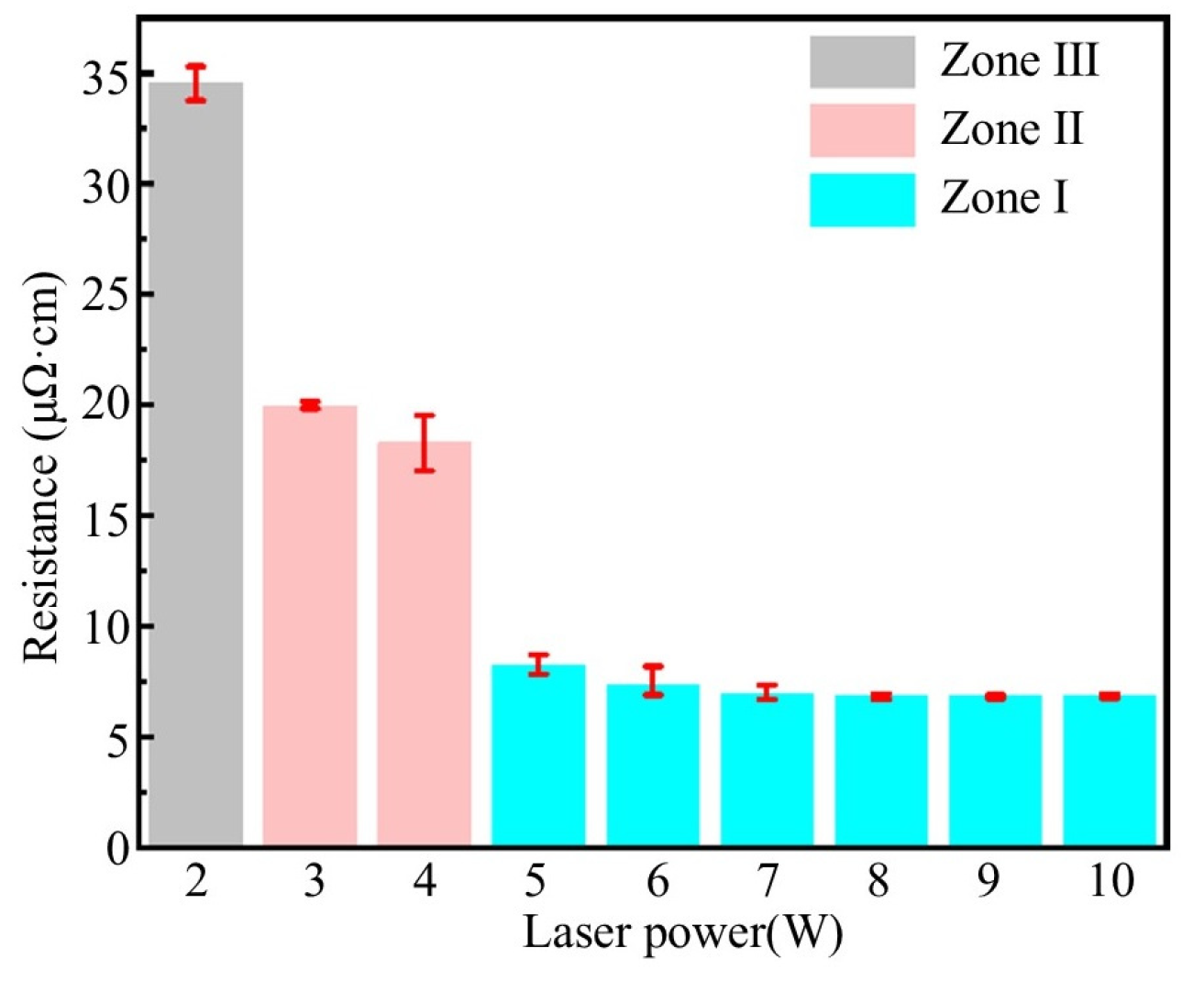
2.3. Influence of the Laser Sintering Process on Resistivity
- Low-power regime (<3 W): resistivity was 34.56 μΩ·cm;
- First transition (3 W): resistivity abruptly decreased by 42.3% to 19.96 μΩ·cm;
- Medium-power regime (3~4 W): resistivity exhibited marginal variation within 18.30~19.96 μΩ·cm (−8.3% variation);
- Second transition (5 W): resistivity dropped sharply by 55.0% to 8.23 μΩ·cm;
- High-power regime (>5 W): absolute value of the resistivity stabilized with minimal fluctuation within 6.81~8.23 μΩ·cm (−17.3% variation).
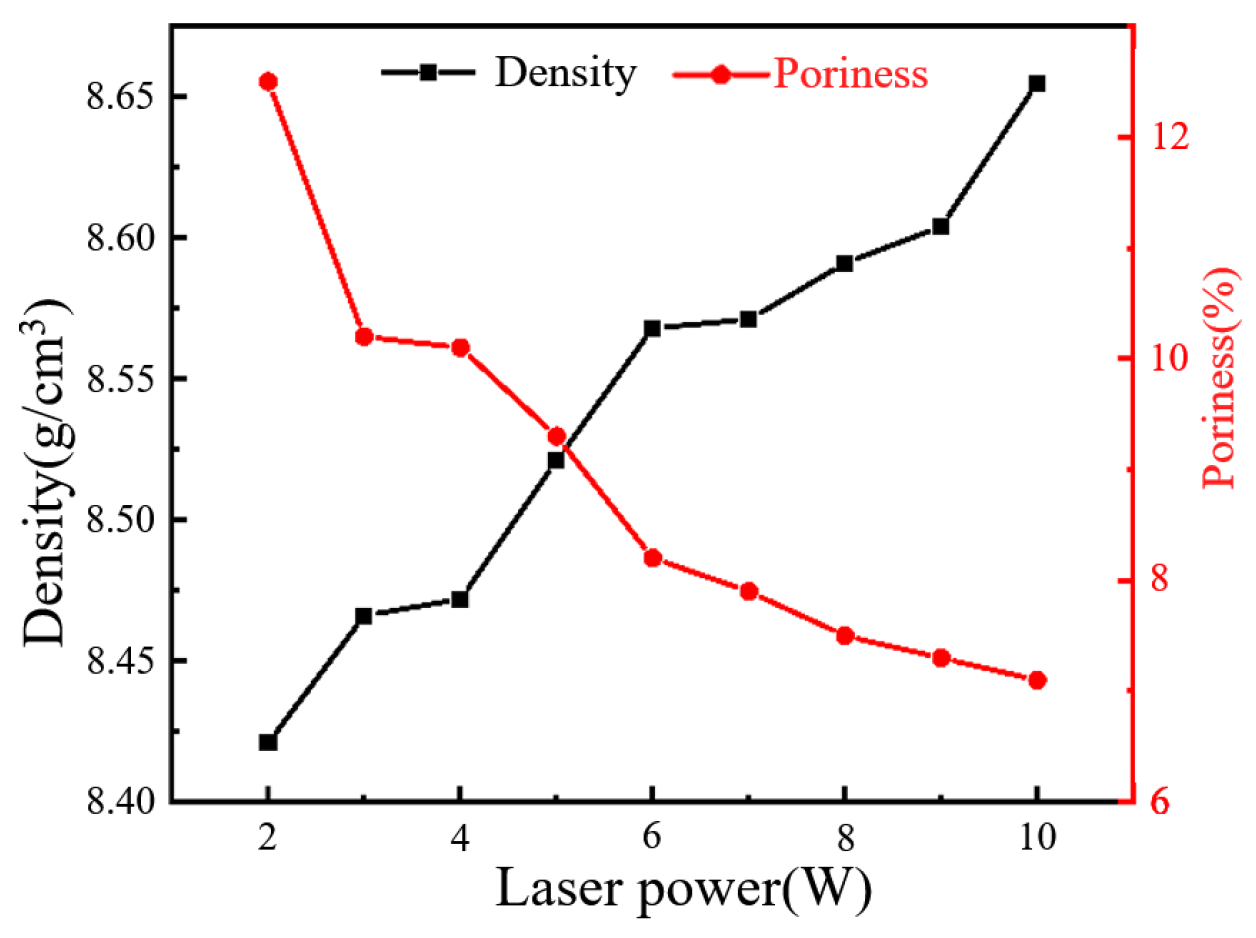
2.4. Influence of Laser Power on the Microstructure
3. Influence of the Process Parameters on Temperature Field Distribution
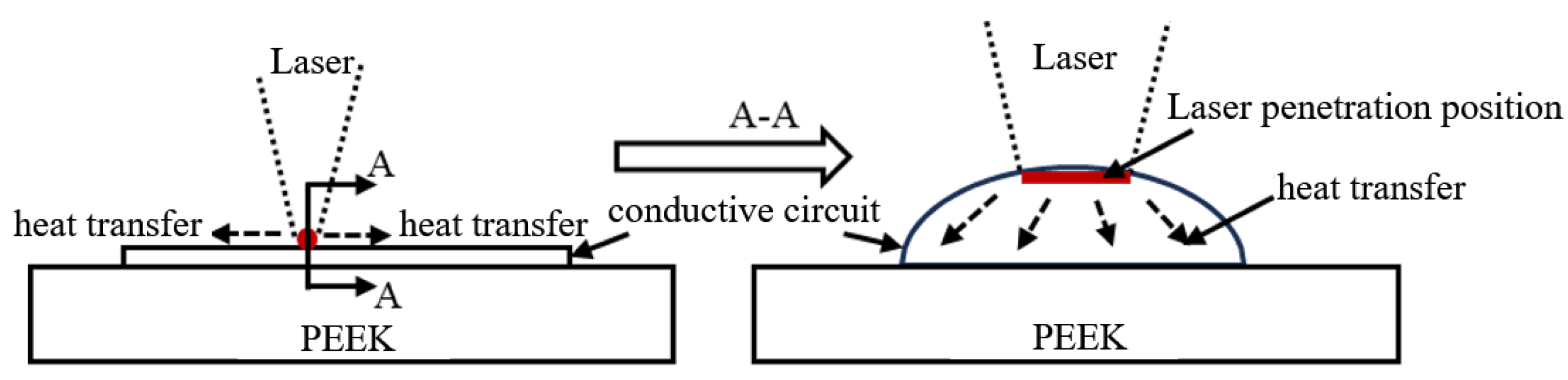
3.1. Analysis of the Laser Action Mechanism
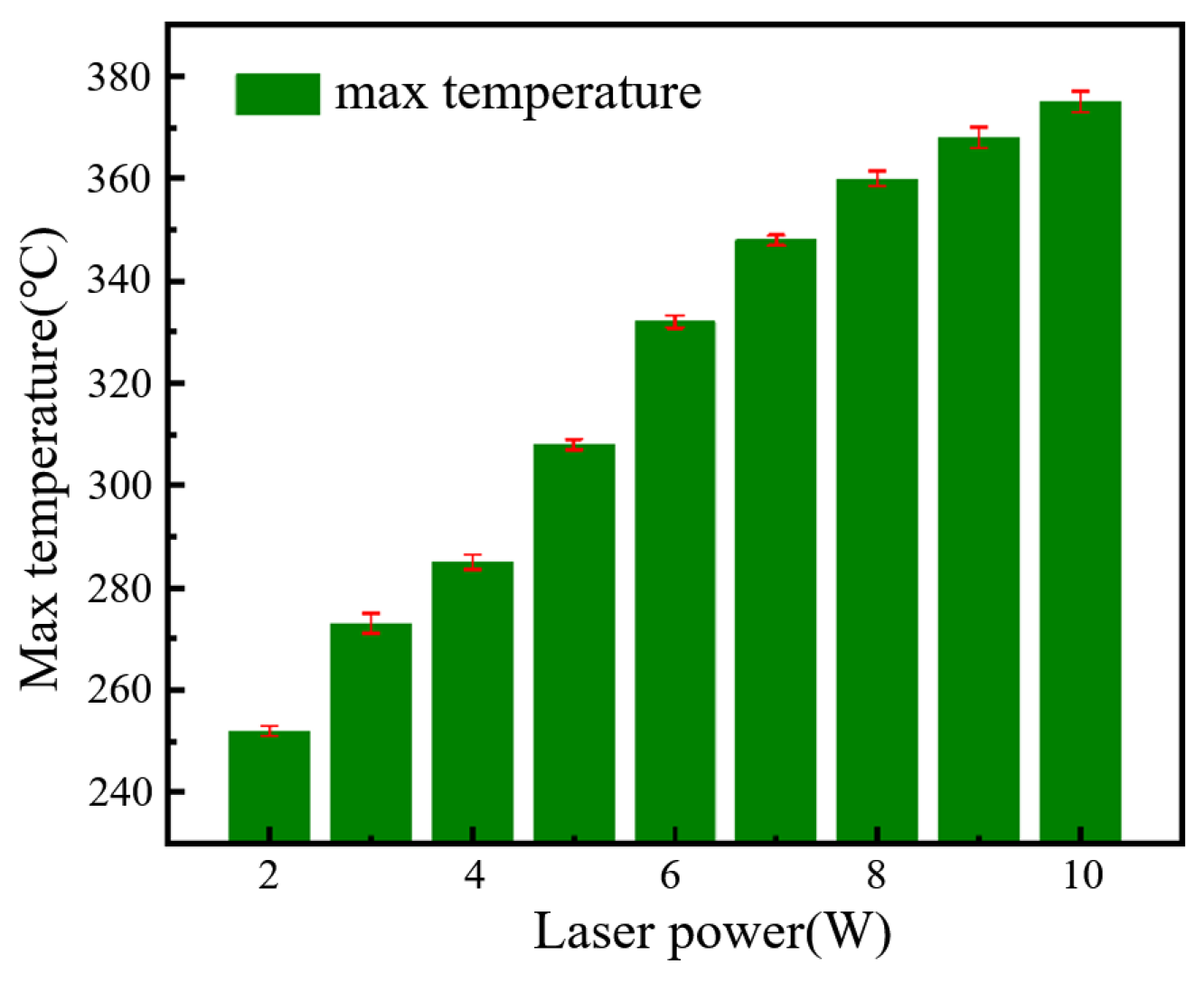
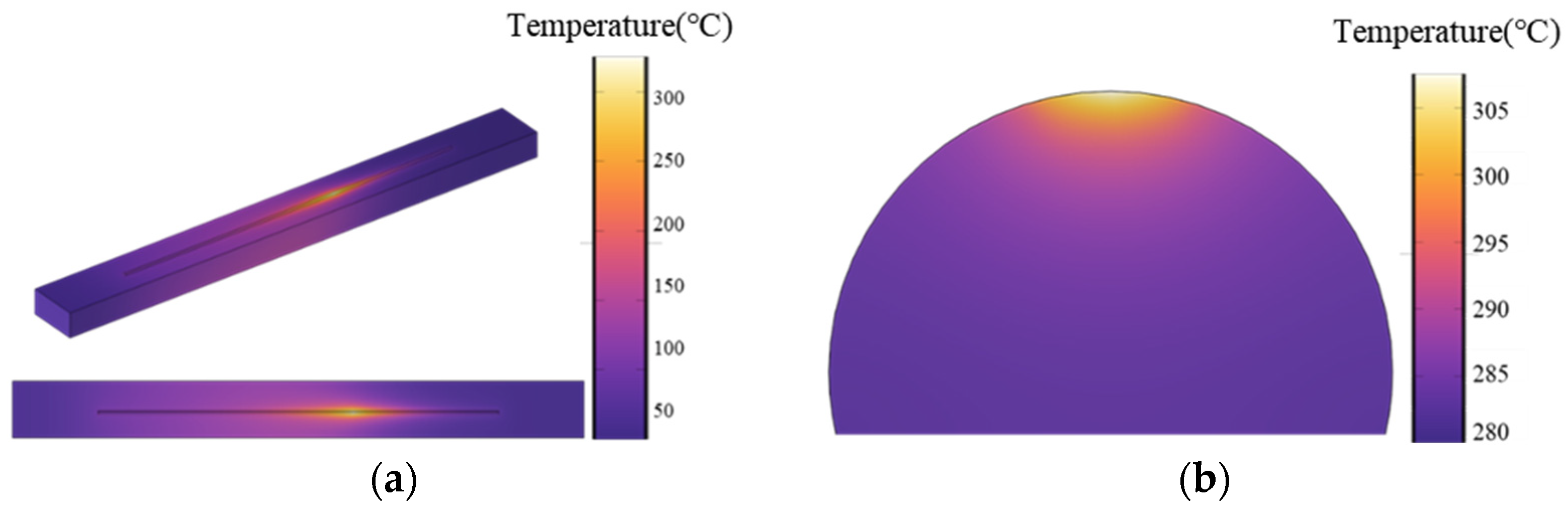
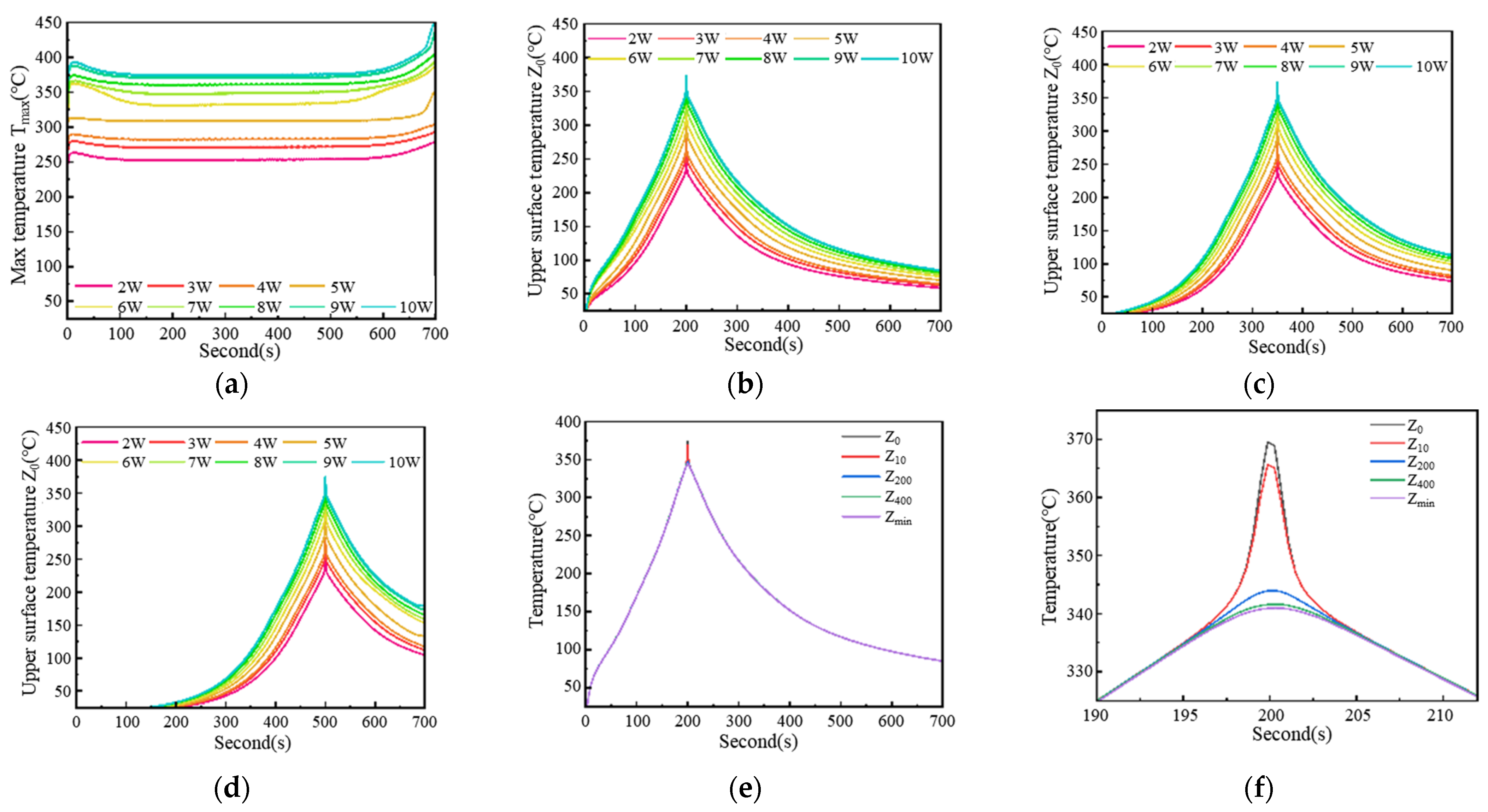
3.2. Temperature Field Monitoring and Simulation in Laser Sintering
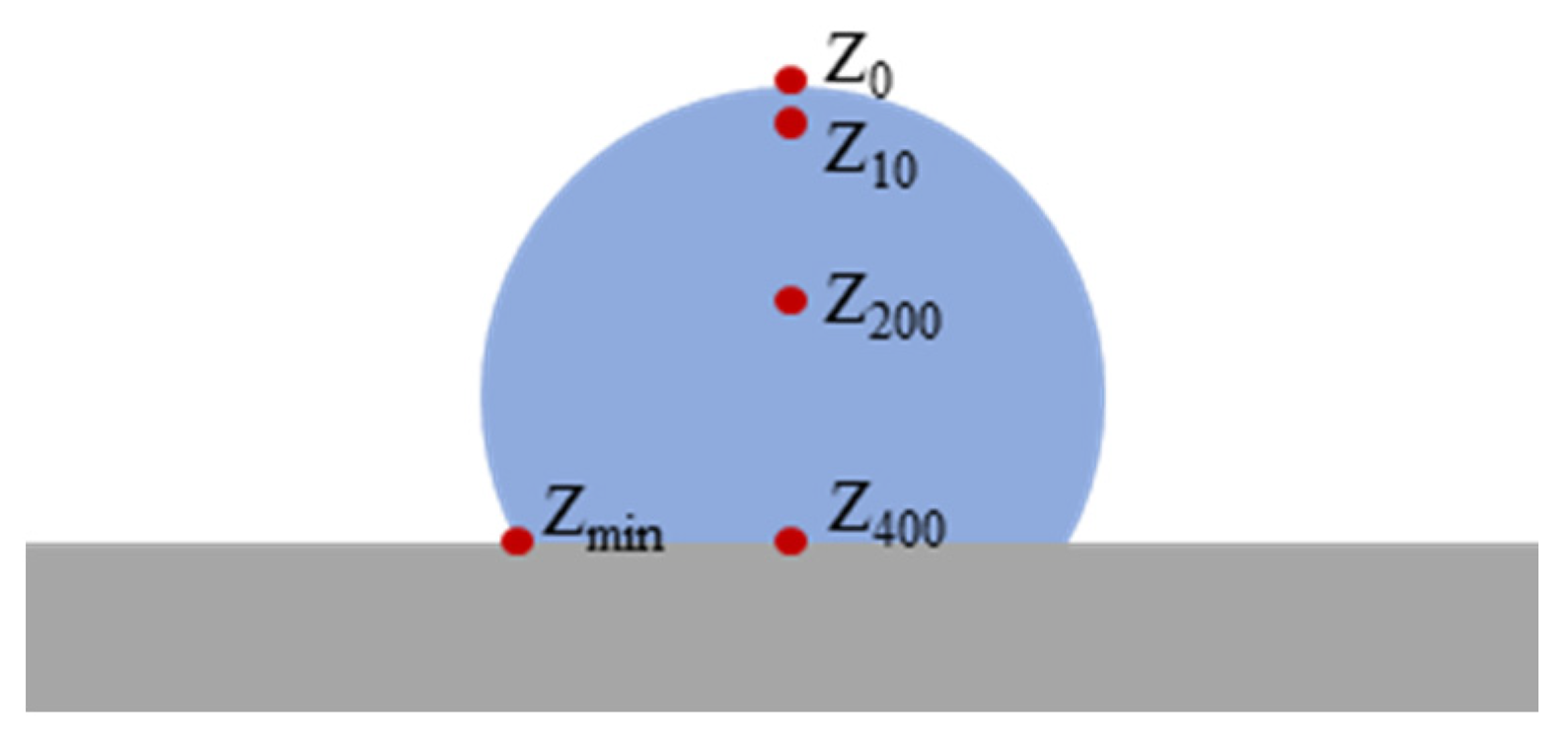
- The maximum temperature within the conductive circuit domain (denoted as Tmax);
- The center point of the upper surface in the conductive circuit cross-section (denoted as Z0);
- A point 10 μm below the surface (denoted as Z10);
- A point 200 μm below the surface (denoted as Z200);
- A point 400 μm below the surface (i.e., the bottom surface, denoted as Z400);
- The edge point of the conductive circuit’s bottom surface farthest from the center of the upper surface (denoted as Zmin).
4. Quantitative Analysis of Temperature Field Effects on Sintering Performance
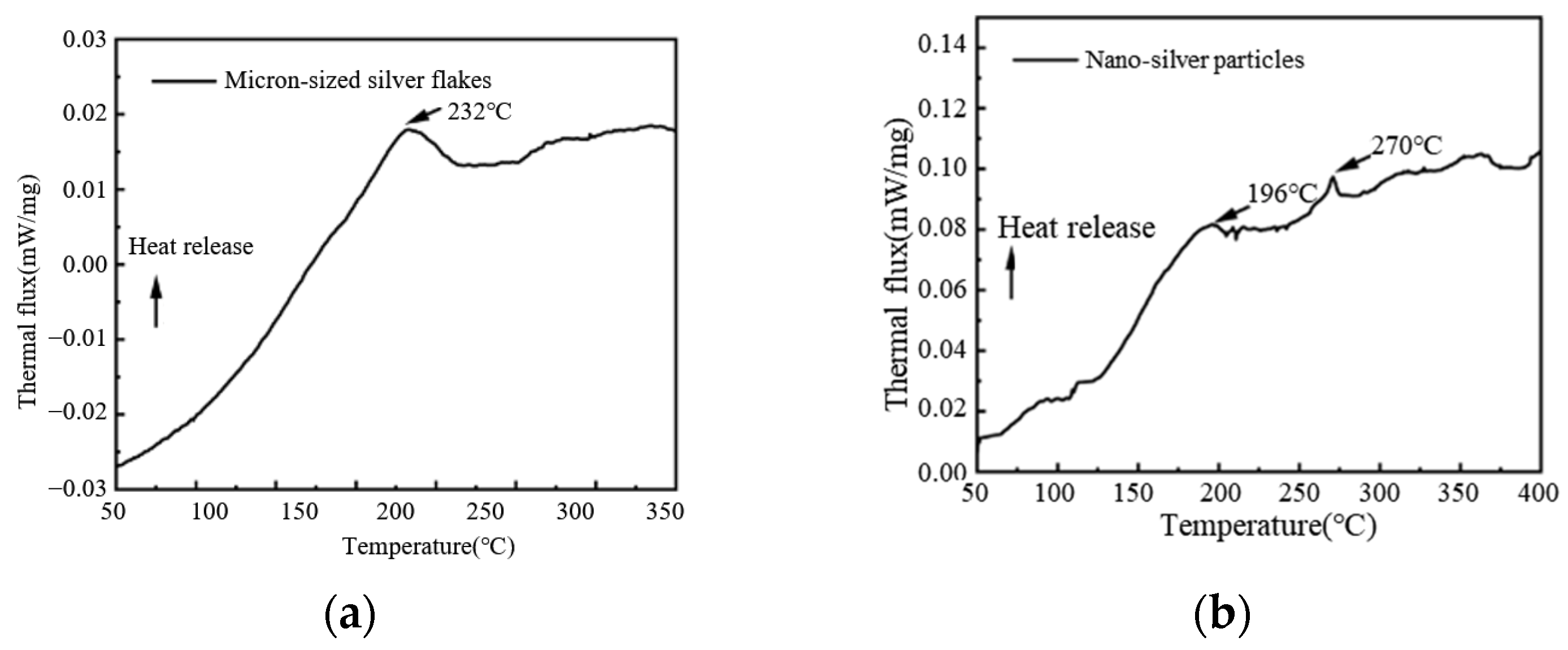
4.1. Relative Relationship Between Effective Sintering Temperature and Thermal Characteristics of Conductive Silver Paste
- non-uniform heating. Unlike the uniform heating in thermal sintering, the top-down heat transfer process in laser sintering results in non-uniform heating across the cross-section of the conductive circuit during sintering.
- non-steady-state temperature changes. Due to the heat transfer along the direction of the conductive circuit, the sintering temperature at a point on the conductive circuit first rises and then falls, creating a preheating and cooling process.
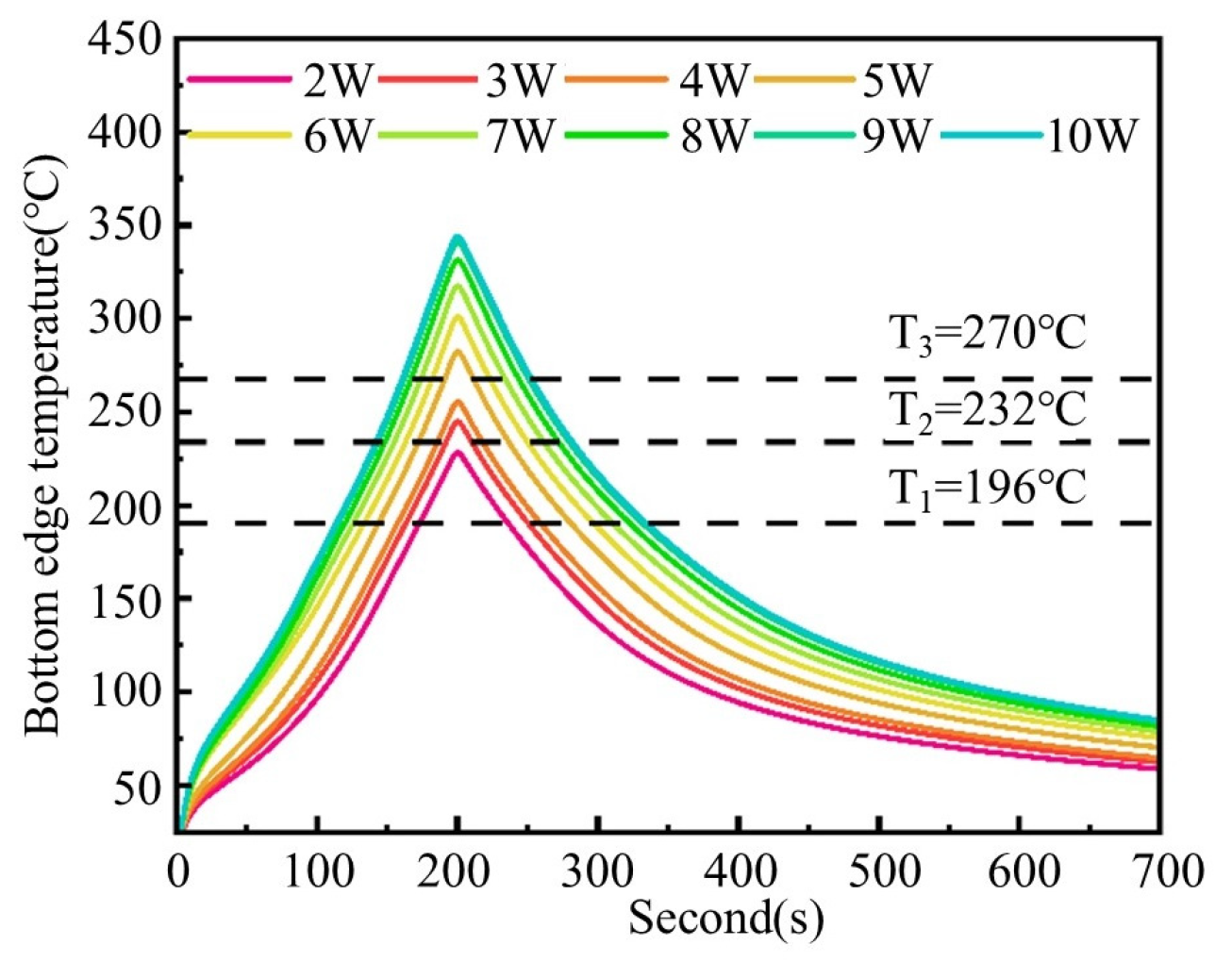
- Zone I (T1 < Ta < T2): When Ta is between T1 and T2, the nano-silver particles initiate sintering, while the micron-sized silver flakes remain below the sintering temperature, resulting in partial consolidation of the conductive silver paste with suboptimal performance.
- Zone II (T2 < Ta < T3): When Ta is between T2 and T3, the sintering of the nano-silver particles intensifies, and the micron-sized silver flakes begin to sinter, thereby causing the sintering performance to improve compared to Zone I.
- Zone III (T3 < Ta < Tp): When Ta is between T3 and Tp, all conductive phases within the conductive silver paste can start to undergo full sintering, and the sintering effect is continuously enhanced with the increase in laser power.
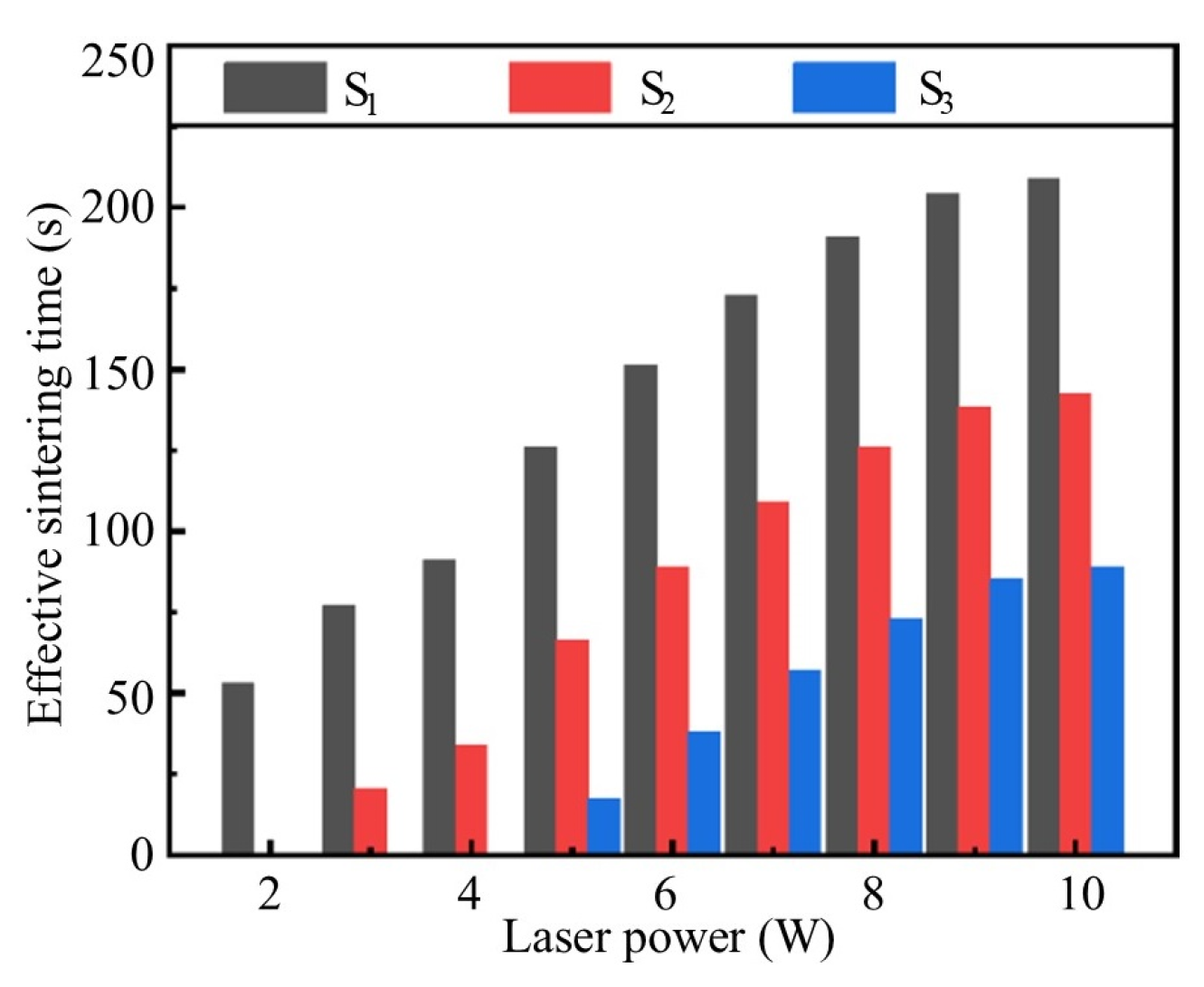
4.2. Influence of Effective Sintering Time on Sintering Performance
- S1: The duration when the sintering temperature exceeds T1 represents the period during which the sintering temperature remains above the first exothermic peak temperature of the nano-silver particles. Within this temperature range, the nano-silver particles undergo initial sintering.
- S2: The duration above temperature T2 represents the time period during which the sintering temperature exceeds the exothermic peak temperature of micron-sized silver flakes, enabling their effective sintering process.
- S3: The duration when the sintering temperature is greater than T3 represents the period when the sintering temperature exceeds the second sintering peak temperature of the nano-silver particles, ensuring thorough sintering of the nanoparticles.
5. Conclusions
- Increasing laser power and reducing laser scanning speed can cause a decrease in the resistivity of conductive circuits. When the laser scanning speed is 0.1 mm/s and the laser power is 10 W, the minimum resistivity is 6.81 μΩ·cm. The laser scanning speed remains constant, the laser power is reduced to 2 W, and the resistivity will increase to 34.56 μΩ·cm. The laser power remains unchanged, the laser scanning speed increases to 0.5 mm/s, and the resistivity is 7.3 μΩ·cm.
- The resistivity variation exhibited a stepwise decreasing trend across three laser power regimes: low-power (<3 W), medium-power (3~4 W), and high-power (>5 W), characterized by rapid inter-regime reduction and gradual intra-regime decline within each power regime. In the low-power range, the resistivity is 34.56 μΩ·cm, and the porosity is 12.5%. In the medium-power range, the resistivity ranges from 18.30 to 19.96 μΩ·cm, and the porosity ranges from 10.1% to 10.2%. In the high-power range, the resistivity is 6.81~8.23 μΩ·cm, and the porosity is 7.1~9.3%.
- The laser sintering parameters determine the final sintering performance by influencing the temperature field through the effective sintering temperature and effective sintering time. Higher laser power elevates the effective sintering temperature beyond the exothermic peak of specific components, leading to rapid inter-regime resistivity reduction. Further increasing the laser power elevated the effective sintering temperature and extended the effective sintering time, thereby reducing the resistivity within the parameter regime and achieving superior sintering performance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FDM | Fused Deposition Modeling |
| PEEK | Polyetheretherketone |
| CCD | Charge-Coupled Device |
| CT | Computed Tomography |
References
- Liu, W.; Xu, R.L.; Wang, C.Q.; Tian, Y.H. Study on Preparation and Rapid Laser Sintering Process of Nano Silver Pastes. In Proceedings of the 18th International Conference on Electronic Packaging Technology (ICEPT), Harbin, China, 16–19 August 2017; pp. 1525–1528. [Google Scholar] [CrossRef]
- Słoma, M. 3D printed electronics with nanomaterials. Nanoscale 2023, 15, 5623–5648. [Google Scholar] [CrossRef] [PubMed]
- Tan, H.W.; Choong, Y.Y.C.; Kuo, C.N.; Low, H.Y.; Chua, C.K. 3D printed electronics: Processes, materials and future trends. Prog. Mater. Sci. 2022, 127, 100945. [Google Scholar] [CrossRef]
- Zhang, B. Controllable Preparation of Organic Conductive Agents and Application in Electrically Conductive Adhesive. Master’s Thesis, Xi’an Technological University, Xi’an, China, 2023. [Google Scholar] [CrossRef]
- Martins, P.; Pereira, N.; Lima, A.C.; Garcia, A.; Mendes-Filipe, C.; Policia, R.; Correia, V.; Lanceros-Mendez, S. Advances in Printing and Electronics: From Engagement to Commitment. Adv. Funct. Mater. 2023, 33, 2213744. [Google Scholar] [CrossRef]
- Wang, K.; Li, X.; Fan, H.; Xiong, S.; Liu, B.; Shuai, C. Preparation of Conductive Silver Paste with Mixed Nanostructured Silver Powders. J. Mater. Eng. Perform. 2025. [Google Scholar] [CrossRef]
- Zhou, H.; Guo, K.; Ma, S.; Wang, C.; Fan, X.; Jia, T.; Zhang, Z.; Xu, H.; Xing, H.; Wang, D. A triple-layer structure flexible sensor based on nano-sintered silver for power electronics with high temperature resistance and high thermal conductivity. Chem. Eng. J. 2022, 432, 134431. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Wang, M.; Zheng, R.; Jin, Y.; Gu, Z. Flexible and strain conductive cotton yarn enabled by low-temperature sintering of silver paste with multifunctional sensing capability in human motion detection and wearable applications. Chem. Eng. J. 2023, 471, 144843. [Google Scholar] [CrossRef]
- Hu, K.; Zhou, Y.; Sitaraman, S.K.; Tentzeris, M.M. Additively manufactured flexible on-package phased array antennas for 5G/mmWave wearable and conformal digital twin and massive MIMO applications. Sci. Rep. 2023, 13, 12515. [Google Scholar] [CrossRef]
- Jang, Y.-R.; Joo, S.-J.; Chu, J.-H.; Uhm, H.-J.; Park, J.-W.; Ryu, C.-H.; Yu, M.-H.; Kim, H.-S. A review on intense pulsed light sintering technologies for conductive electrodes in printed electronics. Int. J. Precis. Eng. Manuf. Technol. 2021, 8, 327–336. [Google Scholar] [CrossRef]
- Hussain, A.; Lee, H.L.; Moon, S.J. Sintering of silver nanoparticle structures and the pursuit of minimum resistivity. Mater. Today Commun. 2023, 34, 105159. [Google Scholar] [CrossRef]
- Jahangir, N.; Cleeman, J.; Hwang, H.J.; Malhotra, R. Towards out-of-chamber damage-free fabrication of highly conductive nanoparticle-based circuits inside 3D printed thermally sensitive polymers. Addit. Manuf. 2019, 30, 100886. [Google Scholar] [CrossRef]
- Ermak, O.; Zenou, M.; Toker, G.B.; Ankri, J.; Shacham-Diamand, Y.; Kotler, Z. Rapid laser sintering of metal nanoparticles inks. Nanotechnology 2016, 27, 385201. [Google Scholar] [CrossRef] [PubMed]
- Perelaer, J.; Klokkenburg, M.; Hendriks, C.E.; Schubert, U.S. Microwave Flash Sintering of Inkjet-Printed Silver Tracks on Polymer Substrates. Adv. Mater. 2009, 21, 4830–4834. [Google Scholar] [CrossRef] [PubMed]
- Ivanisevic, I.; Kassal, P.; Milinkovic, A.; Rogina, A.; Milardovic, S. Combined Chemical and Thermal Sintering for High Conductivity Inkjet-printed Silver Nanoink on Flexible Substrates. Chem. Biochem. Eng. Q. 2019, 33, 377–384. [Google Scholar] [CrossRef]
- Zhao, P.B.; Huang, J.; Nan, J.Z.; Liu, D.C.; Meng, F.B. Laser sintering process optimization of microstrip antenna fabricated by inkjet printing with silver-based MOD ink. Mater. Process. Technol. 2020, 275, 116347. [Google Scholar] [CrossRef]
- Sharif, A.; Farid, N.; McGlynn, P.; Wang, M.; Vijayaraghavan, R.K.; Jilani, A.; Leen, G.; McNally, P.J.; O’Connor, G.M. Ultrashort laser sintering of printed silver nanoparticles on thin, flexible, and porous substrates. J. Phys. D Appl. Phys. 2023, 56, 075102. [Google Scholar] [CrossRef]
- Tan, H.W.; An, J.; Chua, C.K.; Tran, T. Metallic Nanoparticle Inks for 3D Printing of Electronics. Adv. Electron. Mater. 2019, 5, 1800831. [Google Scholar] [CrossRef]
- Paeng, D.; Yeo, J.; Lee, D.; Moon, S.J.; Grigoropoulos, C.P. Laser wavelength effect on laser-induced photo-thermal sintering of silver nanoparticles. Appl. Phys. A-Mater. Sci. Process. 2015, 120, 1229–1240. [Google Scholar] [CrossRef]
- Schwerdtfeger, J.; Singer, R.E.; Körner, C. In situ flaw detection by IR-imaging during electron beam melting. Rapid Prototyp. J. 2012, 18, 259–263. [Google Scholar] [CrossRef]
- Skylar-Scott, M.A.; Gunasekaran, S.; Lewis, J.A. Laser-assisted direct ink writing of planar and 3D metal architectures. Proc. Natl. Acad. Sci. USA 2016, 113, 6137–6142. [Google Scholar] [CrossRef]
- Fu, L. Laser Curing of Inks for Plastic Electronic Applications. Ph.D. Thesis, University of Liverpool, Liverpool, UK, 2014. [Google Scholar]
- Gu, M.F.; Xiao, X.Z.; Liu, T.T.; Li, G.; Liao, W.H. In-situ alleviation of surface modifier passivation effects in silver nanoparticle laser sintering process. J. Manuf. Process. 2025, 139, 239–249. [Google Scholar] [CrossRef]
- Chen, T.; Gu, M. Stoma suppression of laser sintering conductive circuit. Opt. Precis. Eng. 2020, 28, 1958–1966. [Google Scholar] [CrossRef]
- Heavens, O.S. Optical Properties of Thin Solid Films; Courier Corporation: Chelmsford, MA, USA, 1991. [Google Scholar]
- Wang, S.; Li, M.Y.; Ji, H.J.; Wang, C.Q. Rapid pressureless low-temperature sintering of Ag nanoparticles for high-power density electronic packaging. Scr. Mater. 2013, 69, 789–792. [Google Scholar] [CrossRef]





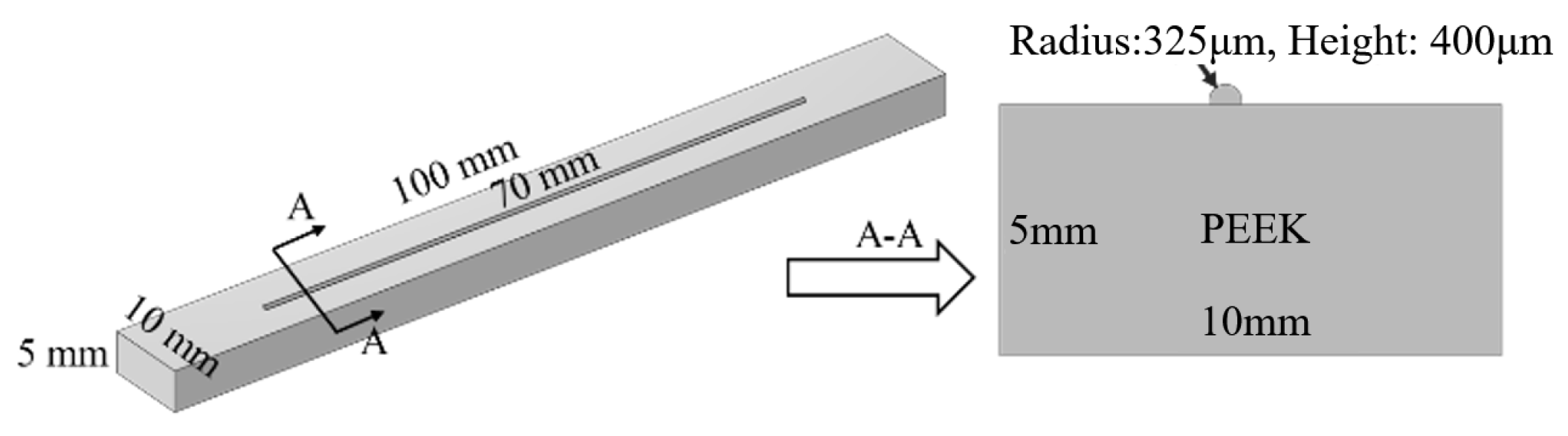
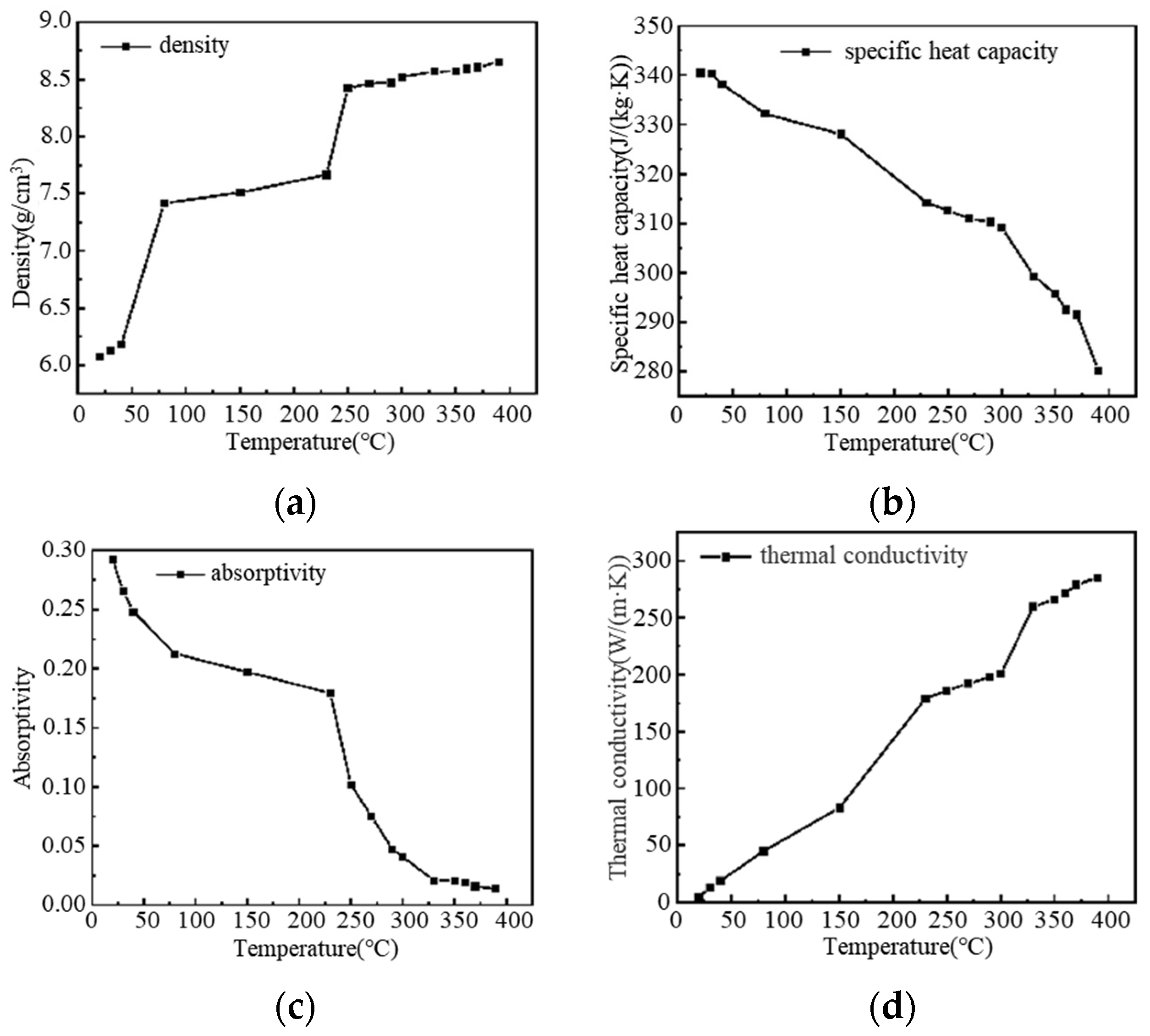

| Categories | Process | Parameters | Size |
|---|---|---|---|
| substrates (PEEK) | FDM | 100% filled; print speed: 80 mm/s layer thickness: 0.2 mm | 100 mm (length) × 30 mm (width) × 5 mm (thickness) |
| circuits | direct writing | nozzle diameter: 0.41 mm; print speed: 8 mm/s; extrusion pressure: 1.5 bar; nozzle height: 400 μm; distance of lines: 10 mm | 70 mm (length) × 650 μm (width) × 400 μm (thickness) |
| Parameter Category | Parameter | Setting |
|---|---|---|
| Fixed parameters | Laser setting | focal length: 100 mm; Defocus distance: 0 mm |
| Scanning passes (n) | n = 1 | |
| Number of samples | 3 samples for each parameter combination | |
| Variable parameters | Laser power | 2 W, 3 W, 4 W, 5 W, 6 W, 7 W, 8 W, 9 W, 10 W |
| Scanning speed | 0.1 mm/s, 0.2 mm/s, 0.3 mm/s, 0.4 mm/s, 0.5 mm/s |
| Laser power (W) | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Experimental monitoring temperature (°C) | 252 | 273 | 285 | 308 | 332 | 348 | 360 | 368 | 375 |
| Sintering simulation temperature (°C) | 253 | 271 | 283 | 309 | 328 | 347 | 361 | 370 | 376 |
| Laser power (W) | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Effective sintering temperature (°C) | 228 | 245 | 255 | 282 | 301 | 317 | 331 | 341 | 346 |
| Laser power (W) | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| S1 (s) | 53 | 77 | 91 | 126 | 151 | 173 | 191 | 204 | 209 |
| S2 (s) | 0 | 21 | 34 | 66 | 89 | 109 | 126 | 138 | 143 |
| S3 (s) | 0 | 0 | 0 | 17 | 38 | 57 | 73 | 85 | 89 |
| Laser Power Regimes | Ta (°C) | S1 (s) | S2 (s) | S3 (s) |
| Low | 228 | 53 | 0 | 0 |
| Medium | 245~255 | 77~91 | 21~34 | 0 |
| High | 282~346 | 126~209 | 66~143 | 17~89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zu, W.; Xiao, X.; Liu, T.; Gu, M.; Li, G.; Liao, W. Effect of Non-Uniform Temperature Field on Sintering Performance of Conductive Silver Paste in Laser Sintering. Materials 2025, 18, 2358. https://doi.org/10.3390/ma18102358
Zu W, Xiao X, Liu T, Gu M, Li G, Liao W. Effect of Non-Uniform Temperature Field on Sintering Performance of Conductive Silver Paste in Laser Sintering. Materials. 2025; 18(10):2358. https://doi.org/10.3390/ma18102358
Chicago/Turabian StyleZu, Wenkai, Xingzhi Xiao, Tingting Liu, Mingfei Gu, Gang Li, and Wenhe Liao. 2025. "Effect of Non-Uniform Temperature Field on Sintering Performance of Conductive Silver Paste in Laser Sintering" Materials 18, no. 10: 2358. https://doi.org/10.3390/ma18102358
APA StyleZu, W., Xiao, X., Liu, T., Gu, M., Li, G., & Liao, W. (2025). Effect of Non-Uniform Temperature Field on Sintering Performance of Conductive Silver Paste in Laser Sintering. Materials, 18(10), 2358. https://doi.org/10.3390/ma18102358







