Band Gap Energy and Lattice Distortion in Anatase TiO2 Thin Films Prepared by Reactive Sputtering with Different Thicknesses
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Structural Characteristics as a Function of the TiO2 Film Thickness
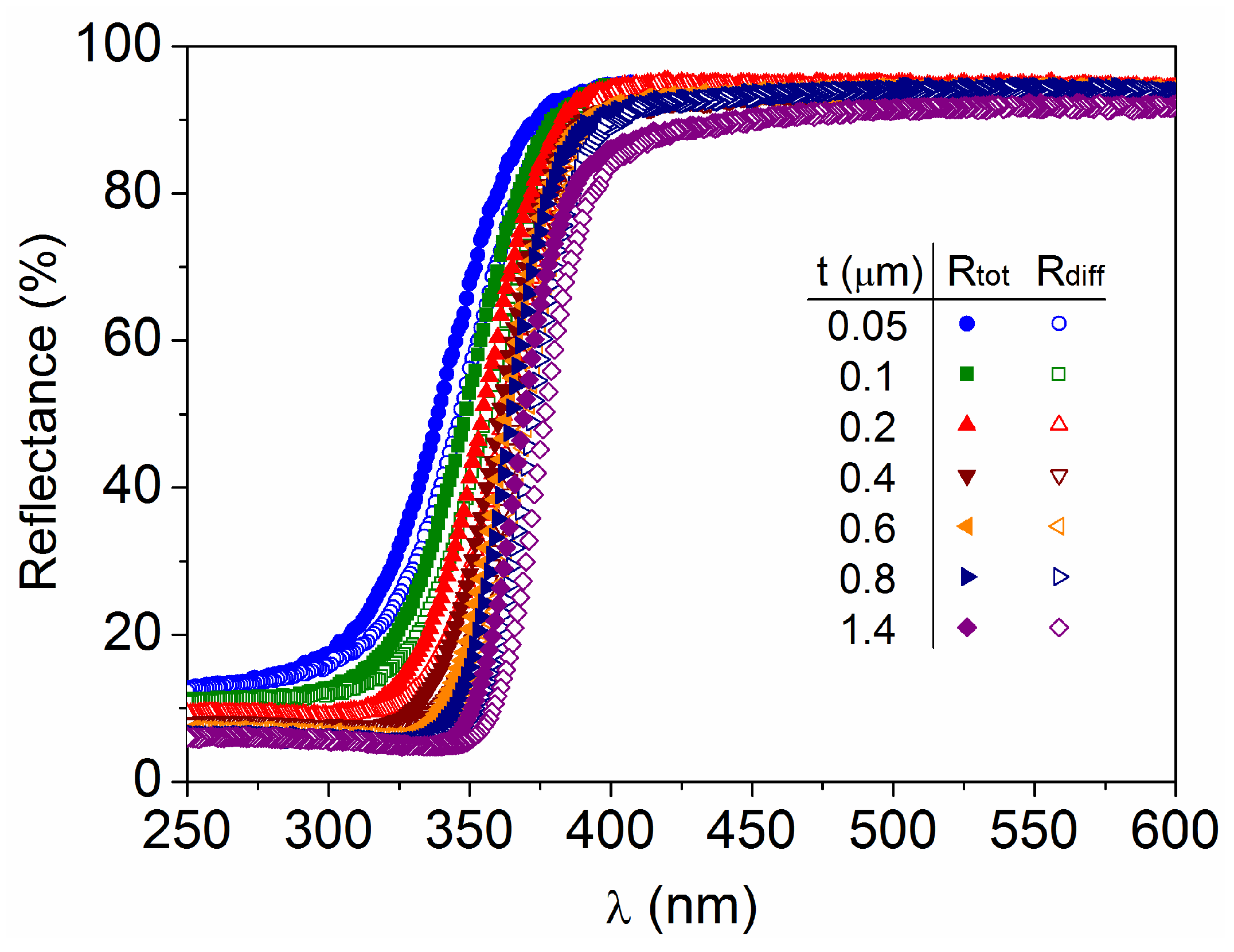
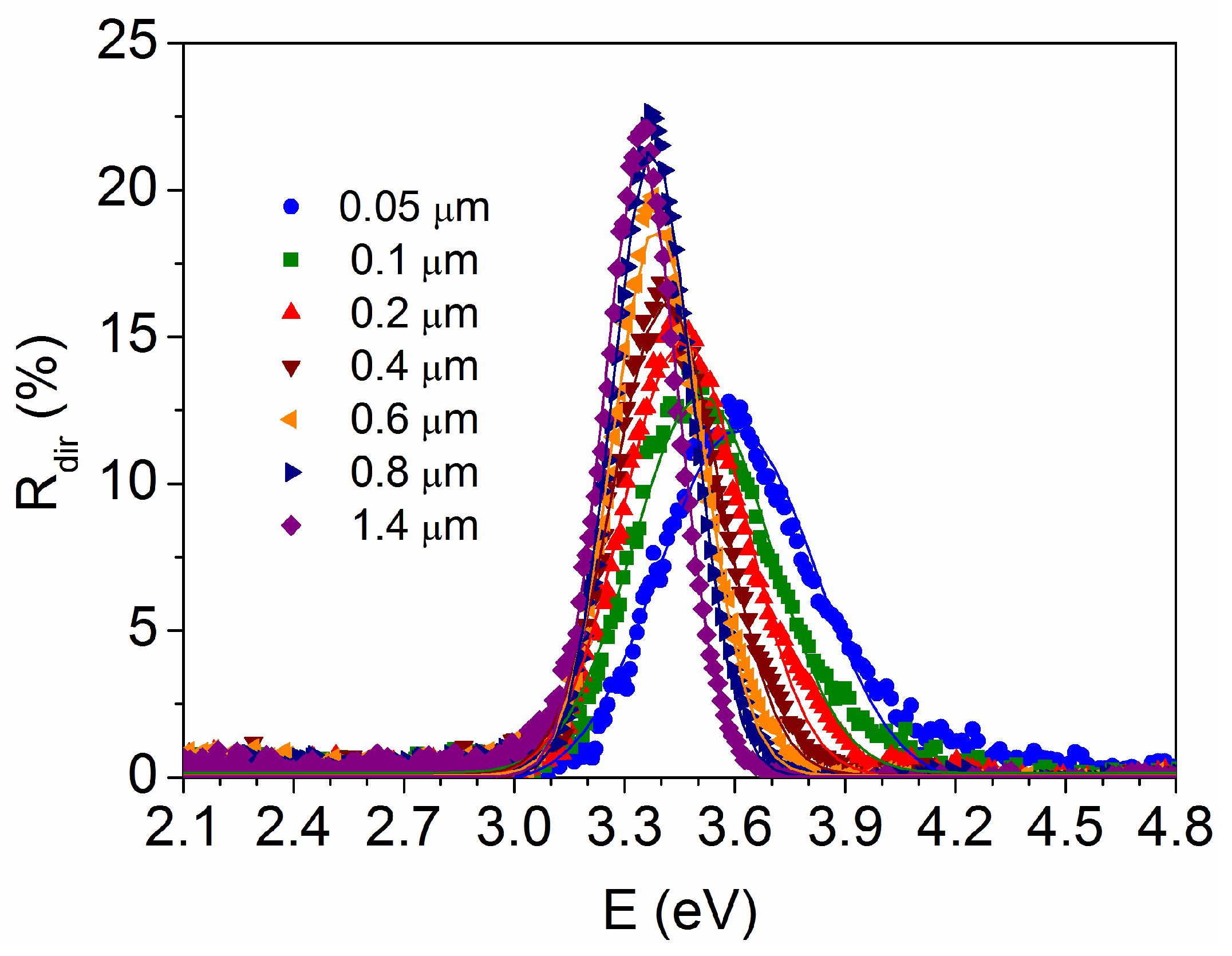
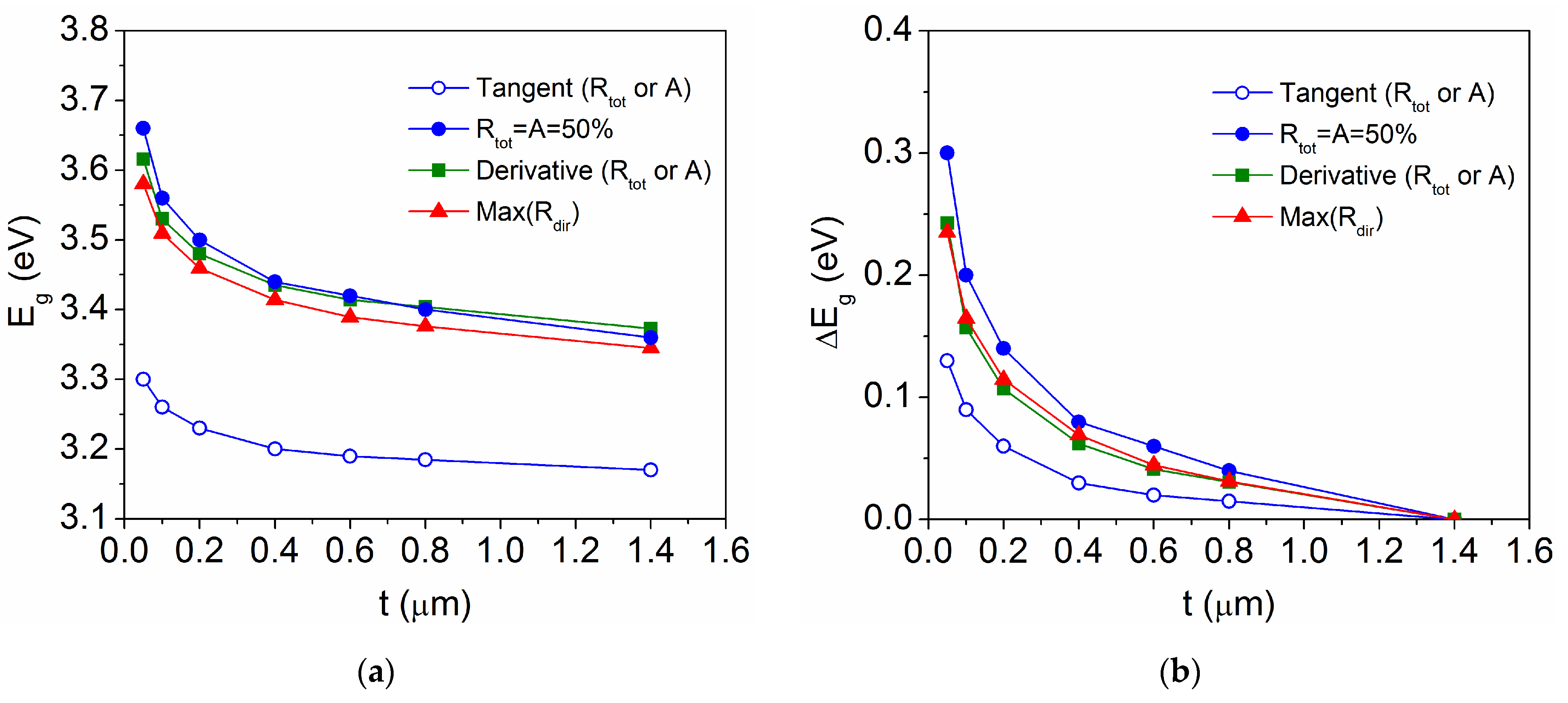
3.2. Optical Characteristics as a Function of the TiO2 Film Thickness
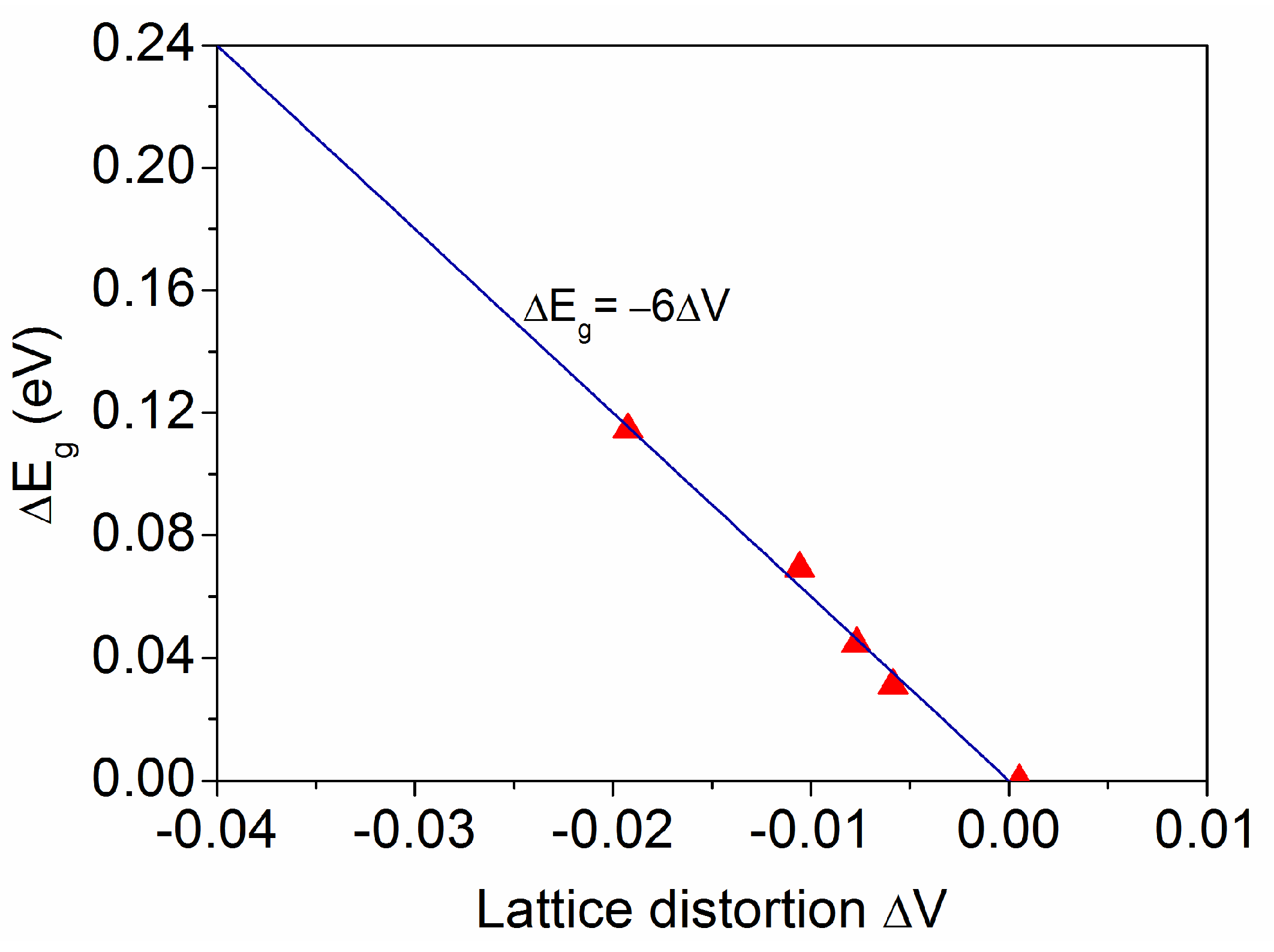
3.3. Relationship Between Band Gap Energy and Unit Cell Volume in TiO2 Thin Films
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aldosari, O.F. Photocatalytic water-splitting for hydrogen production using TiO2-based catalysts: Advances, current challenges, and future perspectives. Catal. Rev. Sci. Eng. 2025, 1–38. [Google Scholar] [CrossRef]
- Ma, H.; Li, Y.; Wang, C.; Li, Y.; Zhang, X. TiO2-based photocatalysts for removal of low-concentration NOx contamination. Catalysts 2025, 15, 103. [Google Scholar] [CrossRef]
- Marcelis, E.J.; ten Elshof, J.E.; Morales-Masis, M. Titanium dioxide: A versatile Earth-abundant optical material for photovoltaics. Adv. Opt. Mater. 2024, 12, 2401423. [Google Scholar] [CrossRef]
- Ziat, Y.; Belkhanchi, H.; Zarhri, Z. DFT analysis of structural, electrical, and optical properties of S, Si, and F-doped GeO2 rutile. Sol. Energy Sustain. Dev. J. 2025, 14, 74–89. [Google Scholar] [CrossRef]
- Ikreedeegh, R.; Tahir, M.; Madi, M. Modified-TiO2 nanotube arrays as a proficient photo-catalyst nanomaterial for energy and environmental applications. Sol. Energy Sustain. Dev. J. 2024, 13, 133–144. [Google Scholar] [CrossRef]
- Song, C.; Xiao, L.; Chen, Y.; Yang, F.; Meng, H.; Zhang, W.; Zhang, Y.; Wu, Y. TiO2-based catalysts with various structures for photocatalytic application: A review. Catalysts 2024, 14, 366. [Google Scholar] [CrossRef]
- Stefanov, B.I.; Niklasson, G.A.; Granqvist, C.G.; Österlund, L. Quantitative relation between photocatalytic activity and degree of <001> orientation for anatase TiO2 thin films. J. Mater. Chem. A 2015, 3, 17369–17375. [Google Scholar] [CrossRef]
- Garg, R.; Gonuguntla, S.; Sk, S.; Iqbal, M.S.; Dada, A.O.; Pal, U.; Ahmadipour, M. Sputtering thin films: Materials, applications, challenges and future directions. Adv. Colloid Interface Sci. 2024, 330, 103203. [Google Scholar] [CrossRef]
- Şeşe, A.; Akkus, M.S. TiO2-coated thin films: A catalyst for sustainable hydrogen production from potassium borohydride. Int. J. Hydrogen Energy, 2025; in press. [Google Scholar] [CrossRef]
- Fresno, F.; Reñones, P.; Alfonso, E.; Guillén, C.; Trigo, J.F.; Herrero, J.; Collado, L.; de la Peña O’Shea, V.A. Influence of surface density on the CO2 photoreduction activity of a DC magnetron sputtered TiO2 catalyst. Appl. Catal. B Environ. 2018, 224, 912–918. [Google Scholar] [CrossRef]
- Cormier, P.A.; Balhamri, A.; Thomann, A.L.; Dussart, R.; Semmar, N.; Lecas, T.; Snyders, R.; Konstantinidis, S. Titanium oxide thin film growth by magnetron sputtering: Total energy flux and its relationship with the phase constitution. Surf. Coat. Technol. 2014, 254, 291–297. [Google Scholar] [CrossRef]
- Guillén, C.; Montero, J.; Herrero, J. Anatase and rutile TiO2 thin films prepared by reactive DC sputtering at high deposition rates on glass and flexible polyimide substrates. J. Mater. Sci. 2014, 49, 5035–5042. [Google Scholar] [CrossRef]
- Guillén, C.; Herrero, J. TiO2 coatings obtained by reactive sputtering at room temperature: Physical properties as a function of the sputtering pressure and film thickness. Thin Solid Films 2017, 636, 193–199. [Google Scholar] [CrossRef]
- Sarngan, P.P.; Lakshmanan, A.; Sarkar, D. Influence of anatase-rutile ratio on band edge position and defect states of TiO2 homojunction catalyst. Chemosphere 2022, 286, 131692. [Google Scholar] [CrossRef]
- Zanatta, A.R. Assessing the amount of the anatase and rutile phases of TiO2 by optical reflectance measurements. Results Phys. 2021, 22, 103864. [Google Scholar] [CrossRef]
- Abbas, Q.A.; Alhelaly, M.T.; Hameed, M.A. The inter-planner parameter and the blue shift of band gap of titanium dioxide thin films prepared using the DC reactive magnetron sputtering. J. Opt. 2024, 53, 1516–1527. [Google Scholar] [CrossRef]
- Vorokh, A.S. Scherrer formula: Estimation of error in determining small nanoparticle size. Nanosyst. Phys. Chem. Math. 2018, 9, 364–369. [Google Scholar] [CrossRef]
- Roos, A. Use of an integrating sphere in solar energy research. Sol. Energy Mater. Sol. Cells 1993, 30, 77–94. [Google Scholar] [CrossRef]
- Zeng, T.; Qiu, Y.; Chen, L.; Song, X. Microstructure and phase evolution of TiO2 precursors prepared by peptization-hydrolysis method using polycarboxylic acid as peptizing agent. Mater. Chem. Phys. 1998, 56, 163–170. [Google Scholar] [CrossRef]
- Khorsand Zak, A.; Majid, W.H.A.; Abrishami, M.E.; Yousefi, R. X-ray analysis of ZnO nanoparticles by Williamson-Hall and size-strain plot methods. Solid State Sci. 2011, 13, 251–256. [Google Scholar] [CrossRef]
- Bilek, M.M.M.; McKenzie, D.R. A comprehensive model of stress generation and relief processes in thin films deposited with energetic ions. Surf. Coat. Technol. 2006, 200, 4345–4354. [Google Scholar] [CrossRef]
- Detor, A.J.; Hodge, A.M.; Chason, E.; Wang, Y.; Xu, H.; Conyers, M.; Nikroo, A.; Hamza, A. Stress and microstructure evolution in thick sputtered films. Acta Mater. 2009, 57, 2055–2065. [Google Scholar] [CrossRef]
- Diebold, U. The surface science of titanium dioxide. Surf. Sci. Rep. 2003, 48, 53–229. [Google Scholar] [CrossRef]
- Tian, F.H.; Wang, X.; Zhao, W.; Zhao, L.; Chu, T.; Yu, S. Adsorption of 2-propanol on anatase TiO2 (101) and (001) surfaces: A density functional theory study. Surf. Sci. 2013, 616, 76–84. [Google Scholar] [CrossRef]
- Chen, M.; Ma, J.; Zhang, B.; He, G.; Li, Y.; Zhang, C.; He, H. Remarkable synergistic effect between {001} facets and surface F ions promoting hole migration on anatase TiO2. Appl. Catal. B Environ. 2017, 207, 397–403. [Google Scholar] [CrossRef]
- Mahmood, A.; Shi, G.; Xie, X.; Sun, J. Assessing the adsorption and photocatalytic activity of TiO2 nanoparticles for the gas phase acetaldehyde: A computational and experimental study. J. Alloys Compd. 2020, 819, 153055. [Google Scholar] [CrossRef]
- Oruç, P.; Turan, N.; Cavdar, S.; Tuğluoğlu, N.; Koralay, H. Investigation of dielectric properties of amorphous, anatase, and rutile TiO2 structures. J. Mater. Sci. Mater. Electron. 2023, 34, 498. [Google Scholar] [CrossRef]
- Sahadat Hossain, M.; Ahmed, S. Easy and green synthesis of TiO2 (Anatase and Rutile): Estimation of crystallite size using Scherrer equation, Williamson-Hall plot, Monshi-Scherrer Model, size-strain plot, Halder- Wagner Model. Results Mater. 2023, 20, 100492. [Google Scholar] [CrossRef]
- Yin, W.J.; Chen, S.; Yang, J.H.; Gong, X.G.; Yan, Y.; Wei, S.H. Effective band gap narrowing of anatase TiO2 by strain along a soft crystal direction. Appl. Phys. Lett. 2010, 96, 2008–2011. [Google Scholar] [CrossRef]
- Arlt, T.; Bermejo, M.; Blanco, M. High-pressure polymorphs of anatase. Phys. Rev. B—Condens. Matter Mater. Phys. 2000, 61, 14414–14419. [Google Scholar] [CrossRef]
- Wagner, J.M.; Bechstedt, F. Properties of strained wurtzite GaN and AlN: Ab initio studies. Phys. Rev. B—Condens. Matter Mater. Phys. 2002, 66, 115202. [Google Scholar] [CrossRef]
- Janssen, G.C.A.M. Stress and strain in polycrystalline thin films. Thin Solid Films 2007, 515, 6654–6664. [Google Scholar] [CrossRef]
- Rajender, G.; Giri, P.K. Strain induced phase formation, microstructural evolution and bandgap narrowing in strained TiO2 nanocrystals grown by ball milling. J. Alloys Compd. 2016, 676, 591–600. [Google Scholar] [CrossRef]
- Qiu, X.; Gou, G.; Zhang, K.; Zhang, X.; Sun, W.; Qin, S.; Luo, X.; Feng, P.; Pan, J.; Gao, W. Investigation on TiO2 photocathodic protection based on lattice distortion and stress engineering. Mater. Today Commun. 2023, 35, 105782. [Google Scholar] [CrossRef]
- Paul, T.C.; Podder, J. Synthesis and characterization of Zn-incorporated TiO2 thin films: Impact of crystallite size on X-ray line broadening and bandgap tuning. Appl. Phys. A Mater. Sci. Process. 2019, 125, 818. [Google Scholar] [CrossRef]
- Kusano, E. Structure-zone modeling of sputter-deposited thin films: A brief review. Appl. Sci. Converg. Technol. 2019, 28, 179–185. [Google Scholar] [CrossRef]
- Welter, E.S.; Garg, S.; Gläser, R.; Goepel, M. Methodological investigation of the band gap determination of solid semiconductors via UV/Vis spectroscopy. ChemPhotoChem 2023, 7, e202300001. [Google Scholar] [CrossRef]
- Serrar, H.; Mecibah, F.Z.; Kribes, I.; Bouachiba, Y.; Mammeri, A.; Bouabellou, A.; Retima, M.; Boughelout, A.; Taabouche, A.; Aouati, R. Argon flow rate effects on the optical waveguide properties of DC sputtered TiO2 thin films. Opt. Mater. 2023, 135, 113259. [Google Scholar] [CrossRef]
- Mullerova, J.; Sutta, P. On some ambiguities of the absorption edge and optical band gaps of amorphous and polycrystalline semiconductors. Commun. Sci. Lett. Univ. Zilina 2017, 19, 9–15. [Google Scholar] [CrossRef]
- Guillén, C.; Montero, J.; Herrero, J. Transparent and conductive electrodes combining AZO and ATO thin films for enhanced light scattering and electrical performance. Appl. Surf. Sci. 2013, 264, 448–452. [Google Scholar] [CrossRef]
- Gal, G.; Mastai, Y.; Hodes, G.; Kronik, L. Band gap determination of semiconductor powders via surface photovoltage spectroscopy. J. Appl. Phys. 1999, 86, 5573–5577. [Google Scholar] [CrossRef]
- Ansari, M.Z.; Munjal, S.; Khare, N. Intrinsic strain dependent redshift in optical band gap of Cu2ZnSnS4 nanostructured thin films. Thin Solid Films 2018, 657, 95–100. [Google Scholar] [CrossRef]
- Khammar, M.; Ynineb, F.; Guitouni, S.; Bouznit, Y.; Attaf, N. Crystallite size and intrinsic strain contribution in band gap energy redshift of ultrasonic-sprayed kesterite CZTS nanostructured thin films. Appl. Phys. A Mater. Sci. Process. 2020, 126, 398. [Google Scholar] [CrossRef]
- Welte, A.; Waldauf, C.; Brabec, C.; Wellmann, P.J. Application of optical absorbance for the investigation of electronic and structural properties of sol-gel processed TiO2 films. Thin Solid Films 2008, 516, 7256–7259. [Google Scholar] [CrossRef]
- Van de Walle, C.G. Band lineups and deformation potentials in the model-solid theory. Phys. Rev. B 1989, 39, 1871–1883. [Google Scholar] [CrossRef]
- Liu, Z.; Menéndez, C.; Shenoy, J.; Hart, J.N.; Sorrell, C.C.; Cazorla, C. Strain engineering of oxide thin films for photocatalytic applications. Nano Energy 2020, 72, 104732. [Google Scholar] [CrossRef]
- Kaur, K.; Singh, C.V. Amorphous TiO2 as a photocatalyst for hydrogen production: A DFT study of structural and electronic properties. Energy Procedia 2012, 29, 291–299. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guillén, C. Band Gap Energy and Lattice Distortion in Anatase TiO2 Thin Films Prepared by Reactive Sputtering with Different Thicknesses. Materials 2025, 18, 2346. https://doi.org/10.3390/ma18102346
Guillén C. Band Gap Energy and Lattice Distortion in Anatase TiO2 Thin Films Prepared by Reactive Sputtering with Different Thicknesses. Materials. 2025; 18(10):2346. https://doi.org/10.3390/ma18102346
Chicago/Turabian StyleGuillén, Cecilia. 2025. "Band Gap Energy and Lattice Distortion in Anatase TiO2 Thin Films Prepared by Reactive Sputtering with Different Thicknesses" Materials 18, no. 10: 2346. https://doi.org/10.3390/ma18102346
APA StyleGuillén, C. (2025). Band Gap Energy and Lattice Distortion in Anatase TiO2 Thin Films Prepared by Reactive Sputtering with Different Thicknesses. Materials, 18(10), 2346. https://doi.org/10.3390/ma18102346





