Multi-Scale Modeling and Damage Mechanisms of Asphalt Pavements Under Coupled Salt–Thermal–Mechanical Effects
Abstract
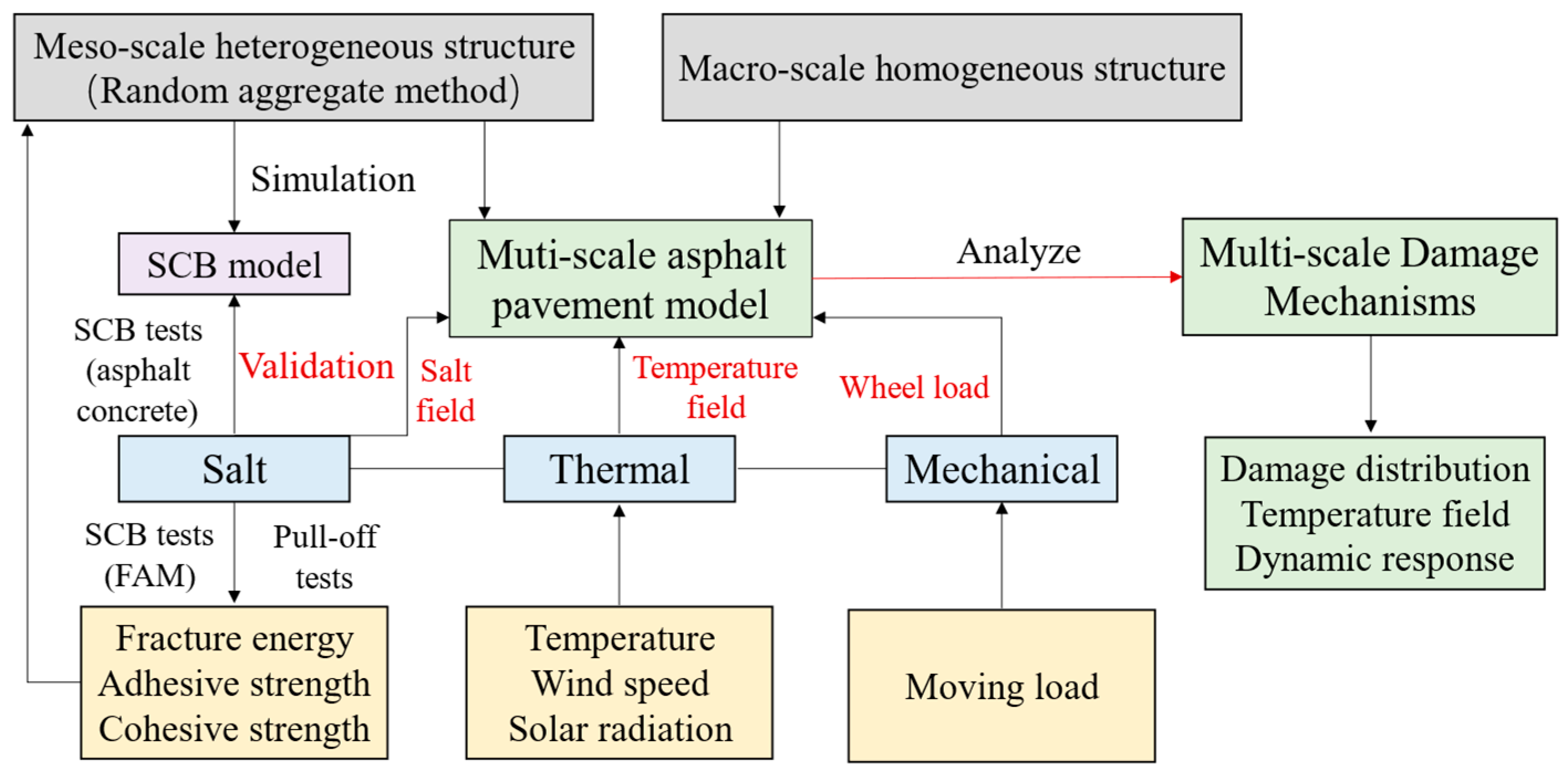
1. Introduction
2. Theories
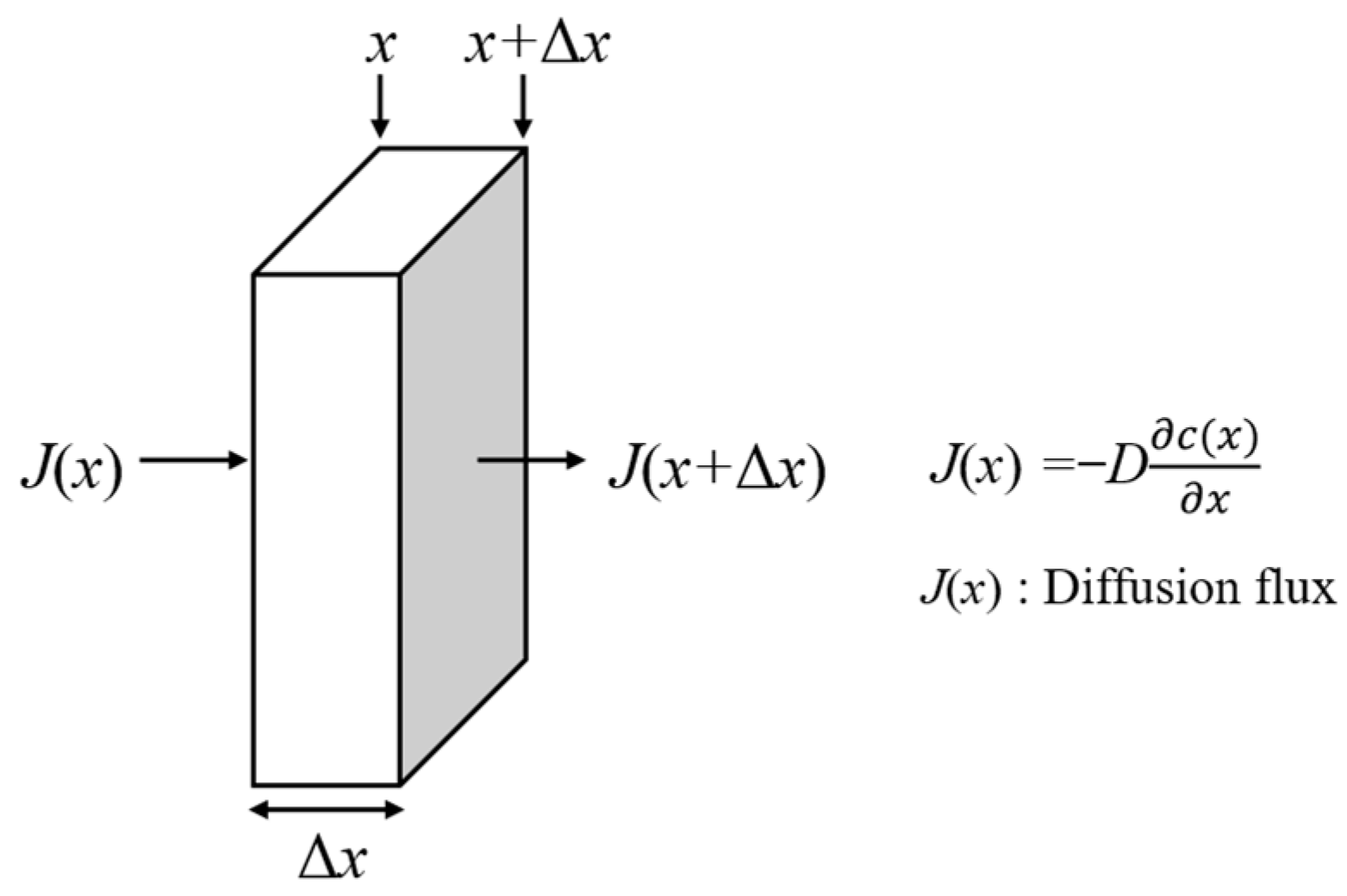
2.1. Diffusion Theory
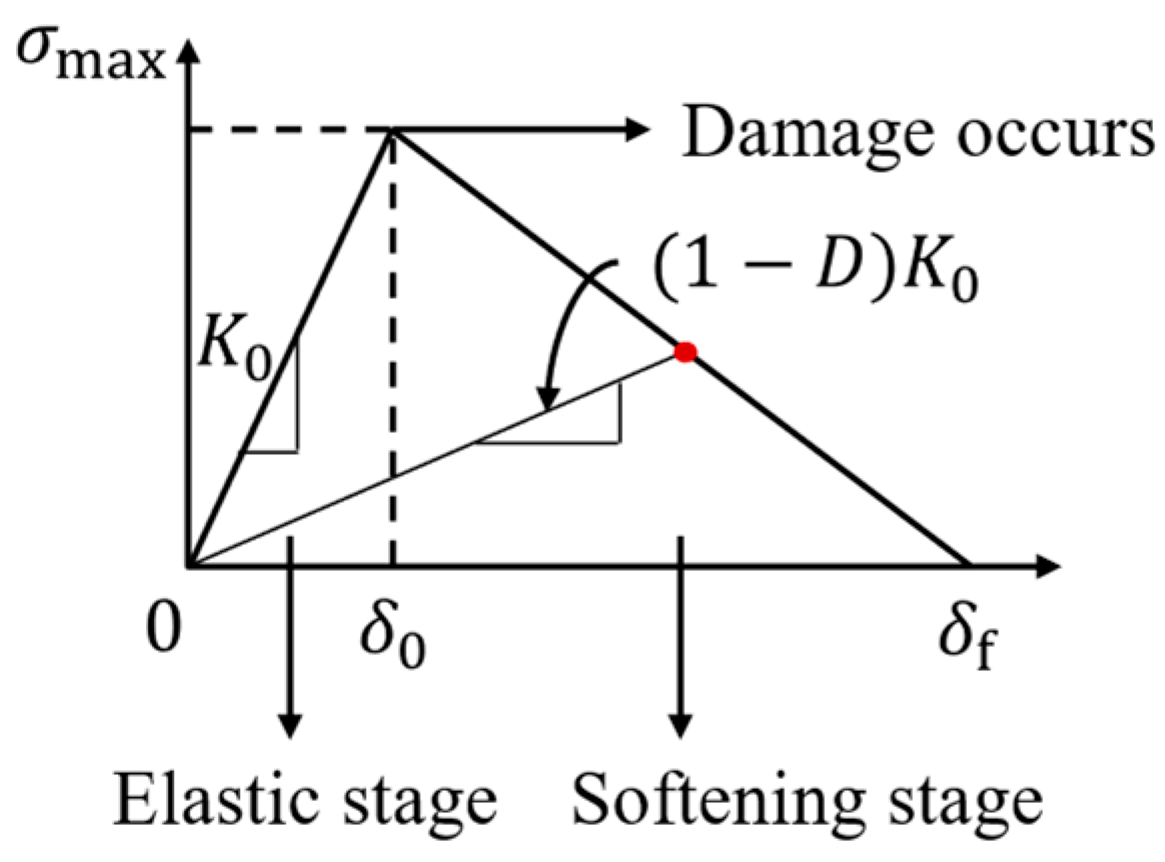
2.2. Damage Theory
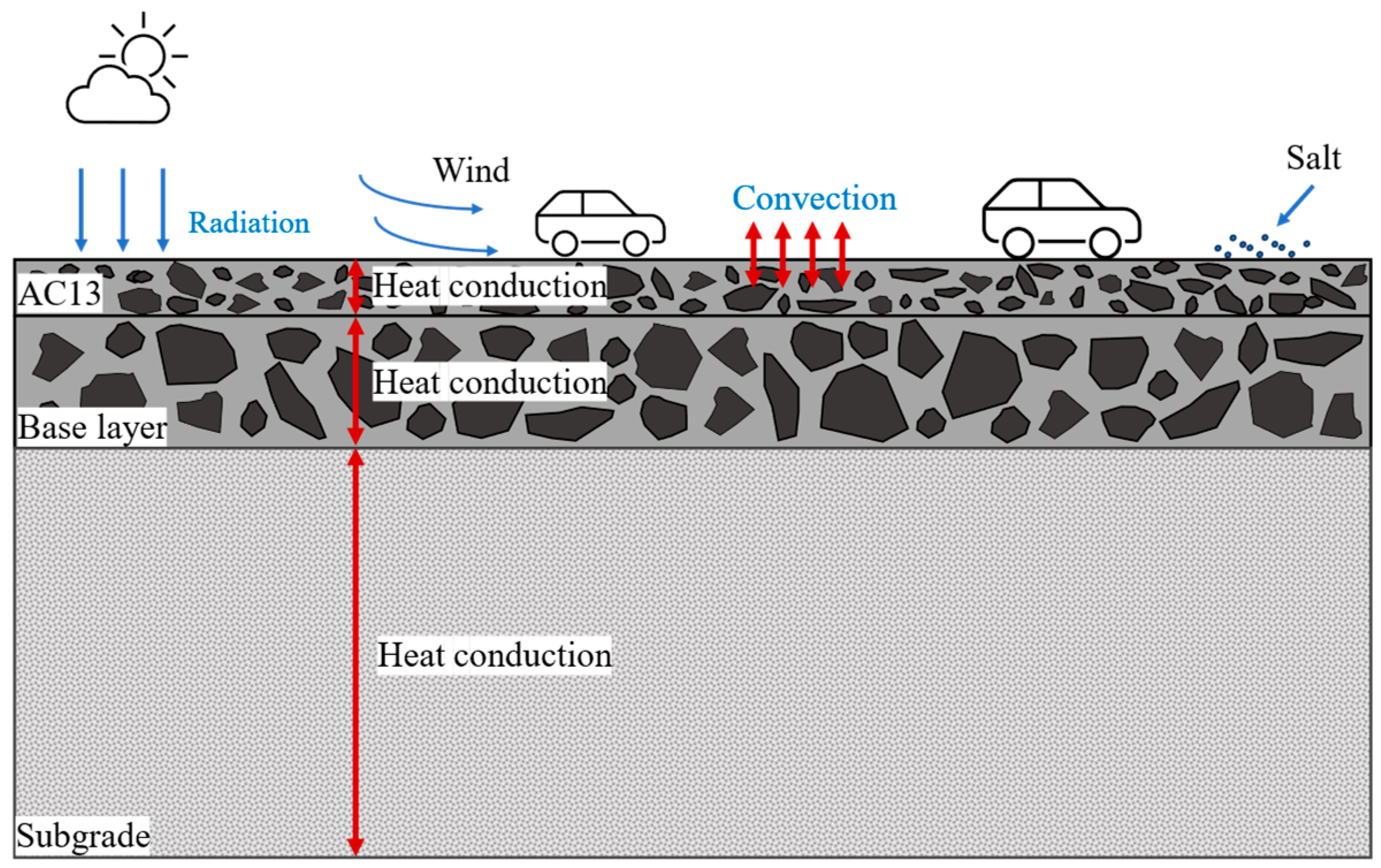
2.3. Heat Transfer Theory
- (1)
- Thermal Radiation
- (2)
- Thermal Convection
- (3)
- Thermal Conduction
3. Materials and Experiments
3.1. Experimental Research Program
3.2. Materials
3.3. Pull-Off Test
- (1)
- The pull-off specimen was positioned within the sleeve of the pull-off apparatus to ensure stable installation, preventing any potential displacement during the testing procedure.
- (2)
- The pull-off rate was set to 0.6 MPa/s. The testing apparatus was then to be activated, which would trigger the automatic commencement of the test, applying the specified pull-off force to the specimen at the predetermined rate.
- (3)
- Upon completion of the test, the values displayed on the screen of the testing apparatus were recorded. Three parallel tests of each group were conducted to ensure statistical validity.
3.4. SCB Test
4. Model Development
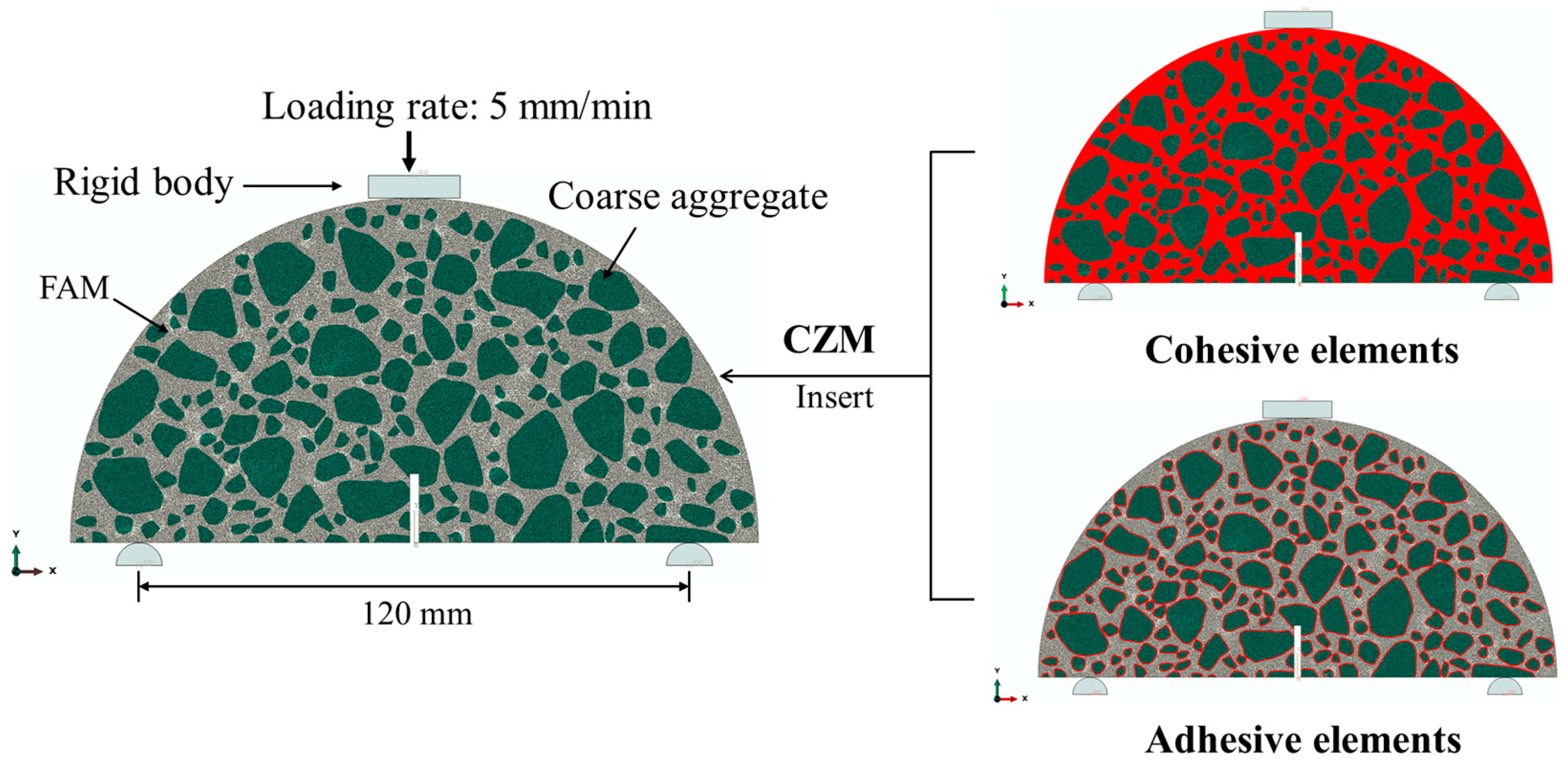
4.1. Heterogeneous SCB Model
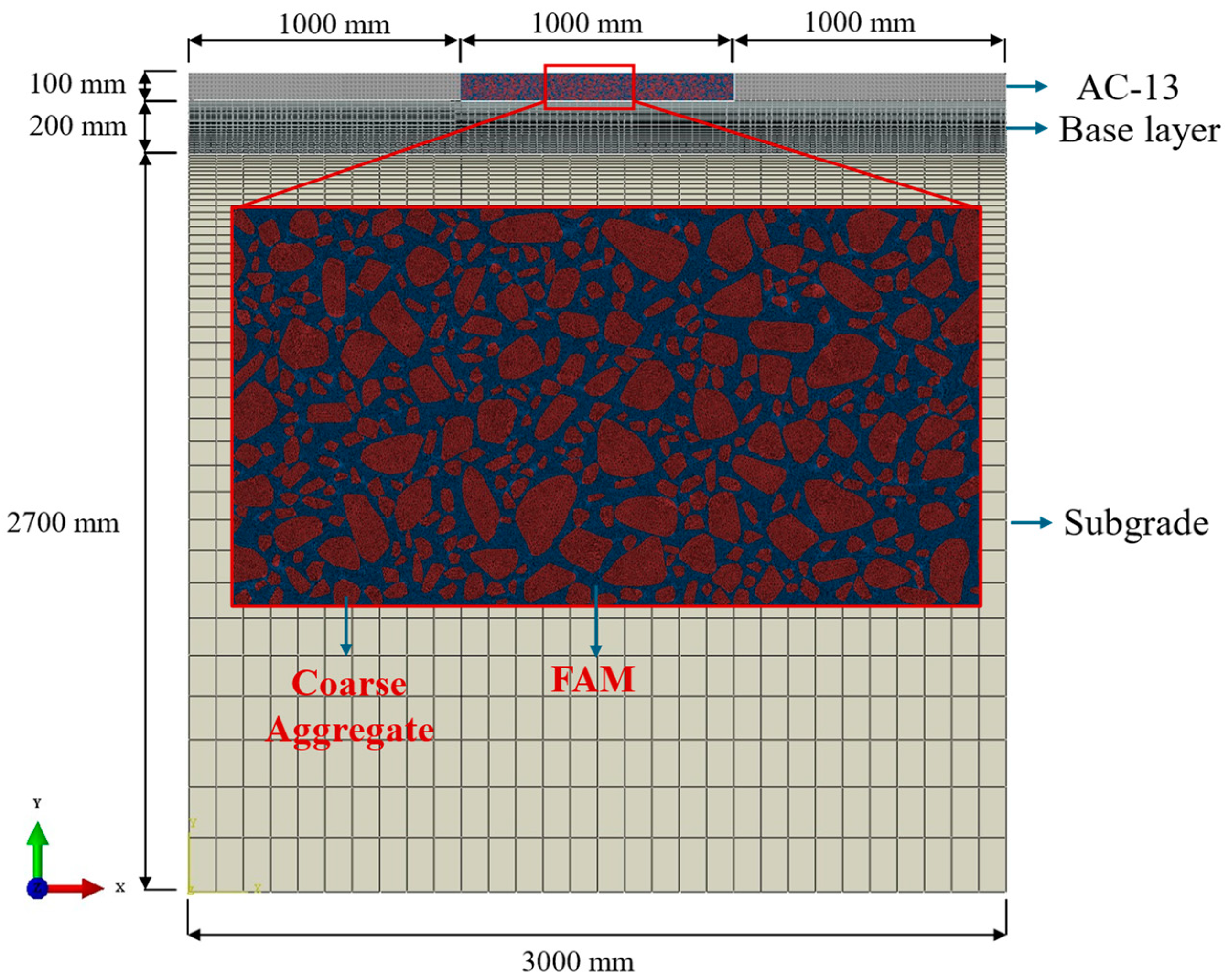
4.2. Multi-Scale FE Pavement Model
- (1)
- Except for the heterogeneous pavement structural regions, all other structural layers were assumed to be homogeneous, continuous, and isotropic.
- (2)
- The materials between the pavement layers were assumed to be tightly bonded, ensuring continuity of temperature and heat flow at the interfaces.
- (3)
- The lateral variation in the pavement temperature field was disregarded under the assumption that heat flow occurs solely in the vertical direction of the pavement.
5. Results and Discussion
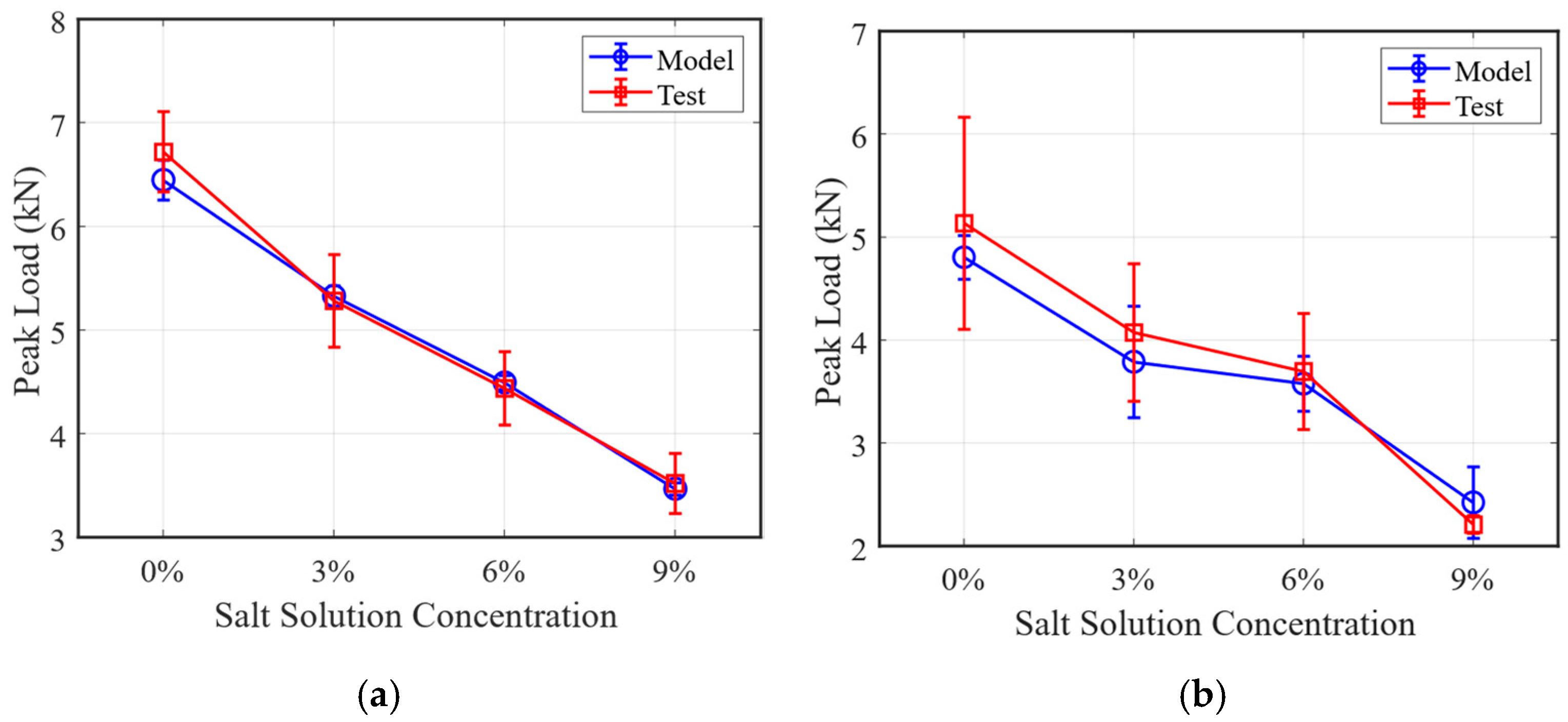
5.1. Model Validation
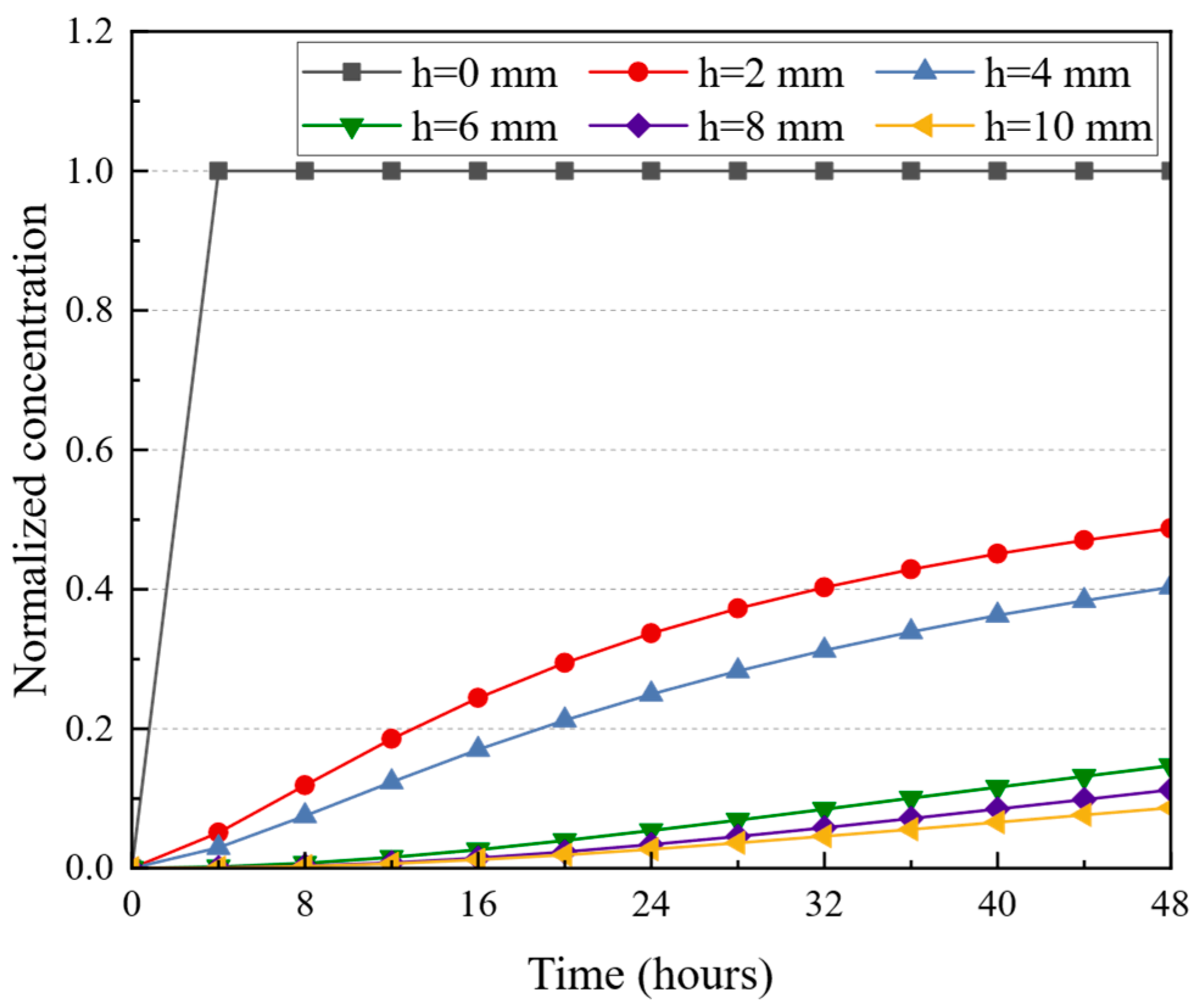
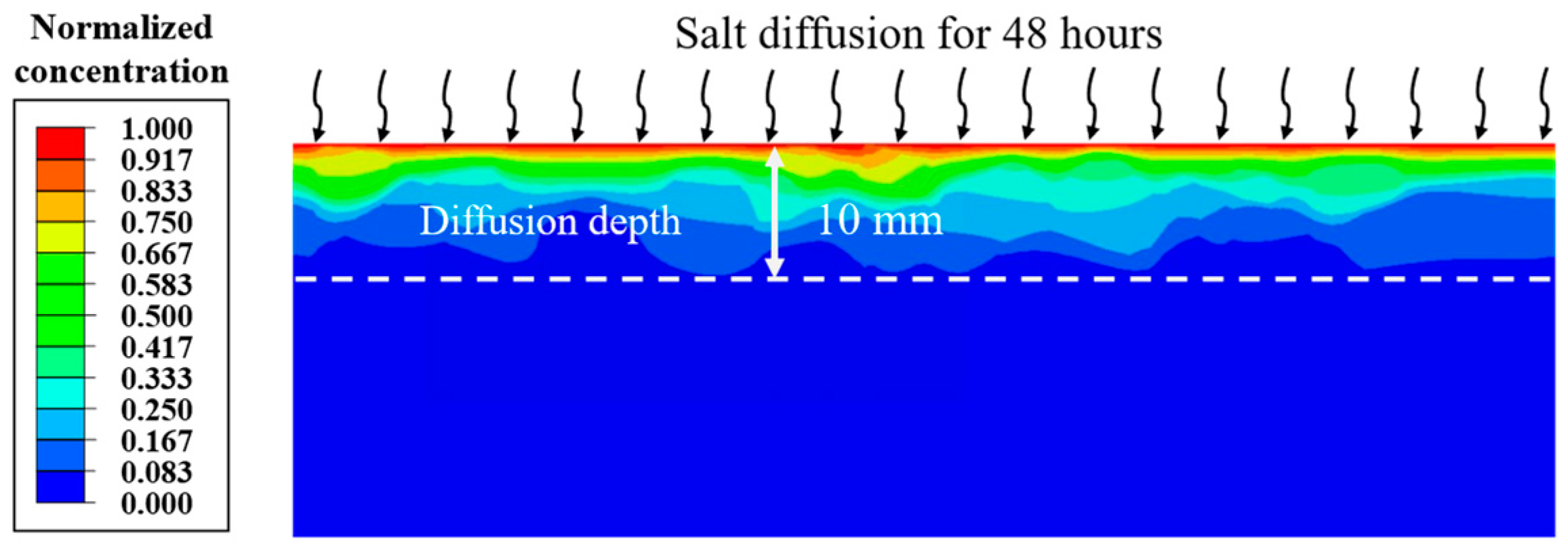
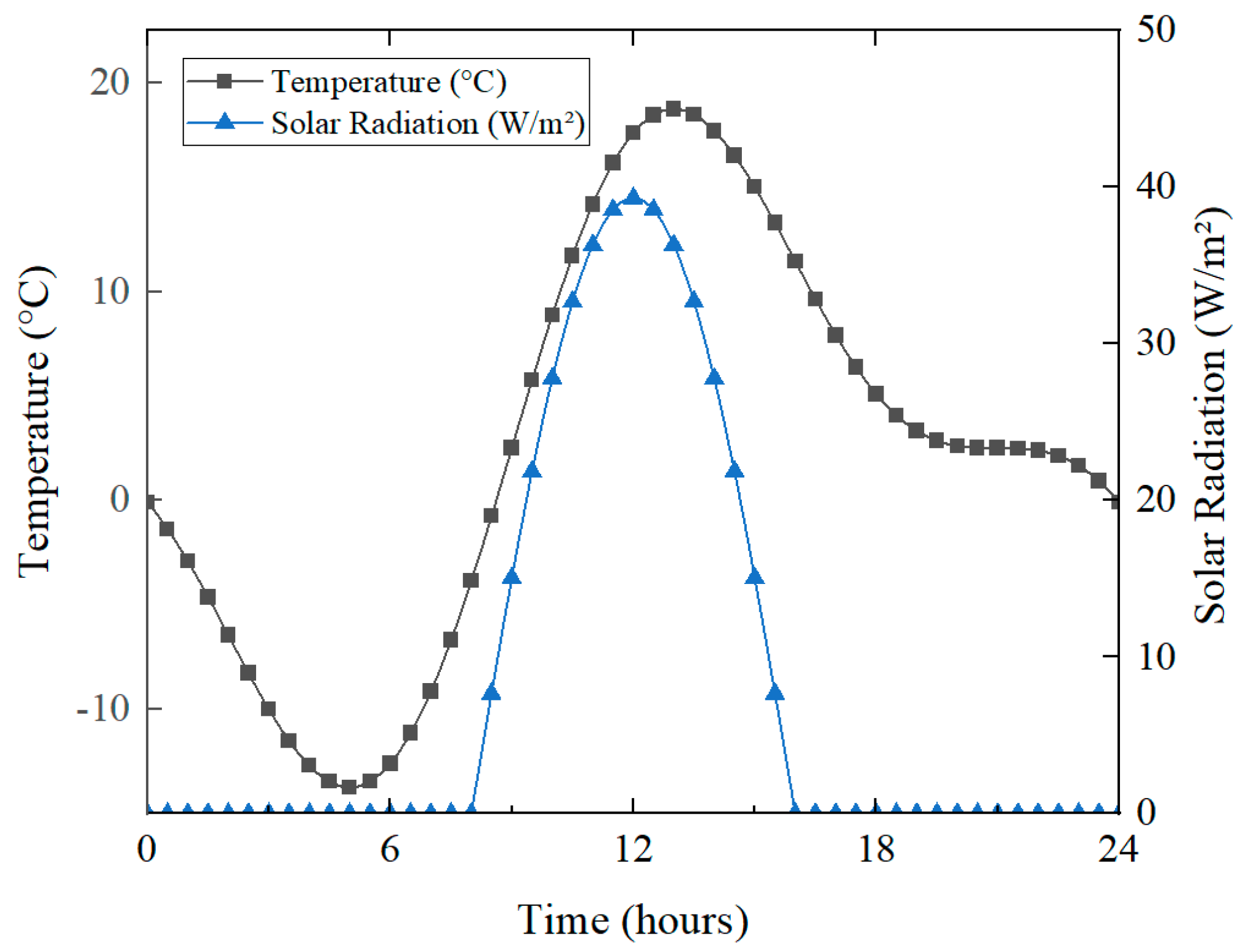
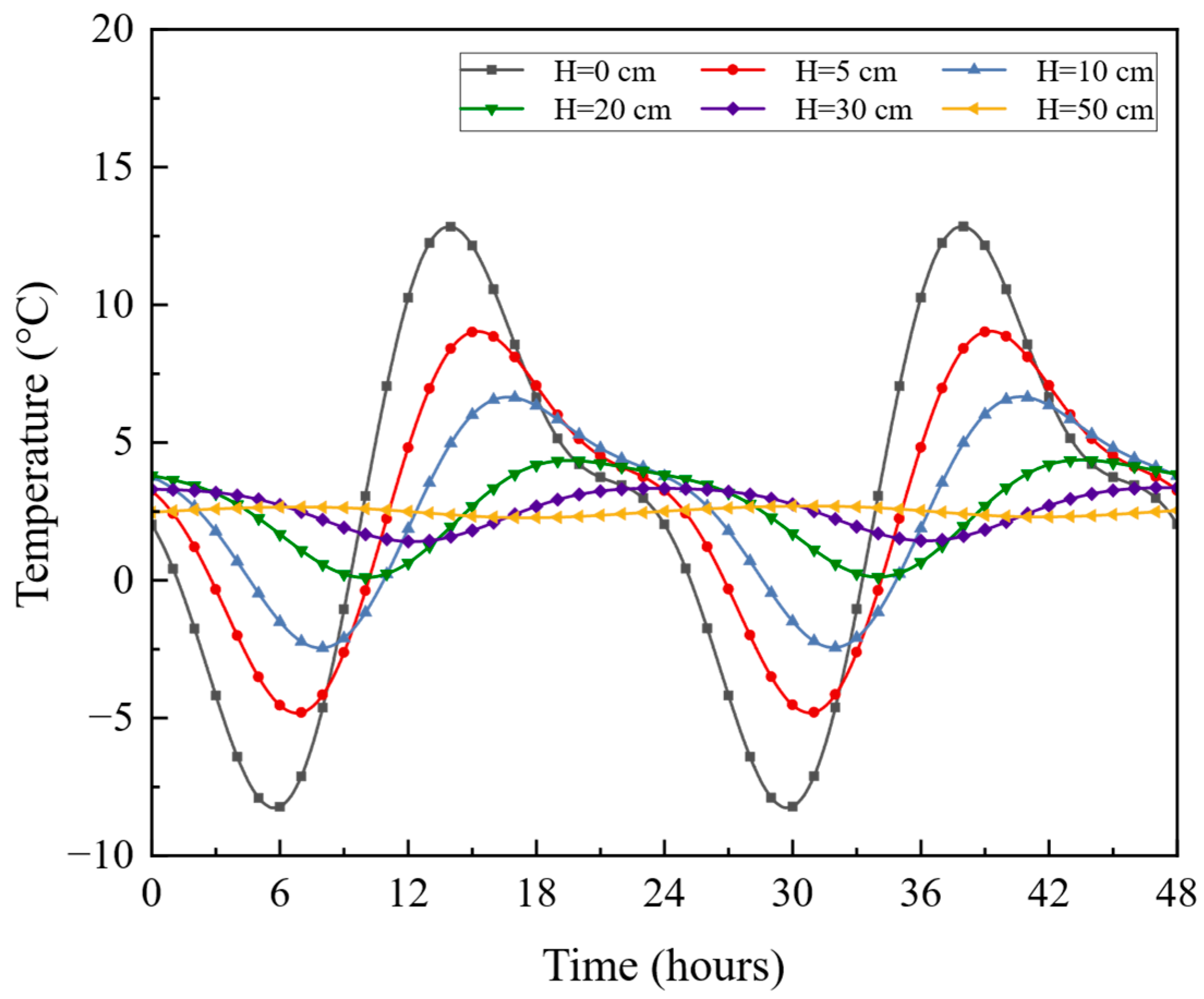
5.2. Analysis of Salt Diffusion and Temperature Field of Pavement
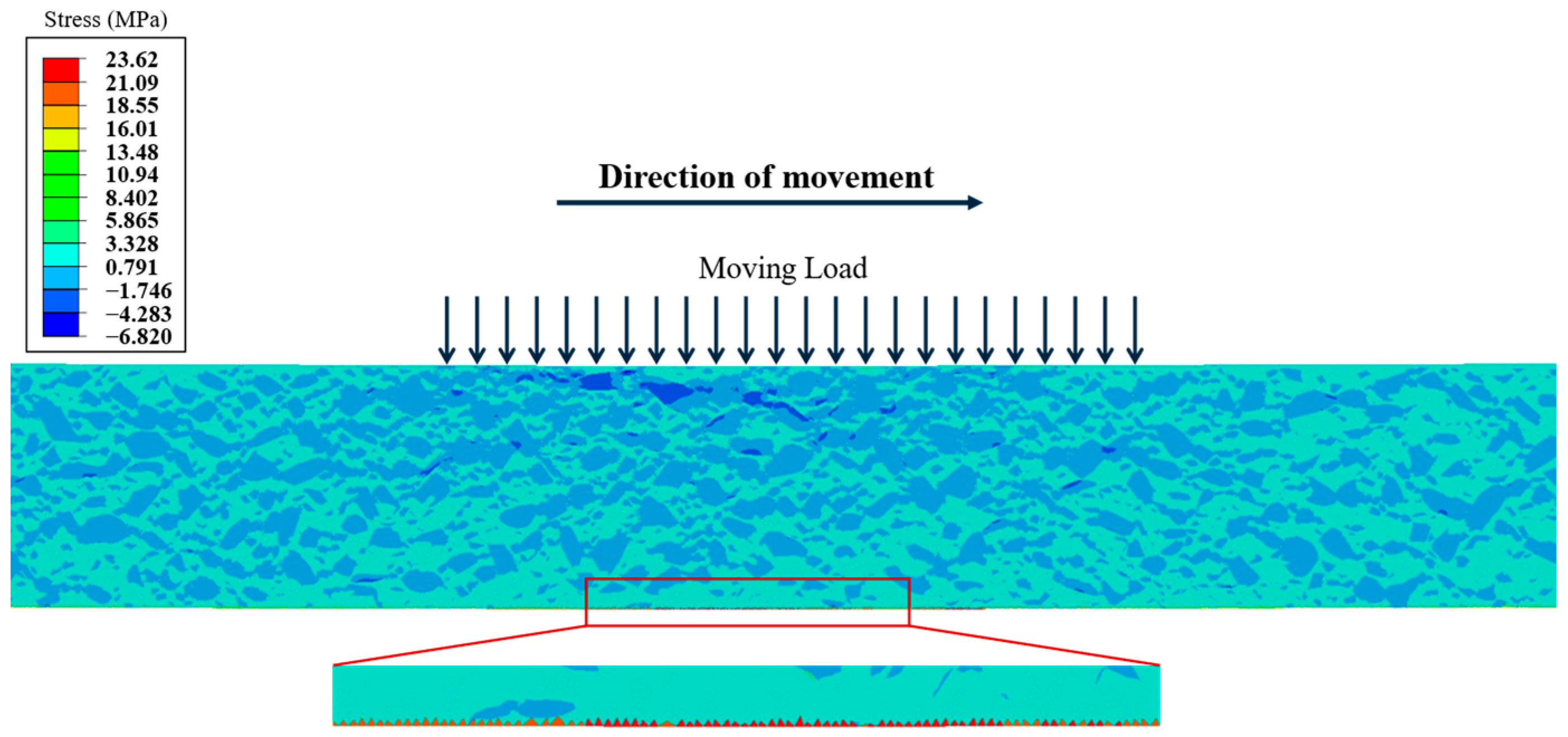
5.3. Responses to Coupled Salt–Thermal–Mechanical Effects
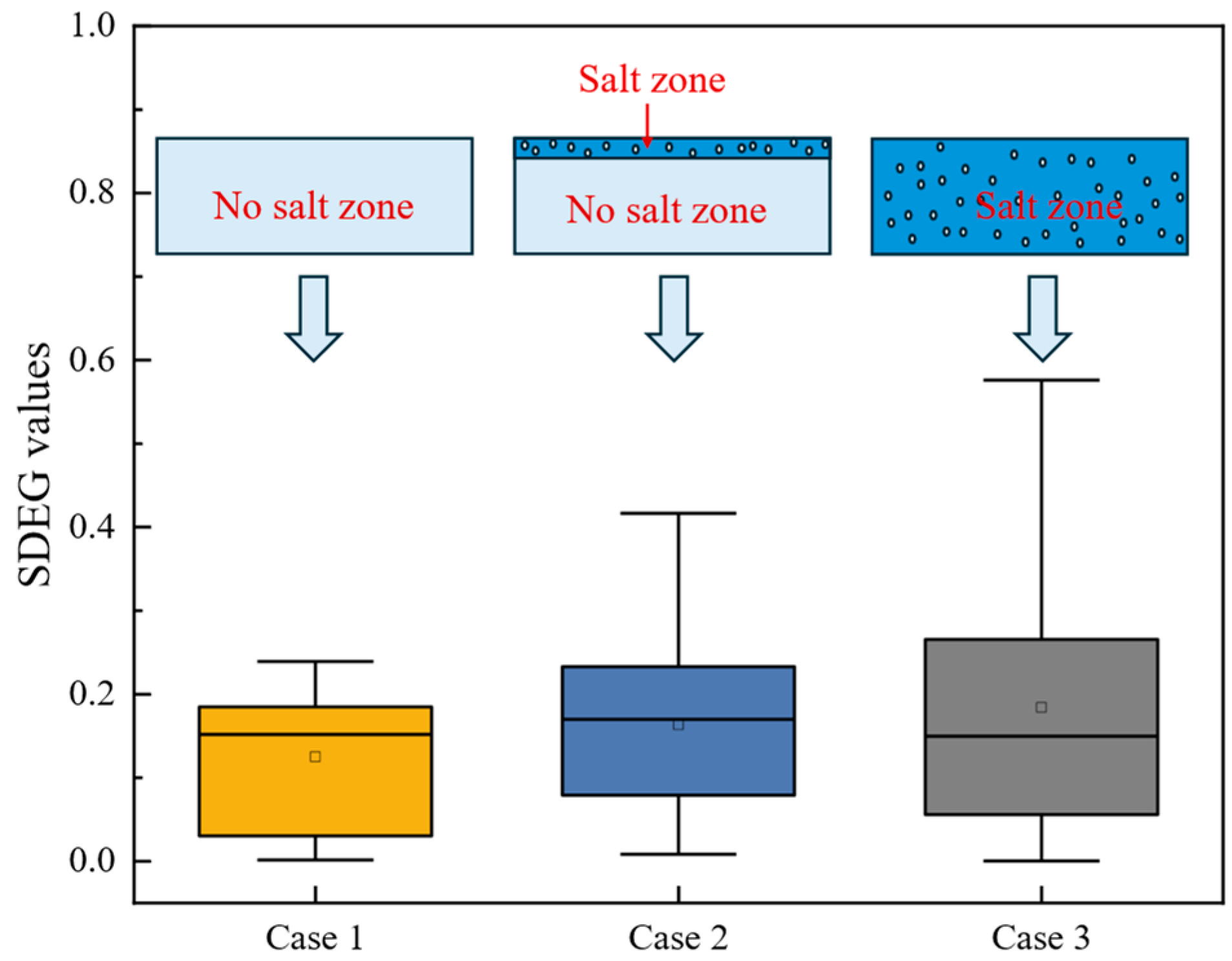
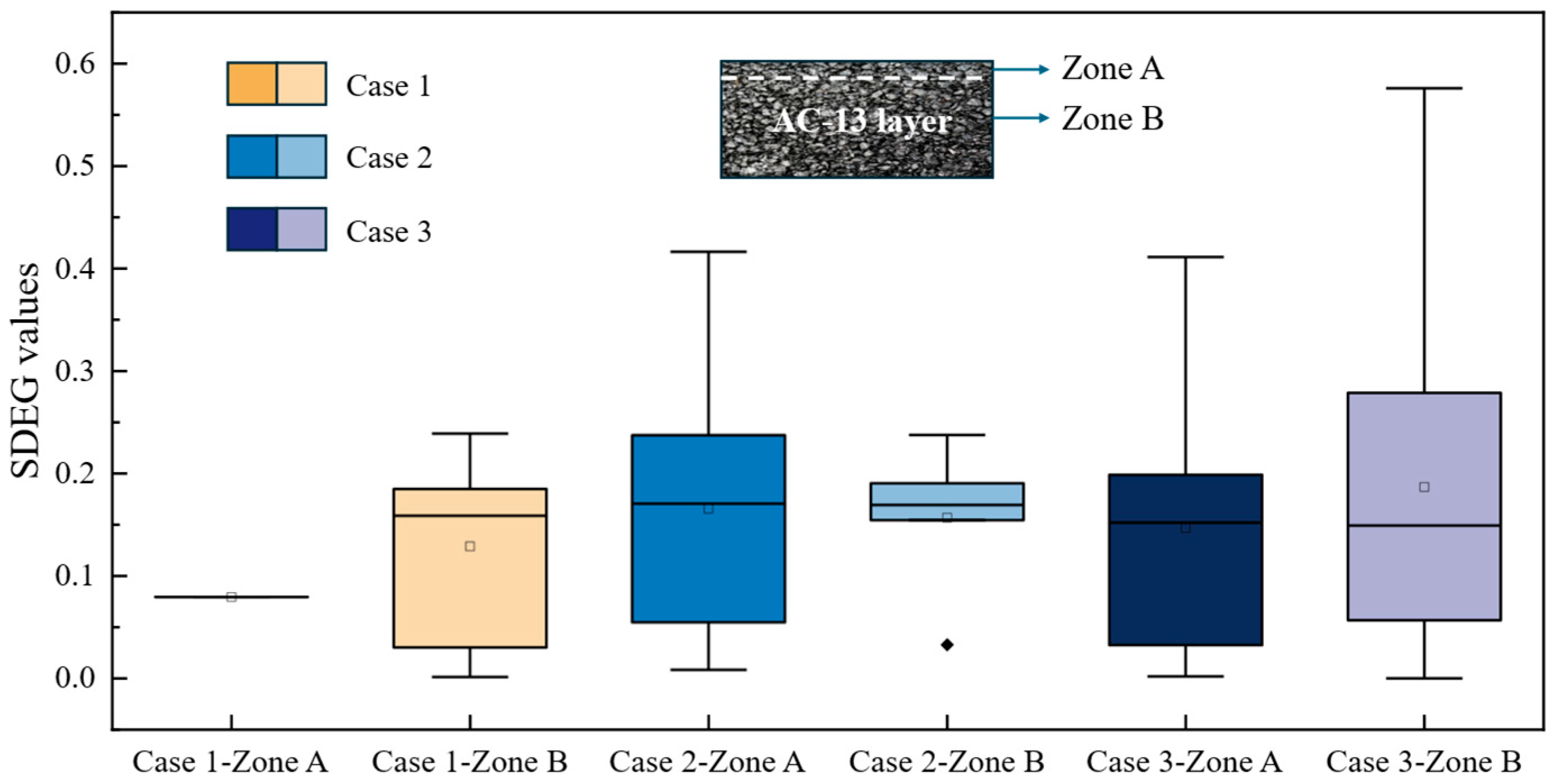
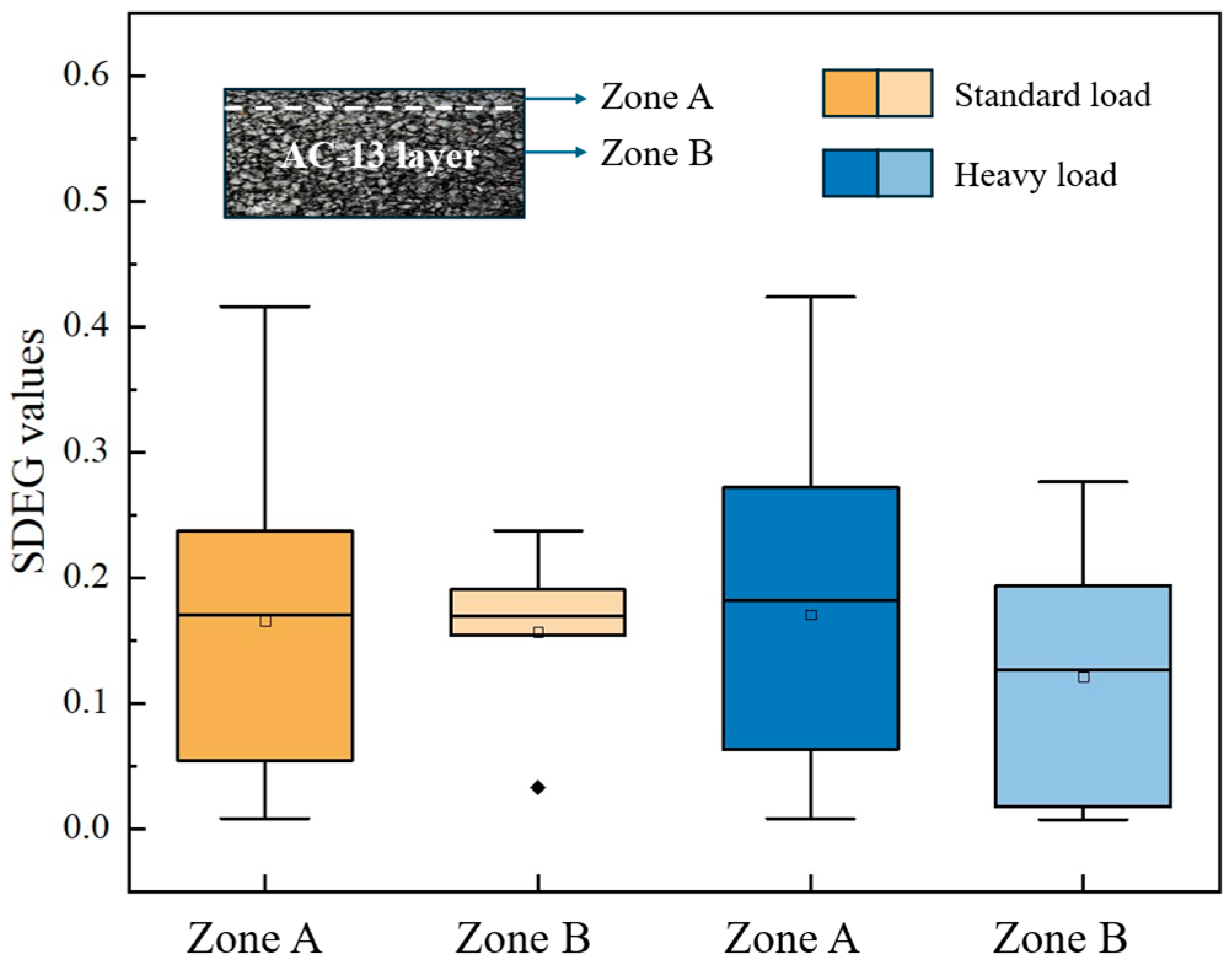
5.4. Effects of Salt
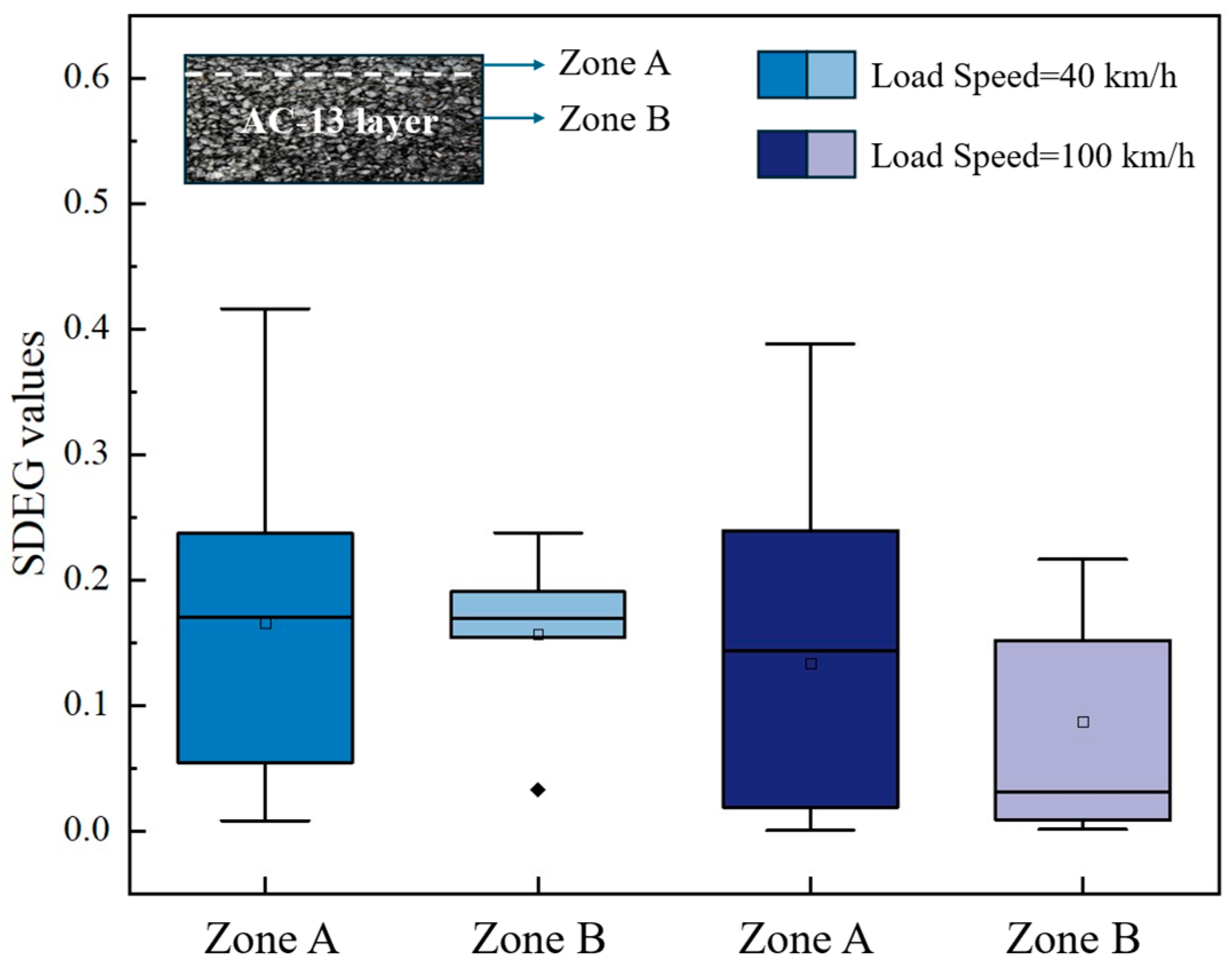
5.5. Effects of Moving Load
6. Conclusions
- (1)
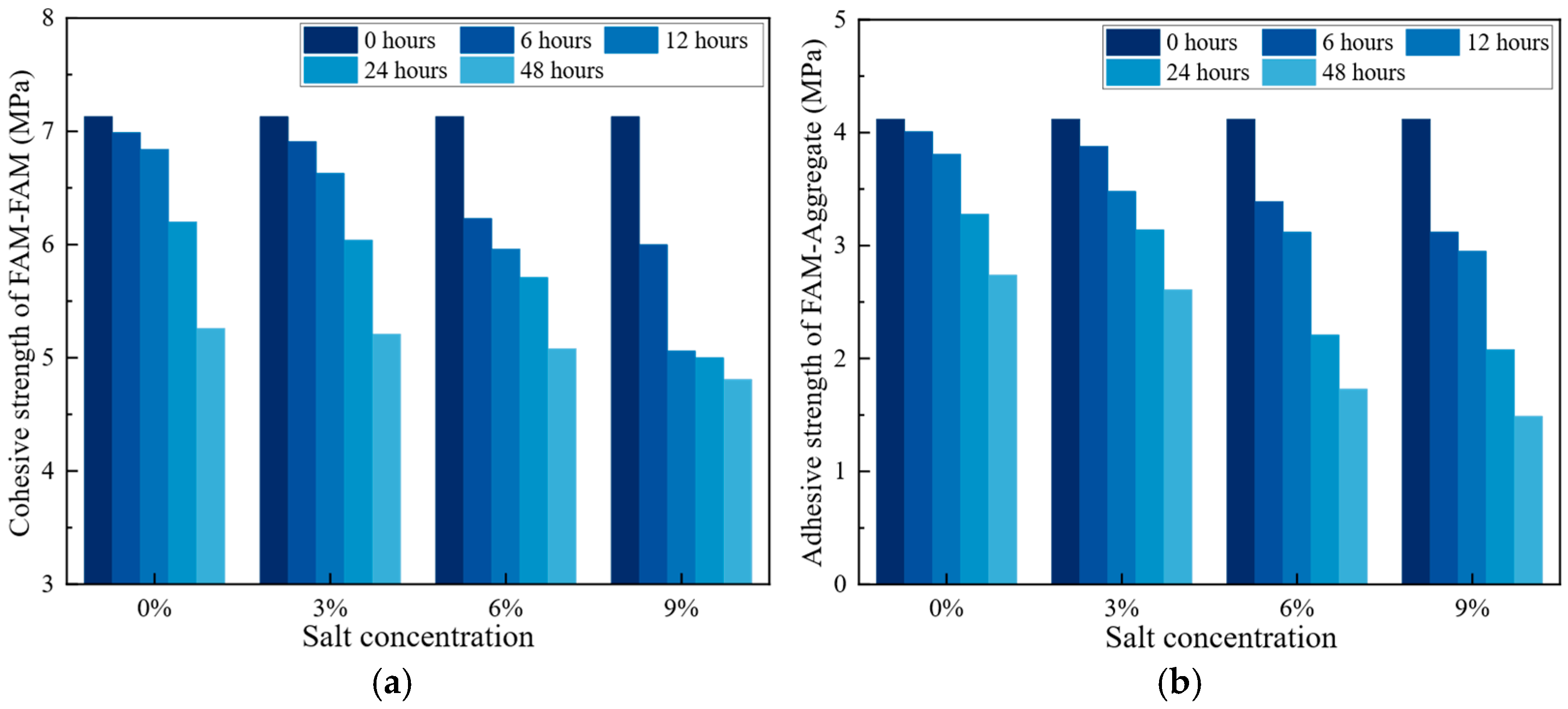
- According to the laboratory tests, at −10 °C, cohesive strength dropped by 26% to 32.5% and adhesive strength by 33.5% to 63.8% after 48 h. At 0 °C, cohesive strength decreased by 24.9% to 44.0% and adhesive strength by 37.9% to 71.6%. Additionally, fracture energy at 0 °C decreased by 4.2% to 13% compared to −10 °C.
- (2)
- Salt ions diffused approximately 10 mm into the pavement after 48 h. The non-uniform distribution of salt within the pavement structure was attributed to the different diffusion coefficients of the aggregate and the FAM.
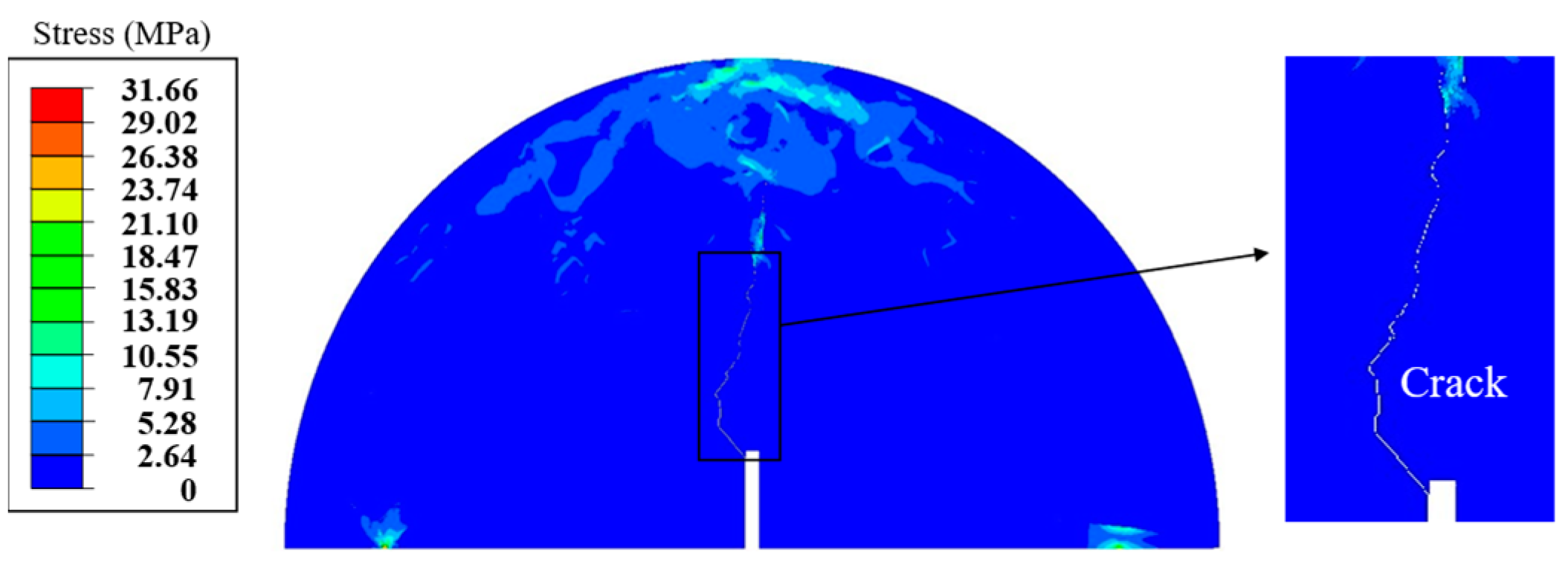
- (3)
- Maximum tensile stress occurred at the bottom of the asphalt layer, with compressive and tensile characteristics exhibited near the moving load’s path. Temperature-related stresses manifested in the surface area even without the moving load, primarily driven by thermal expansion and contraction due to environmental fluctuations.
- (4)
- The presence of salt significantly reduces the load-bearing capacity of the upper layer, resulting in greater damage to cohesive elements compared to the lower layer. Additionally, the detrimental effects of salt on material deterioration in the upper layer are more pronounced than those caused solely by the stresses from moving loads. It is recommended to implement measures to mitigate salt exposure on the upper layer of pavements.
- (5)
- Lower moving speeds lead to increased damage in cohesive elements due to longer stress application times and lower load frequencies, resulting in greater stress accumulation compared to higher speeds.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Leiva-Padilla, P.; Moreno-Navarro, F.; Iglesias, G.R.; Rubio-Gamez, M.C. Thermal characterisation of electroconductive layers for anti-icing and de-snowing applications on roads. Road Mater. Pavement Des. 2022, 23, 168–183. [Google Scholar] [CrossRef]
- Cui, Y.C.; Zhang, L.; Xing, C.; Tan, Y.Q. Anti-icing properties and application of superhydrophobic coatings on asphalt pavement. Constr. Build. Mater. 2024, 419, 135452. [Google Scholar] [CrossRef]
- Zhang, X.M.; Chen, H.; Hoff, I. The mutual effect and reaction mechanism of bitumen and de-icing salt solution. Constr. Build. Mater. 2021, 302, 124213. [Google Scholar] [CrossRef]
- Vega-Zamanillo, A.; Juli-Gándara, L.; Calzada-Pérez, M.A.; Teijón-López-Zuazo, E. Impact of temperature changes and freeze-thaw cycles on the behaviour of asphalt concrete submerged in water with sodium chloride. Appl. Sci. 2020, 10, 1241. [Google Scholar] [CrossRef]
- Wu, Z.M.; Shi, C.J.; Gao, P.W.; Zhang, H.L.; Hu, X. Moisture susceptibility of asphalt mixture subjected to chloride-based deicing salt solutions under simulated environmental conditions. J. Mater. Civ. Eng. 2023, 35, 158718. [Google Scholar] [CrossRef]
- Zhang, K.; Luo, Y.F.; Xie, W.; Wu, J.J. Evaluation of road performance and adhesive characteristic of asphalt binder in salt erosion environment. Mater. Today Commun. 2020, 25, 101593. [Google Scholar] [CrossRef]
- Long, Z.W.; You, L.Y.; Xu, F.; Tang, X.Q.; Ding, Y.H.; Khanal, A.; Miao, Y. Nanomechanical-atomistic insights on interface interactions in asphalt mixtures with various chloride ion erosion statuses. J. Colloid Interface Sci. 2022, 628, 891–909. [Google Scholar] [CrossRef]
- Long, Z.; Guo, N.; Xiao, Y.; You, L.; Xu, F.; Liu, Y.; Tang, X.; Ding, Y. Nanomechanical experiments and molecular dynamics explorations for the deterioration evolution of asphalt driven by chloride salt erosion. J. Mater. Civ. Eng. 2023, 35, 04023382. [Google Scholar] [CrossRef]
- Tang, Y.; Fu, Z.; Hou, Y.; Ma, F.; Wang, W.; Zhang, T.; Yang, P.; Zhao, P. Salt damage on asphalt surfaces under repeated dissolution at molecular scale. Colloids Surf. A-Physicochem. Eng. Asp. 2024, 690, 133829. [Google Scholar] [CrossRef]
- Hamedi, G.H.; Harehdasht, S.L.; Talebi, H. Assessing low-temperature cracking in asphalt mixtures through mix design and thermodynamic parameters. J. Mater. Civ. Eng. 2024, 36, 04024169. [Google Scholar] [CrossRef]
- Krami, K.; Benamara, A.; Radouani, M.; Ettayeb, M. Evaluation of water sensitivity and the impact of thermal cycles on asphalt mixtures with different aggregates and hydrated lime as additive: Experimental study. Case Stud. Constr. Mater. 2024, 20, 145–152. [Google Scholar] [CrossRef]
- Chen, J.Q.; Wang, J.; Shi, Z.; Zhang, Z.; Dan, H.C. Computational fracture analysis of steel slag asphalt mixture subjected to moisture damage. Constr. Build. Mater. 2024, 433, 136697. [Google Scholar] [CrossRef]
- Sobieski, T.; Arámbula-Mercado, E.; Martin, A.E. A method for characterising RAP degree of binder activity. Road Mater. Pavement Des. 2022, 23, 2250–2270. [Google Scholar] [CrossRef]
- Liang, Y.H.; Chen, J.Q.; Li, L. Computational evaluation of the fracture behavior of porous asphalt concrete exposed to moisture and salt erosion. Materials 2024, 17, 1505. [Google Scholar] [CrossRef]
- Wang, L.; Wang, W.; Guan, H.F.; Li, Y.X.; Pei, K.; Chen, B.Y.S. Effect of salt freeze-thaw cycle on crack resistance of steel slag rubber powder modified asphalt mixture. J. Mater. Civ. Eng. 2024, 36, 04023612. [Google Scholar] [CrossRef]
- Xiong, R.; Chu, C.; Qiao, N.; Wang, L.; Yang, F.; Sheng, Y.; Guan, B.; Niu, D.; Geng, J.; Chen, H. Performance evaluation of asphalt mixture exposed to dynamic water and chlorine salt erosion. Constr. Build. Mater. 2019, 201, 121–126. [Google Scholar] [CrossRef]
- Chen, J.Q.; Wu, Q.L.; Wang, H.; Quan, Z.Q.; Dan, H.C. Modeling and analysis of ice condensation on bridge deck pavement surface based on heat transfer theory and finite element method. Appl. Therm. Eng. 2024, 241, 122344. [Google Scholar] [CrossRef]
- Li, Z.; Han, D.; Chen, H.; Zhao, Y. Simulation analysis and optimization of temperature field for hot in-place asphalt pavement recycling. J. Transp. Eng. Part B-Pavements 2023, 149, 04023009. [Google Scholar] [CrossRef]
- Liu, G.; Qian, Z.D.; Wu, X.Y.; Chen, L.L.; Liu, Y. Investigation on the compaction process of steel bridge deck pavement based on DEM-FEM coupling model. Int. J. Pavement Eng. 2023, 24, 2169443. [Google Scholar] [CrossRef]
- Chen, J.Q.; Sun, C.Q.; Sun, X.; Dan, H.C.; Huang, X.Y. Finite difference model for predicting road surface ice formation based on heat transfer and phase transition theory. Cold Reg. Sci. Technol. 2023, 207, 103772. [Google Scholar] [CrossRef]
- Chen, J.Q.; Wang, H.; Xie, P.Y. Pavement temperature prediction: Theoretical models and critical affecting factors. Appl. Therm. Eng. 2019, 158, 113755. [Google Scholar] [CrossRef]
- Dan, H.C.; Zhang, Z.; Chen, J.Q.; Wang, H. Numerical simulation of an indirect tensile test for asphalt mixtures using discrete element method software. J. Mater. Civ. Eng. 2018, 30, 6–10. [Google Scholar] [CrossRef]
- Dan, H.C.; Gao, L.S.; Wang, H.; Tang, J. Discrete-element modeling of mean texture depth and wearing behavior of asphalt mixture. J. Mater. Civ. Eng. 2022, 34, 04022027. [Google Scholar] [CrossRef]
- Niazi, S.; Najmeddine, A.; Shakiba, M. A coupled thermo-hydro-mechanical framework for simulating the failure response of asphalt concrete under freezing conditions. Cold Reg. Sci. Technol. 2024, 218, 104073. [Google Scholar] [CrossRef]
- Xu, J.P.; Zheng, C.F.; Song, Z.F.; Zhou, S.; Chen, W.X. Mesodamage mechanism of asphalt mixtures with different structural types under frost heaving of ice crystals. J. Mater. Civ. Eng. 2023, 35, 04022377. [Google Scholar] [CrossRef]
- Sun, Y.R.; Zhang, Z.; Gong, H.R.; Zhou, C.J.; Chen, J.Y.; Huang, B.S. 3D Multiscale modeling of asphalt pavement responses under coupled temperature-stress fields. J. Eng. Mech. 2022, 148, 04022010. [Google Scholar] [CrossRef]
- Yu, S.J.; Wang, H.; Chen, J.Q. Ravelling susceptibility of porous asphalt pavement in salt environments using multi-scale modelling analysis. Int. J. Pavement Eng. 2025, 26, 2467222. [Google Scholar] [CrossRef]
- Qiu, X.; Deng, J.; Fu, Q.; Lou, Y.; Ye, Y.; Zhang, D. Investigation of chloride salt erosion on asphalt binders and mixtures: Performance evaluation and correlation analysis. Materials 2025, 18, 156. [Google Scholar] [CrossRef]
- Manrique-Sanchez, L.; Caro, S.; Arámbula-Mercado, E. Numerical modelling of ravelling in porous friction courses (PFC). Road Mater. Pavement Des. 2018, 19, 668–689. [Google Scholar] [CrossRef]
- Chen, S.; Yin, D.; Gao, Y.; Zhang, Y.; Ma, T.; Chen, C. Damage behavior of porous asphalt concrete under load–pore pressure effects. J. Mater. Civ. Eng. 2024, 36, 04024041. [Google Scholar] [CrossRef]
- Wang, H.; Wang, J.; Chen, J.Q. Fracture simulation of asphalt concrete with randomly generated aggregate microstructure. Road Mater. Pavement Des. 2018, 19, 1674–1691. [Google Scholar] [CrossRef]
- Xu, Y.Z.; Zheng, C.F.; Feng, Y.P.; Guo, X.D. Low-temperature cohesive and adhesive strength testing of contact surface between bitumen and mineral aggregates by image analysis. Constr. Build. Mater. 2018, 183, 95–101. [Google Scholar] [CrossRef]
- Yee, T.S.; Hamzah, M.O.; Van den Bergh, W. Evaluation of moisture susceptibility of asphalt-aggregate constituents subjected to direct tensile test using imaging technique. Constr. Build. Mater. 2019, 227, 116642. [Google Scholar] [CrossRef]
- Zhang, K.; Luo, Y.; Li, Z.; Zhao, Y.; Zhao, Y. Evaluation of performance deterioration characteristics of asphalt mixture in corrosion environment formed by snow-melting agents. J. Mater. Civ. Eng. 2022, 34, 101593. [Google Scholar] [CrossRef]
- TP105 A; Standard Method of Test for Determining the Fracture Energy of Asphalt Mixtures Using the Semicircular Bend Geometry (SCB). AASHTO: Washington, DC, USA, 2013.
- Pirmohammad, S.; Abdi, M.; Ayatollahi, M.R. Effect of support type on the fracture toughness and energy of asphalt concrete at different temperature conditions. Eng. Fract. Mech. 2021, 254, 107921. [Google Scholar] [CrossRef]
- Kim, K.W.; El Hussein, M. Variation of fracture toughness of asphalt concrete under low temperatures. Constr. Build. Mater. 1997, 11, 403–411. [Google Scholar] [CrossRef]
- Chen, J.; Yu, S.; Huang, W. Two-dimensional microstructure-based model for evaluating the permeability coefficient of heterogeneous construction materials. Materials 2023, 16, 5892. [Google Scholar] [CrossRef]
- Chen, J.Q.; Ouyang, X.; Sun, X. Numerical investigation of asphalt concrete fracture based on heterogeneous structure and cohesive zone model. Appl. Sci. 2022, 12, 11150. [Google Scholar] [CrossRef]
- Teng, G.C.; Zheng, C.F.; Chen, X.Y.; Lan, X.L.; Zhu, Y.M.; Shan, C. Numerical fracture investigation of single-edge notched asphalt concrete beam based on random heterogeneous FEM model. Constr. Build. Mater. 2021, 304, 124581. [Google Scholar] [CrossRef]
- Du, C.; Sun, Y.; Chen, J.; Zhou, C.; Liu, P.; Wang, D.; Oeser, M. Coupled thermomechanical damage behavior analysis of asphalt pavements using a 2d mesostructure-based finite-element method. J. Transp. Eng. Part B-Pavements 2021, 147, 04021012. [Google Scholar] [CrossRef]
- Guo, Q.; Liu, Q.; Zhang, P.; Gao, Y.; Jiao, Y.; Yang, H.; Xu, A. Temperature and pressure dependent behaviors of moisture diffusion in dense asphalt mixture. Constr. Build. Mater. 2020, 246, 118500. [Google Scholar] [CrossRef]





| Type of Tests | Salt Concentration | Temperature | Immersion Duration | Sample Number | |
|---|---|---|---|---|---|
| Pull-off test (FAM) | 0, 3, 6, 9% | −10, 0 °C | 0, 12, 24, 36, 48 h | 120 | |
| SCB test | FAM | 0, 3, 6, 9% | −10, 0 °C | 0, 12, 24, 36, 48 h | 120 |
| Asphalt concrete | 0, 3, 6, 9% | −10, 0 °C | 0, 48 h | 48 | |
| Sieve Size (mm) | 16 | 13.2 | 9.5 | 4.75 | 2.36 | 1.18 | 0.6 | 0.3 | 0.15 | 0.075 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Passing percentage (%) | Asphalt concrete | 100 | 94.7 | 75.3 | 57.7 | 37.6 | 25.2 | 15.7 | 9.3 | 6.7 | 5.0 |
| FAM | 100 | 100 | 100 | 100 | 100 | 67.0 | 41.9 | 24.8 | 17.7 | 13.3 | |
| Type of Material | Elastic Modulus (MPa) | Poisson’s Ratio |
|---|---|---|
| Aggregate | 80,000 | 0.20 |
| FAM | 805 | 0.25 |
| CZM | 805 | 0.25 |
| Temperature (°C) | i | Relaxation Time, ρi (s) | Relaxation Strength, Ei (MPa) FAM | Relaxation Strength, Ei (MPa) Asphalt Concrete | T0 (°C) | C1 | C2 |
|---|---|---|---|---|---|---|---|
| 20 | 1 | 1 × 10−7 | 5218.14 | 2240.85 | 20 (FAM) | 25.4 (FAM) | 233.2 (FAM) |
| 2 | 1 × 10−6 | 5381.72 | 3212.28 | 20 (AC) | 25.7 (AC) | 218.9 (AC) | |
| 3 | 1 × 10−5 | 5499.81 | 3913.62 | - | - | - | |
| 4 | 1 × 10−4 | 5570.35 | 4897.11 | - | - | - | |
| 5 | 1 × 10−3 | 5112.13 | 5645.90 | - | - | - | |
| 6 | 1 × 10−2 | 3608.49 | 5520.75 | - | - | - | |
| 7 | 1 × 10−1 | 1489.17 | 3509.47 | - | - | - | |
| 8 | 1 × 100 | 512.63 | 1405.91 | - | - | - | |
| 9 | 1 × 101 | 154.93 | 531.44 | - | - | - | |
| 10 | 1 × 102 | 55.72 | 171.11 | - | - | - | |
| 11 | 1 × 103 | 13.97 | 68.48 | - | - | - | |
| 12 | 1 × 104 | 6.79 | 18.48 | - | - | - | |
| Equilibrium modulus, Ee | - | - | 34.20 | 197.25 | - | - | - |
| Material | Young’s Modulus (MPa) | Poisson’s Ratio | Coefficient of Thermal Expansion (10−5/°C) | Thermal Conductivity [(J/m·h·°C)] | Specific Heat [(J/kg·°C)] | Density (kg/m3) |
|---|---|---|---|---|---|---|
| Aggregate | 80,000 | 0.20 | 1.20 | 5472 | 920 | 2600 |
| FAM | 805 | 0.25 | 10.52 | 4680 | 923 | 2200 |
| AC-13 | 3592 | 0.35 | 2.19 | 5112 | 916 | 2340 |
| Base layer | 200 | 0.35 | 2.00 | 5616 | 912 | 2200 |
| Subgrade | 70 | 0.40 | 2.00 | 5616 | 1040 | 1800 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Chen, J.; Tang, M.; Liu, Y. Multi-Scale Modeling and Damage Mechanisms of Asphalt Pavements Under Coupled Salt–Thermal–Mechanical Effects. Materials 2025, 18, 2337. https://doi.org/10.3390/ma18102337
Ma J, Chen J, Tang M, Liu Y. Multi-Scale Modeling and Damage Mechanisms of Asphalt Pavements Under Coupled Salt–Thermal–Mechanical Effects. Materials. 2025; 18(10):2337. https://doi.org/10.3390/ma18102337
Chicago/Turabian StyleMa, Jin, Jiaqi Chen, Mingfeng Tang, and Yu Liu. 2025. "Multi-Scale Modeling and Damage Mechanisms of Asphalt Pavements Under Coupled Salt–Thermal–Mechanical Effects" Materials 18, no. 10: 2337. https://doi.org/10.3390/ma18102337
APA StyleMa, J., Chen, J., Tang, M., & Liu, Y. (2025). Multi-Scale Modeling and Damage Mechanisms of Asphalt Pavements Under Coupled Salt–Thermal–Mechanical Effects. Materials, 18(10), 2337. https://doi.org/10.3390/ma18102337







