Strain-Induced Modifications of Thin Film Silicon Membranes Through Physical Bending
Abstract
1. Introduction
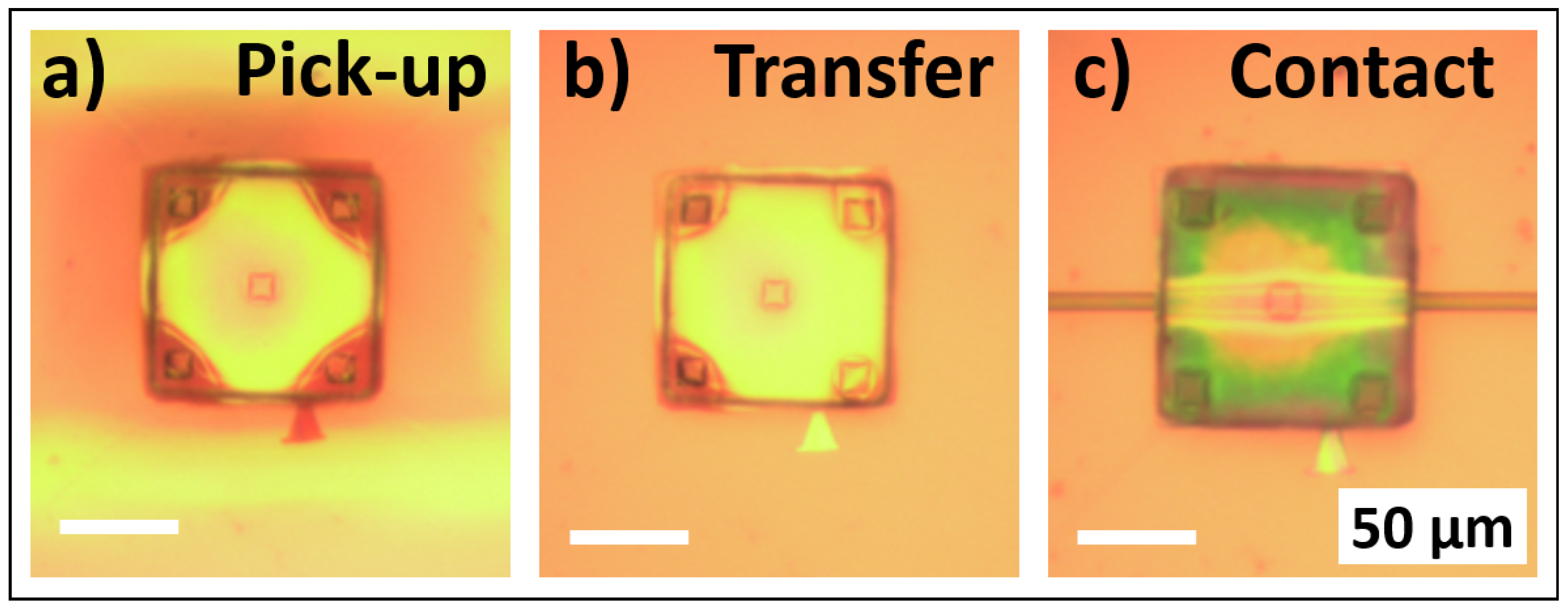
2. Transfer Printing of Silicon Membranes
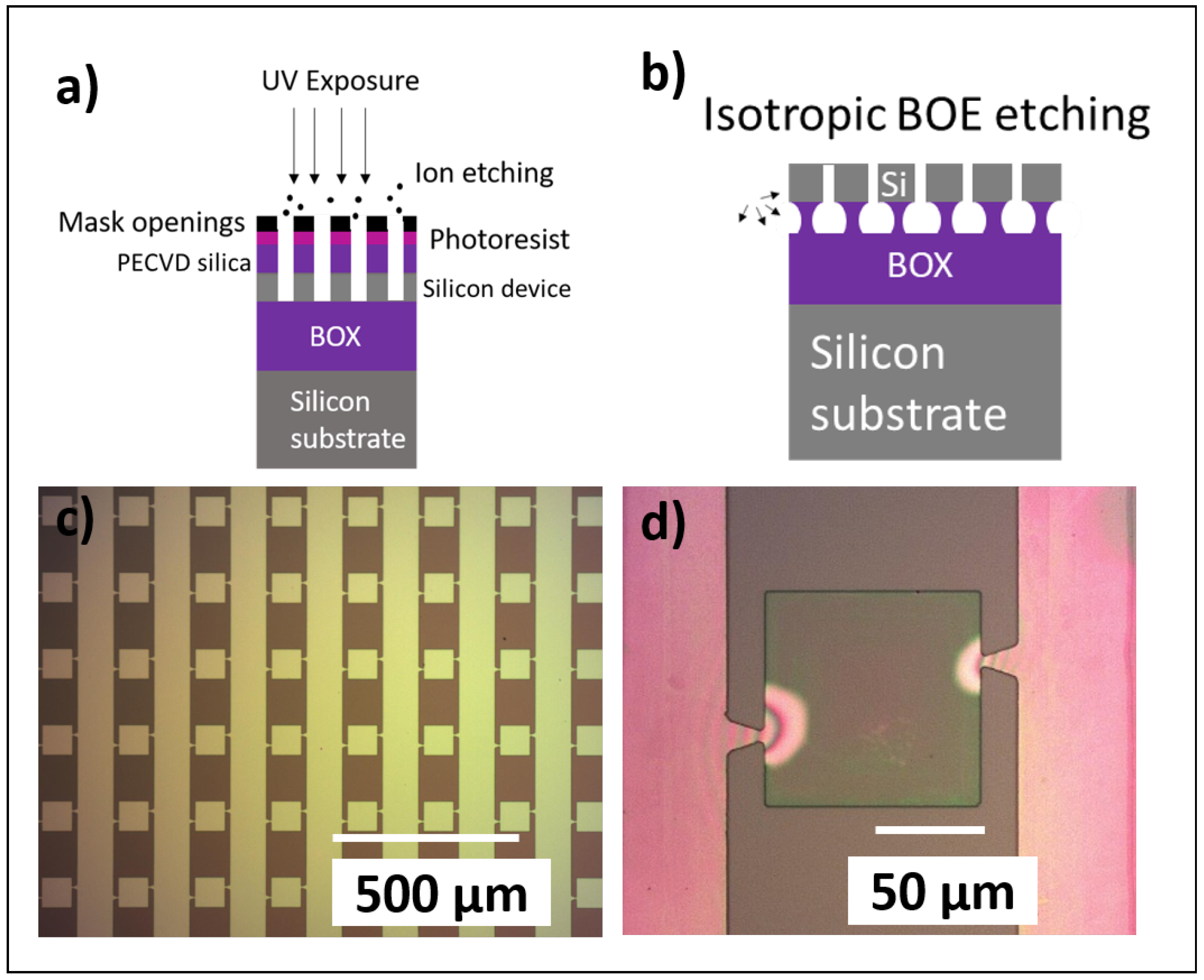
2.1. Fabrication Processes
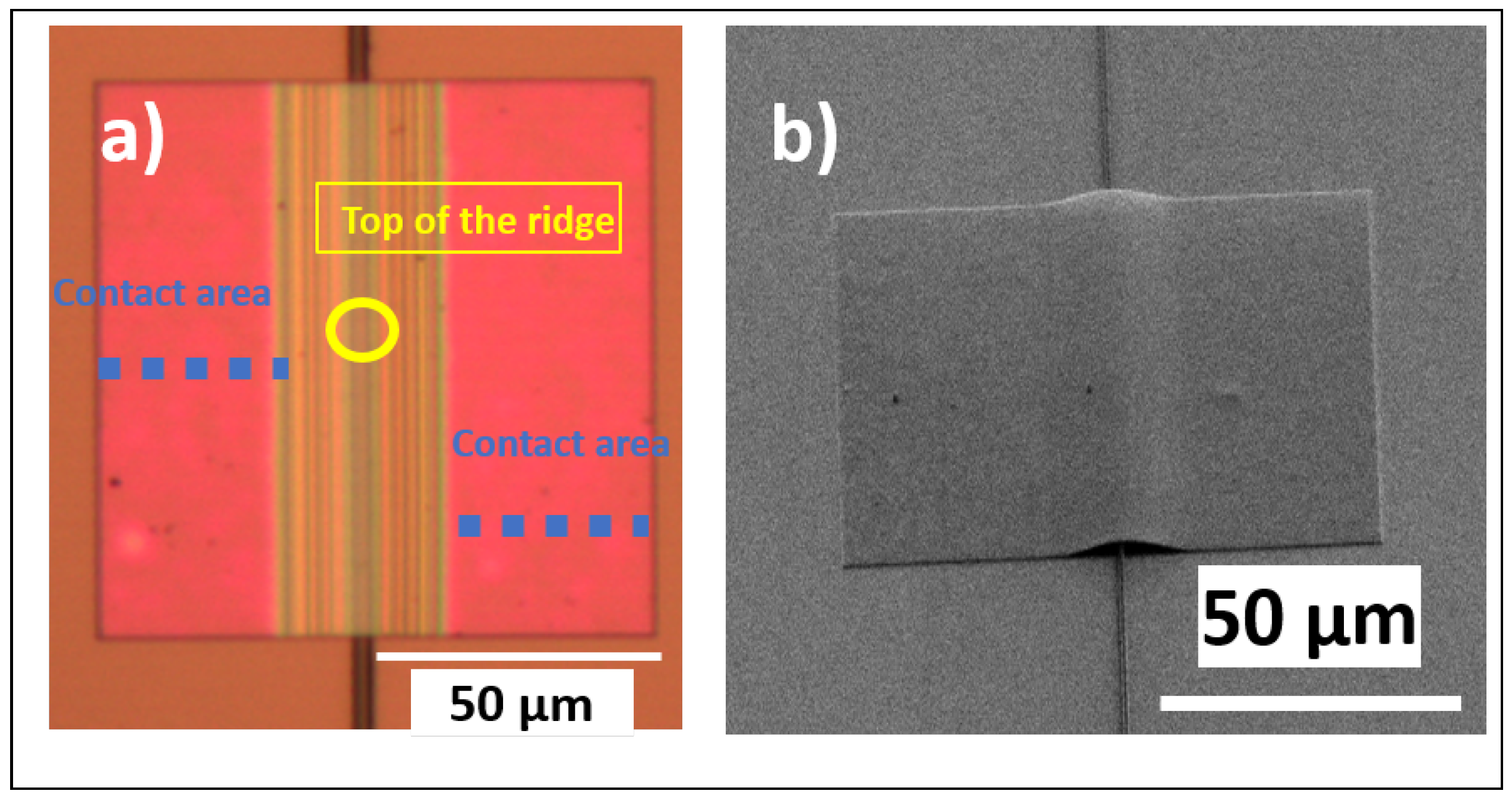
2.2. Printed Membrane Optical Analysis
3. Theoretical Analysis of Membranes’ Mechanical Deformation
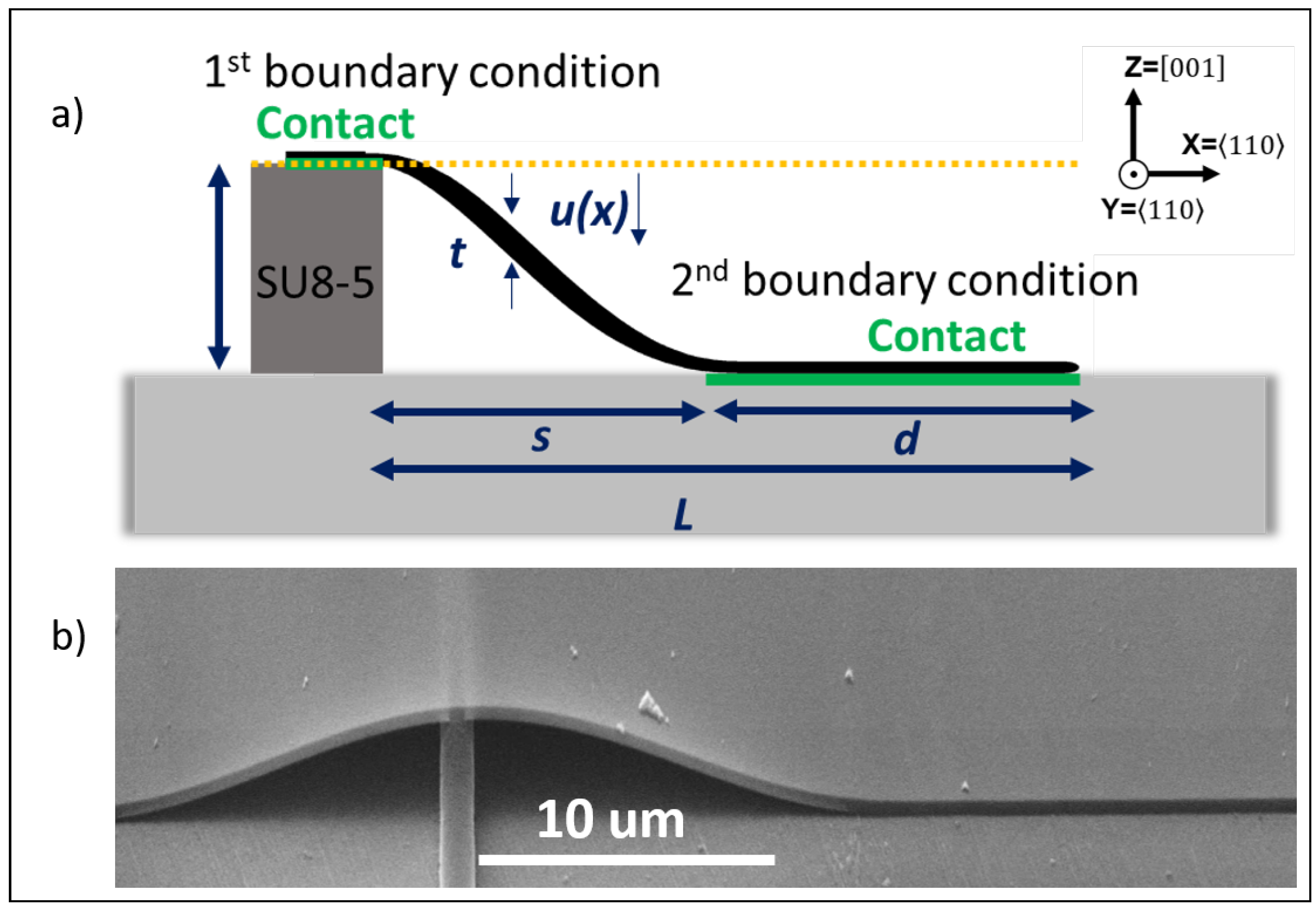
3.1. Analytical Analysis
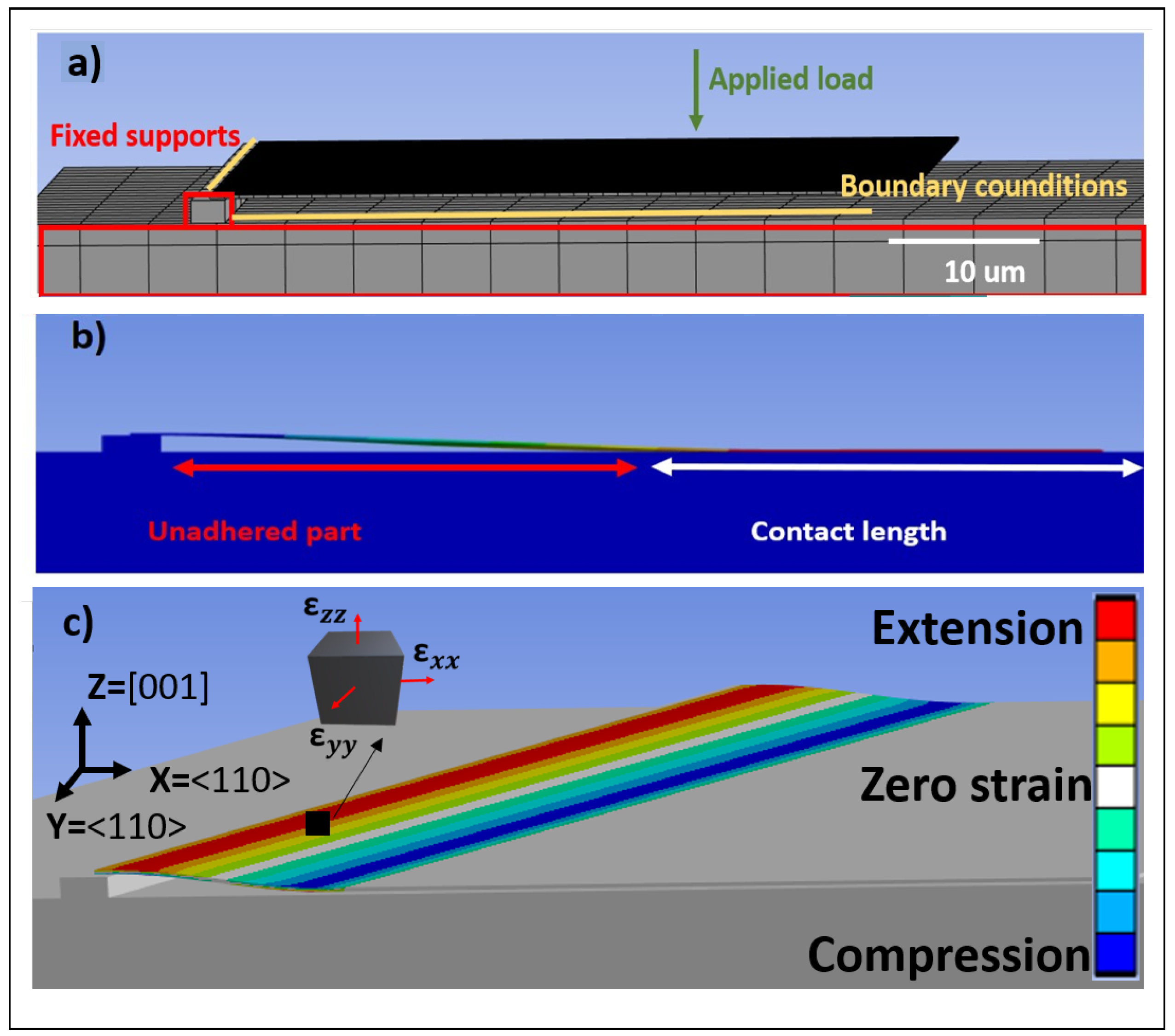
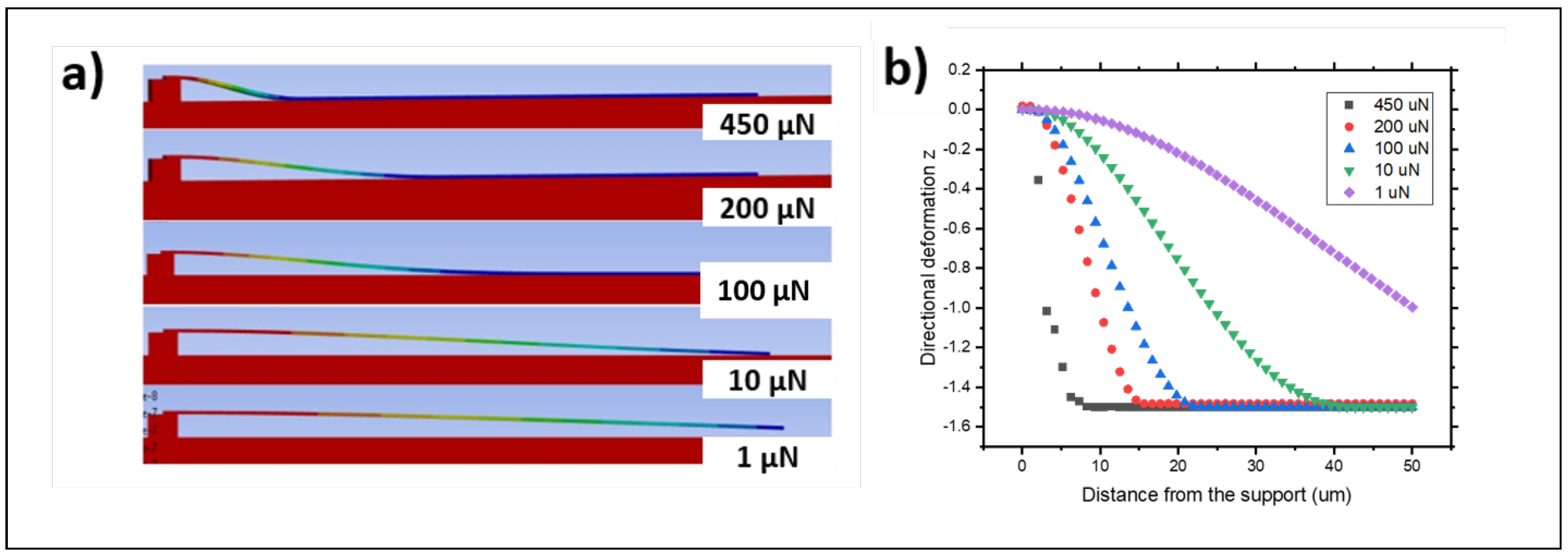
3.2. Finite Element Analysis
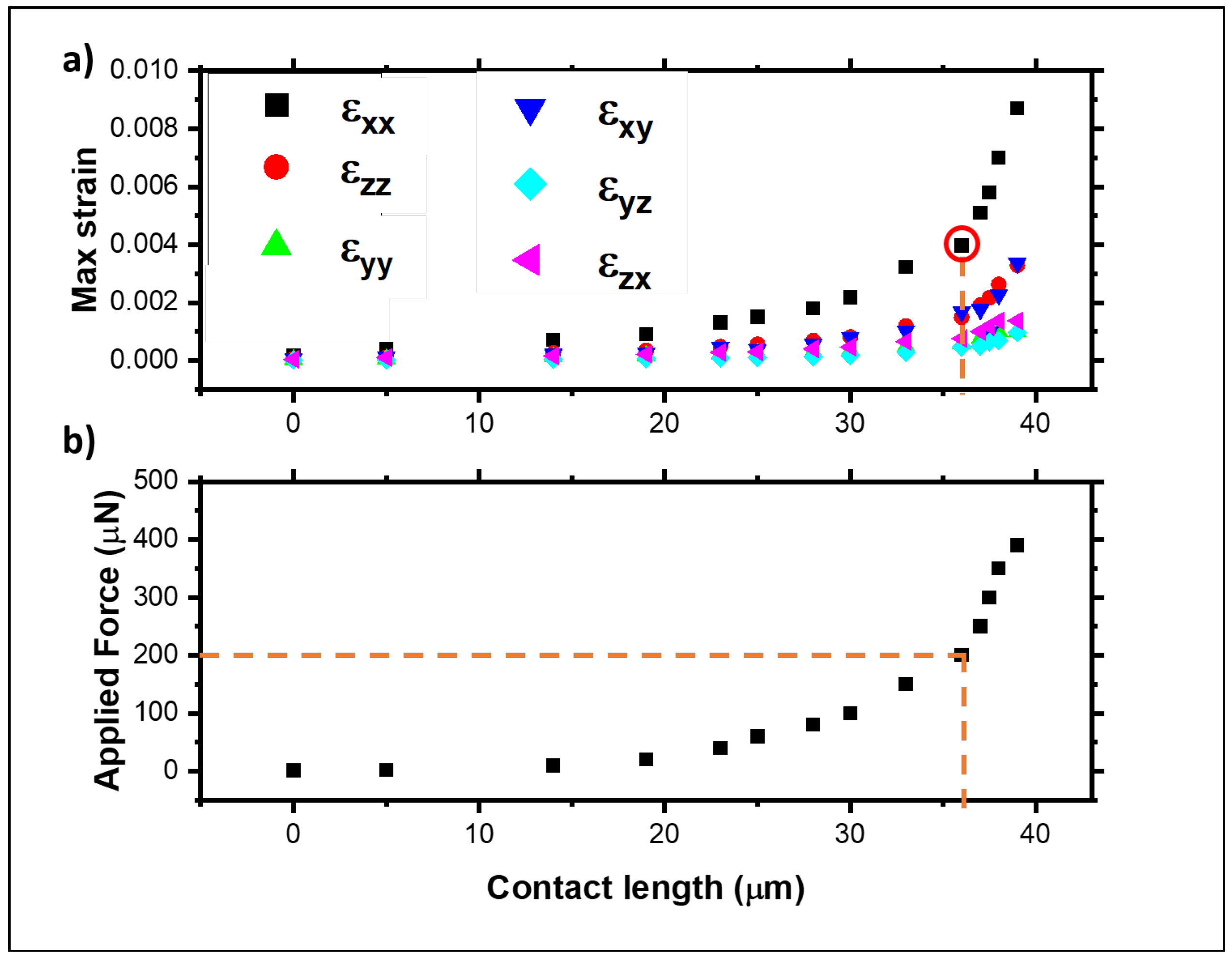
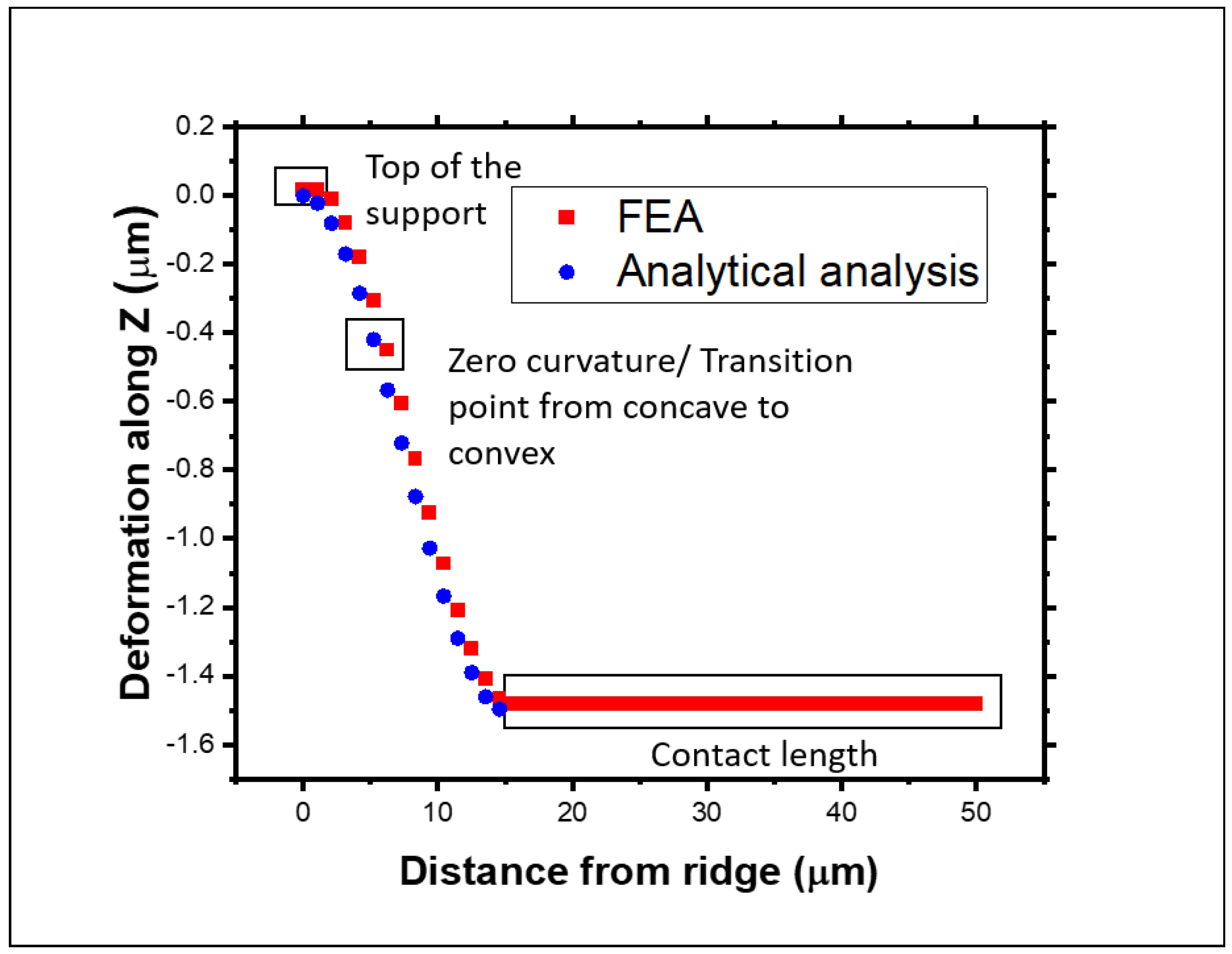
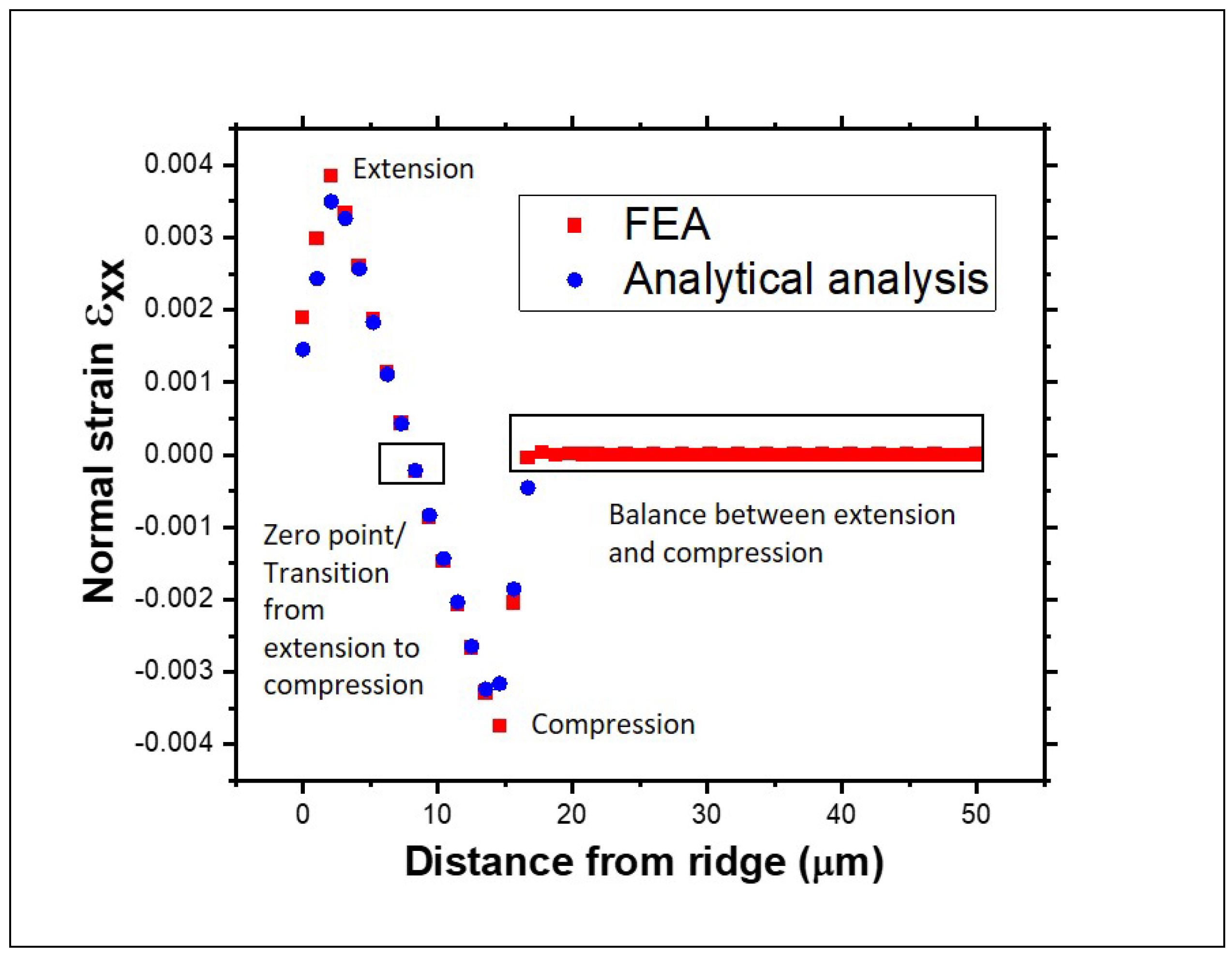
3.3. Comparison of Numerical Model Results
4. Electron Backscatter Diffraction Measurements
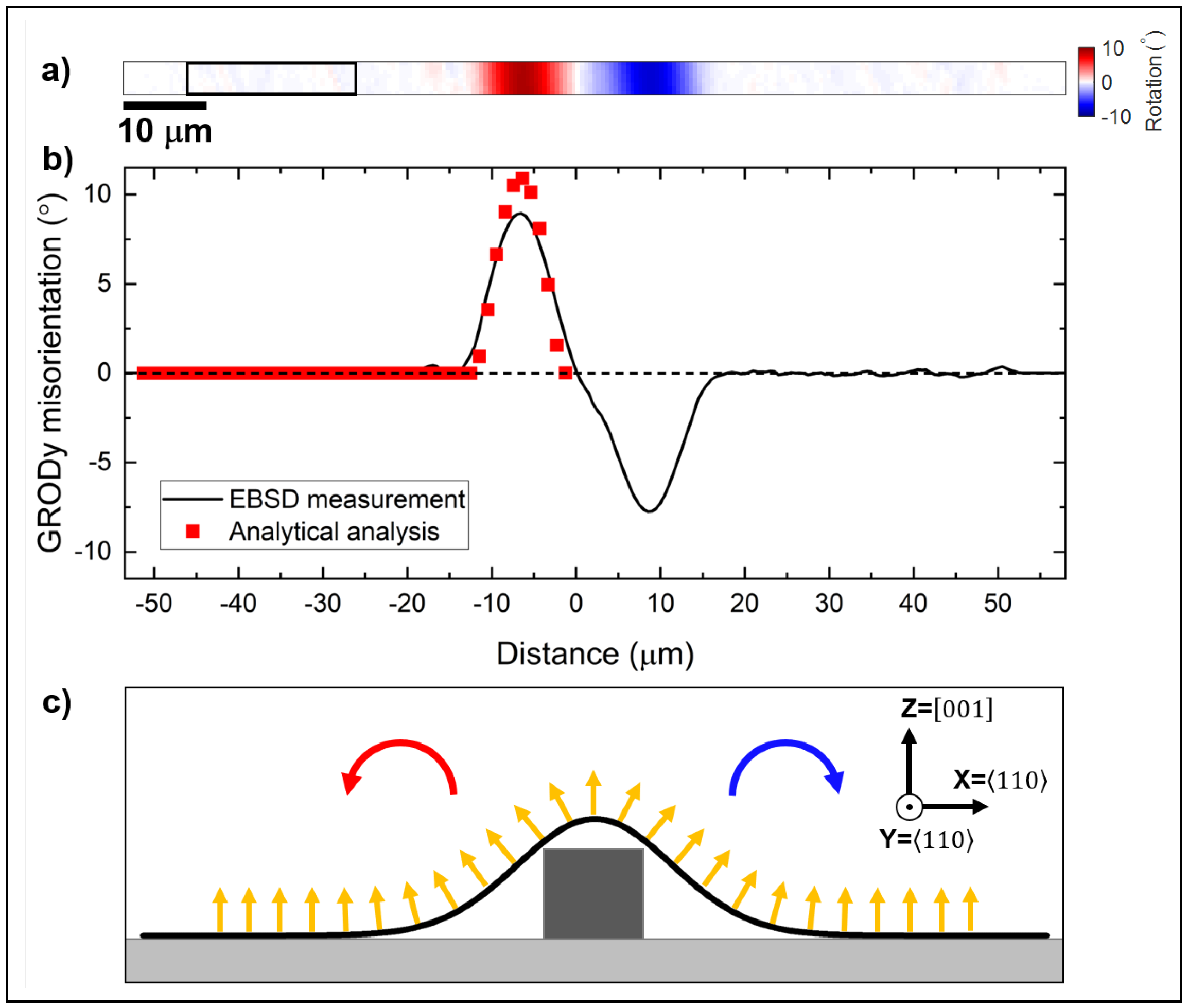
4.1. Radius of Curvature Assessment
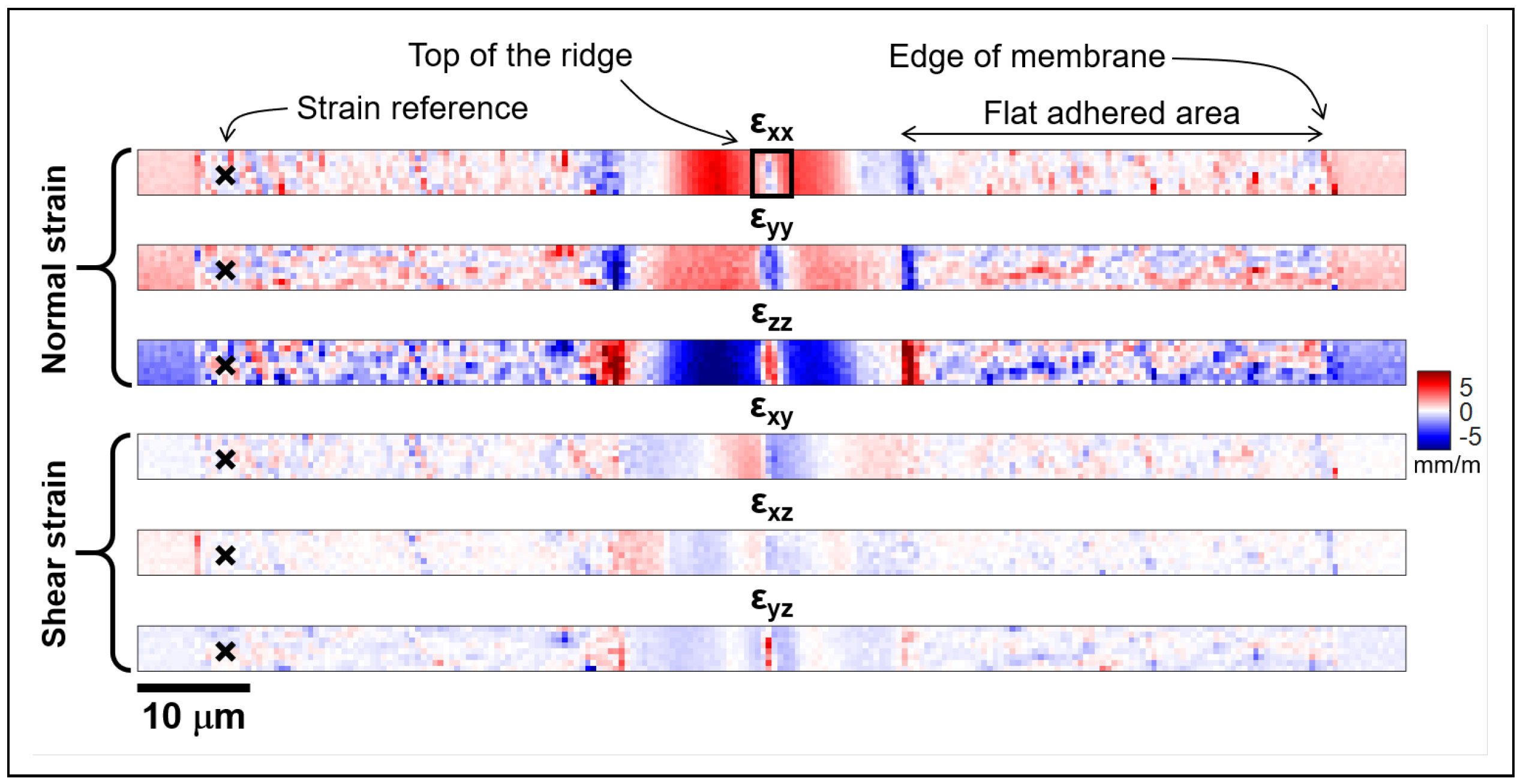
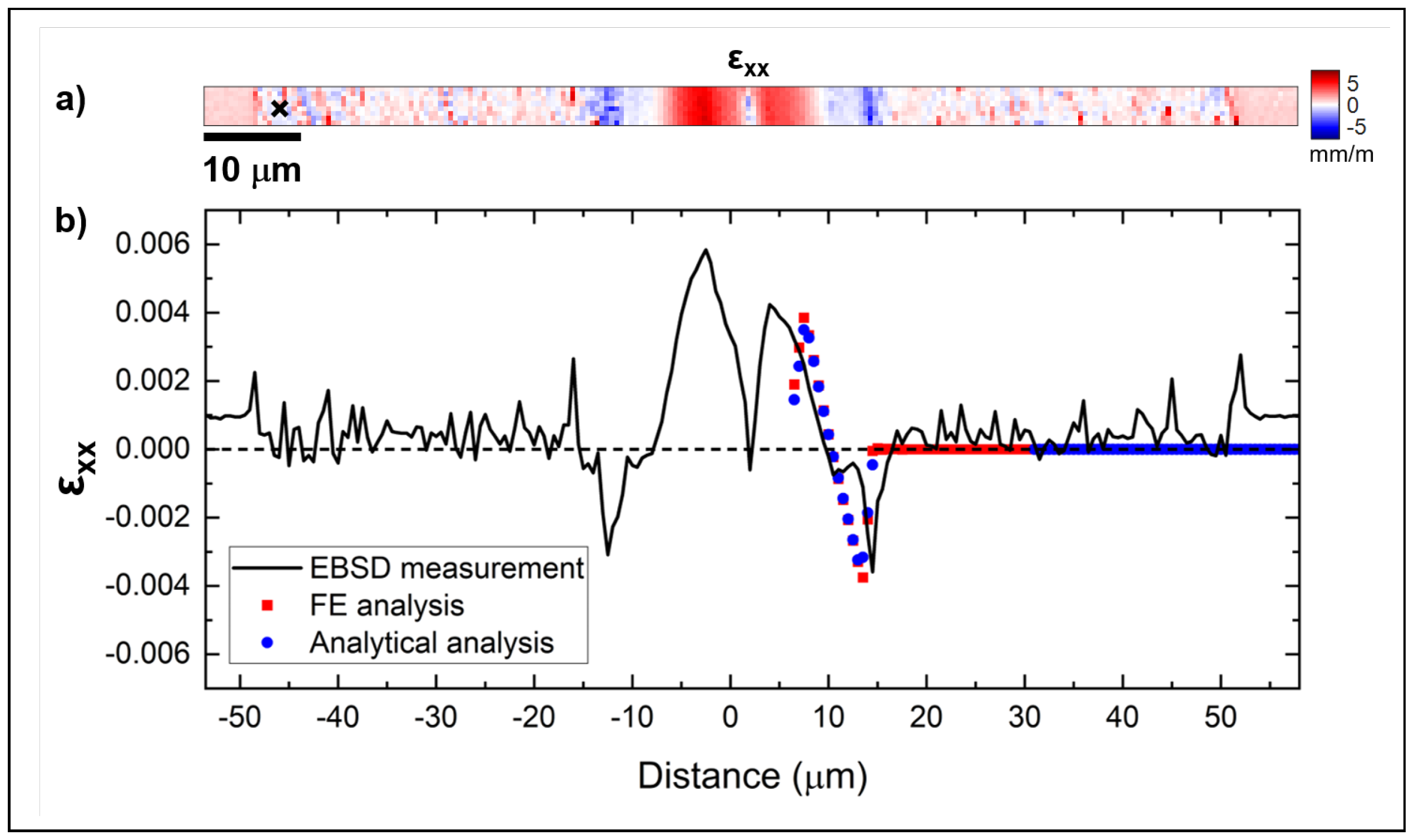
4.2. Normal Strain Assessment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Si | Silicon |
| NMs | Nanomembranes |
| EBSD | Electron Backscatter Diffraction |
| SOI | Silicon-on-insulator |
| BOX | Burried Oxide |
| BOE | Buffered Oxide Etch |
| PDMS | Polydimethylsiloxane |
| KOH | Potassium hydroxide |
| DI | Deionized water |
| SEM | Scanning Electron Microscopy |
| FEA | Finite Element Analysis |
| GROD | Grain Reference Orientation Deviation |
References
- Tsutsui, G.; Mochizuki, S.; Loubet, N.; Bedell, S.; Sadana, D. Strain Engineering in Functional Materials. AIP Adv. 2019, 9, 030701. [Google Scholar] [CrossRef]
- Pešić-Brđanin, T.; Dokić, B.L. Strained silicon layer in CMOS technology. Electronics 2014, 18, 63–69. [Google Scholar] [CrossRef]
- Sweeney, S.J.; Eales, T.D.; Adams, A.R. The impact of strained layers on current and emerging semiconductor laser systems. J. Appl. Phys. 2019, 125, 082538. [Google Scholar] [CrossRef]
- Jacobsen, R.S.; Andersen, K.N.; Borel, P.I.; Fage-Pedersen, J.; Frandsen, L.H.; Hansen, O.; Kristensen, M.; Lavrinenko, A.V.; Moulin, G.; Ou, H.; et al. Strained silicon as a new electro-optic material. Nature 2006, 441, 199–202. [Google Scholar] [CrossRef]
- Maiti, C.; Bera, L.; Chattopadhyay, S. Strained-Si heterostructure field effect transistors. Semicond. Sci. Technol. 1998, 13, 1225. [Google Scholar] [CrossRef]
- Uchida, K.; Kinoshita, A.; Saitoh, M. Carrier transport in (110) nMOSFETs: Subband structures, non-parabolicity, mobility characteristics, and uniaxial stress engineering. In Proceedings of the 2006 International Electron Devices Meeting, San Francisco, CA, USA, 11–13 December 2006; pp. 1–3. [Google Scholar]
- Lee, W.; Hwangbo, Y.; Kim, J.H.; Ahn, J.H. Mobility enhancement of strained Si transistors by transfer printing on plastic substrates. NPG Asia Mater. 2016, 8, e256. [Google Scholar] [CrossRef]
- Liu, X.; Li, F.; Peng, W.; Zhu, Q.; Li, Y.; Zheng, G.; Tian, H.; He, Y. Piezotronic and Piezo-Phototronic Effects-Enhanced Core–Shell Structure-Based Nanowire Field-Effect Transistors. Micromachines 2023, 14, 1335. [Google Scholar] [CrossRef]
- Lee, M.L.; Fitzgerald, E.A.; Bulsara, M.T.; Currie, M.T.; Lochtefeld, A. Strained Si, SiGe, and Ge channels for high-mobility metal-oxide-semiconductor field-effect transistors. J. Appl. Phys. 2005, 97, 011101. [Google Scholar] [CrossRef]
- Numata, T.; Saitoh, M.; Nakabayashi, Y.; Ota, K.; Uchida, K. Source/drain and gate engineering on Si nanowire transistors with reduced parasitic resistance and strained silicon channel. In Proceedings of the 2010 10th IEEE International Conference on Solid-State and Integrated Circuit Technology, Shanghai, China, 1–4 November 2010; pp. 37–40. [Google Scholar]
- Euaruksakul, C.; Li, Z.; Zheng, F.; Himpsel, F.; Ritz, C.; Tanto, B.; Savage, D.; Liu, X.; Lagally, M. Influence of strain on the conduction band structure of strained silicon nanomembranes. Phys. Rev. Lett. 2008, 101, 147403. [Google Scholar] [CrossRef]
- Shiri, D.; Kong, Y.; Buin, A.; Anantram, M. Strain induced change of bandgap and effective mass in silicon nanowires. Appl. Phys. Lett. 2008, 93, 073114. [Google Scholar] [CrossRef]
- Cai, J.; Ishikawa, Y.; Wada, K. Strain induced bandgap and refractive index variation of silicon. Opt. Express 2013, 21, 7162–7170. [Google Scholar] [CrossRef] [PubMed]
- Lafforgue, C.; Berciano, M.; Deniel, L.; Marcaud, G.; Le Roux, X.; Alonso-Ramos, C.; Benedikovic, D.; Vakarin, V.; Ruiz-Caridad, A.; Crozat, P.; et al. High-speed optical modulation based on Pockels effect in strained silicon waveguides. In Proceedings of the 2020 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 10–15 May 2020; Optica Publishing Group: Washington, DC, USA, 2020; p. SM2J-1. [Google Scholar]
- Yang, S.; Chen, Y.; Jiang, C. Strain engineering of two-dimensional materials: Methods, properties, and applications. InfoMat 2021, 3, 397–420. [Google Scholar] [CrossRef]
- Zhou, H.; Seo, J.H.; Paskiewicz, D.M.; Zhu, Y.; Celler, G.K.; Voyles, P.M.; Zhou, W.; Lagally, M.G.; Ma, Z. Fast flexible electronics with strained silicon nanomembranes. Sci. Rep. 2013, 3, 1291. [Google Scholar] [CrossRef] [PubMed]
- Masteghin, M.G.; Tong, V.; Schneider, E.B.; Underwood, C.C.; Peach, T.; Murdin, B.N.; Webb, R.P.; Clowes, S.K.; Cox, D.C. Stress-strain engineering of single-crystalline silicon membranes by ion implantation: Towards direct-gap group-IV semiconductors. Phys. Rev. Mater. 2021, 5, 124603. [Google Scholar] [CrossRef]
- Roberts, M.M.; Klein, L.J.; Savage, D.E.; Slinker, K.A.; Friesen, M.; Celler, G.; Eriksson, M.A.; Lagally, M.G. Elastically relaxed free-standing strained-silicon nanomembranes. Nat. Mater. 2006, 5, 388–393. [Google Scholar] [CrossRef]
- Scott, S.A.; Lagally, M.G. Elastically strain-sharing nanomembranes: Flexible and transferable strained silicon and silicon–germanium alloys. J. Phys. D Appl. Phys. 2007, 40, R75. [Google Scholar] [CrossRef]
- Sánchez-Pérez, J.R.; Boztug, C.; Chen, F.; Sudradjat, F.F.; Paskiewicz, D.M.; Jacobson, R.; Lagally, M.G.; Paiella, R. Direct-bandgap light-emitting germanium in tensilely strained nanomembranes. Proc. Natl. Acad. Sci. USA 2011, 108, 18893–18898. [Google Scholar] [CrossRef] [PubMed]
- Guilhabert, B.; Bommer, S.P.; Wessling, N.K.; Jevtics, D.; Smith, J.A.; Xia, Z.; Ghosh, S.; Kappers, M.; Watson, I.M.; Oliver, R.A.; et al. Advanced Transfer Printing with In-Situ Optical Monitoring for the Integration of Micron-Scale Devices. IEEE J. Sel. Top. Quantum Electron. 2023, 29, 1–11. [Google Scholar] [CrossRef]
- Kim, S.; Wu, J.; Carlson, A.; Jin, S.H.; Kovalsky, A.; Glass, P.; Liu, Z.; Ahmed, N.; Elgan, S.L.; Chen, W.; et al. Microstructured elastomeric surfaces with reversible adhesion and examples of their use in deterministic assembly by transfer printing. Proc. Natl. Acad. Sci. USA 2010, 107, 17095–17100. [Google Scholar] [CrossRef]
- McPhillimy, J.; Guilhabert, B.; Klitis, C.; Dawson, M.D.; Sorel, M.; Strain, M.J. High accuracy transfer printing of single-mode membrane silicon photonic devices. Opt. Express 2018, 26, 16679–16688. [Google Scholar] [CrossRef]
- Hill, P.; Gu, E.; Dawsona, M.D.; Strain, M.J. Thin film diamond membranes bonded on-demand with SOI ring resonators. Diam. Relat. Mater. 2018, 88, 215–221. [Google Scholar] [CrossRef]
- De Boer, M.; Michalske, T. Accurate method for determining adhesion of cantilever beams. J. Appl. Phys. 1999, 86, 817–827. [Google Scholar] [CrossRef]
- Hurst, K.M.; Roberts, C.B.; Ashurst, W.R. A new method to determine adhesion of cantilever beams using beam height experimental data. Tribol. Lett. 2009, 35, 9–15. [Google Scholar] [CrossRef]
- Muhammad, A.; Ali, M.; Shanono, I. Finite Element Analysis of a connecting rod in ANSYS: An overview. IOP Conf. Ser. Mater. Sci. Eng. 2020, 736, 022119. [Google Scholar] [CrossRef]
- Richmond, B.G.; Wright, B.W.; Grosse, I.; Dechow, P.C.; Ross, C.F.; Spencer, M.A.; Strait, D.S. Finite element analysis in functional morphology. Anat. Rec. Part Discov. Mol. Cell. Evol. Biol. 2005, 283, 259–274. [Google Scholar] [CrossRef] [PubMed]
- Winkelmann, A.; Trager-Cowan, C.; Sweeney, F.; Day, A.P.; Parbrook, P. Many-beam dynamical simulation of electron backscatter diffraction patterns. Ultramicroscopy 2007, 107, 414. [Google Scholar] [CrossRef] [PubMed]
- Nolze, G.; Jürgens, M.; Olbricht, J.; Winkelmann, A. Improving the precision of orientation measurements from technical materials via EBSD pattern matching. Acta Mater. 2018, 159, 408. [Google Scholar] [CrossRef]
- Cios, G.; Winkelmann, A.; Nolze, G.; Tokarski, T.; Rychłowski, L.; Dan, L.; Bała, P. Mapping of lattice distortion in martensitic steel–Comparison of different evaluation methods of EBSD patterns. Ultramicroscopy 2023, 253, 113824. [Google Scholar] [CrossRef]
- Winkelmann, A.; Cios, G.; Perzyński, K.; Tokarski, T.; Mehnert, K.; Łukasz, M.; Bała, P. Simulation-based Super-Resolution EBSD for Measurements of Relative Deformation Gradient Tensors. arXiv 2025, arXiv:2502.11628. [Google Scholar]
- Bachmann, F.; Hielscher, R.; Schaeben, H. Texture analysis with MTEX–free and open source software toolbox. Solid State Phenom. 2010, 160, 63. [Google Scholar] [CrossRef]
- Munguía, J.; Bluet, J.; Chouaib, H.; Bremond, G.; Mermoux, M.; Bru-Chevallier, C. Strain dependence of the direct energy bandgap in thin silicon on insulator layers. J. Phys. D Appl. Phys. 2010, 43, 255401. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Margariti, E.; Bruckbauer, J.; Winkelmann, A.; Guilhabert, B.; Gunasekar, N.-K.; Trager-Cowan, C.; Martin, R.; Strain, M. Strain-Induced Modifications of Thin Film Silicon Membranes Through Physical Bending. Materials 2025, 18, 2335. https://doi.org/10.3390/ma18102335
Margariti E, Bruckbauer J, Winkelmann A, Guilhabert B, Gunasekar N-K, Trager-Cowan C, Martin R, Strain M. Strain-Induced Modifications of Thin Film Silicon Membranes Through Physical Bending. Materials. 2025; 18(10):2335. https://doi.org/10.3390/ma18102335
Chicago/Turabian StyleMargariti, Eleni, Jochen Bruckbauer, Aimo Winkelmann, Benoit Guilhabert, Naresh-Kumar Gunasekar, Carol Trager-Cowan, Robert Martin, and Michael Strain. 2025. "Strain-Induced Modifications of Thin Film Silicon Membranes Through Physical Bending" Materials 18, no. 10: 2335. https://doi.org/10.3390/ma18102335
APA StyleMargariti, E., Bruckbauer, J., Winkelmann, A., Guilhabert, B., Gunasekar, N.-K., Trager-Cowan, C., Martin, R., & Strain, M. (2025). Strain-Induced Modifications of Thin Film Silicon Membranes Through Physical Bending. Materials, 18(10), 2335. https://doi.org/10.3390/ma18102335









