Structural Influences on Lithium-Ion Transport in Bismuth Oxides: A Molecular Dynamics Approach
Abstract
:1. Introduction
2. Simulation Details
3. Results and Discussion
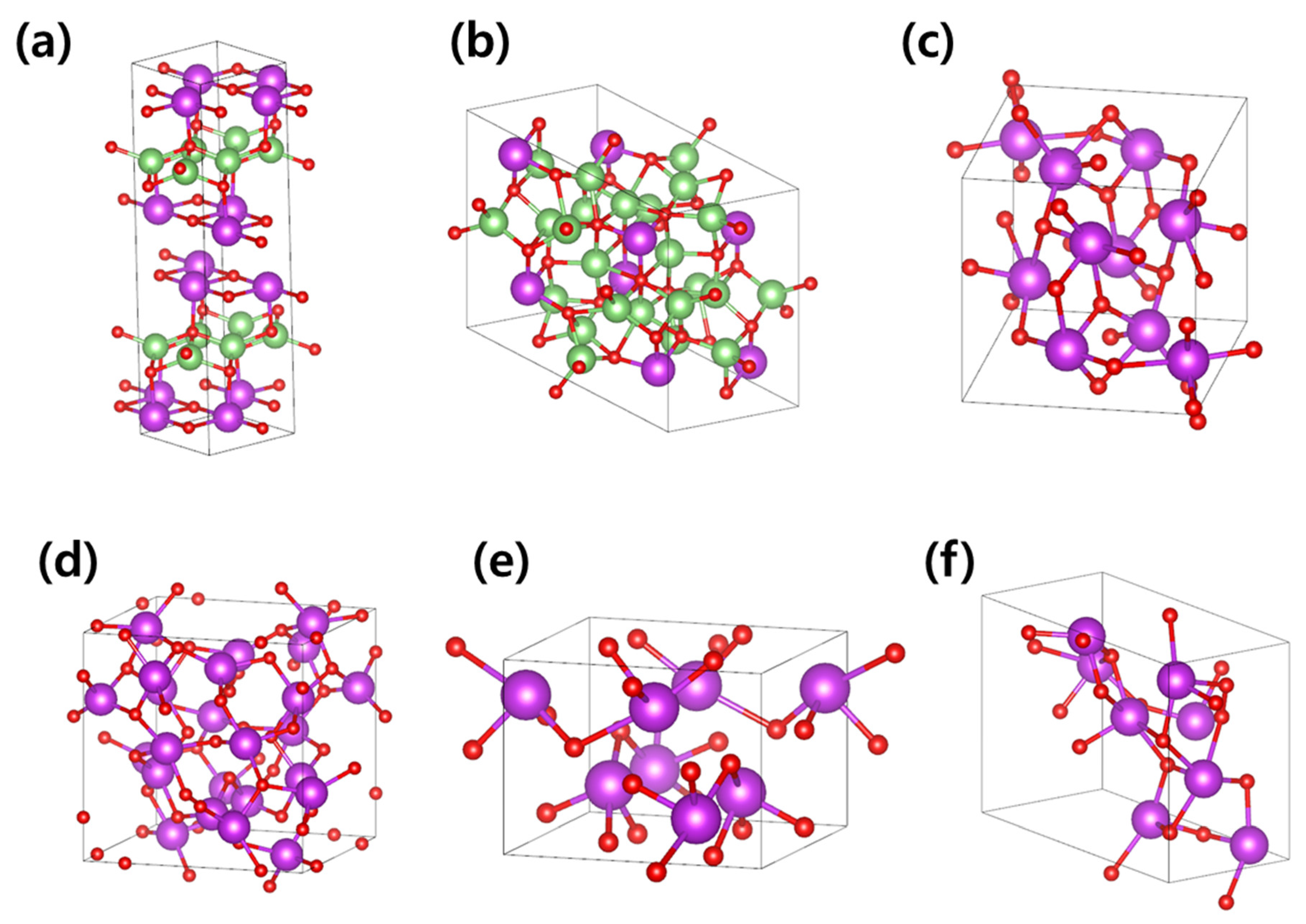
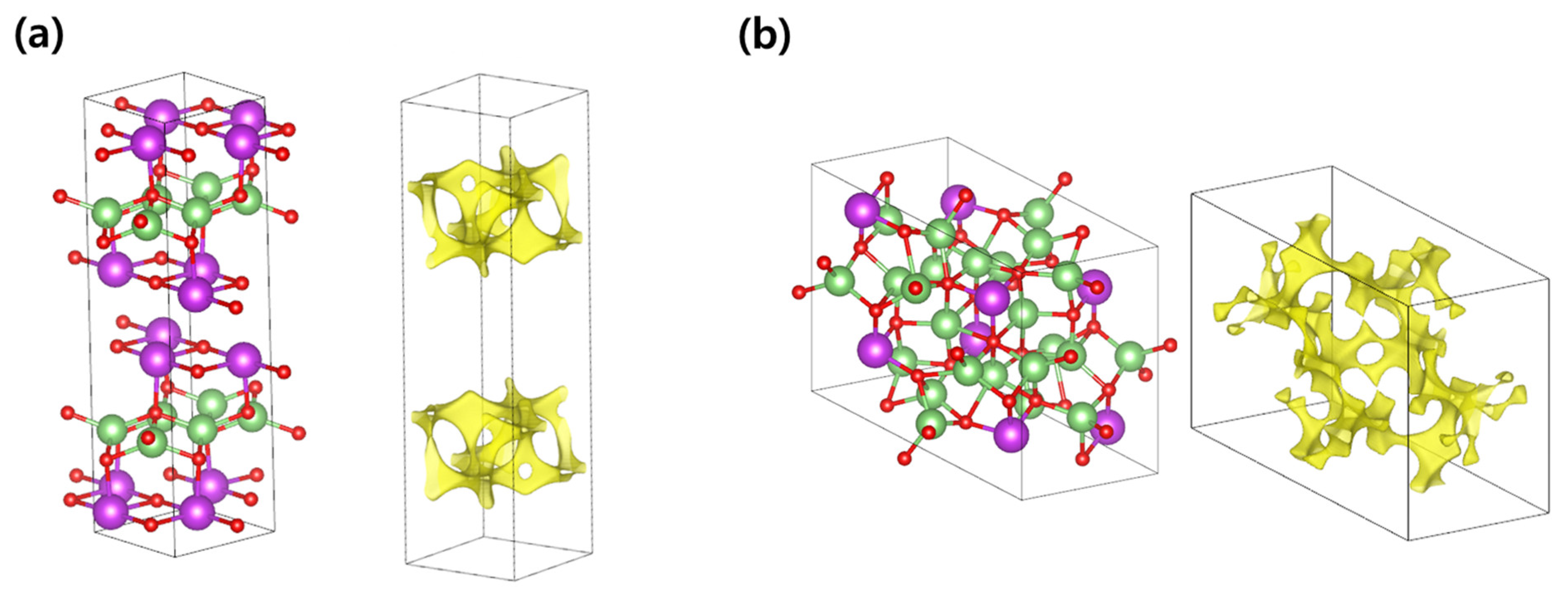
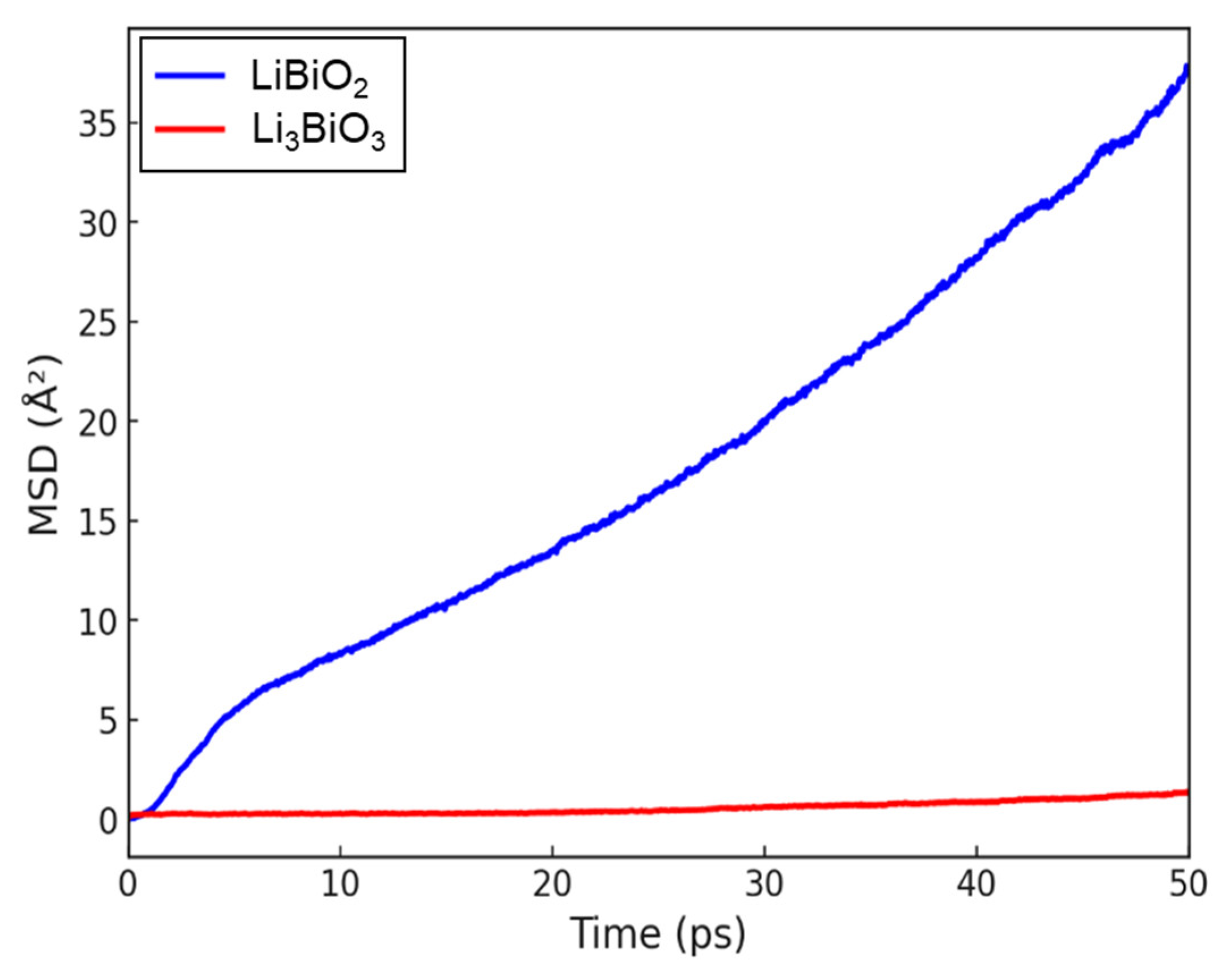
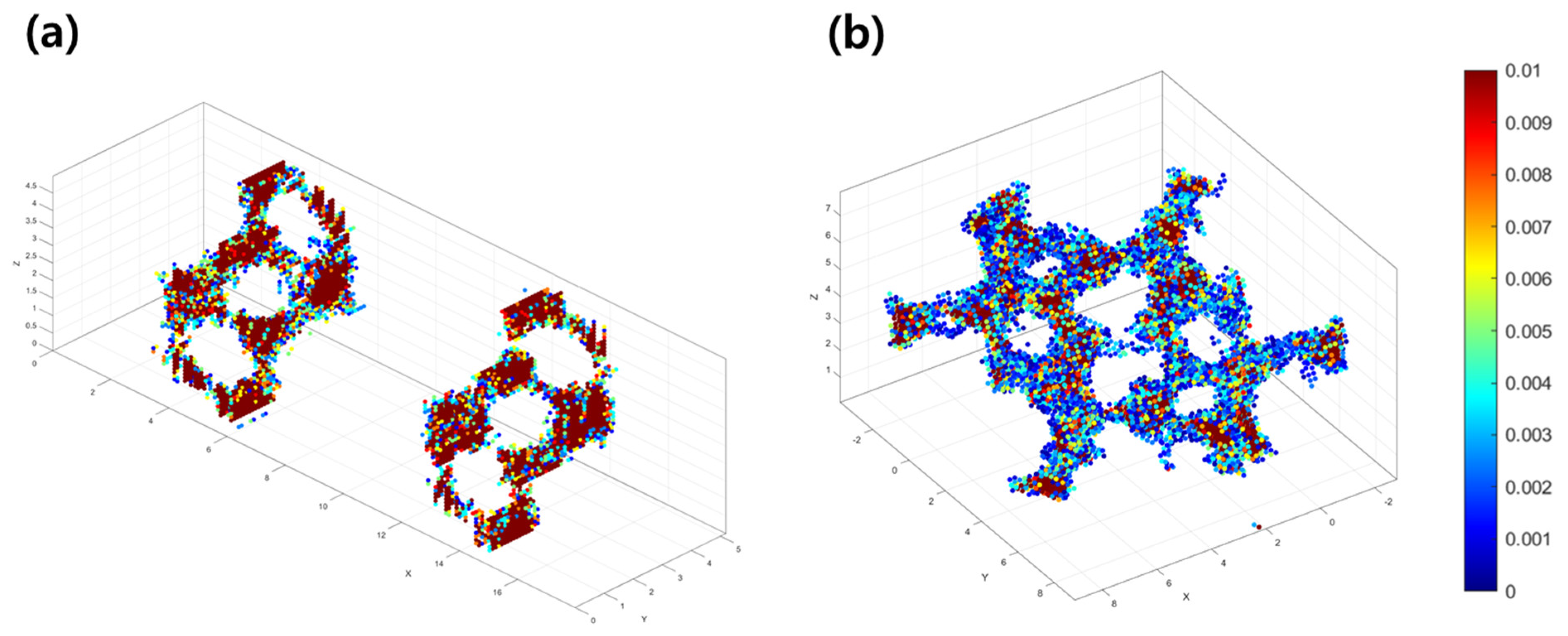
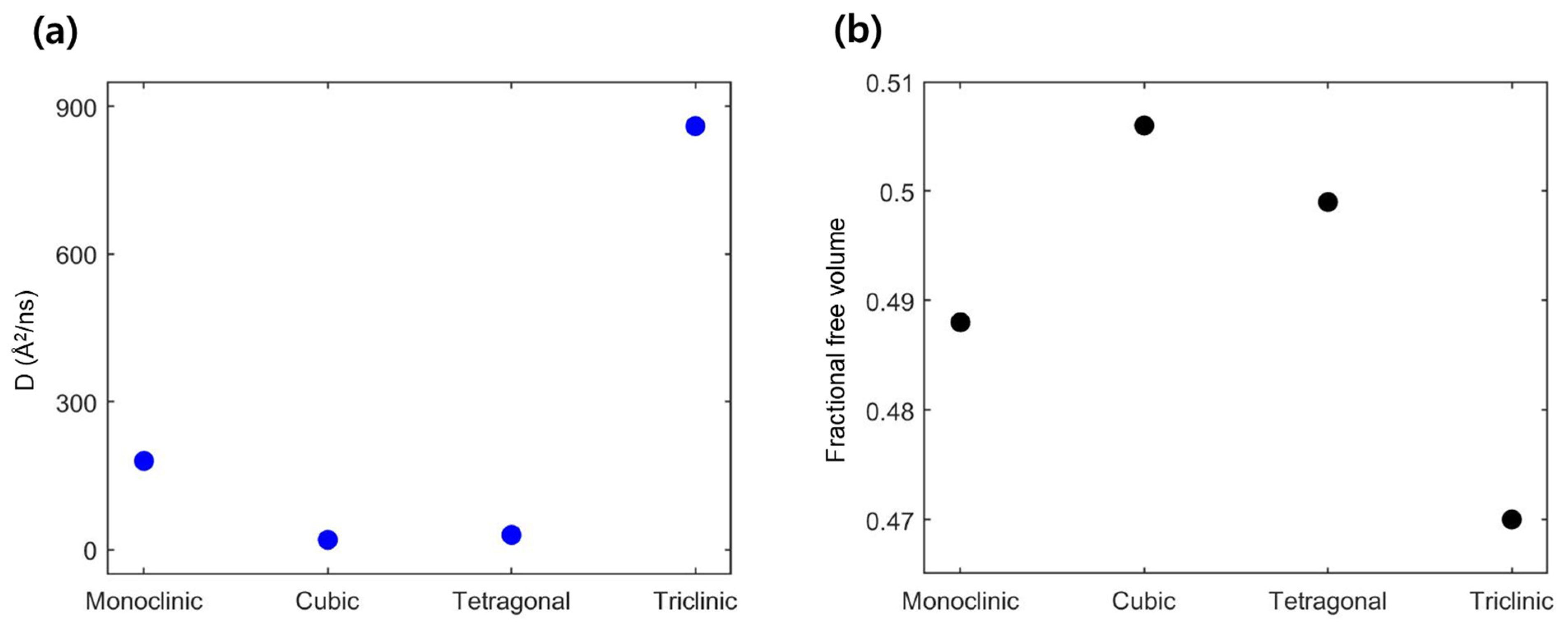
3.1. Li-Contained Bismuth Oxide
3.2. Li-Free Bismuth Oxide
4. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, M.; Lu, J.; Chen, Z.; Amine, K. 30 years of lithium-ion batteries. Adv. Mater. 2018, 30, 1800561. [Google Scholar] [CrossRef] [PubMed]
- Crabtree, G.; Kócs, E.; Trahey, L. The energy-storage frontier: Lithium-ion batteries and beyond. MRS Bull. 2015, 40, 1067–1078. [Google Scholar] [CrossRef]
- Li, W.; Erickson, E.M.; Manthiram, A. High-nickel layered oxide cathodes for lithium-based automotive batteries. Nat. Energy 2020, 5, 26–34. [Google Scholar] [CrossRef]
- Liu, J.; Bao, Z.; Cui, Y.; Dufek, E.J.; Goodenough, J.B.; Khalifah, P.; Zhang, J.G. Pathways for practical high-energy long-cycling lithium metal batteries. Nat. Energy 2019, 4, 180–186. [Google Scholar] [CrossRef]
- Xu, J.; Cai, X.; Cai, S.; Shao, Y.; Hu, C.; Lu, S.; Ding, S. High-energy lithium-ion batteries: Recent progress and a promising future in applications. Energy Environ. Mater. 2023, 6, e12450. [Google Scholar] [CrossRef]
- Chen, T.; Jin, Y.; Lv, H.; Yang, A.; Liu, M.; Chen, B.; Chen, Q. Applications of lithium-ion batteries in grid-scale energy storage systems. Trans. Tianjin Univ. 2020, 26, 208–217. [Google Scholar] [CrossRef]
- Wen, J.; Zhao, D.; Zhang, C. An overview of electricity powered vehicles: Lithium-ion battery energy storage density and energy conversion efficiency. Renew. Energy 2020, 162, 1629–1648. [Google Scholar] [CrossRef]
- Yang, Y.; Okonkwo, E.G.; Huang, G.; Xu, S.; Sun, W.; He, Y. On the sustainability of lithium ion battery industry–A review and perspective. Energy Storage Mater. 2021, 36, 186–212. [Google Scholar] [CrossRef]
- Karuppasamy, K.; Theerthagiri, J.; Vikraman, D.; Yim, C.J.; Hussain, S.; Sharma, R.; Kim, H.S. Ionic liquid-based electrolytes for energy storage devices: A brief review on their limits and applications. Polymers 2020, 12, 918. [Google Scholar] [CrossRef]
- Liu, Y.K.; Zhao, C.Z.; Du, J.; Zhang, X.Q.; Chen, A.B.; Zhang, Q. Research Progresses of Liquid Electrolytes in Lithium-Ion Batteries. Small 2023, 19, 2205315. [Google Scholar] [CrossRef]
- Meng, Y.S.; Srinivasan, V.; Xu, K. Designing better electrolytes. Science 2022, 378, eabq3750. [Google Scholar] [CrossRef] [PubMed]
- Cao, W.; Zhang, J.; Li, H. Batteries with high theoretical energy densities. Energy Storage Mater. 2020, 26, 46–55. [Google Scholar] [CrossRef]
- Gao, M.; Li, H.; Xu, L.; Xue, Q.; Wang, X.; Bai, Y.; Wu, C. Lithium metal batteries for high energy density: Fundamental electrochemistry and challenges. J. Energy Chem. 2021, 59, 666–687. [Google Scholar] [CrossRef]
- Wu, Y.; Xie, L.; Ming, H.; Guo, Y.; Hwang, J.Y.; Wang, W.; Ming, J. An empirical model for the design of batteries with high energy density. ACS Energy Lett. 2020, 5, 807–816. [Google Scholar] [CrossRef]
- Xu, X.; Wang, S.; Wang, H.; Hu, C.; Jin, Y.; Liu, J.; Yan, H. Recent progresses in the suppression method based on the growth mechanism of lithium dendrite. J. Energy Chem. 2018, 27, 513–527. [Google Scholar] [CrossRef]
- Liu, H.; Cheng, X.B.; Jin, Z.; Zhang, R.; Wang, G.; Chen, L.Q.; Zhang, Q. Recent advances in understanding dendrite growth on alkali metal anodes. EnergyChem 2019, 1, 100003. [Google Scholar] [CrossRef]
- Selis, L.A.; Seminario, J.M. Dendrite formation in silicon anodes of lithium-ion batteries. RSC Adv. 2018, 8, 5255–5267. [Google Scholar] [CrossRef]
- Quartarone, E.; Mustarelli, P. Emerging trends in the design of electrolytes for lithium and post-lithium batteries. J. Electrochem. Soc. 2020, 167, 050508. [Google Scholar] [CrossRef]
- Yang, X.; Adair, K.R.; Gao, X.; Sun, X. Recent advances and perspectives on thin electrolytes for high-energy-density solid-state lithium batteries. Energy Environ. Sci. 2021, 14, 643–671. [Google Scholar] [CrossRef]
- Verma, P.; Maire, P.; Novák, P. A review of the features and analyses of the solid electrolyte interphase in Li-ion batteries. Electrochim. Acta 2010, 55, 6332–6341. [Google Scholar] [CrossRef]
- Zheng, F.; Kotobuki, M.; Song, S.; Lai, M.O.; Lu, L. Review on solid electrolytes for all-solid-state lithium-ion batteries. J. Power Sources 2018, 389, 198–213. [Google Scholar] [CrossRef]
- Ye, T.; Li, L.; Zhang, Y. Recent progress in solid electrolytes for energy storage devices. Adv. Funct. Mater. 2020, 30, 2000077. [Google Scholar] [CrossRef]
- Sharma, S.K.; Sharma, G.; Gaur, A.; Arya, A.; Mirsafi, F.S.; Abolhassani, R.; Mishra, Y.K. Progress in electrode and electrolyte materials: Path to all-solid-state Li-ion batteries. Energy Adv. 2022, 1, 457–510. [Google Scholar] [CrossRef]
- Zheng, Y.; Yao, Y.; Ou, J.; Li, M.; Luo, D.; Dou, H.; Li, Z.; Amine, K.; Yu, A.; Chen, Z. A review of composite solid-state electrolytes for lithium batteries: Fundamentals, key materials and advanced structures. Chem. Soc. Rev. 2020, 49, 8790–8839. [Google Scholar] [CrossRef]
- Adenusi, H.; Chass, G.A.; Passerini, S.; Tian, K.V.; Chen, G. Lithium batteries and the solid electrolyte interphase (SEI)—Progress and outlook. Adv. Energy Mater. 2023, 13, 2203307. [Google Scholar] [CrossRef]
- Jiang, P.; Du, G.; Cao, J.; Zhang, X.; Zou, C.; Liu, Y.; Lu, X. Solid-state Li Ion Batteries with Oxide Solid Electrolytes: Progress and Perspective. Energy Technol. 2023, 11, 2201288. [Google Scholar] [CrossRef]
- Reddy, M.V.; Julien, C.M.; Mauger, A.; Zaghib, K. Sulfide and oxide inorganic solid electrolytes for all-solid-state Li batteries: A review. Nanomaterials 2020, 10, 1606. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, L.; Zheng, P.; Sun, J.; Liu, C.; Chai, J.; Liu, Z. Recent advances in stability issues of inorganic solid electrolytes and composite solid electrolytes for all-solid-state batteries. Chem. Rec. 2022, 22, e202200116. [Google Scholar] [CrossRef]
- Wei, R.; Chen, S.; Gao, T.; Liu, W. Challenges, fabrications and horizons of oxide solid electrolytes for solid-state lithium batteries. Nano Sel. 2021, 2, 2256–2274. [Google Scholar] [CrossRef]
- Chen, F.; Jing, M.X.; Yang, H.; Yuan, W.Y.; Liu, M.Q.; Ji, Y.S.; Shen, X.Q. Improved ionic conductivity and Li dendrite suppression of PVDF-based solid electrolyte membrane by LLZO incorporation and mechanical reinforcement. Ionics 2021, 27, 1101–1111. [Google Scholar] [CrossRef]
- Wolfenstine, J.; Allen, J.L.; Sakamoto, J.; Siegel, D.J.; Choe, H. Mechanical behavior of Li-ion-conducting crystalline oxide-based solid electrolytes: A brief review. Ionics 2018, 24, 1271–1276. [Google Scholar] [CrossRef]
- Xue, J.; Zhang, K.; Chen, D.; Zeng, J.; Luo, B. Spark plasma sintering plus heat-treatment of Ta-doped Li₇La₃Zr₂O₁₂ solid electrolyte and its ionic conductivity. Mater. Res. Express 2020, 7, 025518. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, J.; Nie, L.; Hu, X.; Huang, Y.; Yu, Y.; Liu, W. All-solid-state batteries with a limited lithium metal anode at room temperature using a garnet-based electrolyte. Adv. Mater. 2021, 33, 2002325. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, C.Y.; Shi, S.Q.; Wang, Z.X.; Li, H.; Huang, X.J.; Chen, L.Q. The effect of Cr doping on Li ion diffusion in LiFePO₄ from first principles investigations and Monte Carlo simulations. J. Phys. Condens. Matter 2004, 16, 2265. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, Y.; Wang, Z.; Chen, L.; Li, H.; Wu, F. Doping strategy and mechanism for oxide and sulfide solid electrolytes with high ionic conductivity. J. Mater. Chem. A 2022, 10, 4517–4532. [Google Scholar] [CrossRef]
- Sammes, N.M.; Tompsett, G.A.; Näfe, H.; Aldinger, F. Bismuth based oxide electrolytes—Structure and ionic conductivity. Solid State Ionics 1999, 126, 65–80. [Google Scholar] [CrossRef]
- Ahn, J.S.; Camaratta, M.A.; Pergolesi, D.; Lee, K.T.; Yoon, H.; Lee, B.W.; Jung, D.W.; Traversa, E.; Wachsman, E.D. Development of high performance ceria/bismuth oxide bilayered electrolyte SOFCs for lower temperature operation. J. Electrochem. Soc. 2010, 157, B376–B382. [Google Scholar] [CrossRef]
- Hou, J.; Bi, L.; Qian, J.; Zhu, Z.; Zhang, J.; Liu, W. High performance ceria–bismuth bilayer electrolyte low temperature solid oxide fuel cells fabricated by combining co-pressing with drop-coating. J. Mater. Chem. A 2015, 3, 10040–10046. [Google Scholar] [CrossRef]
- Wachsman, E.D.; Lee, K.T. The evolution of low temperature solid oxide fuel cells. J. Mater. Res. 2012, 27, 1920–1930. [Google Scholar]
- Oh, E.O.; Whang, C.M.; Lee, Y.R.; Park, S.Y.; Prasad, D.H.; Yoon, K.J.; Son, J.W.; Lee, J.H.; Lee, H.W. Functionally graded bismuth oxide/zirconia bilayer electrolytes for high-performance solid oxide fuel cells. ACS Appl. Mater. Interfaces 2017, 9, 7743–7750. [Google Scholar]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef]
- Pedone, A.; Malavasi, G.; Menziani, M.C.; Cormack, A.N.; Segre, U. Improved empirical force field for multicomponent oxide glasses and crystals. Phys. Rev. Mater. 2019, 5, 045602. [Google Scholar]
- Sjöberg, S.; Hjelm, J. Diffusion of lithium in lithium-containing glasses and oxides: A molecular dynamics study. J. Phys. Chem. C 2016, 120, 10105–10114. [Google Scholar]
- Pedone, A.; Malavasi, G.; Menziani, M.C.; Cormack, A.N.; Segre, U. A new self-consistent empirical interatomic potential model for oxides, silicates, and silica-based glasses. J. Phys. Chem. B 2006, 110, 11780–11795. [Google Scholar] [CrossRef]
- Ahn, Y.N.; Harris, J.T. The effect of individual elements of alkali aluminosilicate glass on scratch characteristics: A molecular dynamics study. J. Non-Cryst. Solids 2020, 536, 119840. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Nose, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Brown, I.D. Recent developments in the methods and applications of the bond valence model. Chem. Rev. 2009, 109, 6858–6919. [Google Scholar] [CrossRef] [PubMed]
- Nishimura, S.I.; Tanibata, N.; Hayashi, A.; Tatsumisago, M.; Yamada, A. The crystal structure and sodium disorder of high-temperature polymorph β-Na₃PS₄. J. Mater. Chem. A 2017, 5, 25025–25030. [Google Scholar] [CrossRef]
- Adams, S. Bond valence analysis of structure–property relationships in solid electrolytes. J. Power Sources 2006, 159, 200–204. [Google Scholar] [CrossRef]
- Adams, S. Relationship between bond valence and bond softness of alkali halides and chalcogenides. Acta Crystallogr. Sect. B Struct. Sci. 2001, 57, 278–287. [Google Scholar] [CrossRef]
| Method | Bond Length (Å) | Density (g/cm3) | Young’s Modulus (GPa) | Poisson Ratio | ||
|---|---|---|---|---|---|---|
| Bi–Bi | Bi–O | O–O | ||||
| Ab initio MD | 3.6 | 2.2 | 3.0 | 9.1 | 71.0 | 0.26 |
| Classical MD | 3.5 | 2.2 | 3.1 | 10.2 | 67.5 | 0.28 |
| Dji (eV) | aij (Å−2) | r0 (Å) | Cij (eV Å12) | |
|---|---|---|---|---|
| Li0.6–O−1.2 | 0.001114 | 3.429506 | 2.681360 | 1.0 |
| Bi1.8–O−1.2 | 0.000132 | 2.01300 | 4.301589 | 3.0 |
| O−1.2–O−1.2 | 0.042395 | 1.379316 | 3.618701 | 22.0 |
| Temperature (K) | Diffusion Coefficient (Å/ns) | |
|---|---|---|
| LiBiO2 | Li3BiO3 | |
| 500 | 71.3 | 1.7 |
| 1000 | 171.3 | 15.5 |
| 1500 | 320.5 | 64.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, S.-B.; Kim, B.J.; Ahn, Y.N. Structural Influences on Lithium-Ion Transport in Bismuth Oxides: A Molecular Dynamics Approach. Materials 2025, 18, 2287. https://doi.org/10.3390/ma18102287
You S-B, Kim BJ, Ahn YN. Structural Influences on Lithium-Ion Transport in Bismuth Oxides: A Molecular Dynamics Approach. Materials. 2025; 18(10):2287. https://doi.org/10.3390/ma18102287
Chicago/Turabian StyleYou, Seong-Beom, Byeong Jun Kim, and Yong Nam Ahn. 2025. "Structural Influences on Lithium-Ion Transport in Bismuth Oxides: A Molecular Dynamics Approach" Materials 18, no. 10: 2287. https://doi.org/10.3390/ma18102287
APA StyleYou, S.-B., Kim, B. J., & Ahn, Y. N. (2025). Structural Influences on Lithium-Ion Transport in Bismuth Oxides: A Molecular Dynamics Approach. Materials, 18(10), 2287. https://doi.org/10.3390/ma18102287







