Abstract
In this paper, the shear behavior of concrete beams reinforced with FRP stirrups is studied. The shear performances of six concrete beams with a size of 150 mm × 300 mm × 3000 mm under four-point loading up to failure were experimentally analyzed. The critical parameters included the shear span to depth ratio (λ) and stirrup spacing (S). The test results revealed that as λ increased from 1 to 2, 3, and 4, the ultimate shear capacity of the beam decreases by 50.5%, 67.7%, and 69.2%, respectively. Meanwhile, as S increased from 100 mm to 150 mm and 200 mm, the ultimate shear capacity decreased by 16.1% and 44.6%, respectively. A new shear capacity calculation model of concrete beam reinforced with FRP stirrups was also proposed, which further considered the shear capacity of the FRP stirrups on the basis of the shear capacity of an RC beam without stirrups using the strut-and-tie model. Finally, the experiment and calculation results of 56 beam specimens reinforced with FRP stirrups extracted from this paper and previous studies were compared using the calculation models proposed in this paper, in order to evaluate the accuracy of these calculation models.
1. Introduction
To solve the corrosion problem of steel reinforcement in RC (reinforced concrete) structures and improve durability, using fiber-reinforced polymer (FRP) bars instead of steel reinforcement has become an effective method [1]. Currently, common FRP bars mainly includes glass FRP (GFRP), carbon FRP (CFRP), aramid FRP (AFRP), basalt FRP (BFRP), hybrid FRP (HFRP), and so on [2,3,4,5,6]. Among these FRP bars, GFRP bars are the most used feasible substitutes for traditional steel reinforcement due to their superior durability, mature manufacturing process, and relatively cheap price among other advantages [7]. Meanwhile, FRP bars can be used as either longitudinal reinforcement or stirrups instead of steel reinforcement in concrete structures. Because stirrups are closer to the outside of concrete structures (beams, columns, etc.), they are more susceptible to external corrosion than longitudinal reinforcement, resulting in the weakening of the transverse restraint and shear performance of the concrete member [8,9,10]. Therefore, using GFRP bars instead of steel reinforcement as stirrups will more effectively improve the durability of the whole concrete structure. Clearly, research on the performance of GFRP stirrup-reinforced concrete beams has greater significance and advantages.
Over the last 30 years, many scholars have carried out experimental studies on the shear performance of FRP-reinforced concrete beams [11,12,13,14,15,16,17]. It has been found that the shear performance of FRP-reinforced concrete beams is similar to that of concrete beams reinforced by steel, i.e., the shear capacity was also affected by the shear span to depth ratio, longitudinal reinforcement ratio, stirrup ratio and concrete strength [11]. The shear span to depth ratio was the critical factor affecting the failure mode. As the shear span to depth ratio increased, the failure mode changed from diagonal compression failure to shear compression failure, then to diagonal tension failure, and even to flexural failure [12]. Grace et al. [13] experimentally studied the failure mode and ductility of simply supported and continuous concrete beams reinforced with FRP bars. The test results showed that the type of longitudinal bars and stirrups was a key factor in the failure mode. The use of GFRP stirrups increased the deformation and deflection of the beam, and the use of GFRP longitudinal bars caused the beam failure mode to change from flexural failure to shear or flexural–shear failure. Mousavi et al. [14] studied the deflection behavior of concrete beams reinforced with GFRP longitudinal bars and considered that the bond strength of FRP bars was lower than that of steel bars, which led to increased crack depth and reduced the tension-stiffening effect, consequently resulting in greater deflection of concrete beams. Meanwhile, the elastic modulus of FRP longitudinal bars was lower than that of steel bars, so the axial stiffness of the beam after cracking was relatively small, which increased the mid-span deflection of the beam. Said et al. [15] conducted an experimental and analytical study on the shear behavior of concrete beams reinforced with GFRP bars. It was found that when the beam was damaged, the strain of GFRP stirrup was between 0.0043~0.0095. Meanwhile, the shear capacity of concrete beams reinforced with GFRP stirrups was effectively improved compared to their counterpart beams without stirrups. Ahmed et al. [16] found that there were two kinds of failure modes for concrete beams reinforced with FRP stirrups: one was the fracture failure of FRP stirrups, and the other was the crushing failure of concrete at the top flange of the beam near the loading point. Meanwhile, FRP stirrups had no effect on the initial load of shear cracking of the beam, but could enhance the contribution of concrete to its shear capacity after cracking. Similarly, the preliminary research of Hegger et al. [17] showed that when the stirrup ratio of GFRP stirrup was low, the beam failure mode was the fracture of stirrup, while when the stirrup ratio was high, it was the crushing of concrete. Recently, Maranan et al. [9] investigated the shear behaviors of geopolymer beams reinforced with continuous rectangular GFRP spirals. The test results showed that due to the higher strength of the longitudinal and transverse GFRP reinforcements compared with that of the steel reinforcement, the geopolymer concrete beams with GFRP spirals possessed obvious higher shear strength capacity than the ordinary concrete beams with steel spirals.
The shear mechanism of FRP-reinforced concrete beams is quite complex in practice, and most prediction models and design codes/standards are similar to those of steel-reinforced concrete beams [18,19,20,21,22]. According to the research of Razaqpur et al. [23], the shear capacity of FRP reinforced concrete beam is mainly composed of the following six parts:
- (1)
- The shear resistance of uncracked concrete compression zone;
- (2)
- Aggregate interlock;
- (3)
- The dowel action of the longitudinal reinforcement;
- (4)
- Arching action;
- (5)
- Residual tensile stresses across cracks;
- (6)
- Shear carried by the shear reinforcement.
However, different from RC beams reinforced with steel bars, the axial stiffness of the FRP-reinforced concrete beam is relatively low, and its crack width is obviously greater during failure due to the poor plastic deformation capacity and the low elastic modulus of FRP bar. Therefore, when calculating the shear capacity of a FRP-reinforced concrete beam, the friction force and the aggregate interlock force of concrete on both sides of the crack and the tensile stress of concrete between cracks can be ignored [24].
Since the 1990s, some countries have issued their own codes for the shear calculation of FRP-reinforced concrete beams. Among them, the traditional 45° truss model was adopted by the United States [18], while the variable-angle truss model based on the modified pressure field theory was adopted by Canada [19]. In each code, the shear capacity of a given beam was defined as the sum of the contribution of concrete Vc and the contribution of FRP stirrup VFRP. However, the calculation equations of current codes have some limitations. For example, the shear span ratio is generally considered to be a factor affecting the shear capacity of concrete part, but it is not considered in the American and Chinese codes. Additionally, the calculation results of the shear capacity of beams in various codes are conservative, suggesting that these codes underlying applicability to different types of concrete beams reinforced with FRP have not yet been fully explained. However, in order to ensure the applicability of the design equations to general situations, it is necessary to provide a theoretical basis for them and to determine and reasonably consider the critical parameters such as concrete strength and stirrup strength. The purpose of this paper is to solve this problem. In addition, many scholars have also proposed some new more complex shear models using artificial learning methods, such as the genetic algorithm theory [25], the rigid body rotation shear model [26], and so on.
However, to the best of the authors’ knowledge, since FRP reinforced concrete beams are rarely used in actual structures and the calculation of their shear capacity is more complicated, there is limited research on investigations into the shear properties of concrete beams reinforced with types of FRP stirrups. Therefore, comprehensive experiments and theoretical analyses were carried out to investigate the shear capacity of FRP-reinforced concrete beams in this study. The rest of this article is organized as follows: Section 2 introduces in detail the four-point bending test of six reinforced concrete (RC) beams reinforced with FRP stirrups. Section 3 completely discusses the effects of shear span to depth ratio (λ) and stirrup spacing (S) on the deflection, strain, bearing capacity, crack form, and failure mode of FRP-reinforced concrete beams. In Section 4, the calculation formula of the shear capacity of concrete beams without web reinforcement is established based on the strut-and-tie model, and further, a new shear capacity calculation model of concrete beams reinforced with FRP stirrups is proposed by using superposition with the bearing capacity of the FRP stirrup. Finally, the accuracy of the proposed model in this study was evaluated through comparing the test results of 56 beam specimens extracted from this study and previous studies, with the results calculated using models from American, Canadian, and Chinese codes, alongside this study.
2. Experimental Program
2.1. Beam Specimen Design
A total of 6 concrete beams reinforced with GFRP stirrups were tested. The dimensions of all beam specimens were designed to be 150 mm in width, 300 mm in depth, 3000 mm in length and 2700 mm in span [27], as shown in Figure 1. Steel bars with diameter of 20 mm were adopted as the longitudinal reinforcement, and GFRP bars with diameter of 6 mm were adopted as the stirrups. Each beam specimen contained six longitudinal steel bars, two of which were placed on the top, and the other four were arranged in two rows at the bottom of the beam. The concrete cover of each beam was uniformly 20 mm. In this study, four shear span to depth ratios (λ = 1, 2, 3 and 4) and three stirrup spacings (S = 100, 150 and 200 mm) were designed as the parameters influencing the shear capacity of beams. Each beam specimen was identified by a code starting with “B”. More specific parameters and details of the beams are listed in Table 1.
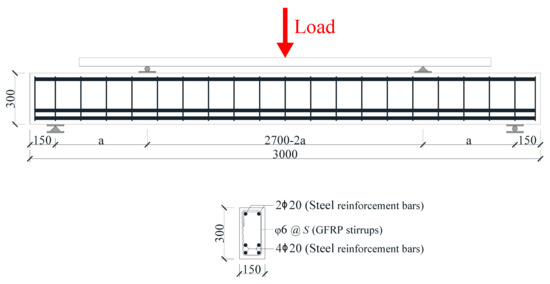
Figure 1.
Configuration and details on concrete beams reinforced with GFRP stirrups (dimensions in mm).

Table 1.
Details of concrete beams reinforced with GFRP stirrups.
2.2. Materials
In this study, ordinary concrete with a compressive strength grade of C30 was used, and the standard value of the cubic compressive strength of concrete fcu was tested to be 33.00 MPa, which was converted into a cylinder compressive strength fc′ of 26.07 MPa (fc′ = 0.78fcu). HRB400 steel bars of diameter of 20 mm were used as longitudinal reinforcements, and GFRP stirrups of diameter of 6 mm were used as shear reinforcements to reinforce the concrete beams. A photograph and schematic diagram of the GFRP stirrups are shown in Figure 2 [27]. According to ASTM D7205/D7205M-06 [28], the tensile properties of GFRP bars were determined using straight GFRP bars with a diameter of 6 mm, and were made of the same material as the GFRP stirrups. The tested tensile strength and elastic modulus of GFRP bars were 716.3 MPa and 55.6 GPa, respectively. The detailed tensile test results of GFRP bars are shown in Table 2.
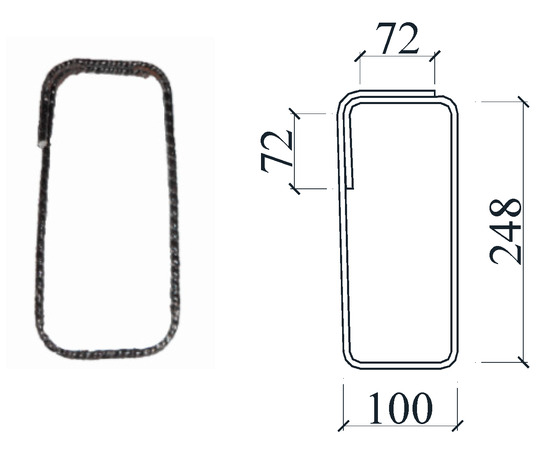
Figure 2.
Photograph and schematic diagram of GFRP stirrup (dimensions in mm) [27].

Table 2.
Tensile test results of GFRP bars.
2.3. Beam Specimen Preparation
In order to accurately measure the deformation of the beam specimen and the strain of the stirrup and longitudinal reinforcement during the loading process, strain gauges were pasted to the designated positions of the GFRP bars and longitudinal steel bars before the concrete was poured, and linear variable differential transformers (LVDTs) were placed at the designated positions against the concrete surface before the test loading. The specific arrangement of strain gauges and LVDTs for each beam specimen is shown in Figure 3. Taking the vertical central axis in the middle of the beam span as the axis of symmetry, all the LVDTs and strain gauges were symmetrically distributed on the left and right sides of the beam. For simplicity, only the LVDTs and strain gauges on the left half span of the beam were marked. A reinforcing cage consisting of GFRP bars and longitudinal steel bars with the strain gauges pasted is shown in Figure 4.
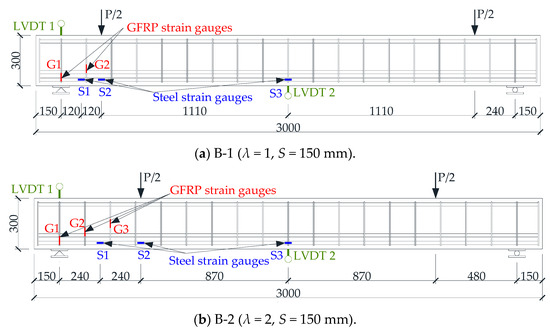
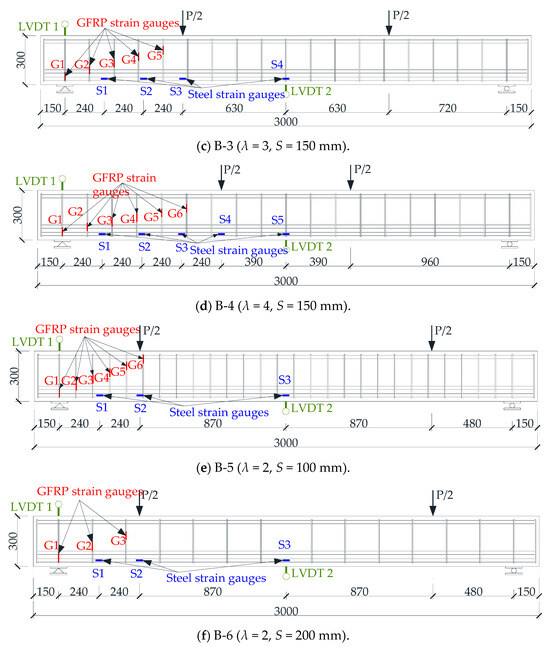
Figure 3.
Schematic diagram of layout of strain gauges and LVDTs.

Figure 4.
Reinforcing cage consisting of steel bars and GFRP stirrups with strain gauges pasted. Note: The top specimen is B-6 (λ = 2, S = 200 mm); the bottom one is B-2 (λ = 2, S = 150 mm).
2.4. Test Set-Up and Loading Program
The beam specimen was simply supported on reinforced concrete piers with a span of 2700 mm, as shown in Figure 5. The loading procedure mainly included two phases, i.e., preloading and formal loading, according to GB 50152-92 [29]. Before each formal loading, the specimen beam was applied with a preload load not exceeding 70% of the calculated value of the cracking test load, and then we checked whether the strain gauge and displacement meter worked normally.

Figure 5.
Experimental set-up of beam specimen.
The formal loading was divided into the following parts:
- (1)
- At the beginning, the load level of each level was 10 kN and maintained for 10 min.
- (2)
- When the load was close to the cracking of concrete, the load level was changed to 5 kN per level. When the first crack appeared in flexural zone of beam between two loading points, the load value was recorded as the first crack load Vcr.
- (3)
- The load level was restored to 10 kN per level after the first crack appeared. When the first oblique crack appeared in the flexural compression zone, the load value was recorded as the first diagonal shear crack Vscr.
- (4)
- When the maximum crack expands to 1.5 mm, the load value of the beam specimen was recorded as the shear capacity of experiment Vexp.
3. Results and Discussions
The test results of the mid-span deflection, crack development, and failure mode of all the beam specimens are summarized in Table 3. The influence of shear span to depth ratio (λ) and stirrup spacing (S) on the shear performances in terms of the load deflection behavior, load–strain behavior, shear capacity, crack patterns, and failure modes of the tested beams were discussed in turn, as follows.

Table 3.
Test results of beam specimens.
3.1. Shear Force–Deflection Response
The effects of shear span to depth ratio (λ) and stirrup spacing (S) on the shear force-deflection responses at midspan of the beam specimens are shown in Figure 6. As is found, before the first crack, the shear-deflection behavior of all beams was nearly linear. After cracking, the effective concrete area decreased, and the moment of inertia decreased, so that the shear force–deflection curve of the beams was still linear, but the stiffness was reduced [30]. Figure 6a revealed that the bending moment increases rapidly with the increase in λ, and the deformation of the beam also increases [31]. It is worth noting that in Figure 6b the deflection of specimen B-6 suddenly increased at 78 kN. This is due to an insufficient stirrup ratio causing some stirrups to reach the limit deformation earlier and brittle fracture. That is to say, the inhibition of GFRP developing into inclined cracks in concrete improves the bearing capacity and ductility of beam specimens. On the other hand, for B-2 and B-5, the slope remains linear, revealing that the contribution of GFRP stirrups to the beam shear capacity remains at a high level. In Summary, GFRP, as a kind of stirrup, exerts its high strength and high ductility to improve the strength and deformation capacity of concrete beams.
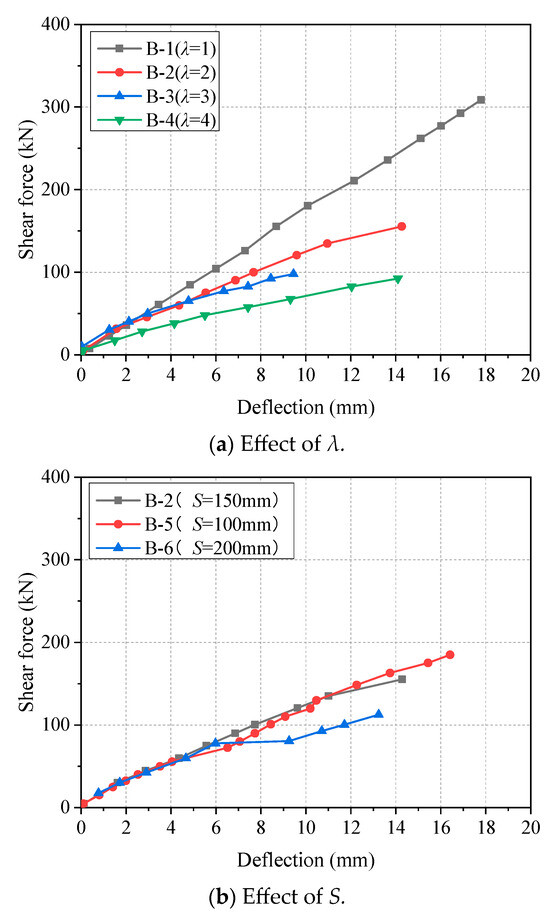
Figure 6.
Shear force–deflection curves at midspan of beam specimens.
3.2. Shear Force–strain Response
The relationships between the shear force and the strain of longitudinal bars of all beam specimens are shown in Figure 7. It can be found that all beams have a similar shear force–strain linear relationship. As shown in Figure 7a, with the increase in λ, the slope of the curve decreases. Since the larger λ leads to the larger bending moment in the purely bending part of the beam, the strain of the longitudinal reinforcement will be greater under the same shear force. As shown in Figure 7b, the influence of S on the strain of steel longitudinal reinforcement is not significant, which is similar to the results of previous tests [31]. In addition, the shear force–strain curves at different positions of longitudinal bars are shown in Figure 8. Generally, the slope of the curve at the position closer to the support is larger. This is because when the position is closer to the support point, the shear force of the beam is larger.
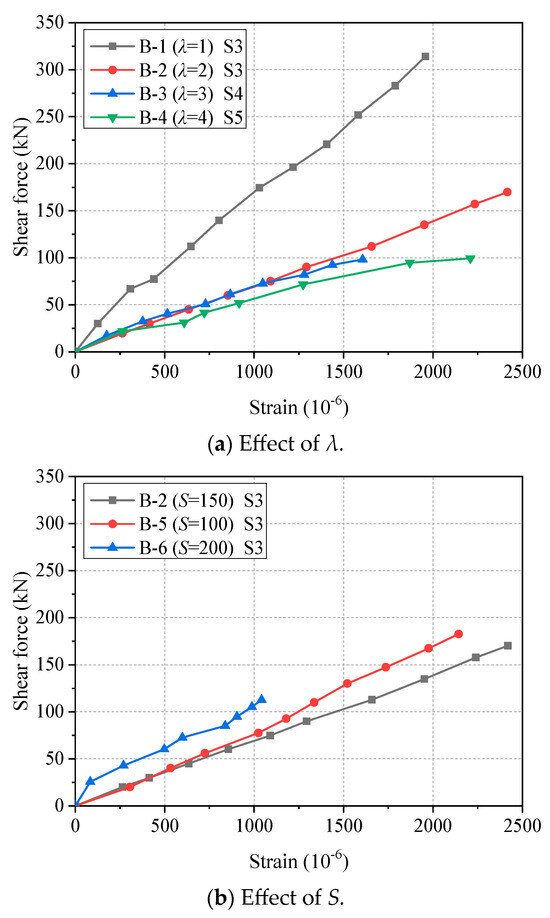
Figure 7.
Shear force–strain curves at midspan of longitudinal steel bars.
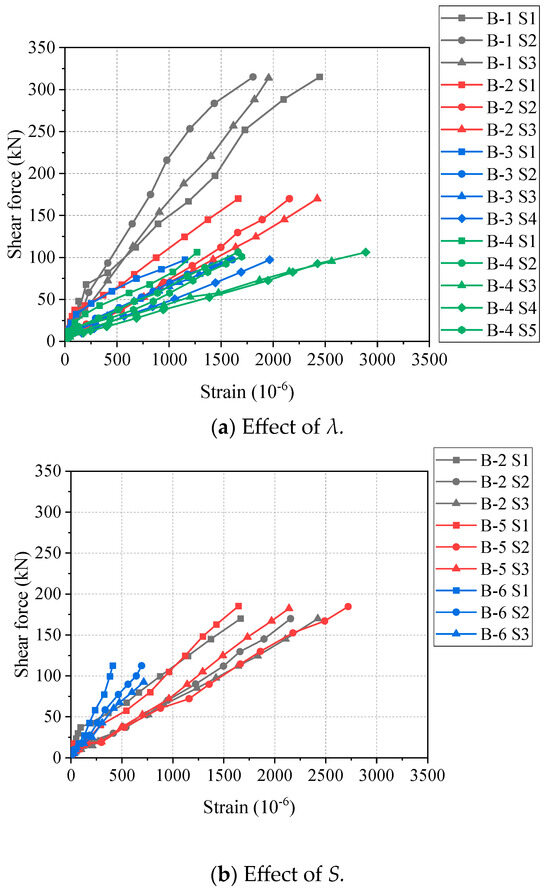
Figure 8.
Shear force–strain curves at different positions of longitudinal steel bars.
Figure 9 illustrates the relationship between the shear force and strain of the GFRP stirrups at different positions between the loading point and support of the beam. All the curves in Figure 9 can be divided into two types according to the different positions: (1) Near the support point (G1), the strain increased slowly with a negative slope as the shear force increased. This is because the stirrups and concrete at the support were locally compressed; (2) for the stirrups between the support and the loading point, the strain suddenly increased after the appearance of cracks. This indicated that the shear contribution of the stirrups increased. The larger changes of the slope illustrate the effectiveness of GFRP stirrups in improving the shear capacity of beams. It is worth noting that the maximum strain of the stirrups of each beam is between 0.002–0.006. Their average value is 0.004, which is consistent with the ultimate strain of 0.004 for stirrups in ACI 440.1R-15 [18].
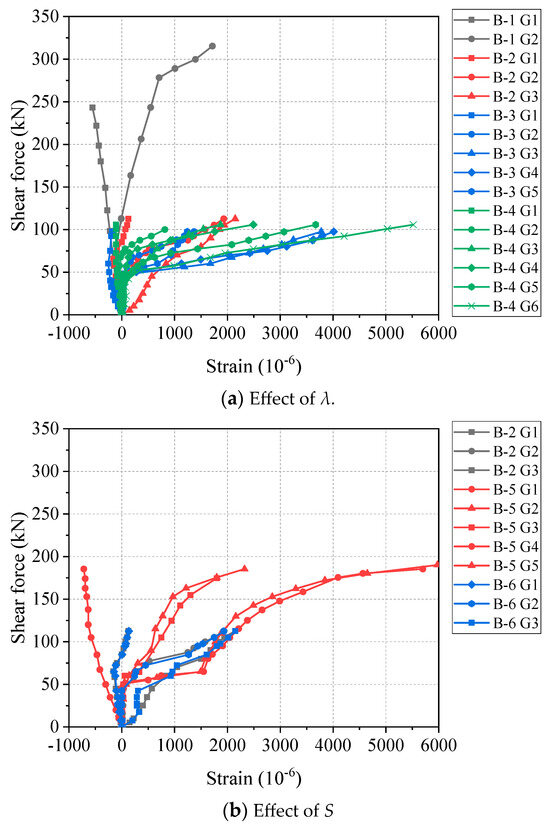
Figure 9.
Shear force–strain curves at different positions of GFRP stirrups.
3.3. Shear Capacity
Figure 10 shows the variation in the ultimate shear force of the beam specimens with λ and S. With the increase in S and λ, the ultimate shear force tended to decrease. On the one hand, as λ increased from 1 to 2, 3, and 4, the ultimate shear force of the beam decreased by 50.5%, 67.7%, and 69.2%, respectively. The increase in λ led to a decrease in the critical shear crack angle, so the bearing capacity of the corresponding section decreased, and the shear capacity decreased accordingly. On the other hand, as S increased from 100 to 150 and 200, the ultimate shear force of the beam decreased by 16.1% and 44.6%, respectively. This was because the decrease in S means denser stirrups, which confined concrete and limited the development of the cracks of the beam.
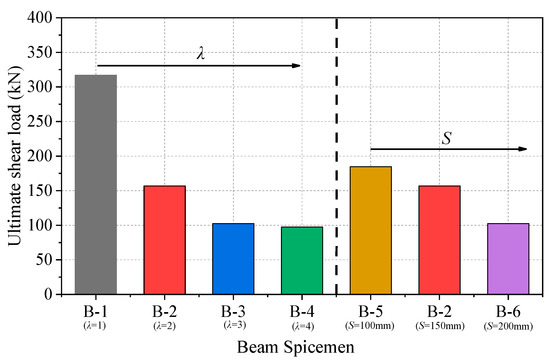
Figure 10.
Ultimate shear force of beam specimens with different λ and S values.
3.4. Crack Patterns
The crack patterns of the beam specimens are shown in Figure 11. Similar crack development can be observed in B-1~B-6. As is found in Table 3, the first cracks of B-1 to B-6 were found under the load of 15 kN~35 kN, and they all appeared in the pure bending zone. The B-1 gave the first crack load of 35 kN. The first crack loads of the B-2, B-3 and B-4 were 43%, 39% and 57% smaller than that of B-1 due to increase in shear span to depth ratio. A comparison was made between B-5, B-2 and B-6, S increased from 100 to 150 and 200, and the load for the first crack was basically unchanged. The results showed that the shear span to depth ratio had an evident influence on the first crack load.

Figure 11.
Crack patterns and failure modes.
The crack development of the beam specimens can be roughly divided into the following three types: (1) For B-1, with the increase in load, several oblique shear cracks appeared in the beam abdomen (e.g., middle zone) between the loading point and the support. The oblique cracks were many and dense when the beam was damaged. (2) For B-2, B-5 and B-6, with the increase in load, many shear inclined cracks appeared in the beam. The beam finally failed along one of the main cracks and the concrete fell off. (3) For B-3 and B-4, the oblique crack in the beam rapidly extended to the point of concentrated load, and formed a long main oblique crack from the loading point to the support.
The relationship curves between the maximum diagonal crack width of beam ωmax and the shear force are shown in Figure 12. The ωmax increases with the increase in shear force, and the slope of the curve increases with the increase in shear force. As can be seen from Figure 12a, the slope of the curve increases faster with the increase in λ. As can be seen from Figure 12b, the curve increases linearly at the beginning, and there is an obvious sudden increase before failure, and the slope of the curve will increase faster with the increase in S. Therefore, λ and S are both important factors affecting crack development.
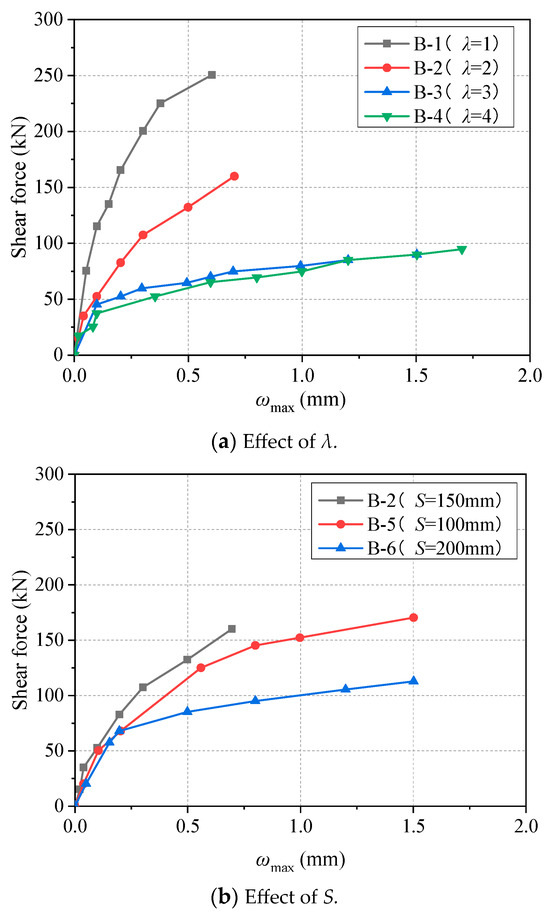
Figure 12.
Relationship curves between the maximum diagonal crack width and shear force of all beam specimens.
3.5. Failure Mode
Compared with previous studies by Said et al. [12,15], we found that there are a total of three types of failure from B-1~B-6., i.e., diagonal compression failure (DC), shear compression failure (SC), and diagonal tension failure (DT). The detailed failure mode of each beam is given in Table 3. Among them, B-1 suffered DC, B-2, B-5 and B-6 suffered SC, and B-3 and B-4 suffered DT.
As we found, λ was the critical factor affecting the failure mode. When λ was relatively small (λ ≤ 1), the diagonal crack extends from near the support point to the loading point. With the increase in load, the crack gradually became horizontal and eventually joined, and finally, the GFRP stirrups and concrete located in the main inclined crack were broken. This was similar to the failure mode of deep beams reinforced with GFRP bars described by Andermatt [32]. When 1 < λ < 3, a crack first appeared at the loading point, and then extended from the support point to the loading plate point to form a critical diagonal crack. The beams could carry the load after the critical diagonal crack formed. Its failure was characterized by the crushing of the concrete near the loading point. When λ ≥ 3, the major diagonal curved cracks appeared in the shear span section of the beam, and developed from the support point to the loading point with the increase in load. As the load continued to increase, parallel cracks formed in the bottom of the shear span section and intersected with the diagonal cracks. Finally, the characteristic of shear tension failure was evident in the concrete cover, and some small concrete pieces inside the stirrups were spilled out.
4. Calculation Model of the Shear Capacities of Concrete Beams Reinforced with FRP Stirrups
4.1. Model Establishment
After the beam specimen appeared oblique cracks, the beam mainly bore the shear force through the tension of the stirrups and some longitudinal reinforcements and the compression of the concrete. As shown in Figure 13, the shear capacity model of the beam was composed of Model 1 and Model 2, which were used to describe beams without a web reinforcement beam and with only stirrups, respectively.
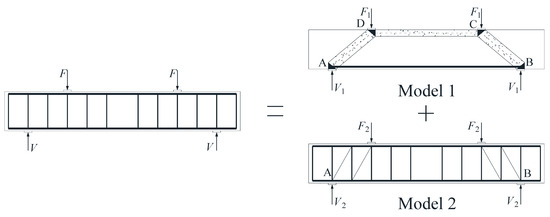
Figure 13.
Shear capacity model of concrete beams reinforced with FRP stirrups.
4.2. Shear Capacity of Concrete Beams without Web Reinforcement: V1
Xiong et al. [33] summarized and put forward the calculation model of shear capacity of concrete beams without web reinforcement. As we found, for concrete beams without web reinforcement, there was an obvious strut-and-tie model when the oblique section of the beam was damaged by shear [34]. As shown in Model 1 in Figure 13, the strut-and-tie model consisted of struts, ties, and nodes. The compressive force was carried by the portions of the concrete between inclined cracks known as struts, and the tension force was carried by the bottom longitudinal reinforcements known as ties. Nodes were the locations where the axes of the struts, ties, and concentrated forces intersected.
4.2.1. Equilibrium Equation
A free-body diagram of a segment of point A from the left support is shown as shown in Figure 14. For equilibrium, the stress of node A of Model 1 must be balanced:
where D is the compression capacity of strut.
where f2max is the compressive stress of strut, and θ is the angle between strut and beam transverse axis, referring to the literature [35].
where da is the height of a concrete horizontal compression bar between nodes C and D. According to reference [36],
where k is the height coefficient of concrete compression area, and can be expressed as follows:
where ρ is the longitudinal reinforcement ratio. n is the elastic modulus ratio of longitudinal reinforcement (Es) to the elastic modulus of concrete (Ec), i.e., and [37].
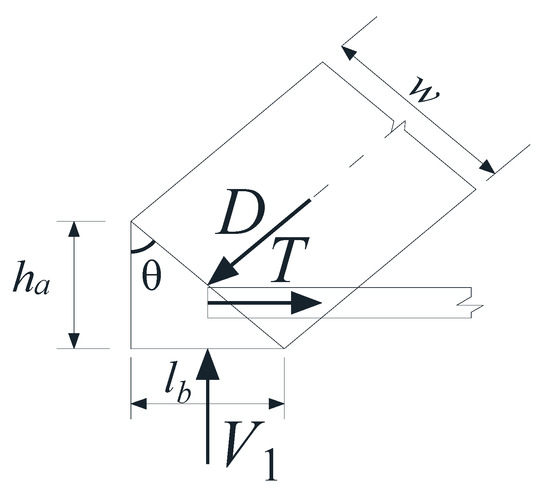
Figure 14.
Force and geometric diagram of point A in Model 1.
4.2.2. Constitutive Equation
When f2max increases to the compressive strength of concrete with oblique cracking βfc′, D reaches its limit, which is equivalent to Model 1 reaching its shear capacity.
According to previous studies [38], the stress–strain relationship in the principal compressive stress direction of softened concrete is as follows:
where fc′ is the specified compressive strength of concrete; β refers to the softening effect coefficient of the compressive strength of cracked concrete, ε0 is the maximum compressive strain of softened concrete (recommended to be taken ε0 as 0.002), εc is the compressive strain of softened concrete, and σc is the compressive stress of softened concrete. The stress–strain curve of softened concrete corresponding to Equation (7) is shown in Figure 15.
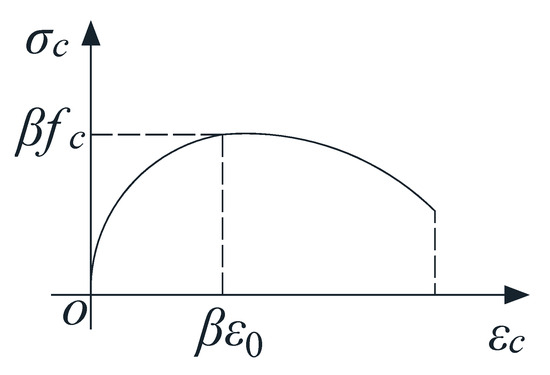
Figure 15.
Stress–strain curve of softened concrete.
Vecchio and Collins obtained the following simplified calculation formula in their research [39]:
where ε1 is the principal tensile strain of concrete in the direction perpendicular to strut.
Therefore, f2max can be expressed as follows:
4.2.3. Compatibility Condition
The strain relationship of beam elements after concrete cracking can be represented by Mohr’s circle [36], and the compatibility conditions for cracked elements are shown in Figure 16. The following formula can be derived from Mohr’s circle:
where εx is the longitudinal strain of the element, εt is the transverse strain of the element, γxt is the shear strain of the element, and ε2 is the principal compressive strain of the strut.
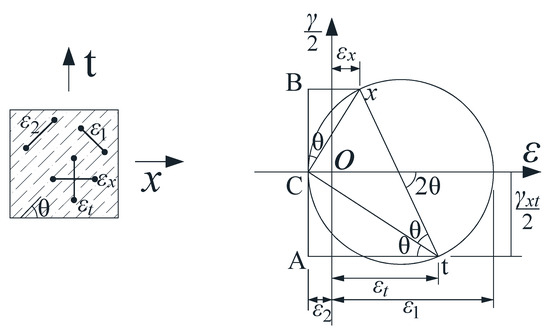
Figure 16.
Compatibility conditions of a cracked element.
The relationship between strains can be obtained from Equations (10) and (11):
The following relationship is obtained from the first strain invariant:
We obtain the following from Equations (8) and (9):
Because ε2 is negative, it can be expressed as follows:
For εx, if the section is near the loading point, εx = 0. If the section is near the support, because it is crossed by longitudinal reinforcement, εx is obtained using following formula [36]:
4.2.4. Parameter w
w, the height of the strut cross-section, has different expression and calculation methods at the support and loading points. This paper specifies the calculation methods at the support and loading point, respectively, as follows:
- (1)
- As shown in Figure 14, w at support point A can be expressed as follows:
- (2)
- As shown in Figure 17, w at load point C can be expressed as follows:
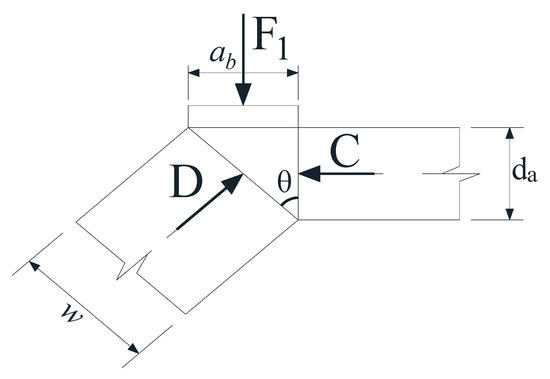
Figure 17.
Force and geometric diagram of point C in Model 1.
4.2.5. Calculation Process
Since w is different at the support and the loading points, the calculation process of shear capacity at the corresponding position is also different. To obtain the shear capacity of the beam, the shear capacity provided by the top (Vt) and the bottom (Vb) of the concrete diagonal strut must be calculated, respectively. It is noted that V1 equals the smaller of Vt and Vb. The calculation process of Vt and Vb is as follows:
- (1)
- The shear capacity provided by the top of strut is Vt.
For the top end of strut, there is no crossing of the tensile reinforcement. The effective strength of concrete is 0.85 fc′ because of C-C-C node [36,40], and Equation (3) can be expressed as follows:
We can combine Equations (1), (18) and (19) to obtain
- (2)
- The shear capacity provided by the bottom of strut is Vb.
We can combine Equations (2), (14)–(16) to obtain
and combine Equations (1), (3) and (9) to obtain
We can also combine Equations (21) and (22) to obtain
Since ε1 is the compressive strain of concrete, the solution of Equation (24) is as follows:
We can then combine Equations (22) and (24) to obtain
The ultimate bearing capacity of concrete beams without web reinforcement is the failure of the top or bottom of the strut, so V1 is the smaller value of Vt and Vb, i.e.
4.3. Shear Capacity Provided by Stirrups: V2
For Model 2, the shear capacity is similar to that provided by steel stirrups in RC beams: . The shear capacity of the beam reinforced with FRP stirrups is calculated according to Equation (27):
where fsv is the effective stress of the FRP stirrup. It can be found from the test phenomenon that when the beam specimens are damaged by shear, the FRP stirrup intersecting the inclined crack does not reach its ultimate tensile strength, so fsv is taken as [18].
Substitute Equation (26) into :
4.4. Calculation Results and Discussion
At present, the design codes and guidelines used to calculate the shear capacities of FRP-reinforced concrete beams mainly include ACI 440.1R-15 [18], CSA S806:12 (reaffirmed 2021) [19], GB 50608-2020 [20], and ISIS-2007 [21]. Based on these design codes and guidelines, the shear capacity of FRP-reinforced concrete beams is divided into the shear capacity contributed by concrete (Vc) and the FRP stirrups (VFRP), and these values are listed in detail in Table 4.

Table 4.
List of design code or guideline equations used to calculate the shear capacities of concrete beams reinforced with FRP bar stirrups.
In order to evaluate the reliability of the shear formula proposed in this paper (i.e., Equation (28)), a database containing 56 test beams was established in this study. The test parameters of 56 beam specimens, including 6 beams in this paper and 50 beams extracted from previously studies [11,41,42,43,44,45,46], are listed in Table 5. The parameters of these specimens include shear span to depth ratio λ, concrete axial compressive strength fc′, FRP stirrup type, and the elastic modulus of the FRP stirrup Esv, etc. The test results of beams reinforced with FRP stirrups were compared with the calculation results of using Equation (28) and the equation mentioned in ACI 440.1R-15, CSA S806:12 (reaffirmed 2021), GB 50608-2020, and ISIS-2007. Further, Figure 18 shows the comparison between the calculation results obtained from the three prediction formulas and the test results. The diagonal line serves as a reference to highlight the deviation between the experimentally observed shear capacity and the shear capacity calculated using the equations.

Table 5.
Summary of calculation results based on Equation (28), ACI-440.1R-15, CSA S806:12 (reaffirmed 2021), GB 50608-2020 and ISIS-2007 and test results of 56 beam specimens reinforced with FRP stirrups.
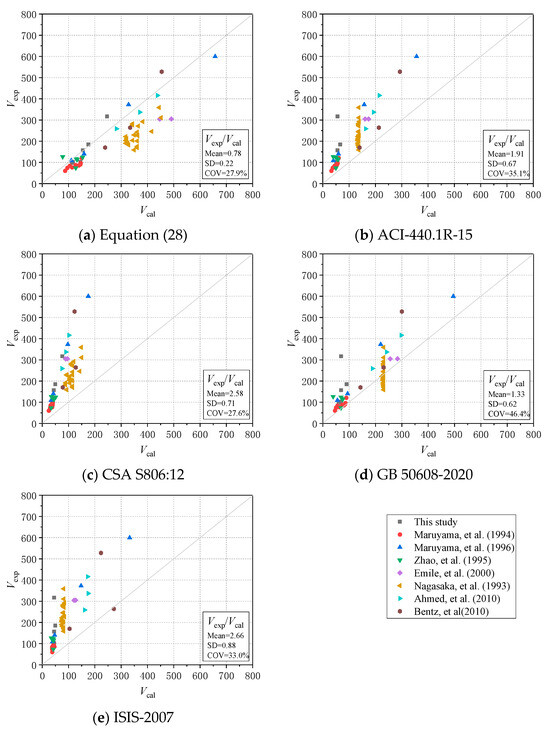
Figure 18.
Comparison between calculation and experimental results [7,41,42,43,44,45,46].
In order to verify the accuracy of the shear capacity calculation model proposed in this paper, the three indicators of the mean value (Mean), standard deviation (SD), and coefficient of variation (COV) of the comparison value Vc/Vexp were calculated, as shown in Table 5 and Figure 18. It can be observed that the calculation results of ACI, CSA, GB and ISIS are quite conservative. The mean values of the experimental calculations (Vexp/Vcal) using ACI, CSA, GB and ISIS are 1.91, 2.58, 1.33 and 2.66, respectively. Because the calculations of ACI, GB, and ISIS did not consider the influence of the shear–span ratio, and alongside the CSA code, we adopted lower reduction factors for both the concrete and stirrup parts, which seriously underestimated the shear capacity. For the results calculated in the GB 50608-2020, some of the shear capacity values of beam specimens with less stirrup spacing were overestimated, but the other points in Figure 18d all located not far above the diagonal line. Moreover, its calculation process is the simplest, so it has more application guidance than others.
It can be seen that the SD value and COV value of the Vc/Vexp are the smallest for Equation (28). The shear capacity calculated by Equation (28) is close to the experimental results, and the mean value and coefficient of variation COV is only 0.77 and 27.4%. It is noted that, similar to GB 50608-2020, the shear capacity of Equation (28) was also overestimated when the stirrup spacing was less than 80 mm. Combined with the experiment results, it can be seen that stirrup spacing of less than 100 mm does not obviously increase the shear capacity. Therefore, the stirrup spacing should have a lower limit of about 100 mm. The calculation results showed that Equation (28) proposed in this paper not only considered the effects of concrete, longitudinal reinforcement and FRP stirrups on shear capacity within other codes and guidelines, but was also more accurate than the models in current codes. In a word, it can be concluded that Equation (28) has a higher precision compared with the existing formulas in the prediction of the shear capacities of concrete beams reinforced with FRP stirrups. In future research, more and more test data on concrete beam reinforced with FRP stirrups should be collected to verify the accuracy and reliability of Equation (28) before it can be used in potential applications or modifications to current design codes.
5. Conclusions
In this study, the shear behavior of concrete beams reinforced with FRP stirrups was investigated, and the deformation and shear capacity of the beam specimens were studied. A shear capacity calculation model based on the strut-and-tie model is proposed and is compared with design codes and guidelines from a database containing 56 beam specimens. The main conclusions can be drawn from this study as follows:
- (1)
- There is a positive linear relationship between the shear force and the mid-span deflection. The shear span to depth ratio λ has a significant effect on the shear–deflection response of beam specimens, and the increase in λ reduced the stiffness of the specimen. Compared with λ, stirrup spacing S has less influence on the ultimate load of the specimen, and when the stirrup spacing is large (S = 200 mm), the stiffness of the specimen decreased in the later stage of loading.
- (2)
- The shear span to depth ratio λ is an important factor affecting the shear capacity and failure mode of beam specimens. When λ increases from 1 to 2, 3, and 4, the ultimate shear capacity of the specimen beam decreases by 50.5%, 67.7%, and 69.2%, respectively. When λ increases from 1 to 2 and 3, and the failure mode was changed from baroclinic failure to shear compression failure and diagonal tension failure.
- (3)
- The shear capacity of RC concrete beams without stirrups was calculated through the strut-and-tie model, then the FRP stirrups’ influence was taken into account. Finally, a new model for calculating the shear capacity of concrete beams with FRP stirrups is established.
- (4)
- By comparing the actual shear capacity of a large number of beams with the predicted capacity based on ACI-440.1R-15, CSA S806:12, GB 50608-2020, ISIS-2007 and Equation (28) proposed in this article, it was concluded that overall, Equation (28) is more accurate for these results than other codes, and its mean and COV values are 0.77 and 27.4%, respectively.
Author Contributions
Conceptualization, project administration, resources, funding acquisition, supervision, writing—review and editing, J.Z.; methodology, investigation, writing—review and editing, X.B.; methodology, investigation, writing—original draft preparation, S.Y.; funding acquisition, supervision, writing—review and editing, Z.W.; investigation, writing—review and editing, H.H.; methodology, writing—review and editing X.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No: 52278282 & 52278284), and the Program for Changjiang Scholars and the Innovative Research Team at the University of the Minister of Education of China (Grant No: IRT_16R67).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| a | Horizontal distance from loading point to supporting point (mm) |
| λ | Shear span to depth ratio |
| S | Stirrup spacing (mm) |
| ρsv | Stirrup reinforcement ratio (%) |
| ρ | Longitudinal reinforcement ratio (%) |
| Vcr | First crack load (kN) |
| Vscr | First diagonal shear crack (kN) |
| Vexp | Shear capacity of experiment (kN) |
| ωmax | Maximum diagonal crack width of beam (mm) |
| Δmax | Maximum deflection (mm) |
| V1 | Shear capacity of concrete beams without web reinforcement (kN) |
| θ | Angle between strut and beam transverse axis (in degree) |
| D | Compression capacity of strut (kN) |
| f2max | Compressive stress of strut (kN) |
| fcu | Standard value of the cubic compressive strength of concrete |
| fc′ | Specified compressive strength of concrete (MPa) |
| β | Softening effect coefficient of the compressive strength of cracked concrete |
| ε0 | Maximum compressive strain of softened concrete |
| εc | Compressive strain of softened concrete |
| σc | Compressive stress of softened concrete (MPa) |
| ε1 | Principal tensile strain of concrete in the direction perpendicular to strut |
| ε2 | Principal compressive strain of strut |
| εx | Longitudinal strain of element |
| εt | Transverse strain of element |
| γxt | Shear strain of element |
| w | Height of strut cross-section (mm) |
| h | Height of beam cross-section (mm) |
| ha | Height of tie cross-section (mm) |
| d | Distance from the extreme compression fibre to the centroid of longitudinal tension force (mm) |
| lb | Width of base plate at support point (mm) |
| ab | Width of base plate at load point (mm) |
| da | Height of concrete horizontal compression bar between nodes C and D (mm) |
| k | Height coefficient of concrete compression area |
| n | Ratio of elastic modulus of longitudinal reinforcement to elastic modulus of concrete |
| Es | Elastic modulus of longitudinal reinforcement (MPa) |
| Ec | Elastic modulus of concrete (MPa) |
| Vt | Shear capacity provided by the top of strut (kN) |
| Vb | Shear capacity provided by the bottom of strut (kN) |
| V2 | Shear capacity provided by stirrups (kN) |
| fsv | Effective stress of FRP stirrup (MPa) |
| Esv | Elastic modulus of FRP stirrup (MPa) |
| Vcal | Shear capacity of calculation (kN) |
References
- Amir, P. 2-Corrosion of Steel in Concrete Structures; Woodhead Publishing: Oxford, UK, 2016; pp. 19–33. [Google Scholar] [CrossRef]
- Xian, G.; Guo, R.; Li, C. Combined effects of sustained bending loading, water immersion and fiber hybrid mode on the mechanical properties of carbon/glass fiber reinforced polymer composite. Compos. Struct. 2022, 281, 115060. [Google Scholar] [CrossRef]
- Xian, G.; Guo, R.; Li, C.; Wang, Y. Mechanical performance evolution and life prediction of prestressed CFRP plate exposed to hygrothermal and freeze-thaw environments. Compos. Struct. 2022, 293, 115719. [Google Scholar] [CrossRef]
- Benmokrane, B.; Zhang, B.; Chennouf, A. Tensile properties and pullout behaviour of AFRP and CFRP rods for grouted anchor applications. Constr. Build. Mater. 2000, 14, 157–170. [Google Scholar] [CrossRef]
- Liu, Y.; Zwingmann, B.; Schlaich, M. Carbon Fiber Reinforced Polymer for Cable Structures A Review. Polymers 2015, 10, 2078–2099. [Google Scholar] [CrossRef]
- Pan, Y.; Yan, D. Study on the durability of GFRP bars and carbon/glass hybrid fiber reinforced polymer (HFRP) bars aged in alkaline solution. Compos. Struct. 2021, 261, 113285. [Google Scholar] [CrossRef]
- Saleh, Z.; Sheikh, M.N.; Remennikov, A.M.; Basu, A. Numerical investigations on the flexural behavior of GFRP-RC beams under monotonic loads. Structures 2019, 20, 255–267. [Google Scholar] [CrossRef]
- Kang, M.R.; Xue, W.C. Research Progress on shear behavior of concrete beams with FRP stirrups. J. North China Univ. Water Resour. Electr. Power (Nat. Sci. Ed.) 2015, 36, 15–20. (In Chinese) [Google Scholar]
- Maranan, G.B.; Manalo, A.C.; Benmokrane, B.; Karunasena, W.; Mendis, P.; Nguyen, T.Q. Shear behaviour of geopolymer-concrete beams transversely reinforced with continuous rectangular GFRP composite spirals. Compos. Struct. 2018, 187, 454–465. [Google Scholar] [CrossRef]
- Maranan, G.B.; Manalo, A.C.; Benmokrane, B.; Karunasena, W.; Mendis, P.; Nguyen, T.Q. Flexural behavior of geopolymer-concrete beams longitudinally reinforced with GFRP and steel hybrid reinforcements. Eng. Struct. 2019, 182, 141–152. [Google Scholar] [CrossRef]
- Bentz, E.C.; Massam, L.; Collins, M.P. Shear Strength of Large Concrete Members with FRP Reinforcement. J. Compos. Constr. 2010, 14, 637–646. [Google Scholar] [CrossRef]
- Liang, X.; Peng, J.; Ren, R. A state-of-the-art review: Shear performance of the concrete beams reinforced with FRP bars. Constr. Build. Mater. 2023, 364, 129996. [Google Scholar] [CrossRef]
- Grace, N.F. Behavior and Ductility of Simple and Continuous FRP Reinforced Beams. Compos. Constr. J. 1998, 2, 186–194. [Google Scholar] [CrossRef]
- Mousavi, S.R.; Esfahani, M.R. Effective moment of inertia prediction of FRP-reinforced concrete beams based on experimental results. Compos. Constr. J. 2012, 16, 490–498. [Google Scholar] [CrossRef]
- Said, M.; Adam, M.A.; Mahmoud, A.A.; Shanour, A.S. Experimental and analytical shear evaluation of concrete beams reinforced with glass fiber reinforced polymers bars. Constr. Build. Mater. 2016, 102, 574–591. [Google Scholar] [CrossRef]
- Ahmed, E.A.; El-Salakawy, E.F.; Benmokrane, B. Shear Performance of RC Bridge Girders Reinforced with Carbon FRP Stirrups. Bridge Eng. J. 2010, 15, 44–54. [Google Scholar] [CrossRef]
- Hegger, J.; Kurth, M. Shear capacity of concrete beams with FRP reinforcement. Proc. Fib Int. Phd Symp. Civ. 2011, 275, 1–14. [Google Scholar] [CrossRef]
- ACI 440.1R-15; Guide for the Design and Construction of Concrete Reinforced with FRP Bars. American Concrete Institute: Farmington Hills, MI, USA, 2015.
- CSA S806:12 (reaffirmed 2021); Design and Construction of Building Structures with Fibre-Reinforced Polymers. Canadian Standards Association (CSA): Toronto, ON, Canada, 2021.
- GB 50608-2010; Technical Code for Infrastructure Application of FRP Composites. China Planning Press: Beijing, China, 2010. (In Chinese)
- Reinforcing Concrete Structures with Fibre Reinforced Polymers, Intelligent Sensing for Innovative Structures (ISIS); SIMTReC: Winnipeg, MB, Canada, 2007.
- Razaqpur, A.G.; Spadea, S. Shear Strength of FRP Reinforced Concrete Members with Stirrups. Compos. Constr. J. 2015, 19, 0401402.1–04014025.15. [Google Scholar] [CrossRef]
- Razaqpur, A.G.; Isgor, B.O.; Greenaway, S.; Selley, A. Concrete Contribution to the Shear Resistance of Fiber Reinforced Polymer Reinforced Concrete Members. Compos. Constr. J. 2004, 8, 452–460. [Google Scholar] [CrossRef]
- Wang, Z.H.; Du, X.L.; Zhan, J.D.; Deng, Z.C. Research Progress on shear behavior of FRP reinforced concrete beams. Compos. Sci. Eng. 2010, 1, 82–85. (In Chinese) [Google Scholar]
- Nehdi, M.; Chabib, H.E.; Said, A.A. Proposed shear design equations for FRP-Reinforced concrete beams based on genetic algorithms approach. Mater. Civ. Eng. J. 2007, 19, 1033–1042. [Google Scholar] [CrossRef]
- Whitehead, P.A.; Ibell, T.J. Rational approach to shear design in fiber-reinforced polymer-prestressed concrete structures. Compos. Constr. J. 2005, 9, 90–100. [Google Scholar] [CrossRef]
- He, H.W. Experimental Study on the Shear Capacity of Concrete Beams with FRP Stirrups. Master’s Dissertation, Zhengzhou University, Zhengzhou, China, 2013. (In Chinese). [Google Scholar]
- D7205/D7205M-06; Standard Test Method for Tensile Properties of Fiber Reinforced Polymer Matrix Composite Bars. ASTM International: West Conshohocken, PA, USA, 2016.
- GB 50152-92; Standard Methods for Testing of Concrete Structures. China Construction Industry Press: Beijing, China, 1992. (In Chinese)
- Hamrani, A.; Alnahhal, W. Shear behavior of basalt FRC beams reinforced with basalt FRP bars and glass FRP stirrups: Experimental and analytical investigations. Eng. Struct. 2021, 242, 112612. [Google Scholar] [CrossRef]
- Fan, X.; Zhou, Z.; Tu, W.; Zhang, M. Shear behaviour of inorganic polymer concrete beams reinforced with basalt FRP bars and stirrups. Compos. Struct. 2021, 255, 112901. [Google Scholar] [CrossRef]
- Andermatt, M.F. Concrete Deep Beams Reinforced with Internal FRP; University of Alberta: Edmonton, AB, Canada, 2010. [Google Scholar] [CrossRef]
- Xiong, J.G.; Fu, G.P. Softened truss model for shear capacity calculation of reinforced concrete short beams without web reinforcement. J. Nanchang Univ. (Eng. Technol.) 2004, 49–53. (In Chinese) [Google Scholar] [CrossRef]
- Xu, X.Z. Theoretical Analysis of the Shear Capacity of Concrete Beams with FRP Stirrups. Master’s Dissertation, Zhengzhou University, Zhengzhou, China, 2015. (In Chinese). [Google Scholar]
- ASCE-ACI Committee 445 on Shear and Torsion. Recent Approaches to Shear Design of Structural concrete. Struct. Eng. J. 1998, 124, 1357–1417. [Google Scholar] [CrossRef]
- Collins, M.P. Prestressed Concrete Structures; Prentice Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- 318-02 and 318R-02; Building Code Requirements for Structural Concrete (ACI 318-02) and Commentary (ACI 318R-02). American Concrete Institute: Farmington Hills, MI, USA, 2002.
- Vecchio, F. Stress-strain characteristics of reinforced concrete in pure shear, Final report. In IABSE Colloquium on Advanced Mechanics of Reinforced Concrete; International Association for Bridge and Structural Engineering: Zurich, Switzerland, 1981; pp. 211–225. [Google Scholar]
- Vecchio, F.J.; Collins, M.P. The Modified Compression-field Theory for Reinforced-concrete Elements Subjected to Shear. Am. Concr. J. Inst. 1986, 83, 219–231. [Google Scholar]
- Schlaich, J. Design and detailing of structural concrete using strut-and-tie models. Struct. Eng. 1991, 69, 113–125. [Google Scholar]
- Maruyama, K.; Zhao, W.J. Flexural and shear behaviour of concrete beams reinforced with FRP rods. Corros. Corros. Prot. Steel Concr. 1994, 1330–1339. [Google Scholar]
- Maruyama, K.; Zhao, W.J. Size effect in shear behavior of FRP reinforced concrete beams, and International Conference on Advanced Composite Materials in Bridges and Structures. CSCE 1996, 227–234. [Google Scholar]
- Zhao, W.; Maruyama, K.; Suzuki, H. Shear behavior of concrete beams reinforced by FRP rods as longitudinal and shear reinforcement. In RILEM Proceedings; Chapman & Hall: Boca Raton, FL, USA, 1995; p. 152. [Google Scholar]
- Emile, S.; Ryan, M.; Sami, R. Fibre reinforced polymer shear reinforcement for concrete members: Behaviour and design guidelines. Can. J. Civil Eng. 2000, 27, 859–872. [Google Scholar] [CrossRef]
- Nagasaka, T.; Fukuyama, H.; Tanigaki, M. Shear performance of concrete beams reinforced with FRP stirrups. ACI Spec. Publ. 1993, 138, 789–812. [Google Scholar]
- Ahmed, E.A.; El-Sayed, A.K.; El-Salakawy, E.; Benmokrane, B. Bend strength of FRP stirrups: Comparison and evaluation of testing methods. Compos. Constr. J. 2010, 14, 3–10. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).