Abstract
This paper reviews quantitative characterization via transmission electron microscopy (TEM) and its application to interfacial phenomena based on the results obtained through the studies. Several signals generated by the interaction between the specimen and the electron beam with a probe size of less than 1 nm are utilized for a quantitative analysis, which yields considerable chemical and physical information. This review describes several phenomena near the interfaces, e.g., clear solid–vapor interface (surface) segregation of yttria in the zirconia nanoparticles by an energy-dispersive X-ray spectroscopy analysis, the evaluation of the local magnetic moment at the grain boundary in terms of electron energy loss spectroscopy equipped with TEM, and grain boundary character dependence of the magnetism. The direct measurement of the stress to the dislocation transferred across the grain boundary and the microstructure evolution focused on the grain boundary formation caused by plastic deformation are discussed as examples of material dynamics associated with the grain boundary. Finally, the outlook for future investigations of interface studies, including the recent progress, is also discussed.
1. Introduction
The microstructures of materials need to be designed and controlled at the nanometer scale to satisfy the recent increase in the demand for engineering materials. Further, the material response to an external field and the corresponding microstructure need to be understood quantitatively for the theoretical modeling of material behavior.
Transmission electron microscopy (TEM) [1] and scanning electron microscopy (SEM) [2] have developed and become commercially available, and microstructure characterization has remarkably progressed in science and technology at the sub-micrometer and nanometer scales. The advantage of electron microscopy over optical microscopy is the use of electrons, which result in an interaction with a specimen. An electron beam provides a high resolution because of its considerably shorter wavelength than light, and electron diffraction can be obtained from crystallographic and geometric information. Further, the emitted X-rays and inelastic electrons, in which the initial energy is lost because of the interaction, are characterized by spectroscopy, i.e., energy-dispersive X-ray spectroscopy (EDS) and electron energy-loss spectroscopy (EELS). Chemical and physical properties, such as the identification of elements and their composition are analyzed by EDS and the valency of ions and an electronic structure are analyzed by EELS. Detailed information on TEM can be found in well-known textbooks [3,4,5,6,7,8]. Moreover, the acquisition of digital data using a charge-coupled device (CCD) [9,10,11] and an imaging plate (IP) film [12,13,14,15,16,17] enables a more efficient quantitative analysis with analytical tools such as EDS and EELS. Figure 1 illustrates the number of articles, including the words “quantitative analysis” and “transmission electron microscopy (or TEM)” in the “title”, “abstract”, or “keywords”. This was referred to by the Scopus [18]. The number of papers has increased steeply since the early 1990s, which is the incipient time in which reports on the CCD and IP were published in the same era. Further, this progress is one of the reasons why quantitative analysis using TEM has been widely conducted.
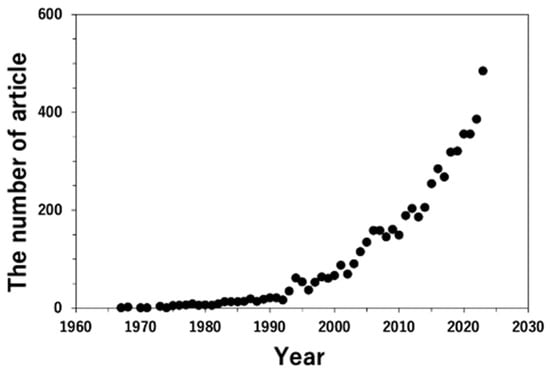
Figure 1.
The change in the number of articles in the fields of “Materials Science”, “Physics and Astronomy”, “Chemistry”, and “Engineering”, which include “quantitative analysis”, and “transmission electron microscopy” or “TEM”, in the title or abstract, or keywords. Data are referred to by scopus.com (accessed on 12 September 2023).
In this article, the quantification analyses by TEM are presented based on some examples from the author’s experiments to highlight their application in the interfaces. The interface, known as an interphase or grain boundary, is a two-dimensional lattice defect in polycrystalline and multiphase materials [19,20,21,22]. The interfaces are high-energy states in comparison with the matrix as a defect-free region, which results in different chemical and physical behaviors. Further, they often govern their mechanical and functional properties and play an important role from an engineering viewpoint [19,21,22,23,24]. Many researchers have attempted to control the grain boundary microstructure to improve its properties based on the concept of “grain boundary engineering” proposed by Watanabe [25,26]. Understanding the structure (both atomic and chemical) and properties of individual interfaces and the relationship between them is essential for controlling the grain boundary and interface structure. Therefore, the nature of the interfaces needs to be understood from a scientific viewpoint for engineering applications. As for studies on grain boundaries and interfaces, the international conference on the intergranular and interphase boundary in materials (IIB) is held every three years [27]. The papers from the recent IIB after 2004 are published as the special issue [28,29,30,31,32,33,34], and it can be pursued as the trend of the research on grain boundaries and interfaces.
This paper reviews the microstructural characterizations of several interfaces using TEM equipped with EDS and EELS. In the next section, the chemical characterization of TEM-EDS is described with application to the solid–vapor (surface) segregation of the zirconia nanoparticle, in which the sample preparation is contrived to analyze the whole of the individual particles. Then, the local magnetic moment characterization at the grain boundary is explained as physical properties characterized by EELS as one of the new characterization techniques. Recently, scanning TEM (STEM) has been recognized as a powerful tool, and both EDS and EELS analyses combined with STEM have become the mainstream for quantitative characterization on a nanoscale. Particularly, a STEM-equipped aberration correction system enables characterization on an atomic scale. However, this article focuses on the TEM characterization that has been conducted so far, and the quantitative characterization of STEM is described later in the section of prospects. The dynamics of the interfaces investigated by in situ straining TEM experiments are also presented. In performing the in situ experiments, the direct measurement succeeded in the dislocation transfer to the grain boundary. Moreover, the dynamics of the microstructure evolved to form grain boundaries during plastic deformation. SEM, which is frequently used for characterizing the microstructures [35,36], and the capability of combining the grain boundary character distribution with electron backscattered diffraction (EBSD), is discussed in detail [37,38,39]. However, the review only discusses the characterization of the interface and the grain boundary by TEM as the other points are beyond the scope of the review.
2. Solid–Vapor Interface (Surface) Segregation Analyzed by TEM-EDS
EDS is commonly used to identify the elements existing in a particular area, and it is one of the most popular attachments equipped with TEM and SEM. Thus far, several textbooks on EDS have been published [5,8,35]. The principles of the quantitative analysis are briefly explained in this section. The inner-shell electron is ejected at a specific energy when the incident electron probe penetrates the specimen. The ionized atom returns to a stable (ground) state by filling the electron from the outer shell because the ionized atom, in which the electron in the inner shell is unoccupied, is known as the excited state. The signal emitted upon returning to the ground state is an X-ray, and the energy-ejecting electrons depend on the elements. Therefore, it is referred to as a characteristic X-ray. The signal was transformed into a current from the detected photons by a detector (converter), and the EDS system displayed the signal as a profile. A quantitative profile, such as the composition of elements x, Cx was evaluated by calculating the peak ratio expressed as
where Ix represents the peak intensity of element x. Equation (1) is the basis for the quantitative EDS analysis. Therefore, it was used in both SEM (bulk specimen) and TEM (thin-film specimen). The coefficient KAB includes the entire process from the X-ray emission to the display as the signal. Consequently, calibration processes are conducted for quantitative evaluations [5,35,40,41]. The thin-film approximation, which excludes the X-ray absorption in the specimen, is generally used for TEM-EDS [5]. As an improved quantitative chemical analysis, the ζ factor analysis proposed by Watanabe has recently gained significant research attention for the quantitative EDS analysis to improve the accuracy of quantities [40,41]. Further, the X-ray efficiency is improved significantly by the configuration of the specimen and X-ray detector and by the enlargement of the detector [42]. Further, the EDS analysis is frequently conducted using aberration (Cs)-corrected scanning transmission electron microscopy (STEM) and chemical analysis on an atomic scale with the simultaneous observation of the atomic structure [43,44,45,46,47,48,49,50]. Several studies on this topic are currently underway [44,45,46,47], but this technique expands our knowledge of the chemical distribution of elements, such as grain boundary segregation in ceramic materials with highly ordered structures [48,49] and metallic materials [50]. In this section, as a case study of the application of EDS, the quantitative analysis around a solid–vapor interface in zirconia (ZrO2) nanoparticles, which includes yttria (Y2O3), i.e., the distribution of Y2O3 near the surface of the nanoparticle, is examined [51].
Figure 2a,b show TEM bright-field images of the ZrO2 nanoparticles prepared by the (a) common method and (b) ion milling method for cross-sectional observation. In the conventional method, a mixture of ZrO2 powder and ethanol is added to a TEM grid. The proposed method is simple and easy to implement; however, because of particle aggregation, the particles overlap with each other, as shown in Figure 2a, and it is difficult to observe the isolated particles. For the cross-sectional observation, particles dispersed ultrasonically are mixed with the epoxy resin and prepared by the standard method of mechanical grinding, dimpling, and ion milling. For the particle–resin mixture, the ZrO2 particles in the TEM specimen are smaller; however, they can be observed individually, as shown in Figure 2b.

Figure 2.
A bright field image of yttria doped zirconia particles taken from the TEM specimens prepared by (a) common method and (b) cross-sectional method. Reprinted from Ref. [51] with permission from John Wiley and Sons.
Figure 3 shows a high-resolution TEM image of ZrO2 particles. The entire particle is flattened by the ion milling process, and the atomic structure inside the particle in Figure 3c, as well as the surface region shown in Figure 3b, is observed clearly. Furthermore, the ion-milled particles are chemically analyzed without considering shadowing because of the rounded shape and uneven surface of the specimen.

Figure 3.
(a) A high-resolution transmission electron micrograph of yttria doped zirconia particle. The FFT pattern in (a) indicates that the particle is tetragonal single phase. Enlarged lattice image of (b) the surface and (c) the internal region of the particle indicated by B and C in (a), respectively. Reprinted from Ref. [51] with permission from John Wiley and Sons.
Figure 4 shows the Y2O3 distribution in a single particle, which is quantitatively analyzed using a point analysis. This figure presents the surface segregation of Y2O3. The Y2O3 content decreases steeply to a few nanometers from the surface, and the contents are recovered up to a nominal composition of approximately 3 mol% within less than 10 nm from the surface, and they remain inside the particles. This chemical inhomogeneity remains as grain boundary segregation after sintering [52], and it plays an important role in the phase transformation in the ZrO2-Y2O3 system. In these ZrO2 particles, a monoclinic region is observed near the surface, in which both phases exhibit a specific orientation relationship. The occurrence of the monoclinic phase is attributed to the stress-induced transformation during sample preparation [53,54,55,56,57,58]. In this study, a quantitative analysis is performed on the composition distribution of the nanoparticle surface segregation.
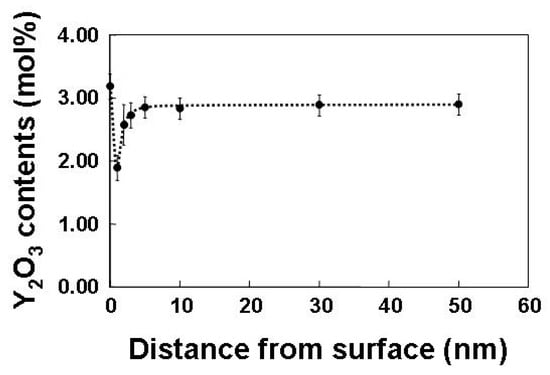
Figure 4.
A composition of yttria estimated by quantitative analysis of EDS spectra in yttria doped zirconia particle as a function of the distance from the surface. Reprinted from Ref. [51] with permission from John Wiley and Sons.
3. Experimental Characterization of the Local Magnetic Moment by TEM-EELS and Its Grain Boundary Character Dependence
In Section 2, the basis of EDS and chemical analysis by EDS is described with a case study of solid–vapor interface segregation in ZrO2 nanoparticles within a few nm from the surface as an example of the chemical analysis, such as the chemical composition and distribution. On the other hand, in EELS, the energy distribution of the electrons, which results in inelastic interactions during the penetration of the specimen, is analyzed for the electronic structure at a high spatial resolution and used as the characterization of the chemical bonding rather than the chemical composition [59]. The detected peaks are categorized into zero loss, plasmon loss, and core loss peaks, which are caused by an elastic interaction (no energy loss), inelastic interaction with valence electrons, and electrons in the inner shell. The characterization of the electronic structure by combining EELS analysis and ab initio calculations has recently been reviewed [60,61]. In addition, EELS has the advantage of analyzing light elements such as carbon, nitrogen, and oxygen because of the high energy resolution, which is less than 1 eV and much higher than that of EDS (approximately 140 eV). A concept similar to EDS was used to perform a quantitative analysis utilizing EELS, and the relationship between the chemical amount, represented as the number of elements, and the peak intensity was expressed by
where Nx, sx, and Ix represent the number of elements x, partial ionization cross section of x, and peak intensity of x above the background, respectively. This equation can be used to perform a quantitative analysis using EELS. However, EDS is frequently used for quantitative chemical analyses because of the high background of the energy loss spectrum and multiple scattering depending on the specimen thickness. A detailed description of the EELS is provided in the references [59,62]. Although quantitative analysis by electron energy loss spectrum is performed for estimating the specimen thickness using the zero-loss peak, etc., there is a report on the relationship between the d-state occupancy in transition metals, and the intensity ratio of the two L edges referred to the white line [63,64]. Pease et al. proposed a relationship between the white line ratio and magnetic moment [65]. Based on their report, we demonstrated the quantitative measurement of the local magnetic moment at the grain boundary in 3D transition metals [66,67,68,69].
Goodenough pointed out the possibility of a nucleation center for the domains of reverse magnetization in ferromagnetic materials [70] to determine the relationship between magnetism and grain boundaries; many researchers have reported these relationships, such as the interaction between the magnetic domain wall and grain boundary [71,72,73,74,75,76] and theoretically [77,78,79,80,81,82,83,84,85]. Recent ab initio calculations demonstrated the grain boundary magnetism that the local magnetic moment increases at the grain boundary; this increase significantly depends on the grain boundary geometry (e.g., misorientation angle) and chemistry (grain boundary segregation) [82,84,85]. However, only a few experimental studies on grain boundary magnetism have been performed, with the exception of neutron diffraction [86]. In this study, the EELS technique proposed by Pease [65] was applied to measure the local magnetic moment at the grain boundary.
Figure 5 shows an example of the electron energy loss spectra of the Fe–L edge obtained from the grain interior (bottom), Σ3 grain boundary (middle), and random grain boundary (top) in pure Fe (99.99 mass% purity). The geometry of the grain boundaries analyzed by EELS was characterized by orientation image microscopy (OIM) with electron backscatter diffraction (EBSD). Further, in the case of TEM, information on both the grain boundary and grain interior was included even if the probe had a diameter of less than 1 nm. The technique proposed by Gu et al. [87,88] was used to extract components only from the grain boundary. The measured L3/L2 ratio, termed the white-line ratio, is summarized as a function of the misorientation angle in Figure 6. The magnetic moment at the grain boundary was enhanced at a high misorientation angle compared to that in the grain interior. Furthermore, the cusp of the magnetic moment can be observed at the S9 boundary. This is the first report on the grain boundary character dependence of local magnetic moments. The grain boundary is the preferred site for segregation, and therefore, the effect of grain boundary segregation on magnetism has been widely examined [84,85,89,90,91,92,93,94,95,96,97]. The effect of grain boundary segregation on the local magnetic moment was investigated.
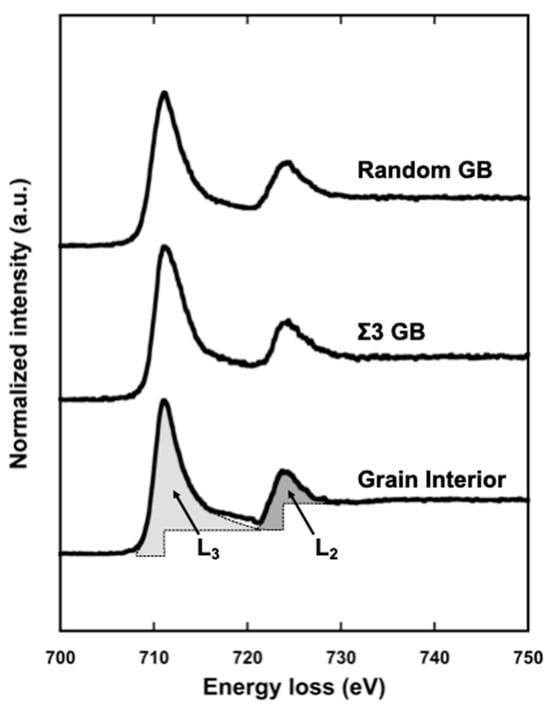
Figure 5.
Typical L edge in EELS spectra obtained from grain interior (bottom), Σ3 grain boundary (middle), and random grain boundary (top) in iron, respectively. The L2 and L3 absorption edges are clearly seen at 710 eV and 725 eV, respectively. Each hatched region shown in the L2 and L3 edge represents schematically the line intensity in L edge obtained from grain interior, which is used in calculating the white-line ratio, R. Reprinted from Ref. [67] with permission from Elsevier.
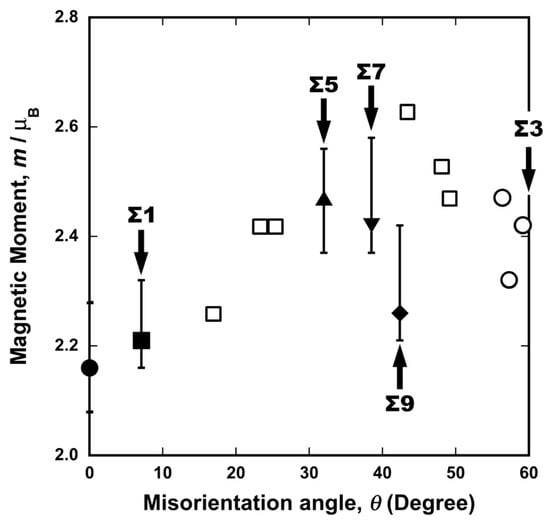
Figure 6.
Experimentally obtained local magnetic moments in pure iron as function of misorientation angle. Moments were measured by the TEM–EELS technique. Solid circle, square, triangles, inverse triangle, and rhombus correspond to the grain interior, Σ1, Σ5, Σ7, Σ9 coincidence boundaries, respectively, and open circles and squares to the Σ3 and random boundary. Reprinted from Ref. [67] with permission from Elsevier.
Figure 7 and Figure 8 show the misorientation-angle dependence of the local magnetic moment obtained in Fe-6 at% Si and Fe-0.8 at% Sn alloys [69]. Both figures include the magnetic moment at the grain boundary obtained for pure Fe as a reference [67]. The local grain boundary moment at the random boundary in the Fe–Si and Fe–Sn alloys was reduced compared to that in pure Fe. However, there is no remarkable change at the Σ5 boundary. These results suggest that the local magnetic moment is determined by combining the physical effect of the geometry and the chemical effect of segregation, as illustrated in Figure 9.
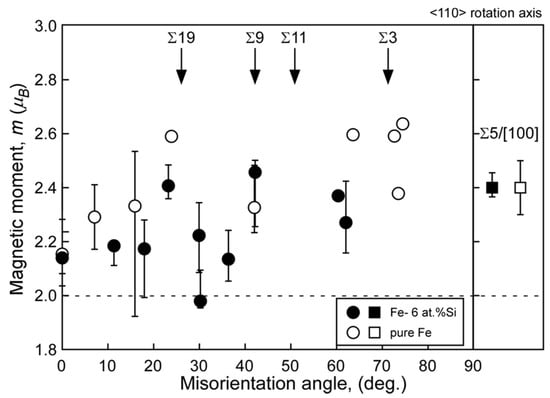
Figure 7.
Local magnetic moments at grain boundaries in the Fe-6 at% Si alloy (solid) and pure Fe (open) as a function of misorientation angle around the <110> rotation axis. For comparison, the local magnetic moment at Σ5 grain boundary with <100> rotation axis in the Fe-6 at% Si alloy are also shown in the figure. The error bar is also shown, and data points that indicate no error bar are data points taken from single EELS measurement. The broken line in this figure indicates the saturated magnetic moment evaluated by a nuclear magnetic resonance (NMR) for the Fe-6 at% Si alloy. Reprinted from Ref. [69] with permission from the Japan Institute of Metals and Materials.
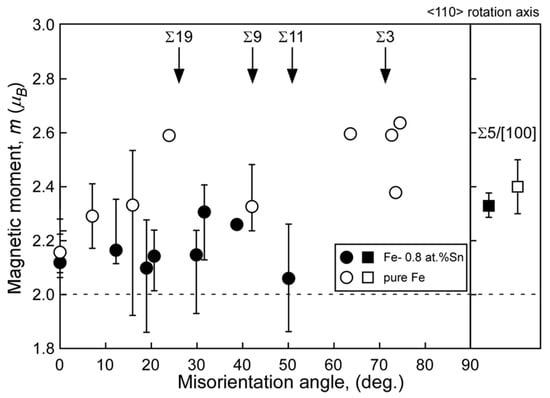
Figure 8.
Local magnetic moments at grain boundaries in the Fe-0.8 at% Sn (solid) alloy and pure Fe (open) as a function of misorientation angle around the <110> rotation axis. For comparison, the local magnetic moment at Σ5 grain boundary around <100> rotation axis in the Fe-0.8 at% Sn alloy is also shown in the figure. The error bar is also shown, and data points indicating no error bar are data points taken from single EELS measurement. The broken line in this figure indicates the saturated magnetic moment evaluated by a vibrating sample magnetometer (VSM) for the Fe-0.8 at% Sn alloy. Reprinted from Ref. [69] with permission from the Japan Institute of Metals and Materials.
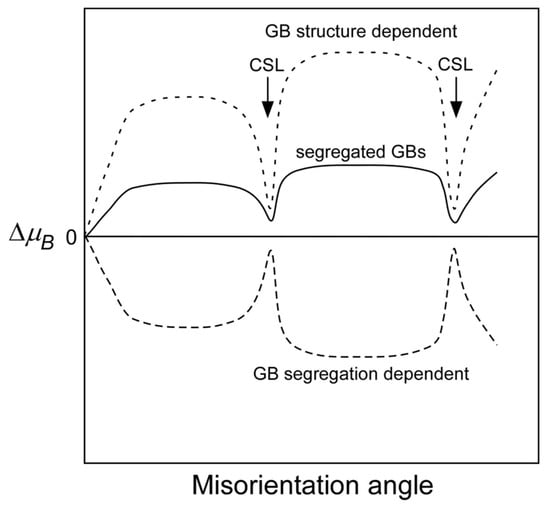
Figure 9.
Schematic explanation of the misorientation dependence of the local magnetic moments at solute (impurity)-segregated grain boundaries, which will be determined by competing between the favoring effect due to the GB structure and disfavoring effect due to grain boundary segregation on the local magnetic moments. Reprinted from Ref. [69] with permission from the Japan Institute of Metals and Materials.
To characterize the magnetic properties by the L edge, X-ray magnetic circular dichroism (XMCD) has been well known [98,99,100,101]. On the other hand, Schattschneider et al. proposed electron magnetic circular dichroism (EMCD) to characterize them in terms of (S)TEM and EELS [102,103,104], and several researchers conducted it [105,106,107]. Muto et al. evaluated the ratio of the orbital (ml) and spin (ms) magnetic moments (ml/ms) [106]. The details of magnetism are clarified at a high spatial resolution by combining these techniques. Further, grain boundary segregation is one of the main factors of grain boundary embrittlement [108,109]; recent ab initio calculations represented the effect of grain boundary segregation and resulting in the local magnetism at the grain boundary on grain boundary embrittlement in Fe–Mn alloys [110]. They also discussed embrittlement from the viewpoint of changes in magnetism at the grain boundary. The relationship between grain boundary segregation and grain boundary embrittlement in steel was reported approximately half a century ago [111,112], and state-of-the-art experiments and theoretical calculations are expected to answer this question.
4. Dynamics and Quantitative Evaluation Associated with the Grain Boundary by In Situ Experiments
The above two sections represented the quantitative analyses by EDS and EELS combined with TEM. EDS and EELS analyses are usually conducted statically because of the time-consuming techniques for signal detection, whereas understanding the dynamics of the materials in external fields is also significantly important to comprehend how response in the materials. The in situ experiment in TEM and SEM is a powerful tool for clarifying the behavior of materials for the various fields, and one can see many reports on the response of the materials under various fields, such as temperature, stress, and atmosphere [113,114,115]. On the other hand, since the publication of the reports by Hall [116] and Petch [117], the Hall–Petch relationship has been well-known for explaining the relationship between mechanical properties and grain size in polycrystalline materials. The grain size corresponds to the grain boundary density; in other words, the mechanical properties are governed by the grain boundaries. The pile-up model is widely accepted for understanding the Hall–Petch relationship [118], and the grain boundary–dislocation interaction has been investigated from both experimental and computational viewpoints [119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143]. Recently, nanoindentation techniques have been employed to understand the mechanical response in the vicinity of an individual grain boundary [128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143]. Moreover, in situ TEM (and SEM) straining experiments are powerful tools for understanding the microstructure evolution of small-scale specimens under the stress field. These have received considerable attention for deformation in the grain interior [144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159], deformation [160,161,162,163,164,165,166,167,168,169,170,171,172,173,174], and fracture [175,176,177,178] around grain boundaries. Among them, some specimen holders can explore the simultaneous mechanical behavior during the microstructure evolution [146,147,150,151,152,154,156,157,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174].
Figure 10 shows the true stress–true strain (S-S) curve of a 4N Al bicrystal pillar, including a single Σ3 grain boundary, obtained by in situ indentation experiments. The S–S curve exhibits an apparent yield phenomenon around the crossing point of the two dashed lines drawn in the S–S curve, and after yielding, a small stress drop is frequently detected. This phenomenon is known as intermittent plasticity [156,179]. Figure 11 shows snapshots captured in the movie during in situ straining for the Σ3 bicrystal pillar. This movie is available as a supplementary movie in Ref. [173]. Figure 11a,d correspond to A to D in Figure 10, respectively. The dislocations were activated and transferred across the grain boundaries before the macroscopic yield phenomenon. The critical resolved shear stress (CRSS) that the dislocation is transferred across the grain boundary was measured from the S–S curve in Figure 10 within 0.06–0.09 GPa. This CRSS matches the stress range estimated from the Hall–Petch coefficient obtained from the macroscopic experiments [180,181].
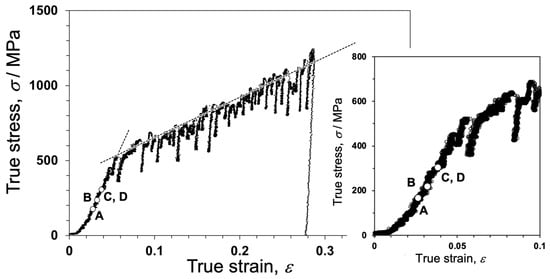
Figure 10.
True stress–true strain (S–S) curve of the bicrystal pillar, including the Σ3 grain boundary. The dashed black lines evaluating the pseudo yield stress in the bicrystal are also drawn in the S–S curve. The initial stage of the S–S curve is also shown. To demonstrate the accuracy of the in situ TEM experiment, S–S curves of the single crystal pillars obtained from each grain composing the bicrystal are shown with this S–S curve in Figure S1 in the supplementary material in Ref. [173]. Reprinted from Ref. [173] with permission from Elsevier.

Figure 11.
(a–d) Snapshots captured the movie during compression for the Σ3 bicrystal pillar. A–D inserted into the lower right on each image correspond to points (A–D) indicated in the S–S curve in Figure 2, respectively. Dislocations indicated by triangles are activated from the contact between indent and sample in the grain A. Details can be represented in Ref. [173]. Reprinted from Ref. [173] with permission from Elsevier.
Further, it also succeeded in capturing grain boundary formation attributed to the dislocation accumulation via in situ straining experiments [159]. Figure 12 shows the dynamics of grain boundary formation in the IF steel during in situ straining. Stress inhomogeneity occurred because the specimen included a concave surface, which resulted in the activation of various slip systems. Tangled dislocations subsequently formed sharp grain boundaries, as shown in micrograph (e) and schematic (f). The line contrast was experimentally recognized as a grain boundary by automated crystal orientation mapping (ACOM) [182], as shown in Figure 13. The orientation of the deformed specimen indicated in the Low-angle annular dark-field (LAADF)-STEM image (a) is analyzed as (b–d), which are imaged in the z (b), y (c), and x directions (d). The coordinates are indicated at the bottom left in (d). Further, the grain boundaries determined from the crystal orientation are represented by black and white lines. The white line corresponds to misorientation angles from 2° to 15°, and the misorientation angle of the black line is greater than 15°. The white and black lines represent the small- and high-angle grain boundaries, respectively. In this case, the misorientation angle of each grain boundary, indicated as the line between a to b and c to d in (d), is evaluated in (e) and quantitatively understood as the existence of sharp peaks or steps in (e). The grain boundary formation can be explained by the dislocation reaction. The grain boundary formation through deformation is recognized as grain refinement in ultrafine-grained metals via severe plastic deformation [183,184]. Also, grain refinement is achieved via grain subdivision during deformation [185,186,187,188,189]. The microstructural evolution obtained in this study is well explained by grain boundary formation. A similar phenomenon was reported in [190]; however, it was observed for a nanowire. This is the first report of a specimen that is close to the bulk scenario. The deformation microstructures in various nanocrystalline materials were also quantitatively analyzed by utilizing a combination of ACOM and in situ straining experiments [191,192,193].
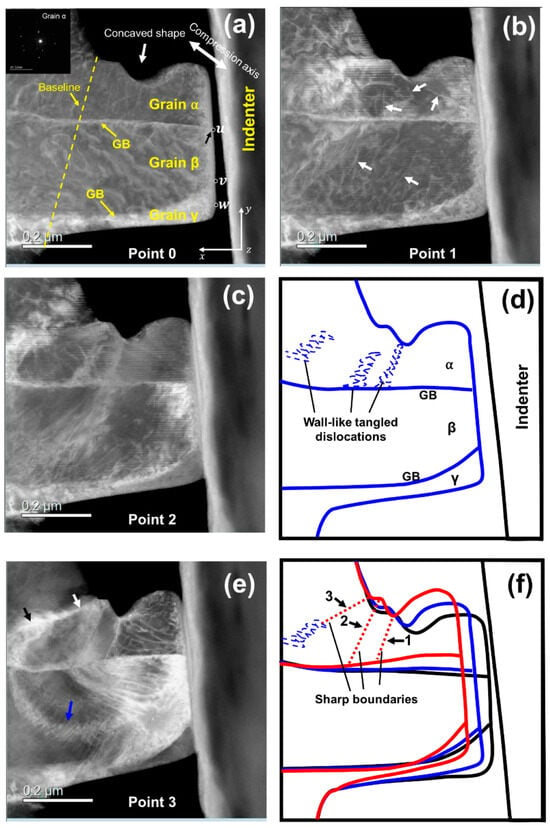
Figure 12.
Dynamic observation of GB formation in bcc iron during TEM in situ compression testing. Low-angle annular dark-field (LAADF)- STEM micrographs of the micropillar (a–c,e), corresponding to points 0–3 in Figure 1 of Ref. [159], respectively. (d) Illustration of the wall-like tangled dislocations in (c). (f) Illustration of the formed GBs and the changes in the geometry of micropillar. The black, blue, and red outer contours represent the geometries of the micropillar in (a,c,e), respectively. The inset in (a) is a selected area electron diffraction pattern of grain α before deformation. Details can be represented in Ref. [159]. Reprinted from Ref. [159] with permission from Elsevier.
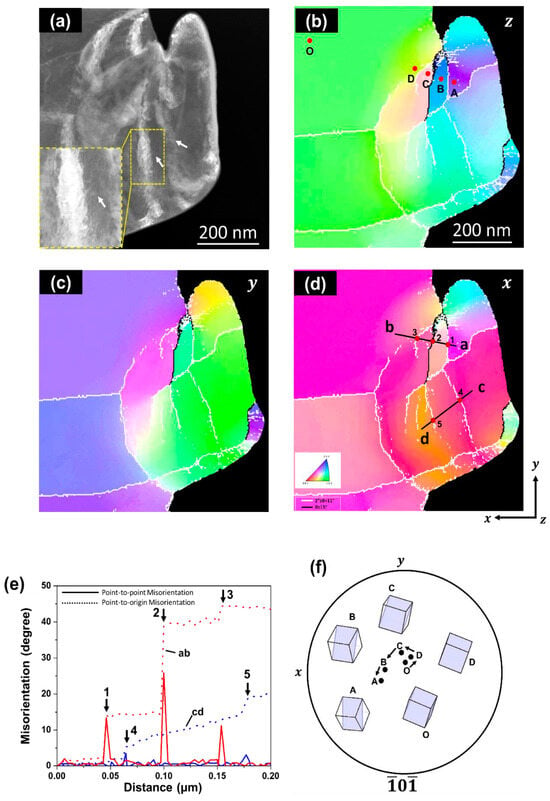
Figure 13.
GB confirmation by precession electron diffraction. (a) LAADF-STEM of micropillar after TEM in situ compression test. Orientation maps obtained by scanning precession electron diffraction measurements from (b) z direction, (c) y direction, and (d) x direction. (e) Misorientation line profile of line segments ab and cd in (d). (f) The crystallographic orientations of the positions of O and A–D are plotted in the pole figure. The orientation at position O at the grain center was used as the original orientation of grain α. In these orientation maps, the grain boundaries with misorientation angles (θ) of 2° ≤ θ ≤ 15° and 15° ≤ θ are defined as low- and high-angle boundaries, which are indicated as white and black lines, respectively. Details can be represented in Ref. [159]. Reprinted from Ref. [159] with permission from Elsevier.
5. Prospects of the Quantitative Characterization of Interface and Grain Boundary by (S)TEM
In the previous sections, it was shown that the quantitative analysis performed by EDS and EELS combined with (S)TEM and related applications to the interface and grain boundaries with the obtained examples. However, new analytical techniques are still being developed for understanding unknown issues of the interfacial phenomena.
The first is an improvement in the accuracy of the quantities. As aforementioned in the first section, STEM is commonly applied to the characterization of the microstructure and the spectroscopic analysis. It is well known that STEM images are generated by the detection of electrons transmitted during the scanning of the specimen, and there are many types of images depending on the interaction between the electron and specimen [194]. High-angle annular dark-field (HAADF) imaging is used to detect scattered electrons at a high angle through the specimen, and the intensity is closely related to the atomic number (Z). Furthermore, the bright contrast in the HAADF image corresponds to the atomic column, and the interpretation of the images is more straightforward than that of the HRTEM images. Therefore, STEM has become a standard technique for characterizing atomic structures. In STEM images, the key to improving spatial resolution is the formation of a probe using an aberration correction technique; currently, a spatial resolution of up to 40.5 pm has been realized [195]. Furthermore, the spatial resolution of spectroscopy is also improved with the fine probe, resulting in the chemical mapping at an atomic scale by EDS and EELS with STEM have been successfully obtained so far [43,44,45,46,47,48,49,50,196]. Moreover, several works on estimating the chemical composition from STEM images have also been reported recently [197,198,199,200,201]. Van Aert et al. [197] and Molina et al. [198] proposed estimating the composition from the intensity of each column in the HAADF-STEM images. Subsequently, the composition of the Al matrix, the vacancies in the Al alloys [199], and the absolute value from the column composition were estimated. These techniques were improved by combining them with image simulations [200]. Recently, the light elements were also quantitatively analyzed [201]. For the further improvement of the chemical analysis, understanding the quantitativeness caused by an interaction of the electron and specimen is important.
On the other hand, chemical and physical properties, such as the grain boundary segregation and the grain boundary energy, are affected by the inhomogeneity of the atomic structure. The inhomogeneity is closely related to the excess volume at the grain boundary. Branova [202] attempted to analyze the excess volume at the grain boundary using HAADF-STEM images. The excess volume is also detected as the local elastic strain. The techniques for the quantitative evaluation of the displacement of atoms and related elastic strain developed by Hÿtch [203,204] and Galindo [205] provided remarkable progress in understanding the strain distribution in the microstructure, especially on the atomic scale. Thus far, there have been many reports on the characterization of elastic strain not only at the grain boundaries as twins [206] and dislocations at the grain boundaries [207,208,209] but also at the interphase boundary in the device [210], heterointerface at an epitaxially grown superlattice [211], and precipitate/matrix interfaces [212,213,214,215,216]. In addition to the strain (stress) field evaluated by the precise measurement of the displacement of atoms, the differential phase-contrast (DPC) imaging by a segmented detector [217] spread a new era in the visualization of electric [218,219] and magnetic fields [220] on an atomic scale. This technique is currently used to characterize heterointerfaces in a functional device [221,222,223].
A novel quantitative analysis of the physical properties using the EELS is also proposed [224,225,226,227]. The core loss edges in EELS are frequently used to analyze the physical and chemical properties related to electrons. In contrast, Oleshko et al. proposed the use of plasmon loss peaks, termed valence EELS (VEELS), to characterize the physical properties of the interphase boundary [224]. Subsequently, Nandy et al. applied VEELS to grain boundaries and discussed the correlation between VEELS and the electron density and volume expansion of the grain boundary [225,226,227]. From a theoretical perspective, Kohyama et al. evaluated the local energy and local stress at the surface and grain boundaries using ab initio calculations [228]. The local energy can be quantitatively evaluated by combining these techniques. Further, a low-loss region was used to characterize the surface plasmons [229] and quantitatively evaluate the bandgap near the Si/SiO2 heterointerface [230]. Further, the remarkable improvement in the energy resolution in EELS using a monochromated electron probe was addressed by Krivanek [231], and a recent energy resolution of less than 10 meV was achieved. This improvement enabled us to evaluate the vibrations, especially the localized vibrational response demonstrated at the heterointerface [232] and grain boundary [233].
In contrast to the analytical viewpoint, the grain boundary engineering proposed by Watanabe in the 1980s from the standpoint of material science [25,26] made a trend to tailor the grain boundary microstructure, which is focused on the geometry of grain boundaries such as the misorientation angle and S-value, termed a “grain boundary character”. In addition to Watanabe’s concept, Raabe proposed “grain boundary segregation engineering” in his review [234] and attempted to control the chemistry of the grain boundary. This concept has spread to the interphase boundary [235] and has been demonstrated [236,237,238]. Atom probe tomography is an important tool for understanding the chemical distribution at specific interfaces and boundaries and the relationship between structure and chemistry [234,235,236,237,238,239,240,241]. However, quantitative analysis using electron microscopy is indispensable because simultaneous observations and analyses can be performed. Furthermore, an in situ study of the mechanical behavior on an atomic scale was performed using a precise MEMS system [242]. The continuous developments of the aforementioned analytical techniques for hardware and software are expected to help elucidate the interfacial phenomena that remain unexplored, which is a direct measurement of the interfacial energy and their distribution in the metastable state/matrix interphase boundary, which only (S)TEM can explore their microstructure, etc.
6. Concluding Remarks
In this article, the quantitative analysis by EDS and EELS equipped with the TEM is described, along with its application to the phenomena accompanied by the interface and the grain boundary. As seen in the references, it is challenging to summarize because of the significant work on the characterization of the interface and the grain boundary, but the points of this article are concluded as follows,
- EDS analysis, which is frequently used in chemical analysis, such as the identification of the elements and the chemical compositions, was explained. Based on this, the solid–vapor (surface) segregation of doped Y2O3 within a few nm from the surface in ZrO2 nanoparticles was explored.
- The TEM-EELS technique, which is often used to understand the electronic structure, is conducted to characterize the local magnetic moments closely related to 3D electrons. Also, the grain boundary character dependence and the effect of the grain boundary segregation of the magnetic moments are quantitatively obtained.
- The characterization of the dynamics of materials by an in situ experiment is also presented. The in situ straining experiments succeeded in the direct stress measurement at the dislocation transfer to the grain boundary and the capture of the microstructure evolution to form grain boundaries during plastic deformation.
- In addition to the application of EDS and EELS to characterize the interface and grain boundary that the author reported so far, the prospects of the characterization of the interface and grain boundary are stated for further improvement of the quantitative analysis.
Funding
This study was partly supported by JSPS KAKENHI Grant numbers, 19106013, 16H06366, 22H01760, and 23K04365.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The authors of this paper used the collections of journals and electronic databases available in Scopus.
Acknowledgments
The author would like to sincerely express their gratitude to Y. Ikuhara and H. Yoshida of the University of Tokyo, and K. Matsui and N. Ohmichi of Tosoh Corp. for their help for the characterization of the zirconia nanoparticle; S. Tsurekawa of Kumamoto University, K. Hirayama of Kumamoto University (now in Kyoto University), T. Fujii of former Tohoku University, and M. Šob of Masaryk University for demonstrating the local magnetic moment measurement using TEM-EELS; T. Ohmura, T. Hara, and H. Li of NIMS, S. Tsurekawa and T. Enami of Kumamoto University, and N. Tsuji of Kyoto University for the in situ (S)TEM straining experiment. The author appreciates the fruitful discussions and encouragement. In addition, the author would like to thank several people at the University of Tokyo, Kumamoto University, and NIMS for their technical assistance.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Ruska, E. The Development of the Electron Microscope and of Electron Microscopy. Available online: https://www.nobelprize.org/prizes/physics/1986/ruska/lecture/ (accessed on 12 September 2023).
- McMullan, D. Scanning electron microscopy 1928–1965. Scanning 1995, 17, 175–185. [Google Scholar] [CrossRef]
- Hirsch, P.B.; Howie, A.; Nicholson, R.B.; Pashley, D.W.; Whelan, M.J.; Marton, L. Electron Microscopy of Thin Crystals, 2nd ed.; Krieger Publishing Company: Malabar, FL, USA, 1977. [Google Scholar]
- Reimer, L.; Kohl, H. Transmission Electron Microscopy, 5th ed.; Springer: New York, NY, USA, 2008. [Google Scholar] [CrossRef]
- Williams, D.B.; Carter, B. Transmission Electron Microscopy, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Fultz, B.; Howe, J.M. Transmission Electron Microscopy and Diffractometry of Materials, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Spence, J.C.H. High-Resolution Electron Microscopy, 4th ed.; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Carter, C.B.; Williams, D.B. (Eds.) Transmission Electron Microscopy Diffraction, Imaging, and Spectroscopy; Springer: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Mooney, P.E.; Fan, G.Y.; Meyer, D.E.; Truong, K.V.; Bui, D.B.; Krivanek, O.L. Slow-Scan CCD Camera for Transmission Electron Microscopy. In Proceedings of the 12th International Congress for Electron Microscopy, Seattle, WA, USA, 12–18 August 1990; San Francisco Press: San Francisco, CA, USA, 1990; Volume 1, p. 164. [Google Scholar]
- Ishizuka, K. Analysis of electron image detection efficiency of slow-scan CCD cameras. Ultramicroscopy 1993, 52, 7–20. [Google Scholar] [CrossRef]
- Fan, G.Y.; Ellisman, M.H. Digital imaging in transmission electron microscopy. J. Microsc. Oxford 2000, 200, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Mori, N.; Oikawa, T.; Katoh, T.; Miyahara, J.; Harada, Y. Application of the “imaging plate” to TEM image recording. Ultramicroscopy 1988, 25, 195–201. [Google Scholar] [CrossRef] [PubMed]
- Mori, N.; Oikawa, T.; Harada, Y.; Miyahara, J. Development of the imaging plate for the transmission electron microscope and its characteristics. J. Electron Microsc. 1990, 39, 433–436. [Google Scholar] [CrossRef]
- Shindo, D.; Hiraga, K.; Oikawa, T.; Mori, N. Quantification of electron diffraction with imaging plate. J. Electron Microsc. 1990, 39, 449–453. [Google Scholar] [CrossRef][Green Version]
- Murakami, Y.; Shindo, D. Lattice modulation preceding to the R-phase transformation in a Ti50Ni48Fe2 alloy studied by TEM with energy-filtering. Mater. Trans. JIM 1999, 40, 1092–1097. [Google Scholar] [CrossRef][Green Version]
- Murakami, Y.; Shibuya, H.; Shindo, D. Precursor effects of martensitic transformations in Ti-based alloys studied by electron microscopy with energy filtering. J. Microsc. 2001, 203, 22–33. [Google Scholar] [CrossRef]
- Ii, S.; Nishida, M.; Murakammi, Y.; Shindo, D. Martensitic transformation in Ti50Pd50.0−XFeX alloy. J. Phys. Arch. 2003, 112, 1035–1038. [Google Scholar] [CrossRef]
- Scopus. Available online: https://www.scopus.com/search/form.uri?display=basic#basic (accessed on 12 September 2023).
- McLean, D. Grain Boundaries in Metals; Clarendon Press: Oxford, UK, 1957. [Google Scholar]
- Gleiter, H.; Charmers, B. Structure of grain boundaries. Prog. Mater. Sci. 1972, 16, 1. [Google Scholar] [CrossRef]
- Sutton, A.P.; Balluffi, R.W. Interfaces in Crystalline Materials; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Howe, J.M. Interfaces in Materials; John Wiley & Sons, Inc.: New York, NY, USA, 1997. [Google Scholar]
- Chadwick, G.A.; Smith, D.A. Grain Boundary Structure and Properties; Academic Press: London, UK, 1976. [Google Scholar]
- Ishida, Y., Ed.; In Proceedings of Fourth Japan Institute of Metals International Symposium on Grain Boundary Structure and Related Phenomena, Minakami, Japan, 25–29 November 1985; The Japan Institute of Metals: Sendai, Japan, 1986.
- Watanabe, T. Approach to grain boundary design for strong and ductile polycrystals. Res. Mech. 1984, 11, 47–84. [Google Scholar]
- Watanabe, T. Grain boundary engineering: Historical perspective and future prospects. J. Mater. Sci. 2011, 46, 4095–4115. [Google Scholar] [CrossRef]
- Intergranular and Interphase Boundaries in Materials, IIB2014. Available online: https://iib2024.org/ (accessed on 12 November 2023).
- Special Issue: Interface Science, Vol. 9, Iss. 3-4. Available online: https://link.springer.com/journal/10793/volumes-and-issues/9-3 (accessed on 12 November 2023).
- Interface Science Section in Journal of Materials Science, Vol. 40, Iss. 11. Available online: https://link.springer.com/journal/10853/volumes-and-issues/40-11 (accessed on 12 November 2023).
- Special Issue: Intergranular and Interphase Boundaries in Materials in Journal of Materials Science, Vol. 43, Iss.11. Available online: https://link.springer.com/journal/10853/volumes-and-issues/43-11 (accessed on 12 November 2023).
- Special Issue: Intergranular and Interphase Boundaries in Materials in Journal of Materials Science, Vol. 46, Iss. 12. Available online: https://link.springer.com/journal/10853/volumes-and-issues/46-12 (accessed on 12 November 2023).
- Special Section: Intergranular and Interphase Boundaries in Journal of Materials Science, Vol. 49, Iss. 11. Available online: https://link.springer.com/journal/10853/volumes-and-issues/49-11 (accessed on 12 November 2023).
- Special Section: Intergranular and Interphase Boundaries in Journal of Materials Science, Vol. 52, Iss. 8. Available online: https://link.springer.com/journal/10853/volumes-and-issues/52-8 (accessed on 12 November 2023).
- Special Section: Interface Science in Journal of Materials Science, Vol. 55, Iss. 22. Available online: https://link.springer.com/journal/10853/volumes-and-issues/55-22 (accessed on 12 November 2023).
- Goldstein, J.I.; Newbury, D.E.; Echlin, P.; Joy, D.C.; Romig, A.D., Jr.; Lyman, C.E.; Fiori, C.; Lifshin, E. Scanning Electron Microscopy and X-ray Analysis, 2nd ed.; Plenum Press: New York, NY, USA; London, UK, 1992. [Google Scholar]
- Reimer, L. Scanning Electron Microscopy, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Wilkinson, A.J.; Meaden, G.; Dingley, D.J. High-resolution elastic strain measurement from electron backscatter diffraction patterns: New levels of sensitivity. Ultramicroscopy 2006, 106, 307–313. [Google Scholar] [CrossRef]
- Schwartz, A.J.; Kumar, M.; Adams, B.L.; Field, D.P. Electron Backscatter Diffraction in Materials Science, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Gutierrez-Urrutia, I.; Zaefferer, S.; Raabe, D. Coupling of electron channeling with EBSD: Toward the quantitative characterization of deformation structures in the SEM. J. Miner. Met. Mater. Soc. 2013, 65, 1229–1236. [Google Scholar] [CrossRef]
- Watanabe, M.; Williams, D.B. The quantitative analysis of thin specimens: A review of progress from the Cliff-Lorimer to the new zeta-factor methods. J. Microsc. 2006, 221, 89–109. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, M. Microscopy hacks: Development of various techniques to assist quantitative nanoanalysis and advanced electron microscopy. Microscopy 2013, 62, 217–241. [Google Scholar] [CrossRef] [PubMed]
- Kawai, S.; Onishi, I.; Ishikawa, T.; Yagi, K.; Iwama, T.; Miyatake, K.; Iwasawa, Y.; Matsushita, M.; Kaneyama, T.; Kondo, Y. A double silicon drift type detector system for EDS with ultrahigh efficiency and throughput for TEM. Microsc. Microanal. 2014, 20, 1150–1151. [Google Scholar] [CrossRef]
- D’Alsonfo, A.J.; Freitag, B.; Klenov, D.; Allen, L.J. Atomic-resolution chemical mapping using energy-dispersive x-ray spectroscopy. Phys. Rev. Lett. 2010, 81, 100101(R). [Google Scholar] [CrossRef]
- Kothleitner, G.; Neish, M.J.; Lugg, N.R.; Findlay, S.D.; Grogger, W.; Hofer, F.; Allen, L.J. Quantitative elemental mapping at atomic resolution using X-ray spectroscopy. Phys. Rev. Lett. 2014, 112, 085501. [Google Scholar] [CrossRef]
- Lugg, N.R.; Kothleitner, G.; Shibata, N.; Ikuhara, Y. On the quantitativeness of EDS STEM. Ultramicroscopy 2015, 151, 150–159. [Google Scholar] [CrossRef] [PubMed]
- MacArthur, K.E.; Yankovich, A.B.; Beche, A.; Luysberg, M.; Brown, H.G.; Findlay, S.D.; Heggen, M.; Allen, L.J. Optimizing experimental conditions for accurate quantitative energy-dispersive X-ray analysis of interfaces at the atomic scale. Microsc. Microanal. 2021, 27, 528–542. [Google Scholar] [CrossRef]
- Watanabe, M.; Egerton, R.F. Evolution in X-ray analysis from micro to atomic scales in aberration-corrected scanning transmission electron microscopes. Microscopy 2022, 71 (Suppl. S1), i132–i147. [Google Scholar] [CrossRef] [PubMed]
- Feng, B.; Yokoi, T.; Kumamoto, A.; Yoshiya, M.; Ikuhara, Y.; Shibata, N. Atomically ordered solute segregation behaviour in an oxide grain boundary. Nat. Commun. 2016, 7, 11079. [Google Scholar] [CrossRef] [PubMed]
- Futazuka, T.; Ishikawa, R.; Shibata, N.; Ikuhara, Y. Grain boundary structural transformation induced by co-segregation of aliovalent dopants. Nat. Commun. 2022, 13, 5299. [Google Scholar] [CrossRef] [PubMed]
- Langenohl, L.; Brink, T.; Richter, G.; Dehm, G.; Liebscher, C.H. Atomic-resolution observations of silver segregation in a [111] tilt grain boundary in copper. Phys. Rev. B 2023, 107, 134112. [Google Scholar] [CrossRef]
- Ii, S.; Yoshida, H.; Matsui, K.; Ohmichi, N.; Ikuhara, Y. Microstructure and surface segregation of 3 mol% Y2O3-doped ZrO2 particles. J. Am. Ceram. Soc. 2006, 89, 2952–2955. [Google Scholar] [CrossRef]
- Matsui, K.; Horikoshi, H.; Ohmichi, N.; Ohgai, M.; Yoshida, H.; Ikuhara, Y. Cubic-Formation and Grain-Growth Mechanisms in Tetragonal Zirconia Polycrystal. J. Am. Ceram. Soc. 2003, 86, 1401–1408. [Google Scholar] [CrossRef]
- Rühle, M.; Heuer, A.H. Phase transformations in ZrO2-containing ceramics: II, The martensitic reaction in t-ZrO2. Adv. Ceram. 1983, 12, 14–32. [Google Scholar]
- Kelly, P.M.; Rose, L.R.F. The martensitic transformation in ceramics-Its role in transformation toughening. Prog. Mater. Sci. 2002, 47, 463–557. [Google Scholar] [CrossRef]
- Bansal, G.K.; Heuer, A.H. On a martensitic phase transformation in zirconia (ZrO2)—I. Mettallographic evidence. Acta Metall. 1972, 20, 1281–12899. [Google Scholar] [CrossRef]
- Bansal, G.K.; Heuer, A.H. On a martensitic phase transformation in zirconia (ZrO2)—II. Crystallographic aspects. Acta Metall. 1974, 22, 409–417. [Google Scholar] [CrossRef]
- Gupta, T.K.; Bechtold, J.H.; Kuznicki, R.C.; Cadoff, L.H.; Rossing, B.R. Stabilization of tetragonal phase in polycrystalline zirconia. J. Mater. Sci. 1977, 12, 2421–2426. [Google Scholar] [CrossRef]
- Gupta, T.K.; Lange, F.F.; Bechtold, J.H. Effect of stress-induced phase transformation on the properties of polycrystalline zirconia containing metastable tetragonal phase. J. Mater. Sci. 1978, 13, 1464–1470. [Google Scholar] [CrossRef]
- Egerton, R.F. Electron Energy-Loss Spectroscopy in the Electron Microscope, 2nd ed.; Plenum Press: New York, NY, USA, 1996. [Google Scholar]
- Mizoguchi, T.; Olovsson, W.; Ikeno, H.; Tanaka, I. Theoretical ELNES using one-particle and multi-particle calculations. Micron 2010, 41, 695–709. [Google Scholar] [CrossRef]
- Ikeno, H.; Mizoguchi, T. Basics and applications of ELNES calculations. Microscopy 2017, 66, 305–327. [Google Scholar] [CrossRef]
- Colliex, C. From early to present and future achievements of EELS in the TEM. Eur. Phys. J. Appl. Phys. 2022, 97, 38. [Google Scholar] [CrossRef]
- Pearson, D.H.; Ahn, C.C.; Fultz, B. White lines and d-electron occupancies for the 3d and 4d transition metals. Phys. Rev. B 1993, 47, 8471–8478. [Google Scholar] [CrossRef] [PubMed]
- Leapman, R.D.; Grunes, L.A.; Fejes, P.L. Study of the L23 edges in the 3d transition metals and their oxides by electron-energy-loss spectroscopy with comparisons to theory. Phys. Rev. B 1982, 26, 614–636. [Google Scholar] [CrossRef]
- Pease, D.M.; Fasihuddin, A.; Daniel, M.; Budnick, J.I. Method of linearizing the 3d L3/L2 white line ratio as a function of magnetic moment. Ultramicroscopy 2001, 88, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Ii, S.; Matsunaga, K.; Hirayama, K.; Fujii, H.; Tsurekawa, S. Experimental Evaluation of Local Magnetic Moment in 3d Transition Metals by TEM/EELS Technique. In Proceedings of the APMC 10: 10th Asia-Pacific Microscopy Conference/ICONN 2012: The 2012 International Conference on Nanoscience and Nanotechnology/ACMM 22: 22nd Australian Conf. on Microscopy and Microanalysis, Perth, WA, Australia, 5–9 February 2012; pp. 414–415. [Google Scholar]
- Ii, S.; Hirayama, K.; Matsunaga, K.; Fujii, H.; Tsurekawa, S. Direct measurement of local magnetic moments at grain boundaries in iron. Scr. Mater. 2013, 68, 253–256. [Google Scholar] [CrossRef]
- Hirayama, K.; Ii, S.; Tsurekawa, S. Transmission electron microscopy/electron energy loss spectroscopy measurements and ab initio calculation of local magnetic moments at nickel grain boundaries. Sci. Technol. Adv. Mater. 2014, 15, 015005. [Google Scholar] [CrossRef]
- Ii, S.; Hirayama, K.; Tsurekawa, S. Experimental confirmation of grain boundary magnetism in Fe–Si and Fe–Sn Alloys by TEM-EELS. Mater. Trans. 2019, 60, 636–641. [Google Scholar] [CrossRef]
- Goodenough, J.B. A theory of domain creation and coercive force in polycrystalline ferromagnetics. Phys. Rev. 1954, 95, 917–932. [Google Scholar] [CrossRef]
- Yamaura, S.; Furuya, Y.; Watanabe, T. The effect of grain boundary microstructure on Barkhausen noise in ferromagnetic materials. Acta Mater. 2001, 49, 3019–3027. [Google Scholar] [CrossRef]
- Kawahara, K.; Ando, K.; Nogiwa, Y.; Yagyu, S.; Tsurekawa, S.; Watanabe, T. Observation of interaction between grain boundaries and magnetic domain by Lorentz microscopy. Ann. Chim. Sci. Mater. 2002, 27, S269–S278. [Google Scholar]
- Hampel, K.; Vvedensky, D.D.; Crampin, S. Magnetic structure near (310) tilt boundaries in iron. Phys. Rev. B 1993, 47, 4810(R). [Google Scholar] [CrossRef]
- Tobin, A.G.; Paul, D.I. Stability of ferromagnetic domain structures at grain boundaries. J. Appl. Phys. 1969, 40, 3611–3614. [Google Scholar] [CrossRef]
- Lin, I.N.; Mishra, R.; Thomas, G. Interaction of magnetic domain walls with microstructural features in spinel ferrites. IEEE Trans. Magn. 1984, 20, 134–139. [Google Scholar] [CrossRef]
- Szmaja, W. Investigations of the domain structure of anisotropic sintered Nd–Fe–B-based permanent magnets. J. Magn. Magn. Mater. 2006, 301, 546–561. [Google Scholar] [CrossRef]
- Crampin, S.; Vvedensky, D.D.; MacLaren, J.M.; Eberhart, M.E. Electronic structure near (210) tilt boundaries in nickel. Phys. Rev. B 1989, 40, 3413–3416. [Google Scholar] [CrossRef]
- Turek, I.; Drchal, V.; Kudrnovský, J.; Šob, M.; Weinberger, P. Electronic Structure of Disordered Alloys, Surface and Interfaces; Kluwer Academic: Boston, MA, USA, 1997; p. 244. [Google Scholar]
- Šob, M.; Turek, I.; Wang, L.; Vitek, V. Application of Ab Initio Electronic Structure Calculations to Grain Boundary Structure. In Proceedings of the 10th International Metallurgical Materials Conference (METAL 2001), Ostrava, Czech Republic, 15–17 May 2001; pp. 1–10. [Google Scholar]
- Wu, R.; Freeman, A.J.; Olson, G.B. First principles determination of the effects of phosphorus and boron on iron grain boundary cohesion. Phys. Rev. B 1996, 53, 7504–7509. [Google Scholar] [CrossRef]
- Siegel, D.J.; Hamilton, J.C. Computational study of carbon segregation and diffusion within a nickel grain boundary. Acta Mater. 2005, 53, 87–96. [Google Scholar] [CrossRef]
- Čák, M.; Šob, M.; Hafner, J. First-principles study of magnetism at grain boundaries in iron and nickel. Phys. Rev. B 2008, 78, 054418. [Google Scholar] [CrossRef]
- Wachowicz, E.; Kiejna, A. Effect of impurities on grain boundary cohesion in bcc iron. Comp. Mater. Sci. 2008, 43, 736–743. [Google Scholar] [CrossRef]
- Všianská, M.; Šob, M. Magnetically dead layers at sp-impurity-decorated grain boundaries and surfaces in nickel. Phys. Rev. B 2011, 84, 014418. [Google Scholar] [CrossRef]
- Všianská, M.; Šob, M. The effect of segregated sp-impurities on grain-boundary and surface structure, magnetism and embrittlement in nickel. Prog. Mater. Sci. 2011, 56, 817–840. [Google Scholar] [CrossRef]
- Fitzsimmons, M.R.; Röll, A.; Burkel, E.; Sickafus, K.E.; Nastasi, M.A.; Smith, G.S.; Pynn, R. The magnetization of a grain boundary in nickel. Nanostruct. Mater. 1995, 6, 539–542. [Google Scholar] [CrossRef]
- Gu, H.; Čeh, M.; Stemmer, S.; Müllejans, H.; Rühle, M. A quantitative approach for spatially-resolved electron energy-loss spectroscopy of grain boundaries and planar defects on a subnanometer scale. Ultramicroscopy 1995, 59, 215–227. [Google Scholar] [CrossRef]
- Gu, H.; Cannon, R.M.; Rühle, M. Composition and chemical width of ultrathin amorphous films at grain boundaries in silicon nitride. J. Mater. Res. 1998, 13, 376–387. [Google Scholar] [CrossRef]
- Szklarz, K.E.; Wayman, M.L. The effects of ferromagnetism on intergranular segregation in iron. Acta Metall. 1981, 29, 341–349. [Google Scholar] [CrossRef]
- Ishida, K.; Yokoyama, S.; Nishizawa, T. Grain boundary segregation in ferromagnetic alloys. Acta Metall. 1985, 33, 255–264. [Google Scholar] [CrossRef]
- Lejček, P.; Hofmann, S.; Paider, V. Solute segregation and classification of [100] tilt grain boundaries in α-iron: Consequences for grain boundary engineering. Acta Mater. 2003, 51, 39513963. [Google Scholar] [CrossRef]
- Ainselie, N.G.; Hoffman, R.E.; Seybolt, A.U. Sulfur segregation at α-iron grain boundaries—I. Acta Metall. 1960, 8, 523–527. [Google Scholar] [CrossRef]
- Seah, M.P.; Hondros, E.D. Use of a “BET” analogue equation to describe grain boundary segregation. Scr. Metall. 1973, 7, 735–737. [Google Scholar] [CrossRef]
- Watanabe, T.; Kitamura, S.; Karashima, S. Grain boundary hardening and segregation in alpha iron-tin alloy. Acta Metall. 1980, 28, 455–463. [Google Scholar] [CrossRef]
- Lejček, P.; Hofmann, S. Grain boundary segregation diagrams of α-iron. Interface Sci. 1993, 1, 163–174. [Google Scholar] [CrossRef]
- Lejček, P.; Hofmann, S.; Janovec, J. Prediction of enthalpy and entropy of solute segregation at individual grain boundaries of α-iron and ferrite steels. Mater. Sci. Eng. A 2007, 462, 76–85. [Google Scholar] [CrossRef]
- Lejček, P. Grain Boundary Segregation in Metals; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- van der Laan, G.; Thole, B.T.; Sawatzky, G.A.; Goedkoop, J.B.; Fuggle, J.C.; Esteva, J.-M.; Karnatak, R.; Remeika, J.P.; Dabkowska, H.A. Experimental proof of magnetic X-ray dichroism. Phys. Rev. B 1986, 34, 6529–6531. [Google Scholar] [CrossRef]
- Van Acker, J.F.; Stadnik, Z.M.; Fuggle, J.C.; Hoekstra, H.J.W.H.; Buschow, K.H.J.; Stroink, G. Magnetic moments and X-ray photoelectron spectroscopy splittings in Fe 3s core levels of materials containing Fe. Phys. Rev. B 1988, 37, 6827–6834. [Google Scholar] [CrossRef]
- Thole, B.T.; Carra, P.; Sette, F.; van der Laan, G. X-ray circular dichroism as a probe of orbital magnetization. Phys. Rev. Lett. 1992, 68, 1943–1946. [Google Scholar] [CrossRef]
- Carra, P.; Thole, B.T.; Altarelli, M.; Wang, X. X-ray circular dichroism and local magnetic fields. Phys. Rev. Lett. 1993, 70, 694–697. [Google Scholar] [CrossRef]
- Hébert, C.; Schattschneider, P. A proposal for dichroic experiments in the electron microscope. Ultramicroscopy 2003, 96, 463–468. [Google Scholar] [CrossRef]
- Schattschneider, P.; Rubino, S.; Hébert, C.; Rusz, J.; Kuneš, J.; Novák, P.; Carlino, E.; Fabrizioli, M.; Panaccione, G.; Rossi, G. Detection of magnetic circular dichroism using a transmission electron microscope. Nature 2006, 441, 486–488. [Google Scholar] [CrossRef]
- Schattschneider, P.; Hébert, C.; Rubino, S.; Stöger-Pollach, M.; Rusz, J.; Novák, P. Magnetic circular dichroism in EELS: Towards 10 nm resolution. Ultramicroscopy 2008, 108, 433–438. [Google Scholar] [CrossRef][Green Version]
- Lidbaum, H.; Rusz, J.; Liebig, A.; Hjörvearsson, B.; Oppeneer, M.; Coronel, E.; Eriksson, O.; Leifer, K. Quantitative magnetic information from reciprocal space maps in transmission electron microscopy. Phys. Rev. Lett. 2009, 102, 037201. [Google Scholar] [CrossRef]
- Muto, S.; Tatsumi, K.; Rusz, J. Parameter-free extraction of EMCD from an energy-filtered diffraction datacube using multivariate curve resolution. Ultramicroscopy 2013, 125, 89–96. [Google Scholar] [CrossRef]
- Muto, S.; Rusz, J.; Tatsumi, K.; Adam, R.; Arai, S.; Kocevski, V.; Oppeneer, P.M.; Burgler, D.E.; Schnerder, C.M. Quantitative characterization of nanoscale polycrystalline magnets with electron magnetic circular dichroism. Nat. Commun. 2014, 5, 3138. [Google Scholar] [CrossRef]
- Geng, W.T.; Freeman, A.J.; Wu, R.; Geller, C.B.; Raynolds, J.E. Embrittling and strengthening effects of hydrogen, boron, and phosphorus on a Σ5 nickel grain boundary. Phys. Rev. B 1999, 60, 7149–7155. [Google Scholar] [CrossRef]
- Tsurekawa, S.; Okamoto, K.; Kawahara, K.; Watanabe, T. The control of grain boundary segregation and segregation-induced brittleness in iron by the application of a magnetic field. J. Mater. Sci. 2005, 40, 895–901. [Google Scholar] [CrossRef]
- Ito, K.; Sawada, H.; Ogata, S. First-principles study on the grain boundary embrittlement of bcc-Fe by Mn segregation. Phys. Rev. Mater. 2019, 3, 013609. [Google Scholar] [CrossRef]
- McMahon, C.J. Intergranular fracture in steels. Mater. Sci. Eng. 1976, 25, 233–239. [Google Scholar] [CrossRef]
- Ozawa, T.; Ishida, Y. Mössbauer effect of 119mSn segregated at the grain boundary of iron. Scr. Metall. 1977, 11, 835–838. [Google Scholar] [CrossRef]
- Taheri, M.L.; Stach, E.A.; Arslan, L.; Crozier, P.A.; Kabius, B.C.; LaGrange, T.; Minor, A.W.; Takeda, S.; Tanese, M.; Wanger, J.B.; et al. Current status and future directions for in situ transmission electron microscopy. Ultramicroscopy 2016, 170, 86–95. [Google Scholar] [CrossRef]
- Zhou, T.; Babu, R.P.; Hou, Z.; Hedström, P. On the role of transmission electron microscopy for precipitation analysis in metallic materials. Crit. Rev. Solid State Mater. 2022, 47, 388–414. [Google Scholar] [CrossRef]
- Sun, L.; Xu, T.; Zhang, Z. (Eds.) . In-Situ Transmission Electron Microscopy; Springer: Singapore, 2023. [Google Scholar] [CrossRef]
- Hall, E.O. The deformation and ageing of mild steel: II characteristics of the Lüders deformation. Proc. Phys. Soc. Sec. B 1951, 64, 742–747. [Google Scholar] [CrossRef]
- Petch, N.J. The cleavage strength of polycrystals. J. Iron Steel Inst. 1953, 174, 25–28. [Google Scholar]
- Anderson, P.M.; Hirth, J.P.; Lothe, J. Theory of Dislocations, 3rd ed.; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Livingston, J.D.; Charmers, B. Multiple slip in bicrystal deformation. Acta Metall. 1957, 5, 322–327. [Google Scholar] [CrossRef]
- Grabski, M.W.; Korski, R. Grain boundaries as sinks for dislocations. Philos. Mag. 1970, 22, 707–715. [Google Scholar] [CrossRef]
- Pumphrey, P.H.; Gleiter, H. The annealing of dislocations in high-angle grain boundaries. Philos. Mag. 1974, 30, 593–602. [Google Scholar] [CrossRef]
- Pond, R.C.; Smith, D.A. On the absorption of dislocations by grain boundaries. Philos. Mag. 1977, 36, 353–366. [Google Scholar] [CrossRef]
- Shen, Z.; Wagoner, R.H.; Clark, W.A.T. Dislocation pile-up and grain boundary interactions in 304 stainless steel. Scr. Metall. 1986, 20, 921–926. [Google Scholar] [CrossRef]
- Shen, Z.; Wagoner, R.H.; Clark, W.A.T. Dislocation and grain boundary interactions in metals. Acta Metall. 1988, 36, 3231–3242. [Google Scholar] [CrossRef]
- Lee, T.C.; Robertson, I.M.; Birnbaum, H.K. An In Situ transmission electron microscope deformation study of the slip transfer mechanisms in metals. Metall. Trans. A 1990, 21, 2437–2447. [Google Scholar] [CrossRef]
- Luster, J.; Morris, M.A. Compatibility of deformation in two-phase Ti-Al alloys: Dependence on microstructure and orientation relationships. Metall. Mater. Trans. A 1995, 26, 1745–1756. [Google Scholar] [CrossRef]
- Kacher, J.; Eftink, B.P.; Cui, B.; Robertson, I.M. Dislocation interactions with grain boundaries. Curr. Opin. Solid State Mater. Sci. 2014, 18, 227–243. [Google Scholar] [CrossRef]
- Wo, P.C.; Ngan, A.H.W. Investigation of slip transmission behavior across grain boundaries in polycrystalline Ni3Al using nanoindentation. J. Mater. Res. 2004, 19, 189–201. [Google Scholar] [CrossRef][Green Version]
- Wang, M.G.; Ngan, A.H.W. Indentation strain burst phenomenon induced by grain boundaries in niobium. J. Mater. Res. 2004, 19, 2478–2486. [Google Scholar] [CrossRef]
- Soer, W.A.; De Hosson, J.T.M. Detection of grain-boundary resistance to slip transfer using nanoindentation. Mater. Lett. 2005, 59, 3192–3195. [Google Scholar] [CrossRef]
- Soer, W.A.; Aifantis, K.E.; De Hosson, J.T.M. Incipient plasticity during nanoindentation at grain boundaries in body-centerd cubic metals. Acta Mater. 2005, 53, 4665–4676. [Google Scholar] [CrossRef]
- Tsurekawa, S.; Chihara, Y.; Tashima, K.; Ii, S.; Lejček, P. Local plastic deformation in the vicinity of grain boundaries in Fe–3 mass% Si alloy bicrystals and tricrystal. J. Mater. Sci. 2014, 49, 4698–4704. [Google Scholar] [CrossRef]
- Aifantis, K.E.; Deng, H.; Shibata, H.; Tsurekawa, S.; Lejček, P.; Hackney, S.A. Interpreting slip transmission through mechanically induced interface energies: A Fe–3%Si case study. J. Mater. Sci. 2018, 54, 1831–1843. [Google Scholar] [CrossRef]
- Tokuda, Y.; Tsurekawa, S.; Molodov, D.A. Local mechanical properties in the vicinity of Σ3/[111] symmetric tilt grain boundary in aluminum bicrystal. Mater. Sci. Eng. A 2018, 716, 37–41. [Google Scholar] [CrossRef]
- Barrales-Mora, L.A.; Tokuda, Y.; Molodov, D.A.; Tsurekawa, S. On incipient plasticity in the vicinity of grain boundaries in aluminum bicrystals: Experimental and simulation nanoindentation study. Mater. Sci. Eng. A 2021, 828, 142100. [Google Scholar] [CrossRef]
- Brandenburg, J.E.; Seo, J.; Eto, K.; Molodov, D.A.; Tsurekawa, S. Influence of symmetrical <10-10> high-angle tilt grain boundaries on the local mechanical properties of magnesium bicrystals. Mater. Sci. Eng. A 2021, 826, 141913. [Google Scholar] [CrossRef]
- Ohmura, T.; Tsuzaki, K.; Yin, F. Nanoindentation-induced deformation behavior in the vicinity of single grain boundary of interstitial-free steel. Mater. Trans. 2005, 46, 2026–2029. [Google Scholar] [CrossRef]
- Ohmura, T.; Zhang, L.; Sekido, K.; Tsuzaki, K. Effects of lattice defects on indentation-induced plasticity initiation behavior in metals. J. Mater. Res. 2012, 27, 1742–1749. [Google Scholar] [CrossRef]
- Nakano, K.; Hayashi, K.; Takeda, K.; Ii, S.; Ohmura, T. Effect of Grain Boundary on the Plastic Deformation in Fe-C Alloys. In Proceedings of the 5th International Symposium of Steel Science (ISSS-2017), Kyoto, Japan, 13–16 November 2017; Li, S., Tsuchiyama, T., Miyamoto, G., Furuhara, T., Eds.; The Iron and Steel Institute of Japan: Tokyo, Japan, 2017; pp. 219–222. [Google Scholar]
- Araki, S.; Mashima, K.; Masumura, T.; Tsuchiyama, T.; Takaki, S.; Ohmura, T. Effect of grain boundary segregation of carbon on critical grain boundary strength of ferritic steel. Scr. Mater. 2019, 169, 38–41. [Google Scholar] [CrossRef]
- Endoh, K.; Ii, S.; Kimura, Y.; Sasaki, T.; Goto, S.; Yokota, T.; Ohmura, T. Effects of grain boundary geometry and boron addition on the local mechanical behavior of interstitial-free (IF) steels. Mater. Trans. 2021, 62, 1479–1488. [Google Scholar] [CrossRef]
- Nakano, K.; Takeda, K.; Ii, S.; Ohmura, T. Evaluation of grain boundary strength through nanoindentation technique. J. Jpn. Inst. Met. Mater. 2021, 85, 40–48. [Google Scholar] [CrossRef]
- Wakeda, M.; Zhang, Y.L.; Ii, S.; Ohmura, T. Multiscale analyses of the interaction between dislocation and Σ9 symmetric tilt grain boundaries in Fe–Si bicrystals by nanoindentation technique. Int. J. Plast. 2021, 145, 103047. [Google Scholar] [CrossRef]
- Saka, H.; Imura, T.; Yukawa, N.; Igarashi, I. Stress measurable tensile device for electron microscopic observation. J. Phys. Soc. Jpn. 1968, 25, 906. [Google Scholar] [CrossRef]
- Saka, H.; Imura, T. On the preparation of tensile test pieces for transmission electron microscopic observation. Jpn. J. Appl. Phys. 1969, 8, 406. [Google Scholar] [CrossRef]
- Minor, A.M.; Asif, S.A.S.; Shan, Z.; Stach, E.A.; Cyrankowski, E.; Wyrobek, T.J.; Warren, O.L. A new view of the onset of plasticity during the nanoindentation of aluminium. Nat. Mater. 2006, 5, 697–702. [Google Scholar] [CrossRef] [PubMed]
- Shan, Z.W.; Mishra, R.K.; Syed Asif, S.A.; Warren, O.L.; Minor, A.M. Mechanical annealing and source-limited deformation in submicrometre-diameter Ni crystals. Nat. Mater. 2008, 7, 115–119. [Google Scholar] [CrossRef]
- Caillard, D. Kinetics of dislocations in pure Fe. Part I. In situ straining experiments at room temperature. Acta Mater. 2010, 58, 3493–3503. [Google Scholar] [CrossRef]
- Caillard, D. Kinetics of dislocations in pure Fe. Part II. In situ straining experiments at low temperature. Acta Mater. 2010, 58, 3504–3515. [Google Scholar] [CrossRef]
- Zhang, L.; Ohmura, T.; Sekido, K.; Nakajima, K.; Hara, T.; Tsuzaki, K. Direct observation of plastic deformation in iron–3% silicon single crystal by in situ nanoindentation in transmission electron microscopy. Scr. Mater. 2011, 64, 919–922. [Google Scholar] [CrossRef]
- Kiener, D.; Hosemann, P.; Maloy, S.A.; Minor, A.M. In situ nanocompression testing of irradiated copper. Nat. Mater. 2011, 10, 608–613. [Google Scholar] [CrossRef]
- Zhang, L.; Ohmura, T.; Sekido, K.; Hara, T.; Nakajima, K.; Tsuzaki, K. Dislocation character transition and related mechanical response in a body-centered cubic single crystal. Scr. Mater. 2012, 67, 388–391. [Google Scholar] [CrossRef]
- Mompiou, F.; Legros, M. Quantitative grain growth and rotation probed by in-situ TEM straining and orientation mapping in small grained Al thin films. Scr. Mater. 2015, 99, 5–8. [Google Scholar] [CrossRef]
- Zhang, L.; Sekido, N.; Ohmura, T. Real time correlation between flow stress and dislocation density in steel during deformation. Mater. Sci. Eng. A 2014, 61, 188–193. [Google Scholar] [CrossRef]
- Miao, B.; Kondo, S.; Tochigi, E.; Wei, J.; Feng, B.; Shibata, N.; Ikuhara, Y. The core structure of 60° mixed basal dislocation in alumina (α-Al2O3) introduced by in situ TEM nanoindentation. Scr. Mater. 2019, 163, 157–162. [Google Scholar] [CrossRef]
- Ii, S.; Enami, T.; Ohmura, T.; Tsurekawa, S. Direct characterization of the relation between the mechanical response and microstructure evolution in aluminum by transmission electron microscopy in situ straining. Materials 2021, 14, 1431. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Gao, S.; Tomota, Y.; Ii, S.; Tsuji, N.; Ohmura, T. Real time correlation between flow stress and dislocation density in steel during deformation. Acta Mater. 2021, 206, 116621. [Google Scholar] [CrossRef]
- Tochigi, E.; Miao, B.; Nakamura, A.; Shibata, N.; Ikuhara, Y. Atomic-scale mechanism of rhombohedral twinning in sapphire. Acta Mater. 2021, 216, 117137. [Google Scholar] [CrossRef]
- Li, H.; Ii, S.; Ohmura, T.; Tsuji, N. Direct observation of grain boundary formation in bcc iron through TEM in situ compression test. Scr. Mater. 2022, 207, 114275. [Google Scholar] [CrossRef]
- Ohmura, T.; Minor, A.M.; Stach, E.A.; Morris, J.M. Dislocation–grain boundary interactions in martensitic steel observed through in situ nanoindentation in a transmission electron microscope. J. Mater. Res. 2004, 19, 3626–3632. [Google Scholar] [CrossRef]
- Soer, W.A.; De Hosson, J.T.M.; Minor, A.M.; Morris, J.M.; Stach, E.A. Effects of solute Mg on grain boundary and dislocation dynamics during nanoindenation of Al-Mg thin films. Acta Mater. 2004, 52, 5783–5790. [Google Scholar] [CrossRef]
- Li, L.L.; An, H.; Imrich, P.J.; Zhang, P.; Zhang, Z.J.; Dehm, G.; Zhang, Z.F. Microcompression and cyclic deformation behaviors of coaxial copper bicrystals with a single twin boundary. Scr. Mater. 2013, 69, 199–202. [Google Scholar] [CrossRef]
- Guo, Y.; Britton, T.B.; Wilkindon, A.J. Slip band–grain boundary interactions in commercial-purity titanium. Acta Mater. 2014, 76, 1–12. [Google Scholar] [CrossRef]
- Imrich, P.J.; Kirchlechner, C.; Kiener, D.; Dehm, G. Internal and external stresses: In situ TEM compression of Cu bicrystals containing a twin boundary. Scr. Mater. 2015, 100, 94–97. [Google Scholar] [CrossRef]
- Kim, Y.; Lee, S.; Jeon, J.B.; Kim, Y.J.; Lee, B.J.; Oh, S.H.; Han, S.M. Effect of a high angle grain boundary on deformation behavior of Al nanopillars. Scr. Mater. 2015, 107, 5–9. [Google Scholar] [CrossRef]
- Imrich, P.J.; Kirchlechner, C.; Kiener, D.; Dehm, G. In situ TEM microcompression of single and bicrystalline samples: Insights and limitations. J. Miner. Met. Mater. Soc. 2015, 67, 1704–1712. [Google Scholar] [CrossRef]
- Kheradmand, N.; Knorr, A.F.; Marx, M.; Deng, Y. Microscopic incompatibility controlling plastic deformation of bicrystals. Acta Mater. 2016, 106, 219–228. [Google Scholar] [CrossRef]
- Malyar, N.V.; Micha, J.S.; Dehm, G.; Kirchlechner, C. Dislocation-twin boundary interaction in small scale Cu bi-crystals loaded in different crystallographic directions. Acta Mater. 2017, 129, 91–97. [Google Scholar] [CrossRef]
- Malyar, N.V.; Micha, J.S.; Dehm, G.; Kirchlechner, C. Size effect in bi-crystalline micropillars with a penetrable high angle grain boundary. Acta Mater. 2017, 129, 312–320. [Google Scholar] [CrossRef]
- Zhang, Z.; Waheed, S.; Balint, D.S.; Dunne, F.P.E. Slip transfer across phase boundaries in dual phase titanium alloys and the effect on strain rate sensitivity. Int. J. Plast. 2018, 104, 23–38. [Google Scholar] [CrossRef]
- Liebig, J.P.; Krauß, S.; Göken, M.; Merle, B. Influence of stacking fault energy and dislocation character on slip transfer at coherent twin boundaries studied by micropillar compression. Acta Mater. 2018, 154, 261–272. [Google Scholar] [CrossRef]
- Weaver, J.S.; Li, N.; Mara, N.A.; Jones, D.R.; Cho, H.; Bronkhorst, C.A.; Fensin, S.J.; Gray, G.T. Slip transmission of high angle grain boundaries in body-centered cubic metals: Micropillar compression of pure Ta single and bi-crystals. Acta Mater. 2018, 156, 356–368. [Google Scholar] [CrossRef]
- Ii, S.; Enami, T.; Ohmura, T.; Tsurekawa, S. Direct measurement of shear stress for dislocation transferring across {111} Σ3 grain boundary in aluminum bicrystal via in situ straining TEM. Scr. Mater. 2022, 221, 114963. [Google Scholar] [CrossRef]
- Kiani, M.T.; Gan, L.T.; Traylor, R.; Yang, R.; Barr, C.M.; Hattar, K.; Fan, J.A.; Gu, X.W. In Situ TEM tensile testing of bicrystals with tailored misorientation angles. Acta Mater. 2022, 224, 117505. [Google Scholar] [CrossRef]
- Ikuhara, Y.; Suzuki, T.; Kubo, Y. Transmission electron microscopy in situ observation of crack propagation in sintered alumina. Philos. Mag. 1992, 66, 323–327. [Google Scholar] [CrossRef]
- Ii, S.; Iwamoto, C.; Matsunaga, K.; Yamamoto, T.; Yoshiya, M.; Ikuhara, Y. Direct observation of intergranular cracks in sintered silicon nitride. Philos. Mag. 2004, 84, 2767–2775. [Google Scholar] [CrossRef]
- Becher, P.F.; Painter, G.S.; Lance, M.J.; Ii, S.; Ikuhara, Y. Direct observations of debonding of reinforcing grains in silicon nitride ceramics sintered with yttria plus alumina additives. J. Am. Ceram. Soc. 2005, 88, 1222–1226. [Google Scholar] [CrossRef]
- Kondo, S.; Ishihara, A.; Tochigi, E.; Shibata, N.; Ikuhara, Y. Direct observation of atomic-scale fracture path within ceramic grain boundary core. Nat. Commum. 2019, 10, 2112. [Google Scholar] [CrossRef] [PubMed]
- Maaß, R.; Derlet, P.M. Micro-plasticity and recent insights from intermittent and small-scale plasticity. Acta Mater. 2018, 143, 338–363. [Google Scholar] [CrossRef]
- Kamikawa, N.; Huang, X.; Tsuji, N.; Hansen, N. Strengthening mechanisms in nanostructured high-purity aluminium deformed to high strain and annealed. Acta Mater. 2009, 57, 4198–4208. [Google Scholar] [CrossRef]
- Wyrzykowski, J.W.; Grabski, M.W. The Hall–Petch relation in aluminium and its dependence on the grain boundary structure. Philos. Mag. A 1986, 53, 505–520. [Google Scholar] [CrossRef]
- Rauch, E.F.; Portillo, J.; Nicolopoulos, S.; Bultreys, D.; Rouvimov, S.; Moeck, P. Automated nanocrystal orientation and phase mapping in the transmission electron microscope on the basis of precession electron diffraction. Z. Kristallogr. 2010, 225, 103–109. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Langdon, T.G. Principles of equal-channel angular pressing as a processing tool for grain refinement. Prog. Mater Sci. 2006, 51, 881–981. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Estrin, Y.; Horita, Z.; Langdon, T.G.; Zehetbauer, M.J.; Zhu, Y.T. Producing bulk ultrafine-grained materials by severe plastic deformation. J. Miner. Met. Mater. Soc. 2006, 58, 33–39. [Google Scholar] [CrossRef]
- Hughes, D.A.; Hansen, N. High angle boundaries formed by grain subdivision mechanisms. Acta Mater. 1997, 45, 3871–3886. [Google Scholar] [CrossRef]
- Hanse, N.; Jensen, D.J. Development of microstructure in FCC metals during cold work. Philos. Trans. A Math. Phys. Eng. Sci. 1997, 357, 1447–1469. [Google Scholar] [CrossRef]
- Hansen, N.; Mehl, R.F.; Medalist, A. New discoveries in deformed metals. Metall. Mater. Trans. A 2001, 32, 2917–2935. [Google Scholar] [CrossRef]
- Hughes, D.A.; Hansen, N.; Bammann, D.J. Geometrically necessary boundaries, incidental dislocation boundaries and geometrically necessary dislocations. Scr. Mater. 2003, 48, 147–153. [Google Scholar] [CrossRef]
- Tsuji, N.; Gholizadeh, R.; Ueji, R.; Kamikawa, N.; Zhao, L.; Tian, Y.; Bai, Y.; Shibata, A. Formation mechanism of ultrafine grained microstructures: Various possibilities for fabricating bulk nanostructured metals and alloys. Mater. Trans. 2019, 60, 1518–1532. [Google Scholar] [CrossRef]
- Wang, L.; Kong, D.; Zhang, Y.; Xiao, L.; Lu, Y.; Chen, Z.; Zhang, Z.; Zou, J.; Zhu, T.; Han, X. Mechanically driven grain boundary formation in nickel nanowires. ACS Nano 2017, 11, 12500–12508. [Google Scholar] [CrossRef] [PubMed]
- Kobler, A.; Kashiwar, A.; Hahn, H.; Kübel, C. Combination of in situ straining and ACOM TEM: A novel method for analysis of plastic deformation of nanocrystalline metals. Ultramicroscopy 2013, 128, 68–81. [Google Scholar] [CrossRef]
- Kobler, A.; Kübel, C. Challenges in quantitative crystallographic characterization of 3D thin films by ACOM-TEM. Ultramicroscopy 2017, 173, 84–94. [Google Scholar] [CrossRef]
- Kashiwar, A.; Hahn, H.; Kübel, C. In situ TEM observation of cooperative grain rotations and the Bauschinger effect in nanocrystalline palladium. Nanomaterials 2021, 11, 432. [Google Scholar] [CrossRef] [PubMed]
- Pennycook, S.J.; Nellist, P.D. Scanning Transmission Electron Microscopy Imaging and Analysis; Springer: New York, NY, USA, 2011. [Google Scholar]
- Morishita, S.; Ishikawa, R.; Kohno, Y.; Sawada, H.; Shibata, N.; Ikuhara, Y. Attainment of 40.5 pm spatial resolution using 300 kV scanning transmission electron microscope equipped with fifth-order aberration corrector. Microscopy 2018, 67, 46–50. [Google Scholar] [CrossRef] [PubMed]
- Kimoto, K.; Asaka, T.; Nagai, T.; Saito, M.; Matsui, Y.; Ishizuka, K. Element-selective imaging of atomic comlumns in a crystal using STEM and EELS. Nature 2007, 450, 702–704. [Google Scholar] [CrossRef]
- Van Aert, S.; Verbeeck, J.; Erni, R.; Bals, S.; Luysberg, M.; Van Dyck, D.; Van Tandeloo, G. Quantitative atomic resolution mapping using high-angle annular dark field scanning transmission electron microscopy. Ultramicroscopy 2009, 109, 1236–1244. [Google Scholar] [CrossRef]
- Molina, S.I.; Sales, D.L.; Galindo, P.L.; Fuster, D.; González, Y.; Alén, B.; González, L.; Varela, M.; Pennycook, S.J. Column-by-column compositional mapping by Z-contrast imaging. Ultramicroscopy 2009, 109, 172–176. [Google Scholar] [CrossRef]
- Bjørge, R.; Dwyer, C.; Weyland, M.; Nakashima, P.N.H.; Etheridge, J.; Holmestad, R. Quantitative HAADF STEM study of β-like precipitates in an Al-Mg-Ge alloy. J. Phys. Conf. Ser. 2011, 371, 012015. [Google Scholar] [CrossRef]
- Martinez, G.T.; Rosenauer, A.; De Backer, A.; Verbeeck, J.; Van Aert, S. Quantitative composition determination at the atomic level using model-based high-angle annular dark field scanning transmission electron microscopy. Ultramicroscopy 2014, 137, 12–19. [Google Scholar] [CrossRef]
- Firoozabadi, S.; Kükelhan, P.; Beyer, A.; Lehr, J.; Heimes, D.; Volz, K. Quantitative composition determination by ADF-STEM at a low-angular regime: A combination of EFSTEM and 4DSTEM. Ultramicroscopy 2022, 240, 113550. [Google Scholar] [CrossRef]
- Buranova, Y.; Rösner, H.; Divinski, S.V.; Imlau, R.; Wilde, G. Quantitative measurements of grain boundary excess volume from HAADF-STEM micrographs. Acta Mater. 2016, 106, 367–373. [Google Scholar] [CrossRef]
- Hÿtch, M.J.; Snoeck, E.; Kilaas, R. Quantitative measurement of displacement and strain fields from HREM micrographs. Ultramicroscopy 1998, 74, 131–146. [Google Scholar] [CrossRef]
- Hÿtch, M.J.; Vermaut, P.; Malarria, J.; Portier, R. Study of atomic displacement fields in shape memory alloys by high-resolution electron microscopy. Mater. Sci. Eng. A 1999, 273–275, 266–270. [Google Scholar] [CrossRef]
- Galindo, P.L.; Kret, S.; Sanchez, A.M.; Laval, J.-Y.; Yáñez, A.; Pizarro, J.; Guerrero, E.; Ben, T.; Molina, S.I. The peak pairs algorithm for strain mapping from HRTEM images. Ultramicroscopy 2007, 107, 1186–1193. [Google Scholar] [CrossRef] [PubMed]
- Sennour, M.; Lartigue-Korinek, S.; Champion, Y.; Hÿtch, M.J. Local strain analysis in twin boundaries in ultrafine grained copper. J. Mater. Sci. 2008, 43, 3806–3811. [Google Scholar] [CrossRef]
- Hÿtch, M.J.; Putaux, J.L.; Thibault, J. Stress and strain around grain-boundary dislocations measured by high-resolution electron microscopy. Philos. Mag. 2006, 86, 4641–4656. [Google Scholar] [CrossRef]
- Zhao, C.W.; Xing, Y.M.; Bai, P.C.; Hou, J.F.; Dai, X.J. Quantitative measurement of deformation field around low-angle grain boundaries by electron microscopy. Phys. B 2008, 403, 1838–1842. [Google Scholar] [CrossRef]
- Couillard, M.; Radtke, G.; Botton, G.A. Strain fields around dislocation arrays in a Σ9 silicon bicrystal measured by scanning transmission electron microscopy. Philos. Mag. 2013, 93, 1250–1267. [Google Scholar] [CrossRef]
- Hüe, F.; Hÿtch, M.; Bender, H.; Houdellier, F.; Claverie, A. Direct mapping of strain in a strained silicon transistor by high-resolution electron microscopy. Phys. Rev. Lett. 2008, 100, 156602. [Google Scholar] [CrossRef] [PubMed]
- Mahalingam, K.; Haugan, H.J.; Brown, G.J.; Eyink, K.G. Quantitative analysis of interfacial strain in InAs/GaSb superlattices by aberration-corrected HRTEM and HAADF-STEM. Ultramicroscopy 2013, 127, 70–75. [Google Scholar] [CrossRef] [PubMed]
- Hernández-Rivera, J.L.; Rivera, J.C.; Koch, C.T.; Özdöl, V.B.; Martínez-Sánchez, R. Study of coherence strain of GP II zones in an aged aluminum composite. J. Alloys Compd. 2012, 536, S159–S164. [Google Scholar] [CrossRef]
- Hernández-Rivera, J.L.; Cruz Rivera, J.J.; Koch, C.T.; Özdöl, V.B.; Martínez-Sánchez, R. Evaluation of strain caused by coherent precipitates in an Al alloy using TEM techniques. Mater. Char. 2012, 73, 61–67. [Google Scholar] [CrossRef]
- Hou, X.; Li, J.J.; Liu, F.; Yan, L.; Bai, P. Coherent strain of Guinier-Preston II zone in an Al-Zn-Mg-Cu alloy. Micron 2019, 124, 102711. [Google Scholar] [CrossRef]
- Hou, X.; Ma, G.; Bai, P.; Lang, F.; Zhao, X.; Liu, F.; Xing, Y. Investigation of the coherent strain evolution of the η’ phase in Al–Zn–Mg–Cu alloys via scanning transmission electron microscopy. J. Alloys Compd. 2021, 856, 158111. [Google Scholar] [CrossRef]
- Tirry, W.; Schryvers, D. Linking a completely three-dimensional nanostrain to a structural transformation eigenstrain. Nat. Mater. 2009, 8, 752–757. [Google Scholar] [CrossRef]
- Shibata, N.; Kondo, Y.; Findley, S.D.; Sawada, H.; Kondo, Y.; Ikuhara, Y. New area detector for atomic-resolution scanning transmission electron microscopy. J. Electron Microsc. 2010, 59, 473–479. [Google Scholar] [CrossRef]
- Shibata, N.; Findley, S.D.; Kohno, Y.; Sawada, H.; Kondo, Y.; Ikuhara, Y. Differential phase-contrast microscopy at atomic resolution. Nat. Phys. 2012, 8, 611–615. [Google Scholar] [CrossRef]
- Shibata, N. Atomic-resolution differential phase contrast electron microscopy. J. Ceram. Soc. Jpn. 2019, 127, 708–714. [Google Scholar] [CrossRef]
- Kohno, Y.; Seki, T.; Findley, S.D.; Ikuhara, Y.; Shibata, N. Real-space visualization of intrinsic magnetic fields of an antiferromagnet. Nature 2022, 602, 234–239. [Google Scholar] [CrossRef] [PubMed]
- Shibata, N.; Findley, S.D.; Sasaki, H.; Matsumoto, T.; Sawada, H.; Kohno, Y.; Otomo, S.; Minato, R.; Ikuhara, Y. Imaging of built-in electric field at a p-n junction by scanning transmission electron microscopy. Sci. Rep. 2015, 5, 10040. [Google Scholar] [CrossRef] [PubMed]
- Toyama, S.; Seki, T.; Kanitani, Y.; Kudo, Y.; Tomiya, S.; Ikuhara, Y.; Shibata, N. Quantitative electric field mapping in semiconductor heterostructures via tilt-scan averaged DPC STEM. Ultramicroscopy 2022, 238, 113538. [Google Scholar] [CrossRef]
- Toyama, S.; Seki, T.; Kanitani, Y.; Kudo, Y.; Tomiya, S.; Ikuhara, Y.; Shibata, N. Real-space observation of a two-dimensional electron gas at semiconductor heterointerfaces. Nat. Nanotechnol. 2023, 18, 521–528. [Google Scholar] [CrossRef]
- Oleshko, V.P.; Howe, J.M. In situ determination and imaging of physical properties of metastable and equilibrium precipitates using valence electron energy-loss spectroscopy and energy-filtering transmission electron microscopy. J. Appl. Phys. 2017, 101, 054308. [Google Scholar] [CrossRef]
- Nandi, P.; Howe, J.M. Determining the volume expansion at grain boundaries using extended energy-loss fine structure analysis. Microsc. Microanal. 2019, 25, 1130–1138. [Google Scholar] [CrossRef]
- Nandi, P.; Sang, X.; Hoglund, E.R.; Unocic, R.R.; Molodov, D.A.; Howe, J.M. Nanoscale mapping of the electron density at Al grain boundaries and correlation with grain-boundary energy. Phys. Rev. Mater. 2019, 3, 053805. [Google Scholar] [CrossRef]
- Nandi, P.; Hoglund, E.R.; Howe, J.M. Observation of grain boundary plasmon and associated deconvolution techniques for low-loss electron energy-loss (EEL) spectra acquired from grain boundaries. Ultramicroscopy 2022, 234, 113478. [Google Scholar] [CrossRef] [PubMed]
- Kohyama, M.; Tanaka, S.; Shiihara, Y. Ab initio local-energy and local-stress calculations for materials science and engineering. Mater. Trans. 2021, 62, 1–15. [Google Scholar] [CrossRef]
- Nelayah, J.; Kociak, M.; Stephan, O.; Garcia de Abajo, F.J.; Tence, M.; Henradr, L.; Taverra, D.; Pastoriza-Santos, I.; Liz-Marzan, L.M.; Colliex, C. Mapping surface plasmons on a single metallic nanoparticle. Nat. Phys. 2007, 3, 348–353. [Google Scholar] [CrossRef]
- Wang, Y.-Y.; Jin, Q.; Zhuang, K.; Choi, J.K.; Nxumalo, J. Band gap measurement by nano-beam STEM with small off-axis angle transmission electron energy loss spectroscopy (TEELS). Ultramicroscopy 2020, 220, 113164. [Google Scholar] [CrossRef]
- Krivanek, O.L.; Dellby, N.; Hachtel, J.A.; Idrobo, J.-C.; Hotz, M.T.; Plotkin-Swing, B.; Bacon, N.J.; Bleloch, A.L.; Corbin, G.J.; Hoffman, M.V.; et al. Progress in ultrahigh energy resolution EELS. Ultramicroscopy 2019, 203, 60–67. [Google Scholar] [CrossRef]
- Hoglund, E.R.; Bao, D.-L.; O’Hara, A.; Makarem, S.; Oiontkowski, Z.T.; Matson, J.R.; Yadav, A.K.; Haislmaier, R.C.; Engel-Herbert, R.; Ihilefeld, J.F.; et al. Emergent interface vibrational structure of oxide superlattices. Nature 2022, 601, 556–561. [Google Scholar] [CrossRef] [PubMed]
- Hoglund, E.R.; Bao, D.-L.; O’Hara, A.; Pfeiler, T.M.; Hoque, M.S.B.; Makarem, S.; Howe, J.M.; Pantelides, S.T.; Hopkins, P.E.; Hachtel, J.A. Direct visualization of localized vibrations at complex grain boundaries. Adv. Mater. 2023, 35, 2208920. [Google Scholar] [CrossRef]
- Raabe, D.; Herbig, M.; Sndlöbes, S.; Li, Y.; Tytko, D.; Kuzmina, M.; Ponge, D.; Choi, P.-P. Grain boundary segregation engineering in metallic alloys: A pathway to the design of interfaces. Curr. Opin. Solid State Mater. Sci. 2014, 18, 253–261. [Google Scholar] [CrossRef]
- Ding, R.; Yao, Y.; Sun, B.; Liu, G.; He, J.; Li, T.; Wan, X.; Dai, Z.; Ponge, D.; Raabe, D.; et al. Chemical boundary engineering: A new route toward lean, ultrastrong yet ductile steels. Sci. Adv. 2020, 6, eaay1430. [Google Scholar] [CrossRef]
- Zhao, H.; Huber, L.; Lu, W.; Peter, N.J.; An, D.; De Geuser, F.; Dehm, G.; Ponge, D.; Neugebauer, J.; Gault, B.; et al. Interplay of chemistry and faceting at grain boundaries in a model Al alloy. Phys. Rev. Lett. 2020, 124, 106102. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Chakraborty, P.; Ponge, D.; Hickel, T.; Sun, B.; Wu, C.-H.; Gault, B.; Raabe, D. Hydrogen trapping and embrittlement in high-strength Al alloys. Nature 2022, 602, 437–441. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Sun, B.; Schökel, A.; Song, W.; Ponge, D.; Raabe, D.; Bleck, W. Phase boundary segregation-induced strengthening and discontinuous yielding in ultrafine-grained duplex medium-Mn steels. Acta Mater. 2020, 200, 389–403. [Google Scholar] [CrossRef]
- Larson, D.J.; Prosa, T.J.; Ulfig, R.M.; Geiser, B.P.; Kelly, T.F. Local Electrode Atom Probe Tomography: A User’s Guide; Springer: New York, NY, USA, 2013. [Google Scholar]
- Millar, M.K.; Forbes, R.G. Atom-Probe Tomography; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Lefebvre-Ulrikson, W.; Vurpullot, F.; Sauvage, X. (Eds.) Atom Probe Tomography; Academic Press: Cambridge, MA, USA, 2016; Available online: https://www.sciencedirect.com/science/book/9780128046470 (accessed on 12 November 2023).
- Tochigi, E.; Sato, T.; Shibata, N.; Fujita, H.; Ikuhara, Y. Atomic-scale analysis of mechanical response of SrTiO3 by MEMS-based in situ STEM mechanical testing. Microsc. Microanal. 2020, 26, 1838–1840. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).