1. Introduction
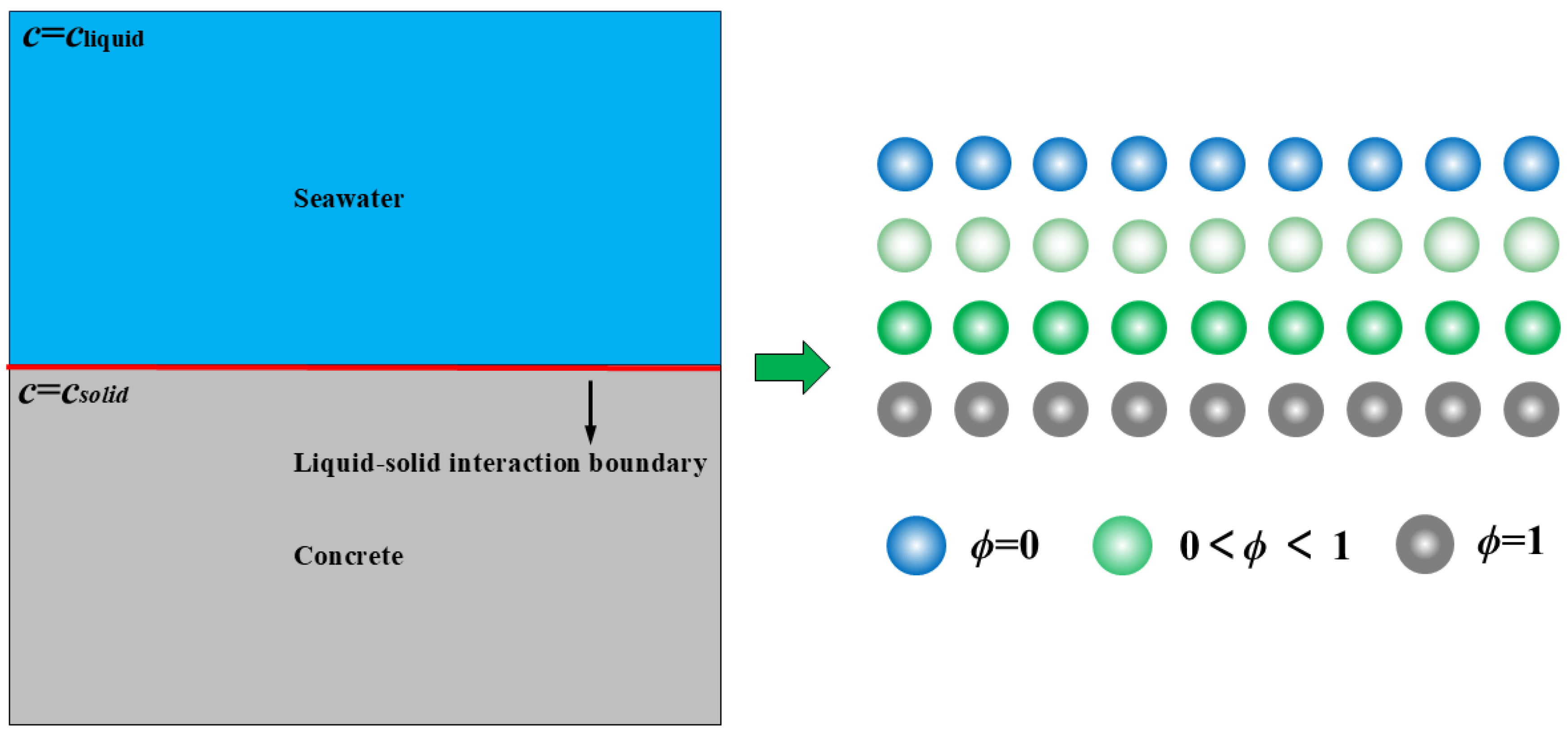
With the continuous growth of the global demand for clean energy, offshore wind power, as a way of developing and utilizing renewable energy, is gradually becoming a research hotspot in the energy field. The pile foundation of offshore wind turbines is a key structure supporting the offshore wind turbine generator set; thus, its safety and durability are directly related to the stable operation of the entire wind power system. However, due to the long-term exposure of the pile foundation of offshore wind turbines to the harsh marine environment, it is affected by various factors such as seawater erosion, chloride ion penetration, and wet–dry cycles, and the problem of corrosion damage is becoming increasingly serious, as shown in
Figure 1. Corrosion damage not only leads to the degradation of the material properties of the pile foundation and reduces its bearing capacity but also may cause structural failure, resulting in huge economic losses and environmental risks. Therefore, in-depth research on the corrosion damage mechanisms of the pile foundation of offshore wind turbines, the establishment of accurate prediction models, and the proposal of effective protection measures are of great practical significance for ensuring the safe operation of offshore wind power facilities, prolonging the service life, and reducing maintenance costs.
Scholars have delved into extensive in-depth investigations regarding the corrosion damage afflicting the pile foundations of offshore wind turbines, primarily manifested across three dimensions: experimental inquiries, theoretical explorations, and numerical simulations. In the realm of experimental research, scholars have resorted to on-site monitoring and laboratory tests to observe and dissect the corrosion damage phenomenon of the pile foundation of offshore wind turbines. On-site monitoring facilitates the direct procurement of corrosion data pertaining to the pile foundation within the authentic marine milieu. Nevertheless, due to the constraints of environmental conditions and monitoring techniques, it is arduous to comprehensively fathom the intricacies of the corrosion process. Conversely, laboratory tests have the capacity to modulate test conditions, thereby facilitating the exploration of the ramifications exerted by a multiplicity of factors upon the corrosion damage of the pile foundation. For instance, Li et al. [
1] conducted a model test on reinforced concrete (RC) marine piles using local electrochemical chloride ingress (LECE) to scrutinize the effect of non-uniform local corrosion on their lateral behavior and discovered that non-uniform local corrosion would give rise to local deterioration of the pile structure, rendering the force–displacement hysteresis curve asymmetric. Liu et al. [
2] investigated the influence of reinforcement corrosion on the flexural performance of lightweight aggregate concrete (LWAC) beams through experiments and numerical simulations and found that longitudinal reinforcement corrosion would reduce the cracking, yielding, and ultimate bending moments of the beams. Hu et al. [
3] delved into the cracking behavior of lightweight aggregate concrete (LWAC) induced by reinforcement corrosion and established and validated a meso-finite element model of LWAC. Mermerdas et al. [
4] explored the effect of different types of calcined kaolin (CK) and high-purity metakaolin (MK) on the corrosion resistance of reinforcement in concrete and ascertained that the incorporation of CK and MK augmented the concrete impedance and diminished the corrosion current density. Liao et al. [
5] probed into the corrosion inhibition mechanism of alanine (ALA) as an anion of layered double hydroxide (LDH) inhibitor on reinforcement and found that the LDHs/ALA exhibited excellent corrosion inhibition performance for reinforcement in a simulated solution containing 0.3 mol/L NaCl. Wang et al. [
6] examined the effect of cracks on chloride ion diffusion and reinforcement corrosion in concrete and found that the chloride ion diffusion region assumed a funnel shape, with the most severe erosion occurring at the crack. Chen et al. [
7] carried out experimental and numerical studies on the corrosion of reinforced concrete members and discovered that the elastic properties of the corrosion products affected the mechanical response of the concrete structure. Zhang et al. [
8] investigated the effect of local corrosion on the lateral impact performance of concrete-filled steel tubular flange girders (CFSTFGs) and found that CFSTFGs mainly underwent overall bending deformation, and the impact resistance of the beam decreased with the increase in the corrosion degree. Song et al. [
9] studied the bond performance between reinforcement and concrete considering the coupling effect of reinforcement corrosion and sulfate attack-induced concrete deterioration and found that with the increase in sulfate concentration, the bond strength decreased and the slip increased. Guo et al. [
10] studied the effect of acid rain corrosion on the eccentric compression performance of reinforced concrete columns and found that acid rain corrosion proceeded from the outside to the inside, altering the mineral composition of concrete. Zhao et al. [
11] studied the seismic performance of circular concrete-filled steel tubular (CFST) columns under local corrosion and found that local corrosion significantly affected the failure mode of CFST columns; Wu et al. [
12] studied the bond performance of reinforced concrete beams considering the effects of concrete compressive strength, longitudinal reinforcement corrosion, stirrup corrosion, and loading rate and found that the increase in concrete strength would augment the bond strength. Zhao et al. [
13] studied the effects of the water–cement ratio, concrete cover thickness, reinforcement spacing, and quantity on the corrosion characteristics of reinforcement and found that the mass loss of reinforcement increased with the increase in the water–cement ratio and decreased with the increase in cover thickness; Xu et al. [
14] studied the seismic performance of prestressed concrete beams in a simulated acid rain corrosion environment and found that the bearing capacity of the beam decreased with the increase in corrosion time. Ding et al. [
15] studied the effect of the reverse osmosis and saturation-based action anti-corrosion technology (RS—AAT) on the chloride ion transport in cracked concrete under wet–dry cycles and immersion conditions and found that the RS-AAT technology could effectively inhibit the chloride ion accumulation around the cracks. Although experimental research can furnish intuitive data and phenomena, due to the complexity of the actual pile foundation of offshore wind turbines, it is challenging to fully replicate the real environment in the test conditions. Moreover, the test period is protracted, and the cost is exorbitant. Therefore, experimental research is incapable of deeply unravelling the internal mechanisms of the corrosion damage of the pile foundation. In the field of theoretical research, scholars have established some simplified mathematical models to depict the corrosion damage process of the pile foundation predicated on the theories of material mechanics, structural mechanics, and electrochemistry. For example, Macdonald et al. [
16] employed a theoretical method based on the point defect model (PDM) to calculate the chloride ion threshold (CT) of reinforcement in concrete and investigated the influence of various factors on the CT value. Chen et al. [
17] explored the applicability of the polarization resistance method for microcell and macrocell corrosion (MMC) through theoretical analysis and the simulation of concrete pore solution experiments and derived a modified Stern–Geary equation applicable to MMC. Mukhti et al. [
18] established an artificial intelligence-assisted model for the automatic assessment of early concrete damage by ultrasonic pulse waves, providing a method for the long-term monitoring and damage assessment of concrete structures. Yang et al. [
19] established a concrete service life prediction model by simulating the sulfate corrosion environment in the Taitema Lake in Xinjiang through laboratory tests. Huang et al. [
20] studied the degradation law of the bond performance of reinforced concrete under chloride ion erosion and established a bond strength prediction model. However, theoretical research is often predicated on certain assumptions and simplified conditions and can only yield analytical solutions under simple boundary conditions. Its applicability to complex practical engineering problems is circumscribed, making it difficult to accurately characterize the corrosion damage behavior of the pile foundation in the complex marine environment.
As an important research method, numerical simulation has been widely applied in the study of corrosion damage of offshore wind turbine pile foundations. Scholars have utilized numerical methods such as the finite element method and the discrete element method to conduct simulation analyses on the corrosion processes of pile foundations. For example, Wu et al. [
21] studied the transport of chloride ions in concrete under uniaxial bending loads and in coastal soft soil environments through experiments and numerical simulations, and they developed a binary time-varying model. Liu et al. [
2] investigated the impact of steel bar corrosion on the flexural performance of lightweight aggregate concrete (LWAC) beams by means of tests and numerical simulations, established a finite element model, and analyzed the flexural performance of LWAC beams with different steel bar corrosion rates. Du et al. [
22] quantitatively evaluated the chloride ion corrosion damage of reinforced concrete beams based on embedded piezoelectric ceramic (PZT) sensors and determined the optimal placement positions of the sensors through three-dimensional finite element simulations. Liu et al. [
3] studied the cracking behavior of LWAC due to corrosion through accelerated corrosion tests and meso-scale finite element methods and established a meso-scale finite element model of LWAC. Wu et al. [
23] conducted quasi-static and dynamic single-shear tests on the dynamic shear behavior of the carbon fiber-reinforced polymer (CFRP)–concrete interface and established a finite element model. Wang et al. [
6] studied the effects of cracks on the diffusion of chloride ions in concrete and the corrosion of steel bars by using methods such as the silver nitrate colorimetric method, XRD, and COMSOL finite element simulation and improved the chloride ion diffusion model. Han et al. [
24] explored the diffusion behavior of chloride ions in rubber concrete under wet–dry cycling conditions through experimental studies and numerical simulations and carried out the simulations using Comsol Multiphysics software. Da et al. [
25] prepared coral aggregate-reinforced concrete beams (CARCB) of different strength grades, conducted shear performance tests, and established a numerical analysis model based on the K&C theory. Li et al. [
26] established a non-uniform corrosion numerical model of reinforced concrete considering the coupling effects of calcium leaching and chloride ion diffusion, which can more accurately predict the corrosion kinetics and rust layer distribution of reinforced concrete under time-varying conditions. Mohammadian et al. [
27] modeled the active corrosion of steel bars in synthetic solutions and studied the impact of the uncertainty of input parameters on the model predictions. Wang et al. [
28] studied the coupling effects of macro-cell corrosion and multi-ion equilibrium in structural concrete through numerical simulations and experimental studies, and carried out the simulations using the DuCOM-PHREEQC integrated analysis platform. Di et al. [
29] studied the transport of chloride ions in marine reinforced concrete (RC) structures through numerical simulation methods and established a 3D meso-scale model of RC multi-phase composite materials. Zeng et al. [
30] conducted a numerical study on the axial compression performance of circular concrete-filled steel tubular short columns under local corrosion by using finite element simulation and analyzed the effects of different corrosion parameters on the column performance. Chen et al. [
31] established a multi-phase meso-scale numerical model to predict the corrosion situation of steel bars in cracked concrete, considering the coupling effects of coarse aggregates (CAs) and cracks on the corrosion of steel bars. Zhang et al. [
32] established a self-balancing steel bar corrosion model and analyzed the corrosion kinetics and rust layer distribution of steel bars under time-varying climate conditions. Xia et al. [
33] established a numerical model coupling mass transport and electrochemical corrosion processes and simulated the evolution of chloride ion transport and steel bar corrosion. Wang et al. [
34] simulated the corrosion process of steel bars in a chloride ion environment by using the concrete meso-structure model of random polygonal coarse aggregates and analyzed the impact of coarse aggregates on the corrosion of steel bars. Dong et al. [
35] proposed a robust numerical solution strategy for evaluating the corrosion situation of reinforced concrete structures under external power supply. Shen et al. [
36] established a strength calculation method and a numerical model of a carbon fiber-reinforced plastic (CFRP) grid: reinforced slender concrete shear walls based on the MVLEM. Hu et al. [
37] established a time-varying analytical model of chloride ion diffusion in the protective layer of a prestressed concrete cylinder pipe (PCCP) and carried out meso-scale numerical simulations of chloride ion diffusion. When dealing with corrosion damage problems, the finite element method requires remeshing to adapt to the changes of the structure during the corrosion processes, which not only increases the computational cost but also may lead to errors in the calculation results. Although the discrete element method can simulate the large deformation and failure processes of the structure, it requires complex parameter calibration and has a relatively low computational efficiency. Therefore, it is necessary to develop a more effective numerical simulation method to overcome these shortcomings. The smoothed particle hydrodynamics method (SPH) is a meshless numerical method with the following advantages: it does not require mesh generation and can avoid the computational difficulties caused by mesh distortion; it has unique advantages in dealing with large deformation and failure problems and can more realistically simulate the mechanical behavior of pile foundations during the corrosion processes; it can conveniently simulate multi-phase media and complex boundary conditions; and it can more accurately reflect the impact of the marine environment on pile foundations. For example, Zhou et al. [
38] proposed the so-called GPD method based on the SPH method, but it has been rarely applied in simulating the corrosion processes of pile foundations.
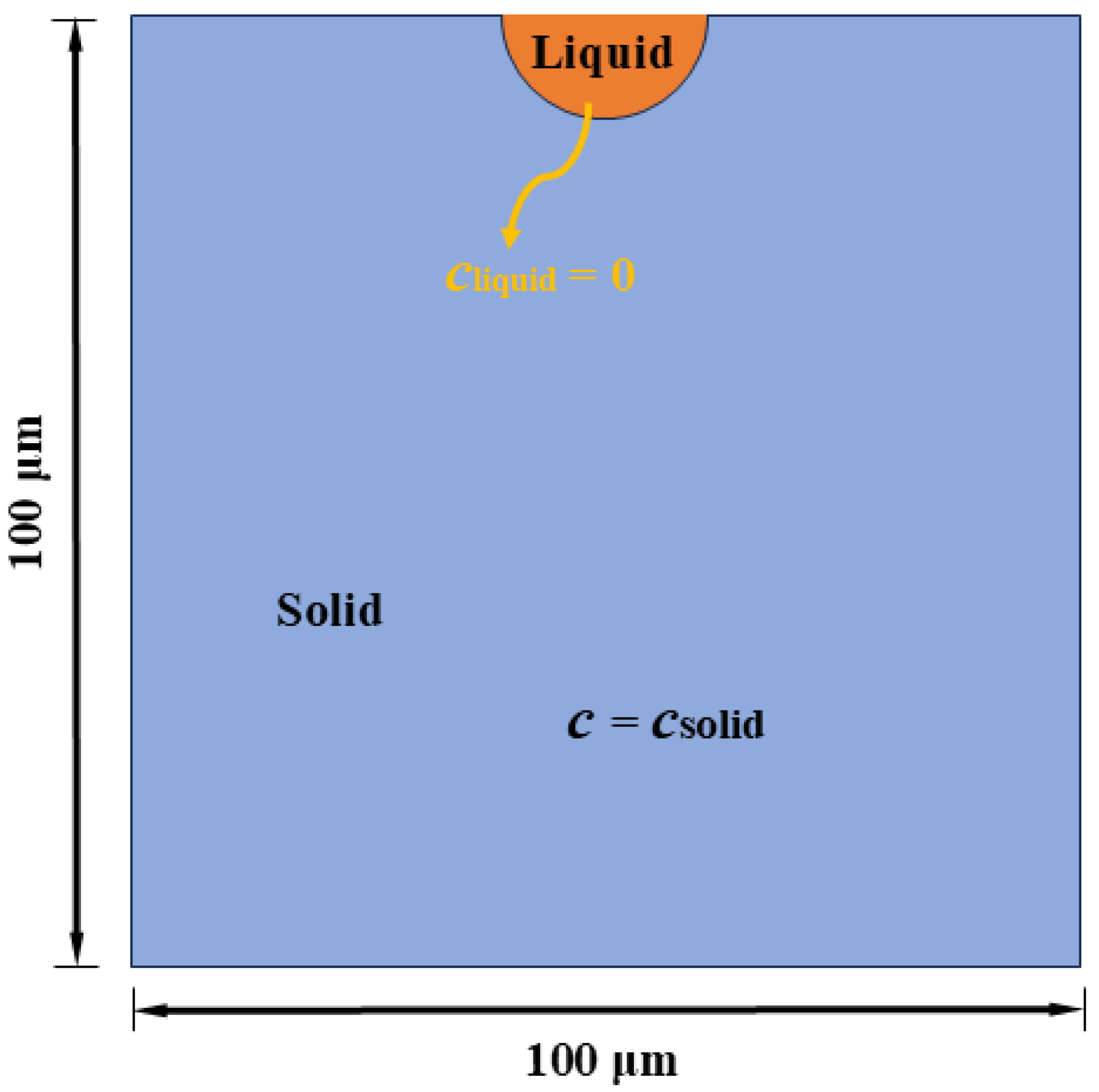
In view of the shortcomings of previous research, a meshless numerical method has been developed to simulate the ion diffusion process and corrosion damage process of pile foundation concrete. In addition, a method for generating the concrete meso-structure within the framework of the smoothed particle hydrodynamics (SPH) method is proposed. Firstly, the rationality of this numerical algorithm is verified through a typical example. Then, concrete pile foundation models under different aggregate percentages, ion concentration diffusion coefficients, and aggregate particle sizes are established to simulate the corrosion damage processes of the concrete pile foundation models under various circumstances. Finally, the simulation results are compared with the corrosion damage morphologies of offshore wind turbine pile foundations, and the application prospects of the SPH method are discussed. The research results can provide some references in applying the SPH method into the simulations of corrosions of concrete piles for offshore wind power and recognizing the corrosion mechanisms of concrete piles for offshore wind power.
3. Generations of Concrete Meso-Structures in the SPH Framework
The generation of concrete meso-structure lies in the generation of random aggregates in concrete. Assuming the random aggregates are circular, the control factors of random aggregates are the coordinates of their centers and radii. The detailed steps are as follows:
(1) Determine the generation range of concrete (x1, y1), the target percentage of aggregate Pagg, the maximum aggregate size Dmax, and the minimum aggregate size Dmin.
(2) Generate random numbers ran1, ran2, and ran3 within the range of (0~1). Determine the three characteristic parameters of the aggregate: the
x-coordinate of the aggregate center
xg, the y-coordinate of the aggregate center
yg, and the radius of the circular aggregate
rg. The expressions of the characteristic parameters of the aggregate can be written as follows:
(3) Judge the position of the generated aggregate with respect to all previously generated circular aggregates. The judgment method is to check whether the distance between the centers of the new aggregate and the previously generated aggregates is greater than the sum of their radii. If they overlap, regenerate the aggregate.
(4) Judge whether the percentage of generated aggregates reaches the target percentage Pagg. If it reaches the target percentage, stop generating aggregates; if not, continue generating aggregates.
For the interfacial transition zone, it is only necessary to set the particles in the outer circle of the aggregate as the interfacial transition zone particles.
5. Discussion
5.1. Comparisons with the Previous Literature
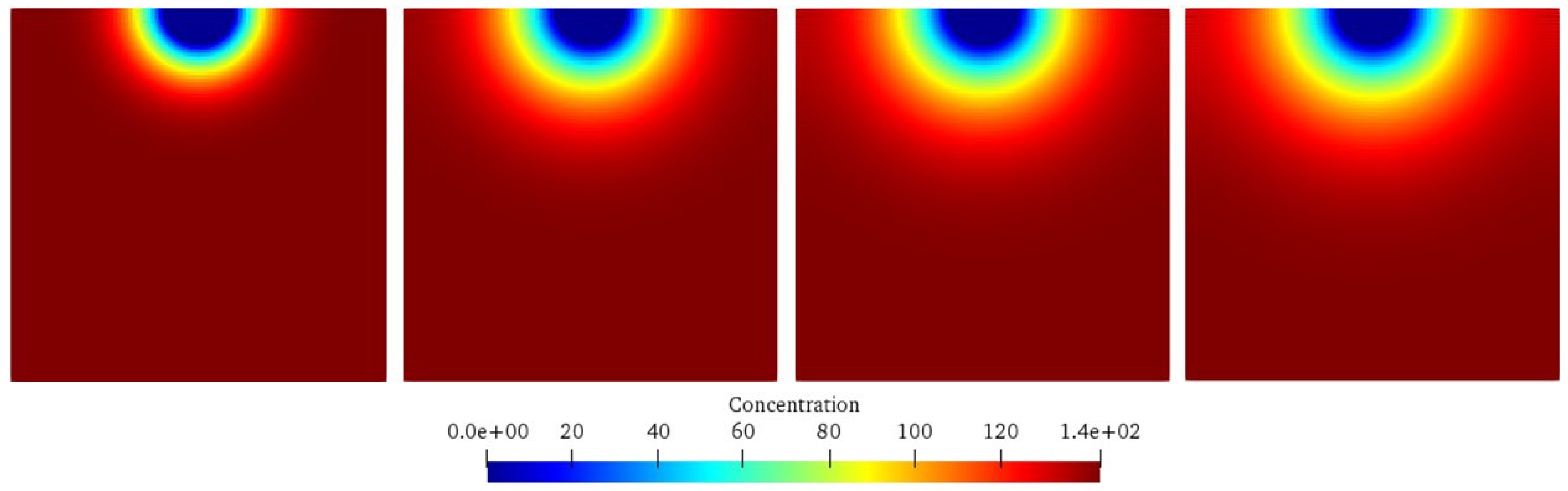
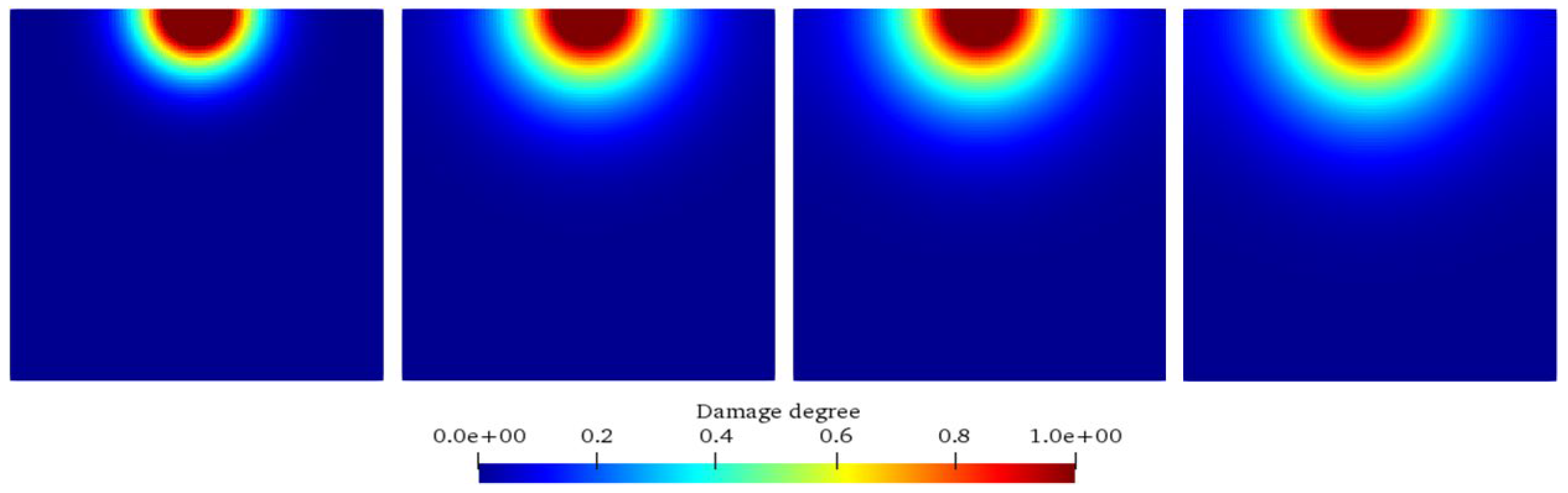
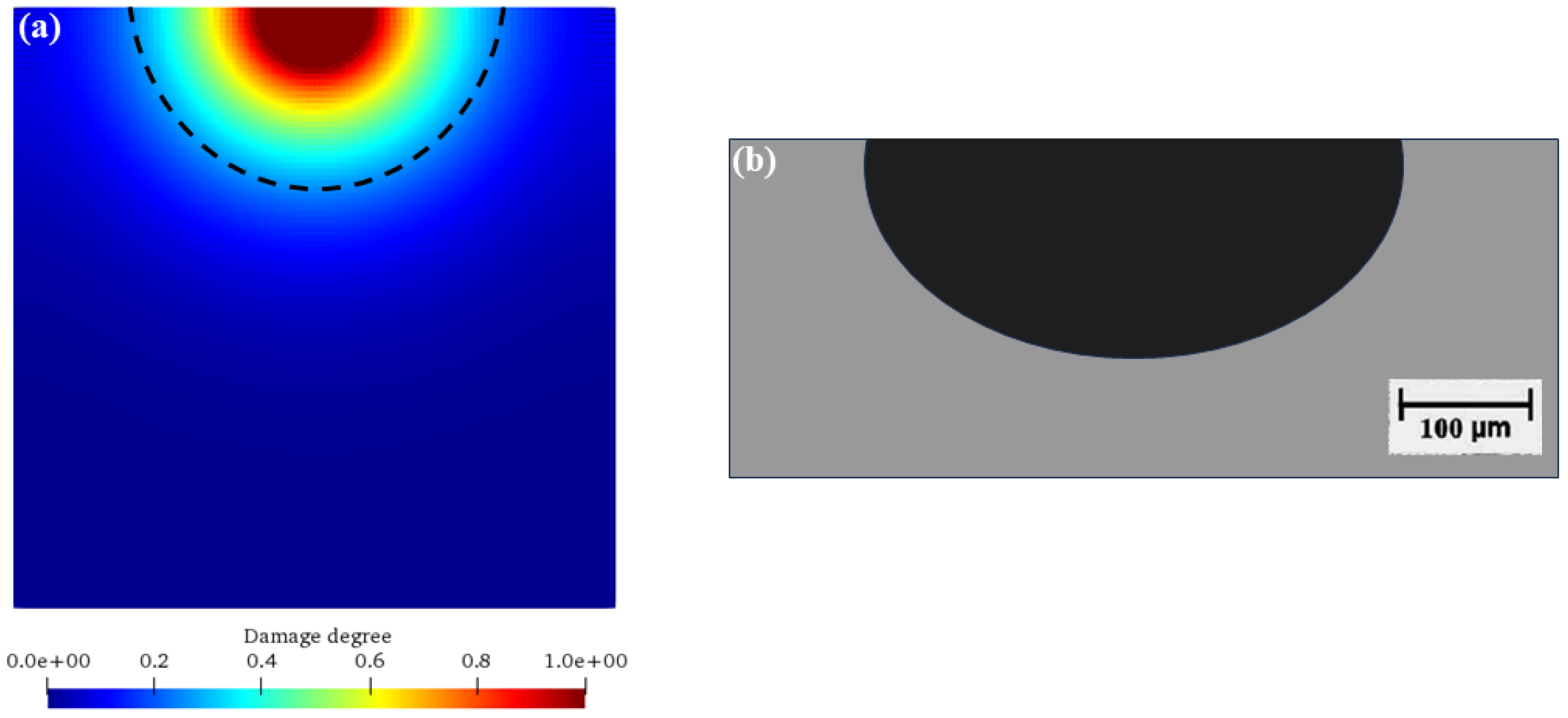
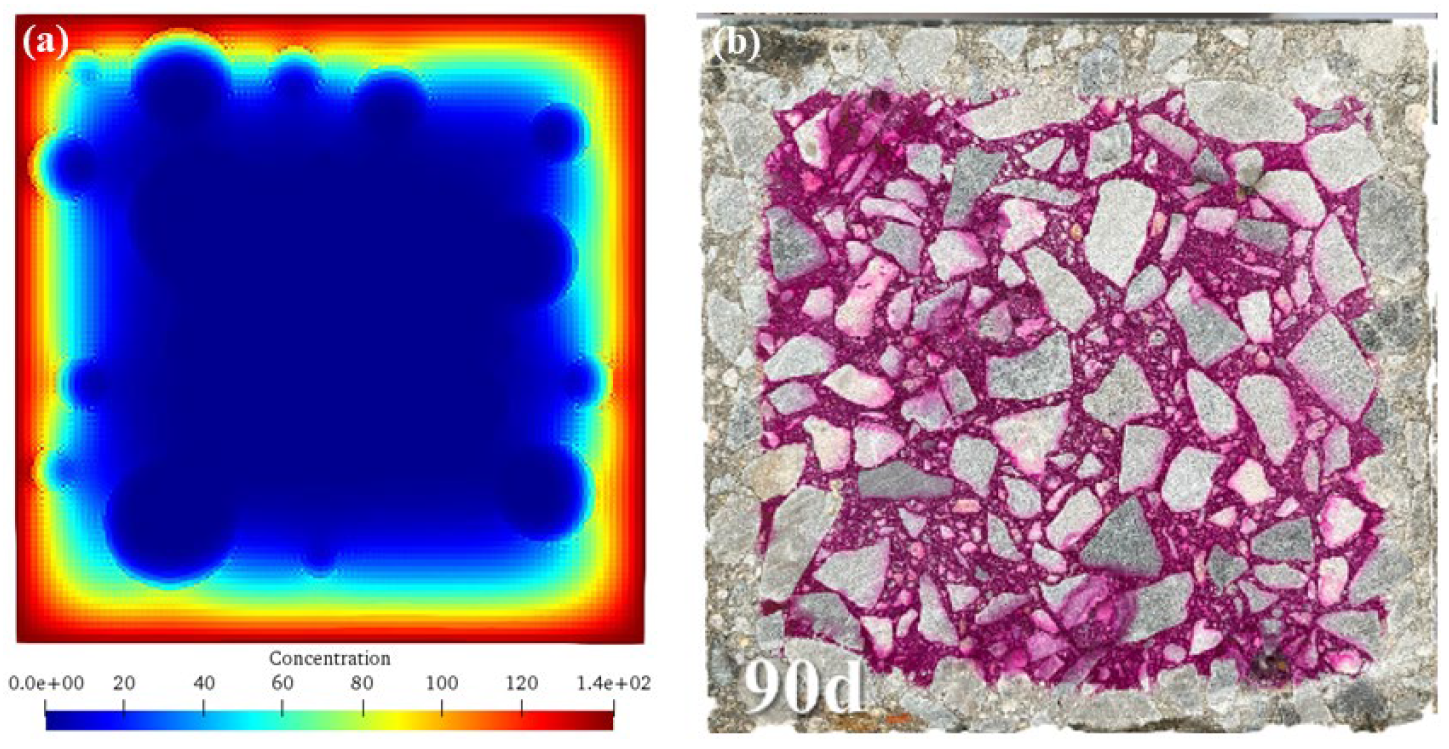
Figure 11 shows the comparisons of numerical results and previous experimental results [
42]. As can be seen, the numerical simulation results of this study (
Figure 11a) ingeniously reveal the corrosion dynamics through the ion concentration cloud diagram. The decreasing ion concentration from the outside to the inside accurately depicts the gradual corrosion process driven by the ion diffusion gradient within the concrete under seawater erosion. This is consistent with the theory of ion transport in concrete, where ions in seawater accumulate at the interface and then penetrate deeper into the interior according to the concentration difference, resulting in a gradually decreasing degree of corrosion with depth. It intuitively demonstrates the complexity of the spatio-temporal evolution of corrosion and highlights the coupling effects of diffusion coefficients, aggregate barriers, and chemical reactions.
The experimental results in the previous literature (
Figure 11b) distinguish the regions with red (uncorroded) and white (corroded) colors, clearly showing the erosion process from the outside to the inside of the concrete. Corresponding to the numerical simulation, it verifies the law that the actual corrosion starts from the surface and then spreads inward, highlighting the intertwined influences of environmental factors and material properties. The high similarity between the two strongly supports the accuracy of the simulation method in this study, indicating that the model can effectively capture the key characteristics of corrosion and fostering trust for engineering applications.
Differences also exist. The numerical simulation shows a continuous ion concentration distribution, while the experimental results present a discrete regional state. This is attributed to the idealized assumptions in the simulation and the practical limitations in the experiment. The precise setting of simulation parameters and the simplification of boundary conditions lead to the ideal continuity, while the experiment is perturbed by factors such as material heterogeneity, slight environmental changes, and measurement errors, resulting in discreteness. These differences drive the optimization of the model, prompting the consideration of more real-world factors to reduce differences and improve accuracy. Overall, the simulation results of this study and the previous experimental results complement each other, injecting strong impetus and opening up new paths for the refinement of the corrosion theory of offshore wind power pile foundations, the optimization of durability design, and the innovation of protection strategies.
5.2. Research Propects
In this study, the chemical damage processes of the concrete of offshore wind power pile foundations were simulated and analyzed using the SPH-based meshless numerical simulation method, and certain achievements have been made. However, there are still many aspects worthy of in-depth discussions.
In terms of the accuracy and reliability of the numerical simulation method, although the rationality of the developed numerical algorithm has been verified by a typical example, there may still be some differences from the actual situation. The actual environment where offshore wind power pile foundations are located is complex and changeable. Factors such as temperature, humidity, and water flow velocity affect the corrosion processes, but the consideration of these factors in this simulation may not be comprehensive enough. Future research can further optimize the model and incorporate more actual environmental factors to improve the simulation accuracy.
Regarding the influences of aggregate characteristics on the chemical damage of concrete, it was found that the aggregate percentage and size have a significant impact on ion diffusion and damage evolution. However, other characteristics of the aggregate, such as the shape, surface roughness, and mineral composition of the aggregate, may also play a role in the corrosion processes. Further research on the comprehensive influence of different aggregate characteristics will help to more comprehensively understand the mechanisms of the role of aggregate in concrete corrosion.
For the ion diffusion coefficient, we only considered the influences of changes within a limited range on concrete corrosion. In fact, in different marine environments, the ion diffusion coefficient may have a larger variation range and may be coupled with other factors to affect the corrosion processes. In the future, we can expand the research range of the ion diffusion coefficient and deeply explore its coupling relationships with other factors (such as aggregate characteristics, environmental factors, etc.).
From the perspective of the durability design of the concrete structure, although the current research provides a basis for understanding the corrosion damage mechanisms, more research is still needed on how to formulate accurate durability design strategies based on the simulation results: for example, how to determine reasonable concrete mix proportions, protective layer thickness, and other design parameters according to the simulation results under different working conditions to ensure the safety and reliability of the pile foundation during the entire service life.
In addition, the application of the SPH method in simulating the corrosion process of complex concrete structures (such as concrete pile foundations with reinforcement) still faces challenges. Determining how to better simulate the interactions between the reinforcement and the concrete as well as the influence of corrosion on this interaction is a problem that needs to be solved in future research, which is crucial for accurately predicting the actual performance of offshore wind power pile foundations. In-depth discussion and further research in these aspects are expected to provide stronger support for the corrosion protection and durability design of offshore wind power pile foundations.
6. Conclusions
(1) The SPH-based meshless numerical simulation method and the concrete meso-structure generation method are reasonable and feasible. The accuracy of the numerical algorithm has been verified by a typical example, and it can predict the damage evolution of concrete during the corrosion process well, providing a powerful tool for studying the corrosion of offshore wind power pile foundations.
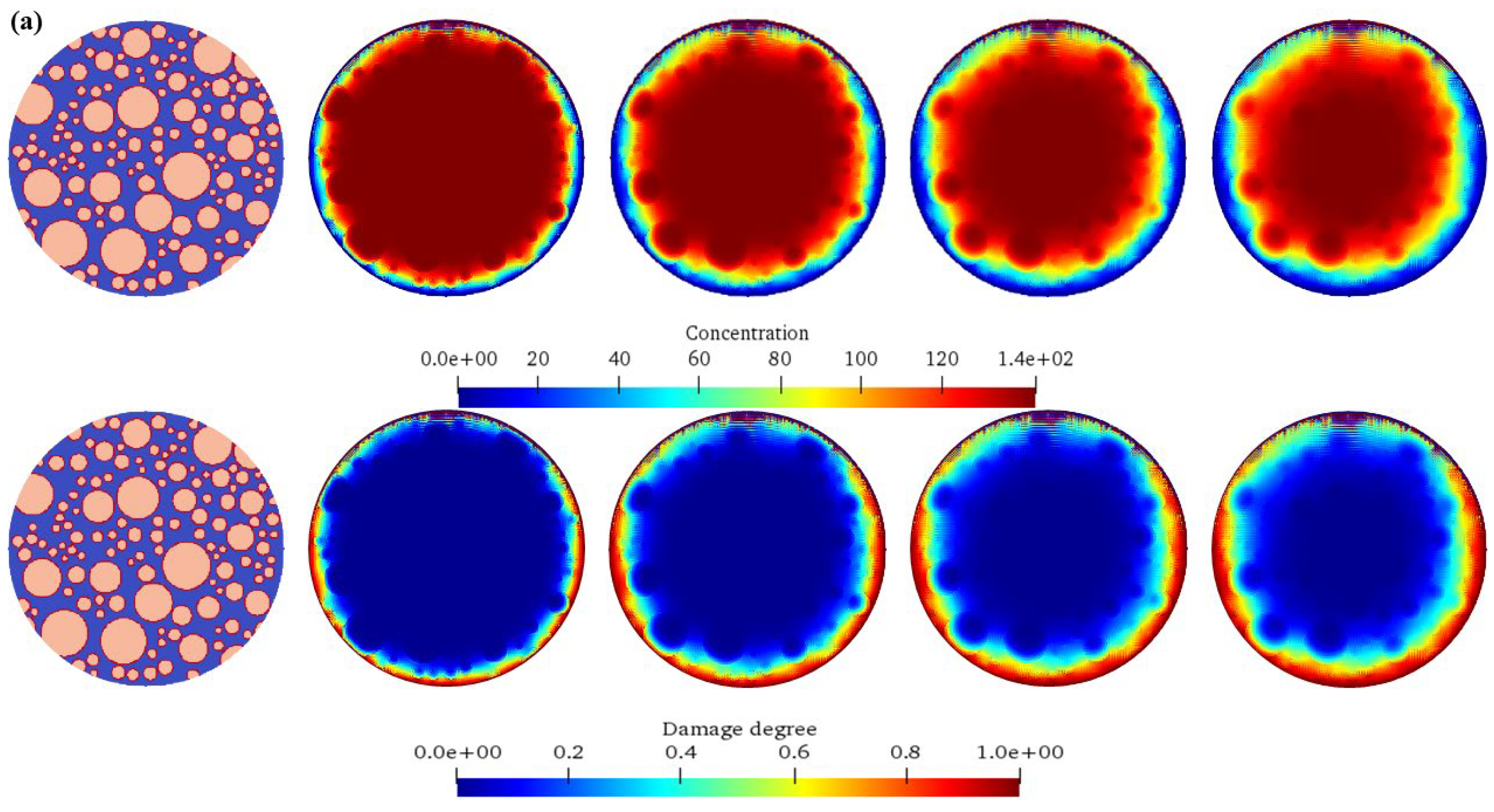
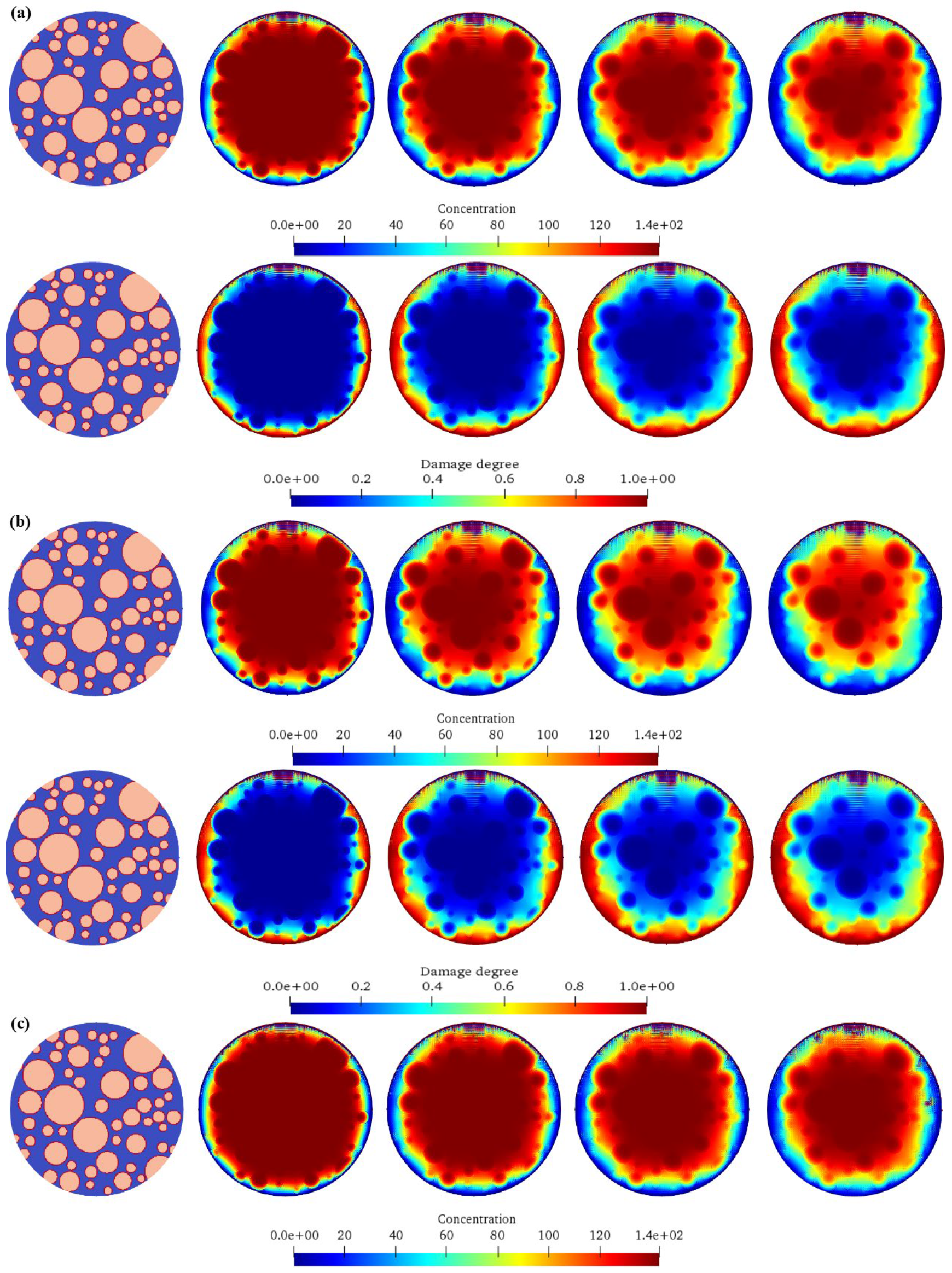
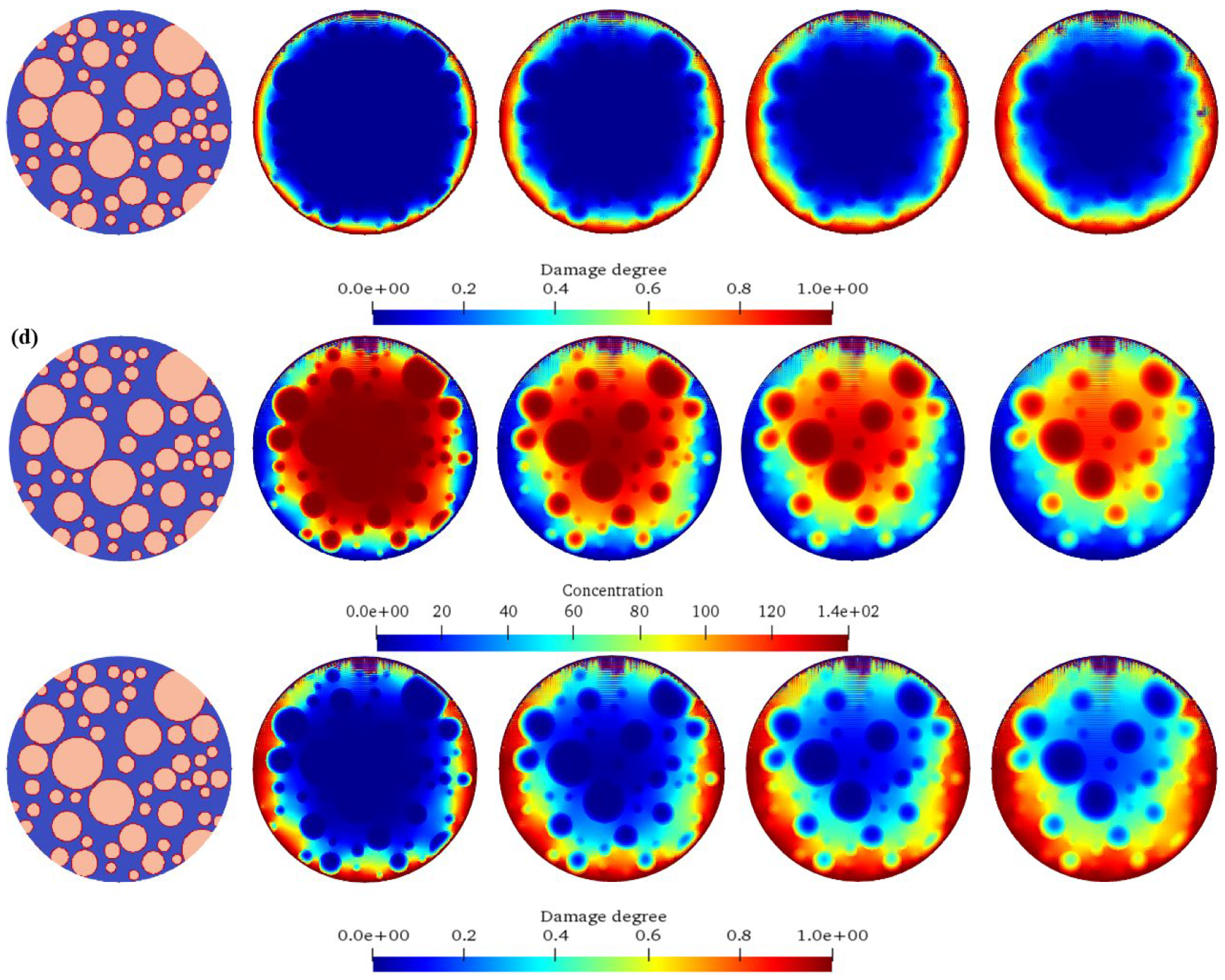
(2) The increase in the aggregate percentage will gradually slow down the diffusion speed of chemical ions, and the ion diffusion path will be more tortuous. The early damage development slows down with the increase in the aggregate size, but the final damage degree will still accumulate. Moreover, the damaged area of the concrete with a high aggregate percentage is relatively scattered, while the damaged area is more likely to be connected into a piece when the aggregate content is low.
(3) The increase in the aggregate size makes the diffusion of chemical ions more difficult, and the large aggregate has a stronger obstruction to the diffusion path. The damage starts later and is concentrated around the large aggregate in the early stage. The concrete with a small aggregate size has a rapid expansion of damage and scattered areas after the damage starts, while the concrete with a large aggregate size has a relatively low damage degree in the same amount of time, but the damage will still develop with the increase in time.
(4) The increase in the ion diffusion coefficient significantly accelerates the ion diffusion process, promotes the earlier and faster development of concrete damage, and significantly deepens the damage degree, indicating that it has a key control effect on the concrete chemical corrosion damage process and directly affects the durability and safety of the concrete structure.
(5) The research results of this study are helpful to deeply understand the corrosion damage mechanism of offshore wind power pile foundations and provide theoretical support for optimizing the durability design, formulating protection strategies, and working on maintenance. However, further research and improvement are still needed in aspects such as the accuracy of the simulation method, the study of aggregate characteristics, the research range of the ion diffusion coefficient, the formulation of durability design strategies, and the application of the SPH method to complex structures.