Electrical Conductivity in Graphite Foils Produced by Rolling and Pressing
Abstract
1. Introduction
2. Materials and Methods
2.1. Production of the Graphite Foil
2.2. Determination of Electrical Conductivity of the Graphite Foil
2.3. Scanning Electron Microscopy Examination of Graphite
2.4. Measuring the Nano-Crystallite Sizes
2.5. Misorientation of Nano-Crystallites
2.6. Identification of the Preferential Crystallographic Orientation of Nano-Crystallites and Calculation of the GF Electrical Conductivity
3. Results and Discussion
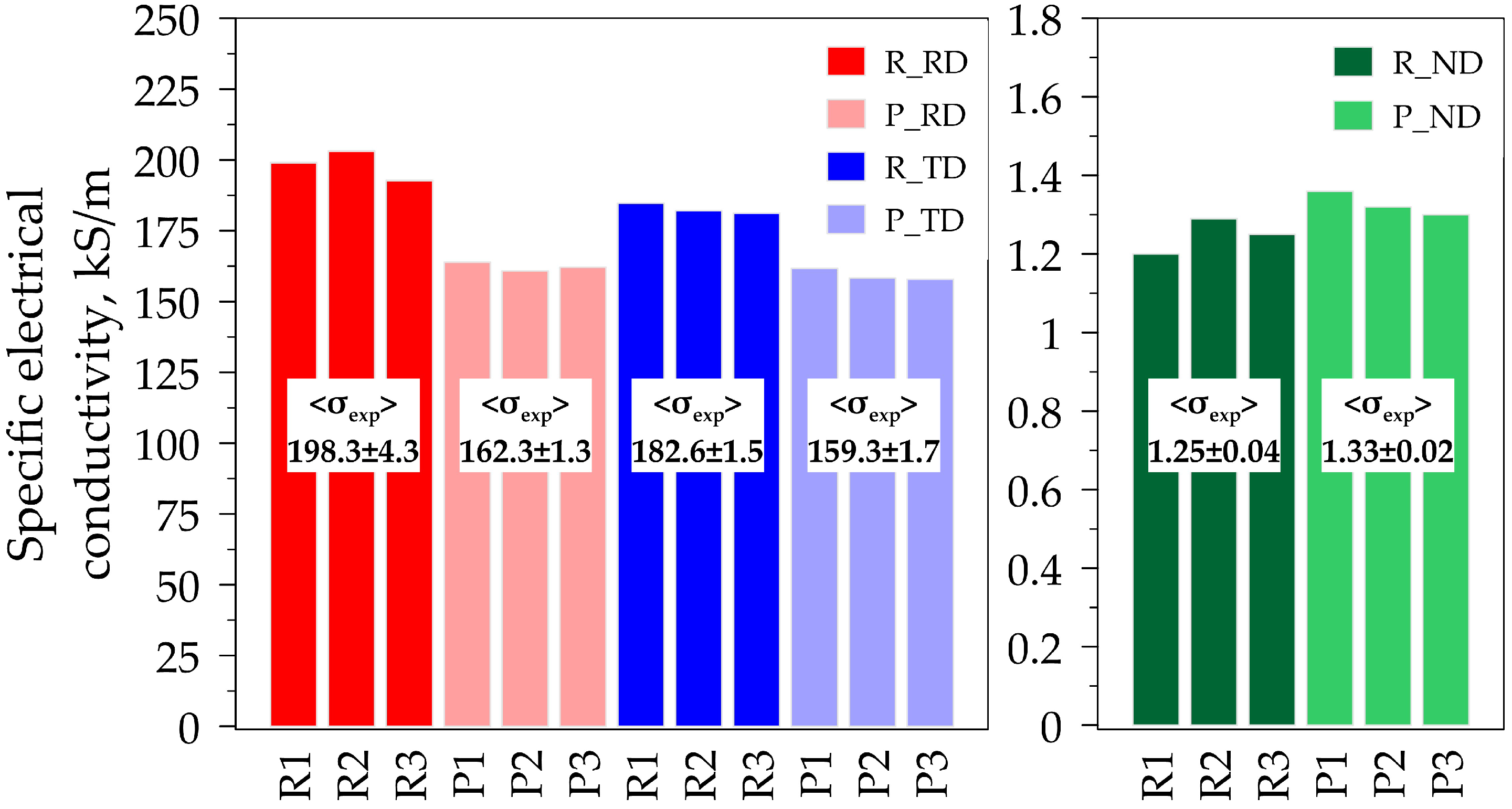
3.1. Experimental Value of Electrical Conductivity for Graphite Foils
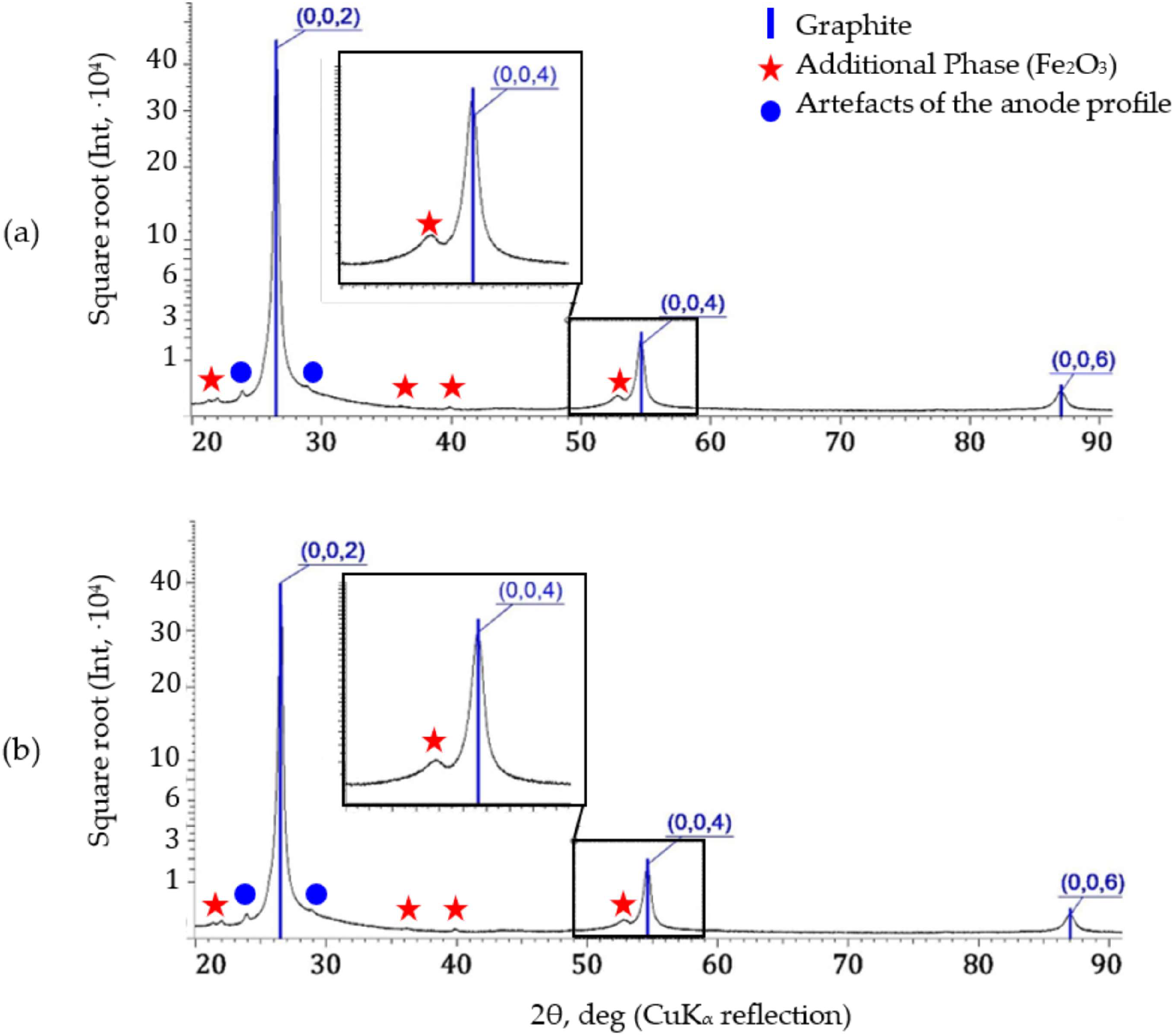
3.2. Phase Composition and Structural Characteristics of GF
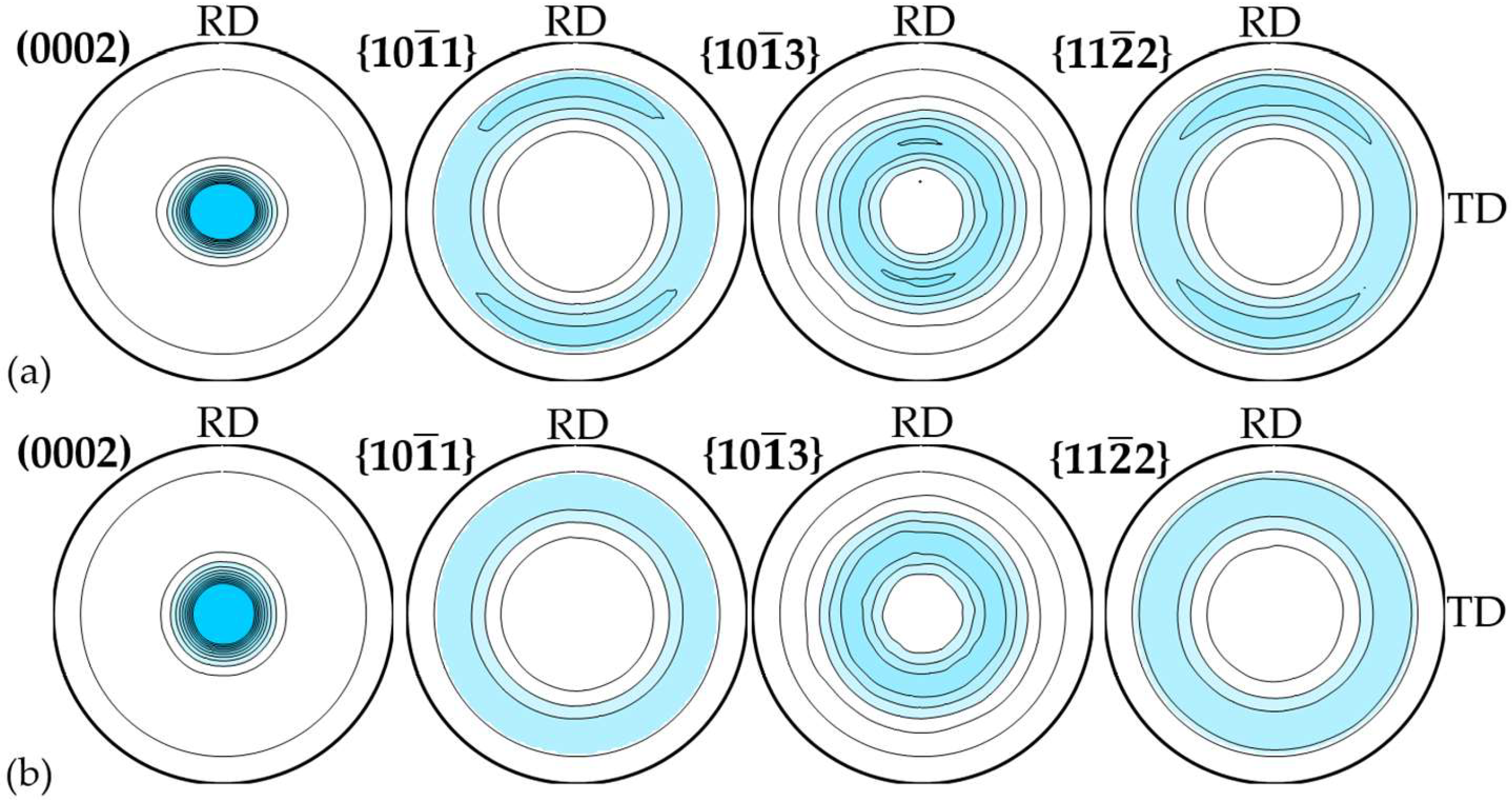
3.3. Crystallographic Texture of GF and the Calculated Values of Electrical Conductivity
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wei, X.H.; Liu, L.; Zhang, J.X.; Shi, J.L.; Guo, Q.G. Mechanical, Electrical, Thermal Performances and Structure Characteristics of Flexible Graphite Sheets. J. Mater. Sci. 2010, 45, 2449–2455. [Google Scholar] [CrossRef]
- Lee, S.-H.; Seo, S.-D.; Jin, Y.-H.; Shim, H.-W.; Kim, D.-W. A Graphite Foil Electrode Covered with Electrochemically Exfoliated Graphene Nanosheets. Electrochem. Commun. 2010, 12, 1419–1422. [Google Scholar] [CrossRef]
- Savchenko, D.V.; Serdan, A.A.; Morozov, V.A.; Van Tendeloo, G.; Ionov, S.G. Improvement of the Oxidation Stability and the Mechanical Properties of Flexible Graphite Foil by Boron Oxide Impregnation. New Carbon Mater. 2012, 27, 12–18. [Google Scholar] [CrossRef]
- Roe, M.; Torrance, A.A. The Surface Failure and Wear of Graphite Seals. Tribol. Int. 2008, 41, 1002–1008. [Google Scholar] [CrossRef]
- Sorokina, N.E.; Redchitz, A.V.; Ionov, S.G.; Avdeev, V.V. Different Exfoliated Graphite as a Base of Sealing Materials. J. Phys. Chem. Solids 2006, 67, 1202–1204. [Google Scholar] [CrossRef]
- Feng, S.; Xu, L.; Li, L.; Bai, S.; Yang, X.; Zhou, X. Sealing Nuclear Graphite with Pyrolytic Carbon. J. Nucl. Mater. 2013, 441, 449–454. [Google Scholar] [CrossRef]
- Jaszak, P. Modeling of the Elastic Properties of Compressed Expanded Graphite-A Material Used in Spiral Wound Gaskets. Int. J. Press. Vessel. Pip. 2020, 187, 104158. [Google Scholar] [CrossRef]
- Nagano, H.; Ohnishi, A.; Nagasaka, Y. Thermophysical Properties of High Thermal Conductivity Graphite Sheet for Spacecraft Thermal Design. In Proceedings of the 34th Thermophysics Conference, Denver, CO, USA, 19–22 June 2000; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2000. [Google Scholar]
- Abidin, M.S.Z.; Razali, M.A.; Peng, T.J. Graphite Paper-Based Device for Energy Storage Application. J. Phys. Conf. Ser. 2023, 2622, 012019. [Google Scholar] [CrossRef]
- Ziv, B.; Haik, O.; Zinigrad, E.; Levi, M.D.; Aurbach, D.; Halalay, I.C. Investigation of Graphite Foil as Current Collector for Cathodes of Li-Ion Batteries. Meet. Abstr. 2012, MA2012-02, 852. [Google Scholar] [CrossRef]
- Zhang, D.; Tan, C.; Zhang, W.; Pan, W.; Wang, Q.; Li, L. Expanded Graphite-Based Materials for Supercapacitors: A Review. Molecules 2022, 27, 716. [Google Scholar] [CrossRef]
- Arvani, M.; Keskinen, J.; Lupo, D.; Honkanen, M. Current Collectors for Low Resistance Aqueous Flexible Printed Supercapacitors. J. Energy Storage 2020, 29, 101384. [Google Scholar] [CrossRef]
- Tarannum, F.; Danayat, S.S.; Nayal, A.; Muthaiah, R.; Annam, R.S.; Garg, J. Large Enhancement in Thermal Conductivity of Solvent−Cast Expanded Graphite/Polyetherimide Composites. Nanomaterials 2022, 12, 1877. [Google Scholar] [CrossRef] [PubMed]
- Bannov, A.G.; Ukhina, A.V.; Maksimovskii, E.A.; Prosanov, I.Y.; Shestakov, A.A.; Lapekin, N.I.; Lazarenko, N.S.; Kurmashov, P.B.; Popov, M.V. Highly Porous Expanded Graphite: Thermal Shock vs. Programmable Heating. Materials 2021, 14, 7687. [Google Scholar] [CrossRef] [PubMed]
- Chow, D.; Burns, N.; Boateng, E.; Van Der Zalm, J.; Kycia, S.; Chen, A. Mechanical Exfoliation of Expanded Graphite to Graphene-Based Materials and Modification with Palladium Nanoparticles for Hydrogen Storage. Nanomaterials 2023, 13, 2588. [Google Scholar] [CrossRef]
- Yurkov, A.L.; Malakho, A.P.; Ivanov, A.V.; Chernova, E.A.; Belogorlov, A.A.; Avdeev, V.V. Studying the Porosity of Graphite Foil with Different Densities: Pore Space Model and Gas Permeability. J. Mater. Sci. 2022, 57, 21156–21171. [Google Scholar] [CrossRef]
- Shulyak, V.A.; Morozov, N.S.; Gracheva, A.V.; Gritskevich, M.D.; Chebotarev, S.N.; Avdeev, V.V. Anisotropy of Electrical and Thermal Conductivity in High-Density Graphite Foils. Nanomaterials 2024, 14, 1162. [Google Scholar] [CrossRef]
- Lu, S.; Blanco, C.; Appleyard, S.; Hammond, C.; Rand, B. Texture studies of carbon and graphite tapes by XRD texture goniometry. J. Mater. Sci. 2002, 37, 5283–5290. [Google Scholar] [CrossRef]
- Hou, B.; Guo, H.; Zhang, N.; Zhi, Q.; Wang, B.; Yang, J. Anisotropic Friction Behavior of Aligned and Oriented Graphite Flakes/Copper Composite. Carbon 2022, 186, 64–74. [Google Scholar] [CrossRef]
- Solfiti, E.; Berto, F. A Review on Thermophysical Properties of Flexible Graphite. Procedia Struct. Integr. 2020, 26, 187–198. [Google Scholar] [CrossRef]
- Kearns, J.J. On the Relationship among ‘f’ Texture Factors for the Principal Planes of Zirconium, Hafnium and Titanium Alloys. J. Nucl. Mater. 2001, 299, 171–174. [Google Scholar] [CrossRef]
- Isaenkova, M.; Krymskaya, O.; Klyukova, K.; Bogomolova, A.; Kozlov, I.; Dzhumaev, P.; Fesenko, V.; Svetogorov, R. Regularities of Changes in the Structure of Different Phases of Deformed Zirconium Alloys as a Result of Raising the Annealing Temperature According to Texture Analysis Data. Metals 2023, 13, 1784. [Google Scholar] [CrossRef]
- Luo, X.; Chugh, R.; Biller, B.C.; Hoi, Y.M.; Chung, D.D.L. Electronic Applications of Flexible Graphite. J. Electron. Mater. 2002, 31, 535–544. [Google Scholar] [CrossRef]
- Zhao, J.; Zhu, X.; Zhang, W.; Qiu, J.; Zhai, F.; Zhang, H.; Cao, G.; Gao, S.; Ding, F.; Xiang, Y. Expanded Graphite Incorporated with Li4 Ti5 O12 Nanoparticles as a High-Rate Lithium-Ion Battery Anode. RSC Adv. 2024, 14, 11276–11283. [Google Scholar] [CrossRef] [PubMed]
- Ma, C.; Ma, C.; Wang, J.; Wang, H.; Shi, J.; Song, Y.; Guo, Q.; Liu, L. Exfoliated Graphite as a Flexible and Conductive Support for Si-Based Li-Ion Battery Anodes. Carbon 2014, 72, 38–46. [Google Scholar] [CrossRef]
- Wen, Y.; He, K.; Zhu, Y.; Han, F.; Xu, Y.; Matsuda, I.; Ishii, Y.; Cumings, J.; Wang, C. Expanded Graphite as Superior Anode for Sodium-Ion Batteries. Nat. Commun. 2014, 5, 4033. [Google Scholar] [CrossRef]
- Liu, Y.; Zeng, J.; Han, D.; Wu, K.; Yu, B.; Chai, S.; Chen, F.; Fu, Q. Graphene Enhanced Flexible Expanded Graphite Film with High Electric, Thermal Conductivities and EMI Shielding at Low Content. Carbon 2018, 133, 435–445. [Google Scholar] [CrossRef]
- Song, R.; Wang, Q.; Mao, B.; Wang, Z.; Tang, D.; Zhang, B.; Zhang, J.; Liu, C.; He, D.; Wu, Z.; et al. Flexible Graphite Films with High Conductivity for Radio-Frequency Antennas. Carbon 2018, 130, 164–169. [Google Scholar] [CrossRef]
- Guan, H.; Chung, D.D.L. Radio-Wave Electrical Conductivity and Absorption-Dominant Interaction with Radio Wave of Exfoliated-Graphite-Based Flexible Graphite, with Relevance to Electromagnetic Shielding and Antennas. Carbon 2020, 157, 549–562. [Google Scholar] [CrossRef]
- Fan, M.; He, H.; Wang, L.; Wang, X.; Tan, B. Preparation and Properties of Carbon Fiber/Flexible Graphite Composite Grounding Material. Materials 2024, 17, 4838. [Google Scholar] [CrossRef]
- Huang, J.; Zhao, Z.; Chen, T.; Zhu, Y.; Lv, Z.; Gong, X.; Niu, Y.; Ma, B. Preparation of Highly Dispersed Expandable Graphite/Polystyrene Composite Foam via Suspension Polymerization with Enhanced Fire Retardation. Carbon 2019, 146, 503–512. [Google Scholar] [CrossRef]
- Darabut, A.M.; Lobko, Y.; Yakovlev, Y.; Rodríguez, M.G.; Veltruská, K.; Šmíd, B.; Kúš, P.; Nováková, J.; Dopita, M.; Vorokhta, M.; et al. Influence of Thermal Treatment on the Structure and Electrical Conductivity of Thermally Expanded Graphite. Adv. Powder Technol. 2022, 33, 103884. [Google Scholar] [CrossRef]
- Hou, B.; Sun, H.; Peng, T.; Zhang, X.; Ren, Y. Rapid Preparation of Expanded Graphite at Low Temperature. New Carbon Mater. 2020, 35, 262–268. [Google Scholar] [CrossRef]
- Rüdorff, W.; Hofmann, U. Über Graphitsalze. Z. Anorg. Allg. Chem. 1938, 238, 1–50. [Google Scholar] [CrossRef]
- Inagaki, M.; Iwashita, N.; Kouno, E. Potential Change with Intercalation of Sulfuric Acid into Graphite by Chemical Oxidation. Carbon 1990, 28, 49–55. [Google Scholar] [CrossRef]
- Saikam, L.; Arthi, P.; Senthil, B.; Shanmugam, M. A Review on Exfoliated Graphite: Synthesis and Applications. Inorg. Chem. Commun. 2023, 152, 110685. [Google Scholar] [CrossRef]
- Krautsou, A.; Shornikova, O.N.; Bulygina, A.I.; Solopov, A.B.; Kustov, A.L.; Avdeev, V.V. Investigation of the Pore Structure of Exfoliated Graphite Based on Highly Oriented Pyrolytic Graphite Nitrate. Russ. J. Phys. Chem. 2023, 97, 1174–1182. [Google Scholar] [CrossRef]
- van der Pauw, L.J. A Method of Measuring Specific Resistivity and Hall Effect of Discs of Arbitrary Shape. Philips Res. Rep. 1958, 13, 220–224. [Google Scholar]
- Oliveira, F.S.; Cipriano, R.B.; Da Silva, F.T.; Romão, E.C.; Dos Santos, C.A.M. Simple Analytical Method for Determining Electrical Resistivity and Sheet Resistance Using the van Der Pauw Procedure. Sci. Rep. 2020, 10, 16379. [Google Scholar] [CrossRef]
- Pang, X.; Zhang, W.; Meng, Y.; Ma, M.; Xu, J. Effect of Expansion Temperature on the Properties of Expanded Graphite and Modified Linear Low Density Polyethylene. Int. Polym. Process. 2022, 37, 271–286. [Google Scholar] [CrossRef]
- Shulyak, V.A.; Morozov, N.S.; Ivanov, A.V.; Gracheva, A.V.; Chebotarev, S.N.; Avdeev, V.V. The Influence of Machining Conditions on the Orientation of Nanocrystallites and Anisotropy of Physical and Mechanical Properties of Flexible Graphite Foils. Nanomaterials 2024, 14, 540. [Google Scholar] [CrossRef]
- Figueira, J.; Loureiro, J.; Vieira, E.; Fortunato, E.; Martins, R.; Pereira, L. Flexible, Scalable, and Efficient Thermoelectric Touch Detector Based on PDMS and Graphite Flakes. Flex. Print. Electron. 2021, 6, 045018. [Google Scholar] [CrossRef]
- Williamson, G.K.; Hall, W.H. X-Ray Line Broadening from Filed Aluminium and Wolfram. Acta Metall. 1953, 1, 22–31. [Google Scholar] [CrossRef]
- Scherrer, P. Bestimmung der Größe und der inneren Struktur von Kolloidteilchen mittels Röntgenstrahlen. Nachrichten Ges. Wiss. Göttingen 1918, 2, 98–100. [Google Scholar]
- Stokes, A.R.; Wilson, A.J.C. The Diffraction of X Rays by Distorted Crystal Aggregates-I. Proc. Phys. Soc. 1944, 56, 174–181. [Google Scholar] [CrossRef]
- Perlovich, Y.A.; Isaenkova, M.G.; Krymskaya, O.A.; Fesenko, V.A.; Babich, Y.A. Optimization of the Procedure for Determining Integral Texture Parameters of Products from Zirconium-Based Alloys Using the Orientation Distribution Function. IOP Conf. Ser. Mater. Sci. Eng. 2016, 130, 012056. [Google Scholar] [CrossRef]
- Kearns, J.J. Thermal Expansion and Preferred Orientation in Zircaloy; Bettis Atomic Power Laboratory: Pittsburgh, PA, USA, 1965. [Google Scholar]
- Isaenkova, M.G.; Tenishev, A.V.; Krymskaya, O.A.; Stolbov, S.D.; Mikhal’chik, V.V.; Fesenko, V.A.; Klyukova, K.E. Influence of the Structural State and Crystallographic Texture of Zr-2.5% Nb Alloy Samples on the Anisotropy of Their Thermal Expansion. Nucl. Mater. Energy 2021, 29, 101071. [Google Scholar] [CrossRef]
- Slack, G.A. Anisotropic Thermal Conductivity of Pyrolytic Graphite. Phys. Rev. 1962, 127, 694–701. [Google Scholar] [CrossRef]


| Processing | Sample Name | Type of the Study |
|---|---|---|
| Rolling | R1, R2, R3 | Study of the structural and textural characteristics |
| R1_RD, R2_RD, R3_RD | Measuring electrical conductivity in different directions | |
| R1_TD, R2_TD, R3_TD | ||
| R1_ND, R2_TD, R3_TD | ||
| Pressing | P1, P2, P3 | Study of the structural and textural characteristics |
| P1_RD, P2_RD, P3_RD | Measuring electrical conductivity in different directions | |
| P1_TD, P2_TD, P3_TD | ||
| P1_ND, P2_ND, P3_ND |
| Sample | Graphite | Additional Phase | ||||
|---|---|---|---|---|---|---|
| a, pm | s, pm | Lc, nm | , % | , °(2θ) | IAP/I(0004) | |
| R1 | 247.36 | 672.27 | 38.5 | 0.55 | 1.05 | 0.118 |
| R2 | 247.47 | 672.29 | 33.8 | 0.42 | 1.06 | 0.119 |
| R3 | 247.48 | 672.29 | 39.6 | 0.56 | 1.02 | 0.113 |
| <R> | 247.44 ± 0.07 | 672.28 ± 0.01 | 37.3 ± 3.1 | 0.51 ± 0.08 | 1.04 ± 0.02 | 0.117 ± 0.003 |
| P1 | 247.08 | 672.29 | 36.5 | 0.51 | 1.14 | 0.112 |
| P2 | 247.16 | 672.25 | 38.5 | 0.56 | 1.11 | 0.110 |
| P3 | 246.72 | 672.29 | 40.8 | 0.59 | 1.13 | 0.107 |
| <P> | 246.99 ± 0.23 | 672.28 ± 0.02 | 38.6 ± 2.2 | 0.55 ± 0.04 | 1.13 ± 0.02 | 0.110 ± 0.003 |
| Sample | Misorientation Angle (MA), ° | Integral Texture f Parameter | |||
|---|---|---|---|---|---|
| ‖RD | ⊥RD | fND | fTD | fRD | |
| R1 | 24.6 ± 0.4 | 27.5 ± 0.5 | 0.818 | 0.084 | 0.098 |
| R2 | 24.3 ± 0.4 | 27.1 ± 0.5 | 0.822 | 0.082 | 0.096 |
| R3 | 24.3 ± 0.4 | 27.2 ± 0.5 | 0.819 | 0.084 | 0.097 |
| <R> | 24.4 ± 0.1 | 27.3 ± 0.2 | 0.820 ± 0.002 | 0.083 ± 0.001 | 0.097 ± 0.001 |
| P1 | 28.1 ± 0.5 | 27.7 ± 0.5 | 0.807 | 0.097 | 0.097 |
| P2 | 26.7 ± 0.5 | 26.8 ± 0.5 | 0.809 | 0.095 | 0.096 |
| P3 | 28.1 ± 0.6 | 28.4 ± 0.6 | 0.790 | 0.105 | 0.105 |
| <P> | 27.6 ± 0.7 | 27.6 ± 0.7 | 0.802 ± 0.009 | 0.099 ± 0.004 | 0.099 ± 0.004 |
| Sample No. | for the Rolled GF (R), kS/m | for the Pressed GF (P), kS/m | ||||
|---|---|---|---|---|---|---|
| RD | TD | ND | RD | TD | ND | |
| 1 | 204.9 | 196.8 | 3.9 | 196.0 | 196.7 | 4.2 |
| 2 | 205.8 | 198.0 | 3.9 | 198.9 | 198.5 | 4.2 |
| 3 | 205.4 | 197.6 | 4.0 | 194.2 | 193.7 | 4.6 |
| Mean values | 205.4 ± 0.4 | 197.5 ± 0.5 | 3.9 ± 0.1 | 196.3 ± 2.1 | 4.3 ± 0.2 | |
| 7.1 | 14.9 | 2.6 | 35.5 | 3.0 | ||
| Specific Electrical Conductivity Anisotropy of the GF by Rolling (R) | Specific Electrical Conductivity Anisotropy of the GF by Pressing (P) | |||
|---|---|---|---|---|
| RD/TD | RD/ND | TD/ND | <RD, TD>/ND | |
| Experiment | 1.09 | 158.63 | 146.09 | 120.99 |
| Calculation | 1.04 | 52.18 | 50.17 | 45.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morozov, N.S.; Shulyak, V.A.; Isaenkova, M.G.; Krymskaya, O.A.; Fesenko, V.A.; Chebotarev, S.N.; Avdeev, V.V. Electrical Conductivity in Graphite Foils Produced by Rolling and Pressing. Materials 2024, 17, 6153. https://doi.org/10.3390/ma17246153
Morozov NS, Shulyak VA, Isaenkova MG, Krymskaya OA, Fesenko VA, Chebotarev SN, Avdeev VV. Electrical Conductivity in Graphite Foils Produced by Rolling and Pressing. Materials. 2024; 17(24):6153. https://doi.org/10.3390/ma17246153
Chicago/Turabian StyleMorozov, Nikolai S., Vladimir A. Shulyak, Margarita G. Isaenkova, Olga A. Krymskaya, Vladimir A. Fesenko, Sergei N. Chebotarev, and Victor V. Avdeev. 2024. "Electrical Conductivity in Graphite Foils Produced by Rolling and Pressing" Materials 17, no. 24: 6153. https://doi.org/10.3390/ma17246153
APA StyleMorozov, N. S., Shulyak, V. A., Isaenkova, M. G., Krymskaya, O. A., Fesenko, V. A., Chebotarev, S. N., & Avdeev, V. V. (2024). Electrical Conductivity in Graphite Foils Produced by Rolling and Pressing. Materials, 17(24), 6153. https://doi.org/10.3390/ma17246153






