Study on the Morphological Distribution and Modeling Methods of River Particles in Upstream and Downstream Sections
Abstract
1. Introduction
2. Modeling Method of Particles
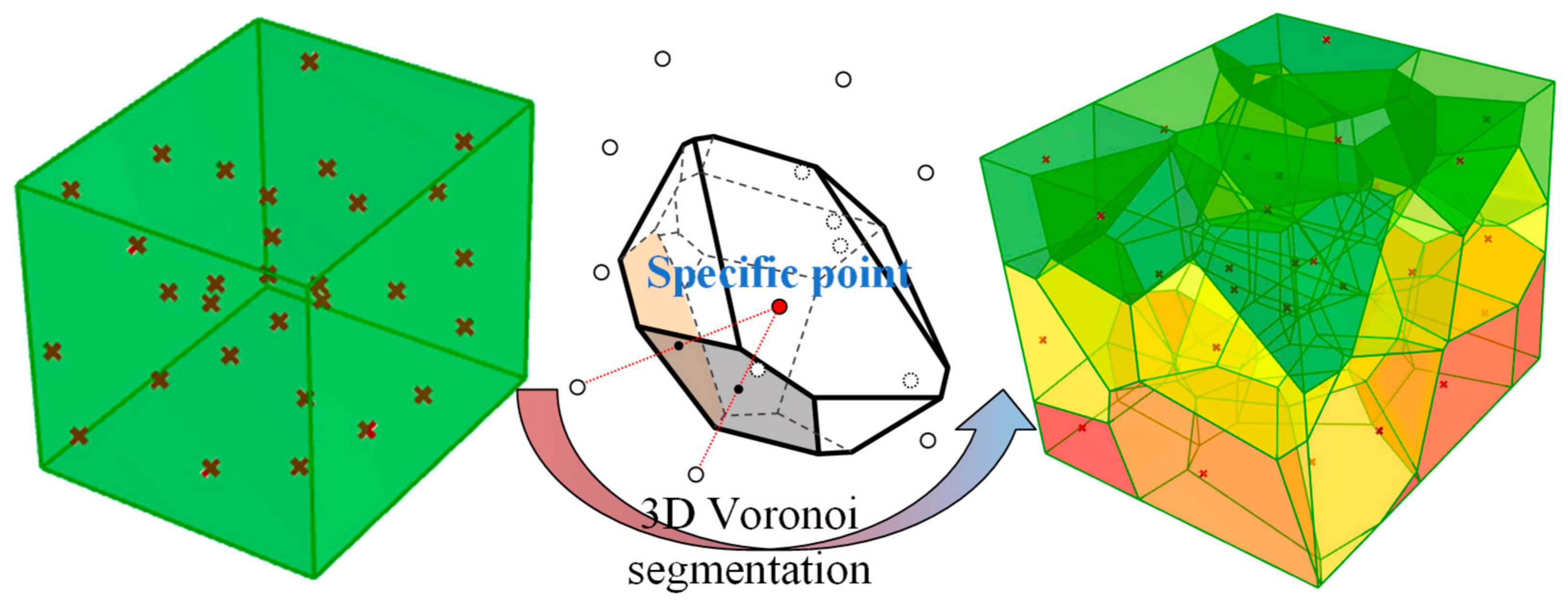
2.1. Simulation of Bedrock Fracture Process
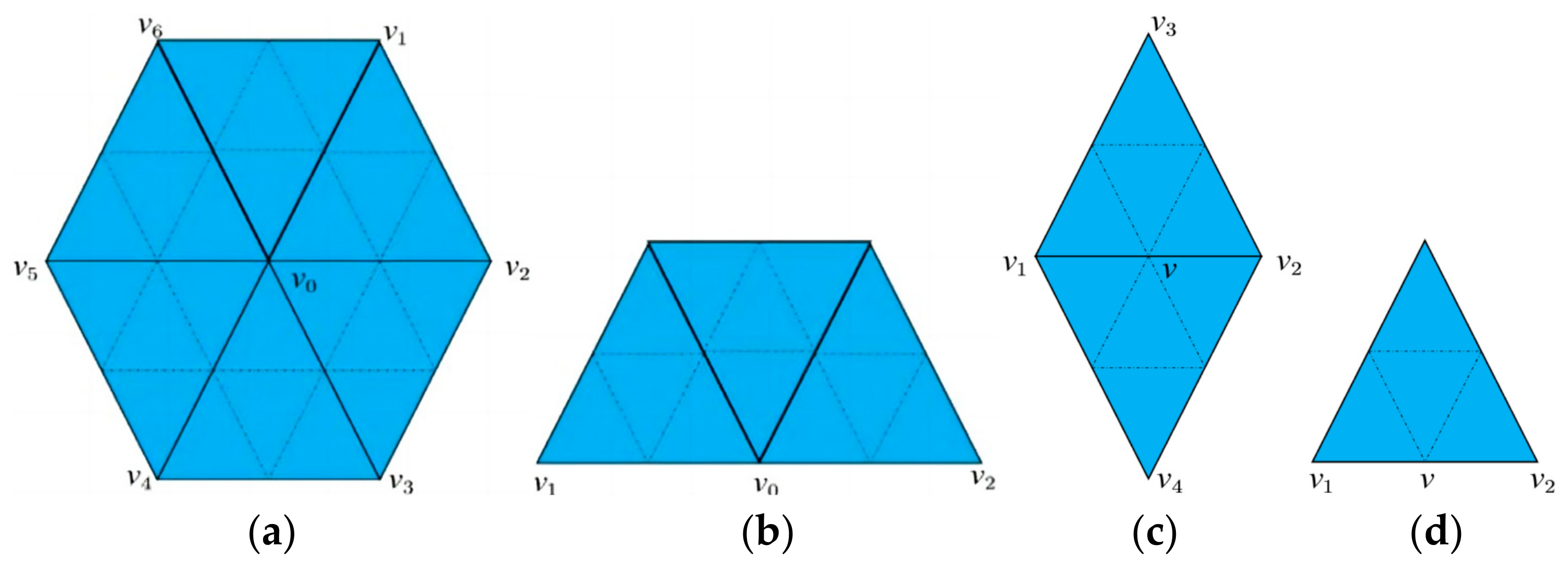
2.2. Particle Abrasion Method
3. Particle Morphology Analysis
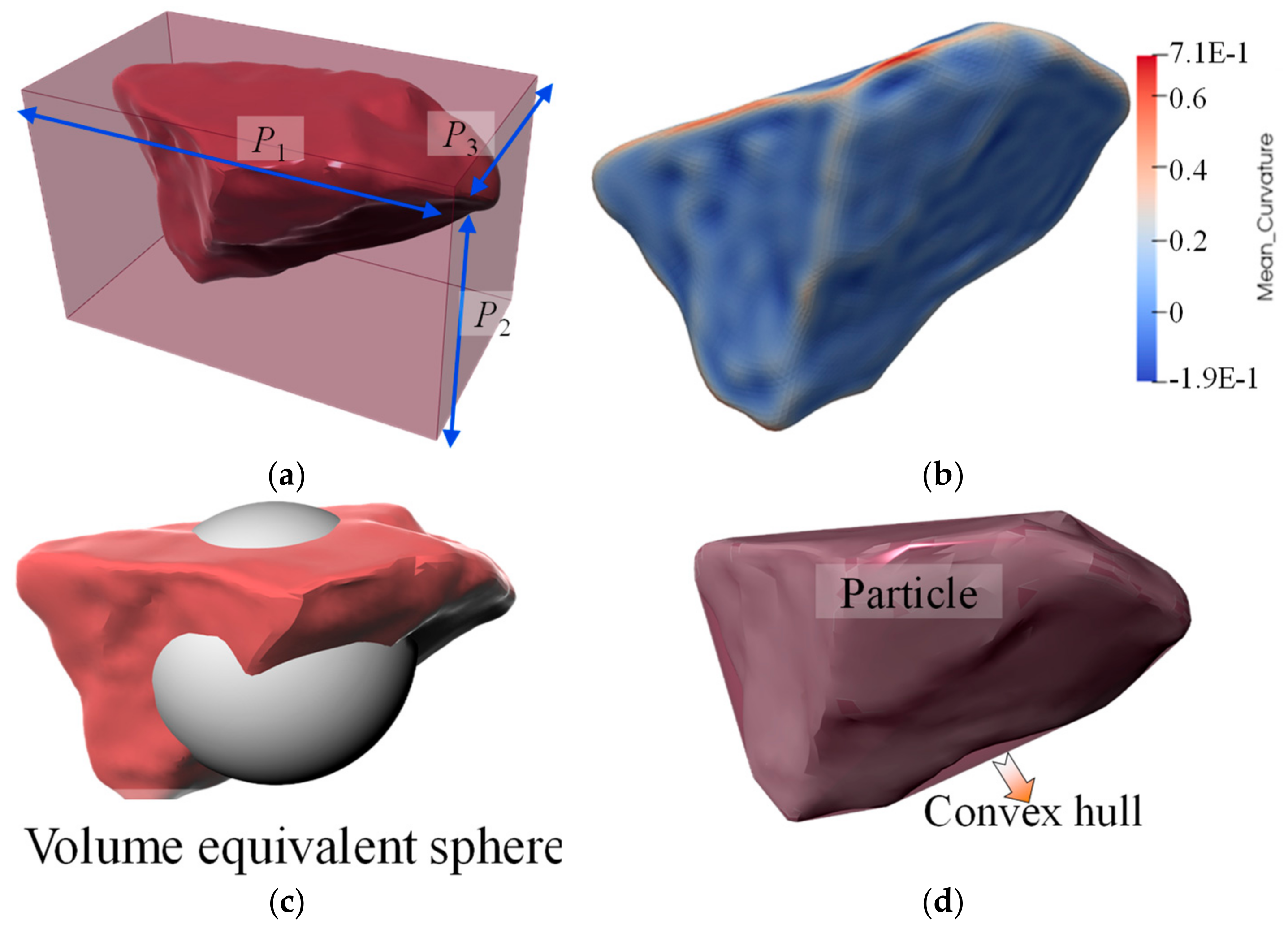
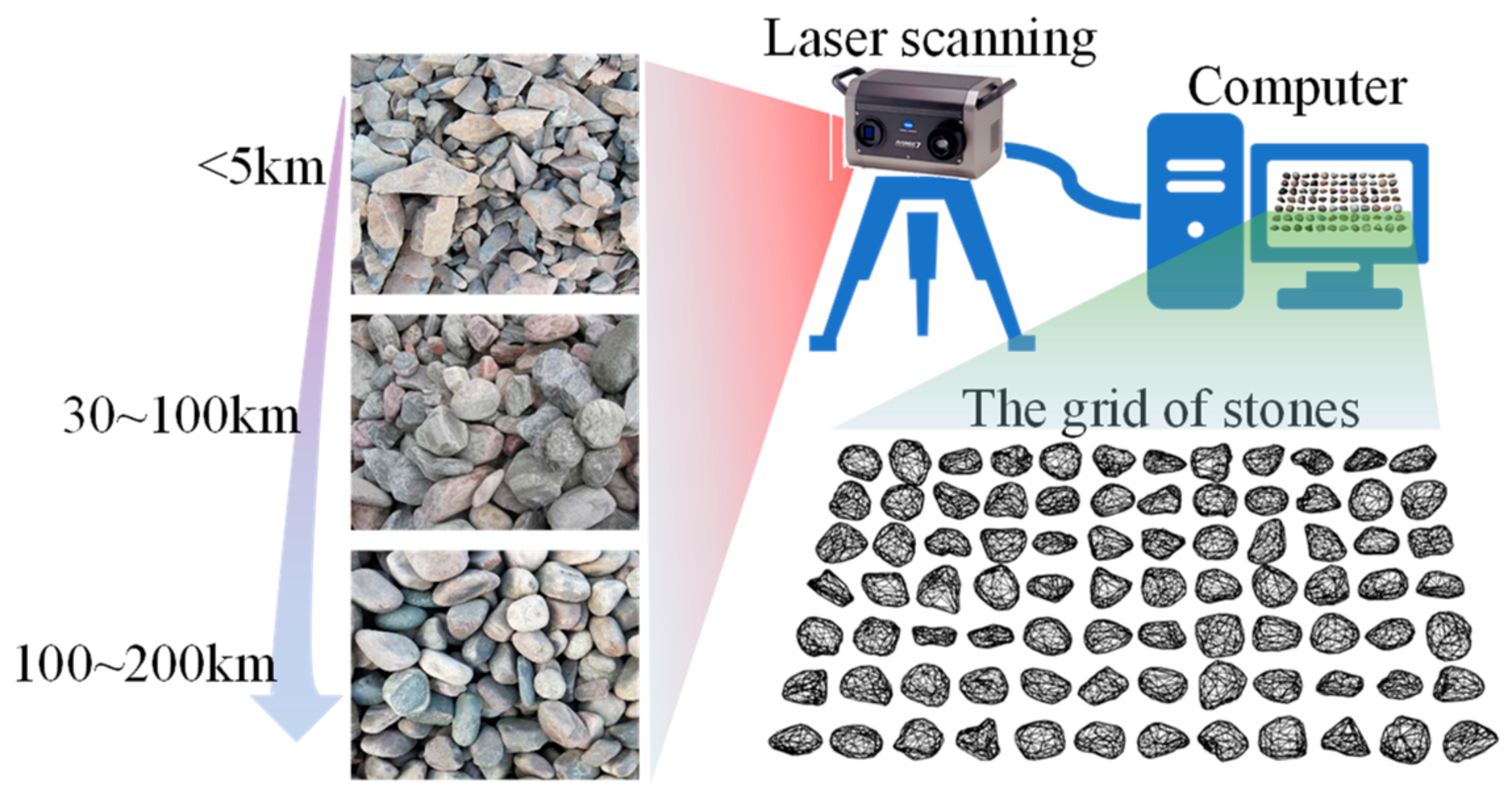
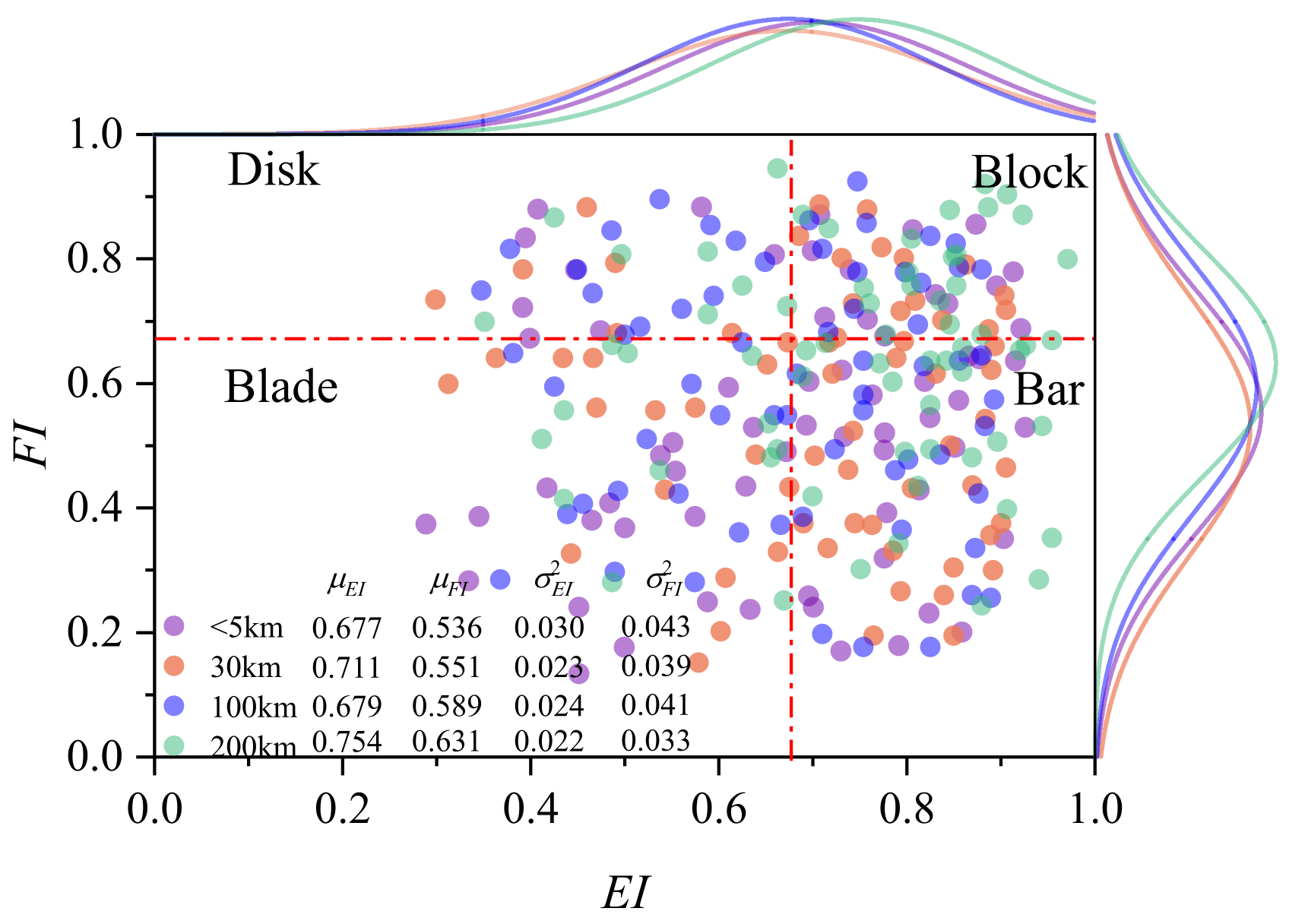
3.1. Particle Morphology Index System
3.2. Particle Morphology Analysis Process
4. Influence of Particle Morphology on the Mechanical Behavior of Granular Materials
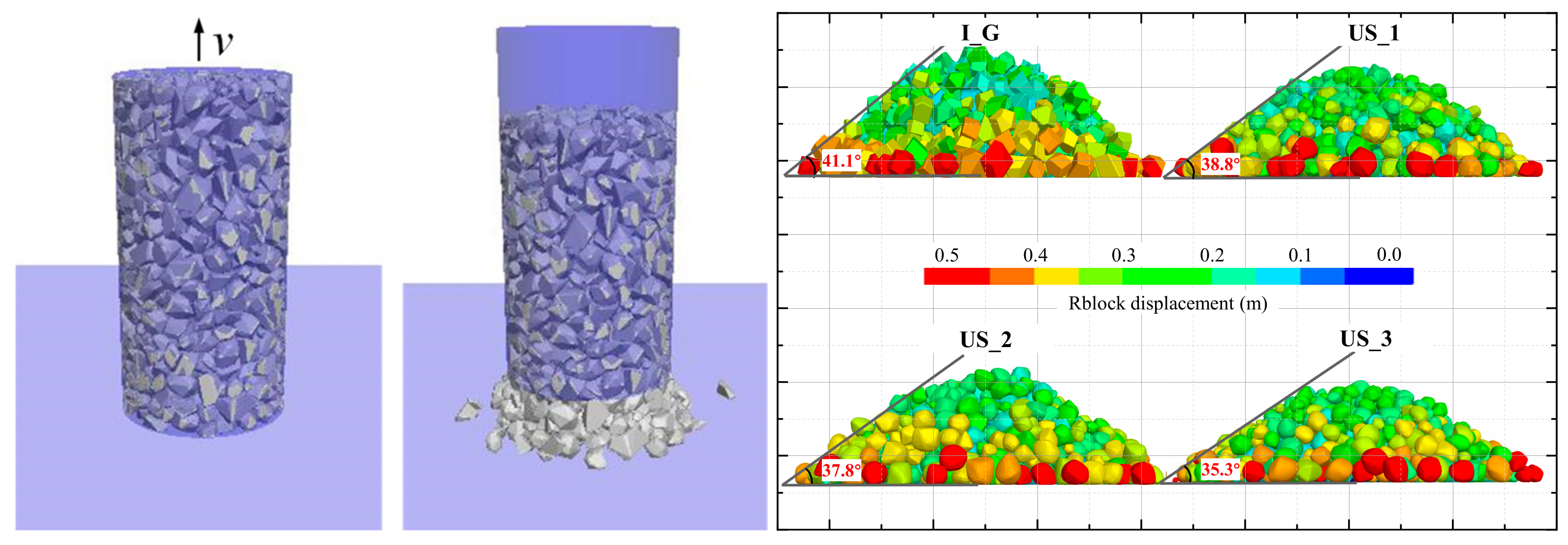
4.1. Experimental Method
4.2. Analysis of Angle of Repose Results
5. Conclusions
- Morphological Characteristics of Upstream and Downstream Particles: This study systematically analyzed the morphological differences in river particles from upstream to downstream sections. Upstream particles exhibited more angular and irregular shapes, while downstream particles showed a gradual rounding due to continuous erosion and transport. These morphological changes highlight the varying impact of river dynamics on particle shape evolution along the river’s course.
- Simulation of Particle Rounding with Loop Subdivision: Additionally, using the Loop subdivision method, the study effectively simulated the trend of particle rounding during transport and abrasion. The method accurately represented the smoothing of sharp edges, replicating the natural process of rounding observed in river particles over time. This modeling approach successfully captured the transition toward more spherical and isotropic particle shapes.
- Angle of Repose Captured by Discrete Element Method (DEM): By employing the Discrete Element Method (DEM), the study accurately captured the natural angle of repose of particles with different degrees of abrasion. The results aligned closely with field observations, validating the DEM’s ability to simulate the mechanical behavior of granular materials. The findings confirmed that angular particles exhibit larger angles of repose due to interlocking, whereas rounder particles tend to slide, resulting in smaller angles.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wentworth, C.K. A laboratory and field study of cobble abrasion. J. Geol. 1919, 27, 507–521. [Google Scholar] [CrossRef]
- Landon, R.E. An analysis of beach pebble abrasion and transportation. J. Geol. 1930, 38, 437–446. [Google Scholar] [CrossRef]
- Jerolmack, D.J.; Reitz, M.D.; Martin, R.L. Sorting out abrasion in a gypsum dune field. J. Geophys. Res. Earth Surface 2011, 116, F02003. [Google Scholar] [CrossRef]
- Krumbein, W.C. The effects of abrasion on the size, shape and roundness of rock fragments. J. Geol. 1941, 49, 482–520. [Google Scholar] [CrossRef]
- Durian, D.J.; Bideaud, H.; Duringer, P.; Schröder, A.; Thalmann, F.; Marques, C.M. What is in a pebble shape? Phys. Rev. Lett. 2006, 97, 028001. [Google Scholar] [CrossRef]
- Cassel, M.; Lavé, J.; Recking, A.; Malavoi, J.R.; Piégay, H. Bedload transport in rivers, size matters but so does shape. Sci. Rep. 2021, 11, 508. [Google Scholar] [CrossRef]
- Domokos, G.; Jerolmack, D.J.; Sipos, A.Á.; Török, Á. How river rocks round: Resolving the shape-size paradox. PLoS ONE 2014, 9, e88657. [Google Scholar] [CrossRef]
- Illenberger, W.K. Pebble shape (and size!). J. Sediment. Res. 1991, 61, 756–767. [Google Scholar]
- Deal, E.; Venditti, J.G.; Benavides, S.J.; Bradley, R.; Zhang, Q.; Kamrin, K.; Perron, J.T. Grain shape effects in bed load sediment transport. Nature 2023, 613, 298–302. [Google Scholar] [CrossRef]
- Kuenen, P.H. Experimental abrasion; 3, fluviatile action on sand. Am. J. Sci. 1959, 257, 172–190. [Google Scholar] [CrossRef]
- Jerolmack, D.J.; Brzinski, I.I.I.T.A. Equivalence of abrupt grain-size transitions in alluvial rivers and eolian sand seas: A hypothesis. Geology 2010, 38, 719–722. [Google Scholar] [CrossRef]
- Domokos, G.; Kun, F.; Sipos, A.A.; Szabó, T. Universality of fragment shapes. Sci. Rep. 2015, 5, 9147. [Google Scholar] [CrossRef]
- Buscarnera, G.; Einav, I. The mechanics of brittle granular materials with coevolving grain size and shape. Proc. R. Soc. A 2021, 477, 20201005. [Google Scholar] [CrossRef] [PubMed]
- Irwin, R.P., III. Paleolakes and the Crustal Dichotomy Boundary on Mars; University of Virginia: Charlottesville, VA, USA, 2005. [Google Scholar]
- Novák-Szabó, T.; Sipos, A.Á.; Shaw, S.; Bertoni, D.; Pozzebon, A.; Grottoli, E.; Sarti, G.; Ciavola, P.; Domokos, G.; Jerolmack, D.J. Universal characteristics of particle shape evolution by bed-load chip. Sci. Adv. 2018, 4, eaao4946. [Google Scholar] [CrossRef] [PubMed]
- Bloore, F.J. The shape of pebbles. J. Int. Assoc. Math. Geol. 1977, 9, 113–122. [Google Scholar] [CrossRef]
- Domokos, G.; Gibbons, G.W. Geometrical and physical models of abrasion. arXiv 2013, arXiv:1307.5633. [Google Scholar]
- Manga, M.; Patel, A.; Dufek, J. Rounding of pumice clasts during transport: Field measurements and laboratory studies. Bull. Volcanol. 2011, 73, 321–333. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, J.; Tan, X.; Yang, H. Modeling of the Particle Abrasion Process and a Discrete Element Method Study of Its Shape Effect. Materials 2024, 17, 3947. [Google Scholar] [CrossRef]
- Li, J.; Konietzky, H.; Frühwirt, T. Voronoi-based DEM simulation approach for sandstone considering grain structure and pore size. Rock Mech. Rock Eng. 2017, 50, 2749–2761. [Google Scholar] [CrossRef]
- Zhou, W.; Ji, X.; Ma, G.; Chen, Y. FDEM simulation of rocks with microstructure generated by Voronoi grain-based model with particle growth. Rock Mech. Rock Eng. 2020, 53, 1909–1921. [Google Scholar] [CrossRef]
- Sanipour, S.; Bahrani, N.; Corkum, A. Simulation of brittle failure around Canada’s mine-by experiment tunnel using 2D continuum-based Voronoi tessellated models. Rock Mech. Rock Eng. 2022, 55, 6387–6408. [Google Scholar] [CrossRef]
- Rógenes, E.; de Farias, M.M.; Rasmussen, L.L. The Continuum Voronoi Block Model for simulation of fracture process in hard rocks. Int. J. Numer. Anal. Methods Geomech. 2022, 46, 89–112. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, J. 3D quantitative shape analysis on form roundness compactness with μCT. Powder Technol. 2016, 291, 262–275. [Google Scholar] [CrossRef]
- Zhou, B.; Wang, J. Generation of a realistic 3D sand assembly using X-ray micro-computed tomography and spherical harmonic-based principal component analysis. Int. J. Numer. Anal. Methods Geomech. 2017, 41, 93–109. [Google Scholar] [CrossRef]
- Fonseca, J.; O’Sullivan, C.; Coop, M.R.; Lee, P.D. Non-invasive characterization of particle morphology of natural sands. Soils Found. 2012, 52, 712–722. [Google Scholar] [CrossRef]
- Ranjan, G.; Rao, A.S. Basic and Applied Soil Mechanics; New Age International: New Dehli, India, 2011. [Google Scholar]
- Tan, X.; Hu, Z.; Cao, M.; Chen, C. 3D discrete element simulation of a geotextile-encased stone column under uniaxial compression testing. Comput. Geotech. 2020, 126, 103769. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| Particle density, ρ (kg/m3) | 2600 |
| Particle coefficient of friction, μc | 0.5 |
| Sidewall–particle friction μs | 0.0 |
| Bottomplate–particle friction μb | 0.5 |
| Particle normal stiffness, kn (N/m) | 1 × 108 |
| Particle tangential stiffness, ks (N/m) | 5 × 107 |
| Damping coefficient, dp | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Z.; Zhang, J.; Tan, X.; Yang, H. Study on the Morphological Distribution and Modeling Methods of River Particles in Upstream and Downstream Sections. Materials 2024, 17, 5290. https://doi.org/10.3390/ma17215290
Hu Z, Zhang J, Tan X, Yang H. Study on the Morphological Distribution and Modeling Methods of River Particles in Upstream and Downstream Sections. Materials. 2024; 17(21):5290. https://doi.org/10.3390/ma17215290
Chicago/Turabian StyleHu, Zhengbo, Junhui Zhang, Xin Tan, and Hao Yang. 2024. "Study on the Morphological Distribution and Modeling Methods of River Particles in Upstream and Downstream Sections" Materials 17, no. 21: 5290. https://doi.org/10.3390/ma17215290
APA StyleHu, Z., Zhang, J., Tan, X., & Yang, H. (2024). Study on the Morphological Distribution and Modeling Methods of River Particles in Upstream and Downstream Sections. Materials, 17(21), 5290. https://doi.org/10.3390/ma17215290









