Experimental Study on Heat Conduction and Water Migration of Composite Bentonite Samples
Abstract
:1. Introduction
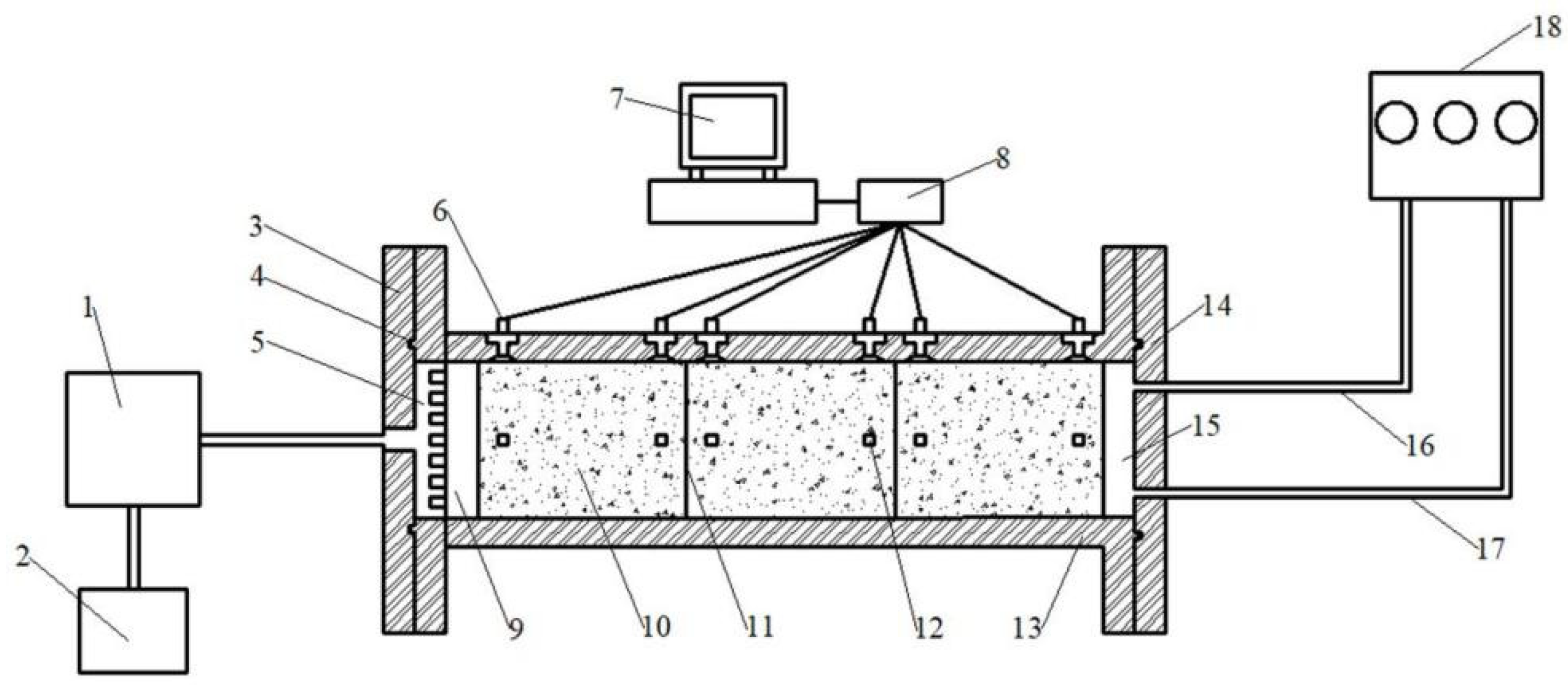
2. Experiment Device
3. Experimental Scheme
4. Experiment Results and Analysis
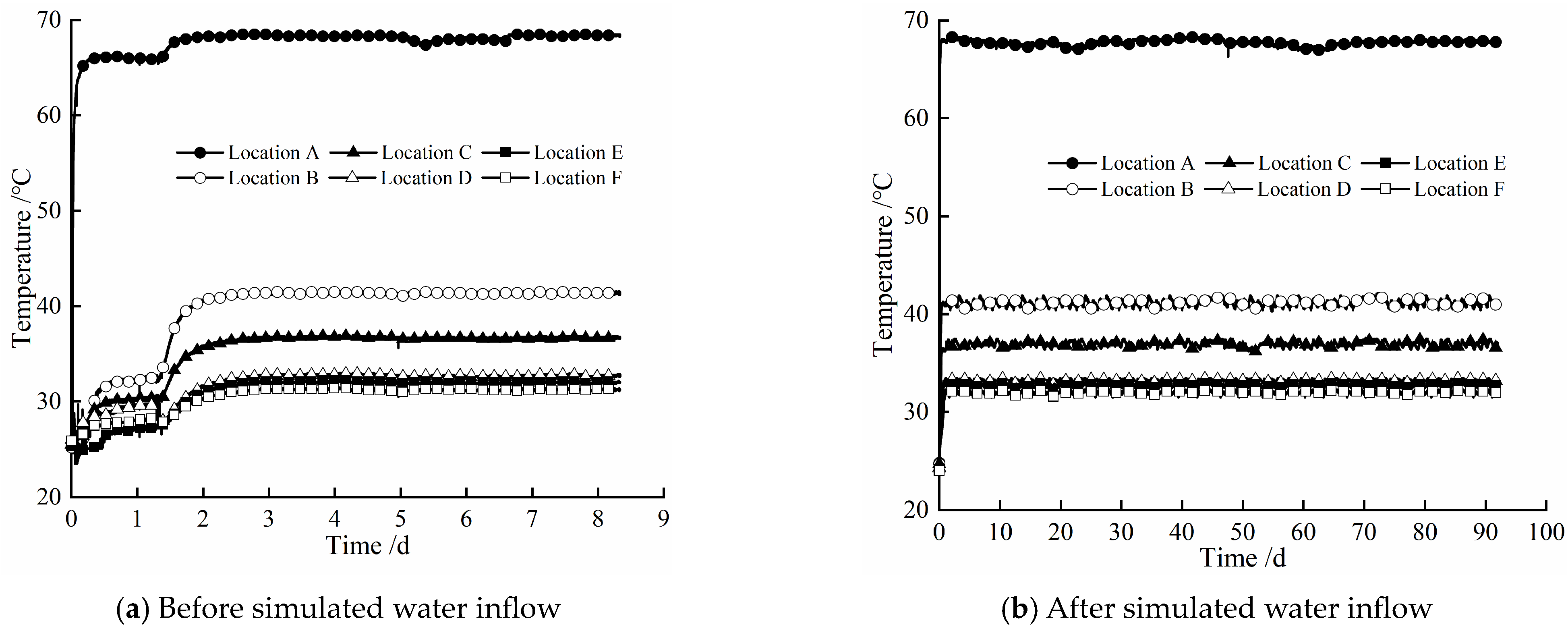
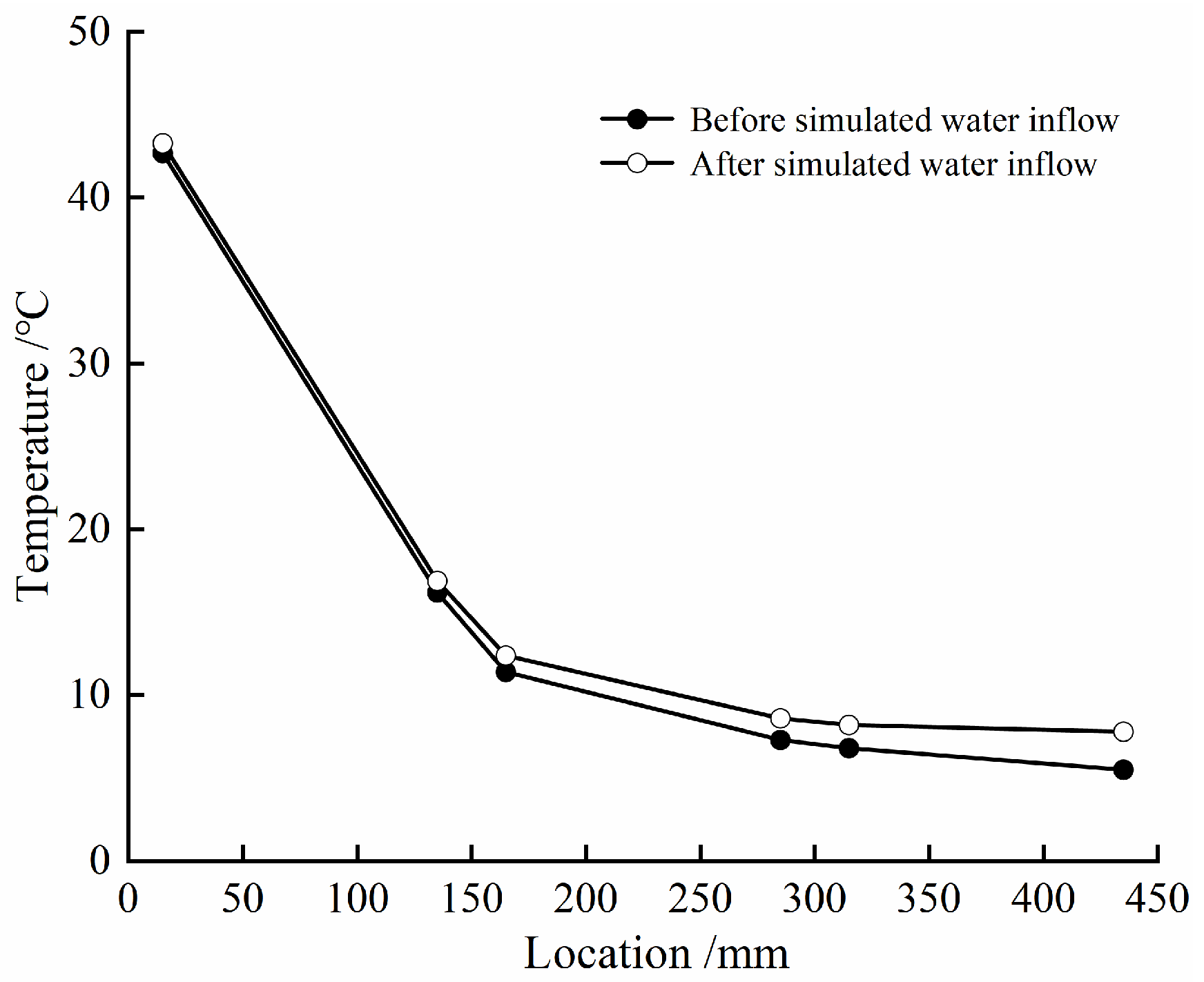
4.1. Temperature Evolution Law
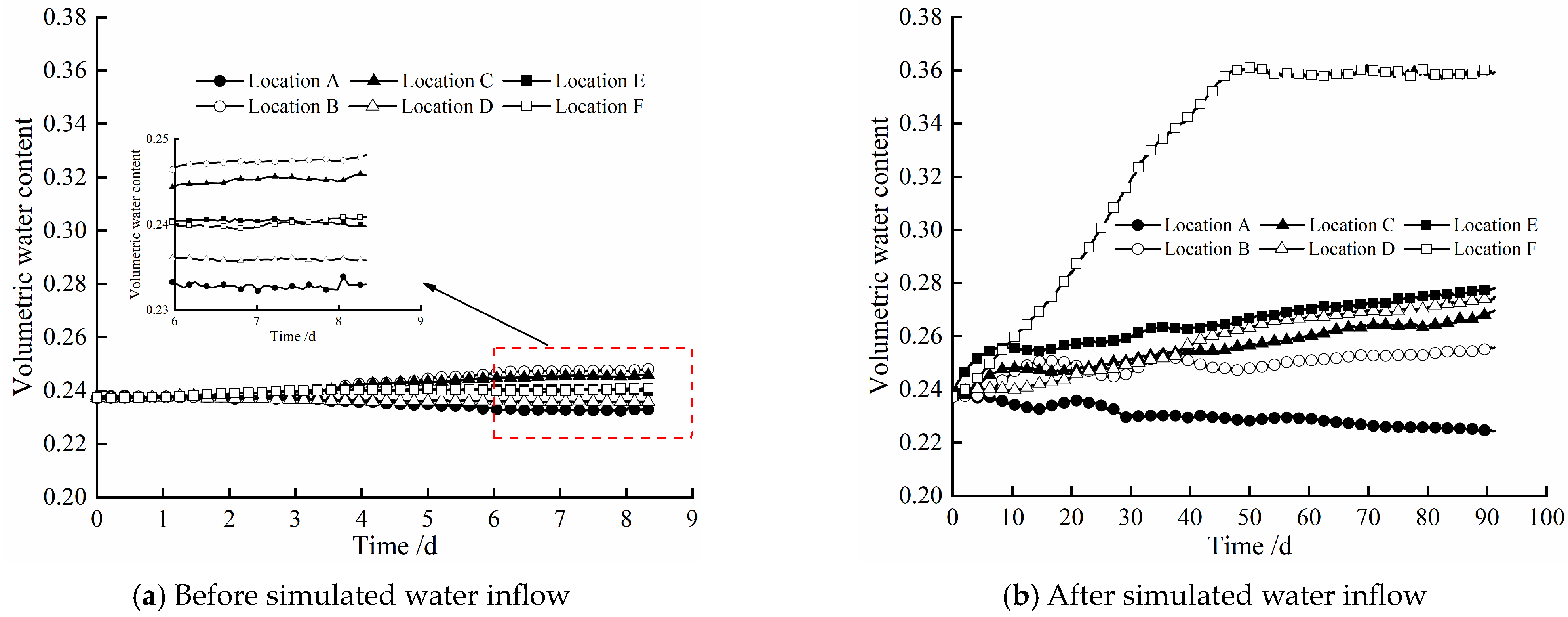
4.2. Water Evolution Law
4.3. Thermal Conductivity at the Joints
4.4. Hydraulic Conductivity at the Joints
4.5. Healing of Joints
5. Conclusions
- (1)
- The variation trend of temperature at different locations of the composite bentonite samples with time is basically similar in the two cases. The loading hydraulic boundary condition makes the temperature near the hydraulic boundary increase slightly in the later stage of the experiment, but it has little effect on the temperature at other locations, which indicates that the change in internal temperature of the composite bentonite samples is mainly affected by the temperature boundary and that the change in the internal water has little effect on it.
- (2)
- Due to the low permeability of the high-pressure compacted bentonite sample, in a short period of time, the loading of hydraulic boundary conditions only makes the volumetric water content of composite bentonite samples near the hydraulic boundary increase significantly but has little effect on other locations. Under the influence of temperature boundary, the internal water near the temperature boundary migrates along the soil pores in the direction of the hydraulic boundary under the action of a temperature gradient, so the volumetric water content gradually decreases with time in a short period of time.
- (3)
- Based on the experimental results, the thermal conductivity and hydraulic conductivity of the joint location after healing of the composite bentonite samples were calculated. The calculation results show that the thermal conductivity and hydraulic conductivity of the joint location after healing can meet the thermal conductivity and low permeability requirements of the HLW repository engineering barrier.
- (4)
- The hydration of the bentonite composite samples produces volume swelling. Under the action of the swelling force, the structural plane between the joint and the sample basically disappears. The process of hydration swelling of the composite bentonite sample is accompanied by the adjustment of stress, the composite bentonite samples are continuously squeezed to the joint area after hydration swelling, the whole composite samples is generally homogenized, and the joints between the composite bentonite samples tend to heal.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, F.; Ye, W.M.; Wang, Q.; Chen, Y.G.; Chen, B. Effective stress incorporating osmotic suction and volume change behavior of compacted GMZ01 bentonite. Acta Geotech. 2020, 15, 1925–1934. [Google Scholar] [CrossRef]
- Dong, X.X.; Chen, Y.G.; Ye, W.M.; Wang, Q. Modeling of water retention behavior of densely compacted Gaomiaozi bentonite based on pore structure evolution. Eng. Geol. 2023, 313, 106977. [Google Scholar] [CrossRef]
- Collin, F.; Li, X.L.; Radu, J.P. Thermo-hydro-mechanical coupling in clay barriers. Eng. Geol. 2002, 64, 179–193. [Google Scholar] [CrossRef]
- Yang, G.S.; Bai, B.; Mao, H.T.; Zhou, R.; Chen, W.X.; Han, F. Study on coupled heat-water-vapor transfer in buffer material based on SPH method. Case Stud. Therm. Eng. 2024, 54, 104019. [Google Scholar] [CrossRef]
- Cui, Y.J.; Tang, A.M. On the chemo-thermo-hydro-mechanical behavior of geological and engineering barriers. J. Rock Geotech. Eng. 2013, 5, 169–178. [Google Scholar] [CrossRef]
- Borah, D.; Nath, H.; Saikia, H. Modification of bentonite clay and its applications: A review. Rev. Inorg. Chem. 2022, 42, 265–282. [Google Scholar] [CrossRef]
- Lv, A.W.; Lv, X.; Xu, X.Y.; Shao, Z.B. Tailored ultra-tough, antimicrobial and recyclable hydrogels based on chitosan and ionic liquid modified montmorillonite with different chain lengths for efficient adsorption of organic dyes in wastewater. Int. J. Biol. Macromol. 2024, 257, 128752. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.B.; Chen, L.; Collin, F.; Liu, Y.M.; Wang, J. Numerical modeling of coupled thermal-hydro-mechanical behavior of GMZ bentonite in the China-Mock-up test. Eng. Geol. 2016, 214, 116–126. [Google Scholar] [CrossRef]
- Yang, G.S.; Liu, Y.M.; Gao, Y.F.; Li, J.; Cai, G.Q. Coupled thermo-hydro-mechanical process in buffer material and self-healing effects with joints. J. Cent. South Univ. 2021, 28, 2905–2918. [Google Scholar] [CrossRef]
- Wu, H.Y.; Bai, B.; Liu, J.J. Temperature-driven coupled transport of pollutants and suspended particles established by granular thermodynamics. Int. J. Heat Mass Transf. 2024, 228, 125645. [Google Scholar] [CrossRef]
- Graupner, B.J.; Shao, H.; Wang, X.R.; Nguyen, T.S.; Li, Z.; Rutqvist, J.; Chen, F.; Birkholzer, J.; Wang, W.; Kolditz, O.; et al. Comparative modelling of the coupled thermal–hydraulic-mechanical (THM) processes in a heated bentonite pellet column with hydration. Environ. Earth Sci. 2018, 77, 84. [Google Scholar] [CrossRef]
- Popp, T.; Rolke, C.; Salzer, K. Hydromechanical properties of bentonite-sand block assemblies with interfaces in engineered barrier systems. Geol. Soc. Lond. Spec. Publ. 2014, 415, 19–33. [Google Scholar] [CrossRef]
- Hoffmann, C.; Alonso, E.E.; Romero, E. Hydro-mechanical behaviour of bentonite pellet mixtures. Phys. Chem. Earth Parts A/B/C 2007, 32, 832–849. [Google Scholar] [CrossRef]
- Chen, B.; Chen, J.Q.; Cao, Y.C. Influence of joint on self-sealing behaviour of highly compacted bentonite in engineering barrier. Chin. J. Rock Mech. Eng. 2012, 31, 618–624. [Google Scholar]
- Wang, Y.; Zhang, H.Y.; Tong, Y.M.; Zhou, G.P. Influence of joint sealing material on the sealing performance of the buffer block barrier. Rock Soil Mech. 2021, 42, 1648–1658. [Google Scholar]
- Jia, L.; Chen, Y.; Ye, W.M.; Cui, Y.J. Effects of a simulated gap on anisotropic swelling pressure of compacted GMZ bentonite. Eng. Geol. 2019, 248, 155–163. [Google Scholar] [CrossRef]
- Meng, Y.H.; Wang, Q.; Su, W.; Ye, W.M.; Chen, Y.G. On the evolution of hydration cracks of compacted bentonite under different boundary conditions. Constr. Build. Mater. 2023, 407, 133387. [Google Scholar] [CrossRef]
- Liu, Y.M.; Wang, J.; Cao, S.F.; Ma, L.K.; Xie, J.L.; Zhao, X.G.; Chen, L. A large-scale THMC experiment of buffer material for geological disposal of high level radioactive waste in China. Rock Soil Mech. 2013, 34, 2756–2762. [Google Scholar]
- Liu, Y.M.; Cai, M.F.; Wang, J. Thermal properties of buffer material for high-level radioactive waste disposal. Chin. J. Rock Mech. Eng. 2007, 26, 3891–3896. [Google Scholar]
- Ye, W.M.; Wang, Q.; Pan, H.; Chen, B. Thermal conductivity of compacted GMZ01 bentonite. Chin. J. Geotech. Eng. 2010, 32, 821–826. [Google Scholar]
- Tsang, C.F.; Barnichon, J.D.; Birkholzer, J. Coupled thermo-hydro-mechanical processes in the near field of a high-level radioactive waste repository in clay formations. Int. J. Rock Mech. Min. Sci. 2012, 49, 31–44. [Google Scholar] [CrossRef]
- Bai, B.; Bai, F.; Hou, J.P. The migration process and temperature effect of aqueous solutions contaminated by heavy metal ions in unsaturated silty soils. Heliyon 2024, 10, e30458. [Google Scholar] [CrossRef] [PubMed]
- Tong, F.; Jing, L.; Zimmerman, R.W. A fully coupled thermo-hydro-mechanical model for simulating multiphase flow, deformation and heat transfer in buffer material and rock masses. Int. J. Rock Mech. Min. Sci. 2010, 47, 205–217. [Google Scholar] [CrossRef]
- Ye, W.M.; Cui, Y.J.; Qian, L.X.; Chen, B. An experimental study of the water transfer through confined compacted GMZ-bentonite. Eng. Geol. 2009, 108, 169–176. [Google Scholar] [CrossRef]
- Bai, B.; Chen, J.; Zhang, B.; Wang, H. Migration trajectories and blocking effect of the fine particles in porous media based on particle flow simulation. AIP Adv. 2024, 14, 045036. [Google Scholar] [CrossRef]
- Chen, Y.G.; Jia, L.Y.; Ye, W.M.; Chen, B.; Cui, Y.J. Advances in experimental investigation on hydraulic fracturing behavior of bentonite-based materials used for HLW disposal. Environ. Earth Sci. 2016, 75, 787. [Google Scholar] [CrossRef]
- Zeng, Z.; Cui, Y.J.; Conil, N.; Talandier, J. Experimental investigation and modeling of the hydraulic conductivity of saturated bentonite–claystone mixture. Int. J. Geomech. 2020, 20, 04020184. [Google Scholar] [CrossRef]
- Tan, Y.; Zhou, G.P.; Zhang, H.Y.; Li, X.Y.; Liu, P. Effect of drying cracks on swelling and self-healing of bentonite-sand blocks used as engineered barriers for radioactive waste disposal. J. Rock Mech. Geotech. Eng. 2024, 16, 1776–1787. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, H.Y.; Tan, Y.; Zhu, J.H. Sealing performance of compacted block joints backfilled with bentonite paste or a particle-powder mixture. Soils Found. 2021, 61, 496–505. [Google Scholar] [CrossRef]
- Harrington, J.F.; Daniels, K.A.; Wiseall, A.C.; Sellin, P. Bentonite homogenisation during the closure of void spaces. Int. J. Rock Mech. Min. Sci. 2020, 136, 104535. [Google Scholar] [CrossRef]



| Mineral | Quality Percentage/% |
|---|---|
| Montmorillonite | 74.4 |
| Quartz | 12.4 |
| Cristobalite | 7.8 |
| Feldspar | 4.3 |
| Calcite | 0.4 |
| Kaolinite | 0.7 |
| Parameter | Value |
|---|---|
| Particle size/μm | <2 |
| Liquid limit/% | 170 |
| Plasticity limit/% | 27.43 |
| Plasticity index | 142.57 |
| Specific gravity/(mg/m3) | 2.66 |
| Location | Experimental Case | Initial Temperature/°C | Final Temperature/°C | ΔT1/°C | ΔT2/°C |
|---|---|---|---|---|---|
| A | Before simulated water inflow | 25.3 | 68.0 | 0.5 | 0.1 |
| After simulated water inflow | 24.8 | 68.1 | |||
| B | Before simulated water inflow | 25.2 | 41.4 | 0.5 | 0.2 |
| After simulated water inflow | 24.7 | 41.6 | |||
| C | Before simulated water inflow | 25.4 | 36.8 | 0.7 | 0.3 |
| After simulated water inflow | 24.7 | 37.1 | |||
| D | Before simulated water inflow | 25.5 | 32.8 | 1.0 | 0.3 |
| After simulated water inflow | 24.5 | 33.1 | |||
| E | Before simulated water inflow | 25.3 | 32.1 | 0.9 | 0.5 |
| After simulated water inflow | 24.4 | 32.6 | |||
| F | Before simulated water inflow | 25.6 | 31.1 | 1.4 | 0.9 |
| After simulated water inflow | 24.2 | 32.0 |
| Experimental Case | k1 | k2 | ΔT/K | λ/(W/(m·K)) | |
|---|---|---|---|---|---|
| Before simulated water inflow | BC joint | 3695.2 | 198.9 | 277.95 | 1.173 |
| DE joint | 273.75 | 1.159 | |||
| After simulated water inflow | BC joint | 276.95 | 1.236 | ||
| 0.269 | DE joint | 273.85 | 1.305 | ||
| Experimental Case | t/s | ΔH/m | q/m3 | K/(m/s) | |
|---|---|---|---|---|---|
| After simulated water inflow | BC joint | 7.884 × 106 | 2.039 | 4.477× 10−6 | 1.084 × 10−12 |
| DE joint | 8.718 × 10−6 | 2.112 × 10−12 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, G.; Bai, B.; Chen, W.; Mao, H.; Liu, Z.; Lan, X. Experimental Study on Heat Conduction and Water Migration of Composite Bentonite Samples. Materials 2024, 17, 4211. https://doi.org/10.3390/ma17174211
Yang G, Bai B, Chen W, Mao H, Liu Z, Lan X. Experimental Study on Heat Conduction and Water Migration of Composite Bentonite Samples. Materials. 2024; 17(17):4211. https://doi.org/10.3390/ma17174211
Chicago/Turabian StyleYang, Gaosheng, Bing Bai, Wenxuan Chen, Haitao Mao, Zhonghua Liu, and Xiaoling Lan. 2024. "Experimental Study on Heat Conduction and Water Migration of Composite Bentonite Samples" Materials 17, no. 17: 4211. https://doi.org/10.3390/ma17174211
APA StyleYang, G., Bai, B., Chen, W., Mao, H., Liu, Z., & Lan, X. (2024). Experimental Study on Heat Conduction and Water Migration of Composite Bentonite Samples. Materials, 17(17), 4211. https://doi.org/10.3390/ma17174211








