Investigating the Effect of Perforations on the Load-Bearing Capacity of Cardboard Packaging
Abstract
1. Introduction
2. Materials and Methods
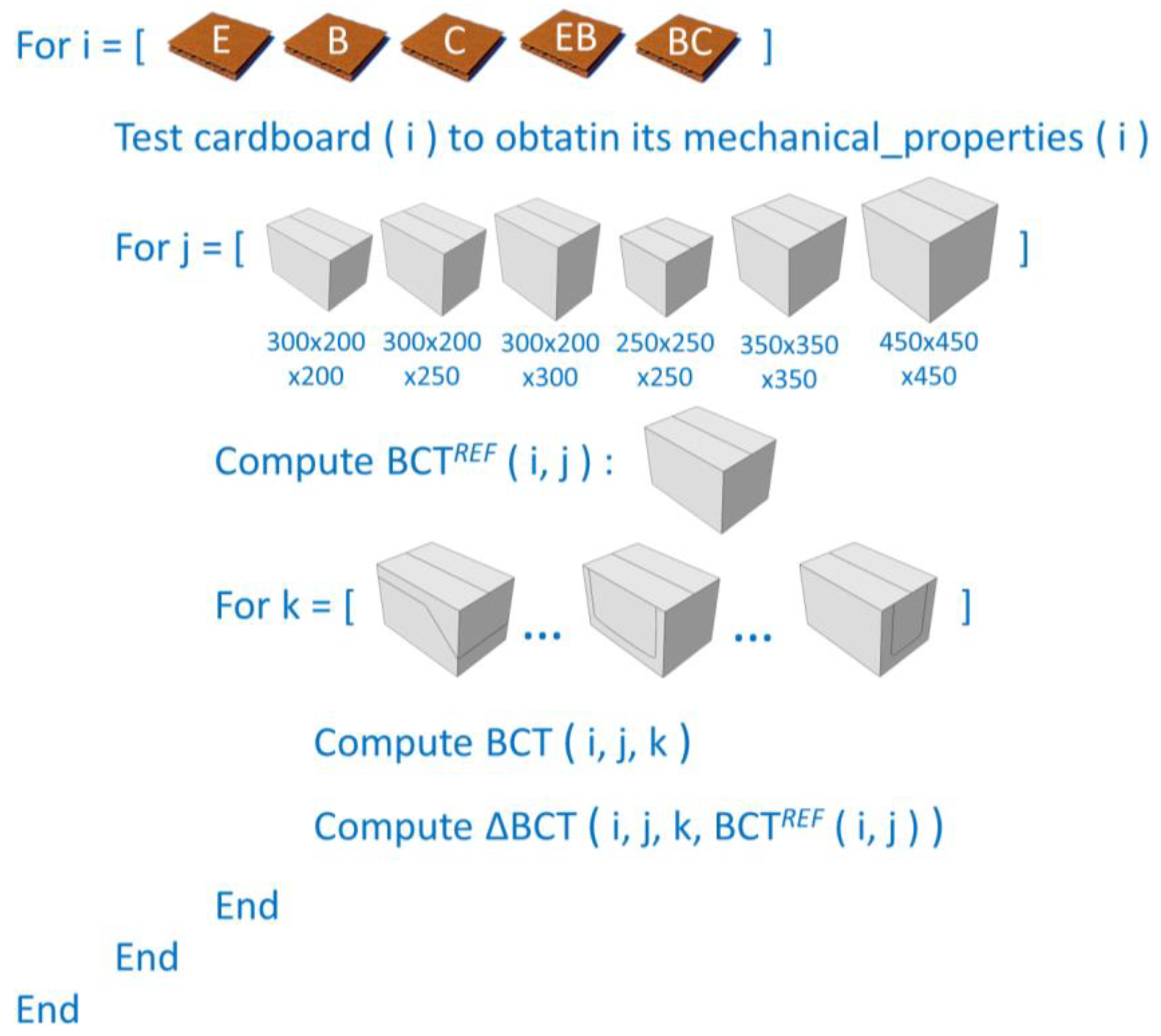
2.1. Workflow of the Study
2.2. Mechanical Properties of Corrugated Cardboards Analyzed
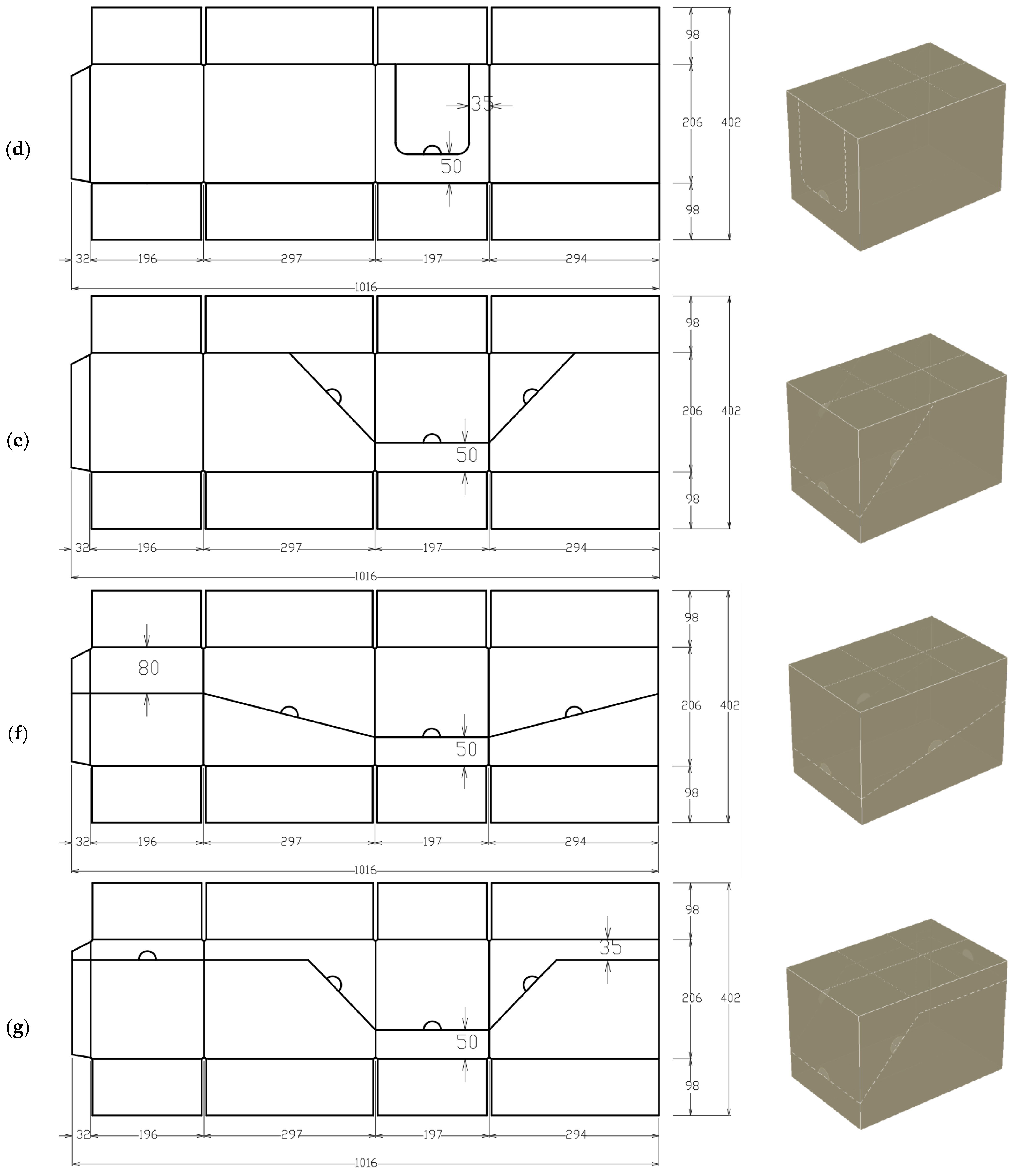
2.3. Finite Element Models of Corrugated Cardboard Boxes with Perforations
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Deshwal, G.K.; Panjagari, N.R.; Alam, T. An Overview of Paper and Paper Based Food Packaging Materials: Health Safety and Environmental Concerns. J. Food Sci. Technol. 2019, 56, 4391–4403. [Google Scholar] [CrossRef] [PubMed]
- Eurostat Online Data Sheet, Packaging Waste Statistics. 2021. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php?title=Packaging_waste_statistics#Generation_and_recycling_per_inhabitant (accessed on 23 July 2024).
- TAPPI/ANSI T402 sp-21; Standard Conditioning and Testing Atmospheres for Paper, Board, Pulp Handsheets, and Related Products. TAPPI: Peachtree Corners, GA, USA, 2023.
- Garbowski, T. Revolutionizing Corrugated Board Production and Optimization with Artificial Intelligence. Bioresources 2024, 19, 2003–2006. [Google Scholar] [CrossRef]
- Garbowski, T. Safety Factors in the Design of Corrugated Board Packaging. Packag. Rev. 2023, 2, 16–22. [Google Scholar]
- Garbowski, T. Evaluating Safety Factors in Corrugated Packaging for Extreme Environmental Conditions. Packag. Rev. 2024, 2, 6–15. [Google Scholar]
- Karabacakoğlu, B.; Tezakıl, F. Electrocoagulation of Corrugated Box Industrial Effluents and Optimization by Response Surface Methodology. Electrocatalysis 2023, 14, 159–169. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. Estimation of the Compressive Strength of Corrugated Cardboard Boxes with Various Perforations. Energies 2021, 14, 1095. [Google Scholar] [CrossRef]
- Luong, V.D.; Abbes, F.; Hoang, M.P.; Duong, P.T.M.; Abbes, B. Finite Element Elastoplastic Homogenization Model of a Corrugated-Core Sandwich Structure. Steel Compos. Struct. 2021, 41, 437–445. [Google Scholar] [CrossRef]
- Luong, V.D.; Abbès, F.; Abbès, B.; Duong, P.T.M.; Nolot, J.-B.; Erre, D.; Guo, Y.-Q. Finite Element Simulation of the Strength of Corrugated Board Boxes under Impact Dynamics. In Proceedings of the International Conference on Advances in Computational Mechanics 2017: ACOME 2017, Phu Quoc Island, Vietnam, 2–4 August 2017; Springer: Singapore, 2018; Volume PartF3. [Google Scholar]
- Di Russo, F.; Desole, M.; Gisario, A.; Genovesi, A.; Barletta, M. Study and Design of Corrugated Cardboard Trays With Microwaves by Experimental Analysis (EA) and Finite Element Methods (FEM). Packag. Technol. Sci. 2024, 37, 857–874. [Google Scholar] [CrossRef]
- Di Russo, F.M.; Desole, M.M.; Gisario, A.; Barletta, M. Evaluation of Wave Configurations in Corrugated Boards by Experimental Analysis (EA) and Finite Element Modeling (FEM): The Role of the Micro-Wave in Packaging Design. Int. J. Adv. Manuf. Technol. 2023, 126, 4963–4982. [Google Scholar] [CrossRef]
- Suarez, B.; Muneta, M.L.M.; Sanz-Bobi, J.D.; Romero, G. Application of Homogenization Approaches to the Numerical Analysis of Seating Made of Multi-Wall Corrugated Cardboard. Compos. Struct. 2021, 262, 113642. [Google Scholar] [CrossRef]
- Suarez, B.; Muneta, L.M.; Romero, G.; Sanz-Bobi, J.D. Efficient Design of Thin Wall Seating Made of a Single Piece of Heavy-Duty Corrugated Cardboard. Materials 2021, 14, 6645. [Google Scholar] [CrossRef] [PubMed]
- Garbowski, T.; Gajewski, T.; Knitter-Piątkowska, A. Influence of Analog and Digital Crease Lines on Mechanical Parameters of Corrugated Board and Packaging. Sensors 2022, 22, 4800. [Google Scholar] [CrossRef] [PubMed]
- Mrówczyński, D.; Gajewski, T.; Garbowski, T. A Simplified Dynamic Strength Analysis of Cardboard Packaging Subjected to Transport Loads. Materials 2023, 16, 5131. [Google Scholar] [CrossRef]
- Kim, S.; Horvath, L.; Russell, J.D.; Park, J. Sustainable and Secure Transport: Achieving Environmental Impact Reductions by Optimizing Pallet-Package Strength Interactions during Transport. Sustainability 2023, 15, 12687. [Google Scholar] [CrossRef]
- Fadiji, T.; Coetzee, C.J.; Berry, T.M.; Opara, U.L. Investigating the Role of Geometrical Configurations of Ventilated Fresh Produce Packaging to Improve the Mechanical Strength—Experimental and Numerical Approaches. Food Packag. Shelf Life 2019, 20, 100312. [Google Scholar] [CrossRef]
- Heposalmi, S.; Matthews, S.; Leminen, V.; Varis, J.; Toghyani, A. FEM as a Package Design Tool for Corrugated Paperboard. Procedia CIRP 2022, 109, 610–616. [Google Scholar] [CrossRef]
- Frank, B. Corrugated Box Compression—A Literature Survey. Packag. Technol. Sci. 2014, 27, 105–128. [Google Scholar] [CrossRef]
- McKee, R.C.; Gander, J.W.; Wachuta, J.R. Compression Strength Formula for Corrugated Boxes. Paperboard Packag. 1963, 48, 149–159. [Google Scholar]
- Frank, B.; Kruger, K. Assessing variation in package modeling. Tappi J. 2021, 20, 231–238. [Google Scholar] [CrossRef]
- Fehér, L.; Pidl, R.; Böröcz, P. Compression Strength Estimation of Corrugated Board Boxes for a Reduction in Sidewall Surface Cutouts—Experimental and Numerical Approaches. Materials 2023, 16, 597. [Google Scholar] [CrossRef]
- Fehér, L.; Mrówczyński, D.; Pidl, R.; Böröcz, P. Compressive Strength of Corrugated Paperboard Packages with Low and High Cutout Rates: Numerical Modelling and Experimental Validation. Materials 2023, 16, 2360. [Google Scholar] [CrossRef] [PubMed]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. Estimation of the Compressive Strength of Corrugated Cardboard Boxes with Various Openings. Energies 2021, 14, 155. [Google Scholar] [CrossRef]
- Duong, P.T.M. Analysis and Simulation for the Double Corrugated Cardboard Plates under Bending and In-Plane Shear Force by Homogenization Method. Int. J. Mech. 2017, 11, 176–181. [Google Scholar]
- Aboura, Z.; Talbi, N.; Allaoui, S.; Benzeggagh, M.L. Elastic Behavior of Corrugated Cardboard: Experiments and Modeling. Compos. Struct. 2004, 63, 53–62. [Google Scholar] [CrossRef]
- Šarčević, I.; Gregor-Svetec, D.; Banić, D. Validation of Elmendorf Method for Testing Perforated Corrugated Cardboard. Teh. Vjesn. 2022, 29, 1883–1888. [Google Scholar] [CrossRef]
- Šarčević, I.; Gregor-Svetec, D.; Banic, D. Effect of perforations on the loss of corrugated cardboard bending stiffness. In Proceedings of the 11th International Symposium on Graphic Engineering and Design, Novi Sad, Serbia, 3–5 November 2022; pp. 73–79. [Google Scholar]
- Sarcevic, I.; Svetec, D.G.; Banic, D. Influence of Perforations on the Reduction of the Compressive Strength of Corrugated Cardboard. J. Phys. Conf. Ser. 2022, 2321, 012016. [Google Scholar] [CrossRef]
- FEMat Systems: BSE System. Available online: http://fematsystems.pl/bse-system_en/ (accessed on 23 July 2024).
- ISO 3037:2022; Corrugated fibreboard—Determination of Edgewise Crush Resistance (Non-Waxed Edge Method). ISO: Geneva, Switzerland, 2022.
- ISO 5628:2019; Paper and Board—Determination of Bending Stiffness—General Principles for Two-Point, Three-Point, and Four-Point Methods. ISO: Geneva, Switzerland, 2019.
- Mrówczyński, D.; Gajewski, T.; Garbowski, T. Sensitivity Analysis of Open-Top Cartons in Terms of Compressive Strength Capacity. Materials 2023, 16, 412. [Google Scholar] [CrossRef]
- Hill, R. A Theory of the Yielding and Plastic Flow of Anisotropic Metals. Proc. R. Soc. Lond. A Math. Phys. Sci. 1948, 193, 281–297. [Google Scholar] [CrossRef]





| Grade | Grammage (g) | Thickness (mm) | Moisture (%) |
|---|---|---|---|
| E | 349 | 1.58 | 7.14 |
| B | 410 | 3.00 | 6.77 |
| C | 449 | 4.10 | 6.94 |
| EB | 789 | 4.47 | 7.08 |
| BC | 673 | 6.76 | 6.92 |
| Board | ||||||||
|---|---|---|---|---|---|---|---|---|
| (MPa) | (MPa) | (–) | (MPa) | (MPa) | (MPa) | (MPa) | (–) | |
| E | 3010 | 1192 | 0.472 | 1762 | 3.0 | 2.7 | 2.57 | 0.95 |
| B | 1494 | 713 | 0.430 | 777 | 3.5 | 5.0 | 1.49 | 0.75 |
| C | 1057 | 641 | 0.381 | 689 | 2.1 | 5.5 | 1.15 | 0.59 |
| EB | 1367 | 753 | 0.400 | 732 | 6.5 | 9.7 | 2.29 | 0.65 |
| BC | 562 | 449 | 0.332 | 402 | 3.2 | 7.9 | 1.19 | 0.50 |
| Dimensions (mm) | B Flute | Reference | C1 | C2 | C3 | C4 | C5 | C6 | C7 |
|---|---|---|---|---|---|---|---|---|---|
| BCT (kN) | 1284 | 953 | 983 | 932 | 1106 | 1057 | 871 | 802 | |
| Δ BCT (%) | – | −25.8 | −23.4 | −27.4 | −13.9 | −17.7 | −32.2 | −37.5 | |
| BCT (kN) | 1326 | 1014 | 1008 | 980 | 1119 | 1113 | 964 | 824 | |
| Δ BCT (%) | – | −23.5 | −24.0 | −26.1 | −15.6 | −16.1 | −27.3 | −37.9 | |
| BCT (kN) | 1361 | 998 | 993 | 973 | 1156 | 1116 | 1022 | 803 | |
| Δ BCT (%) | – | −26.7 | −27.0 | −28.5 | −15.1 | −18.0 | −24.9 | −41.0 |
| Dimensions (mm) | B Flute | Reference | C1 | C2 | C3 | C4 | C5 | C6 | C7 |
|---|---|---|---|---|---|---|---|---|---|
| BCT (kN) | 1477 | 1145 | 1137 | 1070 | 1191 | 1103 | 1024 | 813 | |
| Δ BCT (%) | – | −22.5 | −23.0 | −27.6 | −19.4 | −25.3 | −30.7 | −45.0 | |
| BCT (kN) | 1620 | 1288 | 1285 | 1221 | 1336 | 1275 | 1164 | 915 | |
| Δ BCT (%) | – | −20.5 | −20.7 | −24.6 | −17.5 | −21.3 | −28.1 | −43.5 | |
| BCT (kN) | 1709 | 1387 | 1383 | 1307 | 1430 | 1367 | 1247 | 978 | |
| Δ BCT (%) | – | −18.8 | −19.1 | −23.5 | −16.3 | −20.0 | −27.0 | −42.8 |
| Profile Wave | Reference | C1 | C2 | C3 | C4 | C5 | C6 | C7 | |
|---|---|---|---|---|---|---|---|---|---|
| E | BCT (kN) | 746 | 552 | 567 | 536 | 633 | 612 | 511 | 451 |
| Δ BCT (%) | – | −26.0 | −24.0 | −28.2 | −15.1 | −18.0 | −31.5 | −39.5 | |
| B | BCT (kN) | 1284 | 953 | 983 | 932 | 1106 | 1057 | 871 | 802 |
| Δ BCT (%) | – | −25.8 | −23.4 | −27.4 | −13.9 | −17.7 | −32.2 | −37.5 | |
| C | BCT (kN) | 1676 | 1202 | 1243 | 1192 | 1408 | 1336 | 1101 | 1048 |
| Δ BCT (%) | – | −28.3 | −25.8 | −28.9 | −16.0 | −20.3 | −34.3 | −37.5 | |
| EB | BCT (kN) | 2888 | 2135 | 2208 | 2098 | 2488 | 2372 | 1942 | 1819 |
| Δ BCT (%) | – | −26.1 | −23.5 | −27.4 | −13.9 | −17.9 | −32.8 | −37.0 | |
| BC | BCT (kN) | 3052 | 2199 | 2281 | 2264 | 2611 | 2482 | 2061 | 2006 |
| Δ BCT (%) | – | −27.9 | −25.3 | −25.8 | −14.4 | −18.7 | −32.5 | −34.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andrzejak, K.; Mrówczyński, D.; Gajewski, T.; Garbowski, T. Investigating the Effect of Perforations on the Load-Bearing Capacity of Cardboard Packaging. Materials 2024, 17, 4205. https://doi.org/10.3390/ma17174205
Andrzejak K, Mrówczyński D, Gajewski T, Garbowski T. Investigating the Effect of Perforations on the Load-Bearing Capacity of Cardboard Packaging. Materials. 2024; 17(17):4205. https://doi.org/10.3390/ma17174205
Chicago/Turabian StyleAndrzejak, Kacper, Damian Mrówczyński, Tomasz Gajewski, and Tomasz Garbowski. 2024. "Investigating the Effect of Perforations on the Load-Bearing Capacity of Cardboard Packaging" Materials 17, no. 17: 4205. https://doi.org/10.3390/ma17174205
APA StyleAndrzejak, K., Mrówczyński, D., Gajewski, T., & Garbowski, T. (2024). Investigating the Effect of Perforations on the Load-Bearing Capacity of Cardboard Packaging. Materials, 17(17), 4205. https://doi.org/10.3390/ma17174205









