Axial Compressive Behaviours of Coal Gangue Concrete-Filled Circular Steel Tubular Stub Columns after Chloride Salt Corrosion
Abstract
1. Introduction
2. Finite Element Model and Experimental Verification
2.1. Methodology
2.2. Material Constitutive
2.2.1. Steel Tube
2.2.2. Concrete
2.3. Finite Element Analysis
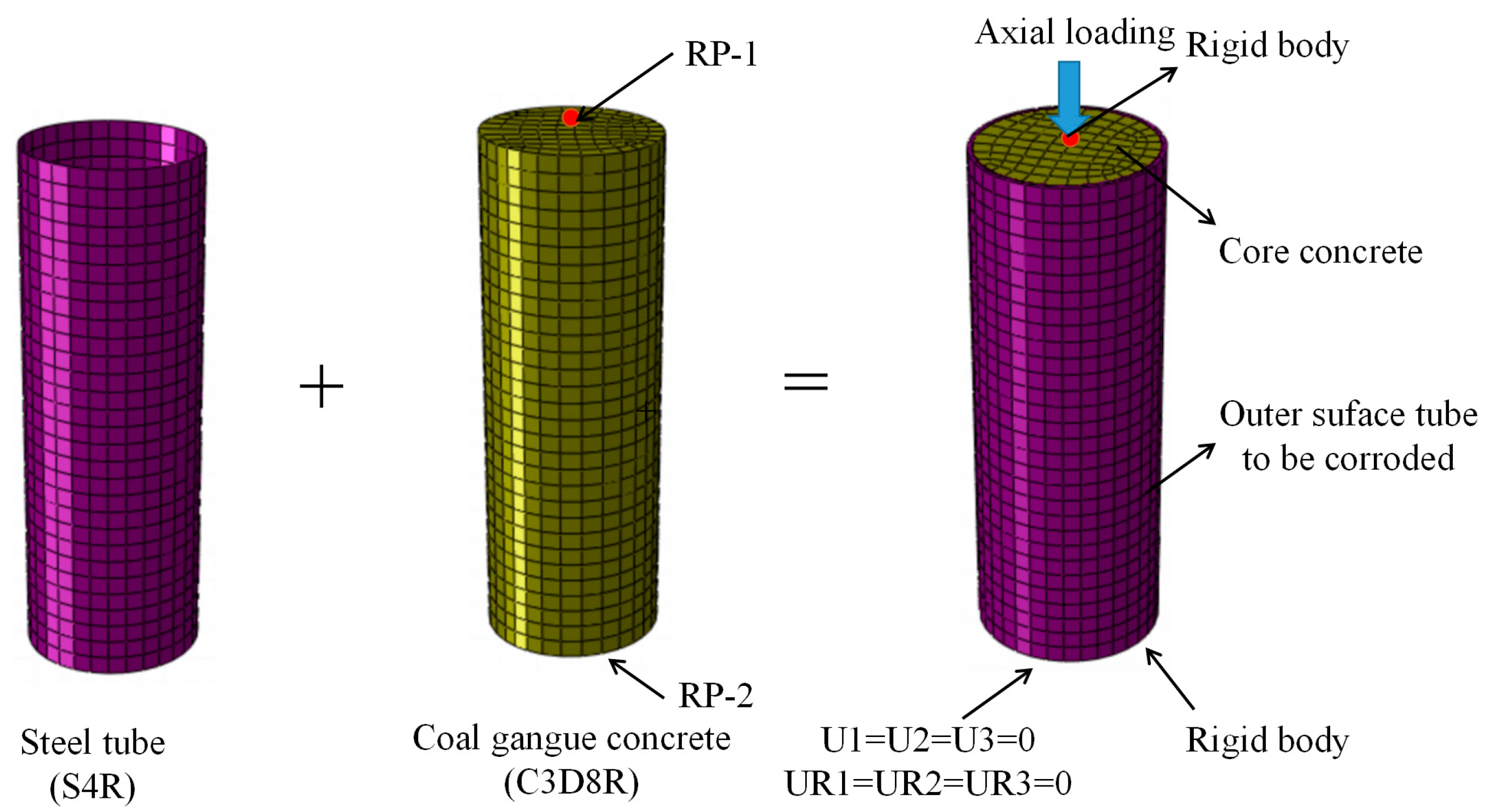
2.3.1. Part and Meshing
2.3.2. Interface Properties
2.3.3. Boundary Condition
2.4. Experimental Verification
2.4.1. Failure Pattern
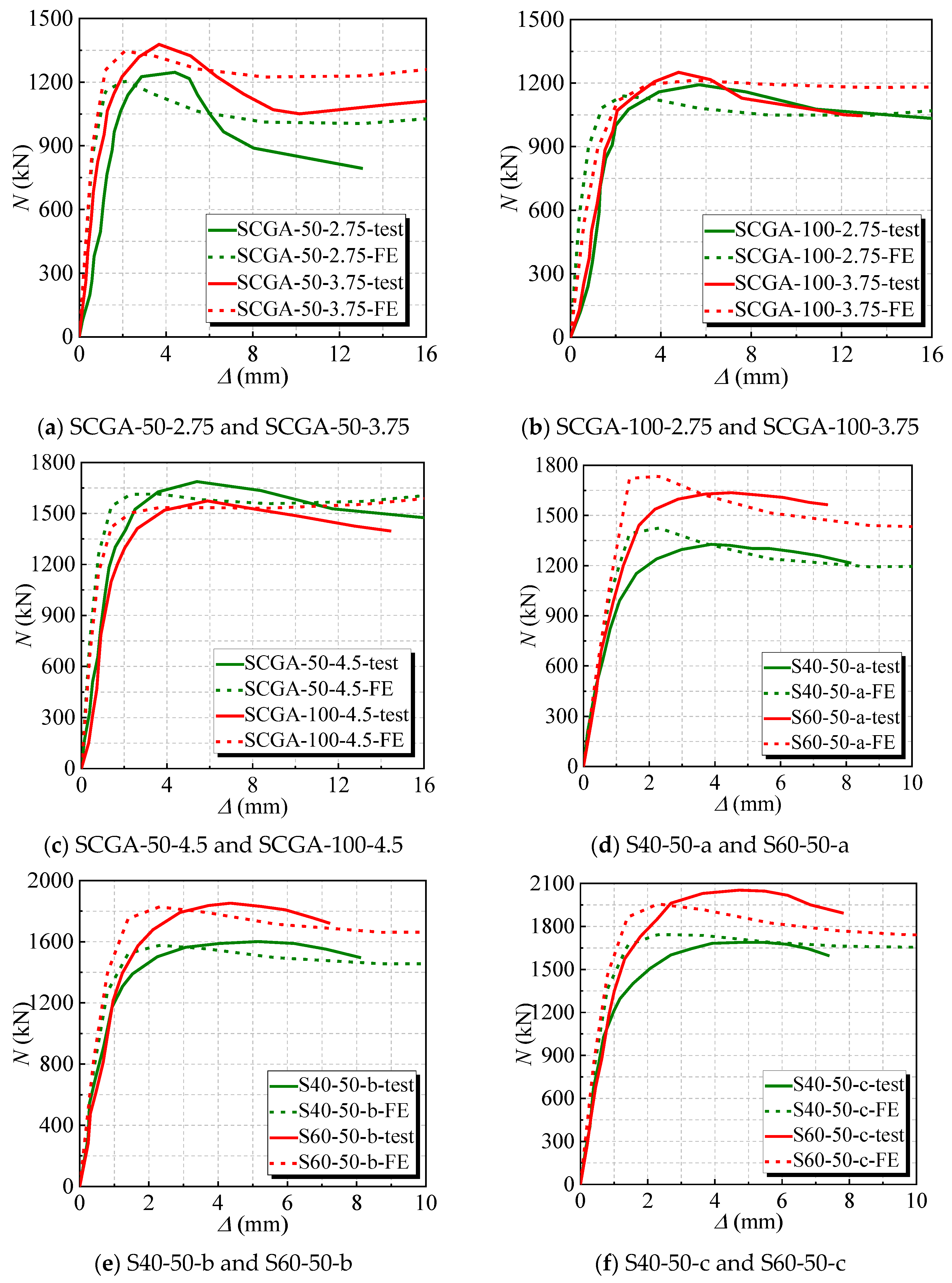
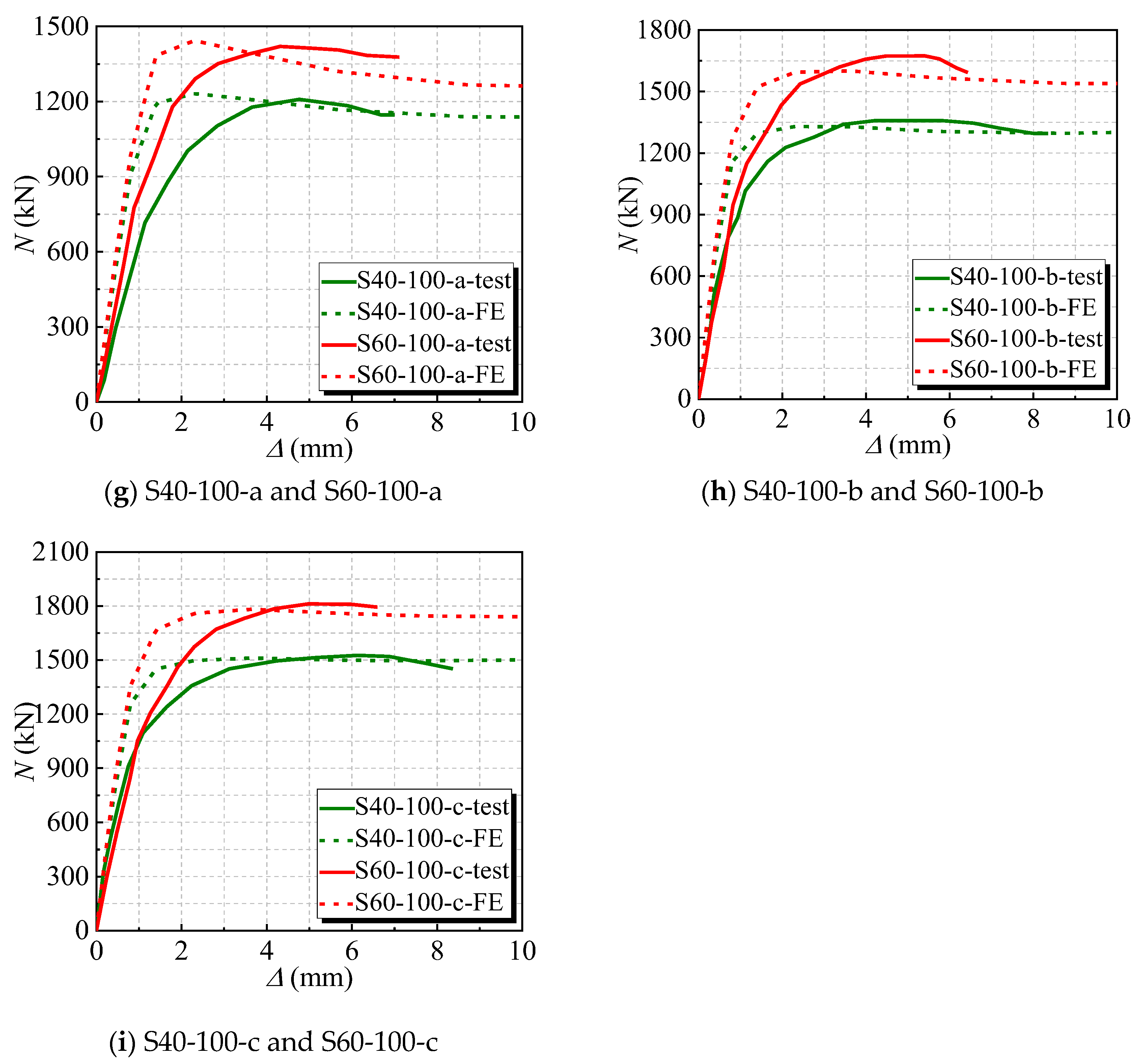
2.4.2. Load (N)-Displacement (∆) Curve
2.4.3. Ultimate Bearing Capacity
3. Numerical Investigations
3.1. Load (N)-Deformation (∆) Curve
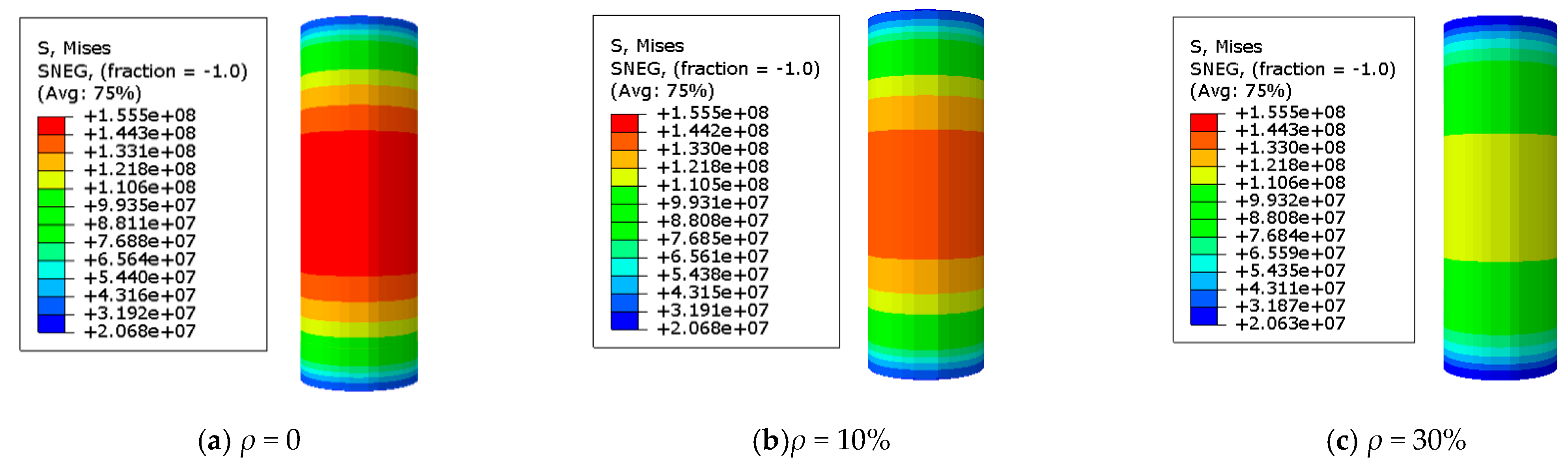
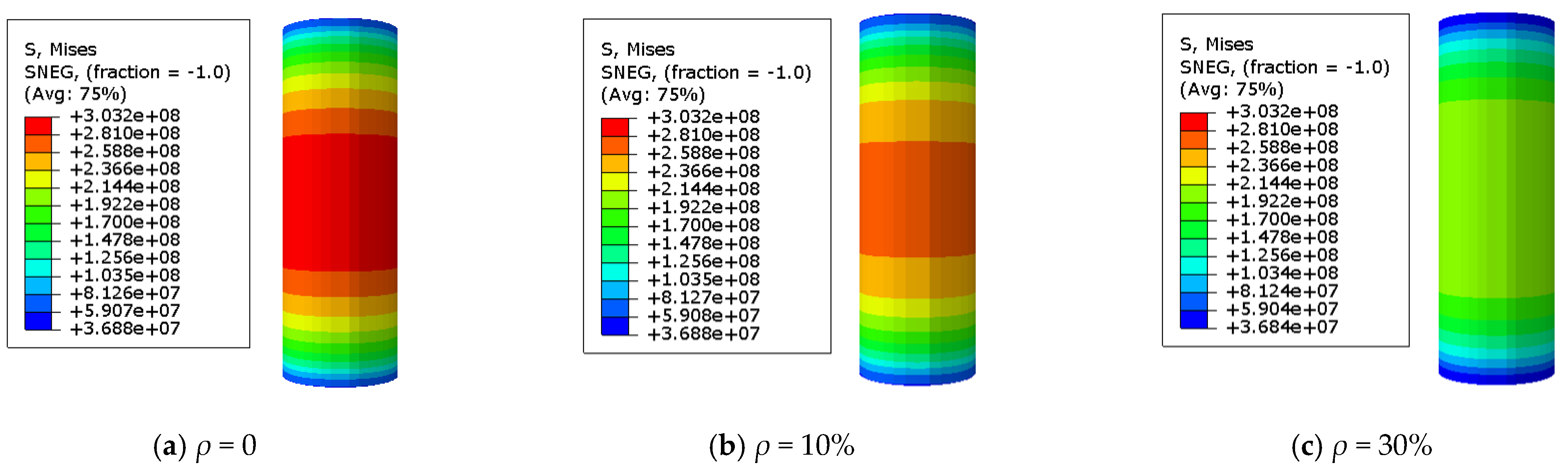
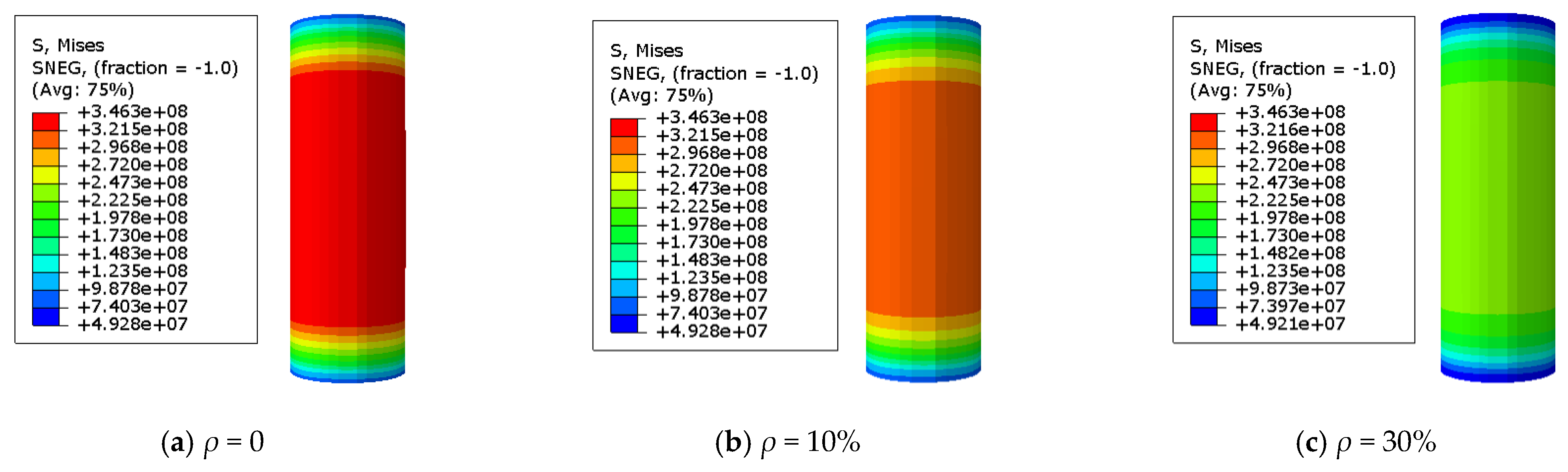
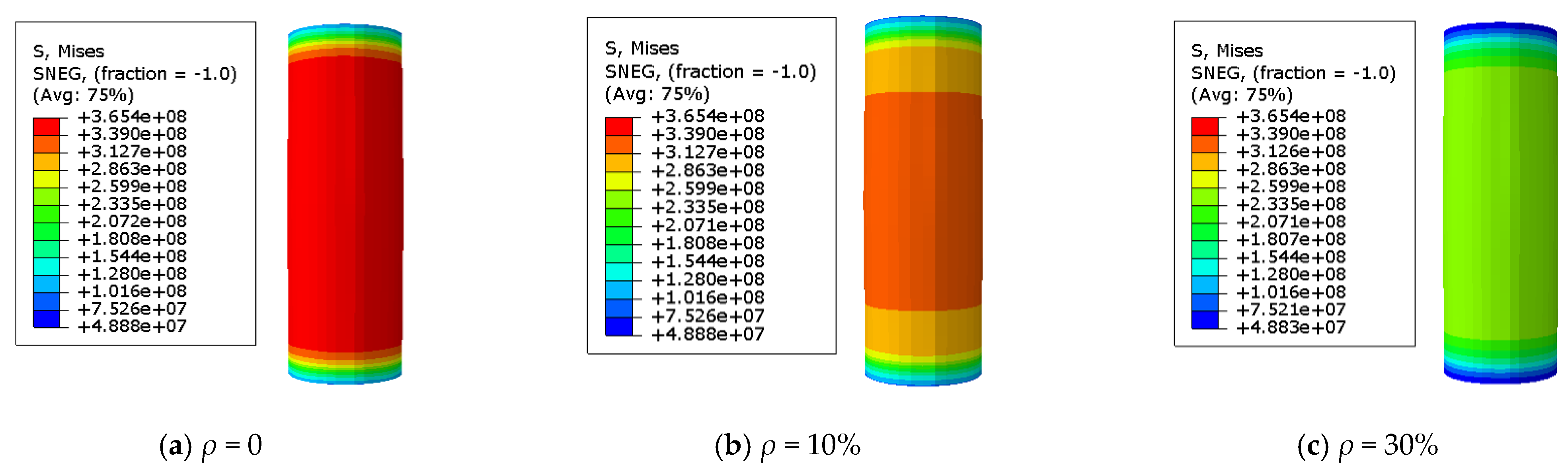
3.2. The Stress Distribution of the Steel Tube
4. Parameter Analysis
5. Simplified Design Method
6. Conclusions
- (1)
- Compared to the FE and Ref. experimental results, it is said that the failure mode of them was shear failure with bulging outward along the height direction of the specimens. The ratio of numerical to experimental values is between 0.929 and 1.074, with a mean of 0.990 and an SD of 0.033. This indicates that the finite element method is relatively accurate.
- (2)
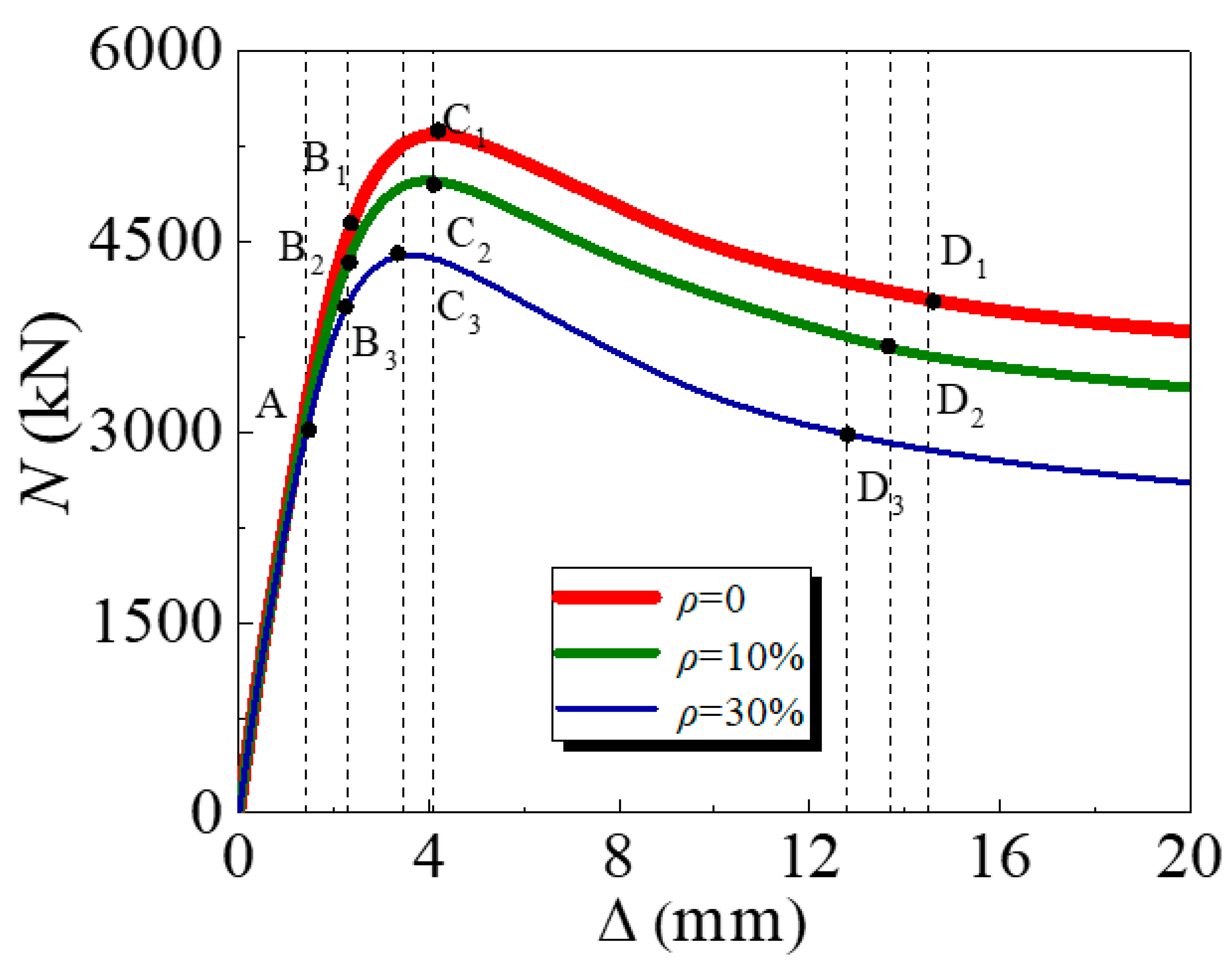
- When the load exceeds the steel yield strength, as the corrosion rate increases, the specimen will enter various characteristic regions. At the same characteristic points, the stress value of the steel tube decreases with increasing corrosion rate due to the lower bearing capacity of the specimen.
- (3)
- The concrete strength, steel yield strength, and steel ratio are positively correlated with the compressive bearing capacity of the specimen. The increase in the steel yield strength and steel ratio will not reduce the loss from corrosion on the compressive bearing capacity of the stub.
- (4)
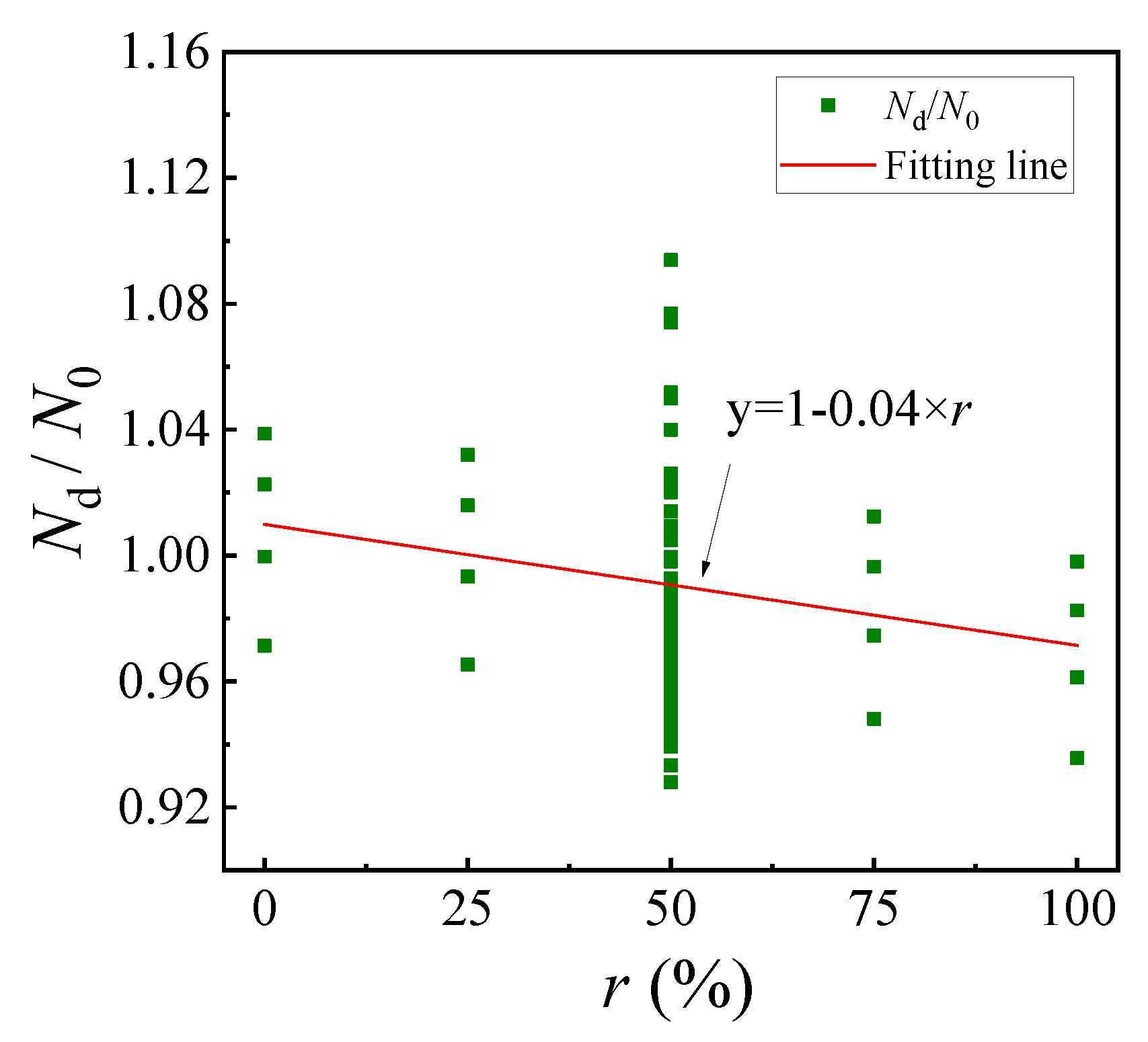
- The corrosion rate and replacement rate are negatively correlated with the Nu of the specimen. When the r of the coal gangue aggregate increases from 0 to 100%, Nu decreases by 3.67%, 3.84%, 3.92%, and 3.91% due to worse mechanical properties of coal gangue, respectively, within the parameter range of this study.
- (5)
- A design method was proposed for predicting the design strength of C-GCFST stub columns with corrosion. The error between the numerical values and designed values is within 9%, which indicates that the predictive effect of this formula is reasonable.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Ac | cross-section area of concrete | Nd | modified ultimate bearing capacity with replacement rate |
| As | cross-section area of steel | Nu | ultimate bearing capacity |
| Ase | cross-section area of steel after exposure | Nf | peak load of the numerical model |
| Asc | total column cross-section | Ne | peak load of the experiment |
| D | section diameter of the specimen | μ | cross-section friction coefficient |
| L | length of the specimen | r | coal gangue aggregate replacement fraction |
| Ec | elastic modulus of concrete | μs | Poisson’s ratio |
| Es | elastic modulus of steel tube | t0 | thickness of steel tube before corrosion |
| Ese | elastic modulus of steel tube with corrosion exposure | t1 | thickness of steel tube after corrosion |
| fsc | compressive strength of the CFST column | θ | steel ratio |
| ξ | hoop coefficient of the CFST | RP-2 | bottom point of the model |
| fc | compressive strength of the coal gangue concrete cylinder | θse | steel ratio after corrosion exposure |
| fcu | compressive strength of concrete cubes | p | contacted pressure in finite element model |
| fb0 | compressive strength of concrete under biaxial loading | β | size of the area encompassed by the descending sections and the strain axis |
| fy | yield strength of steel tube | Ψ | influence of the coal gangue on descending curvature |
| fye | yield strength of steel tube with corrosion exposure | λ | influence of the coal gangue substitute fraction on strain |
| fue | ultimate strength of steel tube with corrosion rate | τbond | bonding force in finite element model |
| ρ | corrosion rate | τcnt | critical value in finite element model |
| N | axial load | σ | stress |
| ∆ | axial displacement | σ0 | peak stress |
| N0 | unmodified ultimate bearing capacity | ε | strain |
| Kc | compressive meridian | ε0 | peak strain |
| U1, U2, U3 | X-, Y-, Z-axis displacement | εe | elastic strain |
| UR1, UR2, UR3 | X-, Y-, Z-axis angle of rotation | εe1, εe2, εe3 | process strain of the compression |
| RP-1 | top point of the model |
References
- Vo, T.L.; Nash, W.; Del Galdo, M.; Rezania, M.; Crane, R.; Nezhad, M.M.; Ferrara, L. Coal mining wastes valorization as raw geomaterials in construction: A review with new perspectives. J. Clean. Prod. 2022, 336, 130213. [Google Scholar] [CrossRef]
- Gao, S.; Zhang, S.M.; Guo, L.H. Application of coal gangue as a coarse aggregate in green concrete production: A review. Materials 2021, 14, 6803. [Google Scholar] [CrossRef] [PubMed]
- Frasson, B.J.; Pinto, R.C.; Rocha, J.C. Influence of different sources of coal gangue used as aluminosilicate powder on the mechanical properties and microstructure of alkali-activated cement. Mater. Construcción 2019, 69, e199. [Google Scholar] [CrossRef]
- Al Khazaleh, M.; Kumar, P.K.; Mohamed, M.J.S.; Kandasamy, A. Influence of coarse coal gangue aggregates on properties of structural concrete with nano silica. Mater. Today Proc. 2023, 72, 2089–2095. [Google Scholar] [CrossRef]
- Wu, H.; Kang, S.; Zhang, H.; Sun, Q.; Shen, R.; Shu, Z. Research of the workability, mechanical and hydration mechanism of coal gangue-construction solid waste backfilling materials. Constr. Build. Mater. 2023, 408, 133833. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, Y.; Wang, Q.; Aganyira, A.K.; Fang, Y. Experimental study and machine learning prediction on compressive strength of spontaneous-combustion coal gangue aggregate concrete. J. Build. Eng. 2023, 71, 106518. [Google Scholar] [CrossRef]
- Cong, X.; Lu, S.; Yao, Y.; Wang, Z. Fabrication and characterization of self-ignition coal gangue autoclaved aerated concrete. Mater. Des. 2016, 97, 155–162. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, G.; Liu, Y.; Li, Z. Mix design for thermal insulation concrete using waste coal gangue as aggregate. Mater. Res. Innov. 2015, 19, S5-878–S5-884. [Google Scholar] [CrossRef]
- Wang, Y.; Qiu, J.; Zeng, C. Shrinkage and Strength Properties of Coal Gangue Ceramsite Lightweight Aggregate Concrete. Adv. Mater. Sci. Eng. 2020, 2020, 3575709. [Google Scholar] [CrossRef]
- Cheng, Y.; Sun, L.; Li, Y.; Liu, M.; He, R.; Jin, X.; Jin, H. Damage Model of Steel Fiber-Reinforced Coal Gangue Concrete under Freeze-Thaw Cycles Based on Weibull Distribution. Materials 2023, 16, 6775. [Google Scholar] [CrossRef]
- Soundararajan, A.; Shanmugasundaram, K. Flexural behaviour of concrete-filled steel hollow sections beams. J. Civ. Eng. Manag. 2008, 14, 107–114. [Google Scholar] [CrossRef]
- Horvath, A.; Kollar, D.; Kovesdi, B. Behaviour of CFST Stub Columns Subjected to Pure Compressive. Int. J. Steel Struct. 2022, 22, 1175–1188. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Q.; Wang, Q.; Zhou, M.; Liu, H.; Guo, H. Axial compressive behavior of circular concrete-filled steel tube stub columns prepared with spontaneous-combustion coal gangue aggregate. J. Build. Eng. 2022, 48, 103987. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, Y.; Liu, H.; Zhou, M.; Wang, Q.; Lin, H. Effect of spontaneous-combustion coal gangue aggregate on axial performance of square concrete-filled steel tube stub columns. Structures 2022, 44, 216–235. [Google Scholar] [CrossRef]
- Gao, S.; Zhao, G.; Guo, L.; Zhou, L.; Yuan, K. Utilization of coal gangue as coarse aggregates in structural concrete. Constr. Build. Mater. 2021, 268, 121212. [Google Scholar] [CrossRef]
- Fang, C.; Li, G.C.; Zhang, L.; Yang, Z.J. Experimental and numerical investigation on seismic performance of ring-beam connection to gangue concrete filled steel tubular columns. Adv. Steel Constr. 2022, 18, 506–516. [Google Scholar]
- Han, L.H.; Hou, C.C.; Wang, Q.L. Behavior of circular CFST stub columns under sustained load and chloride corrosion. J. Constr. Steel Res. 2014, 103, 23–36. [Google Scholar] [CrossRef]
- Han, L.-H.; Hua, Y.-X.; Hou, C.; Wang, Q.-L. Circular concrete-filled steel tubes subjected to coupled tension and chloride corrosion. J. Struct. Eng. 2017, 143, 04017134. [Google Scholar] [CrossRef]
- Hou, C.; Han, L.H.; Zhao, X.L. Full-range analysis on square CFST stub columns and beams under loading and chloride corrosion. Thin-Walled Struct. 2013, 68, 50–64. [Google Scholar] [CrossRef]
- Li, W.; Han, L.H.; Zhao, X.L. Behavior of CFDST stub columns under preload, sustained load and chloride corrosion. J. Constr. Steel Res. 2015, 107, 12–23. [Google Scholar] [CrossRef]
- Li, Y.L.; Zhao, X.L.; Singh, R.R.; Al-Saadi, S. Texts on seawater and sea sand concrete-filled CFRP, BFRP and stainless steel tubular stub columns. Thin-Walled Struct. 2016, 108, 163–184. [Google Scholar] [CrossRef]
- Lyu, X.; Zhang, T.; Wang, W.; Zhang, L.; Xue, G. Behavior of concrete-filled circular steel tubular stub columns exposed to corrosion and freeze—Thaw cycles. Structures 2023, 55, 2266–2279. [Google Scholar] [CrossRef]
- Sultana, S.; Wang, Y.; Sobey, A.J.; Wharton, J.A.; Shenoi, R.A. Influence of corrosion on the ultimate compressive of strength of steel plates and stiffened panels. Thin-Walled Struct. 2015, 96, 95–140. [Google Scholar] [CrossRef]
- Yuan, F.; Chen, M.; Huang, H.; Xie, L.; Wang, C. Circular concrete filled steel tubular (CFST) columns under cyclic load and acid rain attack: Test simulation. Thin-Walled Struct. 2018, 122, 90–101. [Google Scholar] [CrossRef]
- Zeng, W.; Ayough, P.; Wang, Y.H.; Elchalakani, M. Numerical simulation of axially loaded circular concrete-filled steel tubular short columns with localized corrosion. Eng. Struct. 2024, 312, 118243. [Google Scholar] [CrossRef]
- Alraeeini, A.S.; Nikbakht, E. Corrosion effect on the flexural behaviour of concrete filled steel tubulars with single and double skins using engineered cementitious composite. Structures 2022, 44, 1680–1694. [Google Scholar] [CrossRef]
- Zhang, F.; Xia, J.; Li, G.; Guo, Z.; Chang, H.; Wang, K. Degradation of axial ultimate load-bearing capacity of circular thin-walled concrete-filled steel tubular stub columns after corrosion. Materials 2020, 13, 795. [Google Scholar] [CrossRef]
- Li, G.; Hou, C.; Shen, L.M. Life-cycle analysis of FRP-strengthened offshore CFST columns suffering from steel corrosion. Compos. Struct. 2021, 277, 114607. [Google Scholar] [CrossRef]
- Gao, S.; Peng, Z.; Xiaodong, X.L.; Dong, C. Tests on axial strength of circle CFST stub columns under marine atmosphere in cold region. Constr. Build. Mater. 2020, 230, 117073. [Google Scholar] [CrossRef]
- Reddy, S.V.B.; Sivasankar, S. Axial Behaviour of Corroded CFST Columns Wrapped with GFRP Sheets—An Experimental Investigation. Adv. Struct. Eng. 2020, 74, 15–28. [Google Scholar]
- Wang, Y.L.; Cao, M.M.; Sun, H.J. Time-dependent reliability analysis of circular CFST stub columns under environmental corrosion. Pac. Sci. Rev. 2014, 16, 201–206. [Google Scholar] [CrossRef]
- Zhang, T.; Lyu, X.; Liu, H.; Zhang, L.; Wang, J.; Gao, S. Axial performance degradation of squared CFST stubs in severe cold and acid rain area. Constr. Build. Mater. 2020, 262, 176–188. [Google Scholar] [CrossRef]
- Zhao, Z.W.; Mo, S.J.; Gao, T. Axial compression capacity of rectangular CFST columns under random pitting corrosion. Structures 2023, 48, 1230–1243. [Google Scholar] [CrossRef]
- Guo, L.; Huang, H.; Jia, C.; Romanov, K. Axial behavior of square CFST with local corrosion simulated by artificial notch. J. Constr. Steel Res. 2020, 174, 106314. [Google Scholar] [CrossRef]
- Lin, S.Q.; Li, Z.L.; Zhao, Y.G. Behavior of eccentrically loaded circular concrete-filled steel tube stub columns with localized corrosion. Eng. Struct. 2023, 288, 116227. [Google Scholar] [CrossRef]
- Zhao, Z.; Gao, T.; Jian, X.; Mo, S.; Liu, B. Eccentric compression capacity of circular CFST columns under random pitting corrosion. Ocean. Eng. 2023, 288, 115975. [Google Scholar] [CrossRef]
- Luo, S.; Chen, M.; Huang, H.; Xv, K.; Fang, W.; Zhang, R. Eccentric compression test and ultimate load strength analysis of circular CFST long column with local corrosion. Structures 2023, 56, 104937. [Google Scholar] [CrossRef]
- Huang, H.; Guo, L.; Zhao, O.; Gao, S. Experimental and numerical investigation into locally corroded circular concrete-filled steel tubular stub columns strengthened by CFRP. Thin-Walled Struct. 2023, 192, 111174. [Google Scholar] [CrossRef]
- Karagah, H.; Shi, C.; Dawood, M.; Belarbi, A. Experimental investigation of short steel columns with localized corrosion. Thin-Walled Struct. 2015, 87, 191–199. [Google Scholar] [CrossRef]
- Wang, K.; Chen, M.; Zhang, R.; Fang, W. Finite element simulation of load bearing capacity of circular CFST long columns with localized corrosion under eccentric load. Structures 2022, 43, 1629–1642. [Google Scholar] [CrossRef]
- Dinesh, D.; Amritha, E.K. Localized Corrosion Damage Study and Strengthening Strategies on Orthogonal Concrete Filled Steel Tubular Column. In Proceedings of the International Conference on Structural Engineering and Construction Management, Angamaly, India, 7–9 June 2023; Volume 381, pp. 207–220. [Google Scholar]
- Tao, Z.; Wang, Z.B.; Yu, Q. Finite element modelling of concrete-filled steel stub columns under axial compression. J. Constr. Steel Res. 2013, 89, 4320. [Google Scholar] [CrossRef]
- Han, L.H. Concrete Filled Steel Tubular Structures-Theory and Practice, 3rd ed.; Science Press: Beijing, China, 2018. (In Chinese) [Google Scholar]
- Zhang, T.; Xu, Q.; Yang, F.; Gao, S. Study on Degradation Law and the Equivalent Thickness Model of Steel Subjected to Sulfate Corrosion. Materials 2023, 16, 4320. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.Z.; Liu, J.L.; Xu, Q.; Wang, Q.H. Finite Element Analysis of Circular Concrete-filled Steel Tube Stub Columns Using Spontaneous Combustion Coal Gangue Aggregate Subjected to Axial Compressive Load. J. Shenyang Jianzhu Univ. (Nat. Sci.) 2022, 38, 636–644. (In Chinese) [Google Scholar]
- Zhou, M.; Dou, Y.; Zhang, Y.; Zhang, Y.; Zhang, B. Effects of the variety and content of coal gangue coarse aggregate on the mechanical properties of concrete. Constr. Build. Mater. 2019, 220, 386–395. [Google Scholar] [CrossRef]
- Zhang, T.; Zhu, Q.; Liu, H.; Gao, S. Utilization of coal gangue sand in structural concrete as fine aggregate towards sustainable production. Constr. Build. Mater. 2024, 417, 135264. [Google Scholar] [CrossRef]
- Lyu, X.; Zhang, T.; Liu, F.; Liu, Y. Behaviours of stiffened concrete-filled thin-walled square steel tubular stub columns after non-uniform fire exposure. J. Constr. Steel Res. 2022, 188, 107031. [Google Scholar] [CrossRef]
- Wang, J.; Duan, Y.; Lyu, X.; Yu, Y.; Xiao, J. Axial compression behavior of coal gangue coarse aggregate concrete-filled steel tube stub columns. J. Constr. Steel Res. 2024, 215, 108534. [Google Scholar] [CrossRef]
- GB50936-2014; Technical Specification for Steel Stub Concrete Structures. China Architecture Industry Press: Beijing, China, 2014. (In Chinese)





| No. | D (mm) × L (mm) × t (mm) | ρ (%) | Es (GPa) | fye (MPa) | fue (MPa) | μs | Nf (kN) | Ne (kN) | Nf/Ne | Ref. |
|---|---|---|---|---|---|---|---|---|---|---|
| C3-0-10 | 90 × 300 × 3.0 | 10 | 152 | 359 | 431 | 0.282 | 623 | 623 | 1.011 | [22] |
| C3-0-20 | 20 | 134 | 288 | 339 | 0.296 | 570 | 577 | 0.987 | ||
| C3-0-30 | 30 | 122 | 229 | 325 | 0.283 | 549 | 548 | 1.002 | ||
| C4.5-0-10 | 90 × 300 × 4.5 | 10 | 145 | 339 | 403 | 0.266 | 833 | 816 | 1.021 | |
| C4.5-0-20 | 20 | 140 | 305 | 336 | 0.279 | 750 | 745 | 1.007 | ||
| C4.5-0-30 | 30 | 128 | 258 | 318 | 0.309 | 713 | 691 | 1.031 | ||
| Q235-5-0-1/2 | 90 × 270 × 1.78 | 5 | 208 | 242 | 474 | - | 384 | 383 | 1.003 | [29] |
| Q235-10-0-1/2 | 10 | 208 | 242 | 474 | - | 369 | 381 | 0.969 | ||
| Q235-20-0-1/2 | 20 | 208 | 242 | 474 | - | 341 | 354 | 0.965 | ||
| Q345-5-0-1/2 | 90 × 270×1.90 | 5 | 210 | 359 | 531 | - | 490 | 511 | 0.960 | |
| Q345-10-0-1/2 | 10 | 210 | 359 | 531 | - | 474 | 485 | 0.978 | ||
| Q345-20-0-1/2 | 20 | 210 | 359 | 531 | - | 447 | 464 | 0.963 | ||
| SCGA-50-2.75 | 140 × 420 × 2.75 | - | 198 | 278 | 346 | 0.258 | 1207 | 1246 | 0.969 | [13] |
| SCGA-100-2.75 | - | 198 | 278 | 346 | 0.258 | 1139 | 1179 | 0.966 | ||
| SCGA-50-3.75 | 140 × 420 × 3.75 | - | 205 | 285 | 364 | 0.252 | 1347 | 1384 | 0.973 | |
| SCGA-100-3.75 | - | 205 | 285 | 364 | 0.252 | 1213 | 1306 | 0.929 | ||
| SCGA-50-4.50 | 140 × 420 × 4.50 | - | 201 | 338 | 420 | 0.262 | 1614 | 1657 | 0.974 | |
| SCGA-100-4.50 | - | 201 | 338 | 420 | 0.262 | 1535 | 1549 | 0.991 | ||
| S40-50-a | 156 × 450 × 3.0 | - | 201 | 282 | 459 | 0.28 | 1425 | 1327 | 1.074 | [49] |
| S40-100-a | - | 201 | 282 | 459 | 0.28 | 1232 | 1201 | 1.026 | ||
| S60-50-a | - | 201 | 282 | 459 | 0.28 | 1734 | 1630 | 1.064 | ||
| S60-100-a | - | 201 | 282 | 459 | 0.28 | 1443 | 1420 | 1.016 | ||
| S40-50-b | 158 × 450 × 4.0 | - | 206 | 295 | 465 | 0.28 | 1577 | 1659 | 0.951 | |
| S40-100-b | - | 206 | 295 | 465 | 0.28 | 1330 | 1368 | 0.972 | ||
| S60-50-b | - | 206 | 295 | 465 | 0.28 | 1828 | 1865 | 0.980 | ||
| S60-100-b | - | 206 | 295 | 465 | 0.28 | 1600 | 1672 | 0.957 | ||
| S40-50-c | 159 × 450 × 4.5 | - | 204 | 317 | 477 | 0.29 | 1744 | 1718 | 1.015 | |
| S40-100-c | - | 204 | 317 | 477 | 0.29 | 1511 | 1540 | 0.981 | ||
| S60-50-c | - | 204 | 317 | 477 | 0.29 | 1957 | 2039 | 0.960 | ||
| S60-100-c | - | 204 | 317 | 477 | 0.29 | 1782 | 1812 | 0.984 | ||
| Mean value | 0.990 | |||||||||
| SD | 0.033 | |||||||||
| CV | 0.033 | |||||||||
| Parameter | Ranges | Default |
|---|---|---|
| fcu (MPa) | 20, 30, 40, 50, 60 | 30 |
| fy (MPa) | 235, 345, 390, 420, 460 | 345 |
| θ (%) | 1, 2, 3, 4, 5 | 2 |
| r (%) | 0, 25, 50, 75, 100 | 50 |
| ρ (%) | 10, 20, 30, 40 | — |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Wang, H.; Zheng, X.; Gao, S. Axial Compressive Behaviours of Coal Gangue Concrete-Filled Circular Steel Tubular Stub Columns after Chloride Salt Corrosion. Materials 2024, 17, 2782. https://doi.org/10.3390/ma17112782
Zhang T, Wang H, Zheng X, Gao S. Axial Compressive Behaviours of Coal Gangue Concrete-Filled Circular Steel Tubular Stub Columns after Chloride Salt Corrosion. Materials. 2024; 17(11):2782. https://doi.org/10.3390/ma17112782
Chicago/Turabian StyleZhang, Tong, Hongshan Wang, Xuanhe Zheng, and Shan Gao. 2024. "Axial Compressive Behaviours of Coal Gangue Concrete-Filled Circular Steel Tubular Stub Columns after Chloride Salt Corrosion" Materials 17, no. 11: 2782. https://doi.org/10.3390/ma17112782
APA StyleZhang, T., Wang, H., Zheng, X., & Gao, S. (2024). Axial Compressive Behaviours of Coal Gangue Concrete-Filled Circular Steel Tubular Stub Columns after Chloride Salt Corrosion. Materials, 17(11), 2782. https://doi.org/10.3390/ma17112782








