Experimental Analysis of the Influence of Carrier Layer Material on the Performance of the Control System of a Cantilever-Type Piezoelectric Actuator
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
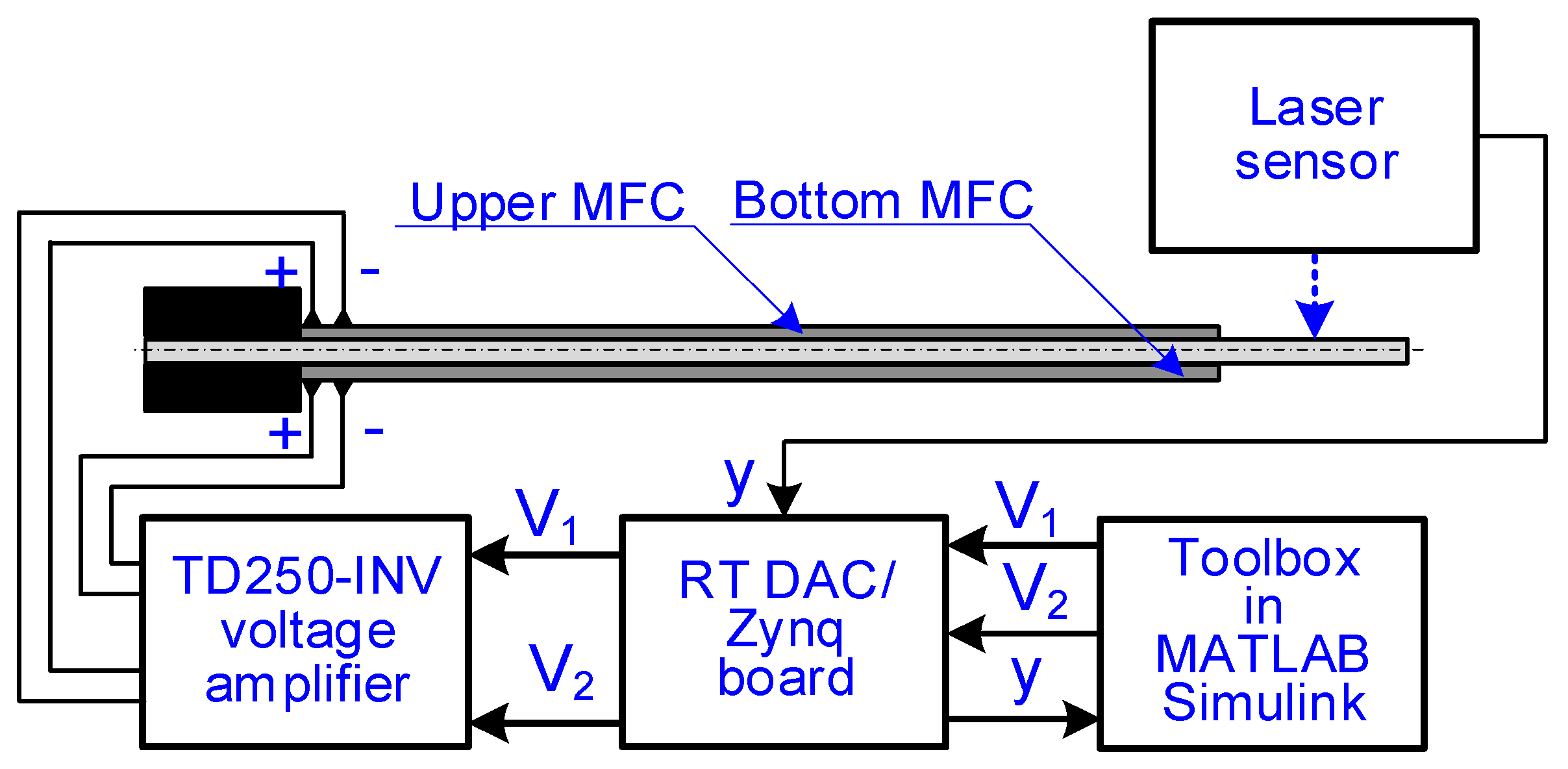
2.2. Laboratory Research Method
2.3. Simulation Research Method
3. Mathematical Model of Piezoelectric Actuator and Synthesis of Control System
3.1. Piezoelectric Actuator
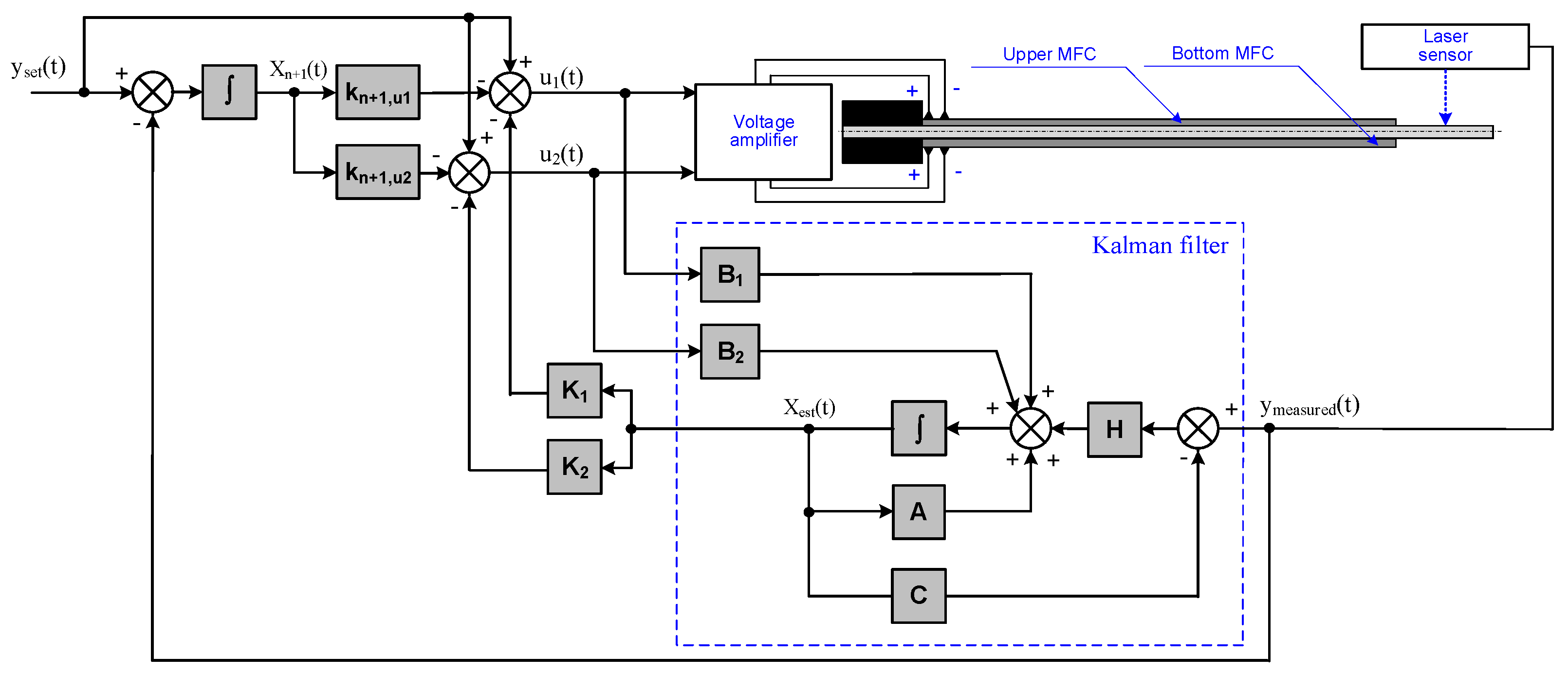
3.2. Synthesis of Control System
4. Results
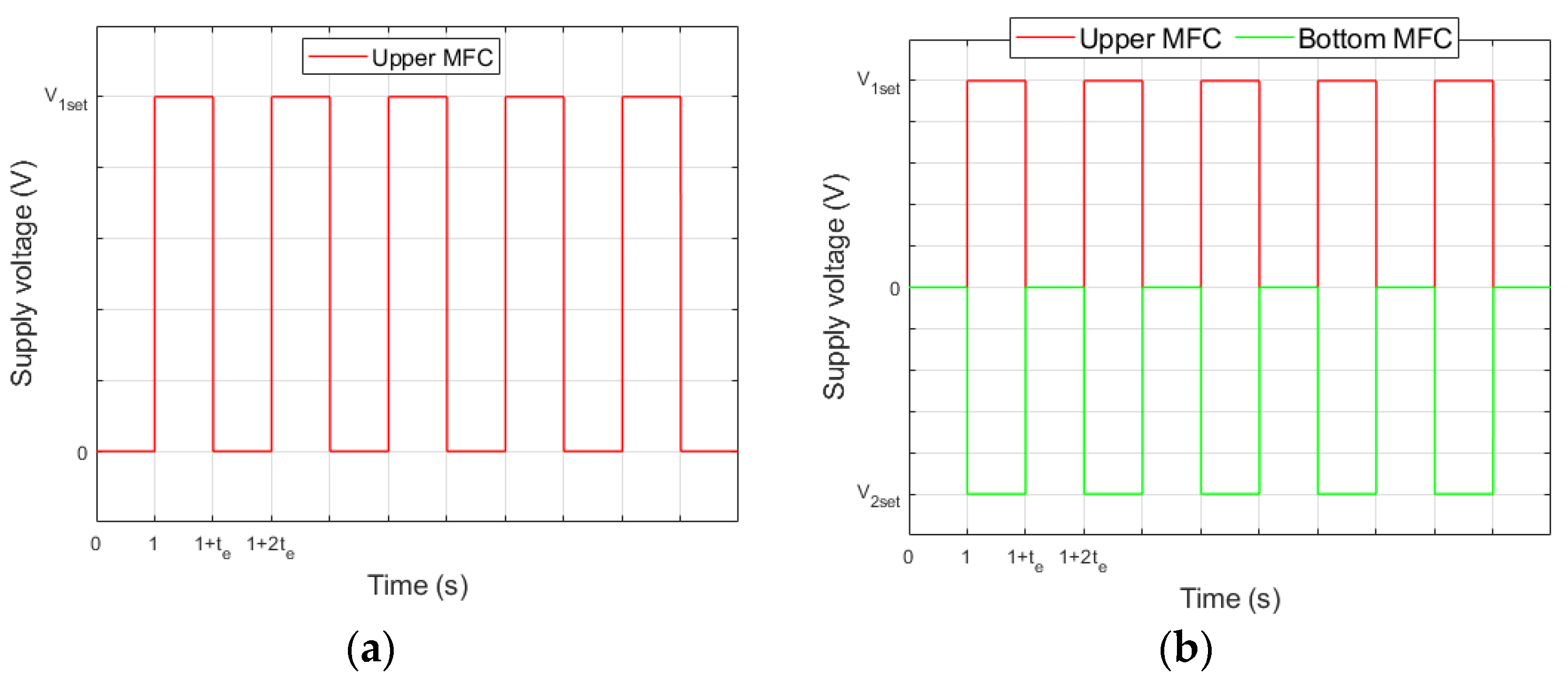
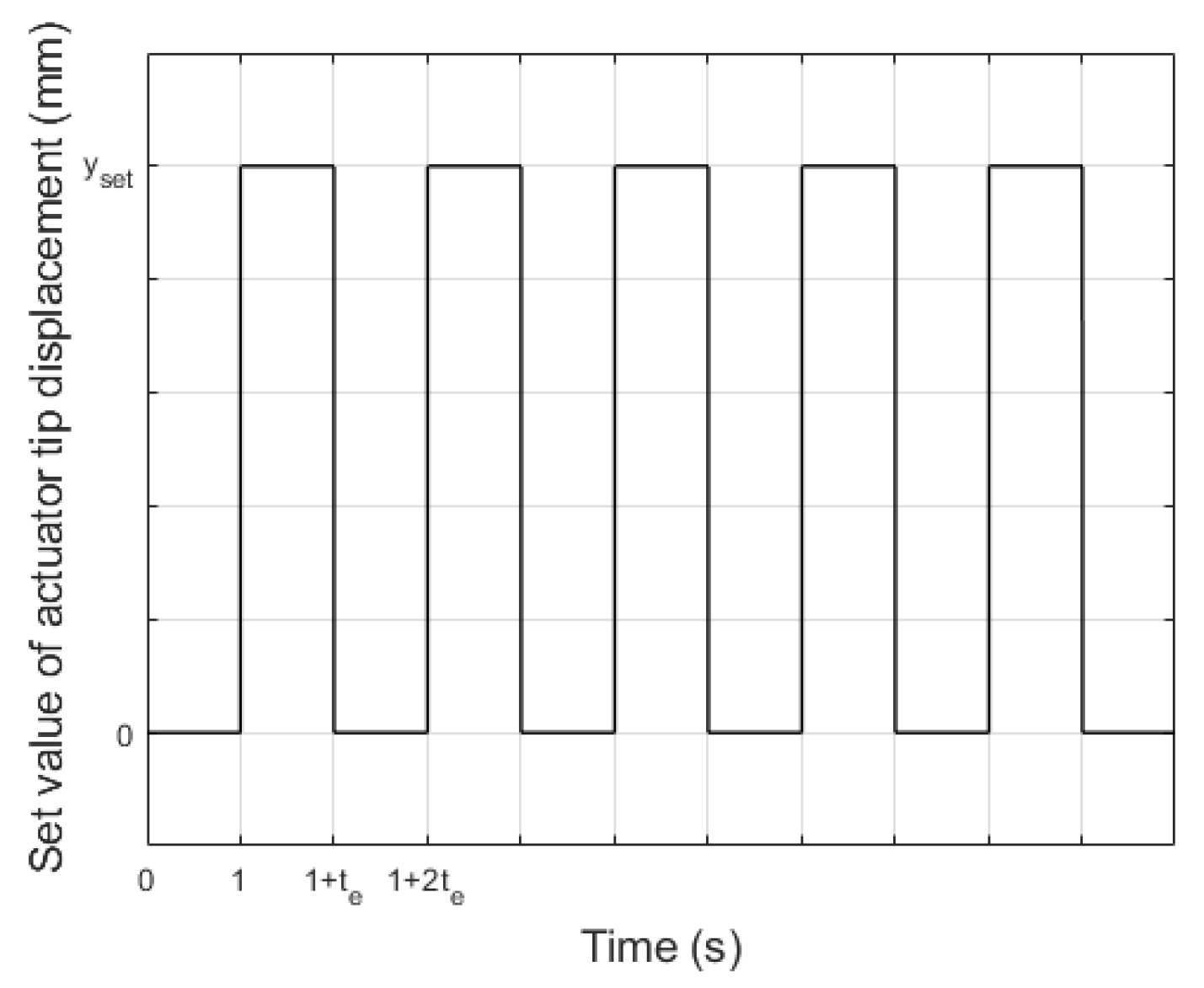
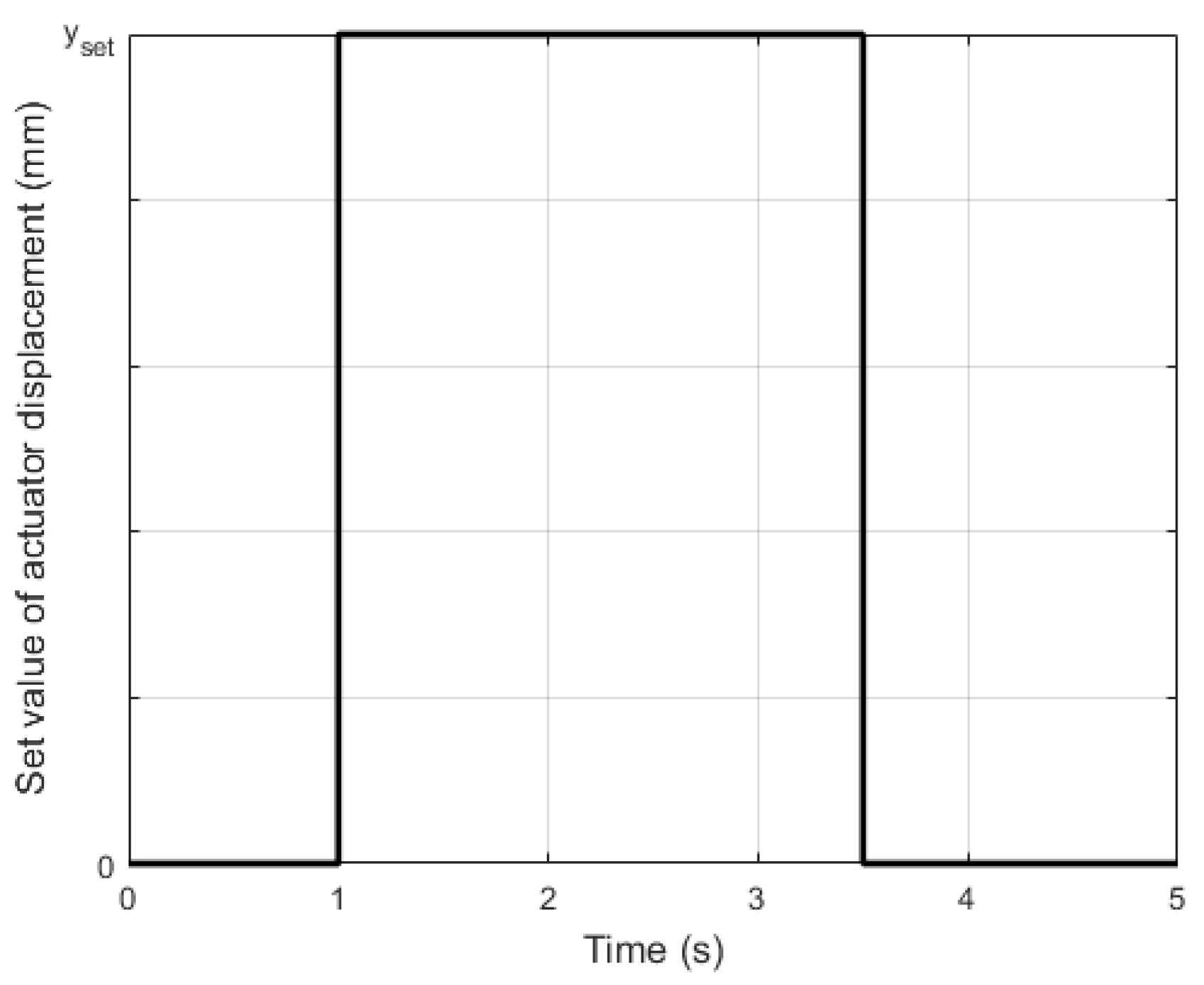
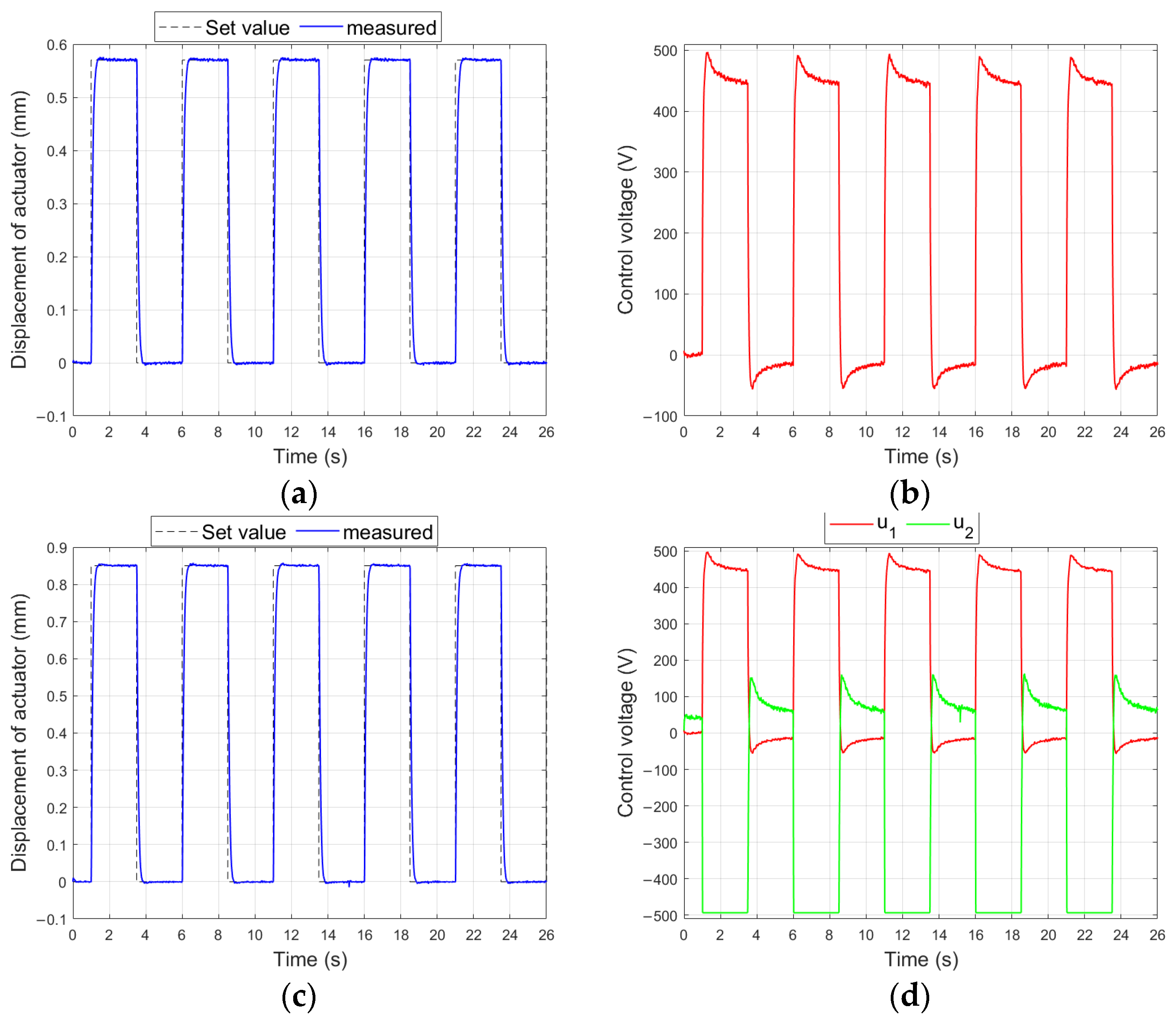
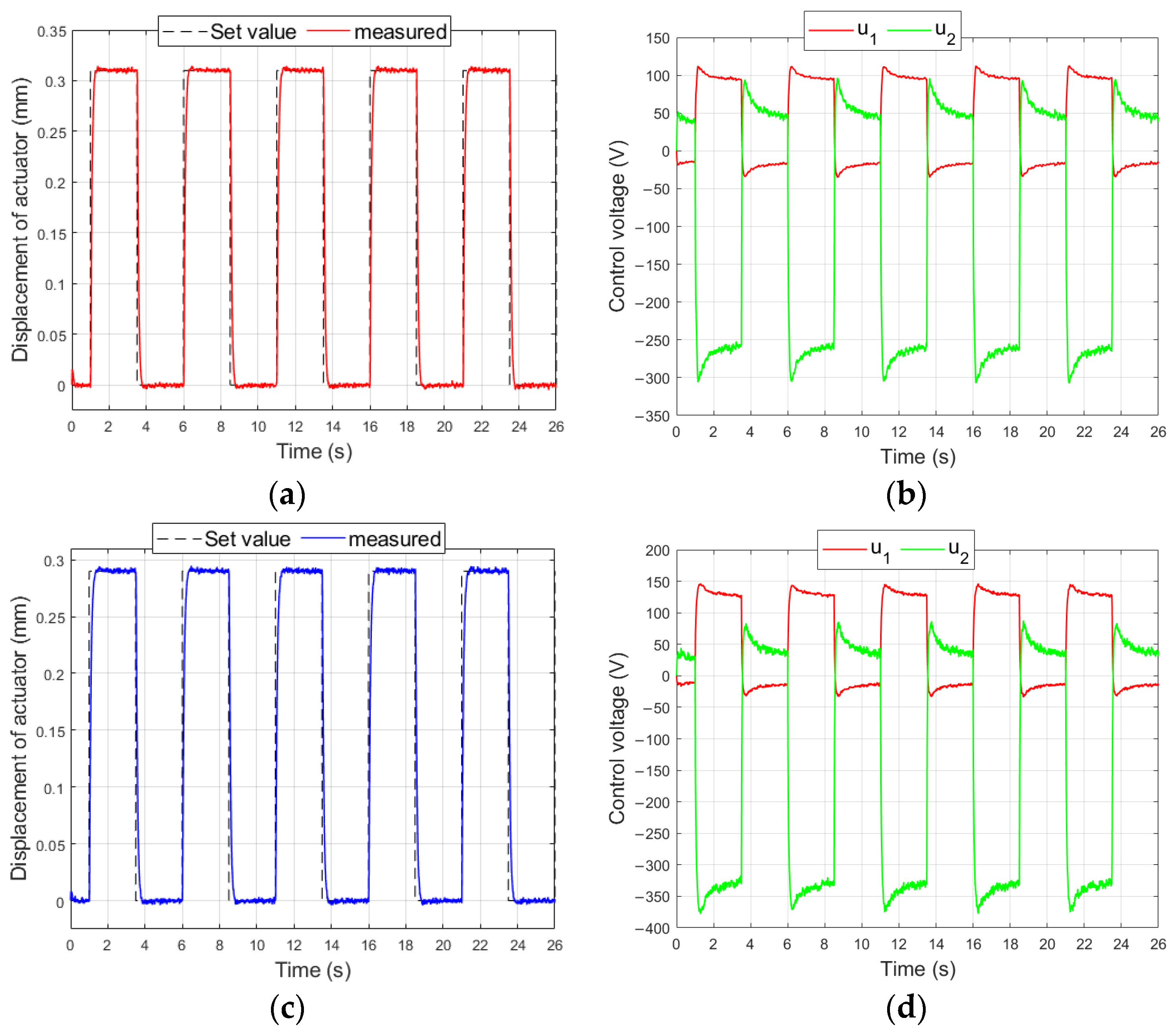
4.1. Description of First Stage of Research
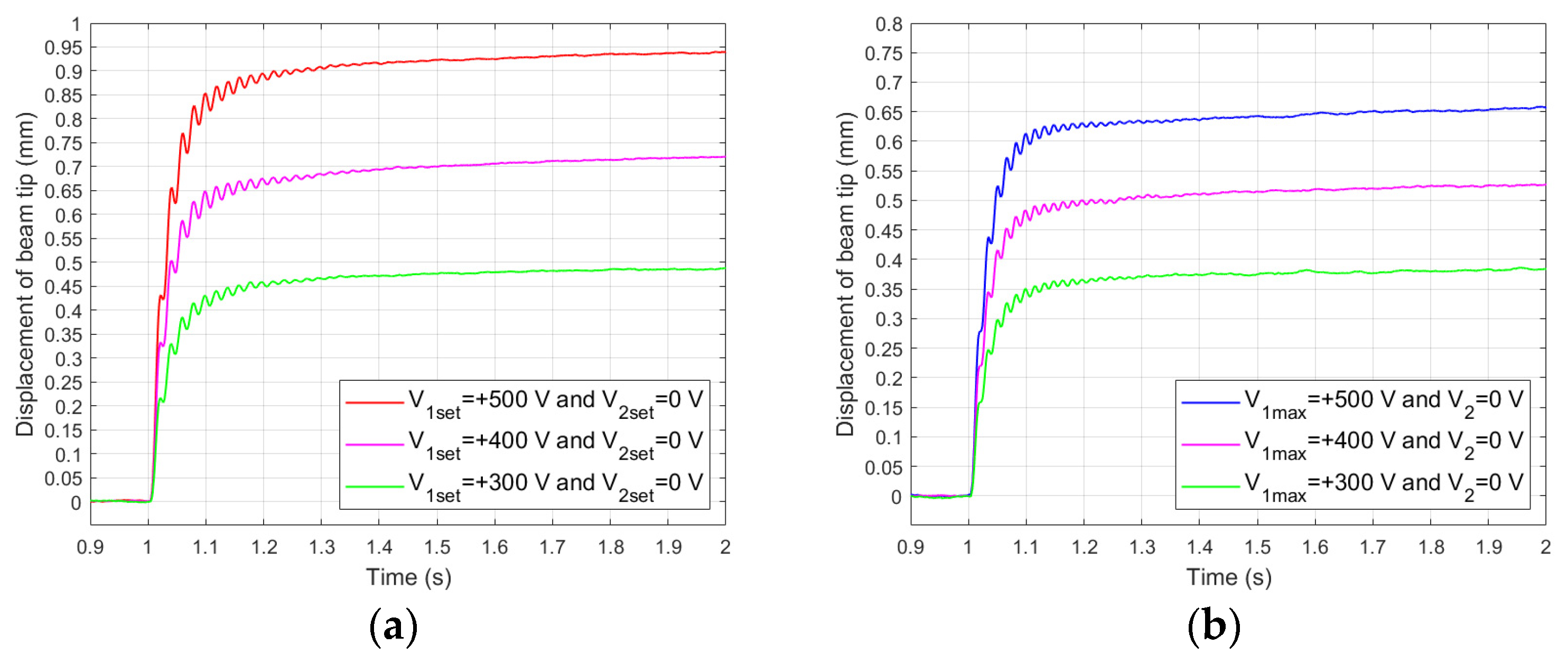
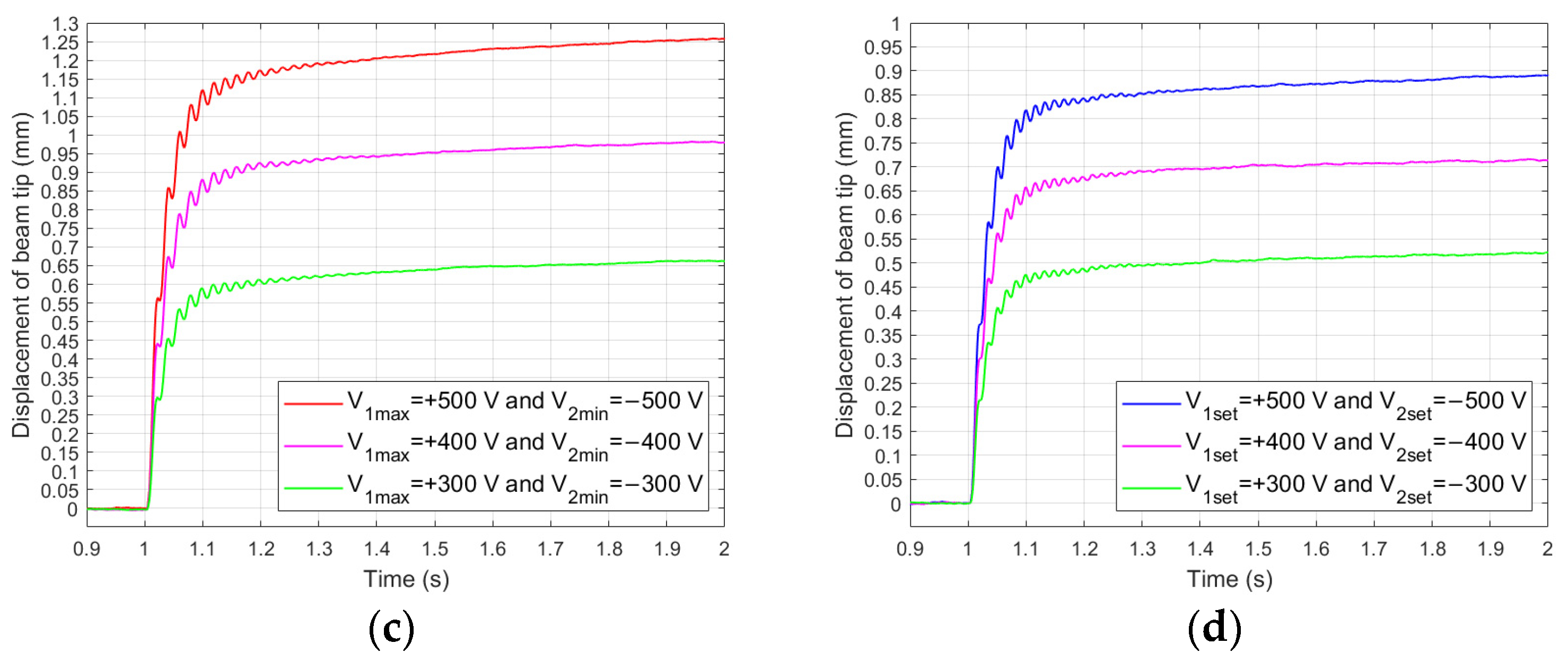
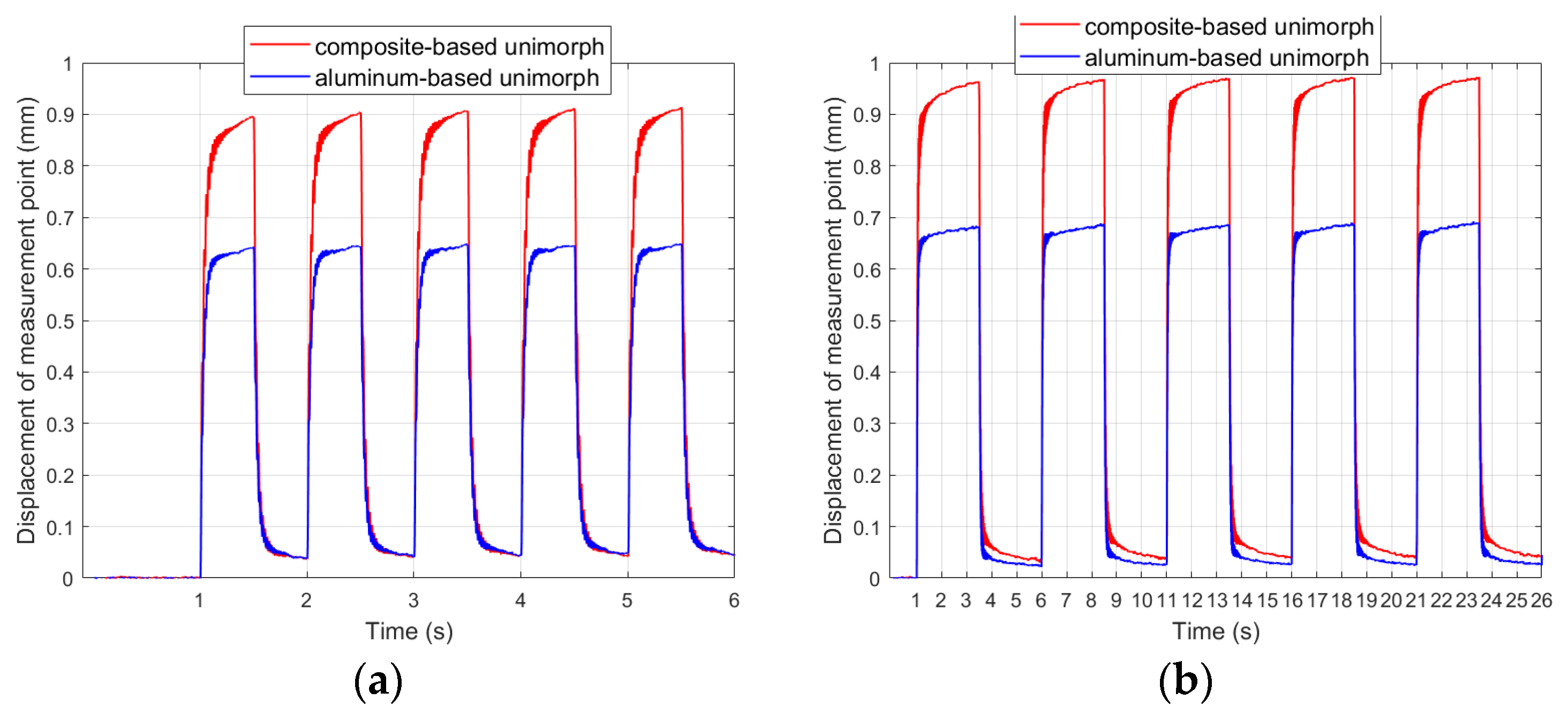
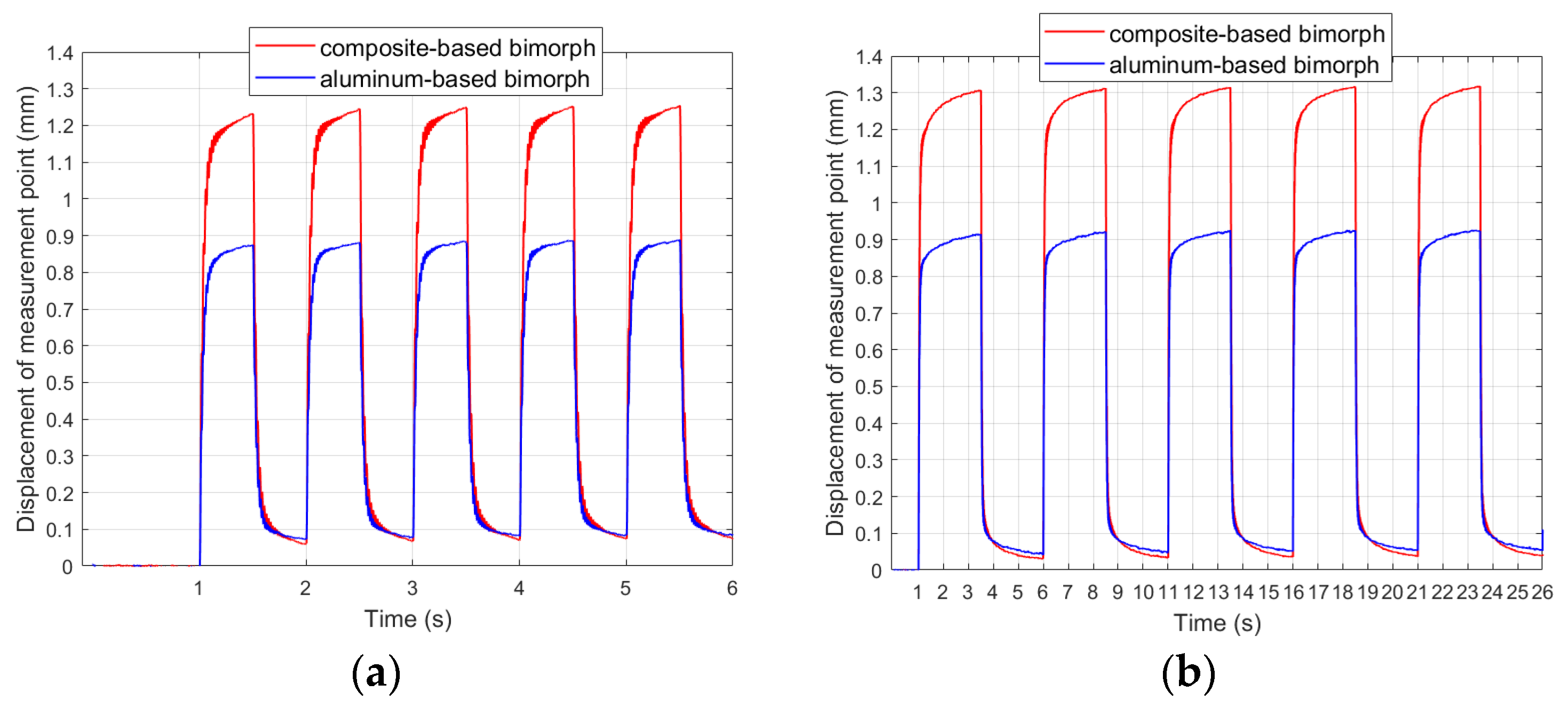
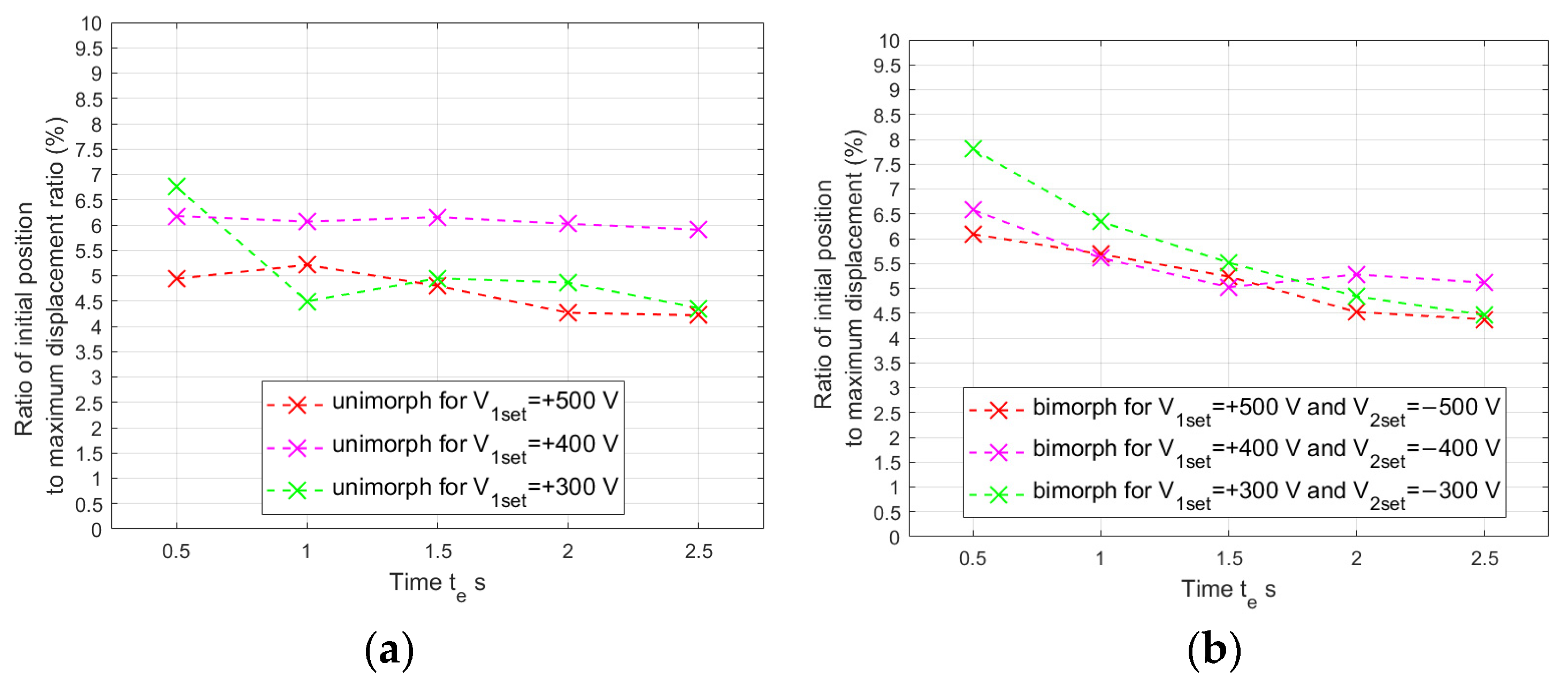
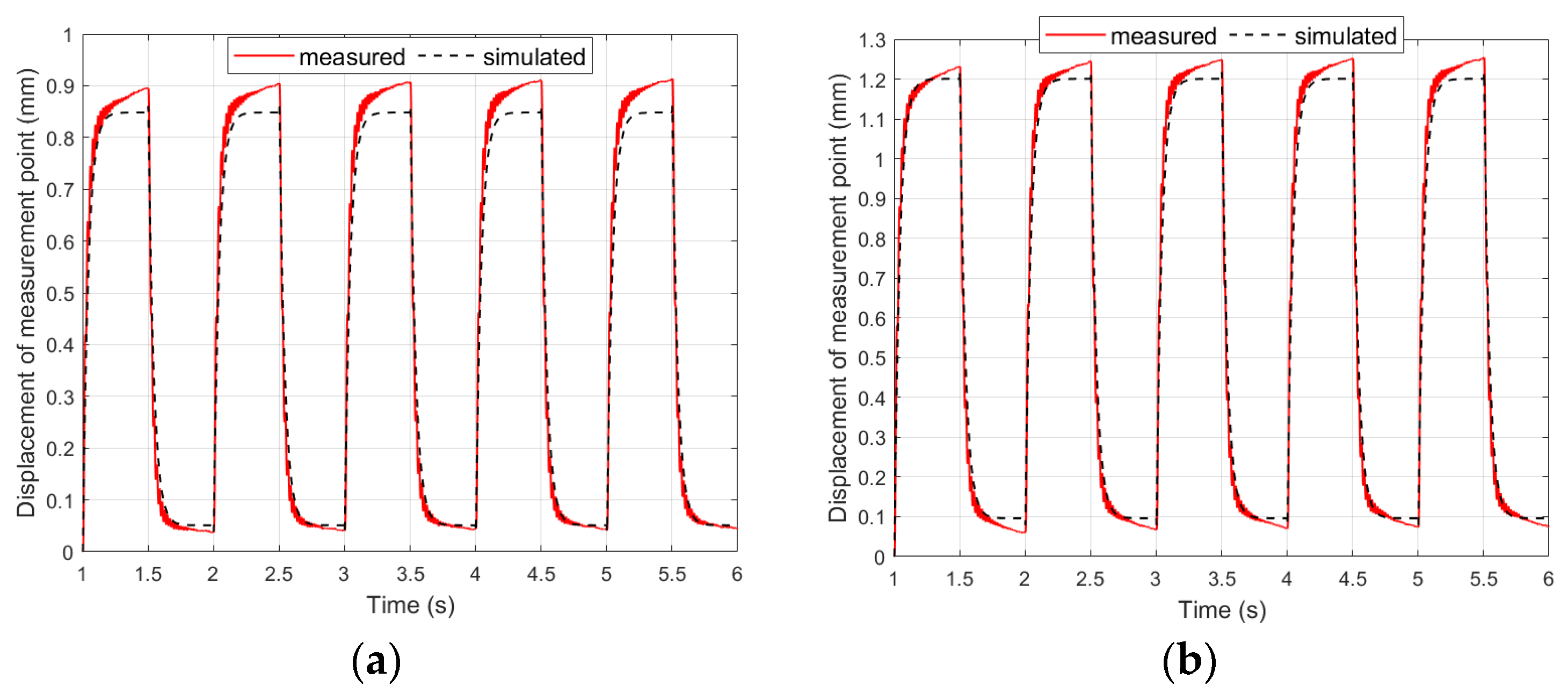
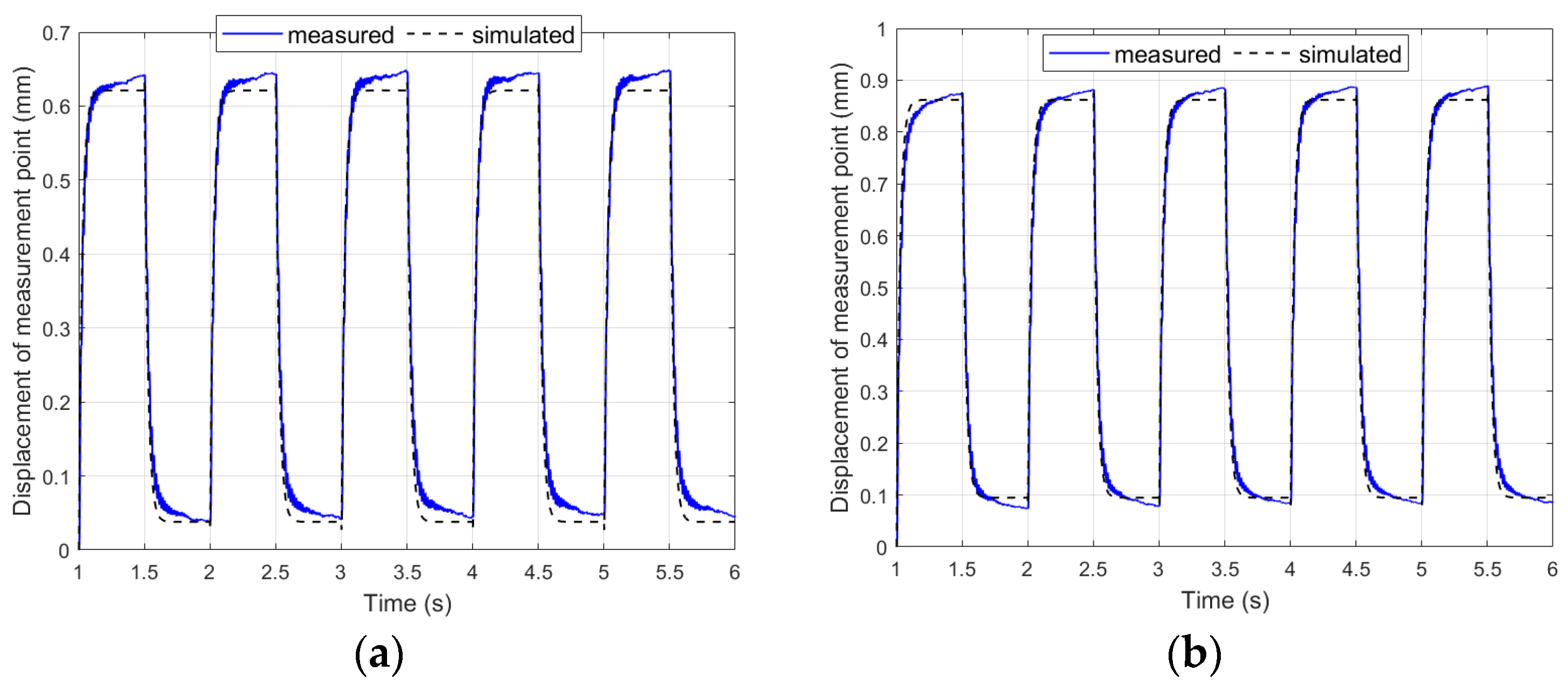
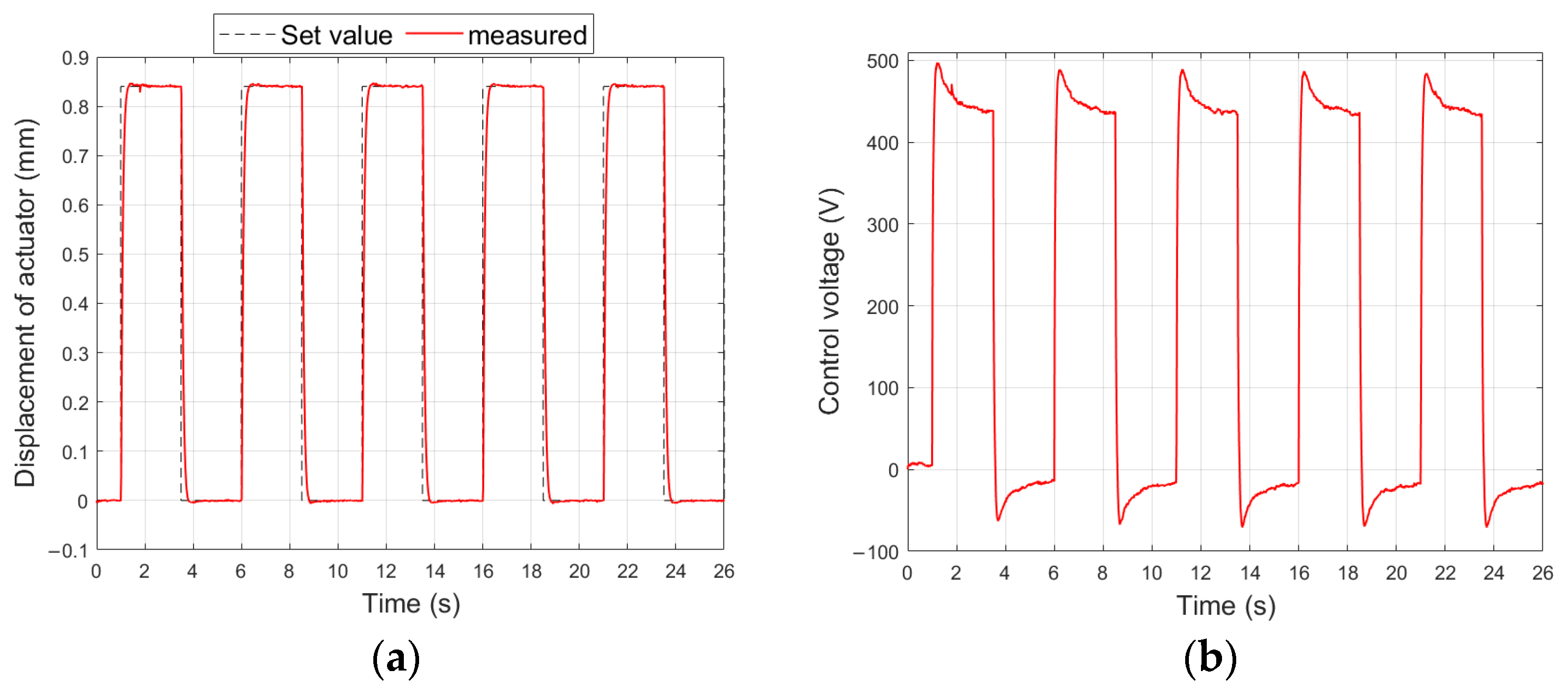
4.2. Results in First Stage of Research
4.3. Description of Second Stage of Research
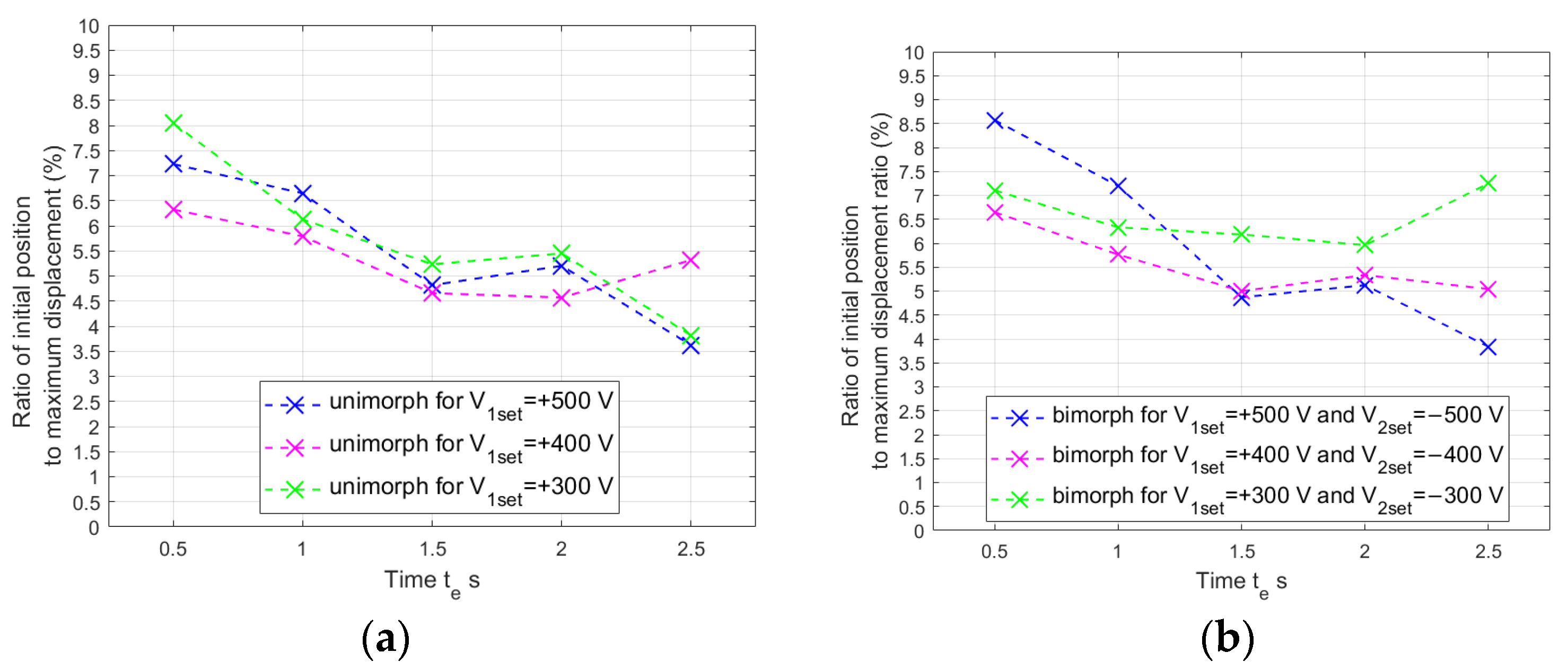
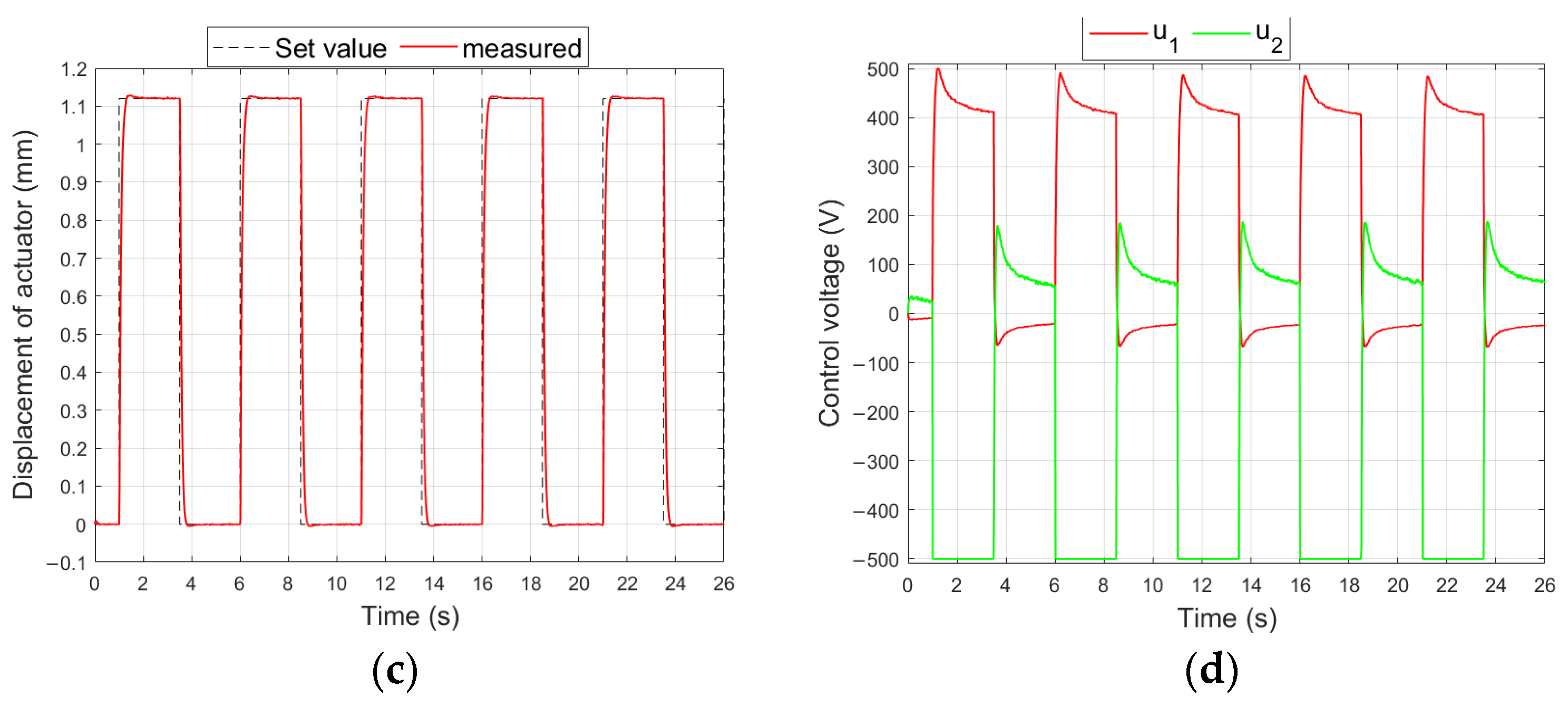
4.4. Results in Second Stage of Research
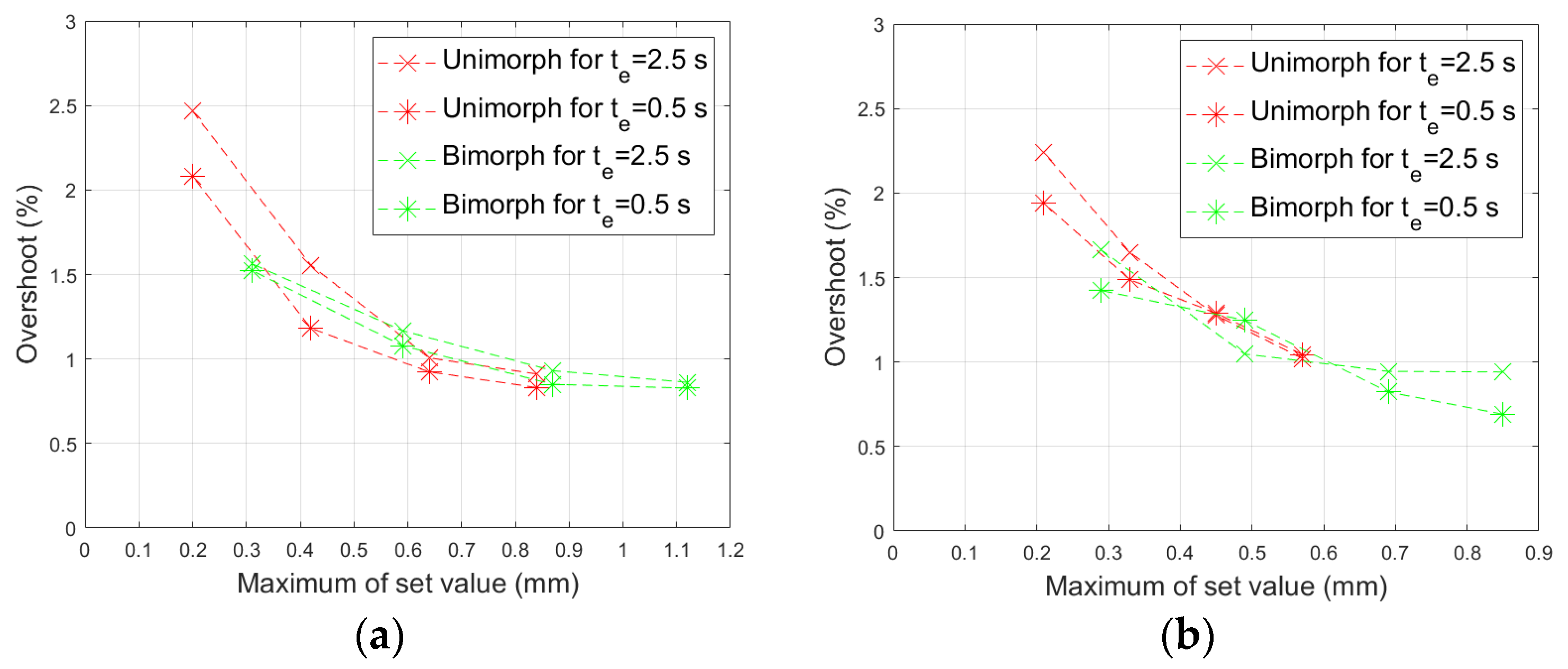
5. Discussion
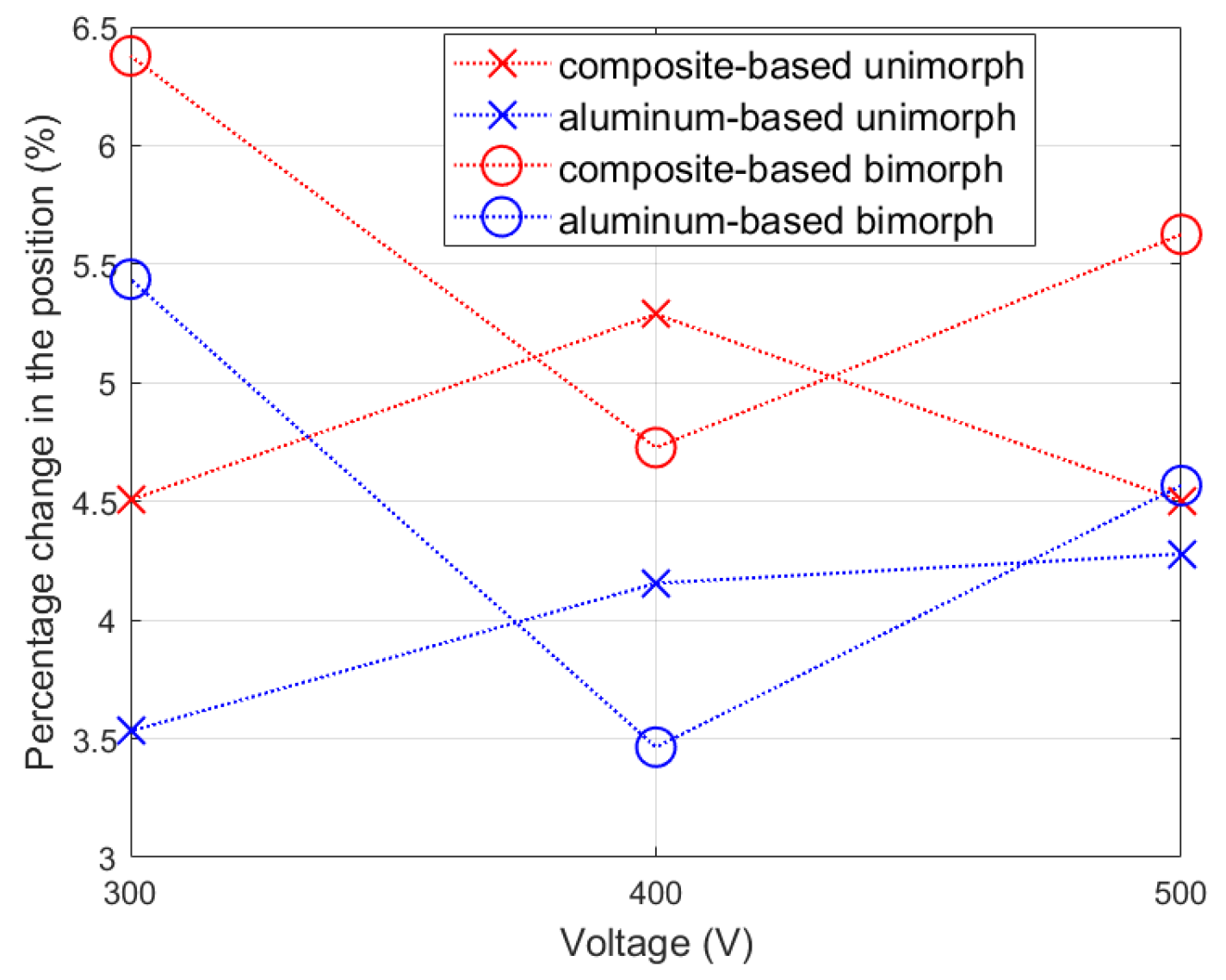
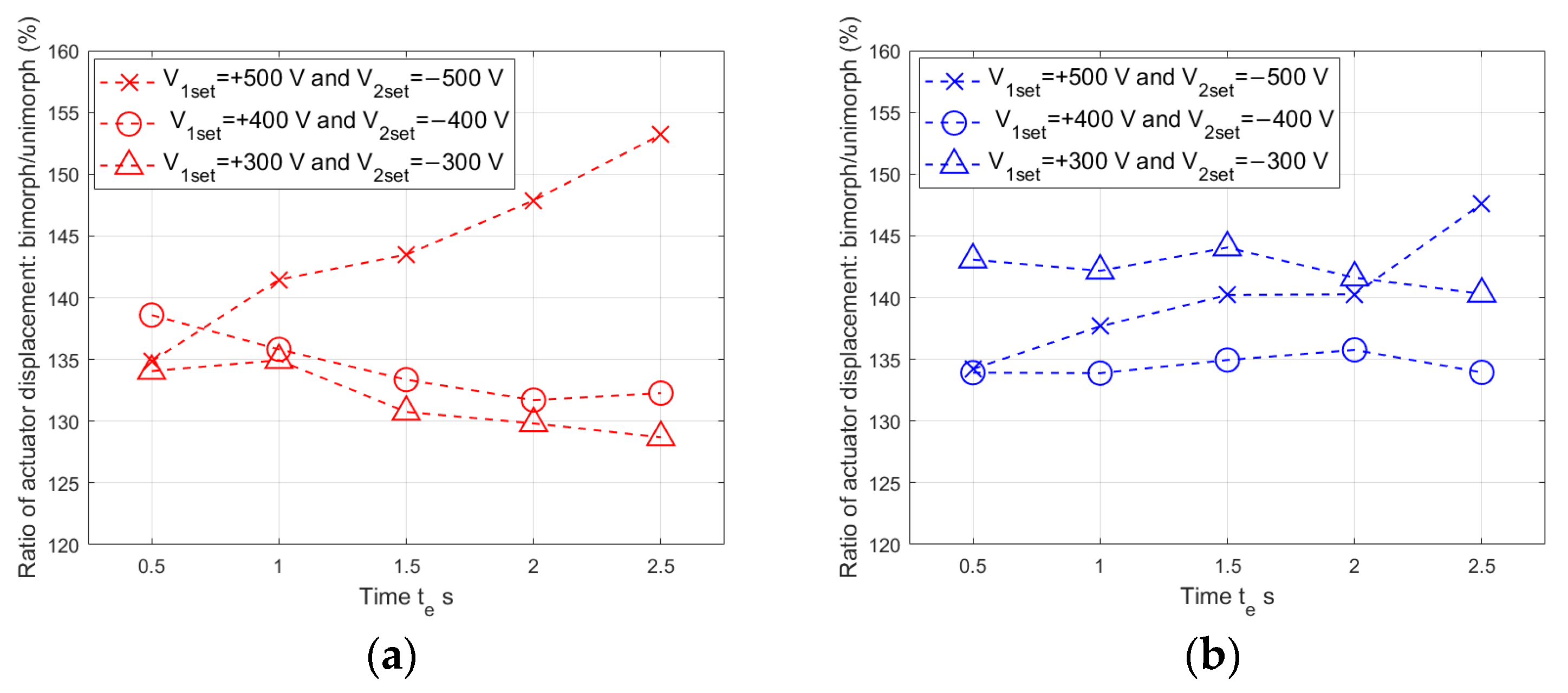
- The control voltage of the compressing MFC should be larger than the control voltage of the stretching MFC. This observation is based on the comparison of the displacements of the unimorph and bimorph for the same carrier layer material.
- The use of Bryson’s rule to determine the weights in the R matrix is not sufficient because it leads to the generation of the maximum possible control voltage, for example ±500 V in the case of the equipment presented in this article. This article proposes a modification to the method of determining the weights by introducing the ratios of the Young’s modulus: see Equation (23). For the same purpose, in the Q matrix, the deviation from 0 of the first state variable should be limited by introducing an appropriately large weight q11. Based on the results of the laboratory experiments, the article proposes a weight value q11 equal to the larger value of Young’s modulus (either the Young’s modulus value of the carrier layer material or of the piezoelectric material);
- The weight in the R matrix that corresponds to the control voltage of the compressing MFC patch should be smaller than the weight corresponding to the control voltage of the stretching MFC patch. This article proposes a modification to the method of determining the weights by introducing the coefficient ε2: see Equation (24).
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mohith, S.; Upadhya, A.R.; Karanth, N.; Kulkarni, S.M.; Rao, M. Recent trends in piezoelectric actuators for precision motion and their applications: A review. Smart Mater. Struct. 2020, 30, 013002. [Google Scholar] [CrossRef]
- Jin, H.; Gao, X.; Ren, K.; Liu, J.; Qiao, L.; Liu, M.; Chen, W.; He, Y.; Dong, S.; Xu, Z.; et al. Review on piezoelectric actuators based on high-performance piezoelectric materials. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 3057–3069. [Google Scholar] [CrossRef]
- Yang, C.; Youcef-Toumi, K. Principle, implementation, and applications of charge control for piezo-actuated nanopositioners: A comprehensive review. Mech. Syst. Signal Process. 2022, 171, 108885. [Google Scholar] [CrossRef]
- Chilibon, I.; Dias, C.; Inacio, P.; Marat-Mendes, J. PZT and PVDF bimorph actuators. J. Optoelectron. Adv. Mater. 2007, 9, 1939–1943. [Google Scholar]
- Ghodsi, M.; Mohammadzaheri, M.; Soltani, P. Analysis of Cantilever Triple-Layer Piezoelectric Harvester (CTLPH): Non-Resonance Applications. Energies 2023, 16, 3129. [Google Scholar] [CrossRef]
- Takagi, K.; Li, J.F.; Yokoyama, S.; Watanabe, R.; Almajid, A.; Taya, M. Design and fabrication of functionally graded PZT/Pt piezoelectric bimorph actuator. Sci. Technol. Adv. Mater. 2002, 3, 217–224. [Google Scholar] [CrossRef]
- Sumit; Kane, S.R.; Sinha, A.K.; Shukla, R. Electric field-induced nonlinear behavior of lead zirconate titanate piezoceramic actuators in bending mode. Mech. Adv. Mater. Struct. 2022, 30, 2111–2120. [Google Scholar] [CrossRef]
- Tan, D.; Yavarow, P.; Erturk, A. Nonlinear elastodynamics of piezoelectric macro-fiber composites with interdigitated electrodes for resonant actuation. Compos. Struct. 2018, 187, 137–143. [Google Scholar] [CrossRef]
- Liu, Y.Z.; Hao, Z.W.; Yu, J.X.; Zhou, X.R.; Lee, P.S.; Sun, Y.; Mu, Z.C.; Zeng, F.L. A high-performance soft actuator based on a poly (vinylidene fluoride) piezoelectric bimorph. Smart Mater. Struct. 2019, 28, 055011. [Google Scholar] [CrossRef]
- Akdogan, E.K.; Allahverdi, M.; Safari, A. Piezoelectric composites for sensor and actuator applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 746–775. [Google Scholar] [CrossRef]
- Dai, Q.; Ng, K. Investigation of electromechanical properties of piezoelectric structural fiber composites with micromechanics analysis and finite element modeling. Mech. Mater. 2012, 53, 29–46. [Google Scholar] [CrossRef]
- Nguyen, C.H.; Kornmann, X. A comparison of dynamic piezoactuation of fiber-based actuators and conventional PZT patches. J. Intell. Mater. Syst. Struct. 2006, 17, 45–55. [Google Scholar] [CrossRef]
- Wang, H.; Xie, X.; Zhang, M.; Wang, B. Analysis of the nonlinear hysteresis of the bimorph beam piezoelectric bending actuator for the deformable mirror systems. J. Astron. Telesc. Instrum. Syst. 2020, 6, 029002. [Google Scholar] [CrossRef]
- Mansour, S.Z.; Seethaler, R.J.; Teo, Y.R.; Yong, Y.K.; Fleming, A.J. Piezoelectric bimorph actuator with integrated strain sensing electrodes. IEEE Sens. J. 2018, 18, 5812–5817. [Google Scholar] [CrossRef]
- Shen, D.; Wen, J.; Ma, J.; Hu, Y.; Wang, R.; Li, J. A novel linear inertial piezoelectric actuator based on asymmetric clamping materials. Sens. Actuators A Phys. 2020, 303, 111746. [Google Scholar] [CrossRef]
- Davis, C.L.; Calkins, F.T.; Butler, G.W. High-frequency jet nozzle actuators for noise reduction. In Smart Structures and Materials 2003: Industrial and Commercial Applications of Smart Structures Technologies; Anderson, E.H., Ed.; Proceedings of SPIE; SPIE: Bellingham, WA, USA, 2003; Volume 5054, pp. 34–44. [Google Scholar]
- Wood, R.J.; Steltz, E.; Fearing, R.S. Optimal energy density piezoelectric bending actuators. Sens. Actuators A Phys. 2005, 119, 476–488. [Google Scholar] [CrossRef]
- Wang, Q.M.; Cross, L.E. Performance analysis of piezoelectric cantilever bending actuators. Ferroelectrics 1998, 215, 187–213. [Google Scholar] [CrossRef]
- Wang, H. Analytical analysis of a beam flexural-mode piezoelectric actuator for deformable mirrors. J. Astron. Telesc. Instrum. Syst. 2015, 1, 049001. [Google Scholar] [CrossRef]
- Mtawa, A.N.; Sun, B.; Gryzagoridis, J. An investigation of the influence of substrate geometry and material properties on the performance of the C-shape piezoelectric actuator. Smart Mater. Struct. 2007, 16, 1036. [Google Scholar] [CrossRef]
- LaCroix, B.W.; Ifju, P.G. Investigating potential substrates to maximize out-of-plane deflection of piezoelectric macro-fiber composite actuators. J. Intell. Mater. Syst. Struct. 2015, 26, 781–795. [Google Scholar] [CrossRef]
- Gan, J.; Zhang, X. A review of nonlinear hysteresis modeling and control of piezoelectric actuators. AIP Adv. 2019, 9, 040702. [Google Scholar] [CrossRef]
- Jung, H.; Gweon, D.G. Creep characteristics of piezoelectric actuators. Rev. Sci. Instrum. 2000, 71, 1896–1900. [Google Scholar] [CrossRef]
- Yang, Y.L.; Wei, Y.D.; Lou, J.Q.; Fu, L.; Tian, G.; Wu, M. Hysteresis modeling and precision trajectory control for a new MFC micromanipulator. Sens. Actuators A Phys. 2016, 247, 37–52. [Google Scholar] [CrossRef]
- Ebrahimi-Tirtashi, A.; Mohajerin, S.; Zakerzadeh, M.R.; Nojoomian, M.A. Vibration control of a piezoelectric cantilever smart beam by 1 adaptive control system. Syst. Sci. Control Eng. 2021, 9, 542–555. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, W.; Zhang, Z.; Jiang, J.; Wu, Z. Theoretical and experimental investigations on modified LQ terminal control scheme of piezo-actuated compliant structures in finite time. J. Sound Vib. 2021, 491, 115762. [Google Scholar] [CrossRef]
- Tsushima, N.; Su, W. Concurrent active piezoelectric control and energy harvesting of highly flexible multifunctional wings. J. Aircr. 2017, 54, 724–736. [Google Scholar] [CrossRef]
- Roundy, S.; Wright, P.K.; Rabaey, J.M. Energy Scavenging for Wireless Sensor Networks; Springer: New York, NY, USA, 2004. [Google Scholar]
- Tian, J.; Guo, Q.; Shi, G. Laminated piezoelectric beam element for dynamic analysis of piezolaminated smart beams and GA-based LQR active vibration control. Compos. Struct. 2020, 252, 112480. [Google Scholar] [CrossRef]
- Smart Material—Home of the MFC. Available online: https://www.smart-material.com/MFC-product-mainV2.html (accessed on 30 July 2022).
- 3M™ Scotch-Weld™ Structural Adhesives. Available online: https://multimedia.3m.com/mws/media/1989908O/04-productselectionguide-epx-en.pdf (accessed on 10 September 2023).
- RT-DAC/Zynq User’s Manual. Available online: http://www.inteco.com.pl/Docs/Rtdac_Zynq.pdf (accessed on 30 July 2023).
- Koo, K.Y.; Park, S.; Lee, J.J.; Yun, C.B. Automated impedance-based structural health monitoring incorporating effective frequency shift for compensating temperature effects. J. Intell. Mater. Syst. Struct. 2009, 20, 367–377. [Google Scholar] [CrossRef]
- Huynh, T.C.; Kim, J.T. Quantification of temperature effect on impedance monitoring via PZT interface for prestressed tendon anchorage. Smart Mater. Struct. 2017, 26, 125004. [Google Scholar] [CrossRef]
- Lining, S.; Changhai, R.; Weibin, R.; Liguo, C.; Minxiu, K. Tracking control of piezoelectric actuator based on a new mathematical model. J. Micromech. Microeng. 2004, 14, 1439. [Google Scholar] [CrossRef]
- Hosea, M.E.; Shampine, L.F. Analysis and implementation of TR-BDF2. Appl. Numer. Math. 1996, 20, 21–37. [Google Scholar] [CrossRef]
- Ismail, M.R.; Omar, F.K.; Ajaj, R.; Ghodsi, M. On the accuracy of lumped parameter model for tapered cantilever piezoelectric energy harvesters with tip mass. In Proceedings of the 2020 Advances in Science and Engineering Technology International Conferences (ASET), Dubai, United Arab Emirates, 4 February–9 April 2020; pp. 1–6. [Google Scholar]
- Wang, B.; Luo, X.; Liu, Y.; Yang, Z. Thickness-variable composite beams for vibration energy harvesting. Compos. Struct. 2020, 244, 112232. [Google Scholar] [CrossRef]
- Grzybek, D. Control System for Multi-Input and Simple-Output Piezoelectric Beam Actuator Based on Macro Fiber Composite. Energies 2022, 15, 2042. [Google Scholar] [CrossRef]
- Deraemaeker, A.; Nasser, H.; Benjeddou, A.; Preumont, A. Mixing rules for the piezoelectric properties of macro fiber composites. J. Intell. Mater. Syst. Struct. 2009, 20, 1475–1482. [Google Scholar] [CrossRef]
- Ghodsi, M.; Mohammadzaheri, M.; Soltani, P.; Ziaifar, H. A new active anti-vibration system using a magnetostrictive bimetal actuator. J. Magn. Magn. Mater. 2022, 557, 169463. [Google Scholar] [CrossRef]
- Li, C.; Shen, L.; Shao, J.; Fang, J. Simulation and experiment of active vibration control based on flexible piezoelectric MFC composed of PZT and PI layer. Polymers 2023, 15, 1819. [Google Scholar] [CrossRef]
- Xu, P.; Lan, X.; Zeng, C.; Zhang, X.; Liu, Y.; Leng, J. Dynamic characteristics and active vibration control effect for shape memory polymer composites. Compos. Struct. 2023, 322, 117327. [Google Scholar] [CrossRef]




| MFC Patch | Carrier Layer | ||||
|---|---|---|---|---|---|
| Dimension | Symbol | Value | Dimension | Symbol | Value |
| Total length | lmfc | 100 | Length | lc | 120 |
| Total width | wmfc | 20 | Width | wc | 20 |
| Total thickness | tmfc | 0.3 | Thickness | tc | 1 |
| Active part length | lmfca | 85 | |||
| Active part width | wmfca | 14 | |||
| Active part thickness | tmfca | 0.18 | |||
| Passive part length | lmfcp | 15 | |||
| Passive part thickness | tmfcp | 0.12 | |||
| Distance between electrodes | tmfce | 0.5 | |||
| Parameter | Composite-Based Actuator | Aluminum-Based Actuator | |
|---|---|---|---|
| Young’s modulus of carrier layer | Yc | 18.6 × 109 Pa [38] | 71 × 109 Pa [26] |
| Density of carrier layer | ρc | 1850 kg/m3 [38] | 2710 kg/m3 [26] |
| Young’s modulus of MFC patch | Ymfc | 30.336 × 109 Pa [30] | |
| Young’s modulus of MFC of piezoceramic fibers in MFC patch | Ymfca | 48.3 × 109 Pa [40] | |
| Density of active part of MFC patch | ρmfca | 5400 kg/m3 [26] | |
| Piezoelectric constant of MFC patch | d33 | 400 × 10−12 C/N [30] | |
| Piezoelectric constant of piezoceramic fibers in MFC patch | d33a | 440 × 10−12 C/N [40] | |
| Experiment No. | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Set voltage V1set (V) | +500 | +400 | +300 | +500 | +400 | +300 |
| Set voltage V2set (V) | 0 | 0 | 0 | −500 | −400 | −300 |
| Experiment No. | V1set (V) | V2set (V) | te (s) | |||||
|---|---|---|---|---|---|---|---|---|
| Unimorph | 7 to 11 | +500 | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 |
| 12 to 16 | +400 | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | |
| 17 to 21 | +300 | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | |
| Bimorph | 22 to 26 | +500 | −500 | 0.5 | 1 | 1.5 | 2 | 2.5 |
| 27 to 31 | +400 | −400 | 0.5 | 1 | 1.5 | 2 | 2.5 | |
| 32 to 36 | +300 | −300 | 0.5 | 1 | 1.5 | 2 | 2.5 | |
| Experiment No. | Composite-Based Actuator | Experiment No. | Aluminum-Based Actuator | |||||
|---|---|---|---|---|---|---|---|---|
| yset (mm) | te (s) | yset (mm) | te (s) | |||||
| Unimorph | 37 to 38 | 0.84 | 2.5 | 0.5 | 39 to 40 | 0.57 | 2.5 | 0.5 |
| 41 to 42 | 0.64 | 2.5 | 0.5 | 43 to 44 | 0.45 | 2.5 | 0.5 | |
| 45 to 46 | 0.42 | 2.5 | 0.5 | 47 to 48 | 0.33 | 2.5 | 0.5 | |
| 49 to 50 | 0.20 | 2.5 | 0.5 | 51 to 52 | 0.21 | 2.5 | 0.5 | |
| Bimorph | 53 to 54 | 1.12 | 2.5 | 0.5 | 55 to 56 | 0.85 | 2.5 | 0.5 |
| 57 to 58 | 0.87 | 2.5 | 0.5 | 59 to 60 | 0.69 | 2.5 | 0.5 | |
| 61 to 62 | 0.59 | 2.5 | 0.5 | 63 to 64 | 0.49 | 2.5 | 0.5 | |
| 65 to 66 | 0.31 | 2.5 | 0.5 | 67 to 68 | 0.29 | 2.5 | 0.5 | |
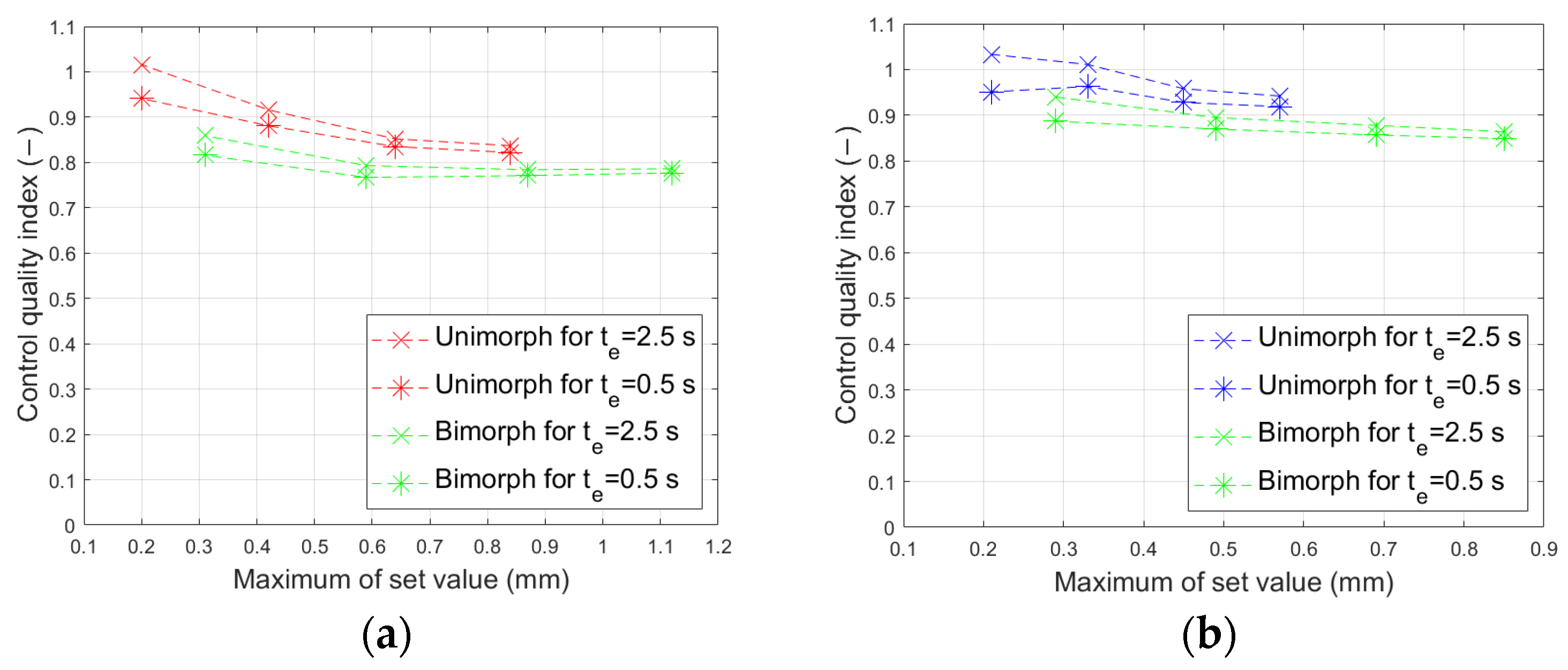
| Experiment No. | Composite-Based | Experiment No. | Aluminum-Based | |||
|---|---|---|---|---|---|---|
| Iq (−) | Iq (−) | |||||
| Unimorph | 37 to 38 | 0.837 | 0.822 | 39 to 40 | 0.942 | 0.919 |
| 41 to 42 | 0.852 | 0.835 | 43 to 44 | 0.958 | 0.928 | |
| 45 to 46 | 0.916 | 0.881 | 47 to 48 | 1.011 | 0.963 | |
| 49 to 50 | 1.016 | 0.941 | 51 to 52 | 1.033 | 0.951 | |
| Bimorph | 53 to 54 | 0.786 | 0.777 | 55 to 56 | 0.864 | 0.849 |
| 57 to 58 | 0.784 | 0.771 | 59 to 60 | 0.878 | 0.857 | |
| 61 to 62 | 0.793 | 0.767 | 63 to 64 | 0.895 | 0.870 | |
| 65 to 66 | 0.859 | 0.816 | 67 to 68 | 0.940 | 0.887 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grzybek, D. Experimental Analysis of the Influence of Carrier Layer Material on the Performance of the Control System of a Cantilever-Type Piezoelectric Actuator. Materials 2024, 17, 96. https://doi.org/10.3390/ma17010096
Grzybek D. Experimental Analysis of the Influence of Carrier Layer Material on the Performance of the Control System of a Cantilever-Type Piezoelectric Actuator. Materials. 2024; 17(1):96. https://doi.org/10.3390/ma17010096
Chicago/Turabian StyleGrzybek, Dariusz. 2024. "Experimental Analysis of the Influence of Carrier Layer Material on the Performance of the Control System of a Cantilever-Type Piezoelectric Actuator" Materials 17, no. 1: 96. https://doi.org/10.3390/ma17010096
APA StyleGrzybek, D. (2024). Experimental Analysis of the Influence of Carrier Layer Material on the Performance of the Control System of a Cantilever-Type Piezoelectric Actuator. Materials, 17(1), 96. https://doi.org/10.3390/ma17010096







