Strength and Deformation Behavior of Graphene Aerogel of Different Morphologies
Abstract
:1. Introduction
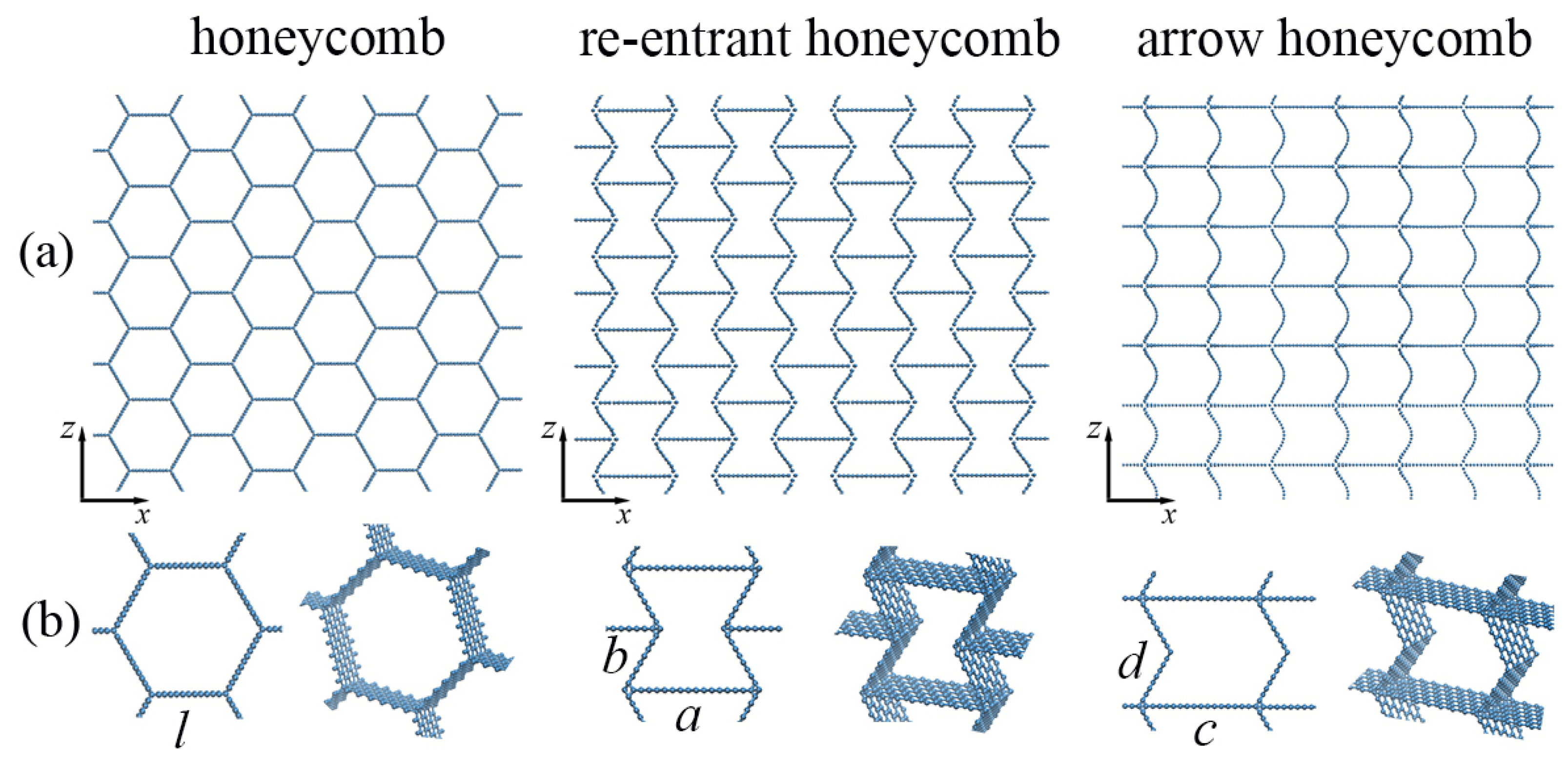
2. Simulation Details
3. Results and Discussion
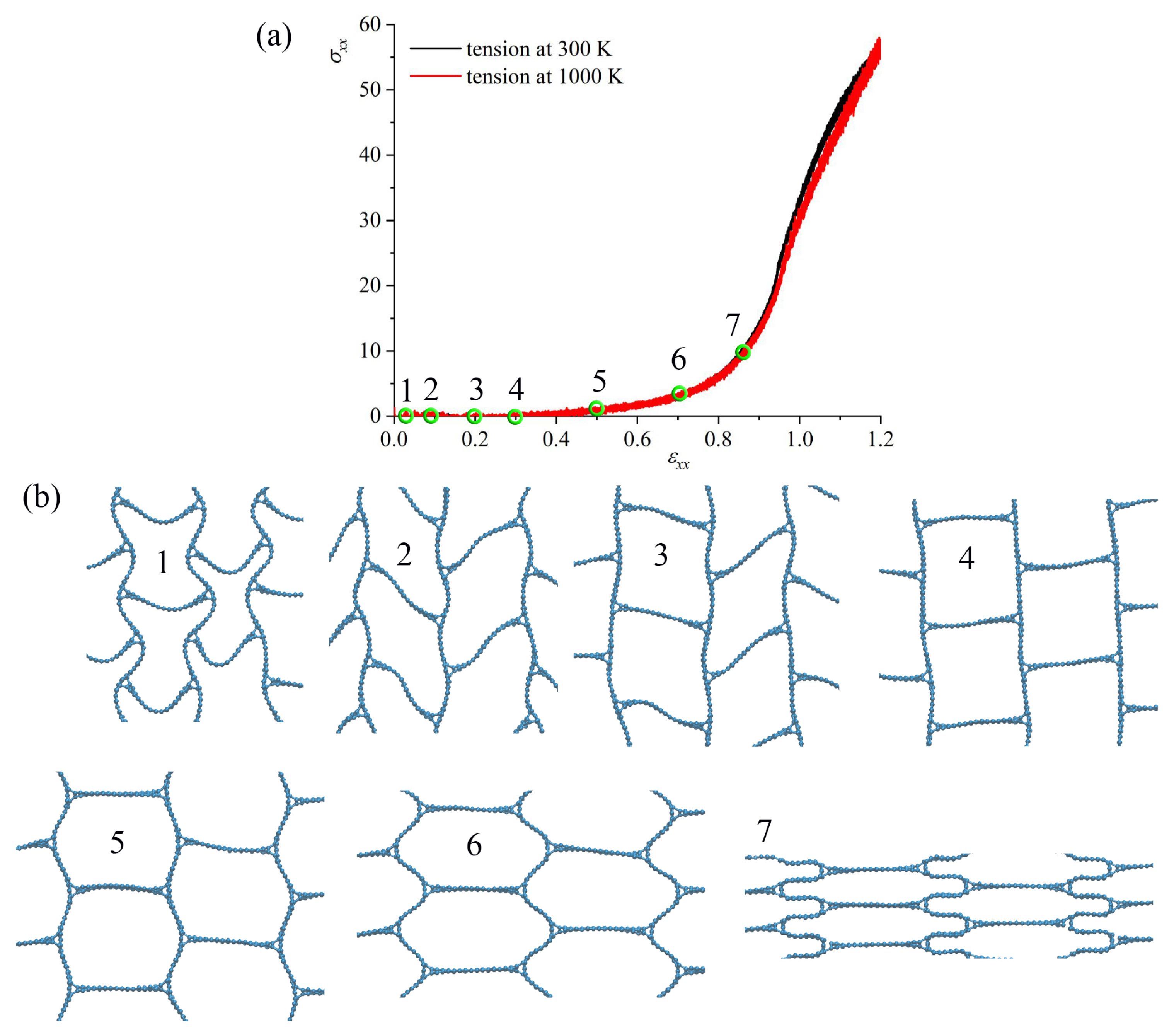
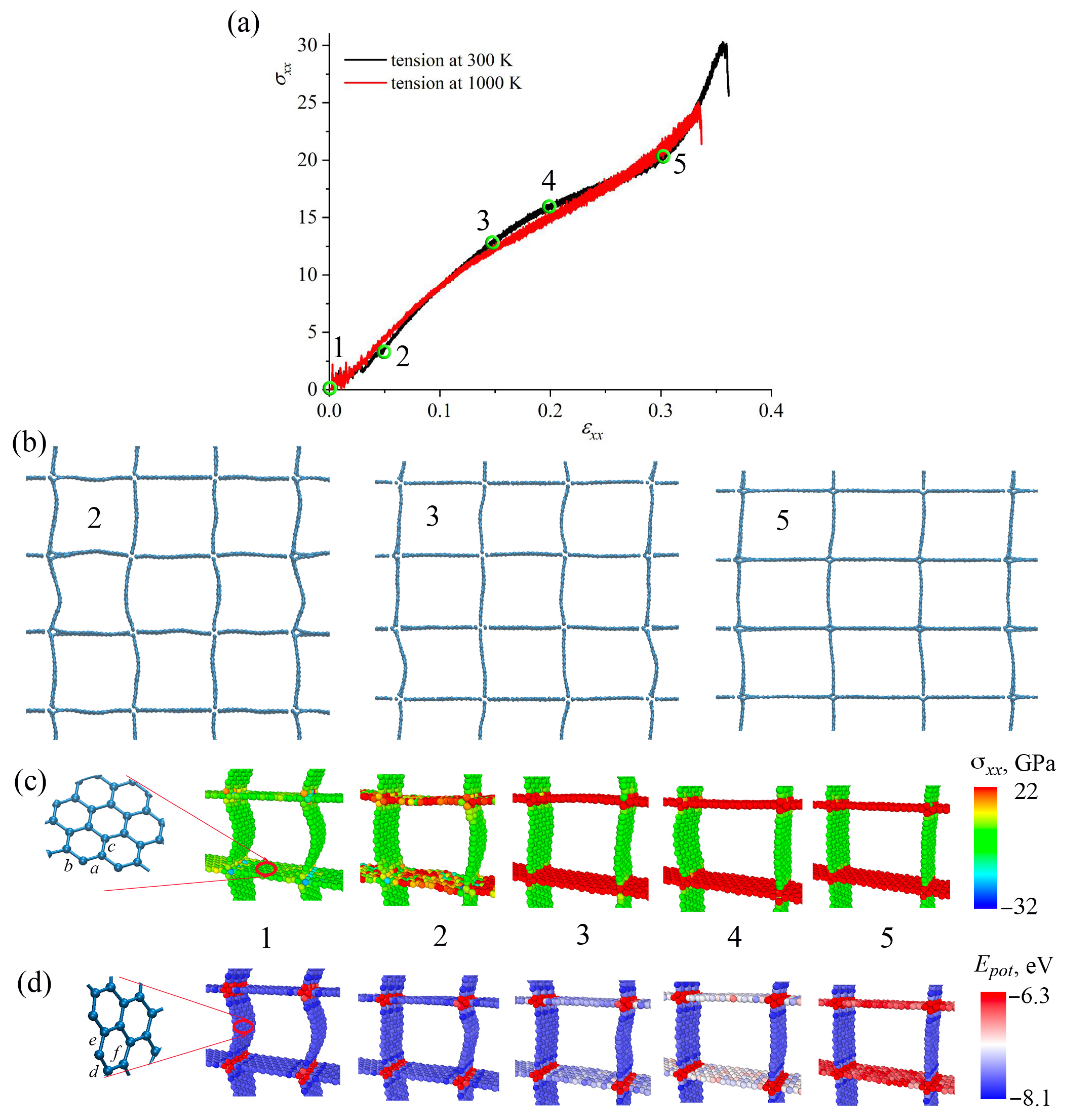
3.1. Effect of Temperature
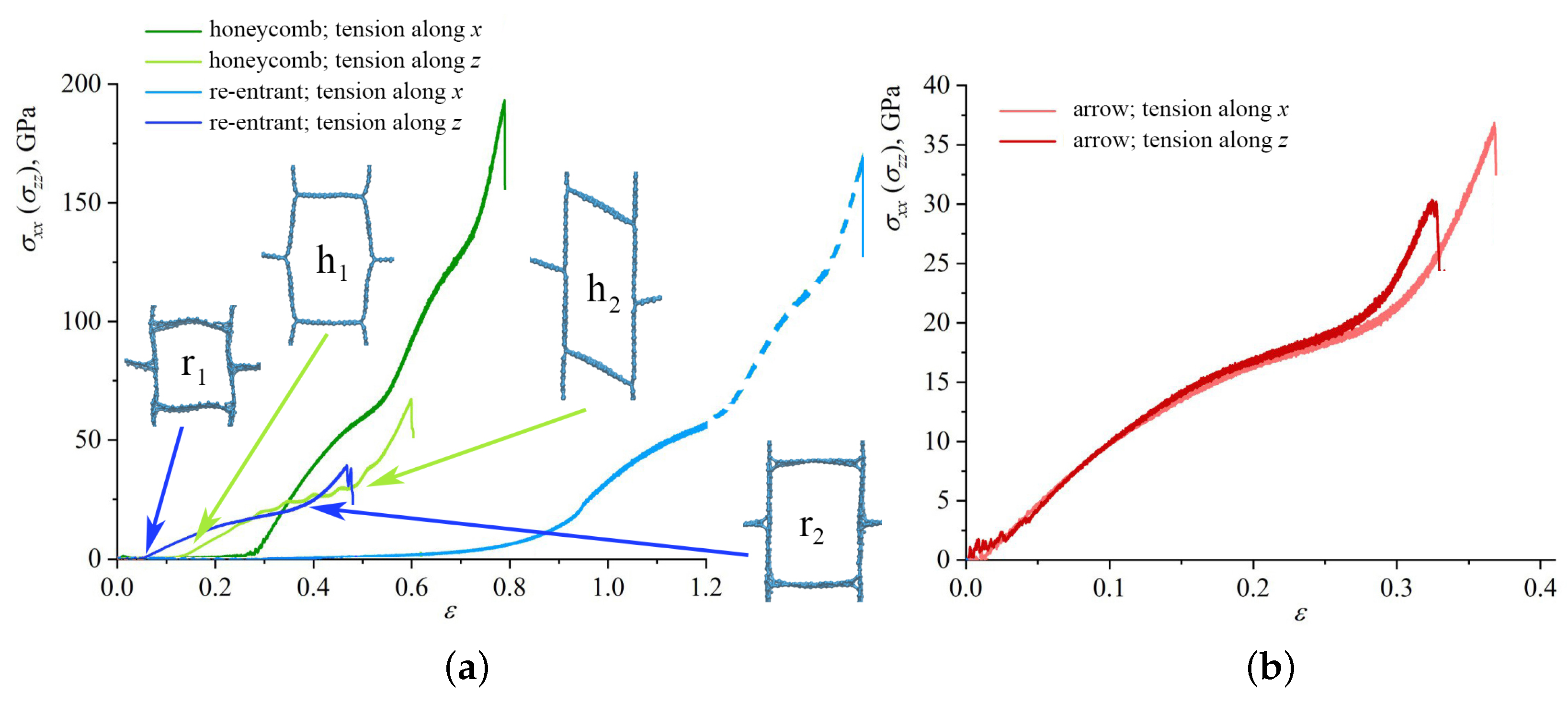
3.2. Effect of Loading Direction
3.3. Elasticity
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GA | graphene aerogel |
| MD | molecular dynamics |
| CNT | carbon nanotubes |
References
- Yu, C.; Song, Y.S. Analysis of Thermoelectric Energy Harvesting with Graphene Aerogel-Supported Form-Stable Phase Change Materials. Nanomaterials 2021, 11, 2192. [Google Scholar] [CrossRef] [PubMed]
- Tafreshi, O.; Mosanenzadeh, S.; Karamikamkar, S.; Saadatnia, Z.; Park, C.; Naguib, H. A review on multifunctional aerogel fibers: Processing, fabrication, functionalization, and applications. Mater. Today Chem. 2022, 23, 100736. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, J.; Zhang, T.; Ma, L.; Lim, C.W.; Ding, F.; Zeng, X.C. Mechanically Robust Tri-Wing Graphene Nanoribbons with Tunable Electronic and Magnetic Properties. Nano Lett. 2010, 10, 494–498. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Kutana, A.; Yang, Y.; Krainyukova, N.V.; Penev, E.S.; Yakobson, B.I. Nanomechanics of carbon honeycomb cellular structures. Carbon 2017, 113, 26–32. [Google Scholar] [CrossRef]
- Kawai, T.; Okada, S.; Miyamoto, Y.; Oshiyama, A. Carbon three-dimensional architecture formed by intersectional collision of graphene patches. Phys. Rev. B 2005, 72, 035428. [Google Scholar] [CrossRef]
- Pang, Z.; Gu, X.; Wei, Y.; Yang, R.; Dresselhaus, M.S. Bottom-up Design of Three-Dimensional Carbon-Honeycomb with Superb Specific Strength and High Thermal Conductivity. Nano Lett. 2016, 17, 179–185. [Google Scholar] [CrossRef] [PubMed]
- Yu, C.; Youn, J.R.; Song, Y.S. Reversible thermo-electric energy harvesting with phase change material (PCM) composites. J. Polym. Res. 2021, 28, 279. [Google Scholar] [CrossRef]
- Wang, H.; Lu, W.; Di, J.; Li, D.; Zhang, X.; Li, M.; Zhang, Z.; Zheng, L.; Li, Q. Ultra-Lightweight and Highly Adaptive All-Carbon Elastic Conductors with Stable Electrical Resistance. Adv. Funct. Mater. 2017, 27, 1606220. [Google Scholar] [CrossRef]
- Thakur, A. Graphene aerogel based energy storage materials—A review. Mater. Today Proc. 2022, 65, 3369–3376. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar] [CrossRef]
- Schaedler, T.A.; Jacobsen, A.J.; Torrents, A.; Sorensen, A.E.; Lian, J.; Greer, J.R.; Valdevit, L.; Carter, W.B. Ultralight Metallic Microlattices. Science 2011, 334, 962–965. [Google Scholar] [CrossRef]
- Yang, J.; Li, X.; Han, S.; Zhang, Y.; Min, P.; Koratkar, N.; Yu, Z.Z. Air-dried, high-density graphene hybrid aerogels for phase change composites with exceptional thermal conductivity and shape stability. J. Mater. Chem. A 2016, 4, 18067–18074. [Google Scholar] [CrossRef]
- Jing, J.; Qian, X.; Si, Y.; Liu, G.; Shi, C. Recent Advances in the Synthesis and Application of Three-Dimensional Graphene-Based Aerogels. Molecules 2022, 27, 924. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Zhao, Z.; Wan, W.; Gogotsi, Y.; Qiu, J. Ultralight and Highly Compressible Graphene Aerogels. Adv. Mater. 2013, 25, 2219–2223. [Google Scholar] [CrossRef] [PubMed]
- Nardecchia, S.; Carriazo, D.; Ferrer, M.L.; Gutiérrez, M.C.; del Monte, F. Three dimensional macroporous architectures and aerogels built of carbon nanotubes and/or graphene: Synthesis and applications. Chem. Soc. Rev. 2013, 42, 794–830. [Google Scholar] [CrossRef]
- Kashani, H.; Ito, Y.; Han, J.; Liu, P.; Chen, M. Extraordinary tensile strength and ductility of scalable nanoporous graphene. Sci. Adv. 2019, 5, eaat6951. [Google Scholar] [CrossRef]
- Afroze, J.D.; Tong, L.; Abden, M.J.; Yuan, Z.; Chen, Y. Hierarchical honeycomb graphene aerogels reinforced by carbon nanotubes with multifunctional mechanical and electrical properties. Carbon 2021, 175, 312–321. [Google Scholar] [CrossRef]
- Peng, X.; Wu, K.; Hu, Y.; Zhuo, H.; Chen, Z.; Jing, S.; Liu, Q.; Liu, C.; Zhong, L. A mechanically strong and sensitive CNT/rGO–CNF carbon aerogel for piezoresistive sensors. J. Mater. Chem. A 2018, 6, 23550–23559. [Google Scholar] [CrossRef]
- Wasalathilake, K.C.; Galpaya, D.G.; Ayoko, G.A.; Yan, C. Understanding the structure-property relationships in hydrothermally reduced graphene oxide hydrogels. Carbon 2018, 137, 282–290. [Google Scholar] [CrossRef]
- Shang, J.J.; Yang, Q.S.; Liu, X. New Coarse-Grained Model and Its Implementation in Simulations of Graphene Assemblies. J. Chem. Theory Comput. 2017, 13, 3706–3714. [Google Scholar] [CrossRef]
- Si, Y.; Wang, X.; Dou, L.; Yu, J.; Ding, B. Ultralight and fire-resistant ceramic nanofibrous aerogels with temperature-invariant superelasticity. Sci. Adv. 2018, 4, eaas8925. [Google Scholar] [CrossRef]
- Fan, Z.; Gong, F.; Nguyen, S.T.; Duong, H.M. Advanced multifunctional graphene aerogel–Poly (methyl methacrylate) composites: Experiments and modeling. Carbon 2015, 81, 396–404. [Google Scholar] [CrossRef]
- Zheng, B.; Liu, C.; Li, Z.; Carraro, C.; Maboudian, R.; Senesky, D.G.; Gu, G.X. Investigation of mechanical properties and structural integrity of graphene aerogels via molecular dynamics simulations. Phys. Chem. Chem. Phys. 2023, 25, 21897–21907. [Google Scholar] [CrossRef] [PubMed]
- Lei, J.; Liu, Z. The structural and mechanical properties of graphene aerogels based on Schwarz-surface-like graphene models. Carbon 2018, 130, 741–748. [Google Scholar] [CrossRef]
- Qin, Z.; Jung, G.S.; Kang, M.J.; Buehler, M.J. The mechanics and design of a lightweight three-dimensional graphene assembly. Sci. Adv. 2017, 3, e1601536. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Zhang, Y.; Li, P.; Gao, C. Strong, Conductive, Lightweight, Neat Graphene Aerogel Fibers with Aligned Pores. ACS Nano 2012, 6, 7103–7113. [Google Scholar] [CrossRef] [PubMed]
- Ha, H.; Shanmuganathan, K.; Ellison, C.J. Mechanically Stable Thermally Crosslinked Poly(acrylic acid)/Reduced Graphene Oxide Aerogels. ACS Appl. Mater. Interfaces 2015, 7, 6220–6229. [Google Scholar] [CrossRef]
- Hong, J.Y.; Yun, S.; Wie, J.J.; Zhang, X.; Dresselhaus, M.S.; Kong, J.; Park, H.S. Cartilage-inspired superelastic ultradurable graphene aerogels prepared by the selective gluing of intersheet joints. Nanoscale 2016, 8, 12900–12909. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, Y.; Xiong, Y.; Zhang, L.; Xu, W.; Duan, G.; Mei, C.; Jiang, S.; Rui, Z.; Zhang, K. Porous aerogel and sponge composites: Assisted by novel nanomaterials for electromagnetic interference shielding. Nano Today 2021, 38, 101204. [Google Scholar] [CrossRef]
- Ren, W.; Cheng, H.M. When two is better than one. Nature 2013, 497, 448–449. [Google Scholar] [CrossRef]
- Guo, F.; Jiang, Y.; Xu, Z.; Xiao, Y.; Fang, B.; Liu, Y.; Gao, W.; Zhao, P.; Wang, H.; Gao, C. Highly stretchable carbon aerogels. Nat. Commun. 2018, 9, 881. [Google Scholar] [CrossRef]
- Wang, H.; Cao, Q.; Peng, Q.; Liu, S. Atomistic Study of Mechanical Behaviors of Carbon Honeycombs. Nanomaterials 2019, 9, 109. [Google Scholar] [CrossRef] [PubMed]
- Tong, H.; Chen, H.; Zhao, Y.; Liu, M.; Cheng, Y.; Lu, J.; Tao, Y.; Du, J.; Wang, H. Robust PDMS-based porous sponge with enhanced recyclability for selective separation of oil-water mixture. Colloids Surf. A Physicochem. Eng. Asp. 2022, 648, 129228. [Google Scholar] [CrossRef]
- Yu, X.; Liang, X.; Zhao, T.; Zhu, P.; Sun, R.; Wong, C.P. Thermally welded honeycomb-like silver nanowires aerogel backfilled with polydimethylsiloxane for electromagnetic interference shielding. Mater. Lett. 2021, 285, 129065. [Google Scholar] [CrossRef]
- Sun, H.; Xu, Z.; Gao, C. Multifunctional, Ultra-Flyweight, Synergistically Assembled Carbon Aerogels. Adv. Mater. 2013, 25, 2554–2560. [Google Scholar] [CrossRef] [PubMed]
- Park, O.K.; Tiwary, C.S.; Yang, Y.; Bhowmick, S.; Vinod, S.; Zhang, Q.; Colvin, V.L.; Asif, S.A.S.; Vajtai, R.; Penev, E.S.; et al. Magnetic field controlled graphene oxide-based origami with enhanced surface area and mechanical properties. Nanoscale 2017, 9, 6991–6997. [Google Scholar] [CrossRef] [PubMed]
- Cao, L.; Fan, F. Deformation and instability of three-dimensional graphene honeycombs under in-plane compression: Atomistic simulations. Extrem. Mech. Lett. 2020, 39, 100861. [Google Scholar] [CrossRef]
- Morris, B.; Becton, M.; Wang, X. Mechanical abnormality in graphene-based lamellar superstructures. Carbon 2018, 137, 196–206. [Google Scholar] [CrossRef]
- Meng, F.; Chen, C.; Hu, D.; Song, J. Deformation behaviors of three-dimensional graphene honeycombs under out-of-plane compression: Atomistic simulations and predictive modeling. J. Mech. Phys. Solids 2017, 109, 241–251. [Google Scholar] [CrossRef]
- Shokrieh, M.M.; Rafiee, R. A review of the mechanical properties of isolated carbon nanotubes and carbon nanotube composites. Mech. Compos. Mater. 2010, 46, 155–172. [Google Scholar] [CrossRef]
- Young, R.J.; Kinloch, I.A.; Gong, L.; Novoselov, K.S. The mechanics of graphene nanocomposites: A review. Compos. Sci. Technol. 2012, 72, 1459–1476. [Google Scholar] [CrossRef]
- Yang, Y.; Shi, E.; Li, P.; Wu, D.; Wu, S.; Shang, Y.; Xu, W.; Cao, A.; Yuan, Q. A compressible mesoporous SiO2 sponge supported by a carbon nanotube network. Nanoscale 2014, 6, 3585. [Google Scholar] [CrossRef]
- Fan, Z.; Tng, D.Z.Y.; Lim, C.X.T.; Liu, P.; Nguyen, S.T.; Xiao, P.; Marconnet, A.; Lim, C.Y.; Duong, H.M. Thermal and electrical properties of graphene/carbon nanotube aerogels. Colloids Surf. A Physicochem. Eng. Asp. 2014, 445, 48–53. [Google Scholar] [CrossRef]
- Qiu, L.; Liu, J.Z.; Chang, S.L.; Wu, Y.; Li, D. Biomimetic superelastic graphene-based cellular monoliths. Nat. Commun. 2012, 3, 1241. [Google Scholar] [CrossRef]
- Zhu, C.; Han, T.Y.J.; Duoss, E.B.; Golobic, A.M.; Kuntz, J.D.; Spadaccini, C.M.; Worsley, M.A. Highly compressible 3D periodic graphene aerogel microlattices. Nat. Commun. 2015, 6, 6962. [Google Scholar] [CrossRef] [PubMed]
- Hyun, S.; Torquato, S. Effective elastic and transport properties of regular honeycombs for all densities. J. Mater. Res. 2000, 15, 1985–1993. [Google Scholar] [CrossRef]
- Grima, J.N.; Oliveri, L.; Attard, D.; Ellul, B.; Gatt, R.; Cicala, G.; Recca, G. Hexagonal Honeycombs with Zero Poisson’s Ratios and Enhanced Stiffness. Adv. Eng. Mater. 2010, 12, 855–862. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S. The elastic properties of hexagonal auxetics under pressure. Phys. Status Solidi (B) 2016, 253, 1261–1269. [Google Scholar] [CrossRef]
- Goldstein, R.; Lisovenko, D.; Chentsov, A.; Lavrentyev, S. Experimental study of defects influence on auxetic behavior of cellular structure with curvilinear elements. Lett. Mater. 2017, 7, 355–358. [Google Scholar] [CrossRef]
- Yang, M.; Zhao, N.; Cui, Y.; Gao, W.; Zhao, Q.; Gao, C.; Bai, H.; Xie, T. Biomimetic Architectured Graphene Aerogel with Exceptional Strength and Resilience. ACS Nano 2017, 11, 6817–6824. [Google Scholar] [CrossRef]
- Available online: https://www.lammps.org (accessed on 24 November 2023).
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in ’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef]
- Patil, S.P.; Shendye, P.; Markert, B. Molecular Investigation of Mechanical Properties and Fracture Behavior of Graphene Aerogel. J. Phys. Chem. B 2020, 124, 6132–6139. [Google Scholar] [CrossRef]
- Baimova, J.; Rysaeva, L.; Rudskoy, A. Deformation behavior of diamond-like phases: Molecular dynamics simulation. Diam. Relat. Mater. 2018, 81, 154–160. [Google Scholar] [CrossRef]
- Shang, J.; Yang, Q.S.; Liu, X.; Wang, C. Compressive deformation mechanism of honeycomb-like graphene aerogels. Carbon 2018, 134, 398–410. [Google Scholar] [CrossRef]
- Rysaeva, L.K.; Baimova, J.A.; Lisovenko, D.S.; Gorodtsov, V.A.; Dmitriev, S.V. Elastic Properties of Fullerites and Diamond-Like Phases. Phys. Status Solidi (B) 2018, 256, 1800049. [Google Scholar] [CrossRef]
- Safina, L.; Baimova, J.; Krylova, K.; Murzaev, R.; Mulyukov, R. Simulation of metal-graphene composites by molecular dynamics: A review. Lett. Mater. 2020, 10, 351–360. [Google Scholar] [CrossRef]
- Wei, Y.; Wu, J.; Yin, H.; Shi, X.; Yang, R.; Dresselhaus, M. The nature of strength enhancement and weakening by pentagon–heptagon defects in graphene. Nat. Mater. 2012, 11, 759–763. [Google Scholar] [CrossRef]
- O’Connor, T.C.; Andzelm, J.; Robbins, M.O. AIREBO-M: A reactive model for hydrocarbons at extreme pressures. J. Chem. Phys. 2015, 142, 024903. [Google Scholar] [CrossRef]
- Du, Y.; Zhou, J.; Ying, P.; Zhang, J. Effects of cell defects on the mechanical and thermal properties of carbon honeycombs. Comput. Mater. Sci. 2021, 187, 110125. [Google Scholar] [CrossRef]
- Hu, J.; Zhou, J.; Zhang, A.; Yi, L.; Wang, J. Temperature dependent mechanical properties of graphene based carbon honeycombs under tension and compression. Phys. Lett. A 2021, 391, 127130. [Google Scholar] [CrossRef]
- Li, B.; Wei, Y.; Meng, F.; Ou, P.; Chen, Y.; Che, L.; Chen, C.; Song, J. Atomistic simulations of vibration and damping in three-dimensional graphene honeycomb nanomechanical resonators. Superlattices Microstruct. 2020, 139, 106420. [Google Scholar] [CrossRef]
- Zhang, P.; Ma, L.; Fan, F.; Zeng, Z.; Peng, C.; Loya, P.E.; Liu, Z.; Gong, Y.; Zhang, J.; Zhang, X.; et al. Fracture toughness of graphene. Nat. Commun. 2014, 5, 3782. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Min, K.; Aluru, N.R. Size and Chirality Dependent Elastic Properties of Graphene Nanoribbons under Uniaxial Tension. Nano Lett. 2009, 9, 3012–3015. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Liu, J.; Yue, S.; Zhao, J.; Ouyang, B.; Jing, Y. Atomistic Simulations on the Tensile Deformation Behaviors of Three-Dimensional Graphene. Phys. Status Solidi (B) 2018, 255, 1700680. [Google Scholar] [CrossRef]
- Jung, G.S.; Irle, S.; Sumpter, B.G. Dynamic aspects of graphene deformation and fracture from approximate density functional theory. Carbon 2022, 190, 183–193. [Google Scholar] [CrossRef]
- Srinivasan, S.G.; van Duin, A.C.T.; Ganesh, P. Development of a ReaxFF Potential for Carbon Condensed Phases and Its Application to the Thermal Fragmentation of a Large Fullerene. J. Phys. Chem. A 2015, 119, 571–580. [Google Scholar] [CrossRef]
- Zhao, H.; Aluru, N.R. Temperature and strain-rate dependent fracture strength of graphene. J. Appl. Phys. 2010, 108, 064321. [Google Scholar] [CrossRef]
- Magnin, Y.; Rondepierre, F.; Cui, W.; Dunstan, D.; San-Miguel, A. Collapse phase diagram of carbon nanotubes with arbitrary number of walls. Collapse modes and macroscopic analog. Carbon 2021, 178, 552–562. [Google Scholar] [CrossRef]
- Gu, X.; Pang, Z.; Wei, Y.; Yang, R. On the influence of junction structures on the mechanical and thermal properties of carbon honeycombs. Carbon 2017, 119, 278–286. [Google Scholar] [CrossRef]
- Qi, P.; Zhu, H.; Borodich, F.; Peng, Q. A Review of the Mechanical Properties of Graphene Aerogel Materials: Experimental Measurements and Computer Simulations. Materials 2023, 16, 1800. [Google Scholar] [CrossRef] [PubMed]
- Qiu, L.; Huang, B.; He, Z.; Wang, Y.; Tian, Z.; Liu, J.Z.; Wang, K.; Song, J.; Gengenbach, T.R.; Li, D. Extremely Low Density and Super-Compressible Graphene Cellular Materials. Adv. Mater. 2017, 29, 1701553. [Google Scholar] [CrossRef] [PubMed]

| Honeycomb | Re-Entrant | Arrow | |||||||
|---|---|---|---|---|---|---|---|---|---|
| GA Matrix | Flakes | CNT | GA Matrix | Flakes | CNT | GA Matrix | Flakes | CNT | |
| , g/cm | 0.58 | 0.86 | 0.92 | 1.01 | 1.31 | 1.58 | 0.69 | 1.21 | 1.0 |
| , GPa | 190 | 156 | 110 | 180 | 160 | 101 | 31 | 27 | 33 |
| 0.79 | 0.76 | 0.72 | 0.8 | 0.76 | 0.7 | 0.36 | 0.37 | 0.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baimova, J.A.; Shcherbinin, S.A. Strength and Deformation Behavior of Graphene Aerogel of Different Morphologies. Materials 2023, 16, 7388. https://doi.org/10.3390/ma16237388
Baimova JA, Shcherbinin SA. Strength and Deformation Behavior of Graphene Aerogel of Different Morphologies. Materials. 2023; 16(23):7388. https://doi.org/10.3390/ma16237388
Chicago/Turabian StyleBaimova, Julia A., and Stepan A. Shcherbinin. 2023. "Strength and Deformation Behavior of Graphene Aerogel of Different Morphologies" Materials 16, no. 23: 7388. https://doi.org/10.3390/ma16237388
APA StyleBaimova, J. A., & Shcherbinin, S. A. (2023). Strength and Deformation Behavior of Graphene Aerogel of Different Morphologies. Materials, 16(23), 7388. https://doi.org/10.3390/ma16237388







