Numerical Simulations of the Low-Velocity Impact Response of Semicylindrical Woven Composite Shells
Abstract
1. Introduction
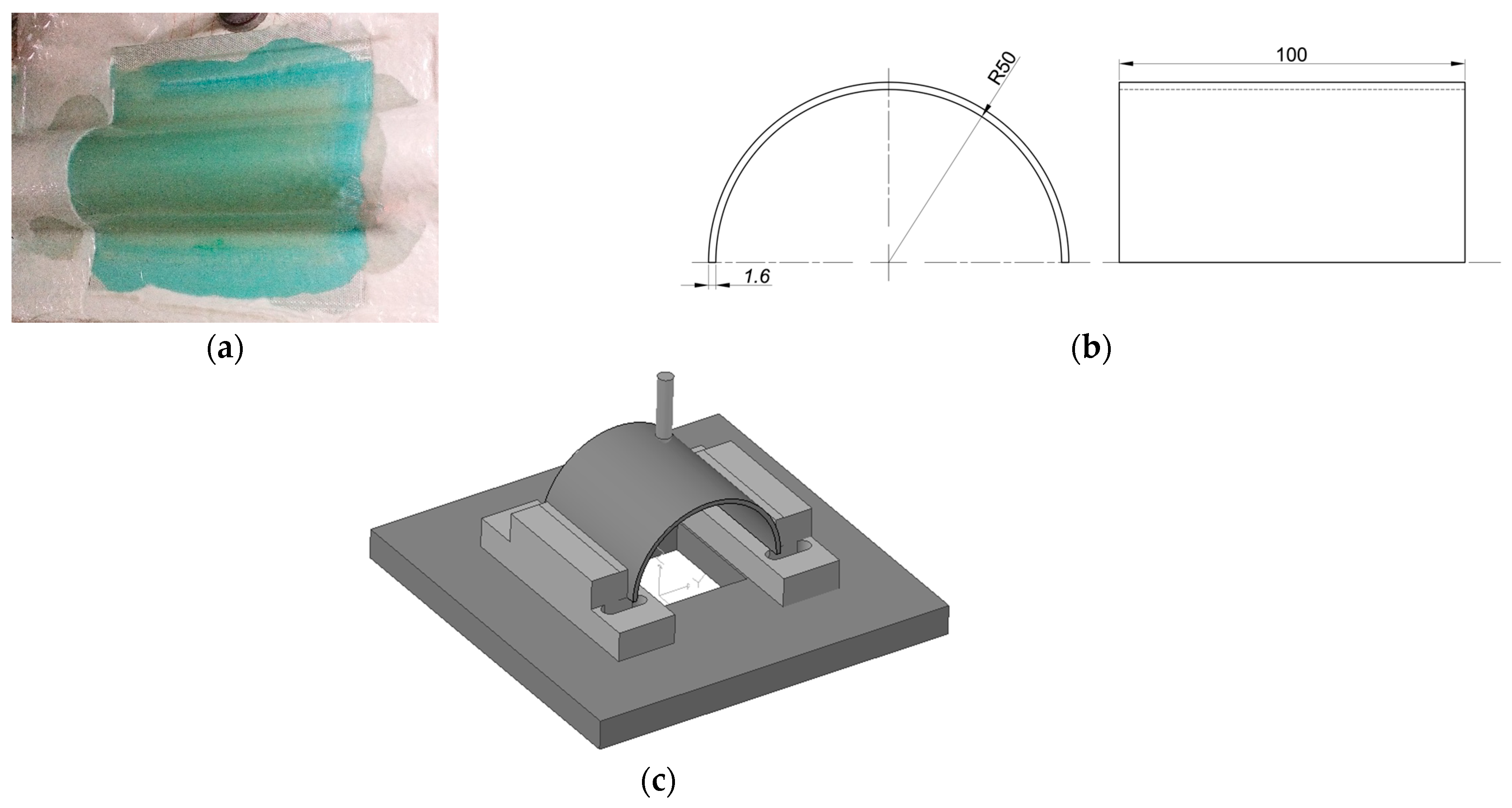
2. Material and Experimental Procedure
3. Damage Models
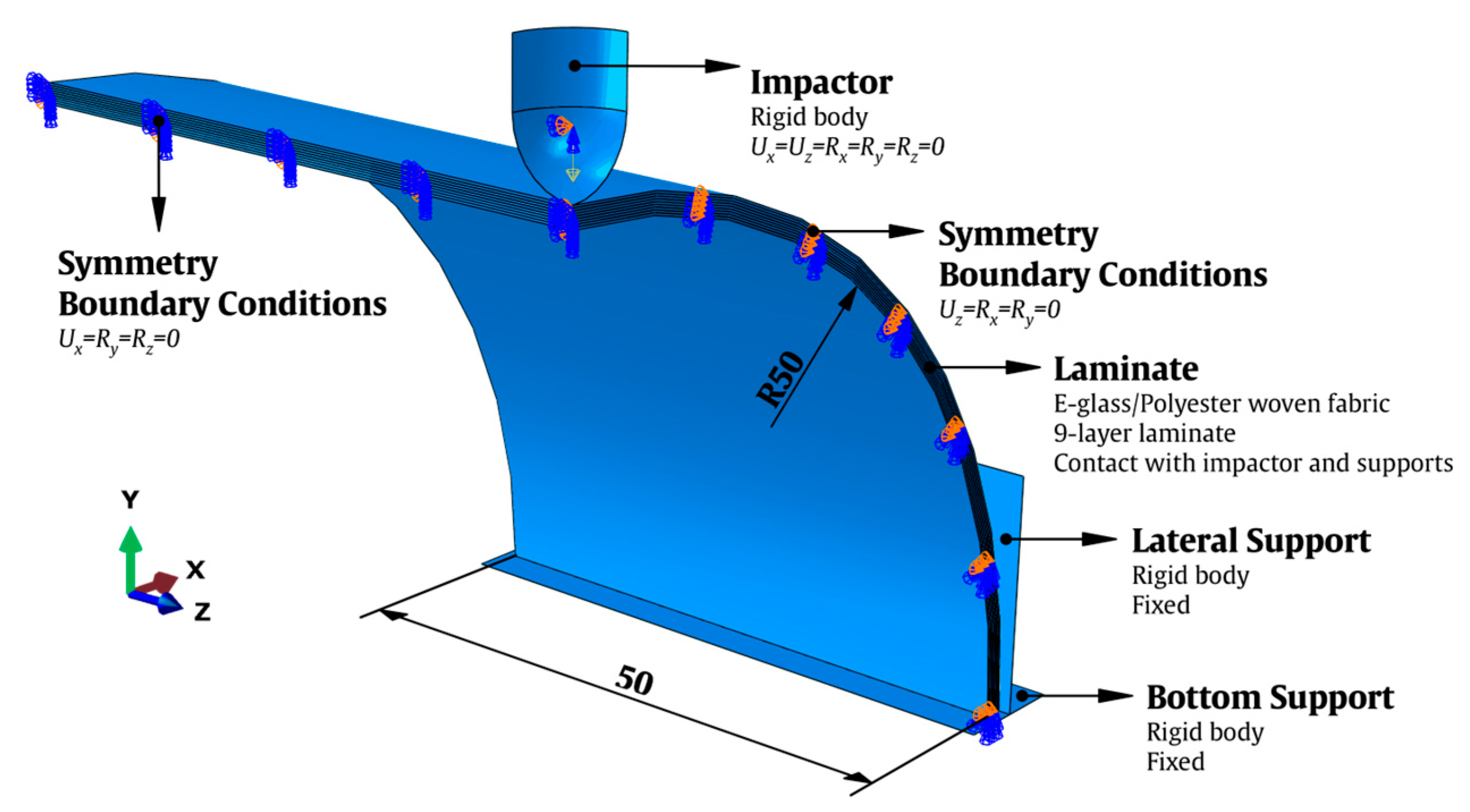
4. Finite Element Model
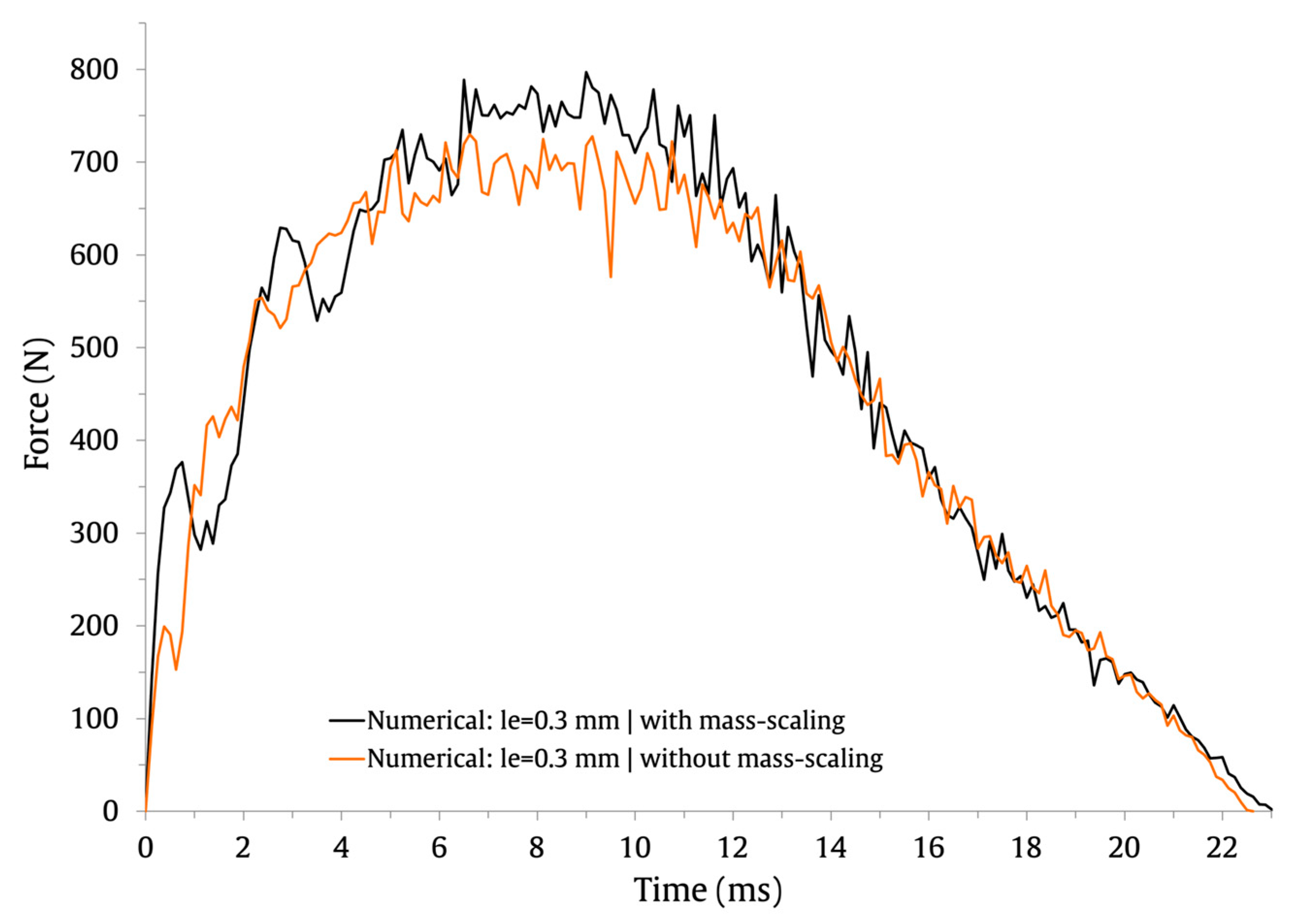
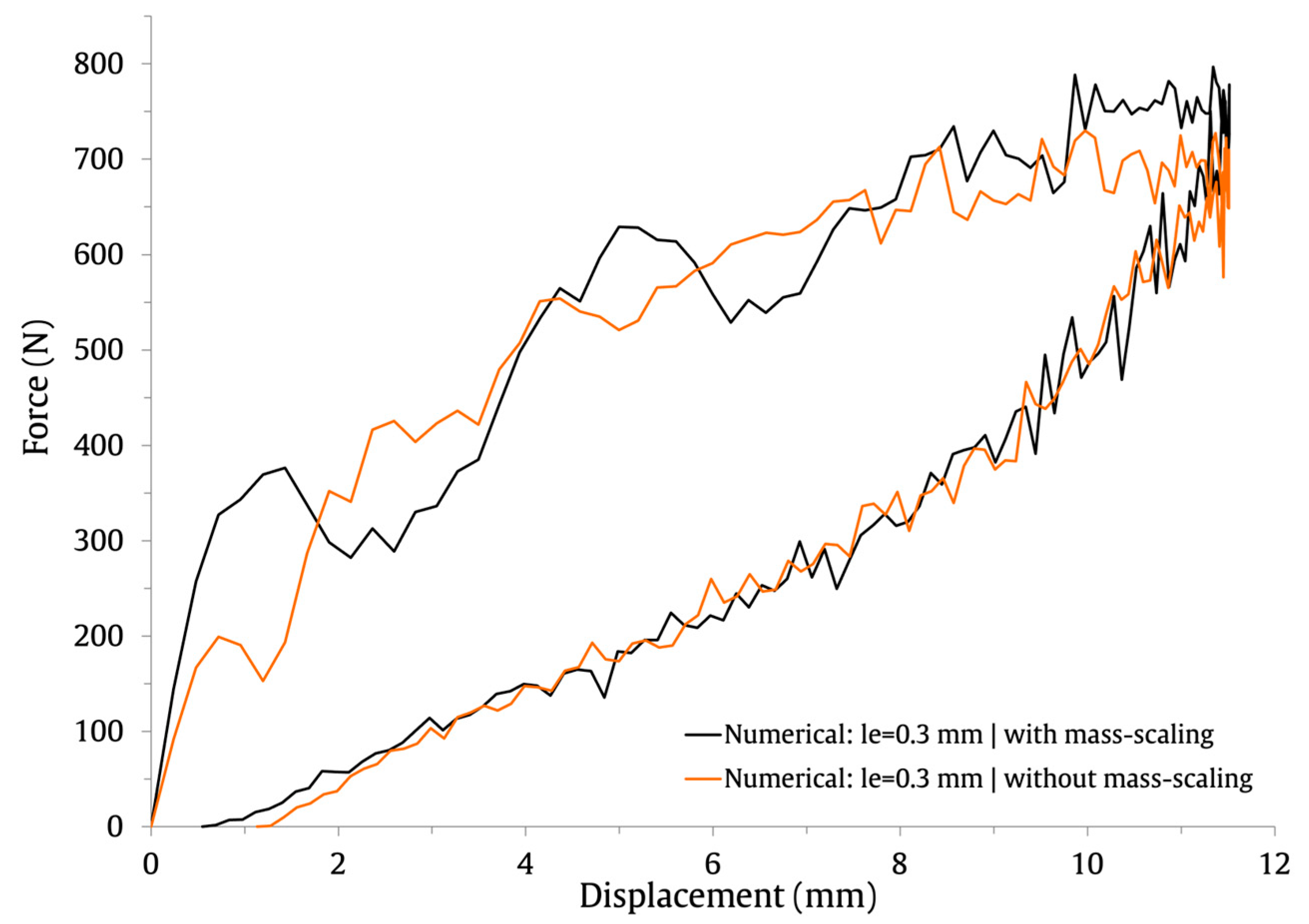
5. Numerical Results
6. Numerical–Experimental Correlation
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Description | Symbol | Description |
| Density | Shear hardening function | ||
| Young’s modulus along fiber direction 1 | Axial damage thresholds | ||
| Young’s modulus along fiber direction 2 | Shear damage threshold | ||
| Though-thickness Young’s modulus | Tensile/compressive strength along the fiber directions | ||
| In-plane shear modulus | Tensile/compressive damage variable along direction 1 | ||
| Out of plane shear modulus | Tensile/compressive damage variable along direction 2 | ||
| In-plane Poisson’s ratio | Shear damage variable | ||
| Tensile strength along direction 1 | Elastic energy density | ||
| Compressive strength along direction 1 | Characteristic length of the element | ||
| Tensile strength along direction 2 | Plastic strain due to shear deformation | ||
| Compressive strength along direction 2 | Elastic normal interlaminar stiffness | ||
| In-plane shear strength | Elastic shear interlaminar stiffness | ||
| Intralaminar fracture toughness along direction 1 and 2 | Elastic tangential interlaminar stiffness | ||
| Parameter in the equation of shear damage | Maximum normal contact stress | ||
| Maximum shear damage | Maximum 1st shear contact stress | ||
| Coefficient in hardening equation | Maximum 2nd shear contact stress | ||
| Power term in hardening equation | Interlaminar normal fracture toughness | ||
| Axial damage activation function | Interlaminar 1st shear fracture toughness | ||
| Shear damage activation function | Interlaminar 2nd shear fracture toughness | ||
| Plasticity activation function | 𝜂 | Benzeggagh–Kenane exponent | |
| Effective tensile/compressive stress | Friction coefficient | ||
| Initial effective shear yield stress | M | Parameter defined for the cohesive zone model | |
| Effective shear stress | Number of elements in the cohesive zone |
References
- Ferreira, L.M.; Graciani, E.; París, F. Predicting Failure Load of a Non-Crimp Fabric Composite by Means of a 3D Finite Element Model Including Progressive Damage. Compos. Struct. 2019, 225, 111115. [Google Scholar] [CrossRef]
- Ferreira, L.; Graciani, E.; París, F. Progressive Damage Study of NCF Composites under Compressive Loading. In Proceedings of the 16th European Conference on Composite Materials, Seville, Spain, 22–26 June 2014; Volume 14, pp. 22–26. [Google Scholar]
- Ferreira, L.M.; Graciani, E.; París, F. Three Dimensional Finite Element Study of the Behaviour and Failure Mechanism of Non-Crimp Fabric Composites under in-Plane Compression. Compos. Struct. 2016, 149, 106–113. [Google Scholar] [CrossRef]
- Ferreira, L.M.; Graciani, E.; París, F. Modelling the Waviness of the Fibres in Non-Crimp Fabric Composites Using 3D Finite Element Models with Straight Tows. Compos. Struct. 2014, 107, 79–87. [Google Scholar] [CrossRef]
- Ferreira, L.; Coelho, C. Modelling Progressive Damage in NCF Composites Using the Continuum Damage Mechanics Method. In Proceedings of the 2022 Advances in Science and Engineering Technology International Conferences (ASET), Dubai, United Arab Emirates, 21–24 February 2022; IEEE: New York, NY, USA; pp. 1–4. [Google Scholar]
- Kim, S.J.; Goo, N.S.; Kim, T.W. The Effect of Curvature on the Dynamic Response and Impact-Induced Damage in Composite Laminates. Compos. Sci. Technol. 1997, 57, 763–773. [Google Scholar] [CrossRef]
- Her, S.-C.; Liang, Y.-C. The Finite Element Analysis of Composite Laminates and Shell Structures Subjected to Low Velocity Impact. Compos. Struct. 2004, 66, 277–285. [Google Scholar] [CrossRef]
- Krishnamurthy, K.; Mahajan, P.; Mittal, R. Impact Response and Damage in Laminated Composite Cylindrical Shells. Compos. Struct. 2003, 59, 15–36. [Google Scholar] [CrossRef]
- Choi, I.H. Finite Element Analysis of Low-Velocity Impact Response of Convex and Concave Composite Laminated Shells. Compos. Struct. 2018, 186, 210–220. [Google Scholar] [CrossRef]
- Kistler, L.S.; Waas, A.M. Impact Response of Cylindrically Curved Laminates Including a Large Deformation Scaling Study. Int. J. Impact Eng. 1998, 21, 61–75. [Google Scholar] [CrossRef]
- Zhao, G.; Cho, C. On Impact Damage of Composite Shells by a Low-Velocity Projectile. J. Compos. Mater. 2004, 38, 1231–1254. [Google Scholar] [CrossRef]
- Kumar, S.; Nageswara Rao, B.; Pradhan, B. Effect of Impactor Parameters and Laminate Characteristics on Impact Response and Damage in Curved Composite Laminates. J. Reinf. Plast. Compos. 2007, 26, 1273–1290. [Google Scholar] [CrossRef]
- Khalili, S.M.R.; Soroush, M.; Davar, A.; Rahmani, O. Finite Element Modeling of Low-Velocity Impact on Laminated Composite Plates and Cylindrical Shells. Compos. Struct. 2011, 93, 1363–1375. [Google Scholar] [CrossRef]
- Albayrak, M.; Kaman, M.O.; Bozkurt, I. Experimental and Numerical Investigation of the Geometrical Effect on Low Velocity Impact Behavior for Curved Composites with a Rubber Interlayer. Appl. Compos. Mater. 2023, 30, 507–538. [Google Scholar] [CrossRef]
- Abaqus, version 2021; Dassault Systemes Simulia Corporation: Providence, RI, USA, 2021.
- Reis, P.N.B.; Sousa, P.; Ferreira, L.M.; Coelho, C.A.C.P. Multi-Impact Response of Semicylindrical Composite Laminated Shells with Different Thicknesses. Compos. Struct. 2023, 310, 116771. [Google Scholar] [CrossRef]
- Silva, M.P.; Santos, P.; Parente, J.M.; Valvez, S.; Reis, P.N.B.; Piedade, A.P. Effect of Post-Cure on the Static and Viscoelastic Properties of a Polyester Resin. Polymers 2020, 12, 1927. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, L.; Coelho, C.; Reis, P. Impact Response of Semi-Cylindrical Composite Laminate Shells Under Repeated Low-Velocity Impacts. In Proceedings of the 2022 Advances in Science and Engineering Technology International Conferences (ASET), Dubai, United Arab Emirates, 21–24 February 2022; pp. 1–5. [Google Scholar]
- Amaro, A.M.; Reis, P.N.B.; Magalhães, A.G.; de Moura, M.F.S.F. The Influence of the Boundary Conditions on Low-Velocity Impact Composite Damage. Strain 2011, 47, e220–e226. [Google Scholar] [CrossRef]
- Johnson, A.F.; Pickett, A.K.; Rozycki, P. Computational Methods for Predicting Impact Damage in Composite Structures. Compos. Sci. Technol. 2001, 61, 2183–2192. [Google Scholar] [CrossRef]
- Ladeveze, P.; LeDantec, E. Damage Modelling of the Elementary Ply for Laminated Composites. Compos. Sci. Technol. 1992, 43, 257–267. [Google Scholar] [CrossRef]
- User, A.A. VUMAT for Fabric Reinforced Composites, Dassault Systèmes; Dassault Systemes Simulia Corporation: Providence, RI, USA, 2008. [Google Scholar]
- Liu, X.; Rouf, K.; Peng, B.; Yu, W. Two-Step Homogenization of Textile Composites Using Mechanics of Structure Genome. Compos. Struct. 2017, 171, 252–262. [Google Scholar] [CrossRef]
- Sridharan, S.; Pankow, M. Performance Evaluation of Two Progressive Damage Models for Composite Laminates under Various Speed Impact Loading. Int. J. Impact Eng. 2020, 143, 103615. [Google Scholar] [CrossRef]
- Bodepati, V.; Mogulanna, K.; Rao, G.S.; Vemuri, M. Numerical Simulation and Experimental Validation of E-Glass/Epoxy Composite Material under Ballistic Impact of 9 Mm Soft Projectile. Plast. Impact Mech. 2017, 173, 740–746. [Google Scholar] [CrossRef]
- Esnaola, A.; Elguezabal, B.; Aurrekoetxea, J.; Gallego, I.; Ulacia, I. Optimization of the Semi-Hexagonal Geometry of a Composite Crush Structure by Finite Element Analysis. Compos. Part B Eng. 2016, 93, 56–66. [Google Scholar] [CrossRef]
- Kostopoulos, V.; Markopoulos, Y.P.; Giannopoulos, G.; Vlachos, D.E. Finite Element Analysis of Impact Damage Response of Composite Motorcycle Safety Helmets. Compos. Part B Eng. 2002, 33, 99–107. [Google Scholar] [CrossRef]
- Hoo Fatt, M.S.; Lin, C. Perforation of Clamped, Woven E-Glass/Polyester Panels. Compos. Part B Eng. 2004, 35, 359–378. [Google Scholar] [CrossRef]
- Alonso, L.; Martínez-Hergueta, F.; Garcia-Gonzalez, D.; Navarro, C.; García-Castillo, S.K.; Teixeira-Dias, F. A Finite Element Approach to Model High-Velocity Impact on Thin Woven GFRP Plates. Int. J. Impact Eng. 2020, 142, 103593. [Google Scholar] [CrossRef]
- Camanho, P.P.; Davila, C.G.; de Moura, M.F. Numerical Simulation of Mixed-Mode Progressive Delamination in Composite Materials. J. Compos. Mater. 2003, 37, 1415–1438. [Google Scholar] [CrossRef]
- Turon, A.; Dávila, C.G.; Camanho, P.P.; Costa, J. An Engineering Solution for Mesh Size Effects in the Simulation of Delamination Using Cohesive Zone Models. Eng. Fract. Mech. 2007, 74, 1665–1682. [Google Scholar] [CrossRef]
- Song, K.; Dávila, C.G.; Rose, C.A. Guidelines and Parameter Selection for the Simulation of Progressive Delamination. In Proceedings of the 2008 ABAQUS User’s Conference, Newport, RI, USA, 19–22 May 2008; Volume 41, pp. 43–44. [Google Scholar]
- Nguyen, K.-H.; Ju, H.-W.; Truong, V.-H.; Kweon, J.-H. Delamination Analysis of Multi-Angle Composite Curved Beams Using an out-of-Autoclave Material. Compos. Struct. 2018, 183, 320–330. [Google Scholar] [CrossRef]
- Zhou, J.; Wen, P.; Wang, S. Numerical Investigation on the Repeated Low-Velocity Impact Behavior of Composite Laminates. Compos. Part B Eng. 2020, 185, 107771. [Google Scholar] [CrossRef]
- Lopes, C.S.; Camanho, P.P.; Gürdal, Z.; Maimí, P.; González, E.V. Low-Velocity Impact Damage on Dispersed Stacking Sequence Laminates. Part II: Numerical Simulations. Compos. Sci. Technol. 2009, 69, 937–947. [Google Scholar] [CrossRef]
- Baluch, A.H.; Falcó, O.; Jiménez, J.L.; Tijs, B.H.A.H.; Lopes, C.S. An Efficient Numerical Approach to the Prediction of Laminate Tolerance to Barely Visible Impact Damage. Compos. Struct. 2019, 225, 111017. [Google Scholar] [CrossRef]
- Falcó, O.; Lopes, C.S.; Sommer, D.E.; Thomson, D.; Ávila, R.L.; Tijs, B.H.A.H. Experimental Analysis and Simulation of Low-Velocity Impact Damage of Composite Laminates. Compos. Struct. 2022, 287, 115278. [Google Scholar] [CrossRef]
- Wang, F.; Wang, B.; Kong, F.; Ouyang, J.; Ma, T.; Chen, Y. Assessment of Degraded Stiffness Matrices for Composite Laminates under Low-Velocity Impact Based on Modified Characteristic Length Model. Compos. Struct. 2021, 272, 114145. [Google Scholar] [CrossRef]
- Schön, J. Coefficient of Friction of Composite Delamination Surfaces. Wear 2000, 237, 77–89. [Google Scholar] [CrossRef]
- Bresciani, L.M.; Manes, A.; Ruggiero, A.; Iannitti, G.; Giglio, M. Experimental Tests and Numerical Modelling of Ballistic Impacts against Kevlar 29 Plain-Woven Fabrics with an Epoxy Matrix: Macro-Homogeneous and Meso-Heterogeneous Approaches. Compos. Part B Eng. 2016, 88, 114–130. [Google Scholar] [CrossRef]
- Hillerborg, A.; Modéer, M.; Petersson, P.-E. Analysis of Crack Formation and Crack Growth in Concrete by Means of Fracture Mechanics and Finite Elements. Cem. Concr. Res. 1976, 6, 773–781. [Google Scholar] [CrossRef]
- Camanho, P.P.; Dávila, C.G. Mixed-Mode Decohesion Finite Elements for the Simulation of Delamination in Composite Materials; NASA Langley Research Center: Hampton, VA, USA, 2002. [Google Scholar]
- Carpinteri, A.; Cornetti, P.; Barpi, F.; Valente, S. Cohesive Crack Model Description of Ductile to Brittle Size-Scale Transition: Dimensional Analysis vs. Renormalization Group Theory. Eng. Fract. Mech. 2003, 70, 1809–1839. [Google Scholar] [CrossRef]
- Falk, M.L.; Needleman, A.; Rice, J.R. A Critical Evaluation of Cohesive Zone Models of Dynamic Fractur. J. Phys. IV 2001, 11, Pr5-43–Pr5-50. [Google Scholar] [CrossRef]
- Schoeppner, G.A.; Abrate, S. Delamination Threshold Loads for Low Velocity Impact on Composite Laminates. Compos. Part Appl. Sci. Manuf. 2000, 31, 903–915. [Google Scholar] [CrossRef]
- Belingardi, G.; Vadori, R. Low Velocity Impact Tests of Laminate Glass-Fiber-Epoxy Matrix Composite Material Plates. Int. J. Impact Eng. 2002, 27, 213–229. [Google Scholar] [CrossRef]





| Property | Symbol | Units | Value |
|---|---|---|---|
| Density | kg/m3 | 1900 | |
| Stiffness properties | GPa | 21.9 | |
| GPa | 21.9 | ||
| GPa | 8.6 | ||
| GPa | 3.4 | ||
| GPa | 2.4 | ||
| - | 0.14 | ||
| Strength properties | MPa | 250 | |
| MPa | 200 | ||
| MPa | 40 | ||
| Fracture toughness | N/mm | 4500 | |
| Shear plasticity | - | 1 | |
| MPa | 25 | ||
| - | 800 | ||
| - | 0.552 |
| Property | Symbol | Units | Value |
|---|---|---|---|
| Stiffness properties | N/mm3 | 106 | |
| Strength properties | MPa | 15 | |
| MPa | 30 | ||
| Fracture toughness | N/mm | 0.3 | |
| N/mm | 0.6 | ||
| - | 1.45 |
| Max. Load (N) | Dif. 1 (%) | Max. Displacement (mm) | Dif. 1 (%) | Contact Time (ms) | Dif. 1 (%) | |
|---|---|---|---|---|---|---|
| With mass scaling | 797 | - | 11.5 | - | 23 | - |
| Without mass scaling | 730 | 8.8 | 11.5 | 0 | 22.6 | 1.8 |
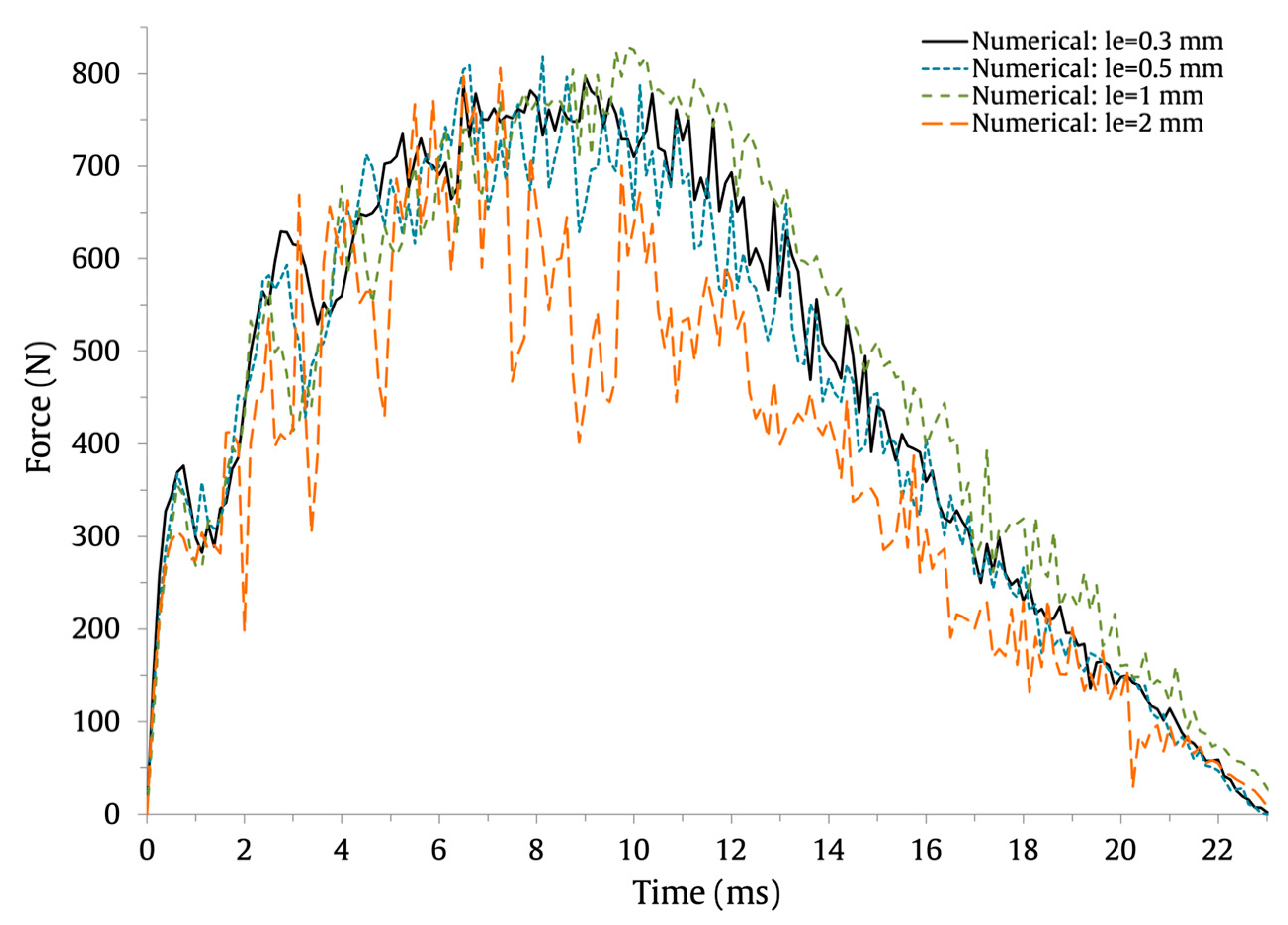
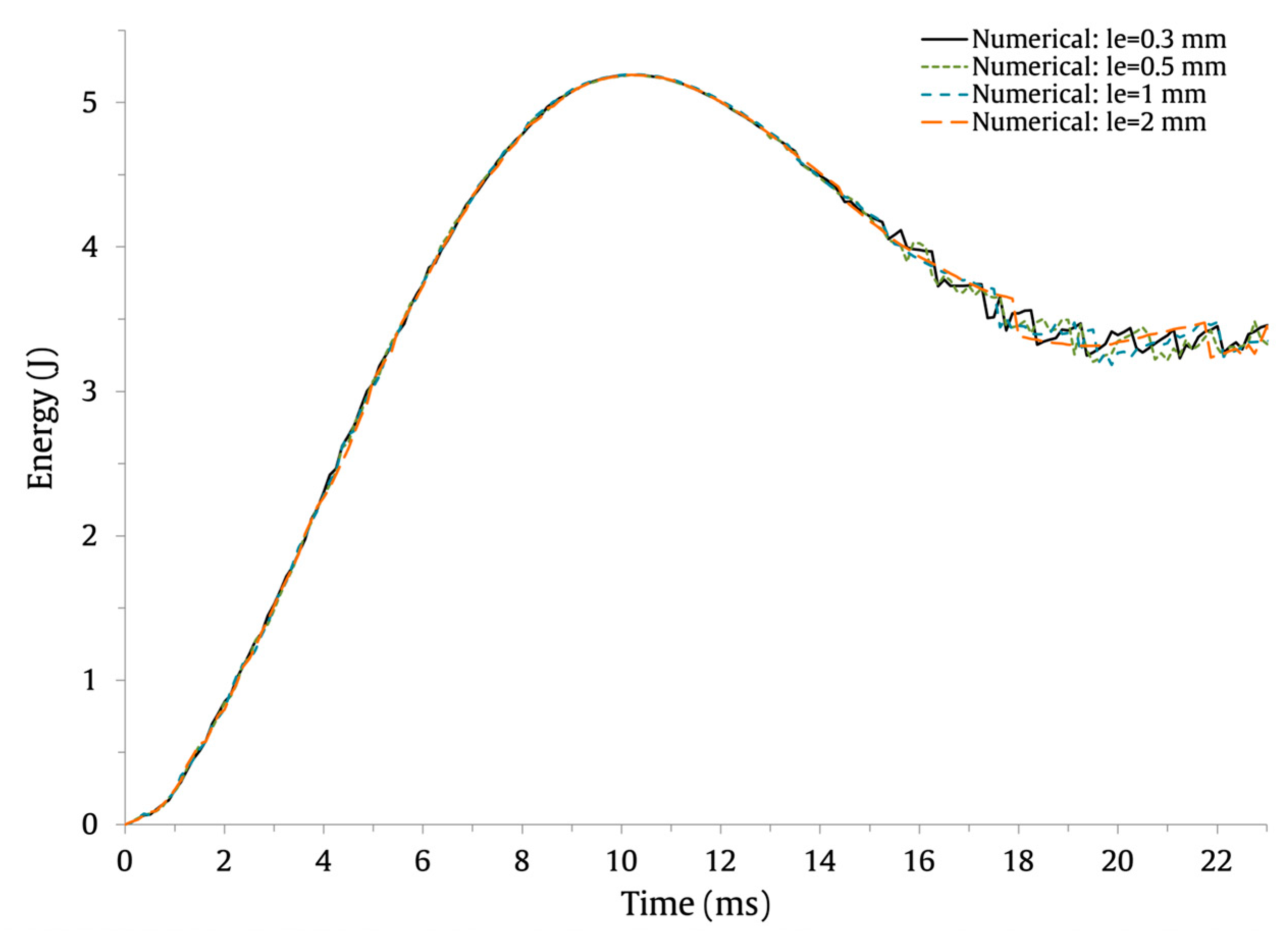
| Mesh Size (mm) | Max. Load (N) | Difference (%) | Max. Displacement (mm) | Difference (%) | Contact Time (ms) | Difference (%) |
|---|---|---|---|---|---|---|
| 0.3 | 797 | - | 11.5 | - | 23 | - |
| 0.5 | 818 | 2.6 | 11.5 | 0 | 23 | 0 |
| 1 | 828 | 3.8 | 11.5 | 0 | 23.5 | 2.2 |
| 2 | 806 | 1.1 | 11.5 | 0 | 23.1 | 0.4 |
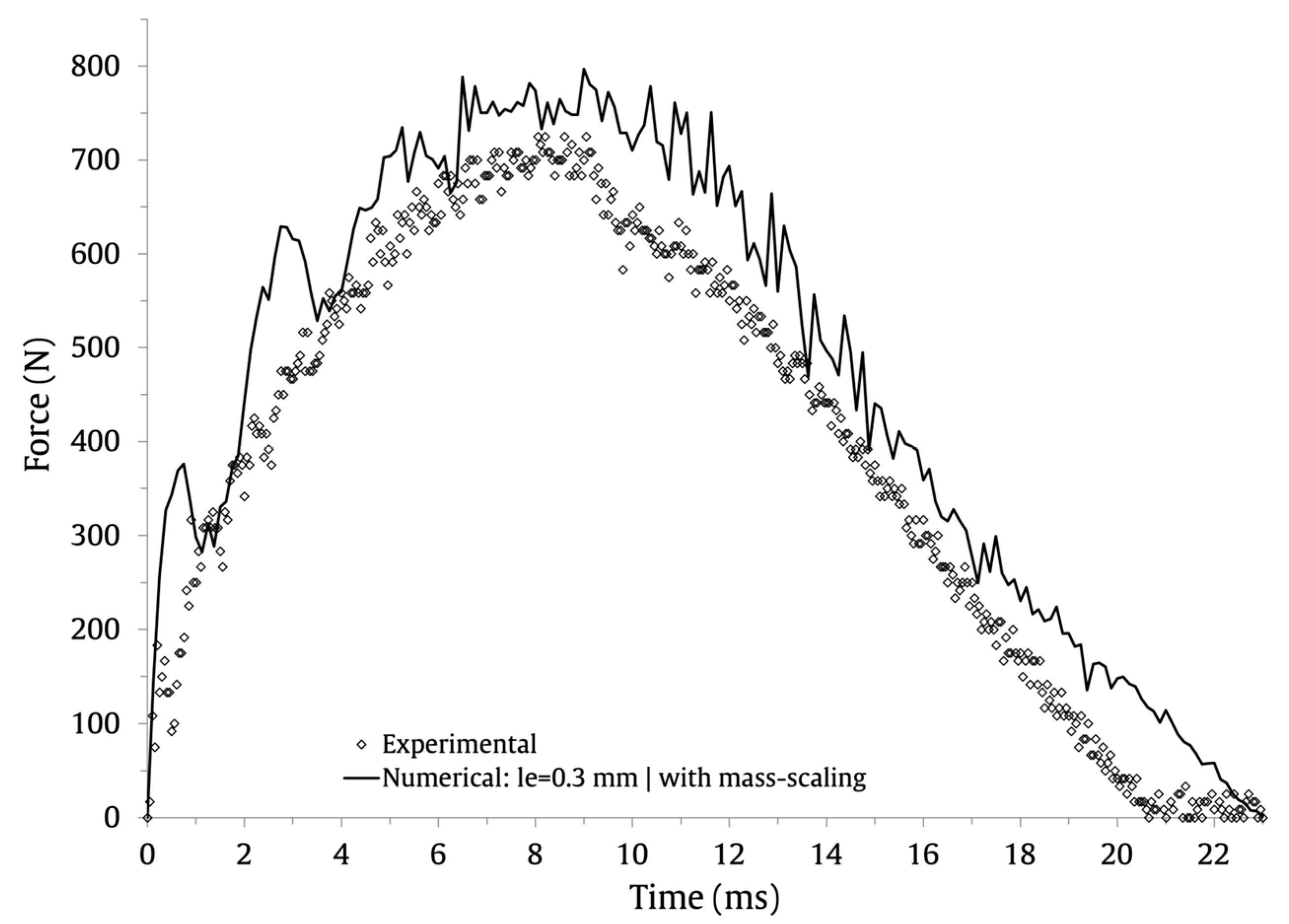
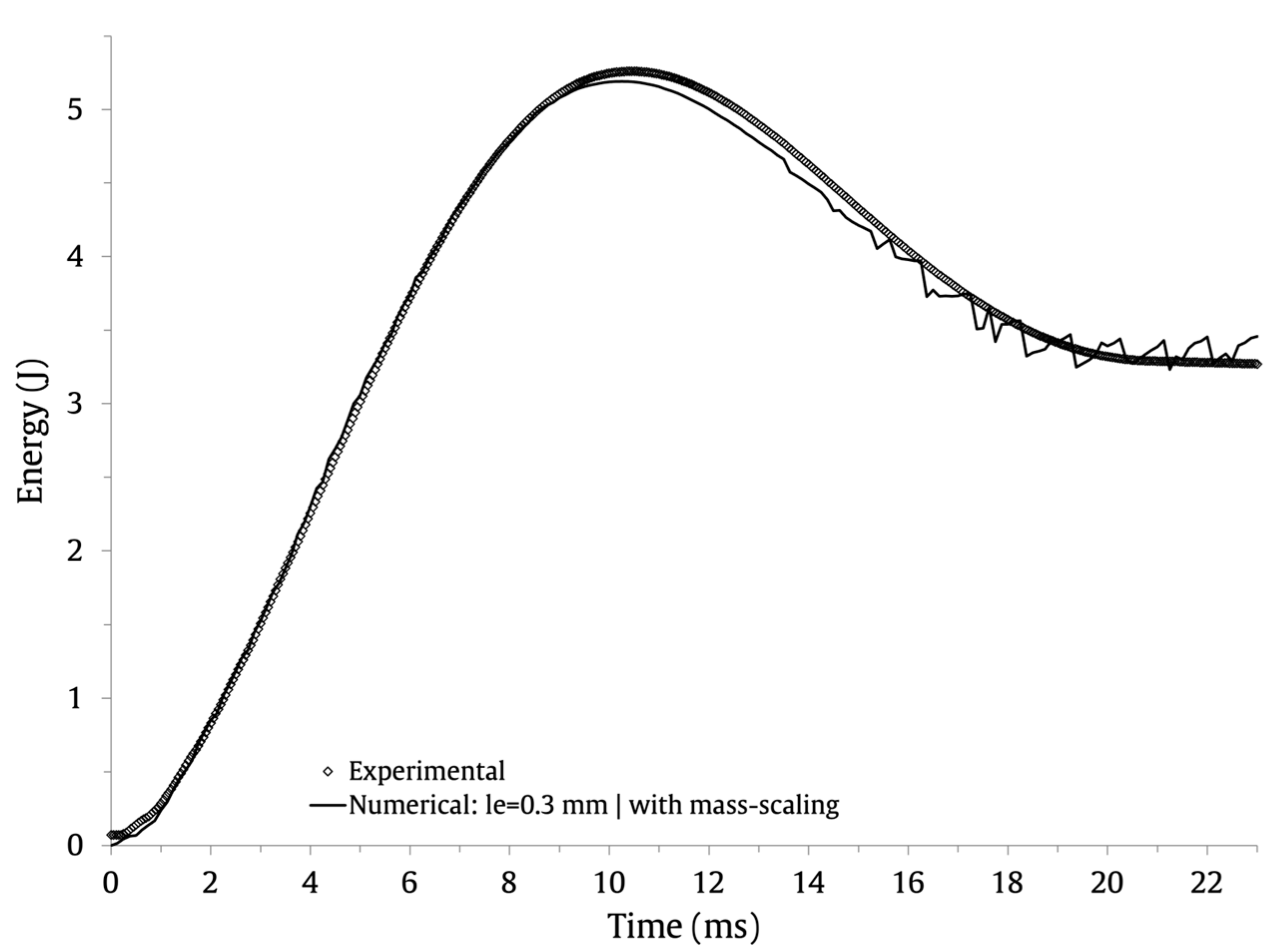
| Mesh Size (mm) | Maximum Load (N) | Maximum Displacement (mm) | Contact Time (ms) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Num. | Exp. | Error (%) | Num. | Exp. | Error (%) | Num. | Exp. | Error (%) | |
| 0.3 | 797 | 757 | 5.0 | 11.5 | 11.2 | 2.7 | 23 | 20.6 | 10.4 |
| 0.5 | 818 | 7.5 | 11.5 | 2.7 | 23 | 10.4 | |||
| 1 | 828 | 8.6 | 11.5 | 2.7 | 23.5 | 12.3 | |||
| 2 | 806 | 6.1 | 11.5 | 2.7 | 23.1 | 10.8 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferreira, L.M.; Coelho, C.A.C.P.; Reis, P.N.B. Numerical Simulations of the Low-Velocity Impact Response of Semicylindrical Woven Composite Shells. Materials 2023, 16, 3442. https://doi.org/10.3390/ma16093442
Ferreira LM, Coelho CACP, Reis PNB. Numerical Simulations of the Low-Velocity Impact Response of Semicylindrical Woven Composite Shells. Materials. 2023; 16(9):3442. https://doi.org/10.3390/ma16093442
Chicago/Turabian StyleFerreira, Luis M., Carlos A. C. P. Coelho, and Paulo N. B. Reis. 2023. "Numerical Simulations of the Low-Velocity Impact Response of Semicylindrical Woven Composite Shells" Materials 16, no. 9: 3442. https://doi.org/10.3390/ma16093442
APA StyleFerreira, L. M., Coelho, C. A. C. P., & Reis, P. N. B. (2023). Numerical Simulations of the Low-Velocity Impact Response of Semicylindrical Woven Composite Shells. Materials, 16(9), 3442. https://doi.org/10.3390/ma16093442









