Stress–Charge Nonlinear Physical Description and Tensor Symmetries for Piezoelectric Materials
Abstract
1. Introduction
2. Stress–Charge Nonlinear Formulation
3. Transformation Laws
4. Symmetry Structure for High-Order Tensors
5. Nonlinear Effects of Piezoelectric Materials
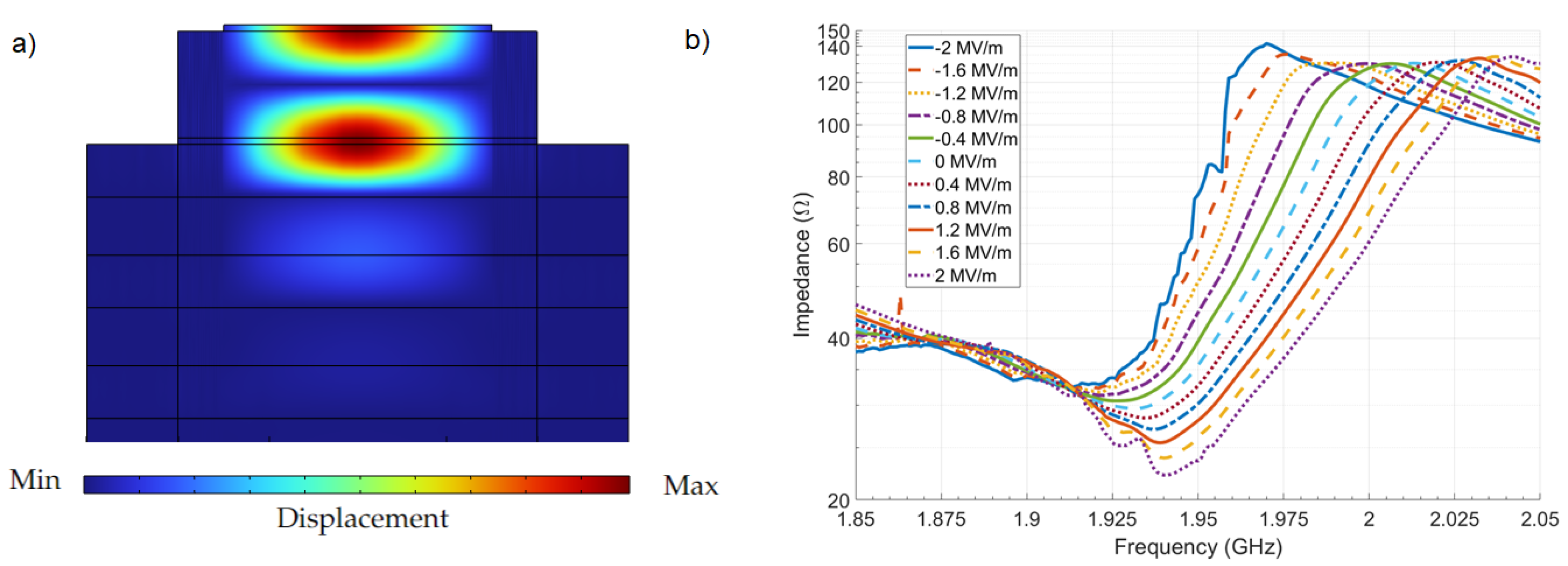
5.1. Variation of Mechanical and Electrical Properties
5.2. Change Response of the PhysicalSystem
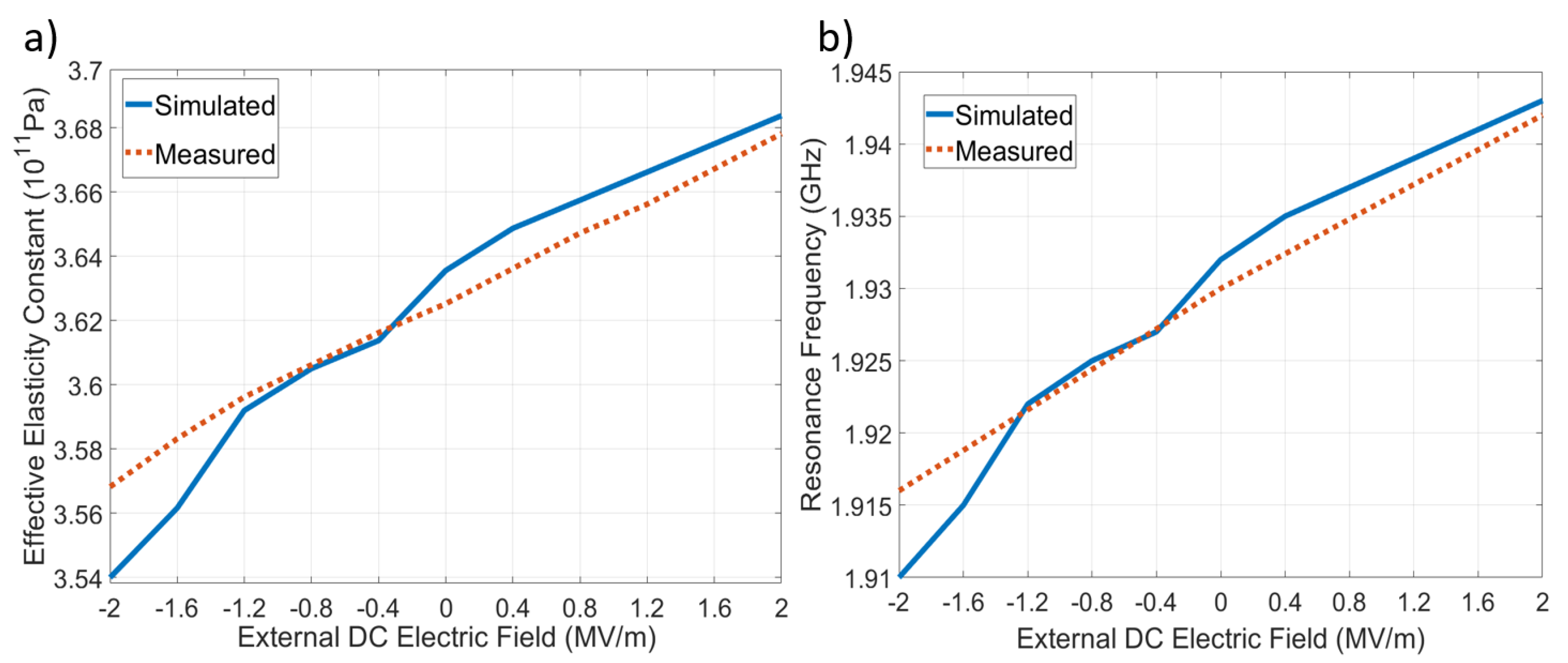
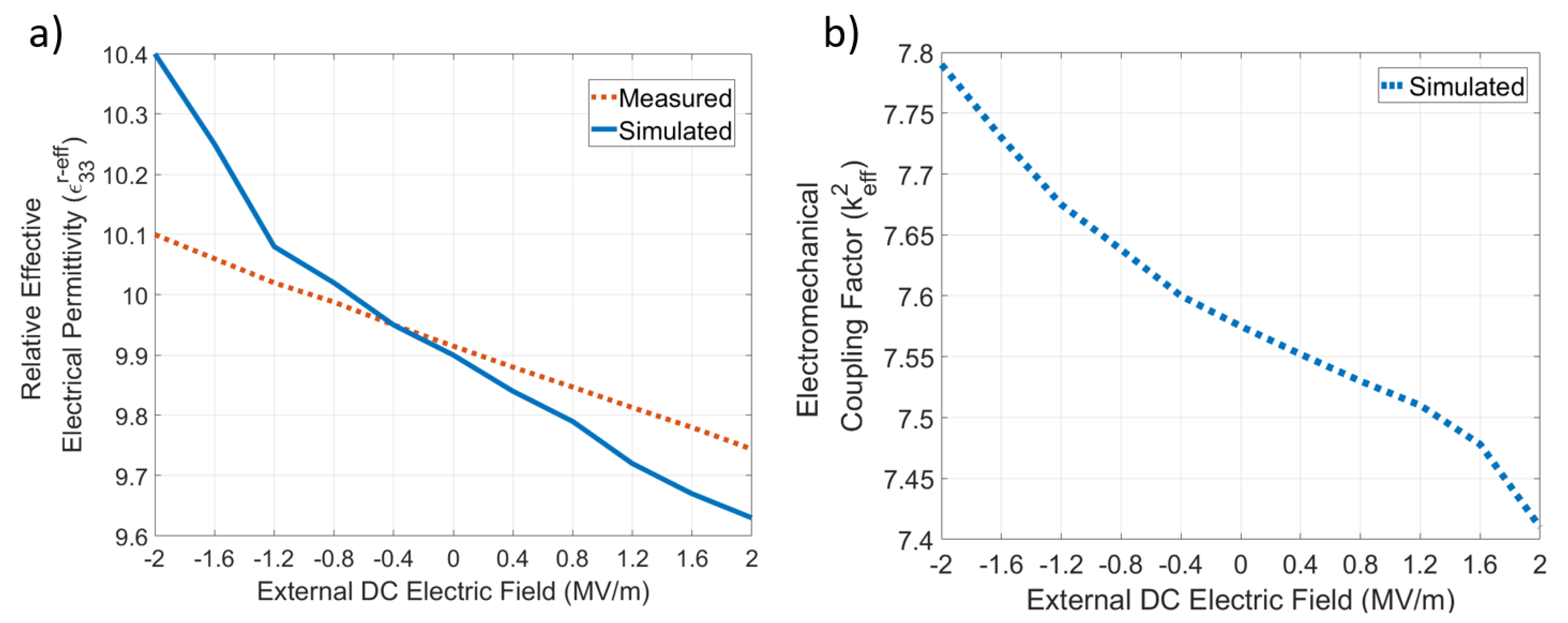
6. Experimental Validation: Simulation
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Laue Group | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Comp. | N | M | O | TII | TI | RI | HII | CI | CII |
| 111 | 111 | 111 | 111 | 111 | 111 | 111 | 111 | 111 | 111 |
| 121 | 121 | 121 | 121 | 121 | 121 | 121 | 121 | 121 | 121 |
| 131 | 131 | 131 | 131 | 131 | 131 | 131 | 131 | 121 | 131 |
| 141 | 141 | 0 | 0 | 0 | 0 | 141 | 0 | 0 | 0 |
| 151 | 151 | 151 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 161 | 161 | 0 | 0 | 161 | 0 | 0 | 161 | 0 | 0 |
| 221 | 221 | 221 | 221 | 221 | 221 | 221 | 221 | 221 | 221 |
| 231 | 231 | 231 | 231 | 231 | 231 | 231 | 231 | 231 | 231 |
| 241 | 241 | 0 | 0 | 0 | 0 | 241 | 0 | 0 | 0 |
| 251 | 251 | 251 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 261 | 261 | 0 | 0 | 261 | 0 | 0 | 261 | 0 | 0 |
| 331 | 331 | 331 | 331 | 331 | 331 | 331 | 331 | 221 | 331 |
| 341 | 341 | 0 | 0 | 0 | 0 | 341 | 0 | 0 | 0 |
| 351 | 351 | 351 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 361 | 361 | 0 | 0 | 361 | 0 | 0 | 361 | 0 | 0 |
| 441 | 441 | 441 | 441 | 441 | 441 | 441 | 441 | 441 | 441 |
| 451 | 451 | 0 | 0 | 451 | 0 | 0 | 451 | 0 | 0 |
| 461 | 461 | 461 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 551 | 551 | 551 | 551 | 551 | 551 | 551 | 551 | 551 | 551 |
| 561 | 561 | 0 | 0 | 0 | 0 | 561 | 0 | 0 | 0 |
| 661 | 661 | 661 | 661 | 661 | 661 | 661 | 661 | 551 | 661 |
| 112 | 112 | 112 | 112 | 221 | 221 | A | A | 221 | 331 |
| 122 | 122 | 122 | 122 | 121 | 121 | B | B | 121 | 131 |
| 132 | 132 | 132 | 132 | 231 | 231 | 231 | 231 | 231 | 231 |
| 142 | 142 | 0 | 0 | 0 | 0 | C | 0 | 0 | 0 |
| 152 | 152 | 152 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 162 | 162 | 0 | 0 | −261 | 0 | 0 | −161 | 0 | 0 |
| 222 | 222 | 222 | 222 | 111 | 111 | D | D | 111 | 111 |
| 232 | 232 | 232 | 232 | 131 | 131 | 131 | 131 | 121 | 121 |
| 242 | 242 | 0 | 0 | 0 | 0 | E | 0 | 0 | 0 |
| 252 | 252 | 252 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 262 | 262 | 0 | 0 | −161 | 0 | 0 | -261 | 0 | 0 |
| 332 | 332 | 332 | 332 | 331 | 331 | 331 | 331 | 221 | 221 |
| 342 | 342 | 0 | 0 | 0 | 0 | −341 | 0 | 0 | 0 |
| 352 | 352 | 352 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 362 | 362 | 0 | 0 | −361 | 0 | 0 | −361 | 0 | 0 |
| 442 | 442 | 442 | 442 | 551 | 551 | 551 | 551 | 551 | 661 |
| 452 | 452 | 0 | 0 | −451 | 0 | 0 | −451 | 0 | 0 |
| 462 | 462 | 462 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 552 | 552 | 552 | 552 | 441 | 441 | 441 | 441 | 441 | 441 |
| 562 | 562 | 0 | 0 | 0 | 0 | F | 0 | 0 | 0 |
| 662 | 662 | 662 | 662 | 661 | 661 | G | G | 551 | 551 |
| 113 | 113 | 113 | 113 | 113 | 113 | 113 | 113 | 221 | 221 |
| 123 | 123 | 123 | 123 | 123 | 123 | 123 | 123 | 231 | 231 |
| 133 | 133 | 133 | 133 | 133 | 133 | 133 | 133 | 121 | 121 |
| 143 | 143 | 0 | 0 | 0 | 0 | 143 | 0 | 0 | 0 |
| 153 | 153 | 153 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 163 | 163 | 0 | 0 | 163 | 0 | 0 | 0 | 0 | 0 |
| 223 | 223 | 223 | 223 | 113 | 113 | 113 | 113 | 221 | 331 |
| 233 | 233 | 233 | 233 | 133 | 133 | 133 | 133 | 121 | 131 |
| 243 | 243 | 0 | 0 | 0 | 0 | −143 | 0 | 0 | 0 |
| 253 | 253 | 253 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 263 | 263 | 0 | 0 | −163 | 0 | 0 | 0 | 0 | 0 |
| 333 | 333 | 333 | 333 | 333 | 333 | 333 | 333 | 111 | 111 |
| 343 | 343 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 353 | 353 | 353 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 363 | 363 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 443 | 443 | 443 | 443 | 443 | 443 | 443 | 443 | 551 | 551 |
| 453 | 453 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 463 | 463 | 463 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 553 | 553 | 553 | 553 | 443 | 443 | 443 | 443 | 551 | 661 |
| 563 | 563 | 0 | 0 | 0 | 0 | 143 | 0 | 0 | 0 |
| 663 | 663 | 663 | 663 | 663 | 663 | H | H | 441 | 441 |
| 114 | 114 | 0 | 0 | 0 | 0 | 114 | 0 | 0 | 0 |
| 124 | 124 | 0 | 0 | 0 | 0 | 124 | 0 | 0 | 0 |
| 134 | 134 | 0 | 0 | 0 | 0 | 134 | 0 | 0 | 0 |
| 144 | 144 | 144 | 144 | 144 | 144 | 144 | 144 | 144 | 144 |
| 154 | 154 | 0 | 0 | 0 | 0 | 0 | 154 | 0 | 0 |
| 164 | 164 | 164 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 224 | 224 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 |
| 234 | 234 | 0 | 0 | 0 | 0 | −134 | 0 | 0 | 0 |
| 244 | 244 | 244 | 244 | 244 | 244 | 244 | 244 | 244 | 244 |
| 254 | 254 | 0 | 0 | 254 | 0 | 0 | 254 | 0 | 0 |
| 264 | 264 | 264 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 334 | 334 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 344 | 344 | 344 | 344 | 344 | 344 | 344 | 344 | 244 | 344 |
| 354 | 354 | 0 | 0 | 354 | 0 | 0 | 354 | 0 | 0 |
| 364 | 364 | 364 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 444 | 444 | 0 | 0 | 0 | 0 | 444 | 0 | 0 | 0 |
| 454 | 454 | 454 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 464 | 464 | 0 | 0 | 464 | 0 | 0 | U | 0 | 0 |
| 554 | 554 | 0 | 0 | 0 | 0 | −444 | 0 | 0 | 0 |
| 564 | 564 | 564 | 564 | 564 | 564 | J | J | 564 | 564 |
| 664 | 664 | 0 | 0 | 0 | 0 | 124 | 0 | 0 | 0 |
| 115 | 115 | 115 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 125 | 125 | 125 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 135 | 135 | 135 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 145 | 145 | 0 | 0 | −254 | 0 | 0 | −254 | 0 | 0 |
| 155 | 155 | 155 | 155 | 244 | 244 | 244 | 244 | 244 | 344 |
| 165 | 165 | 0 | 0 | 0 | 0 | K | 0 | 0 | 0 |
| 225 | 225 | 225 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 235 | 235 | 235 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 245 | 245 | 0 | 0 | 0 | 0 | 0 | −154 | 0 | 0 |
| 255 | 255 | 255 | 255 | 144 | 144 | 144 | 144 | 144 | 144 |
| 265 | 265 | 0 | 0 | 0 | 0 | L | 0 | 0 | 0 |
| 335 | 335 | 335 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 345 | 345 | 0 | 0 | −354 | 0 | 0 | −354 | 0 | 0 |
| 355 | 355 | 355 | 355 | 344 | 344 | 344 | 344 | 244 | 244 |
| 365 | 365 | 0 | 0 | 0 | 0 | 134 | 0 | 0 | 0 |
| 445 | 445 | 445 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 455 | 455 | 0 | 0 | 0 | 0 | −444 | 0 | 0 | 0 |
| 465 | 465 | 465 | 465 | 564 | 564 | J | J | 564 | 564 |
| 555 | 555 | 555 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 565 | 565 | 0 | 0 | −464 | 0 | 0 | −U | 0 | 0 |
| 665 | 665 | 665 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 116 | 116 | 0 | 0 | 116 | 0 | 0 | Y | 0 | 0 |
| 126 | 126 | 0 | 0 | 0 | 0 | 0 | X | 0 | 0 |
| 136 | 136 | 0 | 0 | 136 | 0 | 0 | −361 | 0 | 0 |
| 146 | 146 | 146 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 156 | 156 | 0 | 0 | 0 | 0 | −E/2 + 241/2 | 0 | 0 | 0 |
| 166 | 166 | 166 | 166 | 166 | 166 | D/2−111/ 4−221/4 | D/2−111/ 4−221/4 | 244 | 244 |
| 226 | 226 | 0 | 0 | −116 | 0 | 0 | −3Y−4 × 261 | 0 | 0 |
| 236 | 236 | 0 | 0 | −136 | 0 | 0 | 361 | 0 | 0 |
| 246 | 246 | 246 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 256 | 256 | 0 | 0 | 0 | 0 | −C/2 + 141/2 | 0 | 0 | 0 |
| 266 | 266 | 266 | 266 | 166 | 166 | N/2 | N/2 | 244 | 344 |
| 336 | 336 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 346 | 346 | 346 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 356 | 356 | 0 | 0 | 0 | 0 | 341 | 0 | 0 | 0 |
| 366 | 366 | 366 | 366 | 366 | 366 | O | O | 144 | 144 |
| 446 | 446 | 0 | 0 | 446 | 0 | 0 | 451 | 0 | 0 |
| 456 | 456 | 456 | 456 | 456 | 456 | P | P | 564 | 564 |
| 466 | 466 | 0 | 0 | 0 | 0 | M/2 | 0 | 0 | 0 |
| 556 | 556 | 0 | 0 | −446 | 0 | 0 | −451 | 0 | 0 |
| 566 | 566 | 566 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 666 | 666 | 0 | 0 | 0 | 0 | 0 | X | 0 | 0 |
| Expression | Equivalence | Expression | Equivalence | Expression | Equivalence |
|---|---|---|---|---|---|
| A | 121/2−111/4 + 3/4 × 221 + 661 | J | (244−144)/2 | R | −151/2−251/2−461 |
| B | 111/4 + 121/2 + 221/4−661 | K | (114 + 3 × 124)/2 | S | 251/2−151/2 |
| C | 561−241/2−141/2 | L | (114−124)/2 | T | 141/2−241/2 |
| D | 3/4 × 111 + 121/2−221/4 + 661 | M | 241/2−141/2 + 561 | U | (154−254)/2 |
| E | −141/2−241/2−561 | N | (3 × 111)/4−121/2−221/4−661 | V | −164/2−(3 × 264)/2 |
| F | (141−241)/2 | O | (131−231)/2 | W | 264/2−164/2 |
| G | (111−2 × 121 + 221)/4 | P | (551−441)/2 | X | (261−161)/2 |
| H | (113−123)/2 | Q | 461−251/2−151/2 | Y | −(161 + 3 × 261)/2 |
| I | −(114 + 2 × 124) |
References
- Berlincourt, D. Piezoelectric Crystals and Ceramics. In Ultrasonic Transducer Materials; Mattiat, O.E., Ed.; Springer: Boston, MA, USA, 1971; pp. 63–124. [Google Scholar] [CrossRef]
- Shilpa, G.D.; Sreelakshmi, K.; Ananthaprasad, M.G. PZT thin film deposition techniques, properties and its application in ultrasonic MEMS sensors: A review. IOP Conf. Ser. Mater. Sci. Eng. 2016, 149, 012190. [Google Scholar] [CrossRef]
- Micard, Q.; Condorelli, G.G.; Malandrino, G. Piezoelectric BiFeO3 Thin Films: Optimization of MOCVD Process on Si. Nanomaterials 2020, 10, 630. [Google Scholar] [CrossRef] [PubMed]
- Godard, N.; Grysan, P.; Defay, E.; Glinšek, S. Growth of 100-oriented lead zirconate titanate thin films mediated by a safe solvent. J. Mater. Chem. C 2021, 9, 281–287. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, H.; Yan, J.; Chen, N.; Yan, P.; Yang, F.; Ouyang, J. Large piezoelectricity on Si from highly (001)-oriented PZT thick films via a CMOS-compatible sputtering/RTP process. Materialia 2019, 5, 100228. [Google Scholar] [CrossRef]
- Liu, W.; Xu, W.; Wang, W.; He, L.; Zhou, J.; Radhakrishnan, K.; Yu, H.; Ren, J. RF reactive sputtering AlN thin film at room temperature for CMOS-compatible MEMS application. In Proceedings of the 2017 Joint IEEE International Symposium on the Applications of Ferroelectric (ISAF)/International Workshop on Acoustic Transduction Materials and Devices (IWATMD)/Piezoresponse Force Microscopy (PFM), Atlanta, GA, USA, 7–11 May 2017; pp. 52–55. [Google Scholar] [CrossRef]
- Chen, C.; Shang, Z.; Gong, J.; Zhang, F.; Zhou, H.; Tang, B.; Xu, Y.; Zhang, C.; Yang, Y.; Mu, X. Electric Field Stiffening Effect in c-Oriented Aluminum Nitride Piezoelectric Thin Films. ACS Appl. Mater. Interfaces 2018, 10, 1819–1827. [Google Scholar] [CrossRef]
- Wang, W.; Weinstein, D. Acoustic Bragg reflectors for Q-enhancement of unreleased MEMS resonators. In Proceedings of the 2011 Joint Conference of the IEEE International Frequency Control and the European Frequency and Time Forum (FCS) Proceedings, San Francisco, CA, USA, 2–5 May 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Saddik, G.N.; Boesch, D.S.; Stemmer, S.; York, R.A. Strontium titanate DC electric field switchable and tunable bulk acoustic wave solidly mounted resonator. In Proceedings of the 2008 IEEE MTT-S International Microwave Symposium Digest, Atlanta, GA, USA, 15–20 June 2008; pp. 1263–1266. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, T.; Wang, Q.M. Frequency-temperature compensation of piezoelectric resonators by electric DC bias field. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2005, 52, 1627–1631. [Google Scholar] [CrossRef]
- Piazza, G.; Stephanou, P.J.; Pisano, A.P. Piezoelectric Aluminum Nitride Vibrating Contour-Mode MEMS Resonators. J. Microelectromechanical Syst. 2006, 15, 1406–1418. [Google Scholar] [CrossRef]
- Lin, B.T.; Lee, W.H.; Shieh, J.; Chen, M.J. Ferroelectric AlN ultrathin films prepared by atomic layer epitaxy. In Proceedings of the Behavior and Mechanics of Multifunctional Materials XIII, Denver, CO, USA, 3–7 March 2019; Naguib, H.E., Ed.; International Society for Optics and Photonics, SPIE: Denver, Colorado, 2019; Volume 10968, pp. 287–293. [Google Scholar] [CrossRef]
- Liu, H.; Zhong, J.; Lee, C.; Lee, S.W.; Lin, L. A comprehensive review on piezoelectric energy harvesting technology: Materials, mechanisms, and applications. Appl. Phys. Rev. 2018, 5, 041306. [Google Scholar] [CrossRef]
- Wang, L.P.; Wolf, R.; Wang, Y.; Deng, K.; Zou, L.; Davis, R.; Trolier-McKinstry, S. Design, fabrication, and measurement of high-sensitivity piezoelectric microelectromechanical systems accelerometers. J. Microelectromechanical Syst. 2003, 12, 433–439. [Google Scholar] [CrossRef]
- Wu, Y.; Ma, Y.; Zheng, H.; Ramakrishna, S. Piezoelectric materials for flexible and wearable electronics: A review. Mater. Des. 2021, 211, 110164. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Y.; Zhao, L.; Xu, D.; Chen, W.; Deng, J. Design and Experiments of a Single-Foot Linear Piezoelectric Actuator Operated in a Stepping Mode. IEEE Trans. Ind. Electron. 2018, 65, 8063–8071. [Google Scholar] [CrossRef]
- Wen, W.; Shitang, H.; Shunzhou, L.; Minghua, L.; Yong, P. Enhanced sensitivity of SAW gas sensor coated molecularly imprinted polymer incorporating high frequency stability oscillator. Sens. Actuators B Chem. 2007, 125, 422–427. [Google Scholar] [CrossRef]
- Zhu, Y.; Lee, J.E.Y.; Seshia, A.A. A Resonant Micromachined Electrostatic Charge Sensor. IEEE Sens. J. 2008, 8, 1499–1505. [Google Scholar] [CrossRef]
- Tichy, J.; Erhart, J.; Kittinger, E.; Prívratskȥ, J. Fundamentals of Piezoelectric Sensorics; Springer: Berlin/Heidelberg, Germany, 2010; pp. 55–68. [Google Scholar]
- Ben Hassine, N.; Mercier, D.; Renaux, P.; Chappaz, C.; Basrour, S.; Defay, E. Linear variation of aluminum nitride capacitance versus voltage induced by a piezoelectric-electrostrictive coupling. J. Appl. Phys. 2008, 104, 034110. [Google Scholar] [CrossRef]
- Hall, D.A. Review Nonlinearity in piezoelectric ceramics. J. Mater. Sci. 2001, 36, 4575–4601. [Google Scholar] [CrossRef]
- Asanuma, H.; Komatsuzaki, T. Nonlinear piezoelectricity and damping in partially-covered piezoelectric cantilever with self-sensing synchronized switch damping on inductor circuit. Mech. Syst. Signal Process. 2020, 144, 106867. [Google Scholar] [CrossRef]
- Stanton, S.C.; McGehee, C.C.; Mann, B.P. Nonlinear dynamics for broadband energy harvesting: Investigation of a bistable piezoelectric inertial generator. Phys. D Nonlinear Phenom. 2010, 239, 640–653. [Google Scholar] [CrossRef]
- Jamshidi, R.; Jafari, A.A. Nonlinear vibration of conical shell with a piezoelectric sensor patch and a piezoelectric actuator patch. J. Vib. Control. 2022, 28, 1502–1519. [Google Scholar] [CrossRef]
- Xu, L.; Mu, X.; Chen, X.G.; Zhang, H.Y.; Xiong, R.G. Organic Enantiomeric Ferroelectrics with High Piezoelectric Performance: Imidazolium l- and d-Camphorsulfonate. Chem. Mater. 2021, 33, 5769–5779. [Google Scholar] [CrossRef]
- Tatarenko, A.S.; Murthy, D.V.B.; Srinivasan, G. Hexagonal ferrite-piezoelectric composites for dual magnetic and electric field tunable 8–25 GHz microstripline resonators and phase shifters. Microw. Opt. Technol. Lett. 2012, 54, 1215–1218. [Google Scholar] [CrossRef]
- Serrano, D.E.; Tabrizian, R.; Ayazi, F. Electrostatically tunable piezoelectric-on- silicon micromechanical resonator for real-time clock. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2012, 59, 358–365. [Google Scholar] [CrossRef] [PubMed]
- van Hemert, T.; Reimann, K.; Hueting, R.J.E. Extraction of second order piezoelectric parameters in bulk acoustic wave resonators. Appl. Phys. Lett. 2012, 100, 232901. [Google Scholar] [CrossRef]
- Wang, Q.M.; Zhang, Q.; Xu, B.; Liu, R.; Cross, L.E. Nonlinear piezoelectric behavior of ceramic bending mode actuators under strong electric fields. J. Appl. Phys. 1999, 86, 3352–3360. [Google Scholar] [CrossRef]
- Wang, Q.M.; Zhang, T.; Chen, Q.; Du, X.H. Effect of DC bias field on the complex materials coefficients of piezoelectric resonators. Sens. Actuators A Phys. 2003, 109, 149–155. [Google Scholar] [CrossRef]
- Kusters, J. The Effect of Static Electric Fields on the Elastic Constants of α-Quartz. In Proceedings of the 24th Annual Symposium on Frequency Control, Atlantic City, NJ, USA, 27–29 April 1970; pp. 46–54. [Google Scholar] [CrossRef]
- Newnham, R.E. Properties of Materials: Anisotropy, Symmetry, Structure; Oxford University Press: Oxford, UK, 2005; pp. 147–161. [Google Scholar]
- Defaÿ, E.; Hassine, N.B.; Emery, P.; Parat, G.; Abergel, J.; Devos, A. Tunability of Alluminum Nitride Acoustic Resonators: A Phenomenological Approach. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2011, 58, 2516–2520. [Google Scholar] [CrossRef]
- Hruska, K. Non-linear equations of state of second-order electromechanical effects. Czechoslov. J. Phys. 1964, 14, 309–321. [Google Scholar] [CrossRef]
- Chizhikov, S.I.; Sorokin, N.G.; Petrakov, V.S. The elastoelectric effect in the non-centrosymmetric crystals. Ferroelectrics 1982, 41, 9–25. [Google Scholar] [CrossRef]
- Landis, C.M. Fully coupled, multi-axial, symmetric constitutive laws for polycrystalline ferroelectric ceramics. J. Mech. Phys. Solids 2002, 50, 127–152. [Google Scholar] [CrossRef]
- Delibas, B.; Arockiarajan, A.; Seemann, W. Rate dependent properties of perovskite type tetragonal piezoelectric materials using micromechanical model. Int. J. Solids Struct. 2006, 43, 697–712. [Google Scholar] [CrossRef]
- Auld, B.A. Acoustic Fields And Waves In Solids; Wiley-Interscience: Toronto, Canada, 1973; Volume 1, pp. 386–408. [Google Scholar]
- Hahn, T.; Klapper, H.; Muller, U.; Aroyo, M.I. Point Groups and Crystal Classes; Internation Union of Crystallography: New York, NY, USA, 2016; Volume A, pp. 720–776. [Google Scholar]
- García, L.; Scherer, C. Introduction to Classical Thermodynamics; Trillas: Ciudad de Mexíco, Mexico, 1972; Chapter 9. [Google Scholar]
- Clayton, J.D. Nonlinear Mechanics of Crystals; Springer: London, UK, 2011; pp. 543–566. [Google Scholar]
- Manjunatha, H.; Naidu, K.C.B.; Kumar, N.S.; Pothu, R.; Boddula, R. Applications of Metal–Organic Frameworks (MOFs) and Their Derivatives in Piezo/Ferroelectrics. In Applications of Metal–Organic Frameworks and Their Derived Materials; John Wiley & Sons, Ltd: Hoboken, NJ, USA, 2020; Chapter 2; pp. 41–51. [Google Scholar]
- Kittinger, E.; Tichy, J. Electroelastic effect of crystal rods expressed by fundamental material constants. J. Acoust. Soc. Am. 1987, 83, 647–651. [Google Scholar] [CrossRef]
- Hruska, C.K. Determination of the thirdorder piezoelectric constants of quartz using the extentional mode of rods. J. Appl. Phys. 1989, 66, 1071–1074. [Google Scholar] [CrossRef]
- Tunable Silicon Bulk Acoustic Resonators with Multi-Face AlN transduction; International Frequency Control and the European Frequency and Time Forum: San Francisco, CA, USA, 2011.
- Feldmann, M.; Hénaff, J. Surface Acoustic Waves for Signal Processing; Artech House: Norwood, OH, USA, 1989; Volume 1, pp. 29–41. [Google Scholar]
- Bertotti, G.; Mayergoyz, I.D. The Science of Hysteresis; Elsevier: Amsterdam, The Netherlands, 2005; Volume 3, Chapter 4; pp. 337–451. [Google Scholar]
- Smith, R.C. A Domain Wall Model for Hysteresis in Piezoelectric Materials. J. Intell. Mater. Syst. Struct. 2000, 11, 62–79. [Google Scholar] [CrossRef]
- The Effect Of Static Electric Fields On The Elastic Constants of alpha-Quartz; SPIE Smart Structures + Nondestructive Evaluation: Denver, CO, USA, 2019.
- Ang, W.T.; Garmón, F.A.; Khosla, P.K.; Riviere, C.N. Modeling Rate-Dependent Hysteresis in Piezoelectric Actuators. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003) (Cat. No. 03CH37453), Las Vegas, NV, USA, 27–31 October 2003. [Google Scholar]
- Abdolali, S.; Jahromi, Z. Nonlinear Constitutive Modeling of Piezoelectric Materials. Master’s Thesis, University of Calagary, Calgary, AB, Canada, 2013. [Google Scholar]
- Fulton, C.C.; Gao, H. Electrical Nonlinearity in Fracture of Piezoelectric Ceramics. Appl. Mech. Rev. 1997, 50, S56–S63. [Google Scholar] [CrossRef]
- Eitel, R.E.; Shrout, T.R.; Randall, C.A. Nonlinear contributions to the dielectric permittivity and converse piezoelectric coefficient in piezoelectric ceramics. J. Appl. Phys. 2006, 99, 124110. [Google Scholar] [CrossRef]
| Material Parameter | Symbol | Definition | Order | Units |
|---|---|---|---|---|
| Elasticity Constant | N/m | |||
| Relative Electrical Permittivity | 1 | |||
| Electrical correction term of elasticity constants Strain correction term of piezoelectric coefficient | C/m | |||
| Electrical correction term of piezoelectric coefficient Strain correction term of electrical permittivity | N/Vm | |||
| Electrical correction term of permittivity | C/V | |||
| Strain correction term of elasticity constants | N/m |
| Crystal System | Laue Group | Symbol | Id. | Symbol | Id. | Symbol | Id. |
|---|---|---|---|---|---|---|---|
| Triclinic | N | 1 | 1 | 2 | |||
| Monoclinic | M | 2 | 3 | m | 4 | 2/m | 5 |
| Orthorhombic | O | 222 | 6 | mm2 | 7 | mmm | 8 |
| Tetragonal | TII | 4 | 9 | 10 | 4/m | 11 | |
| Tetragonal | TI | 4 mm | 13 | 2 m | 14 | 4/mmm | 15 |
| Rhombohedral | RI | 32 | 16 | 3 m | 17 | m | 18 |
| Rhombohedral | RII | 3 | 19 | 20 | 422 | 12 | |
| Hexagonal | HII | 6 | 21 | 22 | 6/m | 23 | |
| Hexagonal | HI | 622 | 24 | 6 mm | 25 | m | 26 |
| Cubic | CII | 23 | 28 | m | 29 | 6/mmm | 27 |
| Cubic | CI | 432 | 30 | 4m | 31 | mm | 32 |
| Laue Group | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Comp. | N | M | O | TII | TI | RI | RII | HII | HI | CI | CII |
| 111 | 111 | 111 | 111 | 111 | 111 | 111 | 111 | 111 | 111 | 111 | 111 |
| 121 | 121 | 0 | 0 | 121 | 0 | 0 | 121 | 121 | 0 | 0 | 0 |
| 131 | 131 | 131 | 0 | 0 | 0 | 0 | 131 | 0 | 0 | 0 | 0 |
| 221 | 221 | 221 | 221 | 221 | 221 | 221 | 221 | 221 | 221 | 221 | 221 |
| 231 | 231 | 0 | 0 | 0 | 0 | 231 | 231 | 0 | 0 | 0 | 0 |
| 331 | 331 | 331 | 331 | 331 | 331 | 331 | 331 | 331 | 331 | 331 | 331 |
| 112 | 112 | 112 | 112 | 221 | 221 | 221 | 221 | 221 | 221 | 331 | 331 |
| 122 | 122 | 0 | 0 | −121 | 0 | 0 | −121 | −121 | 0 | 0 | 0 |
| 132 | 132 | 132 | 0 | 0 | 0 | 0 | −131 | 0 | 0 | 0 | 0 |
| 222 | 222 | 222 | 222 | 111 | 111 | 111 | 111 | 111 | 111 | 111 | 111 |
| 232 | 232 | 0 | 0 | 0 | 0 | −231 | −231 | 0 | 0 | 0 | 0 |
| 332 | 332 | 332 | 332 | 331 | 331 | 331 | 331 | 331 | 331 | 221 | 221 |
| 113 | 113 | 113 | 113 | 113 | 113 | 113 | 113 | 113 | 113 | 221 | 221 |
| 123 | 123 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 133 | 133 | 133 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 223 | 223 | 223 | 223 | 113 | 113 | 113 | 113 | 113 | 113 | 331 | 331 |
| 233 | 233 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 333 | 333 | 333 | 333 | 333 | 333 | 333 | 333 | 333 | 333 | 111 | 111 |
| 114 | 114 | 0 | 0 | 0 | 0 | 114 | 114 | 0 | 0 | 0 | 0 |
| 124 | 124 | 124 | 0 | 0 | 0 | 0 | 124 | 0 | 0 | 0 | 0 |
| 134 | 134 | 0 | 0 | 134 | 0 | 0 | 134 | 134 | 0 | 0 | 0 |
| 224 | 224 | 0 | 0 | 0 | 0 | −114 | −114 | 0 | 0 | 0 | 0 |
| 234 | 234 | 234 | 234 | 234 | 234 | 234 | 234 | 234 | 234 | 234 | 234 |
| 334 | 334 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 115 | 115 | 115 | 0 | 0 | 0 | 0 | −124 | 0 | 0 | 0 | 0 |
| 125 | 125 | 0 | 0 | 0 | 0 | 114 | 114 | 0 | 0 | 0 | 0 |
| 135 | 135 | 135 | 135 | 234 | 234 | 234 | 234 | 234 | 234 | 234 | 234 |
| 225 | 225 | 225 | 0 | 0 | 0 | 0 | 124 | 0 | 0 | 0 | 0 |
| 235 | 235 | 0 | 0 | −134 | 0 | 0 | −134 | −134 | 0 | 0 | 0 |
| 335 | 335 | 335 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 116 | 116 | 0 | 0 | 116 | 0 | 0 | −121 | −121 | 0 | 0 | 0 |
| 126 | 126 | 126 | 126 | 126 | 126 | A | A | A | A | 234 | 234 |
| 136 | 136 | 0 | 0 | 0 | 0 | 231 | 231 | 0 | 0 | 0 | 0 |
| 226 | 226 | 0 | 0 | −116 | 0 | 0 | 121 | 121 | 0 | 0 | 0 |
| 236 | 236 | 236 | 0 | 0 | 0 | 0 | −131 | 0 | 0 | 0 | 0 |
| 336 | 336 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Point Group of Symmetry | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Comp. | 1 | 3 | 4 | 6 | 7 | 9 | 10 | 12 | 13 | 14 | 16 | 17 | 19 | 21 | 22 | 24 | 25 | 26 | 28,31 | 30 |
| 111 | 111 | 0 | 111 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 111 | 0 | 111 | 0 | 111 | 0 | 0 | 111 | 0 | 0 |
| 121 | 121 | 0 | 121 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 121 | 0 | 121 | 0 | 121 | 0 | 0 | 121 | 0 | 0 |
| 131 | 131 | 0 | 131 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 131 | 0 | 131 | 0 | 131 | 0 | 0 | 131 | 0 | 0 |
| 141 | 141 | 141 | 0 | 141 | 0 | 141 | 141 | 141 | 0 | 141 | 141 | 0 | 141 | 141 | 0 | 141 | 0 | 0 | 141 | 0 |
| 151 | 151 | 0 | 151 | 0 | 151 | 151 | 151 | 0 | 151 | 0 | 0 | 151 | 151 | 151 | 0 | 0 | 151 | 0 | 0 | 0 |
| 161 | 161 | 161 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 161 | 161 | 0 | 161 | 0 | 0 | 0 | 0 | 0 |
| 221 | 221 | 0 | 221 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | A | 0 | J | 0 | A | 0 | 0 | A | 0 | 0 |
| 231 | 231 | 0 | 231 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −131 | 0 | −131 | 0 | −131 | 0 | 0 | −131 | 0 | 0 |
| 241 | 241 | 241 | 0 | 241 | 0 | 241 | 241 | 241 | 0 | 241 | 241 | 0 | 241 | 241 | 0 | 241 | 0 | 0 | 241 | 241 |
| 251 | 251 | 0 | 251 | 0 | 251 | 251 | 251 | 0 | 251 | 0 | 0 | 251 | 251 | 251 | 0 | 0 | 251 | 0 | 0 | 0 |
| 261 | 261 | 261 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 261 | 261 | 0 | 261 | 0 | 0 | 0 | 0 | 0 |
| 331 | 331 | 0 | 331 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 341 | 341 | 341 | 0 | 341 | 0 | 341 | 341 | 341 | 0 | 341 | 341 | 0 | 341 | 341 | 0 | 341 | 0 | 0 | 341 | −241 |
| 351 | 351 | 0 | 351 | 0 | 351 | 351 | 351 | 0 | 351 | 0 | 0 | 342 | 351 | 351 | 0 | 0 | 351 | 0 | 0 | 0 |
| 361 | 361 | 361 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 361 | 361 | 0 | 361 | 0 | 0 | 0 | 0 | 0 |
| 441 | 441 | 0 | 441 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 441 | 0 | 441 | 0 | 441 | 0 | 0 | 441 | 0 | 0 |
| 451 | 451 | 451 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 451 | 451 | 0 | 451 | 0 | 0 | 0 | 0 | 0 |
| 461 | 461 | 0 | 461 | 0 | 461 | 461 | 461 | 0 | 461 | 0 | 0 | E | E | E | 0 | 0 | E | 0 | 0 | 0 |
| 551 | 551 | 0 | 551 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −441 | 0 | −441 | 0 | −441 | 0 | 0 | −441 | 0 | 0 |
| 561 | 561 | 561 | 0 | 561 | 0 | 561 | 561 | 561 | 0 | 561 | B | 0 | B | B | 0 | B | 0 | 0 | 561 | 0 |
| 661 | 661 | 0 | 661 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 121 | 0 | 121 | 0 | 121 | 0 | 0 | 121 | 0 | 0 |
| 112 | 112 | 112 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | F | F | 0 | F | 0 | 0 | 0 | 0 | 0 |
| 122 | 122 | 122 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | G | G | 0 | G | 0 | 0 | 0 | 0 | 0 |
| 132 | 132 | 132 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 361 | 361 | 0 | 361 | 0 | 0 | 0 | 0 | 0 |
| 142 | 142 | 0 | 142 | 0 | 142 | 251 | −251 | 0 | 251 | 0 | 0 | 251 | 251 | 251 | 0 | 0 | 251 | 0 | 0 | 0 |
| 152 | 152 | 152 | 0 | 152 | 0 | −241 | 241 | −241 | 0 | 241 | −241 | 0 | −241 | −241 | 0 | −241 | 0 | 0 | 341 | −241 |
| 162 | 162 | 0 | 162 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | C | 0 | C | 0 | C | 0 | 0 | C | 0 | 0 |
| 222 | 222 | 222 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | H | H | 0 | H | 0 | 0 | 0 | 0 | 0 |
| 232 | 232 | 232 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −361 | −361 | 0 | −361 | 0 | 0 | 0 | 0 | 0 |
| 242 | 242 | 0 | 242 | 0 | 242 | 151 | −151 | 0 | 151 | 0 | 0 | 151 | 151 | 151 | 0 | 0 | 151 | 0 | 0 | 0 |
| 252 | 252 | 252 | 0 | 252 | 0 | −141 | 141 | −141 | 0 | 141 | −141 | 0 | -141 | −141 | 0 | −141 | 0 | 0 | 141 | 0 |
| 262 | 262 | 0 | 262 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | D | 0 | -D | 0 | -D | 0 | 0 | -D | 0 | 0 |
| 332 | 332 | 332 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 342 | 342 | 0 | 342 | 0 | 342 | 351 | −351 | 0 | 351 | 0 | 0 | 342 | 351 | 351 | 0 | 0 | 351 | 0 | 0 | 0 |
| 352 | 352 | 352 | 0 | 352 | 0 | −341 | 341 | −341 | 0 | 341 | −341 | 0 | -341 | −341 | 0 | −341 | 0 | 0 | 241 | 241 |
| 362 | 362 | 0 | 362 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −131 | 0 | −131 | 0 | −131 | 0 | 0 | −131 | 0 | 0 |
| 442 | 442 | 442 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −451 | −451 | 0 | −451 | 0 | 0 | 0 | 0 | 0 |
| 452 | 452 | 0 | 452 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 441 | 0 | 441 | 0 | 441 | 0 | 0 | 441 | 0 | 0 |
| 462 | 462 | 462 | 0 | 462 | 0 | −561 | 561 | −561 | 0 | 561 | −B | 0 | −B | −B | 0 | −B | 0 | 0 | 561 | 0 |
| 552 | 552 | 552 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 451 | 451 | 0 | 451 | 0 | 0 | 0 | 0 | 0 |
| 562 | 562 | 0 | 562 | 0 | 562 | 461 | −461 | 0 | 461 | 0 | 0 | E | E | E | 0 | 0 | E | 0 | 0 | 0 |
| 662 | 662 | 662 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | G | G | 0 | G | 0 | 0 | 0 | 0 | 0 |
| 113 | 113 | 0 | 113 | 0 | 113 | 113 | 113 | 0 | 113 | 0 | 0 | 113 | 113 | 113 | 0 | 0 | 113 | 0 | 0 | 0 |
| 123 | 123 | 0 | 123 | 0 | 123 | 123 | 0 | 0 | 123 | 0 | 0 | 123 | 123 | 123 | 0 | 0 | 123 | 0 | 0 | 0 |
| 133 | 133 | 0 | 133 | 0 | 133 | 133 | 133 | 0 | 133 | 0 | 0 | 133 | 133 | 133 | 0 | 0 | 133 | 0 | 0 | 0 |
| 143 | 143 | 143 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 143 | 143 | 0 | 143 | 0 | 0 | 0 | 0 | 0 |
| 153 | 153 | 0 | 153 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 153 | 0 | 153 | 0 | 153 | 0 | 0 | 153 | 0 | 0 |
| 163 | 163 | 163 | 0 | 163 | 0 | 163 | 163 | 163 | 0 | 163 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 241 | 241 |
| 223 | 223 | 0 | 223 | 0 | 223 | 113 | −113 | 0 | 113 | 0 | 0 | 113 | 113 | 113 | 0 | 0 | 113 | 0 | 0 | 0 |
| 233 | 233 | 0 | 233 | 0 | 233 | 133 | −133 | 0 | 133 | 0 | 0 | 133 | 133 | 133 | 0 | 0 | 133 | 0 | 0 | 0 |
| 243 | 243 | 243 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −143 | −143 | 0 | −143 | 0 | 0 | 0 | 0 | 0 |
| 253 | 253 | 0 | 253 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −153 | 0 | −153 | 0 | −153 | 0 | 0 | −153 | 0 | 0 |
| 263 | 263 | 263 | 0 | 263 | 0 | −163 | 163 | −163 | 0 | 163 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 341 | −241 |
| 333 | 333 | 0 | 333 | 0 | 333 | 333 | 0 | 0 | 333 | 0 | 0 | 333 | 333 | 333 | 0 | 0 | 333 | 0 | 0 | 0 |
| 343 | 343 | 343 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 353 | 353 | 0 | 353 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 363 | 363 | 363 | 0 | 363 | 0 | 0 | 363 | 0 | 0 | 363 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 141 | 0 |
| 443 | 443 | 0 | 443 | 0 | 443 | 443 | 443 | 0 | 443 | 0 | 0 | 443 | 443 | 443 | 0 | 0 | 443 | 0 | 0 | 0 |
| 453 | 453 | 453 | 0 | 453 | 0 | 0 | 453 | 0 | 0 | 453 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 561 | 0 |
| 463 | 463 | 0 | 463 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −153 | 0 | −153 | 0 | −153 | 0 | 0 | −153 | 0 | 0 |
| 553 | 553 | 0 | 553 | 0 | 553 | 443 | −443 | 0 | 443 | 0 | 0 | 443 | 443 | 443 | 0 | 0 | 443 | 0 | 0 | 0 |
| 563 | 563 | 563 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 143 | 143 | 0 | 143 | 0 | 0 | 0 | 0 | 0 |
| 663 | 663 | 0 | 663 | 0 | 663 | 663 | 0 | 0 | 663 | 0 | 0 | I | I | I | 0 | 0 | I | 0 | 0 | 0 |
| Percent Error | |||
|---|---|---|---|
| Quantity | Symbol | Average | Maximum |
| Effective Elasticity Constant | 0.28 | 0.79 | |
| Relative Effective Electrical Permittivity | 0.92 | 2.9 | |
| Resonance Frequency | 0.15 | 0.3 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaramillo-Alvarado, A.F.; Torres Jacome, A.; Rosales-Quintero, P.; Vazquez-Leal, H.; Diaz-Arango, G.; Huerta-Chua, J.; Martínez-Castillo, J. Stress–Charge Nonlinear Physical Description and Tensor Symmetries for Piezoelectric Materials. Materials 2023, 16, 3432. https://doi.org/10.3390/ma16093432
Jaramillo-Alvarado AF, Torres Jacome A, Rosales-Quintero P, Vazquez-Leal H, Diaz-Arango G, Huerta-Chua J, Martínez-Castillo J. Stress–Charge Nonlinear Physical Description and Tensor Symmetries for Piezoelectric Materials. Materials. 2023; 16(9):3432. https://doi.org/10.3390/ma16093432
Chicago/Turabian StyleJaramillo-Alvarado, A. F., A. Torres Jacome, P. Rosales-Quintero, H. Vazquez-Leal, G. Diaz-Arango, J. Huerta-Chua, and J. Martínez-Castillo. 2023. "Stress–Charge Nonlinear Physical Description and Tensor Symmetries for Piezoelectric Materials" Materials 16, no. 9: 3432. https://doi.org/10.3390/ma16093432
APA StyleJaramillo-Alvarado, A. F., Torres Jacome, A., Rosales-Quintero, P., Vazquez-Leal, H., Diaz-Arango, G., Huerta-Chua, J., & Martínez-Castillo, J. (2023). Stress–Charge Nonlinear Physical Description and Tensor Symmetries for Piezoelectric Materials. Materials, 16(9), 3432. https://doi.org/10.3390/ma16093432









