Cumulative Fatigue Damage of Composite Laminates: Engineering Rule and Life Prediction Aspect
Abstract
1. Introduction
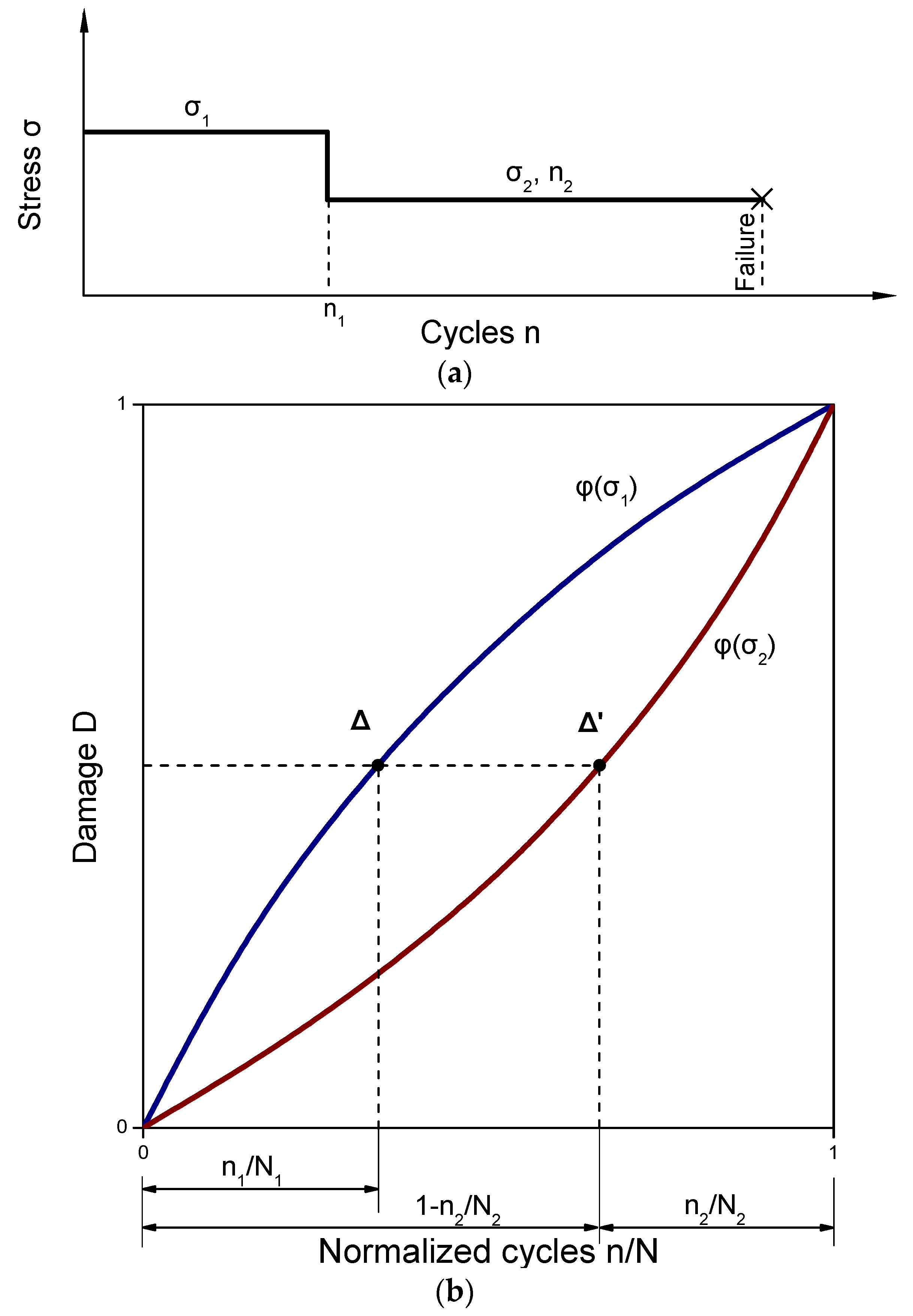
2. Damage Function
3. Damage Analysis under Step Loading
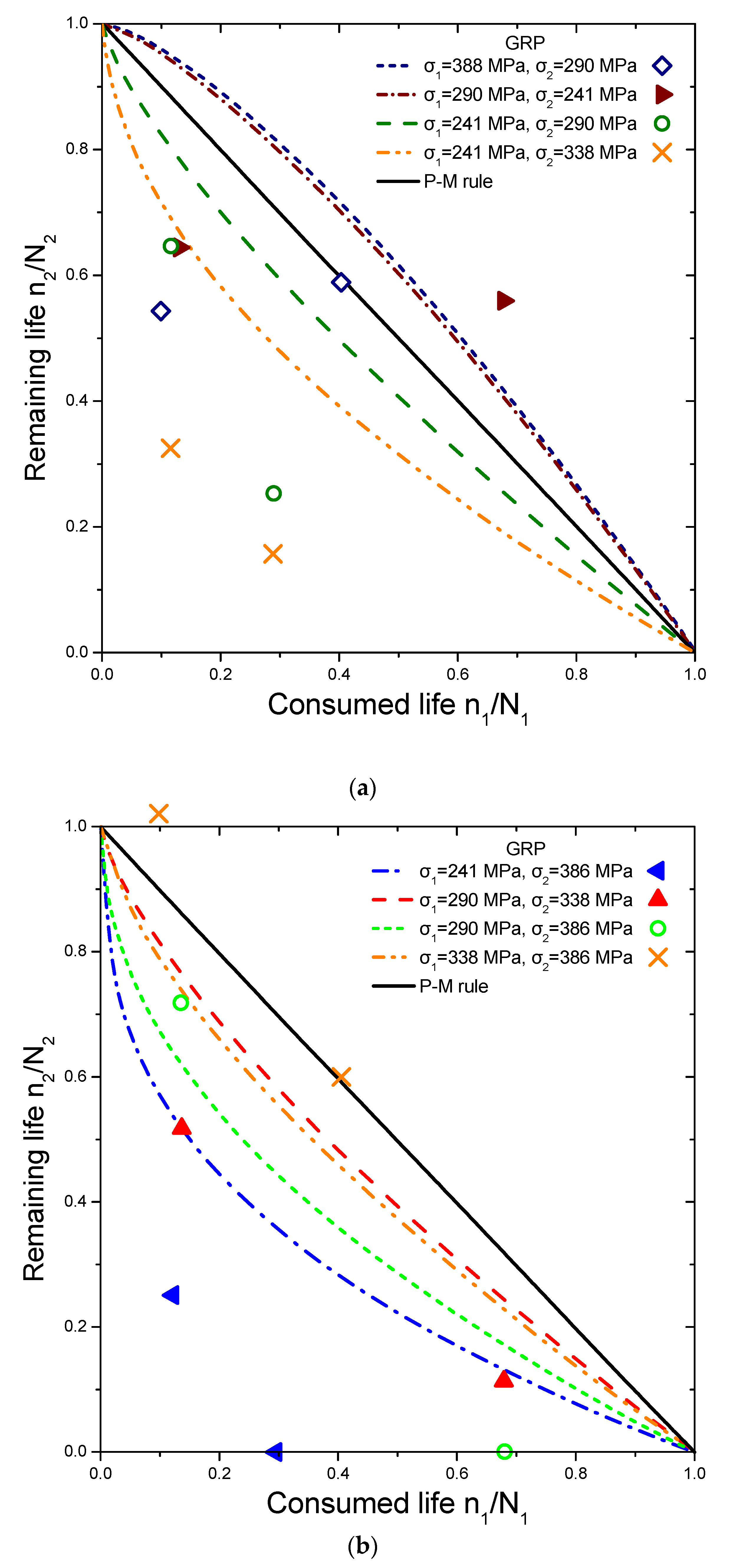
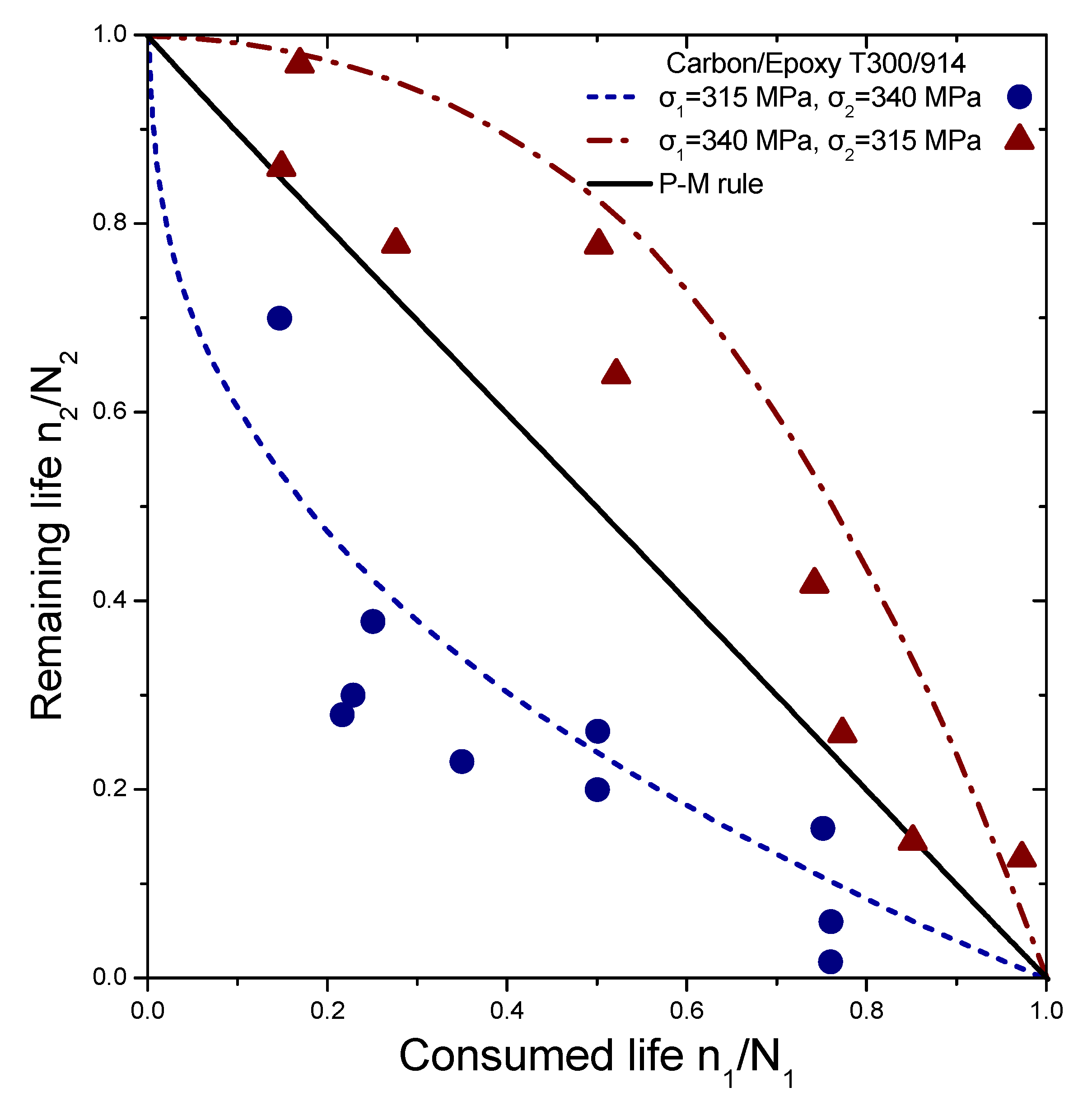
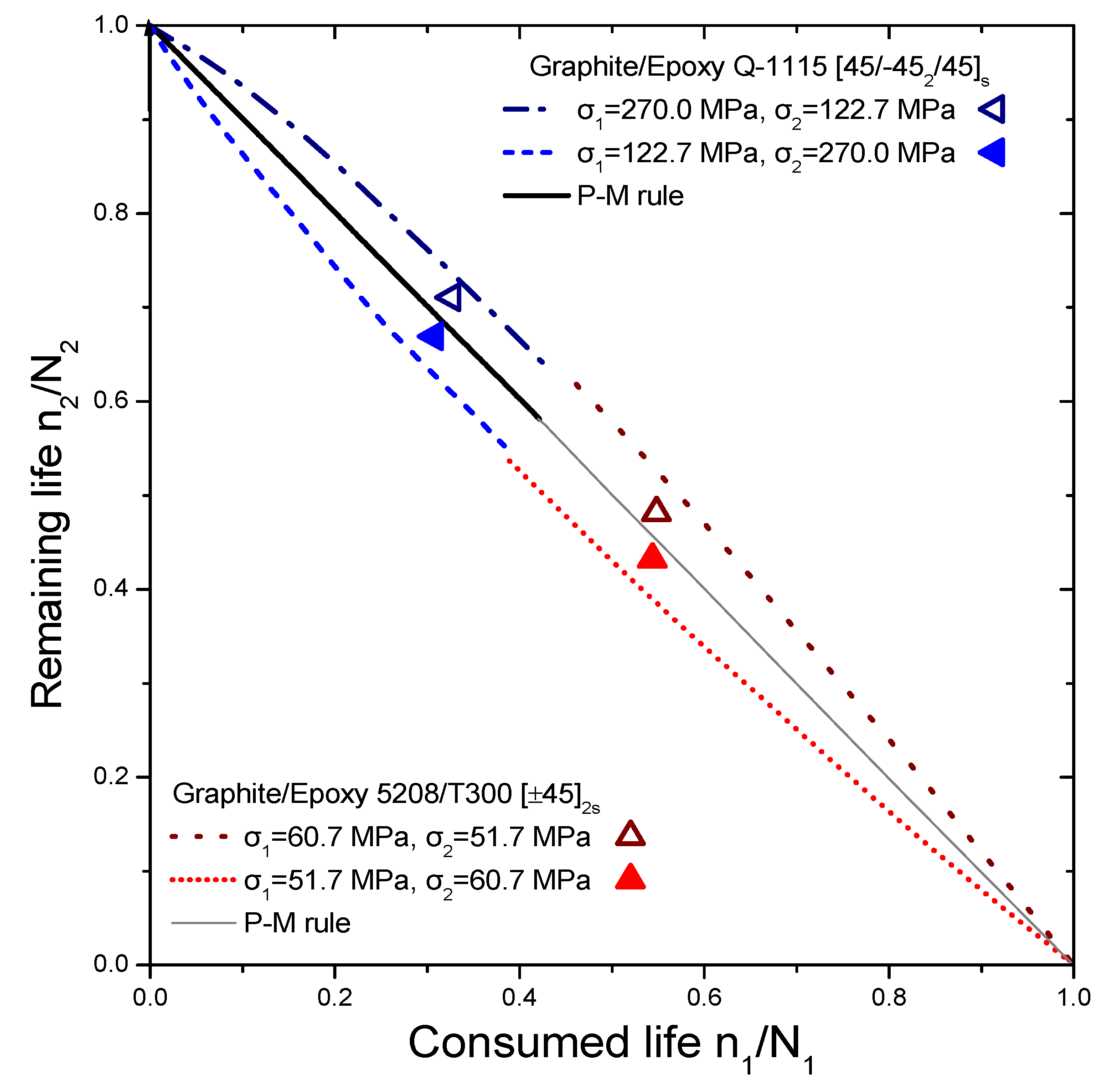
4. Results and Discussion
5. Conclusions
6. Future Developments
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Faidzi, M.K.; Abdullah, S.; Abdullah, M.F.; Singh, S.S.K.; Hui, D. Geometrical effects of different core designs on metal sandwich panel under static and fatigue condition. J. Braz. Soc. Mech. Sci. 2022, 44, 111. [Google Scholar] [CrossRef]
- Li, X.; Sun, Q. Simplification approaches for multi-level load spectra by using equivalent damage rule. Chin. J. Aeronaut. 2021, 34, 119–130. [Google Scholar] [CrossRef]
- Gan, L.; Zhao, X.; Wu, H.; Zhong, Z. Estimation of remaining fatigue life under two-step loading based on kernel-extreme learning machine. Int. J. Fatigue 2021, 148, 106190. [Google Scholar] [CrossRef]
- Hectors, K.; De Waele, W. Cumulative damage and life prediction models for high-cycle fatigue of metals: A review. Metals 2021, 11, 204. [Google Scholar] [CrossRef]
- Xia, F.-L.; Zhu, S.-P.; Liao, D.; Correia, J.A.F.O.; De Jesus, A.M.P. Isodamage curve-based fatigue damage accumulation model considering the exhaustion of static toughness. Eng. Fail. Anal. 2020, 115, 104575. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, C.; Chen, X.; Tan, J. Fatigue reliability analysis of wind turbine drivetrain considering strength degradation and load sharing using survival signature and FTA. Energies 2020, 13, 2108. [Google Scholar] [CrossRef]
- Jia, P.; Liu, H.; Zhu, C.; Wu, W.; Lu, G. Contact fatigue life prediction of a bevel gear under spectrum loading. Front. Mech. Eng. 2020, 15, 123–132. [Google Scholar] [CrossRef]
- Zhu, S.-P.; Liao, D.; Liu, Q.; Correia, J.A.F.O.; De Jesus, A.M.P. Nonlinear fatigue damage accumulation: Isodamage curve-based model and life prediction aspects. Int. J. Fatigue 2019, 128, 105185. [Google Scholar] [CrossRef]
- Zhu, S.-P.; Hao, Y.-Z.; de Oliveira Correia, J.A.F.; Lesiuk, G.; de Jesus, A.M.P. Nonlinear fatigue damage accumulation and life prediction of metals: A comparative study. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 1271–1282. [Google Scholar] [CrossRef]
- Jie, Z.; Li, Y.; Wei, X.; Zhuge, P. Fatigue life prediction of welded joints with artificial corrosion pits based on continuum damage mechanics. J. Constr. Steel Res. 2018, 148, 542–550. [Google Scholar] [CrossRef]
- Palmgren, A. Die Lebensdauer von Kugellagern. Z. Ver. Dtsch. Ing. 1924, 68, 339–341. [Google Scholar]
- Robinson, E.L. Effect of temperature variation on the creep strength of steels. Trans. ASME 1938, 60, 253–259. [Google Scholar] [CrossRef]
- Miner, M.A. Cumulative damage in fatigue. J. Appl. Mech. 1945, 67, A159–A164. [Google Scholar] [CrossRef]
- Aghazadeh Mohandesi, J.; Majidi, B. Fatigue damage accumulation in carbon/epoxy laminated composites. Mater. Des. 2009, 30, 1950–1956. [Google Scholar] [CrossRef]
- Marco, S.M.; Starkey, W.L. A concept of fatigue damage. Trans. ASME 1954, 76, 627–632. [Google Scholar] [CrossRef]
- Found, M.S.; Quaresinin, M. Two-stage fatigue loading of woven carbon fibre reinforced laminates. Fatigue Fract. Eng. Mater. Struct. 2002, 26, 17–26. [Google Scholar] [CrossRef]
- Fissolo, A.; Gourdin, C.; Chen, Y.; Perez, G.; Stelmaszyk, J.M. Investigations into the cumulative fatigue life of an AISI 304L austenitic stainless steel used for pressure water reactors: Application of a double linear damage rule. Int. J. Fatigue 2015, 77, 199–209. [Google Scholar] [CrossRef]
- Huffman, P.J.; Beckman, S.P. A non-linear damage accumulation fatigue model for predicting strain life at variable amplitude loading based on constant amplitude fatigue data. Int. J. Fatigue 2013, 48, 165–169. [Google Scholar] [CrossRef]
- Golos, K.M. A total strain energy density model of metal fatigue. Strength Mater. 1995, 27, 32–41. [Google Scholar] [CrossRef]
- Liu, Y.; Mahadevan, S. Stochastic fatigue damage modeling under variable amplitude loading. Int. J. Fatigue 2007, 29, 1149–1161. [Google Scholar] [CrossRef]
- Stepanskiy, L.G. Cumulative model of very high cycle fatigue. Fatigue. Fract. Eng Mater. Struct. 2012, 35, 513–522. [Google Scholar] [CrossRef]
- Fatemi, A.; Yang, L. Cumulative fatigue damage and life prediction theories: A survey of the state of the art for homogeneous materials. Int. J. Fatigue 1998, 20, 9–34. [Google Scholar] [CrossRef]
- Hwang, W.; Han, K.S. Fatigue of composites-fatigue modules concept and life prediction. Composites 1986, 20, 154–164. [Google Scholar]
- Whitworth, H.A. Modelling stiffness reduction of Gr/ep composite laminates. J. Compos. Mater. 1987, 21, 362–372. [Google Scholar] [CrossRef]
- Brutman, L.J.; Sahu, S.A. New theory to predict cumulative fatigue damage ln: Fiberglass reinforced plastics, composite materials: Testing and design. ASTM STP 1972, 497, 170–188. [Google Scholar]
- Lee, C.-H.; Jen, M.-H.R. Fatigue Response and modelling of variable stress amplitude and frequency in AS-4/PEEK composite laminates, part 2: Analysis and formulation. J. Compos. Mater. 2000, 34, 950–953. [Google Scholar] [CrossRef]
- Epaarachchi, J.A.; Clauseu, P.D. A new cumulative fatigue damage model for glass fibre reinforced plastic composites under step/discrete loading. Compos. Part A 2005, 36, 1236–1245. [Google Scholar] [CrossRef]
- Kachanov, L.M. Time to creep fracture. Izv. Akad. Nauk. SSSR Otd Tekh. Nauk. 1958, 8, 26–31. [Google Scholar]
- Rabotnov, Y.N. The mechanism of delayed fracture. In: Problems of strength of materials and structures. Izv. Akad. Nauk SSSR Mosc. 1959, 5–7. [Google Scholar]
- Rabotnov, Y.N. Creep Problems in Structural Members; North Holland Publishers: Amsterdam, The Netherlands, 1969. [Google Scholar]
- Kachanov, L.M. Introduction to Continuum Damage Mechanics; Martinus Nijhoff: Dordrecht, The Netherlands, 1986. [Google Scholar]
- Lemaitre, J.; Chaboche, J.L. Mechanics of Solid Materials; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Desmorat, R.; Lemaitre, J. Engineering Damage Mechanics; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Fan, Z.C.; Chen, X.D.; Chen, L.; Jiang, J.L. A CDM-based study of fatigue-creep interaction behavior. Int. J. Press Vessels Pip. 2009, 86, 628–632. [Google Scholar] [CrossRef]
- Dattoma, V.; Giancane, S.; Nobile, R.; Panella, F.W. Fatigue life prediction under variable loading based on a new non-linear continuum damage mechanics model. Int. J. Fatigue. 2006, 28, 89–95. [Google Scholar] [CrossRef]
- Hult, J. Continuum damage mechanics–a new design tool. In Materials and Engineering Design: The Next Decade; Dyson, B.F., Hayhurst, D.R., Eds.; Maney Publishing: Leeds, UK, 1989; pp. 199–204. [Google Scholar]
- Chaboch, J.L. Fracture mechanics and damage mechanics: Complementarity of approaches. In Numerical Methods of Fracture Mechanics, Proceedings of the Fourth International Conference, San Antonio, TX, USA, 23–27 March 1987; Luxmoore, A.R., Owen, D.R.J., Rajapakse, Y.P.D., Kanninen, M.F., Eds.; Pineridge Press: Swansea, UK, 1987; pp. 309–324. [Google Scholar]
- Golup, V.P. The nonlinear mechanics of continual damage and its application to problems of creep and fatigue. Int. Appl. Mech. 2000, 36, 303–342. [Google Scholar] [CrossRef]
- Batsoulas, N.D. Creep damage assessment and lifetime predictions for metallic materials under variable loading conditions in elevated temperature applications. Steel Res. Int. 2009, 80, 152–159. [Google Scholar]
- Batsoulas, N.D. Cumulative Fatigue Damage: CDM-based engineering rule and life prediction aspect. Steel Res. Int. 2016, 87, 1670–1677. [Google Scholar] [CrossRef]
- Jen, M.H.R.; Kau, Y.S.; Wu, I.C. Fatigue damage in a centrally notched composite laminate due to two-step spectrum loading. Fatigue 1994, 16, 193–201. [Google Scholar] [CrossRef]
- Manson, S.S.; Halford, G.R. Practical implementation of the double linear change rule and damage curve approach for treating cumulative fatigue damage. Int. J. Fract. 1981, 17, 169–192. [Google Scholar] [CrossRef]
- Hashin, Z.; Rotem, A. A cumulative damage theory of fatigue failure. Mater. Sci. Eng. 1978, 34, 147–160. [Google Scholar] [CrossRef]
- Yao, W.X.; Himmel, N. A new cumulative fatigue damage model for fibre-reinforced plastics. Compos Sci Technol. 2000, 60, 59–64. [Google Scholar] [CrossRef]
- Lee, C.-H.; Jen, M.-H.R. Fatigue Response and modelling of variable stress amplitude and frequency in AS-4/PEEK composite laminates, part 1: Experiments. J. Compos. Mater. 2000, 34, 906–929. [Google Scholar] [CrossRef]
- Gamstedt, E.K.; Sjogre, B.A. An experimental investigation of the sequence effect in block amplitude loading of cross-ply composite laminates. Int. J. Fatigue 2002, 24, 437–466. [Google Scholar] [CrossRef]
- Wu, F.; Yoo, W. A fatigue model of composite materials. Int. J. Fatigue 2010, 32, 134–138. [Google Scholar] [CrossRef]
- Shiri, S.; Pourgol-Mohammed, M.; Yazdani, M. Effect of strength dispersion on fatigue life prediction of composites under two-stage loading. Mater. Des. 2015, 65, 1189–1195. [Google Scholar] [CrossRef]
- Yang, J.N.; Jones, P.l. Effect of load sequence on the statistical fatigue of composites. AIAA J. 1980, 18, 1525–1531. [Google Scholar] [CrossRef]
- Kam, T.Y.; Tsai, S.Y.; Chu, K.H. Fatigue reliability analysis of composite laminates under spectrum stress. Int. J Solids Struct. 1997, 34, 1441–1461. [Google Scholar] [CrossRef]


| Material | σf (MPa) |
|---|---|
| GRP | 506 |
| Carbon/Epoxy T300/914 | 450 |
| Graphite/Epoxy T300/5208 [±45]2s | 94 |
| Graphite/Epoxy Q-1115 [45/−452/45]s | 300 |
| Carbon/Epoxy T800/5208 [0/90/±45]2s | 846 |
| AS-4/PEEK [0/90]4s | 454 |
| AS-4/PEEK [0/45/90/−45]2s | 752 |
| AS-4/PEEK [±45]4s | 967 |
| Applied Stresses (MPa) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| GRP | σ1 | 388 | 290 | 241 | 241 | 241 | 290 | 290 | 338 |
| σ2 | 290 | 241 | 290 | 338 | 386 | 338 | 386 | 386 | |
| Carbon/Epoxy T300/914 | σ1 | 315 | 340 | ||||||
| σ2 | 340 | 315 | |||||||
| Graphite/Epoxy T300/5208 [±45]2s | σ1 | 60.7 | 51.7 | ||||||
| σ2 | 51.7 | 60.7 | |||||||
| Graphite/Epoxy Q-1115 [45/−452/45]s | σ1 | 270.0 | 122.7 | ||||||
| σ2 | 122.7 | 270.0 | |||||||
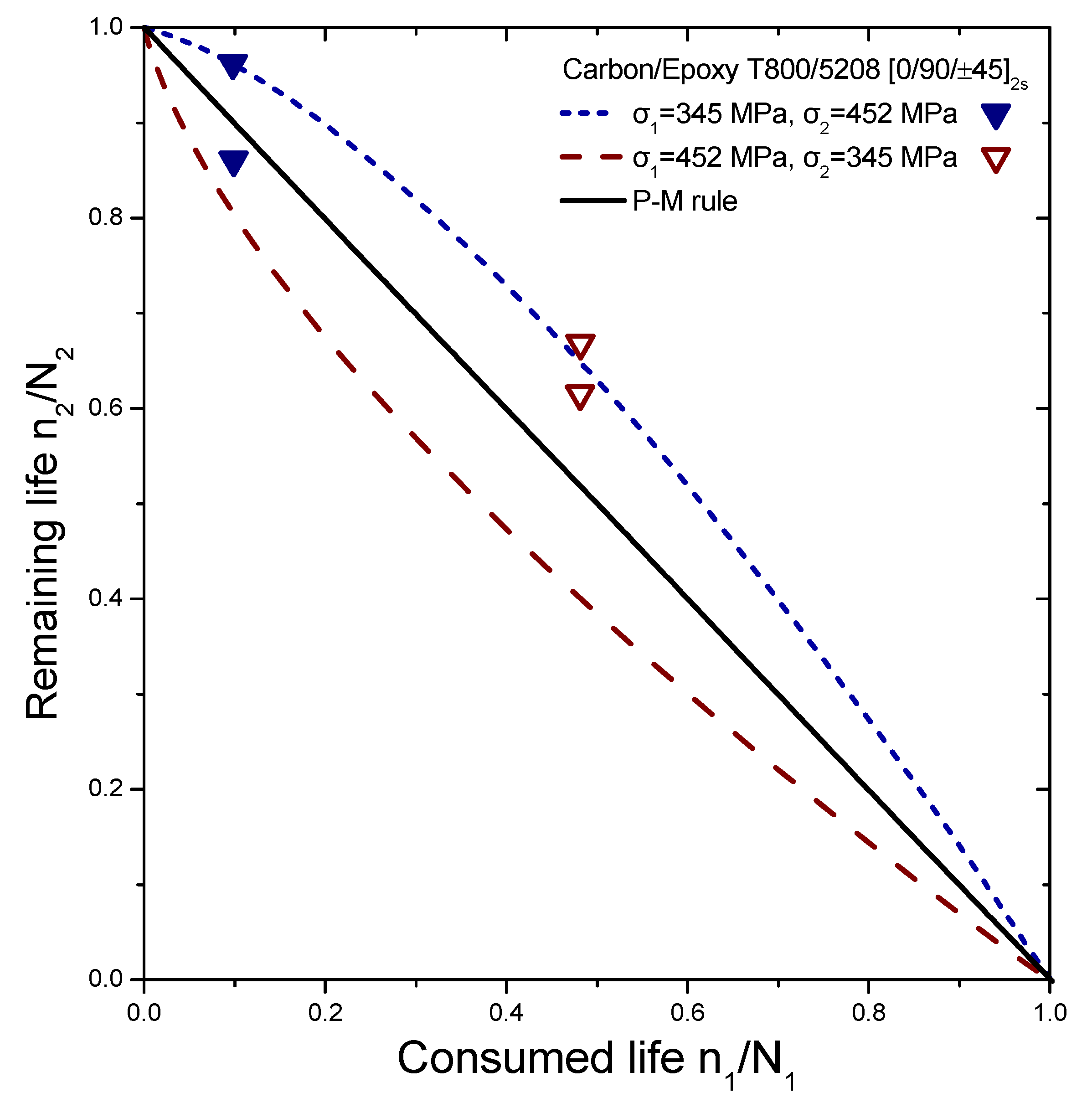
| Carbon/Epoxy T800/5208 [0/90/±45]2s | σ1 | 345 | 452 | ||||||
| σ2 | 452 | 345 | |||||||
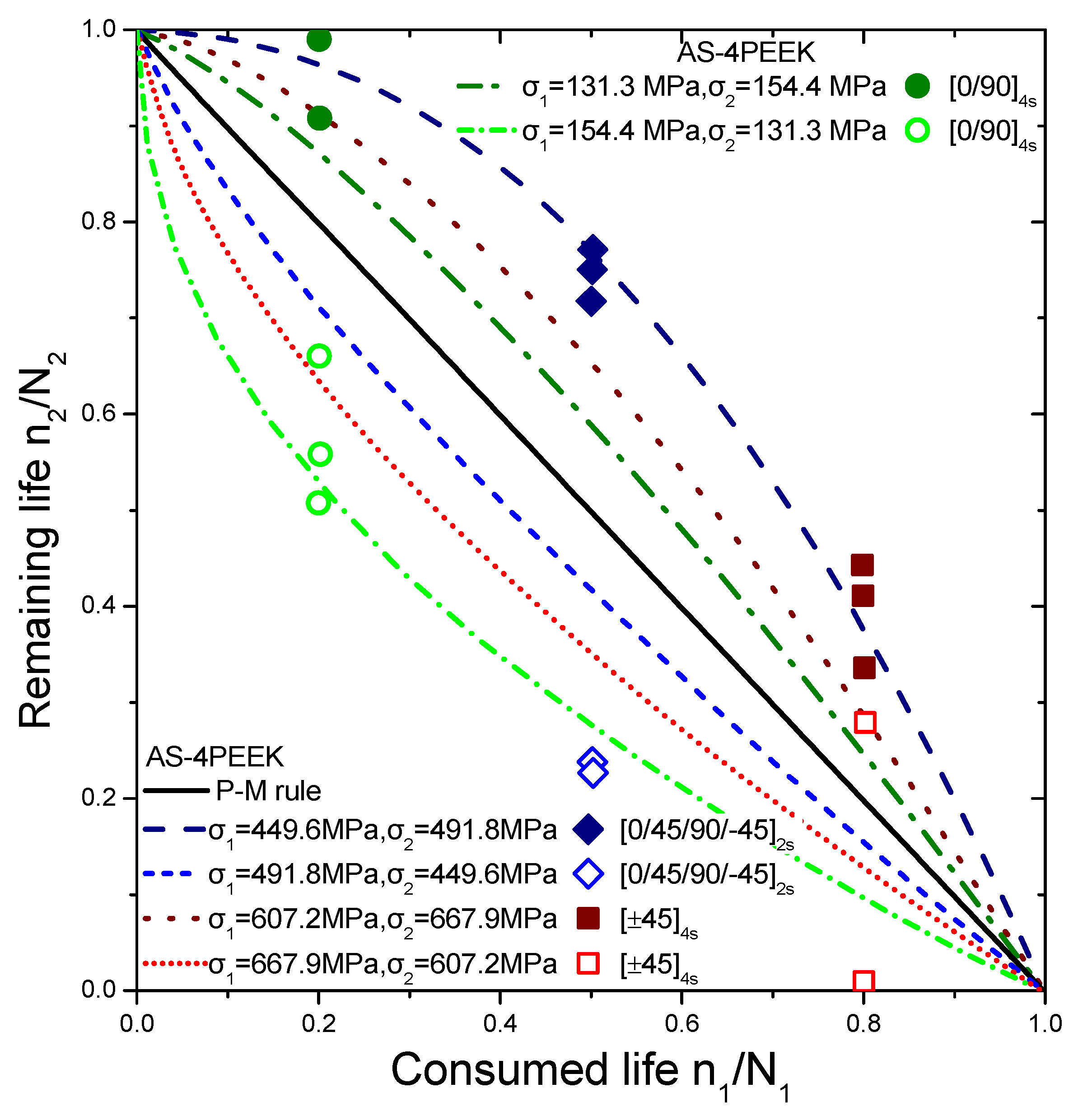
| AS-4PEEK [0/90]4s | σ1 | 131.3 | 154.4 | ||||||
| σ2 | 154.4 | 131.3 | |||||||
| AS-4PEEK [0/45/90/−45]2s | σ1 | 449.6 | 491.8 | ||||||
| σ2 | 491.8 | 449.6 | |||||||
| AS-4PEEK [±45]4s | σ1 | 607.2 | 667.9 | ||||||
| σ2 | 667.9 | 607.2 | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Batsoulas, N.D.; Giannopoulos, G.I. Cumulative Fatigue Damage of Composite Laminates: Engineering Rule and Life Prediction Aspect. Materials 2023, 16, 3271. https://doi.org/10.3390/ma16083271
Batsoulas ND, Giannopoulos GI. Cumulative Fatigue Damage of Composite Laminates: Engineering Rule and Life Prediction Aspect. Materials. 2023; 16(8):3271. https://doi.org/10.3390/ma16083271
Chicago/Turabian StyleBatsoulas, Nikolaos D., and Georgios I. Giannopoulos. 2023. "Cumulative Fatigue Damage of Composite Laminates: Engineering Rule and Life Prediction Aspect" Materials 16, no. 8: 3271. https://doi.org/10.3390/ma16083271
APA StyleBatsoulas, N. D., & Giannopoulos, G. I. (2023). Cumulative Fatigue Damage of Composite Laminates: Engineering Rule and Life Prediction Aspect. Materials, 16(8), 3271. https://doi.org/10.3390/ma16083271







