Theoretical Tolerance Modelling of Dynamics and Stability for Axially Functionally Graded (AFG) Beams
Abstract
1. Introduction
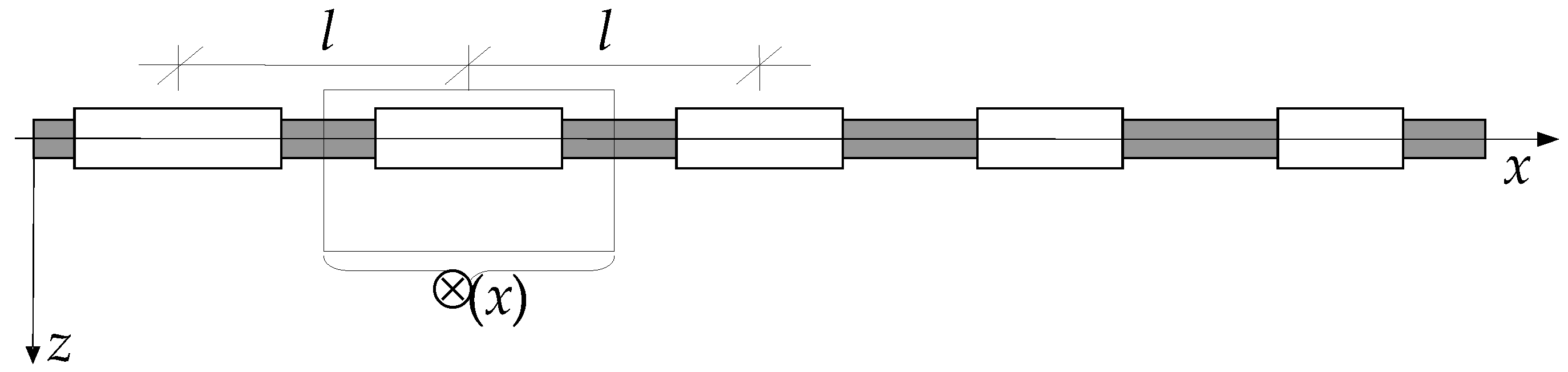
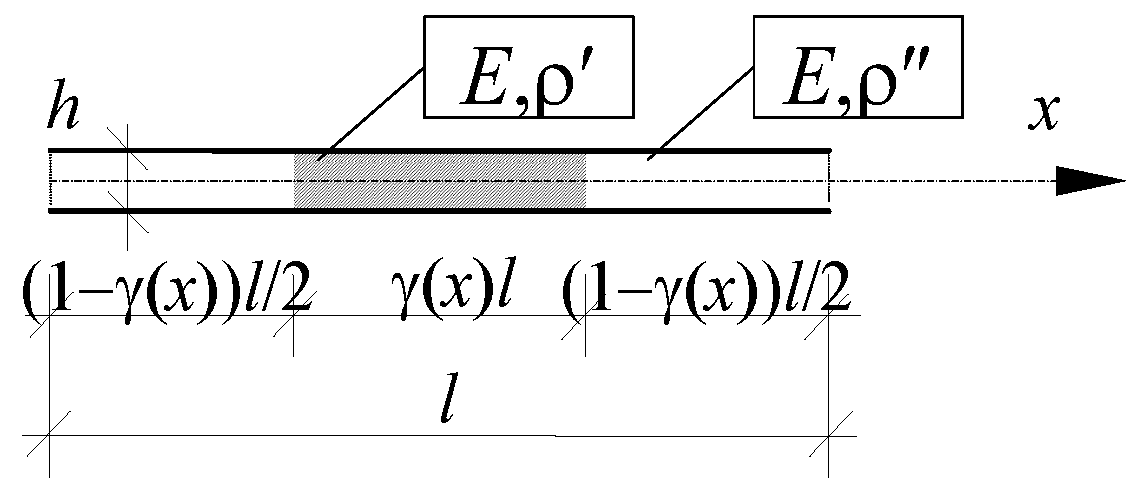
2. Preliminaries of Modelling
3. Tolerance Modelling Approach
3.1. Introductory Concepts
- ∂kg∈O(lα−k) for k = 0,1,…,α, α = 2, ∂0g ≡ g,
- <g>(x) ≈ 0 for every ,
3.2. Assumptions of Modelling
3.3. Modelling Procedure
4. Asymptotic Modelling Approach
4.1. Basic Assumptions
4.2. Modelling Procedure
5. Model Equations
5.1. General Tolerance Model Equations
5.2. Standard Tolerance Model Equations
5.3. Equations of Asymptotic Model
6. Free Vibrations of a Special AFG Beam
6.1. Introduction
6.2. Free Vibration Equations
- The general tolerance model
- The standard tolerance model
- The asymptotic model
6.3. Free Vibration Frequencies—The Ritz Method Applied to the Model Equations
- the general tolerance model
- the standard tolerance model
- the asymptotic model
- the general tolerance model
- the standard tolerance model
- the asymptotic model
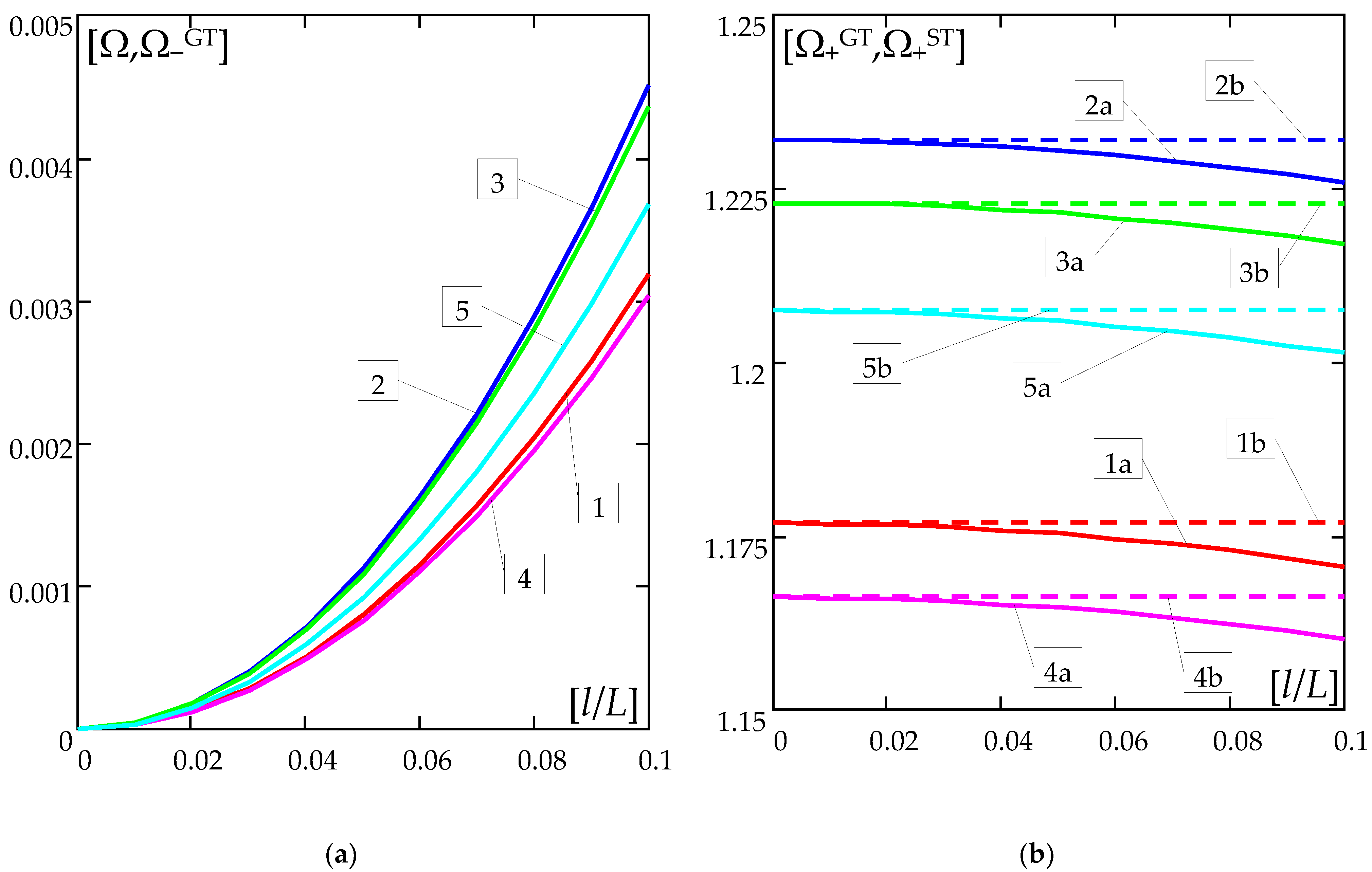
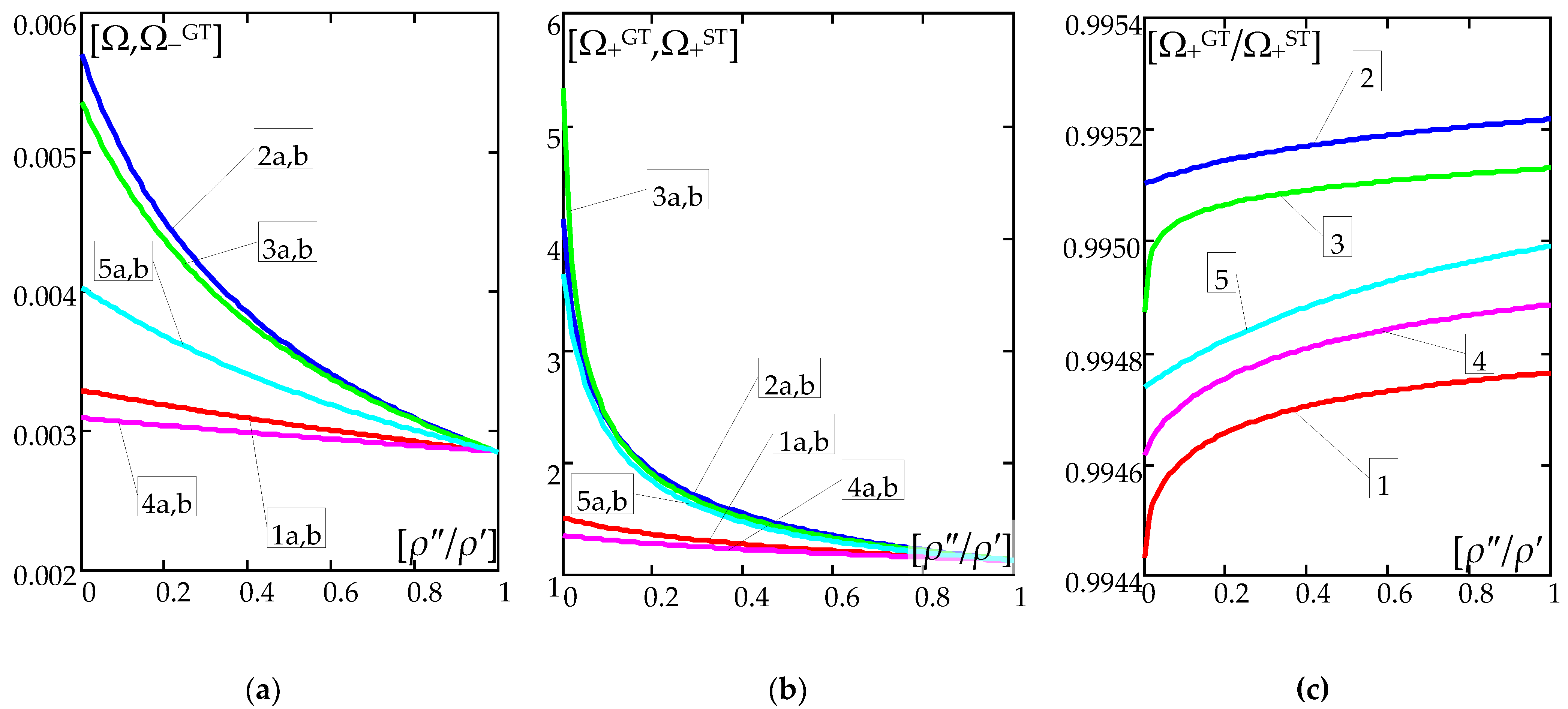
6.4. Free Vibrations—Calculating Results
7. Final Remarks
Funding
Conflicts of Interest
References
- Suresh, S.; Mortensen, A. Fundamentals of Functionally Graded Materials; The University Press: Cambridge, UK, 1998. [Google Scholar]
- Woźniak, C.; Michalak, B.; Jędrysiak, J. (Eds.) Thermomechanics of Microheterogeneous Solids and Structures. Tolerance Averaging Approach; Lodz University of Technology: Lodz, Poland, 2008. [Google Scholar]
- Bensoussan, A.; Lions, J.-L.; Papanicolaou, G. Asymptotic Analysis for Periodic Structures; North-Holland: Amsterdam, The Netherlands, 1978. [Google Scholar]
- Kohn, R.V.; Vogelius, M. A new model of thin plates with rapidly varying thickness. Int. J. Solids Struct. 1984, 20, 333–350. [Google Scholar] [CrossRef]
- Kolpakov, A. Calculation of the characteristics of thin elastic rods with a periodic structure. J. Appl. Math. Mech. 1991, 55, 358–365. [Google Scholar] [CrossRef]
- Kolpakov, A. Application of homogenization method to justification of 1-D model for beam of periodic structure having initial stresses. Int. J. Solids Struct. 1998, 35, 2847–2859. [Google Scholar] [CrossRef]
- Kolpakov, A. The governing equations of a thin elastic stressed beam with a periodic structure. J. Appl. Math. Mech. 1999, 63, 495–504. [Google Scholar] [CrossRef]
- Mao, H.; Shen, F.; Zhang, Y.; Wang, J.; Cui, K.; Wang, H.; Lv, T.; Fu, T.; Tan, T. Microstructure and Mechanical Properties of Carbide Reinforced TiC-Based Ultra-High Temperature Ceramics: A Review. Coatings 2021, 11, 1444. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, L.; Wang, J.; Mao, H.; Cui, K. Microstructure and mechanical properties of high strength porous ceramics with high sewage sludge content. J. Clean. Prod. 2022, 380, 135084. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, Y.; Mao, H.; Cui, K.; Liu, H. Structure evolution, properties and synthesis mechanism of ultra-lightweight eco-friendly ceramics prepared from kaolin clay and sewage sludge. J. Environ. Chem. Eng. 2023, 11, 109061. [Google Scholar] [CrossRef]
- Matysiak, S.J.; Nagórko, W. Microlocal parameters in the modelling of microperiodic plates. Ing. Arch. 1989, 59, 434–444. [Google Scholar] [CrossRef]
- Dallot, J.; Sab, K.; Foret, G. Limit analysis of periodic beams. Eur. J. Mech. A Solids 2009, 28, 166–178. [Google Scholar] [CrossRef]
- Królak, M.; Kowal-Michalska, K.; Mania, R.J.; Świniarski, J. Stability and load carrying capacity of multi-cell thin-walled columns of rectangular cross-sections. J. Theor. Appl. Mech. 2009, 47, 435–456. [Google Scholar]
- Teter, A. Dynamic critical load based on different stability criteria for coupled buckling of columns with stiffened open cross-sections. Thin Walled Struct. 2011, 49, 589–595. [Google Scholar] [CrossRef]
- Hajianmaleki, M.; Qatu, M.S. Vibrations of straight and curved composite beams: A review. Compos. Struct. 2013, 100, 218–232. [Google Scholar] [CrossRef]
- Roque, C.M.C.; Fidalgo, D.S.; Ferreira, A.J.M.; Reddy, J.N. A study of a microstructure-dependent composite laminated Timoshenko beam using a modified couple stress theory and a meshless method. Compos. Struct. 2013, 96, 532–537. [Google Scholar] [CrossRef]
- Batra, R.C.; Xiao, J. Finite deformations of curved laminated St. Venant–Kirchhoff beam using layer-wise third order shear and normal deformable beam theory (TSNDT). Compos. Struct. 2013, 97, 147–164. [Google Scholar] [CrossRef]
- Wittenbeck, L.; Grygorowicz, M.; Paczos, P. Numerical analysis of sandwich beam with corrugated core under three-point bending. AIP Conf. Proc. 2015, 1648, 800007-1–800007-3. [Google Scholar]
- Grygorowicz, M.; Lewiński, J. Bending of I-beam with the transvers shear effect included—FEM calculated. AIP Conf. Proc. 2016, 1738, 480041. [Google Scholar]
- Grygorowicz, M.; Magnucka-Blandzi, E. Mathematical modelling for dynamic stability of sandwich beam with variable mechanical properties of core. Appl. Math. Mech. 2016, 37, 361–374. [Google Scholar] [CrossRef]
- Jopek, H.; Strek, T. Torsion of a two-phased composite bar with helical distribution of constituents. Phys. Status Solidi 2017, 254, 1700050. [Google Scholar] [CrossRef]
- Matuszewska, A.; Strek, T. Vibration properties of auxetic beam. Vib. Phys. Syst. 2018, 29, 2018031. [Google Scholar]
- Arruda, M.R.T.; Castro, L.M.S.; Ferreira, A.J.M.; Garrido, M.; Gonilha, J.; Correia, J.R. Analysis of composite layered beams using Carrera unified formulation with Legendre approximation. Compos. Part B Eng. 2018, 137, 39–50. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Tornabene, F. Strong Formulation Isogeometric Analysis (SFIGA) for laminated composite arbitrarily shaped plates. Compos. Part B Eng. 2016, 96, 173–203. [Google Scholar] [CrossRef]
- Liu, B.; Ferreira, A.J.M.; Xing, Y.F.; Neves, A.M.A. Analysis of composite plates using a layerwise theory and a differential quadrature finite element method. Compos. Struct. 2016, 156, 393–398. [Google Scholar] [CrossRef]
- Pawlus, D. Stability of Three-Layered Annular Plate with Composite Facings. Appl. Compos. Mater. 2017, 24, 141–158. [Google Scholar] [CrossRef]
- Kołakowski, Z.; Mania, R.J. Influence of the coupling matrix B on the interactive buckling of FML-FGM columns with closed cross-sections under axial compression. Compos. Struct. 2017, 173, 70–77. [Google Scholar] [CrossRef]
- Mania, R.J.; Madeo, A.; Zucco, G.; Kubiak, T. Imperfection sensitivity of post-buckling of FML channel section column. Thin Walled Struct. 2017, 114, 32–38. [Google Scholar] [CrossRef]
- Michalski, J.; Strek, T. Response of a Sandwich Plate with Auxetic Anti-tetrachiral Core to Puncture. Lect. Notes Mech. Eng. 2022, 1–14. [Google Scholar]
- Kumar, V.; Singh, S.J.; Saran, V.H.; Harsha, S.P. Vibration Response Analysis of Tapered Porous FGM Plate Resting on Elastic Foundation. Int. J. Struct. Stab. Dyn. 2022, 23, 2350024. [Google Scholar] [CrossRef]
- Kumar, R.; Jana, P. Free vibration analysis of uniform thickness and stepped P-FGM plates: A FSDT-based dynamic stiffness approach. Mech. Based Des. Struct. Mach. 2022. [Google Scholar] [CrossRef]
- Sobhani, E.; Masoodi, A.R. Natural frequency responses of hybrid polymer/carbon fiber/FG-GNP nanocomposites paraboloidal and hyperboloidal shells based on multiscale approaches. Aerosp. Sci. Technol. 2021, 119, 107111. [Google Scholar] [CrossRef]
- Sobhani, E.; Masoodi, A.R. On the circumferential wave responses of connected elliptical-cylindrical shell-like submerged structures strengthened by nano-reinforcer. Ocean. Eng. 2022, 247, 110718. [Google Scholar] [CrossRef]
- Sobhani, E.; Moradi-Dastjerdi, R.; Behdinan, K.; Masoodi, A.R.; Ahmadi-Pari, A.R. Multifunctional trace of various reinforcements on vibrations of three-phase nanocomposite combined hemispherical-cylindrical shells. Compos. Struct. 2022, 279, 114798. [Google Scholar] [CrossRef]
- Bui, T.Q.; Khosravifard, A.; Zhang, C.; Hematiyan, M.R.; Golu, M.V. Dynamic analysis of sandwich beams with functionally graded core using a truly meshfree radial point interpolation method. Eng. Struct. 2013, 47, 90–104. [Google Scholar] [CrossRef]
- Murin, J.; Aminbaghai, M.; Hrabovsky, J.; Kutiš, V.; Kugler, S. Modal analysis of the FGM beams with effect of the shear correction function. Compos. Part B 2013, 45, 1575–1582. [Google Scholar] [CrossRef]
- Carpentieri, G.; Tornabene, F.; Ascione, A.; Fraternali, F. An accurate one-dimensional theory for the dynamics of laminated composite curved beams. J. Sound Vib. 2015, 336, 96–105. [Google Scholar] [CrossRef]
- Roque, C.M.C.; Martins, P.A.L.S.; Ferreira, A.J.M.; Jorge, R.M.N. Differential evolution for free vibration optimization of functionally graded nano beams. Compos. Struct. 2016, 156, 29–34. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Gholipour, A.; Tavallaeinejad, M. Nonlinear bending and forced vibrations of axially functionally graded tapered microbeams. Int. J. Eng. Sci. 2017, 120, 51–62. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H. Bending and vibration analyses of coupled axially functionally graded tapered beams. Nonlinear Dyn. 2018, 91, 17–28. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Vibration analysis of shear-deformable AFG imperfect beams. Compos. Struct. 2018, 200, 910–920. [Google Scholar] [CrossRef]
- Jouneghani, F.Z.; Dimitri, R.; Tornabene, F. Structural response of porous FG nanobeams under hygro-thermo-mechanical loadings. Compos. Part B Eng. 2018, 152, 71–78. [Google Scholar] [CrossRef]
- Brillouin, L. Wave Propagation in Periodic Structures; Dover Pub. Inc.: Dover, UK, 1953. [Google Scholar]
- Xiang, H.-J.; Shi, Z.-F. Analysis of flexural vibration band gaps in periodic beams using differential quadrature method. Comput. Struct. 2009, 87, 1559–1566. [Google Scholar] [CrossRef]
- Yu, D.; Wen, J.; Shen, H.; Xiao, Y.; Wen, X. Propagation of flexural wave in periodic beam on elastic foundations. Phys. Lett. A 2012, 376, 626–630. [Google Scholar] [CrossRef]
- Chen, T. Investigations on flexural wave propagation of a periodic beam using multi-reflection method. Arch. Appl. Mech. 2013, 83, 315–329. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, X.; Wang, W.; Wang, L.; Peng, F.; Li, B. On natural frequencies of non-uniform beams modulated by finite periodic cells. Phys. Lett. A 2016, 380, 3278–3283. [Google Scholar] [CrossRef]
- Gao, F.; Wu, Z.; Li, F.; Hang, C. Numerical and experimental analysis of the vibration and band-gap properties of elastic beams with periodically variable cross sections. Waves Random Complex Media 2019, 29, 299–316. [Google Scholar] [CrossRef]
- Woźniak, C.; Wierzbicki, E. Averaging Techniques in Thermomechanics of Composite Solids. Tolerance Averaging Versus Homogenization; Lodz University of Technology: Częstochowa, Poland, 2000. [Google Scholar]
- Awrejcewicz, J.; Jemielita, G.; Kołakowski, Z.; Matysiak, S.; Nagórko, W.; Pietraszkiewicz, W.; Śniady, P.; Świtka, R.; Szafer, G.; Wągrowska, M.; et al. (Eds.) Mathematical Modelling and Analysis in Continuum Mechanics of Microstructured Media; Silesian University of Technology: Gliwice, Poland, 2010. [Google Scholar]
- Wierzbicki, E.; Woźniak, C. On the dynamics of combined plane periodic structures. Arch. Appl. Mech. 2000, 70, 387–398. [Google Scholar] [CrossRef]
- Jędrysiak, J. On vibrations of thin plates with one-dimensional periodic structure. Int. J. Eng. Sci. 2000, 38, 2023–2043. [Google Scholar] [CrossRef]
- Michalak, B. The meso-shape functions for the meso-structural models of wavy-plates. ZAMM J. Appl. Math. Mech. Z. Angew. Math. Mech. 2001, 81, 639–641. [Google Scholar] [CrossRef]
- Nagórko, W.; Woźniak, C. Nonasymptotic modelling of thin plates reinforced by a system of stiffeners. Electr. J. Polish Agric. Univ. Civ. Eng. 2002, 5, 1–8. [Google Scholar]
- Baron, E. On dynamic behaviour of medium-thickness plates with uniperiodic structure. Arch. Appl. Mech. 2003, 73, 505–516. [Google Scholar] [CrossRef]
- Jędrysiak, J. The length-scale effect in the buckling of thin periodic plates resting on a periodic Winkler foundation. Meccanica 2003, 38, 435–451. [Google Scholar] [CrossRef]
- Mazur-Śniady, K.; Woźniak, C.; Wierzbicki, E. On the modelling of dynamic problems for plates with a periodic structure. Arch. Appl. Mech. 2004, 74, 179–190. [Google Scholar] [CrossRef]
- Tomczyk, B. A non-asymptotic model for the stability analysis of thin biperiodic cylindrical shells. Thin Walled Struct. 2007, 45, 941–944. [Google Scholar] [CrossRef]
- Tomczyk, B. Dynamic stability of micro-periodic cylindrical shells. Mech. Mech. Eng. 2010, 14, 137–150. [Google Scholar]
- Jędrysiak, J.; Paś, A. Dynamics of medium thickness plates interacting with a periodic Winkler’s foundation: Non-asymptotic tolerance modelling. Meccanica 2014, 49, 1577–1585. [Google Scholar] [CrossRef]
- Domagalski, Ł.; Jędrysiak, J. On the tolerance modelling of geometrically nonlinear thin periodic plates. Thin Walled Struct. 2015, 87, 183–190. [Google Scholar] [CrossRef]
- Domagalski, Ł.; Jędrysiak, J. Nonlinear vibrations of periodic beams. J. Theor. Appl. Mech. 2016, 54, 1095–1108. [Google Scholar] [CrossRef]
- Marczak, J.; Jędrysiak, J. Some remarks on modelling of vibrations of periodic sandwich structures with inert core. Compos. Struct. 2018, 202, 752–758. [Google Scholar] [CrossRef]
- Jędrysiak, J. Modelling of Vibrations and Stability for Periodic Slender Visco-Elastic Beams on a Foundation with Damping. Revisiting. Materials 2020, 13, 3939. [Google Scholar] [CrossRef]
- Marczak, J.; Michalak, B.; Wirowski, A. A multi-scale analysis of stress distribution in thin composite plates with dense system of ribs in two directions. Adv. Eng. Softw. 2021, 153, 102960. [Google Scholar] [CrossRef]
- Tomczyk, B.; Gołąbczak, M.; Litawska, A.; Gołąbczak, A. Mathematical modelling of thermoelasticity problems for thin biperiodic cylindrical shells. Contin. Mech. Thermodyn. 2022, 34, 367–385. [Google Scholar] [CrossRef]
- Tomczyk, B.; Bagdasaryan, V.; Gołąbczak, M.; Litawska, A. On the modelling of stability problems for thin cylindrical shells with two-directional micro-periodic structure. Compos. Struct. 2021, 275, 114495. [Google Scholar] [CrossRef]
- Marczak, J.; Jędrysiak, J. The Stability Analysis of Periodic Beams Interacting with Periodic Elastic Foundation with the Use of the Tolerance Averaging Technique. Materials 2021, 14, 5923. [Google Scholar] [CrossRef] [PubMed]
- Jędrysiak, J.; Radzikowska, A. Tolerance averaging of heat conduction in transversally graded laminates. Meccanica 2012, 47, 95–107. [Google Scholar] [CrossRef]
- Michalak, B.; Wirowski, A. Dynamic modelling of thin plate made of certain functionally graded materials. Meccanica 2012, 47, 1487–1498. [Google Scholar] [CrossRef]
- Wirowski, A.; Michalak, B.; Gajdzicki, M. Dynamic modelling of annular plates of functionally graded structure resting on elastic heterogeneous foundation with two modules. J. Mech. 2015, 31, 493–504. [Google Scholar] [CrossRef]
- Perliński, W.; Gajdzicki, M.; Michalak, B. Modelling of annular plates stability with functionally graded structure interacting with elastic heterogeneous subsoil. J. Theor. Appl. Mech. 2014, 52, 485–498. [Google Scholar]
- Michalak, B. 2D tolerance and asymptotic models in elastodynamics of a thin-walled structure with dense system of ribs. Arch. Civ. Mech. Eng. 2015, 15, 449–455. [Google Scholar] [CrossRef]
- Rabenda, M.; Michalak, B. Natural vibrations of prestressed thin functionally graded plates with dense system of ribs in two directions. Compos. Struct. 2015, 133, 1016–1023. [Google Scholar] [CrossRef]
- Ostrowski, P.; Michalak, B. The combined asymptotic-tolerance model of heat conduction in a skeletal micro-heterogeneous hollow cylinder. Compos. Struct. 2015, 134, 343–352. [Google Scholar] [CrossRef]
- Ostrowski, P.; Michalak, B. A contribution to the modelling of heat conduction for cylindrical composite conductors with non-uniform distribution of constituents. Int. J. Heat Mass Transf. 2016, 92, 435–448. [Google Scholar] [CrossRef]
- Pazera, E.; Jędrysiak, J. Effect of microstructure in thermoelasticity problems of functionally graded laminates. Compos. Struct. 2018, 202, 296–303. [Google Scholar] [CrossRef]
- Jędrysiak, J. Tolerance modelling of free vibration frequencies of thin functionally graded plates with one-directional microstructure. Compos. Struct. 2017, 161, 453–468. [Google Scholar] [CrossRef]
- Jędrysiak, J. Tolerance modelling of free vibrations of medium thickness functionally graded plates. Compos. Struct. 2018, 202, 1253–1262. [Google Scholar] [CrossRef]
- Tomczyk, B.; Szczerba, P. Tolerance and asymptotic modelling of dynamic problems for thin microstructured transversally graded shells. Compos. Struct. 2017, 162, 365–373. [Google Scholar] [CrossRef]
- Tomczyk, B.; Szczerba, P. Combined asymptotic-tolerance modelling of dynamic problems for functionally graded shells. Compos. Struct. 2018, 183, 176–184. [Google Scholar] [CrossRef]
- Tomczyk, B.; Szczerba, P. A new asymptotic-tolerance model of dynamic and stability problems for longitudinally graded cylindrical shells. Compos. Struct. 2018, 202, 473–481. [Google Scholar] [CrossRef]
- Jędrysiak, J.; Kaźmierczak-Sobińska, M. Theoretical Analysis of Buckling for Functionally Graded Thin Plates with Microstructure Resting on an Elastic Foundation. Materials 2020, 13, 4031. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jędrysiak, J. Theoretical Tolerance Modelling of Dynamics and Stability for Axially Functionally Graded (AFG) Beams. Materials 2023, 16, 2096. https://doi.org/10.3390/ma16052096
Jędrysiak J. Theoretical Tolerance Modelling of Dynamics and Stability for Axially Functionally Graded (AFG) Beams. Materials. 2023; 16(5):2096. https://doi.org/10.3390/ma16052096
Chicago/Turabian StyleJędrysiak, Jarosław. 2023. "Theoretical Tolerance Modelling of Dynamics and Stability for Axially Functionally Graded (AFG) Beams" Materials 16, no. 5: 2096. https://doi.org/10.3390/ma16052096
APA StyleJędrysiak, J. (2023). Theoretical Tolerance Modelling of Dynamics and Stability for Axially Functionally Graded (AFG) Beams. Materials, 16(5), 2096. https://doi.org/10.3390/ma16052096







